Introduction
Because it may record the past history of ice and climatic change and because it is sensitive to ice-sheet deformation history, the microstructure (grain-sizes and grain shapes) of polar ice is worth studying. During the last 30 years, the main focus has been on the evolution of the average grain-size with depth and thus age. This average grain-size was generally determined by manual counting on two-dimensional (2-D) thin sections of ice.
In the nearly isothermal upper part of cold ice sheets corresponding to the Holocene period, the average grain-size increases with depth (Reference GowGow, 1969; Reference Alley, Perepezko and BentleyAlley and others, 1986b). This is the normal grain-growth process driven by a reduction in the total grain-boundary energy within the material (see, e.g., Reference RalphRalph, 1990; Reference Humphreys and HatherlyHumphreys and Hatherly, 1996; and below). However, a sharp decrease in the average grain-size is generally associated with the Holocene–Last Glacial Maximum (LGM) climatic transition (Reference Duval and LoriusDuval and Lorius, 1980). Several explanations have been proposed for this correlation between grain-size and climate, including soluble impurity drag on grain-boundary migration (Reference Alley and Woods.Alley and Woods,1996), pinning by (insoluble) microparticles (Reference FisherFisher and Koerner, 1986; Reference Li, Jacka and MorganLi and others, 1998), or an effect of surface temperature conditions at the time of deposition (Reference Petit, Duval and LoriusPetit and others, 1987). However, because many parameters, including isotopic record (δD), conductivity and concentrations of different soluble impurities or microparticles, exhibit abrupt changes together at climatic transitions, it is difficult to determine the correct mechanism solely on the basis of correlations between the average grain-size and these parameters.
Here we present a detailed analysis of the microstructure of the shallow part (100–580m) of the European Project for Ice Coring in Antarctica (EPICA) ice core at Dome Concordia (75˚06’ S, 123˚24’ E; 3233ma.s.l.). Using a recently developed image-analysis processing technique (Reference GayGay and Weiss,1999), we were able to extract the complete microstructure (grain boundaries) in two dimensions from thin sections of ice. This allowed us to automatically determine not only the average grain-size but also other parameters such as grain-size distributions or grain-shape anisotropy (Reference Arnaud and DuvalArnaudand others, 2000). In what follows, we discuss the role of soluble and insoluble (microparticles) impurities in the grain-growth process of Antarctic ice, on the basis of this new dataset coupled with an analysis of grain-boundary pinning from classical mean-field models.
Experimental Procedure
Vertical thin sections were prepared in the field from the EPICA ice core at 100–580m depth. They were digitized and analyzed in France using an image-analysis processing technique described by Reference GayGay and Weiss (1999), to extract the microstructure in two dimensions. One section was digitized at approximately each 5 mthrough the core. In addition, thin sections were prepared and digitized at depths corresponding to ``special events’’ revealed by the observation of a dust layer or a dielectric profiling (DEP) peak (Reference Wolff, Basile and SchwanderWolff and others, 1999). Each digitized section represented a surface of about 27.2×20.4 mm2, i.e. about 200–400 grains depending on the average grain-size. the average grain-size (or grain radius) 〈R〉 was calculated over the entire population of grains within a section from the arithmetic average of grain areas, ![]() As detailed by Reference GayGay and Weiss (1999), this method differs from those previously used to manually determine the average grain-size in thin sections of polar ice, such as the linear intercept method (Reference Alley and Woods.Alley and Woods,1996) or the average size of the 50 largest grains within the section (Reference GowGow, 1969). When estimating a ``grain-size’’ within a three-dimensional (3-D) medium from a 2-D section, one should keep in mind stereographic difficulties. Ideally, grain radius should be determined from the cube root of the grain volume in three dimensions. This kind of analysis is difficult to perform experimentally. the scarce information available on the relationship between 3-D parameters and their estimation from 2-D sections comes from 3-D numerical simulations of grain growth (Reference Anderson, Grest and Srolovitz.Anderson and others, 1989). the simulations of Reference Anderson, Grest and Srolovitz.Anderson and others (1989) and Reference WeygandWeygand and others (1998) show that the estimation of 〈R〉 from
As detailed by Reference GayGay and Weiss (1999), this method differs from those previously used to manually determine the average grain-size in thin sections of polar ice, such as the linear intercept method (Reference Alley and Woods.Alley and Woods,1996) or the average size of the 50 largest grains within the section (Reference GowGow, 1969). When estimating a ``grain-size’’ within a three-dimensional (3-D) medium from a 2-D section, one should keep in mind stereographic difficulties. Ideally, grain radius should be determined from the cube root of the grain volume in three dimensions. This kind of analysis is difficult to perform experimentally. the scarce information available on the relationship between 3-D parameters and their estimation from 2-D sections comes from 3-D numerical simulations of grain growth (Reference Anderson, Grest and Srolovitz.Anderson and others, 1989). the simulations of Reference Anderson, Grest and Srolovitz.Anderson and others (1989) and Reference WeygandWeygand and others (1998) show that the estimation of 〈R〉 from ![]() gives the best 2-D estimate of 3-D grain-growth kinetics, therefore validating the procedure followed in the present work. This discussion has been detailed in Reference GayGay and Weiss (1999).
gives the best 2-D estimate of 3-D grain-growth kinetics, therefore validating the procedure followed in the present work. This discussion has been detailed in Reference GayGay and Weiss (1999).
The Grain-Size Profile and the Grain-Growth Process
Figure 1a shows the grain-size profile for the EPICA ice core at 100–580m, i.e. between about 2500 and 28000 BP. the depth– age correspondence comes from Reference Schwander, Jouzel, Hammer, Petit, Udisti and WolffSchwander and others (2001). Grain growth is observed in the Holocene ice, whereas a marked decrease in 〈R〉 is associated with the Holocene–LGM climatic transition. Below the transition, the grain-size appears to remain constant, but the scatter, which is larger than in the Holocene ice, renders a definitive conclusion difficult.
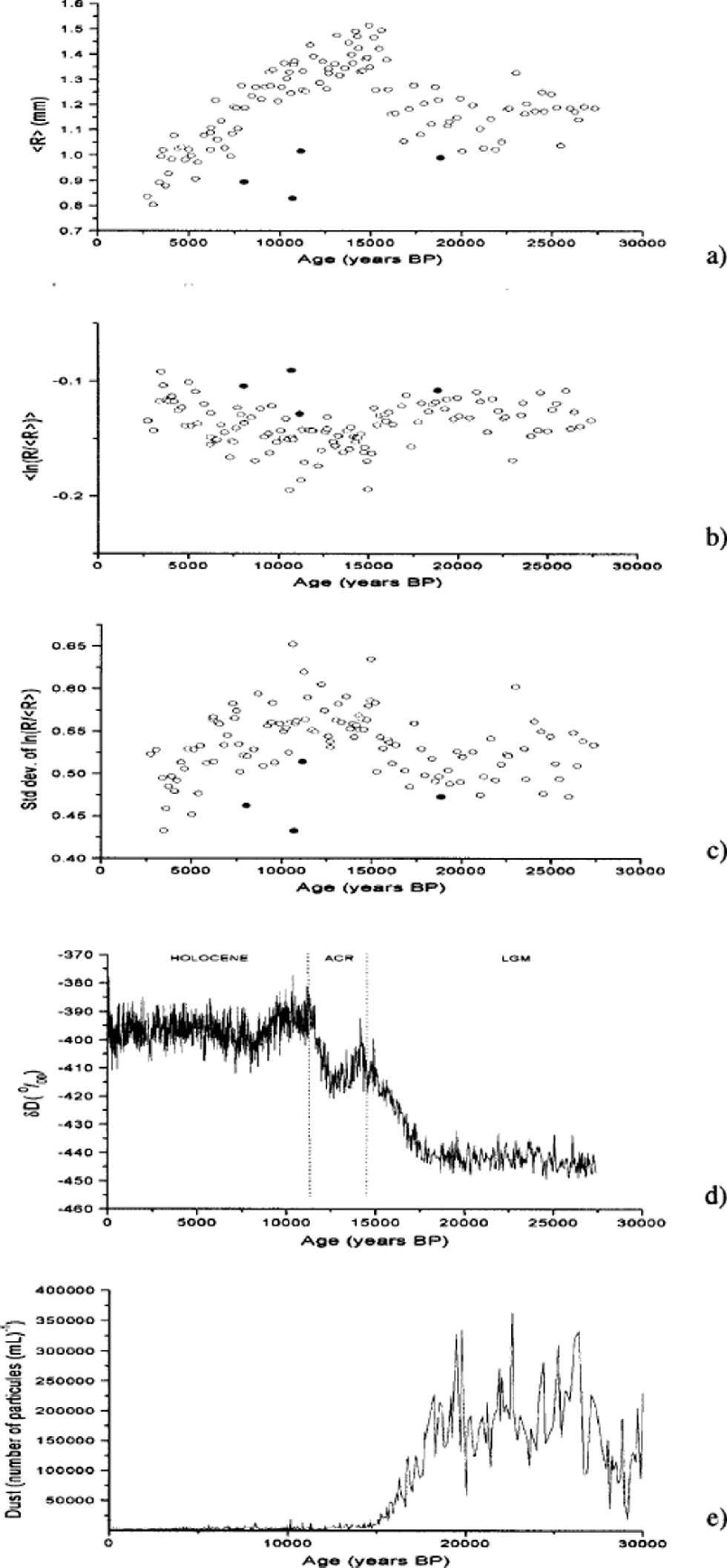
Fig. 1 (a) Average grain-size profile of the EPICA ice core. (b) Normalized grain-size distributions: evolution of 〈ln(R/〈R〉)〉. (c) Normalized grain-size distributions: evolution of the standard deviation of ln(R/〈R〉). (d) Deuterium profile (fromReference JouzelJouzel and others, 2001). (e) Dust number content (from Reference Delmonte and MaggiDelmonte and others, 2002). Closed symbols in (a–c) are ash layers.
To allow an interpretation of our grain-size profile in terms of physical processes, we first recall the classical models of grain-growth kinetics.
Growth kinetics
Ignoring the environment of a grain, i.e. the structural and topological constraints within an assembly of grains, and assuming the boundary is part of a sphere, Reference BurkeBurke and Turnbull (1952) calculated the grain-boundary velocity v (ms–1) in the case where the reduction of grain-boundary
energy is the unique driving force for normal grain growth:
where μ is the mobility, γ is the grain-boundary free energy (Jm–2) and R is the grain radius (m). In Equation (1), γ/R represents the driving force. Further assuming that dR/dt is proportional to v, Reference BurkeBurke and Turnbull (1952) deduced the parabolic grain-growth kinetics:
where K is a constant.
One of the shortcomings of the Burke and Turnbull
analysis was ignorance of the topological space-filling requirements within an assembly of grains. One consequence of these requirements is that large grains grow to the detriment of small grains. the simplest way to model these requirements is by the mean-field approach, which considers an isolated grain embedded in an environment representing the average effect of the whole array of grains. Following the observed difference between grain-growth
kinetics of small and large grains, Reference HillertHillert (1965) proposed the following expression for the velocity of a grain of radius R:
This implies that if R>〈R〉 the grain will grow, but it will shrink if R <〈R〉. This mean-field approach predicts a unimodal grain-size distribution and parabolic grain-growth kinetics (Equation (2)). However, the exponent 1/2 in Equation (2) is an upper bound derived from mean-field approximations. A power law with exponent n of 0.2–0.5 better describes most of the experimental data for many different materials (Reference HigginsHiggins, 1974; Reference Anderson, Grest and Srolovitz.Anderson and others, 1989; Reference RalphRalph, 1990):
where K is an Arrhenius temperature-dependent constant and 〈R〉0 is the average grain-size at t = t0. Departure from the upper bound n = 0.5 has been thought to result from solute drag, interactions with microparticles, the effect of texture, or a non-steady-state regime (Reference RalphRalph,1990).
Following these classical models of grain growth (Reference BurkeBurke and Turnbull, 1952; Reference HillertHillert, 1965), former investigations of grain-growth kinetics in the shallow part of ice sheets assumed parabolic kinetics (Equation (2)), in reasonable agreement with the measurements. However, shallow polar ice could also exhibit n 50.5. A linear fit on a log–log scale of the data of Figure 1 corresponding to Holocene ice gives n =0.307+0.014. A non-linear fit by Equation (4), using the Levenberg–Marquardt algorithm, gives the same exponent, K =7.5 ×10–2 and 〈R〉0 = 0.01 mm.
Grain-size distributions
In the regime of normal grain growth, the distribution of normalized grain-sizes R/〈R〉 remains unchanged, unimodal and is generally well fitted by a lognormal distribution (Reference RalphRalph,1990; Reference Humphreys and HatherlyHumphreys and Hatherly,1996). Note, however, that this lognormal fit has not so far received theoretical support. Moreover, if one starts from a distribution with a different shape (at t = 0), a transient regime is observed with an evolving distribution (Reference Weygand, Bréchet, Lépinoux and GustWeygand, 1998). In the strictest sense, normal grain growth only refers to the ``steady state’’.
For all the thin sections of ice analyzed along the EPICA ice core, the distributions of normalized grain-size are well fitted by lognormal distributions (Reference Arnaud and DuvalArnaud and others, 2000). However, the two independent parameters characterizing the lognormal distribution, i.e. the mean and the standard deviation of ln(R/〈R〉), in part evolve through depth and thus time (Fig. 1b and c). Interestingly, both of them show a break at the Holocene/LGM transition, as does the average grain-size. Moreover, these parameters appear, within the large scatter, to continuously evolve during the Holocene. This could be interpreted as a transient regime (see above).
Grain Growth and Climatic Changes
As already observed by different authors, there is a marked decrease of 〈R〉 associated with the Holocene–LGMclimatic transition (Fig. 1a and d). Several explanations have been proposed for this decrease of 〈R〉:
-
(i) the variation of K with temperature in Equation (4)
-
(ii) A memory effect of the surface temperature conditions at the time of deposition (Reference Petit, Duval and LoriusPetit and others, 1988)
-
(iii) the drag of grain boundaries by soluble impurities
-
(iv) the pinning of grain boundaries by microparticles (dust).
We now review these possibilities in the light of a detailed analysis of ice microstructure, including grain-size distributions.
Note that recrystallization processes such as rotation recrystallization or migration recrystallization create new grains and thus may decrease the average grain-size (Reference Alley, Gow and Meese.Alley and others, 1995; Reference Duval and CastelnauDuval and Castelnau, 1995). However, these mechanisms require significant strain rates and, for migration recrystallization, temperatures above –15˚C, i.e. temperatures encountered near the base of ice sheets (Reference Duval and CastelnauDuval and Castelnau, 1995; De La Reference Chapelle, Castelnau, Lipenkov and DuvalChapelle and others, 1998). At 600m depth, the temperature of the ice measured at Dome Concordia is –50˚C (personal communication from E. Lefebvre, 2001). Consequently, these mechanisms are unlikely to modify the microstructure in large, cold ice sheets at depths of 4600 m (De La Reference Chapelle, Castelnau, Lipenkov and DuvalChapelle and others 1998).
Variation of the grain-growth rate Kwith temperature
Because K is an Arrhenius temperature-dependent constant, a smaller growth rate and therefore smaller grains would be expected in colder ice. However, as noted by Reference Duval and LoriusDuval and Lorius (1980), the difference in growth temperature needed to explain the difference in average grain-size between Holocene and LGM is far too large compared to the present temperature profile, which has, moreover, been smoothed by thermal conduction.
Memory effect of surface temperature conditions at the time of deposition
Reference Petit, Duval and LoriusPetit and others (1987) proposed that the growth rate K could depend on the temperature of the snow at the time of deposition. They assumed that the grain-boundary mobility μ, and consequently K, were proportional to the concentration of interstitials (point defects), c, which in turn was supposed to follow an Arrhenius temperature dependence: ![]() where Ef is an apparent formation energy of interstitials and Ts is the surface temperature at the time of deposition. With this mechanism, the average grain-size becomes a true palaeothermometer. the mechanism was proposed on the basis of a good correlation between the δ18O record and the average grain-size for the former Dome C ice core (Reference Duval and LoriusDuval and Lorius, 1980). Reference Alley, Perepezko and Bentley.Alley and others (1988) questioned this mechanism, arguing that the diffusion of the interstitials within ice would destroy the memory effect proposed by Reference Petit, Duval and LoriusPetit and others (1987). (See also the reply (Reference Petit, Duval and LoriusPetit and others, 1988).)
where Ef is an apparent formation energy of interstitials and Ts is the surface temperature at the time of deposition. With this mechanism, the average grain-size becomes a true palaeothermometer. the mechanism was proposed on the basis of a good correlation between the δ18O record and the average grain-size for the former Dome C ice core (Reference Duval and LoriusDuval and Lorius, 1980). Reference Alley, Perepezko and Bentley.Alley and others (1988) questioned this mechanism, arguing that the diffusion of the interstitials within ice would destroy the memory effect proposed by Reference Petit, Duval and LoriusPetit and others (1987). (See also the reply (Reference Petit, Duval and LoriusPetit and others, 1988).)
In terms of grain-boundary velocity (Equation (3)), the interstitials are assumed to affect the mobility μ, but not the driving force ![]() Besides the objection of Reference Alley, Perepezko and Bentley.Alley and others (1988), the scenario proposed by Reference Petit, Duval and LoriusPetit and others (1987) appears to contradict the observations listed below.
Besides the objection of Reference Alley, Perepezko and Bentley.Alley and others (1988), the scenario proposed by Reference Petit, Duval and LoriusPetit and others (1987) appears to contradict the observations listed below.
(a) A reduced grain-boundary mobility, and therefore a reduced growth rate K, during the LGM would imply an increasing average grain-size during this period, although at a lower rate than during the Holocene, whereas a roughly constant grain-size is observed between 16 000 and 28 000 BP (within a large scatter).
(b) the Antarctic Cold Reversal (ACR), clearly identified in the δD record between 12 000 and 15 000 BP (Fig. 1d; Reference JouzelJouzel and others, 2001), is not marked by any grain-size decrease in the present profile (Fig. 1a), in contradiction with a direct effect of surface temperature. Note that we increased the sampling rate during this period to properly check this point.
(c) Within the context of ``steady-state’’ normal grain growth with a stabilized normalized distribution, a modification of the grain-boundary mobility in Equation (1) or (3) cannot explain a modification of this distribution at the climatic transition. Indeed, a reduction of mobility induced by point defects would apply equally to all grain boundaries, unless one assumes an (improbable) segregation of interstitials depending on the grain-size. In this situation, although the global kinetics would be slowed down, the behaviour of one grain relative to each of the others would remain unchanged, and so too the normalized grain-size distribution.
On the other hand, the normalized grain-size distribution also appears, within a large scatter, to slowly evolve during the Holocene (Fig. 1b and c). This might indicate a transient rather than ``steady-state’’ regime of grain growth. the values of 〈R〉, 〈ln(R/〈R〉) and of the standard deviation of ln(R/〈R〉) observed in the LGM are similar to those observed within the Holocene at about 7500 BP (see Fig. 1a–c). Therefore, a slowing-down of a ``transient’’ growth process by point defects could be a plausible explanation of a simultaneous evolution of these three parameters at the climatic transition.
(d) We identified in the shallow ice of Dome Concordia a few layers with abnormally small grains (Fig. 1a). Some of these correspond to volcanic ash layers detectable by eye (e.g. at 339.5 m depth, i.e. 10700 BP). These layers show exactly the same trend as the ice below the transition for the three independent grain-size parameters (Fig. 1a–c). Because there is no reason to expect a high concentration of interstitials associated with these volcanic dust layers in the Holocene, the scenario of Reference Petit, Duval and LoriusPetit and others (1987) is unable to give a universal explanation for the modification of the ice microstructure.
The drag of soluble impurites by grain boundaries
Two kinds of impurities are found in polar ice: insolubles, which are second-phase particles of dust; and soluble impurities which dissolve as ions when the ice is melted. the exact location and form of these solutes within ice is still largely unknown and probably varies with the nature of the impurity. Sulfates may form hydrates, but it has recently been demonstrated that relatively large concentrations (up to 1 ppm) of Na and Cl can be distributed within the ice lattice as solute atoms (Reference MontagnatMontagnat and others, 2001). While the effect
of dust particles of relatively large size (around 1 μm) is to pin the grain boundaries (see below), solutes are dragged by the moving boundary (Reference Alley, Perepezko and BentleyAlley and others, 1986a; Reference Humphreys and HatherlyHumphreys and Hatherly, 1996). This drag of impurities reduces the grain-boundary mobility μ. Classical models of this effect are of the form (Reference Lucke and DetertLucke and Detert, 1957; Reference Lucke and Stuwe.Lucke and Stuwe, 1971; Reference Humphreys and HatherlyHumphreys and Hatherly, 1996):
where c is the impurity concentration (non-dimensional), μi is the intrinsic mobility of the boundary and α is a constant. More recently Reference Gottstein, Molodov, Shvindlerman., and and RollettGottstein and others (1998) argued that impurity drag modifies the activation enthalpy of mobility rather than the pre-exponential factor, and proposed a slightly different expression for μ(c).
In any case, soluble impurities, like interstitials in the scenario of Reference Petit, Duval and LoriusPetit and others (1987) (see above), are found to modify the mobility and not the driving force. Therefore, the arguments (a) and (c) of the previous section hold. An impurity drag effect is also in contradiction with other observations. Figure 2 shows the relation between liquid conductivity, σ (Reference RöthlisbergerRöthlisberger, 2000), and the non-dimensional parameter R*:
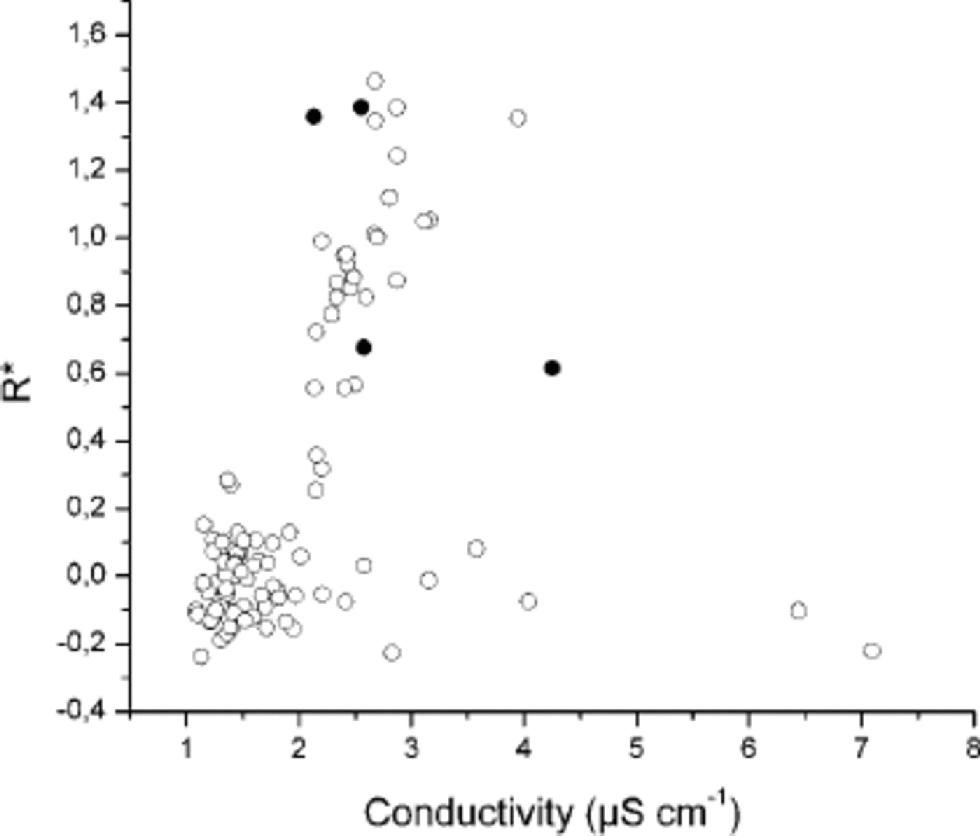
Fig. 2 Correlation between liquid conductivity (from Reference RöthlisbergerRöthlisberger, 2000) and R* (see text for details). Closed symbols are ash layers.
R* aims to quantify the grain-size decrease compared with normal grain growth. 〈R〉 is the measured average grain-size and Rth is the theoretical grain-size calculated for the same depth from grain-growth Equation (4). from relations (1), (2) and (5) it is easily shown that R* should be proportional to the impurity content c if soluble impurities play a major role in grain growth. R* is close to 0 for standard Holocene ice, and above zero for LGM ice as well as for a few anomalous layers within the Holocene. Some authors consider that liquid conductivity measures the total soluble impurity content (Reference FisherFisher and Koerner,1986). Note, however, that this relation between liquid conductivity and soluble impurity content is complex, different species contributing differently to the total conductivity. the global correlation observed between σ and R* (Fig. 2) is not really informative, as many parameters, including isotopic record, conductivity, concentrations of different soluble impurities or of microparticles, and grain-size, exhibit simultaneous changes at climatic transitions. the behaviour of some special layers is more instructive in this respect. These layers, selected on the field from the DEP profile (Reference Wolff, Basile and SchwanderWolff and others, 1999; personal communication from E.W. Reference Wolff, Basile and SchwanderWolff, 1999) show very large conductivities but normal grain-sizes (R* ≈ 0). This shows that large soluble impurity contents do not necessarily imply abnormally small grain-sizes, thus raising doubts about the effectiveness of solute drag in reducing the average grain-size. from continuous flow analysis (CFA) of chemistry of the EPICA ice core (Reference RöthlisbergerRöthlisberger, 2000), one can analyze similar correlations between grain-size and different species (Na+, Ca2+, K+, NO3 –, SO4 2–, ...).Whereas a global correlation is generally found between impurity concentration and R*, in each case some depths lie away from the global correlation, either because a large impurity content is associated with normal grain-size or because small grain-sizes are not associated with large impurity contents.
Pinning of grain boundaries by microparticles
Insoluble second-phase particles can also modify the grain-growth process, but through a rather different mechanism. Large (relative to solute atoms) particles cannot be dragged by moving boundaries. Rather, they pin these boundaries (see, e.g., Reference RalphRalph, 1990; Reference Humphreys and HatherlyHumphreys and Hatherly, 1996). the role of pinning in the grain-growth process depends on the location of particles (see below), as well as on the ratio between the average grain-size and the mean distance between particles. for small grain-sizes compared to large inter-particle distances, most of the boundaries do not ``feel’’ the particles and so the global growth process is unchanged. for small inter-particle distances, most of the boundaries are pinned and the growth process is stopped. Transient behaviour is found in between (Reference Humphreys and HatherlyHumphreys and Hatherly, 1996; Reference Weygand, Bréchet, Lépinoux and GustWeygand, 1998).
C. Zener (cited by Smith, 1948) was the first to model this pinning effect. the interaction between a boundary of free energy γ and a spherical particle of radius r leads to the following restraining force Fz:
Averaging the effect of N particles per unit volume by a mean-field approximation gives an expression for the (average) pinning pressure Pz exerted by the particles per unit area of boundary (Reference Humphreys and HatherlyHumphreys and Hatherly, 1996). Pz depends on where the particles are distributed within the matter. Pz is larger when particles are concentrated along the boundaries or at grain vertices rather than distributed randomly within the volume (the boundaries feel a larger particle density). Corresponding expressions for Pz are given in Table 1. This pinning pressure works against the driving force for grain-boundary motion P = αγ/R. α is a geometrical constant that depends on the model considered (0.25<α ≤1) (Reference Humphreys and HatherlyHumphreys and Hatherly, 1996). In the limiting case P = Pz, the growth process is stopped, and Zener (Reference SmithSmith, 1948) deduced a corresponding limiting (maximum) grain-size Rz whose expressions are given in Table 1. Zener originally set α =1, but more recent models and observations argue for lower values of 0.25–0.5 (Reference Humphreys and HatherlyHumphreys and Hatherly,1996).
Table 1. Pinning of grain boundaries by microparticles. Pz is pinning pressure and Rz is limiting grain size

The number and size distribution of dust particles has been measured along the EPICA ice core using a Coulter counter (Reference Delmonte and MaggiDelmonte and others, 2002). As observed previously in other ice cores (Reference SteffensenSteffensen, 1997; Reference PetitPetit and others, 1999), the dust content is strongly influenced by climate changes, with a much larger number of particles during the LGM than during the Holocene (Fig. 1e), while the average particle size shows only slight change. As listed below, different observations suggest a major role for grain-boundary pinning by dust particles in explaining the variations of average grain-size with climate.
-
(a) In the presence of pinning, Equation (3) can be modified as (Reference HillertHillert,1965):
(8)
Grains in the size range
 neither shrink nor grow. Grains larger or smaller than this will, respectively, grow or shrink but at a reduced rate. Therefore, unlike the drag of solute, pinning does not reduce the mobility μ. Rather, it modifies the driving force for boundary migration non-uniformly. Grain-size distributions are consequently modified by pinning (Reference Riege, Thompson, Frost., Weiland and RollettRiege and others, 1998) as observed at the Holocene–LGM transition (Fig. 1b and c). Analytical models (Reference Abbruzzese and LuckeAbbruzzese and Lucke, 1992), 2-D (Reference Weygand, Bréchet, Lépinoux and GustWeygand, 1998) as well as 3-D (Reference Song, Liu and GuSong and others, 2000) numerical simulations of Zener pinning, and some experimental evidence (Reference Tweed, Nansen and RalphTweed and others, 1982) support narrower normalized distributions (i.e. smaller standard deviation) for pinned microstructures, in agreement with the data of Figure 1c. Similarly, Reference Riege, Thompson, Frost., Weiland and RollettRiege and others (1998) reported a shift of the mean for a 2-D simulation, in agreement with data of Figure 1b.
neither shrink nor grow. Grains larger or smaller than this will, respectively, grow or shrink but at a reduced rate. Therefore, unlike the drag of solute, pinning does not reduce the mobility μ. Rather, it modifies the driving force for boundary migration non-uniformly. Grain-size distributions are consequently modified by pinning (Reference Riege, Thompson, Frost., Weiland and RollettRiege and others, 1998) as observed at the Holocene–LGM transition (Fig. 1b and c). Analytical models (Reference Abbruzzese and LuckeAbbruzzese and Lucke, 1992), 2-D (Reference Weygand, Bréchet, Lépinoux and GustWeygand, 1998) as well as 3-D (Reference Song, Liu and GuSong and others, 2000) numerical simulations of Zener pinning, and some experimental evidence (Reference Tweed, Nansen and RalphTweed and others, 1982) support narrower normalized distributions (i.e. smaller standard deviation) for pinned microstructures, in agreement with the data of Figure 1c. Similarly, Reference Riege, Thompson, Frost., Weiland and RollettRiege and others (1998) reported a shift of the mean for a 2-D simulation, in agreement with data of Figure 1b. -
(b) Several layers of abnormally small grain-sizes have been identified within the Holocene ice, sometimes associated with a visible (by eye) dust layer. This association is another indication of particle pinning. Moreover, these small grain-size layers exhibit exactly the same features as LGM ice: small grains, narrower and shifted (larger mean) normalized distributions (see Fig. 1a–c). This supports a unique mechanism explaining small grains both in LGM ice and in Holocene ice dust layers. Note that Zener pinning is independent of the origin and nature of the second-phase particles: mostly continental dust in LGM ice, and volcanic ashes in Holocene dust layers. This is also in agreement with the observation of small grain-sizes associated with ash layers in the Byrd ice core (Reference Gow and WilliamsonGow and Williamson,1976).
-
(c) from the measured number and size distribution of dust particles, one can apply the mean-field models briefly described above to estimate the limiting grain-sizes Rz associated with Holocene, ACR and LGM (see Table 1). for these estimations, we have taken the following averaged values for the number N of particles mL–1: 3500 for Holocene, 7000 for ACR and 170 000 for LGM (Reference Delmonte and MaggiDelmonte and others, 2002). the average particle radius r is considered to be constant at r= 1μm (Reference Delmonte and MaggiDelmonte and others, 2002); measured variations of r have a negligible effect on Rz .The Rz values given inTable 1 are calculated for α in the range 0.25–0.5 (see above). If the particles are assumed to be randomly distributed within the grains, Rz is extremely large compared to the measured grain-sizes 〈R〉 for Holocene and ACR ice, thus excluding any effect of dust on grain growth, and very large for LGM ice. on the other hand, if the particles are mostly located along the boundaries, as is more likely at the time of snow deposition in central Antarctica (and for which there is some experimental evidence (Reference Barnes and MulvaneyBarnes and others, 2002)), we find Rz values 5–10 times larger than 〈R〉 for Holocene and ACR ice, but very close to 〈R〉 for LGM ice.
These mean-field estimates are in striking agreement with the observed grain-size profile (Fig. 1a). In the Holocene and ACR ice, the dust particle density is too low to have a strong effect on grain growth. This explains why the ACR is not revealed by the grain-size profile. Note, however, that particle pinning might have a limited slowing effect on grain growth during these periods and could explain the departure of the growth exponent n in Equation (4) from the theoretical upper bound of 0.5, especially if the particles are preferentially located at grain vertices. the strong increase in dust density at the climatic transition and during the LGM explains the simultaneous decrease of 〈R〉 at the transition as well as the plateau observed below; 〈R〉 has reached the limiting, asymptotic grain-size Rz around 1–1.2 mm. With this scenario, 〈R〉 should remain constant around this value as long as the number of particles N remains around 170 000 mL–1, and no other recrystallization mechanisms exist. This scenario is also in excellent agreement with Reference FisherFisher and Koerner (1986) who argued that a negative correlation exists between grain-size and N for N>15 000 mL–1, and no correlation below (as for Holocene and ACR here).
Finally, this mechanism explains the large scatter on 〈R〉 observed during the LGM (Fig. 1a). Large fluctuations of the crystal size might be linked to the large variations of dust concentration, whereas the smaller scatter observed during the Holocene is an intrinsic scatter of the measure.
The pinning of grain boundaries by microparticles appears to be the only scenario able to explain qualitatively and quantitatively all the reported observations in a simple way: the grain-size profile (Fig. 1a), the grain-size distributions (Fig.1b and c), the microstructure of ash layers within Holocene ice, etc. It is also in agreement with the fact that layers containing a large amount of soluble impurities, but not necessarily a large amount of dust, may exhibit no significant microstructural changes (Fig. 2)
Conclusion
A detailed analysis of the microstructure of the shallow part (100–580m) of the EPICA ice core at Dome Concordia has been performed using image-analysis processing.The average grain-size profile revealed power-law grain-growth kinetics with an exponent n ≈0.3 in Holocene ice. At the Holocene– LGM transition, the average grain-size strongly decreases, then remains roughly constant down to 580 m depth. Several explanations have been proposed in the literature for this correlation between grain-size and climate. These include soluble impurity drag on grain-boundary migration, pinning by (insoluble) microparticles, and an effect of surface temperature conditions at the time of deposition. We discussed this on the basis of a detailed analysis of the ice microstructure coupled with classical mean-field modeling of grain-growth kinetics, solute drag and particle pinning. It is shown that the pinning of grain boundaries by dust particles located along the boundaries explains qualitatively and quantitatively all the reported observations: the grain-size profile, the grain-size distributions and the microstructure of ash layers within the Holocene ice. This strongly supports a major role for this mechanism in explaining correlations between grain-size and climate in the shallow parts of large ice sheets, although this does not completely rule out a limited effect of some soluble impurities on grain growth. This conclusion is in agreement with Reference FisherFisher and Koerner (1986) and Reference Li, Jacka and MorganLi and others (1998).
Acknowledgements
This work is a contribution to the European Project for Ice Coring in Antarctica (EPICA), a joint European Science Foundation (ESF)/European Commission (EC) scientific programme, funded by the EC under the Environment and Climate Programme and by national contributions from Belgium, Denmark, France, Germany, Italy, the Netherlands, Norway, Sweden, Switzerland and the United Kingdom. We would like to thank two anonymous reviewers for helpful comments.





