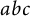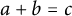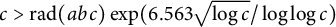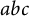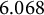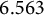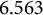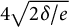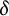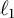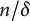1 Introduction
Three natural numbers a, b, c are said to be an
$abc$
triple if they do not share a common factor and satisfy the equation
$$\begin{align*}a + b = c. \end{align*}$$
Informally, the
$abc$
conjecture says that large
$abc$
triples cannot be “very composite,” in the sense of
$abc$
having a prime factorization containing large powers of small primes. The radical of
$abc$
is defined to be the product of the primes in the prime factorization of
$abc$
, i.e.,
The
$abc$
conjecture then states that
$abc$
triples satisfy
$$ \begin{align} c = O\big({\operatorname{\mathrm{rad}}(abc)^{1+\epsilon}}\big) \end{align} $$
for every
$\epsilon>0$
, where the implied big-O constant may depend on
$\epsilon $
.
Presently, the conjecture is far from being proved; not a single
$\epsilon $
is known for which (1.1) holds.Footnote
1
The best-known upper bound is due to Stewart and Yu [Reference Stewart and Yu10] and says that
$abc$
triples satisfy
$$\begin{align*}c = O\big({\exp(\operatorname{\mathrm{rad}}(abc)^{1/3}(\log\operatorname{\mathrm{rad}}(abc))^3)}\big). \end{align*}$$
On the other hand, Stewart and Tijdeman [Reference Stewart and Tijdeman9] proved in 1986 that there are infinitely many
$abc$
triples with
$$ \begin{align} c> \operatorname{\mathrm{rad}}(abc)\exp\big({\kappa\sqrt{\log c}/\log\log c}\big) \end{align} $$
for all
$\kappa <4$
. Such
$abc$
triples are exceptional in the sense that their radical is relatively small in comparison to c and they provide a lower bound on the best possible form of (1.1). In 1997, van Frankenhuysen [Reference van Frankenhuysen3] improved this lower bound by showing that (1.2) holds for
$\kappa =4\sqrt {2}$
, and in 1999, he improved this to
$\kappa =6.068$
using a sphere-packing idea credited to H. W. Lenstra, Jr. We improve this further by showing that there are infinitely many
$abc$
triples satisfying (1.2) with
$\kappa =6.563$
.
2 Preliminaries
Let S be a set of prime numbers. An S-unit is defined to be a rational number whose numerator and denominator in lowest terms are divisible by only the primes in S. That is, one has
This generalizes the notion of units of
$\mathbb {Z}$
; in particular, the
$\emptyset $
-units are
$\pm 1$
. The height of a rational number
$p/q$
in lowest terms is
. This provides a convenient way of measuring the “size” of an S-unit. Finally, if
is a vector in
$\mathbb {R}^n$
, we let
be its standard
$\ell _k$
-norm. The existence of exceptional
$abc$
triples follows from some basic results in the geometry of numbers along with estimates for prime numbers provided by the prime number theorem. In particular, we rely on a result of Rankin [Reference Rankin6] guaranteeing the existence of a short nonzero vector in a suitably chosen lattice.
2.1 The odd prime number lattice
The result involves in an essential way the odd prime number lattice
$L_n$
generated by the rows
,
$\dotsc $
,
of the matrix
where
$p_i$
denotes the ith odd prime number. This lattice has a number of interesting applications. For example, it is used in Schnorr’s factoring algorithm [Reference Schnorr7] and Micciancio’s proof that approximating the shortest vector to within a constant factor is NP-hard under a randomized reduction [Reference Micciancio5]. There is an obvious isomorphism between the points of
$L_n$
and the positive
$ \left \lbrace {p_1,\dotsc ,p_n} \right \rbrace $
-units given by
Furthermore, this relationship works well with a natural notion of size, as shown in the following lemma.
Lemma 2.1
where
and
$p/q=\prod _{i=1}^n p_i^{e_i}$
is expressed in lowest terms.
Proof Without loss of generality, suppose
$p\geq q$
. Then
as required, since
$h(p/q)=p$
by assumption.
2.2 The kernel sublattice
Let P be the set of positive
$ \left \lbrace {p_1,\dotsc ,p_n} \right \rbrace $
-units, and consider the map
$\phi $
reducing the elements of P modulo
$2^m$
. Since each
$p_1$
,
$\dotsc $
,
$p_n$
is odd,
$\phi \colon P\to (\mathbb {Z}/2^m\mathbb {Z})^*$
is well defined. The odd prime number lattice
$L_n$
has an important sublattice that we call the kernel sublattice
$L_{n,m}$
. It consists of those vectors whose associated
$ \left \lbrace {p_1,\dotsc ,p_n} \right \rbrace $
-units lie in the kernel of
$\phi $
. Formally, we define
Figure 1 plots the first two coordinates of vectors in the kernel sublattice for varying m.
Figure 1 Plots of
$\{\ (x,y) : (x,y,z)\in L_{2,m}\ \}$
for
$1\leq m\leq 8$
.
Lemma 2.2
$L_{n,m}$
is a sublattice of
$L_n$
of index
$2^{m-1}$
when
$n\geq 2$
.
Proof Note that
$L_{n,m}$
is discrete and closed under addition and subtraction.
$L_{n,m}$
also contains the n linearly independent vectors
for
$1\leq i\leq n$
, so this demonstrates that
$L_{n,m}$
is a full-rank sublattice of
$L_n$
.
Since
$3$
and
$5$
generate
$(\mathbb {Z}/2^m\mathbb {Z})^*$
, when
$n\geq 2$
, we have
$\phi (P)=(\mathbb {Z}/2^m\mathbb {Z})^*$
. Since
$L_n\cong P$
and
$L_{n,m}\cong \ker \phi $
, it follows that
$L_n/L_{n,m} \cong (\mathbb {Z}/2^m\mathbb {Z})^*$
by the first isomorphism theorem. Thus, the index of
$L_{n,m}$
in
$L_n$
is
$ \left \lvert {(\mathbb {Z}/2^m\mathbb {Z})^*} \right \rvert =2^{m-1}$
.
2.3 Hermite’s constant
The Hermite constant
$\gamma _n$
is defined to be the smallest positive number such that every lattice of dimension n and volume
$\det (L)$
contains a nonzero vector
with
We are interested in the “Manhattan distance”
$\ell _1$
-norm instead of the usual Euclidean norm, so we define the related constants
$\delta _n$
by the smallest positive number such that every full-rank lattice of dimension n contains a nonzero vector
with
By Minkowski’s theorem [Reference Cassels2] applied to a generalized octahedron (a “sphere” in the
$\ell _1$
-norm), every full-rank lattice of dimension n contains a nonzero lattice point
with
. It follows that
$\delta _n \leq (n!)^{1/n} \sim n/e$
, but better bounds on
$\delta _n$
are known. Blichfeldt [Reference Blichfeldt1] showed that
$$\begin{align*}\delta_n \leq \sqrt{\frac{4(n+1)(n+2)}{3\pi(n+3)}}\bigg({\frac{2(n+1)}{n+3}\Big({\frac{n}{2}+1}\Big)!}\bigg)^{1/n} \sim \frac{n}{ \sqrt{1.5\pi e}} , \end{align*}$$
where
. Improving this, Rankin [Reference Rankin6] showed the following.
Lemma 2.3 For all integer n and real
$x\in [1/2,1]$
, we have
$$\begin{align*}\delta_n \leq \Bigg({\frac{2-x}{1-x}}\Bigg)^{x-1}\Bigg({\frac{1+x n}{x}(x n)!}\Bigg)^{1/n}\frac{n^{1-x}}{x!} \sim \Bigg({\frac{2-x}{1-x}}\Bigg)^{x-1}\Bigg({\frac{x}{e}}\Bigg)^x \frac{n}{x!}. \end{align*}$$
Corollary 2.4 Let
$\delta $
be a constant such that
$\delta _n\leq n/\delta +O(\log n)$
. Then a permissible value for
$\delta $
is
$\max \limits _{1/2\leq x\leq 1}\big( {\frac {1-x}{2-x}}\big)^{x-1}\big( {\frac {e}{x}}\big)^x x!\approx 3.65931$
.
Proof Note that
$((1+xn)/x)^{1/n}=1+O((\log n)/n)$
and
$$\begin{align*}(x n)!^{1/n} = \Big({\sqrt{2\pi xn}\mspace{1.5mu}\Big({\frac{xn}{e}}\Big)^{xn} \big({1+O(n^{-1})}\big)}\Big)^{1/n} = \Big({\frac{xn}{e}}\Big)^x \big( {1+O \big({\tfrac{\log n}{n}}\big)}\big). \end{align*}$$
Then, by Lemma 2.3, it follows that
$$\begin{align*}\delta_n \leq \Bigg({\frac{2-x}{1-x}}\Bigg)^{x-1} \Bigg({\frac{x}{e}}\Bigg)^x \frac{n}{x!} + O(\log n), \end{align*}$$
and the function
$x\mapsto \big( {\frac {1-x}{2-x}}\big)^{x-1} \big( {\frac {e}{x}}\big)^x x!$
for
$1/2\leq x\leq 1$
reaches a maximum of approximately
$3.65931$
at
$x\approx 0.645467$
.
The best possible value
$\delta $
can achieve in Corollary 2.4 is unknown, but the Minkowski–Hlawka theorem [Reference Cassels2] applied to a generalized octahedron shows that in any dimension n, there is always a full-rank lattice L with all of its nonzero lattice points
having
; here,
$\zeta $
is the Riemann zeta function. It follows that
$\delta _n>(\zeta (n)\mspace {1.5mu}n!)^{1/n}\mspace {-1.5mu}/2\sim n/(2e)$
, so we must have
$\delta \leq 2e$
.
2.4 A full-rank kernel sublattice
Since
$L_{n,m}\in \mathbb {R}^{n+1}$
is of dimension n (i.e., not full-rank), it is awkward to use Rankin’s result on
$L_{n,m}$
directly. The basis matrix of
$L_{n,m}$
cannot simply be rotated to embed it in
$\mathbb {R}^n$
, since rotation does not preserve the
$\ell _1$
-norm. To circumvent this and work with a full-rank lattice, we adjoin the new basis vector
to
$L_n$
to form a full-rank lattice
$\overline {L}_n$
(and similarly a full-rank lattice
$\overline {L}_{n,m}$
).
Lemma 2.5 The volume of
$\overline {L}_{n,m}$
is
$2^{m-1}n^3\prod _{i=1}^n\log p_i$
when
$n\geq 2$
.
Proof The basis matrix of
$L_n$
adjoined with
is an upper-triangular matrix, so
$\det (\overline {L}_n)=n^3\prod _{i=1}^n\log p_i$
. The index of
$\overline {L}_{n,m}$
in
$\overline {L}_n$
is
$2^{m-1}$
when
$n\geq 2$
by the same argument as in Lemma 2.2, so
$\det (\overline {L}_{n,m})=2^{m-1}\det (\overline {L}_n)$
.
Our choice of m will ultimately be asymptotic to
$n\log _2 n$
, and in this case,
$\det (\overline {L}_{n,m})^{1/(n+1)}$
grows slightly more than linearly in n.
Lemma 2.6 If
$m\sim n\log _2 n$
, then
$\det (\overline {L}_{n,m})^{1/(n+1)}=O(n^{1+\epsilon })$
for all
$\epsilon>0$
.
Proof Lemma 2.5 implies
$\det (\overline {L}_{n,m})^{1/(n+1)} < 2^{m/n} n^{3/n} \big( {\prod _{i=1}^n\log p_i}\big)^{1/n}$
. Note that
$m/n=\log _2 n + o(\log _2 n)<(1+\epsilon )\log _2 n$
for all
$\epsilon>0$
and sufficiently large n. Thus,
$2^{m/n}<n^{1+\epsilon }$
for sufficiently large n, and the remaining factors are
$O(n^\epsilon )$
since
$n^{3/n}=O(1)$
and
$\big( {\prod _{i=1}^n\log p_i}\big)^{1/n}<\log p_n = O(\log n)$
.
Finally, we will require the fact that any vector in
$\overline {L}_n$
including a nontrivial coefficient on
must be sufficiently large (have length at least
$n^3$
in the
$\ell _1$
-norm).
Lemma 2.7 If
, then
.
Proof We have
.
Without loss of generality, suppose that
$e_{n+1}>0$
, and for contradiction, suppose
. Then
$$\begin{align*}\sum_{i=1}^n e_i\log p_i+e_{n+1}n^3 \leq \Bigg\lvert{\sum_{i=1}^n e_i\log p_i+e_{n+1}n^3}\Bigg\rvert < n^3 e_{n+1} - \sum_{i=1}^n \left\lvert {e_i} \right\rvert \log p_i \end{align*}$$
implies
$\sum _{i=1}^n (e_i+ \left \lvert {e_i} \right \rvert ) \log p_i < 0$
, and this is nonsensical since the left-hand side is nonnegative.
2.5 Asymptotic formulae
Let
, and let
$\pi (x)$
be the prime counting function, so that
$n=\pi (x)-1$
. The prime number theorem [Reference Ingham4] states that
$\pi (x)\sim \operatorname {\mathrm {li}}(x)$
where
$\operatorname {\mathrm {li}}(x)$
is the logarithmic integral
$\int _0^x\frac {{\,\mathrm {d}} t}{\log t}$
with asymptotic expansion
$$ \begin{align} \operatorname{\mathrm{li}}(x) = \frac{x}{\log x} + \frac{x}{\log^2 x} + \frac{2x}{\log^3 x} + O \Bigg({\frac{x}{\log^4 x}}\Bigg). \end{align} $$
In fact, the error term
$\pi (x)-\operatorname {\mathrm {li}}(x)$
is
$O(x/\exp (C\log ^{1/2} x))$
for some constant
$C>0$
. The following estimates are consequences of this (cf. [Reference Stewart and Tijdeman9, Lemma 2]). For the convenience of the reader, proofs are given in the Appendix.
Lemma 2.8
$\sum _{i=1}^n\log p_i = n\log p_n - n - p_n/\log ^2 p_n + O(p_n/\log ^3 p_n)$
.
Lemma 2.9
$\sum _{i=1}^n\log \log p_i = n\log \log p_n - p_n/\log ^2 p_n + O(p_n/\log ^3 p_n)$
.
3 Exceptional
triples
For our purposes, the importance of the kernel sublattice is that it lets us show the existence of
$abc$
triples in which c is large relative to
$\operatorname {\mathrm {rad}}(abc)$
. The following lemma shows how this may be done.
Lemma 3.1 For all
$m\lesssim n\log _2 n$
and sufficiently large n, there exists an
$abc$
triple satisfying
$$\begin{align*}\frac{2^{m-1}}{\prod_{i=1}^n p_i}\operatorname{\mathrm{rad}}(abc) \leq c \quad\text{and}\quad 2 \log c \leq \frac{n+O(\log n)}{\delta} \Bigg({2^{m-1}n^3\prod_{i=1}^n\log p_i}\Bigg)^{1/(n+1)}. \end{align*}$$
Proof By the definition of
$\delta $
from Corollary 2.4, for all sufficiently large n, there exists a nonzero
with
Say
. For sufficiently large n, we must have
$e_{n+1}=0$
, since by Lemma 2.7, if
$e_{n+1}\neq 0$
, then
. This would contradict (3.1) since by Lemma 2.6 the right-hand side is
$O(n^{2+\epsilon })$
.
Let
$\prod _{i=1}^n p_i^{e_i}=p/q$
be expressed in lowest terms. By construction of the kernel sublattice, we have that
$p/q \equiv 1\ \ \pmod {2^m}$
. Let
,
, and
, so that a, b, c form an
$abc$
triple. Furthermore, we see that
$$\begin{align*}c \equiv b\quad \pmod{2^m} \end{align*}$$
so that
$c=b+k2^m$
for some positive integer
$k\leq c/2^m$
. Note that a is divisible by
$2$
and any other prime that divides it also divides k, so that
$\operatorname {\mathrm {rad}}(a)\leq 2k\leq c/2^{m-1}$
. Furthermore, by construction of b and c,
$\operatorname {\mathrm {rad}}(bc)\leq \prod _{i=1}^n p_i$
and the first bound follows. The second bound follows from (3.1) and Lemmas 2.1 and 2.5.
3.1 Optimal choice of m
The first bound in Lemma 3.1 allows us to show the existence of infinitely many
$abc$
triples whose ratio of c to
$\operatorname {\mathrm {rad}}(abc)$
grows arbitrarily large. Using the second bound, we can even show that this ratio grows faster than a function of c. It is not immediately clear how to choose m optimally, i.e., to maximize the ratio
$c/\operatorname {\mathrm {rad}}(abc)$
.
For convenience, let R denote the right-hand side of the second inequality in Lemma 3.1 with
. Then
$2^{m-1}= \big( {\frac {\delta R}{n+l_n}}\big)^{n+1}/(n^3\prod _{i=1}^n\log p_i)$
, so the bounds of Lemma 3.1 can be rewritten in terms of R:
$$ \begin{align} \frac{(\delta R/(n+l_n))^{n+1}}{n^3\prod_{i=1}^n p_i\log p_i}\operatorname{\mathrm{rad}}(abc) \leq c \quad\text{and}\quad 2\log c \leq R. \end{align} $$
The question now becomes how to choose R in terms of n so that
$c/\operatorname {\mathrm {rad}}(abc)$
is maximized.
Taking the logarithm of the first inequality in (3.2) gives
$$\begin{align*}(n+1)\log \Bigg({\frac{\delta R}{n+l_n}}\Bigg) - 3\log n - \sum_{i=1}^n \log p_i - \sum_{i=1}^n \log\log p_i + \log\operatorname{\mathrm{rad}}(abc) \leq \log c. \end{align*}$$
Using the asymptotic formulae in Lemmas 2.8 and 2.9 with
$\log (n+l_n)=\log n+O(l_n/n)$
, this becomes
$$ \begin{align} n\log \Bigg({\frac{e\delta R}{np_n\log p_n}}\Bigg) + \frac{2p_n}{\log^2 p_n} + O \Bigg({\frac{p_n}{\log^3 p_n}}\Bigg) + \log\operatorname{\mathrm{rad}}(abc) \leq \log c. \end{align} $$
By the prime number theorem
$n=\operatorname {\mathrm {li}}(p_n)+O(p_n/\log ^2 p_n)$
and (2.1), the leftmost term becomes
$$\begin{align*}n\log \Bigg({\frac{e\delta R}{p_n^2 \big({1+1/\log p_n+O(1/\log^2 p_n)}\big)}}\Bigg) , \end{align*}$$
and with
$\log (1+1/x)=1/x+O(1/x^2)$
as
$x\to \infty $
, this is
$$\begin{align*}n\log \Bigg({\frac{e\delta R}{p_n^2}}\Bigg) - \frac{n}{\log p_n} + O \Bigg({\frac{n}{\log^2 p_n}}\Bigg). \end{align*}$$
Using (2.1) again on the last two terms and putting this back into (3.3), we get
$$ \begin{align} n\log \Bigg({\frac{e\delta R}{p_n^2}}\Bigg) + \frac{p_n}{\log^2 p_n} + O \Bigg({\frac{p_n}{\log^3 p_n}}\Bigg) + \log\operatorname{\mathrm{rad}}(abc) \leq \log c , \end{align} $$
and our goal becomes to choose R as a function of n to maximize
$n\log (e\delta R/p_n^2)$
. Choosing R as asymptotically slow-growing as possible in terms of n will maximize this in terms of R. We must take
$R>p_n^2/(e\delta )$
for the logarithm to be positive, so we take
for some constant k. Note that with this choice
$m\sim n\log _2 n$
, so Lemma 3.1 applies. We have that
$n\log (e\delta R/p_n^2)$
simplifies to
$$\begin{align*}n\log(e\delta k) \sim \frac{p_n}{\log p_n}\log(e\delta k) = \frac{\sqrt{R/k}}{\log\sqrt{R/k}}\log(e\delta k) \sim \frac{2\sqrt{R/k}}{\log R}\log(e\delta k). \end{align*}$$
For fixed R, this is maximized when
. Using
$R=ep_n^2/\delta $
in (3.4),
$$\begin{align*}2n + \frac{p_n}{\log^2 p_n} + O \Bigg({\frac{p_n}{\log^3 p_n}}\Bigg) + \log\operatorname{\mathrm{rad}}(abc) \leq \log c. \end{align*}$$
By the prime number theorem and (2.1) again,
$$\begin{align*}\frac{2p_n}{\log p_n} + \frac{3p_n}{\log^2 p_n} + O \Bigg({\frac{p_n}{\log^3 p_n}}\Bigg) + \log\operatorname{\mathrm{rad}}(abc) \leq \log c. \end{align*}$$
Rewriting in terms of R,
$$\begin{align*}\frac{2\sqrt{\delta R/e}}{\log \sqrt{\delta R/e}} + \frac{3\sqrt{\delta R/e}}{\log^2 \sqrt{\delta R/e}} + O \Bigg({\frac{\sqrt{R}}{\log^3 R}}\Bigg) + \log\operatorname{\mathrm{rad}}(abc) \leq \log c. \end{align*}$$
Simplifying,
$$\begin{align*}\frac{4\sqrt{\delta R/e}}{\log(\delta R/e)} + \frac{12\sqrt{\delta R/e}}{\log^2(\delta R/e)} + O \Bigg({\frac{\sqrt{R}}{\log^3 R}}\Bigg) + \log\operatorname{\mathrm{rad}}(abc) \leq \log c. \end{align*}$$
Using
$1/(x+y)=1/x-y/x^2+O(x^{-3})$
as
$x\to \infty $
, this gives
$$\begin{align*}\frac{4\sqrt{\delta R/e}}{\log (R/2)} + \frac{(12-4\log(2\delta/e))\sqrt{\delta R/e}}{\log^2 R} + O \Bigg({\frac{\sqrt{R}}{\log^3 R}}\Bigg) + \log\operatorname{\mathrm{rad}}(abc) \leq \log c. \end{align*}$$
Using that
$2\delta <e^4$
, the second term on the left is positive, and so for sufficiently large R, the middle two terms are necessarily positive. Therefore, for sufficiently large R, this can be simplified to
$$\begin{align*}\frac{4\sqrt{\delta R/e}}{\log(R/2)} + \log\operatorname{\mathrm{rad}}(abc) \leq \log c. \end{align*}$$
Using that
$2\log c\leq R$
from (3.2) and the increasing monotonicity of
$\sqrt {R}/\log (R/2)$
for sufficiently large R, we finally achieve that
$$\begin{align*}\frac{4\sqrt{2(\delta/e)\log c}}{\log\log c} + \log\operatorname{\mathrm{rad}}(abc) \leq \log c. \end{align*}$$
Taking the exponential, this proves the following theorem.
Theorem 3.1 There are infinitely many
$abc$
triples satisfying
$$\begin{align*}\exp \Bigg({\frac{4\sqrt{2(\delta/e)\log c}}{\log\log c}}\Bigg) \operatorname{\mathrm{rad}}(abc) \leq c. \end{align*}$$
Using the permissible value for
$\delta $
derived by Rankin’s bound in Corollary 2.4, the constant in the exponent becomes approximately
$6.56338$
. As mentioned in Section 2.3, the best-known upper bound on
$\delta $
is
$2e$
, meaning that the constant in the exponent would become
$8$
if this upper bound was shown to be tight.
Appendix
Lemma 2.8
$\sum _{i=1}^n\log p_i = n\log p_n - n - p_n/\log ^2 p_n + O(p_n/\log ^3 p_n)$
.
Proof Let
, so the prime number theorem (with error term) gives
$n=\operatorname {\mathrm {li}}(x)+O(x/\log ^4 x)$
. Rearranging the asymptotic expansion of the logarithmic integral (2.1) gives
$$ \begin{align*} x &= n\log x - \frac{x}{\log x} - \frac{2x}{\log^2 x} + O \Bigg({\frac{x}{\log^3 x}}\Bigg) \\ &= n\log x - n - \frac{x}{\log^2 x} + O \Bigg({\frac{x}{\log^3 x}}\Bigg). \end{align*} $$
An alternate form of the prime number theorem is
$x=\sum _{p\leq x}\log p+O(x/\log ^3 x)$
, so the left-hand side may be replaced by
$\sum _{i=1}^n \log p_i$
from which the result follows.
Lemma 2.9
$\sum _{i=1}^n\log \log p_i = n\log \log p_n - p_n/\log ^2 p_n + O(p_n/\log ^3 p_n)$
.
Proof By Abel’s summation formula with
and
for k up to
, we have
$$\begin{align*}\sum_{i=1}^n\log\log p_i = n\log\log x - \int_2^x\frac{\pi(t)-1}{t\log t}{\,\mathrm{d}} t. \end{align*}$$
We have
$\pi (t)-1=t/\log t+O(t/\log ^2 t)$
by the prime number theorem, so that
$$\begin{align*}\int_2^x\frac{\pi(t)-1}{t\log t}{\,\mathrm{d}} t = \int_2^x\frac{{\,\mathrm{d}} t}{\log^2 t} + O \bigg({\int_2^x\frac{{\,\mathrm{d}} t}{\log^3 t}}\bigg). \end{align*}$$
The first integral on the right works out to
$$\begin{align*}\int_2^x\frac{{\,\mathrm{d}} t}{\log^2 t} = \operatorname{\mathrm{li}}(x) - \frac{x}{\log x} + O(1) = \frac{x}{\log^2 x} + O \Bigg({\frac{x}{\log^3 x}}\Bigg) \end{align*}$$
by the asymptotic expansion of the logarithmic integral. The second integral on the right can split in two (around
$\sqrt x$
) and then estimated by
$$\begin{align*}\int_2^{\sqrt x}\frac{{\,\mathrm{d}} t}{\log^3 t}+\int_{\sqrt x}^x\frac{{\,\mathrm{d}} t}{\log^3 t} \leq \frac{\sqrt x}{\log^3 2}+\frac{x-\sqrt x}{\log^3\sqrt{x}} = O \Bigg({\frac{x}{\log^3 x}}\Bigg). \end{align*}$$
Putting everything together gives
$$ \begin{align*} \sum_{i=1}^n\log\log p_i = n\log\log x - \frac{x}{\log^2 x} + O \Bigg({\frac{x}{\log^3 x}}\Bigg) .\\[-41pt] \end{align*} $$
Acknowledgment
The author would like to thank the reviewer for their detailed review and useful feedback they provided on the first draft of this paper.
Open access
