Article contents
Packing topological entropy for amenable group actions
Published online by Cambridge University Press: 20 October 2021
Abstract
Packing topological entropy is a dynamical analogy of the packing dimension, which can be viewed as a counterpart of Bowen topological entropy. In the present paper we give a systematic study of the packing topological entropy for a continuous G-action dynamical system
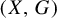 $(X,G)$
, where X is a compact metric space and G is a countable infinite discrete amenable group. We first prove a variational principle for amenable packing topological entropy: for any Borel subset Z of X, the packing topological entropy of Z equals the supremum of upper local entropy over all Borel probability measures for which the subset Z has full measure. Then we obtain an entropy inequality concerning amenable packing entropy. Finally, we show that the packing topological entropy of the set of generic points for any invariant Borel probability measure
$(X,G)$
, where X is a compact metric space and G is a countable infinite discrete amenable group. We first prove a variational principle for amenable packing topological entropy: for any Borel subset Z of X, the packing topological entropy of Z equals the supremum of upper local entropy over all Borel probability measures for which the subset Z has full measure. Then we obtain an entropy inequality concerning amenable packing entropy. Finally, we show that the packing topological entropy of the set of generic points for any invariant Borel probability measure
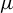 $\mu $
coincides with the metric entropy if either
$\mu $
coincides with the metric entropy if either
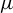 $\mu $
is ergodic or the system satisfies a kind of specification property.
$\mu $
is ergodic or the system satisfies a kind of specification property.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 8
- Cited by



