No CrossRef data available.
Article contents
NORMAL SUBMONOIDS AND CONGRUENCES ON A MONOID
Published online by Cambridge University Press: 18 December 2023
Abstract
A notion of normal submonoid of a monoid M is introduced that generalizes the normal subgroups of a group. When ordered by inclusion, the set  $\mathsf {NorSub}(M)$ of normal submonoids of M is a complete lattice. Joins are explicitly described and the lattice is computed for the finite full transformation monoids
$\mathsf {NorSub}(M)$ of normal submonoids of M is a complete lattice. Joins are explicitly described and the lattice is computed for the finite full transformation monoids 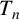 $T_n$,
$T_n$, 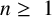 $n\geq ~1$. It is also shown that
$n\geq ~1$. It is also shown that  $\mathsf {NorSub}(M)$ is modular for a specific family of commutative monoids, including all Krull monoids, and that it, as a join semilattice, embeds isomorphically onto a join subsemilattice of the lattice
$\mathsf {NorSub}(M)$ is modular for a specific family of commutative monoids, including all Krull monoids, and that it, as a join semilattice, embeds isomorphically onto a join subsemilattice of the lattice  $\mathsf {Cong}(M)$ of congruences on M. This leads to a new strategy for computing
$\mathsf {Cong}(M)$ of congruences on M. This leads to a new strategy for computing  $\mathsf {Cong}(M)$ consisting of computing
$\mathsf {Cong}(M)$ consisting of computing  $\mathsf {NorSub}(M)$ and the so-called unital congruences on the quotients of M modulo its normal submonoids. This provides a new perspective on Malcev’s computation of the congruences on
$\mathsf {NorSub}(M)$ and the so-called unital congruences on the quotients of M modulo its normal submonoids. This provides a new perspective on Malcev’s computation of the congruences on 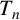 $T_n$.
$T_n$.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by James East
The author is supported by the project PID2019-103849GB-I00 of MCIN/AEI/10.13039/501100011033.



