No CrossRef data available.
Article contents
THE GROWTH OF SOLUTIONS OF MONGE–AMPÈRE EQUATIONS IN HALF SPACES AND ITS APPLICATION
Published online by Cambridge University Press: 31 March 2023
Abstract
We consider the growth of the convex viscosity solution of the Monge–Ampère equation 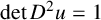 $\det D^2u=1$ outside a bounded domain of the upper half space. We show that if u is a convex quadratic polynomial on the boundary
$\det D^2u=1$ outside a bounded domain of the upper half space. We show that if u is a convex quadratic polynomial on the boundary 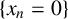 $\{x_n=0\}$ and there exists some
$\{x_n=0\}$ and there exists some 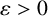 $\varepsilon>0$ such that
$\varepsilon>0$ such that 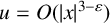 $u=O(|x|^{3-\varepsilon })$ at infinity, then
$u=O(|x|^{3-\varepsilon })$ at infinity, then 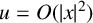 $u=O(|x|^2)$ at infinity. As an application, we improve the asymptotic result at infinity for viscosity solutions of Monge–Ampère equations in half spaces of Jia, Li and Li [‘Asymptotic behavior at infinity of solutions of Monge–Ampère equations in half spaces’, J. Differential Equations 269(1) (2020), 326–348].
$u=O(|x|^2)$ at infinity. As an application, we improve the asymptotic result at infinity for viscosity solutions of Monge–Ampère equations in half spaces of Jia, Li and Li [‘Asymptotic behavior at infinity of solutions of Monge–Ampère equations in half spaces’, J. Differential Equations 269(1) (2020), 326–348].
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 109 , Issue 1 , February 2024 , pp. 125 - 137
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by Natural Science Foundation of Henan Province (Grant No. 222300420321); the second author was supported by Natural Science Foundation of Henan Province (Grant No. 222300420232).



