James Fearon’s seminal work on the “bargaining model” of war set in motion a research agenda that highlights the important effects of informational asymmetries on international conflict (Fearon Reference Fearon1995). The basic claim that uncertainty, misrepresentation, and mutual optimism can substantially increase the likelihood of conflict has gained significant traction in the field. Indeed, it is reasonable to claim that the bargaining model should constitute an important component of an undergraduate international relations (IR) curriculum. Despite the model’s elegance and intuitive logic, however, much of the bargaining literature contains highly technical, game-theoretic notation that is simply unsuited for most undergraduate students. Footnote 1 Even basic treatments in widely used introductory textbooks use basic mathematical notation that might be problematic for certain students (Frieden, Lake, and Schultz Reference Frieden, Lake and Schultz2012).
This article describes a simple card game that clearly illustrates the core logic of Fearon’s bargaining model. The game carefully simulates informational asymmetries and costly conflict while providing students with “incentives to misrepresent” their bargaining strength, as Fearon’s model indicates. The game is highly flexible, and the parameters can be adjusted easily to highlight different components of the bargaining logic.
Research has shown that classroom simulations can be a highly effective pedagogical tool (Frederking Reference Frederking2005; Shellman and Turan Reference Slantchev and Tarar2006). As such, the lack of simulations for teaching this important theory is highly problematic. The simulation described here is somewhat atypical in that it is divorced from real-world political scenarios (Brynen Reference Brynen2010; Wheeler Reference Wheeler2006). I do not present a “role-playing” game or a hypothetical crisis situation. Rather, I describe a game that focuses entirely on the abstract logic of information, bargaining, and conflict. Instructors then can integrate this game with additional simulations that encourage students to apply the bargaining logic to real-world scenarios (Asal Reference Asal2005; Brynen Reference Brynen2010). For instance, instructors might follow this game with an in-depth historical case study of the Korean War or a crisis simulation centered on the India–Pakistan dispute over Kashmir. By integrating this game into a broader lesson plan, instructors can incorporate the bargaining model into even introductory IR courses.
DESCRIBING THE BARGAINING MODEL
Fearon’s argument centers on the idea that war is costly and that if rational states were completely informed regarding the capabilities and resolve of their adversaries, they typically should settle disputes without resorting to war. The costs of conflict create a “bargaining range” of outcomes that both parties should prefer over war. The theory highlights three distinct dynamics that cause rational states to resort to war despite the high costs.
First, due to “informational asymmetries” and uncertainty regarding an adversary’s strength and resolve, states might overestimate their ability to achieve a favorable outcome through war. Essentially, states cannot fully know their adversary’s capabilities and commitment. Furthermore, states have a strong “incentive to misrepresent” and exaggerate their power to secure a better deal. Thus, uncertain states might overestimate their capabilities and stumble into a costly war based on a rational “mutual optimism” (Slantchev and Tarar Reference Wheeler2011).
Second, even if states were fully informed of one another’s power and resolve, they nevertheless could end up in conflict if power is shifting exogenously or if the good in dispute is itself a source of power. Under this “commitment problem” logic, perfectly informed states can negotiate a mutually acceptable deal under current conditions, if they remain static (Powell Reference Reiter2006). However, when relative power is in flux, the declining state cannot trust its adversary to continue abiding by the agreement into the future. Power shifts thus compel declining states to fight now rather than risk fighting later under more dangerous conditions.
Third, Fearon shows that a mutually agreeable negotiated solution might not be possible if the good in dispute is “indivisible” and cannot be continuously divided without diminishing its value. When bargaining over sacred territory or strategically valuable terrain that loses value if it is divided with another actor, there may not be a practicable way to divide that good that still falls within the bargaining range. Thus, issue indivisibilities can prevent a negotiated outcome even when states are fully informed and power levels are stable.
Key Insights of the Bargaining Model
The logic described previously yields at least four key substantive claims. First, greater levels of uncertainty and incentives for states to misrepresent their capabilities increase the probability of conflict. Conversely, greater transparency and increased availability of information should be a force for peace. Second, shifting levels of relative power increase the probability of war. Third, greater flexibility in dividing a disputed good should help states to avoid war. Fourth, as war becomes more costly, states should be more eager to avoid it, thereby increasing the range of outcomes that both prefer over conflict and decreasing the frequency of war.
Although the simulation described herein focuses on the effect of uncertainty, the game can be modified easily to highlight each theoretical claim. The simulation is designed to enable students to effectively describe, explain, and apply the bargaining model’s central claims regarding uncertainty and conflict.
DESCRIBING THE GAME
The game involves pairs of students using a deck of playing cards to “gamble” over pennies. The instructor distributes one deck of shuffled cards and one roll of pennies to each pair of students. For simplicity, I typically remove face cards from each deck, leaving only the cards with a face value of two through nine (i.e., a total of 32 cards). Students divide the pennies in half, giving an equal share to each player.
In the first round of the game, each student is dealt two cards, both of which are face down. Each student also must “ante up” and put one penny in the pot at the start of each hand. After both players look at their own cards, Player 1 (P1) must decide whether to make a demand for the pot or to concede it to Player 2 (P2). If P1 opts to concede, P2 takes the pot, the cards are discarded, and another hand is dealt. If P1 makes a demand, however, P2 must decide whether to “resist” the demand and fight over the pot. If P2 resists, both players turn over their cards and the player with the highest card total (i.e., the summed face values of the two cards) wins the pot and collects the two pennies. Crucially, however, because the players could not agree to a negotiated solution, they both suffer “costs of war” equal to one penny each. The pennies representing the costs of war are removed from the game and set aside. Neither player can ever recoup these losses. The players are not allowed to “split” the pot. Footnote 2 However, if the players turn over their cards and have equal hands, a “stalemate” results. The pot then is split evenly between the two players; however, because they each suffer the costs of war, the one penny that each player takes from the pot is removed from the game.
Crucially, however, because the players could not agree to a negotiated solution, they both suffer “costs of war” equal to one penny each.
There are five potential outcomes. If P1 concedes, she loses the penny she bet at the outset of the hand, and P2 wins that penny. P1’s payoff is -1 and P2’s payoff is +1. Alternatively, if P1 makes a demand and P2 concedes, then P1 takes the pot and gets +1 and P2 gets -1. If P1 issues a demand, P2 resists, and P1 has the better hand, then P1 takes the pot (i.e., +1) but also must pay the costs of conflict such that her net payoff is zero. P2 loses the pot and pays the costs of conflict, netting a payoff of -2. Conversely, if P1 makes a demand, P2 resists, and P2 has the stronger hand, then P2 receives zero and P1 receives -2. Finally, if the players turn over their cards and have equal hands, they split the pot but also suffer the costs of conflict. Each player’s net payoff is then -1. The instructor establishes the number of hands in each round. The players take turns acting first, alternating roles as P1 and P2.
At the end of each round of hands, the instructor asks each student pairing for the “score” of their game—that is, the number of pennies with which each player finished. The pennies are unlikely to be a strong motivator for students, so the instructor may need to offer extra credit to the “winner” of each game. Importantly, however, this competitive scorekeeping is largely a form of misdirection. We do not want to know who won each round but rather how many “wars” occurred or how many pennies were removed from the game. Fortunately, this can be deduced easily by subtracting the sum of P1’s and P2’s scores from the total number of pennies distributed.
Subsequent Rounds
After students complete the first round of hands and the instructor compiles the scores, a new round begins. The cards are reshuffled and the pennies are redistributed to the players in equal shares. Game play remains the same in the second round, with one important exception: the cards now are dealt with one card face down and the other face up. Half of each player’s bargaining strength becomes common knowledge. This, of course, simulates the greater availability of information regarding relative power in a bargaining interaction. The students play the same number of hands as in the first round and according to the same rules.
Although players still have incomplete information regarding their opponent’s hand, there are many scenarios in which players know their own hand to be so weak that backing down is a dominant strategy. Suppose P1 was dealt a four face up and a three face down; P1 thus has a score of seven. If P2’s face-up card is a nine, P1 knows that irrespective of the value of P2’s other card, P2 has the superior hand. If P2 acts first and makes a demand, P1 should always concede. The greater availability of information should allow the players to avoid conflict more frequently.
After completing the second round and tabulating the scores, the pennies are redistributed and the cards are reshuffled. The third round is identical to the first two rounds, except that now both cards are dealt face up. Thus, both players are fully aware of the balance of power between them in the bargaining interaction. Conflict should be easily avoidable, with one important exception. If the players are dealt equal hands—for example, P1 is dealt a six and a five, whereas P2 is dealt a nine and a two—war may be possible. If P1 makes a demand, P2 is indifferent between conceding and resisting. Likewise, even if P1 knows that P2 will resist its demands, P1 is indifferent between making a demand and conceding. Rational players therefore may end up in conflict even in the complete-information game, but only if the players are dealt even hands and they are prohibited from agreeing to split the pot. Footnote 3
MODIFICATIONS
The baseline version of the game described previously emphasizes informational asymmetries and misrepresentation as causes of conflict. However, the game’s parameters can be manipulated to provide an even finer-grained picture of the importance of information or to highlight other components of the bargaining model’s core logic.
First, the instructor can create a finer-grained picture of the effect of information on conflict simply by having the students deal extra cards in each hand. If each hand consists of four cards per player, there is greater uncertainty regarding an opponent’s strength because the range of possible values of their hand is wider. Subsequent rounds then can be adapted to reveal smaller increments of information. In a four-card game, the second round of play has one card face up and three cards face down (i.e., 25% information); the third round has two cards face up and two cards face down (i.e., 50% information); and so on. Each round thus allows smaller additions of information, which potentially results in more subtle shifts in the frequency of conflict.
Second, the instructor can adjust the parameters to simulate more costly conflict and then observe how doing so affects the frequency of war. Subsequent iterations can impose higher costs (e.g., two pennies each), or asymmetrical costs of war, in which one player suffers a greater penalty as the result of conflict. In this case, the instructor should take special note of the players’ scores when counting pennies at the end of the round to determine how asymmetrical costs affect relative bargaining power.
Third, the instructor can simulate greater “divisibility” by allowing the players to agree to split the pot. This can be extended by increasing the size of the pot and allowing players to split it in a greater variety of ways. Theoretically, doing so should significantly reduce the frequency of conflict. In the complete-information game, allowing a negotiated split pot should completely eradicate conflict.
Capturing the effect of power shifts and commitment problems is the most difficult aspect of this simulation. The game must simulate a shifting balance of bargaining power and also provide the declining actor with the means to avert this power shift by initiating costly conflict. For example, the instructor might inform the players at the outset that there will be two rounds of play and that they will keep the pennies they win in the first round when they transition to the second round. But importantly, when the cards are dealt for the second round, P1 must give her four highest cards to P2 and P2 must give his four lowest cards to P1. Thus, P1 will be severely disadvantaged in the second round. However, if P1 wins the first round and secures more pennies than her opponent, she may reduce her vulnerability in round 2. If P1 won round 1 by one penny, she must give up only her three best cards; if she wins round 1 by two pennies, she gives up only her two best cards; and so on. If P1 wins round 1 by four or more pennies, she does not have to give up any of her cards, and round 2 will be played on even terms. This setup provides P1 with an incentive to bargain aggressively in round 1. The short-term costs of conflict may be worth risking for P1 if they offer a better chance of averting a diminished bargaining position in round 2.
Alternatively, the instructor can simulate short-term commitment problems simply by altering the rules so that winners of a hand benefit from a predetermined “bump” to their score in the subsequent hand. If P1 wins the first hand, for example, she then adds two points to her hand in the next round. This simulates a situation in which power is shifting endogenously, and the good in dispute is itself a source of power for future conflicts. Both players face incentives to take an aggressive bargaining stance, and conflict should become more likely.
According to the logic of the bargaining model, the frequency of conflict should be monotonically decreasing as more cards are revealed. The instructor should calculate the average number of “wars” that occurred in each round.
PRESENTING RESULTS
According to the logic of the bargaining model, the frequency of conflict should be monotonically decreasing as more cards are revealed. The instructor should calculate the average number of “wars” that occurred in each round. Footnote 4 The instructor then can show the students how their own behavior tracks with the bargaining model’s expectations and whether conflict was less common as information become more available. Additionally, maintaining a running spreadsheet of game results over time and across classes allows instructors to have informative visual representations of aggregate data ready for immediate presentation. For example, figure 1 illustrates a frequency-weighted scatter plot (i.e., “bubble plot”) showing the number of cards revealed on the x-axis and the frequency of conflict on the y-axis. The fitted bivariate regression line clearly illustrates the pacifying effect of information. Footnote 5 Instructors can compare individual class results to the broader trends that emerge from previous iterations of the game in other classes.
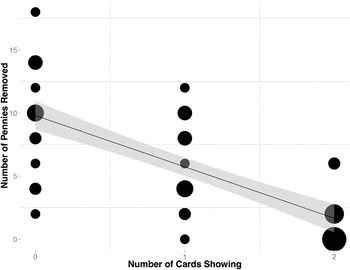
Figure 1 Effect of Information on Frequency of Conflict
It is obvious that the exact nature of the presentation of results will depend on how the instructor manipulates the parameters across various rounds. Figure 1 shows how they might be presented for the baseline simulation described previously. However, simple adjustments in presentation could capture the effects of, for example, increasing costs of war or greater divisibility.
TEACHING POINTS
On completion of the game, instructors should discuss the logic of the simulation and ask for insight on why students played as they did. This section describes questions and prompts that instructors can use to draw out important concepts. Footnote 6
First, the instructor might ask students in a highly conflict-prone pairing to explain why they so often were unable to come to an agreement. Players frequently indicate that they were simply bluffing about the strength of their own hand, hoping to win the pot despite having a weak hand. This directly captures the “incentives to misrepresent” that Fearon highlights as a key cause of war. The instructor then can demonstrate how bluffing became less effective—and therefore less common—as more information was revealed.
Second, the instructor might ask students if they ever resisted their opponent’s demand despite having a weak hand. Students often claim that they would rather “go down fighting” than abjectly concede. This dynamic can prompt a discussion of how states might actually derive a positive utility from fighting because their leaders can project an image of toughness to domestic constituents. Instructors also might ask whether such behavior was intended to project a reputation for firmness to their opponent.
Third, as discussed previously, conflict is indeed possible even in the complete-information game in which the players know one another’s hands. Players occasionally fight simply from spite or because they are dealt even hands and it is arguably rational to do so. In the former case, instructors can use the motivation of spite to highlight the psychological and non-rational components of interstate bargaining. This is an excellent opportunity to illustrate limitations of the bargaining model.
Conversely, if players fought in the complete-information game because they were dealt even hands, the instructor should explain that this was not necessarily the result of irrational behavior. Rather, it resulted from the inability of the players to divide the pot. A quick description of each player’s payoffs will reveal that conflict is perfectly rational when the pot is indivisible but completely irrational and avoidable if the players are allowed to divide the good.
Specific teaching points will depend on how the instructor chooses to manipulate the game’s parameters. If the game is designed so that changes in the costs of conflict are implemented across rounds, with cards dealt face down throughout, the subsequent discussion will focus on how variations in the costs of war affect the probability of conflict. However, for each variation of the game, changing the parameters provides instructors with valuable opportunities to highlight different aspects of the bargaining logic.
CONCLUSION
This article describes a simple card game that clarifies the core logic of the bargaining model of war. The game carefully simulates incomplete information and costly conflict, and its flexibility allows instructors to highlight different aspects of the bargaining model’s core logic. The bargaining framework is now widely used in the IR field, and it is becoming increasingly important to teach this material to undergraduates. Thus, simplifying and illustrating the model’s core logic with minimal notation can be immensely beneficial for students.



