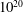2 The accelerator structure

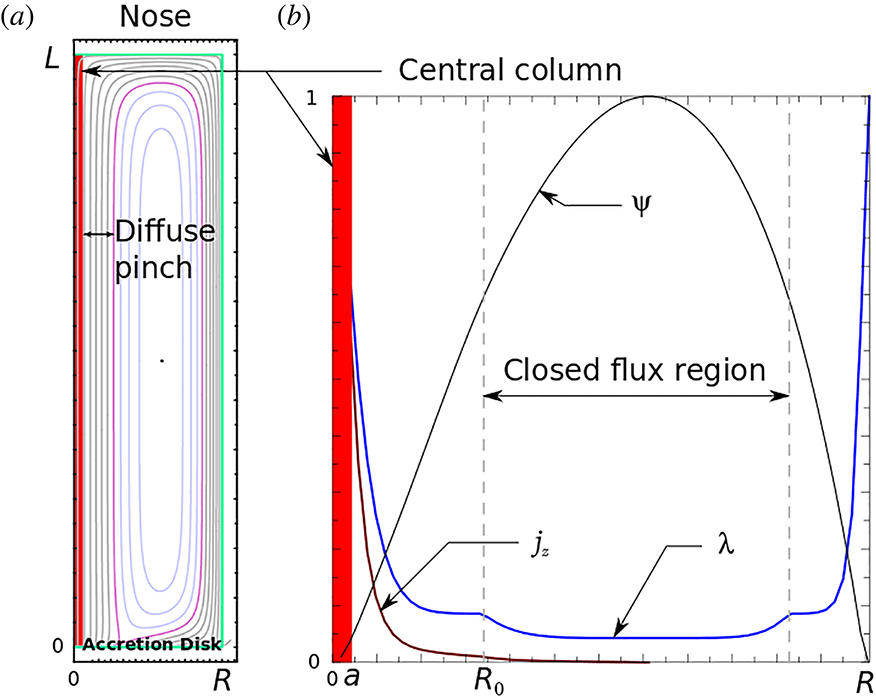
We begin with a description of the accretion disk/jet system, derived in papers I and II. A jet derived from the Grad–Shafranov equation is sketched in figure 1 taken from paper I. The accretion disk dynamo is at the bottom. We employ cylindrical coordinates with z along the jet, in a reference frame fixed in the accretion disk.

Figure 1. (a) A simplified sketch of an accretion disk ejecting a jet, overlaid by a Grad–Shafranov solution for the cross-section of poloildal ( $B_{z}$ , $B_{r}$ ) magnetic flux surfaces, using the accretion disk boundary condition derived in paper I. The axisymmetric calculation box is a cylinder of rotation of radius $R$ and length $L$ . The jet current is concentrated in a central column of radius a given in the text, surrounded by a diffuse pinch of radius $R_{o}$ and an extended outer region of radius $R$ bounded by the return current. Note that the outgoing flux surfaces are straight, finally turning at the ‘nose’. (b) Also drawn are the poloidal flux function $\unicode[STIX]{x1D6F9}$ , the poloidal current $j_{z}$ and the function $\unicode[STIX]{x1D706}=|j_{z}/B_{z}|$ depicted at $z=L/2$ midway up the column.

The left-hand side of figure 1 is a cross-section of axisymmetric magnetic flux surfaces around a core jet, labelled ‘Central Column’. The central column is a force-free ‘screw pinch’ $(\boldsymbol{j}\times \boldsymbol{B}=0)$ surrounded by a diffuse pinch with lower current density that helps guide the central column along its way, giving the radial profiles on the right-hand side, for the current density $|\boldsymbol{j}|$ , $\unicode[STIX]{x1D706}\propto (\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{B}/B^{2})$ and poloidal magnetic flux $\unicode[STIX]{x1D6F9}$ .

Particle acceleration occurs mainly in the central column where most of the electric current and most of the gravitational energy of accretion are deposited, continuing into the ‘nose’ in the figure. Experiments on acceleration need only include this central column, resembling jets produced in spheromak experiments during the early stages of plasma gun injection, before helicity propagation begins to fill in the closed flux in figure 1 (Hooper et al. Reference Hooper, Bulmer, Cohen, Hill, Holcomb, Hudson, McLean, Pearlstein, Romero-Talamas and Sovinec2012). Evidence that spheromak ‘flux cores’ (their central columns) remain collimated during this formation phase, as astrophysical jets do, is discussed in paper II, confirmed by MHD simulations of experiments at Cal Tech (Zhai et al. Reference Zhai, Li, Bellan and Li2014). Collimation by pinch forces persists the full length of the jet, to a length limited only by the available power and the elapsed time.

In paper I, we show that, like spheromak experiments, the central column can be described by an electric circuit with an accelerator voltage $V$ and current $I$ , matched to an exact solution of the diffuse pinch zone in figure 1, defined as the region where disk rotation is approximately Keplerian. The main difference from experiments is that the gun voltage produced by a capacitor bank is replaced by that of a dynamo with rotation frequency $\unicode[STIX]{x1D6FA}$ , giving an electric field $E_{r}=(r\unicode[STIX]{x1D6FA}/c)B_{z}$ integrated across the central column. We obtain (with formulas in cgs units, converted to SI):

Here, the subscript ‘ $a$ ’ denotes values at the central column radius $r=a$ ; and $M_{8}$ is the black hole mass M in units of $10^{8}$ solar masses, giving the Schwarzschild radius $R_{S}=(2MG/c^{2})$ . Equation (2.1b ) integrates $j_{z}=(c/4\unicode[STIX]{x03C0})(r^{-1}\unicode[STIX]{x2202}(rB_{\unicode[STIX]{x1D719}})/\unicode[STIX]{x2202}r)$ over $0<r<a$ . In astrophysical terminology, our jet is a magnetic tower model (Lynden-Bell Reference Lynden-Bell1996, Reference Lynden-Bell2003; Li et al. Reference Li, Lovelace, Finn and Colgate2001, Reference Li, Lapenta, Finn, Li and Colgate2006; Nakamura, Li & Li Reference Nakamura, Li and Li2006) in which magnetic jets are launched vertically ( $B_{r}=0$ at the accretion disk coronal surface). Note that, in the model we propose, ions are ejected by an electrostatic sheath, as in positively charged plasma guns.

We note that our circuit parameters are uniquely determined by considerations of angular momentum conservation in the disk (see papers I and II for details). Experiments suggested below could have similar magnetic field strength, giving gun voltages of a few keV over radial dimensions of $a$ few cm

3 Hyper-resistive acceleration

In paper II, we show that the large inductance of the current-carrying flux loops in figure 1 slows down the jet propagation velocity to $\text{d}L/\text{d}t=0.01c$ . The burden of proof for our accelerator model is how these quasi-static structures propagating at non-relativistic velocities can become the most powerful relativistic accelerators in the Universe.

That quasi-steady ion acceleration can be initiated by MHD kink modes in the central column (or flux core) was demonstrated in the SPHEX spheromak experiment (Al-Karkhy et al. Reference Al-Karkhy, Browning, Cunningham, Gee and Rudbridge1993; Rusbridge et al. Reference Rusbridge, Gee, Browning Cunningham, Duck, Al-Kharky, Martin and Bradley1997). Acceleration was attributed to MHD perturbations $\boldsymbol{E}_{1}$ and $\boldsymbol{B}_{1}$ , shown by measurement to be correlated to give an electric field parallel to the axisymmetrically averaged mean field $\boldsymbol{B}_{o}$ , given by:

Equation (3.1) is a special case of acceleration by turbulence-induced hyper-resistivity appearing in Ohm’s law as (Fowler & Gatto Reference Fowler and Gatto2007):

where $\boldsymbol{R}$ includes hyper-resistivity and also collisional resistivity when it matters; and $\boldsymbol{R},\boldsymbol{E}_{\boldsymbol{o}}$ , the potentials $\unicode[STIX]{x1D6F7}_{o}$ and $\boldsymbol{A}_{o}$ and the magnetic field $\boldsymbol{B}_{o}$ and velocity $\boldsymbol{v}_{o}$ are axisymmetrized mean-field quantities. It is $\boldsymbol{E}_{\boldsymbol{o}\Vert }$ parallel to $\boldsymbol{B}_{o}$ that accelerates cosmic rays to relativistic energies even though $\boldsymbol{B}_{o}$ itself evolves slowly, as noted above, the magnetic evolution being governed by the perpendicular component of (3.2) giving the MHD Ohm’s law. Thus acceleration is essentially electrostatic, as indicated by the middle expression in (3.2), although keeping $\unicode[STIX]{x2202}\boldsymbol{A}_{o}/\unicode[STIX]{x2202}t$ reminds us that transport by $\boldsymbol{R}$ is relative to $\boldsymbol{B}_{o}$ with field lines that do slowly move forward at the nose in our coordinate system fixed in the disk or plasma gun (the ‘lab frame’).

A well-known example of an electric field due to $\boldsymbol{R}$ is the resistive voltage drop due to classical collisional diffusion with $\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}_{o}/\unicode[STIX]{x2202}\unicode[STIX]{x1D719}=\unicode[STIX]{x2202}A_{o\unicode[STIX]{x1D719}}/\unicode[STIX]{x2202}t=0$ and $\boldsymbol{R}=\unicode[STIX]{x1D702}\boldsymbol{j}$ in a constant magnetic field $B_{z}$ , giving the well-known result $v_{or}=-c(R_{\unicode[STIX]{x1D719}}/B_{z})=-c(\unicode[STIX]{x1D702}j_{\unicode[STIX]{x1D719}}/B_{z})=-(c^{2}\unicode[STIX]{x1D702}/B_{z}^{2})\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}r$ with resistivity $\unicode[STIX]{x1D702}$ and pressure $p$ , using also $c^{-1}\boldsymbol{j}\times \boldsymbol{B}=\unicode[STIX]{x1D735}p$ in MHD equilibrium; and from this, $v_{ro}\approx -D(p^{-1}\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}r)$ giving $D\approx (c^{2}\unicode[STIX]{x1D702}p/B_{z}^{2})\approx r_{Le}^{2}\unicode[STIX]{x1D708}_{ee}$ with electron Larmor radius $r_{Le}$ and collision frequency $\unicode[STIX]{x1D708}_{ee}$ .

4 DCLC acceleration

Besides kink modes, another, sometimes stronger, source of hyper-resistivity, when it occurs, may be the DCLC mode mentioned in the Introduction. While kink-mode acceleration of ions in spheromaks is well established, and DCLC momentum transport is well established in fusion mirror devices (Fowler Reference Fowler and Teller1981), to our knowledge the acceleration of ions by DCLC turbulence required for our UHECR accelerator model has not been observed, either in experiments or in simulations. Yet a quasi-linear treatment of DCLC transport (Smith & Cohen Reference Smith and Cohen1983) showed that DCLC resonance acts like a collision with a collision frequency proportional to the ion cyclotron frequency, $\unicode[STIX]{x1D714}_{ci}$ . This can give a momentum transport as large as $D_{p}=p_{i}^{2}\unicode[STIX]{x1D714}_{ci}$ when driven by a non-thermal velocity distribution like that created by kink-mode acceleration, where $p_{i}$ is the ion momentum. This also yields a spatial diffusion of order $D=(D_{p}/m_{i}^{2}\unicode[STIX]{x1D714}_{ci}^{2})=r_{L}^{2}\unicode[STIX]{x1D714}_{ci}$ for ion Larmor radius $r_{L}$ . Note that this scaling is similar to $D\approx \unicode[STIX]{x1D6FE}/k^{2}$ for growth rate $\unicode[STIX]{x1D6FE}\approx \unicode[STIX]{x1D714}_{ci}$ and wavenumber $k\approx r_{L}^{-1}$ (Kadomtsev Reference Kadomtsev1965).

Spatial diffusion by DCLC should in turn produce a hyper-resistive accelerating electric field $E=R\approx (v/c)B\approx (D/ac)B$ , analogous to classical resistive diffusion and hyper-resistive diffusion by kink modes discussed in § 3. Note that the electric field is always perpendicular to the direction of diffusion, whereby the escape of cosmic ray ions out of the current channel simultaneously accelerates these ions along the looping current path, thereby performing in a natural way both the acceleration and ejection functions necessary in quasi-circular accelerators.

5 The DCLC onset condition

Particle acceleration by kink modes produces a momentum distribution of the form:

where $\boldsymbol{p}_{o}$ is particle’s momentum, parallel to $\boldsymbol{B}_{o}$ Here, $m$ is the mass of the particles and $T$ is their temperature. That $f_{ion}$ is roughly a delta function in momentum can be shown as follows. Kink modes that accelerate ions to a velocity $+c$ also accelerate electrons to velocity $-c$ , and counter-streaming ions and electrons interact via the relativistic two-stream instability that spreads the momentum of the streams. One can show that spreading of electron velocities from their origin at $-c$ to $+c$ of the ions produces a quasi-Maxwellian electron momentum distribution with negligible net momentum to carry current in our reference frame fixed in the disk. But the heavier ions maintain their beam-like distribution, giving (5.1b ) with $mT\ll p_{o}^{2}$ whereby most of the current is carried by the ‘runaway’ ion beam, neutralized by the equal charge of the relativistic quasi-Maxwellian electrons.

In a uniform magnetic field, $\boldsymbol{p}_{o}$ would be a constant parallel to constant $\boldsymbol{B}_{o}$ , giving counter-flowing Maxwellian ions and electrons yielding the two-stream instability with finite wavenumber $k_{\Vert }$ as the only unstable mode of interest. But jet magnetic fields are not uniform. For example, in the central column field lines are spirals with components $B_{z}$ and $B_{\unicode[STIX]{x1D719}}$ . Acceleration in a spiral field automatically produces components of $\boldsymbol{p}_{o}$ both parallel and perpendicular to $\boldsymbol{B}$ (equivalently, both the energy and the magnetic moment are accelerated). For a fixed $\boldsymbol{p}_{o}$ , (5.1b ) becomes $f_{ion}\rightarrow \unicode[STIX]{x1D6FF}(\boldsymbol{p}_{\Vert }-\boldsymbol{p}_{\Vert _{o}})\unicode[STIX]{x1D6FF}(\boldsymbol{p}_{\bot }-\boldsymbol{p}_{\bot o})$ . The minimum $\boldsymbol{p}_{\bot o}$ is that for acceleration exactly parallel to $\boldsymbol{B}$ found by balancing the centrifugal force due to line curvature against magnetic attraction, giving $|\boldsymbol{p}_{\bot o}|\approx (r_{Lo}/r)|\boldsymbol{p}_{o}|$ with curvature radius $r$ and Larmor radius $r_{Lo}$ for the full $\boldsymbol{p}_{o}$ . Then, averaging $f_{ion}$ in (5.1b ) over $p_{\Vert }$ gives $f(p_{\bot })=\int \text{d}p_{\Vert }f(\boldsymbol{p})$ which is certain to have a ‘hole’ at $0<|\boldsymbol{p}_{\bot o}|<(r_{Lo}/r)|\boldsymbol{p}_{o}|$ analogous to the ‘ambipolar hole’ in mirror devices (in that case, due to the positive electrostatic potential that confines electrons but ejects ions in these devices). It is the collapse of this hole to achieve a Maxwellian distribution that yields the free energy driving DCLC instability, even for ‘flute-like’ modes with $k_{\Vert }=0$ that are not affected by the two-stream activity (Post & Rosenbluth Reference Post and Rosenbluth1966).

Instability occurs at harmonics of the ion cyclotron frequency. The instability wave itself is a $k_{\Vert }=0$ electron drift wave. Instability occurs when the drift wave frequency $(\propto \text{d}n/\text{d}x)$ equals the ion cyclotron frequency, for any $x$ direction giving a density gradient. Taking $n/(\text{d}n/\text{d}x)=\unicode[STIX]{x1D6E5}$ , one can show that the relativistic condition for onset is:

where the ion Larmor radius $r_{L}$ , the ion cyclotron frequency $\unicode[STIX]{x1D714}_{ci}$ and the ion plasma frequency $\unicode[STIX]{x1D714}_{pi}$ are identical with their non-relativistic counterparts if we replace the rest mass of ions with their relativistic mass. Note that (5.2) is identical to the non-relativistic criterion derived from the DCLC dispersion relation in Fowler (Reference Fowler and Teller1981), while this would not be the case for modes such as two-stream instability involving motion parallel to $\boldsymbol{B}$ (Montgomery & Tidman Reference Montgomery and Tidman1964). The DCLC instability only involves drift waves and ion cyclotron motion perpendicular to $\boldsymbol{B}$ , in which case the momentum derivatives of the Lorentz factor $\unicode[STIX]{x1D6FE}=(p/mv)$ appearing in the two-stream dispersion relation do not appear. Full details will be given in a forthcoming paper.

6 Two stage acceleration

We can show that kink-mode acceleration in the central column is limited by curvature radiation as ions follow the twisting field lines (with $B_{\unicode[STIX]{x1D719}}$ and $B_{z}$ ) that characterize the central column except very near the black hole. (Ion synchrotron radiation also occurs but, due to weak scattering, this only serves to reduce $p_{\bot }$ to the minimum required for ions to follows field lines in the central column.) And the density in the central column will turn out to be too low relative to B to excite DCLC instability by (5.2).

For these reasons, we predict that acceleration of cosmic rays occurs in two stages, first by kink modes in the central column that produce an energetic ion beam entering the nose end of the jet in figure 1, and secondly by DCLC instability in the nose where most of the acceleration takes place. Curvature radiation in the central column limits energies entering the nose to approximately $10^{16}~\text{eV}$ . Both curvature and ion synchrotron radiation cease to matter where field lines flare out radially in the nose, thus allowing DCLC acceleration to extend to of the order of $10^{20}~\text{eV}$ , the maximum energy possible in steady state from an accretion disk dynamo producing $10^{20}$  V.

That kink modes do not spoil jet collimation follows from the relevant wavelengths ( ${\approx}1$ : see paper II) and from the fact the fluctuation levels are weak, as follows. Kinks are driven by $\text{d}|\boldsymbol{j}|/\text{d}r$ where $|\boldsymbol{j}|$ is the current density. We approximate hyper-resistivity $R$ as a diffusion rate $D$ causing flattening of the current profile so as to stabilize the kink modes, giving $R=(v/c)B=(D/ac)B$ . Because the accretion process creating $\text{d}|\boldsymbol{j}|/\text{d}r$ is slow compared to kink growth rates, $D$ needs only to be large enough to flatten $|\boldsymbol{j}|$ in the available time, giving as our estimate $D=a^{2}/t$ for a duration $t$ , during which the jet length $L$ grows to $L=0.01ct$ . We obtain:

Equation (6.1b ) gives the voltage drop along the central column using $V=aB_{a}$ from (2.1a ). The corresponding fluctuation levels are small, of order $E_{1}\approx B_{1}\approx (RB)^{1/2}=10(a/L)^{1/2}B$ . Acting as an electron accelerator, $\unicode[STIX]{x0394}V_{kink}=0.01V$ accounts for all of the synchrotron radiation, showing that most of jet power survives to the nose, where cosmic rays are generated by DCLC acceleration.

By contrast, DCLC fluctuations, giving displacements of the order of the ion Larmor radius $r_{Li}$ , can become comparable to the flux width in the weak magnetic field in the nose.

7 Experiments and simulations to confirm DCLC acceleration

Particle acceleration by DCLC instability probably occurred in the SPHEX experiment cited above, missed in looking only for fluctuations at MHD frequencies (20 kHz while the ion cyclotron frequency was of order 1 MHz). How kink acceleration might cause DCLC instability in SPHEX can differ from jets. In the central column of astrophysical jets, one finds a ${\approx}10^{4}r_{Li}$ , whereas, at ion energies ${>}500~\text{eV}$ observed in SPHEX, the ion Larmor radius is already large, comparable to flux core dimensions. This opens the possibility that DCLC occurs inside the central column (flux core), where also the density is high enough for (5.2) to be satisfied. For the few milli-weber flux and central column radius of order 10 cm ${\approx}\unicode[STIX]{x1D6E5}$ in SPHEX (giving $B<1$  kG), and density $n<10^{14}~\text{cm}^{-3}$ , we estimate $\unicode[STIX]{x1D714}_{ci}/\unicode[STIX]{x1D714}_{pi}<10^{-3}$ . Hydrogen ions are observed at energies 500 eV or higher, giving $r_{Li}\approx 3$  cm, hence $a/r_{Li}<3$ so that (5.2) is well satisfied.

Indirect evidence of DCLC activity in SPHEX includes the observation that accelerated ions were roughly Maxwellian (Rusbridge et al. Reference Rusbridge, Gee, Browning Cunningham, Duck, Al-Kharky, Martin and Bradley1997), as is expected due to velocity space diffusion accompanying DCLC acceleration as discussed above. While two-stream instability was not important in SPHEX but resistivity was important, the fact that kink-mode acceleration did overcome resistance to produce a mono-energetic beam (like (4)) is suggested by evidence that at least 50 % of the current was carried by the ions. At $I=60~\text{kA}$ for this experiment, the minimum density of 500 eV ions required to carry the current is in fact comparable to the observed density ${\approx}10^{14}~\text{cm}^{-3}$ .

The formation stage of spheromak experiments replicates both the central column and its return path forming the nose in figure 1. Experiments could be designed either to produce DCLC and kinks simultaneously in the column, as in SPHEX, or to observe the two-stage acceleration process we predict for cosmic ray acceleration. By making the tank radius 10 times the column radius $a$ , the magnetic field in the nose could become 10 times smaller than that in the column and in the nose.

Equation (5.2) giving a threshold in Larmor radius relative to the flux width $\unicode[STIX]{x1D6E5}$ , applies both in the column and in the nose. In the central column, $\unicode[STIX]{x1D6E5}$ is in the $r$ direction. In the nose, $\unicode[STIX]{x1D6E5}$ is in the $z$ direction. Varying the gun voltage and magnetic field can either reproduce DCLC acceleration coincident with kink acceleration in the flux core, as we suspect was the case in SPHEX described above, or, by postponing DCLC to an advancing nose, to create the two-stage acceleration process of our cosmic ray model. Measurements of cyclotron activity would be the main new diagnostic. Similarly, purely MHD simulations must be replaced by Particle in Cell (PIC) simulations of ions and fluid electrons, as in the linear version of the gyrokinetic toroidal code (GTC) (Deng, Lin & Holod Reference Deng, Lin and Holod2012), cited in our paper II.

The boundary between the above two operating regimes is given by taking the equality in (5.2), with minimum $r_{L}=(v_{\bot }/\unicode[STIX]{x1D714}_{ci})$ for minimum $v_{\bot }$ (perpendicular to $\boldsymbol{B}$ ) given by balancing the magnetic force and centrifugal force, giving $v_{\bot }=c(v_{\Vert }/c)(r_{L}/R_{c})^{1/2}$ and from this $(r_{L}^{}/R_{c})=(v_{\Vert }/\unicode[STIX]{x1D714}_{ci}R_{c})^{2}$ where $R_{c}$ is the magnetic radius of curvature. For $R_{c}\approx \unicode[STIX]{x1D6E5}\approx a$ in the central column, (5.2) with the equality becomes:

Scaling from the SPHEX numbers above gives, with $v_{||}^{2}\propto V_{GUN}=500$  V:

For a fixed $V_{GUN}$ , $a$ and $n$ , adjusting $B$ in the gun to satisfy (7.2) gives $B=10~\text{kG}=1$  T. Other regimes can be found by varying $a$ , $n$ or $V_{GUN}$ . The accelerating voltage $V_{GUN}$ can be varied by including an external inductor to regulate current (as in SPHEX) or bypassing this inductor to utilize the full voltage of the capacitor bank (4 to 6 kV in SPHEX).