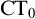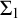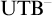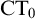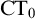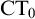1 Introduction
The Global Reflection Principle (GRP) for a theory
![]() $\mathrm {Th}$
is the assertion that all theorems of
$\mathrm {Th}$
is the assertion that all theorems of
![]() $\mathrm {Th}$
are true. As the statement involves the notion of truth for the language of
$\mathrm {Th}$
are true. As the statement involves the notion of truth for the language of
![]() $\mathrm {Th}$
, to uncover its meaning adequately one shall pass to a proper extension of
$\mathrm {Th}$
, to uncover its meaning adequately one shall pass to a proper extension of
![]() $\mathrm {Th}$
in a richer language. Minimal such extensions are called axiomatic theories of truth for
$\mathrm {Th}$
in a richer language. Minimal such extensions are called axiomatic theories of truth for
![]() $\mathrm {Th}$
. Each such theory arises by enriching the language of
$\mathrm {Th}$
. Each such theory arises by enriching the language of
![]() $\mathrm {Th}$
with a single fresh predicate
$\mathrm {Th}$
with a single fresh predicate
![]() $T(x)$
and adding a bunch of axioms characterizing
$T(x)$
and adding a bunch of axioms characterizing
![]() $T(x)$
as a truth predicate for the language of
$T(x)$
as a truth predicate for the language of
![]() $\mathrm {Th}$
. In the paper we focus on one of the most natural such extensions, which comprises straightforward formalizations of the usual inductive Tarski’s conditions in the language of
$\mathrm {Th}$
. In the paper we focus on one of the most natural such extensions, which comprises straightforward formalizations of the usual inductive Tarski’s conditions in the language of
![]() $\mathrm {Th}$
together with the predicate
$\mathrm {Th}$
together with the predicate
![]() $T(x)$
. Let us denote this theory with
$T(x)$
. Let us denote this theory with
![]() $\mathrm {CT}^-$
.Footnote
1
$\mathrm {CT}^-$
.Footnote
1
The GRP lies at the intersection of at least three, to some extent independent, areas of research. The first, which was the starting point for the current paper, is the Tarski Boundary project, that seeks to characterize the extensions of
![]() $\mathrm {CT}^-+\mathrm {Th}$
which are conservative over
$\mathrm {CT}^-+\mathrm {Th}$
which are conservative over
![]() $\mathrm {Th}$
. This is non-trivial for two reasons: on the one hand, if
$\mathrm {Th}$
. This is non-trivial for two reasons: on the one hand, if
![]() $\mathrm {Th}$
can develop enough coding apparatus,Footnote
2
$\mathrm {Th}$
can develop enough coding apparatus,Footnote
2
![]() $\mathrm {CT}^- + \mathrm {Th}$
does not prove any new sentences from the language of
$\mathrm {CT}^- + \mathrm {Th}$
does not prove any new sentences from the language of
![]() $\mathrm {Th}$
. On the other hand, it is an immediate consequence of second Gödels Incompleteness theorem, that
$\mathrm {Th}$
. On the other hand, it is an immediate consequence of second Gödels Incompleteness theorem, that
![]() $\mathrm {CT}^- +\mathrm {Th} +$
GRP is a nonconservative extension of
$\mathrm {CT}^- +\mathrm {Th} +$
GRP is a nonconservative extension of
![]() $\mathrm {Th}$
. Moreover, the “natural” extensions of
$\mathrm {Th}$
. Moreover, the “natural” extensions of
![]() $\mathrm {CT}^- +\mathrm {Th}$
that are nonconservative over
$\mathrm {CT}^- +\mathrm {Th}$
that are nonconservative over
![]() $\mathrm {Th}$
all prove GRP for
$\mathrm {Th}$
all prove GRP for
![]() $\mathrm {Th}$
. Hence, in a sense, GRP is the source of nonconservativity in the realm of truth theories and it seems highly desirable to know what are the minimal resources needed to prove it.
$\mathrm {Th}$
. Hence, in a sense, GRP is the source of nonconservativity in the realm of truth theories and it seems highly desirable to know what are the minimal resources needed to prove it.
The second area is proof theory, especially ordinal analysis as initiated in [Reference Schmerl21] and further developed, e.g., in [Reference Beklemishev and Pakhomov2]. In this approach natural truth-free counterparts of GRP, Uniform Reflection Principles (REF), play central roles in determining the quantitative information about the consequences of theories of predicative strength. To get things right, one adds stratified truth predicates to the picture and studies (partial) uniform reflection principles over axiomatic theories of truth (this is the method used in [Reference Beklemishev and Pakhomov2]). This is how the GRP enters the scene.
Last but not least, axiomatic theories of truth play an important role in the field of model theory of Peano Arithmetic (cf. [Reference Kaye12, Reference Kossak and Schmerl14]). Any subset
![]() $S\subseteq \mathcal {M}$
such that
$S\subseteq \mathcal {M}$
such that
![]() $(\mathcal {M},S)\models \mathrm {CT}^-$
is essentially a full satisfaction class. If
$(\mathcal {M},S)\models \mathrm {CT}^-$
is essentially a full satisfaction class. If
![]() $(\mathcal {M},S)$
additionally satisfies GRP, then S contains all the theorems of
$(\mathcal {M},S)$
additionally satisfies GRP, then S contains all the theorems of
![]() $\mathrm {Th}$
, in the sense of
$\mathrm {Th}$
, in the sense of
![]() $\mathcal {M}$
. Satisfaction classes provide a very powerful tool in constructing interesting models of
$\mathcal {M}$
. Satisfaction classes provide a very powerful tool in constructing interesting models of
![]() $\mathrm {PA}$
and investigating their structure.Footnote
3
$\mathrm {PA}$
and investigating their structure.Footnote
3
The current paper contributes to all the three areas. More specifically:
-
1. We prove that
 $\Delta _0$
-induction for the truth predicate is enough to prove GRP for
$\Delta _0$
-induction for the truth predicate is enough to prove GRP for
 $\mathrm {PA}$
. Coupled with the earlier results by Kotlarski [Reference Kotlarski15], this shows that, over
$\mathrm {PA}$
. Coupled with the earlier results by Kotlarski [Reference Kotlarski15], this shows that, over
 $\mathrm {CT}^- +\mathrm {EA}$
,
$\mathrm {CT}^- +\mathrm {EA}$
,
 $\Delta _0$
induction for the truth predicate is equivalent to GRP for
$\Delta _0$
induction for the truth predicate is equivalent to GRP for
 $\mathrm {PA}$
(we denote this theory with
$\mathrm {PA}$
(we denote this theory with
 $\mathrm {CT}_0$
). This improves on earlier results from [Reference Wcisło and Łełyk25] and provides a direct fix to Kotlarski’s argument in [Reference Kotlarski15].Footnote
4
Additionally, coupled with various developments from the literature, our result shows that the Global Reflection Principle for
$\mathrm {CT}_0$
). This improves on earlier results from [Reference Wcisło and Łełyk25] and provides a direct fix to Kotlarski’s argument in [Reference Kotlarski15].Footnote
4
Additionally, coupled with various developments from the literature, our result shows that the Global Reflection Principle for
 $\mathrm {PA}$
is a very robust notion, being equivalent to various others, apparently very different, truth-theoretic principles, as witnessed by the Many Faces Theorem (Corollary 3.18).
$\mathrm {PA}$
is a very robust notion, being equivalent to various others, apparently very different, truth-theoretic principles, as witnessed by the Many Faces Theorem (Corollary 3.18). -
2. We extend the above result, answering the open problem posed by Beklemishev and Pakhomov in [Reference Beklemishev and Pakhomov2]. We show that not only GRP is provable in
 $\mathrm {CT}_0$
but also
$\mathrm {CT}_0$
but also
 $\Sigma _1$
-Uniform Reflection over a weak truth extension of
$\Sigma _1$
-Uniform Reflection over a weak truth extension of
 $\mathrm {EA}$
, called
$\mathrm {EA}$
, called
 $\mathrm {UTB}^-+\mathrm {EA}$
(which adds to the arithmetical part uniquely Uniform Tarski Biconditionals). The result has some bearings on the analysis performed in [Reference Beklemishev and Pakhomov2].
$\mathrm {UTB}^-+\mathrm {EA}$
(which adds to the arithmetical part uniquely Uniform Tarski Biconditionals). The result has some bearings on the analysis performed in [Reference Beklemishev and Pakhomov2]. -
3. We provide a new conservativity proof for
 $\mathrm {CT}_0$
. Unlike in the first one from [Reference Kotlarski15] we are able to show directly that
$\mathrm {CT}_0$
. Unlike in the first one from [Reference Kotlarski15] we are able to show directly that
 $\mathrm {CT}_0$
is arithmetically conservative over
$\mathrm {CT}_0$
is arithmetically conservative over
 $\omega $
-iterations of uniform reflection over
$\omega $
-iterations of uniform reflection over
 $\mathrm {PA}$
(denote this theory with
$\mathrm {PA}$
(denote this theory with
 $\mathrm {REF}^{\omega }(\mathrm {PA})$
Footnote
5
). The proof is based on an essentially model-theoretic idea of prolonging a (partial) satisfaction class in an end-extension. This proves to be sufficiently robust to characterize finite iterations of Uniform Reflection. We show that a model
$\mathrm {REF}^{\omega }(\mathrm {PA})$
Footnote
5
). The proof is based on an essentially model-theoretic idea of prolonging a (partial) satisfaction class in an end-extension. This proves to be sufficiently robust to characterize finite iterations of Uniform Reflection. We show that a model
 $(\mathcal {M},S)$
, where S is a partial inductive satisfaction class, satisfies n iterations of uniform reflection if and only if a nonstandard restriction of S can be prolonged n times.
$(\mathcal {M},S)$
, where S is a partial inductive satisfaction class, satisfies n iterations of uniform reflection if and only if a nonstandard restriction of S can be prolonged n times.
The paper is organised as follows: in Section 2 we introduce all the relevant preliminaries and context. In particular we develop handy and uniform conventions regarding the definable models and satisfaction classes. Section 3 is devoted to the proof of GRP in
![]() $\mathrm {CT}_0$
. In particular we describe the history of the problem and comment on flaws in Kotlarski’s aforementioned proof [Reference Kotlarski15]. The proof is a streamlined version of the one presented by the author in [Reference Łełyk18]. In Section 4 we extend the result from the previous section answering the question of Beklemishev and Pakhomov in [Reference Beklemishev and Pakhomov2] in the positive: we give a proof of
$\mathrm {CT}_0$
. In particular we describe the history of the problem and comment on flaws in Kotlarski’s aforementioned proof [Reference Kotlarski15]. The proof is a streamlined version of the one presented by the author in [Reference Łełyk18]. In Section 4 we extend the result from the previous section answering the question of Beklemishev and Pakhomov in [Reference Beklemishev and Pakhomov2] in the positive: we give a proof of
![]() $\Sigma _1$
-uniform reflection over
$\Sigma _1$
-uniform reflection over
![]() $\mathrm {UTB}^-+\mathrm {EA}$
in
$\mathrm {UTB}^-+\mathrm {EA}$
in
![]() $\mathrm {CT}_0$
. The proof makes crucial use of the Arithmetized Completeness Theorem. Additionally, the section offers some strengthenings of this main result. In Section 5 we give a proof of the conservativity of
$\mathrm {CT}_0$
. The proof makes crucial use of the Arithmetized Completeness Theorem. Additionally, the section offers some strengthenings of this main result. In Section 5 we give a proof of the conservativity of
![]() $\mathrm {CT}_0$
over
$\mathrm {CT}_0$
over
![]() $\omega $
-iterations of uniform reflection over
$\omega $
-iterations of uniform reflection over
![]() $\mathrm {PA}$
. Extending the work of Kaye and Kotlarski [Reference Kaye and Kotlarski13] we characterize the theory of n-iterated uniform reflection over
$\mathrm {PA}$
. Extending the work of Kaye and Kotlarski [Reference Kaye and Kotlarski13] we characterize the theory of n-iterated uniform reflection over
![]() $\mathrm {PA}$
in terms of models of the form
$\mathrm {PA}$
in terms of models of the form
![]() $(\mathcal {M},S)$
where S is a partial inductive satisfaction class. Finally we examine the structure of models of
$(\mathcal {M},S)$
where S is a partial inductive satisfaction class. Finally we examine the structure of models of
![]() $\mathrm {CT}_0$
and prove a variation of the main result of Section 4.
$\mathrm {CT}_0$
and prove a variation of the main result of Section 4.
To enhance the reading,
![]() $\square $
(as usual) denotes the end of a proof, while
$\square $
(as usual) denotes the end of a proof, while
![]() $\boxplus $
means that the proof is omitted.
$\boxplus $
means that the proof is omitted.
![]() $\triangle $
signalizes the end of a definition, remark, convention, etc.
$\triangle $
signalizes the end of a definition, remark, convention, etc.
2 Setting the stage
In this section we gather all the technical preliminaries needed to follow our reasoning and at the same time develop a useful framework for proving our main results. In particular most of the results contained herein can be found (sometimes under slightly different wording) in [Reference Hájek and Pudlák9, Reference Kaye12].
For starters,
![]() $\mathrm {PA}$
denotes Peano Arithmetic and
$\mathrm {PA}$
denotes Peano Arithmetic and
![]() $\mathcal {L}$
denotes its language, which we stipulate to contain
$\mathcal {L}$
denotes its language, which we stipulate to contain
![]() $+, \times , 0,1, \leq $
as primitive symbols. While studying extensions of
$+, \times , 0,1, \leq $
as primitive symbols. While studying extensions of
![]() $\mathrm {PA}$
in a richer language, we use a handy convention known from [Reference Kossak and Schmerl14]:
$\mathrm {PA}$
in a richer language, we use a handy convention known from [Reference Kossak and Schmerl14]:
![]() $\mathrm {PA}^*$
denotes any theory in the extended language that admits all instantiations of the induction scheme for the extended language. Similarly,
$\mathrm {PA}^*$
denotes any theory in the extended language that admits all instantiations of the induction scheme for the extended language. Similarly,
![]() $I\Sigma _n^*$
denotes the extension of
$I\Sigma _n^*$
denotes the extension of
![]() $\mathrm {PA}$
with induction for
$\mathrm {PA}$
with induction for
![]() $\Sigma _n$
formulae of the extended language. If
$\Sigma _n$
formulae of the extended language. If
![]() $\mathcal {L}'$
is any language then,
$\mathcal {L}'$
is any language then,
![]() $\mathcal {L}^{\prime }_S$
and
$\mathcal {L}^{\prime }_S$
and
![]() $\mathcal {L}^{\prime }_T$
denote the result of extending
$\mathcal {L}^{\prime }_T$
denote the result of extending
![]() $\mathcal {L}'$
with a single binary predicate S or a single unary predicate T, respectively. Most of the extensions of
$\mathcal {L}'$
with a single binary predicate S or a single unary predicate T, respectively. Most of the extensions of
![]() $\mathrm {PA}$
that we study are formulated either in the language
$\mathrm {PA}$
that we study are formulated either in the language
![]() $\mathcal {L}_S$
or
$\mathcal {L}_S$
or
![]() $\mathcal {L}_T$
. Last but not least,
$\mathcal {L}_T$
. Last but not least,
![]() $\mathrm {EA}$
denotes elementary arithmetic, i.e., the extension of
$\mathrm {EA}$
denotes elementary arithmetic, i.e., the extension of
![]() $I\Delta _0$
with a single
$I\Delta _0$
with a single
![]() $\Pi _2$
assertion “
$\Pi _2$
assertion “
![]() $\exp $
is total.” All the theories we study extend
$\exp $
is total.” All the theories we study extend
![]() $\mathrm {EA}$
, possibly in a richer language.
$\mathrm {EA}$
, possibly in a richer language.
![]() $\Delta _0(\exp )$
denote the class of bounded formulae in the language with a symbol for the exponential function
$\Delta _0(\exp )$
denote the class of bounded formulae in the language with a symbol for the exponential function
![]() $\exp $
: it will be used throughout the paper because various syntactical functions needed to state the axioms for the satisfaction predicate are in fact
$\exp $
: it will be used throughout the paper because various syntactical functions needed to state the axioms for the satisfaction predicate are in fact
![]() $\Delta _0(\exp )$
. However, since most of the theories we consider are extensions of
$\Delta _0(\exp )$
. However, since most of the theories we consider are extensions of
![]() $\mathrm {PA}$
, the presence of
$\mathrm {PA}$
, the presence of
![]() $\exp $
as a primitive symbol do not increase their strength. We explain this in more detail in Section 3.
$\exp $
as a primitive symbol do not increase their strength. We explain this in more detail in Section 3.
To smoothly deal with class sized-objects (such as definable models of arithmetical theories) various definitions will be stated in the canonical predicative two-sorted extension of
![]() $\mathrm {PA}$
, i.e.,
$\mathrm {PA}$
, i.e.,
![]() $\mathrm {ACA}_0$
. Uppercase letters
$\mathrm {ACA}_0$
. Uppercase letters
![]() $X,Y,Z$
,
$X,Y,Z$
,
![]() $X_1,Y_1, Z_1,\ldots $
denote second-order variables. In all applications we shall reason about definable classes (perhaps in a richer language) which will be substituted for the free second-order variables. The two sorted language is denoted
$X_1,Y_1, Z_1,\ldots $
denote second-order variables. In all applications we shall reason about definable classes (perhaps in a richer language) which will be substituted for the free second-order variables. The two sorted language is denoted
![]() $\mathcal {L}_{2}$
.
$\mathcal {L}_{2}$
.
2.1 Coding conventions
We assume a standard coding of syntax in
![]() $\mathrm {PA}$
(defined as in [Reference Hájek and Pudlák9]): primitive symbols of the language are assigned numbers in a recursive way, and then terms, formulae, sentences, etc. are treated as well-formed sequences of such numbers. The notion of sequence is based on the definable Ackermanian membership predicate
$\mathrm {PA}$
(defined as in [Reference Hájek and Pudlák9]): primitive symbols of the language are assigned numbers in a recursive way, and then terms, formulae, sentences, etc. are treated as well-formed sequences of such numbers. The notion of sequence is based on the definable Ackermanian membership predicate
![]() $\in $
.
$\in $
.
![]() $\mathrm {Term}(x)$
,
$\mathrm {Term}(x)$
,
![]() $\mathrm {ClTerm}(x)$
,
$\mathrm {ClTerm}(x)$
,
![]() $\mathrm {Var}(x)$
,
$\mathrm {Var}(x)$
,
![]() $\mathrm {Form}(x)$
, and
$\mathrm {Form}(x)$
, and
![]() $\mathrm {Sent}(x)$
denote the arithmetical formulae expressing that x is an arithmetical term, a closed term, a variable, an arithmetical formula, and an arithmetical sentence, respectively.
$\mathrm {Sent}(x)$
denote the arithmetical formulae expressing that x is an arithmetical term, a closed term, a variable, an arithmetical formula, and an arithmetical sentence, respectively.
![]() $x \in \mathrm {Subf}(y)$
expresses that x is a subformula of y. We define
$x \in \mathrm {Subf}(y)$
expresses that x is a subformula of y. We define
![]() $x\in \mathrm {Term}(y)$
and
$x\in \mathrm {Term}(y)$
and
![]() $x\in \mathrm {ClTerm}(y)$
analogously (y is required to be either a formula or a term).
$x\in \mathrm {ClTerm}(y)$
analogously (y is required to be either a formula or a term).
![]() $x\in \mathrm {FV}(y)$
expresses that x is a variable which has a free occurrence in (a formula) y.
$x\in \mathrm {FV}(y)$
expresses that x is a variable which has a free occurrence in (a formula) y.
The choice of coding apparatus is irrelevant as long as the coding is
![]() $\mathrm {PA}$
provably monotone, i.e., the following is provable in
$\mathrm {PA}$
provably monotone, i.e., the following is provable in
![]() $\mathrm {PA}$
:
$\mathrm {PA}$
:
We require a similar condition for (the given formalisation) of
![]() $x\in \mathrm {Term}(y)$
. Various codings which violate this condition are studied in [Reference Grabmayr8, Reference Halbach and Visser11].
$x\in \mathrm {Term}(y)$
. Various codings which violate this condition are studied in [Reference Grabmayr8, Reference Halbach and Visser11].
Throughout the paper we distinguish between variables of the metalanguage, for which we reserve the symbols
![]() $x,y,z, x_0, x_1,\ldots , y_0, y_1,\ldots ,$
and variables of the arithmetized language, which are denoted
$x,y,z, x_0, x_1,\ldots , y_0, y_1,\ldots ,$
and variables of the arithmetized language, which are denoted
![]() $v, v_0, v_1,\ldots $
. We assume a fixed correspondence between the first and the second ones.
$v, v_0, v_1,\ldots $
. We assume a fixed correspondence between the first and the second ones.
![]() $\bar {x}$
,
$\bar {x}$
,
![]() $\bar {v}$
,
$\bar {v}$
,
![]() $\ldots $
denote sequences of variables. For a formula
$\ldots $
denote sequences of variables. For a formula
![]() $\phi $
,
$\phi $
,
![]() $\ulcorner \phi \urcorner $
denotes its Gödel code.
$\ulcorner \phi \urcorner $
denotes its Gödel code.
2.2 Some model theory of
 $\mathrm {PA}$
$\mathrm {PA}$
All the definitions and conventions regarding models of
![]() $\mathrm {PA}$
are as in [Reference Kaye12]. By default
$\mathrm {PA}$
are as in [Reference Kaye12]. By default
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
![]() $\mathcal {K}$
(possibly with indices) range over nonstandard models of
$\mathcal {K}$
(possibly with indices) range over nonstandard models of
![]() $\mathrm {PA}$
and M, N, K denote their respective universes. If
$\mathrm {PA}$
and M, N, K denote their respective universes. If
![]() $\mathcal {M}$
is any model (possibly for
$\mathcal {M}$
is any model (possibly for
![]() $\mathcal {L}_S$
) and
$\mathcal {L}_S$
) and
![]() $\phi (\bar {x})$
a formula (possibly with parameters from
$\phi (\bar {x})$
a formula (possibly with parameters from
![]() $\mathcal {M}$
;
$\mathcal {M}$
;
![]() $\bar {x}$
denotes a sequence of variables), then
$\bar {x}$
denotes a sequence of variables), then
![]() $\phi ^{\mathcal {M}}$
denotes the set definable by
$\phi ^{\mathcal {M}}$
denotes the set definable by
![]() $\phi $
in
$\phi $
in
![]() $\mathcal {M}$
, i.e.,
$\mathcal {M}$
, i.e.,
![]() $\{\bar {a}\in M \ \ | \ \ \mathcal {M}\models \phi (\bar {a}) \}$
. If
$\{\bar {a}\in M \ \ | \ \ \mathcal {M}\models \phi (\bar {a}) \}$
. If
![]() $\mathcal {M}\models \mathrm {PA}$
and
$\mathcal {M}\models \mathrm {PA}$
and
![]() $X\subseteq M^n$
, then
$X\subseteq M^n$
, then
![]() $X{\upharpoonright _{<b}}$
denotes the restriction of X to all elements smaller than b. In the case when
$X{\upharpoonright _{<b}}$
denotes the restriction of X to all elements smaller than b. In the case when
![]() $\mathcal {N}\subseteq \mathcal {M}$
,
$\mathcal {N}\subseteq \mathcal {M}$
,
![]() $X{\upharpoonright _{\mathcal {N}}}$
denotes
$X{\upharpoonright _{\mathcal {N}}}$
denotes
![]() $\bigcup _{b\in N} X{\upharpoonright _{<b}}$
(the restriction of a relation to the submodel).
$\bigcup _{b\in N} X{\upharpoonright _{<b}}$
(the restriction of a relation to the submodel).
Let
![]() $I\subseteq M$
. We write
$I\subseteq M$
. We write
![]() $d> I$
if d is greater than all the elements of I. I is called an initial segment of
$d> I$
if d is greater than all the elements of I. I is called an initial segment of
![]() $\mathcal {M}$
if I is closed downwards with respect to
$\mathcal {M}$
if I is closed downwards with respect to
![]() $\leq $
. We say that I is a cut if I is an initial segment which is closed under successor, i.e.,
$\leq $
. We say that I is a cut if I is an initial segment which is closed under successor, i.e.,
If I is a cut of
![]() $\mathcal {M}$
, then we call
$\mathcal {M}$
, then we call
![]() $\mathcal {M}$
an end-extension of I and write
$\mathcal {M}$
an end-extension of I and write
![]() $I\subseteq _e \mathcal {M}$
(note that I need not be a submodel of
$I\subseteq _e \mathcal {M}$
(note that I need not be a submodel of
![]() $\mathcal {M}$
). Any element
$\mathcal {M}$
). Any element
![]() $c\in M$
such that
$c\in M$
such that
![]() $c>\omega $
is called nonstandard.
$c>\omega $
is called nonstandard.
The following is one of the most basic consequences of induction in models of
![]() $\mathrm {PA}^*$
:
$\mathrm {PA}^*$
:
Lemma 2.1 (Overspill)
If
![]() $\mathcal {M}\models \mathrm {PA}^*$
, then no nontrivial cut of
$\mathcal {M}\models \mathrm {PA}^*$
, then no nontrivial cut of
![]() $\mathcal {M}$
is definable.
$\mathcal {M}$
is definable.
![]() $\boxplus $
$\boxplus $
In particular, if
![]() $\emptyset \subsetneq I\subsetneq _e M$
is a cut and
$\emptyset \subsetneq I\subsetneq _e M$
is a cut and
![]() $\phi (x)$
is any formula such that
$\phi (x)$
is any formula such that
then there exists a
![]() $d>I$
such that
$d>I$
such that
![]() $\mathcal {M}\models \phi (d)$
.
$\mathcal {M}\models \phi (d)$
.
One last notion which is very tightly linked to the topic of satisfaction classes is recursive saturation:
Definition 2.2. Fix
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\bar {a}\in M$
. Let
$\bar {a}\in M$
. Let
![]() $p(x)$
be a set of formulae with at most one variable x and parameters
$p(x)$
be a set of formulae with at most one variable x and parameters
![]() $\bar {a}$
. We say that
$\bar {a}$
. We say that
![]() $p(x)$
is recursive (or computable) if so is the set
$p(x)$
is recursive (or computable) if so is the set
We say that
![]() $p(x)$
is a type over
$p(x)$
is a type over
![]() $\mathcal {M}$
if every finite subset of
$\mathcal {M}$
if every finite subset of
![]() $p(x)$
is satisfied in
$p(x)$
is satisfied in
![]() $\mathcal {M}$
. We say that
$\mathcal {M}$
. We say that
![]() $\mathcal {M}$
is realized if there is a
$\mathcal {M}$
is realized if there is a
![]() $b\in M$
such that for every
$b\in M$
such that for every
![]() $\phi (x)\in p(x)$
,
$\phi (x)\in p(x)$
,
![]() $\mathcal {M}\models \phi (b)$
. We say that
$\mathcal {M}\models \phi (b)$
. We say that
![]() $\mathcal {M}$
is recursively saturated (or computably saturated) if every recursive type over
$\mathcal {M}$
is recursively saturated (or computably saturated) if every recursive type over
![]() $\mathcal {M}$
is realized in
$\mathcal {M}$
is realized in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
![]() $\triangle $
$\triangle $
2.3 Some model theory in
 $\mathrm {PA}$
$\mathrm {PA}$
Models of theories extending Robinson’s arithmetic are infinite objects; thus inside arithmetic they become essentially second-order objects. In what follows a set means a second-order object and we distinguish it from a coded set (a first-order object). The notion of a
![]() $\Delta _n$
set is explained below.
$\Delta _n$
set is explained below.
![]() $x\in X$
should be understood as a membership relation between a first- and a second-order object, whereas
$x\in X$
should be understood as a membership relation between a first- and a second-order object, whereas
![]() $x\in y$
denotes the Ackermanian membership (mentioned earlier) between first-order objects.
$x\in y$
denotes the Ackermanian membership (mentioned earlier) between first-order objects.
We recall the notion of a
![]() $\Delta _n$
-set (see [Reference Hájek and Pudlák9]):
$\Delta _n$
-set (see [Reference Hájek and Pudlák9]):
![]() $\mathrm {Sat}_{\Sigma _n}(x,y) (\mathrm {Sat}_{\Pi _n}(x,y)$
) denotes the arithmetically definable partial satisfaction predicate for
$\mathrm {Sat}_{\Sigma _n}(x,y) (\mathrm {Sat}_{\Pi _n}(x,y)$
) denotes the arithmetically definable partial satisfaction predicate for
![]() $\Sigma _n$
(
$\Sigma _n$
(
![]() $\Pi _n$
respectively) formulae (as in [Reference Kaye12] or [Reference Hájek and Pudlák9]) and
$\Pi _n$
respectively) formulae (as in [Reference Kaye12] or [Reference Hájek and Pudlák9]) and
![]() $\mathrm {Tr}_{\Sigma _n}(x) (\mathrm {Tr}_{\Pi _n}(x))$
abbreviates
$\mathrm {Tr}_{\Sigma _n}(x) (\mathrm {Tr}_{\Pi _n}(x))$
abbreviates
![]() $\mathrm {Sat}_{\Sigma _n}(x,\varepsilon )$
(
$\mathrm {Sat}_{\Sigma _n}(x,\varepsilon )$
(
![]() $\mathrm {Sat}_{\Pi _n}(x,\varepsilon )$
). We stress that the construction of
$\mathrm {Sat}_{\Pi _n}(x,\varepsilon )$
). We stress that the construction of
![]() $\mathrm {Sat}_{\Sigma _n} (\mathrm {Sat}_{\Pi _n})$
is elementary in n, so it gives rise to an
$\mathrm {Sat}_{\Sigma _n} (\mathrm {Sat}_{\Pi _n})$
is elementary in n, so it gives rise to an
![]() $\mathrm {EA}$
-provably total
$\mathrm {EA}$
-provably total
![]() $\Delta _1$
map sending n to (the formula)
$\Delta _1$
map sending n to (the formula)
![]() $\mathrm {Sat}_{\Sigma _n}$
.
$\mathrm {Sat}_{\Sigma _n}$
.
In
![]() $\mathrm {PA}$
, a
$\mathrm {PA}$
, a
![]() $\Sigma _n$
set (
$\Sigma _n$
set (
![]() $\Pi _n$
set) is any
$\Pi _n$
set) is any
![]() $\Sigma _n (\Pi _n)$
formula
$\Sigma _n (\Pi _n)$
formula
![]() $\phi (v)$
with precisely one free variable. We define a
$\phi (v)$
with precisely one free variable. We define a
![]() $\Delta _n$
set to be a pair of formulae
$\Delta _n$
set to be a pair of formulae
![]() $(\phi ,\psi )$
such that
$(\phi ,\psi )$
such that
![]() $\phi $
is
$\phi $
is
![]() $\Sigma _n$
,
$\Sigma _n$
,
![]() $\psi $
is
$\psi $
is
![]() $\Pi _n$
, and
$\Pi _n$
, and
The notions of a
![]() $\Sigma _n (\Pi _n, \Delta _n)$
relation is defined analogously. If X is a
$\Sigma _n (\Pi _n, \Delta _n)$
relation is defined analogously. If X is a
![]() $\Delta _k$
set given by the
$\Delta _k$
set given by the
![]() $\Sigma _k$
formula
$\Sigma _k$
formula
![]() $\phi (v)$
and a
$\phi (v)$
and a
![]() $\Pi _k$
formula
$\Pi _k$
formula
![]() $\psi (v)$
, then
$\psi (v)$
, then
![]() $x\in _k X$
abbreviates
$x\in _k X$
abbreviates
![]() $\mathrm {Sat}_{\Sigma _k}(\phi , x)$
. Note that
$\mathrm {Sat}_{\Sigma _k}(\phi , x)$
. Note that
![]() $x\in _k X$
is
$x\in _k X$
is
![]() $\Delta _k$
.
$\Delta _k$
.
Observe that a set
![]() $A\subseteq M$
is definable from parameters in a model
$A\subseteq M$
is definable from parameters in a model
![]() $\mathcal {M}$
if and only if, for some
$\mathcal {M}$
if and only if, for some
![]() $k\in \omega $
, there exists a
$k\in \omega $
, there exists a
![]() $\Delta _k$
set X such that
$\Delta _k$
set X such that
In the paper, except for side remarks, in which case the definitions below can clearly be adapted, we will only need to talk about models for very specific signatures consisting of two binary functions
![]() $+$
,
$+$
,
![]() $\times $
, one binary relational symbol
$\times $
, one binary relational symbol
![]() $S(x,y)$
, reserved for a satisfaction class and two constants,
$S(x,y)$
, reserved for a satisfaction class and two constants,
![]() $0$
and
$0$
and
![]() $1$
.
$1$
.
We note that since in
![]() $\mathrm {PA}$
models for theories extending some basic arithmetic (which we are uniquely interested in) are class-size objects, we do not always have a satisfaction relation for them. Models without the satisfaction relation will called partial to contrast them with the full ones for which the truth of an arbitrary sentence can be decided.
$\mathrm {PA}$
models for theories extending some basic arithmetic (which we are uniquely interested in) are class-size objects, we do not always have a satisfaction relation for them. Models without the satisfaction relation will called partial to contrast them with the full ones for which the truth of an arbitrary sentence can be decided.
Definition 2.3 (
 $\mathrm {ACA}_0$
; partial model)
$\mathrm {ACA}_0$
; partial model)
We say that
![]() $\mathbf {M} = (U_{\mathbf {M}},+_{\mathbf {M}},\times _{\mathbf {M}}, S_{\mathbf {M}}, 0_{\mathbf {M}}, 1_{\mathbf {M}})$
is a partial model if:
$\mathbf {M} = (U_{\mathbf {M}},+_{\mathbf {M}},\times _{\mathbf {M}}, S_{\mathbf {M}}, 0_{\mathbf {M}}, 1_{\mathbf {M}})$
is a partial model if:
-
1.
 $U_{\mathbf {M}}$
,
$U_{\mathbf {M}}$
,
 $S_{\mathbf {M}}$
are sets and
$S_{\mathbf {M}}$
are sets and
 $S_{\mathbf {M}}\subseteq U_{\mathbf {M}}^2$
,
$S_{\mathbf {M}}\subseteq U_{\mathbf {M}}^2$
, -
2.
 $+_{\mathbf {M}},\times _{\mathbf {M}}$
are functions of type
$+_{\mathbf {M}},\times _{\mathbf {M}}$
are functions of type
 $U_{\mathbf {M}}^2\rightarrow U_{\mathbf {M}}$
,
$U_{\mathbf {M}}^2\rightarrow U_{\mathbf {M}}$
, -
3.
 $0_{\mathbf {M}}\in M$
,
$0_{\mathbf {M}}\in M$
,
 $1_{\mathbf {M}}\in M$
.
$1_{\mathbf {M}}\in M$
.
We say that
![]() $\mathbf {M}$
is a
$\mathbf {M}$
is a
![]() $\Delta _n$
-model if it is a
$\Delta _n$
-model if it is a
![]() $\Delta _n$
set satisfying the above conditions.
$\Delta _n$
set satisfying the above conditions.
![]() $\triangle $
$\triangle $
Definition 2.4. If
![]() $\mathcal {N}$
is any model of
$\mathcal {N}$
is any model of
![]() $\mathrm {PA}$
then we say that
$\mathrm {PA}$
then we say that
![]() $\mathbf {M}$
is a partial
$\mathbf {M}$
is a partial
![]() $\mathcal {N}$
-definable model if for some
$\mathcal {N}$
-definable model if for some
![]() $k\in \omega $
,
$k\in \omega $
,
![]() $\triangle $
$\triangle $
Note that, according to our convention, “
![]() $\mathcal {N}$
-definable
$\mathcal {N}$
-definable
![]() $” $
means
$” $
means
![]() $“\mathcal {N}$
-definable with parameters
$“\mathcal {N}$
-definable with parameters
![]() $.”$
$.”$
Example 2.5 (
 $\mathrm {ACA}_0$
)
$\mathrm {ACA}_0$
)
For every set S,
![]() $\langle v=v, v_1+v_2 = v_3, v_1\cdot v_2 = v_3, S, 0, 1 \rangle $
is a partial model. We denote it with
$\langle v=v, v_1+v_2 = v_3, v_1\cdot v_2 = v_3, S, 0, 1 \rangle $
is a partial model. We denote it with
![]() $\mathbf {V}[S]$
.
$\mathbf {V}[S]$
.
![]() $v=v, v_1+v_2 = v_3,$
and
$v=v, v_1+v_2 = v_3,$
and
![]() $ v_1\cdot v_2 = v_3$
denote sets definable with respective formulae.
$ v_1\cdot v_2 = v_3$
denote sets definable with respective formulae.
![]() $\mathbf {V}$
denotes
$\mathbf {V}$
denotes
![]() $\mathbf {V}[\emptyset ]$
.
$\mathbf {V}[\emptyset ]$
.
![]() $\triangle $
$\triangle $
Remark 2.6. If
![]() $\mathcal {N}\models \mathrm {PA}$
and
$\mathcal {N}\models \mathrm {PA}$
and
![]() $\mathbf {M} = (U_{\mathbf {M}},+_{\mathbf {M}},\times _{\mathbf {M}}, S_{\mathbf {M}}, 0_{\mathbf {M}}, 1_{\mathbf {M}})$
is a partial
$\mathbf {M} = (U_{\mathbf {M}},+_{\mathbf {M}},\times _{\mathbf {M}}, S_{\mathbf {M}}, 0_{\mathbf {M}}, 1_{\mathbf {M}})$
is a partial
![]() $\mathcal {N}$
-definable model, then, outside of
$\mathcal {N}$
-definable model, then, outside of
![]() $\mathcal {N}$
, it gives rise to a model for the signature
$\mathcal {N}$
, it gives rise to a model for the signature
![]() $\{+,\times , S, 0,1\}$
. Indeed, we may define model
$\{+,\times , S, 0,1\}$
. Indeed, we may define model
![]() $\mathcal {M}$
by putting
$\mathcal {M}$
by putting
Such a model will be denoted by
![]() $(\mathbf {M})^{\mathcal {N}}$
.
$(\mathbf {M})^{\mathcal {N}}$
.
![]() $\triangle $
$\triangle $
Definition 2.7.
-
1. For a natural number n,
 $\underline {n}$
denotes the canonical numeral naming n, i.e.,
$\underline {n}$
denotes the canonical numeral naming n, i.e.,  $$\begin{align*}\underbrace{1+(1+\cdots + (1+0)\ldots)}_{n\ \mathrm{ times }\ 1}.\end{align*}$$
$$\begin{align*}\underbrace{1+(1+\cdots + (1+0)\ldots)}_{n\ \mathrm{ times }\ 1}.\end{align*}$$
 $y = \underline {x}$
denotes the formalisation of this relation in
$y = \underline {x}$
denotes the formalisation of this relation in
 $\mathrm {PA}$
. We shall often treat
$\mathrm {PA}$
. We shall often treat
 $\underline {x}$
as a term symbol depending on variable x.
$\underline {x}$
as a term symbol depending on variable x.
-
2. (
 $\mathrm {ACA}_0$
) An assignment is any function with domain
$\mathrm {ACA}_0$
) An assignment is any function with domain
 $\mathrm {dom}(f)\subseteq \mathrm {Var}$
. For a partial model
$\mathrm {dom}(f)\subseteq \mathrm {Var}$
. For a partial model
 $\mathbf {M}$
,
$\mathbf {M}$
,
 $\alpha $
is an
$\alpha $
is an
 $\mathbf {M}$
-assignment if its range is contained in
$\mathbf {M}$
-assignment if its range is contained in
 $U_{\mathbf {M}}$
. We denote it with
$U_{\mathbf {M}}$
. We denote it with
 $\alpha \in \mathrm {Asn}(\mathbf {M})$
.
$\alpha \in \mathrm {Asn}(\mathbf {M})$
.
 $\alpha $
is an
$\alpha $
is an
 $\mathbf {M}$
-assignment for
$\mathbf {M}$
-assignment for
 $\phi $
, symbolically
$\phi $
, symbolically
 $\alpha \in \mathrm {Asn}(\phi , \mathbf {M})$
, if
$\alpha \in \mathrm {Asn}(\phi , \mathbf {M})$
, if
 $\alpha $
is an
$\alpha $
is an
 $\mathbf {M}$
-assignment and
$\mathbf {M}$
-assignment and
 $\mathrm {FV}(\phi )= \mathrm {dom}(\alpha )$
. We naturally extend this definition to coded sequences of terms and formulae: if s is such a sequence, then
$\mathrm {FV}(\phi )= \mathrm {dom}(\alpha )$
. We naturally extend this definition to coded sequences of terms and formulae: if s is such a sequence, then  $$\begin{align*}\alpha \in \mathrm{Asn}(s,\mathbf{M}) := \forall i \in\mathrm{dom}(s)\ \ \alpha \in \mathrm{Asn}(s_i,\mathbf{M}).\end{align*}$$
$$\begin{align*}\alpha \in \mathrm{Asn}(s,\mathbf{M}) := \forall i \in\mathrm{dom}(s)\ \ \alpha \in \mathrm{Asn}(s_i,\mathbf{M}).\end{align*}$$
 $\alpha \in \mathrm {Asn}(s)$
has an analogous meaning.
$\alpha \in \mathrm {Asn}(s)$
has an analogous meaning.
-
3. (
 $\mathrm {ACA}_0$
) If
$\mathrm {ACA}_0$
) If
 $\alpha $
is any assignment and
$\alpha $
is any assignment and
 $\phi $
a formula, then by
$\phi $
a formula, then by
 $\phi [\alpha ]$
we denote the result of the simultaneous substitution of
$\phi [\alpha ]$
we denote the result of the simultaneous substitution of
 $\underline {\alpha (v)}$
for every free occurrence of v, for every
$\underline {\alpha (v)}$
for every free occurrence of v, for every
 $v\in \mathrm {FV}(\phi )\cap \mathrm {dom}(\alpha )$
.
$v\in \mathrm {FV}(\phi )\cap \mathrm {dom}(\alpha )$
.
 $t[\alpha ]$
for a term t is defined analogously. If we are interested in a single substitution in a formula
$t[\alpha ]$
for a term t is defined analogously. If we are interested in a single substitution in a formula
 $\phi $
, then we write
$\phi $
, then we write
 $\phi [x/v]$
, or
$\phi [x/v]$
, or
 $\phi [x]$
if v is clear from context, to mean
$\phi [x]$
if v is clear from context, to mean
 $\phi [\alpha ]$
where
$\phi [\alpha ]$
where
 $\alpha $
is an assignment such that
$\alpha $
is an assignment such that
 $\mathrm {dom}(\alpha ) = \{v\}$
and
$\mathrm {dom}(\alpha ) = \{v\}$
and
 $\alpha (v) = x$
. Abusing the notation a little bit, for a term t,
$\alpha (v) = x$
. Abusing the notation a little bit, for a term t,
 $\phi [t/v]$
denotes the result of substituting t for every free occurrence of v.
$\phi [t/v]$
denotes the result of substituting t for every free occurrence of v.Example 2.8 (
 $\mathrm {PA}$
)
$\mathrm {PA}$
)If
 $\phi = \big ((v_0 + v_1 = v_2) \wedge (\exists v_2\ \ v_2 = v_2)\big )$
and
$\phi = \big ((v_0 + v_1 = v_2) \wedge (\exists v_2\ \ v_2 = v_2)\big )$
and
 $\alpha (v_0) = 2$
,
$\alpha (v_0) = 2$
,
 $\alpha (v_2) = 3$
, then
$\alpha (v_2) = 3$
, then  $$\begin{align*}\phi[\alpha] = \big(((1+1+0) + x_1 = (1+1+1+0)) \wedge (\exists v_2\ \ v_2 = v_2)\big).\end{align*}$$
$$\begin{align*}\phi[\alpha] = \big(((1+1+0) + x_1 = (1+1+1+0)) \wedge (\exists v_2\ \ v_2 = v_2)\big).\end{align*}$$
Note that this is the same as
 $\big ((\underline {2} + x_1 = \underline {3}) \wedge (\exists v_2\ \ v_2 = v_2)\big )$
. We shall use both formats.
$\big ((\underline {2} + x_1 = \underline {3}) \wedge (\exists v_2\ \ v_2 = v_2)\big )$
. We shall use both formats.
 $\triangle $
$\triangle $
-
4. (
 $\mathrm {ACA}_0$
) If
$\mathrm {ACA}_0$
) If
 $\alpha $
is any X-assignment, then
$\alpha $
is any X-assignment, then
 $\alpha {{\upharpoonright _{\phi }}}$
abbreviates
$\alpha {{\upharpoonright _{\phi }}}$
abbreviates
 $\alpha {{\upharpoonright _{\mathrm {FV}(\phi )}}}$
, where
$\alpha {{\upharpoonright _{\mathrm {FV}(\phi )}}}$
, where
 $f{\upharpoonright _A}$
denotes the restriction of a function f to a set A. If
$f{\upharpoonright _A}$
denotes the restriction of a function f to a set A. If
 $\phi $
is clear from context, we will write
$\phi $
is clear from context, we will write
 $\alpha {\upharpoonright _{\cdot }}$
instead of
$\alpha {\upharpoonright _{\cdot }}$
instead of
 $\alpha {\upharpoonright _{\phi }}$
.
$\alpha {\upharpoonright _{\phi }}$
. -
5. (
 $\mathrm {ACA}_0$
) If t is a term and
$\mathrm {ACA}_0$
) If t is a term and
 $\alpha \in \mathrm {Asn}(t)$
, then
$\alpha \in \mathrm {Asn}(t)$
, then
 $t^{\alpha }$
denotes the value of t under
$t^{\alpha }$
denotes the value of t under
 $\alpha $
. It is the same as the value of
$\alpha $
. It is the same as the value of
 $t[\alpha ]$
(
$t[\alpha ]$
(
 $t[\alpha ]$
is a closed term).
$t[\alpha ]$
is a closed term). -
6.
 $(\mathrm {PA})$
If
$(\mathrm {PA})$
If
 $\alpha $
and
$\alpha $
and
 $\beta $
are any two assignments and v is a variable, then
$\beta $
are any two assignments and v is a variable, then
 ${\alpha \leq _v\beta}$
expresses that
${\alpha \leq _v\beta}$
expresses that
 $\beta $
extends
$\beta $
extends
 $\alpha $
by assigning something to the variable v, i.e.,
$\alpha $
by assigning something to the variable v, i.e.,
 $\mathrm {dom}(\beta )=\mathrm {dom}(\alpha )\cup \{v\}$
and for all
$\mathrm {dom}(\beta )=\mathrm {dom}(\alpha )\cup \{v\}$
and for all
 $w\in \mathrm {dom}(\alpha )$
,
$w\in \mathrm {dom}(\alpha )$
,
 $\alpha (w) = \beta (w)$
. Note that if
$\alpha (w) = \beta (w)$
. Note that if
 $\alpha \leq _v \beta $
and
$\alpha \leq _v \beta $
and
 $v\in \mathrm {dom}(\alpha )$
, then
$v\in \mathrm {dom}(\alpha )$
, then
 $\alpha = \beta $
.
$\alpha = \beta $
. -
7. (
 $\mathrm {PA}$
) If c is any (coded) set of variables and a is a number, then
$\mathrm {PA}$
) If c is any (coded) set of variables and a is a number, then
 $[a]_c$
denotes the constant assignment sending everything in c to a. If a variable v is clear from context then we will omit it writing
$[a]_c$
denotes the constant assignment sending everything in c to a. If a variable v is clear from context then we will omit it writing
 $[a]$
instead of
$[a]$
instead of
 $[a]_{v}$
.
$[a]_{v}$
.
 $\triangle $
$\triangle $
Definition 2.9 (
 $\mathrm {ACA}_0$
)
$\mathrm {ACA}_0$
)
Let
![]() $\mathbf {M}$
be a partial model. An
$\mathbf {M}$
be a partial model. An
![]() $\mathbf {M}$
-evaluation of terms is a partial function f of type
$\mathbf {M}$
-evaluation of terms is a partial function f of type
such that for every term t,
![]() $\{t\}\times \mathrm {Asn}(t,\mathbf {M})\subseteq \mathrm {dom}(f)$
and for every terms
$\{t\}\times \mathrm {Asn}(t,\mathbf {M})\subseteq \mathrm {dom}(f)$
and for every terms
![]() $s,t$
and every
$s,t$
and every
![]() $\mathbf {M}$
-assignment
$\mathbf {M}$
-assignment
![]() $\alpha $
:
$\alpha $
:
-
1.
 $\langle t, \alpha \rangle \in \mathrm {dom}(f)\leftrightarrow \mathrm {FV}(t)\subseteq \mathrm {dom}(\alpha )$
,
$\langle t, \alpha \rangle \in \mathrm {dom}(f)\leftrightarrow \mathrm {FV}(t)\subseteq \mathrm {dom}(\alpha )$
, -
2.
 $\alpha \subseteq \beta \wedge \langle t, \alpha \rangle \in \mathrm {dom}(f)\rightarrow f(t,\alpha )=f(t,\beta )$
,
$\alpha \subseteq \beta \wedge \langle t, \alpha \rangle \in \mathrm {dom}(f)\rightarrow f(t,\alpha )=f(t,\beta )$
, -
3.
 $f(0,\alpha ) = 0^{\mathbf {M}}$
,
$f(0,\alpha ) = 0^{\mathbf {M}}$
,
 $f(1,\alpha ) = 1^{\mathbf {M}}$
,
$f(1,\alpha ) = 1^{\mathbf {M}}$
, -
4.
 $f(v,\alpha ) = \left \{\begin {array}{l} \alpha (v), \mathrm { if }\ v\in \mathrm {dom}(\alpha ),\\ \mathrm {undefined,}\ \mathrm { otherwise},\end {array} \right.$
$f(v,\alpha ) = \left \{\begin {array}{l} \alpha (v), \mathrm { if }\ v\in \mathrm {dom}(\alpha ),\\ \mathrm {undefined,}\ \mathrm { otherwise},\end {array} \right.$
-
5.
 $f((s+t),\alpha ) = f(s,\alpha )+^{\mathbf {M}}f(t,\alpha )$
,
$f((s+t),\alpha ) = f(s,\alpha )+^{\mathbf {M}}f(t,\alpha )$
,
 $f((s\cdot t),\alpha ) = f(s,\alpha )\cdot ^{\mathbf {M}} f(t,\alpha )$
.
$f((s\cdot t),\alpha ) = f(s,\alpha )\cdot ^{\mathbf {M}} f(t,\alpha )$
.
 $\triangle $
$\triangle $
Observation 2.10 (
 $\mathrm {ACA}_0$
)
$\mathrm {ACA}_0$
)
For every partial model
![]() $\mathbf {M}$
there exists the unique
$\mathbf {M}$
there exists the unique
![]() $\mathbf {M}$
-evaluation of terms. We shall denote it with
$\mathbf {M}$
-evaluation of terms. We shall denote it with
![]() $\mathrm {val}_{\mathbf {M}}$
. Moreover, if the model is
$\mathrm {val}_{\mathbf {M}}$
. Moreover, if the model is
![]() $\Delta _k$
, then
$\Delta _k$
, then
![]() $\mathrm {val}_{\mathbf {M}}$
can be taken to be
$\mathrm {val}_{\mathbf {M}}$
can be taken to be
![]() $\Delta _k$
as well.
$\Delta _k$
as well.
![]() $\boxplus $
$\boxplus $
Definition 2.11 (
 $\mathrm {ACA}_0$
)
$\mathrm {ACA}_0$
)
Let
![]() $\mathbf {M}$
be a partial model. If X is a set of formulae closed under subformulae, then let
$\mathbf {M}$
be a partial model. If X is a set of formulae closed under subformulae, then let
![]() $s(X)$
denote the set of proper subformulae of formulae from X.
$s(X)$
denote the set of proper subformulae of formulae from X.
![]() $S'$
is called an X-satisfaction relation for
$S'$
is called an X-satisfaction relation for
![]() $\mathbf {M}$
if the conditions below holds.
$\mathbf {M}$
if the conditions below holds.
-
1.
 $X\subseteq \mathrm {Form}_{\mathcal {L}_S}\wedge \forall \phi \forall \psi \big (\psi \in \mathrm {Subf}(\phi )\wedge \phi \in X\rightarrow \psi \in X\big )$
.
$X\subseteq \mathrm {Form}_{\mathcal {L}_S}\wedge \forall \phi \forall \psi \big (\psi \in \mathrm {Subf}(\phi )\wedge \phi \in X\rightarrow \psi \in X\big )$
. -
2.
 $ \forall y,z (S'(y,z)\rightarrow y\in X \wedge z\in \mathrm {Asn}(y,\mathbf {M})\big ).$
$ \forall y,z (S'(y,z)\rightarrow y\in X \wedge z\in \mathrm {Asn}(y,\mathbf {M})\big ).$
-
3.
 $\forall s,t\forall \alpha \in \mathrm {Asn}(s,t,\mathbf {M})\ \ \left (S'(s=t,\alpha )\equiv \mathrm {val}_{\mathbf {M}}(s,\alpha )=\mathrm {val}_{\mathbf {M}}(t,\alpha )\right ).$
$\forall s,t\forall \alpha \in \mathrm {Asn}(s,t,\mathbf {M})\ \ \left (S'(s=t,\alpha )\equiv \mathrm {val}_{\mathbf {M}}(s,\alpha )=\mathrm {val}_{\mathbf {M}}(t,\alpha )\right ).$
-
4.
 $\forall s,t\forall \alpha \in \mathrm {Asn}(s,t,\mathbf {M})\ \ \left (S'(S(s,t),\alpha )\equiv \langle \mathrm {val}_{\mathcal {M}}(s,\alpha ), \mathrm {val}_{\mathcal {M}}(t,\alpha )\rangle \in S_{\mathbf {M}}\right ).$
$\forall s,t\forall \alpha \in \mathrm {Asn}(s,t,\mathbf {M})\ \ \left (S'(S(s,t),\alpha )\equiv \langle \mathrm {val}_{\mathcal {M}}(s,\alpha ), \mathrm {val}_{\mathcal {M}}(t,\alpha )\rangle \in S_{\mathbf {M}}\right ).$
-
5.
 $\forall \phi \in s(X)\forall \alpha \in \mathrm {Asn}(\phi ,\mathbf {M})\ \ \left (S'(\neg \phi ,\alpha )\equiv \neg S'(\phi ,\alpha )\right )$
.
$\forall \phi \in s(X)\forall \alpha \in \mathrm {Asn}(\phi ,\mathbf {M})\ \ \left (S'(\neg \phi ,\alpha )\equiv \neg S'(\phi ,\alpha )\right )$
. -
6.
 $\forall \phi ,\psi \in s(X)\forall \alpha \in \mathrm {Asn}(\phi ,\psi ,\mathbf {M})\ \ \left (S'(\phi \vee \psi ,\alpha )\equiv S'(\phi ,\alpha {\upharpoonright _{\cdot }})\vee S'(\psi ,\alpha {\upharpoonright _{\cdot }})\right )$
.
$\forall \phi ,\psi \in s(X)\forall \alpha \in \mathrm {Asn}(\phi ,\psi ,\mathbf {M})\ \ \left (S'(\phi \vee \psi ,\alpha )\equiv S'(\phi ,\alpha {\upharpoonright _{\cdot }})\vee S'(\psi ,\alpha {\upharpoonright _{\cdot }})\right )$
. -
7.
 $\forall \phi \in s(X) \forall v \forall \alpha \in \mathrm {Asn}(\exists v\phi , \mathbf {M })\ (S'(\exists v\phi ,\alpha )\equiv \exists \beta \geq _v\alpha \big (\beta \in \mathrm {Asn}(\mathbf {M}) \wedge $
$\forall \phi \in s(X) \forall v \forall \alpha \in \mathrm {Asn}(\exists v\phi , \mathbf {M })\ (S'(\exists v\phi ,\alpha )\equiv \exists \beta \geq _v\alpha \big (\beta \in \mathrm {Asn}(\mathbf {M}) \wedge $
 $ S'(\phi , \beta {\upharpoonright _{\cdot }})\big)$
.
$ S'(\phi , \beta {\upharpoonright _{\cdot }})\big)$
.
Let
![]() $\mathrm {CS}^-(X,\mathbf {M}, S')$
denote the conjunction of the above sentences of
$\mathrm {CS}^-(X,\mathbf {M}, S')$
denote the conjunction of the above sentences of
![]() $\mathcal {L}_{\textrm {2}}$
(we treat
$\mathcal {L}_{\textrm {2}}$
(we treat
![]() $\mathbf {M}$
,
$\mathbf {M}$
,
![]() $S'$
, X as second-order variables). In the context of S,
$S'$
, X as second-order variables). In the context of S,
![]() $S(\phi ,\alpha {\upharpoonright _{\cdot }})$
always mean
$S(\phi ,\alpha {\upharpoonright _{\cdot }})$
always mean
![]() $S(\phi ,\alpha {\upharpoonright _{\phi }})$
.
$S(\phi ,\alpha {\upharpoonright _{\phi }})$
.
![]() $\triangle $
$\triangle $
Definition 2.12. (
![]() $\mathrm {PA}$
; measures of complexity of formulae)
$\mathrm {PA}$
; measures of complexity of formulae)
-
1. The depth of a formula
 $\phi $
is the length of the longest path in the syntactic tree of
$\phi $
is the length of the longest path in the syntactic tree of
 $\phi $
. Equivalently, the depth of
$\phi $
. Equivalently, the depth of
 $\phi $
is defined recursively: the depth of an atomic formula is
$\phi $
is defined recursively: the depth of an atomic formula is
 $0$
,
$0$
,
 $\exists $
and
$\exists $
and
 $\neg $
raise the complexity by one, and the depth of the disjunction is the maximum of the depths of the disjuncts plus one.
$\neg $
raise the complexity by one, and the depth of the disjunction is the maximum of the depths of the disjuncts plus one.
 $\phi \in \mathrm {dp}(x)$
expresses that the depth of
$\phi \in \mathrm {dp}(x)$
expresses that the depth of
 $\phi $
is at most x.
$\phi $
is at most x. -
2. Let us fix a canonical syntactical (elementary) transformation, which for a formula
 $\phi (\bar {x})$
returns a formula in the
$\phi (\bar {x})$
returns a formula in the
 $\Sigma _c$
form, that is logically equivalent to
$\Sigma _c$
form, that is logically equivalent to
 $\phi (\bar {x})$
. Denote with
$\phi (\bar {x})$
. Denote with
 $\phi (\bar {x})^{\Sigma }$
the result of applying this transformation. We assume that
$\phi (\bar {x})^{\Sigma }$
the result of applying this transformation. We assume that
 $\mathrm {FV}(\phi (\bar {x}))=\mathrm {FV}(\phi (\bar {x})^{\Sigma })$
. For a number c, let
$\mathrm {FV}(\phi (\bar {x}))=\mathrm {FV}(\phi (\bar {x})^{\Sigma })$
. For a number c, let
 $\Sigma ^*_c$
denote the class of formulae
$\Sigma ^*_c$
denote the class of formulae
 $\phi (x)$
such that
$\phi (x)$
such that
 $\phi (x)^{\Sigma }\in \Sigma _c$
.
$\phi (x)^{\Sigma }\in \Sigma _c$
.
 $\triangle $
$\triangle $
Definition 2.13 (
 $\mathrm {ACA}_0$
)
$\mathrm {ACA}_0$
)
For a number c, a c-full model is a tuple
![]() $(\mathbf {M}, \mathrm {Sat}_{\mathbf {M}})$
where
$(\mathbf {M}, \mathrm {Sat}_{\mathbf {M}})$
where
![]() $\mathbf {M}$
is a partial model, and
$\mathbf {M}$
is a partial model, and
![]() $\mathrm {Sat}_{\mathbf {M}}\subseteq \mathrm {Form}_{\mathcal {L}_S}\times \mathrm {Asn}(\mathbf {M})$
is a
$\mathrm {Sat}_{\mathbf {M}}\subseteq \mathrm {Form}_{\mathcal {L}_S}\times \mathrm {Asn}(\mathbf {M})$
is a
![]() $\Sigma ^*_c$
-satisfaction relation for
$\Sigma ^*_c$
-satisfaction relation for
![]() $\mathbf {M}$
. A model
$\mathbf {M}$
. A model
![]() $(\mathbf {M},\mathrm {Sat}_{\mathbf {M}})$
is a full model if it is a c-full model for every c. Moreover, a tuple
$(\mathbf {M},\mathrm {Sat}_{\mathbf {M}})$
is a full model if it is a c-full model for every c. Moreover, a tuple
![]() $(\mathbf {M}, \mathrm {Sat}_{\mathbf {M}})$
is a depth-c-full model if
$(\mathbf {M}, \mathrm {Sat}_{\mathbf {M}})$
is a depth-c-full model if
![]() $\mathrm {Sat}_{\mathbf {M}}$
is a
$\mathrm {Sat}_{\mathbf {M}}$
is a
![]() $\mathrm {dp}(c)$
-satisfaction relation for
$\mathrm {dp}(c)$
-satisfaction relation for
![]() $\mathbf {M}$
, i.e.,
$\mathbf {M}$
, i.e.,
![]() $\mathrm {CS}^-(\mathrm {dp}(c), \mathbf {M}, \mathrm {Sat}_{\mathbf {M}})$
holds.
$\mathrm {CS}^-(\mathrm {dp}(c), \mathbf {M}, \mathrm {Sat}_{\mathbf {M}})$
holds.
![]() $\triangle $
$\triangle $
We stress that
![]() $(\mathbf {M}, \mathrm {Sat}_{\mathbf {M}})$
being c-full presupposes that
$(\mathbf {M}, \mathrm {Sat}_{\mathbf {M}})$
being c-full presupposes that
![]() $\mathbf {M}$
and
$\mathbf {M}$
and
![]() $\mathrm {Sat}_{\mathbf {M}}$
satisfy full induction (treated as additional predicates).
$\mathrm {Sat}_{\mathbf {M}}$
satisfy full induction (treated as additional predicates).
Observe that if for every
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $(\mathbf {M}, \mathrm {Sat}_{\mathbf {M}})$
is an
$(\mathbf {M}, \mathrm {Sat}_{\mathbf {M}})$
is an
![]() $\mathcal {N}$
-definable n-full model, then we have two satisfaction classes for
$\mathcal {N}$
-definable n-full model, then we have two satisfaction classes for
![]() $\mathbf {M}$
at our disposal: the metatheoretical one and
$\mathbf {M}$
at our disposal: the metatheoretical one and
![]() $\mathrm {Sat}_{\mathbf {M}}$
. The two relations agree in the following sense: for every
$\mathrm {Sat}_{\mathbf {M}}$
. The two relations agree in the following sense: for every
![]() $\phi (x_1,\ldots , x_n)\in \mathcal {L}_S$
and for all
$\phi (x_1,\ldots , x_n)\in \mathcal {L}_S$
and for all
![]() $a_1,\ldots , a_n \in (U_{\mathbf {M}})^{\mathcal {N}}$
,
$a_1,\ldots , a_n \in (U_{\mathbf {M}})^{\mathcal {N}}$
,
where
![]() $[a_1,\ldots , a_n]$
denotes the assignment
$[a_1,\ldots , a_n]$
denotes the assignment
![]() $x_i\mapsto a_i$
,
$x_i\mapsto a_i$
,
![]() $i\leq n$
.
$i\leq n$
.
Convention 2.14. We reserve calligraphic letters
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
![]() $\mathcal {K}$
to talk, both internally and externally, about models with satisfaction relations, while
$\mathcal {K}$
to talk, both internally and externally, about models with satisfaction relations, while
![]() $\mathbf {M}$
,
$\mathbf {M}$
,
![]() $\mathbf {N}$
,
$\mathbf {N}$
,
![]() $\mathbf {K}$
will denote arbitrary partial models.
$\mathbf {K}$
will denote arbitrary partial models.
By the Tarski’s undefinability of truth theorem one obtains that if
![]() $\mathcal {M}$
is any model of
$\mathcal {M}$
is any model of
![]() $\mathrm {PA}$
, then there is no formula
$\mathrm {PA}$
, then there is no formula
![]() $\mathrm {Sat}_{\mathbf {V}}$
with parameters from
$\mathrm {Sat}_{\mathbf {V}}$
with parameters from
![]() $\mathcal {M}$
such that for every n,
$\mathcal {M}$
such that for every n,
![]() $(\mathbf {V},\mathrm {Sat}_{\mathbf {V}})$
is an n-full model. However, relativizing the standard partial truth predicates (see [Reference Hájek and Pudlák9]) one obtains the following observation.
$(\mathbf {V},\mathrm {Sat}_{\mathbf {V}})$
is an n-full model. However, relativizing the standard partial truth predicates (see [Reference Hájek and Pudlák9]) one obtains the following observation.
Observation 2.15 (
 $\mathrm {ACA}_0$
)
$\mathrm {ACA}_0$
)
If
![]() $\mathbf {M}$
is any partial model, then for every k there are uniquely determined predicates
$\mathbf {M}$
is any partial model, then for every k there are uniquely determined predicates
![]() $\mathrm {Sat}_{\mathbf {M}}^k$
such that
$\mathrm {Sat}_{\mathbf {M}}^k$
such that
![]() $(\mathbf {M},\mathrm {Sat}_{\mathbf {M}}^k)$
is a k-full model.
$(\mathbf {M},\mathrm {Sat}_{\mathbf {M}}^k)$
is a k-full model.
![]() $\boxplus $
$\boxplus $
Proposition 2.16 (
 $\mathrm {ACA}_0$
)
$\mathrm {ACA}_0$
)
Let X be closed under subformulae. Suppose that
![]() $\mathrm {Sat}_{\mathbf {M}}$
is an X-satisfaction class for
$\mathrm {Sat}_{\mathbf {M}}$
is an X-satisfaction class for
![]() $\mathbf {M}$
. Let
$\mathbf {M}$
. Let
![]() $Y\subseteq X$
be a set of sentences such that
$Y\subseteq X$
be a set of sentences such that
![]() $\mathbf {M}\models _{\mathrm {Sat}_{\mathbf {M}}} Y$
. Then Y is consistent.
$\mathbf {M}\models _{\mathrm {Sat}_{\mathbf {M}}} Y$
. Then Y is consistent.
Proof. We reason in
![]() $\mathrm {ACA}_0$
and assume the contrary. Then there is a sequent-calculus proof of the sequent
$\mathrm {ACA}_0$
and assume the contrary. Then there is a sequent-calculus proof of the sequent
in the pure first-order logic, where
![]() $\Gamma \subseteq Y$
is a finite set. By cut-elimination we may assume that this proof has a subformula property, so every formula occurring in it is a subformula of a formula from
$\Gamma \subseteq Y$
is a finite set. By cut-elimination we may assume that this proof has a subformula property, so every formula occurring in it is a subformula of a formula from
![]() $\Gamma \cup \{0=1\}$
. By induction on the length of the proof we can show that for every sequent
$\Gamma \cup \{0=1\}$
. By induction on the length of the proof we can show that for every sequent
![]() $\Theta \Rightarrow \Delta $
it holds that
$\Theta \Rightarrow \Delta $
it holds that
This contradicts that the proof ends with
![]() $0=1$
.□
$0=1$
.□
The above notions of partial and full model lead to the definition of two interpretability relations between structures:
Definition 2.17 (Interpretable models; see [Reference Kaye12])
Let
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
be two models of an extension of
$\mathcal {N}$
be two models of an extension of
![]() $\mathrm {PA}$
(not necessarily satisfying
$\mathrm {PA}$
(not necessarily satisfying
![]() $\mathrm {PA}^*$
). We say that
$\mathrm {PA}^*$
). We say that
![]() $\mathcal {M}$
interprets
$\mathcal {M}$
interprets
![]() $\mathcal {N}$
if there exists a partial
$\mathcal {N}$
if there exists a partial
![]() $\mathcal {M}$
-definable model
$\mathcal {M}$
-definable model
![]() $\mathbf {N}$
such that
$\mathbf {N}$
such that
We say that
![]() $\mathcal {M}$
strongly interprets
$\mathcal {M}$
strongly interprets
![]() $\mathcal {N}$
iff there exists
$\mathcal {N}$
iff there exists
![]() $\mathbf {K}$
witnessing that
$\mathbf {K}$
witnessing that
![]() $\mathcal {M}$
interprets
$\mathcal {M}$
interprets
![]() $\mathcal {N}$
and there exists an
$\mathcal {N}$
and there exists an
![]() $\mathcal {M}$
-definable satisfaction predicate
$\mathcal {M}$
-definable satisfaction predicate
![]() $\mathrm {Sat}_{\mathbf {K}}$
making
$\mathrm {Sat}_{\mathbf {K}}$
making
![]() $\mathbf {K}$
a full model. Interpretability and strong interpretability will be denoted by
$\mathbf {K}$
a full model. Interpretability and strong interpretability will be denoted by
![]() $\lhd $
and
$\lhd $
and
![]() $\lhd _S$
, respectively.
$\lhd _S$
, respectively.
![]() $\triangle $
$\triangle $
Observe that, as defined neither interpretability nor strong interpretability is preserved under isomorphism, in the sense that from
![]() $\mathcal {M}\lhd \mathcal {N}$
and
$\mathcal {M}\lhd \mathcal {N}$
and
![]() $\mathcal {N}\simeq \mathcal {K}$
we cannot conclude that
$\mathcal {N}\simeq \mathcal {K}$
we cannot conclude that
![]() $\mathcal {M}\lhd \mathcal {K}$
. The next two propositions uncover the important properties of
$\mathcal {M}\lhd \mathcal {K}$
. The next two propositions uncover the important properties of
![]() $\lhd $
. The following routine notion will come in handy:
$\lhd $
. The following routine notion will come in handy:
Definition 2.18 (
 $\mathrm {ACA}_0$
; relativization)
$\mathrm {ACA}_0$
; relativization)
Suppose that
![]() $\mathbf {M}$
is a partial model. For every formula
$\mathbf {M}$
is a partial model. For every formula
![]() $\phi $
we define its relativization
$\phi $
we define its relativization
![]() $\phi ^{\mathbf {M}}$
by induction on the complexity of
$\phi ^{\mathbf {M}}$
by induction on the complexity of
![]() $\phi $
:
$\phi $
:
 $$ \begin{align*} (s(\bar{v_s}) = t(\bar{v_t}))^{\mathbf{M}} &:= \mathrm{val}_{\mathbf{M}}(s, [\bar{v_s}]) = \mathrm{val}_{\mathbf{M}}(t,[\bar{v_t}]),\\ (S(t(\bar{v})))^{\mathbf{M}} &:= \mathrm{val}_{\mathbf{M}}(t,[\bar{v}]) \in S_{\mathbf{M}},\\ (\phi\vee \psi)^{\mathbf{M}} &:= (\phi)^{\mathbf{M}}\vee (\psi)^{\mathbf{M}},\\ (\neg \phi)^{\mathbf{M}} &:= \neg (\phi)^{\mathbf{M}},\\ (\exists x \phi)^{\mathbf{M}} &:= \exists x \in U_{\mathbf{M}}\ \ (\phi)^{\mathbf{M}}. \end{align*} $$
$$ \begin{align*} (s(\bar{v_s}) = t(\bar{v_t}))^{\mathbf{M}} &:= \mathrm{val}_{\mathbf{M}}(s, [\bar{v_s}]) = \mathrm{val}_{\mathbf{M}}(t,[\bar{v_t}]),\\ (S(t(\bar{v})))^{\mathbf{M}} &:= \mathrm{val}_{\mathbf{M}}(t,[\bar{v}]) \in S_{\mathbf{M}},\\ (\phi\vee \psi)^{\mathbf{M}} &:= (\phi)^{\mathbf{M}}\vee (\psi)^{\mathbf{M}},\\ (\neg \phi)^{\mathbf{M}} &:= \neg (\phi)^{\mathbf{M}},\\ (\exists x \phi)^{\mathbf{M}} &:= \exists x \in U_{\mathbf{M}}\ \ (\phi)^{\mathbf{M}}. \end{align*} $$
Above,
![]() $\mathrm {val}_{\mathbf {M}}(t, [\bar {v_s}])=y$
abbreviates the formula
$\mathrm {val}_{\mathbf {M}}(t, [\bar {v_s}])=y$
abbreviates the formula
![]() $\triangle $
$\triangle $
Proposition 2.19. If
![]() $\mathcal {M}\lhd \mathcal {N}$
and
$\mathcal {M}\lhd \mathcal {N}$
and
![]() $\mathcal {N}\lhd \mathcal {K}$
, then
$\mathcal {N}\lhd \mathcal {K}$
, then
![]() $\mathcal {M}\lhd \mathcal {K}$
.
$\mathcal {M}\lhd \mathcal {K}$
.
Proof. Suppose that
![]() $\mathcal {N} = (\mathbf {N})^{\mathcal {M}}$
and
$\mathcal {N} = (\mathbf {N})^{\mathcal {M}}$
and
![]() $\mathcal {K} = (\mathbf {K})^{\mathcal {N}}$
. Suppose further that
$\mathcal {K} = (\mathbf {K})^{\mathcal {N}}$
. Suppose further that
![]() $\mathbf {N}$
is partial
$\mathbf {N}$
is partial
![]() $\Delta _k$
model in
$\Delta _k$
model in
![]() $\mathcal {M}$
. Hence using partial satisfaction predicate for
$\mathcal {M}$
. Hence using partial satisfaction predicate for
![]() $\Sigma _k$
formulae, we can see that the
$\Sigma _k$
formulae, we can see that the
![]() $\mathbf {K}^{\mathbf {N}}$
(see Definition 2.18) makes sense in
$\mathbf {K}^{\mathbf {N}}$
(see Definition 2.18) makes sense in
![]() $\mathcal {M}$
, and, in
$\mathcal {M}$
, and, in
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathbf {K}^{\mathbf {N}}$
is a partial
$\mathbf {K}^{\mathbf {N}}$
is a partial
![]() $\Delta _k$
model. Moreover it is easy to observe that
$\Delta _k$
model. Moreover it is easy to observe that
which ends the proof.□
The following proposition will play a crucial role in some of our arguments. Its proof consists in internalizing the argument from Remark 2.6 and makes use of the arithmetization of the relativization function introduced above.
Proposition 2.20 (Enayat–Visser)
Suppose that
![]() $\mathcal {M} \lhd _S \mathcal {N}$
and
$\mathcal {M} \lhd _S \mathcal {N}$
and
![]() $\mathcal {N}\lhd \mathcal {K}$
, then
$\mathcal {N}\lhd \mathcal {K}$
, then
![]() $\mathcal {M}\lhd _S \mathcal {K}$
.
$\mathcal {M}\lhd _S \mathcal {K}$
.
Proof. By Proposition 2.19 we have
![]() $\mathcal {M}\lhd \mathcal {K}$
and
$\mathcal {M}\lhd \mathcal {K}$
and
![]() $(\mathbf {K})^{\mathbf {N}}$
is a partial
$(\mathbf {K})^{\mathbf {N}}$
is a partial
![]() $\mathcal {M}$
-definable model witnessing the interpretability. We define the satisfaction relation for
$\mathcal {M}$
-definable model witnessing the interpretability. We define the satisfaction relation for
![]() $(\mathbf {K})^{\mathbf {N}}$
via the formula
$(\mathbf {K})^{\mathbf {N}}$
via the formula
□
In
![]() $\mathrm {PA}$
we can prove that every consistent theory admits a full model. Since in most cases both the theory and the model are infinite objects, this is in fact a parametrized family of theorems:
$\mathrm {PA}$
we can prove that every consistent theory admits a full model. Since in most cases both the theory and the model are infinite objects, this is in fact a parametrized family of theorems:
Theorem 2.21 (Arithmetized Completeness Theorem)
For every
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $\mathrm {PA}^*$
proves the sentence
$\mathrm {PA}^*$
proves the sentence
![]() $\boxplus $
$\boxplus $
Since the proof of this fact (apart from axioms for arithmetical operations) depends only on the presence of induction, it can be proved also in every extension of
![]() $\mathrm {PA}$
which includes full induction scheme (for the extended language). This will be crucial in the second part of the paper. Let us complete this introductory part with two classical observations which give us some information about the structure of interpretable models. The first one shows that in fact interpretability can be seen as refined end-extendibility.
$\mathrm {PA}$
which includes full induction scheme (for the extended language). This will be crucial in the second part of the paper. Let us complete this introductory part with two classical observations which give us some information about the structure of interpretable models. The first one shows that in fact interpretability can be seen as refined end-extendibility.
Definition 2.22. If
![]() $\mathcal {M}$
is a model for a language
$\mathcal {M}$
is a model for a language
![]() $\mathcal {L}'$
extending
$\mathcal {L}'$
extending
![]() $\mathcal {L}$
, then
$\mathcal {L}$
, then
![]() $\mathcal {M}{\upharpoonright _{\mathcal {L}}}$
denote its
$\mathcal {M}{\upharpoonright _{\mathcal {L}}}$
denote its
![]() $\mathcal {L}$
-reduct.
$\mathcal {L}$
-reduct.
![]() $\triangle $
$\triangle $
Proposition 2.23 (Folklore)
Let
![]() $\mathcal {M}, \mathcal {N}$
be models of
$\mathcal {M}, \mathcal {N}$
be models of
![]() $\mathrm {PA}^*$
. If
$\mathrm {PA}^*$
. If
![]() $\mathcal {M}$
interprets
$\mathcal {M}$
interprets
![]() $\mathcal {N}$
, then there exists a unique
$\mathcal {N}$
, then there exists a unique
![]() $\mathcal {M}$
-definable isomorphism between
$\mathcal {M}$
-definable isomorphism between
![]() $\mathcal {M}{\upharpoonright _{\mathcal {L}}}$
and initial segment of
$\mathcal {M}{\upharpoonright _{\mathcal {L}}}$
and initial segment of
![]() $\mathcal {N}{\upharpoonright _{\mathcal {L}}}$
.
$\mathcal {N}{\upharpoonright _{\mathcal {L}}}$
.
Proof. Suppose
![]() $\mathbf {N}:=\langle U_{\mathbf {N}},+_{\mathbf {N}},\times _{\mathbf {N}}, S_{\mathbf {N}}, 0_{\mathbf {N}}, 1_{\mathbf {N}} \rangle $
is an
$\mathbf {N}:=\langle U_{\mathbf {N}},+_{\mathbf {N}},\times _{\mathbf {N}}, S_{\mathbf {N}}, 0_{\mathbf {N}}, 1_{\mathbf {N}} \rangle $
is an
![]() $\mathcal {M}$
definable partial model witnessing the interpretability of
$\mathcal {M}$
definable partial model witnessing the interpretability of
![]() $\mathcal {N}$
in
$\mathcal {N}$
in
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $\mathrm {val}_{\mathbf {N}}$
be a valuation function for
$\mathrm {val}_{\mathbf {N}}$
be a valuation function for
![]() $\mathbf {N}$
. We define the embedding
$\mathbf {N}$
. We define the embedding
![]() $\iota :\mathcal {M}\rightarrow \mathcal {N}$
via the formula
$\iota :\mathcal {M}\rightarrow \mathcal {N}$
via the formula
where
![]() $\underline {x}$
is a canonical numeral (in the sense of
$\underline {x}$
is a canonical numeral (in the sense of
![]() $\mathcal {M}$
) naming x. By the earlier remarks there exists a satisfaction predicate
$\mathcal {M}$
) naming x. By the earlier remarks there exists a satisfaction predicate
![]() $\mathrm {Sat}_{\mathbf {N}}$
making
$\mathrm {Sat}_{\mathbf {N}}$
making
![]() $\mathbf {N}$
a
$\mathbf {N}$
a
![]() $1$
-full model. The fact that
$1$
-full model. The fact that
![]() $\iota $
is an initial embedding follows since for every x we can build a quantifier-free sentence (in the sense of
$\iota $
is an initial embedding follows since for every x we can build a quantifier-free sentence (in the sense of
![]() $\mathcal {M}$
)
$\mathcal {M}$
)
 $$\begin{align*}\forall v\ \ \bigg(v<\underline{x} \rightarrow \bigvee_{z<x} v = \underline{z}\bigg),\end{align*}$$
$$\begin{align*}\forall v\ \ \bigg(v<\underline{x} \rightarrow \bigvee_{z<x} v = \underline{z}\bigg),\end{align*}$$
and by induction on x show that every such sentence is true in
![]() $\mathbf {N}$
according
$\mathbf {N}$
according
![]() $\mathrm {Sat}_{\mathbf {N}}$
. But this is equivalent to
$\mathrm {Sat}_{\mathbf {N}}$
. But this is equivalent to
![]() $\iota $
being an initial embedding. Now, if
$\iota $
being an initial embedding. Now, if
![]() $\iota '$
is any other
$\iota '$
is any other
![]() $\mathcal {M}$
definable isomorphism between
$\mathcal {M}$
definable isomorphism between
![]() $\mathcal {M}$
and an initial segment of
$\mathcal {M}$
and an initial segment of
![]() $\mathcal {N}$
, then it follows that
$\mathcal {N}$
, then it follows that
Then, by induction it follows that
![]() $\mathcal {M}\models \forall x\big (\iota (x) = \iota '(x)\big )$
.□
$\mathcal {M}\models \forall x\big (\iota (x) = \iota '(x)\big )$
.□
If we strengthen the assumption to strong interpretability, then we can conclude that the interpreted model is always
![]() $“$
longer.
$“$
longer.
![]() $”$
$”$
Proposition 2.24 (Folklore)
Let
![]() $\mathcal {M}, \mathcal {N}$
be models of
$\mathcal {M}, \mathcal {N}$
be models of
![]() $\mathrm {PA}^*$
. Suppose that
$\mathrm {PA}^*$
. Suppose that
![]() $\mathcal {M}$
strongly interprets
$\mathcal {M}$
strongly interprets
![]() $\mathcal {N}$
and let
$\mathcal {N}$
and let
![]() $\iota :\mathcal {M}{\upharpoonright _{\mathcal {L}}}\rightarrow \mathcal {N}{\upharpoonright _{\mathcal {L}}}$
be the embedding from Proposition 2.23. Then
$\iota :\mathcal {M}{\upharpoonright _{\mathcal {L}}}\rightarrow \mathcal {N}{\upharpoonright _{\mathcal {L}}}$
be the embedding from Proposition 2.23. Then
![]() $\iota $
is not an elementary embedding. In particular,
$\iota $
is not an elementary embedding. In particular,
![]() $\mathcal {M}$
is isomorphic to a proper initial segment of
$\mathcal {M}$
is isomorphic to a proper initial segment of
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
Proof. Let
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
![]() $\iota $
be as above and let
$\iota $
be as above and let
![]() $\mathbf {N}$
be a partial
$\mathbf {N}$
be a partial
![]() $\mathcal {M}$
-definable model such that
$\mathcal {M}$
-definable model such that
![]() $\mathcal {N} = (\mathbf {N})^{\mathcal {M}}$
. That
$\mathcal {N} = (\mathbf {N})^{\mathcal {M}}$
. That
![]() $\iota $
is not elementary follows from Tarski undefinability of truth theorem. Indeed, since
$\iota $
is not elementary follows from Tarski undefinability of truth theorem. Indeed, since
![]() $\iota $
and
$\iota $
and
![]() $\mathrm {Sat}_{\mathbf {N}}$
are
$\mathrm {Sat}_{\mathbf {N}}$
are
![]() $\mathcal {M}$
definable, we can define in
$\mathcal {M}$
definable, we can define in
![]() $\mathcal {M}$
a predicate
$\mathcal {M}$
a predicate
![]() $S(x,y)$
by putting
$S(x,y)$
by putting
With such a definition for every formula
![]() $\phi (x_1,\ldots , x_n)$
and all
$\phi (x_1,\ldots , x_n)$
and all
![]() $a_1,\ldots , a_n\in M$
we have
$a_1,\ldots , a_n\in M$
we have
Then, if
![]() $\iota $
were elementary, then the condition on the right-hand side would be equivalent to
$\iota $
were elementary, then the condition on the right-hand side would be equivalent to
![]() $\mathcal {M}\models \phi (a_1,\ldots , a_n)$
which contradicts Tarski’s theorem. The last part follows easily from the above and Proposition 2.23.□
$\mathcal {M}\models \phi (a_1,\ldots , a_n)$
which contradicts Tarski’s theorem. The last part follows easily from the above and Proposition 2.23.□
Let us note one immediate corollary. Recall that
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $\kappa $
-like if
$\kappa $
-like if
![]() $|M| = \kappa $
but every proper initial segment of
$|M| = \kappa $
but every proper initial segment of
![]() $\mathcal {M}$
has cardinality strictly smaller than
$\mathcal {M}$
has cardinality strictly smaller than
![]() $\kappa $
.
$\kappa $
.
Corollary 2.25. If
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $\kappa $
-like, then
$\kappa $
-like, then
![]() $\mathcal {M}$
is not strongly interpreted in any model of
$\mathcal {M}$
is not strongly interpreted in any model of
![]() $\mathrm {PA}$
.
$\mathrm {PA}$
.
Proof. Obviously, if
![]() $\mathcal {N}$
interprets
$\mathcal {N}$
interprets
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $|N|\geq |M|$
. Moreover, if
$|N|\geq |M|$
. Moreover, if
![]() $\mathcal {M}$
is strongly interpretable in
$\mathcal {M}$
is strongly interpretable in
![]() $\mathcal {N}$
, then it has a proper initial segment of cardinality
$\mathcal {N}$
, then it has a proper initial segment of cardinality
![]() $|M|$
.□
$|M|$
.□
Moreover, models strongly interpretable in a nonstandard model of
![]() $\mathrm {PA}$
have to be recursively saturated. This is a corollary to the proposition below (see also [Reference Kossak and Schmerl14]):
$\mathrm {PA}$
have to be recursively saturated. This is a corollary to the proposition below (see also [Reference Kossak and Schmerl14]):
Proposition 2.26. Suppose d is a nonstandard element of
![]() $\mathcal {N}$
. If
$\mathcal {N}$
. If
![]() $\mathcal {M}$
is isomorphic to a depth-d-full model, then
$\mathcal {M}$
is isomorphic to a depth-d-full model, then
![]() $\mathcal {M}$
is recursively saturated.
$\mathcal {M}$
is recursively saturated.
Proof. Suppose that
![]() $\mathcal {M} = (\mathbf {M},\mathrm {Sat}_{\mathbf {M}})$
is an
$\mathcal {M} = (\mathbf {M},\mathrm {Sat}_{\mathbf {M}})$
is an
![]() $\mathcal {N}$
definable depth-d-full model,
$\mathcal {N}$
definable depth-d-full model,
![]() $\mathcal {N}$
and d being as above. Fix an arbitrary recursive type
$\mathcal {N}$
and d being as above. Fix an arbitrary recursive type
![]() $p(x) = \{\phi _i(x,a) \ \ | \ \ i\in \omega \}$
with (without loss of generality) a single parameter a and let
$p(x) = \{\phi _i(x,a) \ \ | \ \ i\in \omega \}$
with (without loss of generality) a single parameter a and let
![]() $\sigma (x,y)$
be the
$\sigma (x,y)$
be the
![]() $\Delta _1$
formula representing its recursive enumeration, i.e., for every
$\Delta _1$
formula representing its recursive enumeration, i.e., for every
![]() $i\in \omega $
,
$i\in \omega $
,
Now, since the depth of every
![]() $\phi _i$
is less than d and
$\phi _i$
is less than d and
![]() $p(x)$
is a type we have for every
$p(x)$
is a type we have for every
![]() $n\in \omega $
$n\in \omega $
(
![]() $[x\mapsto z, y\mapsto a]$
denotes the unique assignment sending the variable x to z and the variable y to a). Hence, by overspill for some nonstandard c we have
$[x\mapsto z, y\mapsto a]$
denotes the unique assignment sending the variable x to z and the variable y to a). Hence, by overspill for some nonstandard c we have
which shows that
![]() $p(x)$
is realised in
$p(x)$
is realised in
![]() $\mathcal {M}$
.□
$\mathcal {M}$
.□
2.4 Satisfaction classes
Satisfaction classes provide truth conditions for
![]() $\mathbf {V}$
.Footnote
6
Usually they are studied in the context of nonstandard models of
$\mathbf {V}$
.Footnote
6
Usually they are studied in the context of nonstandard models of
![]() $\mathrm {PA}$
. Let
$\mathrm {PA}$
. Let
![]() $\mathcal {M}$
be such a model.
$\mathcal {M}$
be such a model.
Definition 2.27. We say that
![]() $S\subseteq M^2$
is a partial satisfaction class on
$S\subseteq M^2$
is a partial satisfaction class on
![]() $\mathcal {M}$
if there is a nonstandard c such that
$\mathcal {M}$
if there is a nonstandard c such that
![]() $(\mathcal {M},S)\models \mathrm {CS}^-(\mathrm {dp}(c+1),\mathbf {V}, S)$
. Equivalently the following holds in
$(\mathcal {M},S)\models \mathrm {CS}^-(\mathrm {dp}(c+1),\mathbf {V}, S)$
. Equivalently the following holds in
![]() $(\mathcal {M},S)$
:
$(\mathcal {M},S)$
:
-
1.
 $ \forall x,y \big (S(x,y)\rightarrow \mathrm {Form}(x)\wedge x\in \mathrm {dp}(c) \wedge y\in \mathrm {Asn}(x)\big )$
.
$ \forall x,y \big (S(x,y)\rightarrow \mathrm {Form}(x)\wedge x\in \mathrm {dp}(c) \wedge y\in \mathrm {Asn}(x)\big )$
. -
2.
 $\forall s,t\forall \alpha \in \mathrm {Asn}(s,t)\ \ \left (S(s=t,\alpha )\equiv s^{\alpha }= t^{\alpha }\right )$
.
$\forall s,t\forall \alpha \in \mathrm {Asn}(s,t)\ \ \left (S(s=t,\alpha )\equiv s^{\alpha }= t^{\alpha }\right )$
. -
3.
 $\forall \phi \in \mathrm {dp}(c)\forall \alpha \in \mathrm {Asn}(\phi )\ \ \left (S(\neg \phi ,\alpha )\equiv \neg S(\phi ,\alpha )\right )$
.
$\forall \phi \in \mathrm {dp}(c)\forall \alpha \in \mathrm {Asn}(\phi )\ \ \left (S(\neg \phi ,\alpha )\equiv \neg S(\phi ,\alpha )\right )$
. -
4.
 $\forall \phi ,\psi \in \mathrm {dp}(c)\forall \alpha \in \mathrm {Asn}(\phi ,\psi )\ \ \left (S(\phi \vee \psi ,\alpha )\equiv S(\phi ,\alpha {\upharpoonright _{\phi }})\vee S(\psi ,\alpha {\upharpoonright _{\psi }})\right )$
.
$\forall \phi ,\psi \in \mathrm {dp}(c)\forall \alpha \in \mathrm {Asn}(\phi ,\psi )\ \ \left (S(\phi \vee \psi ,\alpha )\equiv S(\phi ,\alpha {\upharpoonright _{\phi }})\vee S(\psi ,\alpha {\upharpoonright _{\psi }})\right )$
. -
5.
 $\forall \phi \in \mathrm {dp}(c) \forall v \forall \alpha \in \mathrm {Asn}(\exists v\phi )\ \left (S(\exists v\phi ,\alpha )\equiv \exists \beta \geq _v\alpha \big (S(\phi ,\beta {\upharpoonright _{\phi }})\right )$
.
$\forall \phi \in \mathrm {dp}(c) \forall v \forall \alpha \in \mathrm {Asn}(\exists v\phi )\ \left (S(\exists v\phi ,\alpha )\equiv \exists \beta \geq _v\alpha \big (S(\phi ,\beta {\upharpoonright _{\phi }})\right )$
.
Henceforth, the conjunction of
![]() $1$
–
$1$
–
![]() $5$
will be denoted by
$5$
will be denoted by
![]() $\mathrm {CS}^-(c)$
. If additionally
$\mathrm {CS}^-(c)$
. If additionally
![]() $(\mathcal {M},S)\models \mathrm {PA}^*$
, then S is called a partial inductive satisfaction class. If
$(\mathcal {M},S)\models \mathrm {PA}^*$
, then S is called a partial inductive satisfaction class. If
![]() $(\mathcal {M},S)\models \forall x\ \ \mathrm {CS}^-(x)$
, then S is called a full satisfaction class. Further define:
$(\mathcal {M},S)\models \forall x\ \ \mathrm {CS}^-(x)$
, then S is called a full satisfaction class. Further define:
 $$ \begin{align*} \mathrm{UTB}^-&:= \{\mathrm{CS}^-(\underline{n}) \ \ | \ \ n\in \omega \},\\ \mathrm{UTB}_n&:= \mathrm{UTB}^- + I\Sigma_n(S),\\ \mathrm{UTB} &:= \bigcup_{n\in\omega} \mathrm{UTB}_n. \end{align*} $$
$$ \begin{align*} \mathrm{UTB}^-&:= \{\mathrm{CS}^-(\underline{n}) \ \ | \ \ n\in \omega \},\\ \mathrm{UTB}_n&:= \mathrm{UTB}^- + I\Sigma_n(S),\\ \mathrm{UTB} &:= \bigcup_{n\in\omega} \mathrm{UTB}_n. \end{align*} $$
Now we define an analogue of arithmetical hierarchy over the theory of a full satisfaction class.
 $$ \begin{align*} \mathrm{CS}^- &:=\forall x\ \ \mathrm{CS}^-(x),\\ \mathrm{CS}_n &:= \mathrm{CS}^- + I\Sigma_n(S),\\ \mathrm{CS} &:= \bigcup_{n\in\omega} \mathrm{CS}_n. \end{align*} $$
$$ \begin{align*} \mathrm{CS}^- &:=\forall x\ \ \mathrm{CS}^-(x),\\ \mathrm{CS}_n &:= \mathrm{CS}^- + I\Sigma_n(S),\\ \mathrm{CS} &:= \bigcup_{n\in\omega} \mathrm{CS}_n. \end{align*} $$
If S is a partial satisfaction class on
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $b\in M$
, then we put
$b\in M$
, then we put
Note that
![]() $S_b$
is
$S_b$
is
![]() $\Delta _0$
definable from S, and hence for every n, if S is
$\Delta _0$
definable from S, and hence for every n, if S is
![]() $\Sigma _n$
inductive, then so is
$\Sigma _n$
inductive, then so is
![]() $S_b$
.
$S_b$
.
![]() $\triangle $
$\triangle $
Note that if S is a full satisfaction class, then
![]() $(\mathcal {M},S)$
strongly interprets
$(\mathcal {M},S)$
strongly interprets
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathbf {V}$
is a
$\mathbf {V}$
is a
![]() $\Delta _0$
partial model witnessing the interpretation. However,
$\Delta _0$
partial model witnessing the interpretation. However,
![]() $(\mathbf {V},S)$
need not be full, as we need not have any induction for S. In particular, it does not follow that
$(\mathbf {V},S)$
need not be full, as we need not have any induction for S. In particular, it does not follow that
which, arguably, would mean that
![]() $\mathcal {M}$
knows that
$\mathcal {M}$
knows that
![]() $\mathbf {V}$
is a model of
$\mathbf {V}$
is a model of
![]() $\mathrm {PA}$
. Let us call such a satisfaction class
$\mathrm {PA}$
. Let us call such a satisfaction class
![]() $\mathrm {PA}$
-correct. It can be shown that for a countable
$\mathrm {PA}$
-correct. It can be shown that for a countable
![]() $\mathcal {M}$
the following conditions are equivalent:
$\mathcal {M}$
the following conditions are equivalent:
-
1. There exists a full satisfaction class on
 $\mathcal {M}$
.
$\mathcal {M}$
. -
2. There exists a
 $\mathrm {PA}$
-correct full satisfaction class on
$\mathrm {PA}$
-correct full satisfaction class on
 $\mathcal {M}$
.
$\mathcal {M}$
. -
3.
 $\mathcal {M}$
is recursively saturated.
$\mathcal {M}$
is recursively saturated.
The implication
![]() $3.\Rightarrow 2.$
has been shown for the first time in [Reference Kotlarski, Krajewski and Lachlan16]. References [Reference Enayat, Visser, Achourioti, Galinon, Fernández and Fujimoto7, Reference Leigh17] contain different proofs. The implication
$3.\Rightarrow 2.$
has been shown for the first time in [Reference Kotlarski, Krajewski and Lachlan16]. References [Reference Enayat, Visser, Achourioti, Galinon, Fernández and Fujimoto7, Reference Leigh17] contain different proofs. The implication
![]() $1.\Rightarrow 3.$
is a consequence of Lachlan’s theorem (see Theorem 2.31).
$1.\Rightarrow 3.$
is a consequence of Lachlan’s theorem (see Theorem 2.31).
The name
![]() $\mathrm {UTB}^-$
stands for Uniform Tarski Biconditionals
Footnote
7
and is normally used for the theory having as axioms all sentences of the form
$\mathrm {UTB}^-$
stands for Uniform Tarski Biconditionals
Footnote
7
and is normally used for the theory having as axioms all sentences of the form
for every
![]() $\phi (x_1,\ldots ,x_n)\in \mathrm {Form}_{\mathcal {L}}$
.Footnote
8
One can show that, over
$\phi (x_1,\ldots ,x_n)\in \mathrm {Form}_{\mathcal {L}}$
.Footnote
8
One can show that, over
![]() $\mathrm {EA}$
, this set of sentences is equivalent to the one we’ve officially taken as a definition of
$\mathrm {EA}$
, this set of sentences is equivalent to the one we’ve officially taken as a definition of
![]() $\mathrm {UTB}^-$
. By Observation 2.15 each finite portion of
$\mathrm {UTB}^-$
. By Observation 2.15 each finite portion of
![]() $\mathrm {UTB}^-$
is definable in
$\mathrm {UTB}^-$
is definable in
![]() $\mathrm {PA}$
and consequently we obtain the following proposition (which formalizes in
$\mathrm {PA}$
and consequently we obtain the following proposition (which formalizes in
![]() $\mathrm {EA}$
).
$\mathrm {EA}$
).
Proposition 2.28 (
 $\mathrm {EA}$
)
$\mathrm {EA}$
)
If
![]() $\mathrm {Th}$
is any extension of
$\mathrm {Th}$
is any extension of
![]() $\mathrm {PA}$
, then
$\mathrm {PA}$
, then
![]() $\mathrm {UTB}+\mathrm {Th}$
is conservative over
$\mathrm {UTB}+\mathrm {Th}$
is conservative over
![]() $\mathrm {Th}$
.
$\mathrm {Th}$
.
![]() $\boxplus $
$\boxplus $
Furthermore, observe that
![]() $(\mathcal {M}, S)\models \mathrm {CS}^-$
iff S is a full satisfaction class on
$(\mathcal {M}, S)\models \mathrm {CS}^-$
iff S is a full satisfaction class on
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $(\mathcal {M},S)\models \mathrm {CS}$
iff S is a full inductive satisfaction class in the sense of [Reference Kossak and Schmerl14]. For further usage let us observe that the relation of
$(\mathcal {M},S)\models \mathrm {CS}$
iff S is a full inductive satisfaction class in the sense of [Reference Kossak and Schmerl14]. For further usage let us observe that the relation of
![]() $\mathrm {CS}$
to
$\mathrm {CS}$
to
![]() $\mathrm {CS}_n$
is similar to that between
$\mathrm {CS}_n$
is similar to that between
![]() $\mathrm {PA}$
and
$\mathrm {PA}$
and
![]() $I\Sigma _n$
. In particular there are definable partial
$I\Sigma _n$
. In particular there are definable partial
![]() $\mathrm {Sat}_{\Sigma _n}$
satisfaction predicates for
$\mathrm {Sat}_{\Sigma _n}$
satisfaction predicates for
![]() $\Sigma _n \mathcal {L}_{S}$
formulae. Each
$\Sigma _n \mathcal {L}_{S}$
formulae. Each
![]() $\mathrm {Sat}_{\Sigma _n}$
is a
$\mathrm {Sat}_{\Sigma _n}$
is a
![]() $\Sigma _n \mathcal {L}_S$
formula. As a consequence we obtain:
$\Sigma _n \mathcal {L}_S$
formula. As a consequence we obtain:
Proposition 2.29. For every n,
![]() $\mathrm {EA} + \mathrm {CS}_{n+1}\vdash \mathrm {Con}_{\mathrm {EA}+\mathrm {CS}_n}$
.
$\mathrm {EA} + \mathrm {CS}_{n+1}\vdash \mathrm {Con}_{\mathrm {EA}+\mathrm {CS}_n}$
.
![]() $\boxplus $
$\boxplus $
We note that if S is a partial satisfaction class on a model
![]() $\mathcal {M}$
, then for an arbitrary standard formula
$\mathcal {M}$
, then for an arbitrary standard formula
![]() $\phi (x_0,\ldots , x_n)\in \mathcal {L}$
,
$\phi (x_0,\ldots , x_n)\in \mathcal {L}$
,
In particular it follows from Tarski’s theorem that S is never definable in
![]() $\mathcal {M}$
(even if we allow parameters).
$\mathcal {M}$
(even if we allow parameters).
Nonstandard satisfaction classes provide a very useful tool for investigating nonstandard models of
![]() $\mathrm {PA}$
. The first point of interest is that their existence implies recursive saturation. For starters we cite a proposition which directly follows from Proposition 2.26:
$\mathrm {PA}$
. The first point of interest is that their existence implies recursive saturation. For starters we cite a proposition which directly follows from Proposition 2.26:
Proposition 2.30 (Folklore; see [Reference Kaye12])
If S is a partial inductive satisfaction class in
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $\mathcal {M}$
is recursively saturated.
$\mathcal {M}$
is recursively saturated.
Proof. Suppose that
![]() $(\mathcal {M}, S)\models \mathrm {CS}(c)$
for some nonstandard
$(\mathcal {M}, S)\models \mathrm {CS}(c)$
for some nonstandard
![]() $c\in M$
. Then
$c\in M$
. Then
![]() $\mathcal {M}$
is isomorphic to a depth-c-full
$\mathcal {M}$
is isomorphic to a depth-c-full
![]() $\mathcal {M}$
-definable model. Hence by Proposition 2.26 it is recursively saturated.□
$\mathcal {M}$
-definable model. Hence by Proposition 2.26 it is recursively saturated.□
Interestingly, with a much more complicated proof one can strengthen the above proposition lifting the assumption that the chosen satisfaction class is inductive.
Theorem 2.31 (Lachlan; see [Reference Kaye12])
If for some nonstandard c,
![]() $(\mathcal {M},S)\models \mathrm {CS}^-(c)$
, then
$(\mathcal {M},S)\models \mathrm {CS}^-(c)$
, then
![]() $\mathcal {M}$
is recursively saturated.
$\mathcal {M}$
is recursively saturated.
![]() $\boxplus $
$\boxplus $
The converse to Lachlan’s theorem fails, as was shown by Smith.
Theorem 2.32 (Smith [Reference Smith22])
If
![]() $(\mathcal {M},S)\models \mathrm {CS}^-$
, then there is
$(\mathcal {M},S)\models \mathrm {CS}^-$
, then there is
![]() $S'$
such that for some nonstandard
$S'$
such that for some nonstandard
![]() $c\in M (\mathcal {M},S')\models \mathrm {CS}_0(c)$
.
$c\in M (\mathcal {M},S')\models \mathrm {CS}_0(c)$
.
![]() $\boxplus $
$\boxplus $
The condition that
![]() $(\mathcal {M},S')\models I\Delta _0(S)$
implies that
$(\mathcal {M},S')\models I\Delta _0(S)$
implies that
![]() $S'$
is piecewise coded (in the sense of [Reference Hájek and Pudlák9]) or, using set-theoretical notions, a class on
$S'$
is piecewise coded (in the sense of [Reference Hájek and Pudlák9]) or, using set-theoretical notions, a class on
![]() $\mathcal {M}$
. Since
$\mathcal {M}$
. Since
![]() $(\mathcal {M},S')\models \mathrm {CS}^-(c)$
it follows that
$(\mathcal {M},S')\models \mathrm {CS}^-(c)$
it follows that
![]() $S'$
is not definable (even allowing parameters) in
$S'$
is not definable (even allowing parameters) in
![]() $\mathcal {M}$
(or, is a proper class). Since there are recursively saturated models of
$\mathcal {M}$
(or, is a proper class). Since there are recursively saturated models of
![]() $\mathrm {PA}$
in which every class is definable (with parameters; see [Reference Kossak and Schmerl14]), Smith’s result shows that there are recursively saturated models which do not carry a full satisfaction class.
$\mathrm {PA}$
in which every class is definable (with parameters; see [Reference Kossak and Schmerl14]), Smith’s result shows that there are recursively saturated models which do not carry a full satisfaction class.
A common strengthening of theorems of Smith’s and Lachlan’s was obtained by Wcisło in [Reference Wcisło and Łełyk25]:
Theorem 2.33 (Wcisło)
If
![]() $(\mathcal {M},S) \models \mathrm {CS}^-(c)$
then there is an
$(\mathcal {M},S) \models \mathrm {CS}^-(c)$
then there is an
![]() $S'$
and a nonstandard c such that
$S'$
and a nonstandard c such that
![]() $(\mathcal {M},S')\models \mathrm {CS}(c)$
.
$(\mathcal {M},S')\models \mathrm {CS}(c)$
.
![]() $\boxplus $
$\boxplus $
An interesting open problem in the model theory of
![]() $\mathrm {PA}$
is whether the converse to the above theorem is true, i.e., whether every
$\mathrm {PA}$
is whether the converse to the above theorem is true, i.e., whether every
![]() $\mathcal {M}\models \mathrm {PA}$
which admits a partial inductive satisfaction class admits a full satisfaction class. If one allows to prolong the given model, then there is a positive answer to this question.
$\mathcal {M}\models \mathrm {PA}$
which admits a partial inductive satisfaction class admits a full satisfaction class. If one allows to prolong the given model, then there is a positive answer to this question.
Theorem 2.34 (Visser)
If
![]() $(\mathcal {M},S)\models \mathrm {CS}(c)$
for some
$(\mathcal {M},S)\models \mathrm {CS}(c)$
for some
![]() $c\in M$
, then there are
$c\in M$
, then there are
![]() $\mathcal {M}\preceq _e \mathcal {N}$
and
$\mathcal {M}\preceq _e \mathcal {N}$
and
![]() $S'$
such that
$S'$
such that
![]() $(\mathcal {N},S')\models \mathrm {CS}^-$
and
$(\mathcal {N},S')\models \mathrm {CS}^-$
and
![]() $S\subseteq S'$
.
$S\subseteq S'$
.
![]() $\boxplus $
$\boxplus $
The proof of this theorem is given in [Reference Łełyk and Wcisło20, Theorem 43]. In Section 5 we shall give an analogous result for
![]() $\mathcal {M}\models \mathrm {REF}^{\omega }(\mathrm {PA})$
and
$\mathcal {M}\models \mathrm {REF}^{\omega }(\mathrm {PA})$
and
![]() $\mathrm {CS}_0$
instead of
$\mathrm {CS}_0$
instead of
![]() $\mathrm {CS}^-$
.
$\mathrm {CS}^-$
.
Remark 2.35. The theory
![]() $\mathrm {CS}^-$
is a cousin of a compositional truth theory
$\mathrm {CS}^-$
is a cousin of a compositional truth theory
![]() $\mathrm {CT}^-$
which admits a unary predicate T. All compositional axioms of
$\mathrm {CT}^-$
which admits a unary predicate T. All compositional axioms of
![]() $\mathrm {CS}^-$
can be easily adapted to this new setting; however in the case of the universal quantifier we have two natural ways to go. The first candidate is the
$\mathrm {CS}^-$
can be easily adapted to this new setting; however in the case of the universal quantifier we have two natural ways to go. The first candidate is the
![]() $“$
numeral
$“$
numeral
![]() $”$
version, i.e.,
$”$
version, i.e.,
We stress that
![]() $\phi [x/v]$
denotes the result of substituting the numeral naming x for every free occurrence of the variable v. If such an axiom is adopted, then the resulting theory, denote it
$\phi [x/v]$
denotes the result of substituting the numeral naming x for every free occurrence of the variable v. If such an axiom is adopted, then the resulting theory, denote it
![]() $n\mathrm {CT}^-$
, can define the satisfaction predicate satisfying
$n\mathrm {CT}^-$
, can define the satisfaction predicate satisfying
![]() $\mathrm {CS}^-$
via the formula
$\mathrm {CS}^-$
via the formula
Let us stress that the above formula is
![]() $\Delta _0(\exp )$
. The second option is the
$\Delta _0(\exp )$
. The second option is the
![]() $“$
term
$“$
term
![]() $”$
version of
$”$
version of
![]() $\mathrm {CT}^-$
, denote it
$\mathrm {CT}^-$
, denote it
![]() $t\mathrm {CT}^-$
, where the axiom for
$t\mathrm {CT}^-$
, where the axiom for
![]() $\forall $
is the following:
$\forall $
is the following:
Using Enayat–Visser methods from [Reference Enayat, Visser, Achourioti, Galinon, Fernández and Fujimoto7] it can be shown that
![]() $n\mathrm {CT}^-$
and
$n\mathrm {CT}^-$
and
![]() $t\mathrm {CT}^-$
are independent of each other, i.e., neither of them implies the other one (over the remaining axioms of
$t\mathrm {CT}^-$
are independent of each other, i.e., neither of them implies the other one (over the remaining axioms of
![]() $\mathrm {CS}^-$
). Moreover, it is an open problem whether
$\mathrm {CS}^-$
). Moreover, it is an open problem whether
![]() $t\mathrm {CT}^-$
can define the predicate of
$t\mathrm {CT}^-$
can define the predicate of
![]() $\mathrm {CS}^-$
. In this paper
$\mathrm {CS}^-$
. In this paper
![]() $\mathrm {CT}^-$
will be introduced in Section 3 and will denote the numeral version, i.e.,
$\mathrm {CT}^-$
will be introduced in Section 3 and will denote the numeral version, i.e.,
![]() $n\mathrm {CT}^-$
.
$n\mathrm {CT}^-$
.
![]() $\triangle $
$\triangle $
2.5 Reflection principles
Reflection principles are various (families of) statements expressing the soundness of a given theory
![]() $\mathrm {Th}$
in a way which is transparent for
$\mathrm {Th}$
in a way which is transparent for
![]() $\mathrm {Th}$
. In other words, their aim is to capture the meaning of the metatheoretical assertion:
$\mathrm {Th}$
. In other words, their aim is to capture the meaning of the metatheoretical assertion:
Every theorem of
![]() $\mathrm {Th}$
is true.
$\mathrm {Th}$
is true.
In order to avoid the problem of choosing the presentation for (an abstractly given theory
![]() $\mathrm {Th}$
), we will assume that
$\mathrm {Th}$
), we will assume that
![]() $\mathrm {Th}$
is an elementary formula, which, provably in
$\mathrm {Th}$
is an elementary formula, which, provably in
![]() $\mathrm {EA}$
, defines a set of sentences. Such a formula will be called a Gödelized theory. We use
$\mathrm {EA}$
, defines a set of sentences. Such a formula will be called a Gödelized theory. We use
![]() $\mathrm {PA}$
to abbreviate the canonical elementary formula saying “x is an axiom of
$\mathrm {PA}$
to abbreviate the canonical elementary formula saying “x is an axiom of
![]() $\mathrm {PA}^-$
or an axiom of induction.” Having a satisfaction predicate
$\mathrm {PA}^-$
or an axiom of induction.” Having a satisfaction predicate
![]() $S(x,y)$
at our disposal we can express the above in the form of the Global Reflection Principle
$S(x,y)$
at our disposal we can express the above in the form of the Global Reflection Principle
If S satisfies
![]() $\mathrm {UTB}^-$
, then from this one can derive instantiation of the uniform reflection
$\mathrm {UTB}^-$
, then from this one can derive instantiation of the uniform reflection
Hence
![]() $\mathrm {REF}(\mathrm {Th})$
contains all the formulae of the above form for the language of
$\mathrm {REF}(\mathrm {Th})$
contains all the formulae of the above form for the language of
![]() $\mathrm {Th}$
. If
$\mathrm {Th}$
. If
![]() $\Gamma $
is a set of formulae of the language of
$\Gamma $
is a set of formulae of the language of
![]() $\mathrm {Th}$
, then
$\mathrm {Th}$
, then
![]() denote the restriction of
denote the restriction of
![]() $\mathrm {REF}(\mathrm {Th})$
to formulae from class
$\mathrm {REF}(\mathrm {Th})$
to formulae from class
![]() $\Gamma $
. Below we will need also its iterated versions:
$\Gamma $
. Below we will need also its iterated versions:

In the successor step we tacitly fix the canonical representation of
.
The last definition which is relevant to formalizing soundness claims introduces the oracle provability predicates.
Definition 2.36. Let
![]() $\mathrm {Th}$
be any elementary theory.
$\mathrm {Th}$
be any elementary theory.
![]() $\mathrm {Proof}_{\mathrm {Th}}^X(x,y)$
denotes a
$\mathrm {Proof}_{\mathrm {Th}}^X(x,y)$
denotes a
![]() $\Delta ^0_0(\exp )$
formula with a second-order variable X which canonically formalizes the relation: “y is a proof of sentence x from axioms of
$\Delta ^0_0(\exp )$
formula with a second-order variable X which canonically formalizes the relation: “y is a proof of sentence x from axioms of
![]() $\mathrm {Th}$
and sentences belonging to X.”
$\mathrm {Th}$
and sentences belonging to X.”
![]() $\Pr ^X_{\mathrm {Th}}$
is the
$\Pr ^X_{\mathrm {Th}}$
is the
![]() $\Sigma ^0_1$
provability predicate based on it.
$\Sigma ^0_1$
provability predicate based on it.
![]() $\triangle $
$\triangle $
The oracle provability predicate defined above enables us to (uniformly) define a closure conditions on various satisfaction classes. For example we shall often encounter the assertion
which should be read as “Every first-order consequence of true sentences is true,” where “true” abbreviates that
![]() $S(\phi ,\varepsilon )$
holds. In the above assertion we simply substitute the definable class
$S(\phi ,\varepsilon )$
holds. In the above assertion we simply substitute the definable class
![]() $\{x \ \ | \ \ S(x,\varepsilon ) \}$
for the free second-order variable X. Let us also observe that formally
$\{x \ \ | \ \ S(x,\varepsilon ) \}$
for the free second-order variable X. Let us also observe that formally
![]() $\mathrm {Pr}_{\mathrm {Th}}^X$
is the same as
$\mathrm {Pr}_{\mathrm {Th}}^X$
is the same as
![]() $\mathrm {Pr}_{\mathrm {Th}\cup X}$
; however, for heuristic reasons we prefer to keep the lower index for absolute definitions and the upper one for arbitrary sets of formulae.
$\mathrm {Pr}_{\mathrm {Th}\cup X}$
; however, for heuristic reasons we prefer to keep the lower index for absolute definitions and the upper one for arbitrary sets of formulae.
2.5.1 Reflection and internal models
The theory
![]() $\mathrm {REF}(\mathrm {Th})$
admits a model-theoretical characterisation in terms of strongly definable models. Below
$\mathrm {REF}(\mathrm {Th})$
admits a model-theoretical characterisation in terms of strongly definable models. Below
![]() $\mathsf {K}_A(\mathcal {M})$
denote the set of elements of a model M which are definable in
$\mathsf {K}_A(\mathcal {M})$
denote the set of elements of a model M which are definable in
![]() $\mathcal {M}$
with parameters from the set A.
$\mathcal {M}$
with parameters from the set A.
Theorem 2.37 (Kotlarski–Kaye [Reference Kaye and Kotlarski13])
For an arbitrary recursively saturated
![]() $\mathcal {M}$
the following are equivalent:
$\mathcal {M}$
the following are equivalent:
-
1.
 $\mathcal {M}\models \mathrm {REF}(\mathrm {Th})$
.
$\mathcal {M}\models \mathrm {REF}(\mathrm {Th})$
. -
2. There exists a full
 $\mathcal {M}$
-definable model
$\mathcal {M}$
-definable model
 $\mathcal {N} = (\mathbf {N},\mathrm {Sat}_{\mathbf {N}})$
such that:
$\mathcal {N} = (\mathbf {N},\mathrm {Sat}_{\mathbf {N}})$
such that:-
(a)
 $\mathcal {M}\equiv \mathcal {N}$
.
$\mathcal {M}\equiv \mathcal {N}$
. -
(b)
 $\mathsf {K}_{\emptyset }(\mathcal {M}) = \mathsf {K}_{\emptyset }(\mathcal {N})$
.
$\mathsf {K}_{\emptyset }(\mathcal {M}) = \mathsf {K}_{\emptyset }(\mathcal {N})$
. -
(c)
 $\mathcal {M}\models \forall \phi \in \mathrm {Th}\ \ \mathrm {Sat}_{\mathbf {N}}(\phi ,\varepsilon )$
.
$\mathcal {M}\models \forall \phi \in \mathrm {Th}\ \ \mathrm {Sat}_{\mathbf {N}}(\phi ,\varepsilon )$
.
-
Thanks to condition
![]() $(a)$
imposed on
$(a)$
imposed on
![]() $\mathcal {N}$
in the above, Theorem 2.37 can be iterated an arbitrary finite number of times. Let us call the pair
$\mathcal {N}$
in the above, Theorem 2.37 can be iterated an arbitrary finite number of times. Let us call the pair
![]() $(\mathcal {M},\mathcal {N})$
a KK-pair if it satisfies conditions
$(\mathcal {M},\mathcal {N})$
a KK-pair if it satisfies conditions
![]() $1.-3.$
in the thesis of the above theorem. Thus we obtain:
$1.-3.$
in the thesis of the above theorem. Thus we obtain:
Corollary 2.38.
![]() $\mathcal {M}\models \mathrm {REF}(\mathrm {Th})$
if and only if there exists
$\mathcal {M}\models \mathrm {REF}(\mathrm {Th})$
if and only if there exists
![]() $\{\mathcal {M}_i\}_{i\in {\omega }}$
such that
$\{\mathcal {M}_i\}_{i\in {\omega }}$
such that
![]() $\mathcal {M}_0 = \mathcal {M}$
and for each i,
$\mathcal {M}_0 = \mathcal {M}$
and for each i,
![]() $(\mathcal {M}_i,\mathcal {M}_{i+1})$
is a KK-pair.
$(\mathcal {M}_i,\mathcal {M}_{i+1})$
is a KK-pair.
In Section 5 we shall offer a similar in spirit model-theoretical characterization of
![]() $\mathrm {REF}^n(\mathrm {Th})$
and
$\mathrm {REF}^n(\mathrm {Th})$
and
![]() $\mathrm {REF}^{\omega }(\mathrm {Th})$
. The main difference will be that we shall work with models with satisfaction classes.
$\mathrm {REF}^{\omega }(\mathrm {Th})$
. The main difference will be that we shall work with models with satisfaction classes.
2.5.2 Reflection and satisfaction classes
Full satisfaction classes in non-standard models embody the conception of a satisfaction relation for
![]() $\mathbf {V}$
. However, as we have already remarked, not every satisfaction class provides us with a reasonable truth predicate for
$\mathbf {V}$
. However, as we have already remarked, not every satisfaction class provides us with a reasonable truth predicate for
![]() $\mathbf {V}$
. One property that one would require from such a truth predicate is the closure under the internal provability relation. In particular the satisfaction relation for
$\mathbf {V}$
. One property that one would require from such a truth predicate is the closure under the internal provability relation. In particular the satisfaction relation for
![]() $\mathbf {V}$
should make true all the (internal) theorems of first-order logic. This corresponds to the sentence
$\mathbf {V}$
should make true all the (internal) theorems of first-order logic. This corresponds to the sentence
being true in a model
![]() $(\mathcal {M}, S)$
. However, as shown for the first time in [Reference Cieśliński4], over
$(\mathcal {M}, S)$
. However, as shown for the first time in [Reference Cieśliński4], over
![]() $\mathrm {CS}^-$
the above sentence implies GR(
$\mathrm {CS}^-$
the above sentence implies GR(
![]() $\mathrm {PA}$
). In particular, in a countable recursively saturated model
$\mathrm {PA}$
). In particular, in a countable recursively saturated model
![]() $\mathcal {M}$
in which there is a proof of inconsistency of
$\mathcal {M}$
in which there is a proof of inconsistency of
![]() $\mathrm {PA}$
there is no such a reasonable class for
$\mathrm {PA}$
there is no such a reasonable class for
![]() $\mathbf {V}$
(although there are many unreasonable ones). A characterization of models admitting a well-behaved satisfaction class was essentially first given by Kotlarski (in [Reference Kotlarski15]):Footnote
9
$\mathbf {V}$
(although there are many unreasonable ones). A characterization of models admitting a well-behaved satisfaction class was essentially first given by Kotlarski (in [Reference Kotlarski15]):Footnote
9
Theorem 2.39 (Kotlarski)
Suppose
![]() $\mathcal {M}$
is a countable recursively saturated model of
$\mathcal {M}$
is a countable recursively saturated model of
![]() $\mathrm {PA}$
. Then, there exists a full satisfaction class S such that
$\mathrm {PA}$
. Then, there exists a full satisfaction class S such that
![]() $(\mathcal {M},S)\models \mathrm {GR}(\mathrm {PA})$
if and only if
$(\mathcal {M},S)\models \mathrm {GR}(\mathrm {PA})$
if and only if
![]() $\mathcal {M}\models \mathrm {REF}^{\omega }(\mathrm {PA})$
.
$\mathcal {M}\models \mathrm {REF}^{\omega }(\mathrm {PA})$
.
![]() $\boxplus $
$\boxplus $
A different natural question is how much induction is required to prove the global reflection for
![]() $\mathrm {PA}$
. Here a partial answer was given by Wcisło in [Reference Wcisło and Łełyk25], who showed that the satisfaction predicate satisfying
$\mathrm {PA}$
. Here a partial answer was given by Wcisło in [Reference Wcisło and Łełyk25], who showed that the satisfaction predicate satisfying
![]() $\mathrm {CS}^- + \mathrm {GR}(\mathrm {PA})$
is definable in
$\mathrm {CS}^- + \mathrm {GR}(\mathrm {PA})$
is definable in
![]() $\mathrm {CS}_0$
:
$\mathrm {CS}_0$
:
Theorem 2.40 (Wcisło)
There exists an
![]() $\mathcal {L}_S$
formula
$\mathcal {L}_S$
formula
![]() $S'(x,y)$
such that
$S'(x,y)$
such that
![]() $\boxplus $
$\boxplus $
In the above
![]() $\phi [S'/S]$
denotes the result of a uniform substitution of a formula
$\phi [S'/S]$
denotes the result of a uniform substitution of a formula
![]() $S'(s,t)$
for each occurrence of a formula
$S'(s,t)$
for each occurrence of a formula
![]() $S(s,t)$
(renaming variables if necessary). In the next section we improve this result and show that GR
$S(s,t)$
(renaming variables if necessary). In the next section we improve this result and show that GR
![]() $(\mathrm {PA})$
is provable in
$(\mathrm {PA})$
is provable in
![]() $\mathrm {EA} + \mathrm {CS}_0$
.
$\mathrm {EA} + \mathrm {CS}_0$
.
3 Provability of the global reflection principle
In this section we confirm Kotlarski’s claim [Reference Kotlarski15] that, over
![]() $\mathrm {EA}$
, the
$\mathrm {EA}$
, the
![]() $\Delta _0$
induction for a satisfaction predicate is enough to prove the Global Reflection Principle for
$\Delta _0$
induction for a satisfaction predicate is enough to prove the Global Reflection Principle for
![]() $\mathrm {PA}$
. We start by explaining the original strategy and our fix. Unless said otherwise, all theories by default extend
$\mathrm {PA}$
. We start by explaining the original strategy and our fix. Unless said otherwise, all theories by default extend
![]() $\mathrm {EA}$
. However, it is very easy to see that
$\mathrm {EA}$
. However, it is very easy to see that
![]() $\mathrm {CS}_0 + \mathrm {EA}\vdash \mathrm {PA}$
, since for every arithmetical formula
$\mathrm {CS}_0 + \mathrm {EA}\vdash \mathrm {PA}$
, since for every arithmetical formula
![]() $\phi (x)$
,
$\phi (x)$
,
![]() $\psi (x):=T(\phi [x])$
is a
$\psi (x):=T(\phi [x])$
is a
![]() $\Delta _0(\mathcal {L}_T+\exp )$
and consequently, we have an induction axiom for it.
$\Delta _0(\mathcal {L}_T+\exp )$
and consequently, we have an induction axiom for it.
3.1 Kotlarski’s proof
Kotlarski’s proof of GR(
![]() $\mathrm {PA})$
in
$\mathrm {PA})$
in
![]() $\mathrm {CS}_0$
starts by observing that each
$\mathrm {CS}_0$
starts by observing that each
![]() $\Delta _0$
inductive satisfaction class makes all (in the sense of the ground model) the axioms of induction true. The argument runs as follows: working in
$\Delta _0$
inductive satisfaction class makes all (in the sense of the ground model) the axioms of induction true. The argument runs as follows: working in
![]() $\mathrm {CS}_0$
fix a formula
$\mathrm {CS}_0$
fix a formula
![]() $\phi (v)$
with a free variable v. Then,
$\phi (v)$
with a free variable v. Then,
![]() $S(\phi (v), [x])$
is a
$S(\phi (v), [x])$
is a
![]() $\Delta _0(\exp )$
formula with a free variable x, where
$\Delta _0(\exp )$
formula with a free variable x, where
![]() $[x]$
denotes the assignment
$[x]$
denotes the assignment
![]() $\{\langle v, x\rangle \}$
. Hence, the following is an axiom of
$\{\langle v, x\rangle \}$
. Hence, the following is an axiom of
![]() $\mathrm {CS}_0$
:
$\mathrm {CS}_0$
:
Here Kotlarski’s proof of
![]() $\mathrm {PA}$
-correctness ends. However, it is not obvious whether the above is equivalent to
$\mathrm {PA}$
-correctness ends. However, it is not obvious whether the above is equivalent to
![]() $S(\mathrm {Ind}(\phi (v)), \varepsilon )$
, where
$S(\mathrm {Ind}(\phi (v)), \varepsilon )$
, where
![]() $\mathrm {Ind}(\psi )$
denotes the axiom of induction for a formula
$\mathrm {Ind}(\psi )$
denotes the axiom of induction for a formula
![]() $\psi $
. Repeated applications of the compositional clauses yield the equivalence of
$\psi $
. Repeated applications of the compositional clauses yield the equivalence of
![]() $S(\mathrm {Ind}(\phi (v)), \varepsilon )$
with
$S(\mathrm {Ind}(\phi (v)), \varepsilon )$
with
Firstly, on the grounds of
![]() $\mathrm {CS}^-$
alone
$\mathrm {CS}^-$
alone
![]() $S(\phi (v),[{0}])$
neither implies
$S(\phi (v),[{0}])$
neither implies
![]() $S(\phi [0/v],\varepsilon )$
nor is implied by it. Similarly with
$S(\phi [0/v],\varepsilon )$
nor is implied by it. Similarly with
![]() $S(\phi (v), [x+1])$
and
$S(\phi (v), [x+1])$
and
![]() $S(\phi [v+1/v], [x])$
. To see this one should think of a nonstandard
$S(\phi [v+1/v], [x])$
. To see this one should think of a nonstandard
![]() $\phi (v)$
in which v occurs nonstandardly deep in
$\phi (v)$
in which v occurs nonstandardly deep in
![]() $\phi (v)$
(i.e., at a nonstandard level of
$\phi (v)$
(i.e., at a nonstandard level of
![]() $\phi (v)'$
s syntactical tree). For example one can take
$\phi (v)'$
s syntactical tree). For example one can take
![]() $\phi (v)$
to be
$\phi (v)$
to be
for a nonstandard element a. This is the first problem.
The second problem lies in showing that a
![]() $\Delta _0$
–inductive satisfaction class is closed under provability, i.e., proving the sentence
$\Delta _0$
–inductive satisfaction class is closed under provability, i.e., proving the sentence
In the above
![]() $\mathrm {Pr}_{\emptyset }^S$
derives from the oracle provability predicate defined in Definition 2.36. Kotlarski’s idea was to work (internally in
$\mathrm {Pr}_{\emptyset }^S$
derives from the oracle provability predicate defined in Definition 2.36. Kotlarski’s idea was to work (internally in
![]() $\mathrm {PA}$
) with a Hilbert-style proof calculus with Modus Ponens as the only rule of reasoning and then using
$\mathrm {PA}$
) with a Hilbert-style proof calculus with Modus Ponens as the only rule of reasoning and then using
![]() $\Delta _0(\exp )$
induction for an
$\Delta _0(\exp )$
induction for an
![]() $\mathcal {L}_S$
formula
$\mathcal {L}_S$
formula
In
![]() $\theta (x,p)$
all quantifiers can be bounded by p,Footnote
10
that can be taken as a parameter. So it is indeed a
$\theta (x,p)$
all quantifiers can be bounded by p,Footnote
10
that can be taken as a parameter. So it is indeed a
![]() $\Delta _0(\exp )$
-formula. In the base step
$\Delta _0(\exp )$
-formula. In the base step
![]() $\phi $
is either a logical axiom or a true sentence, so it’s truth is either trivial (the latter case) or seems to follow from the compositional axioms. In the inductive step, we have to check that if
$\phi $
is either a logical axiom or a true sentence, so it’s truth is either trivial (the latter case) or seems to follow from the compositional axioms. In the inductive step, we have to check that if
![]() $\phi $
and
$\phi $
and
![]() $\phi \rightarrow \psi $
are true, then so is
$\phi \rightarrow \psi $
are true, then so is
![]() $\psi $
. This is indeed guaranteed by the compositional axioms.
$\psi $
. This is indeed guaranteed by the compositional axioms.
However, problems arise while verifying the base step. For example (working in a nonstandard model) we might encounter the following logical axiom:
for some nonstandard formula
![]() $\phi $
and a term t. Then
$\phi $
and a term t. Then
![]() $S(\psi ,\varepsilon )$
is equivalent to
$S(\psi ,\varepsilon )$
is equivalent to
so we encounter problems similar to the ones discussed while dealing with the truth of induction axioms. Moreover, there are more generic problems: if one does not want to incorporate the rule of universal generalisation, then one has to accept universal generalisations of all instances of propositional tautologies as axioms. In particular (working in a nonstandard model
![]() $(\mathcal {M},S)$
) in the base step one might encounter an axiom of the form
$(\mathcal {M},S)$
) in the base step one might encounter an axiom of the form
If it is true that that for any full satisfaction class S on
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $(\mathcal {M},S)\models \forall \alpha \in \mathrm {Asn}(\phi ) S(\phi \vee \neg \phi ,\alpha )$
, inferring that
$(\mathcal {M},S)\models \forall \alpha \in \mathrm {Asn}(\phi ) S(\phi \vee \neg \phi ,\alpha )$
, inferring that
![]() $(\mathcal {M},S)\models S(\xi , \varepsilon )$
requires some argument which cannot be carried out in
$(\mathcal {M},S)\models S(\xi , \varepsilon )$
requires some argument which cannot be carried out in
![]() $\mathrm {CS}^-$
alone.
$\mathrm {CS}^-$
alone.
3.2 The idea
To fill in the gaps in Kotlarski’s reasoning it is sufficient to establish within
![]() $\mathrm {CS}_0$
a kind of induction on the buildup of formulae. Indeed, what we missed were (inter alia) the following properties:
$\mathrm {CS}_0$
a kind of induction on the buildup of formulae. Indeed, what we missed were (inter alia) the following properties:
 $$ \begin{align*} &\forall\phi\in\mathrm{Form}_{\mathcal{L}}\forall \alpha \in \mathrm{Asn}(\phi)\big(S(\phi,\alpha)\equiv S(\phi[\alpha],\varepsilon)\big).\\ &\forall\phi\in\mathrm{Form}^{\leq 1}_{\mathcal{L}}\forall s,t\forall \alpha\in\mathrm{Asn}(s)\forall \beta\in\mathrm{Asn}(t)\big(s^{\alpha} = t^{\beta}\rightarrow S(\phi[s/v],\alpha)\equiv S(\phi[t/v],\beta)\big). \end{align*} $$
$$ \begin{align*} &\forall\phi\in\mathrm{Form}_{\mathcal{L}}\forall \alpha \in \mathrm{Asn}(\phi)\big(S(\phi,\alpha)\equiv S(\phi[\alpha],\varepsilon)\big).\\ &\forall\phi\in\mathrm{Form}^{\leq 1}_{\mathcal{L}}\forall s,t\forall \alpha\in\mathrm{Asn}(s)\forall \beta\in\mathrm{Asn}(t)\big(s^{\alpha} = t^{\beta}\rightarrow S(\phi[s/v],\alpha)\equiv S(\phi[t/v],\beta)\big). \end{align*} $$
The above hold (provably in
![]() $\mathrm {CS}^-$
) if
$\mathrm {CS}^-$
) if
![]() $\phi $
is an atomic formula and clearly are preserved by taking disjunctions, negations, and applying existential quantification. However, in order to secure the step for
$\phi $
is an atomic formula and clearly are preserved by taking disjunctions, negations, and applying existential quantification. However, in order to secure the step for
![]() $\exists $
we need a
$\exists $
we need a
![]() $\Pi _1$
assumption, saying that the equivalence
$\Pi _1$
assumption, saying that the equivalence
holds under an arbitrary assignment
![]() $\alpha $
. It turns out, however, that such assumptions can be expressed with a
$\alpha $
. It turns out, however, that such assumptions can be expressed with a
![]() $\Delta _0$
formula. Firstly, the above is clearly equivalent to
$\Delta _0$
formula. Firstly, the above is clearly equivalent to
Secondly, if S commuted with the blocks of universal quantifiers, the above could have been further reduced to
where
![]() $\mathrm {ucl}(\cdot )$
is a (definable) function which given a formula returns its universal closure. Our problem thus reduces to showing the equivalence between conditions of types (1) and (2). The standard strategy is to use induction on the length of the quantifier prefix. However, the proof of this once again uses
$\mathrm {ucl}(\cdot )$
is a (definable) function which given a formula returns its universal closure. Our problem thus reduces to showing the equivalence between conditions of types (1) and (2). The standard strategy is to use induction on the length of the quantifier prefix. However, the proof of this once again uses
![]() $\Pi _1$
induction. To bypass this problem, we shall first establish commutation with blocks of uniformly bounded universal quantifiers, i.e., the principle
$\Pi _1$
induction. To bypass this problem, we shall first establish commutation with blocks of uniformly bounded universal quantifiers, i.e., the principle
where
![]() $\mathrm {bucl}(\phi ,x)$
denotes the universal closure of
$\mathrm {bucl}(\phi ,x)$
denotes the universal closure of
![]() $\phi $
, in which every quantifier in the prefix is bounded by (the term) x and
$\phi $
, in which every quantifier in the prefix is bounded by (the term) x and
![]() $\alpha \prec [x]_{\phi }$
says that
$\alpha \prec [x]_{\phi }$
says that
![]() $\mathrm {dom}(\alpha )=\mathrm {FV}(\phi )$
and each value of
$\mathrm {dom}(\alpha )=\mathrm {FV}(\phi )$
and each value of
![]() $\alpha $
is less than x. Having this, we will express
$\alpha $
is less than x. Having this, we will express
![]() $\forall \alpha S(\phi ,\alpha )$
in a
$\forall \alpha S(\phi ,\alpha )$
in a
![]() $\Delta _0$
way via
$\Delta _0$
way via
where v is a variable which do not occur in
![]() $\phi $
. We now proceed to the details.
$\phi $
. We now proceed to the details.
3.3 The proof
One more preparation step will be helpful. We shall expand the language
![]() $\mathcal {L}_S$
with symbols for all primitive recursive functions and extend
$\mathcal {L}_S$
with symbols for all primitive recursive functions and extend
![]() $\mathrm {CS}_0$
with the defining equations of them. Let
$\mathrm {CS}_0$
with the defining equations of them. Let
![]() $\mathcal {L}_S^+$
denote the expanded language and
$\mathcal {L}_S^+$
denote the expanded language and
![]() $\mathrm {CS}_0^+$
the extended theory. Since, trivially,
$\mathrm {CS}_0^+$
the extended theory. Since, trivially,
![]() $\mathrm {CS}_0^+$
is
$\mathrm {CS}_0^+$
is
![]() $\mathcal {L}_S$
-conservative over
$\mathcal {L}_S$
-conservative over
![]() $\mathrm {CS}_0$
, it is sufficient to prove (GR(Th)) in
$\mathrm {CS}_0$
, it is sufficient to prove (GR(Th)) in
![]() $\mathrm {CS}_0^+$
. Let us observe that the latter theory proves
$\mathrm {CS}_0^+$
. Let us observe that the latter theory proves
![]() $\Delta _0$
induction for the language with new function symbols.
$\Delta _0$
induction for the language with new function symbols.
Proposition 3.1.
![]() $\mathrm {CS}_0^+\vdash I\Delta _0(\mathcal {L}_S^+)$
.
$\mathrm {CS}_0^+\vdash I\Delta _0(\mathcal {L}_S^+)$
.
Proof. Fix a model
![]() $\mathcal {M}\models \mathrm {CS}_0^+$
and a
$\mathcal {M}\models \mathrm {CS}_0^+$
and a
![]() $\Delta _0(\mathcal {L}_S^+)$
formula with parameters
$\Delta _0(\mathcal {L}_S^+)$
formula with parameters
![]() $\phi (x)$
. Without loss of generality all the terms occurring in
$\phi (x)$
. Without loss of generality all the terms occurring in
![]() $\phi (x)$
are of the form
$\phi (x)$
are of the form
![]() $f(\underline {n},y)$
where
$f(\underline {n},y)$
where
![]() $f(x,y)$
is a two place p.r. function. Let
$f(x,y)$
is a two place p.r. function. Let
![]() $\psi _f(x,y,z)$
be the
$\psi _f(x,y,z)$
be the
![]() $\Delta _0$
formula of
$\Delta _0$
formula of
![]() $\mathcal {L}$
defining the graph of f. Fix an arbitrary
$\mathcal {L}$
defining the graph of f. Fix an arbitrary
![]() $a\in M$
, assume that
$a\in M$
, assume that
![]() $\phi (a)$
holds, and let b be greater than a and all parameters from
$\phi (a)$
holds, and let b be greater than a and all parameters from
![]() $\phi (x)$
. Without loss of generality assume that b is nonstandard. Let c be such that
$\phi (x)$
. Without loss of generality assume that b is nonstandard. Let c be such that
Now let
![]() $\phi '(x)$
result from
$\phi '(x)$
result from
![]() $\phi (x)$
by recursively changing all subformulae of
$\phi (x)$
by recursively changing all subformulae of
![]() $\phi (x)$
of the form
$\phi (x)$
of the form
into
where z, w are fresh variables.
![]() $\phi '(x)$
is a
$\phi '(x)$
is a
![]() $\Delta _0(\mathcal {L}_S)$
formula and clearly we have
$\Delta _0(\mathcal {L}_S)$
formula and clearly we have
Hence, since
![]() $a<b$
and
$a<b$
and
![]() $\phi (a)$
holds,
$\phi (a)$
holds,
![]() $\phi '(a)$
holds as well. Since for
$\phi '(a)$
holds as well. Since for
![]() $\phi '(x)$
we have an induction axiom there is the least
$\phi '(x)$
we have an induction axiom there is the least
![]() $d<a$
such that
$d<a$
such that
![]() $\phi '(d)$
holds. Hence d is the least element satisfying
$\phi '(d)$
holds. Hence d is the least element satisfying
![]() $\phi (x)$
.□
$\phi (x)$
.□
In the proof below we shall use the following primitive recursive functions (we identify p.r. relations with their characteristic functions):
-
•
 $\prec $
is a primitive recursive product ordering on functions. That is, if
$\prec $
is a primitive recursive product ordering on functions. That is, if
 $\alpha $
and
$\alpha $
and
 $\beta $
are two functions, then
$\beta $
are two functions, then
 $\alpha \prec \beta $
holds if
$\alpha \prec \beta $
holds if
 $\alpha $
is smaller than
$\alpha $
is smaller than
 $\beta $
in the product ordering, i.e.,
$\beta $
in the product ordering, i.e.,  $$\begin{align*}\mathrm{dom}(\alpha)=\mathrm{dom}(\beta) \wedge \forall x\in\mathrm{dom}(\alpha)\ \ \alpha(x)<\beta(x).\end{align*}$$
$$\begin{align*}\mathrm{dom}(\alpha)=\mathrm{dom}(\beta) \wedge \forall x\in\mathrm{dom}(\alpha)\ \ \alpha(x)<\beta(x).\end{align*}$$
 $\preccurlyeq $
is the partial ordering based on
$\preccurlyeq $
is the partial ordering based on
 $\prec $
.
$\prec $
.
-
•
 $\mathrm {bucl}(\phi ,x)$
denotes the universal closure of
$\mathrm {bucl}(\phi ,x)$
denotes the universal closure of
 $\phi $
, in which every quantifier in the prefix is bounded by (the term) x.
$\phi $
, in which every quantifier in the prefix is bounded by (the term) x. -
•
 $\mathrm {bucl}(\phi , x, c)$
returns the formula where
$\mathrm {bucl}(\phi , x, c)$
returns the formula where $$\begin{align*}\forall v_{i_1}<x\ldots \forall v_{i_y}<x\ \ \phi,\end{align*}$$
$$\begin{align*}\forall v_{i_1}<x\ldots \forall v_{i_y}<x\ \ \phi,\end{align*}$$
 $x_{i_1},\ldots , x_{i_y}$
are all the elements of the set c listed in the order of decreasing indices (i.e.,
$x_{i_1},\ldots , x_{i_y}$
are all the elements of the set c listed in the order of decreasing indices (i.e.,
 $i_y<i_{y-1}<\cdots < i_1$
). In particular x has to be a term and c a set of variables. Officially
$i_y<i_{y-1}<\cdots < i_1$
). In particular x has to be a term and c a set of variables. Officially
 $\forall x< t \psi $
abbreviates
$\forall x< t \psi $
abbreviates
 $\forall x\big (x<t \rightarrow \psi )$
; hence the above formula is slightly more complicated than it seems to be. Moreover c need not contain uniquely variables which are free in
$\forall x\big (x<t \rightarrow \psi )$
; hence the above formula is slightly more complicated than it seems to be. Moreover c need not contain uniquely variables which are free in
 $\phi $
; hence some of the quantifiers in the prefix of
$\phi $
; hence some of the quantifiers in the prefix of
 $\mathrm {bucl}(\phi , x, c)$
might be dummy.
$\mathrm {bucl}(\phi , x, c)$
might be dummy.
-
•
 $[x]_{c}$
returns the constant function assigning value x to every variable from the set c.
$[x]_{c}$
returns the constant function assigning value x to every variable from the set c. -
• For a coded set of variables c and a number a,
 $c{\uparrow _a}$
denotes the set consisting of first a elements of c and
$c{\uparrow _a}$
denotes the set consisting of first a elements of c and
 $c{\downarrow ^{a}}$
the set consisting of last a elements of c. For simplicity we assume that the ordering of variables is given by their indices.
$c{\downarrow ^{a}}$
the set consisting of last a elements of c. For simplicity we assume that the ordering of variables is given by their indices. -
• Syntactical relations mentioned at the beginning of Section 2.
Lemma 3.2 (
 $\mathrm {CS}_0^+$
)
$\mathrm {CS}_0^+$
)
For every formula
![]() $\phi $
, every a, every set of variables c, and every assignment
$\phi $
, every a, every set of variables c, and every assignment
![]() $\alpha $
for
$\alpha $
for
![]() $\mathrm {bucl}(\phi , \underline {a}, c)$
,
$\mathrm {bucl}(\phi , \underline {a}, c)$
,
Proof. Fix
![]() $\phi ,a,c$
and let b be the cardinality of c. We formalize the standard argument on the length of the quantifier prefix in
$\phi ,a,c$
and let b be the cardinality of c. We formalize the standard argument on the length of the quantifier prefix in
![]() $\mathrm {bucl}(\phi , \underline {a}, c)$
: starting from the assumption that
$\mathrm {bucl}(\phi , \underline {a}, c)$
: starting from the assumption that
![]() $\forall \beta \prec [a]_{c} S(\phi ,\alpha \cup \beta {{\upharpoonright _{\cdot }}})$
we check that we can prefix
$\forall \beta \prec [a]_{c} S(\phi ,\alpha \cup \beta {{\upharpoonright _{\cdot }}})$
we check that we can prefix
![]() $\phi $
with b quantifiers and arrive at
$\phi $
with b quantifiers and arrive at
![]() $S(\mathrm {bucl}(\phi , \underline {a}, c),\alpha )$
. Formally, we use induction on y up to b in the
$S(\mathrm {bucl}(\phi , \underline {a}, c),\alpha )$
. Formally, we use induction on y up to b in the
![]() $\Delta _0(\mathcal {L}_S^+)$
-formula
$\Delta _0(\mathcal {L}_S^+)$
-formula
Observe that
![]() $c{\uparrow _{b}} = c{\downarrow ^{b}} = c$
,
$c{\uparrow _{b}} = c{\downarrow ^{b}} = c$
,
![]() $c{\downarrow ^{0}} = \emptyset $
. Hence
$c{\downarrow ^{0}} = \emptyset $
. Hence
![]() $\mathrm {bucl}(\phi , \underline {a}, c{\uparrow _{0}}) = \phi $
,
$\mathrm {bucl}(\phi , \underline {a}, c{\uparrow _{0}}) = \phi $
,
![]() $[a]_{c{\downarrow ^{b}}} = [a]_{c}$
. Moreover,
$[a]_{c{\downarrow ^{b}}} = [a]_{c}$
. Moreover,
![]() $\varepsilon $
is the unique assignment
$\varepsilon $
is the unique assignment
![]() $\gamma $
satisfying
$\gamma $
satisfying
![]() $\gamma \prec [a]_{\emptyset }$
. Consequently, for
$\gamma \prec [a]_{\emptyset }$
. Consequently, for
![]() $y=b$
the left-hand side is equivalent to
$y=b$
the left-hand side is equivalent to
![]() $S(\mathrm {bucl}(\phi , \underline {a}, c), \alpha )$
and for
$S(\mathrm {bucl}(\phi , \underline {a}, c), \alpha )$
and for
![]() $y=0$
both sides of the equivalence are the same.
$y=0$
both sides of the equivalence are the same.
Assume that the inductive hypothesis holds for d and let
![]() ${i_d}$
be the index of the
${i_d}$
be the index of the
![]() $(d+1)$
-st variable in c. Observe that
$(d+1)$
-st variable in c. Observe that
Hence by compositional axioms,
![]() $\forall \beta \prec [a]_{c{\downarrow ^{b-(d+1)}}}S(\mathrm {bucl}(\phi , \underline {a}, c{\uparrow _{d+1}}), \alpha \cup \beta {{\upharpoonright _{\cdot }}})$
is equivalent to
$\forall \beta \prec [a]_{c{\downarrow ^{b-(d+1)}}}S(\mathrm {bucl}(\phi , \underline {a}, c{\uparrow _{d+1}}), \alpha \cup \beta {{\upharpoonright _{\cdot }}})$
is equivalent to
Observe that the above is equivalent to
which, by induction hypothesis, is equivalent to
![]() $\forall \beta \prec [a]_{c} S(\phi ,\alpha \cup \beta {{\upharpoonright _{\cdot }}})$
.□
$\forall \beta \prec [a]_{c} S(\phi ,\alpha \cup \beta {{\upharpoonright _{\cdot }}})$
.□
The above lemma motivates the following abbreviation: we define
In the above v is a variable with the least index among those which do not occur in
![]() $\phi $
. In particular
$\phi $
. In particular
![]() $\mathrm {cl}(x,y)$
is a (partial) primitive recursive function, so we have a symbol for it in
$\mathrm {cl}(x,y)$
is a (partial) primitive recursive function, so we have a symbol for it in
![]() $\mathrm {CS}_0^+$
.
$\mathrm {CS}_0^+$
.
![]() $\mathrm {cl}(\phi )$
abbreviates
$\mathrm {cl}(\phi )$
abbreviates
![]() $\mathrm {cl}(\phi ,\mathrm {FV}(\phi ))$
.
$\mathrm {cl}(\phi ,\mathrm {FV}(\phi ))$
.
Now, the following corollary clearly follows from Lemma 3.2.
Corollary 3.3 (
 $\mathrm {CS}_0^+$
)
$\mathrm {CS}_0^+$
)
For all
![]() $\phi $
,
$\phi $
,
![]() $c\subseteq \mathrm {Var}$
and
$c\subseteq \mathrm {Var}$
and
![]() $\alpha \in \mathrm {Asn}(\mathrm {cl}(\phi , c))$
it holds that
$\alpha \in \mathrm {Asn}(\mathrm {cl}(\phi , c))$
it holds that
![]() $S(\mathrm {cl}(\phi , c), \alpha ) \equiv \forall \beta \in \mathrm {Asn}\big (\mathrm {dom}(\beta )= c \rightarrow S(\phi ,\alpha \cup \beta {{\upharpoonright _{\cdot }}})\big )$
.
$S(\mathrm {cl}(\phi , c), \alpha ) \equiv \forall \beta \in \mathrm {Asn}\big (\mathrm {dom}(\beta )= c \rightarrow S(\phi ,\alpha \cup \beta {{\upharpoonright _{\cdot }}})\big )$
.
Proof. Fix
![]() $\phi $
and c. By the compositional axioms and Lemma 3.2
$\phi $
and c. By the compositional axioms and Lemma 3.2
![]() $S(\forall v\mathrm {bucl}(\phi , v, c), \alpha )$
is equivalent to
$S(\forall v\mathrm {bucl}(\phi , v, c), \alpha )$
is equivalent to
![]() $\forall x \forall \beta \prec [x]_{c} S(\phi ,\alpha \cup \beta {\upharpoonright _{\cdot }})$
, which is clearly equivalent to
$\forall x \forall \beta \prec [x]_{c} S(\phi ,\alpha \cup \beta {\upharpoonright _{\cdot }})$
, which is clearly equivalent to
![]() $\forall \beta \big (\mathrm {dom}(\beta ) = c\rightarrow S(\phi ,\alpha \cup \beta {\upharpoonright _{\cdot }}))$
, since each assignment for
$\forall \beta \big (\mathrm {dom}(\beta ) = c\rightarrow S(\phi ,\alpha \cup \beta {\upharpoonright _{\cdot }}))$
, since each assignment for
![]() $\phi $
is dominated by an assignment of the form
$\phi $
is dominated by an assignment of the form
![]() $[a]_{\phi }$
for some a.□
$[a]_{\phi }$
for some a.□
Now, we demonstrate how to use the above corollary for establishing, within
![]() $\mathrm {CS}_0^+$
, the induction on the buildup of formulae. It will be convenient to isolate a few more definitions.
$\mathrm {CS}_0^+$
, the induction on the buildup of formulae. It will be convenient to isolate a few more definitions.
Definition 3.4 (
 $\mathrm {PA}$
)
$\mathrm {PA}$
)
An occurrence of a variable v in a formula
![]() $\phi $
(term s) is a path in a syntactic tree of
$\phi $
(term s) is a path in a syntactic tree of
![]() $\phi $
(term s) ending with v. An occurrence of a subformula
$\phi $
(term s) ending with v. An occurrence of a subformula
![]() $\psi $
of a formula
$\psi $
of a formula
![]() $\phi $
is defined analogously. The fact that
$\phi $
is defined analogously. The fact that
![]() $\psi $
is a subformula occurrence in
$\psi $
is a subformula occurrence in
![]() $\phi $
is denoted
$\phi $
is denoted
![]() $\psi \leq _o\phi $
. The (coded) set of occurrences of variables in a formula
$\psi \leq _o\phi $
. The (coded) set of occurrences of variables in a formula
![]() $\phi $
(term s) will be denoted Occ(
$\phi $
(term s) will be denoted Occ(
![]() $\phi )$
(Occ(s)).
$\phi )$
(Occ(s)).
A substitution of terms for a formula
![]() $\phi $
is a (coded) function
$\phi $
is a (coded) function
![]() $\eta $
such that
$\eta $
such that
![]() $\mathrm {dom}(\eta )\subseteq \mathrm {Occ}(\phi )$
and
$\mathrm {dom}(\eta )\subseteq \mathrm {Occ}(\phi )$
and
![]() $\mathrm {rg}(\eta )\subseteq \mathrm {ClTerm}$
. For a formula
$\mathrm {rg}(\eta )\subseteq \mathrm {ClTerm}$
. For a formula
![]() $\phi $
,
$\phi $
,
![]() $\phi [\eta ]$
denotes the result of applying
$\phi [\eta ]$
denotes the result of applying
![]() $\eta $
to
$\eta $
to
![]() $\phi $
.
$\phi $
.
If
![]() $\eta $
is a substitution of terms for
$\eta $
is a substitution of terms for
![]() $\phi $
and
$\phi $
and
![]() $\psi $
is a subformula of
$\psi $
is a subformula of
![]() $\phi $
, then
$\phi $
, then
![]() $\eta $
naturally gives rise to a substitution of terms for
$\eta $
naturally gives rise to a substitution of terms for
![]() $\psi $
(we look only at those paths that pass through
$\psi $
(we look only at those paths that pass through
![]() $\psi $
and take their suffixes starting from
$\psi $
and take their suffixes starting from
![]() $\psi $
). Such a substitution will be denoted by
$\psi $
). Such a substitution will be denoted by
![]() $\eta {\upharpoonright _{\psi }}$
or simply
$\eta {\upharpoonright _{\psi }}$
or simply
![]() $\eta {\upharpoonright _{\cdot }}$
if it is clear from context which formula should occur in the subscript.
$\eta {\upharpoonright _{\cdot }}$
if it is clear from context which formula should occur in the subscript.
The substitution of terms
![]() $\eta $
for a formula
$\eta $
for a formula
![]() $\phi $
agrees with an assignment
$\phi $
agrees with an assignment
![]() $\alpha \in \mathrm {Asn}(\phi )$
if whenever
$\alpha \in \mathrm {Asn}(\phi )$
if whenever
![]() $p\in \mathrm {dom}(\eta )$
is an occurrence of a variable v in
$p\in \mathrm {dom}(\eta )$
is an occurrence of a variable v in
![]() $\phi $
, then
$\phi $
, then
![]() $({\eta (p)})^{\circ } = \alpha (v)$
. Let
$({\eta (p)})^{\circ } = \alpha (v)$
. Let
![]() $v_p$
denote the variable whose occurrence p is.
$v_p$
denote the variable whose occurrence p is.
Let
![]() $\phi $
be a formula and
$\phi $
be a formula and
![]() $\psi $
an occurrence of its subformula.
$\psi $
an occurrence of its subformula.
![]() $\mathrm {Var}(\phi /\psi )$
denotes the (coded) set of variables whose occurrence in
$\mathrm {Var}(\phi /\psi )$
denotes the (coded) set of variables whose occurrence in
![]() $\psi $
is free in
$\psi $
is free in
![]() $\psi $
but bounded in
$\psi $
but bounded in
![]() $\phi $
.
$\phi $
.
For a subformula
![]() $\psi $
of
$\psi $
of
![]() $\phi $
define
$\phi $
define
![]() $\mathrm {cl}_{\phi }(\psi ):= \forall v^\frown \mathrm {bucl}(\psi , v, \mathrm {Var}(\phi /\psi ))$
where v is the least variable not occurring in
$\mathrm {cl}_{\phi }(\psi ):= \forall v^\frown \mathrm {bucl}(\psi , v, \mathrm {Var}(\phi /\psi ))$
where v is the least variable not occurring in
![]() $\phi $
.
$\phi $
.
![]() $\triangle $
$\triangle $
Example 3.5. Let
![]() $\psi := \big (x_0 = x_1 \wedge \exists x_2( x_2 = ((0+1)+1)\cdot x_0)\big )$
and
$\psi := \big (x_0 = x_1 \wedge \exists x_2( x_2 = ((0+1)+1)\cdot x_0)\big )$
and
![]() $\phi := (\forall x_0 \psi ) \wedge x_0 = x_0$
. Then
$\phi := (\forall x_0 \psi ) \wedge x_0 = x_0$
. Then
Consequently
![]() $\mathrm {cl}_{\phi }(\psi ) = \forall x_3\forall x_0<x_3 \big (x_0 = x_1 \wedge \exists x_2 \big (x_2 = ((0+1)+1)\cdot x_0\big )\big )$
.
$\mathrm {cl}_{\phi }(\psi ) = \forall x_3\forall x_0<x_3 \big (x_0 = x_1 \wedge \exists x_2 \big (x_2 = ((0+1)+1)\cdot x_0\big )\big )$
.
![]() $\triangle $
$\triangle $
Lemma 3.6 (
 $\mathrm {CS}_0^+$
)
$\mathrm {CS}_0^+$
)
Assume that
![]() $\phi $
is a formula,
$\phi $
is a formula,
![]() $\zeta \in \mathrm {Asn}(\phi )$
, and
$\zeta \in \mathrm {Asn}(\phi )$
, and
![]() $\eta $
is a substitution of terms for
$\eta $
is a substitution of terms for
![]() $\phi $
which agrees with
$\phi $
which agrees with
![]() $\zeta $
. Then it holds that
$\zeta $
. Then it holds that
![]() $S(\phi \equiv (\phi [\eta ]),\zeta )$
.
$S(\phi \equiv (\phi [\eta ]),\zeta )$
.
Proof. Fix a formula
![]() $\phi $
, any assignment
$\phi $
, any assignment
![]() $\zeta \in \mathrm {Asn}(\phi )$
, and a substitution of terms
$\zeta \in \mathrm {Asn}(\phi )$
, and a substitution of terms
![]() $\eta $
which agrees with
$\eta $
which agrees with
![]() $\zeta $
. We reason by induction on y in the
$\zeta $
. We reason by induction on y in the
![]() $\Delta _0(\mathcal {L}_S^+)$
-formula
$\Delta _0(\mathcal {L}_S^+)$
-formula
Let us observe that
![]() $S(\mathrm {cl}_{\phi }(\psi \equiv \psi [\eta {{\upharpoonright _{\psi }}}]),\zeta {{\upharpoonright _{\cdot }}})$
makes sense: each occurrence of a free variable of
$S(\mathrm {cl}_{\phi }(\psi \equiv \psi [\eta {{\upharpoonright _{\psi }}}]),\zeta {{\upharpoonright _{\cdot }}})$
makes sense: each occurrence of a free variable of
![]() $\psi \equiv \psi [\eta {{\upharpoonright _{\psi }}}]$
is either an occurrence of a free variable of
$\psi \equiv \psi [\eta {{\upharpoonright _{\psi }}}]$
is either an occurrence of a free variable of
![]() $\phi $
and hence the variable gets assigned a value by
$\phi $
and hence the variable gets assigned a value by
![]() $\zeta {{\upharpoonright _{\psi }}}$
, or is bounded in
$\zeta {{\upharpoonright _{\psi }}}$
, or is bounded in
![]() $\phi $
and so, belonging to
$\phi $
and so, belonging to
![]() $\mathrm {Var}(\phi /\psi )$
, gets bounded by a quantifier occurring in a prefix of
$\mathrm {Var}(\phi /\psi )$
, gets bounded by a quantifier occurring in a prefix of
![]() $\mathrm {cl}_{\phi }(\psi \equiv \psi [\eta {{\upharpoonright _{\psi }}}])$
.
$\mathrm {cl}_{\phi }(\psi \equiv \psi [\eta {{\upharpoonright _{\psi }}}])$
.
Let z be the least variable not occurring in
![]() $\phi $
. We show that
$\phi $
. We show that
![]() $\theta (0)$
holds. The unique sentences of depth
$\theta (0)$
holds. The unique sentences of depth
![]() $0$
are atomic sentences, so let us fix two terms
$0$
are atomic sentences, so let us fix two terms
![]() $s,t$
and argue that
$s,t$
and argue that
holds. Let
![]() $c = \mathrm {Var}(\phi /\psi )$
. Consequently
$c = \mathrm {Var}(\phi /\psi )$
. Consequently
Call the above sentence on the right-hand side
![]() $\xi $
. By Corollary 3.3 we know that
$\xi $
. By Corollary 3.3 we know that
![]() $S(\xi , \zeta {{\upharpoonright _{\cdot }}})$
is equivalent to
$S(\xi , \zeta {{\upharpoonright _{\cdot }}})$
is equivalent to
The last sentence holds, since, by the compositional conditions for atomic sentences and connectives, it is equivalent to the assertion that for every
![]() $\alpha \in \mathrm {Asn}$
such that
$\alpha \in \mathrm {Asn}$
such that
![]() $\mathrm {dom}(\alpha )=c$
$\mathrm {dom}(\alpha )=c$
To avoid double restrictions let us abbreviate
![]() $\zeta {\upharpoonright _{\xi }}$
with
$\zeta {\upharpoonright _{\xi }}$
with
![]() $\zeta _{\xi }$
. Observe that
$\zeta _{\xi }$
. Observe that
![]() $\zeta _{\xi }{\upharpoonright _{s=t}} = \zeta _{\xi }$
. To prove ($) it is sufficient to show that each occurrence of a variable in either s or t gets assigned the same value on both sides. This holds since if
$\zeta _{\xi }{\upharpoonright _{s=t}} = \zeta _{\xi }$
. To prove ($) it is sufficient to show that each occurrence of a variable in either s or t gets assigned the same value on both sides. This holds since if
![]() $o\in Occ(s)$
, then either
$o\in Occ(s)$
, then either
![]() $o\in \mathrm {dom}(\eta {\upharpoonright _{s=t}})$
or not. In the former case by our assumption
$o\in \mathrm {dom}(\eta {\upharpoonright _{s=t}})$
or not. In the former case by our assumption
![]() $\zeta _{\xi }(v_o)=\zeta (v_o) = ({\eta (o)})^{\circ }$
. If
$\zeta _{\xi }(v_o)=\zeta (v_o) = ({\eta (o)})^{\circ }$
. If
![]() $o\notin \mathrm {dom}(\eta {\upharpoonright _{s=t}})$
, then
$o\notin \mathrm {dom}(\eta {\upharpoonright _{s=t}})$
, then
![]() $o\notin \mathrm {dom}(\eta )$
and
$o\notin \mathrm {dom}(\eta )$
and
![]() ${v_o\in \mathrm {dom}(\zeta _{\xi }{{\upharpoonright _{s=t[\eta {{\upharpoonright _{s=t}}}]}}}\cup \alpha )\subseteq \mathrm {dom}(\zeta _{\xi }\cup \alpha )}$
, and hence o get assigned the same value on both sides of the equivalence. Consequently
${v_o\in \mathrm {dom}(\zeta _{\xi }{{\upharpoonright _{s=t[\eta {{\upharpoonright _{s=t}}}]}}}\cup \alpha )\subseteq \mathrm {dom}(\zeta _{\xi }\cup \alpha )}$
, and hence o get assigned the same value on both sides of the equivalence. Consequently
The same holds for t in place of s. Now assume that the thesis holds for y and consider (an occurrence of)
![]() $\psi $
of depth
$\psi $
of depth
![]() $y+1$
. We shall do the case of
$y+1$
. We shall do the case of
![]() $\psi = \psi _1\vee \psi _2$
and
$\psi = \psi _1\vee \psi _2$
and
![]() $\psi = \exists v \psi _3$
. We treat them simultaneously. As previously put
$\psi = \exists v \psi _3$
. We treat them simultaneously. As previously put
![]() $\xi := \mathrm {cl}_{\phi }\big (\psi \equiv (\psi [\eta {{\upharpoonright _{\psi }}}])\big )$
,
$\xi := \mathrm {cl}_{\phi }\big (\psi \equiv (\psi [\eta {{\upharpoonright _{\psi }}}])\big )$
,
![]() $\xi _i := \mathrm {cl}_{\phi }\big (\psi _i\equiv (\psi _i[\eta {{\upharpoonright _{\psi _i}}}])\big )$
,
$\xi _i := \mathrm {cl}_{\phi }\big (\psi _i\equiv (\psi _i[\eta {{\upharpoonright _{\psi _i}}}])\big )$
,
![]() $c = \mathrm {Var}(\phi /\psi )$
, and
$c = \mathrm {Var}(\phi /\psi )$
, and
![]() $c_i = \mathrm {Var}(\phi /\psi _i)$
. Applying the inductive assumption and Corollary 3.3 we have for
$c_i = \mathrm {Var}(\phi /\psi _i)$
. Applying the inductive assumption and Corollary 3.3 we have for
![]() $i\in \{1,2,3\}$
$i\in \{1,2,3\}$
Now observe that
![]() $\zeta {\upharpoonright _{\xi _i}}{\upharpoonright _{\psi _i}} = \zeta {\upharpoonright _{\xi _i}}$
and if
$\zeta {\upharpoonright _{\xi _i}}{\upharpoonright _{\psi _i}} = \zeta {\upharpoonright _{\xi _i}}$
and if
![]() $\mathrm {dom}(\alpha ) = c_i$
, then
$\mathrm {dom}(\alpha ) = c_i$
, then
![]() $\alpha {\upharpoonright _{\psi _i}} = \alpha $
. By this and compositional conditions, for arbitrary
$\alpha {\upharpoonright _{\psi _i}} = \alpha $
. By this and compositional conditions, for arbitrary
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mathrm {dom}(\alpha ) = c_i$
, the succedent of the above implication is equivalent to
$\mathrm {dom}(\alpha ) = c_i$
, the succedent of the above implication is equivalent to
In the case
![]() $\psi = \psi _1\vee \psi _2$
we have
$\psi = \psi _1\vee \psi _2$
we have
![]() $c = c_1\cup c_2$
. Now, by compositional conditions, the following are equivalent for an arbitrary assignment
$c = c_1\cup c_2$
. Now, by compositional conditions, the following are equivalent for an arbitrary assignment
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mathrm {dom}(\alpha ) = c$
:
$\mathrm {dom}(\alpha ) = c$
:
 $$ \begin{align} \left(\bigvee_{i\in\{0,1\}} S(\psi_i, \zeta{{\upharpoonright_{\xi}}}{{\upharpoonright_{\psi_i}}}\cup\alpha{{\upharpoonright_{\psi_i}}})\right) &\equiv\left( \bigvee_{i\in\{0,1\}} S(\psi_i[\eta{{\upharpoonright_{\psi_i}}}], \zeta{{\upharpoonright_{\xi}}}{{\upharpoonright_{\psi_i[\eta{{\upharpoonright_{\psi_i}}}]}}}\cup\alpha{{\upharpoonright_{\psi_i[\eta{{\upharpoonright_{\psi_i}}}]}}})\right). \end{align} $$
$$ \begin{align} \left(\bigvee_{i\in\{0,1\}} S(\psi_i, \zeta{{\upharpoonright_{\xi}}}{{\upharpoonright_{\psi_i}}}\cup\alpha{{\upharpoonright_{\psi_i}}})\right) &\equiv\left( \bigvee_{i\in\{0,1\}} S(\psi_i[\eta{{\upharpoonright_{\psi_i}}}], \zeta{{\upharpoonright_{\xi}}}{{\upharpoonright_{\psi_i[\eta{{\upharpoonright_{\psi_i}}}]}}}\cup\alpha{{\upharpoonright_{\psi_i[\eta{{\upharpoonright_{\psi_i}}}]}}})\right). \end{align} $$
Now observe that
![]() $\zeta {{\upharpoonright _{\xi }}}{{\upharpoonright _{\psi _i}}} = \zeta {{\upharpoonright _{\xi _i}}}{{\upharpoonright _{\psi _i}}} = \zeta {\upharpoonright _{\xi _i}}$
. Indeed, v is a free variable in
$\zeta {{\upharpoonright _{\xi }}}{{\upharpoonright _{\psi _i}}} = \zeta {{\upharpoonright _{\xi _i}}}{{\upharpoonright _{\psi _i}}} = \zeta {\upharpoonright _{\xi _i}}$
. Indeed, v is a free variable in
![]() $\mathrm {cl}_{\phi }(\psi \equiv \psi [\eta {{\upharpoonright _{\psi }}}])$
(
$\mathrm {cl}_{\phi }(\psi \equiv \psi [\eta {{\upharpoonright _{\psi }}}])$
(
![]() $=\xi $
) and a free variable in
$=\xi $
) and a free variable in
![]() $\psi _i$
, if and only if v is a free variable in
$\psi _i$
, if and only if v is a free variable in
![]() $\mathrm {cl}_{\phi }(\psi _i\equiv \psi _i[\eta {\upharpoonright _{\psi _i}}])$
(
$\mathrm {cl}_{\phi }(\psi _i\equiv \psi _i[\eta {\upharpoonright _{\psi _i}}])$
(
![]() $=\xi _i$
) and in
$=\xi _i$
) and in
![]() $\psi _i$
. Hence
$\psi _i$
. Hence
![]() $\mathrm {dom}(\zeta {{\upharpoonright _{\xi }}}{{\upharpoonright _{\psi _i}}})= \mathrm {dom}(\zeta {{\upharpoonright _{\xi _i}}}{{\upharpoonright _{\psi _i}}})$
and this completes our claim. The same reasoning shows also that
$\mathrm {dom}(\zeta {{\upharpoonright _{\xi }}}{{\upharpoonright _{\psi _i}}})= \mathrm {dom}(\zeta {{\upharpoonright _{\xi _i}}}{{\upharpoonright _{\psi _i}}})$
and this completes our claim. The same reasoning shows also that
![]() $\zeta {{\upharpoonright _{\xi }}}{{\upharpoonright _{\psi _i[\eta {\upharpoonright _{\psi _i}}]}}} = \zeta {{\upharpoonright _{\xi _i}}}{{\upharpoonright _{\psi _i[\eta {\upharpoonright _{\psi _i}}]}}}$
. Finally, if
$\zeta {{\upharpoonright _{\xi }}}{{\upharpoonright _{\psi _i[\eta {\upharpoonright _{\psi _i}}]}}} = \zeta {{\upharpoonright _{\xi _i}}}{{\upharpoonright _{\psi _i[\eta {\upharpoonright _{\psi _i}}]}}}$
. Finally, if
![]() $\mathrm {dom}(\alpha ) = c$
, then
$\mathrm {dom}(\alpha ) = c$
, then
![]() $\mathrm {dom}(\alpha {\upharpoonright _{\psi _i}}) = c_i$
. It follows that (3) implies the above condition
$\mathrm {dom}(\alpha {\upharpoonright _{\psi _i}}) = c_i$
. It follows that (3) implies the above condition
![]() $(5)$
and the case of
$(5)$
and the case of
![]() $\vee $
is done.
$\vee $
is done.
In the case of
![]() $\exists $
, we observe that
$\exists $
, we observe that
 $$ \begin{align*} c_3 = \left\{\begin{array}{l} c\cup \{v\},\ \mathrm{ if }\ v\in\ \mathrm{FV}(\psi_3),\\ c,\ \mathrm{ otherwise.}\end{array} \right. \end{align*} $$
$$ \begin{align*} c_3 = \left\{\begin{array}{l} c\cup \{v\},\ \mathrm{ if }\ v\in\ \mathrm{FV}(\psi_3),\\ c,\ \mathrm{ otherwise.}\end{array} \right. \end{align*} $$
The following are equivalent for every
![]() $\alpha \in \mathrm {Asn}$
such that
$\alpha \in \mathrm {Asn}$
such that
![]() $\mathrm {dom}(\alpha ) = c$
:
$\mathrm {dom}(\alpha ) = c$
:
 $$ \begin{align} &\bigg(\exists \beta\geq_v(\alpha\cup \zeta{{\upharpoonright_{\xi}}}){\upharpoonright_{\exists v \psi_3}} S(\psi_3, \beta{{\upharpoonright_{\psi_3}}})\bigg) \nonumber\\ & \quad \equiv \bigg(\exists \beta\geq_v(\alpha\cup \zeta{{\upharpoonright_{\xi}}}){{\upharpoonright_{\exists v\psi_3[\eta{{\upharpoonright_{\exists v\psi_3}}}]}}} S(\psi_3[\eta{{\upharpoonright_{\psi_3}}}], \beta{{\upharpoonright_{\psi_3[\eta{{\upharpoonright_{\psi_3}}}]}}})\bigg). \end{align} $$
$$ \begin{align} &\bigg(\exists \beta\geq_v(\alpha\cup \zeta{{\upharpoonright_{\xi}}}){\upharpoonright_{\exists v \psi_3}} S(\psi_3, \beta{{\upharpoonright_{\psi_3}}})\bigg) \nonumber\\ & \quad \equiv \bigg(\exists \beta\geq_v(\alpha\cup \zeta{{\upharpoonright_{\xi}}}){{\upharpoonright_{\exists v\psi_3[\eta{{\upharpoonright_{\exists v\psi_3}}}]}}} S(\psi_3[\eta{{\upharpoonright_{\psi_3}}}], \beta{{\upharpoonright_{\psi_3[\eta{{\upharpoonright_{\psi_3}}}]}}})\bigg). \end{align} $$
 $$ \begin{align} &\bigg(\exists \beta\geq_v(\alpha\cup \zeta{{\upharpoonright_{\xi}}}) S(\psi_3, \beta{{\upharpoonright_{\psi_3}}})\bigg)\nonumber \\ & \quad \equiv \bigg(\exists \beta\geq_v(\alpha\cup \zeta{{\upharpoonright_{\xi}}}){{\upharpoonright_{\exists v\psi_3[\eta{{\upharpoonright_{\exists v\psi_3}}}]}}} S(\psi_3[\eta{{\upharpoonright_{\psi_3}}}], \beta{{\upharpoonright_{\psi_3[\eta{{\upharpoonright_{\psi_3}}}]}}})\bigg). \end{align} $$
$$ \begin{align} &\bigg(\exists \beta\geq_v(\alpha\cup \zeta{{\upharpoonright_{\xi}}}) S(\psi_3, \beta{{\upharpoonright_{\psi_3}}})\bigg)\nonumber \\ & \quad \equiv \bigg(\exists \beta\geq_v(\alpha\cup \zeta{{\upharpoonright_{\xi}}}){{\upharpoonright_{\exists v\psi_3[\eta{{\upharpoonright_{\exists v\psi_3}}}]}}} S(\psi_3[\eta{{\upharpoonright_{\psi_3}}}], \beta{{\upharpoonright_{\psi_3[\eta{{\upharpoonright_{\psi_3}}}]}}})\bigg). \end{align} $$
Observe that
![]() $v\notin \mathrm {dom}(\zeta {{\upharpoonright _{\xi }}})\cup \mathrm {dom}(\zeta {{\upharpoonright _{\xi _3}}})$
, because every occurrence of v in
$v\notin \mathrm {dom}(\zeta {{\upharpoonright _{\xi }}})\cup \mathrm {dom}(\zeta {{\upharpoonright _{\xi _3}}})$
, because every occurrence of v in
![]() $\exists v\psi _3$
is bounded in
$\exists v\psi _3$
is bounded in
![]() $\phi $
. Hence
$\phi $
. Hence
![]() $\zeta {{\upharpoonright _{\xi }}} = \zeta {{\upharpoonright _{\xi _3}}}$
, and consequently
$\zeta {{\upharpoonright _{\xi }}} = \zeta {{\upharpoonright _{\xi _3}}}$
, and consequently
![]() $\zeta {{\upharpoonright _{\xi }}}{{\upharpoonright _{\psi _3}}} = \zeta {{\upharpoonright _{\xi _3}}}{{\upharpoonright _{\psi _3}}} = \zeta {{\upharpoonright _{\xi _3}}}$
. With this observation the proof in the case
$\zeta {{\upharpoonright _{\xi }}}{{\upharpoonright _{\psi _3}}} = \zeta {{\upharpoonright _{\xi _3}}}{{\upharpoonright _{\psi _3}}} = \zeta {{\upharpoonright _{\xi _3}}}$
. With this observation the proof in the case
![]() $v\notin \mathrm {FV}(\psi _3)$
is straightforward, for
$v\notin \mathrm {FV}(\psi _3)$
is straightforward, for
![]() $(8)$
immediately reduces to (for all
$(8)$
immediately reduces to (for all
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mathrm {dom}(\alpha ) = c_3$
)
$\mathrm {dom}(\alpha ) = c_3$
)
 $$\begin{align*}\bigg(S(\psi_3, \alpha\cup \zeta{{\upharpoonright_{\xi_3}}})\bigg)\equiv \bigg(S(\psi_3[\eta{{\upharpoonright_{\psi_3}}}], (\alpha\cup \zeta{{\upharpoonright_{\xi_3}}}){{\upharpoonright_{\psi_3[\eta{{\upharpoonright_{\psi_3}}}]}}})\bigg).\end{align*}$$
$$\begin{align*}\bigg(S(\psi_3, \alpha\cup \zeta{{\upharpoonright_{\xi_3}}})\bigg)\equiv \bigg(S(\psi_3[\eta{{\upharpoonright_{\psi_3}}}], (\alpha\cup \zeta{{\upharpoonright_{\xi_3}}}){{\upharpoonright_{\psi_3[\eta{{\upharpoonright_{\psi_3}}}]}}})\bigg).\end{align*}$$
The above is the same as our induction assumption. So we may assume that
![]() $v\in \mathrm {FV}(\psi _3)$
. Now fix
$v\in \mathrm {FV}(\psi _3)$
. Now fix
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mathrm {dom}(\alpha ) =c$
. Suppose first that
$\mathrm {dom}(\alpha ) =c$
. Suppose first that
![]() $\beta \geq _v (\alpha \cup \zeta {{\upharpoonright _{\xi _3}}})$
is such that
$\beta \geq _v (\alpha \cup \zeta {{\upharpoonright _{\xi _3}}})$
is such that
![]() $S(\psi _3, \beta {{\upharpoonright _{\psi _3}}})$
holds. Let us observe that in this case,
$S(\psi _3, \beta {{\upharpoonright _{\psi _3}}})$
holds. Let us observe that in this case,
![]() $\beta {\upharpoonright _{\psi _3}} = \beta $
. Moreover
$\beta {\upharpoonright _{\psi _3}} = \beta $
. Moreover
![]() $\mathrm {dom}(\alpha )\cap \mathrm {dom}(\zeta {{\upharpoonright _{\xi _3}}}) = \emptyset $
; hence for some
$\mathrm {dom}(\alpha )\cap \mathrm {dom}(\zeta {{\upharpoonright _{\xi _3}}}) = \emptyset $
; hence for some
![]() $\alpha '$
such that
$\alpha '$
such that
![]() $\mathrm {dom}(\alpha ') = c_3$
,
$\mathrm {dom}(\alpha ') = c_3$
,
![]() $\beta = \alpha '\cup \zeta {\upharpoonright _{\xi _3}}$
. Hence
$\beta = \alpha '\cup \zeta {\upharpoonright _{\xi _3}}$
. Hence
![]() $S(\psi _3[\eta {{\upharpoonright _{\psi _3}}}], \beta {{\upharpoonright _{\psi _3[\eta {{\upharpoonright _{\psi _3}}}]}}})$
follows by induction assumption (3). It is left to show that
$S(\psi _3[\eta {{\upharpoonright _{\psi _3}}}], \beta {{\upharpoonright _{\psi _3[\eta {{\upharpoonright _{\psi _3}}}]}}})$
follows by induction assumption (3). It is left to show that
![]() $\beta {{\upharpoonright _{\psi _3[\eta {{\upharpoonright _{\exists v\psi _3}}}]}}}\geq _v (\alpha \cup \zeta {{\upharpoonright _{\xi }}}){{\upharpoonright _{\exists v\psi _3[\eta {{\upharpoonright _{\exists v\psi _3}}}]}}}$
. This holds since no occurrence of v is in
$\beta {{\upharpoonright _{\psi _3[\eta {{\upharpoonright _{\exists v\psi _3}}}]}}}\geq _v (\alpha \cup \zeta {{\upharpoonright _{\xi }}}){{\upharpoonright _{\exists v\psi _3[\eta {{\upharpoonright _{\exists v\psi _3}}}]}}}$
. This holds since no occurrence of v is in
![]() $\mathrm {dom}(\eta {{\upharpoonright _{\psi _3}}})=\mathrm {dom}(\eta {{\upharpoonright _{\exists v\psi _3}}})$
and
$\mathrm {dom}(\eta {{\upharpoonright _{\psi _3}}})=\mathrm {dom}(\eta {{\upharpoonright _{\exists v\psi _3}}})$
and
![]() $\beta \geq _v (\alpha \cup \zeta {{\upharpoonright _{\xi _3}}})$
. So now assume that for some
$\beta \geq _v (\alpha \cup \zeta {{\upharpoonright _{\xi _3}}})$
. So now assume that for some
![]() $\beta \geq _v(\alpha \cup \zeta {{\upharpoonright _{\xi _3}}}){{\upharpoonright _{\exists v\psi _3[\eta {{\upharpoonright _{\exists v\psi _3}}}]}}} S(\psi _3[\eta {{\upharpoonright _{\psi _3}}}], \beta {{\upharpoonright _{\psi _3[\eta {{\upharpoonright _{\psi _3}}}]}}})$
holds. As no occurrence of v is in
$\beta \geq _v(\alpha \cup \zeta {{\upharpoonright _{\xi _3}}}){{\upharpoonright _{\exists v\psi _3[\eta {{\upharpoonright _{\exists v\psi _3}}}]}}} S(\psi _3[\eta {{\upharpoonright _{\psi _3}}}], \beta {{\upharpoonright _{\psi _3[\eta {{\upharpoonright _{\psi _3}}}]}}})$
holds. As no occurrence of v is in
![]() $\mathrm {dom}(\eta {\upharpoonright _{\psi _3}})$
, we can infer that
$\mathrm {dom}(\eta {\upharpoonright _{\psi _3}})$
, we can infer that
![]() $S(\psi _3[\eta {{\upharpoonright _{\psi _3}}}], \beta )$
holds. Extend
$S(\psi _3[\eta {{\upharpoonright _{\psi _3}}}], \beta )$
holds. Extend
![]() $\alpha $
to
$\alpha $
to
![]() $\alpha '$
such that
$\alpha '$
such that
![]() $\mathrm {dom}(\alpha ') = c_3$
and
$\mathrm {dom}(\alpha ') = c_3$
and
![]() $\alpha '(v) = \beta (v)$
. Then
$\alpha '(v) = \beta (v)$
. Then
![]() $(\alpha '\cup \zeta {\upharpoonright _{\xi _3}}){\upharpoonright _{\psi _3[\eta {{\upharpoonright _{\psi _3}}}]}} = \beta $
and by (3) we obtain
$(\alpha '\cup \zeta {\upharpoonright _{\xi _3}}){\upharpoonright _{\psi _3[\eta {{\upharpoonright _{\psi _3}}}]}} = \beta $
and by (3) we obtain
![]() $S(\psi _3, \alpha '\cup \zeta {\upharpoonright _{\xi _3}})$
. Hence there exists
$S(\psi _3, \alpha '\cup \zeta {\upharpoonright _{\xi _3}})$
. Hence there exists
![]() $\beta '$
such that
$\beta '$
such that
![]() $\beta '\geq _v \alpha \cup \zeta {\upharpoonright _{\xi _3}}$
and
$\beta '\geq _v \alpha \cup \zeta {\upharpoonright _{\xi _3}}$
and
![]() $S(\psi _3,\beta ')$
. This ends the whole proof.□
$S(\psi _3,\beta ')$
. This ends the whole proof.□
Corollary 3.7 (
 $\mathrm {CS}_0^+$
)
$\mathrm {CS}_0^+$
)
For every
![]() $\phi $
,
$\phi $
,
![]() $\psi $
,
$\psi $
,
![]() $\alpha \in \mathrm {Asn}(\phi )$
,
$\alpha \in \mathrm {Asn}(\phi )$
,
![]() $\beta \in \mathrm {Asn}(\psi )$
, if
$\beta \in \mathrm {Asn}(\psi )$
, if
![]() $\phi [\alpha ] = \psi [\beta ]$
, then
$\phi [\alpha ] = \psi [\beta ]$
, then
![]() $S(\phi ,\alpha )\equiv S(\psi , \beta )$
.
$S(\phi ,\alpha )\equiv S(\psi , \beta )$
.
Proof. By Lemma 3.6
![]() $S(\phi ,\alpha )$
is equivalent to
$S(\phi ,\alpha )$
is equivalent to
![]() $S(\phi [\alpha ], \varepsilon )$
and
$S(\phi [\alpha ], \varepsilon )$
and
![]() $S(\psi , \beta )$
is equivalent to
$S(\psi , \beta )$
is equivalent to
![]() $S(\psi [\beta ],\varepsilon )$
.□
$S(\psi [\beta ],\varepsilon )$
.□
Corollary 3.8.
![]() $\mathrm {CS}_0^+\vdash \forall \phi (v) S(\mathrm {Ind}(\phi (v)), \varepsilon )$
.
$\mathrm {CS}_0^+\vdash \forall \phi (v) S(\mathrm {Ind}(\phi (v)), \varepsilon )$
.
Proof. By the previous considerations at the beginning of this section, for a fixed
![]() $\phi (v)$
,
$\phi (v)$
,
![]() $S(\mathrm {Ind}(\phi (v)), \varepsilon )$
is equivalent to
$S(\mathrm {Ind}(\phi (v)), \varepsilon )$
is equivalent to
By Lemma 3.6 and Corollary 3.7 we have
 $$ \begin{align*} &S(\phi[0/v], \varepsilon) \equiv S(\phi(v), [0]),\\ &\forall x \big(S(\phi[v+1/v], [x])\equiv S(\phi(v), [x+1])\big). \end{align*} $$
$$ \begin{align*} &S(\phi[0/v], \varepsilon) \equiv S(\phi(v), [0]),\\ &\forall x \big(S(\phi[v+1/v], [x])\equiv S(\phi(v), [x+1])\big). \end{align*} $$
Hence, finally
![]() $S(\mathrm {Ind}(\phi (v)), \varepsilon )$
is equivalent to the following axiom of
$S(\mathrm {Ind}(\phi (v)), \varepsilon )$
is equivalent to the following axiom of
![]() $\Delta _0(\mathcal {L}_S^+)$
-induction:
$\Delta _0(\mathcal {L}_S^+)$
-induction:
□
Recall that
![]() $\phi (t/v)$
denotes the substitution of t for all (free) occurrences of v in
$\phi (t/v)$
denotes the substitution of t for all (free) occurrences of v in
![]() $\phi (v)$
.
$\phi (v)$
.
Corollary 3.9 (
 $\mathrm {CS}_0^+$
)
$\mathrm {CS}_0^+$
)
For every formula
![]() $\phi (v)$
, term t (possibly having some variables), which is substitutable for v in
$\phi (v)$
, term t (possibly having some variables), which is substitutable for v in
![]() $\phi (v)$
and every
$\phi (v)$
and every
![]() $\alpha \in \mathrm {Asn}(\phi (t/v))$
, if
$\alpha \in \mathrm {Asn}(\phi (t/v))$
, if
![]() $S(\forall v \phi (v), \alpha {{\upharpoonright _{\cdot }}})$
, then
$S(\forall v \phi (v), \alpha {{\upharpoonright _{\cdot }}})$
, then
![]() $S(\phi (t/v),\alpha )$
.
$S(\phi (t/v),\alpha )$
.
Proof. Fix
![]() $\phi (v)$
, t,
$\phi (v)$
, t,
![]() $\alpha $
, as above and suppose
$\alpha $
, as above and suppose
![]() $S(\forall v \phi (v), \alpha {{\upharpoonright _{\cdot }}})$
. By compositional conditions we know that for every
$S(\forall v \phi (v), \alpha {{\upharpoonright _{\cdot }}})$
. By compositional conditions we know that for every
![]() $\beta $
such that
$\beta $
such that
![]() $\beta \geq _v \alpha {{\upharpoonright _{\forall v \phi (v)}}}$
,
$\beta \geq _v \alpha {{\upharpoonright _{\forall v \phi (v)}}}$
,
![]() $S(\phi (v), \beta {{\upharpoonright _{\cdot }}})$
holds. Define
$S(\phi (v), \beta {{\upharpoonright _{\cdot }}})$
holds. Define
![]() $\beta $
such that
$\beta $
such that
![]() $\beta {{\upharpoonright _{\forall v \phi (x)}}} = \alpha {{\upharpoonright _{\forall v \phi (x)}}}$
and
$\beta {{\upharpoonright _{\forall v \phi (x)}}} = \alpha {{\upharpoonright _{\forall v \phi (x)}}}$
and
![]() $\beta (v) = t^{\alpha }$
. Hence, by our assumption we have
$\beta (v) = t^{\alpha }$
. Hence, by our assumption we have
![]() $S(\phi (v), \beta )$
. Let
$S(\phi (v), \beta )$
. Let
![]() $\eta _0$
be a substitution of
$\eta _0$
be a substitution of
![]() $t[\alpha ]$
for every occurrence of v in
$t[\alpha ]$
for every occurrence of v in
![]() $\phi (v)$
. Then
$\phi (v)$
. Then
![]() $\eta _0$
agrees with
$\eta _0$
agrees with
![]() $\beta $
, so by Lemma 3.6 we have
$\beta $
, so by Lemma 3.6 we have
![]() $S(\phi (v)[\eta _0], \beta {\upharpoonright _{.}})$
. Observe that
$S(\phi (v)[\eta _0], \beta {\upharpoonright _{.}})$
. Observe that
![]() $\beta {\upharpoonright _{\phi (v)[\eta _0]}} = \alpha {\upharpoonright _{\phi (v)[\eta _0]}}$
; hence we have
$\beta {\upharpoonright _{\phi (v)[\eta _0]}} = \alpha {\upharpoonright _{\phi (v)[\eta _0]}}$
; hence we have
![]() $S(\phi (v)[\eta _0],\alpha {\upharpoonright _{.}})$
. Let
$S(\phi (v)[\eta _0],\alpha {\upharpoonright _{.}})$
. Let
![]() $\pi $
be a (coded) set of occurrences of the free variables from
$\pi $
be a (coded) set of occurrences of the free variables from
![]() $\phi (t/v)$
that are within the new occurrences of t (observe that there might be some occurrences of t in
$\phi (t/v)$
that are within the new occurrences of t (observe that there might be some occurrences of t in
![]() $\phi (v)$
). Let
$\phi (v)$
). Let
![]() $\eta $
be a substitution of numerals such that for every occurrence
$\eta $
be a substitution of numerals such that for every occurrence
![]() $p\in \pi $
,
$p\in \pi $
,
![]() $\eta (p) = \underline {\alpha (v_p)}$
(recall that
$\eta (p) = \underline {\alpha (v_p)}$
(recall that
![]() $v_p$
is the variable whose occurrence is p). By the definition of
$v_p$
is the variable whose occurrence is p). By the definition of
![]() $\eta $
, we have
$\eta $
, we have
![]() $\phi (v)[\eta _0] = \phi (t/v)[\eta ]$
; hence we can conclude that
$\phi (v)[\eta _0] = \phi (t/v)[\eta ]$
; hence we can conclude that
![]() $S(\phi (t/v)[\eta ], \alpha {\upharpoonright _{.}})$
holds. Since
$S(\phi (t/v)[\eta ], \alpha {\upharpoonright _{.}})$
holds. Since
![]() $\eta $
agrees with
$\eta $
agrees with
![]() $\alpha $
, Lemma 3.6 yields
$\alpha $
, Lemma 3.6 yields
![]() $S(\phi (t/v),\alpha )$
.□
$S(\phi (t/v),\alpha )$
.□
Theorem 3.10.
![]() $\mathrm {CS}_0\vdash \forall \phi \big (\mathrm {Pr}_{\emptyset }^S(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
.
$\mathrm {CS}_0\vdash \forall \phi \big (\mathrm {Pr}_{\emptyset }^S(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
.
Proof. We reason in
![]() $\mathrm {CS}_0^+$
. We fix a sequent calculus for the first-order logic with equality, as in [Reference Takeuti24] (this choice is just a matter of convenienceFootnote
11
). We fix a proof p of a sentence
$\mathrm {CS}_0^+$
. We fix a sequent calculus for the first-order logic with equality, as in [Reference Takeuti24] (this choice is just a matter of convenienceFootnote
11
). We fix a proof p of a sentence
![]() $\phi $
and by induction on its length argue that whenever a sequent
$\phi $
and by induction on its length argue that whenever a sequent
![]() $\Gamma \Rightarrow \Delta $
occurs in p, then
$\Gamma \Rightarrow \Delta $
occurs in p, then
holds, where
![]() $\bigwedge \Gamma $
and
$\bigwedge \Gamma $
and
![]() $\bigvee \Gamma $
denote (the canonically parenthesized) conjunction and disjunction over sentences from sets
$\bigvee \Gamma $
denote (the canonically parenthesized) conjunction and disjunction over sentences from sets
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Delta $
, respectively. To simplify the notation
$\Delta $
, respectively. To simplify the notation
![]() $\bigwedge \Gamma \rightarrow \bigvee \Delta $
will be abbreviated using the sequent notation as
$\bigwedge \Gamma \rightarrow \bigvee \Delta $
will be abbreviated using the sequent notation as
![]() $\Gamma \Rightarrow \Delta $
. In the course of the induction we rely on the fact that the following sentence is provable in
$\Gamma \Rightarrow \Delta $
. In the course of the induction we rely on the fact that the following sentence is provable in
![]() $\mathrm {CS}_0$
:
$\mathrm {CS}_0$
:
The proof of (DC) in
![]() $\mathrm {CT}_0$
consists in a straightforward induction on the size of
$\mathrm {CT}_0$
consists in a straightforward induction on the size of
![]() $\Gamma $
and a similar argument can be given in the case of
$\Gamma $
and a similar argument can be given in the case of
![]() $\bigwedge $
yielding a dual equivalence (see also [Reference Cieśliński3, Reference Wcisło and Łełyk25] for precise arguments). We go back to the main induction on the length of the fixed proof p. In the base step we have to establish that all initial sequents satisfy (9). These include initial sequents for equality and all sequents of the form
$\bigwedge $
yielding a dual equivalence (see also [Reference Cieśliński3, Reference Wcisło and Łełyk25] for precise arguments). We go back to the main induction on the length of the fixed proof p. In the base step we have to establish that all initial sequents satisfy (9). These include initial sequents for equality and all sequents of the form
![]() $\phi \Rightarrow \phi $
. In both cases the proof follows the same pattern: first using Corollary 3.3 we get rid of the quantifier prefix and then verify that the formula following it is satisfied by every assignment. In the case of the initial sequents for equality we use the conditions for atomic sentences from
$\phi \Rightarrow \phi $
. In both cases the proof follows the same pattern: first using Corollary 3.3 we get rid of the quantifier prefix and then verify that the formula following it is satisfied by every assignment. In the case of the initial sequents for equality we use the conditions for atomic sentences from
![]() $\mathrm {CS}^-$
, in case of
$\mathrm {CS}^-$
, in case of
![]() $\phi \Rightarrow \phi $
we use the axioms for
$\phi \Rightarrow \phi $
we use the axioms for
![]() $\neg $
and
$\neg $
and
![]() $\vee $
.
$\vee $
.
In the induction step the cases of quantifier rules are the unique non-obvious ones. Let us consider the dictum de omni rule:
 $$\begin{align*}\frac{\Gamma, \phi(t)\Rightarrow \Delta}{\Gamma, \forall v \phi(v)\Rightarrow\Delta},\end{align*}$$
$$\begin{align*}\frac{\Gamma, \phi(t)\Rightarrow \Delta}{\Gamma, \forall v \phi(v)\Rightarrow\Delta},\end{align*}$$
where
![]() $\phi (v)$
is a formula and t is free for v in
$\phi (v)$
is a formula and t is free for v in
![]() $\phi (v)$
. We may safely assume that v is a free variable in
$\phi (v)$
. We may safely assume that v is a free variable in
![]() $\phi $
. For simplicity abbreviate
$\phi $
. For simplicity abbreviate
![]() $\phi (t/v)$
with simply
$\phi (t/v)$
with simply
![]() $\phi (t)$
. So suppose for every
$\phi (t)$
. So suppose for every
![]() $\alpha \in \mathrm {Asn}\left (\big (\Gamma +\phi (t)\big )\Rightarrow \Delta \right )$
it holds that
$\alpha \in \mathrm {Asn}\left (\big (\Gamma +\phi (t)\big )\Rightarrow \Delta \right )$
it holds that
Fix an arbitrary
![]() $\alpha \in \mathrm {Asn}\left (\big (\Gamma +\forall v\phi (v)\big )\Rightarrow \Delta \right )$
and assume that for every
$\alpha \in \mathrm {Asn}\left (\big (\Gamma +\forall v\phi (v)\big )\Rightarrow \Delta \right )$
and assume that for every
![]() $\theta \in \Gamma \cup \{\forall v \phi (v)\}$
,
$\theta \in \Gamma \cup \{\forall v \phi (v)\}$
,
![]() $S(\theta ,\alpha {{\upharpoonright _{\cdot }}})$
holds. Consider any
$S(\theta ,\alpha {{\upharpoonright _{\cdot }}})$
holds. Consider any
![]() $\beta \in \mathrm {Asn}\left (\big (\Gamma +\phi (t)\big )\Rightarrow \Delta \right )$
such that
$\beta \in \mathrm {Asn}\left (\big (\Gamma +\phi (t)\big )\Rightarrow \Delta \right )$
such that
![]() $\beta {{\upharpoonright _{\big (\Gamma +\forall v\phi (v)\big )\Rightarrow \Delta }}}=\alpha $
. Since
$\beta {{\upharpoonright _{\big (\Gamma +\forall v\phi (v)\big )\Rightarrow \Delta }}}=\alpha $
. Since
![]() $S(\forall v \phi (v), \beta {{\upharpoonright _{\cdot }}})$
, then by Lemma 3.9,
$S(\forall v \phi (v), \beta {{\upharpoonright _{\cdot }}})$
, then by Lemma 3.9,
![]() $S(\phi (t), \beta {{\upharpoonright _{\cdot }}})$
as well. Hence for every
$S(\phi (t), \beta {{\upharpoonright _{\cdot }}})$
as well. Hence for every
![]() $\theta \in \Gamma \cup \{\phi (t)\}\ \mathrm{it\ holds\ that}\ S(\theta , \beta {{\upharpoonright _{\cdot }}})$
. By the induction assumption, for some
$\theta \in \Gamma \cup \{\phi (t)\}\ \mathrm{it\ holds\ that}\ S(\theta , \beta {{\upharpoonright _{\cdot }}})$
. By the induction assumption, for some
![]() $\psi \in \Delta $
,
$\psi \in \Delta $
,
![]() $S(\psi ,\beta {{\upharpoonright _{\cdot }}})$
and since
$S(\psi ,\beta {{\upharpoonright _{\cdot }}})$
and since
![]() $\beta {{\upharpoonright _{\psi }}} = \alpha {{\upharpoonright _{\psi }}}$
, this ends the proof.
$\beta {{\upharpoonright _{\psi }}} = \alpha {{\upharpoonright _{\psi }}}$
, this ends the proof.
Now consider the rule of universal generalisation
 $$\begin{align*}\frac{\Gamma\Rightarrow \Delta,\phi(v)}{\Gamma\Rightarrow\Delta, \forall v\phi(v)},\end{align*}$$
$$\begin{align*}\frac{\Gamma\Rightarrow \Delta,\phi(v)}{\Gamma\Rightarrow\Delta, \forall v\phi(v)},\end{align*}$$
where v does not occur free in the lower sequent. As previously assume that for all
![]() $\alpha \in \mathrm {Asn}\left (\Gamma \Rightarrow (\Delta +\phi (v))\right )$
,
$\alpha \in \mathrm {Asn}\left (\Gamma \Rightarrow (\Delta +\phi (v))\right )$
,
Fix an arbitrary
![]() $\beta \in \mathrm {Asn}\left (\Gamma \Rightarrow \big (\Delta +\forall v\phi (v)\big )\right )$
and arbitrary
$\beta \in \mathrm {Asn}\left (\Gamma \Rightarrow \big (\Delta +\forall v\phi (v)\big )\right )$
and arbitrary
![]() $\gamma \geq _v\beta $
and assume that for all
$\gamma \geq _v\beta $
and assume that for all
![]() $\psi \in \Gamma $
,
$\psi \in \Gamma $
,
![]() $S(\psi , \gamma {{\upharpoonright _{\cdot }}})$
. Since
$S(\psi , \gamma {{\upharpoonright _{\cdot }}})$
. Since
![]() $\gamma {{\upharpoonright _{\Gamma }}} = \beta {{\upharpoonright _{\Gamma }}}$
(v is not a free variable in
$\gamma {{\upharpoonright _{\Gamma }}} = \beta {{\upharpoonright _{\Gamma }}}$
(v is not a free variable in
![]() $\Gamma $
) it follows that there is
$\Gamma $
) it follows that there is
![]() $\psi \in \Delta \cup \{\phi (v)\}$
such that
$\psi \in \Delta \cup \{\phi (v)\}$
such that
![]() $S(\psi ,\gamma {{\upharpoonright _{\cdot }}})$
. If
$S(\psi ,\gamma {{\upharpoonright _{\cdot }}})$
. If
![]() $\psi \in \Delta $
, then we are done, since
$\psi \in \Delta $
, then we are done, since
![]() $\gamma {{\upharpoonright _{\Delta }}} = \beta {{\upharpoonright _{\Delta }}}$
. Otherwise
$\gamma {{\upharpoonright _{\Delta }}} = \beta {{\upharpoonright _{\Delta }}}$
. Otherwise
![]() $S(\phi (v),\gamma {\upharpoonright _{\cdot }})$
and it follows that
$S(\phi (v),\gamma {\upharpoonright _{\cdot }})$
and it follows that
![]() $S(\forall v\phi (v),\beta {{\upharpoonright _{\cdot }}})$
, since
$S(\forall v\phi (v),\beta {{\upharpoonright _{\cdot }}})$
, since
![]() $\gamma $
was arbitrary.
$\gamma $
was arbitrary.
Now, the thesis of the theorem follows, since, for arbitrary
![]() $\phi $
, if
$\phi $
, if
![]() $\mathrm {Pr}_{\emptyset }^S(\phi )$
holds, then there is a sequent calculus proof of
$\mathrm {Pr}_{\emptyset }^S(\phi )$
holds, then there is a sequent calculus proof of
![]() $\Gamma \Rightarrow \phi $
, where for every
$\Gamma \Rightarrow \phi $
, where for every
![]() $\psi \in \Gamma $
we have
$\psi \in \Gamma $
we have
![]() $S(\psi ,\varepsilon )$
. Hence, by the proof above we obtain
$S(\psi ,\varepsilon )$
. Hence, by the proof above we obtain
and since
![]() $\bigwedge \Gamma \rightarrow \phi $
does not admit any free variables, then we have
$\bigwedge \Gamma \rightarrow \phi $
does not admit any free variables, then we have
![]() $S(\bigwedge \Gamma \rightarrow \phi ,\varepsilon )$
. The thesis follows by the conjunctive correctness and compositional conditions: since for every
$S(\bigwedge \Gamma \rightarrow \phi ,\varepsilon )$
. The thesis follows by the conjunctive correctness and compositional conditions: since for every
![]() $\psi \in \Gamma $
we have
$\psi \in \Gamma $
we have
![]() $S(\psi ,\varepsilon )$
, then
$S(\psi ,\varepsilon )$
, then
![]() $S(\bigwedge \Gamma ,\varepsilon )$
holds and an application of Modus Ponens yields
$S(\bigwedge \Gamma ,\varepsilon )$
holds and an application of Modus Ponens yields
![]() $S(\phi ,\varepsilon )$
.□
$S(\phi ,\varepsilon )$
.□
Corollary 3.11. For every Gödelized theory
![]() $\mathrm {Th}$
, we have
$\mathrm {Th}$
, we have
Hence,
Proof. The first part follows directly from Theorem 3.10. Having it, we prove the second one: by induction on n we prove that
For
![]() $n=0$
this follows from the first part. Fix n and assume the thesis holds for it. By the compositional clauses for
$n=0$
this follows from the first part. Fix n and assume the thesis holds for it. By the compositional clauses for
![]() $\mathrm {CS}^-$
we have
$\mathrm {CS}^-$
we have
Consequently, reapplying the first part of this corollary for
![]() $\mathrm {REF}^n(\mathrm {Th})$
substituted for
$\mathrm {REF}^n(\mathrm {Th})$
substituted for
![]() $\mathrm {Th}$
we get the induction thesis for
$\mathrm {Th}$
we get the induction thesis for
![]() $n+1$
.□
$n+1$
.□
The corollary below easily follows from the corollary above and Corollary 3.8.
Corollary 3.12.
![]() $\mathrm {CS}_0\vdash \forall \phi \big (\mathrm {Pr}_{\mathrm {PA}}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
.
$\mathrm {CS}_0\vdash \forall \phi \big (\mathrm {Pr}_{\mathrm {PA}}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
.
![]() $\boxplus $
$\boxplus $
Corollary 3.13.
![]() $\mathrm {CS}_0\vdash \mathrm {REF}^{\omega }(\mathrm {PA})$
.
$\mathrm {CS}_0\vdash \mathrm {REF}^{\omega }(\mathrm {PA})$
.
![]() $\boxplus $
$\boxplus $
3.4 Corollaries
3.4.1 Compositional satisfaction vs. compositional truth
The above results transfer immediately to the setting of the following theory of truth:
Definition 3.14.
![]() $\mathrm {CT}^-$
is the
$\mathrm {CT}^-$
is the
![]() $\mathcal {L}\cup \{T\}$
theory extending
$\mathcal {L}\cup \{T\}$
theory extending
![]() $\mathrm {EA}$
with the following axioms:
$\mathrm {EA}$
with the following axioms:
-
1.
 $\forall x \big (T(x)\rightarrow \mathrm {Sent}(x)\big )$
.
$\forall x \big (T(x)\rightarrow \mathrm {Sent}(x)\big )$
. -
2.
 $\forall s,t\in \mathrm {ClTerm}\big (T(s=t)\equiv ({s})^{\circ }=({t})^{\circ }\big )$
.
$\forall s,t\in \mathrm {ClTerm}\big (T(s=t)\equiv ({s})^{\circ }=({t})^{\circ }\big )$
. -
3.
 $\forall \phi ,\psi \in \mathrm {Sent}\big (T(\phi \vee \psi )\equiv (T(\phi )\vee T(\psi ))\big )$
.
$\forall \phi ,\psi \in \mathrm {Sent}\big (T(\phi \vee \psi )\equiv (T(\phi )\vee T(\psi ))\big )$
. -
4.
 $\forall \phi \in \mathrm {Sent}\big (T(\neg \phi )\equiv \neg T(\phi )\big )$
.
$\forall \phi \in \mathrm {Sent}\big (T(\neg \phi )\equiv \neg T(\phi )\big )$
. -
5.
 $\forall \phi (v)\in \mathrm {Form}^{\leq 1}\big (T(\exists v \phi (v))\equiv \exists x T(\phi [x]\big )$
.
$\forall \phi (v)\in \mathrm {Form}^{\leq 1}\big (T(\exists v \phi (v))\equiv \exists x T(\phi [x]\big )$
.
As usual
![]() $\mathrm {CT}_n$
denotes the result of extending the following theory with induction axioms for
$\mathrm {CT}_n$
denotes the result of extending the following theory with induction axioms for
![]() $\Sigma _n$
formulae of the extended language.
$\Sigma _n$
formulae of the extended language.
![]() $\triangle $
$\triangle $
Let
![]() $\mathcal {L}_T^+$
denote the extension of
$\mathcal {L}_T^+$
denote the extension of
![]() $\mathcal {L}_T$
with function symbols for all p.r. recursive functions and
$\mathcal {L}_T$
with function symbols for all p.r. recursive functions and
![]() $\mathrm {CT}_0^+$
denote the extension of
$\mathrm {CT}_0^+$
denote the extension of
![]() $\mathrm {CT}_0$
with all defining axioms for fresh functions symbols in
$\mathrm {CT}_0$
with all defining axioms for fresh functions symbols in
![]() $\mathcal {L}_{T}^+$
. Then we have an analogue of Proposition 3.1:
$\mathcal {L}_{T}^+$
. Then we have an analogue of Proposition 3.1:
Proposition 3.15.
![]() $\mathrm {CT}_0^+\vdash \mathrm {I}\Delta _0(\mathcal {L}_T^+)$
.
$\mathrm {CT}_0^+\vdash \mathrm {I}\Delta _0(\mathcal {L}_T^+)$
.
![]() $\boxplus $
$\boxplus $
Now we show that the result on the provability of (GR(Th)) in
![]() $\mathrm {CS}_0$
transfers to the setting with the truth predicate.
$\mathrm {CS}_0$
transfers to the setting with the truth predicate.
Corollary 3.16.
![]() $\mathrm {CT}_0\vdash \forall \phi \in \mathrm {Sent}\big (\mathrm {Pr}_{\mathrm {PA}}(\phi )\rightarrow T(\phi )\big )$
.
$\mathrm {CT}_0\vdash \forall \phi \in \mathrm {Sent}\big (\mathrm {Pr}_{\mathrm {PA}}(\phi )\rightarrow T(\phi )\big )$
.
Proof. Work in
![]() $\mathrm {CT}_0^+$
and put
$\mathrm {CT}_0^+$
and put
The above is a
![]() $\Delta _0(\mathcal {L}_T^+)$
formula, so obviously we have
$\Delta _0(\mathcal {L}_T^+)$
formula, so obviously we have
![]() $\mathrm {I}\Delta _0(\mathcal {L}_S^+)$
. Now, we show that
$\mathrm {I}\Delta _0(\mathcal {L}_S^+)$
. Now, we show that
![]() $S(x,y)$
behaves compositionally. We focus on the
$S(x,y)$
behaves compositionally. We focus on the
![]() $\exists $
-axiom. Pick a formula
$\exists $
-axiom. Pick a formula
![]() $\phi (v)$
and
$\phi (v)$
and
![]() $\alpha \in \mathrm {Asn}(\exists v \phi (v))$
. Observe that the following equivalences hold:
$\alpha \in \mathrm {Asn}(\exists v \phi (v))$
. Observe that the following equivalences hold:
 $$ \begin{align*} S(\exists v \phi(v),\alpha)&\equiv T(\exists v \phi(v)[\alpha])\\ &\equiv\exists x T(\phi[\alpha][x]))\\ &\equiv\exists \beta\geq_v\alpha T(\phi[\beta])\\ &\equiv\exists \beta\geq_v\alpha S(\phi,\beta). \end{align*} $$
$$ \begin{align*} S(\exists v \phi(v),\alpha)&\equiv T(\exists v \phi(v)[\alpha])\\ &\equiv\exists x T(\phi[\alpha][x]))\\ &\equiv\exists \beta\geq_v\alpha T(\phi[\beta])\\ &\equiv\exists \beta\geq_v\alpha S(\phi,\beta). \end{align*} $$
In the second and the third equivalence we use the fact that
![]() $v\notin \mathrm {dom}(\alpha )$
. Hence (in
$v\notin \mathrm {dom}(\alpha )$
. Hence (in
![]() $\mathrm {CT}_0$
) by Theorem 3.10 we have
$\mathrm {CT}_0$
) by Theorem 3.10 we have
Translating it back to the language with the truth predicate, we get our thesis.□
The proof of the above corollary proceeds by defining the satisfaction predicate satisfying
![]() $\mathrm {CS}_0^+$
in
$\mathrm {CS}_0^+$
in
![]() $\mathrm {CT}_0^+$
. In fact, the same translation works also in the context of the non-inductive versions of both theories,
$\mathrm {CT}_0^+$
. In fact, the same translation works also in the context of the non-inductive versions of both theories,
![]() $\mathrm {CS}^-$
and
$\mathrm {CS}^-$
and
![]() $\mathrm {CT}^-$
. However, it is not known, whether the reverse is true in the context of these theories, i.e., whether
$\mathrm {CT}^-$
. However, it is not known, whether the reverse is true in the context of these theories, i.e., whether
![]() $\mathrm {CS}^-$
can define the truth predicate of
$\mathrm {CS}^-$
can define the truth predicate of
![]() $\mathrm {CT}^-$
. Using the Enayat–Visser method [Reference Enayat, Visser, Achourioti, Galinon, Fernández and Fujimoto7] of constructing pathological models for
$\mathrm {CT}^-$
. Using the Enayat–Visser method [Reference Enayat, Visser, Achourioti, Galinon, Fernández and Fujimoto7] of constructing pathological models for
![]() $\mathrm {CS}^-$
one can show that standard methods of defining truth from satisfaction do not work. However, the results from the previous section witness that
$\mathrm {CS}^-$
one can show that standard methods of defining truth from satisfaction do not work. However, the results from the previous section witness that
![]() $\Delta _0$
induction is sufficient to overcome these deficiencies of
$\Delta _0$
induction is sufficient to overcome these deficiencies of
![]() $\mathrm {CS}^-$
.
$\mathrm {CS}^-$
.
Proposition 3.17. The truth predicate satisfying
![]() $\mathrm {CT}_0$
is definable in
$\mathrm {CT}_0$
is definable in
![]() $\mathrm {CS}_0$
.
$\mathrm {CS}_0$
.
Proof. Working in
![]() $\mathrm {CS}_0$
, put
$\mathrm {CS}_0$
, put
As previously,
![]() $T(x)$
is a
$T(x)$
is a
![]() $\Delta _0(\mathcal {L}_S)$
formula, so
$\Delta _0(\mathcal {L}_S)$
formula, so
![]() $\mathrm {CS}_0\vdash \mathrm {I}\Delta _0(\mathcal {L}_T)$
. Since sentences are the unique formulae for which
$\mathrm {CS}_0\vdash \mathrm {I}\Delta _0(\mathcal {L}_T)$
. Since sentences are the unique formulae for which
![]() $\varepsilon $
is an assignment, so axiom
$\varepsilon $
is an assignment, so axiom
![]() $1.$
of
$1.$
of
![]() $\mathrm {CS}^-$
implies the corresponding axiom of
$\mathrm {CS}^-$
implies the corresponding axiom of
![]() $\mathrm {CT}^-$
. Once again we focus on the compositional axioms for
$\mathrm {CT}^-$
. Once again we focus on the compositional axioms for
![]() $\exists $
. Working in
$\exists $
. Working in
![]() $\mathrm {CS}_0$
fix
$\mathrm {CS}_0$
fix
![]() $\phi $
and without loss of generality assume that
$\phi $
and without loss of generality assume that
![]() $v\in \mathrm {FV}(\phi )$
. Observe that the following equivalences hold:
$v\in \mathrm {FV}(\phi )$
. Observe that the following equivalences hold:
 $$ \begin{align*} T(\exists v \phi)&\equiv S(\exists v\phi, \varepsilon)\\[3pt] &\equiv \exists \beta\geq_v\varepsilon S(\phi, \beta{\upharpoonright_{\cdot}})\\[3pt] &\equiv \exists x S(\phi, [x])\\[3pt] &\equiv\exists x S(\phi[x],\varepsilon)\\[3pt] &\equiv\exists x T(\phi[x]). \end{align*} $$
$$ \begin{align*} T(\exists v \phi)&\equiv S(\exists v\phi, \varepsilon)\\[3pt] &\equiv \exists \beta\geq_v\varepsilon S(\phi, \beta{\upharpoonright_{\cdot}})\\[3pt] &\equiv \exists x S(\phi, [x])\\[3pt] &\equiv\exists x S(\phi[x],\varepsilon)\\[3pt] &\equiv\exists x T(\phi[x]). \end{align*} $$
The proof of the fourth equivalence involves the crucial use of Lemma 3.6.□
3.4.2 Many faces theorem
Corollary 3.16 coupled with some known results from the literature, shows that the Global Reflection Principle is a very robust notion. Not only it is equivalent to bounded induction but is immune to, apparently significant, variations. This is summarized in the corollary below (we state it for the theory of compositional truth; however all the equivalences should transfer to the setting of a satisfaction predicate without significant changes).
![]() $\mathrm {Pr}^T_{\mathrm {Sent}}(\phi )$
asserts that
$\mathrm {Pr}^T_{\mathrm {Sent}}(\phi )$
asserts that
![]() $\phi $
is provable from the set of true sentences in pure sentential logic, while DC is a truth variant of the principles from the proof of Theorem 3.10.
$\phi $
is provable from the set of true sentences in pure sentential logic, while DC is a truth variant of the principles from the proof of Theorem 3.10.
Corollary 3.18. Over
![]() $\mathrm {CT}^- +\mathrm {EA}$
the following theories are equivalent:
$\mathrm {CT}^- +\mathrm {EA}$
the following theories are equivalent:
-
1. I
 $\Delta _0(\mathcal {L}_T)$
;
$\Delta _0(\mathcal {L}_T)$
; -
2.
 $\forall \phi \big (\mathrm {Pr}_{\mathrm {PA}}(\phi )\rightarrow T(\phi )\big )$
;
$\forall \phi \big (\mathrm {Pr}_{\mathrm {PA}}(\phi )\rightarrow T(\phi )\big )$
; -
3.
 $\forall \phi \big (\mathrm {Pr}_{\emptyset }(\phi )\rightarrow T(\phi )\big )$
;
$\forall \phi \big (\mathrm {Pr}_{\emptyset }(\phi )\rightarrow T(\phi )\big )$
; -
4.
 $\forall \phi \big (\mathrm {Pr}^T_{\emptyset }(\phi )\rightarrow T(\phi )\big )$
;
$\forall \phi \big (\mathrm {Pr}^T_{\emptyset }(\phi )\rightarrow T(\phi )\big )$
; -
5.
 $\forall \phi \big (\mathrm {Pr}^T_{\mathrm {Sent}}(\phi )\rightarrow T(\phi )\big )$
;
$\forall \phi \big (\mathrm {Pr}^T_{\mathrm {Sent}}(\phi )\rightarrow T(\phi )\big )$
; -
6.
 $\mathrm {DC}$
.
$\mathrm {DC}$
.
The implication 3.
![]() $\Rightarrow $
4. is established in [Reference Cieśliński5]. The equivalence between 5. and 1. is demonstrated in [Reference Cieśliński3]. Much later it was significantly fine-tuned in [Reference Enayat and Pakhomov6], yielding the implication 6.
$\Rightarrow $
4. is established in [Reference Cieśliński5]. The equivalence between 5. and 1. is demonstrated in [Reference Cieśliński3]. Much later it was significantly fine-tuned in [Reference Enayat and Pakhomov6], yielding the implication 6.
![]() $\Rightarrow $
1.
$\Rightarrow $
1.
![]() $\boxplus $
$\boxplus $
3.4.3 Fullness
The following is one of the most useful properties of
![]() $\mathrm {CS}_0$
. It implies that every model of
$\mathrm {CS}_0$
. It implies that every model of
![]() $\mathrm {CS}_0$
is full, a theorem first demonstrated by Wcisło and presented in [Reference Wcisło and Łełyk25]. The proof below is an observation also due to Wcisło which crucially uses the provability of (GR(Th)). It’s proof is included also in [Reference Łełyk and Wcisło20] (Fact 33) but we give it here for completeness. In the definition below we fix a canonical elementary translation transforming a given formula
$\mathrm {CS}_0$
is full, a theorem first demonstrated by Wcisło and presented in [Reference Wcisło and Łełyk25]. The proof below is an observation also due to Wcisło which crucially uses the provability of (GR(Th)). It’s proof is included also in [Reference Łełyk and Wcisło20] (Fact 33) but we give it here for completeness. In the definition below we fix a canonical elementary translation transforming a given formula
![]() $\phi $
into one in the
$\phi $
into one in the
![]() $\Sigma _n$
form. We assume that it formalizes in
$\Sigma _n$
form. We assume that it formalizes in
![]() $\mathrm {PA}$
.
$\mathrm {PA}$
.
Recall (Definition 2.12) that
![]() $\phi (x)^{\Sigma }$
denotes the canonical
$\phi (x)^{\Sigma }$
denotes the canonical
![]() $\Sigma _c$
form of
$\Sigma _c$
form of
![]() $\phi (x)$
and
$\phi (x)$
and
![]() $\Sigma ^*_c:= \{\phi \ \ | \ \ \phi ^{\Sigma }\in \Sigma _c \}$
. Moreover recall that
$\Sigma ^*_c:= \{\phi \ \ | \ \ \phi ^{\Sigma }\in \Sigma _c \}$
. Moreover recall that
![]() $S_c$
denotes the restriction of S to all formulae which are equivalent to sentences of
$S_c$
denotes the restriction of S to all formulae which are equivalent to sentences of
![]() $\Sigma _c$
complexity (in the sense of
$\Sigma _c$
complexity (in the sense of
![]() $\mathcal {M}$
). More precisely
$\mathcal {M}$
). More precisely
Theorem 3.19. Suppose that
![]() $(\mathcal {M},S)\models \mathrm {CS}^-+\mathrm {GR}(\mathrm {PA})$
. Then for every c,
$(\mathcal {M},S)\models \mathrm {CS}^-+\mathrm {GR}(\mathrm {PA})$
. Then for every c,
![]() $(\mathcal {M}, S_c)\models \mathrm {CS}(\Sigma ^*_c)$
.
$(\mathcal {M}, S_c)\models \mathrm {CS}(\Sigma ^*_c)$
.
Proof. Fix a model
![]() $(\mathcal {M},S)\models \mathrm {CS}^- + \mathrm {GR}(\mathrm {PA})$
and
$(\mathcal {M},S)\models \mathrm {CS}^- + \mathrm {GR}(\mathrm {PA})$
and
![]() $c\in M$
. It will be easier to switch to the truth predicate, so put
$c\in M$
. It will be easier to switch to the truth predicate, so put
![]() $T:= S(x,\varepsilon )$
. Since for every formula
$T:= S(x,\varepsilon )$
. Since for every formula
![]() $\phi \in \Sigma _c^*$
and every
$\phi \in \Sigma _c^*$
and every
![]() $\alpha \in \mathrm {Asn}(\phi )$
we have
$\alpha \in \mathrm {Asn}(\phi )$
we have
it is sufficient to show that
![]() $(\mathcal {M},T_c)\models \mathrm {Ind}(\mathcal {L}_T)$
, where
$(\mathcal {M},T_c)\models \mathrm {Ind}(\mathcal {L}_T)$
, where
![]() $T_c$
is the restriction of T to the formulae of
$T_c$
is the restriction of T to the formulae of
![]() $\Sigma _c^*$
complexity, i.e.,
$\Sigma _c^*$
complexity, i.e.,
From now on we work in
![]() $(\mathcal {M},T)$
. By the classical metamathematics of
$(\mathcal {M},T)$
. By the classical metamathematics of
![]() $\mathrm {PA}$
, for every c there is a formula
$\mathrm {PA}$
, for every c there is a formula
![]() $\mathrm {Sat}_{\Sigma _c}$
such that for every
$\mathrm {Sat}_{\Sigma _c}$
such that for every
![]() $\phi \in \Sigma _c^*$
and every
$\phi \in \Sigma _c^*$
and every
![]() $\alpha \in \mathrm {Asn}(\phi )$
we have
$\alpha \in \mathrm {Asn}(\phi )$
we have
Hence, by GR(PA) we conclude that for every sentence
![]() $\phi \in \Sigma ^*_c$
$\phi \in \Sigma ^*_c$
Put
![]() $\xi (v):=\mathrm {Sat}_{\Sigma _c}(v,\varepsilon )$
and
$\xi (v):=\mathrm {Sat}_{\Sigma _c}(v,\varepsilon )$
and
![]() $T'(x):= T(\xi [x])\wedge x\in \Sigma ^*_c$
. Then we see that
$T'(x):= T(\xi [x])\wedge x\in \Sigma ^*_c$
. Then we see that
Consequently,
![]() $T'$
satisfies the compositional axioms of
$T'$
satisfies the compositional axioms of
![]() $\mathrm {CT}^-$
for formulae from the
$\mathrm {CT}^-$
for formulae from the
![]() $\Sigma _c^*$
class. We shall now show
$\Sigma _c^*$
class. We shall now show
![]() $(\mathcal {M},T')\models \mathrm {Ind}(\mathcal {L}_T)$
. Thus let
$(\mathcal {M},T')\models \mathrm {Ind}(\mathcal {L}_T)$
. Thus let
![]() $\eta [T']$
be an arbitrary axiom of induction for a formula with
$\eta [T']$
be an arbitrary axiom of induction for a formula with
![]() $T'$
(we mark all occurrences of
$T'$
(we mark all occurrences of
![]() $T'$
in
$T'$
in
![]() $\eta $
). We may assume that
$\eta $
). We may assume that
![]() $\eta [T']$
is in the semirelational form (as defined in [Reference Łełyk and Wcisło19]). Since, using the notation of [Reference Łełyk and Wcisło19],
$\eta [T']$
is in the semirelational form (as defined in [Reference Łełyk and Wcisło19]). Since, using the notation of [Reference Łełyk and Wcisło19],
![]() $T'$
is of the form
$T'$
is of the form
![]() $T\ast \xi $
, by Lemma 25 in [Reference Łełyk and Wcisło19] we have
$T\ast \xi $
, by Lemma 25 in [Reference Łełyk and Wcisło19] we have
However,
![]() $\eta [\xi ]$
is an axiom of induction (in the sense of
$\eta [\xi ]$
is an axiom of induction (in the sense of
![]() $\mathcal {M}$
) for an arithmetical formula
$\mathcal {M}$
) for an arithmetical formula
![]() $\eta [\xi ]$
, hence
$\eta [\xi ]$
, hence
![]() $T(\eta [\xi ])$
by GR(PA).□
$T(\eta [\xi ])$
by GR(PA).□
Remark 3.20. A very similar reasoning was used in Kotlarski in [Reference Kotlarski15]. However various parts of this paper are negatively influenced by the significant gaps already discussed at the beginning of this section. We decided to reprove it in a rigorous way. Essentially the same proof is given in [Reference Łełyk and Wcisło20].
![]() $\triangle $
$\triangle $
Corollary 3.21. For any
![]() $(\mathcal {M},S)\models \mathrm {CS}^-$
the following conditions are equivalent:
$(\mathcal {M},S)\models \mathrm {CS}^-$
the following conditions are equivalent:
-
1.
 $(\mathcal {M},S)\models \mathrm {GR}(\mathrm {PA})$
.
$(\mathcal {M},S)\models \mathrm {GR}(\mathrm {PA})$
. -
2. For every
 $c\in M$
,
$c\in M$
,
 $(\mathcal {M},S)\models \mathrm {CS}(\Sigma ^*_c)$
.
$(\mathcal {M},S)\models \mathrm {CS}(\Sigma ^*_c)$
. -
3.
 $(\mathcal {M},S)\models \mathrm {CS}_0$
.
$(\mathcal {M},S)\models \mathrm {CS}_0$
.
Proof. We show the remaining implication
![]() $2.\Rightarrow 3$
. By the classical fact in the metamathematics of
$2.\Rightarrow 3$
. By the classical fact in the metamathematics of
![]() $\mathrm {PA}$
, a subset of the model satisfies
$\mathrm {PA}$
, a subset of the model satisfies
![]() $\Delta _0$
-induction if and only if it is piecewise coded, i.e., it is sufficient to show
$\Delta _0$
-induction if and only if it is piecewise coded, i.e., it is sufficient to show
where
![]() $(x)_i$
denotes the i-th projection of x. Working in
$(x)_i$
denotes the i-th projection of x. Working in
![]() $(\mathcal {M},S)$
fix an arbitrary c. Obviously, if a formula
$(\mathcal {M},S)$
fix an arbitrary c. Obviously, if a formula
![]() $\phi <c$
then
$\phi <c$
then
![]() $\phi \in \Sigma ^*_c$
. Hence, it is sufficient to find a d such that
$\phi \in \Sigma ^*_c$
. Hence, it is sufficient to find a d such that
This clearly can be done as
![]() $S_c$
satisfies full induction.□
$S_c$
satisfies full induction.□
4 Consequences of the global reflection principle
In this section we focus on the
![]() $\Delta _0$
-inductive truth predicate. We remind the Reader that by default all theories extend
$\Delta _0$
-inductive truth predicate. We remind the Reader that by default all theories extend
![]() $\mathrm {EA}$
. We extend the result from the previous section and prove the following theorem.
$\mathrm {EA}$
. We extend the result from the previous section and prove the following theorem.
Theorem 4.1. For every
![]() $\phi (x)\in \Sigma _1(\mathcal {L}_T)$
and every
$\phi (x)\in \Sigma _1(\mathcal {L}_T)$
and every
![]() $n\in \omega $
the following sentence is provable in
$n\in \omega $
the following sentence is provable in
![]() $\mathrm {CT}_0$
:
$\mathrm {CT}_0$
:
Corollary 4.2.
![]() .
.
The above answers affirmatively the question of Beklemishev and Pakhomov from [Reference Beklemishev and Pakhomov2].
Convention 4.3. Working in an extension of
![]() $\mathrm {UTB}^-$
, it makes sense to treat the predicate T as a theory composed of all true sentences. Thus, we shall often write (for a Gödelized theory
$\mathrm {UTB}^-$
, it makes sense to treat the predicate T as a theory composed of all true sentences. Thus, we shall often write (for a Gödelized theory
![]() $\mathrm {Th}$
)
$\mathrm {Th}$
)
to denote the theory consisting of all sentences
for
![]() $\phi (x)\in \Gamma $
.
$\phi (x)\in \Gamma $
.
![]() $\triangle $
$\triangle $
Let us start by explaining that Theorem 4.1 really improves on the results from the previous section. Let
![]() $\mathrm {Th}$
be a Gödelized theory extending EA in a language
$\mathrm {Th}$
be a Gödelized theory extending EA in a language
![]() $\mathcal {L}'$
and let
$\mathcal {L}'$
and let
![]() $\mathrm {UTB}^-(\mathrm {Th})$
denote the extension of
$\mathrm {UTB}^-(\mathrm {Th})$
denote the extension of
![]() $\mathrm {Th}$
with
$\mathrm {Th}$
with
![]() $\mathrm {UTB}^-$
axioms. It is enough to observe that over
$\mathrm {UTB}^-$
axioms. It is enough to observe that over
![]() $\mathrm {EA}$
$\mathrm {EA}$
Indeed, working in
fix an arbitrary
![]() $\mathcal {L}_{\mathrm {Th}}$
sentence
$\mathcal {L}_{\mathrm {Th}}$
sentence
![]() $\phi $
and assume
$\phi $
and assume
![]() $\mathrm {Pr}_{\mathrm {Th}}(\phi )$
. By the axioms of
$\mathrm {Pr}_{\mathrm {Th}}(\phi )$
. By the axioms of
![]() $\mathrm {UTB}^-(\mathrm {Th})$
we immediately obtain
$\mathrm {UTB}^-(\mathrm {Th})$
we immediately obtain
![]() $\mathrm {Pr}_{\mathrm {UTB}^-(\mathrm {Th})}(\ulcorner T(\phi ) \urcorner )$
. Therefore, by the
$\mathrm {Pr}_{\mathrm {UTB}^-(\mathrm {Th})}(\ulcorner T(\phi ) \urcorner )$
. Therefore, by the
![]() $\Delta _0$
reflection for
$\Delta _0$
reflection for
![]() $\mathrm {UTB}^-(\mathrm {Th})$
we obtain,
$\mathrm {UTB}^-(\mathrm {Th})$
we obtain,
![]() $T(\phi )$
.
$T(\phi )$
.
Proof of Theorem 4.1 starts with a lemma:Footnote 12
Lemma 4.4. For every
![]() $\phi \in \Delta _0(\mathcal {L}_T)$
,
$\phi \in \Delta _0(\mathcal {L}_T)$
,
Proof. Fix
![]() $(\mathcal {M},T)\models \mathrm {CT}_0$
,
$(\mathcal {M},T)\models \mathrm {CT}_0$
,
![]() $\phi (x)\in \Delta _0(\mathcal {L}_T)$
and
$\phi (x)\in \Delta _0(\mathcal {L}_T)$
and
![]() $a\in M$
and any proof p such that
$a\in M$
and any proof p such that
![]() $(\mathcal {M},T)\models \mathrm {Proof}_{\mathrm {UTB}}^T(p,\phi [a])$
. Since in
$(\mathcal {M},T)\models \mathrm {Proof}_{\mathrm {UTB}}^T(p,\phi [a])$
. Since in
![]() $\phi $
all the quantifiers are bounded, then there is a
$\phi $
all the quantifiers are bounded, then there is a
![]() $b\in M$
such that for every
$b\in M$
such that for every
![]() $(\mathcal {M}', T')$
satisfying (1)
$(\mathcal {M}', T')$
satisfying (1)
![]() $\mathcal {M}\subseteq _e \mathcal {M}'$
and (2)
$\mathcal {M}\subseteq _e \mathcal {M}'$
and (2)
![]() $T'{\upharpoonright _{<b}} = T{\upharpoonright _{<b}}$
we have
$T'{\upharpoonright _{<b}} = T{\upharpoonright _{<b}}$
we have
Recall that for
![]() $X\subseteq M$
,
$X\subseteq M$
,
![]() $X{\upharpoonright _{<b}}$
denotes the set of elements of X below b. Fix any such b. In short, b is big enough so that any end-extension of
$X{\upharpoonright _{<b}}$
denotes the set of elements of X below b. Fix any such b. In short, b is big enough so that any end-extension of
![]() $(\mathcal {M},T)$
which agrees with T up to b is absolute with respect to
$(\mathcal {M},T)$
which agrees with T up to b is absolute with respect to
![]() $\phi (a)$
. Without loss of generality assume that
$\phi (a)$
. Without loss of generality assume that
![]() $p<b$
and let c be big enough so that any formula (with code) smaller than b belongs to
$p<b$
and let c be big enough so that any formula (with code) smaller than b belongs to
![]() $(\Sigma ^*_{c-1})^{\mathcal {M}}$
. By Theorem 3.19,
$(\Sigma ^*_{c-1})^{\mathcal {M}}$
. By Theorem 3.19,
![]() $(\mathcal {M}, T_c)\models \mathrm {CT}(\Sigma _c^*)$
. Now we work in
$(\mathcal {M}, T_c)\models \mathrm {CT}(\Sigma _c^*)$
. Now we work in
![]() $(\mathcal {M},T_c)$
. Consider the theory
$(\mathcal {M},T_c)$
. Consider the theory
By GR(PA) (Corollary 3.12)
![]() $\mathrm {Th}$
is consistent and by the trivial conservativity proof for
$\mathrm {Th}$
is consistent and by the trivial conservativity proof for
![]() $\mathrm {UTB}$
it follows that
$\mathrm {UTB}$
it follows that
![]() $\mathrm {UTB}+\mathrm {Th}$
is consistent as well. Hence, by the Arithmetized Completeness Theorem (for
$\mathrm {UTB}+\mathrm {Th}$
is consistent as well. Hence, by the Arithmetized Completeness Theorem (for
![]() $\mathrm {PA}^*$
) there is a full model
$\mathrm {PA}^*$
) there is a full model
![]() $((\mathcal {N}, T'), \mathrm {Sat}_{(\mathcal {N}, T')})$
such that
$((\mathcal {N}, T'), \mathrm {Sat}_{(\mathcal {N}, T')})$
such that
Since
![]() $(\mathcal {N}, T')$
is strongly interpretable in
$(\mathcal {N}, T')$
is strongly interpretable in
![]() $(\mathcal {M},T_c)$
, then, by Proposition 2.24,
$(\mathcal {M},T_c)$
, then, by Proposition 2.24,
![]() $\mathcal {M}\subseteq _e \mathcal {N}$
. Since internally in
$\mathcal {M}\subseteq _e \mathcal {N}$
. Since internally in
![]() $(\mathcal {M}, T_c)$
,
$(\mathcal {M}, T_c)$
,
![]() $(\mathcal {N},T')$
is a model of
$(\mathcal {N},T')$
is a model of
![]() $\mathrm {UTB}+\mathrm {Th}$
, then every sentence occurring in p is true in
$\mathrm {UTB}+\mathrm {Th}$
, then every sentence occurring in p is true in
![]() $(\mathcal {N},T')$
. So we see that
$(\mathcal {N},T')$
. So we see that
![]() $(\mathcal {N}, T')\models \phi (a)$
. We show that
$(\mathcal {N}, T')\models \phi (a)$
. We show that
![]() $T'{\upharpoonright _{<b}} = T{\upharpoonright _{<b}}$
. Fix any sentence
$T'{\upharpoonright _{<b}} = T{\upharpoonright _{<b}}$
. Fix any sentence
![]() $\psi $
such that
$\psi $
such that
![]() $\psi <b$
. Then, by the choice of c,
$\psi <b$
. Then, by the choice of c,
![]() $\psi \in \Sigma ^*_{c-1}$
and hence the following conditions are equivalent:
$\psi \in \Sigma ^*_{c-1}$
and hence the following conditions are equivalent:
-
1.
 $\psi \in T{\upharpoonright _{<b}}$
.
$\psi \in T{\upharpoonright _{<b}}$
. -
2.
 $\psi \in \mathrm {Th}$
.
$\psi \in \mathrm {Th}$
. -
3.
 $(\mathcal {M}, T_c)\models \big [\mathcal {N}\models _{\mathrm {Sat}_{(\mathcal {N}, T')}}\psi \big ]$
.
$(\mathcal {M}, T_c)\models \big [\mathcal {N}\models _{\mathrm {Sat}_{(\mathcal {N}, T')}}\psi \big ]$
. -
4.
 $(\mathcal {N},T')\models T(\psi )$
.
$(\mathcal {N},T')\models T(\psi )$
. -
5.
 $\psi \in T'{\upharpoonright _{<b}}$
.
$\psi \in T'{\upharpoonright _{<b}}$
.
The equivalence between
![]() $3.$
and
$3.$
and
![]() $4.$
follows by (B). Hence it follows by (A) that
$4.$
follows by (B). Hence it follows by (A) that
![]() $(\mathcal {M},T)\models \phi (a)$
, which suffices to prove the claim.□
$(\mathcal {M},T)\models \phi (a)$
, which suffices to prove the claim.□
Remark 4.5. The above proof generalises to the case in which
![]() $\mathrm {PA}$
is replaced with a (formalized) theory
$\mathrm {PA}$
is replaced with a (formalized) theory
![]() $\mathrm {Th}$
in an expanded (at most countable) language
$\mathrm {Th}$
in an expanded (at most countable) language
![]() $\mathcal {L}'$
(we assume a fixed Gödel coding of
$\mathcal {L}'$
(we assume a fixed Gödel coding of
![]() $\mathcal {L}'$
) such that
$\mathcal {L}'$
) such that
![]() $\mathrm {Th}\vdash \mathrm {Ind}_{\mathcal {L}'}$
. This allows us to obtain:
$\mathrm {Th}\vdash \mathrm {Ind}_{\mathcal {L}'}$
. This allows us to obtain:
Lemma 4.6. For every
![]() $\phi \in \Delta _0(\mathcal {L}^{\prime }_{T})$
,
$\phi \in \Delta _0(\mathcal {L}^{\prime }_{T})$
,
In order to bypass the problems with infinitely many additional predicates in
![]() $\mathcal {L}'$
it is sufficient to work with an
$\mathcal {L}'$
it is sufficient to work with an
![]() $\mathcal {M}$
-bounded fragment of
$\mathcal {M}$
-bounded fragment of
![]() $\mathrm {Th}$
and consider only the fragment of
$\mathrm {Th}$
and consider only the fragment of
![]() $\mathcal {L}'$
consisting of predicates which occur in a formula in the fixed proof p.
$\mathcal {L}'$
consisting of predicates which occur in a formula in the fixed proof p.
![]() $\triangle $
$\triangle $
The following lemma suffices to complete the proof of Theorem 4.1.
Lemma 4.7 (Bounding lemma)
For every formula
![]() $\phi (x)\in \Delta _0(\mathcal {L}_T)$
and every
$\phi (x)\in \Delta _0(\mathcal {L}_T)$
and every
![]() $n\in \omega $
, the following implication is provable in
$n\in \omega $
, the following implication is provable in
![]() $\mathrm {CT}_0$
:
$\mathrm {CT}_0$
:
Before we prove it, let us show a proposition which was the motivation for the proof of the above lemma:
Proposition 4.8 (
 $\Sigma _1$
-completeness for
$\Sigma _1$
-completeness for
 $\mathrm {UTB}^-$
)
$\mathrm {UTB}^-$
)
For every
![]() $\Delta _0(\mathcal {L}_T)$
formula
$\Delta _0(\mathcal {L}_T)$
formula
![]() $\phi (x)$
, if
$\phi (x)$
, if
![]() $(\mathbb {N}, \mathrm {Th}(\mathbb {N}))\models \exists x \phi (x)$
, then for some
$(\mathbb {N}, \mathrm {Th}(\mathbb {N}))\models \exists x \phi (x)$
, then for some
![]() $n\in \omega\ \mathrm {Th}(\mathbb {N})+ \mathrm {UTB}^-\vdash \exists x<\underline {n} \phi (x)$
.
$n\in \omega\ \mathrm {Th}(\mathbb {N})+ \mathrm {UTB}^-\vdash \exists x<\underline {n} \phi (x)$
.
Proof. Suppose that for every n,
![]() $\mathrm {UTB}^- + \mathrm {Th}(\mathbb {N}) + \forall x<\underline {n}\neg \phi (x)$
is consistent. A trivial compactness argument then shows that
$\mathrm {UTB}^- + \mathrm {Th}(\mathbb {N}) + \forall x<\underline {n}\neg \phi (x)$
is consistent. A trivial compactness argument then shows that
![]() ${\mathrm {Th}(\mathbb {N}) {{\kern-1.6pt}+{\kern-1.6pt}} \mathrm {UTB}^- {{\kern-1.6pt}+{\kern-1.6pt}} \{\forall x<\underline {n}\phi (x) \, | \, n {{\kern-1.6pt}\in{\kern-1.6pt}} \omega \}}$
is consistent as well. So let us take
${\mathrm {Th}(\mathbb {N}) {{\kern-1.6pt}+{\kern-1.6pt}} \mathrm {UTB}^- {{\kern-1.6pt}+{\kern-1.6pt}} \{\forall x<\underline {n}\phi (x) \, | \, n {{\kern-1.6pt}\in{\kern-1.6pt}} \omega \}}$
is consistent as well. So let us take
![]() ${(\mathcal {M},T)\models \mathrm {Th}(\mathbb {N}) {{\kern-1.2pt}+{\kern-1.2pt}} \mathrm {UTB}^- {{\kern-1.2pt}+{\kern-1.2pt}} \{\forall x<\underline {n}\phi (x) \ | \ n {{\kern-0.9pt}\in{\kern-0.9pt}} \omega \}}$
and look at
${(\mathcal {M},T)\models \mathrm {Th}(\mathbb {N}) {{\kern-1.2pt}+{\kern-1.2pt}} \mathrm {UTB}^- {{\kern-1.2pt}+{\kern-1.2pt}} \{\forall x<\underline {n}\phi (x) \ | \ n {{\kern-0.9pt}\in{\kern-0.9pt}} \omega \}}$
and look at
![]() $(\mathbb {N}, T{\upharpoonright _{\mathbb {N}}})$
. Since
$(\mathbb {N}, T{\upharpoonright _{\mathbb {N}}})$
. Since
![]() $\mathbb {N}\preceq _e \mathcal {M}$
,
$\mathbb {N}\preceq _e \mathcal {M}$
,
![]() $(\mathbb {N}, T{\upharpoonright _{\mathbb {N}}})\models \mathrm {UTB}^-$
, and, consequently
$(\mathbb {N}, T{\upharpoonright _{\mathbb {N}}})\models \mathrm {UTB}^-$
, and, consequently
![]() $T{\upharpoonright _{\mathbb {N}}} = \mathrm {Th}(\mathbb {N})$
, because in
$T{\upharpoonright _{\mathbb {N}}} = \mathrm {Th}(\mathbb {N})$
, because in
![]() $\mathbb {N}$
there is only one interpretation for the
$\mathbb {N}$
there is only one interpretation for the
![]() $\mathrm {UTB}^-$
-truth predicate. Since
$\mathrm {UTB}^-$
-truth predicate. Since
![]() $\phi (x)\in \Delta _0(\mathcal {L}_T)$
, then
$\phi (x)\in \Delta _0(\mathcal {L}_T)$
, then
![]() $(\mathbb {N},\mathrm {Th}(\mathbb {N}))\models \forall x \neg \phi (x)$
, which suffices to end the proof.□
$(\mathbb {N},\mathrm {Th}(\mathbb {N}))\models \forall x \neg \phi (x)$
, which suffices to end the proof.□
Remark 4.9. Essentially the same proof shows that already
![]() $\mathrm {TB}^-$
(a non-uniform version of
$\mathrm {TB}^-$
(a non-uniform version of
![]() $\mathrm {UTB}^-$
based solely on Tarski biconditionals for arithmetical sentences) is
$\mathrm {UTB}^-$
based solely on Tarski biconditionals for arithmetical sentences) is
![]() $\Sigma _1$
-complete in the above sense.
$\Sigma _1$
-complete in the above sense.
![]() $\triangle $
$\triangle $
Proof of Lemma 4.7. Fix
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $\phi (x)\in \Delta _0(\mathcal {L}_T)$
, and a model
$\phi (x)\in \Delta _0(\mathcal {L}_T)$
, and a model
![]() $(\mathcal {M},T)\models \mathrm {CT}_0$
. Assume that for all
$(\mathcal {M},T)\models \mathrm {CT}_0$
. Assume that for all
![]() $a\in M$
,
$a\in M$
,
![]() $(\mathcal {M},T)\models \neg \mathrm {Pr}_{\mathrm {UTB}}^T(\forall v{<}\underline {a} \neg \phi (v))$
. By formalizing in
$(\mathcal {M},T)\models \neg \mathrm {Pr}_{\mathrm {UTB}}^T(\forall v{<}\underline {a} \neg \phi (v))$
. By formalizing in
![]() $\mathrm {PA}$
the trivial compactness argument, we see that for an
$\mathrm {PA}$
the trivial compactness argument, we see that for an
![]() $(\mathcal {M},T)$
-definable theory
$(\mathcal {M},T)$
-definable theory
![]() $(\mathcal {M},T)\models \mathrm {Con}_{\mathrm {Th}}$
. However, contrary to what happened in the proof of
$(\mathcal {M},T)\models \mathrm {Con}_{\mathrm {Th}}$
. However, contrary to what happened in the proof of
![]() $\Sigma _1$
-completeness for
$\Sigma _1$
-completeness for
![]() $\mathrm {UTB}^-$
(Proposition 4.8), there need not be an
$\mathrm {UTB}^-$
(Proposition 4.8), there need not be an
![]() $(\mathcal {M},T)$
-definable full model of
$(\mathcal {M},T)$
-definable full model of
![]() $\mathrm {Th}$
, since we may not have
$\mathrm {Th}$
, since we may not have
![]() $\Sigma _1$
-induction for
$\Sigma _1$
-induction for
![]() $\mathcal {L}_T$
. As a remedy, we shall work with restrictions of T. For an arbitrary c we shall show that
$\mathcal {L}_T$
. As a remedy, we shall work with restrictions of T. For an arbitrary c we shall show that
![]() $\neg \mathrm {Pr}^{T{\upharpoonright _{c}}}_{\mathrm {UTB}_n{\upharpoonright _{c}}}(\forall v \neg \phi (v))$
, which suffices to prove the claim by a trivial compactness argument
$\neg \mathrm {Pr}^{T{\upharpoonright _{c}}}_{\mathrm {UTB}_n{\upharpoonright _{c}}}(\forall v \neg \phi (v))$
, which suffices to prove the claim by a trivial compactness argument
![]() $(\mathrm {UTB}_n{\upharpoonright _{c}}$
denotes the first
$(\mathrm {UTB}_n{\upharpoonright _{c}}$
denotes the first
![]() $c-1$
axioms of
$c-1$
axioms of
![]() $\mathrm {UTB}_n$
). Fix c and let
$\mathrm {UTB}_n$
). Fix c and let
![]() $c<b$
be big enough so that every formula in
$c<b$
be big enough so that every formula in
![]() $T{\upharpoonright _{c}}$
and every axiom of
$T{\upharpoonright _{c}}$
and every axiom of
![]() $\mathrm {UTB}^-{\upharpoonright _{c}}$
belongs to
$\mathrm {UTB}^-{\upharpoonright _{c}}$
belongs to
![]() $\Sigma _{b-1}^*$
. Working in
$\Sigma _{b-1}^*$
. Working in
![]() $(\mathcal {M}, T_b)$
consider
$(\mathcal {M}, T_b)$
consider
Since
![]() $\mathrm {Th}_{b}\subseteq \mathrm {Th}$
, then
$\mathrm {Th}_{b}\subseteq \mathrm {Th}$
, then
![]() $\mathrm {Th}_{b}$
is consistent.
$\mathrm {Th}_{b}$
is consistent.
![]() $\mathrm {Th}_b$
is definable in
$\mathrm {Th}_b$
is definable in
![]() $(\mathcal {M}, T_b)\models \mathrm {PA}^*$
; hence we can fix a full model
$(\mathcal {M}, T_b)\models \mathrm {PA}^*$
; hence we can fix a full model
![]() $((\mathcal {N}, T'), \mathrm {Sat}_{(\mathcal {N}, T')})$
such that
$((\mathcal {N}, T'), \mathrm {Sat}_{(\mathcal {N}, T')})$
such that
Consider a model
![]() $(\mathcal {M}, T'{\upharpoonright _{M}})$
(i.e., we restrict
$(\mathcal {M}, T'{\upharpoonright _{M}})$
(i.e., we restrict
![]() $T'$
to model M). Since
$T'$
to model M). Since
![]() $(\mathcal {M}, T'{\upharpoonright _{M}})\subseteq _e (\mathcal {N}, T')$
and
$(\mathcal {M}, T'{\upharpoonright _{M}})\subseteq _e (\mathcal {N}, T')$
and
![]() $\phi (x)\in \Delta _0(\mathcal {L}_T)$
, then
$\phi (x)\in \Delta _0(\mathcal {L}_T)$
, then
![]() $(\mathcal {M}, T'{\upharpoonright _{M}})\models \forall x\neg \phi (x)$
. We check that
$(\mathcal {M}, T'{\upharpoonright _{M}})\models \forall x\neg \phi (x)$
. We check that
![]() $(\mathcal {M},T'{\upharpoonright _{M}})\models \mathrm {CS}^-(\Sigma ^*_{b})$
. To this end it is sufficient to show that for every
$(\mathcal {M},T'{\upharpoonright _{M}})\models \mathrm {CS}^-(\Sigma ^*_{b})$
. To this end it is sufficient to show that for every
![]() $\phi \in \Sigma _{b}^*$
we have
$\phi \in \Sigma _{b}^*$
we have
So fix an arbitrary such
![]() $\phi $
. Now the following conditions are equivalent:
$\phi $
. Now the following conditions are equivalent:
-
1.
 $\phi \in T'{\upharpoonright _{M}}$
;
$\phi \in T'{\upharpoonright _{M}}$
; -
2.
 $(\mathcal {N},T')\models T(\phi )$
;
$(\mathcal {N},T')\models T(\phi )$
; -
3.
 $(M, T_b)\models \big [(\mathcal {N}, T')\models _{\mathrm {Sat}_{(\mathcal {N}, T')}} \phi \big ]$
;
$(M, T_b)\models \big [(\mathcal {N}, T')\models _{\mathrm {Sat}_{(\mathcal {N}, T')}} \phi \big ]$
; -
4.
 $(\mathcal {M}, T)\models T(\phi )$
.
$(\mathcal {M}, T)\models T(\phi )$
.
Now, the equivalence between (2) and (3) is by the fact that
![]() $(\mathcal {N},T')$
is an
$(\mathcal {N},T')$
is an
![]() $(\mathcal {M},T_b)$
-definable full model of
$(\mathcal {M},T_b)$
-definable full model of
![]() $\mathrm {UTB}$
. The equivalence between (3) and (4) holds because
$\mathrm {UTB}$
. The equivalence between (3) and (4) holds because
![]() $\mathcal {N}$
satisfies all sentences from
$\mathcal {N}$
satisfies all sentences from
![]() $\Sigma _b^*$
, which T deems true in
$\Sigma _b^*$
, which T deems true in
![]() $\mathcal {M}$
. Since
$\mathcal {M}$
. Since
![]() $T'{\upharpoonright _{M}}$
is
$T'{\upharpoonright _{M}}$
is
![]() $(\mathcal {M}, T_b)$
-definable it satisfies full
$(\mathcal {M}, T_b)$
-definable it satisfies full
![]() $\mathcal {L}_T$
induction. To sum up, we have just concluded that
$\mathcal {L}_T$
induction. To sum up, we have just concluded that
We work in
![]() $(\mathcal {M}, T'{\upharpoonright _{M}})$
. First observe that
$(\mathcal {M}, T'{\upharpoonright _{M}})$
. First observe that
![]() $T^{\prime }_b$
makes
$T^{\prime }_b$
makes
![]() $\mathbf {V}$
(i.e., the class of all numbers; see Example 2.5) a b-full model for the arithmetical vocabulary (because
$\mathbf {V}$
(i.e., the class of all numbers; see Example 2.5) a b-full model for the arithmetical vocabulary (because
![]() $T^{\prime }_b = T_b$
, by (*)). For a fixed
$T^{\prime }_b = T_b$
, by (*)). For a fixed
![]() $k\in \omega $
let
$k\in \omega $
let
![]() $X_k$
consist of all Boolean combinations of sentences from
$X_k$
consist of all Boolean combinations of sentences from
![]() $\Sigma ^*_b(\mathcal {L})\cup \Sigma ^*_k(\mathcal {L}_T)$
. Observe that for all
$\Sigma ^*_b(\mathcal {L})\cup \Sigma ^*_k(\mathcal {L}_T)$
. Observe that for all
![]() $k\in \omega $
, all the uniform Tarski biconditionals are in
$k\in \omega $
, all the uniform Tarski biconditionals are in
![]() $X_k$
and this class is closed under subformulae. Now for every
$X_k$
and this class is closed under subformulae. Now for every
![]() $k\in \omega $
, there exists an
$k\in \omega $
, there exists an
![]() $(\mathcal {M}, T'{\upharpoonright _{M}})$
definable satisfaction class for
$(\mathcal {M}, T'{\upharpoonright _{M}})$
definable satisfaction class for
![]() $\mathbf {V}[T]$
and sentences from
$\mathbf {V}[T]$
and sentences from
![]() $X_k$
. Denote such a satisfaction predicate with
$X_k$
. Denote such a satisfaction predicate with
![]() $\mathrm {Sat}_{\Sigma _{k}}^{T^{\prime }_b}$
. Then
$\mathrm {Sat}_{\Sigma _{k}}^{T^{\prime }_b}$
. Then
![]() $\mathrm {Sat}_{\Sigma _{n+2}}^{T^{\prime }_{b}}$
makes
$\mathrm {Sat}_{\Sigma _{n+2}}^{T^{\prime }_{b}}$
makes
![]() $\mathbf {V}[T]$
an
$\mathbf {V}[T]$
an
![]() $X_{n}$
-model for the definable restricted theory
$X_{n}$
-model for the definable restricted theory
By Proposition 2.16 this is enough to show that this theory is consistent.□
Remark 4.10. The proof of Lemma 4.4 can be modified to yield a new proof of Theorem 1 from [Reference Beklemishev and Pakhomov2] (for finite languages). Let us restate it and prove it here:
Theorem 4.11 (Beklemishev–Pakhomov)
Let
![]() $\mathcal {L}'$
be an arbitrary finite language with a fixed Gödel numbering and
$\mathcal {L}'$
be an arbitrary finite language with a fixed Gödel numbering and
![]() $\mathrm {Th}$
be a Gödelized
$\mathrm {Th}$
be a Gödelized
![]() $\mathcal {L}'$
theory. Then,
$\mathcal {L}'$
theory. Then,
is
![]() $\mathcal {L}'$
-conservative over
$\mathcal {L}'$
-conservative over
![]() $\mathrm {REF}(\mathrm {Th})$
.
$\mathrm {REF}(\mathrm {Th})$
.
Proof. Pick any
![]() $(\mathcal {M},S)\models \text {REF}(\mathrm {Th}) + \mathrm {CS}(\Sigma ^*_c(\mathcal {L}'))$
(the satisfaction class is defined for
$(\mathcal {M},S)\models \text {REF}(\mathrm {Th}) + \mathrm {CS}(\Sigma ^*_c(\mathcal {L}'))$
(the satisfaction class is defined for
![]() $\mathcal {L}'$
). Using overspill, as in the proof of Lemma 5.3 we may pick a nonstandard
$\mathcal {L}'$
). Using overspill, as in the proof of Lemma 5.3 we may pick a nonstandard
![]() $d<c$
such that
$d<c$
such that
Then, in
![]() $(\mathcal {M},S)$
the
$(\mathcal {M},S)$
the
![]() $\mathcal {L}^{\prime }_S$
-theory
$\mathcal {L}^{\prime }_S$
-theory
![]() $\mathrm {Th}+\mathrm {UTB}^-(\mathcal {L}')+\{\phi \in \Sigma ^*_d(\mathcal {L}') \ \ | \ \ S(\phi ,\varepsilon ) \}$
is consistent, so let
$\mathrm {Th}+\mathrm {UTB}^-(\mathcal {L}')+\{\phi \in \Sigma ^*_d(\mathcal {L}') \ \ | \ \ S(\phi ,\varepsilon ) \}$
is consistent, so let
![]() $(\mathcal {N}, S')$
be its full model. We claim that
$(\mathcal {N}, S')$
be its full model. We claim that
![]() $\mathrm {UTB}^-(\mathcal {L}')$
holds in
$\mathrm {UTB}^-(\mathcal {L}')$
holds in
![]() $(\mathcal {M},S'{\upharpoonright _{M}})$
since, in
$(\mathcal {M},S'{\upharpoonright _{M}})$
since, in
![]() $\mathcal {M}$
, S and
$\mathcal {M}$
, S and
![]() $S'{\upharpoonright _{M}}$
coincide on all formulae from
$S'{\upharpoonright _{M}}$
coincide on all formulae from
![]() $\Sigma ^*_d$
. To show
$\Sigma ^*_d$
. To show
![]() $\Delta _0$
reflection, we use the fact that
$\Delta _0$
reflection, we use the fact that
![]() $(\mathcal {N},S')$
is strongly interpretable in
$(\mathcal {N},S')$
is strongly interpretable in
![]() $(\mathcal {M},S)$
. Fix a
$(\mathcal {M},S)$
. Fix a
![]() $\Delta _0(\mathcal {L}^{\prime }_T)$
-formula
$\Delta _0(\mathcal {L}^{\prime }_T)$
-formula
![]() $\phi (x)$
and working in
$\phi (x)$
and working in
![]() $(\mathcal {M},S)$
assume that p is a proof of
$(\mathcal {M},S)$
assume that p is a proof of
![]() $\phi (\underline {a})$
(for some element a) from the axioms of
$\phi (\underline {a})$
(for some element a) from the axioms of
![]() $\mathrm {UTB}^-(\mathcal {L}')+\mathrm {Th}$
. Since
$\mathrm {UTB}^-(\mathcal {L}')+\mathrm {Th}$
. Since
 $$\begin{align*}(\mathcal{M},S)\models \bigg[(\mathcal{N},S')\models_{\mathrm{Sat}_{(\mathcal{N},S')}} \mathrm{UTB}^- +\mathrm{Th}\bigg],\end{align*}$$
$$\begin{align*}(\mathcal{M},S)\models \bigg[(\mathcal{N},S')\models_{\mathrm{Sat}_{(\mathcal{N},S')}} \mathrm{UTB}^- +\mathrm{Th}\bigg],\end{align*}$$
then
![]() $(\mathcal {N},S')\models \phi (a)$
and since
$(\mathcal {N},S')\models \phi (a)$
and since
![]() $(\mathcal {M},S'{\upharpoonright _{M}})\subseteq _e(\mathcal {N},S')$
,
$(\mathcal {M},S'{\upharpoonright _{M}})\subseteq _e(\mathcal {N},S')$
,
![]() $\phi (a)$
holds in
$\phi (a)$
holds in
![]() $(\mathcal {M},S'{\upharpoonright _{M}})$
by absoluteness of bounded formulae.□
$(\mathcal {M},S'{\upharpoonright _{M}})$
by absoluteness of bounded formulae.□
![]() $\triangle $
$\triangle $
5 The arithmetical part of
 $\mathrm {CT}_0$
$\mathrm {CT}_0$
In this section we reprove the following result of Kotlarski [Reference Kotlarski15].Footnote 13
Theorem 5.1 (Kotlarski and Smoryński)
![]() $\mathrm {CT}_0$
is arithmetically conservative over
$\mathrm {CT}_0$
is arithmetically conservative over
![]() $\mathrm {REF}^{\omega }(\mathrm {PA})$
.
$\mathrm {REF}^{\omega }(\mathrm {PA})$
.
The idea of Kotlarski’s argument is to mimic the Henkin proof of Completeness Theorem in a countable recursively saturated model. Also, [Reference Beklemishev and Pakhomov2] gives a different, syntactic proof of Theorem 5.1. We choose a still different path and our main ingredient is the following:
Theorem 5.2. Let
![]() $\mathrm {Th}$
be any Gödelized
$\mathrm {Th}$
be any Gödelized
![]() $\mathcal {L}$
theory. Suppose that
$\mathcal {L}$
theory. Suppose that
![]() $\mathcal {M}\models \mathrm {REF}^{\omega }(\mathrm {Th})$
and S is a satisfaction class for
$\mathcal {M}\models \mathrm {REF}^{\omega }(\mathrm {Th})$
and S is a satisfaction class for
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
for some nonstandard c. Then there exists a nonstandard
![]() $d\in M$
and
$d\in M$
and
![]() $(\mathcal {N}, S')\models \mathrm {CS}_0 + \forall x \big (\mathrm {Th}(x)\rightarrow S(x,\varepsilon )\big )$
such that
$(\mathcal {N}, S')\models \mathrm {CS}_0 + \forall x \big (\mathrm {Th}(x)\rightarrow S(x,\varepsilon )\big )$
such that
![]() $\mathcal {M}\subsetneq _e\mathcal {N}$
and
$\mathcal {M}\subsetneq _e\mathcal {N}$
and
![]() $S_d\subseteq S'$
.
$S_d\subseteq S'$
.
Observe that the conditions
![]() $\mathcal {M}\subsetneq _e \mathcal {N}$
and
$\mathcal {M}\subsetneq _e \mathcal {N}$
and
![]() $S_d\subseteq S'$
jointly imply that
$S_d\subseteq S'$
jointly imply that
![]() $\mathcal {M}\precneqq _e\mathcal {N}$
(assuming
$\mathcal {M}\precneqq _e\mathcal {N}$
(assuming
![]() $S_d$
and
$S_d$
and
![]() $S'$
are satisfaction classes). The construction of
$S'$
are satisfaction classes). The construction of
![]() $(\mathcal {N},S')$
proceeds in
$(\mathcal {N},S')$
proceeds in
![]() $\omega $
-stages and is motivated by Corollary 3.21:
$\omega $
-stages and is motivated by Corollary 3.21:
![]() $\mathcal {N}$
will admit a cofinal
$\mathcal {N}$
will admit a cofinal
![]() $\omega $
-sequence
$\omega $
-sequence
![]() $a_0,\ldots , a_n,\ldots $
and at the n-th stage of the construction we shall build a satisfaction class for all formulae of complexity
$a_0,\ldots , a_n,\ldots $
and at the n-th stage of the construction we shall build a satisfaction class for all formulae of complexity
![]() $a_n$
. The following lemma makes this idea more precise. Henceforth
$a_n$
. The following lemma makes this idea more precise. Henceforth
![]() $\mathrm {Th}$
is any Gödelized theory in
$\mathrm {Th}$
is any Gödelized theory in
![]() $\mathcal {L}$
.Footnote
14
$\mathcal {L}$
.Footnote
14
Lemma 5.3. Suppose that
![]() $\mathcal {M}\models \mathrm {REF}^{\omega }(\mathrm {Th})$
, c is a nonstandard element of M, and
$\mathcal {M}\models \mathrm {REF}^{\omega }(\mathrm {Th})$
, c is a nonstandard element of M, and
![]() $(\mathcal {M},S)\models \mathrm {CS}(\Sigma ^*_c(\mathcal {L}))$
. Then there exist a nonstandard
$(\mathcal {M},S)\models \mathrm {CS}(\Sigma ^*_c(\mathcal {L}))$
. Then there exist a nonstandard
![]() $d\in M$
and a sequence
$d\in M$
and a sequence
![]() $\{(\mathcal {M}_n, S_n,c_n)\}_{n\in \omega }$
such that
$\{(\mathcal {M}_n, S_n,c_n)\}_{n\in \omega }$
such that
![]() $(\mathcal {M}_0,S_0, c_0) = (\mathcal {M},S_d,d)$
and for each n:
$(\mathcal {M}_0,S_0, c_0) = (\mathcal {M},S_d,d)$
and for each n:
-
1.
 $\mathcal {M}_n\preceq _e \mathcal {M}_{n+1}$
and
$\mathcal {M}_n\preceq _e \mathcal {M}_{n+1}$
and
 $S_n\subseteq S_{n+1}$
.
$S_n\subseteq S_{n+1}$
. -
2.
 $(\mathcal {M}_{n+1}, S_{n+1})\models \mathrm {CS}(\Sigma ^*_{c_{n+1}}(\mathcal {L})) + \forall \phi \in \Sigma _{c_{n+1}}^*\big (\mathrm {Th}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
.
$(\mathcal {M}_{n+1}, S_{n+1})\models \mathrm {CS}(\Sigma ^*_{c_{n+1}}(\mathcal {L})) + \forall \phi \in \Sigma _{c_{n+1}}^*\big (\mathrm {Th}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
. -
3.
 $c_{n+1}\in M_{n+1}\setminus M_n$
.
$c_{n+1}\in M_{n+1}\setminus M_n$
.
Thus
![]() $\{(\mathcal {M}_n, S_n,c_n)\}_{n\in \omega }$
consists of proper end-extensions and each satisfaction class
$\{(\mathcal {M}_n, S_n,c_n)\}_{n\in \omega }$
consists of proper end-extensions and each satisfaction class
![]() $S_{n+1}$
in the sequence decides all formulae in the sense of
$S_{n+1}$
in the sequence decides all formulae in the sense of
![]() $M_n$
. Let us show that Lemma 5.3 immediately implies Theorem 5.2.
$M_n$
. Let us show that Lemma 5.3 immediately implies Theorem 5.2.
Proof of Theorem 5.2 modulo Lemma 5.3. Fix
![]() $\mathcal {M}\models \mathrm {REF}^{\omega }(\mathrm {Th})$
and S such that
$\mathcal {M}\models \mathrm {REF}^{\omega }(\mathrm {Th})$
and S such that
![]() $(\mathcal {M},S)\models \mathrm {CS}(\Sigma ^*_c)$
. Fix a chain
$(\mathcal {M},S)\models \mathrm {CS}(\Sigma ^*_c)$
. Fix a chain
![]() $\{(\mathcal {M}_n,S_n, c_n)\}_{n\in \omega }$
as in the thesis of Lemma 5.3. Put
$\{(\mathcal {M}_n,S_n, c_n)\}_{n\in \omega }$
as in the thesis of Lemma 5.3. Put
![]() $\mathcal {N} = \bigcup _n\mathcal {M}_n$
,
$\mathcal {N} = \bigcup _n\mathcal {M}_n$
,
![]() $S' = \bigcup _n S_n$
. It is straightforward to verify that
$S' = \bigcup _n S_n$
. It is straightforward to verify that
![]() $(\mathcal {N},S')\models \mathrm {CS}^-+\forall \phi \big (\mathrm {Th}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
. Let us check one direction of the quantifier axiom. Assume that
$(\mathcal {N},S')\models \mathrm {CS}^-+\forall \phi \big (\mathrm {Th}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
. Let us check one direction of the quantifier axiom. Assume that
![]() $(\mathcal {N},S')\models \exists \beta \geq _v\alpha S(\phi (v),\beta )$
. Let k be big enough so that
$(\mathcal {N},S')\models \exists \beta \geq _v\alpha S(\phi (v),\beta )$
. Let k be big enough so that
![]() $(\mathcal {M}_n, S_n)\models \exists \beta \geq _v\alpha S(\phi (v),\beta )$
and
$(\mathcal {M}_n, S_n)\models \exists \beta \geq _v\alpha S(\phi (v),\beta )$
and
![]() $\phi (v)\in \Sigma ^*_{c_n-1}$
. It follows that
$\phi (v)\in \Sigma ^*_{c_n-1}$
. It follows that
![]() $(\mathcal {M}_n, S_n)\models S(\exists v \phi (v), \alpha )$
. Hence
$(\mathcal {M}_n, S_n)\models S(\exists v \phi (v), \alpha )$
. Hence
![]() $(\mathcal {N},S')\models S(\exists v \phi (v), \alpha )$
. The argument in the rest of cases is similar.
$(\mathcal {N},S')\models S(\exists v \phi (v), \alpha )$
. The argument in the rest of cases is similar.
To check
![]() $\Delta _0(\mathcal {L}_T)$
-induction, we verify that S is coded, i.e., for every
$\Delta _0(\mathcal {L}_T)$
-induction, we verify that S is coded, i.e., for every
![]() $c\in N$
there exists a
$c\in N$
there exists a
![]() $d\in N$
such that
$d\in N$
such that
holds (recall that
![]() $(x)_i$
denotes the projection of x to the i-th coordinate). Take any c and let n be big enough so that
$(x)_i$
denotes the projection of x to the i-th coordinate). Take any c and let n be big enough so that
![]() $c\in M_n$
and each formula smaller than c is of complexity
$c\in M_n$
and each formula smaller than c is of complexity
![]() $\Sigma _{c_n}^*$
. By using induction in
$\Sigma _{c_n}^*$
. By using induction in
![]() $(M_{n+1}, S_{n+1})$
we can find the appropriate
$(M_{n+1}, S_{n+1})$
we can find the appropriate
![]() $d\in M_n$
and since
$d\in M_n$
and since
![]() $(\mathcal {M}_n, S_{n+1}{\upharpoonright _{M_n}})\subseteq _e (\mathcal {N},S')$
, this d will work also for
$(\mathcal {M}_n, S_{n+1}{\upharpoonright _{M_n}})\subseteq _e (\mathcal {N},S')$
, this d will work also for
![]() $(\mathcal {N}, S')$
.□
$(\mathcal {N}, S')$
.□
The proof of Lemma 5.3 consists in prolonging the given satisfaction class S until its domain catches up with the universes of models constructed along the way. As it turns out this notion of a satisfaction class being prolongable is worth isolating.
Definition 5.4. Suppose
![]() $(\mathcal {M},S, X)\models \mathrm {CS}(X)$
and for every n,
$(\mathcal {M},S, X)\models \mathrm {CS}(X)$
and for every n,
![]() $(\mathcal {M}, X)\models \Sigma ^*_n\subseteq X$
.
$(\mathcal {M}, X)\models \Sigma ^*_n\subseteq X$
.
-
1. S is
 $0$
-prolongable if there is
$0$
-prolongable if there is
 $\mathcal {N}$
such that
$\mathcal {N}$
such that
 $\mathcal {M}\subsetneq _e \mathcal {N}$
,
$\mathcal {M}\subsetneq _e \mathcal {N}$
,
 $\mathcal {N}$
is strongly interpreted in
$\mathcal {N}$
is strongly interpreted in
 $(\mathcal {M}, S)$
via a satisfaction class
$(\mathcal {M}, S)$
via a satisfaction class
 $\mathrm {Sat}_{\mathcal {N}}$
, and for all
$\mathrm {Sat}_{\mathcal {N}}$
, and for all
 $\phi \in s(X)$
and
$\phi \in s(X)$
and
 $\alpha \in \mathrm {Asn}(\phi )$
,
$\alpha \in \mathrm {Asn}(\phi )$
,  $$\begin{align*}(\mathcal{M},S)\models \bigg[S(\phi,\alpha)\equiv \mathcal{N}\models_{\mathrm{Sat}_{\mathcal{N}}}\phi[\alpha]\bigg].\end{align*}$$
$$\begin{align*}(\mathcal{M},S)\models \bigg[S(\phi,\alpha)\equiv \mathcal{N}\models_{\mathrm{Sat}_{\mathcal{N}}}\phi[\alpha]\bigg].\end{align*}$$
-
2. S is
 $n+1$
prolongable if there is
$n+1$
prolongable if there is
 $\mathcal {N}$
such that
$\mathcal {N}$
such that
 $\mathcal {M}\preceq _e \mathcal {N}$
,
$\mathcal {M}\preceq _e \mathcal {N}$
,
 $c\in N\setminus M$
, and
$c\in N\setminus M$
, and
 $S'\subseteq N^2$
such that
$S'\subseteq N^2$
such that
 $(\mathcal {N},S')\models \mathrm {CS}(\Sigma ^*_c)$
,
$(\mathcal {N},S')\models \mathrm {CS}(\Sigma ^*_c)$
,
 $S\subseteq S'$
, and
$S\subseteq S'$
, and
 $S'$
is n-prolongable.
$S'$
is n-prolongable.
 $\triangle $
$\triangle $
Let us observe that if
![]() $\mathcal {N}$
witnesses the
$\mathcal {N}$
witnesses the
![]() $0$
-prolongability of S, then
$0$
-prolongability of S, then
![]() $\mathcal {N}\models \mathrm {PA}$
. The following lemma is the key element of our reasoning:
$\mathcal {N}\models \mathrm {PA}$
. The following lemma is the key element of our reasoning:
Convention 5.5. Let
![]() $\mathrm {GR}(X, S, Z)$
denote the following sentence of
$\mathrm {GR}(X, S, Z)$
denote the following sentence of
![]() $\mathcal {L}_{\mathrm {2}}$
:
$\mathcal {L}_{\mathrm {2}}$
:
Moreover, if S is a satisfaction class on
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $(\mathcal {M},S)\models \mathrm {GR}(X,S,S+Y)$
will abbreviate
$(\mathcal {M},S)\models \mathrm {GR}(X,S,S+Y)$
will abbreviate
![]() $(\mathcal {M},S)\models \mathrm {GR}(X,S,\{\phi \in \mathrm {Sent}_{\mathcal {L}} \ \ | \ \ S(\phi ,\varepsilon ) \}\cup Y)$
.
$(\mathcal {M},S)\models \mathrm {GR}(X,S,\{\phi \in \mathrm {Sent}_{\mathcal {L}} \ \ | \ \ S(\phi ,\varepsilon ) \}\cup Y)$
.
![]() $\triangle $
$\triangle $
Lemma 5.6. Suppose that
![]() $(\mathcal {M}, S, c)\models \mathrm {CS}(\Sigma ^*_c)\wedge \mathrm {GR}(\Sigma ^*_c,S,S+\mathrm {REF}(\mathrm {Th}))$
. Then there exists
$(\mathcal {M}, S, c)\models \mathrm {CS}(\Sigma ^*_c)\wedge \mathrm {GR}(\Sigma ^*_c,S,S+\mathrm {REF}(\mathrm {Th}))$
. Then there exists
![]() $(\mathcal {N},S', c')\models \mathrm {CS}(\Sigma ^*_{c'})\wedge \mathrm {GR}(\Sigma ^*_{c'},S',S'+\mathrm {Th})$
such that:
$(\mathcal {N},S', c')\models \mathrm {CS}(\Sigma ^*_{c'})\wedge \mathrm {GR}(\Sigma ^*_{c'},S',S'+\mathrm {Th})$
such that:
-
1.
 $(\mathcal {N}, S', c')$
is strongly interpretable in
$(\mathcal {N}, S', c')$
is strongly interpretable in
 $(\mathcal {M},S,c)$
.
$(\mathcal {M},S,c)$
. -
2.
 $c'\in N\setminus M$
.
$c'\in N\setminus M$
. -
3.
 $S\subseteq S'$
.
$S\subseteq S'$
.
Proof. Fix
![]() $(\mathcal {M},S,c)$
as in the assumption and work in it. Consider the following
$(\mathcal {M},S,c)$
as in the assumption and work in it. Consider the following
![]() $\mathcal {L}_{S'}\cup \{c'\}$
theory, where
$\mathcal {L}_{S'}\cup \{c'\}$
theory, where
![]() $c'$
is a fresh constant and
$c'$
is a fresh constant and
![]() $S'$
is a fresh predicate:
$S'$
is a fresh predicate:
We shall show that the theory is consistent. The proof proceeds in two stages. In the first one, we fix a full model of
![]() $\mathrm {REF}(\mathrm {Th}) + \{\phi \ \ | \ \ S(\phi ,\varepsilon ) \}$
, i.e., a full model
$\mathrm {REF}(\mathrm {Th}) + \{\phi \ \ | \ \ S(\phi ,\varepsilon ) \}$
, i.e., a full model
![]() $(\mathcal {N}', \mathrm {Sat}_{\mathcal {N}'})$
such that
$(\mathcal {N}', \mathrm {Sat}_{\mathcal {N}'})$
such that
![]() $\mathcal {N}'\models _{\mathrm {Sat}_{\mathcal {N}'}}\mathrm {REF}(\mathrm {Th}) + \{\phi \ \ | \ \ S(\phi ,\varepsilon ) \}$
. Such a model exists by the Arithmetized Completeness Theorem, since by our assumption every consequence of
$\mathcal {N}'\models _{\mathrm {Sat}_{\mathcal {N}'}}\mathrm {REF}(\mathrm {Th}) + \{\phi \ \ | \ \ S(\phi ,\varepsilon ) \}$
. Such a model exists by the Arithmetized Completeness Theorem, since by our assumption every consequence of
![]() $\mathrm {REF}(\mathrm {Th})$
and the set of true sentences (in the sense of S) is true, in the sense of S (recall that
$\mathrm {REF}(\mathrm {Th})$
and the set of true sentences (in the sense of S) is true, in the sense of S (recall that
![]() $(\mathcal {M}, S)\models \mathrm {PA}^*$
). Let us observe that
$(\mathcal {M}, S)\models \mathrm {PA}^*$
). Let us observe that
![]() $\mathcal {N}'\models _{\mathrm {Sat}_{\mathcal {N}'}} \mathrm {PA}$
, since
$\mathcal {N}'\models _{\mathrm {Sat}_{\mathcal {N}'}} \mathrm {PA}$
, since
![]() $\mathrm {REF}(\mathrm {EA})\vdash \mathrm {PA}$
(and the proof formalizes in
$\mathrm {REF}(\mathrm {EA})\vdash \mathrm {PA}$
(and the proof formalizes in
![]() $\mathrm {EA}$
) and
$\mathrm {EA}$
) and
![]() $\mathrm {Th}\supseteq \mathrm {EA}$
. Now, using
$\mathrm {Th}\supseteq \mathrm {EA}$
. Now, using
![]() $\mathcal {N}'$
we formalize the standard argument that any model of
$\mathcal {N}'$
we formalize the standard argument that any model of
![]() $\mathrm {PA}$
admits an elementary extension to a model with a fully inductive, partial nonstandard satisfaction class. We reason in
$\mathrm {PA}$
admits an elementary extension to a model with a fully inductive, partial nonstandard satisfaction class. We reason in
![]() $(\mathcal {M},S,c)$
. We show that
$(\mathcal {M},S,c)$
. We show that
is consistent. Let A be a finite (in the sense of
![]() $\mathcal {M}$
) fragment of this theory and let
$\mathcal {M}$
) fragment of this theory and let
![]() $a-1$
be the greatest d such that
$a-1$
be the greatest d such that
![]() $\ulcorner c>\underline {d} \urcorner \in A$
. We shall find the interpretation for
$\ulcorner c>\underline {d} \urcorner \in A$
. We shall find the interpretation for
![]() $S'$
in
$S'$
in
![]() $\mathcal {N}'$
. Consider the arithmetical partial truth predicate
$\mathcal {N}'$
. Consider the arithmetical partial truth predicate
![]() $\mathrm {Sat}_{a}$
for formulae from
$\mathrm {Sat}_{a}$
for formulae from
![]() $\Sigma ^*_a$
and interpret
$\Sigma ^*_a$
and interpret
![]() $S'$
as
$S'$
as
![]() $\mathrm {Sat}_a$
. Then
$\mathrm {Sat}_a$
. Then
![]() $\mathcal {N}'\models \mathrm {CS}(\Sigma ^*_a, \mathrm {Sat}_a)$
. Moreover, as
$\mathcal {N}'\models \mathrm {CS}(\Sigma ^*_a, \mathrm {Sat}_a)$
. Moreover, as
![]() $\mathcal {N}'\models \mathrm {REF}(\mathrm {Th})$
,
$\mathcal {N}'\models \mathrm {REF}(\mathrm {Th})$
,
![]() $\mathcal {N}'\models \mathrm {GR}(\Sigma ^*_a, \mathrm {Sat}_a, \mathrm {Sat}_a+\mathrm {Th})$
(see, e.g., [Reference Beklemishev1]). So A is consistent and by the formalized compactness theorem, so is the entire theory. Let
$\mathcal {N}'\models \mathrm {GR}(\Sigma ^*_a, \mathrm {Sat}_a, \mathrm {Sat}_a+\mathrm {Th})$
(see, e.g., [Reference Beklemishev1]). So A is consistent and by the formalized compactness theorem, so is the entire theory. Let
![]() $(\mathcal {N}, S',c')$
be its full model. Then
$(\mathcal {N}, S',c')$
be its full model. Then
![]() $\mathcal {N}$
is clearly an end-extension of
$\mathcal {N}$
is clearly an end-extension of
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $c'\in N\setminus M$
. Moreover
$c'\in N\setminus M$
. Moreover
![]() $(\mathcal {N}, S', c')\models \mathrm {CS}(\Sigma ^*_{c'}, S')\wedge \mathrm {GR}(\Sigma ^*_{c'}, S', S' + \mathrm {Th})$
and
$(\mathcal {N}, S', c')\models \mathrm {CS}(\Sigma ^*_{c'}, S')\wedge \mathrm {GR}(\Sigma ^*_{c'}, S', S' + \mathrm {Th})$
and
![]() $S\subseteq S'$
, by construction.□
$S\subseteq S'$
, by construction.□
The following lemma isolates the relation between prolongability and global reflection.
Lemma 5.7. Suppose that
![]() $(\mathcal {M},S, c)\models \mathrm {CS}(\Sigma ^*_c)$
where c is nonstandard. Then the following conditions are equivalent:
$(\mathcal {M},S, c)\models \mathrm {CS}(\Sigma ^*_c)$
where c is nonstandard. Then the following conditions are equivalent:
-
1. S is n-prolongable.
-
2.
 $(\mathcal {M},S, c)\models \mathrm {GR}(\Sigma ^*_c,S,S+\mathrm {REF}^n(\mathrm {EA}))$
.
$(\mathcal {M},S, c)\models \mathrm {GR}(\Sigma ^*_c,S,S+\mathrm {REF}^n(\mathrm {EA}))$
.
Proof. We prove by induction on n that
 $$ \begin{align*} \forall \mathcal{M}\forall S \forall c\in M\setminus \omega &\bigg[(\mathcal{M},S, c)\models \mathrm{CS}(\Sigma^*_c) \Longrightarrow \big(S\ \mathrm{ is }\ n\mathrm{-prolongable}\\ & \quad \iff (\mathcal{M},S, c)\models\mathrm{GR}(\Sigma^*_c,S,S+\mathrm{REF}^n(\mathrm{EA}))\big)\bigg]. \end{align*} $$
$$ \begin{align*} \forall \mathcal{M}\forall S \forall c\in M\setminus \omega &\bigg[(\mathcal{M},S, c)\models \mathrm{CS}(\Sigma^*_c) \Longrightarrow \big(S\ \mathrm{ is }\ n\mathrm{-prolongable}\\ & \quad \iff (\mathcal{M},S, c)\models\mathrm{GR}(\Sigma^*_c,S,S+\mathrm{REF}^n(\mathrm{EA}))\big)\bigg]. \end{align*} $$
For the base step fix
![]() $\mathcal {M}$
, S, X as above and assume first that S is
$\mathcal {M}$
, S, X as above and assume first that S is
![]() $0$
-prolongable. Fix
$0$
-prolongable. Fix
![]() $\mathcal {N}$
as in the definition of
$\mathcal {N}$
as in the definition of
![]() $0$
-prolongability. Working in
$0$
-prolongability. Working in
![]() $(\mathcal {M},S)$
take any proof p of a sentence
$(\mathcal {M},S)$
take any proof p of a sentence
![]() $\phi \in s(\Sigma ^*_c)$
from
$\phi \in s(\Sigma ^*_c)$
from
![]() $\mathrm {EA}$
. Since
$\mathrm {EA}$
. Since
![]() $\mathrm {EA}$
is a finite theory
$\mathrm {EA}$
is a finite theory
![]() $\mathcal {N}\models _{\mathrm {Sat}_{\mathcal {N}}} \mathrm {EA}$
. Then, since p is a proof from true axioms in the sense of
$\mathcal {N}\models _{\mathrm {Sat}_{\mathcal {N}}} \mathrm {EA}$
. Then, since p is a proof from true axioms in the sense of
![]() $\mathrm {Sat}_{\mathcal {N}}$
, then
$\mathrm {Sat}_{\mathcal {N}}$
, then
![]() $\mathrm {Sat}_{\mathcal {N}}(\phi ,\varepsilon )$
. Hence, since
$\mathrm {Sat}_{\mathcal {N}}(\phi ,\varepsilon )$
. Hence, since
![]() $\phi $
is a formula from
$\phi $
is a formula from
![]() $s(\Sigma ^*_c)$
,
$s(\Sigma ^*_c)$
,
![]() $S(\phi ,\varepsilon )$
holds by the definition of
$S(\phi ,\varepsilon )$
holds by the definition of
![]() $0$
-prolongability.
$0$
-prolongability.
Suppose now that
![]() $(\mathcal {M},S, c)\models \forall \phi \in s(\Sigma ^*_c)\big ( \mathrm {Pr}^S_{\mathrm {EA}}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
. Consider the following
$(\mathcal {M},S, c)\models \forall \phi \in s(\Sigma ^*_c)\big ( \mathrm {Pr}^S_{\mathrm {EA}}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
. Consider the following
![]() $(\mathcal {M},S,c)$
-definable theory
$(\mathcal {M},S,c)$
-definable theory
![]() $\mathrm {Th}:= \{\phi \in \Sigma ^*_c \ \ | \ \ S(\phi ,\varepsilon ) \}$
. By our assumption,
$\mathrm {Th}:= \{\phi \in \Sigma ^*_c \ \ | \ \ S(\phi ,\varepsilon ) \}$
. By our assumption,
![]() $(\mathcal {M},S,c)\models \mathrm {Con}_{\mathrm {Th}}$
. Work in
$(\mathcal {M},S,c)\models \mathrm {Con}_{\mathrm {Th}}$
. Work in
![]() $(\mathcal {M},S,c)$
. By the Arithmetized Completeness Theorem (we use the assumption that
$(\mathcal {M},S,c)$
. By the Arithmetized Completeness Theorem (we use the assumption that
![]() $(\mathcal {M},S,c)\models \mathrm {PA}^*$
), we have a full model
$(\mathcal {M},S,c)\models \mathrm {PA}^*$
), we have a full model
![]() $\mathcal {N}\models _{\mathrm {Sat}_{\mathcal {N}}}\mathrm {Th}$
. Hence, obviously
$\mathcal {N}\models _{\mathrm {Sat}_{\mathcal {N}}}\mathrm {Th}$
. Hence, obviously
![]() $\mathrm {Sat}_{\mathcal {N}}$
and S coincide on
$\mathrm {Sat}_{\mathcal {N}}$
and S coincide on
![]() $s(\Sigma ^*_c)$
(observe that they need not coincide on
$s(\Sigma ^*_c)$
(observe that they need not coincide on
![]() $\Sigma ^*_c$
).
$\Sigma ^*_c$
).
Now assume that the equivalence holds for n. Fix
![]() $\mathcal {M}$
, S,
$\mathcal {M}$
, S,
![]() $\Sigma ^*_c$
as above and assume first that S is
$\Sigma ^*_c$
as above and assume first that S is
![]() $(n+1)$
-prolongable and pick
$(n+1)$
-prolongable and pick
![]() $(\mathcal {N}, S',c')\models \mathrm {CS}(\Sigma ^*_{c'})$
such that
$(\mathcal {N}, S',c')\models \mathrm {CS}(\Sigma ^*_{c'})$
such that
![]() $S\subseteq S'$
and
$S\subseteq S'$
and
![]() $S'$
is n-prolongable. By the induction assumption
$S'$
is n-prolongable. By the induction assumption
![]() $(\mathcal {N},S',c')\models \forall \phi \in s(\Sigma ^*_{c'})\big ( \mathrm {Pr}^S_{\mathrm {REF}^n(\mathrm {EA})}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
. By compositional clauses, it follows that for every
$(\mathcal {N},S',c')\models \forall \phi \in s(\Sigma ^*_{c'})\big ( \mathrm {Pr}^S_{\mathrm {REF}^n(\mathrm {EA})}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
. By compositional clauses, it follows that for every
![]() $\phi (v)\in M$
$\phi (v)\in M$
Hence in particular, if
![]() $\psi \in M$
is any axiom of
$\psi \in M$
is any axiom of
![]() $\mathrm {EA}+\mathrm {REF}^{n+1}(\mathrm {EA})$
, then
$\mathrm {EA}+\mathrm {REF}^{n+1}(\mathrm {EA})$
, then
![]() $(\mathcal {N},S')\models S(\psi , \varepsilon )$
. So suppose
$(\mathcal {N},S')\models S(\psi , \varepsilon )$
. So suppose
![]() $p\in M$
is a proof of a sentence
$p\in M$
is a proof of a sentence
![]() $\phi \in s(\Sigma ^*_c)$
from the axioms of
$\phi \in s(\Sigma ^*_c)$
from the axioms of
![]() $\mathrm {REF}^{n+1}(\mathrm {EA})$
. Work in
$\mathrm {REF}^{n+1}(\mathrm {EA})$
. Work in
![]() $(\mathcal {N}, S')$
. By the previous argument, if
$(\mathcal {N}, S')$
. By the previous argument, if
![]() $\theta $
is a premise of p, then
$\theta $
is a premise of p, then
![]() $S(\theta ,\varepsilon )$
holds. Since all the formulae occurring in p belong to
$S(\theta ,\varepsilon )$
holds. Since all the formulae occurring in p belong to
![]() $\Sigma _{c'}^*$
, then we have
$\Sigma _{c'}^*$
, then we have
![]() $(\mathcal {N},S')\models S(\phi ,\varepsilon )$
. However,
$(\mathcal {N},S')\models S(\phi ,\varepsilon )$
. However,
![]() $S'$
and S coincide on
$S'$
and S coincide on
![]() $s(\Sigma ^*_c)$
.
$s(\Sigma ^*_c)$
.
Now, working in
![]() $(\mathcal {M},S,c)$
, assume
$(\mathcal {M},S,c)$
, assume
![]() $\forall \phi \in s(\Sigma ^*_c)\big ( \mathrm {Pr}^S_{\mathrm {REF}^{n+1}(\mathrm {EA})}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
. We apply Lemma 5.6 to
$\forall \phi \in s(\Sigma ^*_c)\big ( \mathrm {Pr}^S_{\mathrm {REF}^{n+1}(\mathrm {EA})}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
. We apply Lemma 5.6 to
![]() $\mathrm {Th}:= \mathrm {REF}^n(\mathrm {EA})$
and conclude that there is
$\mathrm {Th}:= \mathrm {REF}^n(\mathrm {EA})$
and conclude that there is
![]() $(\mathcal {N},S',c')$
as in the thesis of the lemma. By our inductive assumption applied to
$(\mathcal {N},S',c')$
as in the thesis of the lemma. By our inductive assumption applied to
![]() $(\mathcal {N},S', c')$
, it follows that
$(\mathcal {N},S', c')$
, it follows that
![]() $S'$
is n-prolongable. Hence S is
$S'$
is n-prolongable. Hence S is
![]() $n+1$
-prolongable, which ends the proof.□
$n+1$
-prolongable, which ends the proof.□
Corollary 5.8. The following conditions are equivalent for a model
![]() $(\mathcal {M},S,c)\models \mathrm {CS}(\Sigma ^*_c, S)$
:
$(\mathcal {M},S,c)\models \mathrm {CS}(\Sigma ^*_c, S)$
:
-
1.
 $(\mathcal {M},S,c)$
is n-prolongable.
$(\mathcal {M},S,c)$
is n-prolongable. -
2. There exists an
 $(\mathcal {M},S,c)$
-definable sequence of models
$(\mathcal {M},S,c)$
-definable sequence of models
 $\{(\mathcal {M}_k, S_k,c_k)\}_{k\leq n\in \omega }$
such that
$\{(\mathcal {M}_k, S_k,c_k)\}_{k\leq n\in \omega }$
such that
 $(\mathcal {M}_0,S_0, c_0) = (\mathcal {M},S,c)$
and for each
$(\mathcal {M}_0,S_0, c_0) = (\mathcal {M},S,c)$
and for each
 $k<n$
:
$k<n$
:-
(a)
 $\mathcal {M}_k\precneqq _e \mathcal {M}_{k+1}$
and
$\mathcal {M}_k\precneqq _e \mathcal {M}_{k+1}$
and
 $S_k\subseteq S_{k+1}$
.
$S_k\subseteq S_{k+1}$
. -
(b)
 $(\mathcal {M}_k, S_k, c_k)\models \mathrm {CS}(\Sigma ^*_{c_k})$
.
$(\mathcal {M}_k, S_k, c_k)\models \mathrm {CS}(\Sigma ^*_{c_k})$
. -
(c)
 $c_{k+1}\in M_{k+1}\setminus M_{k}$
.
$c_{k+1}\in M_{k+1}\setminus M_{k}$
. -
(d)
 $(\mathcal {M}_{k+1}, S_{k+1}, c_{k+1})$
is strongly interpretable in
$(\mathcal {M}_{k+1}, S_{k+1}, c_{k+1})$
is strongly interpretable in
 $(\mathcal {M}_k, S_{k}, c_k)$
.
$(\mathcal {M}_k, S_{k}, c_k)$
.
-
Corollary 5.9. The following conditions are equivalent for a model
![]() $(\mathcal {M},S,c)\models \mathrm {CS}(\Sigma ^*_c, S)$
and for every
$(\mathcal {M},S,c)\models \mathrm {CS}(\Sigma ^*_c, S)$
and for every
![]() $n\in \omega $
:
$n\in \omega $
:
-
1.
 $\mathcal {M}\models \mathrm {REF}^{n+1}(\mathrm {EA})$
.
$\mathcal {M}\models \mathrm {REF}^{n+1}(\mathrm {EA})$
. -
2. There exists
 $b\in M\setminus \omega $
such that
$b\in M\setminus \omega $
such that
 $S_b$
is n-prolongable.
$S_b$
is n-prolongable.
Proof.
![]() $(2)\Rightarrow (1)$
follows immediately from Lemma 5.7. We prove
$(2)\Rightarrow (1)$
follows immediately from Lemma 5.7. We prove
![]() $(1)\Rightarrow (2)$
. Fix
$(1)\Rightarrow (2)$
. Fix
![]() $(\mathcal {M}, S, c)$
as in the assumptions. Let
$(\mathcal {M}, S, c)$
as in the assumptions. Let
![]() $\mathrm {Sat}_k$
be an arithmetically definable truth predicate for
$\mathrm {Sat}_k$
be an arithmetically definable truth predicate for
![]() $\Sigma ^*_k$
(as in the proof of Lemma 5.6). By induction in
$\Sigma ^*_k$
(as in the proof of Lemma 5.6). By induction in
![]() $(\mathcal {M},S,c)$
, we have
$(\mathcal {M},S,c)$
, we have
for every k. Since
![]() $\mathcal {M}\models \mathrm {REF}^{n+1}(\mathrm {EA})$
, then, for every k, we have
$\mathcal {M}\models \mathrm {REF}^{n+1}(\mathrm {EA})$
, then, for every k, we have
Hence for every
![]() $l\in \omega $
,
$l\in \omega $
,
![]() $(\mathcal {M},S,c)\models \forall x<l\forall \phi \in \Sigma ^*_x \big (\mathrm {Pr}^{S_x}_{\mathrm {REF}^n(\mathrm {EA})}(\phi )\rightarrow S_x(\phi ,\varepsilon )\big ).$
By the overspill principle we can find a
$(\mathcal {M},S,c)\models \forall x<l\forall \phi \in \Sigma ^*_x \big (\mathrm {Pr}^{S_x}_{\mathrm {REF}^n(\mathrm {EA})}(\phi )\rightarrow S_x(\phi ,\varepsilon )\big ).$
By the overspill principle we can find a
![]() $b>\omega $
,
$b>\omega $
,
![]() $b\leq c$
, such that
$b\leq c$
, such that
Hence
![]() $S_{b-1}$
is n-prolongable.□
$S_{b-1}$
is n-prolongable.□
Since
![]() $\mathrm {REF}(\mathrm {EA})=\mathrm {PA}$
, the following is the most memorizable version of our main lemma:
$\mathrm {REF}(\mathrm {EA})=\mathrm {PA}$
, the following is the most memorizable version of our main lemma:
Theorem 5.10. The following conditions are equivalent for a model
![]() $(\mathcal {M},S,c)\models \mathrm {CS}(\Sigma ^*_c)$
and for every
$(\mathcal {M},S,c)\models \mathrm {CS}(\Sigma ^*_c)$
and for every
![]() $n\in \omega $
:
$n\in \omega $
:
-
1.
 $\mathcal {M}\models \mathrm {REF}^{n}(\mathrm {PA})$
.
$\mathcal {M}\models \mathrm {REF}^{n}(\mathrm {PA})$
. -
2. There exists
 $b\in M\setminus \omega $
such that
$b\in M\setminus \omega $
such that
 $S_b$
is n-prolongable.
$S_b$
is n-prolongable.
Now, we have all that is needed to finish our conservativity proof for
![]() $\mathrm {CT}_0$
:
$\mathrm {CT}_0$
:
Proof of Lemma 5.3. Suppose
![]() $(\mathcal {M},S, c)\models \mathrm {CS}(\Sigma ^*_c)$
and
$(\mathcal {M},S, c)\models \mathrm {CS}(\Sigma ^*_c)$
and
![]() $\mathcal {M}\models \mathrm {REF}^{\omega }(\mathrm {Th})$
. Let
$\mathcal {M}\models \mathrm {REF}^{\omega }(\mathrm {Th})$
. Let
![]() $\mathrm {Sat}_n$
be the arithmetical partial truth predicate for formulae in
$\mathrm {Sat}_n$
be the arithmetical partial truth predicate for formulae in
![]() $\Sigma ^*_{n}$
. By assumption on
$\Sigma ^*_{n}$
. By assumption on
![]() $\mathcal {M}$
it follows that for every n
$\mathcal {M}$
it follows that for every n
By induction, for every
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $\mathrm {Sat}_n$
and
$\mathrm {Sat}_n$
and
![]() $S_n$
coincide. Hence for every
$S_n$
coincide. Hence for every
![]() $n\in \omega $
we have
$n\in \omega $
we have
By overspill it follows that for some
![]() $d>\omega $
$d>\omega $
We define the chain
![]() $(\mathcal {M}_n, S_n, c_n)$
by induction. Assume that
$(\mathcal {M}_n, S_n, c_n)$
by induction. Assume that
![]() $(\mathcal {M}_k, S_k, c_k)$
has been defined and it satisfies
$(\mathcal {M}_k, S_k, c_k)$
has been defined and it satisfies
![]() $\mathrm {GR}(\Sigma ^*_{c_k}, S_{c_k}, S_{c_k} + \mathrm {REF}^{d-k}(\mathrm {Th}))$
. To get
$\mathrm {GR}(\Sigma ^*_{c_k}, S_{c_k}, S_{c_k} + \mathrm {REF}^{d-k}(\mathrm {Th}))$
. To get
![]() $(\mathcal {M}_{k+1}, S_{k+1}, c_{k+1})$
we apply Lemma 5.6 to
$(\mathcal {M}_{k+1}, S_{k+1}, c_{k+1})$
we apply Lemma 5.6 to
![]() $\mathrm {Th}' = \mathrm {REF}^{d-(k+1)}(\mathrm {Th})$
.□
$\mathrm {Th}' = \mathrm {REF}^{d-(k+1)}(\mathrm {Th})$
.□
Corollary 5.11. The arithmetical consequences of
![]() $\mathrm {CT}_0+\forall \phi \big (\mathrm {Th}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
and
$\mathrm {CT}_0+\forall \phi \big (\mathrm {Th}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
and
![]() $\mathrm {REF}^{\omega }(\mathrm {Th})$
coincide.
$\mathrm {REF}^{\omega }(\mathrm {Th})$
coincide.
Proof. Conservativity part follows from Theorem 5.2. That
![]() $\mathrm {CT}_0+\forall \phi \big (\mathrm {Th}(\phi )\rightarrow S(\phi ,\varepsilon )\big )\vdash \mathrm {REF}^{\omega }(\mathrm {Th})$
was established in Corollary 3.11.□
$\mathrm {CT}_0+\forall \phi \big (\mathrm {Th}(\phi )\rightarrow S(\phi ,\varepsilon )\big )\vdash \mathrm {REF}^{\omega }(\mathrm {Th})$
was established in Corollary 3.11.□
It might seem that in the above proof the limit model is a very specific model of
![]() $\mathrm {CS}_0$
. Quite surprisingly every model of
$\mathrm {CS}_0$
. Quite surprisingly every model of
![]() $\mathrm {CS}_0$
is of this form. One of the crucial steps in the proof is worth isolating as a lemma.
$\mathrm {CS}_0$
is of this form. One of the crucial steps in the proof is worth isolating as a lemma.
Lemma 5.12. Suppose that
![]() $(\mathcal {M}, S)\models \mathrm {CS}_0$
,
$(\mathcal {M}, S)\models \mathrm {CS}_0$
,
![]() $(\mathcal {M}_0, S{\upharpoonright _{M_0}})\subseteq (\mathcal {M},S)$
,
$(\mathcal {M}_0, S{\upharpoonright _{M_0}})\subseteq (\mathcal {M},S)$
,
![]() $d_1\in M_0$
, and
$d_1\in M_0$
, and
![]() $(\mathcal {M}_0,S_{d_1}{\upharpoonright _{M_0}})\models \mathrm {CS}^-(\Sigma _{d_1}^*)$
. Then for every
$(\mathcal {M}_0,S_{d_1}{\upharpoonright _{M_0}})\models \mathrm {CS}^-(\Sigma _{d_1}^*)$
. Then for every
![]() $d_0\in M_0$
such that
$d_0\in M_0$
such that
![]() $d_1-d_0$
is nonstandard,
$d_1-d_0$
is nonstandard,
![]() $(\mathcal {M}_0, S_{d_0}{\upharpoonright _{M_0}})\models \mathrm {CS}(\Sigma ^*_{d_0})$
.
$(\mathcal {M}_0, S_{d_0}{\upharpoonright _{M_0}})\models \mathrm {CS}(\Sigma ^*_{d_0})$
.
Proof. Let us fix
![]() $\mathcal {M},S,\mathcal {M}_0, d_1, d_1$
as above. Since
$\mathcal {M},S,\mathcal {M}_0, d_1, d_1$
as above. Since
![]() $(\mathcal {M}_0, S_{d_1}{\upharpoonright _{M_0}})\models \mathrm {CS}^-(\Sigma ^*_{d_1})$
, it follows that
$(\mathcal {M}_0, S_{d_1}{\upharpoonright _{M_0}})\models \mathrm {CS}^-(\Sigma ^*_{d_1})$
, it follows that
We prove that induction axioms hold in
![]() $(\mathcal {M}_0,S_{d_0}{\upharpoonright _{M_0}})$
as well. By the assumptions, it follows that
$(\mathcal {M}_0,S_{d_0}{\upharpoonright _{M_0}})$
as well. By the assumptions, it follows that
![]() $(\mathcal {M}, S_{d_1})\models \forall \phi \in \Sigma ^*_{d_1}\big (\mathrm {Pr}_{\mathrm {PA}}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
, hence also
$(\mathcal {M}, S_{d_1})\models \forall \phi \in \Sigma ^*_{d_1}\big (\mathrm {Pr}_{\mathrm {PA}}(\phi )\rightarrow S(\phi ,\varepsilon )\big )$
, hence also
Let
![]() $\mathrm {Sat}_{\Sigma _{d_0}}$
be as in the proof of Theorem 3.19 and let us abbreviate
$\mathrm {Sat}_{\Sigma _{d_0}}$
be as in the proof of Theorem 3.19 and let us abbreviate
![]() $S(\phi ,\varepsilon )$
with
$S(\phi ,\varepsilon )$
with
![]() $T(\phi )$
and
$T(\phi )$
and
![]() $\mathrm {Sat}_{\Sigma _{d_0}}(x,\varepsilon )$
with
$\mathrm {Sat}_{\Sigma _{d_0}}(x,\varepsilon )$
with
![]() $Tr_{d_0}(x)$
. Observe that
$Tr_{d_0}(x)$
. Observe that
![]() $Tr_{d_0}\in \Sigma _{d_0}^*$
. It follows that
$Tr_{d_0}\in \Sigma _{d_0}^*$
. It follows that
Since
![]() $S_{d_0}$
coincides with
$S_{d_0}$
coincides with
![]() $S_{d_1}$
on
$S_{d_1}$
on
![]() $(\Sigma ^*_{d_0})^{\mathcal {M}_0}$
, then
$(\Sigma ^*_{d_0})^{\mathcal {M}_0}$
, then
Since
![]() $T(Tr_{{d_0}}(\underline {x^{\Sigma }}))$
defines and
$T(Tr_{{d_0}}(\underline {x^{\Sigma }}))$
defines and
![]() $S_{d_0}{\upharpoonright _{M_0}}$
in
$S_{d_0}{\upharpoonright _{M_0}}$
in
![]() $(\mathcal {M}_0, S_{d_1}{\upharpoonright _{M_0}})$
it is sufficient to show that
$(\mathcal {M}_0, S_{d_1}{\upharpoonright _{M_0}})$
it is sufficient to show that
where
![]() $\eta $
is an arbitrary instance of an induction axiom for a fresh predicate letter P, in a semi-relational form. Fix
$\eta $
is an arbitrary instance of an induction axiom for a fresh predicate letter P, in a semi-relational form. Fix
![]() $\eta $
. Since
$\eta $
. Since
![]() $\mathcal {M}_0\models \mathrm {Pr}_{\mathrm {PA}}(\eta [Tr_{{d_0}}(\underline {x^{\Sigma }})/P])$
and
$\mathcal {M}_0\models \mathrm {Pr}_{\mathrm {PA}}(\eta [Tr_{{d_0}}(\underline {x^{\Sigma }})/P])$
and
![]() $\eta [Tr_{{d_0}}(\underline {x^{\Sigma }})/P]\in \Sigma ^*_{d_1}$
, we have
$\eta [Tr_{{d_0}}(\underline {x^{\Sigma }})/P]\in \Sigma ^*_{d_1}$
, we have
(*) follows as in [Reference Łełyk and Wcisło19] and Theorem 3.19.□
Theorem 5.13. Suppose
![]() $(\mathcal {M},S)\models \mathrm {CS}_0$
has cofinality
$(\mathcal {M},S)\models \mathrm {CS}_0$
has cofinality
![]() $\kappa $
. Then there is a chain
$\kappa $
. Then there is a chain
![]() $\{(\mathcal {M}_{\alpha }, S_{\alpha }, c_{\alpha })\}_{\alpha \in \kappa }$
such that
$\{(\mathcal {M}_{\alpha }, S_{\alpha }, c_{\alpha })\}_{\alpha \in \kappa }$
such that
![]() $\bigcup _{\alpha \in \kappa }\mathcal {M}_{\alpha } = \mathcal {M}$
,
$\bigcup _{\alpha \in \kappa }\mathcal {M}_{\alpha } = \mathcal {M}$
,
![]() $\bigcup _{\alpha \in \kappa }S_{\alpha }$
and for every
$\bigcup _{\alpha \in \kappa }S_{\alpha }$
and for every
![]() $\alpha <\beta <\kappa $
:
$\alpha <\beta <\kappa $
:
-
1.
 $\mathcal {M}_{\alpha }\preceq _e \mathcal {M}_{\beta }$
and
$\mathcal {M}_{\alpha }\preceq _e \mathcal {M}_{\beta }$
and
 $S_{\alpha }\subseteq S_{\beta }$
.
$S_{\alpha }\subseteq S_{\beta }$
. -
2.
 $(\mathcal {M}_{\beta }, S_{\beta })\models \mathrm {CS}(\Sigma ^*_{c_{\beta }})$
.
$(\mathcal {M}_{\beta }, S_{\beta })\models \mathrm {CS}(\Sigma ^*_{c_{\beta }})$
. -
3.
 $c_{\beta }\in M_{\beta }\setminus M_{\alpha }$
.
$c_{\beta }\in M_{\beta }\setminus M_{\alpha }$
.
We note that the above chain need not be continuous.
Proof. Fix
![]() $(\mathcal {M},S)\models \mathrm {CS}_0$
and a cofinal sequence
$(\mathcal {M},S)\models \mathrm {CS}_0$
and a cofinal sequence
![]() $\{d_{\alpha }\}_{\alpha \in \kappa }$
. In the base step we build
$\{d_{\alpha }\}_{\alpha \in \kappa }$
. In the base step we build
![]() $(\mathcal {M}_0,S_0,d_0)\models \mathrm {CS}(\Sigma ^*_{d_0})$
. Consider the formula
$(\mathcal {M}_0,S_0,d_0)\models \mathrm {CS}(\Sigma ^*_{d_0})$
. Consider the formula
![]() $\theta '(x,y,z)$
$\theta '(x,y,z)$
where
![]() $\theta (x,y,c)$
is
$\theta (x,y,c)$
is
 $$ \begin{align*} \forall \phi\in\Sigma^*_y \forall i<x\forall \alpha<c_i &\bigg(\phi<c_i \wedge\alpha\in\mathrm{Asn}(\exists v\phi) \wedge S(\exists v \phi,\alpha) \\ & \quad\rightarrow \exists \beta<c_{i+1}\big(\beta\sim_v \alpha \wedge S(\phi,\beta{\upharpoonright_{\phi}})\big)\bigg). \end{align*} $$
$$ \begin{align*} \forall \phi\in\Sigma^*_y \forall i<x\forall \alpha<c_i &\bigg(\phi<c_i \wedge\alpha\in\mathrm{Asn}(\exists v\phi) \wedge S(\exists v \phi,\alpha) \\ & \quad\rightarrow \exists \beta<c_{i+1}\big(\beta\sim_v \alpha \wedge S(\phi,\beta{\upharpoonright_{\phi}})\big)\bigg). \end{align*} $$
Thus
![]() $\theta '(x,y,z)$
expresses that there is a witness-bounding sequence c of length x and starting from z, which works for those formulae of
$\theta '(x,y,z)$
expresses that there is a witness-bounding sequence c of length x and starting from z, which works for those formulae of
![]() $\Sigma _y^*$
complexity which are below some of the elements of the sequence. Let e be such that
$\Sigma _y^*$
complexity which are below some of the elements of the sequence. Let e be such that
![]() $e-d_0$
is nonstandard. We reason in
$e-d_0$
is nonstandard. We reason in
![]() $(\mathcal {M},S_{e})\models \mathrm {CS}(\Sigma ^*_{e})$
and by a straightforward induction conclude that
$(\mathcal {M},S_{e})\models \mathrm {CS}(\Sigma ^*_{e})$
and by a straightforward induction conclude that
We let a be an arbitrary nonstandard number and we fix c witnessing
![]() $\theta '(a,e,e)$
. We define
$\theta '(a,e,e)$
. We define
Clearly if
![]() $b_1,b_2<c_i$
, for some i, then
$b_1,b_2<c_i$
, for some i, then
![]() $b_1+b_2, b_1\cdot b_2<c_{i+1}$
by the assumption on c. Hence
$b_1+b_2, b_1\cdot b_2<c_{i+1}$
by the assumption on c. Hence
![]() $\mathcal {M}_0\subseteq \mathcal {M}$
. We check that
$\mathcal {M}_0\subseteq \mathcal {M}$
. We check that
![]() $(\mathcal {M}_0, S_{e}{\upharpoonright _{M_0}})\models \mathrm {CS}^-(\Sigma ^*_{e})$
. The unique non-trivial step is the one for quantifiers: fix any formula
$(\mathcal {M}_0, S_{e}{\upharpoonright _{M_0}})\models \mathrm {CS}^-(\Sigma ^*_{e})$
. The unique non-trivial step is the one for quantifiers: fix any formula
![]() $\phi (v,\bar {w})\in \Sigma ^*_{e}\cap M_0$
,
$\phi (v,\bar {w})\in \Sigma ^*_{e}\cap M_0$
,
![]() $\alpha \in M_0$
and assume that
$\alpha \in M_0$
and assume that
![]() $(\mathcal {M}_0,S_{e}{\upharpoonright _{M_0}})\models S(\exists v \phi (v,\bar {w}),\alpha )$
and
$(\mathcal {M}_0,S_{e}{\upharpoonright _{M_0}})\models S(\exists v \phi (v,\bar {w}),\alpha )$
and
![]() $\alpha ,\phi <c_i$
. Then
$\alpha ,\phi <c_i$
. Then
Hence by the properties of c there is
![]() $\beta <c_{i+1}$
,
$\beta <c_{i+1}$
,
![]() $\beta \sim _v \alpha $
such that
$\beta \sim _v \alpha $
such that
To conclude that
![]() $S_0:=S_{d_0}$
is fully inductive, we apply Corollary 5.12 for
$S_0:=S_{d_0}$
is fully inductive, we apply Corollary 5.12 for
![]() $\mathcal {M}' = \mathcal {M}_0$
,
$\mathcal {M}' = \mathcal {M}_0$
,
![]() $d_0=d_0$
, and
$d_0=d_0$
, and
![]() $d_1 = e$
.
$d_1 = e$
.
In the successor step assume that
![]() $(\mathcal {M}_{\alpha }, S_{\alpha }, c_{\alpha })$
has been constructed and w.l.o.g. assume that
$(\mathcal {M}_{\alpha }, S_{\alpha }, c_{\alpha })$
has been constructed and w.l.o.g. assume that
![]() $d_{\alpha +1}\notin M_{\alpha }$
. We pick
$d_{\alpha +1}\notin M_{\alpha }$
. We pick
![]() $e\in M$
such that
$e\in M$
such that
![]() $e-d_{\alpha +1}$
is nonstandard and repeat the reasoning from the base step with
$e-d_{\alpha +1}$
is nonstandard and repeat the reasoning from the base step with
![]() $d_{\alpha +1}$
replacing
$d_{\alpha +1}$
replacing
![]() $d_0$
. In the limit step, we assume that for every
$d_0$
. In the limit step, we assume that for every
![]() $\alpha <\beta $
,
$\alpha <\beta $
,
![]() $(\mathcal {M}_{\alpha }, S_{\alpha }, c_{\alpha })$
has been constructed. We take
$(\mathcal {M}_{\alpha }, S_{\alpha }, c_{\alpha })$
has been constructed. We take
![]() $(\mathcal {M}^{\prime }_{\beta }, S^{\prime }_{\beta }) = \bigcup _{\alpha <\beta } (\mathcal {M}_{\alpha }, S_{\alpha })$
and assume (by the regularity of
$(\mathcal {M}^{\prime }_{\beta }, S^{\prime }_{\beta }) = \bigcup _{\alpha <\beta } (\mathcal {M}_{\alpha }, S_{\alpha })$
and assume (by the regularity of
![]() $\kappa $
) that
$\kappa $
) that
![]() $\gamma $
is the least such that
$\gamma $
is the least such that
![]() $d_{\gamma }\notin M^{\prime }_{\beta }$
. We put
$d_{\gamma }\notin M^{\prime }_{\beta }$
. We put
![]() $c_{\beta } = d_{\gamma }$
and repeat the reasoning from the base step with
$c_{\beta } = d_{\gamma }$
and repeat the reasoning from the base step with
![]() $c_{\beta }$
replacing
$c_{\beta }$
replacing
![]() $d_0$
.□
$d_0$
.□
The construction from Lemma 5.3 enables us to extend the result from Section 4.
Theorem 5.14.
![]() is
is
![]() $\Pi _1(\mathcal {L}_T)$
conservative over
$\Pi _1(\mathcal {L}_T)$
conservative over
![]() $\mathrm {CT}_0$
.
$\mathrm {CT}_0$
.
Proof. Fix
![]() $(\mathcal {M},T)\models \mathrm {CT}_0$
. We shall find
$(\mathcal {M},T)\models \mathrm {CT}_0$
. We shall find
, which suffices to end the proof. Firstly, turn
![]() $(\mathcal {M},T)$
into a model
$(\mathcal {M},T)$
into a model
![]() $(\mathcal {M},S)\models \mathrm {CS}_0$
in the canonical way. Secondly, assume that there exists
$(\mathcal {M},S)\models \mathrm {CS}_0$
in the canonical way. Secondly, assume that there exists
![]() $\{(\mathcal {M}_i, S_i, c_i)\}_{i\in \omega }$
such that
$\{(\mathcal {M}_i, S_i, c_i)\}_{i\in \omega }$
such that
![]() $(\mathcal {M}_0, S_0) = (\mathcal {M},S)$
, the rest of the chain is as in the thesis of Lemma 5.3 and for each
$(\mathcal {M}_0, S_0) = (\mathcal {M},S)$
, the rest of the chain is as in the thesis of Lemma 5.3 and for each
![]() $i>0$
,
$i>0$
,
![]() $(\mathcal {M}_{i+1}, S_{i+1}, c_{i+1})$
is strongly interpreted in its predecessor
$(\mathcal {M}_{i+1}, S_{i+1}, c_{i+1})$
is strongly interpreted in its predecessor
![]() $(\mathcal {M}_{i}, S_{i}, c_{i})$
. Let
$(\mathcal {M}_{i}, S_{i}, c_{i})$
. Let
![]() $\mathrm {Sat}_{i+1}$
denote the satisfaction relation witnessing the interpretability of
$\mathrm {Sat}_{i+1}$
denote the satisfaction relation witnessing the interpretability of
![]() $(\mathcal {M}_{i+1}, S_{i+1}, c_{i+1})$
in
$(\mathcal {M}_{i+1}, S_{i+1}, c_{i+1})$
in
![]() $(\mathcal {M}_{i}, S_{i}, c_{i})$
. Put
$(\mathcal {M}_{i}, S_{i}, c_{i})$
. Put
![]() $(\mathcal {M}_{\infty }, S_{\infty }) = \bigcup _{i\in \omega } (\mathcal {M}_i, S_i)$
and define
$(\mathcal {M}_{\infty }, S_{\infty }) = \bigcup _{i\in \omega } (\mathcal {M}_i, S_i)$
and define
![]() $T_{\infty }:= \{\phi \in M_{\infty } \ \ | \ \ S(\phi ,\varepsilon ) \}$
. By the proof of Theorem 5.2,
$T_{\infty }:= \{\phi \in M_{\infty } \ \ | \ \ S(\phi ,\varepsilon ) \}$
. By the proof of Theorem 5.2,
![]() $(\mathcal {M}_{\infty }, S_{\infty })\models \mathrm {CS}_0$
, and hence
$(\mathcal {M}_{\infty }, S_{\infty })\models \mathrm {CS}_0$
, and hence
![]() $(\mathcal {M}_{\infty }, T_{\infty })\models \mathrm {CT}_0$
, so it is sufficient to show that
$(\mathcal {M}_{\infty }, T_{\infty })\models \mathrm {CT}_0$
, so it is sufficient to show that
Suppose that for some
![]() $\phi (x)\in \Sigma _1(\mathcal {L}_T)$
and
$\phi (x)\in \Sigma _1(\mathcal {L}_T)$
and
![]() $c\in M$
,
$c\in M$
,
![]() $(\mathcal {M}_{\infty },T_{\infty })\models \mathrm {Pr}_{\mathrm {UTB}}^T(\phi (\underline {c}))$
. Let p be the witnessing proof and fix any
$(\mathcal {M}_{\infty },T_{\infty })\models \mathrm {Pr}_{\mathrm {UTB}}^T(\phi (\underline {c}))$
. Let p be the witnessing proof and fix any
![]() $i\in \omega $
such that
$i\in \omega $
such that
![]() $p<c_i$
. Hence
$p<c_i$
. Hence
![]() $(\mathcal {M}_{i}, S_{i})\models \mathrm {Pr}_{\mathrm {UTB}}^S(\phi (\underline {c}))$
. We reason in
$(\mathcal {M}_{i}, S_{i})\models \mathrm {Pr}_{\mathrm {UTB}}^S(\phi (\underline {c}))$
. We reason in
![]() $(\mathcal {M}_{i}, S_{i})$
. Since every next model in the chain is strongly interpretable in the previous one, we have (in
$(\mathcal {M}_{i}, S_{i})$
. Since every next model in the chain is strongly interpretable in the previous one, we have (in
![]() $(\mathcal {M}_{i}, S_{i})$
)
$(\mathcal {M}_{i}, S_{i})$
)
Consider (in
![]() $(\mathcal {M}_i, S_i)$
) the model
$(\mathcal {M}_i, S_i)$
) the model
![]() $(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})$
. This model is interpretable in
$(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})$
. This model is interpretable in
![]() $(\mathcal {M}_{i+1}, S_{i+1})$
; hence by Proposition 2.20 it is a full model (in the sense of
$(\mathcal {M}_{i+1}, S_{i+1})$
; hence by Proposition 2.20 it is a full model (in the sense of
![]() $(\mathcal {M}_{i}, S_{i})$
; i.e., it is strongly interpretable in
$(\mathcal {M}_{i}, S_{i})$
; i.e., it is strongly interpretable in
![]() $(\mathcal {M}_{i}, S_{i})$
). Let
$(\mathcal {M}_{i}, S_{i})$
). Let
![]() $\mathrm {Sat}_{i+1}'$
denote the respective satisfaction class. We shall show that
$\mathrm {Sat}_{i+1}'$
denote the respective satisfaction class. We shall show that
This suffices to end the proof, since
![]() $\phi (c)$
is a
$\phi (c)$
is a
![]() $\Sigma _1(\mathcal {L}_T)$
formula and
$\Sigma _1(\mathcal {L}_T)$
formula and
![]() $(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}}) \subseteq _e (\mathcal {M}_{\infty },T_{\infty })$
. Reasoning in
$(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}}) \subseteq _e (\mathcal {M}_{\infty },T_{\infty })$
. Reasoning in
![]() $(\mathcal {M}_{i}, S_{i})$
we see that since
$(\mathcal {M}_{i}, S_{i})$
we see that since
![]() $S_{i+2}{\upharpoonright _{M_{i+1}}}$
is definable in
$S_{i+2}{\upharpoonright _{M_{i+1}}}$
is definable in
![]() $(M_{i+1}, S_{i+1})$
, which satisfies full induction, also
$(M_{i+1}, S_{i+1})$
, which satisfies full induction, also
![]() $(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})$
satisfies full induction. Moreover, since
$(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})$
satisfies full induction. Moreover, since
![]() $S_{i+1}\subseteq S_{i+2}{\upharpoonright _{M_{i+1}}}$
we know that for every e (
$S_{i+1}\subseteq S_{i+2}{\upharpoonright _{M_{i+1}}}$
we know that for every e (
![]() $\in M_{i}$
)
$\in M_{i}$
)
![]() $(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})\models _{\mathrm {Sat}_{i+1}'} \mathrm {CS}(\Sigma ^*_e)$
. Hence,
$(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})\models _{\mathrm {Sat}_{i+1}'} \mathrm {CS}(\Sigma ^*_e)$
. Hence,
Moreover, if
![]() $\psi $
is an assumption of proof p and an arithmetical sentence, then
$\psi $
is an assumption of proof p and an arithmetical sentence, then
![]() $\psi \in T_{\omega }$
; hence, by the choice of i,
$\psi \in T_{\omega }$
; hence, by the choice of i,
![]() $\psi \in S_i$
. It follows that
$\psi \in S_i$
. It follows that
![]() $(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})\models _{\mathrm {Sat}_{i+1}'}\psi ,$
since
$(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})\models _{\mathrm {Sat}_{i+1}'}\psi ,$
since
![]() $\mathrm {Sat}_{i+1}'$
coincides with
$\mathrm {Sat}_{i+1}'$
coincides with
![]() $\mathrm {Sat}_{i+1}$
on sentences from
$\mathrm {Sat}_{i+1}$
on sentences from
![]() $M_i$
. We conclude, still working in
$M_i$
. We conclude, still working in
![]() $(\mathcal {M}_i, S_i)$
, that
$(\mathcal {M}_i, S_i)$
, that
![]() $\mathrm {Sat}_{i+1}'$
makes every premise of p true in
$\mathrm {Sat}_{i+1}'$
makes every premise of p true in
![]() $(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})$
. So p’s conclusion,
$(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})$
. So p’s conclusion,
![]() $\phi (c)$
, must be deemed true in
$\phi (c)$
, must be deemed true in
![]() $(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})$
by
$(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})$
by
![]() $\mathrm {Sat}_{i+1}'$
. Since
$\mathrm {Sat}_{i+1}'$
. Since
![]() $\phi (c)$
is a standard formula with a parameter, we can conclude that
$\phi (c)$
is a standard formula with a parameter, we can conclude that
![]() $(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})\models \phi (\underline {c})$
.
$(\mathcal {M}_{i+1}, S_{i+2}{\upharpoonright _{M_{i+1}}})\models \phi (\underline {c})$
.
Now, we show how to justify the existence of the chain
![]() $\{(\mathcal {M}_i, S_i, c_i)\}_{i\in \omega }$
. Let B
$\{(\mathcal {M}_i, S_i, c_i)\}_{i\in \omega }$
. Let B
![]() $\Sigma _1(\mathcal {L}_T)$
denote the extension of
$\Sigma _1(\mathcal {L}_T)$
denote the extension of
![]() $\mathrm {CT}_0$
with
$\mathrm {CT}_0$
with
![]() $\Sigma _1$
collection scheme for the language with the truth predicate. As shown in [Reference Łełyk and Wcisło20], B
$\Sigma _1$
collection scheme for the language with the truth predicate. As shown in [Reference Łełyk and Wcisło20], B
![]() $\Sigma _1(\mathcal {L}_T)$
is
$\Sigma _1(\mathcal {L}_T)$
is
![]() $\Pi _2$
conservative over
$\Pi _2$
conservative over
![]() $\mathrm {CT}_0$
. So we can assume that the above model
$\mathrm {CT}_0$
. So we can assume that the above model
![]() $(\mathcal {M},T)$
is a countable recursively saturated (in the extended language) model of
$(\mathcal {M},T)$
is a countable recursively saturated (in the extended language) model of
![]() $\mathrm {CT}^- + \text {B}\Sigma _1(\mathcal {L}_T)$
. By the classical result of Wilkie–Paris [Reference Wilkie, Paris, Fenstad, Frolov and Hilpinen26] there exists a proper end-extension
$\mathrm {CT}^- + \text {B}\Sigma _1(\mathcal {L}_T)$
. By the classical result of Wilkie–Paris [Reference Wilkie, Paris, Fenstad, Frolov and Hilpinen26] there exists a proper end-extension
![]() $(\mathcal {M}', T')\models \mathrm {CT}_0$
of
$(\mathcal {M}', T')\models \mathrm {CT}_0$
of
![]() $(\mathcal {M},T)$
.Footnote
15
Hence it is sufficient to start the construction of the chain from
$(\mathcal {M},T)$
.Footnote
15
Hence it is sufficient to start the construction of the chain from
![]() $(\mathcal {M}', T^{\prime }_a)$
, where
$(\mathcal {M}', T^{\prime }_a)$
, where
![]() $a\in M'\setminus M$
and then proceed as in the proof of Lemma 5.3.□
$a\in M'\setminus M$
and then proceed as in the proof of Lemma 5.3.□
6 Two open problems
We conclude our paper with two open problems:
Question 1. Does the statement of Theorem 5.13 remain true if we require for every
![]() $\alpha <\beta $
,
$\alpha <\beta $
,
![]() $\mathcal {M}_{\beta }$
is strongly interpretable in
$\mathcal {M}_{\beta }$
is strongly interpretable in
![]() $\mathcal {M}_{\alpha }$
?
$\mathcal {M}_{\alpha }$
?
Acknowledgements
The paper summarizes the developments obtained during the years 2015–2019, some of them being included in the author’s Ph.D. thesis [Reference Łełyk18]. Special thanks go to thesis’ supervisor Cezary Cieśliński, who also brought our attention to the problem of the scope of arithmetical consequences of
![]() $\mathrm {CT}_0$
. We thank Ali Enayat and Albert Visser for many important insights which turned out to be crucial in solving problems presented in this paper. Last but not least, we are extremely grateful to Bartosz Wcisło whose constant encouragement and support during all these years were essential for bringing this work to the daylight.
$\mathrm {CT}_0$
. We thank Ali Enayat and Albert Visser for many important insights which turned out to be crucial in solving problems presented in this paper. Last but not least, we are extremely grateful to Bartosz Wcisło whose constant encouragement and support during all these years were essential for bringing this work to the daylight.
The current version of the paper benefited a lot from remarks and suggestions by Ali Enayat.
We are grateful to Lev Beklemishev and Fedor Pakhomov for bringing our attention to the open problem on the status of
![]() $\Sigma _1$
-uniform reflection over
$\Sigma _1$
-uniform reflection over
![]() $\mathrm {UTB}^-+\mathrm {EA}$
.
$\mathrm {UTB}^-+\mathrm {EA}$
.
This research was supported by an NCN Maestro grant 2019/34/A/HS1/00399, “Epistemic and semantic commitments of foundational theories.”