Introduction

Cosmogenic nuclide techniques are revolutionizing the study of geomorphic processes and landscape history. The ability to date rock surfaces and sediments, over a wide range of time-scales, allows us to address many problems that were previously unsolvable (reviewed in Reference NishiizumiNishiizumi and others, 1993; Reference Cerling and CraigCerling and Craig, 1994). For example, in reconstructing past glacial events, attempts to establish chronologies have often been frustrated by the lack of suitable organic material for radiocarbon dating. All too frequently, only undatable rocks and sediments were available for analysis. Now, with cosmogenic nuclide techniques, the rocks and sediments can be dated. Determination of exposure histories of features such as moraine boulders, glacial pavements and trimlines, lava flows, shore platforms, alluvial fans, landslides, cliff surfaces, and meteorite impact deposits has been the major application (e.g. Reference Craig and PoredaCraig and Poreda, 1986; Reference KurzKurz, 1986; Reference Phillips, Leavy, Jannik, Elmore and KubikPhillips and others, 1986, Reference Phillips, Zreda, Smith, Elmore, Kubik and Sharma1990, Reference Phillips1991, Reference Phillips, Zreda, Benson, Plummer, Elmore and Sharma1996a, Reference Phillips, Zreda, Flinsch, Elmore and Sharmab, Reference Phillips1997; Reference Klein, Middleton, Giegengack and SharmaKlein and others, 1988; Reference CerlingCerling, 1990; Reference Nishiizumi, Kohl, Arnold, Klein, Fink and MiddletonNishiizumi and others, 1991a, Reference Nishiizumib, Reference Nishiizumi1993; Reference Gosse, Klein, Evenson, Lawn and MiddletonGosse and others, 1995a, Reference Gosse, Evenson, Klein, Lawn and Middletonb; Reference Brook, Nesje, Lehman, Raisbeck and YiouBrook and others, 1996b; Reference Stone, Evans, Fifield, Allan and CresswellStone and others, 1998b). However, cosmogenic nuclide techniques can also be applied to determine the erosion rates of surfaces and to date burial events (e.g. Reference NishiizumiNishiizumi and others, 1993; Reference Granger, Kirchner and FinkelGranger and others, 1996, 1997; Reference Davis, Bierman, Marsella, Caffee and SouthonDavis and others, 1999).

This paper provides an overview of cosmogenic radionuclide techniques and the underlying assumptions, uncertainties and sample requirements, as well as theoretical considerations that illustrate potential uses of the techniques in glaciology and glacial geomorphology.

In-Situ Cosmogenic Radionuclides

The Earth is continually bombarded by cosmic rays which are largely attenuated by the atmosphere. Those cosmic rays that do reach the Earth’s surface interact with atomic nuclei in minerals near the Earth’s surface to produce in-situ cosmogenic nuclides, such as stable ³He and ²¹Ne and radioactive ¹⁰Be, ¹⁴C, ²⁶Al, ³⁶Cl (Reference Cerling and CraigCerling and Craig, 1994). Recent advances in nuclear instrumentation allow measurement of very low concentrations of these rare nuclides. Three cosmogenic radionuclides are commonly used in applications of the cosmogenic nuclide technique to problems in glaciology and glacial geomorphology: ¹⁰Be and ²⁶Al, which are created by nuclear reactions in quartz (Reference Nishiizumi, Lal, Klein, Middleton and ArnoldNishiizumi and others, 1986); and ³⁶Cl which is produced by cosmic-ray interactions with ³⁵Cl, ³⁹K and ⁴⁰Ca (Reference PhillipsPhillips and others, 1997). The half-lives for ¹⁰Be, ²⁶Al and ³⁶Cl are: 1.51 ± 0.03 × 10⁶ a (Reference HofmannHofmann and others, 1987); 7.05 ± 0.2 × 10⁵ a (Reference Norris, Gancarz, Rokop and ThomasNorris and others, 1983); and 3.01 × 10⁵ a (Reference Lederer and ShirleyLederer and Shirley, 1978) respectively. Quartz and the target materials for 36Cl are found in a large variety of rocks and sediments making the technique widely applicable.

With prolonged exposure, cosmogenic radionuclides accumulate within exposed rock as a function of time and depth below the surface (Figs 1 and 2). Time elapsed T (years) since initial rock surface exposure can be calculated from cosmogenic nuclide concentrations N (atoms g^-1) in the sample according to Reference LalLal (1991):

(1)

where P is the local cosmogenic radionuclide production rate (atoms g^-1a^-1), x is depth below the surface (cm), λ is the radioactive decay constant (a^-1), ε is the surface-erosion rate (cm a^-1), N _i is the inherited concentration of cosmogenic radionuclides (atom g^-1), μ is the absorption coefficient (cm^-1) in the target; μ = ρ/Λ where ρ is the average density of the rock (g cm^-3), and Λ is the exponential production attenuation length in rocks (150 g cm^-2; Reference Brown, Brook, Raisbeck, Yiou and KurzBrown and others, 1992).

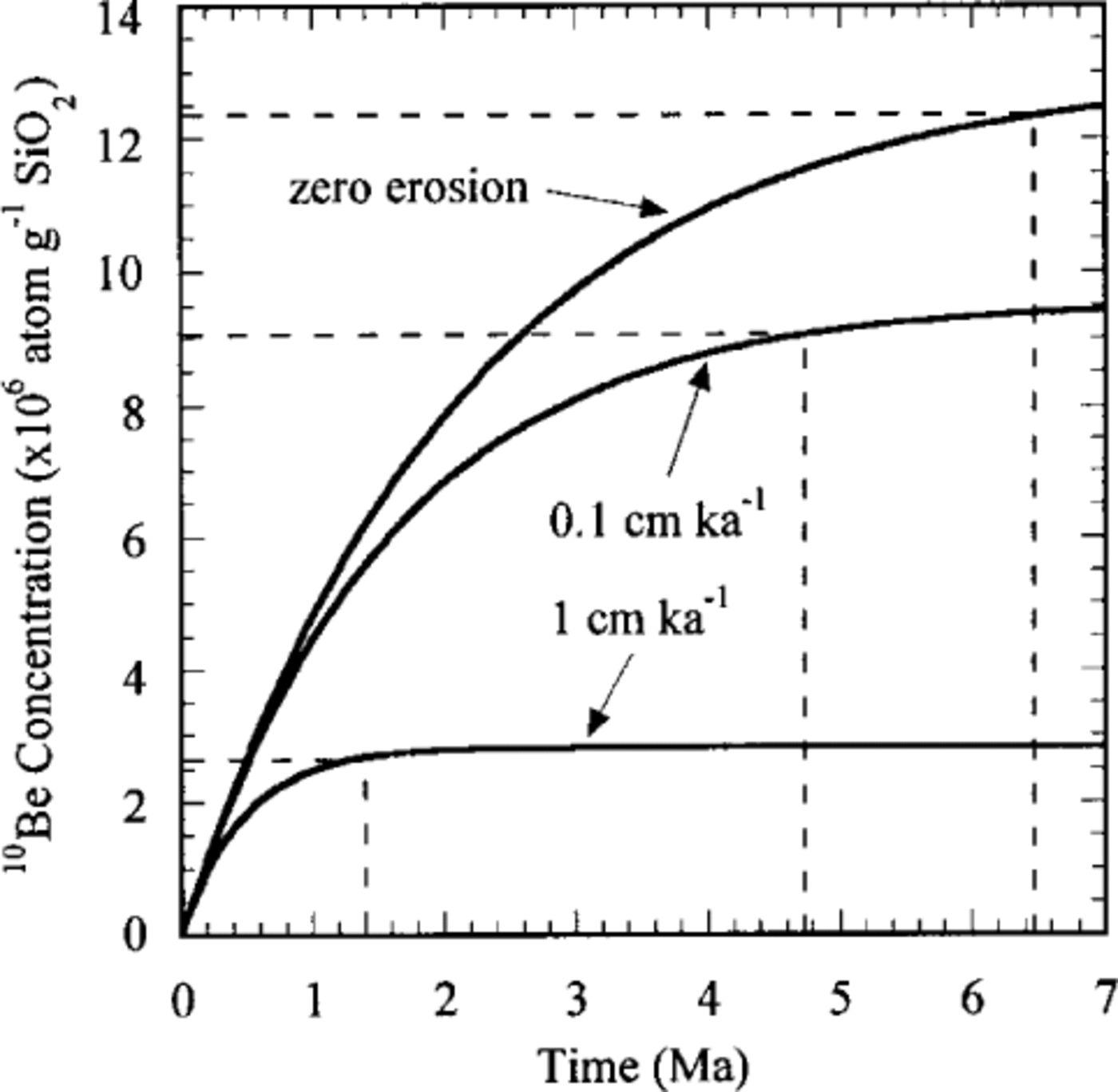
Fig. 1. Increase in surface ¹⁰Be concentration with time under different steady-state erosion rates calculated using Equation (1) with ¹⁰Be production rate of 6.0 atomsg ^-1 (SiO₂) a^-1. Dashed lines intersect concentration curves at 95% cosmogenic radionuclide saturation in the sample, representing the maximum age currently measurable forgiven production and erosion rate.

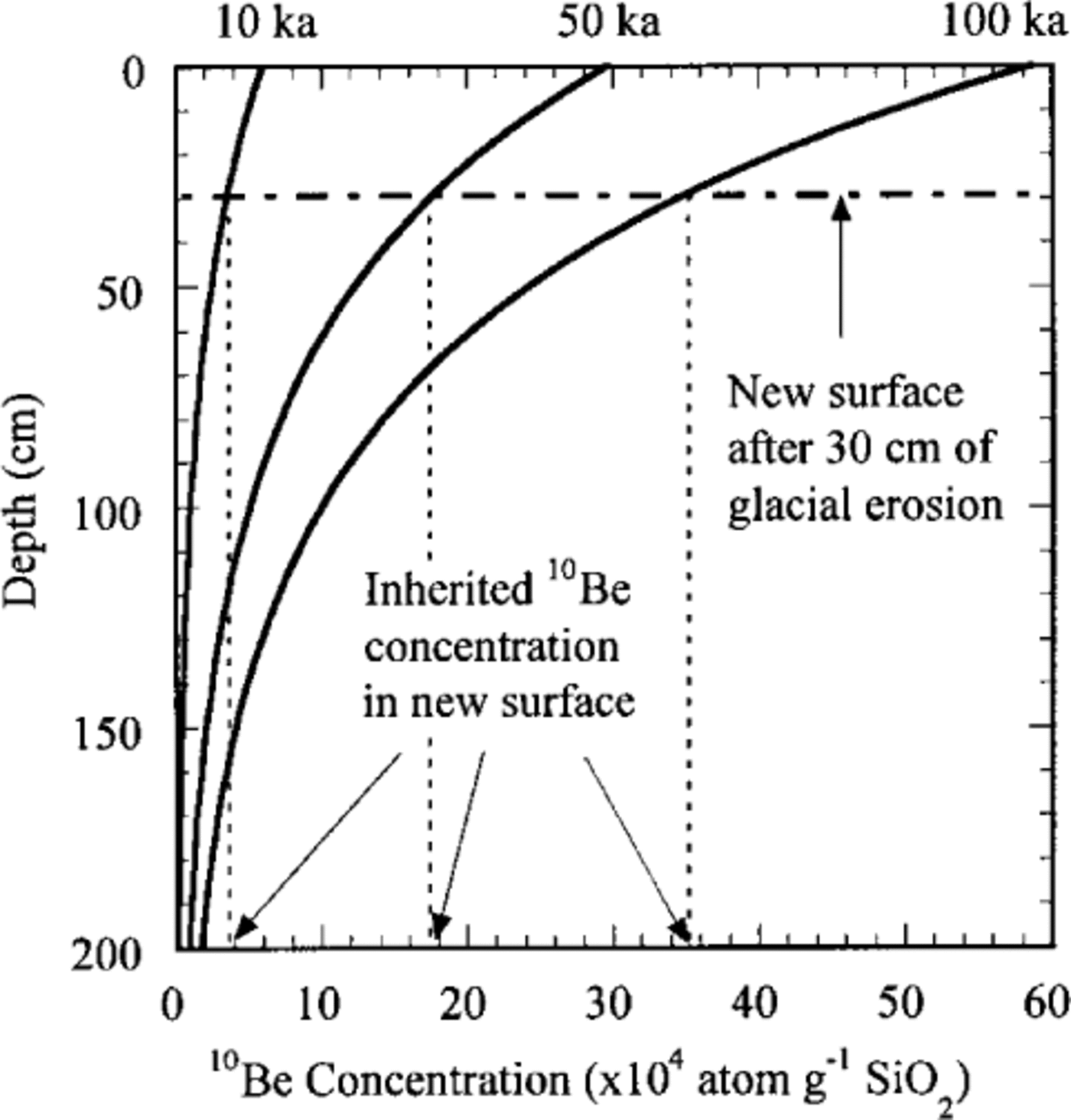
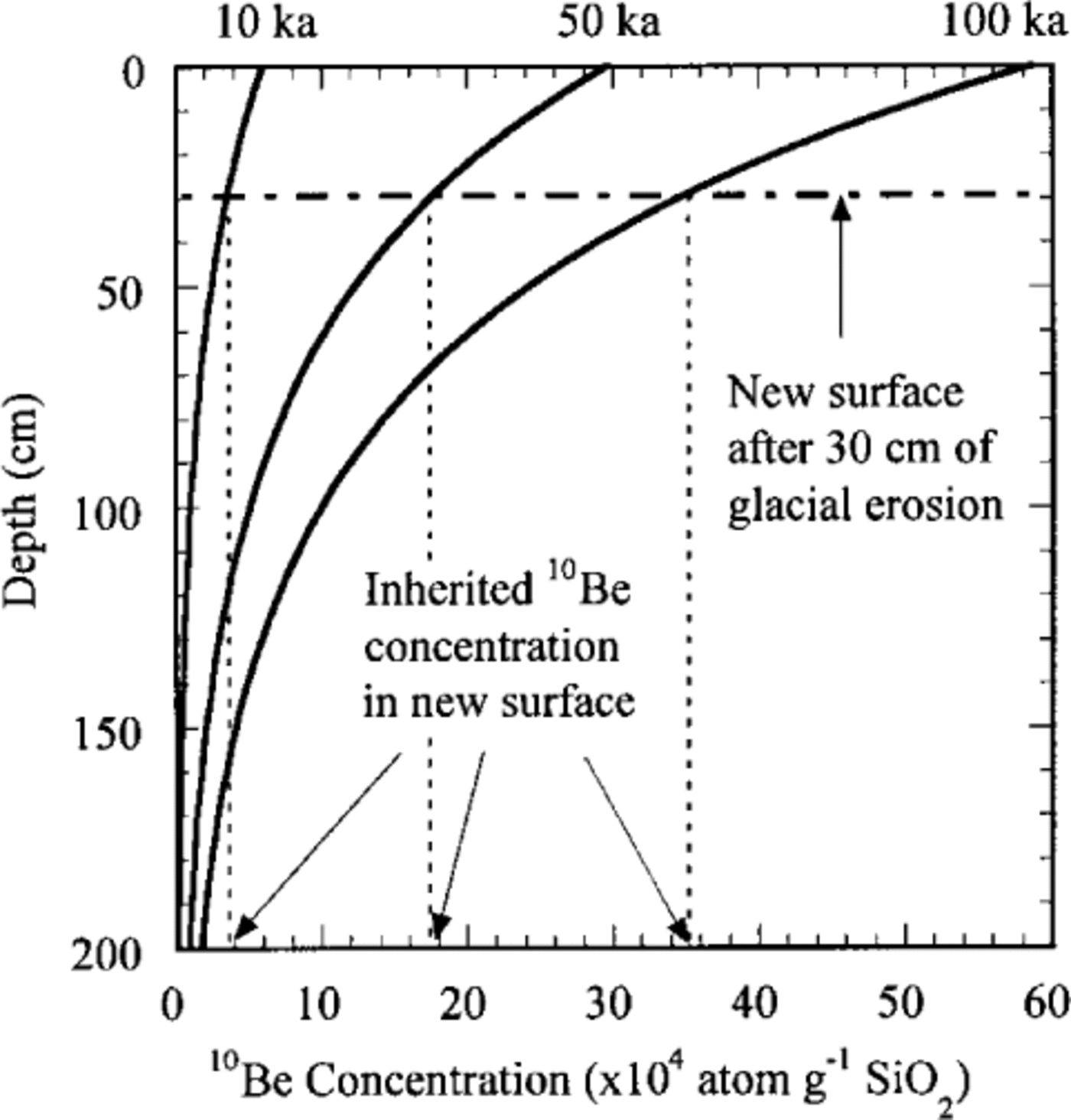
Fig. 2. Exponential decrease in ¹⁰Be concentration with depth for a surface production rate of 6.0 atomsg^-1 (SiO²) a 1 and a rock density of 2.75g cm^-3 after 10, 50 and 100 ka (solid curves). The effect of shallow glacial scouring on inheritance is shown for the case where 30 cm of bedrock is removed (thick dot-dash line). For example, if 30 cm is removed after 50 ka of exposure, the new surface has an inherited ¹⁰Be concentration of ~ 17.5 × 10⁴ atomsg^-1 equivalent to an apparent exposure age of ~ 29 ka.

Cosmogenic radionuclide measurements require accelerator mass spectrometry (AMS) because cosmogenic nuclide concentrations in a sample are typically < 106 atoms g 1 (Reference Elmore and PhillipsElmore and Phillips, 1987). AMS measurements are made to a precision of 1% to 7%, where precision is a measure of the exactness with which the result is determined and how reproducible the result is, without reference to what the result means.

Uncertainties of Cosmogenic Radionuclide Methods

In addition to AMS measurement precision limits, there are also inherent systematic errors in the use of cosmogenic radionuclides, particularly in sampling and in our current understanding of spatial and temporal variations in cosmogenic radionuclide production rates. The uncertainties resulting from these errors must be estimated and combined with uncertainties related to the statistical distribution of results when multiple samples are analyzed. Systematic uncertainties, unlike analytical ones, are not reduced by additional measurements, and so may dominate overall uncertainty.

The concentration of cosmogenic radionuclides in a sample depends not only on time, but also on production rate integrated over the entire exposure time, depth below the surface, geometry of the sampled surface, surface-erosion rate or burial rate, and the initial cosmogenic radionuclide concentration (Equation (1)). A sampling strategy for the application of cosmogenic radionuclide techniques should be designed to minimize systematic error and uncertainties in subsequent age and erosion determination. To minimize the depth correction required as a result of the exponential decrease in cosmogenic radionuclide production with depth (Fig. 2), samples are usually collected from within 5 cm of the rock surface. The extent of sample shielding from exposure to cosmic rays by surrounding topography and sample geometry is accounted for in geometric and shielding corrections, based on measuring sample-surface inclination and vertical angles to the horizon. Erosion of a rock surface removes accumulated cosmogenic radionuclides, making calculated exposure ages too young. Burial has the same effect because it shields the surface from cosmic rays. To minimize the impact of burial or erosion, surface samples are selected that have no evidence of erosion since initial exposure and are unlikely to have ever been buried.

The largest systematic uncertainty in surface-exposure ages is the production-rate estimate. The thickness of atmosphere cosmic-ray particles have to penetrate to reach the surface affects the production rate. Thus, at low latitudes and low elevations, surface-production rates are lowest. Similarly, the geomagnetic dipole field shields the Earth from low-energy cosmic rays. This shielding effect is strongest at the magnetic Equator and virtually absent at the magnetic poles (Reference Lal and PetersLal and Peters, 1967). Estimates of production rates have been derived from measured cosmogenic radionuclide concentrations in independently dated surfaces and from theoretical calculations (Tables 1 and 2). For specific localities, most workers adjust the production rate for latitude and altitude using the scaling factors of Reference LalLal (1991).

Table 1. Published ³⁶ Clproduction rates (sea-level and ≥60° geomagnetic latitude).

Theoretical calculation.

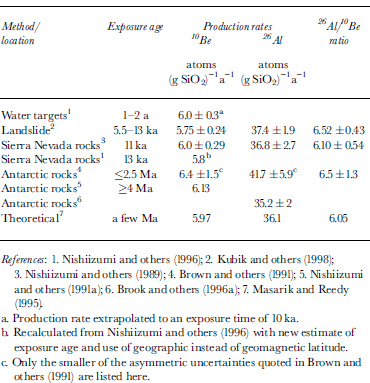
Table 2. Published ¹⁰Be and ²⁶Al production rates (sea-level and >60° geomagnetic latitude) and ²⁶Al/¹⁰Be ratios.

Recently, data from marine cores and the Greenland Icecore Project (GRIP) core have provided a high-resolution correlation between cosmogenic radionuclide production and geomagnetic field-strength variations over the last 200 ka (Reference Frank, Schwartz, Baumann, Kubik, Suterand and ManginiFrank and others, 1997; Reference Baumgartner, Beer, Masarik, Wagner, Meynadier and SynalBaumgartner and others, 1998), allowing some magnetic corrections to be made. However, several issues related to the systematics of cosmogenic radionuclide production are still being determined (e.g. Reference Gosse and KleinGosse and Klein, 1996). These include production-rate coefficients and pre-200 ka fluctuations in the dipole geomagnetic field intensity. After these issues have been resolved, cosmogenic ages calculated on the basis of our present understanding of the controlling factors will need to be revised. It is anticipated that the magnitude of these corrections will not exceed 15% (Reference PhillipsPhillips and others, 1997). Systematic production uncertainties do not impact on comparisons between results using the same production-rate estimate. For example, if the aim is to determine the age differences between a series of moraines, cosmogenic radionuclide data can be utilized at the analytical precision of 3–7%, assuming constant production rate. If production rates vary, that variation must be accounted for.

Surface Exposure Ages and Erosion Rates

Surface-exposure dating has been the most widely used cosmogenic radionuclide technique in glacial geomorphology to date, and has proven useful for constraining glacial chronologies in alpine areas (e.g. Reference Phillips, Zreda, Smith, Elmore, Kubik and SharmaPhillips and others, 1990, Reference Phillips, Zreda, Benson, Plummer, Elmore and Sharma1996a, Reference Phillips, Zreda, Flinsch, Elmore and Sharmab, Reference Phillips1997; Reference Gosse, Klein, Evenson, Lawn and MiddletonGosse and others, 1995a, b) as well as in ice- sheet dominated terrain such as Antarctica (Reference Ivy-Ochs, Schlüchter, Kubik, Dittrich-Hannen and BeerIvy-Ochs and others, 1995; Reference Fabel, Stone, Fifield, Cresswell and RicciFabel and others, 1997) and northern Europe (e.g. Reference Brook, Brown, Kurz, Raisbeck and YiouBrook and others, 1996b). Unlike other techniques, surface-exposure dating can be used to date glacial events directly because it avoids the inaccuracies of methods which produce bracketing ages by dating prior or subsequent events, such as burial of organic matter by moraine. The time range of the method is in the order of a thousand to several million years (Fig. 1). Age limits depend on which isotope is being used, how fast the sampled surface is eroding, and local cosmogenic radionuclide production rates (e.g. Reference Brown, Brook, Raisbeck, Yiou and KurzBrown and others, 1992; Reference NishiizumiNishiizumi and others, 1993; Reference BiermanBierman, 1994).

Using Equation (1) to calculate exposure time (T) from a measured cosmogenic radionuclide concentration (N) in a sample requires that the post-exposure steady-state erosion rate (e) is known. For surfaces that show evidence of very little postglacial erosion, such as intact striations and glacial polish, a post-exposure steady-state erosion rate of zero is assumed. If independent erosion-rate evidence is not available, there is no unique solution to Equation (1), rather, the inferred results consist of paired erosion rates and ages. If the exposure time can be independently constrained, the cosmogenic radionuclide concentration can be used to calculate the post-exposure steady-state erosion rate for the surface.

Although independent age control is often not available, steady-state bedrock-erosion rates can be calculated. Because production decreases exponentially with depth below the surface (Fig. 2), the accumulated cosmogenic radionuclide concentration in a mineral grain records the speed with which that grain has been uncovered; slower erosion rates imply longer exposure times near the surface, and thus higher concentrations. Reference LalLal (1991) showed that the cosmogenic radionuclide concentration N, in a steadily eroding outcrop surface, is inversely proportional to the outcrop’s erosion rate ε:

(2)

The radionuclide concentration N averages the erosion rate over a time-scale of order 1/με, the time required to erode a layer of thickness 1/μ from the surface. Equation (2) assumes that the half-life, λ, is much longer than 1/με. Because cosmogenic radionuclides are insensitive to recent changes in erosion rates, they are particularly useful for estimating long-term rates of erosion (Reference Brook, Brown, Kurz, Raisbeck and YiouBrook and others, 1996b; Reference Granger, Kirchner and FinkelGranger and others, 1996).

Additionally, Reference LalLal (1991) showed that the cosmogenic radionuclide ratio derived from measurement of two cosmogenic radionuclides in the same sample varies with exposure time and erosion rate because of the difference in their respective decay rates (see section on Burial dating below). Hence, in theory it is possible to simultaneously calculate an erosion rate and exposure age for a sample by measuring the concentration of two cosmogenic radionuclides. The applicability of this has only been demonstrated for areas with long exposure histories and very slow erosion rates (e.g. Reference NishiizumiNishiizumi and others, 1993).

Erosion and Inheritance

A concern in exposure-age dating in glaciated landscapes is the extent to which insufficient glacial erosion might yield erroneous deglaciation ages due to remnant cosmogenic radionuclide concentrations in exposed surfaces (Reference Fabel, Stone, Fifield, Cresswell and RicciFabel and others, 1997). This is a concern if the exposure age “clock” is only partially reset because erosion does not remove all of the surface and near-surface rock in which cosmogenic radionuclides accumulated prior to the glacial event. However, accounting for this problem provides a unique new opportunity to back-calculate the amount of rock lost due to erosion (Reference Horn, Harbor, Elmore, Sharma and DunneHorn and others, 1996; Reference Briner and SwansonBriner and Swanson, 1998). We are applying this approach to determine the spatial dis-tribution of valley-scale glacial erosion based on the exponential decrease in cosmogenic radionuclide concentration with depth in a rock surface (Fig. 2) and the inherited cosmogenic radionuclide concentration in the sample (Reference FabelFabel and others, 1998). Inheritance refers to the remnant cosmogenic radionuclide concentration from a prior exposure history. For example, for exposed bedrock with a density of 2.75 g cm^-3, the cosmogenic radionuclide production rate at a depth of ~ 175 cm is <5% of the surface-production rate and is not measurable with current AMS precision. If a surface which has been exposed for a few thousand years is overridden by ice which erodes in excess of ~ 175 cm of bed-rock, the existing cosmogenic radionuclide signal is 95% removed leaving a “fresh” surface exposed after retreat. If, on the other hand, glacial erosion removes < 175 cm of rock, the subsequently exposed surface contains a measurable cosmogenic radionuclide concentration inherited from prior exposure (Fig. 2).

Inherited concentrations can be calculated if the ages of the penultimate and final deglaciation can be constrained, either independently or from multiple surface-exposure ages. The difference between the deglaciation age and the age given by the samples with inheritance provides the concentration of inherited cosmogenic radionuclides, and the difference between the penultimate and final deglaciation limits is the time available for erosion. Using the exponential decrease in cosmogenic radionuclide concentration with depth (Fig. 2), it is possible to back-calculate how much rock had to be eroded to leave the sampled surface with the inherited cosmogenic radionuclide concentration:

(3)

where x is the depth of rock removed, N _meas is the measured cosmogenic radionuclide concentration, and N _deg and N _prior are the modeled cosmogenic radionuclide concentrations (using Equation (1)) for the penultimate and final deglaciation ages.

For example, we have measured ¹⁰Be and ²⁶Al in bedrock samples collected from a valley profile in the Wind River Range, Wyoming. The samples were striated and polished, indicating very minor erosion since the last deglaciation. The erosion rates obtained from calculated cosmogenic radionuclide inheritance in the samples for the period between the penultimate and last glaciation range from > 3.0 cm ka^-1 in the valley bottom to < 0.22 cm ka^-1 near the upper limit of the Last Glacial Maximum ice in the valley (unpublished data). The calculations assume that the penultimate Bull Lake glaciation (Reference PhillipsPhillips and others, 1997) left a comogenic radionuclide-free surface and the youngest surface-exposure ages provide the final deglaciation age. From the available data, it is not possible to determine if the calculated erosion rates are purely glacial or if they are a mixture between subaerial (during the Interglacial) and glacial erosion. In other applications of this concept, Reference Briner and SwansonBriner and Swanson (1998) calculated glacial erosion rates for a large roche moutonnée in the area of Puget Sound, Washington, U.S.A., using ³⁶Cl inheritance. Erosion-rate data for the last glacial advance yielded 9— 35 cm ka^-1 from the stoss side, and in excess of 63–72 cm ka^-1 on summit surfaces, while the quarried lee region yielded deglaciation ages and corresponding erosion depths of ≥ 2 m.

Burial Dating

One cosmogenic radionuclide application that has received relatively little attention in glacial geomorphology so far is dating sediment burial using the radioactive decay of ²⁶Al and ¹⁰Be. The method has been used to date sediments in river terraces, alluvial fans and caves (Reference Granger, Kirchner and FinkelGranger and others, 1996; 1997), and relies on the fact that ²⁶Al is produced six- times faster than ¹⁰Be, regardless of the absolute production rate (Table 2, column 5). Thus if a quartz-bearing rock accumulates ²⁶Al and ¹⁰Be while exposed at the surface, then its ²⁶Al/¹⁰Be ratio will be six. If this rock is subsequently buried deep enough that it is completely shielded, its ²⁶Al/¹⁰Be ratio will diminish over time because ²⁶Al decays faster than ¹⁰Be. Thus, the departure of the ²⁶Al/ ¹⁰Be ratio in the buried rock from an initial value of six can be used to determine the time since burial.

Following Reference LalLal (1991) and Reference Granger, Kirchner and FinkelGranger and others (1997), the ²⁶Al/¹⁰Be ratio (N ₂₆/N ₁₀) in a steadily eroding outcrop will change with erosion rate • as follows:

(4)

where the suffixes 26 and 10 make the symbols (defined in Equation (1)) specific to ²⁶Al and ¹⁰Be respectively. For erosion rates much faster than λ₂₆/μ, the ²⁶Al/¹⁰Be ratio approaches (N ₂₆/N ₁₀) = P ₂₆/P ₁₀=~ 6.0 (Table 2, column 5); for erosion rates much slower than λ₁₀/μ, it approaches (P ₂₆ λ₁₀/ P ₁₀ λ₂₆ =~ 2.7 (Fig. 3). When minerals exposed near the Earth’s surface are shielded from cosmic rays (e.g. by burial beneath a till), then the cosmogenic radionuclide production ceases and ²⁶Al and ¹⁰Be decay according to:

(5)

where T _burial is the time since burial and (N ₂₆)_i and (N ₁₀)_i represent initial ²⁶Al and ¹⁰Be concentrations. Because ²⁶Al decays faster than ¹⁰Be, the ratio N ₂₆/N ₁₀ decreases exponentially over time (Fig. 3):

(6)

Fig. 3. ²⁶Al/¹⁰Be ratio plotted against ¹⁰Be concentration (after Reference Granger, Kirchner and FinkelGranger and others, 1997). The 0 ma curve represents the ²⁶Al/¹⁰Be ratio in a steadily eroding rock, as determined by Equation (4). Erosion rates are shown from 0.1 cm ka^-1 calculated for a ¹⁰Be production rate of 6.0 atomsg^-1 (SiO₂) a^-1. When a sample is shielded from cosmic rays, radioactive decay causes the ²⁶Al/¹⁰Be ratio to decline parallel to the straight dashed lines, according to Equation (6). Isochrons are shown as thin curves (labeled Ma). The black square is a hypothetical sample with a measured ²⁶Al and ¹⁰Be concentration. The ²⁶Al/¹⁰Be ratio and ¹⁰Be concentration indicate a burial age of ~ 1.5 Ma. The pre-burial erosion rate may be calculated by backtracking ²⁶Al/¹⁰Be ratios parallel to the dashed decay lines (large arrow) to intercept the 0 Ma exposure line, providing a steady-state erosion estimate of 0.1-1 cm ka^-1 for this sample.

Equations (4)–(6) can be solved iteratively and can be used to estimate burial times and pre-burial erosion rates (Reference Granger, Kirchner and FinkelGranger and others, 1997).

Geological requirements for the method to be applicable are simply that: (1) quartz must be exposed at the surface for long enough to accumulate measurable cosmogenic radionuclide concentrations (typically > 10 ka); (2) the quartz must be buried quickly with respect to radioactive decay; (3) the quartz must be buried deeply with respect to cosmic-ray penetration (typically >5m); and (4) the sediment must have a simple history of exposure prior to burial (Reference Granger, Kirchner and FinkelGranger and others, 1997), i.e. no inherited cosmogenic signal.

One possible glaciological application of burial dating is to determine the age of material buried by till. This is useful because the time of till deposition may be considerably different from the time the till is exposed by glacial retreat. Additionally, there may be situations where multiple phases of till deposition prevent surface-exposure dating of all but the most recent depositional event. Burial dating till material itself is problematic, since the material has probably only experienced limited exposure. However, the burial-dating method can be applied to sediments or palaeosols which are likely to have been exposed in excess of 10 ka prior to being buried by the till. By determining the burial age of these types of samples, it is possible to obtain an age for till deposition. Precision of burial dating using ²⁶Al and ¹⁰Be is limited to ~200 ka, thus burial dating is mainly useful for dating older events which have previously been difficult to date, or for which only limiting ages, such as palaeomagnetic dates, exist. The method is currently being successfully applied to buried fluvial and lacustrine sediments from palaeochannels and proglacial lakes to determine which ice-sheet advances caused the major drainage rearrangements documented in the mid-west of the U.S.A. (Reference Granger and SmithGranger and Smith, 1998).

Shielding and Complex Exposure Histories

Although surface-exposure ages, erosion rates, and burial ages can be obtained for well-constrained situations, complex surface-exposure histories are problematic. Interpretation of cosmogenic radionuclide concentrations is much more difficult if a surface has experienced multiple exposure periods, erosion and periods of burial. Current exposure- age calculations are usually based on models that assume steady-state erosion and free-surface exposure, i.e. without shielding of the surface by sediment or ice in the past. Thus, reported ages are generally based on the simplest likely geo- morphological history.

Surface shielding lowers the cosmogenic radionuclide production rate. If a surface has been exposed, subsequently shielded and only recently re-exposed, then the cosmogenic radionuclide concentration will have decreased by radioactive decay during the shielding period. In theory, the ratio of two nuclides with different half-lives could be used to distinguish between continuous exposure at the surface and periodic shielding (personal communication from D. Lal, 1998). This may have considerable potential for constraining the duration of ice-sheet occupation.

To illustrate the effect of multiple-shielding events on the cosmogenic radionuclide concentration in a bedrock surface, consider a bimodal cyclic exposure history of a surface which is exposed for T_l years followed by shielding for T ₂ years. The surface-erosion rate is assumed to be zero. For multiple cycles with full exposure for time T_l , followed by partial exposure at K times the full intensity for a time period T ₂, with a radioactive decay constant λ, and surface production rate P, the cosmogenic radionuclide concentration attains a value C _n, after n cycles:

(7)

where K = 1 represents no shielding (i.e. there are no glacial periods in the record) and K = 0 represents full shielding during glacial periods. These simulations show that shielding history produces a change in cosmogenic radionuclide ratios (Fig. 4). Assuming full shielding during glacial periods (at least 5.5 m of ice), with multiple radionuclides we can in theory solve for T ₂, the portion of time ice-shielding has been effective, i.e. we have the possibility of constraining the lengths of glacial periods using cosmogenic radionuclide techniques.

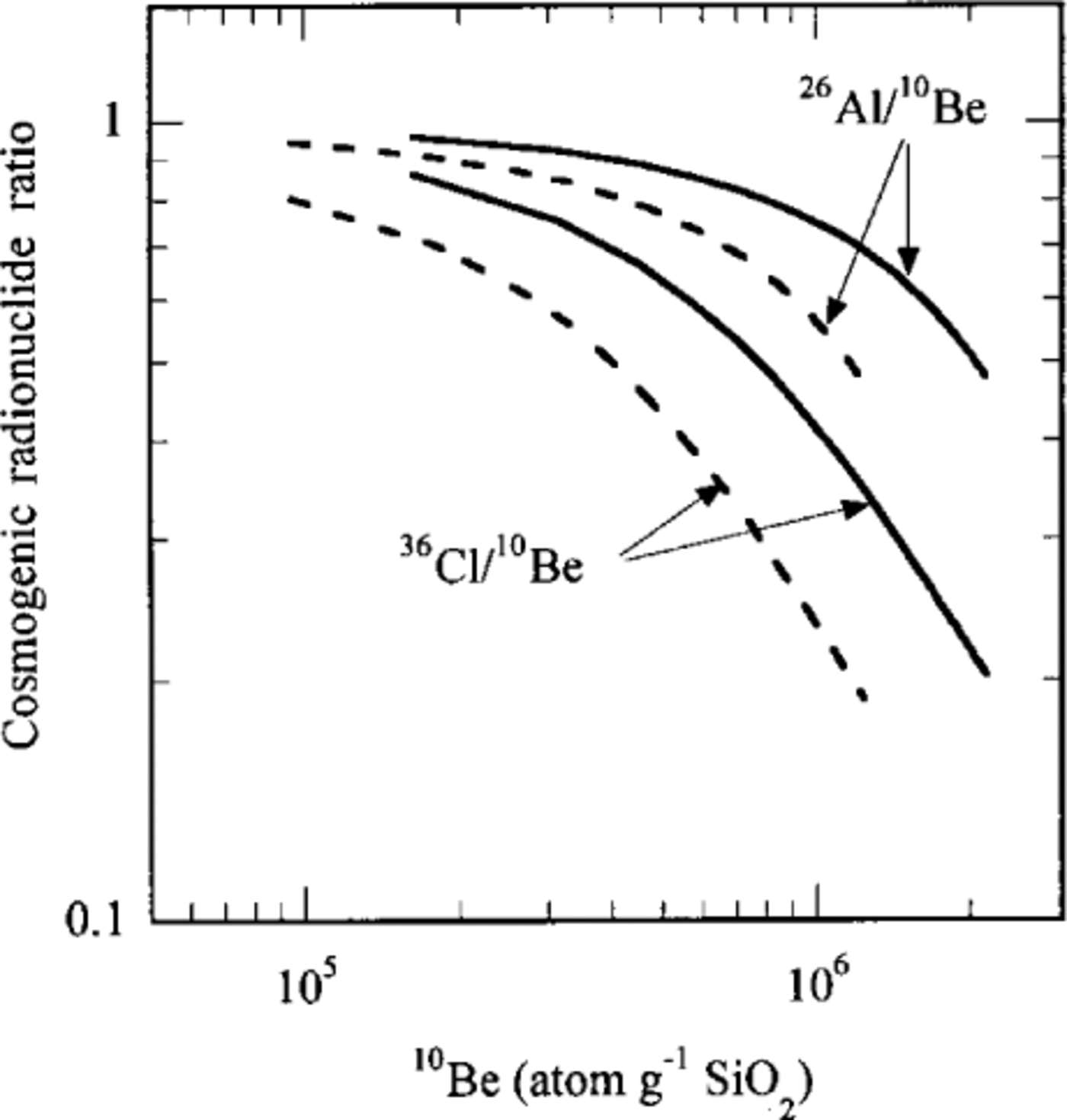
Fig. 4. ²⁶Al/¹⁰Be and ³⁶Cl/¹⁰Be ratios plotted against ¹⁰Be concentration. The solid curves show the cosmogenic radionuclide buildup in a rock surface calculated using Equation (7) for 50 cycles of T ₁ = 80 ka and T ₂ = 30 ka with both T ₁ and T ₂ at full production (no shielding).These curves are identical to the steady-state erosion curve calculated in Figure 3 using Equation (4) except that here the erosion rate is zero and surface production rates for¹⁰Be ²⁶Al and ³⁶Cl are1atomsg^-1a^-1. The dashed curves are calculated in the same way, but with T ₂ at zero production (shielded). Shielding the surface during part of its history decreases the ²³Al/¹⁰Be and ³⁶Cl/¹⁰Be ratios in the samples when compared to a free exposure history. .Note the effect is more dramatic for ¹⁰Be and ³⁶Cl. This is because of the larger difference in the radioactive decay rate between ¹⁰Be ratio ³⁶Cl when compared to ¹⁰Be and²⁶Al.

The minimum measurable difference in the cosmogenic radionuclide ratios resulting from multiple-exposure histories versus an exposure history without shielding is ~ 7%. With this in mind, we set up an exposure model to compare expected cosmogenic radionuclide ratios for continuous and complex exposure histories. The model takes into account pre-burial, burial, and post-burial time, subaerial erosion during non-glaciated times, and glacial erosion by the burying ice. The cosmogenic radionuclide concentrations for a surface which experiences burial through part of its exposure history (N _complex) and for a surface which has not been shielded during the same time interval (N _simple) are calculated for each individual isotope according to:

(8a)

(8b)

where ε _s and ε _g are subaerial and glacial-erosion rate (cm ka^-1) respectively, and T _pre, T _burial and T _post are the pre-burial, burial and post-burial times (a) respectively. All other symbols are defined in Equation (1).

The results shown in Figure 5 are for ³⁶Cl/¹⁰Be ratios and provide minimum requirements for the method to be applicable since ³⁶Cl/¹⁰Be is more sensitive to complex histories then ²⁶Al/¹⁰Be (Fig. 4). The results of the modeling indicate that to get a measurable difference in the ³⁶Cl/¹⁰Be ratio requires a minimum burial time of ~70 ka. Pre-burial erosion reduces this minimum burial time (Fig. 5a). Glacial erosion, although reducing the cosmogenic radionuclide concentration in the surface, does not affect the minimum burial time because the ³⁶Cl/¹⁰Be ratio depends on radioactive decay which is constant regardless of the subglacial erosion rate. Obviously, if glacial erosion exceeds ~175 cm, all inherited cosmogenic radionuclide information is lost. The most dramatic effect, and ultimately the critical factor influencing the feasibility of applying the complex exposure model in the real world, is the post-burial exposure time (Fig. 5b). The ³⁶Cl/¹⁰Be ratio will only be measurable if the surface has experienced limited post-burial exposure (< ~7 ka for a burial time of 100 ka) because renewed cosmogenic radionuclide accumulation rapidly obliterates the ³⁶Cl/¹⁰Be signal inherited after the burial event. This is enhanced by glacial erosion since it reduces the inherited cosmogenic radionuclide concentration. Subaerial erosion after burial has a buffering effect because the net rate of cosmogenic radionuclide accumulation in the surface is reduced (Fig. 5b). In summary, measurable differences in ³⁶Cl/¹⁰Be ratios between simple (continuous) surface exposure and more complex exposure histories will only occur if the burial time exceeds ~70 ka and the surface has been exposed for less than a few thousand years. This suggests the technique might best be applied to surfaces that are still buried by till and thus have no complications resulting from recent exposure.

Fig. 5. Sensitivity plots of a complex exposure model to length of burial (a) and length of post-burial exposure (b). Percentage difference in ³⁶Cl/¹⁰Be ratios is the difference in ³⁶Cl/¹⁰Be for a surface which has been exposed continuously, compared to a surface which has experienced burial. The horizontal dashed line marks the 7% ratio difference which is the minimum requirement for AMS. 5a) Pre-burial time set at 50 ka and post-burial time at 0 ka. Labels denote subaerial-erosion rates during pre-burial exposure. Plots including glacial erosion during burial are covered by the 0 cm ka^-1 line (see text). 5b) Pre-burial and burial times set at 100 ka. Labels denote glacial-erosion rates for the duration of burial. Note, even with zero erosion, the percentage difference in ³⁶Cl/¹⁰Be ratio drops below 7% after ~ 7 ka.

There are additional problems in using ³⁶Cl and ¹⁰Be because they are not obtained from the same mineral and the ³⁶Cl production rates are not as well constrained as those for ¹⁰Be. Nonetheless, testing of this technique is in progress on samples collected in northern Sweden where Reference Kleman and StroevenKleman and Stroeven (1997) have mapped palaeosurfaces which appear to have been buried by non-erosive ice for the last 110 ka, and which have only recently been deglaciated (< 8.5 ka). Although this deglaciation age is greater than the minimum set by the complex history model, technical improvements in AMS may reduce the limiting 7% difference in the ³⁶Cl/¹⁰Be ratios.

Conclusion

Cosmogenic radionuclide techniques have great potential for addressing numerous chronological and process problems in glaciology and glacial geomorphology. Standard surface-exposure dating provides a means for establishing glacial chronologies directly from deposits and surfaces created by glacial events over time-scales of thousands to millions of years. In addition to such established uses, there are as yet untapped cosmogenic radionuclide applications for glaciology and glacial geomorphology. The burial age of previously exposed sediments, derived from the ratio of two cosmogenic radionuclides, can provide chronological control for glacial advances and till deposition. This pro-vides the potential for constraining glaciological models of former valley glaciers and ice sheets. In places where both cosmogenic radionuclide inheritance and independent age control exist, the rate, spatial patterns, and magnitude of glacial erosion can be determined from single cosmogenic radionuclide measurements. This provides the potential for constraining models that link ice dynamics and erosion processes.

The usefulness of the techniques is somewhat tempered by the limitations inherent in the methods. Age errors for surface-exposure dating lie in the ±15 % range due to analytical and systematic uncertainties. Burial dating is only feasible for samples which have initial cosmogenic radionuclide concentrations equivalent to > 10 ka exposure. To obtain a measurable change in the cosmogenic radionuclide ratio burial time has to exceed ~70 ka for ³⁶Cl/¹⁰Be and ~200 ka for ²⁶Al/¹⁰Be. Complex exposure histories may only be determined if burial times are long and the length of the post-burial exposure time is short. Where glacial erosion has completely removed the cosmogenic radionuclide signal, the data provide a minimum estimate of the depth of rock removed.

Despite these limitations, the usefulness of cosmogenic radionuclide techniques has been demonstrated by many applications that have yielded important new results. Some of these, as well as potential future applications of cosmogenic radionuclide techniques in glacial geomorphology and glaciology have been outlined here. However, as with any recently established and currently developing technique, there are still relatively few workers in this field. Thus there are considerable opportunities for glaciologists and geomorphologists to make significant new advances by being the first to apply this method to address classic problems in their area of interest.