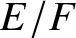1 Introduction
In 1986, Gross and Zagier [Reference Gross and ZagierGZ86] proved a remarkable formula that relates the Néron–Tate heights of Heegner points on a rational elliptic curve to the central derivative of the corresponding Rankin–Selberg L-function. A decade later, Kudla [Reference Kudla and RapoportKud97] revealed another striking relation between Gillet–Soulé heights of special cycles on Shimura curves and derivatives of Siegel Eisenstein series of genus 2, suggesting an arithmetic version of theta lifting and the Siegel–Weil formula (see, for example, [Reference Kudla and RapoportKud02, Reference KudlaKud03]). This was later further developed in his joint work with Rapoport and Yang [Reference Kudla, Rapoport and YangKRY06]. For the higher dimensional case, in a series of papers starting from the late 1990s, Kudla and Rapoport developed the theory of special cycles on integral models of Shimura varieties for GSpin groups in lower rank cases and for unitary groups of arbitrary ranks [Reference KudlaKR11, Reference KudlaKR14]. They also studied special cycles on the relevant Rapoport–Zink spaces over non-Archimedean local fields. In particular, they formulated a conjecture relating the arithmetic intersection number of special cycles on the unitary Rapoport–Zink space to the first derivative of local Whittaker functions [Reference KudlaKR11, Conjecture 1.3].
In his thesis work [Reference LiuLiu11a, Reference LiuLiu11b], one of us studied special cycles as elements in the Chow group of the unitary Shimura variety over its reflex field (rather than in the arithmetic Chow group of a certain integral model) and the Beilinson–Bloch height of the arithmetic theta lifting (rather than the Gillet–Soulé height). In particular, in the setting of unitary groups, he proposed an explicit conjectural formula for the Beilinson–Bloch height in terms of the central L-derivative and local doubling zeta integrals. Such a formula is completely parallel to the Rallis inner product formula [Reference RallisRal84], which computes the Petersson inner product of the global theta lifting and hence was named arithmetic inner product formula in [Reference LiuLiu11a] and can be regarded as a higher dimensional generalisation of the Gross–Zagier formula.Footnote 1 In the case of ![]() $\mathrm {U}(1,1)$ over an arbitrary CM extension, such a conjectural formula was completely confirmed in [Reference LiuLiu11b], while the case for
$\mathrm {U}(1,1)$ over an arbitrary CM extension, such a conjectural formula was completely confirmed in [Reference LiuLiu11b], while the case for ![]() $\mathrm {U}(r,r)$ with
$\mathrm {U}(r,r)$ with ![]() $r\geqslant 2$ is significantly harder. Recently, the Kudla–Rapoport conjecture has been proved by W. Zhang and one of us in [Reference Li and ZhangLZa],Footnote 2 and it has become possible to attack the cases for higher rank groups.
$r\geqslant 2$ is significantly harder. Recently, the Kudla–Rapoport conjecture has been proved by W. Zhang and one of us in [Reference Li and ZhangLZa],Footnote 2 and it has become possible to attack the cases for higher rank groups.
In [Reference Li and LiuLL21], we proved that for certain cuspidal automorphic representations ![]() $\pi $ of
$\pi $ of ![]() $\mathrm {U}(r,r)$, if the central derivative
$\mathrm {U}(r,r)$, if the central derivative ![]() $L'(1/2,\pi )$ is nonvanishing, then the
$L'(1/2,\pi )$ is nonvanishing, then the ![]() $\pi $-nearly isotypic localisation of the Chow group of a certain unitary Shimura variety over its reflex field does not vanish. This proved part of the Beilinson–Bloch conjecture for Chow groups and L-functions (see [Reference Li and LiuLL21, Section 1] for a precise formulation in our setting). Moreover, assuming the modularity of Kudla’s generating functions of special cycles, we further proved the arithmetic inner product formula relating
$\pi $-nearly isotypic localisation of the Chow group of a certain unitary Shimura variety over its reflex field does not vanish. This proved part of the Beilinson–Bloch conjecture for Chow groups and L-functions (see [Reference Li and LiuLL21, Section 1] for a precise formulation in our setting). Moreover, assuming the modularity of Kudla’s generating functions of special cycles, we further proved the arithmetic inner product formula relating ![]() $L'(1/2,\pi )$ and the height of arithmetic theta liftings. In this article, we improve the main results from [Reference Li and LiuLL21] in two directions: First, we allow ramified places in the CM extension
$L'(1/2,\pi )$ and the height of arithmetic theta liftings. In this article, we improve the main results from [Reference Li and LiuLL21] in two directions: First, we allow ramified places in the CM extension ![]() $E/F$ at which we consider representations that are spherical with respect to a certain special maximal compact subgroup, by formulating and proving an analogue of the Kudla–Rapoport conjecture for exotic smooth Rapoport–Zink spaces. Second, we lift the restriction on the components at split places of the automorphic representation, by proving a more general vanishing result on certain cohomology of integral models of unitary Shimura varieties with Drinfeld level structures. However, for technical reasons, we will still assume
$E/F$ at which we consider representations that are spherical with respect to a certain special maximal compact subgroup, by formulating and proving an analogue of the Kudla–Rapoport conjecture for exotic smooth Rapoport–Zink spaces. Second, we lift the restriction on the components at split places of the automorphic representation, by proving a more general vanishing result on certain cohomology of integral models of unitary Shimura varieties with Drinfeld level structures. However, for technical reasons, we will still assume ![]() $F\neq \mathbb {Q}$ (see Remark 4.33).
$F\neq \mathbb {Q}$ (see Remark 4.33).
1.1 Main results
Let ![]() $E/F$ be a CM extension of number fields with the complex conjugation
$E/F$ be a CM extension of number fields with the complex conjugation ![]() $\mathtt {c}$. Denote by
$\mathtt {c}$. Denote by  $\mathtt {V}_F^{(\infty )}$ and
$\mathtt {V}_F^{(\infty )}$ and  $\mathtt {V}_F^{\mathrm {fin}}$ the set of Archimedean and non-Archimedean places of F, respectively. Denote by
$\mathtt {V}_F^{\mathrm {fin}}$ the set of Archimedean and non-Archimedean places of F, respectively. Denote by  $\mathtt {V}_F^{\mathrm {spl}}$,
$\mathtt {V}_F^{\mathrm {spl}}$,  $\mathtt {V}_F^{\mathrm {int}}$ and
$\mathtt {V}_F^{\mathrm {int}}$ and ![]() $\mathtt {V}_F^{\mathrm {ram}}$ the subsets of
$\mathtt {V}_F^{\mathrm {ram}}$ the subsets of  $\mathtt {V}_F^{\mathrm {fin}}$ of those that are split, inert and ramified in E, respectively.
$\mathtt {V}_F^{\mathrm {fin}}$ of those that are split, inert and ramified in E, respectively.
Take an even positive integer ![]() $n=2r$. We equip
$n=2r$. We equip ![]() $W_r := E^n$ with the skew-hermitian form (with respect to the involution
$W_r := E^n$ with the skew-hermitian form (with respect to the involution ![]() $\mathtt {c}$) given by the matrix
$\mathtt {c}$) given by the matrix  $\left (\begin {smallmatrix}&1_r\\ -1_r &\end {smallmatrix}\right )$. Put
$\left (\begin {smallmatrix}&1_r\\ -1_r &\end {smallmatrix}\right )$. Put ![]() $G_r := \mathrm {U}(W_r)$, the unitary group of
$G_r := \mathrm {U}(W_r)$, the unitary group of ![]() $W_r$, which is a quasi-split reductive group over F. For every
$W_r$, which is a quasi-split reductive group over F. For every  $v\in \mathtt {V}_F^{\mathrm {fin}}$, we denote by
$v\in \mathtt {V}_F^{\mathrm {fin}}$, we denote by ![]() $K_{r,v}\subseteq G_r(F_v)$ the stabiliser of the lattice
$K_{r,v}\subseteq G_r(F_v)$ the stabiliser of the lattice ![]() $O_{E_v}^n$, which is a special maximal compact subgroup.
$O_{E_v}^n$, which is a special maximal compact subgroup.
We start from an informal discussion on the arithmetic inner product formula. Let ![]() $\pi $ be a tempered automorphic representation of
$\pi $ be a tempered automorphic representation of ![]() $G_r(\mathbb {A}_F)$, which by theta dichotomy gives rise to a unique up to isomorphism hermitian space
$G_r(\mathbb {A}_F)$, which by theta dichotomy gives rise to a unique up to isomorphism hermitian space ![]() $V_\pi $ of rank n over
$V_\pi $ of rank n over ![]() $\mathbb {A}_E$. It is known that the hermitian space
$\mathbb {A}_E$. It is known that the hermitian space ![]() $V_\pi $ is coherent (respectively incoherent); that is,
$V_\pi $ is coherent (respectively incoherent); that is, ![]() $V_\pi $ is (respectively is not) the base change of a hermitian space over E, if and only if the global root number
$V_\pi $ is (respectively is not) the base change of a hermitian space over E, if and only if the global root number ![]() $\varepsilon (\pi )$ equals
$\varepsilon (\pi )$ equals ![]() $1$ (respectively
$1$ (respectively ![]() $-1$). When
$-1$). When ![]() $\varepsilon (\pi )=1$, we have the global theta lifting of
$\varepsilon (\pi )=1$, we have the global theta lifting of ![]() $\pi $, which is a space of automorphic forms on
$\pi $, which is a space of automorphic forms on ![]() $\mathrm {U}(V_\pi )(\mathbb {A}_F)$, and the famous Rallis inner product formula [Reference RallisRal84] computes the Petersson inner product of the global theta lifting in terms of the central L-value
$\mathrm {U}(V_\pi )(\mathbb {A}_F)$, and the famous Rallis inner product formula [Reference RallisRal84] computes the Petersson inner product of the global theta lifting in terms of the central L-value  $L(\tfrac {1}{2},\pi )$ of
$L(\tfrac {1}{2},\pi )$ of ![]() $\pi $. When
$\pi $. When ![]() $\varepsilon (\pi )=-1$, we have the arithmetic theta lifting of
$\varepsilon (\pi )=-1$, we have the arithmetic theta lifting of ![]() $\pi $, which is a space of algebraic cycles on the Shimura variety associated to
$\pi $, which is a space of algebraic cycles on the Shimura variety associated to ![]() $V_\pi $, and the conjectural arithmetic inner product formula [Reference LiuLiu11a] computes the height of the arithmetic theta lifting in terms of the central L-derivative
$V_\pi $, and the conjectural arithmetic inner product formula [Reference LiuLiu11a] computes the height of the arithmetic theta lifting in terms of the central L-derivative  $L'(\tfrac {1}{2},\pi )$ of
$L'(\tfrac {1}{2},\pi )$ of ![]() $\pi $. In our previous article [Reference Li and LiuLL21], we verified the arithmetic inner product formula, under certain hypotheses, when
$\pi $. In our previous article [Reference Li and LiuLL21], we verified the arithmetic inner product formula, under certain hypotheses, when ![]() $E/F$ and
$E/F$ and ![]() $\pi $ satisfy certain local conditions (see [Reference Li and LiuLL21, Assumption 1.3]). In particular, we want
$\pi $ satisfy certain local conditions (see [Reference Li and LiuLL21, Assumption 1.3]). In particular, we want ![]() $\mathtt {V}_F^{\mathrm {ram}}=\emptyset $, which forces
$\mathtt {V}_F^{\mathrm {ram}}=\emptyset $, which forces ![]() $[F:\mathbb {Q}]$ to be even, and we want the representation
$[F:\mathbb {Q}]$ to be even, and we want the representation ![]() $\pi $ to be either unramified or almost unramified at
$\pi $ to be either unramified or almost unramified at  $v\in \mathtt {V}_F^{\mathrm {int}}$. Computing local root numbers, we have
$v\in \mathtt {V}_F^{\mathrm {int}}$. Computing local root numbers, we have ![]() $\varepsilon (\pi _v)=(-1)^r$ if
$\varepsilon (\pi _v)=(-1)^r$ if  $v\in \mathtt {V}_F^{(\infty )}$,
$v\in \mathtt {V}_F^{(\infty )}$, ![]() $\varepsilon (\pi _v)=1$ if
$\varepsilon (\pi _v)=1$ if  $v\in \mathtt {V}_F^{\mathrm {spl}}$ or
$v\in \mathtt {V}_F^{\mathrm {spl}}$ or ![]() $\pi _v$ is unramified,
$\pi _v$ is unramified, ![]() $\varepsilon (\pi _v)=-1$ if (
$\varepsilon (\pi _v)=-1$ if ( $v\in \mathtt {V}_F^{\mathrm {int}}$ and)
$v\in \mathtt {V}_F^{\mathrm {int}}$ and) ![]() $\pi _v$ is almost unramified. It follows that
$\pi _v$ is almost unramified. It follows that ![]() $\varepsilon (\pi )=(-1)^{r[F:\mathbb {Q}]+|\mathtt {S}_\pi |}$, where
$\varepsilon (\pi )=(-1)^{r[F:\mathbb {Q}]+|\mathtt {S}_\pi |}$, where  $\mathtt {S}_\pi \subseteq \mathtt {V}_F^{\mathrm {int}}$ denotes the (finite) subset at which
$\mathtt {S}_\pi \subseteq \mathtt {V}_F^{\mathrm {int}}$ denotes the (finite) subset at which ![]() $\pi $ is almost unramified, which equals
$\pi $ is almost unramified, which equals ![]() $(-1)^{|\mathtt {S}_\pi |}$ as
$(-1)^{|\mathtt {S}_\pi |}$ as ![]() $[F:\mathbb {Q}]$ is even. In this article, we improve our results so that
$[F:\mathbb {Q}]$ is even. In this article, we improve our results so that ![]() $\mathtt {V}_F^{\mathrm {ram}}$ can be nonempty; hence,
$\mathtt {V}_F^{\mathrm {ram}}$ can be nonempty; hence, ![]() $[F:\mathbb {Q}]$ can be odd and we will still have
$[F:\mathbb {Q}]$ can be odd and we will still have ![]() $\varepsilon (\pi )=(-1)^{r[F:\mathbb {Q}]+|\mathtt {S}_\pi |}$. To show the significance of such improvement, now we may have
$\varepsilon (\pi )=(-1)^{r[F:\mathbb {Q}]+|\mathtt {S}_\pi |}$. To show the significance of such improvement, now we may have ![]() $\varepsilon (\pi )=-1$ but
$\varepsilon (\pi )=-1$ but ![]() $\mathtt {S}_\pi =\emptyset $, so that we can accommodate
$\mathtt {S}_\pi =\emptyset $, so that we can accommodate ![]() $\pi $ that comes from certain explicit motives like symmetric power of elliptic curves (see Example 1.10).
$\pi $ that comes from certain explicit motives like symmetric power of elliptic curves (see Example 1.10).
The reader may read the introduction of [Reference Li and LiuLL21] for more background. Now we describe in more detail our setup and main results in the current article.
Definition 1.1. We define the subset ![]() $\mathtt {V}_F^\heartsuit $ of
$\mathtt {V}_F^\heartsuit $ of  $\mathtt {V}_F^{\mathrm {spl}}\cup \mathtt {V}_F^{\mathrm {int}}$ consisting of v satisfying that for every
$\mathtt {V}_F^{\mathrm {spl}}\cup \mathtt {V}_F^{\mathrm {int}}$ consisting of v satisfying that for every  $v'\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {ram}}$, where p is the underlying rational prime of v, the subfield of
$v'\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {ram}}$, where p is the underlying rational prime of v, the subfield of ![]() $\overline {F_v}$ generated by
$\overline {F_v}$ generated by ![]() $F_v$ and the Galois closure of
$F_v$ and the Galois closure of ![]() $E_{v'}$ is unramified over
$E_{v'}$ is unramified over ![]() $F_v$.
$F_v$.
Remark 1.2. The purpose of this technical definition is that for certain places v in  $\mathtt {V}_F^{\mathrm {spl}}\cup \mathtt {V}_F^{\mathrm {int}}$, we need to have a CM type of E such that its reflex field does not contain more ramification over p than
$\mathtt {V}_F^{\mathrm {spl}}\cup \mathtt {V}_F^{\mathrm {int}}$, we need to have a CM type of E such that its reflex field does not contain more ramification over p than ![]() $F_v$ does – this is possible for
$F_v$ does – this is possible for ![]() $v\in \mathtt {V}_F^\heartsuit $. Note that
$v\in \mathtt {V}_F^\heartsuit $. Note that
• the complement
 $(\mathtt {V}_F^{\mathrm {spl}}\cup \mathtt {V}_F^{\mathrm {int}})\setminus \mathtt {V}_F^\heartsuit $ is finite;
$(\mathtt {V}_F^{\mathrm {spl}}\cup \mathtt {V}_F^{\mathrm {int}})\setminus \mathtt {V}_F^\heartsuit $ is finite;• when E is Galois, or contains an imaginary quadratic field, or satisfies
 $\mathtt {V}_F^{\mathrm {ram}}=\emptyset $, we have
$\mathtt {V}_F^{\mathrm {ram}}=\emptyset $, we have  $\mathtt {V}_F^\heartsuit =\mathtt {V}_F^{\mathrm {spl}}\cup \mathtt {V}_F^{\mathrm {int}}$.
$\mathtt {V}_F^\heartsuit =\mathtt {V}_F^{\mathrm {spl}}\cup \mathtt {V}_F^{\mathrm {int}}$.
Assumption 1.3. Suppose that ![]() $F\neq \mathbb {Q}$, that
$F\neq \mathbb {Q}$, that  $\mathtt {V}_F^{\mathrm {spl}}$ contains all 2-adic places and that every prime in
$\mathtt {V}_F^{\mathrm {spl}}$ contains all 2-adic places and that every prime in ![]() $\mathtt {V}_F^{\mathrm {ram}}$ is unramified over
$\mathtt {V}_F^{\mathrm {ram}}$ is unramified over ![]() $\mathbb {Q}$. We consider a cuspidal automorphic representation
$\mathbb {Q}$. We consider a cuspidal automorphic representation ![]() $\pi $ of
$\pi $ of ![]() $G_r(\mathbb {A}_F)$ realised on a space
$G_r(\mathbb {A}_F)$ realised on a space ![]() $\mathcal {V}_\pi $ of cusp forms satisfying the following:
$\mathcal {V}_\pi $ of cusp forms satisfying the following:
(1) For every
 $v\in \mathtt {V}_F^{(\infty )}$,
$v\in \mathtt {V}_F^{(\infty )}$,  $\pi _v$ is the holomorphic discrete series representation of Harish-Chandra parameter
$\pi _v$ is the holomorphic discrete series representation of Harish-Chandra parameter  $\{\tfrac {1-n}{2},\tfrac {3-n}{2},\dots ,\tfrac {n-3}{2},\tfrac {n-1}{2}\}$ (see [Reference Li and LiuLL21, Remark 1.4(1)]).
$\{\tfrac {1-n}{2},\tfrac {3-n}{2},\dots ,\tfrac {n-3}{2},\tfrac {n-1}{2}\}$ (see [Reference Li and LiuLL21, Remark 1.4(1)]).(2) For every
 $v\in \mathtt {V}_F^{\mathrm {ram}}$,
$v\in \mathtt {V}_F^{\mathrm {ram}}$,  $\pi _v$ is spherical with respect to
$\pi _v$ is spherical with respect to  $K_{r,v}$; that is,
$K_{r,v}$; that is,  $\pi _v^{K_{r,v}}\neq \{0\}$.
$\pi _v^{K_{r,v}}\neq \{0\}$.(3) For every
 $v\in \mathtt {V}_F^{\mathrm {int}}$,
$v\in \mathtt {V}_F^{\mathrm {int}}$,  $\pi _v$ is either unramified or almost unramified with respect to
$\pi _v$ is either unramified or almost unramified with respect to  $K_{r,v}$ (see [Reference Li and LiuLL21, Remark 1.4(3)]); moreover, if
$K_{r,v}$ (see [Reference Li and LiuLL21, Remark 1.4(3)]); moreover, if  $\pi _v$ is almost unramified, then v is unramified over
$\pi _v$ is almost unramified, then v is unramified over  $\mathbb {Q}$.
$\mathbb {Q}$.(4) For every
 $v\in \mathtt {V}_F^{\mathrm {fin}}$,
$v\in \mathtt {V}_F^{\mathrm {fin}}$,  $\pi _v$ is tempered.
$\pi _v$ is tempered.(5) We have
 $\mathtt {R}_\pi \cup \mathtt {S}_\pi \subseteq \mathtt {V}_F^\heartsuit $ (Definition 1.1), where
$\mathtt {R}_\pi \cup \mathtt {S}_\pi \subseteq \mathtt {V}_F^\heartsuit $ (Definition 1.1), where•
 $\mathtt {R}_\pi \subseteq \mathtt {V}_F^{\mathrm {spl}}$ denotes the (finite) subset for which
$\mathtt {R}_\pi \subseteq \mathtt {V}_F^{\mathrm {spl}}$ denotes the (finite) subset for which  $\pi _v$ is ramified,
$\pi _v$ is ramified,•
 $\mathtt {S}_\pi \subseteq \mathtt {V}_F^{\mathrm {int}}$ denotes the (finite) subset for which
$\mathtt {S}_\pi \subseteq \mathtt {V}_F^{\mathrm {int}}$ denotes the (finite) subset for which  $\pi _v$ is almost unramified.
$\pi _v$ is almost unramified.
Comparing Assumption 1.3 with [Reference Li and LiuLL21, Assumption 1.3], we have lifted the restriction that ![]() $\mathtt {V}_F^{\mathrm {ram}}=\emptyset $ (by allowing
$\mathtt {V}_F^{\mathrm {ram}}=\emptyset $ (by allowing ![]() $\pi _v$ to be a certain type of representations for
$\pi _v$ to be a certain type of representations for ![]() $v\in \mathtt {V}_F^{\mathrm {ram}}$) and also the restriction on
$v\in \mathtt {V}_F^{\mathrm {ram}}$) and also the restriction on ![]() $\pi _v$ for
$\pi _v$ for  $v\in \mathtt {V}_F^{\mathrm {spl}}$. Note that (5) is not really a new restriction since when
$v\in \mathtt {V}_F^{\mathrm {spl}}$. Note that (5) is not really a new restriction since when ![]() $\mathtt {V}_F^{\mathrm {ram}}=\emptyset $, it is automatic by Remark 1.2.
$\mathtt {V}_F^{\mathrm {ram}}=\emptyset $, it is automatic by Remark 1.2.
Suppose that we are in Assumption 1.3. Denote by ![]() $L(s,\pi )$ the doubling L-function. Then we have
$L(s,\pi )$ the doubling L-function. Then we have ![]() $\varepsilon (\pi )=(-1)^{r[F:\mathbb {Q}]+|\mathtt {S}_\pi |}$ for the global (doubling) root number, so that the vanishing order of
$\varepsilon (\pi )=(-1)^{r[F:\mathbb {Q}]+|\mathtt {S}_\pi |}$ for the global (doubling) root number, so that the vanishing order of ![]() $L(s,\pi )$ at the centre
$L(s,\pi )$ at the centre  $s=\tfrac {1}{2}$ has the same parity as
$s=\tfrac {1}{2}$ has the same parity as ![]() $r[F:\mathbb {Q}]+|\mathtt {S}_\pi |$. The cuspidal automorphic representation
$r[F:\mathbb {Q}]+|\mathtt {S}_\pi |$. The cuspidal automorphic representation ![]() $\pi $ determines a hermitian space
$\pi $ determines a hermitian space ![]() $V_\pi $ over
$V_\pi $ over ![]() $\mathbb {A}_E$ of rank n via local theta dichotomy (so that the local theta lifting of
$\mathbb {A}_E$ of rank n via local theta dichotomy (so that the local theta lifting of ![]() $\pi _v$ to
$\pi _v$ to ![]() $\mathrm {U}(V_\pi )(F_v)$ is nontrivial for every place v of F), unique up to isomorphism, which is totally positive definite and satisfies that for every
$\mathrm {U}(V_\pi )(F_v)$ is nontrivial for every place v of F), unique up to isomorphism, which is totally positive definite and satisfies that for every  $v\in \mathtt {V}_F^{\mathrm {fin}}$, the local Hasse invariant
$v\in \mathtt {V}_F^{\mathrm {fin}}$, the local Hasse invariant ![]() $\epsilon (V_\pi \otimes _{\mathbb {A}_F}F_v)=1$ if and only if
$\epsilon (V_\pi \otimes _{\mathbb {A}_F}F_v)=1$ if and only if ![]() $v\not \in \mathtt {S}_\pi $.
$v\not \in \mathtt {S}_\pi $.
Now suppose that ![]() $r[F:\mathbb {Q}]+|\mathtt {S}_\pi |$ is odd; hence,
$r[F:\mathbb {Q}]+|\mathtt {S}_\pi |$ is odd; hence, ![]() $\varepsilon (\pi )=-1$, which is equivalent to that
$\varepsilon (\pi )=-1$, which is equivalent to that ![]() $V_\pi $ is incoherent. In what follows, we take
$V_\pi $ is incoherent. In what follows, we take ![]() $V=V_\pi $ in the context of [Reference Li and LiuLL21, Conjecture 1.1]; hence,
$V=V_\pi $ in the context of [Reference Li and LiuLL21, Conjecture 1.1]; hence, ![]() $H=\mathrm {U}(V_\pi )$. Let
$H=\mathrm {U}(V_\pi )$. Let ![]() $\mathtt {R}$ be a finite subset of
$\mathtt {R}$ be a finite subset of  $\mathtt {V}_F^{\mathrm {fin}}$. We fix a special maximal subgroup
$\mathtt {V}_F^{\mathrm {fin}}$. We fix a special maximal subgroup ![]() $L^{\mathtt {R}}$ of
$L^{\mathtt {R}}$ of  $H(\mathbb {A}_F^{\infty ,\mathtt {R}})$ that is the stabiliser of a lattice
$H(\mathbb {A}_F^{\infty ,\mathtt {R}})$ that is the stabiliser of a lattice ![]() $\Lambda ^{\mathtt {R}}$ in
$\Lambda ^{\mathtt {R}}$ in  $V\otimes _{\mathbb {A}_F}\mathbb {A}_F^{\infty ,\mathtt {R}}$ (see Notation 4.2(H6) for more details). For a field
$V\otimes _{\mathbb {A}_F}\mathbb {A}_F^{\infty ,\mathtt {R}}$ (see Notation 4.2(H6) for more details). For a field ![]() $\mathbb {L}$, we denote by
$\mathbb {L}$, we denote by ![]() $\mathbb {T}^{\mathtt {R}}_{\mathbb {L}}$ the (abstract) Hecke algebra
$\mathbb {T}^{\mathtt {R}}_{\mathbb {L}}$ the (abstract) Hecke algebra  $\mathbb {L}[L^{\mathtt {R}}\backslash H(\mathbb {A}_F^{\infty ,\mathtt {R}})/L^{\mathtt {R}}]$, which is a commutative
$\mathbb {L}[L^{\mathtt {R}}\backslash H(\mathbb {A}_F^{\infty ,\mathtt {R}})/L^{\mathtt {R}}]$, which is a commutative ![]() $\mathbb {L}$-algebra. When
$\mathbb {L}$-algebra. When ![]() $\mathtt {R}$ contains
$\mathtt {R}$ contains ![]() $\mathtt {R}_\pi $, the cuspidal automorphic representation
$\mathtt {R}_\pi $, the cuspidal automorphic representation ![]() $\pi $ gives rise to a character
$\pi $ gives rise to a character
 $$ \begin{align*} \chi_\pi^{\mathtt{R}}\colon\mathbb{T}^{\mathtt{R}}_{\mathbb{Q}^{\mathrm{ac}}}\to\mathbb{Q}^{\mathrm{ac}}, \end{align*} $$
$$ \begin{align*} \chi_\pi^{\mathtt{R}}\colon\mathbb{T}^{\mathtt{R}}_{\mathbb{Q}^{\mathrm{ac}}}\to\mathbb{Q}^{\mathrm{ac}}, \end{align*} $$where ![]() $\mathbb {Q}^{\mathrm {ac}}$ denotes the subfield of
$\mathbb {Q}^{\mathrm {ac}}$ denotes the subfield of ![]() $\mathbb {C}$ of algebraic numbers, and we put
$\mathbb {C}$ of algebraic numbers, and we put
which is a maximal ideal of  $\mathbb {T}^{\mathtt {R}}_{\mathbb {Q}^{\mathrm {ac}}}$.
$\mathbb {T}^{\mathtt {R}}_{\mathbb {Q}^{\mathrm {ac}}}$.
In what follows, we will fix an arbitrary embedding ![]() $\boldsymbol {\iota }\colon E\hookrightarrow \mathbb {C}$ and denote by
$\boldsymbol {\iota }\colon E\hookrightarrow \mathbb {C}$ and denote by ![]() $\{X_L\}$ the system of unitary Shimura varieties of dimension
$\{X_L\}$ the system of unitary Shimura varieties of dimension ![]() $n-1$ over
$n-1$ over ![]() $\boldsymbol {\iota }(E)$ indexed by open compact subgroups
$\boldsymbol {\iota }(E)$ indexed by open compact subgroups ![]() $L\subseteq H(\mathbb {A}_F^\infty )$ (see Subsection 4.2 for more details). The following is the first main theorem of this article.
$L\subseteq H(\mathbb {A}_F^\infty )$ (see Subsection 4.2 for more details). The following is the first main theorem of this article.
Theorem 1.4. Let ![]() $(\pi ,\mathcal {V}_\pi )$ be as in Assumption 1.3 with
$(\pi ,\mathcal {V}_\pi )$ be as in Assumption 1.3 with ![]() $r[F:\mathbb {Q}]+|\mathtt {S}_\pi |$ odd, for which we assume [Reference Li and LiuLL21, Hypothesis 6.6]. If
$r[F:\mathbb {Q}]+|\mathtt {S}_\pi |$ odd, for which we assume [Reference Li and LiuLL21, Hypothesis 6.6]. If  $L'(\tfrac {1}{2},\pi )\neq 0$ – that is,
$L'(\tfrac {1}{2},\pi )\neq 0$ – that is,  $\operatorname {\mathrm {ord}}_{s=\frac {1}{2}}L(s,\pi )=1$ – then as long as
$\operatorname {\mathrm {ord}}_{s=\frac {1}{2}}L(s,\pi )=1$ – then as long as ![]() $\mathtt {R}$ satisfies
$\mathtt {R}$ satisfies ![]() $\mathtt {R}_\pi \subseteq \mathtt {R}$ and
$\mathtt {R}_\pi \subseteq \mathtt {R}$ and  $|\mathtt {R}\cap \mathtt {V}_F^{\mathrm {spl}}\cap \mathtt {V}_F^\heartsuit |\geqslant 2$, the nonvanishing
$|\mathtt {R}\cap \mathtt {V}_F^{\mathrm {spl}}\cap \mathtt {V}_F^\heartsuit |\geqslant 2$, the nonvanishing
 $$ \begin{align*} \varinjlim_{L_{\mathtt{R}}}\left(\operatorname{\mathrm{CH}}^r(X_{L_{\mathtt{R}}L^{\mathtt{R}}})^0_{\mathbb{Q}^{\mathrm{ac}}}\right)_{\mathfrak{m}_\pi^{\mathtt{R}}}\neq 0 \end{align*} $$
$$ \begin{align*} \varinjlim_{L_{\mathtt{R}}}\left(\operatorname{\mathrm{CH}}^r(X_{L_{\mathtt{R}}L^{\mathtt{R}}})^0_{\mathbb{Q}^{\mathrm{ac}}}\right)_{\mathfrak{m}_\pi^{\mathtt{R}}}\neq 0 \end{align*} $$holds, where the colimit is taken over all open compact subgroups ![]() $L_{\mathtt {R}}$ of
$L_{\mathtt {R}}$ of ![]() $H(F_{\mathtt {R}})$.
$H(F_{\mathtt {R}})$.
Our remaining results rely on Hypothesis 4.11 on the modularity of Kudla’s generating functions of special cycles and hence are conditional at this moment.
Theorem 1.5. Let ![]() $(\pi ,\mathcal {V}_\pi )$ be as in Assumption 1.3 with
$(\pi ,\mathcal {V}_\pi )$ be as in Assumption 1.3 with ![]() $r[F:\mathbb {Q}]+|\mathtt {S}_\pi |$ odd, for which we assume [Reference Li and LiuLL21, Hypothesis 6.6]. Assume Hypothesis 4.11 on the modularity of generating functions of codimension r.
$r[F:\mathbb {Q}]+|\mathtt {S}_\pi |$ odd, for which we assume [Reference Li and LiuLL21, Hypothesis 6.6]. Assume Hypothesis 4.11 on the modularity of generating functions of codimension r.
(1) For every collection of elements
•
 $\varphi _1=\otimes _v\varphi _{1v}\in \mathcal {V}_{\pi }$ and
$\varphi _1=\otimes _v\varphi _{1v}\in \mathcal {V}_{\pi }$ and  $\varphi _2=\otimes _v\varphi _{2v}\in \mathcal {V}_{\pi }$ such that for every
$\varphi _2=\otimes _v\varphi _{2v}\in \mathcal {V}_{\pi }$ such that for every  $v\in \mathtt {V}_F^{(\infty )}$,
$v\in \mathtt {V}_F^{(\infty )}$,  $\varphi _{1v}$ and
$\varphi _{1v}$ and  $\varphi _{2v}$ have the lowest weight and satisfy
$\varphi _{2v}$ have the lowest weight and satisfy  $\langle \varphi _{1v}^{\mathtt {c}},\varphi _{2v}\rangle _{\pi _v}=1$,
$\langle \varphi _{1v}^{\mathtt {c}},\varphi _{2v}\rangle _{\pi _v}=1$,•
 $\phi ^\infty _1=\otimes _v\phi ^\infty _{1v}\in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )$ and
$\phi ^\infty _1=\otimes _v\phi ^\infty _{1v}\in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )$ and  $\phi ^\infty _2=\otimes _v\phi ^\infty _{2v}\in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )$,
$\phi ^\infty _2=\otimes _v\phi ^\infty _{2v}\in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )$,
the identity
holds. Here, $$ \begin{align*} \langle\Theta_{\phi^\infty_1}(\varphi_1),\Theta_{\phi^\infty_2}(\varphi_2)\rangle_{X,E}^\natural= \frac{L'(\tfrac{1}{2},\pi)}{b_{2r}(0)}\cdot C_r^{[F:\mathbb{Q}]} \cdot\prod_{v\in\mathtt{V}_F^{\mathrm{fin}}}\mathfrak{Z}^\natural_{\pi_v,V_v}(\varphi^{\mathtt{c}}_{1v},\varphi_{2v},\phi_{1v}^\infty\otimes(\phi_{2v}^\infty)^{\mathtt{c}}) \end{align*} $$
$$ \begin{align*} \langle\Theta_{\phi^\infty_1}(\varphi_1),\Theta_{\phi^\infty_2}(\varphi_2)\rangle_{X,E}^\natural= \frac{L'(\tfrac{1}{2},\pi)}{b_{2r}(0)}\cdot C_r^{[F:\mathbb{Q}]} \cdot\prod_{v\in\mathtt{V}_F^{\mathrm{fin}}}\mathfrak{Z}^\natural_{\pi_v,V_v}(\varphi^{\mathtt{c}}_{1v},\varphi_{2v},\phi_{1v}^\infty\otimes(\phi_{2v}^\infty)^{\mathtt{c}}) \end{align*} $$•
 $\Theta _{\phi ^\infty _i}(\varphi _i)\in \varinjlim _L\operatorname {\mathrm {CH}}^r(X_L)^0_{\mathbb {C}}$ is the arithmetic theta lifting (Definition 4.12), which is only well-defined under Hypothesis 4.11;
$\Theta _{\phi ^\infty _i}(\varphi _i)\in \varinjlim _L\operatorname {\mathrm {CH}}^r(X_L)^0_{\mathbb {C}}$ is the arithmetic theta lifting (Definition 4.12), which is only well-defined under Hypothesis 4.11;•
 $\langle \Theta _{\phi ^\infty _1}(\varphi _1),\Theta _{\phi ^\infty _2}(\varphi _2)\rangle _{X,E}^\natural $ is the normalised height pairing (Definition 4.17),Footnote 3 which is constructed based on Beilinson’s notion of height pairing;
$\langle \Theta _{\phi ^\infty _1}(\varphi _1),\Theta _{\phi ^\infty _2}(\varphi _2)\rangle _{X,E}^\natural $ is the normalised height pairing (Definition 4.17),Footnote 3 which is constructed based on Beilinson’s notion of height pairing;•
 $b_{2r}(0)$ is defined in Notation 4.1(F4), which equals
$b_{2r}(0)$ is defined in Notation 4.1(F4), which equals  $L(M_r^\vee (1))$ where
$L(M_r^\vee (1))$ where  $M_r$ is the motive associated to
$M_r$ is the motive associated to  $G_r$ by Gross [Reference GrossGro97]; in particular, it is a positive real number;
$G_r$ by Gross [Reference GrossGro97]; in particular, it is a positive real number;•
 $C_r=(-1)^r2^{-2r}\pi ^{r^2}\frac {\Gamma (1)\cdots \Gamma (r)}{\Gamma (r+1)\cdots \Gamma (2r)}$, which is the exact value of a certain Archimedean doubling zeta integral; and
$C_r=(-1)^r2^{-2r}\pi ^{r^2}\frac {\Gamma (1)\cdots \Gamma (r)}{\Gamma (r+1)\cdots \Gamma (2r)}$, which is the exact value of a certain Archimedean doubling zeta integral; and•
 $\mathfrak {Z}^\natural _{\pi _v,V_v}(\varphi ^{\mathtt {c}}_{1v},\varphi _{2v},\phi _{1v}^\infty \otimes (\phi _{2v}^\infty )^{\mathtt {c}})$ is the normalised local doubling zeta integral [Reference Li and LiuLL21, Section 3], which equals
$\mathfrak {Z}^\natural _{\pi _v,V_v}(\varphi ^{\mathtt {c}}_{1v},\varphi _{2v},\phi _{1v}^\infty \otimes (\phi _{2v}^\infty )^{\mathtt {c}})$ is the normalised local doubling zeta integral [Reference Li and LiuLL21, Section 3], which equals  $1$ for all but finitely many v.
$1$ for all but finitely many v.
(2) In the context of [Reference Li and LiuLL21, Conjecture 1.1], take (
 $V=V_\pi $ and)
$V=V_\pi $ and)  $\tilde \pi ^\infty $ to be the theta lifting of
$\tilde \pi ^\infty $ to be the theta lifting of  $\pi ^\infty $ to
$\pi ^\infty $ to  $H(\mathbb {A}_F^\infty )$. If
$H(\mathbb {A}_F^\infty )$. If  $L'(\tfrac {1}{2},\pi )\neq 0$ – that is,
$L'(\tfrac {1}{2},\pi )\neq 0$ – that is,  $\operatorname {\mathrm {ord}}_{s=\frac {1}{2}}L(s,\pi )=1$ – then holds.
$\operatorname {\mathrm {ord}}_{s=\frac {1}{2}}L(s,\pi )=1$ – then holds. $$ \begin{align*} \operatorname{\mathrm{Hom}}_{H(\mathbb{A}_F^\infty)}\left(\tilde\pi^\infty,\varinjlim_{L}\operatorname{\mathrm{CH}}^r(X_L)^0_{\mathbb{C}}\right)\neq0 \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hom}}_{H(\mathbb{A}_F^\infty)}\left(\tilde\pi^\infty,\varinjlim_{L}\operatorname{\mathrm{CH}}^r(X_L)^0_{\mathbb{C}}\right)\neq0 \end{align*} $$
Remark 1.6. We have the following remarks concerning Theorem 1.5.
(1) Part (1) verifies the so-called arithmetic inner product formula, a conjecture proposed by one of us [Reference LiuLiu11a, Conjecture 3.11].
(2) The arithmetic inner product formula in part (1) is perfectly parallel to the classical Rallis inner product formula. In fact, suppose that V is totally positive definite but coherent. We have the classical theta lifting
 $\theta _{\phi ^\infty }(\varphi )$ where we use standard Gaussian functions at Archimedean places. Then the Rallis inner product formula in this case reads as in which
$\theta _{\phi ^\infty }(\varphi )$ where we use standard Gaussian functions at Archimedean places. Then the Rallis inner product formula in this case reads as in which $$ \begin{align*} \langle\theta_{\phi^\infty_1}(\varphi_1),\theta_{\phi^\infty_2}(\varphi_2)\rangle_H= \frac{L(\tfrac{1}{2},\pi)}{b_{2r}(0)}\cdot C_r^{[F:\mathbb{Q}]} \cdot\prod_{v\in\mathtt{V}_F^{\mathrm{fin}}}\mathfrak{Z}^\natural_{\pi_v,V_v}(\varphi^{\mathtt{c}}_{1v},\varphi_{2v},\phi_{1v}^\infty\otimes(\phi_{2v}^\infty)^{\mathtt{c}}), \end{align*} $$
$$ \begin{align*} \langle\theta_{\phi^\infty_1}(\varphi_1),\theta_{\phi^\infty_2}(\varphi_2)\rangle_H= \frac{L(\tfrac{1}{2},\pi)}{b_{2r}(0)}\cdot C_r^{[F:\mathbb{Q}]} \cdot\prod_{v\in\mathtt{V}_F^{\mathrm{fin}}}\mathfrak{Z}^\natural_{\pi_v,V_v}(\varphi^{\mathtt{c}}_{1v},\varphi_{2v},\phi_{1v}^\infty\otimes(\phi_{2v}^\infty)^{\mathtt{c}}), \end{align*} $$ $\langle ,\rangle _H$ denotes the Petersson inner product with respect to the Tamagawa measure on
$\langle ,\rangle _H$ denotes the Petersson inner product with respect to the Tamagawa measure on  $H(\mathbb {A}_F)$.
$H(\mathbb {A}_F)$.
In the case where ![]() $\mathtt {R}_\pi =\emptyset $, we have a very explicit height formula for test vectors that are new everywhere.
$\mathtt {R}_\pi =\emptyset $, we have a very explicit height formula for test vectors that are new everywhere.
Corollary 1.7. Let ![]() $(\pi ,\mathcal {V}_\pi )$ be as in Assumption 1.3 with
$(\pi ,\mathcal {V}_\pi )$ be as in Assumption 1.3 with ![]() $r[F:\mathbb {Q}]+|\mathtt {S}_\pi |$ odd, for which we assume [Reference Li and LiuLL21, Hypothesis 6.6]. Assume Hypothesis 4.11 on the modularity of generating functions of codimension r. In the situation of Theorem 1.5(1), suppose further that
$r[F:\mathbb {Q}]+|\mathtt {S}_\pi |$ odd, for which we assume [Reference Li and LiuLL21, Hypothesis 6.6]. Assume Hypothesis 4.11 on the modularity of generating functions of codimension r. In the situation of Theorem 1.5(1), suppose further that
•
 $\mathtt {R}_\pi =\emptyset $;
$\mathtt {R}_\pi =\emptyset $;•
 $\varphi _1=\varphi _2=\varphi \in \mathcal {V}_\pi ^{[r]\emptyset }$ (see Notation 4.3(G8) for the precise definition of the 1-dimensional space
$\varphi _1=\varphi _2=\varphi \in \mathcal {V}_\pi ^{[r]\emptyset }$ (see Notation 4.3(G8) for the precise definition of the 1-dimensional space  $\mathcal {V}_\pi ^{[r]\emptyset }$ of holomorphic new forms) such that for every
$\mathcal {V}_\pi ^{[r]\emptyset }$ of holomorphic new forms) such that for every  $v\in \mathtt {V}_F$,
$v\in \mathtt {V}_F$,  $\langle \varphi _v^{\mathtt {c}},\varphi _v\rangle _{\pi _v}=1$; and
$\langle \varphi _v^{\mathtt {c}},\varphi _v\rangle _{\pi _v}=1$; and•
 $\phi ^\infty _1=\phi ^\infty _2=\phi ^\infty $ such that for every
$\phi ^\infty _1=\phi ^\infty _2=\phi ^\infty $ such that for every  $v\in \mathtt {V}_F^{\mathrm {fin}}$,
$v\in \mathtt {V}_F^{\mathrm {fin}}$,  .
.
Then the identity
 $$ \begin{align*} \langle\Theta_{\phi^\infty}(\varphi),\Theta_{\phi^\infty}(\varphi)\rangle_{X,E}^\natural=(-1)^r\cdot \frac{L'(\tfrac{1}{2},\pi)}{b_{2r}(0)}\cdot |C_r|^{[F:\mathbb{Q}]} \cdot\prod_{v\in\mathtt{S}_\pi}\frac{q_v^{r-1}(q_v+1)}{(q_v^{2r-1}+1)(q_v^{2r}-1)} \end{align*} $$
$$ \begin{align*} \langle\Theta_{\phi^\infty}(\varphi),\Theta_{\phi^\infty}(\varphi)\rangle_{X,E}^\natural=(-1)^r\cdot \frac{L'(\tfrac{1}{2},\pi)}{b_{2r}(0)}\cdot |C_r|^{[F:\mathbb{Q}]} \cdot\prod_{v\in\mathtt{S}_\pi}\frac{q_v^{r-1}(q_v+1)}{(q_v^{2r-1}+1)(q_v^{2r}-1)} \end{align*} $$holds, where ![]() $q_v$ is the residue cardinality of
$q_v$ is the residue cardinality of ![]() $F_v$.
$F_v$.
Remark 1.8. Assuming the conjecture on the injectivity of the étale Abel–Jacobi map, one can show that the cycle ![]() $\Theta _{\phi ^\infty }(\varphi )$ is a primitive cycle of codimension r. By [Reference BeĭlinsonBeĭ87, Conjecture 5.5], we expect that
$\Theta _{\phi ^\infty }(\varphi )$ is a primitive cycle of codimension r. By [Reference BeĭlinsonBeĭ87, Conjecture 5.5], we expect that  $(-1)^r\langle \Theta _{\phi ^\infty }(\varphi ),\Theta _{\phi ^\infty }(\varphi )\rangle _{X,E}^\natural \geqslant 0$ holds, which, in the situation of Corollary 1.7, is equivalent to
$(-1)^r\langle \Theta _{\phi ^\infty }(\varphi ),\Theta _{\phi ^\infty }(\varphi )\rangle _{X,E}^\natural \geqslant 0$ holds, which, in the situation of Corollary 1.7, is equivalent to  $L'(\tfrac {1}{2},\pi )\geqslant 0$.
$L'(\tfrac {1}{2},\pi )\geqslant 0$.
Remark 1.9. When ![]() $\mathtt {S}_\pi =\emptyset $, Theorem 1.4, Theorem 1.5 and Corollary 1.7 hold without [Reference Li and LiuLL21, Hypothesis 6.6]. See Remark 4.32 for more details.
$\mathtt {S}_\pi =\emptyset $, Theorem 1.4, Theorem 1.5 and Corollary 1.7 hold without [Reference Li and LiuLL21, Hypothesis 6.6]. See Remark 4.32 for more details.
Example 1.10. Suppose that ![]() $E/F$ satisfies the conditions in Assumption 1.3 and that
$E/F$ satisfies the conditions in Assumption 1.3 and that ![]() $r\geqslant 2$. Consider an elliptic curve A over F without complex multiplication, satisfying that
$r\geqslant 2$. Consider an elliptic curve A over F without complex multiplication, satisfying that ![]() $\operatorname {\mathrm {Sym}}^{2r-1}A$ and hence
$\operatorname {\mathrm {Sym}}^{2r-1}A$ and hence ![]() $\operatorname {\mathrm {Sym}}^{2r-1}A_E$ are modular. Let
$\operatorname {\mathrm {Sym}}^{2r-1}A_E$ are modular. Let ![]() $\Pi $ be the cuspidal automorphic representation of
$\Pi $ be the cuspidal automorphic representation of ![]() $\operatorname {\mathrm {GL}}_n(\mathbb {A}_E)$ corresponding to
$\operatorname {\mathrm {GL}}_n(\mathbb {A}_E)$ corresponding to ![]() $\operatorname {\mathrm {Sym}}^{2r-1}A_E$, which satisfies
$\operatorname {\mathrm {Sym}}^{2r-1}A_E$, which satisfies ![]() $\Pi ^\vee \simeq \Pi \circ \mathtt {c}$. Then there exists a cuspidal automorphic representation
$\Pi ^\vee \simeq \Pi \circ \mathtt {c}$. Then there exists a cuspidal automorphic representation ![]() $\pi $ of
$\pi $ of ![]() $G_r(\mathbb {A}_F)$ as in Assumption 1.3 with
$G_r(\mathbb {A}_F)$ as in Assumption 1.3 with ![]() $\Pi $ its base change if and only if A has good reduction at every
$\Pi $ its base change if and only if A has good reduction at every  $v\in \mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {V}_F^{\mathrm {spl}}$.Footnote 4 Moreover, if this is the case, then we have
$v\in \mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {V}_F^{\mathrm {spl}}$.Footnote 4 Moreover, if this is the case, then we have ![]() $\mathtt {S}_\pi =\emptyset $; hence,
$\mathtt {S}_\pi =\emptyset $; hence, ![]() $\varepsilon (\pi )=(-1)^{r[F:\mathbb {Q}]}$. In particular, the above results apply when both r and
$\varepsilon (\pi )=(-1)^{r[F:\mathbb {Q}]}$. In particular, the above results apply when both r and ![]() $[F:\mathbb {Q}]$ are odd.
$[F:\mathbb {Q}]$ are odd.
1.2 Two new ingredients
The proofs of our main theorems follow the same line in [Reference Li and LiuLL21], with two new (main) ingredients, responsible for the two improvements we mentioned at the beginning.
The first new ingredient is formulating and proving an analogue of the Kudla–Rapoport conjecture in the case where ![]() $E/F$ is ramified and the level structure is the one that gives the exotic smooth model (see Subsection 2.1). Here, F is a p-adic field with p odd. Let
$E/F$ is ramified and the level structure is the one that gives the exotic smooth model (see Subsection 2.1). Here, F is a p-adic field with p odd. Let ![]() $\boldsymbol {L}$ be an
$\boldsymbol {L}$ be an ![]() $O_E$-lattice of a nonsplit (nondegenerate) hermitian space
$O_E$-lattice of a nonsplit (nondegenerate) hermitian space ![]() $\boldsymbol {V}$ over E of (even) rank n. Then one can associate an intersection number
$\boldsymbol {V}$ over E of (even) rank n. Then one can associate an intersection number ![]() $\mathrm {Int}(\boldsymbol {L})$ of special divisors on a formally smooth relative Rapoport–Zink space classifying quasi-isogenies of certain unitary
$\mathrm {Int}(\boldsymbol {L})$ of special divisors on a formally smooth relative Rapoport–Zink space classifying quasi-isogenies of certain unitary ![]() $O_F$-divisible groups and also the derivative of the representation density function
$O_F$-divisible groups and also the derivative of the representation density function ![]() $\partial \mathrm {Den}(\boldsymbol {L})$ given by
$\partial \mathrm {Den}(\boldsymbol {L})$ given by ![]() $\boldsymbol {L}$. We show in Theorem 2.7 the formula
$\boldsymbol {L}$. We show in Theorem 2.7 the formula
This is parallel to the Kudla–Rapoport conjecture proved in [Reference Li and ZhangLZa], originally stated for the case where ![]() $E/F$ is unramified. The proof follows from the same strategy as in [Reference Li and ZhangLZa], namely, we write
$E/F$ is unramified. The proof follows from the same strategy as in [Reference Li and ZhangLZa], namely, we write ![]() $\boldsymbol {L}=L^\flat +\langle x\rangle $ for a sublattice
$\boldsymbol {L}=L^\flat +\langle x\rangle $ for a sublattice ![]() $L^\flat $ of
$L^\flat $ of ![]() $\boldsymbol {L}$ such that
$\boldsymbol {L}$ such that ![]() $V_{L^\flat } := L^\flat \otimes _{O_F}F$ is nondegenerate and regard x as a variable. Thus, it motivates us to define a function
$V_{L^\flat } := L^\flat \otimes _{O_F}F$ is nondegenerate and regard x as a variable. Thus, it motivates us to define a function ![]() $\mathrm {Int}_{L^\flat }$ on
$\mathrm {Int}_{L^\flat }$ on ![]() $\boldsymbol {V}\setminus V_{L^\flat }$ by the formula
$\boldsymbol {V}\setminus V_{L^\flat }$ by the formula ![]() $\mathrm {Int}_{L^\flat }(x)=\mathrm {Int}(L^\flat +\langle x\rangle )$ and similarly for
$\mathrm {Int}_{L^\flat }(x)=\mathrm {Int}(L^\flat +\langle x\rangle )$ and similarly for ![]() $\partial \mathrm {Den}_{L^\flat }$. For
$\partial \mathrm {Den}_{L^\flat }$. For ![]() $\mathrm {Int}_{L^\flat }$, there is a natural decomposition
$\mathrm {Int}_{L^\flat }$, there is a natural decomposition  $\mathrm {Int}_{L^\flat }=\mathrm {Int}_{L^\flat }^{\mathrm {h}}+\mathrm {Int}_{L^\flat }^{\mathrm {v}}$ according to the horizontal and vertical parts of the special cycle defined by
$\mathrm {Int}_{L^\flat }=\mathrm {Int}_{L^\flat }^{\mathrm {h}}+\mathrm {Int}_{L^\flat }^{\mathrm {v}}$ according to the horizontal and vertical parts of the special cycle defined by ![]() $L^\flat $. In a parallel manner, we have the decomposition
$L^\flat $. In a parallel manner, we have the decomposition  $\partial \mathrm {Den}_{L^\flat }=\partial \mathrm {Den}_{L^\flat }^{\mathrm {h}}+\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$ by simply matching
$\partial \mathrm {Den}_{L^\flat }=\partial \mathrm {Den}_{L^\flat }^{\mathrm {h}}+\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$ by simply matching  $\partial \mathrm {Den}_{L^\flat }^{\mathrm {h}}$ with
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {h}}$ with  $\mathrm {Int}_{L^\flat }^{\mathrm {h}}$. Thus, it suffices to show that
$\mathrm {Int}_{L^\flat }^{\mathrm {h}}$. Thus, it suffices to show that ![]() $\mathrm {Int}_{L^\flat }^{\mathrm {v}}=\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$. By some sophisticated induction argument on
$\mathrm {Int}_{L^\flat }^{\mathrm {v}}=\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$. By some sophisticated induction argument on ![]() $L^\flat $, it suffices to show the following remarkable property for both
$L^\flat $, it suffices to show the following remarkable property for both ![]() $\mathrm {Int}_{L^\flat }^{\mathrm {v}}$ and
$\mathrm {Int}_{L^\flat }^{\mathrm {v}}$ and ![]() $\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$: they extend (uniquely) to compactly supported locally constant functions on
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$: they extend (uniquely) to compactly supported locally constant functions on ![]() $\boldsymbol {V}$, whose Fourier transforms are supported in the set
$\boldsymbol {V}$, whose Fourier transforms are supported in the set ![]() $\{x\in \boldsymbol {V}\mathbin {|} (x,x)_{\boldsymbol {V}}\in O_F\}$. However, there are some new difficulties in our case:
$\{x\in \boldsymbol {V}\mathbin {|} (x,x)_{\boldsymbol {V}}\in O_F\}$. However, there are some new difficulties in our case:
• The isomorphism class of an
 $O_E$-lattice is not determined by its fundamental invariants and there is a parity constraint for the valuation of an
$O_E$-lattice is not determined by its fundamental invariants and there is a parity constraint for the valuation of an  $O_E$-lattice. This will make the induction argument on
$O_E$-lattice. This will make the induction argument on  $L^\flat $ much more complicated than the one in [Reference Li and ZhangLZa] (see Subsection 2.7).
$L^\flat $ much more complicated than the one in [Reference Li and ZhangLZa] (see Subsection 2.7).• The comparison of our relative Rapoport–Zink space to an (absolute) Rapoport–Zink space is not known. This is needed in the p-adic uniformisation of Shimura varieties. We solve this problem when
 $F/\mathbb {Q}_p$ is unramified, which is the reason for us to assume that every prime in
$F/\mathbb {Q}_p$ is unramified, which is the reason for us to assume that every prime in  $\mathtt {V}_F^{\mathrm {ram}}$ is unramified over
$\mathtt {V}_F^{\mathrm {ram}}$ is unramified over  $\mathbb {Q}$ in Assumption 1.3. See Subsection 2.8.
$\mathbb {Q}$ in Assumption 1.3. See Subsection 2.8.• Due to the parity constraint, the computation of
 $\mathrm {Int}_{L^\flat }^{\mathrm {v}}$ can only be reduced to the case where
$\mathrm {Int}_{L^\flat }^{\mathrm {v}}$ can only be reduced to the case where  $n=4$ (rather than
$n=4$ (rather than  $n=3$ in [Reference Li and ZhangLZa]). After that, we have to compute certain intersection multiplicity, for which we use a new argument based on the linear invariance of the K-theoretic intersection of special divisors. See Lemma 2.55.
$n=3$ in [Reference Li and ZhangLZa]). After that, we have to compute certain intersection multiplicity, for which we use a new argument based on the linear invariance of the K-theoretic intersection of special divisors. See Lemma 2.55.
Here come three more remarks:
• First, we need to extend the result of [Reference Cho and YamauchiCY20] on a counting formula for
 $\partial \mathrm {Den}(\boldsymbol {L})$ to hermitian spaces over a ramified extension
$\partial \mathrm {Den}(\boldsymbol {L})$ to hermitian spaces over a ramified extension  $E/F$ (Lemma 2.19).
$E/F$ (Lemma 2.19).• Second, we have found a simpler argument for the properties of
 $\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$ (Proposition 2.22) which does not use any functional equation or induction formula. This argument is applicable to [Reference Li and ZhangLZa] to give a new proof of the main result on the analytic side there. Also note that we prove the vanishing property in Proposition 2.22 directly, while in [Reference Li and ZhangLZa] it is only deduced after proving
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$ (Proposition 2.22) which does not use any functional equation or induction formula. This argument is applicable to [Reference Li and ZhangLZa] to give a new proof of the main result on the analytic side there. Also note that we prove the vanishing property in Proposition 2.22 directly, while in [Reference Li and ZhangLZa] it is only deduced after proving  $\mathrm {Int}_{L^\flat }^{\mathrm {v}}=\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$.Footnote 5
$\mathrm {Int}_{L^\flat }^{\mathrm {v}}=\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$.Footnote 5• Finally, unlike the case in [Reference Li and ZhangLZa], the parity of the dimension of the hermitian space plays a crucial role in the exotic smooth case. In particular, we will not study the case where
 $\boldsymbol {V}$ has odd dimension.
$\boldsymbol {V}$ has odd dimension.
The second new ingredient is a vanishing result on certain cohomology of integral models of unitary Shimura varieties with Drinfeld level structures. For  $v\in \mathtt {V}_F^{\mathrm {spl}}\cap \mathtt {V}_F^\heartsuit $ with p the underlying rational prime, we have a tower of integral models
$v\in \mathtt {V}_F^{\mathrm {spl}}\cap \mathtt {V}_F^\heartsuit $ with p the underlying rational prime, we have a tower of integral models ![]() $\{\mathcal {X}_m\}_{m\geqslant 0}$ defined by Drinfeld level structures (at v), with an action by
$\{\mathcal {X}_m\}_{m\geqslant 0}$ defined by Drinfeld level structures (at v), with an action by  $\mathbb {T}^{\mathtt {R}\cup \mathtt {V}_F^{(p)}}_{\mathbb {Q}^{\mathrm {ac}}}$ via Hecke correspondences. We show in Theorem 4.21 that
$\mathbb {T}^{\mathtt {R}\cup \mathtt {V}_F^{(p)}}_{\mathbb {Q}^{\mathrm {ac}}}$ via Hecke correspondences. We show in Theorem 4.21 that
with ![]() $\ell \neq p$ and
$\ell \neq p$ and  $\mathfrak {m} := \mathfrak {m}_\pi ^{\mathtt {R}}\cap \mathbb {S}^{\mathtt {R}\cup \mathtt {V}_F^{(p)}}_{\mathbb {Q}^{\mathrm {ac}}}$, where
$\mathfrak {m} := \mathfrak {m}_\pi ^{\mathtt {R}}\cap \mathbb {S}^{\mathtt {R}\cup \mathtt {V}_F^{(p)}}_{\mathbb {Q}^{\mathrm {ac}}}$, where  $\mathbb {S}^{\mathtt {R}\cup \mathtt {V}_F^{(p)}}_{\mathbb {Q}^{\mathrm {ac}}}$ is the subalgebra of
$\mathbb {S}^{\mathtt {R}\cup \mathtt {V}_F^{(p)}}_{\mathbb {Q}^{\mathrm {ac}}}$ is the subalgebra of  $\mathbb {T}^{\mathtt {R}\cup \mathtt {V}_F^{(p)}}_{\mathbb {Q}^{\mathrm {ac}}}$ consisting of those supported at split places. We reduce this vanishing property to some other vanishing properties for cohomology of Newton strata of
$\mathbb {T}^{\mathtt {R}\cup \mathtt {V}_F^{(p)}}_{\mathbb {Q}^{\mathrm {ac}}}$ consisting of those supported at split places. We reduce this vanishing property to some other vanishing properties for cohomology of Newton strata of ![]() $\mathcal {X}_m$, by using a key result of Mantovan [Reference MantovanMan08] saying that the closure of every refined Newton stratum is smooth. For the vanishing properties for Newton strata, we generalise an argument of [Reference Taylor and YoshidaTY07, Proposition 4.4]. However, since in our case the representation
$\mathcal {X}_m$, by using a key result of Mantovan [Reference MantovanMan08] saying that the closure of every refined Newton stratum is smooth. For the vanishing properties for Newton strata, we generalise an argument of [Reference Taylor and YoshidaTY07, Proposition 4.4]. However, since in our case the representation ![]() $\pi _v$ has arbitrary level and our group has nontrivial endoscopy, we need a more sophisticated trace formula, which was provided in [Reference Caraiani and ScholzeCS17].
$\pi _v$ has arbitrary level and our group has nontrivial endoscopy, we need a more sophisticated trace formula, which was provided in [Reference Caraiani and ScholzeCS17].
1.3 Notation and conventions
• When we have a function f on a product set
 $A_1\times \cdots \times A_m$, we will write
$A_1\times \cdots \times A_m$, we will write  $f(a_1,\dots ,a_m)$ instead of
$f(a_1,\dots ,a_m)$ instead of  $f((a_1,\dots ,a_m))$ for its value at an element
$f((a_1,\dots ,a_m))$ for its value at an element  $(a_1,\dots ,a_m)\in A_1\times \cdots \times A_m$.
$(a_1,\dots ,a_m)\in A_1\times \cdots \times A_m$.• For a set S, we denote by
 the characteristic function of S.
the characteristic function of S.• All rings are commutative and unital, and ring homomorphisms preserve units. However, we use the word algebra in the general sense, which is not necessarily commutative or unital.
• For a (formal) subscheme Z of a (formal) scheme X, we denote by
 $\mathscr {I}_Z$ the ideal sheaf of Z, which is a subsheaf of the structure sheaf
$\mathscr {I}_Z$ the ideal sheaf of Z, which is a subsheaf of the structure sheaf  $\mathscr {O}_X$ of X.
$\mathscr {O}_X$ of X.• For a ring R, we denote by
 $\operatorname {\mathrm {Sch}}_{/R}$ the category of schemes over R, by
$\operatorname {\mathrm {Sch}}_{/R}$ the category of schemes over R, by  $\operatorname {\mathrm {Sch}}^{\prime }_{/R}$ the subcategory of locally Noetherian schemes over R. When R is discretely valued, we also denote by
$\operatorname {\mathrm {Sch}}^{\prime }_{/R}$ the subcategory of locally Noetherian schemes over R. When R is discretely valued, we also denote by  $\operatorname {\mathrm {Sch}}_{/R}^{\mathrm {v}}$ the subcategory of schemes over R on which uniformisers of R are locally nilpotent.
$\operatorname {\mathrm {Sch}}_{/R}^{\mathrm {v}}$ the subcategory of schemes over R on which uniformisers of R are locally nilpotent.• If a base ring is not specified in the tensor operation
 $\otimes $, then it is
$\otimes $, then it is  $\mathbb {Z}$.
$\mathbb {Z}$.• For an abelian group A and a ring R, we put
 $A_R := A\otimes R$.
$A_R := A\otimes R$.• For an integer
 $m\geqslant 0$, we denote by
$m\geqslant 0$, we denote by  $0_m$ and
$0_m$ and  $1_m$ the null and identity matrices of rank m, respectively. We also denote by
$1_m$ the null and identity matrices of rank m, respectively. We also denote by  $\mathtt {w}_m$ the matrix
$\mathtt {w}_m$ the matrix  $\left (\begin {smallmatrix}&1_m\\ -1_m &\end {smallmatrix}\right )$.
$\left (\begin {smallmatrix}&1_m\\ -1_m &\end {smallmatrix}\right )$.• We denote by
 $\mathtt {c}\colon \mathbb {C}\to \mathbb {C}$ the complex conjugation. For an element x in a complex space with a default underlying real structure, we denote by
$\mathtt {c}\colon \mathbb {C}\to \mathbb {C}$ the complex conjugation. For an element x in a complex space with a default underlying real structure, we denote by  $x^{\mathtt {c}}$ its complex conjugation.
$x^{\mathtt {c}}$ its complex conjugation.• For a field K, we denote by
 $\overline {K}$ the abstract algebraic closure of K. However, for aesthetic reasons, we will write
$\overline {K}$ the abstract algebraic closure of K. However, for aesthetic reasons, we will write  $\overline {\mathbb {Q}}_p$ instead of
$\overline {\mathbb {Q}}_p$ instead of  $\overline {\mathbb {Q}_p}$ and will denote by
$\overline {\mathbb {Q}_p}$ and will denote by  $\overline {\mathbb {F}}_p$ its residue field. On the other hand, we denote by
$\overline {\mathbb {F}}_p$ its residue field. On the other hand, we denote by  $\mathbb {Q}^{\mathrm {ac}}$ the algebraic closure of
$\mathbb {Q}^{\mathrm {ac}}$ the algebraic closure of  $\mathbb {Q}$ inside
$\mathbb {Q}$ inside  $\mathbb {C}$.
$\mathbb {C}$.• For a number field K, we denote by
 $\psi _K\colon K\backslash \mathbb {A}_K\to \mathbb {C}^\times $ the standard additive character, namely,
$\psi _K\colon K\backslash \mathbb {A}_K\to \mathbb {C}^\times $ the standard additive character, namely,  $\psi _K := \psi _{\mathbb {Q}}\circ \operatorname {\mathrm {Tr}}_{K/\mathbb {Q}}$ in which
$\psi _K := \psi _{\mathbb {Q}}\circ \operatorname {\mathrm {Tr}}_{K/\mathbb {Q}}$ in which  $\psi _{\mathbb {Q}}\colon \mathbb {Q}\backslash \mathbb {A}\to \mathbb {C}^\times $ is the unique character such that
$\psi _{\mathbb {Q}}\colon \mathbb {Q}\backslash \mathbb {A}\to \mathbb {C}^\times $ is the unique character such that  $\psi _{\mathbb {Q},\infty }(x)=\mathrm {e}^{2\pi ix}$.
$\psi _{\mathbb {Q},\infty }(x)=\mathrm {e}^{2\pi ix}$.• Throughout the entire article, all parabolic inductions are unitarily normalised.
2 Intersection of special cycles at ramified places
Throughout this section, we fix a ramified quadratic extension ![]() $E/F$ of p-adic fields with p odd, with
$E/F$ of p-adic fields with p odd, with ![]() $\mathtt {c}\in \operatorname {\mathrm {Gal}}(E/F)$ the Galois involution. We fix a uniformiser
$\mathtt {c}\in \operatorname {\mathrm {Gal}}(E/F)$ the Galois involution. We fix a uniformiser ![]() $u\in E$ satisfying
$u\in E$ satisfying ![]() $u^{\mathtt {c}}=-u$. Let k be the residue field of F and denote by q the cardinality of k. Let
$u^{\mathtt {c}}=-u$. Let k be the residue field of F and denote by q the cardinality of k. Let ![]() $n=2r$ be an even positive integer.
$n=2r$ be an even positive integer.
In Subsection 2.1, we introduce our relative Rapoport–Zink space and state the main theorem (Theorem 2.7) on the relation between intersection numbers and derivatives of representation densities. In Subsection 2.2, we study derivatives of representation densities. In Subsection 2.3, we recall the Bruhat–Tits stratification on the relative Rapoport–Zink space from [Reference WuWu] and deduce some consequences. In Subsection 2.4, we prove the linear invariance on the K-theoretic intersection of special divisors, following [Reference HowardHow19]. In Subsection 2.5, we prove Theorem 2.7 when ![]() $r=1$, which is needed for the proof when
$r=1$, which is needed for the proof when ![]() $r>1$. In Subsection 2.6, we study intersection numbers. In Subsection 2.7, we prove Theorem 2.7 for general r. In Subsection 2.8, we compare our relative Rapoport–Zink space to certain (absolute) Rapoport–Zink space assuming
$r>1$. In Subsection 2.6, we study intersection numbers. In Subsection 2.7, we prove Theorem 2.7 for general r. In Subsection 2.8, we compare our relative Rapoport–Zink space to certain (absolute) Rapoport–Zink space assuming ![]() $F/\mathbb {Q}_p$ is unramified.
$F/\mathbb {Q}_p$ is unramified.
Here are two preliminary definitions for this section:
• A hermitian
 $O_E$-module is a finitely generated free
$O_E$-module is a finitely generated free  $O_E$-module L together with an
$O_E$-module L together with an  $O_F$-bilinear pairing
$O_F$-bilinear pairing  $(\,,\,)_L\colon L\times L\to E$ such that the induced E-valued pairing on
$(\,,\,)_L\colon L\times L\to E$ such that the induced E-valued pairing on  $L\otimes _{O_F}F$ is a nondegenerate hermitian pairing (with respect to
$L\otimes _{O_F}F$ is a nondegenerate hermitian pairing (with respect to  $\mathtt {c}$). When we say that a hermitian
$\mathtt {c}$). When we say that a hermitian  $O_E$-module L is contained in a hermitian
$O_E$-module L is contained in a hermitian  $O_E$-module or a hermitian E-space M, we require that the restriction of the pairing
$O_E$-module or a hermitian E-space M, we require that the restriction of the pairing  $(\,,\,)_M$ to L coincides with
$(\,,\,)_M$ to L coincides with  $(\,,\,)_L$.
$(\,,\,)_L$.• Let X be an object of an additive category with a notion of dual.
– We say that a morphism
 $\sigma _X\colon X\to X^\vee $ is a symmetrisation if
$\sigma _X\colon X\to X^\vee $ is a symmetrisation if  $\sigma _X$ is an isomorphism and the composite morphism
$\sigma _X$ is an isomorphism and the composite morphism  $X\to X^{\vee \vee }\xrightarrow {\sigma _X^\vee }X^\vee $ coincides with
$X\to X^{\vee \vee }\xrightarrow {\sigma _X^\vee }X^\vee $ coincides with  $\sigma _X$.
$\sigma _X$.– Given an action
 $\iota _X\colon O_E\to \operatorname {\mathrm {End}}(X)$, we say that a morphism
$\iota _X\colon O_E\to \operatorname {\mathrm {End}}(X)$, we say that a morphism  $\lambda _X\colon X\to X^\vee $ is
$\lambda _X\colon X\to X^\vee $ is  $\iota _X$-compatible if
$\iota _X$-compatible if  $\lambda _X\circ \iota _X(\alpha )=\iota _X(\alpha ^{\mathtt {c}})^\vee \circ \lambda _X$ holds for every
$\lambda _X\circ \iota _X(\alpha )=\iota _X(\alpha ^{\mathtt {c}})^\vee \circ \lambda _X$ holds for every  $\alpha \in O_E$.
$\alpha \in O_E$.
2.1 A Kudla–Rapoport type formula
We fix an embedding ![]() $\varphi _0\colon E\to \mathbb {C}_p$ and let
$\varphi _0\colon E\to \mathbb {C}_p$ and let ![]() $\breve {E}$ be the maximal complete unramified extension of
$\breve {E}$ be the maximal complete unramified extension of ![]() $\varphi _0(E)$ in
$\varphi _0(E)$ in ![]() $\mathbb {C}_p$. We regard E as a subfield of
$\mathbb {C}_p$. We regard E as a subfield of ![]() $\breve {E}$ via
$\breve {E}$ via ![]() $\varphi _0$ and hence identify the residue field of
$\varphi _0$ and hence identify the residue field of ![]() $\breve {E}$ with an algebraic closure
$\breve {E}$ with an algebraic closure ![]() $\overline {k}$ of k.
$\overline {k}$ of k.
Definition 2.1. Let S be an object of ![]() $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}$. We define a category
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}$. We define a category ![]() $\mathrm {Exo}_{(n-1,1)}(S)$ whose objects are triples
$\mathrm {Exo}_{(n-1,1)}(S)$ whose objects are triples ![]() $(X,\iota _X,\lambda _X)$ in which
$(X,\iota _X,\lambda _X)$ in which
• X is an
 $O_F$-divisible groupFootnote 6 over S of dimension
$O_F$-divisible groupFootnote 6 over S of dimension  $n=2r$ and (relative) height
$n=2r$ and (relative) height  $2n$;
$2n$;•
 $\iota _X\colon O_E\to \operatorname {\mathrm {End}}(X)$ is an action of
$\iota _X\colon O_E\to \operatorname {\mathrm {End}}(X)$ is an action of  $O_E$ on X satisfying:
$O_E$ on X satisfying:– (Kottwitz condition): the characteristic polynomial of
 $\iota _X(u)$ on the locally free
$\iota _X(u)$ on the locally free  $\mathscr {O}_S$-module
$\mathscr {O}_S$-module  $\operatorname {\mathrm {Lie}}(X)$ is
$\operatorname {\mathrm {Lie}}(X)$ is  $(T-u)^{n-1}(T+u)\in \mathscr {O}_S[T]$,
$(T-u)^{n-1}(T+u)\in \mathscr {O}_S[T]$,– (Wedge condition): we have
 $$ \begin{align*} \bigwedge^2\left(\iota_X(u)-u\mathbin{|}\operatorname{\mathrm{Lie}}(X)\right)&=0, \end{align*} $$
$$ \begin{align*} \bigwedge^2\left(\iota_X(u)-u\mathbin{|}\operatorname{\mathrm{Lie}}(X)\right)&=0, \end{align*} $$– (Spin condition): for every geometric point s of S, the action of
 $\iota _X(u)$ on
$\iota _X(u)$ on  $\operatorname {\mathrm {Lie}}(X_s)$ is nonzero;
$\operatorname {\mathrm {Lie}}(X_s)$ is nonzero;
•
 $\lambda _X\colon X\to X^\vee $ is a
$\lambda _X\colon X\to X^\vee $ is a  $\iota _X$-compatible polarisation such that
$\iota _X$-compatible polarisation such that  $\operatorname {\mathrm {ker}}(\lambda _X)=X[\iota _X(u)]$.
$\operatorname {\mathrm {ker}}(\lambda _X)=X[\iota _X(u)]$.
A morphism (respectively quasi-morphism) from ![]() $(X,\iota _X,\lambda _X)$ to
$(X,\iota _X,\lambda _X)$ to ![]() $(Y,\iota _Y,\lambda _Y)$ is an
$(Y,\iota _Y,\lambda _Y)$ is an ![]() $O_E$-linear isomorphism (respectively quasi-isogeny)
$O_E$-linear isomorphism (respectively quasi-isogeny) ![]() $\rho \colon X\to Y$ of height zero such that
$\rho \colon X\to Y$ of height zero such that ![]() $\rho ^*\lambda _Y=\lambda _X$.
$\rho ^*\lambda _Y=\lambda _X$.
When S belongs to  $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$, we denote by
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$, we denote by  $\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}(S)$ the subcategory of
$\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}(S)$ the subcategory of ![]() $\mathrm {Exo}_{(n-1,1)}(S)$ consisting of
$\mathrm {Exo}_{(n-1,1)}(S)$ consisting of ![]() $(X,\iota _X,\lambda _X)$ in which X is supersingular.Footnote 7
$(X,\iota _X,\lambda _X)$ in which X is supersingular.Footnote 7
Remark 2.2. Giving a ![]() $\iota _X$-compatible polarisation
$\iota _X$-compatible polarisation ![]() $\lambda _X$ of X satisfying
$\lambda _X$ of X satisfying ![]() $\operatorname {\mathrm {ker}}(\lambda _X)=X[\iota _X(u)]$ is equivalent to giving a
$\operatorname {\mathrm {ker}}(\lambda _X)=X[\iota _X(u)]$ is equivalent to giving a ![]() $\iota _X$-compatible symmetrisation
$\iota _X$-compatible symmetrisation ![]() $\sigma _X$ of X. In fact, since
$\sigma _X$ of X. In fact, since ![]() $\operatorname {\mathrm {ker}}(\lambda _X)=X[\iota _X(u)]$, there is a unique morphism
$\operatorname {\mathrm {ker}}(\lambda _X)=X[\iota _X(u)]$, there is a unique morphism ![]() $\sigma _X\colon X\to X^\vee $ satisfying
$\sigma _X\colon X\to X^\vee $ satisfying ![]() $\lambda _X=\sigma _X\circ \iota _X(u)$, which is, in fact, an isomorphism satisfying
$\lambda _X=\sigma _X\circ \iota _X(u)$, which is, in fact, an isomorphism satisfying
 $$ \begin{align*} \sigma_X^\vee=\iota_X(u^{-1})^\vee\circ\lambda_X^\vee=-\iota_X(u^{-1})^\vee\circ\lambda_X =-\lambda_X\circ\iota_X(u^{-1,\mathtt{c}})=\lambda_X\circ\iota_X(u^{-1})=\sigma_X \end{align*} $$
$$ \begin{align*} \sigma_X^\vee=\iota_X(u^{-1})^\vee\circ\lambda_X^\vee=-\iota_X(u^{-1})^\vee\circ\lambda_X =-\lambda_X\circ\iota_X(u^{-1,\mathtt{c}})=\lambda_X\circ\iota_X(u^{-1})=\sigma_X \end{align*} $$and is clearly ![]() $\iota _X$-compatible. Conversely, given a
$\iota _X$-compatible. Conversely, given a ![]() $\iota _X$-compatible symmetrisation
$\iota _X$-compatible symmetrisation ![]() $\sigma _X$ of X, we may recover
$\sigma _X$ of X, we may recover ![]() $\lambda _X$ as
$\lambda _X$ as ![]() $\sigma _X\circ \iota _X(u)$. In what follows, we call
$\sigma _X\circ \iota _X(u)$. In what follows, we call ![]() $\sigma _X$ the symmetrisation of
$\sigma _X$ the symmetrisation of ![]() $\lambda _X$.
$\lambda _X$.
To define our relative Rapoport–Zink space, we fix an object
 $$ \begin{align*} (\boldsymbol{X},\iota_{\boldsymbol{X}},\lambda_{\boldsymbol{X}})\in\mathrm{Exo}_{(n-1,1)}^{\mathrm{b}}(\overline{k}). \end{align*} $$
$$ \begin{align*} (\boldsymbol{X},\iota_{\boldsymbol{X}},\lambda_{\boldsymbol{X}})\in\mathrm{Exo}_{(n-1,1)}^{\mathrm{b}}(\overline{k}). \end{align*} $$Definition 2.3. We define a functor ![]() $\mathcal {N} := \mathcal {N}_{(\boldsymbol {X},\iota _{\boldsymbol {X}},\lambda _{\boldsymbol {X}})}$ on
$\mathcal {N} := \mathcal {N}_{(\boldsymbol {X},\iota _{\boldsymbol {X}},\lambda _{\boldsymbol {X}})}$ on  $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$ such that for every object S of
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$ such that for every object S of  $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$,
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$, ![]() $\mathcal {N}(S)$ consists of quadruples
$\mathcal {N}(S)$ consists of quadruples ![]() $(X,\iota _X,\lambda _X;\rho _X)$ in which
$(X,\iota _X,\lambda _X;\rho _X)$ in which
•
 $(X,\iota _X,\lambda _X)$ is an object of
$(X,\iota _X,\lambda _X)$ is an object of  $\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}(S)$;
$\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}(S)$;•
 $\rho _X$ is a quasi-morphism from
$\rho _X$ is a quasi-morphism from  $(X,\iota _X,\lambda _X)\times _S(S\otimes _{O_{\breve {E}}}\overline {k})$ to
$(X,\iota _X,\lambda _X)\times _S(S\otimes _{O_{\breve {E}}}\overline {k})$ to  $(\boldsymbol {X},\iota _{\boldsymbol {X}},\lambda _{\boldsymbol {X}})\otimes _{\overline {k}}(S\otimes _{O_{\breve {E}}}\overline {k})$ in the category
$(\boldsymbol {X},\iota _{\boldsymbol {X}},\lambda _{\boldsymbol {X}})\otimes _{\overline {k}}(S\otimes _{O_{\breve {E}}}\overline {k})$ in the category  $\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}(S\otimes _{O_{\breve {E}}}\overline {k})$.
$\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}(S\otimes _{O_{\breve {E}}}\overline {k})$.
Lemma 2.4. The functor ![]() $\mathcal {N}$ is a separated formal scheme formally smooth over
$\mathcal {N}$ is a separated formal scheme formally smooth over ![]() $\operatorname {\mathrm {Spf}} O_{\breve {E}}$ of relative dimension
$\operatorname {\mathrm {Spf}} O_{\breve {E}}$ of relative dimension ![]() $n-1$. Moreover,
$n-1$. Moreover, ![]() $\mathcal {N}$ has two connected components.
$\mathcal {N}$ has two connected components.
Proof. It follows from [Reference Rapoport, Smithling and ZhangRZ96] that ![]() $\mathcal {N}$ is a separated formal scheme over
$\mathcal {N}$ is a separated formal scheme over ![]() $\operatorname {\mathrm {Spf}} O_{\breve {E}}$. The formal smoothness of
$\operatorname {\mathrm {Spf}} O_{\breve {E}}$. The formal smoothness of ![]() $\mathcal {N}$ follow from the smoothness of its local model, which is [Reference Rapoport, Smithling and ZhangRSZ17, Proposition 3.10], and the dimension also follows. For the last assertion, our moduli functor
$\mathcal {N}$ follow from the smoothness of its local model, which is [Reference Rapoport, Smithling and ZhangRSZ17, Proposition 3.10], and the dimension also follows. For the last assertion, our moduli functor ![]() $\mathcal {N}$ is the disjoint union of
$\mathcal {N}$ is the disjoint union of ![]() $\mathcal {N}_{(0,0)}$ and
$\mathcal {N}_{(0,0)}$ and ![]() $\mathcal {N}_{(0,1)}$ from [Reference WuWu, Section 3.4], each of which is connected by [Reference WuWu, Theorem 5.18(2)].Footnote 8
$\mathcal {N}_{(0,1)}$ from [Reference WuWu, Section 3.4], each of which is connected by [Reference WuWu, Theorem 5.18(2)].Footnote 8
To study special cycles on ![]() $\mathcal {N}$, we fix a triple
$\mathcal {N}$, we fix a triple ![]() $(X_0,\iota _{X_0},\lambda _{X_0})$ where
$(X_0,\iota _{X_0},\lambda _{X_0})$ where
•
 $X_0$ is a supersingular
$X_0$ is a supersingular  $O_F$-divisible group over
$O_F$-divisible group over  $\operatorname {\mathrm {Spec}} O_{\breve {E}}$ of dimension
$\operatorname {\mathrm {Spec}} O_{\breve {E}}$ of dimension  $1$ and height
$1$ and height  $2$;
$2$;•
 $\iota _{X_0}\colon O_E\to \operatorname {\mathrm {End}}(X_0)$ is an
$\iota _{X_0}\colon O_E\to \operatorname {\mathrm {End}}(X_0)$ is an  $O_E$-action on
$O_E$-action on  $X_0$ such that the induced action on
$X_0$ such that the induced action on  $\operatorname {\mathrm {Lie}}(X_0)$ is given by
$\operatorname {\mathrm {Lie}}(X_0)$ is given by  $\varphi _0$;
$\varphi _0$;•
 $\lambda _{X_0}\colon X_0\to X_0^\vee $ is a
$\lambda _{X_0}\colon X_0\to X_0^\vee $ is a  $\iota _{X_0}$-compatible principal polarisation.
$\iota _{X_0}$-compatible principal polarisation.
Note that ![]() $\iota _{X_0}$ induces an isomorphism
$\iota _{X_0}$ induces an isomorphism  $\iota _{X_0}\colon O_E\xrightarrow {\sim }\operatorname {\mathrm {End}}_{O_E}(X_0)$. Put
$\iota _{X_0}\colon O_E\xrightarrow {\sim }\operatorname {\mathrm {End}}_{O_E}(X_0)$. Put
 $$ \begin{align*} \boldsymbol{V} := \operatorname{\mathrm{Hom}}_{O_E}(X_0\otimes_{O_{\breve{E}}}\overline{k},\boldsymbol{X})\otimes\mathbb{Q}, \end{align*} $$
$$ \begin{align*} \boldsymbol{V} := \operatorname{\mathrm{Hom}}_{O_E}(X_0\otimes_{O_{\breve{E}}}\overline{k},\boldsymbol{X})\otimes\mathbb{Q}, \end{align*} $$which is a vector space over E of dimension n. We have a pairing
sending ![]() $(x,y)\in \boldsymbol {V}^2$ to the composition of quasi-homomorphisms
$(x,y)\in \boldsymbol {V}^2$ to the composition of quasi-homomorphisms
 $$ \begin{align*} X_0\xrightarrow{x}\boldsymbol{X}\xrightarrow{\lambda_{\boldsymbol{X}}}\boldsymbol{X}^\vee\xrightarrow{y^\vee}X_0^\vee\xrightarrow{u^{-2}\lambda_{X_0}^{-1}}X_0 \end{align*} $$
$$ \begin{align*} X_0\xrightarrow{x}\boldsymbol{X}\xrightarrow{\lambda_{\boldsymbol{X}}}\boldsymbol{X}^\vee\xrightarrow{y^\vee}X_0^\vee\xrightarrow{u^{-2}\lambda_{X_0}^{-1}}X_0 \end{align*} $$as an element in ![]() $\operatorname {\mathrm {End}}_{O_E}(X_0)\otimes \mathbb {Q}$ and hence in E via
$\operatorname {\mathrm {End}}_{O_E}(X_0)\otimes \mathbb {Q}$ and hence in E via ![]() $\iota _{X_0}^{-1}$. It is known that
$\iota _{X_0}^{-1}$. It is known that ![]() $(\,,\,)_{\boldsymbol {V}}$ is a nondegenerate and nonsplit hermitian form on
$(\,,\,)_{\boldsymbol {V}}$ is a nondegenerate and nonsplit hermitian form on ![]() $\boldsymbol {V}$ [Reference Rapoport, Smithling and ZhangRSZ17, Lemma 3.5].Footnote 9
$\boldsymbol {V}$ [Reference Rapoport, Smithling and ZhangRSZ17, Lemma 3.5].Footnote 9
Definition 2.5. For every nonzero element ![]() $x\in \boldsymbol {V}$, we define the special divisor
$x\in \boldsymbol {V}$, we define the special divisor ![]() $\mathcal {N}(x)$ of
$\mathcal {N}(x)$ of ![]() $\mathcal {N}$ to be the maximal closed formal subscheme over which the quasi-homomorphism
$\mathcal {N}$ to be the maximal closed formal subscheme over which the quasi-homomorphism
 $$ \begin{align*} \rho_X^{-1}\circ x\colon(X_0\otimes_{O_{\breve{E}}}\overline{k})\otimes_k(S\otimes_{O_{\breve{E}}}\overline{k})\to X\times_S(S\otimes_{O_{\breve{E}}}\overline{k}) \end{align*} $$
$$ \begin{align*} \rho_X^{-1}\circ x\colon(X_0\otimes_{O_{\breve{E}}}\overline{k})\otimes_k(S\otimes_{O_{\breve{E}}}\overline{k})\to X\times_S(S\otimes_{O_{\breve{E}}}\overline{k}) \end{align*} $$lifts (uniquely) to a homomorphism ![]() $X_0\otimes _{O_{\breve {E}}}S\to X$.
$X_0\otimes _{O_{\breve {E}}}S\to X$.
Definition 2.6. For an ![]() $O_E$-lattice
$O_E$-lattice ![]() $\boldsymbol {L}$ of
$\boldsymbol {L}$ of ![]() $\boldsymbol {V}$, the Serre intersection multiplicity
$\boldsymbol {V}$, the Serre intersection multiplicity
 $$ \begin{align*} \chi\left(\mathscr{O}_{\mathcal{N}(x_1)}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\cdots\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x_n)}\right) \end{align*} $$
$$ \begin{align*} \chi\left(\mathscr{O}_{\mathcal{N}(x_1)}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\cdots\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x_n)}\right) \end{align*} $$does not depend on the choice of a basis ![]() $\{x_1,\dots ,x_n\}$ of
$\{x_1,\dots ,x_n\}$ of ![]() $\boldsymbol {L}$ by Corollary 2.35, which we define to be
$\boldsymbol {L}$ by Corollary 2.35, which we define to be ![]() $\mathrm {Int}(\boldsymbol {L})$.
$\mathrm {Int}(\boldsymbol {L})$.
Theorem 2.7. For every ![]() $O_E$-lattice
$O_E$-lattice ![]() $\boldsymbol {L}$ of
$\boldsymbol {L}$ of ![]() $\boldsymbol {V}$, we have
$\boldsymbol {V}$, we have
where ![]() $\partial \mathrm {Den}(\boldsymbol {L})$ is defined in Definition 2.16.
$\partial \mathrm {Den}(\boldsymbol {L})$ is defined in Definition 2.16.
The strategy of proving this theorem described in Subsection 1.2 motivates the following definition, which will be frequently used in the rest of Section 2.
Definition 2.8. We define ![]() $\flat (\boldsymbol {V})$ to be the set of hermitian
$\flat (\boldsymbol {V})$ to be the set of hermitian ![]() $O_E$-modules contained in
$O_E$-modules contained in ![]() $\boldsymbol {V}$ of rank
$\boldsymbol {V}$ of rank ![]() $n-1$. In what follows, for
$n-1$. In what follows, for ![]() $L^\flat \in \flat (\boldsymbol {V})$, we put
$L^\flat \in \flat (\boldsymbol {V})$, we put ![]() $V_{L^\flat } := L^\flat \otimes _{O_F}F$ and write
$V_{L^\flat } := L^\flat \otimes _{O_F}F$ and write  $V_{L^\flat }^\perp $ for the orthogonal complement of
$V_{L^\flat }^\perp $ for the orthogonal complement of ![]() $V_{L^\flat }$ in
$V_{L^\flat }$ in ![]() $\boldsymbol {V}$.
$\boldsymbol {V}$.
Remark 2.9. Let S be an object of ![]() $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}$. We have another category
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}$. We have another category ![]() $\mathrm {Exo}_{(n,0)}(S)$ whose objects are triples
$\mathrm {Exo}_{(n,0)}(S)$ whose objects are triples ![]() $(X,\iota _X,\lambda _X)$ in which
$(X,\iota _X,\lambda _X)$ in which
• X is an
 $O_F$-divisible group over S of dimension
$O_F$-divisible group over S of dimension  $n=2r$ and (relative) height
$n=2r$ and (relative) height  $2n$;
$2n$;•
 $\iota _X\colon O_E\to \operatorname {\mathrm {End}}(X)$ is an action of
$\iota _X\colon O_E\to \operatorname {\mathrm {End}}(X)$ is an action of  $O_E$ on X such that
$O_E$ on X such that  $\iota _X(u)-u$ annihilates
$\iota _X(u)-u$ annihilates  $\operatorname {\mathrm {Lie}}(X)$;
$\operatorname {\mathrm {Lie}}(X)$;•
 $\lambda _X\colon X\to X^\vee $ is a
$\lambda _X\colon X\to X^\vee $ is a  $\iota _X$-compatible polarisation such that
$\iota _X$-compatible polarisation such that  $\operatorname {\mathrm {ker}}(\lambda _X)=X[\iota _X(u)]$.
$\operatorname {\mathrm {ker}}(\lambda _X)=X[\iota _X(u)]$.
Morphisms are defined similarly as in Definition 2.1.
For later use, we fix a nontrivial additive character ![]() $\psi _F\colon F\to \mathbb {C}^\times $ of conductor
$\psi _F\colon F\to \mathbb {C}^\times $ of conductor ![]() $O_F$. For a locally constant compactly supported function
$O_F$. For a locally constant compactly supported function ![]() $\phi $ on a hermitian space V over E, its Fourier transform
$\phi $ on a hermitian space V over E, its Fourier transform ![]() $\widehat \phi $ is defined by
$\widehat \phi $ is defined by
 $$ \begin{align*} \widehat\phi(x)=\int_V\phi(y)\psi_F(\operatorname{\mathrm{Tr}}_{E/F}(x,y)_V)\,\mathrm{d} y \end{align*} $$
$$ \begin{align*} \widehat\phi(x)=\int_V\phi(y)\psi_F(\operatorname{\mathrm{Tr}}_{E/F}(x,y)_V)\,\mathrm{d} y \end{align*} $$where ![]() $\mathrm {d}y$ is the self-dual Haar measure on V.
$\mathrm {d}y$ is the self-dual Haar measure on V.
2.2 Fourier transform of analytic side
In this subsection, we study local densities of hermitian lattices. We first introduce some notion about ![]() $O_E$-lattices in hermitian spaces.
$O_E$-lattices in hermitian spaces.
Definition 2.10. Let V be a hermitian space over E of dimension m, equipped with the hermitian form ![]() $(\,,\,)_V$.
$(\,,\,)_V$.
(1) For a subset X of V,
• we denote by
 $X^{\mathrm {int}}$ the subset
$X^{\mathrm {int}}$ the subset  $\{x\in X\mathbin {|} (x,x)_V\in O_F\}$;
$\{x\in X\mathbin {|} (x,x)_V\in O_F\}$;• we denote by
 $\langle X\rangle $ the
$\langle X\rangle $ the  $O_E$-submodule of V generated by X; when
$O_E$-submodule of V generated by X; when  $X=\{x,\dots \}$ is explicitly presented, we simply write
$X=\{x,\dots \}$ is explicitly presented, we simply write  $\langle x,\dots \rangle $ instead of
$\langle x,\dots \rangle $ instead of  $\langle \{x,\dots \}\rangle $.
$\langle \{x,\dots \}\rangle $.
(2) For an
 $O_E$-lattice L of V, we put We say that L is
$O_E$-lattice L of V, we put We say that L is $$ \begin{align*} L^\vee := &\ \{x\in V\mathbin{|}\operatorname{\mathrm{Tr}}_{E/F}(x,y)_V\in O_F\text{ for every } y\in L\} \\ =&\ \{x\in V\mathbin{|} (x,y)_V\in u^{-1}O_E\text{ for every } y\in L\}. \end{align*} $$
$$ \begin{align*} L^\vee := &\ \{x\in V\mathbin{|}\operatorname{\mathrm{Tr}}_{E/F}(x,y)_V\in O_F\text{ for every } y\in L\} \\ =&\ \{x\in V\mathbin{|} (x,y)_V\in u^{-1}O_E\text{ for every } y\in L\}. \end{align*} $$• integral if
 $L\subseteq L^\vee $;
$L\subseteq L^\vee $;• vertex if it is integral such that
 $L^\vee /L$ is annihilated by u; and
$L^\vee /L$ is annihilated by u; and• self-dual if
 $L=L^\vee $.
$L=L^\vee $.
(3) For an integral
 $O_E$-lattice L of V, we define
$O_E$-lattice L of V, we define• the fundamental invariants of L unique integers
 $0\leqslant a_1\leqslant \cdots \leqslant a_m$ such that
$0\leqslant a_1\leqslant \cdots \leqslant a_m$ such that  $L^\vee /L\simeq O_E/(u^{a_1})\oplus \cdots \oplus O_E/(u^{a_m})$ as
$L^\vee /L\simeq O_E/(u^{a_1})\oplus \cdots \oplus O_E/(u^{a_m})$ as  $O_E$-modules;
$O_E$-modules;• the type
 $t(L)$ of L to be the number of nonzero elements in its fundamental invariants; and
$t(L)$ of L to be the number of nonzero elements in its fundamental invariants; and• the valuation of L to be
 $\operatorname {\mathrm {val}}(L) := \sum _{i=1}^ma_i$; when L is generated by a single element x, we simply write
$\operatorname {\mathrm {val}}(L) := \sum _{i=1}^ma_i$; when L is generated by a single element x, we simply write  $\operatorname {\mathrm {val}}(x)$ instead of
$\operatorname {\mathrm {val}}(x)$ instead of  $\operatorname {\mathrm {val}}(\langle x\rangle )$.
$\operatorname {\mathrm {val}}(\langle x\rangle )$.
The above notation and definitions make sense without specifying V, namely, they apply to hermitian ![]() $O_E$-modules.
$O_E$-modules.
Definition 2.11. For a hermitian ![]() $O_E$-module L, we say that a basis
$O_E$-module L, we say that a basis ![]() $\{e_1,\dots ,e_m\}$ of L is a normal basis if its moment matrix
$\{e_1,\dots ,e_m\}$ of L is a normal basis if its moment matrix  $T=((e_i,e_j)_L)_{i,j=1}^m$ is conjugate to
$T=((e_i,e_j)_L)_{i,j=1}^m$ is conjugate to
 $$ \begin{align*} \begin{pmatrix} \beta_1 u^{2b_1} \end{pmatrix} \oplus\cdots\oplus \begin{pmatrix} \beta_s u^{2b_s} \end{pmatrix} \oplus \begin{pmatrix} 0 & u^{2c_1-1} \\ -u^{2c_1-1} & 0 \end{pmatrix} \oplus\cdots\oplus \begin{pmatrix} 0 & u^{2c_t-1} \\ -u^{2c_t-1} & 0 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} \beta_1 u^{2b_1} \end{pmatrix} \oplus\cdots\oplus \begin{pmatrix} \beta_s u^{2b_s} \end{pmatrix} \oplus \begin{pmatrix} 0 & u^{2c_1-1} \\ -u^{2c_1-1} & 0 \end{pmatrix} \oplus\cdots\oplus \begin{pmatrix} 0 & u^{2c_t-1} \\ -u^{2c_t-1} & 0 \end{pmatrix} \end{align*} $$by a permutation matrix, for some ![]() $\beta _1,\dots ,\beta _s\in O_F^\times $ and
$\beta _1,\dots ,\beta _s\in O_F^\times $ and ![]() $b_1,\dots ,b_s,c_1,\dots ,c_t\in \mathbb {Z}$.
$b_1,\dots ,b_s,c_1,\dots ,c_t\in \mathbb {Z}$.
Lemma 2.12. In the above definition, we have
(1) normal basis exists;
(2) the invariants
 $s,t$ and
$s,t$ and  $b_1,\dots ,b_s,c_1,\dots ,c_t$ depend only on L;
$b_1,\dots ,b_s,c_1,\dots ,c_t$ depend only on L;(3) when L is integral, the fundamental invariants of L are the unique nondecreasing rearrangement of
 $(2b_1+1,\dots ,2b_s+1,2c_1,2c_1,\dots ,2c_t,2c_t)$.
$(2b_1+1,\dots ,2b_s+1,2c_1,2c_1,\dots ,2c_t,2c_t)$.
Proof. Part (1) follows from [Reference JacobowitzJac62, Propositions 4.3 & 8.1]. Part (2) follows from the canonicity of the Jordan splitting on [Reference JacobowitzJac62, Page 449]. Part (3) follows from a direct calculation of ![]() $L^\vee $.
$L^\vee $.
Remark 2.13. The above lemma implies that for an integral hermitian ![]() $O_E$-module L of rank m with fundamental invariants
$O_E$-module L of rank m with fundamental invariants ![]() $(a_1,\dots ,a_m)$,
$(a_1,\dots ,a_m)$,
(1) L is vertex if and only if
 $a_m\leqslant 1$ and self-dual if and only if
$a_m\leqslant 1$ and self-dual if and only if  $a_m=0$;
$a_m=0$;(2)
 $t(L)$ and
$t(L)$ and  $\operatorname {\mathrm {val}}(L)$ must have the same parity with m.
$\operatorname {\mathrm {val}}(L)$ must have the same parity with m.
Definition 2.14. Let M and L be two hermitian ![]() $O_E$-modules. We denote by
$O_E$-modules. We denote by ![]() $\mathrm {Herm}_{L,M}$ the scheme of hermitian
$\mathrm {Herm}_{L,M}$ the scheme of hermitian ![]() $O_E$-module homomorphisms from L to M, which is a scheme of finite type over
$O_E$-module homomorphisms from L to M, which is a scheme of finite type over ![]() $O_F$. We define the local density to be
$O_F$. We define the local density to be
 $$ \begin{align*} \mathrm{Den}(M,L) := \lim_{N\to+\infty}\frac{\left|\mathrm{Herm}_{L,M}(O_F/(u^{2N}))\right|}{q^{N\cdot d_{L,M}}} \end{align*} $$
$$ \begin{align*} \mathrm{Den}(M,L) := \lim_{N\to+\infty}\frac{\left|\mathrm{Herm}_{L,M}(O_F/(u^{2N}))\right|}{q^{N\cdot d_{L,M}}} \end{align*} $$where ![]() $d_{L,M}$ is the dimension of
$d_{L,M}$ is the dimension of ![]() $\mathrm {Herm}_{L,M}\otimes _{O_F}F$.
$\mathrm {Herm}_{L,M}\otimes _{O_F}F$.
Denote by H the standard hyperbolic hermitian ![]() $O_E$-module (of rank 2) given by the matrix
$O_E$-module (of rank 2) given by the matrix  $\left (\begin {smallmatrix} 0 & u^{-1}\\ -u^{-1} & 0\end {smallmatrix}\right )$. For an integer
$\left (\begin {smallmatrix} 0 & u^{-1}\\ -u^{-1} & 0\end {smallmatrix}\right )$. For an integer ![]() $s\geqslant 0$, put
$s\geqslant 0$, put ![]() $H_s := H^{\oplus s}$. Then
$H_s := H^{\oplus s}$. Then ![]() $H_s$ is a self-dual hermitian
$H_s$ is a self-dual hermitian ![]() $O_E$-module of rank
$O_E$-module of rank ![]() $2s$. The following lemma is a variant of a result of Cho–Yamauchi [Reference Cho and YamauchiCY20] when
$2s$. The following lemma is a variant of a result of Cho–Yamauchi [Reference Cho and YamauchiCY20] when ![]() $E/F$ is ramified.
$E/F$ is ramified.
Lemma 2.15. Let L be a hermitian ![]() $O_E$-module of rank m. Then we have
$O_E$-module of rank m. Then we have
 $$ \begin{align*} \mathrm{Den}(H_s,L)=\sum_{L\subseteq L'\subseteq L^{\prime vee}}|L'/L|^{m-2s} \prod_{s-\frac{m+t(L')}{2}<i\leqslant s}(1-q^{-2i}) \end{align*} $$
$$ \begin{align*} \mathrm{Den}(H_s,L)=\sum_{L\subseteq L'\subseteq L^{\prime vee}}|L'/L|^{m-2s} \prod_{s-\frac{m+t(L')}{2}<i\leqslant s}(1-q^{-2i}) \end{align*} $$for every integer ![]() $s\geqslant m$, where the sum is taken over integral
$s\geqslant m$, where the sum is taken over integral ![]() $O_E$-lattices of
$O_E$-lattices of ![]() $L\otimes _{O_F}F$ containing L.
$L\otimes _{O_F}F$ containing L.
Proof. Put ![]() $V := L\otimes _{O_F}F$. For an integral
$V := L\otimes _{O_F}F$. For an integral ![]() $O_E$-lattice
$O_E$-lattice ![]() $L'$ of V, we equip the k-vector space
$L'$ of V, we equip the k-vector space ![]() $L^{\prime }_k := L'\otimes _{O_E}O_E/(u)$ with a k-valued pairing
$L^{\prime }_k := L'\otimes _{O_E}O_E/(u)$ with a k-valued pairing ![]() $\langle \,,\,\rangle _{L^{\prime }_k}$ by the formula
$\langle \,,\,\rangle _{L^{\prime }_k}$ by the formula
 $$ \begin{align*} \langle x,y\rangle_{L^{\prime}_k} := u\cdot (x^\sharp,y^\sharp)_V\mod(u) \end{align*} $$
$$ \begin{align*} \langle x,y\rangle_{L^{\prime}_k} := u\cdot (x^\sharp,y^\sharp)_V\mod(u) \end{align*} $$where ![]() $x^\sharp $ and
$x^\sharp $ and ![]() $y^\sharp $ are arbitrary lifts of x and y, respectively. Then
$y^\sharp $ are arbitrary lifts of x and y, respectively. Then ![]() $L^{\prime }_k$ becomes a symplectic space over k of dimension m whose radical has dimension
$L^{\prime }_k$ becomes a symplectic space over k of dimension m whose radical has dimension ![]() $t(L')$. Similarly, we have
$t(L')$. Similarly, we have ![]() $H_{s,k}$, which is a nondegenerate symplectic space over k of dimension
$H_{s,k}$, which is a nondegenerate symplectic space over k of dimension ![]() $2s$. We denote by
$2s$. We denote by ![]() $\operatorname {\mathrm {Isom}}_{L^{\prime }_k,H_{s,k}}$ the k-scheme of isometries from
$\operatorname {\mathrm {Isom}}_{L^{\prime }_k,H_{s,k}}$ the k-scheme of isometries from ![]() $L^{\prime }_k$ to
$L^{\prime }_k$ to ![]() $H_{s,k}$.
$H_{s,k}$.
By the same argument in [Reference Cho and YamauchiCY20, Section 3.3], we have
 $$ \begin{align*} \mathrm{Den}(H_s,L)=q^{-m(4s-m+1)/2}\cdot\sum_{L\subseteq L'\subseteq L^{\prime \vee}}|L'/L|^{m-2s}\left|\operatorname{\mathrm{Isom}}_{L^{\prime}_k,H_{s,k}}(k)\right|. \end{align*} $$
$$ \begin{align*} \mathrm{Den}(H_s,L)=q^{-m(4s-m+1)/2}\cdot\sum_{L\subseteq L'\subseteq L^{\prime \vee}}|L'/L|^{m-2s}\left|\operatorname{\mathrm{Isom}}_{L^{\prime}_k,H_{s,k}}(k)\right|. \end{align*} $$Thus, it remains to show that
 $$ \begin{align} \left|\operatorname{\mathrm{Isom}}_{L^{\prime}_k,H_{s,k}}(k)\right|=q^{m(4s-m+1)/2}\prod_{s-\frac{m+t(L')}{2}<i\leqslant s}(1-q^{-2i}). \end{align} $$
$$ \begin{align} \left|\operatorname{\mathrm{Isom}}_{L^{\prime}_k,H_{s,k}}(k)\right|=q^{m(4s-m+1)/2}\prod_{s-\frac{m+t(L')}{2}<i\leqslant s}(1-q^{-2i}). \end{align} $$ We fix a decomposition ![]() $L^{\prime }_k=L_0\oplus L_1$ in which
$L^{\prime }_k=L_0\oplus L_1$ in which ![]() $L_0$ is nondegenerate and
$L_0$ is nondegenerate and ![]() $L_1$ is the radical of
$L_1$ is the radical of ![]() $L^{\prime }_k$. We have a morphism
$L^{\prime }_k$. We have a morphism ![]() $\pi \colon \operatorname {\mathrm {Isom}}_{L^{\prime }_k,H_{s,k}}\to \operatorname {\mathrm {Isom}}_{L_0,H_{s,k}}$ given by restriction, such that for every element
$\pi \colon \operatorname {\mathrm {Isom}}_{L^{\prime }_k,H_{s,k}}\to \operatorname {\mathrm {Isom}}_{L_0,H_{s,k}}$ given by restriction, such that for every element ![]() $f\in \operatorname {\mathrm {Isom}}_{L_0,H_{s,k}}(k)$, the fibre
$f\in \operatorname {\mathrm {Isom}}_{L_0,H_{s,k}}(k)$, the fibre ![]() $\pi ^{-1}f$ is isomorphic to
$\pi ^{-1}f$ is isomorphic to ![]() $\operatorname {\mathrm {Isom}}_{L_1,\operatorname {\mathrm {im}}(f)^\perp }$. As
$\operatorname {\mathrm {Isom}}_{L_1,\operatorname {\mathrm {im}}(f)^\perp }$. As ![]() $\operatorname {\mathrm {im}}(f)^\perp $ is isomorphic to
$\operatorname {\mathrm {im}}(f)^\perp $ is isomorphic to  $H_{s-\frac {m-t(L')}{2},k}$, it suffices to show (2.2) in the two extremal cases:
$H_{s-\frac {m-t(L')}{2},k}$, it suffices to show (2.2) in the two extremal cases: ![]() $t(L')=0$ and
$t(L')=0$ and ![]() $t(L')=m$.
$t(L')=m$.
Suppose that ![]() $t(L')=0$; that is,
$t(L')=0$; that is, ![]() $L^{\prime }_k$ is nondegenerate. Note that
$L^{\prime }_k$ is nondegenerate. Note that ![]() $\operatorname {\mathrm {Sp}}(H_{s,k})$ acts on
$\operatorname {\mathrm {Sp}}(H_{s,k})$ acts on ![]() $\operatorname {\mathrm {Isom}}_{L^{\prime }_k,H_{s,k}}$ transitively, with the stabiliser isomorphic to
$\operatorname {\mathrm {Isom}}_{L^{\prime }_k,H_{s,k}}$ transitively, with the stabiliser isomorphic to ![]() $\operatorname {\mathrm {Sp}}(H_{s-\frac {m}{2},k})$. Thus, we have
$\operatorname {\mathrm {Sp}}(H_{s-\frac {m}{2},k})$. Thus, we have
 $$ \begin{align*} \left|\operatorname{\mathrm{Isom}}_{L^{\prime}_k,H_{s,k}}(k)\right|&=\frac{|\operatorname{\mathrm{Sp}}(H_{s,k})(k)|}{\left|\operatorname{\mathrm{Sp}}(H_{s-\frac{m}{2},k})(k)\right|} \\ &=\frac{q^{s^2}\prod_{i=1}^s(q^{2i}-1)}{q^{\left(s-\frac{m}{2}\right)^2}\prod_{i=1}^{s-\frac{m}{2}}(q^{2i}-1)} \\ &=q^{m(4s-m+1)/2}\prod_{s-\frac{m}{2}<i\leqslant s}(1-q^{-2i}), \end{align*} $$
$$ \begin{align*} \left|\operatorname{\mathrm{Isom}}_{L^{\prime}_k,H_{s,k}}(k)\right|&=\frac{|\operatorname{\mathrm{Sp}}(H_{s,k})(k)|}{\left|\operatorname{\mathrm{Sp}}(H_{s-\frac{m}{2},k})(k)\right|} \\ &=\frac{q^{s^2}\prod_{i=1}^s(q^{2i}-1)}{q^{\left(s-\frac{m}{2}\right)^2}\prod_{i=1}^{s-\frac{m}{2}}(q^{2i}-1)} \\ &=q^{m(4s-m+1)/2}\prod_{s-\frac{m}{2}<i\leqslant s}(1-q^{-2i}), \end{align*} $$which confirms (2.2).
Suppose that ![]() $t(L')=m$; that is,
$t(L')=m$; that is, ![]() $L^{\prime }_k$ is isotropic. Note that
$L^{\prime }_k$ is isotropic. Note that ![]() $\operatorname {\mathrm {Sp}}(H_{s,k})$ acts on
$\operatorname {\mathrm {Sp}}(H_{s,k})$ acts on ![]() $\operatorname {\mathrm {Isom}}_{L^{\prime }_k,H_{s,k}}$ transitively, with the stabiliser Q fitting into a short exact sequence
$\operatorname {\mathrm {Isom}}_{L^{\prime }_k,H_{s,k}}$ transitively, with the stabiliser Q fitting into a short exact sequence
in which ![]() $U_m$ is a unipotent subgroup of
$U_m$ is a unipotent subgroup of ![]() $\operatorname {\mathrm {Sp}}(H_{s,k})$ of Levi type
$\operatorname {\mathrm {Sp}}(H_{s,k})$ of Levi type ![]() $\operatorname {\mathrm {GL}}_{m,k}\times ^(H_{s-m,k})$. Thus, we have
$\operatorname {\mathrm {GL}}_{m,k}\times ^(H_{s-m,k})$. Thus, we have
 $$ \begin{align*} |\operatorname{\mathrm{Isom}}_{L^{\prime}_k,H_{s,k}}(k)| &=\frac{|\operatorname{\mathrm{Sp}}(H_{s,k})(k)|}{|U_m(k)|\cdot|\operatorname{\mathrm{Sp}}(H_{s-m,k})(k)|} \\ &=\frac{q^{s^2}\prod_{i=1}^s(q^{2i}-1)}{q^{m(2s-2m)+\frac{m(m+1)}{2}}\cdot q^{\left(s-m\right)^2}\prod_{i=1}^{s-m}(q^{2i}-1)} \\ &=q^{m(4s-m+1)/2}\prod_{s-m<i\leqslant s}(1-q^{-2i}), \end{align*} $$
$$ \begin{align*} |\operatorname{\mathrm{Isom}}_{L^{\prime}_k,H_{s,k}}(k)| &=\frac{|\operatorname{\mathrm{Sp}}(H_{s,k})(k)|}{|U_m(k)|\cdot|\operatorname{\mathrm{Sp}}(H_{s-m,k})(k)|} \\ &=\frac{q^{s^2}\prod_{i=1}^s(q^{2i}-1)}{q^{m(2s-2m)+\frac{m(m+1)}{2}}\cdot q^{\left(s-m\right)^2}\prod_{i=1}^{s-m}(q^{2i}-1)} \\ &=q^{m(4s-m+1)/2}\prod_{s-m<i\leqslant s}(1-q^{-2i}), \end{align*} $$which confirms (2.2).
Thus, (2.2) is proved and the lemma follows.
Now we fix a hermitian space ![]() $\boldsymbol {V}$ over E of dimension
$\boldsymbol {V}$ over E of dimension ![]() $n=2r$ that is nonsplit.
$n=2r$ that is nonsplit.
Definition 2.16. For an ![]() $O_E$-lattice
$O_E$-lattice ![]() $\boldsymbol {L}$ of
$\boldsymbol {L}$ of ![]() $\boldsymbol {V}$, define the (normalised) local Siegel series of
$\boldsymbol {V}$, define the (normalised) local Siegel series of ![]() $\boldsymbol {L}$ to be the polynomial
$\boldsymbol {L}$ to be the polynomial ![]() $\mathrm {Den}(X,\boldsymbol {L})\in \mathbb {Z}[X]$, which exists by Lemma 2.19, such that for every integer
$\mathrm {Den}(X,\boldsymbol {L})\in \mathbb {Z}[X]$, which exists by Lemma 2.19, such that for every integer ![]() $s\geqslant 0$,
$s\geqslant 0$,
 $$ \begin{align*} \mathrm{Den}(q^{-s},\boldsymbol{L})=\frac{\mathrm{Den}(H_{r+s},\boldsymbol{L})}{\prod_{i=s+1}^{r+s}(1-q^{-2i})}, \end{align*} $$
$$ \begin{align*} \mathrm{Den}(q^{-s},\boldsymbol{L})=\frac{\mathrm{Den}(H_{r+s},\boldsymbol{L})}{\prod_{i=s+1}^{r+s}(1-q^{-2i})}, \end{align*} $$where ![]() $\mathrm {Den}$ is defined in Definition 2.14. We then put
$\mathrm {Den}$ is defined in Definition 2.14. We then put
 $$ \begin{align*} \partial\mathrm{Den}(\boldsymbol{L}) := -\left.\frac{\,\mathrm{d}}{\,\mathrm{d} X}\right|_{X=1}\mathrm{Den}(X,\boldsymbol{L}). \end{align*} $$
$$ \begin{align*} \partial\mathrm{Den}(\boldsymbol{L}) := -\left.\frac{\,\mathrm{d}}{\,\mathrm{d} X}\right|_{X=1}\mathrm{Den}(X,\boldsymbol{L}). \end{align*} $$Remark 2.17. Since ![]() $\boldsymbol {V}$ is nonsplit, we have
$\boldsymbol {V}$ is nonsplit, we have ![]() $\mathrm {Den}(1,\boldsymbol {L})=\mathrm {Den}(H_r,\boldsymbol {L})=0$.
$\mathrm {Den}(1,\boldsymbol {L})=\mathrm {Den}(H_r,\boldsymbol {L})=0$.
Remark 2.18. Let ![]() $\boldsymbol {L}$ be an
$\boldsymbol {L}$ be an ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}$. Let
$\boldsymbol {V}$. Let ![]() $T\in \operatorname {\mathrm {GL}}_n(E)$ be a matrix that represents
$T\in \operatorname {\mathrm {GL}}_n(E)$ be a matrix that represents ![]() $\boldsymbol {L}$ and consider the Tth Whittaker function
$\boldsymbol {L}$ and consider the Tth Whittaker function
of the Schwartz function
at the identity element ![]() $1_{4r}$. By [Reference KudlaKR14, Proposition 10.1],Footnote 10 we have
$1_{4r}$. By [Reference KudlaKR14, Proposition 10.1],Footnote 10 we have
for every integer ![]() $s\geqslant 0$. Thus, we obtain
$s\geqslant 0$. Thus, we obtain

by Definition 2.16.
Lemma 2.19. For every ![]() $O_E$-lattice
$O_E$-lattice ![]() $\boldsymbol {L}$ of
$\boldsymbol {L}$ of ![]() $\boldsymbol {V}$, we have
$\boldsymbol {V}$, we have
 $$ \begin{align} \mathrm{Den}(X,\boldsymbol{L})=\sum_{\boldsymbol{L}\subseteq L\subseteq L^\vee}X^{2\mathrm{length}_{O_E}(L/\boldsymbol{L})}\prod_{i=0}^{\frac{t(L)}{2}-1}(1-q^{2i}X^2) \end{align} $$
$$ \begin{align} \mathrm{Den}(X,\boldsymbol{L})=\sum_{\boldsymbol{L}\subseteq L\subseteq L^\vee}X^{2\mathrm{length}_{O_E}(L/\boldsymbol{L})}\prod_{i=0}^{\frac{t(L)}{2}-1}(1-q^{2i}X^2) \end{align} $$and
 $$ \begin{align} \partial\mathrm{Den}(\boldsymbol{L})=2\sum_{\boldsymbol{L}\subseteq L\subseteq L^\vee}\prod_{i=1}^{\frac{t(L)}{2}-1}(1-q^{2i}), \end{align} $$
$$ \begin{align} \partial\mathrm{Den}(\boldsymbol{L})=2\sum_{\boldsymbol{L}\subseteq L\subseteq L^\vee}\prod_{i=1}^{\frac{t(L)}{2}-1}(1-q^{2i}), \end{align} $$where both sums are taken over integral ![]() $O_E$-lattices of
$O_E$-lattices of ![]() $\boldsymbol {V}$ containing
$\boldsymbol {V}$ containing ![]() $\boldsymbol {L}$.Footnote 11
$\boldsymbol {L}$.Footnote 11
Proof. The identity (2.3) is a direct consequence of Lemma 2.15 and Definition 2.16. The identity (2.4) is a consequence of (2.3).
Definition 2.20. Let ![]() $L^\flat $ be an element of
$L^\flat $ be an element of ![]() $\flat (\boldsymbol {V})$ (Definition 2.8). For
$\flat (\boldsymbol {V})$ (Definition 2.8). For ![]() $x\in \boldsymbol {V}\setminus V_{L^\flat }$, we put
$x\in \boldsymbol {V}\setminus V_{L^\flat }$, we put

Here in the second formula, L in the summation is an ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}$.
$\boldsymbol {V}$.
Remark 2.21. We have
(1) The summation in
 $\partial \mathrm {Den}_{L^\flat }^{\mathrm {h}}(x)$ equals twice the number of integral
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {h}}(x)$ equals twice the number of integral  $O_E$-lattices L of
$O_E$-lattices L of  $\boldsymbol {V}$ that contains
$\boldsymbol {V}$ that contains  $L^\flat +\langle x\rangle $ and such that
$L^\flat +\langle x\rangle $ and such that  $t(L\cap V_{L^\flat })=1$.
$t(L\cap V_{L^\flat })=1$.(2) There exists a compact subset
 $C_{L^\flat }$ of
$C_{L^\flat }$ of  $\boldsymbol {V}$ such that
$\boldsymbol {V}$ such that  $\partial \mathrm {Den}_{L^\flat }$,
$\partial \mathrm {Den}_{L^\flat }$,  $\partial \mathrm {Den}_{L^\flat }^{\mathrm {h}}$ and
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {h}}$ and  $\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$ vanish outside
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$ vanish outside  $C_{L^\flat }$ and are locally constant functions on
$C_{L^\flat }$ and are locally constant functions on  $C_{L^\flat }\setminus V_{L^\flat }$.
$C_{L^\flat }\setminus V_{L^\flat }$.(3) For an integral
 $O_E$-lattice L of
$O_E$-lattice L of  $\boldsymbol {V}$, if
$\boldsymbol {V}$, if  $t(L\cap V_{L^\flat })=1$, then
$t(L\cap V_{L^\flat })=1$, then  $t(L)=2$ by Lemma 2.23(1) and the fact that
$t(L)=2$ by Lemma 2.23(1) and the fact that  $\boldsymbol {V}$ is nonsplit.
$\boldsymbol {V}$ is nonsplit.(4) By (3) and Lemma 2.19, we have
for
 $x\in \boldsymbol {V}\setminus V_{L^\flat }$.
$x\in \boldsymbol {V}\setminus V_{L^\flat }$.
The following is our main result of this subsection.
Proposition 2.22. Let ![]() $L^\flat $ be an element of
$L^\flat $ be an element of ![]() $\flat (\boldsymbol {V})$. Then
$\flat (\boldsymbol {V})$. Then ![]() $\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$ extends (uniquely) to a (compactly supported) locally constant function on
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$ extends (uniquely) to a (compactly supported) locally constant function on ![]() $\boldsymbol {V}$, which we still denote by
$\boldsymbol {V}$, which we still denote by ![]() $\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$. Moreover, the support of
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$. Moreover, the support of  $\widehat {\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}}$ is contained in
$\widehat {\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}}$ is contained in ![]() $\boldsymbol {V}^{\mathrm {int}}$ (Definition 2.10).
$\boldsymbol {V}^{\mathrm {int}}$ (Definition 2.10).
We need some lemmas for preparation.
Lemma 2.23. Let L be an integral hermitian ![]() $O_E$-module of with fundamental invariants
$O_E$-module of with fundamental invariants ![]() $(a_1,\dots ,a_m)$.
$(a_1,\dots ,a_m)$.
(1) If
 $T=((e_i,e_j)_L)_{i,j=1}^m$ is the moment matrix of an arbitrary basis
$T=((e_i,e_j)_L)_{i,j=1}^m$ is the moment matrix of an arbitrary basis  $\{e_1,\dots ,e_m\}$ of L, then for every
$\{e_1,\dots ,e_m\}$ of L, then for every  $1\leqslant i\leqslant m$,
$1\leqslant i\leqslant m$,  $a_1+\cdots +a_i-i$ equals the minimal E-valuation of the determinant of all i-by-i minors of T.
$a_1+\cdots +a_i-i$ equals the minimal E-valuation of the determinant of all i-by-i minors of T.(2) If
 $L=L'+\langle x\rangle $ for some (integral) hermitian
$L=L'+\langle x\rangle $ for some (integral) hermitian  $O_E$-module
$O_E$-module  $L'$ contained in L of rank
$L'$ contained in L of rank  $m-1$, then we have where
$m-1$, then we have where $$ \begin{align*} t(L)= \begin{cases} t(L')+1, &\text{if } x'\in uL^{\prime\vee}+L', \\ t(L')-1, &\text{otherwise,} \end{cases} \end{align*} $$
$$ \begin{align*} t(L)= \begin{cases} t(L')+1, &\text{if } x'\in uL^{\prime\vee}+L', \\ t(L')-1, &\text{otherwise,} \end{cases} \end{align*} $$ $x'$ is the unique element in
$x'$ is the unique element in  $L^{\prime \vee }$ such that
$L^{\prime \vee }$ such that  $(x',y)_L=(x,y)_L$ for every
$(x',y)_L=(x,y)_L$ for every  $y\in L'$.
$y\in L'$.
Proof. Part (1) is simply the well-known method of computing the Smith normal form of ![]() $uT$ (over
$uT$ (over ![]() $O_E$) using ideals generated by determinants of minors. For (2), take a normal basis
$O_E$) using ideals generated by determinants of minors. For (2), take a normal basis ![]() $\{x_1,\dots ,x_{m-1}\}$ of L (Definition 2.11) such that
$\{x_1,\dots ,x_{m-1}\}$ of L (Definition 2.11) such that ![]() $\langle x_1,\dots ,x_{m-1-t(L')}\rangle $ is self-dual. Applying (1) to the basis
$\langle x_1,\dots ,x_{m-1-t(L')}\rangle $ is self-dual. Applying (1) to the basis ![]() $\{x_1,\dots ,x_{m-1},x\}$ of L, we know that
$\{x_1,\dots ,x_{m-1},x\}$ of L, we know that ![]() $t(L)=t(L')+1$ if
$t(L)=t(L')+1$ if ![]() $(x_i,x)_L\in O_E$ for every
$(x_i,x)_L\in O_E$ for every ![]() $m-t(L')\leqslant i\leqslant {m-1}$; otherwise, we have
$m-t(L')\leqslant i\leqslant {m-1}$; otherwise, we have ![]() $t(L)=t(L')-1$. In particular, (2) follows.
$t(L)=t(L')-1$. In particular, (2) follows.
In the rest of this subsection, in order to shorten formulae, we put
 $$ \begin{align*} \mu(t) := \prod_{i=1}^{\frac{t}{2}-1}(1-q^{2i}) \end{align*} $$
$$ \begin{align*} \mu(t) := \prod_{i=1}^{\frac{t}{2}-1}(1-q^{2i}) \end{align*} $$for every positive even integer t.
Lemma 2.24. Take ![]() $L^\flat \in \flat (\boldsymbol {V})$ that is integral. For every compact subset X of
$L^\flat \in \flat (\boldsymbol {V})$ that is integral. For every compact subset X of ![]() $\boldsymbol {V}$ not contained in
$\boldsymbol {V}$ not contained in ![]() $V_{L^\flat }$, we denote by
$V_{L^\flat }$, we denote by ![]() $\delta _X$ the maximal integer such that the image of X under the projection map
$\delta _X$ the maximal integer such that the image of X under the projection map  $\boldsymbol {V}\to V_{L^\flat }^\perp $ induced by the orthogonal decomposition
$\boldsymbol {V}\to V_{L^\flat }^\perp $ induced by the orthogonal decomposition  $\boldsymbol {V}=V_{L^\flat }\oplus V_{L^\flat }^\perp $ is contained in
$\boldsymbol {V}=V_{L^\flat }\oplus V_{L^\flat }^\perp $ is contained in  $u^{\delta _X}(V_{L^\flat }^\perp )^{\mathrm {int}}$. We denote by
$u^{\delta _X}(V_{L^\flat }^\perp )^{\mathrm {int}}$. We denote by ![]() $\mathfrak {L}$ the set of
$\mathfrak {L}$ the set of ![]() $O_E$-lattices of
$O_E$-lattices of ![]() $\boldsymbol {V}$ containing
$\boldsymbol {V}$ containing ![]() $L^\flat $ and by
$L^\flat $ and by ![]() $\mathfrak {E}$ the set of triples
$\mathfrak {E}$ the set of triples ![]() $(L^{\flat \prime },\delta ,\varepsilon )$ in which
$(L^{\flat \prime },\delta ,\varepsilon )$ in which ![]() $L^{\flat \prime }$ is an
$L^{\flat \prime }$ is an ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $V_{L^\flat }$ containing
$V_{L^\flat }$ containing ![]() $L^\flat $,
$L^\flat $, ![]() $\delta \in \mathbb {Z}$ and
$\delta \in \mathbb {Z}$ and  $\varepsilon \colon u^\delta (V_{L^\flat }^\perp )^{\mathrm {int}}\to L^{\flat \prime }\otimes _{O_F}F/O_F$ is an
$\varepsilon \colon u^\delta (V_{L^\flat }^\perp )^{\mathrm {int}}\to L^{\flat \prime }\otimes _{O_F}F/O_F$ is an ![]() $O_E$-linear map.
$O_E$-linear map.
(1) The map
 $\mathfrak {L}\to \mathfrak {E}$ sending L to the triple
$\mathfrak {L}\to \mathfrak {E}$ sending L to the triple  $(L\cap V_{L^\flat },\delta _L,\varepsilon _L)$ is a bijection, where
$(L\cap V_{L^\flat },\delta _L,\varepsilon _L)$ is a bijection, where  $\varepsilon _L$ is the extension map
$\varepsilon _L$ is the extension map  $u^{\delta _L}(V_{L^\flat }^\perp )^{\mathrm {int}}\to (L\cap V_{L^\flat })\otimes _{O_F}F/O_F$ induced by the short exact sequence Moreover, L is integral if and only if the following hold:
$u^{\delta _L}(V_{L^\flat }^\perp )^{\mathrm {int}}\to (L\cap V_{L^\flat })\otimes _{O_F}F/O_F$ induced by the short exact sequence Moreover, L is integral if and only if the following hold: $$ \begin{align*} 0 \to L\cap V_{L^\flat} \to L \to u^{\delta_L}(V_{L^\flat}^\perp)^{\mathrm{int}} \to 0. \end{align*} $$
$$ \begin{align*} 0 \to L\cap V_{L^\flat} \to L \to u^{\delta_L}(V_{L^\flat}^\perp)^{\mathrm{int}} \to 0. \end{align*} $$•
 $L\cap V_{L^\flat }$ is integral;
$L\cap V_{L^\flat }$ is integral;• the image of
 $\varepsilon $ is contained in
$\varepsilon $ is contained in  $(L\cap V_{L^\flat })^\vee /(L\cap V_{L^\flat })$;
$(L\cap V_{L^\flat })^\vee /(L\cap V_{L^\flat })$;•
 $\varepsilon _L(x)+x\subseteq \boldsymbol {V}^{\mathrm {int}}$ for every
$\varepsilon _L(x)+x\subseteq \boldsymbol {V}^{\mathrm {int}}$ for every  $x\in u^{\delta _L}(V_{L^\flat }^\perp )^{\mathrm {int}}$.Footnote 12
$x\in u^{\delta _L}(V_{L^\flat }^\perp )^{\mathrm {int}}$.Footnote 12
(2) For
 $L\in \mathfrak {L}$ that is integral and corresponds to
$L\in \mathfrak {L}$ that is integral and corresponds to  $(L^{\flat \prime },\delta ,\varepsilon )\in \mathfrak {E}$, we have
$(L^{\flat \prime },\delta ,\varepsilon )\in \mathfrak {E}$, we have  $$ \begin{align*} t(L)= \begin{cases} t(L^{\flat\prime})+1, &\text{if the image of } \varepsilon \text{ is contained in } (u(L^{\flat\prime})^\vee+L^{\flat\prime})/L^{\flat\prime}, \\ t(L^{\flat\prime})-1, &\text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} t(L)= \begin{cases} t(L^{\flat\prime})+1, &\text{if the image of } \varepsilon \text{ is contained in } (u(L^{\flat\prime})^\vee+L^{\flat\prime})/L^{\flat\prime}, \\ t(L^{\flat\prime})-1, &\text{otherwise.} \end{cases} \end{align*} $$(3) For every fixed integral
 $O_E$-lattice
$O_E$-lattice  $L^{\flat \prime }$ of
$L^{\flat \prime }$ of  $V_{L^\flat }$ containing
$V_{L^\flat }$ containing  $L^\flat $, the sum is convergent, and if
$L^\flat $, the sum is convergent, and if $$ \begin{align*} \sum_{\substack{L\subseteq L^\vee \\ L\cap V_{L^\flat}=L^{\flat\prime}}}q^{-\delta_L}|\mu(t(L))| \end{align*} $$
$$ \begin{align*} \sum_{\substack{L\subseteq L^\vee \\ L\cap V_{L^\flat}=L^{\flat\prime}}}q^{-\delta_L}|\mu(t(L))| \end{align*} $$ $t(L^{\flat \prime })>1$, then we have for every
$t(L^{\flat \prime })>1$, then we have for every $$ \begin{align*} \sum_{\substack{L\subseteq L^\vee \\ L\cap V_{L^\flat}=L^{\flat\prime}\\ z\in L^\vee}}q^{-\delta_L}\mu(t(L))=0 \end{align*} $$
$$ \begin{align*} \sum_{\substack{L\subseteq L^\vee \\ L\cap V_{L^\flat}=L^{\flat\prime}\\ z\in L^\vee}}q^{-\delta_L}\mu(t(L))=0 \end{align*} $$ $z\in \boldsymbol {V}\setminus \boldsymbol {V}^{\mathrm {int}}$.
$z\in \boldsymbol {V}\setminus \boldsymbol {V}^{\mathrm {int}}$.(4) For every fixed integral
 $O_E$-lattice
$O_E$-lattice  $L^{\flat \prime }$ of
$L^{\flat \prime }$ of  $V_{L^\flat }$ containing
$V_{L^\flat }$ containing  $L^\flat $ with
$L^\flat $ with  $t(L^{\flat \prime })>1$, we have
$t(L^{\flat \prime })>1$, we have  $$ \begin{align*} \sum_{\substack{L\subseteq L^\vee \\ L\cap V_{L^\flat}=L^{\flat\prime}\\ \delta_L=0}}\mu(t(L))=0. \end{align*} $$
$$ \begin{align*} \sum_{\substack{L\subseteq L^\vee \\ L\cap V_{L^\flat}=L^{\flat\prime}\\ \delta_L=0}}\mu(t(L))=0. \end{align*} $$
Proof. For (1), the inverse map ![]() $\mathfrak {E}\to \mathfrak {L}$ is the one that sends
$\mathfrak {E}\to \mathfrak {L}$ is the one that sends ![]() $(L^{\flat \prime },\delta ,\varepsilon )$ to the
$(L^{\flat \prime },\delta ,\varepsilon )$ to the ![]() $O_E$-lattice L generated by
$O_E$-lattice L generated by ![]() $L^{\flat \prime }$ and
$L^{\flat \prime }$ and ![]() $\varepsilon _L(x)+x$ for every
$\varepsilon _L(x)+x$ for every  $x\in u^{\delta _L}(V_{L^\flat }^\perp )^{\mathrm {int}}$. The rest of (1) is straightforward.
$x\in u^{\delta _L}(V_{L^\flat }^\perp )^{\mathrm {int}}$. The rest of (1) is straightforward.
Part (2) is simply Lemma 2.23(2).
Part (4) follows by applying (3) to generators z of ![]() $O_E$-modules
$O_E$-modules  $u^{-1}(V_{L^\flat }^\perp )^{\mathrm {int}}$ and
$u^{-1}(V_{L^\flat }^\perp )^{\mathrm {int}}$ and  $u^{-2}(V_{L^\flat }^\perp )^{\mathrm {int}}$ and then taking the difference.
$u^{-2}(V_{L^\flat }^\perp )^{\mathrm {int}}$ and then taking the difference.
Now we prove (3), which is the most difficult one. For every ![]() $x\in \boldsymbol {V}$, we denote by
$x\in \boldsymbol {V}$, we denote by ![]() $x'\in V_{L^\flat }$ the first component of x with respect to the orthogonal decomposition
$x'\in V_{L^\flat }$ the first component of x with respect to the orthogonal decomposition  $\boldsymbol {V}=V_{L^\flat }\oplus V_{L^\flat }^\perp $. Put
$\boldsymbol {V}=V_{L^\flat }\oplus V_{L^\flat }^\perp $. Put
Note that both ![]() $\Omega $ and
$\Omega $ and ![]() $\Omega ^\circ $ are open compact subsets of
$\Omega ^\circ $ are open compact subsets of ![]() $\boldsymbol {V}$ stable under the translation by
$\boldsymbol {V}$ stable under the translation by ![]() $L^{\prime \flat }$. For an element
$L^{\prime \flat }$. For an element ![]() $L\in \mathfrak {L}$ corresponding to
$L\in \mathfrak {L}$ corresponding to ![]() $(L^{\flat \prime },\delta ,\varepsilon )\in \mathfrak {E}$ from (1), L is integral if and only
$(L^{\flat \prime },\delta ,\varepsilon )\in \mathfrak {E}$ from (1), L is integral if and only ![]() $\varepsilon (x)+x\subseteq \Omega $ for every
$\varepsilon (x)+x\subseteq \Omega $ for every  $x\in u^\delta (V_{L^\flat }^\perp )^{\mathrm {int}}$. By (2), for such L,
$x\in u^\delta (V_{L^\flat }^\perp )^{\mathrm {int}}$. By (2), for such L,
 $$ \begin{align*} t(L)= \begin{cases} t(L^{\flat\prime})+1, &\text{if } \varepsilon(x)+x\subseteq\Omega^\circ \text{ for every } x\in u^\delta(V_{L^\flat}^\perp)^{\mathrm{int}}\setminus u^{\delta+1}(V_{L^\flat}^\perp)^{\mathrm{int}}, \\ t(L^{\flat\prime})-1, &\text{if } \varepsilon(x)+x\subseteq\Omega\setminus\Omega^\circ \text{ for every } x\in u^\delta(V_{L^\flat}^\perp)^{\mathrm{int}}\setminus u^{\delta+1}(V_{L^\flat}^\perp)^{\mathrm{int}}. \end{cases} \end{align*} $$
$$ \begin{align*} t(L)= \begin{cases} t(L^{\flat\prime})+1, &\text{if } \varepsilon(x)+x\subseteq\Omega^\circ \text{ for every } x\in u^\delta(V_{L^\flat}^\perp)^{\mathrm{int}}\setminus u^{\delta+1}(V_{L^\flat}^\perp)^{\mathrm{int}}, \\ t(L^{\flat\prime})-1, &\text{if } \varepsilon(x)+x\subseteq\Omega\setminus\Omega^\circ \text{ for every } x\in u^\delta(V_{L^\flat}^\perp)^{\mathrm{int}}\setminus u^{\delta+1}(V_{L^\flat}^\perp)^{\mathrm{int}}. \end{cases} \end{align*} $$Thus, we may replace the term corresponding to L in the summation in (3) by an integration over the region  $\bigcup _{x\in u^\delta (V_{L^\flat }^\perp )^{\mathrm {int}}\setminus u^{\delta +1}(V_{L^\flat }^\perp )^{\mathrm {int}}}(\varepsilon (x)+x)$ of
$\bigcup _{x\in u^\delta (V_{L^\flat }^\perp )^{\mathrm {int}}\setminus u^{\delta +1}(V_{L^\flat }^\perp )^{\mathrm {int}}}(\varepsilon (x)+x)$ of ![]() $\Omega $. It follows that
$\Omega $. It follows that
 $$ \begin{align*} \sum_{\substack{L\subseteq L^\vee \\ L\cap V_{L^\flat}=L^{\flat\prime}}}q^{-\delta_L}|\mu(t(L))| =\frac{1}{C}\left(\int_{\Omega^\circ\setminus V_{L^\flat}}|\mu(t(L^{\flat\prime})+1)|\,\mathrm{d} x+\int_{\Omega\setminus(\Omega^\circ\cup V_{L^\flat})}|\mu(t(L^{\flat\prime})-1)|\,\mathrm{d} x\right), \end{align*} $$
$$ \begin{align*} \sum_{\substack{L\subseteq L^\vee \\ L\cap V_{L^\flat}=L^{\flat\prime}}}q^{-\delta_L}|\mu(t(L))| =\frac{1}{C}\left(\int_{\Omega^\circ\setminus V_{L^\flat}}|\mu(t(L^{\flat\prime})+1)|\,\mathrm{d} x+\int_{\Omega\setminus(\Omega^\circ\cup V_{L^\flat})}|\mu(t(L^{\flat\prime})-1)|\,\mathrm{d} x\right), \end{align*} $$which is convergent, where
 $$ \begin{align*} C=\operatorname{\mathrm{vol}}(L^{\flat\prime})\cdot\operatorname{\mathrm{vol}}((V_{L^\flat}^\perp)^{\mathrm{int}}\setminus u(V_{L^\flat}^\perp)^{\mathrm{int}}). \end{align*} $$
$$ \begin{align*} C=\operatorname{\mathrm{vol}}(L^{\flat\prime})\cdot\operatorname{\mathrm{vol}}((V_{L^\flat}^\perp)^{\mathrm{int}}\setminus u(V_{L^\flat}^\perp)^{\mathrm{int}}). \end{align*} $$ Now we take an element ![]() $z\in \boldsymbol {V}\setminus \boldsymbol {V}^{\mathrm {int}}$. We may assume
$z\in \boldsymbol {V}\setminus \boldsymbol {V}^{\mathrm {int}}$. We may assume ![]() $z'\in (L^{\flat \prime })^\vee $ since otherwise the summation in (3) is empty. Put
$z'\in (L^{\flat \prime })^\vee $ since otherwise the summation in (3) is empty. Put
 $$ \begin{align*} \Omega_z := \{x\in\Omega\mathbin{|}(x,z)_{\boldsymbol{V}}\in u^{-1}O_E\},\qquad \Omega^\circ_z := \{x\in\Omega^\circ\mathbin{|}(x,z)_{\boldsymbol{V}}\in u^{-1}O_E\}, \end{align*} $$
$$ \begin{align*} \Omega_z := \{x\in\Omega\mathbin{|}(x,z)_{\boldsymbol{V}}\in u^{-1}O_E\},\qquad \Omega^\circ_z := \{x\in\Omega^\circ\mathbin{|}(x,z)_{\boldsymbol{V}}\in u^{-1}O_E\}, \end{align*} $$both stable under the translation by ![]() $L^{\prime \flat }$ since
$L^{\prime \flat }$ since ![]() $z'\in (L^{\flat \prime })^\vee $. Similarly, we have
$z'\in (L^{\flat \prime })^\vee $. Similarly, we have
 $$ \begin{align*} \sum_{\substack{L\subseteq L^\vee \\ L\cap V_{L^\flat}=L^{\flat\prime}\\ z\in L^\vee}}q^{-\delta_L}\mu(t(L)) &=\frac{1}{C}\left(\int_{\Omega_z^\circ\setminus V_{L^\flat}}\mu(t(L^{\flat\prime})+1)\,\mathrm{d} x+\int_{\Omega_z\setminus(\Omega_z^\circ\cup V_{L^\flat})}\mu(t(L^{\flat\prime})-1)\,\mathrm{d} x\right) \\ &=\frac{\mu(t(L^{\flat\prime})-1)}{C}\left(\operatorname{\mathrm{vol}}(\Omega_z\setminus\Omega_z^\circ)+\left(1-q^{t(L^{\flat\prime})-1}\right)\operatorname{\mathrm{vol}}(\Omega_z^\circ)\right) \\ &=\frac{\mu(t(L^{\flat\prime})-1)}{C}\left(\operatorname{\mathrm{vol}}(\Omega_z)-q^{t(L^{\flat\prime})-1}\operatorname{\mathrm{vol}}(\Omega_z^\circ)\right), \end{align*} $$
$$ \begin{align*} \sum_{\substack{L\subseteq L^\vee \\ L\cap V_{L^\flat}=L^{\flat\prime}\\ z\in L^\vee}}q^{-\delta_L}\mu(t(L)) &=\frac{1}{C}\left(\int_{\Omega_z^\circ\setminus V_{L^\flat}}\mu(t(L^{\flat\prime})+1)\,\mathrm{d} x+\int_{\Omega_z\setminus(\Omega_z^\circ\cup V_{L^\flat})}\mu(t(L^{\flat\prime})-1)\,\mathrm{d} x\right) \\ &=\frac{\mu(t(L^{\flat\prime})-1)}{C}\left(\operatorname{\mathrm{vol}}(\Omega_z\setminus\Omega_z^\circ)+\left(1-q^{t(L^{\flat\prime})-1}\right)\operatorname{\mathrm{vol}}(\Omega_z^\circ)\right) \\ &=\frac{\mu(t(L^{\flat\prime})-1)}{C}\left(\operatorname{\mathrm{vol}}(\Omega_z)-q^{t(L^{\flat\prime})-1}\operatorname{\mathrm{vol}}(\Omega_z^\circ)\right), \end{align*} $$where we have used ![]() $t(L^{\flat \prime })>1$ in the second equality. Thus, it remains to show that
$t(L^{\flat \prime })>1$ in the second equality. Thus, it remains to show that
 $$ \begin{align} \operatorname{\mathrm{vol}}(\Omega_z)=q^{t(L^{\flat\prime})-1}\operatorname{\mathrm{vol}}(\Omega_z^\circ). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{vol}}(\Omega_z)=q^{t(L^{\flat\prime})-1}\operatorname{\mathrm{vol}}(\Omega_z^\circ). \end{align} $$ We fix an orthogonal decomposition ![]() $L^{\flat \prime }=L_0\oplus L_1$ in which
$L^{\flat \prime }=L_0\oplus L_1$ in which ![]() $L_0$ is self-dual and
$L_0$ is self-dual and ![]() $L_1$ is of both rank and type
$L_1$ is of both rank and type ![]() $t(L^{\flat \prime })$. Since both
$t(L^{\flat \prime })$. Since both ![]() $\Omega _z$ and
$\Omega _z$ and ![]() $\Omega _z^\circ $ depend only on the coset
$\Omega _z^\circ $ depend only on the coset ![]() $z+L^{\flat \prime }$, we may assume
$z+L^{\flat \prime }$, we may assume ![]() $z'\in L_1^\vee $ and anisotropic. Let
$z'\in L_1^\vee $ and anisotropic. Let ![]() $V_2\subseteq \boldsymbol {V}$ be the orthogonal complement of
$V_2\subseteq \boldsymbol {V}$ be the orthogonal complement of ![]() $L_0+\langle z\rangle $. We claim
$L_0+\langle z\rangle $. We claim
(*) There exists an integral
 $O_E$-lattice
$O_E$-lattice  $L_2$ of
$L_2$ of  $V_2$ of of type
$V_2$ of of type  $t(L^{\flat \prime })$ such that (2.6)for
$t(L^{\flat \prime })$ such that (2.6)for $$ \begin{align} (u^i L_2^\vee)^{\mathrm{int}}=\{x\in V_2^{\mathrm{int}}\mathbin{|} x'\in u^iL_1^\vee\} \end{align} $$
$$ \begin{align} (u^i L_2^\vee)^{\mathrm{int}}=\{x\in V_2^{\mathrm{int}}\mathbin{|} x'\in u^iL_1^\vee\} \end{align} $$ $i=0,1$.
$i=0,1$.
Assuming (![]() $*$), by construction, we have
$*$), by construction, we have
Now we use the condition ![]() $z\not \in \boldsymbol {V}^{\mathrm {int}}$, which implies that
$z\not \in \boldsymbol {V}^{\mathrm {int}}$, which implies that ![]() $\langle z\rangle ^\vee \subseteq u\langle z\rangle \cap \boldsymbol {V}^{\mathrm {int}}$. Combining with (2.6), we obtain
$\langle z\rangle ^\vee \subseteq u\langle z\rangle \cap \boldsymbol {V}^{\mathrm {int}}$. Combining with (2.6), we obtain
 $$ \begin{align*} \Omega_z=L_0\times\langle z\rangle^\vee\times(L_2^\vee)^{\mathrm{int}},\qquad \Omega_z^\circ=L_0\times\langle z\rangle^\vee\times(uL_2^\vee)^{\mathrm{int}}. \end{align*} $$
$$ \begin{align*} \Omega_z=L_0\times\langle z\rangle^\vee\times(L_2^\vee)^{\mathrm{int}},\qquad \Omega_z^\circ=L_0\times\langle z\rangle^\vee\times(uL_2^\vee)^{\mathrm{int}}. \end{align*} $$Thus, (2.5) follows from Lemma 2.25. Part (3) is proved.
Now we show (![]() $*$). There are two cases.
$*$). There are two cases.
First, we assume ![]() $z\neq z'$; that is,
$z\neq z'$; that is, ![]() $z\not \in V_{L^\flat }$. Let
$z\not \in V_{L^\flat }$. Let ![]() $L_2$ be the unique
$L_2$ be the unique ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $V_2$ satisfying
$V_2$ satisfying
Then (2.6) clearly holds. Thus, it remains to show that ![]() $L_2$ is integral of type
$L_2$ is integral of type ![]() $t(L^{\flat \prime })$. Put
$t(L^{\flat \prime })$. Put  $w := z-z'\in V_{L^\flat }^\perp $, which is nonzero and hence anisotropic. Then
$w := z-z'\in V_{L^\flat }^\perp $, which is nonzero and hence anisotropic. Then
 $$ \begin{align*} \bar{z} := z'-\frac{(z',z')_{\boldsymbol{V}}}{(w,w)_{\boldsymbol{V}}}w \end{align*} $$
$$ \begin{align*} \bar{z} := z'-\frac{(z',z')_{\boldsymbol{V}}}{(w,w)_{\boldsymbol{V}}}w \end{align*} $$is the unique element in ![]() $V_2$ such that
$V_2$ such that ![]() $\bar {z}'=z'$. To compute
$\bar {z}'=z'$. To compute ![]() $L_2$, we write
$L_2$, we write
for some ![]() $y\in V_{L^\flat }\cap V_2$ and
$y\in V_{L^\flat }\cap V_2$ and ![]() $\alpha \in E\setminus uO_E$, where
$\alpha \in E\setminus uO_E$, where ![]() $M := L_1^\vee \cap V_2$. Then
$M := L_1^\vee \cap V_2$. Then
Since ![]() $M^\vee /M^\dagger $ is isomorphic to an
$M^\vee /M^\dagger $ is isomorphic to an ![]() $O_E$-submodule of
$O_E$-submodule of ![]() $E/u^{-1}O_E$, we may take an element
$E/u^{-1}O_E$, we may take an element ![]() $y^\dagger \in M^\vee $ that generates
$y^\dagger \in M^\vee $ that generates ![]() $M^\vee /M^\dagger $. Then we have
$M^\vee /M^\dagger $. Then we have
for some ![]() $\alpha ^\dagger \in E^\times $ such that
$\alpha ^\dagger \in E^\times $ such that ![]() $(y^\dagger ,y)_{\boldsymbol {V}}+\alpha ^\dagger \alpha ^{\mathtt {c}}(z',z')_{\boldsymbol {V}}\in u^{-1}O_E$. Now by (2.7), we have
$(y^\dagger ,y)_{\boldsymbol {V}}+\alpha ^\dagger \alpha ^{\mathtt {c}}(z',z')_{\boldsymbol {V}}\in u^{-1}O_E$. Now by (2.7), we have
By the same argument, we have
where
 $$ \begin{align*} \rho := \frac{(z',z')_{\boldsymbol{V}}}{(\bar{z},\bar{z})_{\boldsymbol{V}}}. \end{align*} $$
$$ \begin{align*} \rho := \frac{(z',z')_{\boldsymbol{V}}}{(\bar{z},\bar{z})_{\boldsymbol{V}}}. \end{align*} $$By Lemma 2.23(2), we have ![]() $t(L_2)=t(L_1)=t(L^{\flat \prime })$ as long as
$t(L_2)=t(L_1)=t(L^{\flat \prime })$ as long as ![]() $L_2$ is integral. Thus, it suffices to show that
$L_2$ is integral. Thus, it suffices to show that ![]() $y^\dagger +\alpha ^\dagger \rho \bar {z}\in \boldsymbol {V}^{\mathrm {int}}$. We compute
$y^\dagger +\alpha ^\dagger \rho \bar {z}\in \boldsymbol {V}^{\mathrm {int}}$. We compute
 $$ \begin{align*} &(y^\dagger+\alpha^\dagger\rho\bar{z},y^\dagger+\alpha^\dagger\rho\bar{z})_{\boldsymbol{V}}-(y^\dagger+\alpha^\dagger z',y^\dagger+\alpha^\dagger z')_{\boldsymbol{V}} \\ &=(\alpha^\dagger\rho\bar{z},\alpha^\dagger\rho\bar{z})_{\boldsymbol{V}}-(\alpha^\dagger z',\alpha^\dagger z')_{\boldsymbol{V}} \\ &=\operatorname{\mathrm{Nm}}_{E/F}(\alpha^\dagger)\left(\frac{(z',z')_{\boldsymbol{V}}^2}{(\bar{z},\bar{z})_{\boldsymbol{V}}}-(z',z')_{\boldsymbol{V}}\right) \\ &=\operatorname{\mathrm{Nm}}_{E/F}(\alpha^\dagger)(z',z')_{\boldsymbol{V}}\left(\frac{(z',z')_{\boldsymbol{V}}}{(z',z')_{\boldsymbol{V}}+\frac{(z',z')_{\boldsymbol{V}}^2}{(w,w)_{\boldsymbol{V}}}}-1\right) \\ &=\operatorname{\mathrm{Nm}}_{E/F}(\alpha^\dagger)(z',z')_{\boldsymbol{V}}\left(\frac{(w,w)_{\boldsymbol{V}}}{(z',z')_{\boldsymbol{V}}+(w,w)_{\boldsymbol{V}}}-1\right) \\ &=\frac{-(\alpha^\dagger)^{\mathtt{c}}}{\alpha^\dagger}\frac{(\alpha^\dagger z',z')_{\boldsymbol{V}}^2}{(z,z)_{\boldsymbol{V}}}. \end{align*} $$
$$ \begin{align*} &(y^\dagger+\alpha^\dagger\rho\bar{z},y^\dagger+\alpha^\dagger\rho\bar{z})_{\boldsymbol{V}}-(y^\dagger+\alpha^\dagger z',y^\dagger+\alpha^\dagger z')_{\boldsymbol{V}} \\ &=(\alpha^\dagger\rho\bar{z},\alpha^\dagger\rho\bar{z})_{\boldsymbol{V}}-(\alpha^\dagger z',\alpha^\dagger z')_{\boldsymbol{V}} \\ &=\operatorname{\mathrm{Nm}}_{E/F}(\alpha^\dagger)\left(\frac{(z',z')_{\boldsymbol{V}}^2}{(\bar{z},\bar{z})_{\boldsymbol{V}}}-(z',z')_{\boldsymbol{V}}\right) \\ &=\operatorname{\mathrm{Nm}}_{E/F}(\alpha^\dagger)(z',z')_{\boldsymbol{V}}\left(\frac{(z',z')_{\boldsymbol{V}}}{(z',z')_{\boldsymbol{V}}+\frac{(z',z')_{\boldsymbol{V}}^2}{(w,w)_{\boldsymbol{V}}}}-1\right) \\ &=\operatorname{\mathrm{Nm}}_{E/F}(\alpha^\dagger)(z',z')_{\boldsymbol{V}}\left(\frac{(w,w)_{\boldsymbol{V}}}{(z',z')_{\boldsymbol{V}}+(w,w)_{\boldsymbol{V}}}-1\right) \\ &=\frac{-(\alpha^\dagger)^{\mathtt{c}}}{\alpha^\dagger}\frac{(\alpha^\dagger z',z')_{\boldsymbol{V}}^2}{(z,z)_{\boldsymbol{V}}}. \end{align*} $$As ![]() $z'\in L_1^\vee $, we have
$z'\in L_1^\vee $, we have ![]() $(\alpha ^\dagger z',z')_{\boldsymbol {V}}\in u^{-1}O_E$. As
$(\alpha ^\dagger z',z')_{\boldsymbol {V}}\in u^{-1}O_E$. As ![]() $z\not \in \boldsymbol {V}^{\mathrm {int}}$, we have
$z\not \in \boldsymbol {V}^{\mathrm {int}}$, we have ![]() $(z,z)_{\boldsymbol {V}}\not \in u^{-1}O_E$. Together, we have
$(z,z)_{\boldsymbol {V}}\not \in u^{-1}O_E$. Together, we have  $\frac {(\alpha ^\dagger z',z')_{\boldsymbol {V}}^2}{(z,z)_{\boldsymbol {V}}}\in O_F$. Thus,
$\frac {(\alpha ^\dagger z',z')_{\boldsymbol {V}}^2}{(z,z)_{\boldsymbol {V}}}\in O_F$. Thus, ![]() $y^\dagger +\alpha ^\dagger \rho \bar {z}\in \boldsymbol {V}^{\mathrm {int}}$ as
$y^\dagger +\alpha ^\dagger \rho \bar {z}\in \boldsymbol {V}^{\mathrm {int}}$ as ![]() $y^\dagger +\alpha ^\dagger z'\in \boldsymbol {V}^{\mathrm {int}}$; hence,
$y^\dagger +\alpha ^\dagger z'\in \boldsymbol {V}^{\mathrm {int}}$; hence, ![]() $L_2$ meets the requirement in (
$L_2$ meets the requirement in (![]() $*$).
$*$).
Second, we assume ![]() $z=z'$; that is,
$z=z'$; that is, ![]() $z\in V_{L^\flat }$. Take
$z\in V_{L^\flat }$. Take  $L_2=(L_1^\vee \cap V_2)^\vee \oplus u^\delta (V_{L^\flat }^\perp )^{\mathrm {int}}$ for some integer
$L_2=(L_1^\vee \cap V_2)^\vee \oplus u^\delta (V_{L^\flat }^\perp )^{\mathrm {int}}$ for some integer ![]() $\delta \geqslant 0$ determined later. We show that
$\delta \geqslant 0$ determined later. We show that ![]() $(L_1^\vee \cap V_2)^\vee $ is an integral hermitian
$(L_1^\vee \cap V_2)^\vee $ is an integral hermitian ![]() $O_E$-module of type
$O_E$-module of type ![]() $t(L^{\flat \prime })-1$. As in the previous case, we write
$t(L^{\flat \prime })-1$. As in the previous case, we write
for some ![]() $y\in V_{L^\flat }\cap V_2$ and
$y\in V_{L^\flat }\cap V_2$ and ![]() $\alpha \in E\setminus uO_E$, where
$\alpha \in E\setminus uO_E$, where ![]() $M := L_1^\vee \cap V_2$. Then
$M := L_1^\vee \cap V_2$. Then
so that ![]() $M^\vee $ is generated by
$M^\vee $ is generated by ![]() $M^\dagger $ and
$M^\dagger $ and ![]() $y^\dagger $. As
$y^\dagger $. As ![]() $L_1$ is of type
$L_1$ is of type ![]() $t(L^{\flat \prime })$, which is its rank, we have
$t(L^{\flat \prime })$, which is its rank, we have ![]() $L_1\subseteq uL_1^\vee $; that is,
$L_1\subseteq uL_1^\vee $; that is,
hence, ![]() $M^\dagger \subseteq uM$. As
$M^\dagger \subseteq uM$. As ![]() $z'\in L_1^\vee $, we have
$z'\in L_1^\vee $, we have ![]() $(\alpha z',z')_{\boldsymbol {V}}\in u^{-1}O_E$. As
$(\alpha z',z')_{\boldsymbol {V}}\in u^{-1}O_E$. As ![]() $z'=z\not \in \boldsymbol {V}^{\mathrm {int}}$, we have
$z'=z\not \in \boldsymbol {V}^{\mathrm {int}}$, we have ![]() $(z',z')_{\boldsymbol {V}}\not \in u^{-1}O_E$; hence,
$(z',z')_{\boldsymbol {V}}\not \in u^{-1}O_E$; hence, ![]() $\alpha ^\dagger \in uO_E$. Again, as
$\alpha ^\dagger \in uO_E$. Again, as ![]() $z'\in L_1^\vee $, we have
$z'\in L_1^\vee $, we have  $\alpha ^\dagger z'\in uL_1^\vee $; hence,
$\alpha ^\dagger z'\in uL_1^\vee $; hence,  $y^\dagger \in uL_1^\vee \cap V_2= uM$. Together, we obtain
$y^\dagger \in uL_1^\vee \cap V_2= uM$. Together, we obtain ![]() $M^\vee \subseteq uM$; that is,
$M^\vee \subseteq uM$; that is, ![]() $(L_1^\vee \cap V_2)^\vee $ is an integral hermitian
$(L_1^\vee \cap V_2)^\vee $ is an integral hermitian ![]() $O_E$-module of type
$O_E$-module of type ![]() $t(L^{\flat \prime })-1$.
$t(L^{\flat \prime })-1$.
Consequently, ![]() $L_2$ is an integral
$L_2$ is an integral ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $V_2$ of type
$V_2$ of type ![]() $t(L^{\flat \prime })$. Since
$t(L^{\flat \prime })$. Since  $L_2^\vee =(L_1^\vee \cap V_2)\oplus u^{-\delta -1}(V_{L^\flat }^\perp )^{\mathrm {int}}$, it is clear that for
$L_2^\vee =(L_1^\vee \cap V_2)\oplus u^{-\delta -1}(V_{L^\flat }^\perp )^{\mathrm {int}}$, it is clear that for ![]() $\delta $ sufficiently large, (2.6) holds for
$\delta $ sufficiently large, (2.6) holds for ![]() $i=0,1$. Thus, (
$i=0,1$. Thus, (![]() $*$) is proved.
$*$) is proved.
The lemma is all proved.
Lemma 2.25. Let L be an integral hermitian ![]() $O_E$-module of rank
$O_E$-module of rank ![]() $2m+1$ for some integer
$2m+1$ for some integer ![]() $m\geqslant 0$ with
$m\geqslant 0$ with ![]() $t(L)=2m+1$. Then we have
$t(L)=2m+1$. Then we have
 $$ \begin{align} \left|(L^\vee)^{\mathrm{int}}/L\right|=q^{2m}\cdot\left|(uL^\vee)^{\mathrm{int}}/L\right|. \end{align} $$
$$ \begin{align} \left|(L^\vee)^{\mathrm{int}}/L\right|=q^{2m}\cdot\left|(uL^\vee)^{\mathrm{int}}/L\right|. \end{align} $$Note that both ![]() $(L^\vee )^{\mathrm {int}}$ and
$(L^\vee )^{\mathrm {int}}$ and ![]() $(uL^\vee )^{\mathrm {int}}$ are stable under the translation by L as
$(uL^\vee )^{\mathrm {int}}$ are stable under the translation by L as ![]() $t(L)=2m+1$.
$t(L)=2m+1$.
Proof. Put ![]() $V := L\otimes _{O_F}F$. We prove by induction on
$V := L\otimes _{O_F}F$. We prove by induction on ![]() $\operatorname {\mathrm {val}}(L)$ for integral
$\operatorname {\mathrm {val}}(L)$ for integral ![]() $O_E$-lattices L of V with
$O_E$-lattices L of V with ![]() $t(L)=2m+1$ that (2.8) holds.
$t(L)=2m+1$ that (2.8) holds.
The initial case is such that ![]() $\operatorname {\mathrm {val}}(L)=2m+1$; that is,
$\operatorname {\mathrm {val}}(L)=2m+1$; that is, ![]() $L^\vee =u^{-1}L$. The pairing
$L^\vee =u^{-1}L$. The pairing ![]() $u^2(\,,\,)_V$ induces a nondegenerate quadratic form on
$u^2(\,,\,)_V$ induces a nondegenerate quadratic form on ![]() $L^\vee /L$. It is clear that
$L^\vee /L$. It is clear that ![]() $(L^\vee )^{\mathrm {int}}/L$ is exactly the set of isotropic vectors in
$(L^\vee )^{\mathrm {int}}/L$ is exactly the set of isotropic vectors in ![]() $L^\vee /L$ under the previous form. In particular, we have
$L^\vee /L$ under the previous form. In particular, we have
 $$ \begin{align*} \left|(L^\vee)^{\mathrm{int}}/L\right|=q^{2m}=q^{2m}\cdot\left|(uL^\vee)^{\mathrm{int}}/L\right|. \end{align*} $$
$$ \begin{align*} \left|(L^\vee)^{\mathrm{int}}/L\right|=q^{2m}=q^{2m}\cdot\left|(uL^\vee)^{\mathrm{int}}/L\right|. \end{align*} $$ Now we consider L with ![]() $\operatorname {\mathrm {val}}(L)>2m+1$ and suppose that (2.8) holds for such
$\operatorname {\mathrm {val}}(L)>2m+1$ and suppose that (2.8) holds for such ![]() $L'$ with
$L'$ with ![]() $\operatorname {\mathrm {val}}(L')<\operatorname {\mathrm {val}}(L)$. Choose an orthogonal decomposition
$\operatorname {\mathrm {val}}(L')<\operatorname {\mathrm {val}}(L)$. Choose an orthogonal decomposition ![]() $L=L_0\oplus L_1$ in which
$L=L_0\oplus L_1$ in which ![]() $L_0$ is an integral hermitian
$L_0$ is an integral hermitian ![]() $O_E$-module with fundamental invariants
$O_E$-module with fundamental invariants ![]() $(1,\dots ,1)$ and such that all fundamental invariants of
$(1,\dots ,1)$ and such that all fundamental invariants of ![]() $L_1$ are at least
$L_1$ are at least ![]() $2$. In particular,
$2$. In particular, ![]() $L_1$ has positive rank. It is easy to see that we may choose a hermitian
$L_1$ has positive rank. It is easy to see that we may choose a hermitian ![]() $O_E$-module
$O_E$-module ![]() $L^{\prime }_1$ contained in
$L^{\prime }_1$ contained in ![]() $u^{-1}L_1$ satisfying
$u^{-1}L_1$ satisfying ![]() $L_1\varsubsetneq L^{\prime }_1$ and
$L_1\varsubsetneq L^{\prime }_1$ and ![]() $t(L^{\prime }_1)=t(L_1)$. Put
$t(L^{\prime }_1)=t(L_1)$. Put ![]() $L' := L_0\oplus L^{\prime }_1$. By the induction hypothesis, we have
$L' := L_0\oplus L^{\prime }_1$. By the induction hypothesis, we have
 $$ \begin{align*} \left|(L^{\prime \vee})^{\mathrm{int}}/L'\right|=q^{2m}\cdot\left|(uL^{\prime \vee})^{\mathrm{int}}/L'\right|. \end{align*} $$
$$ \begin{align*} \left|(L^{\prime \vee})^{\mathrm{int}}/L'\right|=q^{2m}\cdot\left|(uL^{\prime \vee})^{\mathrm{int}}/L'\right|. \end{align*} $$It remains to show that
 $$ \begin{align} \left|((L^\vee)^{\mathrm{int}}\setminus (L^{\prime \vee})^{\mathrm{int}})/L\right|=q^{2m}\cdot\left|((uL^\vee)^{\mathrm{int}}\setminus(uL^{\prime \vee})^{\mathrm{int}})/L\right|. \end{align} $$
$$ \begin{align} \left|((L^\vee)^{\mathrm{int}}\setminus (L^{\prime \vee})^{\mathrm{int}})/L\right|=q^{2m}\cdot\left|((uL^\vee)^{\mathrm{int}}\setminus(uL^{\prime \vee})^{\mathrm{int}})/L\right|. \end{align} $$We claim that the map
given by the multiplication by u is ![]() $q^{2m}$-to-
$q^{2m}$-to-![]() $1$.
$1$.
Take an element ![]() $x\in (uL^\vee )^{\mathrm {int}}\setminus (uL^{\prime \vee })^{\mathrm {int}}$. Its preimage is bijective to the set of elements
$x\in (uL^\vee )^{\mathrm {int}}\setminus (uL^{\prime \vee })^{\mathrm {int}}$. Its preimage is bijective to the set of elements ![]() $(y_0,y_1)\in L_0/uL_0\oplus L_1/uL_1$ such that
$(y_0,y_1)\in L_0/uL_0\oplus L_1/uL_1$ such that ![]() $u^{-1}(x+(y_0,y_1))\in V^{\mathrm {int}}$, which amounts to the equation
$u^{-1}(x+(y_0,y_1))\in V^{\mathrm {int}}$, which amounts to the equation
 $$ \begin{align*} (x,x)_V+\operatorname{\mathrm{Tr}}_{E/F}(x,y_0)_V+\operatorname{\mathrm{Tr}}_{E/F}(x,y_1)_V+(y_0,y_0)_V \in u^2 O_F. \end{align*} $$
$$ \begin{align*} (x,x)_V+\operatorname{\mathrm{Tr}}_{E/F}(x,y_0)_V+\operatorname{\mathrm{Tr}}_{E/F}(x,y_1)_V+(y_0,y_0)_V \in u^2 O_F. \end{align*} $$Since  $x\in (uL_0^\vee )\times ((uL_1^\vee )^{\mathrm {int}}\setminus (u^2L_1^\vee )^{\mathrm {int}})$, there exists
$x\in (uL_0^\vee )\times ((uL_1^\vee )^{\mathrm {int}}\setminus (u^2L_1^\vee )^{\mathrm {int}})$, there exists ![]() $y_1\in L_1$ such that
$y_1\in L_1$ such that ![]() $(x,y_1)_V\in O_E^\times $. In other words, for each
$(x,y_1)_V\in O_E^\times $. In other words, for each ![]() $y_0$, the above relation defines a nontrivial linear equation on
$y_0$, the above relation defines a nontrivial linear equation on ![]() $L_1/uL_1$. Thus, the preimage of x has cardinality
$L_1/uL_1$. Thus, the preimage of x has cardinality ![]() $q^{2m}$. We obtain (2.9) and hence complete the induction process.
$q^{2m}$. We obtain (2.9) and hence complete the induction process.
Proof of Proposition 2.22.
We fix an element ![]() $L^\flat \in \flat (\boldsymbol {V})$. If
$L^\flat \in \flat (\boldsymbol {V})$. If ![]() $L^\flat $ is not integral, then
$L^\flat $ is not integral, then ![]() $\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}\equiv 0$; hence, the proposition is trivial. Thus, we now assume
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}\equiv 0$; hence, the proposition is trivial. Thus, we now assume ![]() $L^\flat $ integral and will freely adopt notation from Lemma 2.24.
$L^\flat $ integral and will freely adopt notation from Lemma 2.24.
To show that ![]() $\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$ extends to a compactly supported locally constant function on
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}$ extends to a compactly supported locally constant function on ![]() $\boldsymbol {V}$, it suffices to show that for every
$\boldsymbol {V}$, it suffices to show that for every ![]() $y\in V_{L^\flat }/L^\flat $, there exists an integer
$y\in V_{L^\flat }/L^\flat $, there exists an integer ![]() $\delta (y)>0$ such that
$\delta (y)>0$ such that ![]() $\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}(y+x)$ is constant for
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}(y+x)$ is constant for  $x\in u^{\delta (y)}(V_{L^\flat }^\perp )^{\mathrm {int}}\setminus \{0\}$. If
$x\in u^{\delta (y)}(V_{L^\flat }^\perp )^{\mathrm {int}}\setminus \{0\}$. If ![]() $L^\flat +\langle y\rangle $ is not integral, then there exists
$L^\flat +\langle y\rangle $ is not integral, then there exists ![]() $\delta (y)>0$ such that
$\delta (y)>0$ such that ![]() $L^\flat +\langle y+x\rangle $ is not integral for
$L^\flat +\langle y+x\rangle $ is not integral for  $x\in u^{\delta (y)}(V_{L^\flat }^\perp )^{\mathrm {int}}\setminus \{0\}$, which implies
$x\in u^{\delta (y)}(V_{L^\flat }^\perp )^{\mathrm {int}}\setminus \{0\}$, which implies ![]() $\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}(y+x)=0$.
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}(y+x)=0$.
Now we fix an element ![]() $y\in V_{L^\flat }/L^\flat $ such that
$y\in V_{L^\flat }/L^\flat $ such that ![]() $L^\flat +\langle y\rangle $ is integral. We claim that we may take
$L^\flat +\langle y\rangle $ is integral. We claim that we may take ![]() $\delta (y)=a_{n-1}$, which is the maximal element in the fundamental invariants of
$\delta (y)=a_{n-1}$, which is the maximal element in the fundamental invariants of ![]() $L^\flat $. It amounts to showing that for every fixed pair
$L^\flat $. It amounts to showing that for every fixed pair ![]() $(f_1,f_2)$ of generators of the
$(f_1,f_2)$ of generators of the ![]() $O_E$-module
$O_E$-module  $(V_{L^\flat }^\perp )^{\mathrm {int}}$, we have
$(V_{L^\flat }^\perp )^{\mathrm {int}}$, we have
 $$ \begin{align} \partial\mathrm{Den}_{L^\flat}^{\mathrm{v}}(y+u^\delta f_1)-\partial\mathrm{Den}_{L^\flat}^{\mathrm{v}}(y+u^{\delta-1} f_2)=0 \end{align} $$
$$ \begin{align} \partial\mathrm{Den}_{L^\flat}^{\mathrm{v}}(y+u^\delta f_1)-\partial\mathrm{Den}_{L^\flat}^{\mathrm{v}}(y+u^{\delta-1} f_2)=0 \end{align} $$for ![]() $\delta>a_{n-1}$. For every
$\delta>a_{n-1}$. For every ![]() $\delta '\in \mathbb {Z}$, we define two sets
$\delta '\in \mathbb {Z}$, we define two sets
 $$ \begin{align*} \mathfrak{L}_1^{\delta'}& := \{L\in\mathfrak{L}\mathbin{|} L\subseteq L^\vee,\delta_L=\delta',y+u^\delta f_1\in L\},\\ \mathfrak{L}_2^{\delta'}& := \{L\in\mathfrak{L}\mathbin{|} L\subseteq L^\vee,\delta_L=\delta',y+u^{\delta-1}f_2\in L\}. \end{align*} $$
$$ \begin{align*} \mathfrak{L}_1^{\delta'}& := \{L\in\mathfrak{L}\mathbin{|} L\subseteq L^\vee,\delta_L=\delta',y+u^\delta f_1\in L\},\\ \mathfrak{L}_2^{\delta'}& := \{L\in\mathfrak{L}\mathbin{|} L\subseteq L^\vee,\delta_L=\delta',y+u^{\delta-1}f_2\in L\}. \end{align*} $$By Remark 2.21(4), we have
 $$ \begin{align*} \partial\mathrm{Den}_{L^\flat}^{\mathrm{v}}(y+u^\delta f_1)&=2\sum_{\delta'\leqslant\delta}\sum_{\substack{L\in\mathfrak{L}_1^{\delta'}\\ t(L\cap V_{L^\flat})>1}}\mu(t(L)) =2\sum_{\substack{L^\flat\subseteq L^{\flat\prime}\subseteq (L^{\flat\prime})^\vee\\t(L^{\flat\prime})>1}}\sum_{\delta'\leqslant\delta} \sum_{\substack{L\in\mathfrak{L}_1^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L));\\ \partial\mathrm{Den}_{L^\flat}^{\mathrm{v}}(y+u^{\delta-1}f_2)&=2\sum_{\delta'\leqslant\delta-1}\sum_{\substack{L\in\mathfrak{L}_2^{\delta'}\\ t(L\cap V_{L^\flat})>1}}\mu(t(L)) =2\sum_{\substack{L^\flat\subseteq L^{\flat\prime}\subseteq (L^{\flat\prime})^\vee\\t(L^{\flat\prime})>1}}\sum_{\delta'\leqslant\delta-1} \sum_{\substack{L\in\mathfrak{L}_2^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L)). \end{align*} $$
$$ \begin{align*} \partial\mathrm{Den}_{L^\flat}^{\mathrm{v}}(y+u^\delta f_1)&=2\sum_{\delta'\leqslant\delta}\sum_{\substack{L\in\mathfrak{L}_1^{\delta'}\\ t(L\cap V_{L^\flat})>1}}\mu(t(L)) =2\sum_{\substack{L^\flat\subseteq L^{\flat\prime}\subseteq (L^{\flat\prime})^\vee\\t(L^{\flat\prime})>1}}\sum_{\delta'\leqslant\delta} \sum_{\substack{L\in\mathfrak{L}_1^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L));\\ \partial\mathrm{Den}_{L^\flat}^{\mathrm{v}}(y+u^{\delta-1}f_2)&=2\sum_{\delta'\leqslant\delta-1}\sum_{\substack{L\in\mathfrak{L}_2^{\delta'}\\ t(L\cap V_{L^\flat})>1}}\mu(t(L)) =2\sum_{\substack{L^\flat\subseteq L^{\flat\prime}\subseteq (L^{\flat\prime})^\vee\\t(L^{\flat\prime})>1}}\sum_{\delta'\leqslant\delta-1} \sum_{\substack{L\in\mathfrak{L}_2^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L)). \end{align*} $$Now we claim that
 $$ \begin{align} \sum_{\delta'\leqslant\delta} \sum_{\substack{L\in\mathfrak{L}_1^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L))- \sum_{\delta'\leqslant\delta-1} \sum_{\substack{L\in\mathfrak{L}_2^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L))=0 \end{align} $$
$$ \begin{align} \sum_{\delta'\leqslant\delta} \sum_{\substack{L\in\mathfrak{L}_1^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L))- \sum_{\delta'\leqslant\delta-1} \sum_{\substack{L\in\mathfrak{L}_2^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L))=0 \end{align} $$for every ![]() $L^{\flat \prime }$ in the summation. Since
$L^{\flat \prime }$ in the summation. Since ![]() $\delta>a_{n-1}$, it follows that for
$\delta>a_{n-1}$, it follows that for ![]() $\delta '<0$, we have
$\delta '<0$, we have
 $$ \begin{align*} \mathfrak{L}_1^{\delta'}=\mathfrak{L}_2^{\delta'}=\{L\in\mathfrak{L}\mathbin{|} L\subseteq L^\vee,\delta_L=\delta',y\in L\}. \end{align*} $$
$$ \begin{align*} \mathfrak{L}_1^{\delta'}=\mathfrak{L}_2^{\delta'}=\{L\in\mathfrak{L}\mathbin{|} L\subseteq L^\vee,\delta_L=\delta',y\in L\}. \end{align*} $$Thus, the left-hand side of (2.11) equals
 $$ \begin{align} \sum_{\delta'=0}^\delta \sum_{\substack{L\in\mathfrak{L}_1^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L))- \sum_{\delta'=0}^{\delta-1} \sum_{\substack{L\in\mathfrak{L}_2^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L)). \end{align} $$
$$ \begin{align} \sum_{\delta'=0}^\delta \sum_{\substack{L\in\mathfrak{L}_1^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L))- \sum_{\delta'=0}^{\delta-1} \sum_{\substack{L\in\mathfrak{L}_2^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L)). \end{align} $$However, we also have  $\mathfrak {L}_1^0=\{L\in \mathfrak {L}\mathbin {|} L\subseteq L^\vee ,\delta _L=\delta ',y\in L\}$, which implies
$\mathfrak {L}_1^0=\{L\in \mathfrak {L}\mathbin {|} L\subseteq L^\vee ,\delta _L=\delta ',y\in L\}$, which implies

which vanishes by Lemma 2.24(4). Thus, we obtain
 $$ \begin{align} (2.12) =\sum_{\delta'=1}^{\delta} \sum_{\substack{L\in\mathfrak{L}_1^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L))- \sum_{\delta'=0}^{\delta-1} \sum_{\substack{L\in\mathfrak{L}_2^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L)). \end{align} $$
$$ \begin{align} (2.12) =\sum_{\delta'=1}^{\delta} \sum_{\substack{L\in\mathfrak{L}_1^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L))- \sum_{\delta'=0}^{\delta-1} \sum_{\substack{L\in\mathfrak{L}_2^{\delta'}\\ L\cap V_{L^\flat}=L^{\flat\prime}}}\mu(t(L)). \end{align} $$Finally, the automorphism of ![]() $\mathfrak {E}$ sending
$\mathfrak {E}$ sending ![]() $(L^{\flat \prime },\delta ',\varepsilon )$ to
$(L^{\flat \prime },\delta ',\varepsilon )$ to ![]() $(L^{\flat \prime },\delta '-1,\varepsilon \circ (u\alpha \cdot ))$, where
$(L^{\flat \prime },\delta '-1,\varepsilon \circ (u\alpha \cdot ))$, where ![]() $\alpha \in O_E^\times $ is the element satisfying
$\alpha \in O_E^\times $ is the element satisfying ![]() $f_1=\alpha f_2$, induces a bijection from
$f_1=\alpha f_2$, induces a bijection from  $\mathfrak {L}_1^{\delta '}$ to
$\mathfrak {L}_1^{\delta '}$ to  $\mathfrak {L}_2^{\delta '-1}$ preserving both
$\mathfrak {L}_2^{\delta '-1}$ preserving both ![]() $L\cap V_{L^\flat }$ and
$L\cap V_{L^\flat }$ and ![]() $t(L)$. Thus, (2.13) vanishes; hence, (2.11) and (2.10) hold.
$t(L)$. Thus, (2.13) vanishes; hence, (2.11) and (2.10) hold.
Now we show that the support of  $\widehat {\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}}$ is contained in
$\widehat {\partial \mathrm {Den}_{L^\flat }^{\mathrm {v}}}$ is contained in ![]() $\boldsymbol {V}^{\mathrm {int}}$. Take an element
$\boldsymbol {V}^{\mathrm {int}}$. Take an element ![]() $z\in \boldsymbol {V}\setminus \boldsymbol {V}^{\mathrm {int}}$. Using Remark 2.21(4), we have
$z\in \boldsymbol {V}\setminus \boldsymbol {V}^{\mathrm {int}}$. Using Remark 2.21(4), we have

which is valid and vanishes by Lemma 2.24(3).
Proposition 2.22 is proved.
2.3 Bruhat–Tits stratification
Let the setup be as in Subsection 2.1. We first generalise Definition 2.5 to a more general context. For every subset X of ![]() $\boldsymbol {V}$ such that
$\boldsymbol {V}$ such that ![]() $\langle X\rangle $ is finitely generated, we put
$\langle X\rangle $ is finitely generated, we put
 $$ \begin{align*} \mathcal{N}(X) := \bigcap_{x\in X}\mathcal{N}(x), \end{align*} $$
$$ \begin{align*} \mathcal{N}(X) := \bigcap_{x\in X}\mathcal{N}(x), \end{align*} $$which is always a finite intersection and depends only on ![]() $\langle X\rangle $. Clearly, we have
$\langle X\rangle $. Clearly, we have ![]() $\mathcal {N}(X')\subseteq \mathcal {N}(X)$ if
$\mathcal {N}(X')\subseteq \mathcal {N}(X)$ if ![]() $\langle X\rangle \subseteq \langle X'\rangle $. When
$\langle X\rangle \subseteq \langle X'\rangle $. When ![]() $X=\{x,\dots \}$ is explicitly presented, we simply write
$X=\{x,\dots \}$ is explicitly presented, we simply write ![]() $\mathcal {N}(x,\dots )$ instead of
$\mathcal {N}(x,\dots )$ instead of ![]() $\mathcal {N}(\{x,\dots \})$.
$\mathcal {N}(\{x,\dots \})$.
Remark 2.26. When ![]() $\langle X\rangle $ is an
$\langle X\rangle $ is an ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}$, the formal subscheme
$\boldsymbol {V}$, the formal subscheme ![]() $\mathcal {N}(X)$ is a proper closed subscheme of
$\mathcal {N}(X)$ is a proper closed subscheme of ![]() $\mathcal {N}$. This can be proved by the same argument for [Reference Li and ZhangLZa, Lemma 2.10.1].
$\mathcal {N}$. This can be proved by the same argument for [Reference Li and ZhangLZa, Lemma 2.10.1].
Definition 2.27. Let ![]() $\Lambda $ be a vertex
$\Lambda $ be a vertex ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}$ (Definition 2.10).
$\boldsymbol {V}$ (Definition 2.10).
(1) We equip the k-vector space
 $\Lambda ^\vee /\Lambda $ with a k-valued pairing
$\Lambda ^\vee /\Lambda $ with a k-valued pairing  $(\,,\,)_{\Lambda ^\vee /\Lambda }$ by the formula where
$(\,,\,)_{\Lambda ^\vee /\Lambda }$ by the formula where $$ \begin{align*} (x,y)_{\Lambda^\vee/\Lambda} := u^2\operatorname{\mathrm{Tr}}_{E/F}(x^\sharp,y^\sharp)_{\boldsymbol{V}}\mod(u^2) \end{align*} $$
$$ \begin{align*} (x,y)_{\Lambda^\vee/\Lambda} := u^2\operatorname{\mathrm{Tr}}_{E/F}(x^\sharp,y^\sharp)_{\boldsymbol{V}}\mod(u^2) \end{align*} $$ $x^\sharp $ and
$x^\sharp $ and  $y^\sharp $ are arbitrary lifts of x and y, respectively. Then
$y^\sharp $ are arbitrary lifts of x and y, respectively. Then  $\Lambda ^\vee /\Lambda $ becomes a nonsplit (nondegenerate) quadratic space over k of (even positive) dimension
$\Lambda ^\vee /\Lambda $ becomes a nonsplit (nondegenerate) quadratic space over k of (even positive) dimension  $t(\Lambda )$.
$t(\Lambda )$.(2) Let
 $\mathcal {V}_\Lambda $ be the reduced subscheme of
$\mathcal {V}_\Lambda $ be the reduced subscheme of  $\mathcal {N}(\Lambda )$ and put
$\mathcal {N}(\Lambda )$ and put  $$ \begin{align*} \mathcal{V}_\Lambda^\circ := \mathcal{V}_\Lambda-\bigcup_{\Lambda\subsetneqq\Lambda'}\mathcal{V}_{\Lambda'}. \end{align*} $$
$$ \begin{align*} \mathcal{V}_\Lambda^\circ := \mathcal{V}_\Lambda-\bigcup_{\Lambda\subsetneqq\Lambda'}\mathcal{V}_{\Lambda'}. \end{align*} $$
Proposition 2.28 Bruhat–Tits stratification, [Reference WuWu]
The reduced subscheme ![]() $\mathcal {N}_{\mathrm {red}}$ is a disjoint union of
$\mathcal {N}_{\mathrm {red}}$ is a disjoint union of ![]() $ \mathcal {V}_\Lambda ^\circ $ for all vertex
$ \mathcal {V}_\Lambda ^\circ $ for all vertex ![]() $O_E$-lattices
$O_E$-lattices ![]() $\Lambda $ of
$\Lambda $ of ![]() $\boldsymbol {V}$ in the sense of stratification, such that
$\boldsymbol {V}$ in the sense of stratification, such that ![]() $\mathcal {V}_{\Lambda }\cap \mathcal {V}_{\Lambda '}$ coincides with
$\mathcal {V}_{\Lambda }\cap \mathcal {V}_{\Lambda '}$ coincides with ![]() $\mathcal {V}_{\Lambda +\Lambda '}$ (respectively is empty) if
$\mathcal {V}_{\Lambda +\Lambda '}$ (respectively is empty) if ![]() $\Lambda +\Lambda '$ is (respectively is not) a vertex
$\Lambda +\Lambda '$ is (respectively is not) a vertex ![]() $O_E$-lattice.
$O_E$-lattice.
Moreover, for every vertex ![]() $O_E$-lattice
$O_E$-lattice ![]() $\Lambda $,
$\Lambda $,
(1)
 $\mathcal {V}_\Lambda $ is canonically isomorphic to the generalised Deligne–Lusztig variety of
$\mathcal {V}_\Lambda $ is canonically isomorphic to the generalised Deligne–Lusztig variety of  $\operatorname {\mathrm {O}}(\Lambda ^\vee /\Lambda )$ over
$\operatorname {\mathrm {O}}(\Lambda ^\vee /\Lambda )$ over  $\overline {k}$ classifying maximal isotropic subspaces U of
$\overline {k}$ classifying maximal isotropic subspaces U of  $(\Lambda ^\vee /\Lambda )\otimes _k\overline {k}$ satisfying where
$(\Lambda ^\vee /\Lambda )\otimes _k\overline {k}$ satisfying where $$ \begin{align*} \dim(U\cap\delta(U))=\tfrac{t(\Lambda)}{2}-1, \end{align*} $$
$$ \begin{align*} \dim(U\cap\delta(U))=\tfrac{t(\Lambda)}{2}-1, \end{align*} $$ $\delta \in \operatorname {\mathrm {Gal}}(\overline {k}/k)$ denotes the Frobenius element;
$\delta \in \operatorname {\mathrm {Gal}}(\overline {k}/k)$ denotes the Frobenius element;(2) the intersection of
 $\mathcal {V}_\Lambda $ with each connected component of
$\mathcal {V}_\Lambda $ with each connected component of  $\mathcal {N}_{\mathrm {red}}$ is connected, nonempty and smooth projective over
$\mathcal {N}_{\mathrm {red}}$ is connected, nonempty and smooth projective over  $\overline {k}$ of dimension
$\overline {k}$ of dimension  $\tfrac {t(\Lambda )}{2}-1$.
$\tfrac {t(\Lambda )}{2}-1$.
Proof. This follows from [Reference WuWu, Proposition 5.13 & Theorem 5.18]. Note that we use lattices in ![]() $\boldsymbol {V}$, which is different from the hermitian space C used in [Reference WuWu], to parametrise strata. By the obvious analogue of [Reference KudlaKR11, Lemma 3.9], we may naturally identify
$\boldsymbol {V}$, which is different from the hermitian space C used in [Reference WuWu], to parametrise strata. By the obvious analogue of [Reference KudlaKR11, Lemma 3.9], we may naturally identify ![]() $\boldsymbol {V}$ with C, after which the stratum
$\boldsymbol {V}$ with C, after which the stratum ![]() $\mathcal {S}_\Lambda $ in [Reference WuWu] coincides with our stratum
$\mathcal {S}_\Lambda $ in [Reference WuWu] coincides with our stratum ![]() $\mathcal {V}_{u\Lambda ^\vee }$.
$\mathcal {V}_{u\Lambda ^\vee }$.
Remark 2.29. In the above proposition, when ![]() $t(\Lambda )=4$,
$t(\Lambda )=4$, ![]() $\mathcal {V}_\Lambda $ is isomorphic to two copies of
$\mathcal {V}_\Lambda $ is isomorphic to two copies of ![]() $\mathbb {P}^1_{\overline {k}}$, though we do not need this explicit description in the following.
$\mathbb {P}^1_{\overline {k}}$, though we do not need this explicit description in the following.
Corollary 2.30. For every nonzero element ![]() $x\in \boldsymbol {V}$, we have
$x\in \boldsymbol {V}$, we have
 $$ \begin{align*} \mathcal{N}(x)_{\mathrm{red}}=\bigcup_{x\in\Lambda}\mathcal{V}^\circ_\Lambda \end{align*} $$
$$ \begin{align*} \mathcal{N}(x)_{\mathrm{red}}=\bigcup_{x\in\Lambda}\mathcal{V}^\circ_\Lambda \end{align*} $$where the union is taken over all vertex ![]() $O_E$-lattices of
$O_E$-lattices of ![]() $\boldsymbol {V}$ containing x.
$\boldsymbol {V}$ containing x.
Proof. Since ![]() $\mathcal {N}(x)_{\mathrm {red}}$ is a reduced closed subscheme of
$\mathcal {N}(x)_{\mathrm {red}}$ is a reduced closed subscheme of ![]() $\mathcal {N}_{\mathrm {red}}$, it suffices to check that
$\mathcal {N}_{\mathrm {red}}$, it suffices to check that
 $$ \begin{align*} \mathcal{N}(x)(\overline{k})=\bigcup_{x\in\Lambda}\mathcal{V}^\circ_\Lambda(\overline{k}). \end{align*} $$
$$ \begin{align*} \mathcal{N}(x)(\overline{k})=\bigcup_{x\in\Lambda}\mathcal{V}^\circ_\Lambda(\overline{k}). \end{align*} $$By Definition 2.27(2), we have
 $$ \begin{align*} \mathcal{N}(x)(\overline{k})\supseteq\bigcup_{x\in\Lambda}\mathcal{V}^\circ_\Lambda(\overline{k}). \end{align*} $$
$$ \begin{align*} \mathcal{N}(x)(\overline{k})\supseteq\bigcup_{x\in\Lambda}\mathcal{V}^\circ_\Lambda(\overline{k}). \end{align*} $$For the other direction, by Proposition 2.28, we have to show that if ![]() $\Lambda $ does not contain x, then
$\Lambda $ does not contain x, then  $\mathcal {N}(x)(\overline {k})\cap \mathcal {V}^\circ _\Lambda (\overline {k})=\emptyset $. Suppose that we have
$\mathcal {N}(x)(\overline {k})\cap \mathcal {V}^\circ _\Lambda (\overline {k})=\emptyset $. Suppose that we have  $s\in \mathcal {N}(x)(\overline {k})\cap \mathcal {V}^\circ _\Lambda (\overline {k})$; then s should belong to
$s\in \mathcal {N}(x)(\overline {k})\cap \mathcal {V}^\circ _\Lambda (\overline {k})$; then s should belong to ![]() $\mathcal {V}_{\Lambda '}(\overline {k})$ where
$\mathcal {V}_{\Lambda '}(\overline {k})$ where ![]() $\Lambda '$ is the
$\Lambda '$ is the ![]() $O_E$-lattice generated by
$O_E$-lattice generated by ![]() $\Lambda $ and x. In particular,
$\Lambda $ and x. In particular, ![]() $\Lambda '$ is vertex and strictly contains
$\Lambda '$ is vertex and strictly contains ![]() $\Lambda $. But this contradicts with the definition of
$\Lambda $. But this contradicts with the definition of ![]() $\mathcal {V}^\circ _\Lambda $. The corollary follows.
$\mathcal {V}^\circ _\Lambda $. The corollary follows.
Corollary 2.31. Suppose that ![]() $r\geqslant 2$. For every nonzero element
$r\geqslant 2$. For every nonzero element ![]() $x\in \boldsymbol {V}$, the intersection of
$x\in \boldsymbol {V}$, the intersection of ![]() $\mathcal {N}(x)$ with each connected component of
$\mathcal {N}(x)$ with each connected component of ![]() $\mathcal {N}_{\mathrm {red}}$ is strictly a closed subscheme of the latter.
$\mathcal {N}_{\mathrm {red}}$ is strictly a closed subscheme of the latter.
Proof. By Corollary 2.30 and Proposition 2.28(2), it suffices to show that the intersection of all vertex ![]() $O_E$-lattices of
$O_E$-lattices of ![]() $\boldsymbol {V}$ is
$\boldsymbol {V}$ is ![]() $\{0\}$.
$\{0\}$.
Take a nonsplit hermitian subspace ![]() $V_2$ of
$V_2$ of ![]() $\boldsymbol {V}$ of dimension
$\boldsymbol {V}$ of dimension ![]() $2$ and an
$2$ and an ![]() $O_E$-lattice
$O_E$-lattice ![]() $L_2$ of
$L_2$ of ![]() $V_2$ of fundamental invariants
$V_2$ of fundamental invariants ![]() $(1,1)$. Then the orthogonal complement
$(1,1)$. Then the orthogonal complement ![]() $V_2^\perp $ of
$V_2^\perp $ of ![]() $V_2$ in
$V_2$ in ![]() $\boldsymbol {V}$ admits a self-dual
$\boldsymbol {V}$ admits a self-dual ![]() $O_E$-lattice
$O_E$-lattice ![]() $L_1$. Choose a normal basis (Definition 2.11)
$L_1$. Choose a normal basis (Definition 2.11) ![]() $\{e_1,\dots ,e_{2r-2}\}$ of
$\{e_1,\dots ,e_{2r-2}\}$ of ![]() $L_1$ under which the moment matrix is given by
$L_1$ under which the moment matrix is given by  $\left (\begin {smallmatrix} 0 & u^{-1}\\ -u^{-1} & 0 \end {smallmatrix}\right )^{\oplus r-1}$. For every tuple
$\left (\begin {smallmatrix} 0 & u^{-1}\\ -u^{-1} & 0 \end {smallmatrix}\right )^{\oplus r-1}$. For every tuple ![]() $a=(a_1,\dots ,a_{2r-2})\in \mathbb {Z}^{2r-2}$ satisfying
$a=(a_1,\dots ,a_{2r-2})\in \mathbb {Z}^{2r-2}$ satisfying ![]() $a_{2i-1}+a_{2i}=0$ for
$a_{2i-1}+a_{2i}=0$ for ![]() $1\leqslant i\leqslant r-1$, the
$1\leqslant i\leqslant r-1$, the ![]() $O_E$-lattice
$O_E$-lattice
is integral with fundamental invariants ![]() $(0,\dots ,0,1,1)$ and, hence, vertex. It is clear that the intersection of all such
$(0,\dots ,0,1,1)$ and, hence, vertex. It is clear that the intersection of all such ![]() $\Lambda _a$ is
$\Lambda _a$ is ![]() $L_2$. Since
$L_2$. Since ![]() $r\geqslant 2$, the intersection of all
$r\geqslant 2$, the intersection of all ![]() $2$-dimensional nonsplit hermitian subspaces of
$2$-dimensional nonsplit hermitian subspaces of ![]() $\boldsymbol {V}$ is
$\boldsymbol {V}$ is ![]() $\{0\}$. Thus, the intersection of all vertex
$\{0\}$. Thus, the intersection of all vertex ![]() $O_E$-lattices of
$O_E$-lattices of ![]() $\boldsymbol {V}$ is
$\boldsymbol {V}$ is ![]() $\{0\}$.
$\{0\}$.
Lemma 2.32. Let ![]() $\Lambda $ be a vertex
$\Lambda $ be a vertex ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}$. For each connected component
$\boldsymbol {V}$. For each connected component ![]() $\mathcal {V}_\Lambda ^+$ of
$\mathcal {V}_\Lambda ^+$ of ![]() $\mathcal {V}_\Lambda $ and integer
$\mathcal {V}_\Lambda $ and integer ![]() $d\geqslant 0$, the group of d-cycles of
$d\geqslant 0$, the group of d-cycles of ![]() $\mathcal {V}_\Lambda ^+$, up to
$\mathcal {V}_\Lambda ^+$, up to ![]() $\ell $-adic homological equivalence for every rational prime
$\ell $-adic homological equivalence for every rational prime ![]() $\ell \neq p$, is generated by
$\ell \neq p$, is generated by ![]() $\mathcal {V}_{\Lambda '}\cap \mathcal {V}_\Lambda ^+$ for all vertex
$\mathcal {V}_{\Lambda '}\cap \mathcal {V}_\Lambda ^+$ for all vertex ![]() $O_E$-lattices
$O_E$-lattices ![]() $\Lambda '$ containing
$\Lambda '$ containing ![]() $\Lambda $ with
$\Lambda $ with ![]() $t(\Lambda ')=2d+2$.
$t(\Lambda ')=2d+2$.
Proof. Let ![]() $k'$ be the quadratic extension of k in
$k'$ be the quadratic extension of k in ![]() $\overline {k}$. Note that
$\overline {k}$. Note that ![]() $\mathcal {V}_\Lambda ^+$ has a canonical structure over
$\mathcal {V}_\Lambda ^+$ has a canonical structure over ![]() $k'$, so that
$k'$, so that ![]() $\mathcal {V}_\Lambda ^{\circ +} := \mathcal {V}_\Lambda ^\circ \cap \mathcal {V}_\Lambda ^+$ (over
$\mathcal {V}_\Lambda ^{\circ +} := \mathcal {V}_\Lambda ^\circ \cap \mathcal {V}_\Lambda ^+$ (over ![]() $k'$) is the classical Deligne–Lusztig variety of
$k'$) is the classical Deligne–Lusztig variety of ![]() $\operatorname {\mathrm {SO}}(\Lambda ^\vee /\Lambda )$ of Coxeter type.
$\operatorname {\mathrm {SO}}(\Lambda ^\vee /\Lambda )$ of Coxeter type.
Recall that ![]() $\delta $ is the Frobenius element of
$\delta $ is the Frobenius element of ![]() $\operatorname {\mathrm {Gal}}(\overline {k}/k)$. Fix a rational prime
$\operatorname {\mathrm {Gal}}(\overline {k}/k)$. Fix a rational prime ![]() $\ell $ different from p. For every finite-dimensional
$\ell $ different from p. For every finite-dimensional ![]() $\overline {\mathbb {Q}}_\ell $-vector space V with an action by
$\overline {\mathbb {Q}}_\ell $-vector space V with an action by ![]() $\delta ^2$, we denote by
$\delta ^2$, we denote by ![]() $V^\dagger $ the subspace consisting of elements on which
$V^\dagger $ the subspace consisting of elements on which ![]() $\delta ^2$ acts by roots of unity. Then for the lemma, it suffices to show that for every
$\delta ^2$ acts by roots of unity. Then for the lemma, it suffices to show that for every ![]() $d\geqslant 0$,
$d\geqslant 0$,  $\mathrm {H}_{2d}(\mathcal {V}_\Lambda ^+,\overline {\mathbb {Q}}_\ell (-d))^\dagger $ is generated by (the cycle class of)
$\mathrm {H}_{2d}(\mathcal {V}_\Lambda ^+,\overline {\mathbb {Q}}_\ell (-d))^\dagger $ is generated by (the cycle class of) ![]() $\mathcal {V}_{\Lambda '}\cap \mathcal {V}_\Lambda ^+$ for all vertex
$\mathcal {V}_{\Lambda '}\cap \mathcal {V}_\Lambda ^+$ for all vertex ![]() $O_E$-lattices
$O_E$-lattices ![]() $\Lambda '$ containing
$\Lambda '$ containing ![]() $\Lambda $ with
$\Lambda $ with ![]() $t(\Lambda ')=2d+2$. By the same argument for [Reference Li and ZhangLZa, Theorem 5.3.2], it reduces to the following claim:
$t(\Lambda ')=2d+2$. By the same argument for [Reference Li and ZhangLZa, Theorem 5.3.2], it reduces to the following claim:
(*) The action of
 $\delta ^2$ on
$\delta ^2$ on  $V := \bigoplus _{j\geqslant 0}\mathrm {H}^{2j}(\mathcal {V}_\Lambda ^{\circ +},\overline {\mathbb {Q}}_\ell (j))$ is semisimple and
$V := \bigoplus _{j\geqslant 0}\mathrm {H}^{2j}(\mathcal {V}_\Lambda ^{\circ +},\overline {\mathbb {Q}}_\ell (j))$ is semisimple and  $V^\dagger =\mathrm {H}^0(\mathcal {V}_\Lambda ^{\circ +},\overline {\mathbb {Q}}_\ell )$.
$V^\dagger =\mathrm {H}^0(\mathcal {V}_\Lambda ^{\circ +},\overline {\mathbb {Q}}_\ell )$.
There are three cases.
When ![]() $t(\Lambda )=2$,
$t(\Lambda )=2$, ![]() $\mathcal {V}_\Lambda ^{\circ +}$ is isomorphic to
$\mathcal {V}_\Lambda ^{\circ +}$ is isomorphic to ![]() $\operatorname {\mathrm {Spec}}\overline {k}$; hence, (
$\operatorname {\mathrm {Spec}}\overline {k}$; hence, (![]() $*$) is trivial.
$*$) is trivial.
When ![]() $t(\Lambda )=4$,
$t(\Lambda )=4$, ![]() $\mathcal {V}_\Lambda ^{\circ +}$ is an affine curve; hence, (
$\mathcal {V}_\Lambda ^{\circ +}$ is an affine curve; hence, (![]() $*$) is again trivial.
$*$) is again trivial.
When ![]() $t(\Lambda )\geqslant 6$, by Case
$t(\Lambda )\geqslant 6$, by Case ![]() (with
(with  $n=\tfrac {t(\Lambda )}{2}\geqslant 3$) in [Reference LusztigLus76, Section 7.3], the action of
$n=\tfrac {t(\Lambda )}{2}\geqslant 3$) in [Reference LusztigLus76, Section 7.3], the action of ![]() $\delta ^2$ on
$\delta ^2$ on  $\bigoplus _{j\geqslant 0}\mathrm {H}^j_c(\mathcal {V}_\Lambda ^{\circ +},\overline {\mathbb {Q}}_\ell )$ has eigenvalues
$\bigoplus _{j\geqslant 0}\mathrm {H}^j_c(\mathcal {V}_\Lambda ^{\circ +},\overline {\mathbb {Q}}_\ell )$ has eigenvalues ![]() $\{1,q^2,q^4,\dots ,q^{t(\Lambda )-2}\}$ and the eigenvalue
$\{1,q^2,q^4,\dots ,q^{t(\Lambda )-2}\}$ and the eigenvalue ![]() $q^{2j}$ appears in
$q^{2j}$ appears in 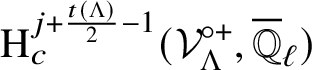 $\mathrm {H}^{j+\frac {t(\Lambda )}{2}-1}_c(\mathcal {V}_\Lambda ^{\circ +},\overline {\mathbb {Q}}_\ell )$. Moreover by [Reference LusztigLus76, Theorem 6.1], the action of
$\mathrm {H}^{j+\frac {t(\Lambda )}{2}-1}_c(\mathcal {V}_\Lambda ^{\circ +},\overline {\mathbb {Q}}_\ell )$. Moreover by [Reference LusztigLus76, Theorem 6.1], the action of ![]() $\delta ^2$ is semisimple. Thus, (
$\delta ^2$ is semisimple. Thus, (![]() $*$) follows from the Poincaré duality.
$*$) follows from the Poincaré duality.
The lemma is proved.
2.4 Linear invariance of intersection numbers
Let the setup be as in Subsection 2.1. For every nonzero element ![]() $x\in \boldsymbol {V}$, we define a chain complex of locally free
$x\in \boldsymbol {V}$, we define a chain complex of locally free ![]() $\mathscr {O}_{\mathcal {N}}$-modules
$\mathscr {O}_{\mathcal {N}}$-modules
supported in degrees ![]() $1$ and
$1$ and ![]() $0$ with the map
$0$ with the map ![]() $\mathscr {I}_{\mathcal {N}(x)} \to \mathscr {O}_{\mathcal {N}}$ being the natural inclusion. We extend the definition to
$\mathscr {I}_{\mathcal {N}(x)} \to \mathscr {O}_{\mathcal {N}}$ being the natural inclusion. We extend the definition to ![]() $x=0$ by setting
$x=0$ by setting
 $$ \begin{align} C(0) := \left(\cdots\to 0 \to \omega \xrightarrow{0} \mathscr{O}_{\mathcal{N}} \to 0\right) \end{align} $$
$$ \begin{align} C(0) := \left(\cdots\to 0 \to \omega \xrightarrow{0} \mathscr{O}_{\mathcal{N}} \to 0\right) \end{align} $$supported in degrees ![]() $1$ and
$1$ and ![]() $0$, where
$0$, where ![]() $\omega $ is the line bundle from Definition 2.38.
$\omega $ is the line bundle from Definition 2.38.
The following is our main result of this subsection.
Proposition 2.33. Let ![]() $0\leqslant m\leqslant n$ be an integer. Suppose that
$0\leqslant m\leqslant n$ be an integer. Suppose that ![]() $x_1,\dots ,x_m\in \boldsymbol {V}$ and
$x_1,\dots ,x_m\in \boldsymbol {V}$ and ![]() $y_1,\dots ,y_m\in \boldsymbol {V}$ generate the same
$y_1,\dots ,y_m\in \boldsymbol {V}$ generate the same ![]() $O_E$-submodule. Then we have an isomorphism
$O_E$-submodule. Then we have an isomorphism
of ![]() $\mathscr {O}_{\mathcal {N}}$-modules for every i.
$\mathscr {O}_{\mathcal {N}}$-modules for every i.
Proposition 2.33 has the following two immediate corollaries.
Corollary 2.34. Let ![]() $0\leqslant m\leqslant n$ be an integer. Suppose that
$0\leqslant m\leqslant n$ be an integer. Suppose that ![]() $x_1,\dots ,x_m\in \boldsymbol {V}$ and
$x_1,\dots ,x_m\in \boldsymbol {V}$ and ![]() $y_1,\dots ,y_m\in \boldsymbol {V}$ generate the same
$y_1,\dots ,y_m\in \boldsymbol {V}$ generate the same ![]() $O_E$-submodule. Then we have
$O_E$-submodule. Then we have
in ![]() $\mathrm {K}_0(\mathcal {N})$, where
$\mathrm {K}_0(\mathcal {N})$, where ![]() $\mathrm {K}_0(\mathcal {N})$ denotes the K-group of
$\mathrm {K}_0(\mathcal {N})$ denotes the K-group of ![]() $\mathcal {N}$ [Reference Li and LiuLL21, Section B].
$\mathcal {N}$ [Reference Li and LiuLL21, Section B].
Corollary 2.35. Suppose that ![]() $x_1,\dots ,x_n\in \boldsymbol {V}$ generate an
$x_1,\dots ,x_n\in \boldsymbol {V}$ generate an ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}$. The Serre intersection multiplicity
$\boldsymbol {V}$. The Serre intersection multiplicity
 $$ \begin{align*} \chi\left(\mathscr{O}_{\mathcal{N}(x_1)}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\cdots\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x_n)}\right) := \sum_{i,j\geqslant 0}(-1)^{i+j}\mathrm{length}_{O_{\breve{E}}} \mathrm{H}^j\left(\mathcal{N},\mathrm{H}_i\left(\mathscr{O}_{\mathcal{N}(x_1)}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\cdots\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x_n)}\right)\right) \end{align*} $$
$$ \begin{align*} \chi\left(\mathscr{O}_{\mathcal{N}(x_1)}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\cdots\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x_n)}\right) := \sum_{i,j\geqslant 0}(-1)^{i+j}\mathrm{length}_{O_{\breve{E}}} \mathrm{H}^j\left(\mathcal{N},\mathrm{H}_i\left(\mathscr{O}_{\mathcal{N}(x_1)}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\cdots\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x_n)}\right)\right) \end{align*} $$depends only on the ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}$ generated by
$\boldsymbol {V}$ generated by ![]() $x_1,\dots ,x_n$. Note that by construction, the element
$x_1,\dots ,x_n$. Note that by construction, the element ![]() $[C(x_1)\otimes _{\mathscr {O}_{\mathcal {N}}}\cdots \otimes _{\mathscr {O}_{\mathcal {N}}} C(x_m)]$ belongs to the image of the map
$[C(x_1)\otimes _{\mathscr {O}_{\mathcal {N}}}\cdots \otimes _{\mathscr {O}_{\mathcal {N}}} C(x_m)]$ belongs to the image of the map  $\mathrm {K}_0^{\mathcal {N}(x_1,\dots ,x_m)}(\mathcal {N})\to \mathrm {K}_0(\mathcal {N})$; hence, the above number is finite by Remark 2.26.
$\mathrm {K}_0^{\mathcal {N}(x_1,\dots ,x_m)}(\mathcal {N})\to \mathrm {K}_0(\mathcal {N})$; hence, the above number is finite by Remark 2.26.
Now we start to prove Proposition 2.33, following [Reference HowardHow19]. Let ![]() $(X,\iota _X,\lambda _X)$ be the universal object over
$(X,\iota _X,\lambda _X)$ be the universal object over ![]() $\mathcal {N}$. We have a short exact sequence
$\mathcal {N}$. We have a short exact sequence
of locally free ![]() $\mathscr {O}_{\mathcal {N}}$-modules, where
$\mathscr {O}_{\mathcal {N}}$-modules, where ![]() $\mathrm {D}(X)$ denotes the covariant crystal of X restricted to the Zariski site of
$\mathrm {D}(X)$ denotes the covariant crystal of X restricted to the Zariski site of ![]() $\mathcal {N}$. Then
$\mathcal {N}$. Then ![]() $\iota _X$ induces actions of
$\iota _X$ induces actions of ![]() $O_E$ on all terms such that the short exact sequence is
$O_E$ on all terms such that the short exact sequence is ![]() $O_E$-linear.
$O_E$-linear.
We define an ![]() $\mathscr {O}_{\mathcal {N}}$-submodule
$\mathscr {O}_{\mathcal {N}}$-submodule ![]() $F_X$ of
$F_X$ of ![]() $\operatorname {\mathrm {Lie}}(X)$ as the kernel of
$\operatorname {\mathrm {Lie}}(X)$ as the kernel of ![]() $\iota _X(u)-u$ on
$\iota _X(u)-u$ on ![]() $\operatorname {\mathrm {Lie}}(X)$, which is stable under the
$\operatorname {\mathrm {Lie}}(X)$, which is stable under the ![]() $O_E$-action.
$O_E$-action.
Lemma 2.36. The ![]() $\mathscr {O}_{\mathcal {N}}$-submodule
$\mathscr {O}_{\mathcal {N}}$-submodule ![]() $F_X$ is locally free of rank
$F_X$ is locally free of rank ![]() $n-1$ and is locally a direct summand of
$n-1$ and is locally a direct summand of ![]() $\operatorname {\mathrm {Lie}}(X)$.
$\operatorname {\mathrm {Lie}}(X)$.
Proof. Let ![]() $s\in \mathcal {N}(\overline {k})$ be a closed point. By the wedge condition and the spin condition in Definition 2.1, we know that the map
$s\in \mathcal {N}(\overline {k})$ be a closed point. By the wedge condition and the spin condition in Definition 2.1, we know that the map
has rank ![]() $1$ on both generic and special fibres. Thus,
$1$ on both generic and special fibres. Thus, ![]() $F_X\otimes _{\mathscr {O}_{\mathcal {N}}}\mathscr {O}_{\mathcal {N},s}$ is a direct summand of
$F_X\otimes _{\mathscr {O}_{\mathcal {N}}}\mathscr {O}_{\mathcal {N},s}$ is a direct summand of ![]() $\operatorname {\mathrm {Lie}}(X)\otimes _{\mathscr {O}_{\mathcal {N}}}\mathscr {O}_{\mathcal {N},s}$ of rank
$\operatorname {\mathrm {Lie}}(X)\otimes _{\mathscr {O}_{\mathcal {N}}}\mathscr {O}_{\mathcal {N},s}$ of rank ![]() $n-1$. The lemma follows.
$n-1$. The lemma follows.
The symmetrisation ![]() $\sigma _X$ of the polarisation
$\sigma _X$ of the polarisation ![]() $\lambda _X$ (Remark 2.2) induces a perfect symmetric
$\lambda _X$ (Remark 2.2) induces a perfect symmetric ![]() $\mathscr {O}_{\mathcal {N}}$-bilinear pairing
$\mathscr {O}_{\mathcal {N}}$-bilinear pairing
satisfying ![]() $(\iota _X(\alpha )x,y)=(x,\iota _X(\alpha ^{\mathtt {c}})y)$ for every
$(\iota _X(\alpha )x,y)=(x,\iota _X(\alpha ^{\mathtt {c}})y)$ for every ![]() $\alpha \in O_E$ and
$\alpha \in O_E$ and ![]() $x,y\in \mathrm {D}(X)$. As
$x,y\in \mathrm {D}(X)$. As ![]() $\operatorname {\mathrm {Fil}}(X)$ is a maximal isotropic
$\operatorname {\mathrm {Fil}}(X)$ is a maximal isotropic ![]() $\mathscr {O}_{\mathcal {N}}$-submodule of
$\mathscr {O}_{\mathcal {N}}$-submodule of ![]() $\mathrm {D}(X)$ with respect to
$\mathrm {D}(X)$ with respect to ![]() $(\,,\,)$, we have an induced perfect
$(\,,\,)$, we have an induced perfect ![]() $\mathscr {O}_{\mathcal {N}}$-bilinear pairing
$\mathscr {O}_{\mathcal {N}}$-bilinear pairing
under which we denote by ![]() $F_X^\perp \subseteq \operatorname {\mathrm {Fil}}(X)$ the annihilator of
$F_X^\perp \subseteq \operatorname {\mathrm {Fil}}(X)$ the annihilator of ![]() $F_X$. Then the
$F_X$. Then the ![]() $\mathscr {O}_{\mathcal {N}}$-submodule
$\mathscr {O}_{\mathcal {N}}$-submodule ![]() $F_X^\perp $ is locally free of rank
$F_X^\perp $ is locally free of rank ![]() $1$ and is locally a direct summand of
$1$ and is locally a direct summand of ![]() $\operatorname {\mathrm {Fil}}(X)$.
$\operatorname {\mathrm {Fil}}(X)$.
Following [Reference HowardHow19, Section 3], we put
 $$ \begin{align*} \epsilon & := u\otimes 1 + 1\otimes u \in O_E\otimes_{O_F}\mathscr{O}_{\mathcal{N}},\\ \epsilon^{\mathtt{c}} & := -u\otimes 1 + 1\otimes u \in O_E\otimes_{O_F}\mathscr{O}_{\mathcal{N}}. \end{align*} $$
$$ \begin{align*} \epsilon & := u\otimes 1 + 1\otimes u \in O_E\otimes_{O_F}\mathscr{O}_{\mathcal{N}},\\ \epsilon^{\mathtt{c}} & := -u\otimes 1 + 1\otimes u \in O_E\otimes_{O_F}\mathscr{O}_{\mathcal{N}}. \end{align*} $$Lemma 2.37. There are inclusions of ![]() $\mathscr {O}_{\mathcal {N}}$-modules
$\mathscr {O}_{\mathcal {N}}$-modules ![]() $F_X^\perp \subseteq \epsilon \mathrm {D}(X)\subseteq \mathrm {D}(X)$, which are locally direct summands. The map
$F_X^\perp \subseteq \epsilon \mathrm {D}(X)\subseteq \mathrm {D}(X)$, which are locally direct summands. The map ![]() $\epsilon \colon \mathrm {D}(X)\to \epsilon \mathrm {D}(X)$ descends to a surjective map
$\epsilon \colon \mathrm {D}(X)\to \epsilon \mathrm {D}(X)$ descends to a surjective map
 $$ \begin{align*} \operatorname{\mathrm{Lie}}(X)\xrightarrow{\epsilon}\epsilon\mathrm{D}(X)/F_X^\perp, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Lie}}(X)\xrightarrow{\epsilon}\epsilon\mathrm{D}(X)/F_X^\perp, \end{align*} $$whose kernel ![]() $L_X$ is locally a direct summand
$L_X$ is locally a direct summand ![]() $\mathscr {O}_{\mathcal {N}}$-submodule of
$\mathscr {O}_{\mathcal {N}}$-submodule of ![]() $\operatorname {\mathrm {Lie}}(X)$ of rank
$\operatorname {\mathrm {Lie}}(X)$ of rank ![]() $1$. Moreover, the
$1$. Moreover, the ![]() $O_E$-action stabilises
$O_E$-action stabilises ![]() $L_X$ and
$L_X$ and ![]() $O_E$ acts on
$O_E$ acts on ![]() $\operatorname {\mathrm {Lie}}(X)/L_X$ and
$\operatorname {\mathrm {Lie}}(X)/L_X$ and ![]() $L_X$ via
$L_X$ via ![]() $\varphi _0$ and
$\varphi _0$ and ![]() $\varphi _0^{\mathtt {c}}$, respectively.
$\varphi _0^{\mathtt {c}}$, respectively.
Proof. This follows from the same proof for [Reference HowardHow19, Proposition 3.3].
Definition 2.38. We define the line bundle of modular forms ![]() $\omega $ to be
$\omega $ to be  $L_X^{-1}$, where
$L_X^{-1}$, where ![]() $L_X$ is the line bundle on
$L_X$ is the line bundle on ![]() $\mathcal {N}$ from Lemma 2.37.
$\mathcal {N}$ from Lemma 2.37.
For every closed formal subscheme Z of ![]() $\mathcal {N}$, we denote by
$\mathcal {N}$, we denote by ![]() $\widetilde {Z}$ the closed formal subscheme defined by the sheaf
$\widetilde {Z}$ the closed formal subscheme defined by the sheaf  $\mathscr {I}_Z^2$. Take a nonzero element
$\mathscr {I}_Z^2$. Take a nonzero element ![]() $x\in \boldsymbol {V}$. By the definition of
$x\in \boldsymbol {V}$. By the definition of ![]() $\mathcal {N}(x)$, we have a distinguished morphism
$\mathcal {N}(x)$, we have a distinguished morphism
 $$ \begin{align*} X_0\mathbin{|}_{\mathcal{N}(x)}\xrightarrow{x} X\mathbin{|}_{\mathcal{N}(x)} \end{align*} $$
$$ \begin{align*} X_0\mathbin{|}_{\mathcal{N}(x)}\xrightarrow{x} X\mathbin{|}_{\mathcal{N}(x)} \end{align*} $$of ![]() $O_F$-divisible groups, which induces an
$O_F$-divisible groups, which induces an ![]() $O_E$-linear map
$O_E$-linear map
 $$ \begin{align*} \mathrm{D}(X_0)\mathbin{|}_{\mathcal{N}(x)}\xrightarrow{x}\mathrm{D}(X)\mathbin{|}_{\mathcal{N}(x)} \end{align*} $$
$$ \begin{align*} \mathrm{D}(X_0)\mathbin{|}_{\mathcal{N}(x)}\xrightarrow{x}\mathrm{D}(X)\mathbin{|}_{\mathcal{N}(x)} \end{align*} $$of vector bundles. By the Grothendieck–Messing theory, the above map admits a canonical extension
 $$ \begin{align*} \mathrm{D}(X_0)\mathbin{|}_{\widetilde{\mathcal{N}(x)}}\xrightarrow{\tilde{x}}\mathrm{D}(X)\mathbin{|}_{\widetilde{\mathcal{N}(x)}}, \end{align*} $$
$$ \begin{align*} \mathrm{D}(X_0)\mathbin{|}_{\widetilde{\mathcal{N}(x)}}\xrightarrow{\tilde{x}}\mathrm{D}(X)\mathbin{|}_{\widetilde{\mathcal{N}(x)}}, \end{align*} $$which further restricts to a map
 $$ \begin{align} \operatorname{\mathrm{Fil}}(X_0)\mathbin{|}_{\widetilde{\mathcal{N}(x)}}\xrightarrow{\tilde{x}}\operatorname{\mathrm{Lie}}(X)\mathbin{|}_{\widetilde{\mathcal{N}(x)}}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Fil}}(X_0)\mathbin{|}_{\widetilde{\mathcal{N}(x)}}\xrightarrow{\tilde{x}}\operatorname{\mathrm{Lie}}(X)\mathbin{|}_{\widetilde{\mathcal{N}(x)}}. \end{align} $$ From now on, we fix a generator ![]() $\gamma $ of the rank
$\gamma $ of the rank ![]() $1$ free
$1$ free ![]() $O_{\breve {E}}$-module
$O_{\breve {E}}$-module ![]() $\operatorname {\mathrm {Fil}}(X_0)$.
$\operatorname {\mathrm {Fil}}(X_0)$.
Lemma 2.39. The image ![]() $\tilde {x}(\gamma )$ is a section of
$\tilde {x}(\gamma )$ is a section of ![]() $L_X$ over
$L_X$ over  $\widetilde {\mathcal {N}(x)}$, whose vanishing locus coincides with
$\widetilde {\mathcal {N}(x)}$, whose vanishing locus coincides with ![]() $\mathcal {N}(x)$, where
$\mathcal {N}(x)$, where ![]() $\tilde {x}$ is the map (2.15).
$\tilde {x}$ is the map (2.15).
Proof. This follows from the same proof for [Reference HowardHow19, Proposition 4.1].
The following lemma is parallel to [Reference KudlaKR11, Proposition 3.5].
Lemma 2.40. For every nonzero element ![]() $x\in \boldsymbol {V}$, the closed formal subscheme
$x\in \boldsymbol {V}$, the closed formal subscheme ![]() $\mathcal {N}(x)$ of
$\mathcal {N}(x)$ of ![]() $\mathcal {N}$ is either empty or a relative Cartier divisor.
$\mathcal {N}$ is either empty or a relative Cartier divisor.
Proof. The case ![]() $r=1$ has been proved in [Reference Rapoport, Smithling and ZhangRSZ17, Proposition 6.6]. Thus, we now assume
$r=1$ has been proved in [Reference Rapoport, Smithling and ZhangRSZ17, Proposition 6.6]. Thus, we now assume ![]() $r\geqslant 2$.
$r\geqslant 2$.
We may assume that ![]() $\mathcal {N}(x)$ is nonempty. By the same argument in the proof of [Reference HowardHow19, Proposition 4.3],
$\mathcal {N}(x)$ is nonempty. By the same argument in the proof of [Reference HowardHow19, Proposition 4.3], ![]() $\mathcal {N}(x)$ is locally defined by one equation. It remains to show that such an equation is not divisible by u. Since
$\mathcal {N}(x)$ is locally defined by one equation. It remains to show that such an equation is not divisible by u. Since ![]() $r\geqslant 2$, this follows from [Reference KudlaKR11, Lemma 3.6], Lemma 2.4 and Corollary 2.31.
$r\geqslant 2$, this follows from [Reference KudlaKR11, Lemma 3.6], Lemma 2.4 and Corollary 2.31.
Proof of Proposition 2.33.
The proof of [Reference HowardHow19, Theorem 5.1] can be applied in the same way to Proposition 2.33, using Lemma 2.39 and Lemma 2.40.
To end this subsection, we prove some results that will be used later.
Lemma 2.41. The ![]() $\mathscr {O}_{\mathcal {N}}$-submodule
$\mathscr {O}_{\mathcal {N}}$-submodule ![]() $L_X$ from Lemma 2.37 coincides with the image of the map
$L_X$ from Lemma 2.37 coincides with the image of the map ![]() $\iota _X(u)-u\colon \operatorname {\mathrm {Lie}}(X)\to \operatorname {\mathrm {Lie}}(X)$.
$\iota _X(u)-u\colon \operatorname {\mathrm {Lie}}(X)\to \operatorname {\mathrm {Lie}}(X)$.
Proof. Denote by ![]() $L^{\prime }_X$ the image of the map
$L^{\prime }_X$ the image of the map ![]() $\iota _X(u)-u\colon \operatorname {\mathrm {Lie}}(X)\to \operatorname {\mathrm {Lie}}(X)$. As we have
$\iota _X(u)-u\colon \operatorname {\mathrm {Lie}}(X)\to \operatorname {\mathrm {Lie}}(X)$. As we have ![]() $L^{\prime }_X\simeq \operatorname {\mathrm {Lie}}(X)/F_X$,
$L^{\prime }_X\simeq \operatorname {\mathrm {Lie}}(X)/F_X$, ![]() $L^{\prime }_X$ is a locally free
$L^{\prime }_X$ is a locally free ![]() $\mathscr {O}_{\mathcal {N}}$-submodule of
$\mathscr {O}_{\mathcal {N}}$-submodule of ![]() $\operatorname {\mathrm {Lie}}(X)$ of rank
$\operatorname {\mathrm {Lie}}(X)$ of rank ![]() $1$ by Lemma 2.36. By the spin condition in Definition 2.1, for every closed point
$1$ by Lemma 2.36. By the spin condition in Definition 2.1, for every closed point ![]() $s\in \mathcal {N}(\overline {k})$, the induced map
$s\in \mathcal {N}(\overline {k})$, the induced map  $L^{\prime }_X\otimes _{\mathscr {O}_{\mathcal {N}}}\overline {k}\to \operatorname {\mathrm {Lie}}(X)\otimes _{\mathscr {O}_{\mathcal {N}}}\overline {k}$ over the residue field at s is injective. Thus, the quotient
$L^{\prime }_X\otimes _{\mathscr {O}_{\mathcal {N}}}\overline {k}\to \operatorname {\mathrm {Lie}}(X)\otimes _{\mathscr {O}_{\mathcal {N}}}\overline {k}$ over the residue field at s is injective. Thus, the quotient ![]() $\mathscr {O}_{\mathcal {N}}$-module
$\mathscr {O}_{\mathcal {N}}$-module ![]() $\operatorname {\mathrm {Lie}}(X)/L^{\prime }_X$ is locally free. It remains to show that
$\operatorname {\mathrm {Lie}}(X)/L^{\prime }_X$ is locally free. It remains to show that ![]() $L^{\prime }_X\subseteq L_X$.
$L^{\prime }_X\subseteq L_X$.
By definition, every section of ![]() $L^{\prime }_X$ can be locally written as the image of
$L^{\prime }_X$ can be locally written as the image of ![]() $(\iota _X(u)-u)x$ for some section x of
$(\iota _X(u)-u)x$ for some section x of ![]() $\mathrm {D}(X)$. We need to show that
$\mathrm {D}(X)$. We need to show that
(1)
 $\epsilon (\iota _X(u)-u)x$ is a section of
$\epsilon (\iota _X(u)-u)x$ is a section of  $\operatorname {\mathrm {Fil}}(X)$;
$\operatorname {\mathrm {Fil}}(X)$;(2)
 $(\epsilon (\iota _X(u)-u)x,y)=0$ for every section y of
$(\epsilon (\iota _X(u)-u)x,y)=0$ for every section y of  $F_X$.
$F_X$.
For (1), we have ![]() $\epsilon (\iota _X(u)-u)x=(\iota _X(u)+u)(\iota _X(u)-u)x=(\iota _X(u^2)-u^2)x$. Since
$\epsilon (\iota _X(u)-u)x=(\iota _X(u)+u)(\iota _X(u)-u)x=(\iota _X(u^2)-u^2)x$. Since ![]() $\iota _X(u^2)-u^2$ acts by zero on
$\iota _X(u^2)-u^2$ acts by zero on ![]() $\operatorname {\mathrm {Lie}}(X)$, (1) follows.
$\operatorname {\mathrm {Lie}}(X)$, (1) follows.
For (2), we have ![]() $(\epsilon (\iota _X(u)-u)x,y)=((\iota _X(u)-u)x,(-\iota _X(u)+u)y)=0$ as y is a section of
$(\epsilon (\iota _X(u)-u)x,y)=((\iota _X(u)-u)x,(-\iota _X(u)+u)y)=0$ as y is a section of ![]() $\operatorname {\mathrm {ker}}(\iota _X(u)-u)$. Thus, (2) follows.
$\operatorname {\mathrm {ker}}(\iota _X(u)-u)$. Thus, (2) follows.
The lemma is proved.
Lemma 2.42. Let ![]() $\Lambda $ be a vertex
$\Lambda $ be a vertex ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}$ with
$\boldsymbol {V}$ with ![]() $t(\Lambda )=4$. Then
$t(\Lambda )=4$. Then ![]() $\omega $ has degree
$\omega $ has degree ![]() $q-1$ on each connected component of (the smooth projective curve)
$q-1$ on each connected component of (the smooth projective curve) ![]() $\mathcal {V}_\Lambda $ (Definition 2.27).
$\mathcal {V}_\Lambda $ (Definition 2.27).
Proof. Let ![]() $\delta $ be the Frobenius element of
$\delta $ be the Frobenius element of ![]() $\operatorname {\mathrm {Gal}}(\overline {k}/k)$.
$\operatorname {\mathrm {Gal}}(\overline {k}/k)$.
Let ![]() $s\in \mathcal {N}(\overline {k})$ be a closed point represented by the quadruple
$s\in \mathcal {N}(\overline {k})$ be a closed point represented by the quadruple ![]() $(X,\iota _X,\lambda _X;\rho _X)$. Let
$(X,\iota _X,\lambda _X;\rho _X)$. Let ![]() $\mathsf {M}$ be the covariant
$\mathsf {M}$ be the covariant ![]() $O_F$-Dieudonné module of X equipped with the
$O_F$-Dieudonné module of X equipped with the ![]() $O_E$-action
$O_E$-action ![]() $\iota _X$, which becomes a free
$\iota _X$, which becomes a free ![]() $O_{\breve {E}}$-module. We have
$O_{\breve {E}}$-module. We have ![]() $\operatorname {\mathrm {Lie}}(X)=\mathsf {M}/\mathsf {V}\mathsf {M}$. By Definition 2.38 and Lemma 2.41, the fibre
$\operatorname {\mathrm {Lie}}(X)=\mathsf {M}/\mathsf {V}\mathsf {M}$. By Definition 2.38 and Lemma 2.41, the fibre ![]() $\omega ^{-1}\mathbin {|}_s$ is canonically identified with
$\omega ^{-1}\mathbin {|}_s$ is canonically identified with ![]() $((u\otimes 1)\mathsf {M}+\mathsf {V}\mathsf {M})/\mathsf {V}\mathsf {M}$. By the identification between
$((u\otimes 1)\mathsf {M}+\mathsf {V}\mathsf {M})/\mathsf {V}\mathsf {M}$. By the identification between ![]() $\mathcal {V}_\Lambda $ and the generalised Deligne–Lusztig variety of
$\mathcal {V}_\Lambda $ and the generalised Deligne–Lusztig variety of ![]() $\operatorname {\mathrm {O}}(\Lambda ^\vee /\Lambda )$ in Proposition 2.28 given in [Reference WuWu, Proposition 4.29 & Proposition 5.13], we know that
$\operatorname {\mathrm {O}}(\Lambda ^\vee /\Lambda )$ in Proposition 2.28 given in [Reference WuWu, Proposition 4.29 & Proposition 5.13], we know that ![]() $\omega ^{-1}\mathbin {|}_{\mathcal {V}_\Lambda }$ coincides with
$\omega ^{-1}\mathbin {|}_{\mathcal {V}_\Lambda }$ coincides with ![]() $(\delta (U)+U)/U$ where U is the tautological subbundle of
$(\delta (U)+U)/U$ where U is the tautological subbundle of ![]() $(\Lambda ^\vee /\Lambda )\otimes _k\mathscr {O}_{\mathcal {V}_\Lambda }$.
$(\Lambda ^\vee /\Lambda )\otimes _k\mathscr {O}_{\mathcal {V}_\Lambda }$.
To compute the degree of ![]() $(\delta (U)+U)/U$, let
$(\delta (U)+U)/U$, let ![]() $\mathcal {V}_\Lambda ^+$ and
$\mathcal {V}_\Lambda ^+$ and ![]() $\mathcal {V}_\Lambda ^-$ be the two connected components of
$\mathcal {V}_\Lambda ^-$ be the two connected components of ![]() $\mathcal {V}_\Lambda $. Let
$\mathcal {V}_\Lambda $. Let ![]() $\mathcal {L}_\Lambda $ be the scheme over
$\mathcal {L}_\Lambda $ be the scheme over ![]() $\overline {k}$ classifying lines in
$\overline {k}$ classifying lines in ![]() $\Lambda ^\vee /\Lambda $ with the tautological bundle L. We may identify
$\Lambda ^\vee /\Lambda $ with the tautological bundle L. We may identify ![]() $\mathcal {V}_\Lambda ^+$ and
$\mathcal {V}_\Lambda ^+$ and ![]() $\mathcal {V}_\Lambda ^-$ as two closed subschemes of
$\mathcal {V}_\Lambda ^-$ as two closed subschemes of ![]() $\mathcal {L}_\Lambda $ via the assignment
$\mathcal {L}_\Lambda $ via the assignment ![]() $U\mapsto \delta (U)\cap U$ (see [Reference Howard and PappasHP14, Section 3.2] for more details). Then,
$U\mapsto \delta (U)\cap U$ (see [Reference Howard and PappasHP14, Section 3.2] for more details). Then, ![]() $\mathcal {V}_\Lambda ^+$ and
$\mathcal {V}_\Lambda ^+$ and ![]() $\mathcal {V}_\Lambda ^-$ are the two irreducible components of the locus where L and
$\mathcal {V}_\Lambda ^-$ are the two irreducible components of the locus where L and ![]() $\delta (L)$ generate an isotropic subspace and the assignment
$\delta (L)$ generate an isotropic subspace and the assignment ![]() $L\mapsto \delta (L)$ switches
$L\mapsto \delta (L)$ switches ![]() $\mathcal {V}_\Lambda ^+$ and
$\mathcal {V}_\Lambda ^+$ and ![]() $\mathcal {V}_\Lambda ^-$. Let
$\mathcal {V}_\Lambda ^-$. Let ![]() $\mathcal {I}_\Lambda $ be the locus where L is isotropic and
$\mathcal {I}_\Lambda $ be the locus where L is isotropic and ![]() $L=\delta (L)$. Then
$L=\delta (L)$. Then ![]() $\mathcal {I}_\Lambda $ is a disjoint union of
$\mathcal {I}_\Lambda $ is a disjoint union of ![]() $q^2+1$ copies of
$q^2+1$ copies of ![]() $\operatorname {\mathrm {Spec}}\overline {k}$ since there are exactly
$\operatorname {\mathrm {Spec}}\overline {k}$ since there are exactly ![]() $q^2+1$ isotropic lines in
$q^2+1$ isotropic lines in ![]() $\Lambda ^\vee /\Lambda $ and is contained in
$\Lambda ^\vee /\Lambda $ and is contained in ![]() $\mathcal {V}_\Lambda ^+\cap \mathcal {V}_\Lambda ^-$. Note that the map
$\mathcal {V}_\Lambda ^+\cap \mathcal {V}_\Lambda ^-$. Note that the map ![]() $\delta (U)/(\delta (U)\cap U)\to (\delta (U)+U)/U$ is an isomorphism and there is a short exact sequence
$\delta (U)/(\delta (U)\cap U)\to (\delta (U)+U)/U$ is an isomorphism and there is a short exact sequence
of ![]() $\mathscr {O}_{\mathcal {V}_\Lambda ^\pm }$-modules. Since
$\mathscr {O}_{\mathcal {V}_\Lambda ^\pm }$-modules. Since ![]() $\delta (U)\cap U$ is the restriction of the tautological bundle L on
$\delta (U)\cap U$ is the restriction of the tautological bundle L on ![]() $\mathcal {L}_\Lambda $, we have
$\mathcal {L}_\Lambda $, we have
 $$ \begin{align*} \deg\left(\omega^{-1}\mathbin{|}_{\mathcal{V}_\Lambda^\pm}\right)&=\deg\left((\delta(U)+U)/U\mathbin{|}_{\mathcal{V}_\Lambda^\pm}\right)\\ &=\deg\left(\delta(\delta(U)\cap U)\mathbin{|}_{\mathcal{V}_\Lambda^\pm}\right)+(q^2+1) \\ &=\deg\left(L^{\otimes q}\mathbin{|}_{\mathcal{V}_\Lambda^\pm}\right)+(q^2+1) \\ &=-q\deg(\mathcal{V}_\Lambda^\pm)+(q^2+1), \end{align*} $$
$$ \begin{align*} \deg\left(\omega^{-1}\mathbin{|}_{\mathcal{V}_\Lambda^\pm}\right)&=\deg\left((\delta(U)+U)/U\mathbin{|}_{\mathcal{V}_\Lambda^\pm}\right)\\ &=\deg\left(\delta(\delta(U)\cap U)\mathbin{|}_{\mathcal{V}_\Lambda^\pm}\right)+(q^2+1) \\ &=\deg\left(L^{\otimes q}\mathbin{|}_{\mathcal{V}_\Lambda^\pm}\right)+(q^2+1) \\ &=-q\deg(\mathcal{V}_\Lambda^\pm)+(q^2+1), \end{align*} $$where ![]() $\deg (\mathcal {V}_\Lambda ^\pm )$ denotes the degree of the curve
$\deg (\mathcal {V}_\Lambda ^\pm )$ denotes the degree of the curve ![]() $\mathcal {V}_\Lambda ^\pm $ in the projective space
$\mathcal {V}_\Lambda ^\pm $ in the projective space ![]() $\mathcal {L}_\Lambda $. Thus, it remains to show that
$\mathcal {L}_\Lambda $. Thus, it remains to show that ![]() $\deg (\mathcal {V}_\Lambda ^\pm )=q+1$.
$\deg (\mathcal {V}_\Lambda ^\pm )=q+1$.
To compute the degree, take a ![]() $3$-dimensional quadratic subspace H of
$3$-dimensional quadratic subspace H of ![]() $\Lambda ^\vee /\Lambda $. Let
$\Lambda ^\vee /\Lambda $. Let  $\mathcal {L}_\Lambda ^H$ be the hyperplane of
$\mathcal {L}_\Lambda ^H$ be the hyperplane of ![]() $\mathcal {L}_\Lambda $ that consists of lines contained in H. Then
$\mathcal {L}_\Lambda $ that consists of lines contained in H. Then  $\mathcal {L}_\Lambda ^H\cap \mathcal {V}_\Lambda $ is the subscheme of lines
$\mathcal {L}_\Lambda ^H\cap \mathcal {V}_\Lambda $ is the subscheme of lines ![]() $L\subseteq H$ that is isotropic and fixed by
$L\subseteq H$ that is isotropic and fixed by ![]() $\delta $, which is a disjoint union of
$\delta $, which is a disjoint union of ![]() $q+1$ copies of
$q+1$ copies of ![]() $\operatorname {\mathrm {Spec}}\overline {k}$ since there are exactly
$\operatorname {\mathrm {Spec}}\overline {k}$ since there are exactly ![]() $q+1$ isotropic lines in H. As
$q+1$ isotropic lines in H. As  $\mathcal {L}_\Lambda ^H\cap \mathcal {V}_\Lambda $ is contained in
$\mathcal {L}_\Lambda ^H\cap \mathcal {V}_\Lambda $ is contained in ![]() $\mathcal {I}_\Lambda $, it is contained in
$\mathcal {I}_\Lambda $, it is contained in ![]() $\mathcal {V}_\Lambda ^+\cap \mathcal {V}_\Lambda ^-$. Therefore, we have
$\mathcal {V}_\Lambda ^+\cap \mathcal {V}_\Lambda ^-$. Therefore, we have ![]() $\deg (\mathcal {V}_\Lambda ^\pm )=q+1$.
$\deg (\mathcal {V}_\Lambda ^\pm )=q+1$.
The lemma is proved.
2.5 Proof of Theorem 2.7 when  $r=1$
$r=1$
Let the setup be as in Subsection 2.1. In this subsection, we assume ![]() $r=1$. Note that since
$r=1$. Note that since ![]() $\boldsymbol {V}$ is nonsplit, the fundamental invariants of an integral
$\boldsymbol {V}$ is nonsplit, the fundamental invariants of an integral ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}$ must consist of two positive odd integers.
$\boldsymbol {V}$ must consist of two positive odd integers.
Lemma 2.43. Let ![]() $\boldsymbol {L}$ be an integral
$\boldsymbol {L}$ be an integral ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}$ with fundamental invariants
$\boldsymbol {V}$ with fundamental invariants ![]() $(2b_1+1,2b_2+1)$. Then
$(2b_1+1,2b_2+1)$. Then
 $$ \begin{align*} \partial\mathrm{Den}(\boldsymbol{L})=2\sum_{j=0}^{b_1}\left(1+q+\cdots+q^j+(b_2-j)q^j\right). \end{align*} $$
$$ \begin{align*} \partial\mathrm{Den}(\boldsymbol{L})=2\sum_{j=0}^{b_1}\left(1+q+\cdots+q^j+(b_2-j)q^j\right). \end{align*} $$Proof. We denote by ![]() $\mathfrak {L}$ the set of integral
$\mathfrak {L}$ the set of integral ![]() $O_E$-lattices of
$O_E$-lattices of ![]() $\boldsymbol {V}$ containing
$\boldsymbol {V}$ containing ![]() $\boldsymbol {L}$. We now count
$\boldsymbol {L}$. We now count ![]() $\mathfrak {L}$.
$\mathfrak {L}$.
Fix an orthogonal basis ![]() $\{e_1,e_2\}$ of
$\{e_1,e_2\}$ of ![]() $\boldsymbol {V}$ with
$\boldsymbol {V}$ with ![]() $(e_1,e_1)_{\boldsymbol {V}}\in O_F^\times $ and
$(e_1,e_1)_{\boldsymbol {V}}\in O_F^\times $ and ![]() $(e_2,e_2)_{\boldsymbol {V}}\in O_F^\times $ and such that
$(e_2,e_2)_{\boldsymbol {V}}\in O_F^\times $ and such that ![]() $\boldsymbol {L}=\langle u^{b_1}e_1\rangle +\langle u^{b_2}e_2\rangle $. For every
$\boldsymbol {L}=\langle u^{b_1}e_1\rangle +\langle u^{b_2}e_2\rangle $. For every ![]() $L\in \mathfrak {L}$, we let
$L\in \mathfrak {L}$, we let ![]() $j(L)$ be the unique integer such that
$j(L)$ be the unique integer such that ![]() $L\cap \langle e_1\rangle \otimes _{O_F}F=\langle u^{j(L)}e_1\rangle $ and let
$L\cap \langle e_1\rangle \otimes _{O_F}F=\langle u^{j(L)}e_1\rangle $ and let ![]() $k(L)$ be the unique integer such that the image of L under the natural projection map
$k(L)$ be the unique integer such that the image of L under the natural projection map ![]() $\boldsymbol {V}\to \langle e_2\rangle \otimes _{O_F}F$ is
$\boldsymbol {V}\to \langle e_2\rangle \otimes _{O_F}F$ is ![]() $\langle u^{k(L)}e_2\rangle $. Then by Lemma 2.23(1), L is uniquely determined by
$\langle u^{k(L)}e_2\rangle $. Then by Lemma 2.23(1), L is uniquely determined by ![]() $j(L)$,
$j(L)$, ![]() $k(L)$ and the extension map
$k(L)$ and the extension map ![]() $\varepsilon _L\colon \langle u^{k(L)}e_2\rangle \to \langle u^{j(L)}e_1\rangle \otimes _{O_F}F/O_F$. The condition that L contains
$\varepsilon _L\colon \langle u^{k(L)}e_2\rangle \to \langle u^{j(L)}e_1\rangle \otimes _{O_F}F/O_F$. The condition that L contains ![]() $\boldsymbol {L}$ is equivalent to that
$\boldsymbol {L}$ is equivalent to that ![]() $j(L)\leqslant b_1$,
$j(L)\leqslant b_1$, ![]() $k(L)\leqslant b_2$ and that
$k(L)\leqslant b_2$ and that ![]() $\varepsilon _L$ vanishes on
$\varepsilon _L$ vanishes on ![]() $\langle u^{b_2}e_2\rangle $. Since
$\langle u^{b_2}e_2\rangle $. Since ![]() $\boldsymbol {L}$ is nonsplit, the condition that L is integral is equivalent to that
$\boldsymbol {L}$ is nonsplit, the condition that L is integral is equivalent to that ![]() $j(L)\geqslant 0$,
$j(L)\geqslant 0$, ![]() $k(L)\geqslant 0$ and that the image of
$k(L)\geqslant 0$ and that the image of ![]() $\varepsilon _L$ is contained in
$\varepsilon _L$ is contained in ![]() $\langle e_1\rangle /\langle u^{j(L)}e_1\rangle $. Thus, the number of
$\langle e_1\rangle /\langle u^{j(L)}e_1\rangle $. Thus, the number of ![]() $L\in \mathfrak {L}$ with
$L\in \mathfrak {L}$ with ![]() $j(L)=j$ for some fixed
$j(L)=j$ for some fixed ![]() $0\leqslant j\leqslant b_1$ equals
$0\leqslant j\leqslant b_1$ equals ![]() $1+q+\cdots +q^j+(b_2-j)q^j$. Summing over all
$1+q+\cdots +q^j+(b_2-j)q^j$. Summing over all ![]() $0\leqslant j\leqslant b_1$, we obtain
$0\leqslant j\leqslant b_1$, we obtain
 $$ \begin{align*} |\mathfrak{L}|=\sum_{j=0}^{b_1}\left(1+q+\cdots+q^j+(b_2-j)q^j\right). \end{align*} $$
$$ \begin{align*} |\mathfrak{L}|=\sum_{j=0}^{b_1}\left(1+q+\cdots+q^j+(b_2-j)q^j\right). \end{align*} $$The lemma then follows from (2.4) as ![]() $t(\boldsymbol {L})=2$.
$t(\boldsymbol {L})=2$.
Proposition 2.44. Theorem 2.7 holds when ![]() $r=1$. More explicitly, for an integral
$r=1$. More explicitly, for an integral ![]() $O_E$-lattice
$O_E$-lattice ![]() $\boldsymbol {L}$ of
$\boldsymbol {L}$ of ![]() $\boldsymbol {V}$ with fundamental invariants
$\boldsymbol {V}$ with fundamental invariants ![]() $(2b_1+1,2b_2+1)$, we have
$(2b_1+1,2b_2+1)$, we have
 $$ \begin{align*} \mathrm{Int}(\boldsymbol{L})=\partial\mathrm{Den}(\boldsymbol{L})=2\sum_{j=0}^{b_1}\left(1+q+\cdots+q^j+(b_2-j)q^j\right). \end{align*} $$
$$ \begin{align*} \mathrm{Int}(\boldsymbol{L})=\partial\mathrm{Den}(\boldsymbol{L})=2\sum_{j=0}^{b_1}\left(1+q+\cdots+q^j+(b_2-j)q^j\right). \end{align*} $$Proof. If ![]() $\boldsymbol {L}$ is not integral, then
$\boldsymbol {L}$ is not integral, then ![]() $\mathrm {Int}(\boldsymbol {L})=\partial \mathrm {Den}(\boldsymbol {L})=0$. If
$\mathrm {Int}(\boldsymbol {L})=\partial \mathrm {Den}(\boldsymbol {L})=0$. If ![]() $\boldsymbol {L}$ is integral with fundamental invariants
$\boldsymbol {L}$ is integral with fundamental invariants ![]() $(2b_1+1,2b_2+1)$. We may take an orthogonal basis
$(2b_1+1,2b_2+1)$. We may take an orthogonal basis ![]() $\{x_1,x_2\}$ of
$\{x_1,x_2\}$ of ![]() $\boldsymbol {L}$ such that
$\boldsymbol {L}$ such that ![]() $\operatorname {\mathrm {val}}(x_1)=2b_1+1$ and
$\operatorname {\mathrm {val}}(x_1)=2b_1+1$ and ![]() $\operatorname {\mathrm {val}}(x_2)=2b_2+1$.
$\operatorname {\mathrm {val}}(x_2)=2b_2+1$.
Put ![]() $\boldsymbol {D} := \operatorname {\mathrm {End}}_{O_F}(X_0)\otimes \mathbb {Q}$, which is a division quaternion algebra over F with the F-linear embedding
$\boldsymbol {D} := \operatorname {\mathrm {End}}_{O_F}(X_0)\otimes \mathbb {Q}$, which is a division quaternion algebra over F with the F-linear embedding ![]() $\iota _{X_0}\colon E\to \boldsymbol {D}$. By the Serre construction, we may naturally identify
$\iota _{X_0}\colon E\to \boldsymbol {D}$. By the Serre construction, we may naturally identify ![]() $\boldsymbol {D}$ with
$\boldsymbol {D}$ with ![]() $\boldsymbol {V}$ and we have an identity
$\boldsymbol {V}$ and we have an identity

of divisors, decomposing the special divisor as a sum of quasi-canonical lifting divisors (see [Reference Rapoport, Smithling and ZhangRSZ17, Section 6 & Proposition 7.1]).
We claim that for every ![]() $0\leqslant j\leqslant b_1$, the identity
$0\leqslant j\leqslant b_1$, the identity

holds. In fact, this can be proved in the same way as for [Reference KudlaKR11, Proposition 8.4] using Keating’s formula [Reference VollaardVol07, Theorem 2.1]. Notice that in [Reference KudlaKR11, Proposition 8.4] we replace ![]() $e_s$ by
$e_s$ by ![]() $2q^j$ since
$2q^j$ since ![]() $E/F$ is ramified and the factor
$E/F$ is ramified and the factor ![]() $2$ comes from the fact that
$2$ comes from the fact that ![]() $\mathcal {Z}_l$ has two connected components. By (2.16) and (2.17), we have
$\mathcal {Z}_l$ has two connected components. By (2.16) and (2.17), we have
 $$ \begin{align*} \mathrm{Int}(\boldsymbol{L})=\mathrm{length}_{O_{\breve{E}}}\mathcal{N}(x_1)\cap\mathcal{N}(x_2)=\sum_{j=0}^{b_1}2\left(1+q+\cdots+q^j+(b_2-l)q^j\right). \end{align*} $$
$$ \begin{align*} \mathrm{Int}(\boldsymbol{L})=\mathrm{length}_{O_{\breve{E}}}\mathcal{N}(x_1)\cap\mathcal{N}(x_2)=\sum_{j=0}^{b_1}2\left(1+q+\cdots+q^j+(b_2-l)q^j\right). \end{align*} $$The proposition follows by Lemma 2.43.
Definition 2.45. For ![]() $L^\flat \in \flat (\boldsymbol {V})$, we put
$L^\flat \in \flat (\boldsymbol {V})$, we put
as an effective divisor by (the ![]() $r=1$ case of) Lemma 2.40.
$r=1$ case of) Lemma 2.40.
Corollary 2.46. Take an element ![]() $L^\flat \in \flat (\boldsymbol {V})$. For every
$L^\flat \in \flat (\boldsymbol {V})$. For every ![]() $x\in \boldsymbol {V}\setminus V_{L^\flat }$, we have
$x\in \boldsymbol {V}\setminus V_{L^\flat }$, we have

2.6 Fourier transform of geometric side
Let the setup be as in Subsection 2.1. We will freely use notation concerning K-groups of formal schemes from [Reference Li and LiuLL21, Section B] and [Reference ZhangZha21, Appendix B], based on the work [Reference Gillet and SoulGS87].
Definition 2.47. Let ![]() $\mathcal {X}$ be a formal scheme over
$\mathcal {X}$ be a formal scheme over ![]() $\operatorname {\mathrm {Spf}} O_{\breve {E}}$.
$\operatorname {\mathrm {Spf}} O_{\breve {E}}$.
(1) We denote by
 $\mathcal {X}^{\mathrm {h}}$ the closed formal subscheme of
$\mathcal {X}^{\mathrm {h}}$ the closed formal subscheme of  $\mathcal {X}$ defined by the ideal sheaf
$\mathcal {X}$ defined by the ideal sheaf  $\mathscr {O}_{\mathcal {X}}[p^\infty ]$.
$\mathscr {O}_{\mathcal {X}}[p^\infty ]$.(2) For every closed formal subscheme
 $\mathcal {Z}$ of
$\mathcal {Z}$ of  $\mathcal {X}$, we denote by
$\mathcal {X}$, we denote by  $\mathrm {K}_0(\mathcal {X},\mathcal {Z})$ the image of the map
$\mathrm {K}_0(\mathcal {X},\mathcal {Z})$ the image of the map  $\mathrm {K}_0^{\mathcal {Z}}(\mathcal {X})\to \mathrm {K}_0(\mathcal {X})$ and similarly by
$\mathrm {K}_0^{\mathcal {Z}}(\mathcal {X})\to \mathrm {K}_0(\mathcal {X})$ and similarly by  $\mathrm {F}^m\mathrm {K}_0(\mathcal {X},\mathcal {Z})$ the image of the map
$\mathrm {F}^m\mathrm {K}_0(\mathcal {X},\mathcal {Z})$ the image of the map  $\mathrm {F}^m\mathrm {K}_0^{\mathcal {Z}}(\mathcal {X})\to \mathrm {K}_0(\mathcal {X})$ for
$\mathrm {F}^m\mathrm {K}_0^{\mathcal {Z}}(\mathcal {X})\to \mathrm {K}_0(\mathcal {X})$ for  $m\geqslant 0$.
$m\geqslant 0$.
Definition 2.48. Let X be a subset of ![]() $\boldsymbol {V}$ such that
$\boldsymbol {V}$ such that ![]() $\langle X\rangle $ is finitely generated of rank m.
$\langle X\rangle $ is finitely generated of rank m.
(1) We denote by
 the element
the element  $[C(x_1)\otimes _{\mathscr {O}_{\mathcal {N}}}\cdots \otimes _{\mathscr {O}_{\mathcal {N}}} C(x_m)]$ from Subsection 2.4 for a basis
$[C(x_1)\otimes _{\mathscr {O}_{\mathcal {N}}}\cdots \otimes _{\mathscr {O}_{\mathcal {N}}} C(x_m)]$ from Subsection 2.4 for a basis  $\{x_1,\dots ,x_m\}$ of the
$\{x_1,\dots ,x_m\}$ of the  $O_E$-module generated by X, which is independent of the choice of the basis by Corollary 2.34.
$O_E$-module generated by X, which is independent of the choice of the basis by Corollary 2.34.(2) We denote by
 the class of
the class of  $\mathcal {N}(X)^{\mathrm {h}}$.
$\mathcal {N}(X)^{\mathrm {h}}$.(3) We put
 .
.
Lemma 2.49. Let ![]() $L^\flat $ be an element of
$L^\flat $ be an element of ![]() $\flat (\boldsymbol {V})$ (Definition 2.8). We have
$\flat (\boldsymbol {V})$ (Definition 2.8). We have
(1)
 $\mathcal {N}(L^\flat )^{\mathrm {h}}$ is either empty or finite flat over
$\mathcal {N}(L^\flat )^{\mathrm {h}}$ is either empty or finite flat over  $\operatorname {\mathrm {Spf}} O_{\breve {E}}$;
$\operatorname {\mathrm {Spf}} O_{\breve {E}}$;(2) all of
 ,
,  and
and  belong to
belong to  $\mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N},\mathcal {N}(L^\flat ))$;
$\mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N},\mathcal {N}(L^\flat ))$;(3) there exist finitely many vertex
 $O_E$-lattices
$O_E$-lattices  $\Lambda _1,\dots ,\Lambda _m$ of
$\Lambda _1,\dots ,\Lambda _m$ of  $\boldsymbol {V}$ of type n such that
$\boldsymbol {V}$ of type n such that  belongs to
belongs to  $\sum _{i=1}^m\mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N},\mathcal {V}_{\Lambda _i})$.
$\sum _{i=1}^m\mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N},\mathcal {V}_{\Lambda _i})$.
Proof. Part (1) follows from Lemma 2.54 and Lemma 2.53.
Take a basis ![]() $\{x_1,\dots ,x_{n-1}\}$ of the
$\{x_1,\dots ,x_{n-1}\}$ of the ![]() $O_E$-module
$O_E$-module ![]() $L^\flat $.
$L^\flat $.
For (2), it suffices to show ![]() by (1). By definition,
by (1). By definition, ![]() is the cup product of the classes in
is the cup product of the classes in ![]() $\mathrm {K}_0(\mathcal {N})$ of
$\mathrm {K}_0(\mathcal {N})$ of ![]() $\mathcal {N}(x_1),\dots ,\mathcal {N}(x_{n-1})$, each being a divisor by Lemma 2.40. Thus,
$\mathcal {N}(x_1),\dots ,\mathcal {N}(x_{n-1})$, each being a divisor by Lemma 2.40. Thus, ![]() belongs to
belongs to ![]() $\mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N},\mathcal {N}(L^\flat ))$ by (the analogue for formal schemes of) [Reference Gillet and SoulGS87, Proposition 5.5].
$\mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N},\mathcal {N}(L^\flat ))$ by (the analogue for formal schemes of) [Reference Gillet and SoulGS87, Proposition 5.5].
For (3), by the same argument for [Reference Li and ZhangLZa, Lemma 5.1.1], we know that there exists a proper closed subscheme Z of ![]() $\mathcal {N}$ containing the reduced fibre of
$\mathcal {N}$ containing the reduced fibre of ![]() $\mathcal {N}(L^\flat )^{\mathrm {h}}$, such that
$\mathcal {N}(L^\flat )^{\mathrm {h}}$, such that ![]() $\mathcal {N}(L^\flat )$ is contained in
$\mathcal {N}(L^\flat )$ is contained in ![]() $\mathcal {N}(L^\flat )^{\mathrm {h}}\bigcup Z$. By (1) and (2), there exists a closed reduced 1-dimensional subscheme C of Z containing the reduced fibre of
$\mathcal {N}(L^\flat )^{\mathrm {h}}\bigcup Z$. By (1) and (2), there exists a closed reduced 1-dimensional subscheme C of Z containing the reduced fibre of ![]() $\mathcal {N}(L^\flat )^{\mathrm {h}}$, such that
$\mathcal {N}(L^\flat )^{\mathrm {h}}$, such that ![]() belongs to
belongs to ![]() $\mathrm {K}_0(\mathcal {N},C\cup \mathcal {N}(L^\flat )^{\mathrm {h}})$. By [Reference Gillet and SoulGS87, Lemma 1.9] (and its notation),
$\mathrm {K}_0(\mathcal {N},C\cup \mathcal {N}(L^\flat )^{\mathrm {h}})$. By [Reference Gillet and SoulGS87, Lemma 1.9] (and its notation), ![]() belongs to the image of the natural map
belongs to the image of the natural map  $\mathrm {K}^{\prime }_0(C\cup \mathcal {N}(L^\flat )^{\mathrm {h}})\to \mathrm {K}_0(\mathcal {X})$ that sends a coherent
$\mathrm {K}^{\prime }_0(C\cup \mathcal {N}(L^\flat )^{\mathrm {h}})\to \mathrm {K}_0(\mathcal {X})$ that sends a coherent ![]() $\mathscr {O}_{C\cup \mathcal {N}(L^\flat )^{\mathrm {h}}}$-module M to any finite projective resolution of M on
$\mathscr {O}_{C\cup \mathcal {N}(L^\flat )^{\mathrm {h}}}$-module M to any finite projective resolution of M on ![]() $\mathcal {X}$. It follows, by the definition of
$\mathcal {X}$. It follows, by the definition of ![]() , that
, that ![]() can be represented by a finite complex of coherent sheaves on
can be represented by a finite complex of coherent sheaves on ![]() $C\cup \mathcal {N}(L^\flat )^{\mathrm {h}}$ that are Artinian on
$C\cup \mathcal {N}(L^\flat )^{\mathrm {h}}$ that are Artinian on ![]() $\mathcal {N}(L^\flat )^{\mathrm {h}}$, which implies that
$\mathcal {N}(L^\flat )^{\mathrm {h}}$, which implies that ![]() belongs to the image of the map
belongs to the image of the map ![]() $\mathrm {K}^{\prime }_0(C)\to \mathrm {K}_0(\mathcal {N})$. Let
$\mathrm {K}^{\prime }_0(C)\to \mathrm {K}_0(\mathcal {N})$. Let ![]() $C_1,\dots ,C_m$ be the irreducible components of C. It is clear that the map
$C_1,\dots ,C_m$ be the irreducible components of C. It is clear that the map  $\bigoplus _{i=1}^m\mathrm {K}^{\prime }_0(C_i)\to \mathrm {K}^{\prime }_0(C)$ is surjective, which implies that
$\bigoplus _{i=1}^m\mathrm {K}^{\prime }_0(C_i)\to \mathrm {K}^{\prime }_0(C)$ is surjective, which implies that ![]() belongs to
belongs to ![]() $\sum _{i=1}^m\mathrm {K}_0(\mathcal {N},C_i)$. Finally, for each
$\sum _{i=1}^m\mathrm {K}_0(\mathcal {N},C_i)$. Finally, for each ![]() $1\leqslant i\leqslant m$, we may choose a vertex
$1\leqslant i\leqslant m$, we may choose a vertex ![]() $O_E$-lattice
$O_E$-lattice ![]() $\Lambda _i$ of
$\Lambda _i$ of ![]() $\boldsymbol {V}$ of type n such that
$\boldsymbol {V}$ of type n such that ![]() $C_i\subseteq \mathcal {V}_{\Lambda _i}$ by Proposition 2.28. Then (3) follows.
$C_i\subseteq \mathcal {V}_{\Lambda _i}$ by Proposition 2.28. Then (3) follows.
Definition 2.50. Let ![]() $L^\flat $ be an element of
$L^\flat $ be an element of ![]() $\flat (\boldsymbol {V})$ (Definition 2.8). For
$\flat (\boldsymbol {V})$ (Definition 2.8). For ![]() $x\in \boldsymbol {V}\setminus V_{L^\flat }$, we put
$x\in \boldsymbol {V}\setminus V_{L^\flat }$, we put

Here, the intersection numbers are well-defined since ![]() $\mathcal {N}(L^\flat )\cap \mathcal {N}(x)$ is a proper closed subscheme of
$\mathcal {N}(L^\flat )\cap \mathcal {N}(x)$ is a proper closed subscheme of ![]() $\mathcal {N}$ by Remark 2.26. Note that
$\mathcal {N}$ by Remark 2.26. Note that ![]() $\mathrm {Int}_{L^\flat }(x)=\mathrm {Int}(L^\flat +\langle x\rangle )$ (Definition 2.6).
$\mathrm {Int}_{L^\flat }(x)=\mathrm {Int}(L^\flat +\langle x\rangle )$ (Definition 2.6).
The following is our main result of this subsection.
Proposition 2.51. Let ![]() $L^\flat $ be an element of
$L^\flat $ be an element of ![]() $\flat (\boldsymbol {V})$ (Definition 2.8).
$\flat (\boldsymbol {V})$ (Definition 2.8).
(1) We have
 $\mathrm {Int}_{L^\flat }^{\mathrm {h}}(x)=\partial \mathrm {Den}_{L^\flat }^{\mathrm {h}}(x)$ for
$\mathrm {Int}_{L^\flat }^{\mathrm {h}}(x)=\partial \mathrm {Den}_{L^\flat }^{\mathrm {h}}(x)$ for  $x\in \boldsymbol {V}\setminus V_{L^\flat }$, where
$x\in \boldsymbol {V}\setminus V_{L^\flat }$, where  $\partial \mathrm {Den}_{L^\flat }^{\mathrm {h}}$ is from Definition 2.20.
$\partial \mathrm {Den}_{L^\flat }^{\mathrm {h}}$ is from Definition 2.20.(2) The function
 $\mathrm {Int}_{L^\flat }^{\mathrm {v}}$ extends (uniquely) to a (compactly supported) locally constant function on
$\mathrm {Int}_{L^\flat }^{\mathrm {v}}$ extends (uniquely) to a (compactly supported) locally constant function on  $\boldsymbol {V}$, which we still denote by
$\boldsymbol {V}$, which we still denote by  $\mathrm {Int}_{L^\flat }^{\mathrm {v}}$. Moreover, we have In particular, the support of
$\mathrm {Int}_{L^\flat }^{\mathrm {v}}$. Moreover, we have In particular, the support of $$ \begin{align*} \widehat{\mathrm{Int}_{L^\flat}^{\mathrm{v}}}=-\mathrm{Int}_{L^\flat}^{\mathrm{v}}. \end{align*} $$
$$ \begin{align*} \widehat{\mathrm{Int}_{L^\flat}^{\mathrm{v}}}=-\mathrm{Int}_{L^\flat}^{\mathrm{v}}. \end{align*} $$ $\widehat {\mathrm {Int}_{L^\flat }^{\mathrm {v}}}$ is contained in
$\widehat {\mathrm {Int}_{L^\flat }^{\mathrm {v}}}$ is contained in  $\boldsymbol {V}^{\mathrm {int}}$ (Definition 2.10).
$\boldsymbol {V}^{\mathrm {int}}$ (Definition 2.10).
The rest of this subsection is devoted to the proof of this proposition.
Remark 2.52 Cancellation law for special cycles
Let ![]() $\boldsymbol {V}'$ be a hermitian subspace of
$\boldsymbol {V}'$ be a hermitian subspace of ![]() $\boldsymbol {V}$ that is nonsplit and of positive even dimension
$\boldsymbol {V}$ that is nonsplit and of positive even dimension ![]() $n'$. Let L be an integral hermitian
$n'$. Let L be an integral hermitian ![]() $O_E$-module contained in
$O_E$-module contained in ![]() $\boldsymbol {V}$ such that
$\boldsymbol {V}$ such that ![]() $L\cap \boldsymbol {V}^{\prime \perp }$ is a self-dual
$L\cap \boldsymbol {V}^{\prime \perp }$ is a self-dual ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}^{\prime \perp }$. We may choose
$\boldsymbol {V}^{\prime \perp }$. We may choose
• an object
 $(\boldsymbol {X}',\iota _{\boldsymbol {X}'},\lambda _{\boldsymbol {X}'})\in \mathrm {Exo}_{(n'-1,1)}^{\mathrm {b}}(\overline {k})$ (Definition 2.1),
$(\boldsymbol {X}',\iota _{\boldsymbol {X}'},\lambda _{\boldsymbol {X}'})\in \mathrm {Exo}_{(n'-1,1)}^{\mathrm {b}}(\overline {k})$ (Definition 2.1),• an object
 $(Y,\iota _Y,\lambda _Y)\in \mathrm {Exo}_{(n-n',0)}(O_{\breve {E}})$ (Remark 2.9),Footnote 13
$(Y,\iota _Y,\lambda _Y)\in \mathrm {Exo}_{(n-n',0)}(O_{\breve {E}})$ (Remark 2.9),Footnote 13• a quasi-morphism
 $\varrho $ from
$\varrho $ from  $(Y,\iota _Y,\lambda _Y)\otimes _{O_{\breve {E}}}\overline {k}\oplus (\boldsymbol {X}',\iota _{\boldsymbol {X}'},\lambda _{\boldsymbol {X}'})$ to
$(Y,\iota _Y,\lambda _Y)\otimes _{O_{\breve {E}}}\overline {k}\oplus (\boldsymbol {X}',\iota _{\boldsymbol {X}'},\lambda _{\boldsymbol {X}'})$ to  $(\boldsymbol {X},\iota _{\boldsymbol {X}},\lambda _{\boldsymbol {X}})$ in the category
$(\boldsymbol {X},\iota _{\boldsymbol {X}},\lambda _{\boldsymbol {X}})$ in the category  $\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}(S\otimes _{O_{\breve {E}}}\overline {k})$ satisfying
$\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}(S\otimes _{O_{\breve {E}}}\overline {k})$ satisfying–
 $\varrho $ identifies
$\varrho $ identifies  $\operatorname {\mathrm {Hom}}_{O_E}(X_0\otimes _{O_{\breve {E}}}\overline {k},\boldsymbol {X}')\otimes \mathbb {Q}$ with
$\operatorname {\mathrm {Hom}}_{O_E}(X_0\otimes _{O_{\breve {E}}}\overline {k},\boldsymbol {X}')\otimes \mathbb {Q}$ with  $\boldsymbol {V}'$ as hermitian spaces;
$\boldsymbol {V}'$ as hermitian spaces;–
 $\varrho $ identifies
$\varrho $ identifies  $\operatorname {\mathrm {Hom}}_{O_E}(X_0\otimes _{O_{\breve {E}}}\overline {k},Y\otimes _{O_{\breve {E}}}\overline {k})$ with
$\operatorname {\mathrm {Hom}}_{O_E}(X_0\otimes _{O_{\breve {E}}}\overline {k},Y\otimes _{O_{\breve {E}}}\overline {k})$ with  $L\cap \boldsymbol {V}^{\prime \perp }$ as hermitian
$L\cap \boldsymbol {V}^{\prime \perp }$ as hermitian  $O_E$-modules.
$O_E$-modules.
Let ![]() $\mathcal {N}' := \mathcal {N}_{(\boldsymbol {X}',\iota _{\boldsymbol {X}'},\lambda _{\boldsymbol {X}'})}$ be the relative Rapoport–Zink space for the triple
$\mathcal {N}' := \mathcal {N}_{(\boldsymbol {X}',\iota _{\boldsymbol {X}'},\lambda _{\boldsymbol {X}'})}$ be the relative Rapoport–Zink space for the triple ![]() $(\boldsymbol {X}',\iota _{\boldsymbol {X}'},\lambda _{\boldsymbol {X}'})$ (Definition 2.3). We have a morphism
$(\boldsymbol {X}',\iota _{\boldsymbol {X}'},\lambda _{\boldsymbol {X}'})$ (Definition 2.3). We have a morphism ![]() $\mathcal {N}'\to \mathcal {N}$ such that for every object S of
$\mathcal {N}'\to \mathcal {N}$ such that for every object S of  $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$,
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$, ![]() $\mathcal {N}(S)$ it sends an object
$\mathcal {N}(S)$ it sends an object ![]() $(X',\iota _{X'},\lambda _{X'};\rho _{X'})\in \mathcal {N}'(S)$ to the object
$(X',\iota _{X'},\lambda _{X'};\rho _{X'})\in \mathcal {N}'(S)$ to the object
We have
(1) The morphism
 $\mathcal {N}'\to \mathcal {N}$ above identifies
$\mathcal {N}'\to \mathcal {N}$ above identifies  $\mathcal {N}'$ with the closed formal subscheme
$\mathcal {N}'$ with the closed formal subscheme  $\mathcal {N}(L\cap \boldsymbol {V}^{\prime \perp })$ of
$\mathcal {N}(L\cap \boldsymbol {V}^{\prime \perp })$ of  $\mathcal {N}$.
$\mathcal {N}$.(2) Suppose that
 $L\cap \boldsymbol {V}'\neq \{0\}$; then
$L\cap \boldsymbol {V}'\neq \{0\}$; then  $\mathcal {N}(L)$ coincides with the image of
$\mathcal {N}(L)$ coincides with the image of  $\mathcal {N}'(L\cap \boldsymbol {V}')$ under the morphism
$\mathcal {N}'(L\cap \boldsymbol {V}')$ under the morphism  $\mathcal {N}'\to \mathcal {N}$ above.
$\mathcal {N}'\to \mathcal {N}$ above.(3) For a nonzero element
 $x\in \boldsymbol {V}$ written as
$x\in \boldsymbol {V}$ written as  $x=y+x'$ with respect to the orthogonal decomposition
$x=y+x'$ with respect to the orthogonal decomposition  $\boldsymbol {V}=\boldsymbol {V}^{\prime \perp }\oplus \boldsymbol {V}'$, we have
$\boldsymbol {V}=\boldsymbol {V}^{\prime \perp }\oplus \boldsymbol {V}'$, we have  $$ \begin{align*} \mathcal{N}'\times_{\mathcal{N}}\mathcal{N}(x)= \begin{cases} \emptyset,&\text{if } y\not\in L\cap\boldsymbol{V}^{\prime\perp}, \\ \mathcal{N}',&\text{if } y\in L\cap\boldsymbol{V}^{\prime\perp} \text{ and } x'=0, \\ \mathcal{N}'(x'),&\text{if } y\in L\cap\boldsymbol{V}^{\prime\perp} \text{ and } x'\neq 0. \end{cases} \end{align*} $$
$$ \begin{align*} \mathcal{N}'\times_{\mathcal{N}}\mathcal{N}(x)= \begin{cases} \emptyset,&\text{if } y\not\in L\cap\boldsymbol{V}^{\prime\perp}, \\ \mathcal{N}',&\text{if } y\in L\cap\boldsymbol{V}^{\prime\perp} \text{ and } x'=0, \\ \mathcal{N}'(x'),&\text{if } y\in L\cap\boldsymbol{V}^{\prime\perp} \text{ and } x'\neq 0. \end{cases} \end{align*} $$(4) If L is an
 $O_E$-lattice of
$O_E$-lattice of  $\boldsymbol {V}$, then we have
$\boldsymbol {V}$, then we have  $\mathrm {Int}(L)=\mathrm {Int}(L\cap \boldsymbol {V}')$.
$\mathrm {Int}(L)=\mathrm {Int}(L\cap \boldsymbol {V}')$.
These follow from the similar argument for the cancellation law in [Reference Li and ZhangLZa, Section 2.11]. Indeed, we may choose compatible framing objects for ![]() $\mathcal {N}'$ and
$\mathcal {N}'$ and ![]() $\mathcal {N}$ as in [Reference Rapoport, Smithling and ZhangRSZ17, Page 2207]. Note that the hermitian form on
$\mathcal {N}$ as in [Reference Rapoport, Smithling and ZhangRSZ17, Page 2207]. Note that the hermitian form on ![]() $\boldsymbol {V}$ in [Reference Rapoport, Smithling and ZhangRSZ17] is the scaled form
$\boldsymbol {V}$ in [Reference Rapoport, Smithling and ZhangRSZ17] is the scaled form ![]() $u^2(\,,\,)_{\boldsymbol {V}}$ and thus u-modular lattices in [Reference Rapoport, Smithling and ZhangRSZ17] correspond to our self-dual lattices.
$u^2(\,,\,)_{\boldsymbol {V}}$ and thus u-modular lattices in [Reference Rapoport, Smithling and ZhangRSZ17] correspond to our self-dual lattices.
Lemma 2.53. Let ![]() $L^{\flat \prime }\in \flat (\boldsymbol {V})$ be an element that is integral and satisfies
$L^{\flat \prime }\in \flat (\boldsymbol {V})$ be an element that is integral and satisfies ![]() $t(L^{\flat \prime })=1$.
$t(L^{\flat \prime })=1$.
(1) The formal subscheme
 $\mathcal {N}(L^{\flat \prime })$ is finite flat over
$\mathcal {N}(L^{\flat \prime })$ is finite flat over  $\operatorname {\mathrm {Spf}} O_{\breve {E}}$.
$\operatorname {\mathrm {Spf}} O_{\breve {E}}$.(2) If we put
 $\mathcal {N}(L^{\flat \prime })^\circ := \mathcal {N}(L^{\flat \prime })-\mathcal {N}(L^{\flat \prime }_-)$ as an element in
$\mathcal {N}(L^{\flat \prime })^\circ := \mathcal {N}(L^{\flat \prime })-\mathcal {N}(L^{\flat \prime }_-)$ as an element in  $\mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N})$, then for every
$\mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N})$, then for every  $x\in \boldsymbol {V}\setminus V_{L^\flat }$, Here,
$x\in \boldsymbol {V}\setminus V_{L^\flat }$, Here,
 $L^{\flat \prime }_-$ is the unique element in
$L^{\flat \prime }_-$ is the unique element in  $\flat (\boldsymbol {V})$ satisfying
$\flat (\boldsymbol {V})$ satisfying  $L^{\flat \prime }\subseteq L^{\flat \prime }_-\subseteq (L^{\flat \prime })^\vee $ with
$L^{\flat \prime }\subseteq L^{\flat \prime }_-\subseteq (L^{\flat \prime })^\vee $ with  $|L^{\flat \prime }_-/L^{\flat \prime }|=q$ (so that
$|L^{\flat \prime }_-/L^{\flat \prime }|=q$ (so that  $L^{\flat \prime }_-$ is either not integral or is integral with
$L^{\flat \prime }_-$ is either not integral or is integral with  $t(L^{\flat \prime }_-)=1$).
$t(L^{\flat \prime }_-)=1$).
Proof. Since ![]() $t(L^{\flat \prime })=1$, we may choose a
$t(L^{\flat \prime })=1$, we may choose a ![]() $2$-dimensional (nonsplit) hermitian subspace
$2$-dimensional (nonsplit) hermitian subspace ![]() $\boldsymbol {V}'$ of
$\boldsymbol {V}'$ of ![]() $\boldsymbol {V}$ such that
$\boldsymbol {V}$ such that ![]() $L^{\flat \prime }\cap \boldsymbol {V}^{\prime \perp }$ is a self-dual
$L^{\flat \prime }\cap \boldsymbol {V}^{\prime \perp }$ is a self-dual ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}^{\prime \perp }$. We adopt the construction in Remark 2.52.
$\boldsymbol {V}^{\prime \perp }$. We adopt the construction in Remark 2.52.
For (1), we have ![]() $\mathcal {N}(L^{\flat \prime })=\mathcal {N}'(L^{\flat \prime }\cap \boldsymbol {V}')$, which is finite flat over
$\mathcal {N}(L^{\flat \prime })=\mathcal {N}'(L^{\flat \prime }\cap \boldsymbol {V}')$, which is finite flat over ![]() $\operatorname {\mathrm {Spf}} O_{\breve {E}}$ by (the
$\operatorname {\mathrm {Spf}} O_{\breve {E}}$ by (the ![]() $r=1$ case of) Lemma 2.40.
$r=1$ case of) Lemma 2.40.
For (2), we write ![]() $x=y+x'$ with respect to the orthogonal decomposition
$x=y+x'$ with respect to the orthogonal decomposition ![]() $\boldsymbol {V}=\boldsymbol {V}^{\prime \perp }\oplus \boldsymbol {V}'$. Since
$\boldsymbol {V}=\boldsymbol {V}^{\prime \perp }\oplus \boldsymbol {V}'$. Since ![]() $x\not \in V_{L^\flat }$, we have
$x\not \in V_{L^\flat }$, we have ![]() $x'\neq 0$. By Remark 2.52(2),
$x'\neq 0$. By Remark 2.52(2), ![]() $\mathcal {N}(L^{\flat \prime })^\circ $ coincides with (the class of)
$\mathcal {N}(L^{\flat \prime })^\circ $ coincides with (the class of) ![]() $\mathcal {N}'(L^{\flat \prime }\cap \boldsymbol {V}')^\circ $ in
$\mathcal {N}'(L^{\flat \prime }\cap \boldsymbol {V}')^\circ $ in ![]() $\mathrm {F}^1\mathrm {K}_0(\mathcal {N}')$ under the map
$\mathrm {F}^1\mathrm {K}_0(\mathcal {N}')$ under the map ![]() $\mathrm {F}^1\mathrm {K}_0(\mathcal {N}')\to \mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N})$. There are two cases.
$\mathrm {F}^1\mathrm {K}_0(\mathcal {N}')\to \mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N})$. There are two cases.
If ![]() $y\not \in L^{\flat \prime }\cap \boldsymbol {V}^{\prime \perp }$, then
$y\not \in L^{\flat \prime }\cap \boldsymbol {V}^{\prime \perp }$, then ![]() by Remark 2.52(3) and there is no integral
by Remark 2.52(3) and there is no integral ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}$ containing
$\boldsymbol {V}$ containing ![]() $L^{\flat \prime }+\langle x\rangle $. Thus, (2) follows.
$L^{\flat \prime }+\langle x\rangle $. Thus, (2) follows.
If ![]() $y\in L^{\flat \prime }\cap \boldsymbol {V}^{\prime \perp }$, then by Remark 2.52(3), we have
$y\in L^{\flat \prime }\cap \boldsymbol {V}^{\prime \perp }$, then by Remark 2.52(3), we have

By Corollary 2.46, we have

Thus, (2) follows.
Lemma 2.54. Let ![]() $L^\flat $ be an element of
$L^\flat $ be an element of ![]() $\flat (\boldsymbol {V})$ (Definition 2.8). We have
$\flat (\boldsymbol {V})$ (Definition 2.8). We have
 $$ \begin{align*} \mathcal{N}(L^\flat)^{\mathrm{h}}=\bigcup_{\substack{L^\flat\subseteq L^{\flat\prime}\subseteq(L^{\flat\prime})^\vee \\ t(L^{\flat\prime})=1}} \mathcal{N}(L^{\flat\prime})^\circ \end{align*} $$
$$ \begin{align*} \mathcal{N}(L^\flat)^{\mathrm{h}}=\bigcup_{\substack{L^\flat\subseteq L^{\flat\prime}\subseteq(L^{\flat\prime})^\vee \\ t(L^{\flat\prime})=1}} \mathcal{N}(L^{\flat\prime})^\circ \end{align*} $$as closed formal subschemes of ![]() $\mathcal {N}$ and the identity
$\mathcal {N}$ and the identity

in ![]() $\mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N})/\mathrm {F}^n\mathrm {K}_0(\mathcal {N})$, where
$\mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N})/\mathrm {F}^n\mathrm {K}_0(\mathcal {N})$, where ![]() $\mathcal {N}(L^{\flat \prime })^\circ $ is introduced in Lemma 2.53(2).
$\mathcal {N}(L^{\flat \prime })^\circ $ is introduced in Lemma 2.53(2).
Proof. This lemma can be proved by the same way as for [Reference Li and ZhangLZa, Theorem 4.2.1], as long as we establish the following claim replacing [Reference Li and ZhangLZa, Lemma 4.5.1] in the case where ![]() $E/F$ is ramified.
$E/F$ is ramified.
• Let L be a self-dual hermitian
 $O_E$-module of rank n and
$O_E$-module of rank n and  $L^\flat $ a hermitian
$L^\flat $ a hermitian  $O_E$-module contained in L. If
$O_E$-module contained in L. If  $L/L^\flat $ is free, then
$L/L^\flat $ is free, then  $L^\flat $ is integral with
$L^\flat $ is integral with  $t(L^\flat )=1$.
$t(L^\flat )=1$.
However, this is just a special case of Lemma 2.23(2).
Lemma 2.55. Let ![]() $\Lambda $ be a vertex
$\Lambda $ be a vertex ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}$ with
$\boldsymbol {V}$ with ![]() $t(\Lambda )=4$. Take an arbitrary connected component
$t(\Lambda )=4$. Take an arbitrary connected component ![]() $\mathcal {V}_\Lambda ^+$ of the smooth projective curve
$\mathcal {V}_\Lambda ^+$ of the smooth projective curve ![]() $\mathcal {V}_\Lambda $ from Proposition 2.28, regarded as an element in
$\mathcal {V}_\Lambda $ from Proposition 2.28, regarded as an element in ![]() $\mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N})$. For every
$\mathrm {F}^{n-1}\mathrm {K}_0(\mathcal {N})$. For every ![]() $x\in \boldsymbol {V}\setminus \{0\}$, put
$x\in \boldsymbol {V}\setminus \{0\}$, put  . Then
. Then ![]() $\mathrm {Int}_{\mathcal {V}_\Lambda ^+}$ extends (uniquely) to a compactly supported locally constant function on
$\mathrm {Int}_{\mathcal {V}_\Lambda ^+}$ extends (uniquely) to a compactly supported locally constant function on ![]() $\boldsymbol {V}$, which we still denote by
$\boldsymbol {V}$, which we still denote by ![]() $\mathrm {Int}_{\mathcal {V}_\Lambda ^+}$. Moreover, we have
$\mathrm {Int}_{\mathcal {V}_\Lambda ^+}$. Moreover, we have
 $$ \begin{align*} \widehat{\mathrm{Int}_{\mathcal{V}_\Lambda^+}}=-\mathrm{Int}_{\mathcal{V}_\Lambda^+}. \end{align*} $$
$$ \begin{align*} \widehat{\mathrm{Int}_{\mathcal{V}_\Lambda^+}}=-\mathrm{Int}_{\mathcal{V}_\Lambda^+}. \end{align*} $$Proof. Since ![]() $t(\Lambda )=4$, we may choose a
$t(\Lambda )=4$, we may choose a ![]() $4$-dimensional (nonsplit) hermitian subspace
$4$-dimensional (nonsplit) hermitian subspace ![]() $\boldsymbol {V}'$ of
$\boldsymbol {V}'$ of ![]() $\boldsymbol {V}$ such that
$\boldsymbol {V}$ such that ![]() $\Lambda \cap \boldsymbol {V}^{\prime \perp }$ is a self-dual
$\Lambda \cap \boldsymbol {V}^{\prime \perp }$ is a self-dual ![]() $O_E$-lattice of
$O_E$-lattice of ![]() $\boldsymbol {V}^{\prime \perp }$. We adopt the construction in Remark 2.52. Write
$\boldsymbol {V}^{\prime \perp }$. We adopt the construction in Remark 2.52. Write ![]() $x=y+x'$ with respect to the orthogonal decomposition
$x=y+x'$ with respect to the orthogonal decomposition ![]() $\boldsymbol {V}=\boldsymbol {V}^{\prime \perp }\oplus \boldsymbol {V}'$. Put
$\boldsymbol {V}=\boldsymbol {V}^{\prime \perp }\oplus \boldsymbol {V}'$. Put ![]() $\Lambda ' := \Lambda \cap \boldsymbol {V}'$. By Remark 2.52(2) and Definition 2.27(2),
$\Lambda ' := \Lambda \cap \boldsymbol {V}'$. By Remark 2.52(2) and Definition 2.27(2), ![]() $\mathcal {V}_\Lambda $ coincides with
$\mathcal {V}_\Lambda $ coincides with ![]() $\mathcal {V}_{\Lambda '}$ under the natural morphism
$\mathcal {V}_{\Lambda '}$ under the natural morphism ![]() $\mathcal {N}'\to \mathcal {N}$. Denote by
$\mathcal {N}'\to \mathcal {N}$. Denote by ![]() $\mathcal {V}_{\Lambda '}^+$ the connected component of
$\mathcal {V}_{\Lambda '}^+$ the connected component of ![]() $\mathcal {V}_{\Lambda '}$ that corresponds to
$\mathcal {V}_{\Lambda '}$ that corresponds to ![]() $\mathcal {V}_\Lambda ^+$. By Remark 2.52(3), we have
$\mathcal {V}_\Lambda ^+$. By Remark 2.52(3), we have

In other words, we have
. Therefore, it suffices to consider the case where ![]() $n=4$.
$n=4$.
We now give an explicit formula for ![]() $\mathrm {Int}_{\mathcal {V}_\Lambda ^+}(x)$ when
$\mathrm {Int}_{\mathcal {V}_\Lambda ^+}(x)$ when ![]() $n=4$. Let
$n=4$. Let ![]() $\mathcal {N}^+$ be the connected component of
$\mathcal {N}^+$ be the connected component of ![]() $\mathcal {N}$ that contains
$\mathcal {N}$ that contains ![]() $\mathcal {V}_\Lambda ^+$ and put
$\mathcal {V}_\Lambda ^+$ and put ![]() $Z^+ := Z\cap \mathcal {N}^+$ for every formal subscheme Z of
$Z^+ := Z\cap \mathcal {N}^+$ for every formal subscheme Z of ![]() $\mathcal {N}$. Put
$\mathcal {N}$. Put ![]() $\Lambda (x) := \Lambda +\langle x\rangle $. There are three cases.
$\Lambda (x) := \Lambda +\langle x\rangle $. There are three cases.
(1) Suppose that
 $\Lambda (x)$ is not integral. By Corollary 2.30,
$\Lambda (x)$ is not integral. By Corollary 2.30,  $\mathcal {V}_\Lambda $ has empty intersection with
$\mathcal {V}_\Lambda $ has empty intersection with  $\mathcal {N}(x)$. Thus, we have
$\mathcal {N}(x)$. Thus, we have  $\mathrm {Int}_{\mathcal {V}_\Lambda ^+}(x)=0$.
$\mathrm {Int}_{\mathcal {V}_\Lambda ^+}(x)=0$.(2) Suppose that
 $\Lambda (x)$ is integral but
$\Lambda (x)$ is integral but  $x\not \in \Lambda $. Then
$x\not \in \Lambda $. Then  $\Lambda (x)$ has fundamental invariants
$\Lambda (x)$ has fundamental invariants  $(0,0,1,1)$. By Corollary 2.30,
$(0,0,1,1)$. By Corollary 2.30,  $\mathcal {V}_\Lambda ^+\cap \mathcal {N}(x)_{\mathrm {red}}=\mathcal {V}_{\Lambda (x)}^+$, which is a
$\mathcal {V}_\Lambda ^+\cap \mathcal {N}(x)_{\mathrm {red}}=\mathcal {V}_{\Lambda (x)}^+$, which is a  $\overline {k}$-point. Thus, we have
$\overline {k}$-point. Thus, we have  $\mathrm {Int}_{\mathcal {V}_\Lambda ^+}(x)\geqslant 1$. Choose a normal basis (Definition 2.11)
$\mathrm {Int}_{\mathcal {V}_\Lambda ^+}(x)\geqslant 1$. Choose a normal basis (Definition 2.11)  $\{x_1,x_2,x_3,x_4\}$ of
$\{x_1,x_2,x_3,x_4\}$ of  $\Lambda $ and write
$\Lambda $ and write  $x=\lambda _1x_1+\lambda _2x_2+\lambda _3x_3+\lambda _4x_4$ with
$x=\lambda _1x_1+\lambda _2x_2+\lambda _3x_3+\lambda _4x_4$ with  $\lambda _i\in E$. Without loss of generality, we may assume
$\lambda _i\in E$. Without loss of generality, we may assume  $\lambda _4\not \in O_E$. Since
$\lambda _4\not \in O_E$. Since  $ux\in \Lambda $, we have
$ux\in \Lambda $, we have  $\Lambda (x)=\langle x_1,x_2,x_3,x\rangle $. By Corollary 2.30,
$\Lambda (x)=\langle x_1,x_2,x_3,x\rangle $. By Corollary 2.30,  $\mathcal {N}(x_1)\cap \mathcal {N}(x_2)\cap \mathcal {N}(x_3)$ contains
$\mathcal {N}(x_1)\cap \mathcal {N}(x_2)\cap \mathcal {N}(x_3)$ contains  $\mathcal {V}_\Lambda $ as a closed subscheme. By Remark 2.52 and Proposition 2.44 applied to
$\mathcal {V}_\Lambda $ as a closed subscheme. By Remark 2.52 and Proposition 2.44 applied to  $\boldsymbol {V}'$ spanned by
$\boldsymbol {V}'$ spanned by  $x_3$ and
$x_3$ and  $x_4$,
$x_4$,  $\mathcal {N}(\Lambda (x))$ is a
$\mathcal {N}(\Lambda (x))$ is a  $0$-dimensional scheme and
$0$-dimensional scheme and  $\mathrm {Int}(\Lambda (x))=2$. It follows that by Lemma 2.56. Thus, we obtain
$\mathrm {Int}(\Lambda (x))=2$. It follows that by Lemma 2.56. Thus, we obtain $$ \begin{align*} \mathrm{Int}_{\mathcal{V}_\Lambda^+}(x)&\leqslant\mathrm{length}_{O_{\breve{E}}}\left(\mathcal{N}(x_1)\cap\mathcal{N}(x_2)\cap\mathcal{N}(x_3)\right)\cap\mathcal{N}(x)^+ =\mathrm{Int}^+(\Lambda(x))=1 \end{align*} $$
$$ \begin{align*} \mathrm{Int}_{\mathcal{V}_\Lambda^+}(x)&\leqslant\mathrm{length}_{O_{\breve{E}}}\left(\mathcal{N}(x_1)\cap\mathcal{N}(x_2)\cap\mathcal{N}(x_3)\right)\cap\mathcal{N}(x)^+ =\mathrm{Int}^+(\Lambda(x))=1 \end{align*} $$ $\mathrm {Int}^+(\Lambda (x))=1$; hence,
$\mathrm {Int}^+(\Lambda (x))=1$; hence,  $\mathrm {Int}_{\mathcal {V}_\Lambda ^+}(x)=1$.
$\mathrm {Int}_{\mathcal {V}_\Lambda ^+}(x)=1$.(3) Suppose that
 $x\in \Lambda $. Then
$x\in \Lambda $. Then  $\mathcal {V}_\Lambda ^+$ is a closed subscheme of
$\mathcal {V}_\Lambda ^+$ is a closed subscheme of  $\mathcal {N}(x)$, which implies However, by Corollary 2.34, we have
$\mathcal {N}(x)$, which implies However, by Corollary 2.34, we have $$ \begin{align*} \mathscr{O}_{\mathcal{V}_{\Lambda^+}}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x)} =\left(\mathscr{O}_{\mathcal{V}_{\Lambda^+}}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}(x)}}\mathscr{O}_{\mathcal{N}(x)}\right)\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x)} =\mathscr{O}_{\mathcal{V}_{\Lambda^+}}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}(x)}}\left(\mathscr{O}_{\mathcal{N}(x)}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x)}\right). \end{align*} $$in
$$ \begin{align*} \mathscr{O}_{\mathcal{V}_{\Lambda^+}}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x)} =\left(\mathscr{O}_{\mathcal{V}_{\Lambda^+}}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}(x)}}\mathscr{O}_{\mathcal{N}(x)}\right)\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x)} =\mathscr{O}_{\mathcal{V}_{\Lambda^+}}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}(x)}}\left(\mathscr{O}_{\mathcal{N}(x)}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x)}\right). \end{align*} $$in $$ \begin{align*} \mathscr{O}_{\mathcal{N}(x)}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x)}=\mathscr{O}_{\mathcal{N}(x)}\otimes_{\mathscr{O}_{\mathcal{N}}}C(0) \end{align*} $$
$$ \begin{align*} \mathscr{O}_{\mathcal{N}(x)}\overset{\mathbb{L}}\otimes_{\mathscr{O}_{\mathcal{N}}}\mathscr{O}_{\mathcal{N}(x)}=\mathscr{O}_{\mathcal{N}(x)}\otimes_{\mathscr{O}_{\mathcal{N}}}C(0) \end{align*} $$ $\mathrm {K}_0(\mathcal {N})$, where
$\mathrm {K}_0(\mathcal {N})$, where  $C(0)$ is the complex (2.14). Thus, we obtain by Lemma 2.42.
$C(0)$ is the complex (2.14). Thus, we obtain by Lemma 2.42. $$ \begin{align*} \mathrm{Int}_{\mathcal{V}_\Lambda^+}(x)&=\chi\left(C(0)\mathbin{|}_{\mathcal{V}_\Lambda^+}\right)=\deg\left(\mathscr{O}_{\mathcal{V}_\Lambda^+}\right)-\deg\left(\omega\mathbin{|}_{\mathcal{V}_\Lambda^+}\right) =-\deg\left(\omega\mathbin{|}_{\mathcal{V}_\Lambda^+}\right)=1-q \end{align*} $$
$$ \begin{align*} \mathrm{Int}_{\mathcal{V}_\Lambda^+}(x)&=\chi\left(C(0)\mathbin{|}_{\mathcal{V}_\Lambda^+}\right)=\deg\left(\mathscr{O}_{\mathcal{V}_\Lambda^+}\right)-\deg\left(\omega\mathbin{|}_{\mathcal{V}_\Lambda^+}\right) =-\deg\left(\omega\mathbin{|}_{\mathcal{V}_\Lambda^+}\right)=1-q \end{align*} $$
Since there are exactly ![]() $q^2+1$ vertex
$q^2+1$ vertex ![]() $O_E$-lattices of
$O_E$-lattices of ![]() $\boldsymbol {V}$ properly containing
$\boldsymbol {V}$ properly containing ![]() $\Lambda $, combining (1–3), we obtain
$\Lambda $, combining (1–3), we obtain

It follows that

• If
 $x\in \Lambda $, then
$x\in \Lambda $, then  $\widehat {\mathrm {Int}_{\mathcal {V}_\Lambda ^+}}(x)=-\frac {1+q}{q}+\frac {q^2+1}{q}=q-1$.
$\widehat {\mathrm {Int}_{\mathcal {V}_\Lambda ^+}}(x)=-\frac {1+q}{q}+\frac {q^2+1}{q}=q-1$.• If
 $\Lambda (x)$ is integral but
$\Lambda (x)$ is integral but  $x\not \in \Lambda $, then the number of
$x\not \in \Lambda $, then the number of  $\Lambda '$ in the summation of (2.18) is such that
$\Lambda '$ in the summation of (2.18) is such that  $x\in \Lambda ^{\prime \vee }$ is exactly
$x\in \Lambda ^{\prime \vee }$ is exactly  $1$ (namely,
$1$ (namely,  $\Lambda (x)$ itself). Thus, we have
$\Lambda (x)$ itself). Thus, we have  $\widehat {\mathrm {Int}_{\mathcal {V}_\Lambda ^+}}(x)=-\frac {1+q}{q}+\frac {1}{q}=-1$.
$\widehat {\mathrm {Int}_{\mathcal {V}_\Lambda ^+}}(x)=-\frac {1+q}{q}+\frac {1}{q}=-1$.• If
 $\Lambda (x)$ is not integral but
$\Lambda (x)$ is not integral but  $x\in \Lambda ^\vee $, then the set of
$x\in \Lambda ^\vee $, then the set of  $\Lambda '$ in the summation of (2.18) satisfying
$\Lambda '$ in the summation of (2.18) satisfying  $x\in \Lambda ^{\prime \vee }$ is bijective to the set of isotropic lines in
$x\in \Lambda ^{\prime \vee }$ is bijective to the set of isotropic lines in  $\Lambda ^\vee /\Lambda $ perpendicular to x. Now since
$\Lambda ^\vee /\Lambda $ perpendicular to x. Now since  $\Lambda (x)$ is not integral, x is anisotropic in
$\Lambda (x)$ is not integral, x is anisotropic in  $\Lambda ^\vee /\Lambda $, which implies that the previous set has cardinality
$\Lambda ^\vee /\Lambda $, which implies that the previous set has cardinality  $q+1$. Thus, we have
$q+1$. Thus, we have  $\widehat {\mathrm {Int}_{\mathcal {V}_\Lambda ^+}}(x)=-\frac {1+q}{q}+\frac {q+1}{q}=0$.
$\widehat {\mathrm {Int}_{\mathcal {V}_\Lambda ^+}}(x)=-\frac {1+q}{q}+\frac {q+1}{q}=0$.• If
 $x\not \in \Lambda ^\vee $, then
$x\not \in \Lambda ^\vee $, then  $\widehat {\mathrm {Int}_{\mathcal {V}_\Lambda ^+}}(x)=0$.
$\widehat {\mathrm {Int}_{\mathcal {V}_\Lambda ^+}}(x)=0$.
Therefore, we have  $\widehat {\mathrm {Int}_{\mathcal {V}_\Lambda ^+}}=-\mathrm {Int}_{\mathcal {V}_\Lambda ^+}$. The lemma is proved.
$\widehat {\mathrm {Int}_{\mathcal {V}_\Lambda ^+}}=-\mathrm {Int}_{\mathcal {V}_\Lambda ^+}$. The lemma is proved.
Lemma 2.56. Denote the two connected components of ![]() $\mathcal {N}$ by
$\mathcal {N}$ by ![]() $\mathcal {N}^+$ and
$\mathcal {N}^+$ and ![]() $\mathcal {N}^-$ and
$\mathcal {N}^-$ and ![]() $\mathrm {Int}^\pm (\boldsymbol {L})$ the intersection multiplicity in Definition 2.6 on
$\mathrm {Int}^\pm (\boldsymbol {L})$ the intersection multiplicity in Definition 2.6 on ![]() $\mathcal {N}^\pm $. Then
$\mathcal {N}^\pm $. Then
 $$ \begin{align*} \mathrm{Int}^+(\boldsymbol{L})=\mathrm{Int}^-(\boldsymbol{L})=\tfrac{1}{2}\mathrm{Int}(\boldsymbol{L}). \end{align*} $$
$$ \begin{align*} \mathrm{Int}^+(\boldsymbol{L})=\mathrm{Int}^-(\boldsymbol{L})=\tfrac{1}{2}\mathrm{Int}(\boldsymbol{L}). \end{align*} $$Proof. Choose a normal basis (Definition 2.11) ![]() $\{x_1,\dots ,x_n\}$ of
$\{x_1,\dots ,x_n\}$ of ![]() $\boldsymbol {L}$. Since
$\boldsymbol {L}$. Since ![]() $\boldsymbol {V}$ is nonsplit, there exists an anisotropic element in the basis, say,
$\boldsymbol {V}$ is nonsplit, there exists an anisotropic element in the basis, say, ![]() $x_n$. Let
$x_n$. Let ![]() $\theta $ the unique element in
$\theta $ the unique element in ![]() $\mathrm {U}(\boldsymbol {V})(F)$ satisfying
$\mathrm {U}(\boldsymbol {V})(F)$ satisfying ![]() $\theta (x_i)=1$ for
$\theta (x_i)=1$ for ![]() $1\leqslant i\leqslant n-1$ and
$1\leqslant i\leqslant n-1$ and ![]() $\theta (x_n)=-x_n$. Then
$\theta (x_n)=-x_n$. Then ![]() $\theta $ induces an automorphism of
$\theta $ induces an automorphism of ![]() $\mathcal {N}$, preserving
$\mathcal {N}$, preserving ![]() $\mathcal {N}(x_i)$ for
$\mathcal {N}(x_i)$ for ![]() $1\leqslant i\leqslant n$, but switching
$1\leqslant i\leqslant n$, but switching ![]() $\mathcal {N}^+$ and
$\mathcal {N}^+$ and ![]() $\mathcal {N}^-$ as
$\mathcal {N}^-$ as ![]() $\det \theta =-1$. Thus, we have
$\det \theta =-1$. Thus, we have ![]() $\mathrm {Int}^+(\boldsymbol {L})=\mathrm {Int}^-(\boldsymbol {L})$. Since
$\mathrm {Int}^+(\boldsymbol {L})=\mathrm {Int}^-(\boldsymbol {L})$. Since ![]() $\mathrm {Int}(\boldsymbol {L})=\mathrm {Int}^+(\boldsymbol {L})+\mathrm {Int}^-(\boldsymbol {L})$, the lemma follows.
$\mathrm {Int}(\boldsymbol {L})=\mathrm {Int}^+(\boldsymbol {L})+\mathrm {Int}^-(\boldsymbol {L})$, the lemma follows.
Proof of Proposition 2.51.
We first consider (1). By Lemma 2.54, we have for ![]() $x\in \boldsymbol {V}\setminus V_{L^\flat }$,
$x\in \boldsymbol {V}\setminus V_{L^\flat }$,

which, by Lemma 2.53, equals

Thus, Proposition 2.51(1) follows from Definition 2.20.
We first consider (2). We may assume ![]() $r\geqslant 2$ since otherwise
$r\geqslant 2$ since otherwise ![]() $\mathrm {Int}_{L^\flat }^{\mathrm {v}}\equiv 0$; hence, (2) is trivial. We write
$\mathrm {Int}_{L^\flat }^{\mathrm {v}}\equiv 0$; hence, (2) is trivial. We write ![]() $\mathcal {N}=\mathcal {N}^+\cup \mathcal {N}^-$ for the two connected components. For every vertex
$\mathcal {N}=\mathcal {N}^+\cup \mathcal {N}^-$ for the two connected components. For every vertex ![]() $O_E$-lattice
$O_E$-lattice ![]() $\Lambda $ of
$\Lambda $ of ![]() $\boldsymbol {V}$, we put
$\boldsymbol {V}$, we put ![]() $\mathcal {V}_\Lambda ^\pm := \mathcal {V}_\Lambda \cap \mathcal {N}^\pm $. Since the natural map
$\mathcal {V}_\Lambda ^\pm := \mathcal {V}_\Lambda \cap \mathcal {N}^\pm $. Since the natural map  $\mathrm {F}^{\frac {t(\Lambda )}{2}-2}\mathrm {K}_0(\mathcal {V}_\Lambda )\to \mathrm {F}^{n-1}\mathrm {K}_0^{\mathcal {V}_\Lambda }(\mathcal {N})$ is an isomorphism, by Lemma 2.49(3) and Lemma 2.32, there exist rational numbers
$\mathrm {F}^{\frac {t(\Lambda )}{2}-2}\mathrm {K}_0(\mathcal {V}_\Lambda )\to \mathrm {F}^{n-1}\mathrm {K}_0^{\mathcal {V}_\Lambda }(\mathcal {N})$ is an isomorphism, by Lemma 2.49(3) and Lemma 2.32, there exist rational numbers ![]() $c_\Lambda ^\pm $ for vertex
$c_\Lambda ^\pm $ for vertex ![]() $O_E$-lattices
$O_E$-lattices ![]() $\Lambda $ of
$\Lambda $ of ![]() $\boldsymbol {V}$ with
$\boldsymbol {V}$ with ![]() $t(\Lambda )=4$, of which all but finitely many are zero, such that
$t(\Lambda )=4$, of which all but finitely many are zero, such that

has zero intersection with ![]() $\mathrm {F}^1\mathrm {K}_0(\mathcal {N})$. Thus, Proposition 2.51(2) follows from Lemma 2.55.
$\mathrm {F}^1\mathrm {K}_0(\mathcal {N})$. Thus, Proposition 2.51(2) follows from Lemma 2.55.
2.7 Proof of Theorem 2.7
Let the setup be as in Subsection 2.1. In this subsection, for an element ![]() $L^\flat \in \flat (\boldsymbol {V})$ (Definition 2.8), we set
$L^\flat \in \flat (\boldsymbol {V})$ (Definition 2.8), we set ![]() $\operatorname {\mathrm {val}}(L^\flat )=-1$ if
$\operatorname {\mathrm {val}}(L^\flat )=-1$ if ![]() $L^\flat $ is not integral.
$L^\flat $ is not integral.
Lemma 2.57. Suppose that ![]() $r\geqslant 2$ and take an integral element
$r\geqslant 2$ and take an integral element ![]() $L^\flat \in \flat (\boldsymbol {V})$ whose fundamental invariants
$L^\flat \in \flat (\boldsymbol {V})$ whose fundamental invariants ![]() $(a_1,\dots ,a_{n-2},a_{n-1})$ satisfy
$(a_1,\dots ,a_{n-2},a_{n-1})$ satisfy ![]() $a_{n-2}<a_{n-1}$ (in particular,
$a_{n-2}<a_{n-1}$ (in particular, ![]() $a_{n-1}$ is odd). Then the number of integral
$a_{n-1}$ is odd). Then the number of integral ![]() $O_E$-lattices of
$O_E$-lattices of ![]() $\boldsymbol {V}$ containing
$\boldsymbol {V}$ containing ![]() $L^\flat $ with fundamental invariants
$L^\flat $ with fundamental invariants ![]() $(a_1,\dots ,a_{n-2},a_{n-1}-1,a_{n-1}-1)$ is either
$(a_1,\dots ,a_{n-2},a_{n-1}-1,a_{n-1}-1)$ is either ![]() $0$ or
$0$ or ![]() $2$. When the number is
$2$. When the number is ![]() $2$ and those lattices are denoted by
$2$ and those lattices are denoted by ![]() $L^{\flat +}$ and
$L^{\flat +}$ and ![]() $L^{\flat -}$, we have
$L^{\flat -}$, we have
(1)
 $L^{\flat \pm }\cap V_{L^\flat }=L^\flat $;
$L^{\flat \pm }\cap V_{L^\flat }=L^\flat $;(2)
 $a_{n-1}\geqslant 3$;
$a_{n-1}\geqslant 3$;(3) there are orthogonal decompositions
 $L^\flat =L^\flat _\leftarrow \oplus L^\flat _\rightarrow $ and
$L^\flat =L^\flat _\leftarrow \oplus L^\flat _\rightarrow $ and  $L^{\flat \pm }=L^\flat _\leftarrow \oplus L^{\flat \pm }_\rightarrow $, in which
$L^{\flat \pm }=L^\flat _\leftarrow \oplus L^{\flat \pm }_\rightarrow $, in which  $L^\flat _\leftarrow $,
$L^\flat _\leftarrow $,  $L^\flat _\rightarrow $ and
$L^\flat _\rightarrow $ and  $L^{\flat \pm }_\rightarrow $ are integral hermitian
$L^{\flat \pm }_\rightarrow $ are integral hermitian  $O_E$-modules with fundamental invariants
$O_E$-modules with fundamental invariants  $(a_1,\dots ,a_{n-2})$,
$(a_1,\dots ,a_{n-2})$,  $(a_{n-1})$ and
$(a_{n-1})$ and  $(a_{n-1}-1,a_{n-1}-1)$, respectively.
$(a_{n-1}-1,a_{n-1}-1)$, respectively.
Proof. Let L be an integral ![]() $O_E$-lattice L of
$O_E$-lattice L of ![]() $\boldsymbol {V}$ containing
$\boldsymbol {V}$ containing ![]() $L^\flat $ with fundamental invariants
$L^\flat $ with fundamental invariants ![]() $(a_1,\dots ,a_{n-2},a_{n-1}-1,a_{n-1}-1)$.
$(a_1,\dots ,a_{n-2},a_{n-1}-1,a_{n-1}-1)$.
We first claim that (1) must hold. We have ![]() $\operatorname {\mathrm {val}}(L\cap V_{L^\flat })\geqslant a_1+\cdots +a_{n-2}+a_{n-1}-1$ by Lemma 2.23(1). Since
$\operatorname {\mathrm {val}}(L\cap V_{L^\flat })\geqslant a_1+\cdots +a_{n-2}+a_{n-1}-1$ by Lemma 2.23(1). Since ![]() $L\cap V_{L^\flat }$ contains
$L\cap V_{L^\flat }$ contains ![]() $L^\flat $ and
$L^\flat $ and ![]() $\operatorname {\mathrm {val}}(L\cap V_{L^\flat })$ is odd, we must have
$\operatorname {\mathrm {val}}(L\cap V_{L^\flat })$ is odd, we must have ![]() $L\cap V_{L^\flat }=L^\flat $.
$L\cap V_{L^\flat }=L^\flat $.
Choose a normal basis ![]() $(e_1,\dots ,e_{n-1})$ of
$(e_1,\dots ,e_{n-1})$ of ![]() $L^\flat $ (Definition 2.11) and rearrange them such that for every
$L^\flat $ (Definition 2.11) and rearrange them such that for every ![]() $1\leqslant i\leqslant n-1$, exactly one of the following three happens:
$1\leqslant i\leqslant n-1$, exactly one of the following three happens:
(a)
 $(e_i,e_i)_{\boldsymbol {V}}=\beta _i u^{a_i-1}$ for some
$(e_i,e_i)_{\boldsymbol {V}}=\beta _i u^{a_i-1}$ for some  $\beta _i\in O_F^\times $;
$\beta _i\in O_F^\times $;(b)
 $(e_i,e_{i+1})_{\boldsymbol {V}}=u^{a_i-1}$;
$(e_i,e_{i+1})_{\boldsymbol {V}}=u^{a_i-1}$;(c)
 $(e_i,e_{i-1})_{\boldsymbol {V}}=-u^{a_i-1}$.
$(e_i,e_{i-1})_{\boldsymbol {V}}=-u^{a_i-1}$.
By the claim on (1), we may write ![]() $L=L^\flat +\langle x\rangle $ in which
$L=L^\flat +\langle x\rangle $ in which
for some ![]() $\lambda _i\in (E\setminus O_E)\cup \{0\}$ and
$\lambda _i\in (E\setminus O_E)\cup \{0\}$ and  $0\neq x_n\in V_{L^\flat }^\perp $. Let T be the moment matrix with respect to the basis
$0\neq x_n\in V_{L^\flat }^\perp $. Let T be the moment matrix with respect to the basis ![]() $\{e_1,\dots ,e_{n-1},x\}$ of L.
$\{e_1,\dots ,e_{n-1},x\}$ of L.
We show by induction that for ![]() $1\leqslant i\leqslant n-2$,
$1\leqslant i\leqslant n-2$, ![]() $\lambda _i=0$. Suppose we know
$\lambda _i=0$. Suppose we know ![]() $\lambda _1=\cdots \lambda _{i-1}=0$. For
$\lambda _1=\cdots \lambda _{i-1}=0$. For ![]() $\lambda _i$ (with
$\lambda _i$ (with ![]() $1\leqslant i\leqslant n-2$), there are three cases.
$1\leqslant i\leqslant n-2$), there are three cases.
• If
 $e_i$ is in the situation (a) above, then applying Lemma 2.23(1) to the i-by-i minor of T consisting of rows
$e_i$ is in the situation (a) above, then applying Lemma 2.23(1) to the i-by-i minor of T consisting of rows  $\{1,\dots ,i\}$ and columns
$\{1,\dots ,i\}$ and columns  $\{1,\dots ,i-1,n\}$, we obtain
$\{1,\dots ,i-1,n\}$, we obtain  $\operatorname {\mathrm {val}}_E(\lambda _i\beta _i u^{a_i-1})\geqslant a_i-1$, which implies
$\operatorname {\mathrm {val}}_E(\lambda _i\beta _i u^{a_i-1})\geqslant a_i-1$, which implies  $\lambda _i=0$.
$\lambda _i=0$.• If
 $e_i$ is in the situation (b) above, then applying Lemma 2.23(1) to the i-by-i minor of T consisting of rows
$e_i$ is in the situation (b) above, then applying Lemma 2.23(1) to the i-by-i minor of T consisting of rows  $\{1,\dots ,i-1,i+1\}$ and columns
$\{1,\dots ,i-1,i+1\}$ and columns  $\{1,\dots ,i-1,n\}$, we obtain
$\{1,\dots ,i-1,n\}$, we obtain  $\operatorname {\mathrm {val}}_E(-\lambda _i u^{a_i-1})\geqslant a_i-1$, which implies
$\operatorname {\mathrm {val}}_E(-\lambda _i u^{a_i-1})\geqslant a_i-1$, which implies  $\lambda _i=0$.
$\lambda _i=0$.• If
 $e_i$ is in the situation (c) above, then applying Lemma 2.23(1) to the i-by-i minor of T consisting of rows
$e_i$ is in the situation (c) above, then applying Lemma 2.23(1) to the i-by-i minor of T consisting of rows  $\{1,\dots ,i\}$ and columns
$\{1,\dots ,i\}$ and columns  $\{1,\dots ,i-1,n\}$, we obtain
$\{1,\dots ,i-1,n\}$, we obtain  $\operatorname {\mathrm {val}}_E(\lambda _i u^{a_i-1})\geqslant a_i-1$, which implies
$\operatorname {\mathrm {val}}_E(\lambda _i u^{a_i-1})\geqslant a_i-1$, which implies  $\lambda _i=0$.
$\lambda _i=0$.
Note that ![]() $e_{n-1}$ is in the situation (a). Applying Lemma 2.23(1) to the
$e_{n-1}$ is in the situation (a). Applying Lemma 2.23(1) to the ![]() $(n-1)$-by-
$(n-1)$-by-![]() $(n-1)$ minor of T consisting of rows
$(n-1)$ minor of T consisting of rows ![]() $\{1,\dots ,n-1\}$ and columns
$\{1,\dots ,n-1\}$ and columns ![]() $\{1,\dots ,n-2,n\}$, we obtain
$\{1,\dots ,n-2,n\}$, we obtain ![]() $\operatorname {\mathrm {val}}_E(\lambda _{n-1}\beta _{n-1}u^{a_{n-1}-1})\geqslant a_{n-1}-2$, which implies
$\operatorname {\mathrm {val}}_E(\lambda _{n-1}\beta _{n-1}u^{a_{n-1}-1})\geqslant a_{n-1}-2$, which implies ![]() $\lambda _{n-1}\in u^{-1}O_E$. On the other hand,
$\lambda _{n-1}\in u^{-1}O_E$. On the other hand, ![]() $\lambda _{n-1}\neq 0$ since otherwise
$\lambda _{n-1}\neq 0$ since otherwise ![]() $a_{n-1}$ will appear in the fundamental invariants of L, which is a contradiction. Thus, we have
$a_{n-1}$ will appear in the fundamental invariants of L, which is a contradiction. Thus, we have ![]() $\lambda _{n-1}\in u^{-1}O_E\setminus O_E$. After rescaling by an element in
$\lambda _{n-1}\in u^{-1}O_E\setminus O_E$. After rescaling by an element in ![]() $O_E^\times $, we may assume
$O_E^\times $, we may assume ![]() $\lambda _{n-1}=u^{-1}$. Applying Lemma 2.23(1) to the
$\lambda _{n-1}=u^{-1}$. Applying Lemma 2.23(1) to the ![]() $(n-1)$-by-
$(n-1)$-by-![]() $(n-1)$ minor of T consisting of rows
$(n-1)$ minor of T consisting of rows ![]() $\{1,\dots ,n-2,n\}$ and columns
$\{1,\dots ,n-2,n\}$ and columns ![]() $\{1,\dots ,n-2,n\}$, we obtain
$\{1,\dots ,n-2,n\}$, we obtain
 $$ \begin{align} \operatorname{\mathrm{val}}_E\left((x_n,x_n)_{\boldsymbol{V}}-u^{-2}\beta_{n-1}u^{a_{n-1}-1}\right)\geqslant a_{n-1}-2. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{val}}_E\left((x_n,x_n)_{\boldsymbol{V}}-u^{-2}\beta_{n-1}u^{a_{n-1}-1}\right)\geqslant a_{n-1}-2. \end{align} $$We note the following facts.
• The set of
 $x_n\in V_{L^\flat }^\perp $ satisfying (2.19) is stable under the multiplication by
$x_n\in V_{L^\flat }^\perp $ satisfying (2.19) is stable under the multiplication by  $1+uO_E$.
$1+uO_E$.• The set of orbits of such
 $x_n$ under the multiplication by
$x_n$ under the multiplication by  $1+uO_E$ is bijective to the set of L.
$1+uO_E$ is bijective to the set of L.• The number of orbits is either
 $0$ or
$0$ or  $2$.
$2$.• If the number is
 $2$, then
$2$, then  $a_{n-1}\geqslant 3$, since
$a_{n-1}\geqslant 3$, since  $\boldsymbol {V}$ is nonsplit.
$\boldsymbol {V}$ is nonsplit.
Thus, the main part of the lemma is proved, with the properties (1) and (2) included. For (3), we simply take ![]() $L^\flat _\leftarrow =\langle e_1,\dots ,e_{n-2}\rangle $ with
$L^\flat _\leftarrow =\langle e_1,\dots ,e_{n-2}\rangle $ with ![]() $L^\flat _\rightarrow $ and
$L^\flat _\rightarrow $ and ![]() $L^{\flat \pm }_\rightarrow $ uniquely determined.
$L^{\flat \pm }_\rightarrow $ uniquely determined.
The lemma is proved.
In the rest of subsection, we say that ![]() $L^\flat $ is special if
$L^\flat $ is special if ![]() $L^\flat $ is like in Lemma 2.57 for which the number is
$L^\flat $ is like in Lemma 2.57 for which the number is ![]() $2$. We now define an open compact subset
$2$. We now define an open compact subset ![]() $S_{L^\flat }$ of
$S_{L^\flat }$ of ![]() $\boldsymbol {V}$ for an integral element
$\boldsymbol {V}$ for an integral element ![]() $L^\flat \in \flat (\boldsymbol {V})$ in the following way:
$L^\flat \in \flat (\boldsymbol {V})$ in the following way:
 $$ \begin{align*} S_{L^\flat} := \begin{cases} L^{\flat+}\cup L^{\flat-}, &\text{if } L^\flat \text{ is special,}\\ L^\flat+(V_{L^\flat}^\perp)^{\mathrm{int}}, &\text{if } L^\flat \text{ is not special.} \end{cases} \end{align*} $$
$$ \begin{align*} S_{L^\flat} := \begin{cases} L^{\flat+}\cup L^{\flat-}, &\text{if } L^\flat \text{ is special,}\\ L^\flat+(V_{L^\flat}^\perp)^{\mathrm{int}}, &\text{if } L^\flat \text{ is not special.} \end{cases} \end{align*} $$Lemma 2.58. Take an integral element ![]() $L^\flat \in \flat (\boldsymbol {V})$. Then for every
$L^\flat \in \flat (\boldsymbol {V})$. Then for every ![]() $x\in \boldsymbol {V}\setminus (V_{L^\flat }\cup S_{L^\flat })$, we may write
$x\in \boldsymbol {V}\setminus (V_{L^\flat }\cup S_{L^\flat })$, we may write
for some ![]() $L^{\flat \prime }\in \flat (\boldsymbol {V})$ satisfying
$L^{\flat \prime }\in \flat (\boldsymbol {V})$ satisfying ![]() $\operatorname {\mathrm {val}}(L^{\flat \prime })<\operatorname {\mathrm {val}}(L^\flat )$.
$\operatorname {\mathrm {val}}(L^{\flat \prime })<\operatorname {\mathrm {val}}(L^\flat )$.
Proof. Take an element ![]() $x\in \boldsymbol {V}\setminus (V_{L^\flat }\cup S_{L^\flat })$. Put
$x\in \boldsymbol {V}\setminus (V_{L^\flat }\cup S_{L^\flat })$. Put ![]() $L := L^\flat +\langle x\rangle $. If L is not integral, then by Lemma 2.12, we may write
$L := L^\flat +\langle x\rangle $. If L is not integral, then by Lemma 2.12, we may write ![]() $L=L^{\flat \prime }+\langle x'\rangle $ with
$L=L^{\flat \prime }+\langle x'\rangle $ with ![]() $L^{\flat \prime }\in \flat (\boldsymbol {V})$ that is not integral; hence, the lemma follows.
$L^{\flat \prime }\in \flat (\boldsymbol {V})$ that is not integral; hence, the lemma follows.
In what follows, we assume L integral and write its fundamental invariants as ![]() $(a^{\prime }_1,\dots ,a^{\prime }_n)$. By Lemma 2.12, it suffices to show that
$(a^{\prime }_1,\dots ,a^{\prime }_n)$. By Lemma 2.12, it suffices to show that
Choose a normal basis ![]() $(e_1,\dots ,e_{n-1})$ of
$(e_1,\dots ,e_{n-1})$ of ![]() $L^\flat $ (Definition 2.11) and rearrange them such that for every
$L^\flat $ (Definition 2.11) and rearrange them such that for every ![]() $1\leqslant i\leqslant n-1$, exactly one of the following three happens:
$1\leqslant i\leqslant n-1$, exactly one of the following three happens:
(a)
 $(e_i,e_i)_{\boldsymbol {V}}=\beta _i u^{a_i-1}$ for some
$(e_i,e_i)_{\boldsymbol {V}}=\beta _i u^{a_i-1}$ for some  $\beta _i\in O_F^\times $;
$\beta _i\in O_F^\times $;(b)
 $(e_i,e_{i+1})_{\boldsymbol {V}}=u^{a_i-1}$;
$(e_i,e_{i+1})_{\boldsymbol {V}}=u^{a_i-1}$;(c)
 $(e_i,e_{i-1})_{\boldsymbol {V}}=-u^{a_i-1}$.
$(e_i,e_{i-1})_{\boldsymbol {V}}=-u^{a_i-1}$.
Write ![]() $x=\lambda _1 e_1+\cdots +\lambda _{n-1}e_{n-1}+x_n$ for some
$x=\lambda _1 e_1+\cdots +\lambda _{n-1}e_{n-1}+x_n$ for some ![]() $\lambda _i\in (E\setminus O_E)\cup \{0\}$ and
$\lambda _i\in (E\setminus O_E)\cup \{0\}$ and  $0\neq x_n\in V_{L^\flat }^\perp $. Let T be the moment matrix with respect to the basis
$0\neq x_n\in V_{L^\flat }^\perp $. Let T be the moment matrix with respect to the basis ![]() $\{e_1,\dots ,e_{n-1},x\}$ of L.
$\{e_1,\dots ,e_{n-1},x\}$ of L.
If ![]() $\lambda _1=\cdots =\lambda _{n-1}=0$, then since
$\lambda _1=\cdots =\lambda _{n-1}=0$, then since ![]() $x\not \in S_{L^\flat }$, we have either
$x\not \in S_{L^\flat }$, we have either ![]() $\langle x\rangle $ is not integral or
$\langle x\rangle $ is not integral or ![]() $\operatorname {\mathrm {val}}(x)\leqslant a_{n-1}-2$ (only possible when
$\operatorname {\mathrm {val}}(x)\leqslant a_{n-1}-2$ (only possible when ![]() $L^\flat $ is special), which implies (2.20).
$L^\flat $ is special), which implies (2.20).
If ![]() $\lambda _i\neq 0$ for some
$\lambda _i\neq 0$ for some ![]() $1\leqslant i\leqslant n-1$ such that
$1\leqslant i\leqslant n-1$ such that ![]() $e_i$ is in the situation (b) or (c); then applying Lemma 2.23(1) to the
$e_i$ is in the situation (b) or (c); then applying Lemma 2.23(1) to the ![]() $(n-1)$-by-
$(n-1)$-by-![]() $(n-1)$ minor of T deleting the ith row and the ith column, we obtain (2.20).
$(n-1)$ minor of T deleting the ith row and the ith column, we obtain (2.20).
If ![]() $\lambda _i\not \in u^{-1}O_E$ for some
$\lambda _i\not \in u^{-1}O_E$ for some ![]() $1\leqslant i\leqslant n-1$ such that
$1\leqslant i\leqslant n-1$ such that ![]() $e_i$ is in the situation (a); then applying Lemma 2.23(1) to the
$e_i$ is in the situation (a); then applying Lemma 2.23(1) to the ![]() $(n-1)$-by-
$(n-1)$-by-![]() $(n-1)$ minor of T deleting the ith row and the nth column, we obtain (2.20).
$(n-1)$ minor of T deleting the ith row and the nth column, we obtain (2.20).
If ![]() $\lambda _i\neq 0$ and
$\lambda _i\neq 0$ and ![]() $\lambda _j\neq 0$ for
$\lambda _j\neq 0$ for ![]() $1\leqslant i<j\leqslant n-1$ such that both
$1\leqslant i<j\leqslant n-1$ such that both ![]() $e_i$ and
$e_i$ and ![]() $e_j$ are in the situation (a), then applying Lemma 2.23(1) to the
$e_j$ are in the situation (a), then applying Lemma 2.23(1) to the ![]() $(n-1)$-by-
$(n-1)$-by-![]() $(n-1)$ minor of T deleting the ith row and the jth column, we obtain (2.20).
$(n-1)$ minor of T deleting the ith row and the jth column, we obtain (2.20).
The remaining case is that ![]() $\lambda _i\in u^{-1}O_E\setminus O_E$ for a unique element
$\lambda _i\in u^{-1}O_E\setminus O_E$ for a unique element ![]() $1\leqslant i\leqslant n-1$ such that
$1\leqslant i\leqslant n-1$ such that ![]() $e_i$ is in the situation (a). Then
$e_i$ is in the situation (a). Then ![]() $L^\flat +\langle x\rangle $ is the orthogonal sum of
$L^\flat +\langle x\rangle $ is the orthogonal sum of ![]() $\langle e_1,\dots ,\widehat {e_i},\dots ,e_{n-1}\rangle $ and
$\langle e_1,\dots ,\widehat {e_i},\dots ,e_{n-1}\rangle $ and ![]() $\langle e_i,x\rangle $. In particular, if we write the fundamental invariants of
$\langle e_i,x\rangle $. In particular, if we write the fundamental invariants of ![]() $\langle e_i,x\rangle $ as
$\langle e_i,x\rangle $ as ![]() $(b_1,b_2)$, then the fundamental invariant of
$(b_1,b_2)$, then the fundamental invariant of ![]() $L^\flat +\langle x\rangle $ is the nondecreasing rearrangement of
$L^\flat +\langle x\rangle $ is the nondecreasing rearrangement of ![]() $(a_1,\dots ,\widehat {a_i},\dots ,a_{n-1},b_1,b_2)$. We have two cases:
$(a_1,\dots ,\widehat {a_i},\dots ,a_{n-1},b_1,b_2)$. We have two cases:
• If
 $(x,x)_{\boldsymbol {V}}\in u^{e_i-1}O_F$, then
$(x,x)_{\boldsymbol {V}}\in u^{e_i-1}O_F$, then  $(b_1,b_2)=(a_i-1,a_i-1)$. Thus, we have either (2.20) or
$(b_1,b_2)=(a_i-1,a_i-1)$. Thus, we have either (2.20) or  $i=n-1$,
$i=n-1$,  $a_{n-2}<a_{n-1}$ and
$a_{n-2}<a_{n-1}$ and  $L^\flat +\langle x\rangle $ has fundamental invariants
$L^\flat +\langle x\rangle $ has fundamental invariants  $(a_1,\dots ,a_{n-2},a_{n-1}-1,a_{n-1}-1)$ (hence
$(a_1,\dots ,a_{n-2},a_{n-1}-1,a_{n-1}-1)$ (hence  $L^\flat $ is special). The latter case is not possible as
$L^\flat $ is special). The latter case is not possible as  $x\not \in S_{L^\flat }$.
$x\not \in S_{L^\flat }$.• If
 $(x,x)_{\boldsymbol {V}}\not \in u^{e_i-1}O_F$, then
$(x,x)_{\boldsymbol {V}}\not \in u^{e_i-1}O_F$, then  $b_1\leqslant a_i-2$. Thus, we have (2.20).
$b_1\leqslant a_i-2$. Thus, we have (2.20).
The lemma is proved.
Proof of Theorem 2.7.
For every element ![]() $L^\flat \in \flat (\boldsymbol {V})$, we define a function
$L^\flat \in \flat (\boldsymbol {V})$, we define a function
which is a compactly supported locally constant function on ![]() $\boldsymbol {V}$ by Proposition 2.22 and Proposition 2.51(2). It enjoys the following properties:
$\boldsymbol {V}$ by Proposition 2.22 and Proposition 2.51(2). It enjoys the following properties:
(1) For
 $x\in \boldsymbol {V}\setminus V_{L^\flat }$, we have
$x\in \boldsymbol {V}\setminus V_{L^\flat }$, we have  $\Phi _{L^\flat }(x)=\partial \mathrm {Den}_{L^\flat }(x)-\mathrm {Int}_{L^\flat }(x)$ by Proposition 2.51(1).
$\Phi _{L^\flat }(x)=\partial \mathrm {Den}_{L^\flat }(x)-\mathrm {Int}_{L^\flat }(x)$ by Proposition 2.51(1).(2)
 $\Phi _{L^\flat }$ is invariant under the translation by
$\Phi _{L^\flat }$ is invariant under the translation by  $L^\flat $, which follows from (1) and the similar properties for
$L^\flat $, which follows from (1) and the similar properties for  $\partial \mathrm {Den}_{L^\flat }$ and
$\partial \mathrm {Den}_{L^\flat }$ and  $\mathrm {Int}_{L^\flat }$.
$\mathrm {Int}_{L^\flat }$.(3) The support of
 $\widehat {\Phi _{L^\flat }}$ is contained in
$\widehat {\Phi _{L^\flat }}$ is contained in  $\boldsymbol {V}^{\mathrm {int}}$, by Proposition 2.22 and Proposition 2.51(2).
$\boldsymbol {V}^{\mathrm {int}}$, by Proposition 2.22 and Proposition 2.51(2).
We prove by induction on ![]() $\operatorname {\mathrm {val}}(L^\flat )$ that
$\operatorname {\mathrm {val}}(L^\flat )$ that ![]() $\Phi _{L^\flat }\equiv 0$.
$\Phi _{L^\flat }\equiv 0$.
The initial case is that ![]() $\operatorname {\mathrm {val}}(L^\flat )=-1$; that is,
$\operatorname {\mathrm {val}}(L^\flat )=-1$; that is, ![]() $L^\flat $ is not integral. Then we have
$L^\flat $ is not integral. Then we have ![]() $\partial \mathrm {Den}_{L^\flat }=\mathrm {Int}_{L^\flat }=0$; hence,
$\partial \mathrm {Den}_{L^\flat }=\mathrm {Int}_{L^\flat }=0$; hence, ![]() $\Phi _{L^\flat }\equiv 0$ by (1).
$\Phi _{L^\flat }\equiv 0$ by (1).
Now consider ![]() $L^\flat $ that is integral and assume
$L^\flat $ that is integral and assume ![]() $\Phi _{L^{\flat \prime }}\equiv 0$ for every
$\Phi _{L^{\flat \prime }}\equiv 0$ for every ![]() $L^{\flat \prime }\in \flat (\boldsymbol {V})$ satisfying
$L^{\flat \prime }\in \flat (\boldsymbol {V})$ satisfying ![]() $\operatorname {\mathrm {val}}(L^{\flat \prime })<\operatorname {\mathrm {val}}(L^\flat )$. For every
$\operatorname {\mathrm {val}}(L^{\flat \prime })<\operatorname {\mathrm {val}}(L^\flat )$. For every ![]() $x\in \boldsymbol {V}\setminus (V_{L^\flat }\cup S_{L^\flat })$, by Lemma 2.58, we may write
$x\in \boldsymbol {V}\setminus (V_{L^\flat }\cup S_{L^\flat })$, by Lemma 2.58, we may write ![]() $L^\flat +\langle x\rangle = L^{\flat \prime }+\langle x'\rangle $ with some
$L^\flat +\langle x\rangle = L^{\flat \prime }+\langle x'\rangle $ with some ![]() $L^{\flat \prime }\in \flat (\boldsymbol {V})$ satisfying
$L^{\flat \prime }\in \flat (\boldsymbol {V})$ satisfying ![]() $\operatorname {\mathrm {val}}(L^{\flat \prime })<\operatorname {\mathrm {val}}(L^\flat )$ and we have
$\operatorname {\mathrm {val}}(L^{\flat \prime })<\operatorname {\mathrm {val}}(L^\flat )$ and we have
 $$ \begin{align*} \Phi_{L^\flat}(x)&=\partial\mathrm{Den}_{L^\flat}(x)-\mathrm{Int}_{L^\flat}(x) \\ &=\partial\mathrm{Den}(L^\flat+\langle x\rangle)-\mathrm{Int}(L^\flat+\langle x\rangle) \\ &=\partial\mathrm{Den}(L^{\flat\prime}+\langle x'\rangle)-\mathrm{Int}(L^{\flat\prime}+\langle x'\rangle) \\ &=\Phi_{L^{\flat\prime}}(x')=0 \end{align*} $$
$$ \begin{align*} \Phi_{L^\flat}(x)&=\partial\mathrm{Den}_{L^\flat}(x)-\mathrm{Int}_{L^\flat}(x) \\ &=\partial\mathrm{Den}(L^\flat+\langle x\rangle)-\mathrm{Int}(L^\flat+\langle x\rangle) \\ &=\partial\mathrm{Den}(L^{\flat\prime}+\langle x'\rangle)-\mathrm{Int}(L^{\flat\prime}+\langle x'\rangle) \\ &=\Phi_{L^{\flat\prime}}(x')=0 \end{align*} $$by the induction hypothesis. Thus, the support of ![]() $\Phi _{L^\flat }$ is contained in
$\Phi _{L^\flat }$ is contained in ![]() $S_{L^\flat }$. There are two cases.
$S_{L^\flat }$. There are two cases.
Suppose that ![]() $L^\flat $ is not special. By (2), we may write
$L^\flat $ is not special. By (2), we may write ![]() for a locally constant function
for a locally constant function ![]() $\phi $ on
$\phi $ on  $V_{L^\flat }^\perp $ supported on
$V_{L^\flat }^\perp $ supported on  $(V_{L^\flat }^\perp )^{\mathrm {int}}$. Then
$(V_{L^\flat }^\perp )^{\mathrm {int}}$. Then  for some
for some ![]() $C\in \mathbb {Q}^\times $. Now since
$C\in \mathbb {Q}^\times $. Now since ![]() $\widehat \phi $ is invariant under the translation by
$\widehat \phi $ is invariant under the translation by  $u^{-1}(V_{L^\flat }^\perp )^{\mathrm {int}}$, we must have
$u^{-1}(V_{L^\flat }^\perp )^{\mathrm {int}}$, we must have ![]() $\widehat \phi =0$ by (3); that is,
$\widehat \phi =0$ by (3); that is, ![]() $\Phi _{L^\flat }\equiv 0$.
$\Phi _{L^\flat }\equiv 0$.
Suppose that ![]() $L^\flat $ is special. We fix the orthogonal decompositions
$L^\flat $ is special. We fix the orthogonal decompositions ![]() $L^\flat =L^\flat _\leftarrow \oplus L^\flat _\rightarrow $ and
$L^\flat =L^\flat _\leftarrow \oplus L^\flat _\rightarrow $ and ![]() $L^{\flat \pm }=L^\flat _\leftarrow \oplus L^{\flat \pm }_\rightarrow $ from Lemma 2.57. Put
$L^{\flat \pm }=L^\flat _\leftarrow \oplus L^{\flat \pm }_\rightarrow $ from Lemma 2.57. Put ![]() $V_\leftarrow := L^\flat _\leftarrow \otimes _{O_F}F$ and denote by
$V_\leftarrow := L^\flat _\leftarrow \otimes _{O_F}F$ and denote by ![]() $V_\rightarrow $ the orthogonal complement of
$V_\rightarrow $ the orthogonal complement of ![]() $V_\leftarrow $ in
$V_\leftarrow $ in ![]() $\boldsymbol {V}$. Then both
$\boldsymbol {V}$. Then both ![]() $L^{\flat +}_\rightarrow $ and
$L^{\flat +}_\rightarrow $ and ![]() $L^{\flat -}_\rightarrow $ are integral
$L^{\flat -}_\rightarrow $ are integral ![]() $O_E$-lattices of
$O_E$-lattices of ![]() $V_\rightarrow $ with fundamental invariants
$V_\rightarrow $ with fundamental invariants ![]() $(a_{n-1}-1,a_{n-1}-1)$. Moreover, we have
$(a_{n-1}-1,a_{n-1}-1)$. Moreover, we have ![]() $S_{L^\flat }=L^\flat _\leftarrow \times (L^{\flat +}_\rightarrow \cup L^{\flat -}_\rightarrow )$. Thus, by (2), we may write
$S_{L^\flat }=L^\flat _\leftarrow \times (L^{\flat +}_\rightarrow \cup L^{\flat -}_\rightarrow )$. Thus, by (2), we may write ![]() for a locally constant function
for a locally constant function ![]() $\phi $ on
$\phi $ on ![]() $V_\rightarrow $ supported on
$V_\rightarrow $ supported on ![]() $L^{\flat +}_\rightarrow \cup L^{\flat -}_\rightarrow $. Since
$L^{\flat +}_\rightarrow \cup L^{\flat -}_\rightarrow $. Since ![]() $a_{n-1}\geqslant 3$ by Lemma 2.57, we have
$a_{n-1}\geqslant 3$ by Lemma 2.57, we have ![]() $L^{\flat +}_\rightarrow \cup L^{\flat -}_\rightarrow \subseteq uV_\rightarrow ^{\mathrm {int}}$, which implies that the support of
$L^{\flat +}_\rightarrow \cup L^{\flat -}_\rightarrow \subseteq uV_\rightarrow ^{\mathrm {int}}$, which implies that the support of ![]() $\phi $ is contained in
$\phi $ is contained in ![]() $uV_\rightarrow ^{\mathrm {int}}$. On the other hand, by (3), the support of
$uV_\rightarrow ^{\mathrm {int}}$. On the other hand, by (3), the support of ![]() $\widehat \phi $ is contained in
$\widehat \phi $ is contained in ![]() $V_\rightarrow ^{\mathrm {int}}$. Together, we must have
$V_\rightarrow ^{\mathrm {int}}$. Together, we must have ![]() $\phi =0$ by the uncertainty principle [Reference Li and ZhangLZa, Proposition 8.1.6]; that is,
$\phi =0$ by the uncertainty principle [Reference Li and ZhangLZa, Proposition 8.1.6]; that is, ![]() $\Phi _{L^\flat }\equiv 0$.
$\Phi _{L^\flat }\equiv 0$.
By (1), we have ![]() $\partial \mathrm {Den}_{L^\flat }(x)=\mathrm {Int}_{L^\flat }(x)$ for every
$\partial \mathrm {Den}_{L^\flat }(x)=\mathrm {Int}_{L^\flat }(x)$ for every ![]() $x\in \boldsymbol {V}\setminus V_{L^\flat }$. In particular, Theorem 2.7 follows as every
$x\in \boldsymbol {V}\setminus V_{L^\flat }$. In particular, Theorem 2.7 follows as every ![]() $O_E$-lattice
$O_E$-lattice ![]() $\boldsymbol {L}$ of
$\boldsymbol {L}$ of ![]() $\boldsymbol {V}$ is of the form
$\boldsymbol {V}$ is of the form ![]() $L^\flat +\langle x\rangle $ for some
$L^\flat +\langle x\rangle $ for some ![]() $L^\flat \in \flat (\boldsymbol {V})$.
$L^\flat \in \flat (\boldsymbol {V})$.
2.8 Comparison with absolute Rapoport–Zink spaces
Let the setup be as in Subsection 2.1. In this subsection, we compare ![]() $\mathcal {N}$ to certain (absolute) Rapoport–Zink space under the assumption that F is unramified over
$\mathcal {N}$ to certain (absolute) Rapoport–Zink space under the assumption that F is unramified over ![]() $\mathbb {Q}_p$. Put
$\mathbb {Q}_p$. Put ![]() $f := [F:\mathbb {Q}_p]$; hence,
$f := [F:\mathbb {Q}_p]$; hence, ![]() $q=p^f$. This subsection is redundant if
$q=p^f$. This subsection is redundant if ![]() $f=1$.
$f=1$.
To begin with, we fix a subset ![]() $\Phi $ of
$\Phi $ of ![]() $\operatorname {\mathrm {Hom}}(E,\mathbb {C}_p)=\operatorname {\mathrm {Hom}}(E,\breve {E})$ containing
$\operatorname {\mathrm {Hom}}(E,\mathbb {C}_p)=\operatorname {\mathrm {Hom}}(E,\breve {E})$ containing ![]() $\varphi _0$ and satisfying
$\varphi _0$ and satisfying ![]() $\operatorname {\mathrm {Hom}}(E,\breve {E})=\Phi \coprod \Phi ^{\mathtt {c}}$. Recall that we have regarded E as a subfield of
$\operatorname {\mathrm {Hom}}(E,\breve {E})=\Phi \coprod \Phi ^{\mathtt {c}}$. Recall that we have regarded E as a subfield of ![]() $\breve {E}$ via
$\breve {E}$ via ![]() $\varphi _0$. We introduce more notation.
$\varphi _0$. We introduce more notation.
• For every ring R, we denote by
 $\mathsf {W}(R)$ the p-typical Witt ring of R, with
$\mathsf {W}(R)$ the p-typical Witt ring of R, with  $\mathsf {F}$,
$\mathsf {F}$,  $\mathsf {V}$,
$\mathsf {V}$,  $[\;]$ and
$[\;]$ and  $\mathsf {I}(R)$ its (p-typical) Frobenius, the Verschiebung, the Teichmüller lift and the augmentation ideal, respectively. For an
$\mathsf {I}(R)$ its (p-typical) Frobenius, the Verschiebung, the Teichmüller lift and the augmentation ideal, respectively. For an  $\mathsf {F}^i$-linear map
$\mathsf {F}^i$-linear map  $\mathsf {f}\colon \mathsf {P}\to \mathsf {Q}$ between
$\mathsf {f}\colon \mathsf {P}\to \mathsf {Q}$ between  $\mathsf {W}(R)$-modules with
$\mathsf {W}(R)$-modules with  $i\geqslant 1$, we denote by its induced
$i\geqslant 1$, we denote by its induced
 $\mathsf {W}(R)$-linear map.
$\mathsf {W}(R)$-linear map.• For
 $i\in \mathbb {Z}/f\mathbb {Z}$, put
$i\in \mathbb {Z}/f\mathbb {Z}$, put  $\psi _i := \mathsf {F}^i\colon O_F\to O_F$, define
$\psi _i := \mathsf {F}^i\colon O_F\to O_F$, define  $\hat \psi _i\colon O_F\to \mathsf {W}(O_F)$ to be the composition of
$\hat \psi _i\colon O_F\to \mathsf {W}(O_F)$ to be the composition of  $\psi _i$ with the Cartier homomorphism
$\psi _i$ with the Cartier homomorphism  $O_F\to \mathsf {W}(O_F)$ and denote by
$O_F\to \mathsf {W}(O_F)$ and denote by  $\varphi _i$ the unique element in
$\varphi _i$ the unique element in  $\Phi $ above
$\Phi $ above  $\psi _i$.
$\psi _i$.• For
 $i\in \mathbb {Z}/f\mathbb {Z}$, let
$i\in \mathbb {Z}/f\mathbb {Z}$, let  $\epsilon _i$ be the unique unit in
$\epsilon _i$ be the unique unit in  $\mathsf {W}(O_F)$ satisfying
$\mathsf {W}(O_F)$ satisfying 
which exists by [Reference Ahsendorf, Cheng and ZinkACZ16, Lemma 2.24]. We then fix a unit
 $\mu _u$ in
$\mu _u$ in  $\mathsf {W}(O_{\breve {F}})$, where
$\mathsf {W}(O_{\breve {F}})$, where  $\breve {F}$ denotes the complete maximal unramified extension of F in
$\breve {F}$ denotes the complete maximal unramified extension of F in  $\breve {E}$, such that (2.21)which is possible since the right-hand side is a unit in
$\breve {E}$, such that (2.21)which is possible since the right-hand side is a unit in
 $\mathsf {W}(O_F)$.
$\mathsf {W}(O_F)$.• For a p-divisible group X over an object S of
 $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$ with an action by
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$ with an action by  $O_F$, we have a decomposition of
$O_F$, we have a decomposition of $$ \begin{align*} \operatorname{\mathrm{Lie}}(X)=\bigoplus_{i=0}^{f-1}\operatorname{\mathrm{Lie}}_{\psi_i}(X) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Lie}}(X)=\bigoplus_{i=0}^{f-1}\operatorname{\mathrm{Lie}}_{\psi_i}(X) \end{align*} $$ $\mathscr {O}_S$-modules according to the action of
$\mathscr {O}_S$-modules according to the action of  $O_F$ on
$O_F$ on  $\operatorname {\mathrm {Lie}}(X)$.
$\operatorname {\mathrm {Lie}}(X)$.
Definition 2.59. Let S be an object of ![]() $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}$. We define a category
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}$. We define a category  $\mathrm {Exo}_{(n-1,1)}^\Phi (S)$ whose objects are triples
$\mathrm {Exo}_{(n-1,1)}^\Phi (S)$ whose objects are triples ![]() $(X,\iota _X,\lambda _X)$ in which
$(X,\iota _X,\lambda _X)$ in which
• X is a p-divisible group over S of dimension
 $nf$ and height
$nf$ and height  $2nf$;
$2nf$;•
 $\iota _X\colon O_E\to \operatorname {\mathrm {End}}(X)$ is an action of
$\iota _X\colon O_E\to \operatorname {\mathrm {End}}(X)$ is an action of  $O_E$ on X satisfying:
$O_E$ on X satisfying:– (Kottwitz condition): the characteristic polynomial of
 $\iota _X(u)$ on the
$\iota _X(u)$ on the  $\mathscr {O}_S$-module
$\mathscr {O}_S$-module  $\operatorname {\mathrm {Lie}}_{\psi _0}(X)$ is
$\operatorname {\mathrm {Lie}}_{\psi _0}(X)$ is  $(T-u)^{n-1}(T+u)\in \mathscr {O}_S[T]$,
$(T-u)^{n-1}(T+u)\in \mathscr {O}_S[T]$,– (Wedge condition): we have
 $$ \begin{align*} \bigwedge^2\left(\iota_X(u)-u\mathbin{|}\operatorname{\mathrm{Lie}}_{\psi_0}(X)\right)&=0, \end{align*} $$
$$ \begin{align*} \bigwedge^2\left(\iota_X(u)-u\mathbin{|}\operatorname{\mathrm{Lie}}_{\psi_0}(X)\right)&=0, \end{align*} $$– (Spin condition): for every geometric point s of S, the action of
 $\iota _X(u)$ on
$\iota _X(u)$ on  $\operatorname {\mathrm {Lie}}_{\psi _0}(X_s)$ is nonzero;
$\operatorname {\mathrm {Lie}}_{\psi _0}(X_s)$ is nonzero;– (Banal condition): for
 $1\leqslant i\leqslant f-1$,
$1\leqslant i\leqslant f-1$,  $O_E$ acts on
$O_E$ acts on  $\operatorname {\mathrm {Lie}}_{\psi _i}(X)$ via
$\operatorname {\mathrm {Lie}}_{\psi _i}(X)$ via  $\varphi _i$;
$\varphi _i$;
•
 $\lambda _X\colon X\to X^\vee $ is a
$\lambda _X\colon X\to X^\vee $ is a  $\iota _X$-compatible polarisation such that
$\iota _X$-compatible polarisation such that  $\operatorname {\mathrm {ker}}(\lambda _X)=X[\iota _X(u)]$.
$\operatorname {\mathrm {ker}}(\lambda _X)=X[\iota _X(u)]$.
A morphism (respectively quasi-morphism) from ![]() $(X,\iota _X,\lambda _X)$ to
$(X,\iota _X,\lambda _X)$ to ![]() $(Y,\iota _Y,\lambda _Y)$ is an
$(Y,\iota _Y,\lambda _Y)$ is an ![]() $O_E$-linear isomorphism (respectively quasi-isogeny)
$O_E$-linear isomorphism (respectively quasi-isogeny) ![]() $\rho \colon X\to Y$ of height zero such that
$\rho \colon X\to Y$ of height zero such that ![]() $\rho ^*\lambda _Y=\lambda _X$.
$\rho ^*\lambda _Y=\lambda _X$.
When S belongs to  $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$, we denote by
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$, we denote by  $\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S)$ the subcategory of
$\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S)$ the subcategory of  $\mathrm {Exo}_{(n-1,1)}^\Phi (S)$ consisting of
$\mathrm {Exo}_{(n-1,1)}^\Phi (S)$ consisting of ![]() $(X,\iota _X,\lambda _X)$ in which X is supersingular.
$(X,\iota _X,\lambda _X)$ in which X is supersingular.
Note that both  $\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}$ and
$\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}$ and  $\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}$ are prestacks (that is, presheaves valued in groupoids) on
$\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}$ are prestacks (that is, presheaves valued in groupoids) on  $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$. Now we construct a morphism
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$. Now we construct a morphism
 $$ \begin{align} -^{\mathrm{rel}}\colon\mathrm{Exo}_{(n-1,1)}^{\Phi,\mathrm{b}}\to\mathrm{Exo}_{(n-1,1)}^{\mathrm{b}} \end{align} $$
$$ \begin{align} -^{\mathrm{rel}}\colon\mathrm{Exo}_{(n-1,1)}^{\Phi,\mathrm{b}}\to\mathrm{Exo}_{(n-1,1)}^{\mathrm{b}} \end{align} $$of prestacks on  $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$. We will use the theory of displays [Reference ZinkZin02, Reference LauLau08] and
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$. We will use the theory of displays [Reference ZinkZin02, Reference LauLau08] and ![]() $O_F$-displays [Reference Ahsendorf, Cheng and ZinkACZ16].
$O_F$-displays [Reference Ahsendorf, Cheng and ZinkACZ16].
Let ![]() $S=\operatorname {\mathrm {Spec}} R$ be an affine scheme in
$S=\operatorname {\mathrm {Spec}} R$ be an affine scheme in  $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$. Take an object
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$. Take an object ![]() $(X,\iota _X,\lambda _X)$ of
$(X,\iota _X,\lambda _X)$ of  $\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S)$. Write
$\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S)$. Write ![]() $(\mathsf {P},\mathsf {Q},\mathsf {F},\dot {\mathsf {F}})$ for the display of X (as a formal p-divisible group). The action of
$(\mathsf {P},\mathsf {Q},\mathsf {F},\dot {\mathsf {F}})$ for the display of X (as a formal p-divisible group). The action of ![]() $O_F$ on
$O_F$ on ![]() $\mathsf {P}$ induces decompositions
$\mathsf {P}$ induces decompositions
 $$ \begin{align*} \mathsf{P}=\bigoplus_{i=0}^{f-1}\mathsf{P}_i,\quad \mathsf{Q}=\bigoplus_{i=0}^{f-1}\mathsf{Q}_i,\quad \mathsf{F}=\sum_{i=0}^{f-1}\mathsf{F}_i,\quad \dot{\mathsf{F}}=\sum_{i=0}^{f-1}\dot{\mathsf{F}}_i, \end{align*} $$
$$ \begin{align*} \mathsf{P}=\bigoplus_{i=0}^{f-1}\mathsf{P}_i,\quad \mathsf{Q}=\bigoplus_{i=0}^{f-1}\mathsf{Q}_i,\quad \mathsf{F}=\sum_{i=0}^{f-1}\mathsf{F}_i,\quad \dot{\mathsf{F}}=\sum_{i=0}^{f-1}\dot{\mathsf{F}}_i, \end{align*} $$where ![]() $\mathsf {P}_i$ is the
$\mathsf {P}_i$ is the ![]() $\mathsf {W}(R)$-submodule on which
$\mathsf {W}(R)$-submodule on which ![]() $O_F$ acts via
$O_F$ acts via ![]() $\hat \psi _i$ and
$\hat \psi _i$ and ![]() $\mathsf {Q}_i=\mathsf {Q}\cap \mathsf {P}_i$. It is clear that the above decomposition is
$\mathsf {Q}_i=\mathsf {Q}\cap \mathsf {P}_i$. It is clear that the above decomposition is ![]() $O_E$-linear and
$O_E$-linear and ![]() $\mathsf {P}_i$ is a projective
$\mathsf {P}_i$ is a projective ![]() $O_E\otimes _{O_F,\hat \psi _i}\mathsf {W}(R)$-module of rank n.
$O_E\otimes _{O_F,\hat \psi _i}\mathsf {W}(R)$-module of rank n.
Lemma 2.60. For ![]() $1\leqslant i\leqslant f-1$, we have
$1\leqslant i\leqslant f-1$, we have
and the map
is a Frobenius linear epimorphism and, hence, isomorphism.
Proof. The banal condition in Definition 2.59 implies that for ![]() $1\leqslant i\leqslant f-1$,
$1\leqslant i\leqslant f-1$,
To show the reverse inclusion, it suffices to show that the image of
in ![]() $\mathsf {P}_i/\mathsf {I}(R)\mathsf {P}_i=\mathsf {P}_i\otimes _{\mathsf {W}(R)}R$ is a projective R-module of rank n. But the image is the same as
$\mathsf {P}_i/\mathsf {I}(R)\mathsf {P}_i=\mathsf {P}_i\otimes _{\mathsf {W}(R)}R$ is a projective R-module of rank n. But the image is the same as ![]() $(u\otimes 1 - 1\otimes \varphi _i(u))\mathsf {P}_i\otimes _{\mathsf {W}(R)}R$, which has rank n since
$(u\otimes 1 - 1\otimes \varphi _i(u))\mathsf {P}_i\otimes _{\mathsf {W}(R)}R$, which has rank n since ![]() $\mathsf {P}_i$ is projective over
$\mathsf {P}_i$ is projective over ![]() $O_E\otimes _{O_F,\hat \psi _i}\mathsf {W}(R)$ of rank n.
$O_E\otimes _{O_F,\hat \psi _i}\mathsf {W}(R)$ of rank n.
Now we show that  $(\mathsf {F}^{\prime }_i)^\natural $ is surjective. It suffices to show that
$(\mathsf {F}^{\prime }_i)^\natural $ is surjective. It suffices to show that  $\operatorname {\mathrm {coker}}(\mathsf {F}^{\prime }_i)^\natural \otimes _{\mathsf {W}(R)}\kappa $ vanishes for every homomorphism
$\operatorname {\mathrm {coker}}(\mathsf {F}^{\prime }_i)^\natural \otimes _{\mathsf {W}(R)}\kappa $ vanishes for every homomorphism ![]() $\mathsf {W}(R)\to \kappa $ with
$\mathsf {W}(R)\to \kappa $ with ![]() $\kappa $ a perfect field of characteristic p. Since
$\kappa $ a perfect field of characteristic p. Since ![]() $\mathsf {W}(R)\to \kappa $ necessarily vanishes on
$\mathsf {W}(R)\to \kappa $ necessarily vanishes on ![]() $\mathsf {I}(R)$, it lifts to a homomorphism
$\mathsf {I}(R)$, it lifts to a homomorphism ![]() $\mathsf {W}(R)\to \mathsf {W}(\kappa )$. Thus, we may just assume that R is a perfect field of characteristic p. Since
$\mathsf {W}(R)\to \mathsf {W}(\kappa )$. Thus, we may just assume that R is a perfect field of characteristic p. Since
in which ![]() $\epsilon _i$ is a unit in
$\epsilon _i$ is a unit in ![]() $\mathsf {W}(O_F)$, the image of the map
$\mathsf {W}(O_F)$, the image of the map
contains
. As R is a perfect field of characteristic p, we have
; hence, (2.23) is surjective. Thus, ![]() $\mathsf {F}^{\prime }_i$ is a Frobenius linear epimorphism as
$\mathsf {F}^{\prime }_i$ is a Frobenius linear epimorphism as ![]() $\mathsf {F}_i$ is.
$\mathsf {F}_i$ is.
The lemma is proved.
Now we put
 $$ \begin{align*} \mathsf{P}^{\mathrm{rel}} := \mathsf{P}_0,\quad \mathsf{Q}^{\mathrm{rel}} := \mathsf{Q}_0,\quad \mathsf{F}^{\mathrm{rel}} := \mathsf{F}^{\prime}_{f-1}\circ\cdots\circ\mathsf{F}^{\prime}_1\circ\mathsf{F}_0,\quad \dot{\mathsf{F}}^{\mathrm{rel}} := \mathsf{F}^{\prime}_{f-1}\circ\cdots\circ\mathsf{F}^{\prime}_1\circ\dot{\mathsf{F}}_0. \end{align*} $$
$$ \begin{align*} \mathsf{P}^{\mathrm{rel}} := \mathsf{P}_0,\quad \mathsf{Q}^{\mathrm{rel}} := \mathsf{Q}_0,\quad \mathsf{F}^{\mathrm{rel}} := \mathsf{F}^{\prime}_{f-1}\circ\cdots\circ\mathsf{F}^{\prime}_1\circ\mathsf{F}_0,\quad \dot{\mathsf{F}}^{\mathrm{rel}} := \mathsf{F}^{\prime}_{f-1}\circ\cdots\circ\mathsf{F}^{\prime}_1\circ\dot{\mathsf{F}}_0. \end{align*} $$Then ![]() $(\mathsf {P}^{\mathrm {rel}},\mathsf {Q}^{\mathrm {rel}},\mathsf {F}^{\mathrm {rel}},\dot {\mathsf {F}}^{\mathrm {rel}})$ defines an f(-
$(\mathsf {P}^{\mathrm {rel}},\mathsf {Q}^{\mathrm {rel}},\mathsf {F}^{\mathrm {rel}},\dot {\mathsf {F}}^{\mathrm {rel}})$ defines an f(-![]() $\mathbb {Z}_p$)-display in the sense of [Reference Ahsendorf, Cheng and ZinkACZ16, Definition 2.1] with an
$\mathbb {Z}_p$)-display in the sense of [Reference Ahsendorf, Cheng and ZinkACZ16, Definition 2.1] with an ![]() $O_E$-action, for which the Kottwitz condition, the wedge condition and the spin condition are obviously inherited. It remains to construct the polarisation
$O_E$-action, for which the Kottwitz condition, the wedge condition and the spin condition are obviously inherited. It remains to construct the polarisation ![]() $\lambda _{X^{\mathrm {rel}}}$. By Remark 2.61, we have the collection of perfect symmetric
$\lambda _{X^{\mathrm {rel}}}$. By Remark 2.61, we have the collection of perfect symmetric ![]() $\mathsf {W}(R)$-bilinear pairings
$\mathsf {W}(R)$-bilinear pairings ![]() $\{(\,,\,)_i\mathbin {|} i\in \mathbb {Z}/f\mathbb {Z}\}$ coming from
$\{(\,,\,)_i\mathbin {|} i\in \mathbb {Z}/f\mathbb {Z}\}$ coming from ![]() $\lambda _X$. For
$\lambda _X$. For ![]() $x,y\in \mathsf {P}_0$, put
$x,y\in \mathsf {P}_0$, put  $x_i := (\mathsf {F}^{\prime }_{i-1}\circ \cdots \circ \mathsf {F}^{\prime }_1\circ \dot {\mathsf {F}}_0)(x)$ and
$x_i := (\mathsf {F}^{\prime }_{i-1}\circ \cdots \circ \mathsf {F}^{\prime }_1\circ \dot {\mathsf {F}}_0)(x)$ and  $y_i := (\mathsf {F}^{\prime }_{i-1}\circ \cdots \circ \mathsf {F}^{\prime }_1\circ \dot {\mathsf {F}}_0)(y)$ for
$y_i := (\mathsf {F}^{\prime }_{i-1}\circ \cdots \circ \mathsf {F}^{\prime }_1\circ \dot {\mathsf {F}}_0)(y)$ for ![]() $1\leqslant i\leqslant f$ and we have
$1\leqslant i\leqslant f$ and we have

Put ![]() $(\,,\,)^{\mathrm {rel}} := \mu _u(\,,\,)_0$, which satisfies
$(\,,\,)^{\mathrm {rel}} := \mu _u(\,,\,)_0$, which satisfies

by (2.21). Then the f(-![]() $\mathbb {Z}_p$)-display
$\mathbb {Z}_p$)-display ![]() $(\mathsf {P}^{\mathrm {rel}},\mathsf {Q}^{\mathrm {rel}},\mathsf {F}^{\mathrm {rel}},\dot {\mathsf {F}}^{\mathrm {rel}})$ with
$(\mathsf {P}^{\mathrm {rel}},\mathsf {Q}^{\mathrm {rel}},\mathsf {F}^{\mathrm {rel}},\dot {\mathsf {F}}^{\mathrm {rel}})$ with ![]() $O_E$-action together with the pairing
$O_E$-action together with the pairing ![]() $(\,,\,)^{\mathrm {rel}}$ define an object
$(\,,\,)^{\mathrm {rel}}$ define an object ![]() $(X,\iota _X,\lambda _X)^{\mathrm {rel}}$ of
$(X,\iota _X,\lambda _X)^{\mathrm {rel}}$ of  $\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}(S)$, as explained in the proof of [Reference MihatschMih22, Proposition 3.4] and Remark 2.61. It is clear that the construction is functorial in S.
$\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}(S)$, as explained in the proof of [Reference MihatschMih22, Proposition 3.4] and Remark 2.61. It is clear that the construction is functorial in S.
Remark 2.61. For an object ![]() $(X,\iota _X,\lambda _X)$ of
$(X,\iota _X,\lambda _X)$ of  $\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S)$ with
$\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S)$ with ![]() $(\mathsf {P},\mathsf {Q},\mathsf {F},\dot {\mathsf {F}})$ the display of X, we have a similar claim as in Remark 2.2 concerning the polarisation
$(\mathsf {P},\mathsf {Q},\mathsf {F},\dot {\mathsf {F}})$ the display of X, we have a similar claim as in Remark 2.2 concerning the polarisation ![]() $\lambda _X$. In particular, as discussed in [Reference MihatschMih22, Section 11.1], the polarisation
$\lambda _X$. In particular, as discussed in [Reference MihatschMih22, Section 11.1], the polarisation ![]() $\lambda _X$, or, rather, its symmetrisation, is equivalent to a collection of perfect symmetric
$\lambda _X$, or, rather, its symmetrisation, is equivalent to a collection of perfect symmetric ![]() $\mathsf {W}(R)$-bilinear pairings
$\mathsf {W}(R)$-bilinear pairings
satisfying ![]() $(\iota _X(\alpha )x,y)_i=(x,\iota _X(\alpha ^{\mathtt {c}})y)_i$ for every
$(\iota _X(\alpha )x,y)_i=(x,\iota _X(\alpha ^{\mathtt {c}})y)_i$ for every ![]() $\alpha \in O_E$ and
$\alpha \in O_E$ and  for every
for every ![]() $i\in \mathbb {Z}/f\mathbb {Z}$.
$i\in \mathbb {Z}/f\mathbb {Z}$.
Similarly, for an object ![]() $(X',\iota _{X'},\lambda _{X'})$ of
$(X',\iota _{X'},\lambda _{X'})$ of  $\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}(S)$ with
$\mathrm {Exo}_{(n-1,1)}^{\mathrm {b}}(S)$ with ![]() $(\mathsf {P}',\mathsf {Q}',\mathsf {F}',\dot {\mathsf {F}}')$ the f(-
$(\mathsf {P}',\mathsf {Q}',\mathsf {F}',\dot {\mathsf {F}}')$ the f(-![]() $\mathbb {Z}_p$)-display of
$\mathbb {Z}_p$)-display of ![]() $X'$, the polarisation
$X'$, the polarisation ![]() $\lambda _{X'}$ is equivalent to a perfect symmetric
$\lambda _{X'}$ is equivalent to a perfect symmetric ![]() $\mathsf {W}(R)$-bilinear pairing
$\mathsf {W}(R)$-bilinear pairing
satisfying ![]() $(\iota _{X'}(\alpha )x,y)'=(x,\iota _{X'}(\alpha ^{\mathtt {c}})y)'$ for every
$(\iota _{X'}(\alpha )x,y)'=(x,\iota _{X'}(\alpha ^{\mathtt {c}})y)'$ for every ![]() $\alpha \in O_E$ and
$\alpha \in O_E$ and  .
.
Proposition 2.62. The morphism (2.22) is an isomorphism.
Proof. It suffices to show that for every affine scheme ![]() $S=\operatorname {\mathrm {Spec}} R$ in
$S=\operatorname {\mathrm {Spec}} R$ in  $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$, the functor
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$, the functor ![]() $-^{\mathrm {rel}}(S)$ is fully faithful and essentially surjective.
$-^{\mathrm {rel}}(S)$ is fully faithful and essentially surjective.
We first show that ![]() $-^{\mathrm {rel}}(S)$ is fully faithful. Take an object
$-^{\mathrm {rel}}(S)$ is fully faithful. Take an object ![]() $(X,\iota _X,\lambda _X)$ of
$(X,\iota _X,\lambda _X)$ of  $\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S)$. It suffices to show that the natural map
$\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S)$. It suffices to show that the natural map ![]() $\operatorname {\mathrm {Aut}}((X,\iota _X,\lambda _X))\to \operatorname {\mathrm {Aut}}((X,\iota _X,\lambda _X)^{\mathrm {rel}})$ is an isomorphism, which follows from a stronger statement that the map
$\operatorname {\mathrm {Aut}}((X,\iota _X,\lambda _X))\to \operatorname {\mathrm {Aut}}((X,\iota _X,\lambda _X)^{\mathrm {rel}})$ is an isomorphism, which follows from a stronger statement that the map ![]() $\operatorname {\mathrm {End}}_{O_E}(X)\to \operatorname {\mathrm {End}}_{O_E}(X^{\mathrm {rel}})$ is an isomorphism, where
$\operatorname {\mathrm {End}}_{O_E}(X)\to \operatorname {\mathrm {End}}_{O_E}(X^{\mathrm {rel}})$ is an isomorphism, where ![]() $X^{\mathrm {rel}}$ denotes the first entry of
$X^{\mathrm {rel}}$ denotes the first entry of ![]() $(X,\iota _X,\lambda _X)^{\mathrm {rel}}$, which is an
$(X,\iota _X,\lambda _X)^{\mathrm {rel}}$, which is an ![]() $O_F$-divisible group. For the latter, it amounts to showing that the natural map
$O_F$-divisible group. For the latter, it amounts to showing that the natural map
is an isomorphism. For the injectivity, let ![]() $\mathsf {f}$ be an element in the source, which decomposes as
$\mathsf {f}$ be an element in the source, which decomposes as  $\mathsf {f}=\sum _{i=0}^{f-1}\mathsf {f}_i$ for endomorphisms
$\mathsf {f}=\sum _{i=0}^{f-1}\mathsf {f}_i$ for endomorphisms ![]() $\mathsf {f}_i\colon \mathsf {P}_i\to \mathsf {P}_i$ preserving
$\mathsf {f}_i\colon \mathsf {P}_i\to \mathsf {P}_i$ preserving ![]() $\mathsf {Q}_i$ and commuting with
$\mathsf {Q}_i$ and commuting with ![]() $\mathsf {F}$ and
$\mathsf {F}$ and ![]() $\dot {\mathsf {F}}$. Since for every
$\dot {\mathsf {F}}$. Since for every ![]() $i\in \mathbb {Z}/f\mathbb {Z}$,
$i\in \mathbb {Z}/f\mathbb {Z}$, ![]() $\dot {\mathsf {F}}_i$ is a Frobenius linear surjective map from
$\dot {\mathsf {F}}_i$ is a Frobenius linear surjective map from ![]() $\mathsf {Q}_i$ to
$\mathsf {Q}_i$ to ![]() $\mathsf {P}_{i+1}$, the map
$\mathsf {P}_{i+1}$, the map ![]() $\mathsf {f}$ is determined by
$\mathsf {f}$ is determined by ![]() $\mathsf {f}_0$. Thus, (2.24) is injective. For the surjectivity, let
$\mathsf {f}_0$. Thus, (2.24) is injective. For the surjectivity, let ![]() $\mathsf {f}^{\mathrm {rel}}$ be an element in the target. Put
$\mathsf {f}^{\mathrm {rel}}$ be an element in the target. Put ![]() $\mathsf {f}_0 := \mathsf {f}^{\mathrm {rel}}\colon \mathsf {P}_0\to \mathsf {P}_0$. By Lemma 2.63(2), there is a unique endomorphism
$\mathsf {f}_0 := \mathsf {f}^{\mathrm {rel}}\colon \mathsf {P}_0\to \mathsf {P}_0$. By Lemma 2.63(2), there is a unique endomorphism ![]() $\mathsf {f}_1$ of
$\mathsf {f}_1$ of ![]() $\mathsf {P}_1$ rendering the following diagram
$\mathsf {P}_1$ rendering the following diagram

commutative. For ![]() $2\leqslant i\leqslant f-1$, we define
$2\leqslant i\leqslant f-1$, we define ![]() $\mathsf {f}_i$ to be the unique endomorphism of
$\mathsf {f}_i$ to be the unique endomorphism of ![]() $\mathsf {P}_i$ satisfying that
$\mathsf {P}_i$ satisfying that
 $$ \begin{align*} \mathsf{f}_i\circ(\mathsf{F}^{\prime}_{i-1}\circ\cdots\circ\mathsf{F}^{\prime}_1)^\natural=(\mathsf{F}^{\prime}_{i-1}\circ\cdots\circ\mathsf{F}^{\prime}_1)^\natural\circ(1\otimes\mathsf{f}_i). \end{align*} $$
$$ \begin{align*} \mathsf{f}_i\circ(\mathsf{F}^{\prime}_{i-1}\circ\cdots\circ\mathsf{F}^{\prime}_1)^\natural=(\mathsf{F}^{\prime}_{i-1}\circ\cdots\circ\mathsf{F}^{\prime}_1)^\natural\circ(1\otimes\mathsf{f}_i). \end{align*} $$Then  $\mathsf {f} := \sum _{i=0}^{f-1}\mathsf {f}_i$ is an
$\mathsf {f} := \sum _{i=0}^{f-1}\mathsf {f}_i$ is an ![]() $O_E$-linear endomorphism of
$O_E$-linear endomorphism of ![]() $\mathsf {P}$, which commutes with
$\mathsf {P}$, which commutes with ![]() $\dot {\mathsf {F}}$ and hence
$\dot {\mathsf {F}}$ and hence ![]() $\mathsf {F}$. It remains to check that
$\mathsf {F}$. It remains to check that ![]() $\mathsf {f}(\mathsf {Q})\subseteq \mathsf {Q}$, which follows from Lemma 2.60.
$\mathsf {f}(\mathsf {Q})\subseteq \mathsf {Q}$, which follows from Lemma 2.60.
We then show that ![]() $-^{\mathrm {rel}}(S)$ is essentially surjective. Take an object
$-^{\mathrm {rel}}(S)$ is essentially surjective. Take an object
 $$ \begin{align*} (X',\iota_{X'},\lambda_{X'})\in\mathrm{Exo}_{(n-1,1)}^{\mathrm{b}}(S) \end{align*} $$
$$ \begin{align*} (X',\iota_{X'},\lambda_{X'})\in\mathrm{Exo}_{(n-1,1)}^{\mathrm{b}}(S) \end{align*} $$in which ![]() $X'$ is given by an f(-
$X'$ is given by an f(-![]() $\mathbb {Z}_p$)-display
$\mathbb {Z}_p$)-display ![]() $(\mathsf {P}',\mathsf {Q}',\mathsf {F}',\dot {\mathsf {F}}')$. For
$(\mathsf {P}',\mathsf {Q}',\mathsf {F}',\dot {\mathsf {F}}')$. For ![]() $0\leqslant i\leqslant f-1$, put
$0\leqslant i\leqslant f-1$, put

Denote by ![]() $\mathsf {u}_0\colon \mathsf {P}_0\to \mathsf {P}_0$ the endomorphism given by the action of
$\mathsf {u}_0\colon \mathsf {P}_0\to \mathsf {P}_0$ the endomorphism given by the action of ![]() $u\in O_E$ on
$u\in O_E$ on ![]() $\mathsf {P}'$. Put
$\mathsf {P}'$. Put ![]() $\mathsf {Q}_0=\mathsf {Q}'$ and for
$\mathsf {Q}_0=\mathsf {Q}'$ and for ![]() $1\leqslant i\leqslant f-1$, put
$1\leqslant i\leqslant f-1$, put
Fix a normal decomposition ![]() $\mathsf {P}'=\mathsf {L}'\oplus \mathsf {T}'$ for
$\mathsf {P}'=\mathsf {L}'\oplus \mathsf {T}'$ for ![]() $\mathsf {Q}'$ and let
$\mathsf {Q}'$ and let
be the corresponding ![]() $\mathsf {F}^f$-linear isomorphism. For
$\mathsf {F}^f$-linear isomorphism. For ![]() $0\leqslant i<f-1$, let
$0\leqslant i<f-1$, let ![]() $\ddot {\mathsf {F}}_i\colon \mathsf {P}_i\to \mathsf {P}_{i+1}$ be the Frobenius linear isomorphism induced by the identity map on
$\ddot {\mathsf {F}}_i\colon \mathsf {P}_i\to \mathsf {P}_{i+1}$ be the Frobenius linear isomorphism induced by the identity map on ![]() $\mathsf {P}'$ and, finally, let
$\mathsf {P}'$ and, finally, let ![]() $\ddot {\mathsf {F}}_{f-1}\colon \mathsf {P}_{f-1}\to \mathsf {P}_0$ be the Frobenius linear isomorphism induced by
$\ddot {\mathsf {F}}_{f-1}\colon \mathsf {P}_{f-1}\to \mathsf {P}_0$ be the Frobenius linear isomorphism induced by ![]() $\ddot {\mathsf {F}}'$. Let
$\ddot {\mathsf {F}}'$. Let ![]() $\dot {\mathsf {F}}_0\colon \mathsf {Q}_0\to \mathsf {P}_1$ be the map defined by the formula
$\dot {\mathsf {F}}_0\colon \mathsf {Q}_0\to \mathsf {P}_1$ be the map defined by the formula
for ![]() $l\in \mathsf {L}'$,
$l\in \mathsf {L}'$, ![]() $t\in \mathsf {T}'$ and
$t\in \mathsf {T}'$ and ![]() $w\in \mathsf {W}(R)$, which is a Frobenius linear epimorphism. By Lemma 2.63(2), there is a unique endomorphism
$w\in \mathsf {W}(R)$, which is a Frobenius linear epimorphism. By Lemma 2.63(2), there is a unique endomorphism ![]() $\mathsf {u}_1$ of
$\mathsf {u}_1$ of ![]() $\mathsf {P}_1$ rendering the following diagram
$\mathsf {P}_1$ rendering the following diagram

commutative.Footnote 14 For ![]() $2\leqslant i\leqslant f-1$, we define
$2\leqslant i\leqslant f-1$, we define ![]() $\mathsf {u}_i$ to be the unique endomorphism of
$\mathsf {u}_i$ to be the unique endomorphism of ![]() $\mathsf {P}_i$ satisfying that
$\mathsf {P}_i$ satisfying that
and define a map ![]() $\dot {\mathsf {F}}_i\colon \mathsf {Q}_i\to \mathsf {P}_{i+1}$ by the following (compatible) formulae:
$\dot {\mathsf {F}}_i\colon \mathsf {Q}_i\to \mathsf {P}_{i+1}$ by the following (compatible) formulae:

for ![]() $x\in \mathsf {P}_i$ and
$x\in \mathsf {P}_i$ and ![]() $w\in \mathsf {W}(R)$, which is a Frobenius linear epimorphism. Put
$w\in \mathsf {W}(R)$, which is a Frobenius linear epimorphism. Put
 $$ \begin{align*} \mathsf{P} := \bigoplus_{i=0}^{f-1}\mathsf{P}_i,\quad \mathsf{Q} := \bigoplus_{i=0}^{f-1}\mathsf{Q}_i,\quad \dot{\mathsf{F}} := \sum_{i=0}^{f-1}\dot{\mathsf{F}}_i,\quad \mathsf{u} := \sum_{i=0}^{f-1}\mathsf{u}_i. \end{align*} $$
$$ \begin{align*} \mathsf{P} := \bigoplus_{i=0}^{f-1}\mathsf{P}_i,\quad \mathsf{Q} := \bigoplus_{i=0}^{f-1}\mathsf{Q}_i,\quad \dot{\mathsf{F}} := \sum_{i=0}^{f-1}\dot{\mathsf{F}}_i,\quad \mathsf{u} := \sum_{i=0}^{f-1}\mathsf{u}_i. \end{align*} $$Then it is straightforward to check that ![]() $(\mathsf {P},\mathsf {Q},\mathsf {F},\dot {\mathsf {F}})$ is a display with an action by
$(\mathsf {P},\mathsf {Q},\mathsf {F},\dot {\mathsf {F}})$ is a display with an action by ![]() $O_E$ for which u acts by
$O_E$ for which u acts by ![]() $\mathsf {u}$, where
$\mathsf {u}$, where ![]() $\mathsf {F}$ is determined by
$\mathsf {F}$ is determined by ![]() $\dot {\mathsf {F}}$ in the usual way. Now we construct a collection of perfect symmetric
$\dot {\mathsf {F}}$ in the usual way. Now we construct a collection of perfect symmetric ![]() $\mathsf {W}(R)$-bilinear pairings
$\mathsf {W}(R)$-bilinear pairings ![]() $\{(\,,\,)_i\mathbin {|} i\in \mathbb {Z}/f\mathbb {Z}\}$ as in Remark 2.61. Put
$\{(\,,\,)_i\mathbin {|} i\in \mathbb {Z}/f\mathbb {Z}\}$ as in Remark 2.61. Put ![]() $(\,,\,)_0 := \mu _u^{-1}(\,,\,)'$, where
$(\,,\,)_0 := \mu _u^{-1}(\,,\,)'$, where ![]() $(\,,\,)'$ is the pairing induced by
$(\,,\,)'$ is the pairing induced by ![]() $\lambda _{X'}$. Define inductively for
$\lambda _{X'}$. Define inductively for ![]() $1\leqslant i\leqslant f-1$ the unique (perfect symmetric
$1\leqslant i\leqslant f-1$ the unique (perfect symmetric ![]() $\mathsf {W}(R)$-bilinear) pairing
$\mathsf {W}(R)$-bilinear) pairing ![]() $(\,,\,)_i$ satisfying
$(\,,\,)_i$ satisfying

. It is clear that we also have

. Then the display ![]() $(\mathsf {P},\mathsf {Q},\mathsf {F},\dot {\mathsf {F}})$ with the
$(\mathsf {P},\mathsf {Q},\mathsf {F},\dot {\mathsf {F}})$ with the ![]() $O_E$-action together with the collection of pairings
$O_E$-action together with the collection of pairings ![]() $\{(\,,\,)_i\mathbin {|} i\in \mathbb {Z}/f\mathbb {Z}\}$ define an object
$\{(\,,\,)_i\mathbin {|} i\in \mathbb {Z}/f\mathbb {Z}\}$ define an object  $(X,\iota _X,\lambda _X)\in \mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S)$, which satisfies
$(X,\iota _X,\lambda _X)\in \mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S)$, which satisfies ![]() $(X,\iota _X,\lambda _X)^{\mathrm {rel}}\simeq (X',\iota _{X'},\lambda _{X'})$ by construction.
$(X,\iota _X,\lambda _X)^{\mathrm {rel}}\simeq (X',\iota _{X'},\lambda _{X'})$ by construction.
The proposition is proved.
Lemma 2.63. Let R be a ring on which p is nilpotent. For a pair ![]() $(\mathsf {P},\mathsf {Q})$ in which
$(\mathsf {P},\mathsf {Q})$ in which ![]() $\mathsf {P}$ is a projective
$\mathsf {P}$ is a projective ![]() $\mathsf {W}(R)$-module of finite rank and
$\mathsf {W}(R)$-module of finite rank and ![]() $\mathsf {Q}$ is a submodule of
$\mathsf {Q}$ is a submodule of ![]() $\mathsf {P}$ containing
$\mathsf {P}$ containing ![]() $\mathsf {I}(R)\mathsf {P}$ such that
$\mathsf {I}(R)\mathsf {P}$ such that ![]() $\mathsf {P}/\mathsf {Q}$ is a projective R-module, we define
$\mathsf {P}/\mathsf {Q}$ is a projective R-module, we define ![]() $\mathsf {Q}^\star $ to be the image of
$\mathsf {Q}^\star $ to be the image of ![]() $J(R)\mathsf {P}$ under the map
$J(R)\mathsf {P}$ under the map  that is the base change of the inclusion map
that is the base change of the inclusion map ![]() $\mathsf {I}(R)\mathsf {P}\to \mathsf {Q}$, where
$\mathsf {I}(R)\mathsf {P}\to \mathsf {Q}$, where ![]() $J(R)$ denotes the kernel of
$J(R)$ denotes the kernel of  . Then for every Frobenius linear epimorphism
. Then for every Frobenius linear epimorphism ![]() $\dot {\mathsf {F}}\colon \mathsf {Q}\to \mathsf {P}'$ with
$\dot {\mathsf {F}}\colon \mathsf {Q}\to \mathsf {P}'$ with ![]() $\mathsf {P}'$ a projective
$\mathsf {P}'$ a projective ![]() $\mathsf {W}(R)$-module of the same rank as
$\mathsf {W}(R)$-module of the same rank as ![]() $\mathsf {P}$, we have
$\mathsf {P}$, we have
(1) the kernel of
 $\dot {\mathsf {F}}^\natural $ coincides with
$\dot {\mathsf {F}}^\natural $ coincides with  $\mathsf {Q}^\star $;
$\mathsf {Q}^\star $;(2) for every endomorphism
 $\mathsf {f}\colon \mathsf {P}\to \mathsf {P}$ that preserves
$\mathsf {f}\colon \mathsf {P}\to \mathsf {P}$ that preserves  $\mathsf {Q}$, there exists a unique endomorphism
$\mathsf {Q}$, there exists a unique endomorphism  $\mathsf {f}'\colon \mathsf {P}'\to \mathsf {P}'$ rendering the following diagram commutative.
$\mathsf {f}'\colon \mathsf {P}'\to \mathsf {P}'$ rendering the following diagram commutative.
Proof. We first claim that ![]() $\mathsf {J}(R)$ is contained in the kernel of the map
$\mathsf {J}(R)$ is contained in the kernel of the map

that is the base change of the inclusion map ![]() $\mathsf {I}(R)\to \mathsf {W}(R)$. Take an element
$\mathsf {I}(R)\to \mathsf {W}(R)$. Take an element ![]() in
in  . If
. If ![]() $x\in J(R)$, then
$x\in J(R)$, then ![]() $\sum a_ib_i=0$. But the image of x under (2.25) is
$\sum a_ib_i=0$. But the image of x under (2.25) is ![]() , which equals
, which equals ![]() $p\sum a_ib_i$. Thus,
$p\sum a_ib_i$. Thus, ![]() $J(R)$ is contained in the kernel of (2.25).
$J(R)$ is contained in the kernel of (2.25).
For (1), choose a normal decomposition ![]() $\mathsf {P}=\mathsf {L}\oplus \mathsf {T}$ of
$\mathsf {P}=\mathsf {L}\oplus \mathsf {T}$ of ![]() $\mathsf {W}(R)$-modules such that
$\mathsf {W}(R)$-modules such that ![]() $\mathsf {Q}=\mathsf {L}\oplus \mathsf {I}(R)\mathsf {T}$. By (the proof of) [Reference LauLau10, Lemma 2.5], there exists a Frobenius linear automorphism
$\mathsf {Q}=\mathsf {L}\oplus \mathsf {I}(R)\mathsf {T}$. By (the proof of) [Reference LauLau10, Lemma 2.5], there exists a Frobenius linear automorphism ![]() $\Psi $ of P such that
$\Psi $ of P such that

for ![]() $l\in \mathsf {L}$,
$l\in \mathsf {L}$, ![]() $t\in \mathsf {T}$ and
$t\in \mathsf {T}$ and ![]() $a\in \mathsf {I}(R)$. Thus,
$a\in \mathsf {I}(R)$. Thus, ![]() $\operatorname {\mathrm {ker}}\dot {\mathsf {F}}^\natural $ equals the submodule
$\operatorname {\mathrm {ker}}\dot {\mathsf {F}}^\natural $ equals the submodule ![]() $J(R)\mathsf {T}$ of
$J(R)\mathsf {T}$ of

. However, by the claim above, the image of ![]() $J(R)\mathsf {L}$ under the map
$J(R)\mathsf {L}$ under the map

vanishes. Thus, we have ![]() $J(R)\mathsf {T}=\mathsf {Q}^\star $.
$J(R)\mathsf {T}=\mathsf {Q}^\star $.
For (2), the uniqueness follows since ![]() $\dot {\mathsf {F}}^\natural $ is surjective, and the existence follows since the map
$\dot {\mathsf {F}}^\natural $ is surjective, and the existence follows since the map ![]() $1\otimes (\mathsf {f}\mathbin {|}_{\mathsf {Q}})$ preserves
$1\otimes (\mathsf {f}\mathbin {|}_{\mathsf {Q}})$ preserves ![]() $\mathsf {Q}^\star $, which is a consequence of the definition of
$\mathsf {Q}^\star $, which is a consequence of the definition of ![]() $\mathsf {Q}^\star $.
$\mathsf {Q}^\star $.
To define our (absolute) Rapoport–Zink space, we fix an object
 $$ \begin{align*} (\boldsymbol{X},\iota_{\boldsymbol{X}},\lambda_{\boldsymbol{X}})\in\mathrm{Exo}_{(n-1,1)}^{\Phi,\mathrm{b}}(\overline{k}). \end{align*} $$
$$ \begin{align*} (\boldsymbol{X},\iota_{\boldsymbol{X}},\lambda_{\boldsymbol{X}})\in\mathrm{Exo}_{(n-1,1)}^{\Phi,\mathrm{b}}(\overline{k}). \end{align*} $$Definition 2.64. We define a functor  $\mathcal {N}^\Phi := \mathcal {N}^\Phi _{(\boldsymbol {X},\iota _{\boldsymbol {X}},\lambda _{\boldsymbol {X}})}$ on
$\mathcal {N}^\Phi := \mathcal {N}^\Phi _{(\boldsymbol {X},\iota _{\boldsymbol {X}},\lambda _{\boldsymbol {X}})}$ on  $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$ such that for every object S of
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$ such that for every object S of  $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$,
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$, ![]() $\mathcal {N}(S)$ consists of quadruples
$\mathcal {N}(S)$ consists of quadruples ![]() $(X,\iota _X,\lambda _X;\rho _X)$ in which
$(X,\iota _X,\lambda _X;\rho _X)$ in which
•
 $(X,\iota _X,\lambda _X)$ is an object of
$(X,\iota _X,\lambda _X)$ is an object of  $\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S)$;
$\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S)$;•
 $\rho _X$ is a quasi-morphism from
$\rho _X$ is a quasi-morphism from  $(X,\iota _X,\lambda _X)\times _S(S\otimes _{O_{\breve {E}}}\overline {k})$ to
$(X,\iota _X,\lambda _X)\times _S(S\otimes _{O_{\breve {E}}}\overline {k})$ to  $(\boldsymbol {X},\iota _{\boldsymbol {X}},\lambda _{\boldsymbol {X}})\otimes _{\overline {k}}(S\otimes _{O_{\breve {E}}}\overline {k})$ in the category
$(\boldsymbol {X},\iota _{\boldsymbol {X}},\lambda _{\boldsymbol {X}})\otimes _{\overline {k}}(S\otimes _{O_{\breve {E}}}\overline {k})$ in the category  $\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S\otimes _{O_{\breve {E}}}\overline {k})$.
$\mathrm {Exo}_{(n-1,1)}^{\Phi ,\mathrm {b}}(S\otimes _{O_{\breve {E}}}\overline {k})$.
Corollary 2.65. The morphism
 $$ \begin{align*} \mathcal{N}^\Phi=\mathcal{N}^\Phi_{(\boldsymbol{X},\iota_{\boldsymbol{X}},\lambda_{\boldsymbol{X}})}\to\mathcal{N} := \mathcal{N}_{(\boldsymbol{X},\iota_{\boldsymbol{X}},\lambda_{\boldsymbol{X}})^{\mathrm{rel}}} \end{align*} $$
$$ \begin{align*} \mathcal{N}^\Phi=\mathcal{N}^\Phi_{(\boldsymbol{X},\iota_{\boldsymbol{X}},\lambda_{\boldsymbol{X}})}\to\mathcal{N} := \mathcal{N}_{(\boldsymbol{X},\iota_{\boldsymbol{X}},\lambda_{\boldsymbol{X}})^{\mathrm{rel}}} \end{align*} $$sending ![]() $(X,\iota _X,\lambda _X;\rho _X)$ to
$(X,\iota _X,\lambda _X;\rho _X)$ to  $((X,\iota _X,\lambda _X)^{\mathrm {rel}};\rho _X^{\mathrm {rel}})$ is an isomorphism.
$((X,\iota _X,\lambda _X)^{\mathrm {rel}};\rho _X^{\mathrm {rel}})$ is an isomorphism.
Proof. This follows immediately from Proposition 2.62.
Now we study special divisors on ![]() $\mathcal {N}^\Phi $ and their relation with those on
$\mathcal {N}^\Phi $ and their relation with those on ![]() $\mathcal {N}$. Fix a triple
$\mathcal {N}$. Fix a triple ![]() $(X_0,\iota _{X_0},\lambda _{X_0})$ where
$(X_0,\iota _{X_0},\lambda _{X_0})$ where
•
 $X_0$ is a supersingular p-divisible group over
$X_0$ is a supersingular p-divisible group over  $\operatorname {\mathrm {Spec}} O_{\breve {E}}$ of dimension f and height
$\operatorname {\mathrm {Spec}} O_{\breve {E}}$ of dimension f and height  $2f$;
$2f$;•
 $\iota _{X_0}\colon O_E\to \operatorname {\mathrm {End}}(X_0)$ is an
$\iota _{X_0}\colon O_E\to \operatorname {\mathrm {End}}(X_0)$ is an  $O_E$-action on
$O_E$-action on  $X_0$ such that for
$X_0$ such that for  $0\leqslant i\leqslant f-1$, the summand
$0\leqslant i\leqslant f-1$, the summand  $\operatorname {\mathrm {Lie}}_{\psi _i}(X)$ has rank
$\operatorname {\mathrm {Lie}}_{\psi _i}(X)$ has rank  $1$ on which
$1$ on which  $O_E$ acts via
$O_E$ acts via  $\varphi _i$;
$\varphi _i$;•
 $\lambda _{X_0}\colon X_0\to X_0^\vee $ is a
$\lambda _{X_0}\colon X_0\to X_0^\vee $ is a  $\iota _{X_0}$-compatible principal polarisation.
$\iota _{X_0}$-compatible principal polarisation.
Note that ![]() $\iota _{X_0}$ induces an isomorphism
$\iota _{X_0}$ induces an isomorphism  $\iota _{X_0}\colon O_E\xrightarrow {\sim }\operatorname {\mathrm {End}}_{O_E}(X_0)$. Put
$\iota _{X_0}\colon O_E\xrightarrow {\sim }\operatorname {\mathrm {End}}_{O_E}(X_0)$. Put
 $$ \begin{align*} \boldsymbol{V} := \operatorname{\mathrm{Hom}}_{O_E}(X_0\otimes_{O_{\breve{E}}}\overline{k},\boldsymbol{X})\otimes\mathbb{Q}, \end{align*} $$
$$ \begin{align*} \boldsymbol{V} := \operatorname{\mathrm{Hom}}_{O_E}(X_0\otimes_{O_{\breve{E}}}\overline{k},\boldsymbol{X})\otimes\mathbb{Q}, \end{align*} $$which is a vector space over E of dimension n, equipped with a natural hermitian form similar to (2.1). By a construction similar to (2.22), we obtain a triple ![]() $(X_0,\iota _{X_0},\lambda _{X_0})^{\mathrm {rel}}$ as in the definition of special divisors on
$(X_0,\iota _{X_0},\lambda _{X_0})^{\mathrm {rel}}$ as in the definition of special divisors on ![]() $\mathcal {N}$ (Definition 2.5) and a canonical map
$\mathcal {N}$ (Definition 2.5) and a canonical map
 $$ \begin{align*} \operatorname{\mathrm{Hom}}_{O_E}(X_0\otimes_{O_{\breve{E}}}\overline{k},\boldsymbol{X})\to\operatorname{\mathrm{Hom}}_{O_E}(X_0^{\mathrm{rel}}\otimes_{O_{\breve{E}}}\overline{k},\boldsymbol{X}^{\mathrm{rel}}), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hom}}_{O_E}(X_0\otimes_{O_{\breve{E}}}\overline{k},\boldsymbol{X})\to\operatorname{\mathrm{Hom}}_{O_E}(X_0^{\mathrm{rel}}\otimes_{O_{\breve{E}}}\overline{k},\boldsymbol{X}^{\mathrm{rel}}), \end{align*} $$which induces a map
 $$ \begin{align} -^{\mathrm{rel}}\colon\boldsymbol{V}\to\boldsymbol{V}^{\mathrm{rel}} := \operatorname{\mathrm{Hom}}_{O_E}(X_0^{\mathrm{rel}}\otimes_{O_{\breve{E}}}\overline{k},\boldsymbol{X}^{\mathrm{rel}})\otimes\mathbb{Q}. \end{align} $$
$$ \begin{align} -^{\mathrm{rel}}\colon\boldsymbol{V}\to\boldsymbol{V}^{\mathrm{rel}} := \operatorname{\mathrm{Hom}}_{O_E}(X_0^{\mathrm{rel}}\otimes_{O_{\breve{E}}}\overline{k},\boldsymbol{X}^{\mathrm{rel}})\otimes\mathbb{Q}. \end{align} $$For every nonzero element ![]() $x\in \boldsymbol {V}$, we have similarly a closed formal subscheme
$x\in \boldsymbol {V}$, we have similarly a closed formal subscheme ![]() $\mathcal {N}^\Phi (x)$ of
$\mathcal {N}^\Phi (x)$ of ![]() $\mathcal {N}^\Phi $ defined similarly as in Definition 2.5.
$\mathcal {N}^\Phi $ defined similarly as in Definition 2.5.
Corollary 2.66. The map (2.26) is an isomorphism of hermitian spaces. Moreover, under the isomorphism in Corollary 2.65, we have ![]() $\mathcal {N}^\Phi (x)=\mathcal {N}(x^{\mathrm {rel}})$.
$\mathcal {N}^\Phi (x)=\mathcal {N}(x^{\mathrm {rel}})$.
Proof. By the definition of ![]() $-^{\mathrm {rel}}$, the map (2.26) is clearly an isometry. Since both
$-^{\mathrm {rel}}$, the map (2.26) is clearly an isometry. Since both ![]() $\mathsf {V}$ and
$\mathsf {V}$ and ![]() $\mathsf {V}^{\mathrm {rel}}$ have dimension n, (2.26) is an isomorphism of hermitian spaces. The second assertion follows from Corollary 2.65 and construction of
$\mathsf {V}^{\mathrm {rel}}$ have dimension n, (2.26) is an isomorphism of hermitian spaces. The second assertion follows from Corollary 2.65 and construction of ![]() $-^{\mathrm {rel}}$, parallel to [Reference MihatschMih22, Remark 4.4].
$-^{\mathrm {rel}}$, parallel to [Reference MihatschMih22, Remark 4.4].
Remark 2.67. Let S be an object of ![]() $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}$. We have another category
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}$. We have another category  $\mathrm {Exo}_{(n,0)}^\Phi (S)$ whose objects are triples
$\mathrm {Exo}_{(n,0)}^\Phi (S)$ whose objects are triples ![]() $(X,\iota _X,\lambda _X)$ in which
$(X,\iota _X,\lambda _X)$ in which
• X is a p-divisible group over S of dimension
 $nf$ and height
$nf$ and height  $2nf$;
$2nf$;•
 $\iota _X\colon O_E\to \operatorname {\mathrm {End}}(X)$ is an action of
$\iota _X\colon O_E\to \operatorname {\mathrm {End}}(X)$ is an action of  $O_E$ on X such that for
$O_E$ on X such that for  $0\leqslant i\leqslant f-1$,
$0\leqslant i\leqslant f-1$,  $O_E$ acts on
$O_E$ acts on  $\operatorname {\mathrm {Lie}}_{\psi _i}(X)$ via
$\operatorname {\mathrm {Lie}}_{\psi _i}(X)$ via  $\varphi _i$;
$\varphi _i$;•
 $\lambda _X\colon X\to X^\vee $ is a
$\lambda _X\colon X\to X^\vee $ is a  $\iota _X$-compatible polarisation such that
$\iota _X$-compatible polarisation such that  $\operatorname {\mathrm {ker}}(\lambda _X)=X[\iota _X(u)]$.
$\operatorname {\mathrm {ker}}(\lambda _X)=X[\iota _X(u)]$.
Morphisms are defined similarly as in Definition 2.59. The category  $\mathrm {Exo}_{(n,0)}^\Phi (S)$ is a connected groupoid. Moreover, one can show that there is a canonical isomorphism
$\mathrm {Exo}_{(n,0)}^\Phi (S)$ is a connected groupoid. Moreover, one can show that there is a canonical isomorphism  $\mathrm {Exo}_{(n,0)}^\Phi \to \mathrm {Exo}_{(n,0)}$ of prestacks after restriction to
$\mathrm {Exo}_{(n,0)}^\Phi \to \mathrm {Exo}_{(n,0)}$ of prestacks after restriction to  $\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$ similar to (2.22).
$\operatorname {\mathrm {Sch}}_{/O_{\breve {E}}}^{\mathrm {v}}$ similar to (2.22).
Remark 2.68. It is desirable to extend the results in this subsection to a general finite extension ![]() $F/\mathbb {Q}_p$. We hope to address this problem in the future.
$F/\mathbb {Q}_p$. We hope to address this problem in the future.
3 Local theta lifting at ramified places
Throughout this section, we fix a ramified quadratic extension ![]() $E/F$ of p-adic fields with p odd, with
$E/F$ of p-adic fields with p odd, with ![]() $\mathtt {c}\in \operatorname {\mathrm {Gal}}(E/F)$ the Galois involution. We fix a uniformiser
$\mathtt {c}\in \operatorname {\mathrm {Gal}}(E/F)$ the Galois involution. We fix a uniformiser ![]() $u\in E$ satisfying
$u\in E$ satisfying ![]() $u^{\mathtt {c}}=-u$ and denote by q the cardinality of
$u^{\mathtt {c}}=-u$ and denote by q the cardinality of ![]() $O_E/(u)$. Let
$O_E/(u)$. Let ![]() $n=2r$ be an even positive integer. We fix a nontrivial additive character
$n=2r$ be an even positive integer. We fix a nontrivial additive character ![]() $\psi _F\colon F\to \mathbb {C}^\times $ of conductor
$\psi _F\colon F\to \mathbb {C}^\times $ of conductor ![]() $O_F$.
$O_F$.
The goal of this section is to compute the doubling L-function, the doubling epsilon factor, the spherical doubling zeta integral and the local theta lifting for a tempered admissible irreducible representation ![]() $\pi $ of
$\pi $ of ![]() $G_r(F)$ that is spherical with respect to the standard special maximal compact subgroup.
$G_r(F)$ that is spherical with respect to the standard special maximal compact subgroup.
3.1 Weil representation and spherical module
We equip ![]() $W_r := E^{2r}$ with the skew-hermitian form given by the matrix
$W_r := E^{2r}$ with the skew-hermitian form given by the matrix  $\left (\begin {smallmatrix}&1_r\\ -1_r &\end {smallmatrix}\right )$. We denote by
$\left (\begin {smallmatrix}&1_r\\ -1_r &\end {smallmatrix}\right )$. We denote by ![]() $\{e_1,\dots ,e_{2r}\}$ the natural basis of
$\{e_1,\dots ,e_{2r}\}$ the natural basis of ![]() $W_r$. Denote by
$W_r$. Denote by ![]() $G_r$ the unitary group of
$G_r$ the unitary group of ![]() $W_r$, which is a reductive group over F. We write elements of
$W_r$, which is a reductive group over F. We write elements of ![]() $W_r$ in row form, on which
$W_r$ in row form, on which ![]() $G_r$ acts from the right. Let
$G_r$ acts from the right. Let ![]() $K_r\subseteq G_r(F)$ be the stabiliser of the lattice
$K_r\subseteq G_r(F)$ be the stabiliser of the lattice  $O_E^{2r}\subseteq W_r$, which is a special maximal compact subgroup. We fix the Haar measure
$O_E^{2r}\subseteq W_r$, which is a special maximal compact subgroup. We fix the Haar measure ![]() $\mathrm {d}g$ on
$\mathrm {d}g$ on ![]() $G_r(F)$ that gives
$G_r(F)$ that gives ![]() $K_r$ volume
$K_r$ volume ![]() $1$. Let
$1$. Let ![]() $P_r$ be the Borel subgroup of
$P_r$ be the Borel subgroup of ![]() $G_r$ consisting of elements of the form
$G_r$ consisting of elements of the form

in which a is a lower-triangular matrix in ![]() $\operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_r$. Let
$\operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_r$. Let ![]() $P_r^0$ be the maximal parabolic subgroup of
$P_r^0$ be the maximal parabolic subgroup of ![]() $G_r$ containing
$G_r$ containing ![]() $P_r$ with the unipotent radical
$P_r$ with the unipotent radical ![]() $N_r^0$, such that the standard diagonal Levi factor
$N_r^0$, such that the standard diagonal Levi factor ![]() $M_r^0$ of
$M_r^0$ of ![]() $P_r^0$ is isomorphic to
$P_r^0$ is isomorphic to ![]() $\operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_r$.
$\operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_r$.
We fix a a split hermitian space ![]() $(V,(\,,\,)_V)$ over E of dimension
$(V,(\,,\,)_V)$ over E of dimension ![]() $n=2r$ and a self-dual lattice
$n=2r$ and a self-dual lattice ![]() $\Lambda _V$ of V, namely,
$\Lambda _V$ of V, namely, ![]() $\Lambda _V=\Lambda _V^\vee := \{x\in V\mathbin {|}\operatorname {\mathrm {Tr}}_{E/F}(x,y)_V\in O_F\text { for every } y\in \Lambda _V\}$. Put
$\Lambda _V=\Lambda _V^\vee := \{x\in V\mathbin {|}\operatorname {\mathrm {Tr}}_{E/F}(x,y)_V\in O_F\text { for every } y\in \Lambda _V\}$. Put ![]() $H_V := \mathrm {U}(V)$ and let
$H_V := \mathrm {U}(V)$ and let ![]() $L_V$ be the stabiliser of
$L_V$ be the stabiliser of ![]() $\Lambda _V$ in
$\Lambda _V$ in ![]() $H_V(F)$. We fix the Haar measure
$H_V(F)$. We fix the Haar measure ![]() $\mathrm {d}h$ on
$\mathrm {d}h$ on ![]() $H_V(F)$ that gives
$H_V(F)$ that gives ![]() $L_V$ volume
$L_V$ volume ![]() $1$.
$1$.
Remark 3.1. We have
(1) There exists an isomorphism
 $\kappa \colon W_r\to V$ of E-vector spaces satisfying
$\kappa \colon W_r\to V$ of E-vector spaces satisfying  $(\kappa (e_i),\kappa (e_j))_V=0$,
$(\kappa (e_i),\kappa (e_j))_V=0$,  $(\kappa (e_{r+i}),\kappa (e_{r+j}))_V=0$ and
$(\kappa (e_{r+i}),\kappa (e_{r+j}))_V=0$ and  $(\kappa (e_i),\kappa (e_{r+j}))_V=u^{-1}\delta _{ij}$ for
$(\kappa (e_i),\kappa (e_{r+j}))_V=u^{-1}\delta _{ij}$ for  $1\leqslant i,j\leqslant r$ and such that
$1\leqslant i,j\leqslant r$ and such that  $L_V$ is generated by
$L_V$ is generated by  $\{\kappa (e_i)\mathbin {|} 1\leqslant i\leqslant 2r\}$ as an
$\{\kappa (e_i)\mathbin {|} 1\leqslant i\leqslant 2r\}$ as an  $O_E$-submodule.
$O_E$-submodule.(2) The double coset
 $K_r\backslash G_r(F)/K_r$ has representatives where
$K_r\backslash G_r(F)/K_r$ has representatives where $$ \begin{align*} \begin{pmatrix} u^{a_1} & &&&& \\ & \ddots &&&& \\ & & u^{a_r} &&& \\ &&& (-u)^{-a_1} && \\ &&&& \ddots & \\ &&&&& (-u)^{-a_r} \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} u^{a_1} & &&&& \\ & \ddots &&&& \\ & & u^{a_r} &&& \\ &&& (-u)^{-a_1} && \\ &&&& \ddots & \\ &&&&& (-u)^{-a_r} \end{pmatrix} \end{align*} $$ $0\leqslant a_1\leqslant \cdots \leqslant a_r$ are integers.
$0\leqslant a_1\leqslant \cdots \leqslant a_r$ are integers.
We introduce two Hecke algebras:
Then by the remark above, both ![]() $\mathcal {H}_{W_r}$ and
$\mathcal {H}_{W_r}$ and ![]() $\mathcal {H}_V$ are commutative complex algebras and are canonically isomorphic to
$\mathcal {H}_V$ are commutative complex algebras and are canonically isomorphic to  $\mathcal {T}_r := \mathbb {C}[T_1^{\pm 1},\dots ,T_r^{\pm 1}]^{\{\pm 1\}^r\rtimes \mathfrak {S}_r}$.
$\mathcal {T}_r := \mathbb {C}[T_1^{\pm 1},\dots ,T_r^{\pm 1}]^{\{\pm 1\}^r\rtimes \mathfrak {S}_r}$.
Let ![]() $(\omega _{W_r,V},\mathcal {V}_{W_r,V})$ be the Weil representation of
$(\omega _{W_r,V},\mathcal {V}_{W_r,V})$ be the Weil representation of ![]() $G_r(F)\times H_V(F)$ (with respect to the additive character
$G_r(F)\times H_V(F)$ (with respect to the additive character ![]() $\psi _F$ and the trivial splitting character). We recall the action under the Schrödinger model
$\psi _F$ and the trivial splitting character). We recall the action under the Schrödinger model ![]() $\mathcal {V}_{W_r,V}\simeq C^\infty _c(V^r)$ as follows:
$\mathcal {V}_{W_r,V}\simeq C^\infty _c(V^r)$ as follows:
• for
 $a\in \operatorname {\mathrm {GL}}_r(E)$ and
$a\in \operatorname {\mathrm {GL}}_r(E)$ and  $\phi \in C^\infty _c(V^r)$, we have
$\phi \in C^\infty _c(V^r)$, we have 
• for
 $b\in \mathrm {Herm}_r(F)$ and
$b\in \mathrm {Herm}_r(F)$ and  $\phi \in C^\infty _c(V^r)$, we have where
$\phi \in C^\infty _c(V^r)$, we have where $$ \begin{align*} \omega_{W_r,V}\left(\left(\begin{smallmatrix} 1_r & b \\ & 1_r \end{smallmatrix}\right)\right)\phi(x)=\psi_F(\operatorname{\mathrm{tr}} bT(x))\cdot \phi(x) \end{align*} $$
$$ \begin{align*} \omega_{W_r,V}\left(\left(\begin{smallmatrix} 1_r & b \\ & 1_r \end{smallmatrix}\right)\right)\phi(x)=\psi_F(\operatorname{\mathrm{tr}} bT(x))\cdot \phi(x) \end{align*} $$ $T(x) := \left ((x_i,x_j)_V\right )_{1\leqslant i,j\leqslant r}$ is the moment matrix of
$T(x) := \left ((x_i,x_j)_V\right )_{1\leqslant i,j\leqslant r}$ is the moment matrix of  $x=(x_1,\dots ,x_r)$;
$x=(x_1,\dots ,x_r)$;• for
 $\phi \in C^\infty _c(V^r)$, we have
$\phi \in C^\infty _c(V^r)$, we have  $$ \begin{align*} \omega_{W_r,V}\left(\left(\begin{smallmatrix} & 1_r \\ -1_r & \end{smallmatrix}\right)\right)\phi(x)=\widehat\phi(x); \end{align*} $$
$$ \begin{align*} \omega_{W_r,V}\left(\left(\begin{smallmatrix} & 1_r \\ -1_r & \end{smallmatrix}\right)\right)\phi(x)=\widehat\phi(x); \end{align*} $$• for
 $h\in H_V(F)$ and
$h\in H_V(F)$ and  $\phi \in C^\infty _c(V^r)$, we have
$\phi \in C^\infty _c(V^r)$, we have  $$ \begin{align*} \omega_{W_r,V}(h)\phi(x)=\phi(h^{-1}x). \end{align*} $$
$$ \begin{align*} \omega_{W_r,V}(h)\phi(x)=\phi(h^{-1}x). \end{align*} $$
Here, we recall the Fourier transform ![]() $C^\infty _c(V^r)\to C^\infty _c(V^r)$ sending
$C^\infty _c(V^r)\to C^\infty _c(V^r)$ sending ![]() $\phi $ to
$\phi $ to ![]() $\widehat \phi $ defined by the formula
$\widehat \phi $ defined by the formula
 $$ \begin{align*} \widehat\phi(x) := \int_{V^r}\phi(y)\psi_F\left(\sum_{i=1}^r\operatorname{\mathrm{Tr}}_{E/F}(x_i,y_i)_V\right)\,\mathrm{d} y, \end{align*} $$
$$ \begin{align*} \widehat\phi(x) := \int_{V^r}\phi(y)\psi_F\left(\sum_{i=1}^r\operatorname{\mathrm{Tr}}_{E/F}(x_i,y_i)_V\right)\,\mathrm{d} y, \end{align*} $$where ![]() $\mathrm {d}y$ is the self-dual Haar measure on
$\mathrm {d}y$ is the self-dual Haar measure on ![]() $V^r$.
$V^r$.
Definition 3.2. We define the spherical module ![]() $\mathcal {S}_{W_r,V}$ to be the subspace of
$\mathcal {S}_{W_r,V}$ to be the subspace of ![]() $\mathcal {V}_{W_r,V}$ consisting of elements that are fixed by
$\mathcal {V}_{W_r,V}$ consisting of elements that are fixed by ![]() $K_r\times L_V$, as a module over
$K_r\times L_V$, as a module over ![]() $\mathcal {H}_{W_r}\otimes _{\mathbb {C}}\mathcal {H}_V$ via the representation
$\mathcal {H}_{W_r}\otimes _{\mathbb {C}}\mathcal {H}_V$ via the representation ![]() $\omega _{W_r,V}$. We denote by
$\omega _{W_r,V}$. We denote by ![]() $\mathrm {Sph}(V^r)$ the corresponding subspace of
$\mathrm {Sph}(V^r)$ the corresponding subspace of ![]() $C^\infty _c(V^r)$ under the Schrödinger model.
$C^\infty _c(V^r)$ under the Schrödinger model.
Lemma 3.3. The function ![]() belongs to
belongs to ![]() $\mathrm {Sph}(V^r)$.
$\mathrm {Sph}(V^r)$.
Proof. It suffices to check that

which follows from the fact that ![]() $\Lambda _V^\vee =\Lambda _V$. The lemma follows.
$\Lambda _V^\vee =\Lambda _V$. The lemma follows.
Proposition 3.4. The annihilator of the ![]() $\mathcal {H}_{W_r}\otimes _{\mathbb {C}}\mathcal {H}_V$-module
$\mathcal {H}_{W_r}\otimes _{\mathbb {C}}\mathcal {H}_V$-module ![]() $\mathcal {S}_{W_r,V}$ is
$\mathcal {S}_{W_r,V}$ is ![]() $\mathcal {I}_{W_r,V}$, where
$\mathcal {I}_{W_r,V}$, where ![]() $\mathcal {I}_{W_r,V}$ denotes the diagonal ideal of
$\mathcal {I}_{W_r,V}$ denotes the diagonal ideal of ![]() $\mathcal {H}_{W_r}\otimes _{\mathbb {C}}\mathcal {H}_V$.
$\mathcal {H}_{W_r}\otimes _{\mathbb {C}}\mathcal {H}_V$.
Proof. The same proof of [Reference LiuLiu22, Proposition 4.4] (with ![]() $\epsilon =+$ and
$\epsilon =+$ and ![]() $d=r$) works in this case as well, using Lemma 3.3.
$d=r$) works in this case as well, using Lemma 3.3.
In what follows, we review the construction of unramified principal series of ![]() $G_r(F)$ and
$G_r(F)$ and ![]() $H_V(F)$.
$H_V(F)$.
We identify ![]() $M_r$, the standard diagonal Levi factor of
$M_r$, the standard diagonal Levi factor of ![]() $P_r$, with
$P_r$, with ![]() $(\operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_1)^r$, under which we write an element of
$(\operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_1)^r$, under which we write an element of ![]() $M_r(F)$ as
$M_r(F)$ as ![]() $a=(a_1,\dots ,a_r)$ with
$a=(a_1,\dots ,a_r)$ with ![]() $a_i\in E^\times $ its eigenvalue on
$a_i\in E^\times $ its eigenvalue on ![]() $e_i$ for
$e_i$ for ![]() $1\leqslant i\leqslant r$. For every tuple
$1\leqslant i\leqslant r$. For every tuple  $\sigma =(\sigma _1,\dots ,\sigma _r)\in (\mathbb {C}/\tfrac {2\pi i}{\log q}\mathbb {Z})^r$, we define a character
$\sigma =(\sigma _1,\dots ,\sigma _r)\in (\mathbb {C}/\tfrac {2\pi i}{\log q}\mathbb {Z})^r$, we define a character ![]() $\chi ^\sigma _r$ of
$\chi ^\sigma _r$ of ![]() $M_r(F)$ and hence
$M_r(F)$ and hence ![]() $P_r(F)$ by the formula
$P_r(F)$ by the formula
 $$ \begin{align*} \chi^\sigma_r(a)=\prod_{i=1}^r|a_i|_E^{\sigma_i+i-1/2}. \end{align*} $$
$$ \begin{align*} \chi^\sigma_r(a)=\prod_{i=1}^r|a_i|_E^{\sigma_i+i-1/2}. \end{align*} $$We then have the normalised principal series
which is an admissible representation of ![]() $G_r(F)$ via the right translation. We denote by
$G_r(F)$ via the right translation. We denote by ![]() $\pi ^\sigma _{W_r}$ the unique irreducible constituent of
$\pi ^\sigma _{W_r}$ the unique irreducible constituent of ![]() $\mathrm {I}^\sigma _{W_r}$ that has nonzero
$\mathrm {I}^\sigma _{W_r}$ that has nonzero ![]() $K_r$-invariants.
$K_r$-invariants.
For V, we fix a basis ![]() $\{v_r,\dots ,v_1,v_{-1},\dots ,v_{-r}\}$ of the
$\{v_r,\dots ,v_1,v_{-1},\dots ,v_{-r}\}$ of the ![]() $O_E$-lattice
$O_E$-lattice ![]() $\Lambda _V$, satisfying
$\Lambda _V$, satisfying ![]() $(v_i,v_j)_V=u^{-1}\delta _{i,-j}$ for every
$(v_i,v_j)_V=u^{-1}\delta _{i,-j}$ for every ![]() $1\leqslant i,j\leqslant r$. We have an increasing filtration
$1\leqslant i,j\leqslant r$. We have an increasing filtration
of isotropic E-subspaces of V where ![]() $Z_i$ are the E-subspaces of V spanned by
$Z_i$ are the E-subspaces of V spanned by ![]() $\{v_r,\dots ,v_i\}$. Let
$\{v_r,\dots ,v_i\}$. Let ![]() $Q_V$ be the (minimal) parabolic subgroup of
$Q_V$ be the (minimal) parabolic subgroup of ![]() $H_V$ that stabilises (3.1). Let
$H_V$ that stabilises (3.1). Let ![]() $M_V$ be the Levi factor of
$M_V$ be the Levi factor of ![]() $Q_V$ stabilising the lines spanned by
$Q_V$ stabilising the lines spanned by ![]() $v_i$ for every i. Then we have the canonical isomorphism
$v_i$ for every i. Then we have the canonical isomorphism ![]() $M_V=(\operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_1)^r$, under which we write an element of
$M_V=(\operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_1)^r$, under which we write an element of ![]() $M_V(F)$ as
$M_V(F)$ as ![]() $b=(b_1,\dots ,b_r)$ with
$b=(b_1,\dots ,b_r)$ with ![]() $b_i\in E^\times $ its eigenvalue on
$b_i\in E^\times $ its eigenvalue on ![]() $v_i$ for
$v_i$ for ![]() $1\leqslant i\leqslant r$. For every tuple
$1\leqslant i\leqslant r$. For every tuple  $\sigma =(\sigma _1,\dots ,\sigma _r)\in (\mathbb {C}/\tfrac {2\pi i}{\log q}\mathbb {Z})^r$, we define a character
$\sigma =(\sigma _1,\dots ,\sigma _r)\in (\mathbb {C}/\tfrac {2\pi i}{\log q}\mathbb {Z})^r$, we define a character ![]() $\chi ^\sigma _V$ of
$\chi ^\sigma _V$ of ![]() $M_V(F)$ and hence
$M_V(F)$ and hence ![]() $Q_V(F)$ by the formula
$Q_V(F)$ by the formula
 $$ \begin{align*} \chi^\sigma_V(b)=\prod_{i=1}^r|b_i|_E^{\sigma_i+i-1/2}. \end{align*} $$
$$ \begin{align*} \chi^\sigma_V(b)=\prod_{i=1}^r|b_i|_E^{\sigma_i+i-1/2}. \end{align*} $$We then have the normalised principal series
which is an admissible representation of ![]() $H_V(F)$ via the right translation. We denote by
$H_V(F)$ via the right translation. We denote by ![]() $\pi ^\sigma _V$ the unique irreducible constituent of
$\pi ^\sigma _V$ the unique irreducible constituent of ![]() $\mathrm {I}^\sigma _V$ that has nonzero
$\mathrm {I}^\sigma _V$ that has nonzero ![]() $L_V$-invariants.
$L_V$-invariants.
3.2 Doubling zeta integral and doubling L-factor
In this section, we compute certain doubling zeta integrals and doubling L-factors for irreducible admissible representations ![]() $\pi $ of
$\pi $ of ![]() $G_r(F)$ satisfying
$G_r(F)$ satisfying ![]() $\pi ^{K_r}\neq \{0\}$. We will freely use notation from [Reference LiuLiu22, Section 5].
$\pi ^{K_r}\neq \{0\}$. We will freely use notation from [Reference LiuLiu22, Section 5].
We have the degenerate principal series  $\mathrm {I}^\Box _r(s) := \operatorname {\mathrm {Ind}}_{P_r^\Box }^{G_r^\Box }(|\;|_E^s\circ \Delta )$ of
$\mathrm {I}^\Box _r(s) := \operatorname {\mathrm {Ind}}_{P_r^\Box }^{G_r^\Box }(|\;|_E^s\circ \Delta )$ of ![]() $G_r^\Box (F)$. Let
$G_r^\Box (F)$. Let  $\mathfrak {f}^{(s)}_r$ be the unique section of
$\mathfrak {f}^{(s)}_r$ be the unique section of ![]() $\mathrm {I}^\Box _r(s)$ such that for every
$\mathrm {I}^\Box _r(s)$ such that for every ![]() $g\in pK_r$ with
$g\in pK_r$ with ![]() $p\in P_r^\Box (F)$,
$p\in P_r^\Box (F)$,
 $$ \begin{align*} \mathfrak{f}_r^{(s)}(g)=|\Delta(p)|_E^{s+r}. \end{align*} $$
$$ \begin{align*} \mathfrak{f}_r^{(s)}(g)=|\Delta(p)|_E^{s+r}. \end{align*} $$It is a holomorphic standard and hence good section.
Remark 3.5. By definition, we have  $\mathrm {I}^\Box _r(s)\subseteq \mathrm {I}^{\sigma ^\Box _s}_{W_{2r}}$, where
$\mathrm {I}^\Box _r(s)\subseteq \mathrm {I}^{\sigma ^\Box _s}_{W_{2r}}$, where
 $$ \begin{align*} \sigma^\Box_s := (s+r-\tfrac{1}{2},s+r-\tfrac{3}{2},\dots,s-r+\tfrac{3}{2},s-r+\tfrac{1}{2})\in(\mathbb{C}/\tfrac{2\pi i}{\log q}\mathbb{Z})^{2r}. \end{align*} $$
$$ \begin{align*} \sigma^\Box_s := (s+r-\tfrac{1}{2},s+r-\tfrac{3}{2},\dots,s-r+\tfrac{3}{2},s-r+\tfrac{1}{2})\in(\mathbb{C}/\tfrac{2\pi i}{\log q}\mathbb{Z})^{2r}. \end{align*} $$Moreover, if we denote by ![]() $\varphi ^{\sigma ^\Box _s}$ the unique section in
$\varphi ^{\sigma ^\Box _s}$ the unique section in  $\mathrm {I}^{\sigma ^\Box _s}_{W_{2r}}$ that is fixed by
$\mathrm {I}^{\sigma ^\Box _s}_{W_{2r}}$ that is fixed by ![]() $K_{2r}$ and such that
$K_{2r}$ and such that ![]() $\varphi ^{\sigma ^\Box _s}(1_{4r})=1$, then
$\varphi ^{\sigma ^\Box _s}(1_{4r})=1$, then  $\mathfrak {f}_r^{(s)}=\varphi ^{\sigma ^\Box _s}$.
$\mathfrak {f}_r^{(s)}=\varphi ^{\sigma ^\Box _s}$.
Let ![]() $\pi $ be an irreducible admissible representation of
$\pi $ be an irreducible admissible representation of ![]() $G_r(F)$. For every element
$G_r(F)$. For every element ![]() $\xi \in \pi ^\vee \boxtimes \pi $, we denote by
$\xi \in \pi ^\vee \boxtimes \pi $, we denote by ![]() $H_\xi \in C^\infty (G_r(F))$ its associated matrix coefficient. Then for every meromorphic section
$H_\xi \in C^\infty (G_r(F))$ its associated matrix coefficient. Then for every meromorphic section ![]() $f^{(s)}$ of
$f^{(s)}$ of ![]() $\mathrm {I}^\Box _r(s)$, we have the (doubling) zeta integral
$\mathrm {I}^\Box _r(s)$, we have the (doubling) zeta integral
 $$ \begin{align*} Z(\xi,f^{(s)}) := \int_{G_r(F)}H_\xi(g)f^{(s)}(\mathbf{w}_r(g,1_{2r}))\,\mathrm{d} g, \end{align*} $$
$$ \begin{align*} Z(\xi,f^{(s)}) := \int_{G_r(F)}H_\xi(g)f^{(s)}(\mathbf{w}_r(g,1_{2r}))\,\mathrm{d} g, \end{align*} $$which is absolutely convergent for ![]() $\mathrm {Re}\, s$ large enough and has a meromorphic continuation. We let
$\mathrm {Re}\, s$ large enough and has a meromorphic continuation. We let ![]() $L(s,\pi )$ and
$L(s,\pi )$ and ![]() $\varepsilon (s,\pi ,\psi _F)$ be the doubling L-factor and the doubling epsilon factor of
$\varepsilon (s,\pi ,\psi _F)$ be the doubling L-factor and the doubling epsilon factor of ![]() $\pi $, respectively, defined in [Reference YamanaYam14, Theorem 5.2].
$\pi $, respectively, defined in [Reference YamanaYam14, Theorem 5.2].
Take an element  $\sigma =(\sigma _1,\dots ,\sigma _r)\in (\mathbb {C}/\tfrac {2\pi i}{\log q}\mathbb {Z})^r$. We define an L-factor
$\sigma =(\sigma _1,\dots ,\sigma _r)\in (\mathbb {C}/\tfrac {2\pi i}{\log q}\mathbb {Z})^r$. We define an L-factor
 $$ \begin{align*} L^\sigma(s) := \prod_{i=1}^r\frac{1}{(1-q^{\sigma_i-s})(1-q^{-\sigma_i-s})}. \end{align*} $$
$$ \begin{align*} L^\sigma(s) := \prod_{i=1}^r\frac{1}{(1-q^{\sigma_i-s})(1-q^{-\sigma_i-s})}. \end{align*} $$Let ![]() $\xi ^\sigma $ be a generator of the 1-dimensional space
$\xi ^\sigma $ be a generator of the 1-dimensional space  $((\pi _{W_r}^\sigma )^\vee )^{K_r}\boxtimes (\pi _{W_r}^\sigma )^{K_r}$, which satisfies
$((\pi _{W_r}^\sigma )^\vee )^{K_r}\boxtimes (\pi _{W_r}^\sigma )^{K_r}$, which satisfies ![]() $H_{\xi ^\sigma }(1_{2r})\neq 0$. We normalise
$H_{\xi ^\sigma }(1_{2r})\neq 0$. We normalise ![]() $\xi ^\sigma $ such that
$\xi ^\sigma $ such that ![]() $H_{\xi ^\sigma }(1_{2r})=1$, which makes it unique.
$H_{\xi ^\sigma }(1_{2r})=1$, which makes it unique.
Proposition 3.6. For  $\sigma \in (\mathbb {C}/\tfrac {2\pi i}{\log q}\mathbb {Z})^r$, we have
$\sigma \in (\mathbb {C}/\tfrac {2\pi i}{\log q}\mathbb {Z})^r$, we have
 $$ \begin{align*} Z(\xi^\sigma,\mathfrak{f}_r^{(s)})=\frac{L^\sigma(s+\tfrac{1}{2})}{b_{2r}(s)}, \end{align*} $$
$$ \begin{align*} Z(\xi^\sigma,\mathfrak{f}_r^{(s)})=\frac{L^\sigma(s+\tfrac{1}{2})}{b_{2r}(s)}, \end{align*} $$where  $b_{2r}(s) := \prod _{i=1}^{r}\frac {1}{1-q^{-2s-2i}}$.
$b_{2r}(s) := \prod _{i=1}^{r}\frac {1}{1-q^{-2s-2i}}$.
Proof. We have an isomorphism ![]() $m\colon \operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_r\to M_r^0$ sending a to
$m\colon \operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_r\to M_r^0$ sending a to  . Let
. Let ![]() $\tau $ be the unramified constituent of the normalised induction of
$\tau $ be the unramified constituent of the normalised induction of ![]() $\boxtimes _{i=1}^r|\;|_E^{\sigma _i}$, as a representation of
$\boxtimes _{i=1}^r|\;|_E^{\sigma _i}$, as a representation of ![]() $\operatorname {\mathrm {GL}}_r(E)$. We fix vectors
$\operatorname {\mathrm {GL}}_r(E)$. We fix vectors ![]() $v_0\in \tau $ and
$v_0\in \tau $ and ![]() $v_0^\vee \in \tau ^\vee $ fixed by
$v_0^\vee \in \tau ^\vee $ fixed by ![]() $M_r^0(F)\cap K_r=m(\operatorname {\mathrm {GL}}_r(O_E))$ such that
$M_r^0(F)\cap K_r=m(\operatorname {\mathrm {GL}}_r(O_E))$ such that ![]() $\langle v_0^\vee ,v_0\rangle _\tau =1$.
$\langle v_0^\vee ,v_0\rangle _\tau =1$.
By a similar argument in [Reference Gelbart, Piatetski-Shapiro and RallisGPSR87, Section 6] or in the proof of [Reference LiuLiu22, Proposition 5.6], we have
 $$ \begin{align} Z(\xi^\sigma,\mathfrak{f}_r^{(s)})=C_{\mathbf{w}^{\prime}_r}(s)\int_{\operatorname{\mathrm{GL}}_r(E)}\varphi^{\mathbf{w}^{\prime}_r\sigma^\Box_s}(\mathbf{w}^{\prime\prime}_r(m(a),1_{2r})) |\mathrm{det}\: a|_E^{-r/2}\langle\tau^\vee(a)v^\vee_0,v_0\rangle_\tau\,\mathrm{d} a, \end{align} $$
$$ \begin{align} Z(\xi^\sigma,\mathfrak{f}_r^{(s)})=C_{\mathbf{w}^{\prime}_r}(s)\int_{\operatorname{\mathrm{GL}}_r(E)}\varphi^{\mathbf{w}^{\prime}_r\sigma^\Box_s}(\mathbf{w}^{\prime\prime}_r(m(a),1_{2r})) |\mathrm{det}\: a|_E^{-r/2}\langle\tau^\vee(a)v^\vee_0,v_0\rangle_\tau\,\mathrm{d} a, \end{align} $$where
 $$ \begin{align*} C_{\mathbf{w}^{\prime}_r}(s)=\prod_{i=1}^r\frac{\zeta_E(2s+2i)}{\zeta_E(2s+r+i)}\prod_{i=1}^r\frac{\zeta_F(2s+2i-1)}{\zeta_F(2s+2i)} =\prod_{i=1}^r\frac{\zeta_E(2s+2i-1)}{\zeta_E(2s+r+i)}. \end{align*} $$
$$ \begin{align*} C_{\mathbf{w}^{\prime}_r}(s)=\prod_{i=1}^r\frac{\zeta_E(2s+2i)}{\zeta_E(2s+r+i)}\prod_{i=1}^r\frac{\zeta_F(2s+2i-1)}{\zeta_F(2s+2i)} =\prod_{i=1}^r\frac{\zeta_E(2s+2i-1)}{\zeta_E(2s+r+i)}. \end{align*} $$See the proof of [Reference LiuLiu22, Proposition 5.6] for unexplained notation. By [Reference Gelbart, Piatetski-Shapiro and RallisGPSR87, Proposition 6.1], we have
 $$ \begin{align*} \int_{\operatorname{\mathrm{GL}}_r(E)}\varphi^{\mathbf{w}^{\prime}_r\sigma^\Box_s}(\mathbf{w}^{\prime\prime}_r(m(a),1_{2r})) |\mathrm{det}\: a|_E^{-r/2}\langle\tau^\vee(a)v^\vee_0,v_0\rangle_\tau\,\mathrm{d} a =\frac{L(s+\tfrac{1}{2},\tau)L(s+\tfrac{1}{2},\tau^\vee)}{\prod_{i=1}^r\zeta_E(2s+i)}. \end{align*} $$
$$ \begin{align*} \int_{\operatorname{\mathrm{GL}}_r(E)}\varphi^{\mathbf{w}^{\prime}_r\sigma^\Box_s}(\mathbf{w}^{\prime\prime}_r(m(a),1_{2r})) |\mathrm{det}\: a|_E^{-r/2}\langle\tau^\vee(a)v^\vee_0,v_0\rangle_\tau\,\mathrm{d} a =\frac{L(s+\tfrac{1}{2},\tau)L(s+\tfrac{1}{2},\tau^\vee)}{\prod_{i=1}^r\zeta_E(2s+i)}. \end{align*} $$Combining with (3.2), we have
 $$ \begin{align*} Z(\xi^\sigma,\mathfrak{f}_r^{(s)})&=\left(\prod_{i=1}^r\frac{\zeta_E(2s+2i-1)}{\zeta_E(2s+r+i)}\right)\cdot \left(\frac{L(s+\tfrac{1}{2},\tau)L(s+\tfrac{1}{2},\tau^\vee)}{\prod_{i=1}^r\zeta_E(2s+i)}\right) \\ &=\frac{L(s+\tfrac{1}{2},\tau)L(s+\tfrac{1}{2},\tau^\vee)}{\prod_{i=1}^r\zeta_E(2s+2i)} \\ &=\frac{L^\sigma(s+\tfrac{1}{2})}{b_{2r}(s)}. \end{align*} $$
$$ \begin{align*} Z(\xi^\sigma,\mathfrak{f}_r^{(s)})&=\left(\prod_{i=1}^r\frac{\zeta_E(2s+2i-1)}{\zeta_E(2s+r+i)}\right)\cdot \left(\frac{L(s+\tfrac{1}{2},\tau)L(s+\tfrac{1}{2},\tau^\vee)}{\prod_{i=1}^r\zeta_E(2s+i)}\right) \\ &=\frac{L(s+\tfrac{1}{2},\tau)L(s+\tfrac{1}{2},\tau^\vee)}{\prod_{i=1}^r\zeta_E(2s+2i)} \\ &=\frac{L^\sigma(s+\tfrac{1}{2})}{b_{2r}(s)}. \end{align*} $$The proposition is proved.
Proposition 3.7. For  $\sigma \in (\mathbb {C}/\tfrac {2\pi i}{\log q}\mathbb {Z})^r$, we have
$\sigma \in (\mathbb {C}/\tfrac {2\pi i}{\log q}\mathbb {Z})^r$, we have
and ![]() $\varepsilon (s,\pi ^\sigma _{W_r},\psi _F)=1$.
$\varepsilon (s,\pi ^\sigma _{W_r},\psi _F)=1$.
Proof. It follows from the same argument for [Reference YamanaYam14, Proposition 7.1], using Proposition 3.6.
Remark 3.8. It is clear that the base change ![]() $\operatorname {\mathrm {BC}}(\pi ^\sigma _{W_r})$ is well-defined, which is an unramified irreducible admissible representation of
$\operatorname {\mathrm {BC}}(\pi ^\sigma _{W_r})$ is well-defined, which is an unramified irreducible admissible representation of ![]() $\operatorname {\mathrm {GL}}_n(E)$, and we have
$\operatorname {\mathrm {GL}}_n(E)$, and we have ![]() $L(s,\pi ^\sigma _{W_r})=L(s,\operatorname {\mathrm {BC}}(\pi ^\sigma _{W_r}))$ by Proposition 3.7.
$L(s,\pi ^\sigma _{W_r})=L(s,\operatorname {\mathrm {BC}}(\pi ^\sigma _{W_r}))$ by Proposition 3.7.
For an irreducible admissible representation ![]() $\pi $ of
$\pi $ of ![]() $G_r(F)$, let
$G_r(F)$, let ![]() $\Theta (\pi ,V)$ be the
$\Theta (\pi ,V)$ be the ![]() $\pi $-isotypic quotient of
$\pi $-isotypic quotient of ![]() $\mathcal {V}_{W_r,V}$, which is an admissible representation of
$\mathcal {V}_{W_r,V}$, which is an admissible representation of ![]() $H_V(F)$ and
$H_V(F)$ and ![]() $\theta (\pi ,V)$ its maximal semisimple quotient. By [Reference WaldspurgerWal90],
$\theta (\pi ,V)$ its maximal semisimple quotient. By [Reference WaldspurgerWal90], ![]() $\theta (\pi ,V)$ is either zero or an irreducible admissible representation of
$\theta (\pi ,V)$ is either zero or an irreducible admissible representation of ![]() $H_V(F)$, known as the theta lifting of
$H_V(F)$, known as the theta lifting of ![]() $\pi $ to V (with respect to the additive character
$\pi $ to V (with respect to the additive character ![]() $\psi _F$ and the trivial splitting character).
$\psi _F$ and the trivial splitting character).
Proposition 3.9. For an irreducible admissible representation ![]() $\pi $ of
$\pi $ of ![]() $G_r(F)$ of the form
$G_r(F)$ of the form ![]() $\pi _{W_r}^\sigma $ for an element
$\pi _{W_r}^\sigma $ for an element  $\sigma =(\sigma _1,\dots ,\sigma _r)\in (i\mathbb {R}/\tfrac {2\pi i}{\log q}\mathbb {Z})^r$, we have
$\sigma =(\sigma _1,\dots ,\sigma _r)\in (i\mathbb {R}/\tfrac {2\pi i}{\log q}\mathbb {Z})^r$, we have ![]() $\theta (\pi ,V)\simeq \pi _V^\sigma $.
$\theta (\pi ,V)\simeq \pi _V^\sigma $.
Proof. By the same argument in the proof of [Reference LiuLiu22, Theorem 6.2], we have ![]() $\Theta (\pi ,V)^{L_V}\neq \{0\}$. By our assumption on
$\Theta (\pi ,V)^{L_V}\neq \{0\}$. By our assumption on ![]() $\sigma $,
$\sigma $, ![]() $\pi $ is tempered. By (the same argument for) [Reference Gan and IchinoGI16, Theorem 4.1(v)],
$\pi $ is tempered. By (the same argument for) [Reference Gan and IchinoGI16, Theorem 4.1(v)], ![]() $\Theta (\pi ,V)$ is a semisimple representation of
$\Theta (\pi ,V)$ is a semisimple representation of ![]() $H_V(F)$; hence,
$H_V(F)$; hence, ![]() $\Theta (\pi ,V)=\theta (\pi ,V)$. In particular, we have
$\Theta (\pi ,V)=\theta (\pi ,V)$. In particular, we have ![]() $\theta (\pi ,V)^{L_V}\neq \{0\}$. By Proposition 3.4, the diagonal ideal
$\theta (\pi ,V)^{L_V}\neq \{0\}$. By Proposition 3.4, the diagonal ideal ![]() $\mathcal {I}_{W_r,V}$ annihilates
$\mathcal {I}_{W_r,V}$ annihilates  $(\pi _{W_r}^\sigma )^{K_r}\boxtimes \theta (\pi ,V)^{L_V}$, which implies that
$(\pi _{W_r}^\sigma )^{K_r}\boxtimes \theta (\pi ,V)^{L_V}$, which implies that ![]() $\theta (\pi ,V)\simeq \pi _V^\sigma $.
$\theta (\pi ,V)\simeq \pi _V^\sigma $.
4 Arithmetic inner product formula
In this section, we collect all local ingredients and deduce our main theorems, following the same line as in [Reference Li and LiuLL21]. In Subsections 4.1 and 4.2, we recall the doubling method and the arithmetic theta lifting from [Reference Li and LiuLL21], respectively. In Subsection 4.3, we prove the vanishing of local indices at split places, by proving the second main ingredient of this article, namely, Theorem 4.21. In Subsection 4.4, we recall the formula for local indices at inert places. In Subsection 4.5, we compute local indices at ramified places, based on the Kudla–Rapoport type formula Theorem 2.7. In Subsection 4.6, we recall the formula for local indices at Archimedean places. The deduction of the main results of the article is explained in Subsection 4.7, which is a straightforward modification of [Reference Li and LiuLL21, Section 11].
4.1 Recollection on doubling method
For the readers’ convenience, we copy three groups of notation from [Reference Li and LiuLL21, Section 2] to here. The only difference is item (H5), which reflects the fact that we are able to study certain places in ![]() $\mathtt {V}_F^{\mathrm {ram}}$ in the current article.
$\mathtt {V}_F^{\mathrm {ram}}$ in the current article.
Notation 4.1. Let ![]() $E/F$ be a CM extension of number fields, so that
$E/F$ be a CM extension of number fields, so that ![]() $\mathtt {c}$ is a well-defined element in
$\mathtt {c}$ is a well-defined element in ![]() $\operatorname {\mathrm {Gal}}(E/F)$. We continue to fix an embedding
$\operatorname {\mathrm {Gal}}(E/F)$. We continue to fix an embedding ![]() $\boldsymbol {\iota }\colon E\hookrightarrow \mathbb {C}$. We denote by
$\boldsymbol {\iota }\colon E\hookrightarrow \mathbb {C}$. We denote by ![]() $\mathbf {u}$ the (Archimedean) place of E induced by
$\mathbf {u}$ the (Archimedean) place of E induced by ![]() $\boldsymbol {\iota }$ and regard E as a subfield of
$\boldsymbol {\iota }$ and regard E as a subfield of ![]() $\mathbb {C}$ via
$\mathbb {C}$ via ![]() $\boldsymbol {\iota }$.
$\boldsymbol {\iota }$.
(F1) We denote by
•
 $\mathtt {V}_F$ and
$\mathtt {V}_F$ and  $\mathtt {V}_F^{\mathrm {fin}}$ the set of all places and non-Archimedean places of F, respectively;
$\mathtt {V}_F^{\mathrm {fin}}$ the set of all places and non-Archimedean places of F, respectively;•
 $\mathtt {V}_F^{\mathrm {spl}}$,
$\mathtt {V}_F^{\mathrm {spl}}$,  $\mathtt {V}_F^{\mathrm {int}}$ and
$\mathtt {V}_F^{\mathrm {int}}$ and  $\mathtt {V}_F^{\mathrm {ram}}$ the subsets of
$\mathtt {V}_F^{\mathrm {ram}}$ the subsets of  $\mathtt {V}_F^{\mathrm {fin}}$ of those that are split, inert and ramified in E, respectively;
$\mathtt {V}_F^{\mathrm {fin}}$ of those that are split, inert and ramified in E, respectively;•
 $\mathtt {V}_F^{(\diamond )}$ the subset of
$\mathtt {V}_F^{(\diamond )}$ the subset of  $\mathtt {V}_F$ of places above
$\mathtt {V}_F$ of places above  $\diamond $ for every place
$\diamond $ for every place  $\diamond $ of
$\diamond $ of  $\mathbb {Q}$; and
$\mathbb {Q}$; and•
 $\mathtt {V}_E^?$ the places of E above
$\mathtt {V}_E^?$ the places of E above  $\mathtt {V}_F^?$.
$\mathtt {V}_F^?$.
Moreover,
• for every place
 $u\in \mathtt {V}_E$ of E, we denote by
$u\in \mathtt {V}_E$ of E, we denote by  $\underline {u}\in \mathtt {V}_F$ the underlying place of F;
$\underline {u}\in \mathtt {V}_F$ the underlying place of F;• for every
 $v\in \mathtt {V}_F^{\mathrm {fin}}$, we denote by
$v\in \mathtt {V}_F^{\mathrm {fin}}$, we denote by  $\mathfrak {p}_v$ the maximal ideal of
$\mathfrak {p}_v$ the maximal ideal of  $O_{F_v}$ and put
$O_{F_v}$ and put  $q_v := |O_{F_v}/\mathfrak {p}_v|$;
$q_v := |O_{F_v}/\mathfrak {p}_v|$;• for every
 $v\in \mathtt {V}_F$, we put
$v\in \mathtt {V}_F$, we put  $E_v := E\otimes _FF_v$ and denote by
$E_v := E\otimes _FF_v$ and denote by  $|\;|_{E_v}\colon E_v^\times \to \mathbb {C}^\times $ the normalised norm character.
$|\;|_{E_v}\colon E_v^\times \to \mathbb {C}^\times $ the normalised norm character.
(F2) Let
 $m\geqslant 0$ be an integer.
$m\geqslant 0$ be an integer.• We denote by
 $\mathrm {Herm}_m$ the subscheme of
$\mathrm {Herm}_m$ the subscheme of  $\operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {Mat}}_{m,m}$ of m-by-m matrices b satisfying
$\operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {Mat}}_{m,m}$ of m-by-m matrices b satisfying  . Put
. Put  $\mathrm {Herm}_m^\circ := \mathrm {Herm}_m\cap \operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_m$.
$\mathrm {Herm}_m^\circ := \mathrm {Herm}_m\cap \operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_m$.• For every ordered partition
 $m=m_1+\cdots +m_s$ with
$m=m_1+\cdots +m_s$ with  $m_i$ a positive integer, we denote by
$m_i$ a positive integer, we denote by  $\partial _{m_1,\dots ,m_s}\colon \mathrm {Herm}_m\to \mathrm {Herm}_{m_1}\times \cdots \times \mathrm {Herm}_{m_s}$ the morphism that extracts the diagonal blocks with corresponding ranks.
$\partial _{m_1,\dots ,m_s}\colon \mathrm {Herm}_m\to \mathrm {Herm}_{m_1}\times \cdots \times \mathrm {Herm}_{m_s}$ the morphism that extracts the diagonal blocks with corresponding ranks.• We denote by
 $\mathrm {Herm}_m(F)^+$ (respectively
$\mathrm {Herm}_m(F)^+$ (respectively  $\mathrm {Herm}^\circ _m(F)^+$) the subset of
$\mathrm {Herm}^\circ _m(F)^+$) the subset of  $\mathrm {Herm}_m(F)$ of elements that are totally semi-positive definite (respectively totally positive definite).
$\mathrm {Herm}_m(F)$ of elements that are totally semi-positive definite (respectively totally positive definite).
(F3) For every
 $u\in \mathtt {V}_E^{(\infty )}$, we fix an embedding
$u\in \mathtt {V}_E^{(\infty )}$, we fix an embedding  $\iota _u\colon E\hookrightarrow \mathbb {C}$ inducing u (with
$\iota _u\colon E\hookrightarrow \mathbb {C}$ inducing u (with  $\iota _{\mathbf {u}}=\boldsymbol {\iota }$) and identify
$\iota _{\mathbf {u}}=\boldsymbol {\iota }$) and identify  $E_u$ with
$E_u$ with  $\mathbb {C}$ via
$\mathbb {C}$ via  $\iota _u$.
$\iota _u$.(F4) Let
 $\eta := \eta _{E/F}\colon \mathbb {A}_F^\times \to \mathbb {C}^\times $ be the quadratic character associated to
$\eta := \eta _{E/F}\colon \mathbb {A}_F^\times \to \mathbb {C}^\times $ be the quadratic character associated to  $E/F$. For every
$E/F$. For every  $v\in \mathtt {V}_F$ and every positive integer m, put Put
$v\in \mathtt {V}_F$ and every positive integer m, put Put $$ \begin{align*} b_{m,v}(s) := \prod_{i=1}^m L(2s+i,\eta_v^{m-i}). \end{align*} $$
$$ \begin{align*} b_{m,v}(s) := \prod_{i=1}^m L(2s+i,\eta_v^{m-i}). \end{align*} $$ $b_m(s) := \prod _{v\in \mathtt {V}_F}b_{m,v}(s)$.
$b_m(s) := \prod _{v\in \mathtt {V}_F}b_{m,v}(s)$.(F5) For every element
 $T\in \mathrm {Herm}_m(\mathbb {A}_F)$, we have the character given by the formula
$T\in \mathrm {Herm}_m(\mathbb {A}_F)$, we have the character given by the formula $$ \begin{align*} \psi_T\colon\mathrm{Herm}_m(\mathbb{A}_F)\to\mathbb{C}^\times \end{align*} $$
$$ \begin{align*} \psi_T\colon\mathrm{Herm}_m(\mathbb{A}_F)\to\mathbb{C}^\times \end{align*} $$ $\psi _T(b) := \psi _F(\operatorname {\mathrm {tr}} bT)$.
$\psi _T(b) := \psi _F(\operatorname {\mathrm {tr}} bT)$.(F6) Let R be a commutative F-algebra. A (skew-)hermitian space over
 $R\otimes _FE$ is a free
$R\otimes _FE$ is a free  $R\otimes _FE$-module V of finite rank, equipped with a (skew-)hermitian form
$R\otimes _FE$-module V of finite rank, equipped with a (skew-)hermitian form  $(\,,\,)_V$ with respect to the involution
$(\,,\,)_V$ with respect to the involution  $\mathtt {c}$ that is nondegenerate.
$\mathtt {c}$ that is nondegenerate.
Notation 4.2. We fix an even positive integer ![]() $n=2r$. Let
$n=2r$. Let ![]() $(V,(\,,\,)_V)$ be a hermitian space over
$(V,(\,,\,)_V)$ be a hermitian space over ![]() $\mathbb {A}_E$ of rank n that is totally positive definite.
$\mathbb {A}_E$ of rank n that is totally positive definite.
(H1) For every commutative
 $\mathbb {A}_F$-algebra R and every integer
$\mathbb {A}_F$-algebra R and every integer  $m\geqslant 0$, we denote by the moment matrix of an element
$m\geqslant 0$, we denote by the moment matrix of an element $$ \begin{align*} T(x) := \left((x_i,x_j)_V\right)_{i,j}\in\mathrm{Herm}_m(R) \end{align*} $$
$$ \begin{align*} T(x) := \left((x_i,x_j)_V\right)_{i,j}\in\mathrm{Herm}_m(R) \end{align*} $$ $x=(x_1,\dots ,x_m)\in V^m\otimes _{\mathbb {A}_F}R$.
$x=(x_1,\dots ,x_m)\in V^m\otimes _{\mathbb {A}_F}R$.(H2) For every
 $v\in \mathtt {V}_F$, we put
$v\in \mathtt {V}_F$, we put  $V_v := V\otimes _{\mathbb {A}_F}F_v$, which is a hermitian space over
$V_v := V\otimes _{\mathbb {A}_F}F_v$, which is a hermitian space over  $E_v$, and define the local Hasse invariant of
$E_v$, and define the local Hasse invariant of  $V_v$ to be
$V_v$ to be  $\epsilon (V_v) := \eta _v((-1)^r\mathrm {det}\: V_v)\in \{\pm 1\}$, which equals
$\epsilon (V_v) := \eta _v((-1)^r\mathrm {det}\: V_v)\in \{\pm 1\}$, which equals  $1$ for all but finitely many v. In what follows, we will abbreviate
$1$ for all but finitely many v. In what follows, we will abbreviate  $\epsilon (V_v)$ as
$\epsilon (V_v)$ as  $\epsilon _v$. Recall that V is coherent (respectively incoherent) if
$\epsilon _v$. Recall that V is coherent (respectively incoherent) if  $\prod _{v\in \mathtt {V}_F}\epsilon _v=1$ (respectively
$\prod _{v\in \mathtt {V}_F}\epsilon _v=1$ (respectively  $\prod _{v\in \mathtt {V}_F}\epsilon _v=-1$).
$\prod _{v\in \mathtt {V}_F}\epsilon _v=-1$).(H3) Let v be a place of F and
 $m\geqslant 0$ an integer.
$m\geqslant 0$ an integer.• For
 $T\in \mathrm {Herm}_m(F_v)$, we put
$T\in \mathrm {Herm}_m(F_v)$, we put  $(V^m_v)_T := \{x\in V^m_v\mathbin {|} T(x)=T\}$ and
$(V^m_v)_T := \{x\in V^m_v\mathbin {|} T(x)=T\}$ and  $$ \begin{align*} (V^m_v)_{\mathrm{reg}} := \bigcup_{T\in\mathrm{Herm}_m^\circ(F_v)}(V^m_v)_T. \end{align*} $$
$$ \begin{align*} (V^m_v)_{\mathrm{reg}} := \bigcup_{T\in\mathrm{Herm}_m^\circ(F_v)}(V^m_v)_T. \end{align*} $$• We denote by
 $\mathscr {S}(V_v^m)$ the space of (complex-valued) Bruhat–Schwartz functions on
$\mathscr {S}(V_v^m)$ the space of (complex-valued) Bruhat–Schwartz functions on  $V_v^m$. When
$V_v^m$. When  $v\in \mathtt {V}_F^{(\infty )}$, we have the Gaussian function
$v\in \mathtt {V}_F^{(\infty )}$, we have the Gaussian function  $\phi ^0_v\in \mathscr {S}(V_v^m)$ given by the formula
$\phi ^0_v\in \mathscr {S}(V_v^m)$ given by the formula  $\phi ^0_v(x)=\mathrm {e}^{-2\pi \operatorname {\mathrm {tr}} T(x)}$.
$\phi ^0_v(x)=\mathrm {e}^{-2\pi \operatorname {\mathrm {tr}} T(x)}$.• We have a Fourier transform map
 $\widehat {\phantom {a}}\colon \mathscr {S}(V_v^m)\to \mathscr {S}(V_v^m)$ sending
$\widehat {\phantom {a}}\colon \mathscr {S}(V_v^m)\to \mathscr {S}(V_v^m)$ sending  $\phi $ to
$\phi $ to  $\widehat \phi $ defined by the formula where
$\widehat \phi $ defined by the formula where $$ \begin{align*} \widehat\phi(x) := \int_{V_v^m}\phi(y)\psi_{E,v}\left(\sum_{i=1}^m(x_i,y_i)_V\right)\,\mathrm{d} y, \end{align*} $$
$$ \begin{align*} \widehat\phi(x) := \int_{V_v^m}\phi(y)\psi_{E,v}\left(\sum_{i=1}^m(x_i,y_i)_V\right)\,\mathrm{d} y, \end{align*} $$ $\mathrm {d}y$ is the self-dual Haar measure on
$\mathrm {d}y$ is the self-dual Haar measure on  $V_v^m$ with respect to
$V_v^m$ with respect to  $\psi _{E,v}$.
$\psi _{E,v}$.• In what follows, we will always use this self-dual Haar measure on
 $V_v^m$.
$V_v^m$.
(H4) Let
 $m\geqslant 0$ be an integer. For
$m\geqslant 0$ be an integer. For  $T\in \mathrm {Herm}_m(F)$, we put which is a finite subset of
$T\in \mathrm {Herm}_m(F)$, we put which is a finite subset of $$ \begin{align*} \operatorname{\mathrm{Diff}}(T,V) := \{v\in\mathtt{V}_F\mathbin{|}(V^m_v)_T=\emptyset\}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Diff}}(T,V) := \{v\in\mathtt{V}_F\mathbin{|}(V^m_v)_T=\emptyset\}, \end{align*} $$ $\mathtt {V}_F\setminus \mathtt {V}_F^{\mathrm {spl}}$.
$\mathtt {V}_F\setminus \mathtt {V}_F^{\mathrm {spl}}$.(H5) Take a nonempty finite subset
 $\mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {fin}}$ that contains Let
$\mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {fin}}$ that contains Let $$ \begin{align*} \{v\in\mathtt{V}_F^{\mathrm{ram}}\mathbin{|}\text{either } \epsilon_v=-1, \text{ or } v\mid 2 \text{ or } v \text{ is ramified over } \mathbb{Q}\}. \end{align*} $$
$$ \begin{align*} \{v\in\mathtt{V}_F^{\mathrm{ram}}\mathbin{|}\text{either } \epsilon_v=-1, \text{ or } v\mid 2 \text{ or } v \text{ is ramified over } \mathbb{Q}\}. \end{align*} $$ $\mathtt {S}$ be the subset of
$\mathtt {S}$ be the subset of  $\mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R}$ consisting of v such that
$\mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R}$ consisting of v such that  $\epsilon _v=-1$, which is contained in
$\epsilon _v=-1$, which is contained in  $\mathtt {V}_F^{\mathrm {int}}$.
$\mathtt {V}_F^{\mathrm {int}}$.(H6) We fix a
 $\prod _{v\in \mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R}}O_{E_v}$-lattice
$\prod _{v\in \mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R}}O_{E_v}$-lattice  $\Lambda ^{\mathtt {R}}$ in
$\Lambda ^{\mathtt {R}}$ in  $V\otimes _{\mathbb {A}_F}\mathbb {A}_F^{\infty ,\mathtt {R}}$ such that for every
$V\otimes _{\mathbb {A}_F}\mathbb {A}_F^{\infty ,\mathtt {R}}$ such that for every  $v\in \mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R}$,
$v\in \mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R}$,  $\Lambda ^{\mathtt {R}}_v$ is a subgroup of
$\Lambda ^{\mathtt {R}}_v$ is a subgroup of  $(\Lambda ^{\mathtt {R}}_v)^\vee $ of index
$(\Lambda ^{\mathtt {R}}_v)^\vee $ of index  $q_v^{1-\epsilon _v}$, where is the
$q_v^{1-\epsilon _v}$, where is the $$ \begin{align*} (\Lambda^{\mathtt{R}}_v)^\vee := \{x\in V_v\mathbin{|}\psi_{E,v}((x,y)_V)=1\text{ for every }y\in\Lambda^{\mathtt{R}}_v\} \end{align*} $$
$$ \begin{align*} (\Lambda^{\mathtt{R}}_v)^\vee := \{x\in V_v\mathbin{|}\psi_{E,v}((x,y)_V)=1\text{ for every }y\in\Lambda^{\mathtt{R}}_v\} \end{align*} $$ $\psi _{E,v}$-dual lattice of
$\psi _{E,v}$-dual lattice of  $\Lambda ^{\mathtt {R}}_v$.
$\Lambda ^{\mathtt {R}}_v$.(H7) Put
 $H := \mathrm {U}(V)$, which is a reductive group over
$H := \mathrm {U}(V)$, which is a reductive group over  $\mathbb {A}_F$.
$\mathbb {A}_F$.(H8) Denote by
 $L^{\mathtt {R}}\subseteq H(\mathbb {A}_F^{\infty ,\mathtt {R}})$ the stabiliser of
$L^{\mathtt {R}}\subseteq H(\mathbb {A}_F^{\infty ,\mathtt {R}})$ the stabiliser of  $\Lambda ^{\mathtt {R}}$, which is a special maximal subgroup. We have the (abstract) Hecke algebra away from
$\Lambda ^{\mathtt {R}}$, which is a special maximal subgroup. We have the (abstract) Hecke algebra away from  $\mathtt {R}$ which is a ring with the unit
$\mathtt {R}$ which is a ring with the unit $$ \begin{align*} \mathbb{T}^{\mathtt{R}} := \mathbb{Z}[L^{\mathtt{R}}\backslash H(\mathbb{A}_F^{\infty,\mathtt{R}})/L^{\mathtt{R}}], \end{align*} $$
$$ \begin{align*} \mathbb{T}^{\mathtt{R}} := \mathbb{Z}[L^{\mathtt{R}}\backslash H(\mathbb{A}_F^{\infty,\mathtt{R}})/L^{\mathtt{R}}], \end{align*} $$ and denote by
and denote by  $\mathbb {S}^{\mathtt {R}}$ the subring of
$\mathbb {S}^{\mathtt {R}}$ the subring of
 $\mathbb {T}^{\mathtt {R}}$.
$\mathbb {T}^{\mathtt {R}}$.(H9) Suppose that V is incoherent, namely,
 $\prod _{v\in \mathtt {V}_F}\epsilon _v=-1$. For every
$\prod _{v\in \mathtt {V}_F}\epsilon _v=-1$. For every  $u\in \mathtt {V}_E\setminus \mathtt {V}_E^{\mathrm {spl}}$, we fix a u-nearby space
$u\in \mathtt {V}_E\setminus \mathtt {V}_E^{\mathrm {spl}}$, we fix a u-nearby space  of V, which is a hermitian space over E and an isomorphism
of V, which is a hermitian space over E and an isomorphism  . More precisely,
. More precisely,• if
 $u\in \mathtt {V}_E^{(\infty )}$, then
$u\in \mathtt {V}_E^{(\infty )}$, then  is the hermitian space over E, unique up to isomorphism, that has signature
is the hermitian space over E, unique up to isomorphism, that has signature  $(n-1,1)$ at u and satisfies
$(n-1,1)$ at u and satisfies  ;
;• if
 $u\in \mathtt {V}_E^{\mathrm {fin}}\setminus \mathtt {V}_E^{\mathrm {spl}}$, then
$u\in \mathtt {V}_E^{\mathrm {fin}}\setminus \mathtt {V}_E^{\mathrm {spl}}$, then  is the hermitian space over E, unique up to isomorphism, that satisfies
is the hermitian space over E, unique up to isomorphism, that satisfies  .
.
Put
 , which is a reductive group over F. Then
, which is a reductive group over F. Then  and
and  $H(\mathbb {A}_F^{\underline {u}})$ are identified.
$H(\mathbb {A}_F^{\underline {u}})$ are identified.
Notation 4.3. Let ![]() $m\geqslant 0$ be an integer. We equip
$m\geqslant 0$ be an integer. We equip ![]() $W_m=E^{2m}$ and
$W_m=E^{2m}$ and ![]() $\bar {W}_m=E^{2m}$ the skew-hermitian forms given by the matrices
$\bar {W}_m=E^{2m}$ the skew-hermitian forms given by the matrices ![]() $\mathtt {w}_m$ and
$\mathtt {w}_m$ and ![]() $-\mathtt {w}_m$, respectively.
$-\mathtt {w}_m$, respectively.
(G1) Let
 $G_m$ be the unitary group of both
$G_m$ be the unitary group of both  $W_m$ and
$W_m$ and  $\bar {W}_m$. We write elements of
$\bar {W}_m$. We write elements of  $W_m$ and
$W_m$ and  $\bar {W}_m$ in row form, on which
$\bar {W}_m$ in row form, on which  $G_m$ acts from the right.
$G_m$ acts from the right.(G2) We denote by
 $\{e_1,\dots ,e_{2m}\}$ and
$\{e_1,\dots ,e_{2m}\}$ and  $\{\bar {e}_1,\dots ,\bar {e}_{2m}\}$ the natural bases of
$\{\bar {e}_1,\dots ,\bar {e}_{2m}\}$ the natural bases of  $W_m$ and
$W_m$ and  $\bar {W}_m$, respectively.
$\bar {W}_m$, respectively.(G3) Let
 $P_m\subseteq G_m$ be the parabolic subgroup stabilising the subspace generated by
$P_m\subseteq G_m$ be the parabolic subgroup stabilising the subspace generated by  $\{e_{m+1},\dots ,e_{2m}\}$ and
$\{e_{m+1},\dots ,e_{2m}\}$ and  $N_m\subseteq P_m$ its unipotent radical.
$N_m\subseteq P_m$ its unipotent radical.(G4) We have
• a homomorphism
 $m\colon \operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_m\to P_m$ sending a to which identifies
$m\colon \operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_m\to P_m$ sending a to which identifies
 $\operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_m$ as a Levi factor of
$\operatorname {\mathrm {Res}}_{E/F}\operatorname {\mathrm {GL}}_m$ as a Levi factor of  $P_m$;
$P_m$;• a homomorphism
 $n\colon \mathrm {Herm}_m\to N_m$ sending b to which is an isomorphism.
$n\colon \mathrm {Herm}_m\to N_m$ sending b to which is an isomorphism. $$ \begin{align*} n(b) := \begin{pmatrix} 1_m & b \\ & 1_m \\ \end{pmatrix} , \end{align*} $$
$$ \begin{align*} n(b) := \begin{pmatrix} 1_m & b \\ & 1_m \\ \end{pmatrix} , \end{align*} $$
(G5) We define a maximal compact subgroup
 $K_m=\prod _{v\in \mathtt {V}_F}K_{m,v}$ of
$K_m=\prod _{v\in \mathtt {V}_F}K_{m,v}$ of  $G_m(\mathbb {A}_F)$ in the following way:
$G_m(\mathbb {A}_F)$ in the following way:• for
 $v\in \mathtt {V}_F^{\mathrm {fin}}$,
$v\in \mathtt {V}_F^{\mathrm {fin}}$,  $K_{m,v}$ is the stabiliser of the lattice
$K_{m,v}$ is the stabiliser of the lattice  $O_{E_v}^{2m}$;
$O_{E_v}^{2m}$;• for
 $v\in \mathtt {V}_F^{(\infty )}$,
$v\in \mathtt {V}_F^{(\infty )}$,  $K_{m,v}$ is the subgroup of the form in which
$K_{m,v}$ is the subgroup of the form in which $$ \begin{align*} [k_1,k_2] := \frac{1}{2} \begin{pmatrix} k_1+k_2 & -ik_1+ik_2 \\ ik_1-ik_2 & k_1+k_2 \\ \end{pmatrix} , \end{align*} $$
$$ \begin{align*} [k_1,k_2] := \frac{1}{2} \begin{pmatrix} k_1+k_2 & -ik_1+ik_2 \\ ik_1-ik_2 & k_1+k_2 \\ \end{pmatrix} , \end{align*} $$ $k_i\in \operatorname {\mathrm {GL}}_m(\mathbb {C})$ satisfies
$k_i\in \operatorname {\mathrm {GL}}_m(\mathbb {C})$ satisfies  for
for  $i=1,2$. Here, we have identified
$i=1,2$. Here, we have identified  $G_m(F_v)$ as a subgroup of
$G_m(F_v)$ as a subgroup of  $\operatorname {\mathrm {GL}}_{2m}(\mathbb {C})$ via the embedding
$\operatorname {\mathrm {GL}}_{2m}(\mathbb {C})$ via the embedding  $\iota _u$ with
$\iota _u$ with  $v=\underline {u}$ in Notation 4.1(F3).
$v=\underline {u}$ in Notation 4.1(F3).
(G6) For every
 $v\in \mathtt {V}_F^{(\infty )}$, we have a character
$v\in \mathtt {V}_F^{(\infty )}$, we have a character  $\kappa _{m,v}\colon K_{m,v}\to \mathbb {C}^\times $ that sends
$\kappa _{m,v}\colon K_{m,v}\to \mathbb {C}^\times $ that sends  $[k_1,k_2]$ to
$[k_1,k_2]$ to  $\mathrm {det}\: k_1/\mathrm {det}\: k_2$.Footnote 15
$\mathrm {det}\: k_1/\mathrm {det}\: k_2$.Footnote 15(G7) For every
 $v\in \mathtt {V}_F$, we define a Haar measure
$v\in \mathtt {V}_F$, we define a Haar measure  $\mathrm {d}g_v$ on
$\mathrm {d}g_v$ on  $G_m(F_v)$ as follows:
$G_m(F_v)$ as follows:• for
 $v\in \mathtt {V}_F^{\mathrm {fin}}$,
$v\in \mathtt {V}_F^{\mathrm {fin}}$,  $\mathrm {d}g_v$ is the Haar measure under which
$\mathrm {d}g_v$ is the Haar measure under which  $K_{m,v}$ has volume
$K_{m,v}$ has volume  $1$;
$1$;• for
 $v\in \mathtt {V}_F^{(\infty )}$,
$v\in \mathtt {V}_F^{(\infty )}$,  $\mathrm {d}g_v$ is the product of the measure on
$\mathrm {d}g_v$ is the product of the measure on  $K_{m,v}$ of total volume
$K_{m,v}$ of total volume  $1$ and the standard hyperbolic measure on
$1$ and the standard hyperbolic measure on  $G_m(F_v)/K_{m,v}$ (see, for example, [Reference Eischen and LiuEL, Section 2.1]).
$G_m(F_v)/K_{m,v}$ (see, for example, [Reference Eischen and LiuEL, Section 2.1]).
Put
 $\mathrm {d}g=\prod _{v}\mathrm {d}g_v$, which is a Haar measure on
$\mathrm {d}g=\prod _{v}\mathrm {d}g_v$, which is a Haar measure on  $G_m(\mathbb {A}_F)$.
$G_m(\mathbb {A}_F)$.(G8) We denote by
 $\mathcal {A}(G_m(F)\backslash G_m(\mathbb {A}_F))$ the space of both
$\mathcal {A}(G_m(F)\backslash G_m(\mathbb {A}_F))$ the space of both  $\mathcal {Z}(\mathfrak {g}_{m,\infty })$-finite and
$\mathcal {Z}(\mathfrak {g}_{m,\infty })$-finite and  $K_{m,\infty }$-finite automorphic forms on
$K_{m,\infty }$-finite automorphic forms on  $G_m(\mathbb {A}_F)$, where
$G_m(\mathbb {A}_F)$, where  $\mathcal {Z}(\mathfrak {g}_{m,\infty })$ denotes the centre of the complexified universal enveloping algebra of the Lie algebra
$\mathcal {Z}(\mathfrak {g}_{m,\infty })$ denotes the centre of the complexified universal enveloping algebra of the Lie algebra  $\mathfrak {g}_{m,\infty }$ of
$\mathfrak {g}_{m,\infty }$ of  $G_m\otimes _FF_\infty $. We denote by
$G_m\otimes _FF_\infty $. We denote by•
 $\mathcal {A}^{[r]}(G_m(F)\backslash G_m(\mathbb {A}_F))$ the maximal subspace of
$\mathcal {A}^{[r]}(G_m(F)\backslash G_m(\mathbb {A}_F))$ the maximal subspace of  $\mathcal {A}(G_m(F)\backslash G_m(\mathbb {A}_F))$ on which for every
$\mathcal {A}(G_m(F)\backslash G_m(\mathbb {A}_F))$ on which for every  $v\in \mathtt {V}_F^{(\infty )}$,
$v\in \mathtt {V}_F^{(\infty )}$,  $K_{m,v}$ acts by the character
$K_{m,v}$ acts by the character  $\kappa _{m,v}^r$,
$\kappa _{m,v}^r$,•
 $\mathcal {A}^{[r]\mathtt {R}}(G_m(F)\backslash G_m(\mathbb {A}_F))$ the maximal subspace of
$\mathcal {A}^{[r]\mathtt {R}}(G_m(F)\backslash G_m(\mathbb {A}_F))$ the maximal subspace of  $\mathcal {A}^{[r]}(G_m(F)\backslash G_m(\mathbb {A}_F))$ on which
$\mathcal {A}^{[r]}(G_m(F)\backslash G_m(\mathbb {A}_F))$ on which– for every
 $v\in \mathtt {V}_F^{\mathrm {fin}}\setminus (\mathtt {R}\cup \mathtt {S})$,
$v\in \mathtt {V}_F^{\mathrm {fin}}\setminus (\mathtt {R}\cup \mathtt {S})$,  $K_{m,v}$ acts trivially and
$K_{m,v}$ acts trivially and– for every
 $v\in \mathtt {S}$, the standard Iwahori subgroup
$v\in \mathtt {S}$, the standard Iwahori subgroup  $I_{m,v}$ acts trivially and
$I_{m,v}$ acts trivially and  $\mathbb {C}[I_{m,v}\backslash K_{m,v}/I_{m,v}]$ acts by the character
$\mathbb {C}[I_{m,v}\backslash K_{m,v}/I_{m,v}]$ acts by the character  $\kappa _{m,v}^-$ ([Reference LiuLiu22, Definition 2.1]),
$\kappa _{m,v}^-$ ([Reference LiuLiu22, Definition 2.1]),
•
 $\mathcal {A}_{\mathrm {cusp}}(G_m(F)\backslash G_m(\mathbb {A}_F))$ the subspace of
$\mathcal {A}_{\mathrm {cusp}}(G_m(F)\backslash G_m(\mathbb {A}_F))$ the subspace of  $\mathcal {A}(G_m(F)\backslash G_m(\mathbb {A}_F))$ of cusp forms and by
$\mathcal {A}(G_m(F)\backslash G_m(\mathbb {A}_F))$ of cusp forms and by  $\langle \,,\,\rangle _{G_m}$ the hermitian form on
$\langle \,,\,\rangle _{G_m}$ the hermitian form on  $\mathcal {A}_{\mathrm {cusp}}(G_m(F)\backslash G_m(\mathbb {A}_F))$ given by the Petersson inner product with respect to the Haar measure
$\mathcal {A}_{\mathrm {cusp}}(G_m(F)\backslash G_m(\mathbb {A}_F))$ given by the Petersson inner product with respect to the Haar measure  $\mathrm {d}g$.
$\mathrm {d}g$.
For a subspace
 $\mathcal {V}$ of
$\mathcal {V}$ of  $\mathcal {A}(G_m(F)\backslash G_m(\mathbb {A}_F))$, we denote by
$\mathcal {A}(G_m(F)\backslash G_m(\mathbb {A}_F))$, we denote by•
 $\mathcal {V}^{[r]}$ the intersection of
$\mathcal {V}^{[r]}$ the intersection of  $\mathcal {V}$ and
$\mathcal {V}$ and  $\mathcal {A}^{[r]}(G_m(F)\backslash G_m(\mathbb {A}_F))$,
$\mathcal {A}^{[r]}(G_m(F)\backslash G_m(\mathbb {A}_F))$,•
 $\mathcal {V}^{[r]\mathtt {R}}$ the intersection of
$\mathcal {V}^{[r]\mathtt {R}}$ the intersection of  $\mathcal {V}$ and
$\mathcal {V}$ and  $\mathcal {A}^{[r]\mathtt {R}}(G_m(F)\backslash G_m(\mathbb {A}_F))$,
$\mathcal {A}^{[r]\mathtt {R}}(G_m(F)\backslash G_m(\mathbb {A}_F))$,•
 $\mathcal {V}^{\mathtt {c}}$ the subspace
$\mathcal {V}^{\mathtt {c}}$ the subspace  $\{\varphi ^{\mathtt {c}}\mathbin {|}\varphi \in \mathcal {V}\}$.
$\{\varphi ^{\mathtt {c}}\mathbin {|}\varphi \in \mathcal {V}\}$.
Assumption 4.4. In what follows, we will consider an irreducible automorphic subrepresentation ![]() $(\pi ,\mathcal {V}_\pi )$ of
$(\pi ,\mathcal {V}_\pi )$ of ![]() $\mathcal {A}_{\mathrm {cusp}}(G_r(F)\backslash G_r(\mathbb {A}_F))$ satisfying that
$\mathcal {A}_{\mathrm {cusp}}(G_r(F)\backslash G_r(\mathbb {A}_F))$ satisfying that
(1) for every
 $v\in \mathtt {V}_F^{(\infty )}$,
$v\in \mathtt {V}_F^{(\infty )}$,  $\pi _v$ is the (unique up to isomorphism) discrete series representation whose restriction to
$\pi _v$ is the (unique up to isomorphism) discrete series representation whose restriction to  $K_{r,v}$ contains the character
$K_{r,v}$ contains the character  $\kappa _{r,v}^r$;
$\kappa _{r,v}^r$;(2) for every
 $v\in \mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R}$,
$v\in \mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R}$,  $\pi _v$ is unramified (respectively almost unramified) with respect to
$\pi _v$ is unramified (respectively almost unramified) with respect to  $K_{r,v}$ if
$K_{r,v}$ if  $\epsilon _v=1$ (respectively
$\epsilon _v=1$ (respectively  $\epsilon _v=-1$);
$\epsilon _v=-1$);(3) for every
 $v\in \mathtt {V}_F^{\mathrm {fin}}$,
$v\in \mathtt {V}_F^{\mathrm {fin}}$,  $\pi _v$ is tempered.
$\pi _v$ is tempered.
We realise the contragredient representation ![]() $\pi ^\vee $ on
$\pi ^\vee $ on ![]() $\mathcal {V}_\pi ^{\mathtt {c}}$ via the Petersson inner product
$\mathcal {V}_\pi ^{\mathtt {c}}$ via the Petersson inner product ![]() $\langle \,,\,\rangle _{G_r}$ (Notation 4.3(G8)). By (1) and (2), we have
$\langle \,,\,\rangle _{G_r}$ (Notation 4.3(G8)). By (1) and (2), we have  $\mathcal {V}_\pi ^{[r]\mathtt {R}}\neq \{0\}$, where
$\mathcal {V}_\pi ^{[r]\mathtt {R}}\neq \{0\}$, where  $\mathcal {V}_\pi ^{[r]\mathtt {R}}$ is defined in Notation 4.3(G8).
$\mathcal {V}_\pi ^{[r]\mathtt {R}}$ is defined in Notation 4.3(G8).
Remark 4.5. By Proposition 4.8(2), we know that when  $\mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$, V coincides with the hermitian space over
$\mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$, V coincides with the hermitian space over ![]() $\mathbb {A}_E$ of rank n determined by
$\mathbb {A}_E$ of rank n determined by ![]() $\pi $ via local theta dichotomy.
$\pi $ via local theta dichotomy.
Definition 4.6. We define the L-function for ![]() $\pi $ as the Euler product
$\pi $ as the Euler product ![]() $L(s,\pi ) := \prod _{v}L(s,\pi _v)$ over all places of F, in which
$L(s,\pi ) := \prod _{v}L(s,\pi _v)$ over all places of F, in which
(1) for
 $v\in \mathtt {V}_F^{\mathrm {fin}}$,
$v\in \mathtt {V}_F^{\mathrm {fin}}$,  $L(s,\pi _v)$ is the doubling L-function defined in [Reference YamanaYam14, Theorem 5.2];
$L(s,\pi _v)$ is the doubling L-function defined in [Reference YamanaYam14, Theorem 5.2];(2) for
 $v\in \mathtt {V}_F^{(\infty )}$,
$v\in \mathtt {V}_F^{(\infty )}$,  $L(s,\pi _v)$ is the L-function of the standard base change
$L(s,\pi _v)$ is the L-function of the standard base change  $\operatorname {\mathrm {BC}}(\pi _v)$ of
$\operatorname {\mathrm {BC}}(\pi _v)$ of  $\pi _v$. By Assumption 4.4(1),
$\pi _v$. By Assumption 4.4(1),  $\operatorname {\mathrm {BC}}(\pi _v)$ is the principal series representation of
$\operatorname {\mathrm {BC}}(\pi _v)$ is the principal series representation of  $\operatorname {\mathrm {GL}}_n(\mathbb {C})$ that is the normalised induction of
$\operatorname {\mathrm {GL}}_n(\mathbb {C})$ that is the normalised induction of  $\arg ^{n-1}\boxtimes \arg ^{n-3}\boxtimes \cdots \boxtimes \arg ^{3-n}\boxtimes \arg ^{1-n}$, where
$\arg ^{n-1}\boxtimes \arg ^{n-3}\boxtimes \cdots \boxtimes \arg ^{3-n}\boxtimes \arg ^{1-n}$, where  $\arg \colon \mathbb {C}^\times \to \mathbb {C}^\times $ is the argument character.
$\arg \colon \mathbb {C}^\times \to \mathbb {C}^\times $ is the argument character.
Remark 4.7. Let v be a place of F.
(1) For
 $v\in \mathtt {V}_F^{(\infty )}$, the doubling L-function is only well-defined up to an entire function without zeros. However, one can show that
$v\in \mathtt {V}_F^{(\infty )}$, the doubling L-function is only well-defined up to an entire function without zeros. However, one can show that  $L(s,\pi _v)$ satisfies the requirement for the doubling L-function in [Reference YamanaYam14, Theorem 5.2].
$L(s,\pi _v)$ satisfies the requirement for the doubling L-function in [Reference YamanaYam14, Theorem 5.2].(2) For
 $v\in \mathtt {V}_F^{\mathrm {spl}}$, the standard base change
$v\in \mathtt {V}_F^{\mathrm {spl}}$, the standard base change  $\operatorname {\mathrm {BC}}(\pi _v)$ is well-defined and we have
$\operatorname {\mathrm {BC}}(\pi _v)$ is well-defined and we have  $L(s,\pi _v)=L(s,\operatorname {\mathrm {BC}}(\pi _v))$ by [Reference YamanaYam14, Theorem 7.2].
$L(s,\pi _v)=L(s,\operatorname {\mathrm {BC}}(\pi _v))$ by [Reference YamanaYam14, Theorem 7.2].(3) For
 $v\in \mathtt {V}_F^{\mathrm {int}}\setminus \mathtt {R}$, the standard base change
$v\in \mathtt {V}_F^{\mathrm {int}}\setminus \mathtt {R}$, the standard base change  $\operatorname {\mathrm {BC}}(\pi _v)$ is well-defined and we have
$\operatorname {\mathrm {BC}}(\pi _v)$ is well-defined and we have  $L(s,\pi _v)=L(s,\operatorname {\mathrm {BC}}(\pi _v))$ by [Reference LiuLiu22, Remark 1.4].
$L(s,\pi _v)=L(s,\operatorname {\mathrm {BC}}(\pi _v))$ by [Reference LiuLiu22, Remark 1.4].(4) For
 $v\in \mathtt {V}_F^{\mathrm {ram}}\setminus \mathtt {R}$, the standard base change
$v\in \mathtt {V}_F^{\mathrm {ram}}\setminus \mathtt {R}$, the standard base change  $\operatorname {\mathrm {BC}}(\pi _v)$ is well-defined and we have
$\operatorname {\mathrm {BC}}(\pi _v)$ is well-defined and we have  $L(s,\pi _v)=L(s,\operatorname {\mathrm {BC}}(\pi _v))$ by Remark 3.8.
$L(s,\pi _v)=L(s,\operatorname {\mathrm {BC}}(\pi _v))$ by Remark 3.8.
In particular, when  $\mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$, we have
$\mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$, we have ![]() $L(s,\pi )=\prod _{v}L(s,\operatorname {\mathrm {BC}}(\pi _v))$.
$L(s,\pi )=\prod _{v}L(s,\operatorname {\mathrm {BC}}(\pi _v))$.
Recall that we have the normalised doubling integral
 $$ \begin{align*} \mathfrak{Z}^\natural_{\pi_v,V_v}\colon\pi_v^\vee\otimes\pi_v\otimes\mathscr{S}(V_v^{2r})\to\mathbb{C} \end{align*} $$
$$ \begin{align*} \mathfrak{Z}^\natural_{\pi_v,V_v}\colon\pi_v^\vee\otimes\pi_v\otimes\mathscr{S}(V_v^{2r})\to\mathbb{C} \end{align*} $$from [Reference Li and LiuLL21, Section 3].
Proposition 4.8. Let ![]() $(\pi ,\mathcal {V}_\pi )$ be as in Assumption 4.4.
$(\pi ,\mathcal {V}_\pi )$ be as in Assumption 4.4.
(1) For every
 $v\in \mathtt {V}_F^{\mathrm {fin}}$, we have
$v\in \mathtt {V}_F^{\mathrm {fin}}$, we have  $$ \begin{align*} \dim_{\mathbb{C}}\operatorname{\mathrm{Hom}}_{G_r(F_v)\times G_r(F_v)}(\mathrm{I}^\Box_{r,v}(0),\pi_v\boxtimes\pi_v^\vee)=1. \end{align*} $$
$$ \begin{align*} \dim_{\mathbb{C}}\operatorname{\mathrm{Hom}}_{G_r(F_v)\times G_r(F_v)}(\mathrm{I}^\Box_{r,v}(0),\pi_v\boxtimes\pi_v^\vee)=1. \end{align*} $$(2) For every
 $v\in (\mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R})\cup \mathtt {V}_F^{\mathrm {spl}}$,
$v\in (\mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R})\cup \mathtt {V}_F^{\mathrm {spl}}$,  $V_v$ is the unique hermitian space over
$V_v$ is the unique hermitian space over  $E_v$ of rank
$E_v$ of rank  $2r$, up to isomorphism, such that
$2r$, up to isomorphism, such that  $\mathfrak {Z}^\natural _{\pi _v,V_v}\neq 0$.
$\mathfrak {Z}^\natural _{\pi _v,V_v}\neq 0$.(3) For every
 $v\in \mathtt {V}_F^{\mathrm {fin}}$,
$v\in \mathtt {V}_F^{\mathrm {fin}}$,  $\operatorname {\mathrm {Hom}}_{G_r(F_v)}(\mathscr {S}(V_v^r),\pi _v)$ is irreducible as a representation of
$\operatorname {\mathrm {Hom}}_{G_r(F_v)}(\mathscr {S}(V_v^r),\pi _v)$ is irreducible as a representation of  $H(F_v)$ and is nonzero if
$H(F_v)$ and is nonzero if  $v\in (\mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R})\cup \mathtt {V}_F^{\mathrm {spl}}$.
$v\in (\mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R})\cup \mathtt {V}_F^{\mathrm {spl}}$.
Proof. This is same as [Reference Li and LiuLL21, Proposition 3.6] except that in (2) we have to take care of the case where ![]() $v\in \mathtt {V}_F^{\mathrm {ram}}$, which is a consequence of Proposition 3.9.
$v\in \mathtt {V}_F^{\mathrm {ram}}$, which is a consequence of Proposition 3.9.
Proposition 4.9. Let ![]() $(\pi ,\mathcal {V}_\pi )$ be as in Assumption 4.4 such that
$(\pi ,\mathcal {V}_\pi )$ be as in Assumption 4.4 such that  $L(\tfrac {1}{2},\pi )=0$. Take
$L(\tfrac {1}{2},\pi )=0$. Take
•
 $\varphi _1=\otimes _v\varphi _{1v}\in \mathcal {V}_\pi ^{[r]\mathtt {R}}$ and
$\varphi _1=\otimes _v\varphi _{1v}\in \mathcal {V}_\pi ^{[r]\mathtt {R}}$ and  $\varphi _2=\otimes _v\varphi _{2v}\in \mathcal {V}_\pi ^{[r]\mathtt {R}}$ such that
$\varphi _2=\otimes _v\varphi _{2v}\in \mathcal {V}_\pi ^{[r]\mathtt {R}}$ such that  $\langle \varphi _{1v}^{\mathtt {c}},\varphi _{2v}\rangle _{\pi _v}=1$ for
$\langle \varphi _{1v}^{\mathtt {c}},\varphi _{2v}\rangle _{\pi _v}=1$ for  $v\in \mathtt {V}_F\setminus \mathtt {R}$,Footnote 16 and
$v\in \mathtt {V}_F\setminus \mathtt {R}$,Footnote 16 and•
 $\Phi =\otimes _v\Phi _v\in \mathscr {S}(V^{2r})$ such that
$\Phi =\otimes _v\Phi _v\in \mathscr {S}(V^{2r})$ such that  $\Phi _v$ is the Gaussian function (Notation 4.2(H3)) for
$\Phi _v$ is the Gaussian function (Notation 4.2(H3)) for  $v\in \mathtt {V}_F^{(\infty )}$ and
$v\in \mathtt {V}_F^{(\infty )}$ and  for
for  $v\in \mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R}$.
$v\in \mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R}$.
Then we have
 $$ \begin{align*} &\quad\int_{G_r(F)\backslash G_r(\mathbb{A}_F)}\int_{G_r(F)\backslash G_r(\mathbb{A}_F)}\varphi_2(g_2)\varphi_1^{\mathtt{c}}(g_1)E'(0,(g_1,g_2),\Phi)\,\mathrm{d} g_1\,\mathrm{d} g_2 \\ &=\frac{L'(\tfrac{1}{2},\pi)}{b_{2r}(0)}\cdot C_r^{[F:\mathbb{Q}]} \cdot\prod_{v\in\mathtt{V}_F^{\mathrm{fin}}}\mathfrak{Z}^\natural_{\pi_v,V_v}(\varphi^{\mathtt{c}}_{1v},\varphi_{2v},\Phi_v) \\ &=\frac{L'(\tfrac{1}{2},\pi)}{b_{2r}(0)}\cdot C_r^{[F:\mathbb{Q}]} \cdot\prod_{v\in\mathtt{S}}\frac{(-1)^rq_v^{r-1}(q_v+1)}{(q_v^{2r-1}+1)(q_v^{2r}-1)} \cdot\prod_{v\in\mathtt{R}}\mathfrak{Z}^\natural_{\pi_v,V_v}(\varphi^{\mathtt{c}}_{1v},\varphi_{2v},\Phi_v), \end{align*} $$
$$ \begin{align*} &\quad\int_{G_r(F)\backslash G_r(\mathbb{A}_F)}\int_{G_r(F)\backslash G_r(\mathbb{A}_F)}\varphi_2(g_2)\varphi_1^{\mathtt{c}}(g_1)E'(0,(g_1,g_2),\Phi)\,\mathrm{d} g_1\,\mathrm{d} g_2 \\ &=\frac{L'(\tfrac{1}{2},\pi)}{b_{2r}(0)}\cdot C_r^{[F:\mathbb{Q}]} \cdot\prod_{v\in\mathtt{V}_F^{\mathrm{fin}}}\mathfrak{Z}^\natural_{\pi_v,V_v}(\varphi^{\mathtt{c}}_{1v},\varphi_{2v},\Phi_v) \\ &=\frac{L'(\tfrac{1}{2},\pi)}{b_{2r}(0)}\cdot C_r^{[F:\mathbb{Q}]} \cdot\prod_{v\in\mathtt{S}}\frac{(-1)^rq_v^{r-1}(q_v+1)}{(q_v^{2r-1}+1)(q_v^{2r}-1)} \cdot\prod_{v\in\mathtt{R}}\mathfrak{Z}^\natural_{\pi_v,V_v}(\varphi^{\mathtt{c}}_{1v},\varphi_{2v},\Phi_v), \end{align*} $$where
 $$ \begin{align*} C_r := (-1)^r2^{-2r}\pi^{r^2}\frac{\Gamma(1)\cdots\Gamma(r)}{\Gamma(r+1)\cdots\Gamma(2r)}, \end{align*} $$
$$ \begin{align*} C_r := (-1)^r2^{-2r}\pi^{r^2}\frac{\Gamma(1)\cdots\Gamma(r)}{\Gamma(r+1)\cdots\Gamma(2r)}, \end{align*} $$and the measure on ![]() $G_r(\mathbb {A}_F)$ is the one defined in Notation 4.3(G7).
$G_r(\mathbb {A}_F)$ is the one defined in Notation 4.3(G7).
Proof. The proof is same as [Reference Li and LiuLL21, Proposition 3.7], with the additional input
 $$ \begin{align*} \mathfrak{Z}^\natural_{\pi_v,V_v}(\varphi^{\mathtt{c}}_{1v},\varphi_{2v},\Phi_v)=1 \end{align*} $$
$$ \begin{align*} \mathfrak{Z}^\natural_{\pi_v,V_v}(\varphi^{\mathtt{c}}_{1v},\varphi_{2v},\Phi_v)=1 \end{align*} $$for ![]() $v\in \mathtt {V}_F^{\mathrm {ram}}\setminus \mathtt {R}$ by Proposition 3.6.
$v\in \mathtt {V}_F^{\mathrm {ram}}\setminus \mathtt {R}$ by Proposition 3.6.
Suppose that V is incoherent. By [Reference LiuLiu11b, Section 2B], we have
(1) Take
 $u\in \mathtt {V}_E\setminus \mathtt {V}_E^{\mathrm {spl}}$ and
$u\in \mathtt {V}_E\setminus \mathtt {V}_E^{\mathrm {spl}}$ and  , where we recall from Notation 4.2(H9) that
, where we recall from Notation 4.2(H9) that  is the u-nearby hermitian space, such that
is the u-nearby hermitian space, such that  (Notation 4.2(H3)) for v in a nonempty subset
(Notation 4.2(H3)) for v in a nonempty subset  $\mathtt {R}'\subseteq \mathtt {R}$. Then for every
$\mathtt {R}'\subseteq \mathtt {R}$. Then for every  $g\in P_r^\Box (F_{\mathtt {R}'})G_r^\Box (\mathbb {A}_F^{\mathtt {R}'})$, we have
$g\in P_r^\Box (F_{\mathtt {R}'})G_r^\Box (\mathbb {A}_F^{\mathtt {R}'})$, we have 
(2) Take
 $\Phi =\otimes _v\Phi _v\in \mathscr {S}(V^{2r})$ such that
$\Phi =\otimes _v\Phi _v\in \mathscr {S}(V^{2r})$ such that  $\operatorname {\mathrm {supp}}(\Phi _v)\subseteq (V^{2r}_v)_{\mathrm {reg}}$ for v in a subset
$\operatorname {\mathrm {supp}}(\Phi _v)\subseteq (V^{2r}_v)_{\mathrm {reg}}$ for v in a subset  $\mathtt {R}'\subseteq \mathtt {R}$ of cardinality at least
$\mathtt {R}'\subseteq \mathtt {R}$ of cardinality at least  $2$. Then for every
$2$. Then for every  $g\in P_r^\Box (F_{\mathtt {R}'})G_r^\Box (\mathbb {A}_F^{\mathtt {R}'})$, we have where
$g\in P_r^\Box (F_{\mathtt {R}'})G_r^\Box (\mathbb {A}_F^{\mathtt {R}'})$, we have where $$ \begin{align*} E'(0,g,\Phi)=\sum_{w\in\mathtt{V}_F\setminus\mathtt{V}_F^{\mathrm{spl}}}\mathfrak{E}(g,\Phi)_w, \end{align*} $$Here,
$$ \begin{align*} E'(0,g,\Phi)=\sum_{w\in\mathtt{V}_F\setminus\mathtt{V}_F^{\mathrm{spl}}}\mathfrak{E}(g,\Phi)_w, \end{align*} $$Here, $$ \begin{align*} \mathfrak{E}(g,\Phi)_w := \sum_{\substack{T^\Box\in\mathrm{Herm}_{2r}^\circ(F)\\ \operatorname{\mathrm{Diff}}(T^\Box,V)=\{w\}}}W^{\prime}_{T^\Box}(0,g_w,\Phi_w) \prod_{v\in\mathtt{V}_F\setminus\{w\}} W_{T^\Box}(0,g_v,\Phi_v). \end{align*} $$
$$ \begin{align*} \mathfrak{E}(g,\Phi)_w := \sum_{\substack{T^\Box\in\mathrm{Herm}_{2r}^\circ(F)\\ \operatorname{\mathrm{Diff}}(T^\Box,V)=\{w\}}}W^{\prime}_{T^\Box}(0,g_w,\Phi_w) \prod_{v\in\mathtt{V}_F\setminus\{w\}} W_{T^\Box}(0,g_v,\Phi_v). \end{align*} $$ $\operatorname {\mathrm {Diff}}(T^\Box ,V)$ is defined in Notation 4.2(H4).
$\operatorname {\mathrm {Diff}}(T^\Box ,V)$ is defined in Notation 4.2(H4).
Definition 4.10. Suppose that V is incoherent. Take an element  $u\in \mathtt {V}_E\setminus \mathtt {V}_E^{\mathrm {spl}}$ and a pair
$u\in \mathtt {V}_E\setminus \mathtt {V}_E^{\mathrm {spl}}$ and a pair ![]() $(T_1,T_2)$ of elements in
$(T_1,T_2)$ of elements in ![]() $\mathrm {Herm}_r(F)$.
$\mathrm {Herm}_r(F)$.
(1) For
 , we put
, we put 
(2) For
 $\Phi =\otimes _v\Phi _v\in \mathscr {S}(V^{2r})$, we put
$\Phi =\otimes _v\Phi _v\in \mathscr {S}(V^{2r})$, we put  $$ \begin{align*} \mathfrak{E}_{T_1,T_2}(g,\Phi)_u := \sum_{\substack{T^\Box\in\mathrm{Herm}_{2r}^\circ(F)\\ \operatorname{\mathrm{Diff}}(T^\Box,V)=\{\underline{u}\}\\ \partial_{r,r}T^\Box=(T_1,T_2)}} W^{\prime}_{T^\Box}(0,g_{\underline{u}},\Phi_{\underline{u}})\prod_{v\in\mathtt{V}_F\setminus\{\underline{u}\}}W_{T^\Box}(0,g_v,\Phi_v). \end{align*} $$
$$ \begin{align*} \mathfrak{E}_{T_1,T_2}(g,\Phi)_u := \sum_{\substack{T^\Box\in\mathrm{Herm}_{2r}^\circ(F)\\ \operatorname{\mathrm{Diff}}(T^\Box,V)=\{\underline{u}\}\\ \partial_{r,r}T^\Box=(T_1,T_2)}} W^{\prime}_{T^\Box}(0,g_{\underline{u}},\Phi_{\underline{u}})\prod_{v\in\mathtt{V}_F\setminus\{\underline{u}\}}W_{T^\Box}(0,g_v,\Phi_v). \end{align*} $$
Here, ![]() $\partial _{r,r}\colon \mathrm {Herm}_{2r}\to \mathrm {Herm}_r\times \mathrm {Herm}_r$ is defined in Notation 4.1(F2).
$\partial _{r,r}\colon \mathrm {Herm}_{2r}\to \mathrm {Herm}_r\times \mathrm {Herm}_r$ is defined in Notation 4.1(F2).
4.2 Recollection on arithmetic theta lifting
From this moment, we will assume ![]() $F\neq \mathbb {Q}$.
$F\neq \mathbb {Q}$.
Recall that we have fixed a ![]() $\mathbf {u}$-nearby space
$\mathbf {u}$-nearby space
and an isomorphism

from Notation 4.2(H9). For every open compact subgroup ![]() $L\subseteq H(\mathbb {A}_F^\infty )$, we have the Shimura variety
$L\subseteq H(\mathbb {A}_F^\infty )$, we have the Shimura variety ![]() $X_L$ associated to
$X_L$ associated to
of the level L, which is a smooth quasi-projective scheme over E (which is regarded as a subfield of ![]() $\mathbb {C}$ via
$\mathbb {C}$ via ![]() $\boldsymbol {\iota }$) of dimension
$\boldsymbol {\iota }$) of dimension ![]() $n-1$. We remind the reader of its complex uniformisation
$n-1$. We remind the reader of its complex uniformisation
where ![]() $\mathfrak {D}$ denotes the complex manifold of negative lines in
$\mathfrak {D}$ denotes the complex manifold of negative lines in
and the Deligne homomorphism is the one adopted in [Reference Liu, Tian, Xiao, Zhang and ZhuLTXZZ, Section 3.2]. In what follows, for a place ![]() $u\in \mathtt {V}_E$, we put
$u\in \mathtt {V}_E$, we put ![]() $X_{L,u} := X_L\otimes _EE_u$ as a scheme over
$X_{L,u} := X_L\otimes _EE_u$ as a scheme over ![]() $E_u$.
$E_u$.
For every ![]() $\phi ^\infty \in \mathscr {S}(V^m\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^L$ and
$\phi ^\infty \in \mathscr {S}(V^m\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^L$ and ![]() $T\in \mathrm {Herm}_m(F)$, we put
$T\in \mathrm {Herm}_m(F)$, we put
 $$ \begin{align*} Z_T(\phi^\infty)_L := \sum_{\substack{x\in L\backslash V^m\otimes_{\mathbb{A}_F}\mathbb{A}_F^\infty\\ T(x)=T}}\phi^\infty(x)Z(x)_L, \end{align*} $$
$$ \begin{align*} Z_T(\phi^\infty)_L := \sum_{\substack{x\in L\backslash V^m\otimes_{\mathbb{A}_F}\mathbb{A}_F^\infty\\ T(x)=T}}\phi^\infty(x)Z(x)_L, \end{align*} $$where ![]() $Z(x)_L$ is Kudla’s special cycle recalled in [Reference Li and LiuLL21, Definition 4.1]. As the above summation is finite,
$Z(x)_L$ is Kudla’s special cycle recalled in [Reference Li and LiuLL21, Definition 4.1]. As the above summation is finite, ![]() $Z_T(\phi ^\infty )_L$ is a well-defined element in
$Z_T(\phi ^\infty )_L$ is a well-defined element in ![]() $\operatorname {\mathrm {CH}}^m(X_L)_{\mathbb {C}}$. For every
$\operatorname {\mathrm {CH}}^m(X_L)_{\mathbb {C}}$. For every ![]() $g\in G_m(\mathbb {A}_F)$, Kudla’s generating function is defined to be
$g\in G_m(\mathbb {A}_F)$, Kudla’s generating function is defined to be
 $$ \begin{align*} Z_{\phi^\infty}(g)_L := \sum_{T\in\mathrm{Herm}_m(F)^+} \omega_{m,\infty}(g_\infty)\phi^0_\infty(T)\cdot Z_T(\omega_m^\infty(g^\infty)\phi^\infty)_L \end{align*} $$
$$ \begin{align*} Z_{\phi^\infty}(g)_L := \sum_{T\in\mathrm{Herm}_m(F)^+} \omega_{m,\infty}(g_\infty)\phi^0_\infty(T)\cdot Z_T(\omega_m^\infty(g^\infty)\phi^\infty)_L \end{align*} $$as a formal sum valued in ![]() $\operatorname {\mathrm {CH}}^m(X_L)_{\mathbb {C}}$, where
$\operatorname {\mathrm {CH}}^m(X_L)_{\mathbb {C}}$, where
 $$ \begin{align*} \omega_{m,\infty}(g_\infty)\phi^0_\infty(T) := \prod_{v\in\mathtt{V}_F^{(\infty)}}\omega_{m,v}(g_v)\phi^0_v(T). \end{align*} $$
$$ \begin{align*} \omega_{m,\infty}(g_\infty)\phi^0_\infty(T) := \prod_{v\in\mathtt{V}_F^{(\infty)}}\omega_{m,v}(g_v)\phi^0_v(T). \end{align*} $$Here, we note that for  $v\in \mathtt {V}_F^{(\infty )}$, the function
$v\in \mathtt {V}_F^{(\infty )}$, the function ![]() $\omega _{m,v}(g_v)\phi ^0_v$ factors through the moment map
$\omega _{m,v}(g_v)\phi ^0_v$ factors through the moment map ![]() $V_v^m\to \mathrm {Herm}_m(F_v)$ (see Notation 4.2(H1)).
$V_v^m\to \mathrm {Herm}_m(F_v)$ (see Notation 4.2(H1)).
Hypothesis 4.11 Modularity of generating functions of codimension m, [Reference Li and LiuLL21, Hypothesis 4.5]
For every open compact subgroup ![]() $L\subseteq H(\mathbb {A}_F^\infty )$, every
$L\subseteq H(\mathbb {A}_F^\infty )$, every ![]() $\phi ^\infty \in \mathscr {S}(V^m\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^L$ and every complex linear map
$\phi ^\infty \in \mathscr {S}(V^m\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^L$ and every complex linear map ![]() $l\colon \operatorname {\mathrm {CH}}^m(X_L)_{\mathbb {C}}\to \mathbb {C}$, the assignment
$l\colon \operatorname {\mathrm {CH}}^m(X_L)_{\mathbb {C}}\to \mathbb {C}$, the assignment
is absolutely convergent and gives an element in ![]() $\mathcal {A}^{[r]}(G_m(F)\backslash G_m(\mathbb {A}_F))$. In other words, the function
$\mathcal {A}^{[r]}(G_m(F)\backslash G_m(\mathbb {A}_F))$. In other words, the function ![]() $Z_{\phi ^\infty }(-)_L$ defines an element in
$Z_{\phi ^\infty }(-)_L$ defines an element in  $\operatorname {\mathrm {Hom}}_{\mathbb {C}}(\operatorname {\mathrm {CH}}^m(X_L)_{\mathbb {C}}^\vee ,\mathcal {A}^{[r]}(G_m(F)\backslash G_m(\mathbb {A}_F)))$.
$\operatorname {\mathrm {Hom}}_{\mathbb {C}}(\operatorname {\mathrm {CH}}^m(X_L)_{\mathbb {C}}^\vee ,\mathcal {A}^{[r]}(G_m(F)\backslash G_m(\mathbb {A}_F)))$.
Definition 4.12. Let ![]() $(\pi ,\mathcal {V}_\pi )$ be as in Assumption 4.4. Assume Hypothesis 4.11 on the modularity of generating functions of codimension r. For every
$(\pi ,\mathcal {V}_\pi )$ be as in Assumption 4.4. Assume Hypothesis 4.11 on the modularity of generating functions of codimension r. For every  $\varphi \in \mathcal {V}_\pi ^{[r]}$, every open compact subgroup
$\varphi \in \mathcal {V}_\pi ^{[r]}$, every open compact subgroup ![]() $L\subseteq H(\mathbb {A}_F^\infty )$ and every
$L\subseteq H(\mathbb {A}_F^\infty )$ and every ![]() $\phi ^\infty \in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^L$, we put
$\phi ^\infty \in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^L$, we put
 $$ \begin{align*} \Theta_{\phi^\infty}(\varphi)_L := \int_{G_r(F)\backslash G_r(\mathbb{A}_F)} \varphi^{\mathtt{c}}(g)Z_{\phi^\infty}(g)_L\,\mathrm{d} g, \end{align*} $$
$$ \begin{align*} \Theta_{\phi^\infty}(\varphi)_L := \int_{G_r(F)\backslash G_r(\mathbb{A}_F)} \varphi^{\mathtt{c}}(g)Z_{\phi^\infty}(g)_L\,\mathrm{d} g, \end{align*} $$which is an element in ![]() $\operatorname {\mathrm {CH}}^r(X_L)_{\mathbb {C}}$ by [Reference Li and LiuLL21, Proposition 4.7]. It is clear that the image of
$\operatorname {\mathrm {CH}}^r(X_L)_{\mathbb {C}}$ by [Reference Li and LiuLL21, Proposition 4.7]. It is clear that the image of ![]() $\Theta _{\phi ^\infty }(\varphi )_L$ in
$\Theta _{\phi ^\infty }(\varphi )_L$ in
 $$ \begin{align*} \operatorname{\mathrm{CH}}^r(X)_{\mathbb{C}} := \varinjlim_L\operatorname{\mathrm{CH}}^r(X_L)_{\mathbb{C}} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{CH}}^r(X)_{\mathbb{C}} := \varinjlim_L\operatorname{\mathrm{CH}}^r(X_L)_{\mathbb{C}} \end{align*} $$depends only on ![]() $\varphi $ and
$\varphi $ and ![]() $\phi ^\infty $, which we denote by
$\phi ^\infty $, which we denote by ![]() $\Theta _{\phi ^\infty }(\varphi )$. Finally, we define the arithmetic theta lifting of
$\Theta _{\phi ^\infty }(\varphi )$. Finally, we define the arithmetic theta lifting of ![]() $(\pi ,\mathcal {V}_\pi )$ to V (with respect to
$(\pi ,\mathcal {V}_\pi )$ to V (with respect to ![]() $\boldsymbol {\iota }$) to be the complex subspace
$\boldsymbol {\iota }$) to be the complex subspace ![]() $\Theta (\pi ,V)$ of
$\Theta (\pi ,V)$ of ![]() $\operatorname {\mathrm {CH}}^r(X)_{\mathbb {C}}$ spanned by
$\operatorname {\mathrm {CH}}^r(X)_{\mathbb {C}}$ spanned by ![]() $\Theta _{\phi ^\infty }(\varphi )$ for all
$\Theta _{\phi ^\infty }(\varphi )$ for all  $\varphi \in \mathcal {V}_\pi ^{[r]}$ and
$\varphi \in \mathcal {V}_\pi ^{[r]}$ and ![]() $\phi ^\infty \in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )$.
$\phi ^\infty \in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )$.
We recall Beilinson’s height pairing for our particular use from [Reference Li and LiuLL21, Section 6]. We have a map
 $$ \begin{align*} \langle\,,\,\rangle_{X_L,E}^\ell\colon \operatorname{\mathrm{CH}}^r(X_L)^{\langle\ell\rangle}_{\mathbb{C}}\times\operatorname{\mathrm{CH}}^r(X_L)^{\langle\ell\rangle}_{\mathbb{C}}\to\mathbb{C}\otimes_{\mathbb{Q}}\mathbb{Q}_\ell \end{align*} $$
$$ \begin{align*} \langle\,,\,\rangle_{X_L,E}^\ell\colon \operatorname{\mathrm{CH}}^r(X_L)^{\langle\ell\rangle}_{\mathbb{C}}\times\operatorname{\mathrm{CH}}^r(X_L)^{\langle\ell\rangle}_{\mathbb{C}}\to\mathbb{C}\otimes_{\mathbb{Q}}\mathbb{Q}_\ell \end{align*} $$that is complex linear in the first variable and conjugate symmetric. Here, ![]() $\ell $ is a rational prime such that
$\ell $ is a rational prime such that ![]() $X_{L,u}$ has smooth projective reduction for every
$X_{L,u}$ has smooth projective reduction for every  $u\in \mathtt {V}_E^{(\ell )}$. For a pair
$u\in \mathtt {V}_E^{(\ell )}$. For a pair ![]() $(c_1,c_2)$ of elements in
$(c_1,c_2)$ of elements in  $\mathrm {Z}^r(X_L)^{\langle \ell \rangle }_{\mathbb {C}}\times \mathrm {Z}^r(X_L)^{\langle \ell \rangle }_{\mathbb {C}}$ with disjoint supports, we have
$\mathrm {Z}^r(X_L)^{\langle \ell \rangle }_{\mathbb {C}}\times \mathrm {Z}^r(X_L)^{\langle \ell \rangle }_{\mathbb {C}}$ with disjoint supports, we have
 $$ \begin{align*} \langle c_1,c_2\rangle_{X_L,E}^\ell=\sum_{u\in\mathtt{V}_E^{(\infty)}}2\langle c_1,c_2\rangle_{X_{L,u},E_u}+ \sum_{u\in\mathtt{V}_E^{\mathrm{fin}}}\log q_u\cdot \langle c_1,c_2\rangle_{X_{L,u},E_u}^\ell, \end{align*} $$
$$ \begin{align*} \langle c_1,c_2\rangle_{X_L,E}^\ell=\sum_{u\in\mathtt{V}_E^{(\infty)}}2\langle c_1,c_2\rangle_{X_{L,u},E_u}+ \sum_{u\in\mathtt{V}_E^{\mathrm{fin}}}\log q_u\cdot \langle c_1,c_2\rangle_{X_{L,u},E_u}^\ell, \end{align*} $$in which
•
 $q_u$ is the residue cardinality of
$q_u$ is the residue cardinality of  $E_u$ for
$E_u$ for  $u\in \mathtt {V}_E^{\mathrm {fin}}$;
$u\in \mathtt {V}_E^{\mathrm {fin}}$;•
 $\langle c_1,c_2\rangle _{X_{L,u},E_u}^\ell \in \mathbb {C}\otimes _{\mathbb {Q}}\mathbb {Q}_\ell $ is the non-Archimedean local index recalled in [Reference Li and LiuLL21, Section B] for
$\langle c_1,c_2\rangle _{X_{L,u},E_u}^\ell \in \mathbb {C}\otimes _{\mathbb {Q}}\mathbb {Q}_\ell $ is the non-Archimedean local index recalled in [Reference Li and LiuLL21, Section B] for  $u\in \mathtt {V}_E^{\mathrm {fin}}$ (see [Reference Li and LiuLL21, Remark B.11] when u is above
$u\in \mathtt {V}_E^{\mathrm {fin}}$ (see [Reference Li and LiuLL21, Remark B.11] when u is above  $\ell $), which equals zero for all but finitely many u;
$\ell $), which equals zero for all but finitely many u;•
 $\langle c_1,c_2\rangle _{X_{L,u},E_u}\in \mathbb {C}$ is the Archimedean local index for
$\langle c_1,c_2\rangle _{X_{L,u},E_u}\in \mathbb {C}$ is the Archimedean local index for  $u\in \mathtt {V}_E^{(\infty )}$, recalled in [Reference Li and LiuLL21, Section 10].
$u\in \mathtt {V}_E^{(\infty )}$, recalled in [Reference Li and LiuLL21, Section 10].
Definition 4.13. We say that a rational prime ![]() $\ell $ is
$\ell $ is ![]() $\mathtt {R}$-good if
$\mathtt {R}$-good if ![]() $\ell $ is unramified in E and satisfies
$\ell $ is unramified in E and satisfies  $\mathtt {V}_F^{(\ell )}\subseteq \mathtt {V}_F^{\mathrm {fin}}\setminus (\mathtt {R}\cup \mathtt {S})$.
$\mathtt {V}_F^{(\ell )}\subseteq \mathtt {V}_F^{\mathrm {fin}}\setminus (\mathtt {R}\cup \mathtt {S})$.
Definition 4.14. For every open compact subgroup ![]() $L_{\mathtt {R}}$ of
$L_{\mathtt {R}}$ of ![]() $H(F_{\mathtt {R}})$ and every subfield
$H(F_{\mathtt {R}})$ and every subfield ![]() $\mathbb {L}$ of
$\mathbb {L}$ of ![]() $\mathbb {C}$, we define
$\mathbb {C}$, we define
(1)
 $(\mathbb {S}^{\mathtt {R}}_{\mathbb {L}})^0_{L_{\mathtt {R}}}$ to be the subalgebra of
$(\mathbb {S}^{\mathtt {R}}_{\mathbb {L}})^0_{L_{\mathtt {R}}}$ to be the subalgebra of  $\mathbb {S}^{\mathtt {R}}_{\mathbb {L}}$ (Notation 4.2(H8)) of elements that annihilate
$\mathbb {S}^{\mathtt {R}}_{\mathbb {L}}$ (Notation 4.2(H8)) of elements that annihilate  $$ \begin{align*} \bigoplus_{i\neq 2r-1}\mathrm{H}^i_{\mathrm{dR}}(X_{L_{\mathtt{R}} L^{\mathtt{R}}}/E)\otimes_{\mathbb{Q}}\mathbb{L}, \end{align*} $$
$$ \begin{align*} \bigoplus_{i\neq 2r-1}\mathrm{H}^i_{\mathrm{dR}}(X_{L_{\mathtt{R}} L^{\mathtt{R}}}/E)\otimes_{\mathbb{Q}}\mathbb{L}, \end{align*} $$(2) for every rational prime
 $\ell $,
$\ell $,  $(\mathbb {S}^{\mathtt {R}}_{\mathbb {L}})^{\langle \ell \rangle }_{L_{\mathtt {R}}}$ to be the subalgebra of
$(\mathbb {S}^{\mathtt {R}}_{\mathbb {L}})^{\langle \ell \rangle }_{L_{\mathtt {R}}}$ to be the subalgebra of  $\mathbb {S}^{\mathtt {R}}_{\mathbb {L}}$ of elements that annihilate
$\mathbb {S}^{\mathtt {R}}_{\mathbb {L}}$ of elements that annihilate  $$ \begin{align*} \bigoplus_{u\in\mathtt{V}_E^{\mathrm{fin}}\setminus\mathtt{V}_E^{(\ell)}}\mathrm{H}^{2r}(X_{L_{\mathtt{R}} L^{\mathtt{R}},u},\mathbb{Q}_\ell(r))\otimes_{\mathbb{Q}}\mathbb{L}. \end{align*} $$
$$ \begin{align*} \bigoplus_{u\in\mathtt{V}_E^{\mathrm{fin}}\setminus\mathtt{V}_E^{(\ell)}}\mathrm{H}^{2r}(X_{L_{\mathtt{R}} L^{\mathtt{R}},u},\mathbb{Q}_\ell(r))\otimes_{\mathbb{Q}}\mathbb{L}. \end{align*} $$
Here, ![]() $L^{\mathtt {R}}$ is defined in Notation 4.2(H8).
$L^{\mathtt {R}}$ is defined in Notation 4.2(H8).
Definition 4.15. Consider a nonempty subset ![]() $\mathtt {R}'\subseteq \mathtt {R}$, an
$\mathtt {R}'\subseteq \mathtt {R}$, an ![]() $\mathtt {R}$-good rational prime
$\mathtt {R}$-good rational prime ![]() $\ell $ and an open compact subgroup L of
$\ell $ and an open compact subgroup L of ![]() $H(\mathbb {A}_F^\infty )$ of the form
$H(\mathbb {A}_F^\infty )$ of the form ![]() $L_{\mathtt {R}} L^{\mathtt {R}}$ where
$L_{\mathtt {R}} L^{\mathtt {R}}$ where ![]() $L^{\mathtt {R}}$ is defined in Notation 4.2(H8). An
$L^{\mathtt {R}}$ is defined in Notation 4.2(H8). An ![]() $(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple is a sextuple
$(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple is a sextuple ![]() $(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ in which
$(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ in which
• for
 $i=1,2$,
$i=1,2$,  $\phi ^\infty _i=\otimes _v\phi ^\infty _{iv}\in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^L$ in which
$\phi ^\infty _i=\otimes _v\phi ^\infty _{iv}\in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^L$ in which  for
for  $v\in \mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R}$, satisfying that
$v\in \mathtt {V}_F^{\mathrm {fin}}\setminus \mathtt {R}$, satisfying that  $\operatorname {\mathrm {supp}}(\phi ^\infty _{1v}\otimes (\phi ^\infty _{2v})^{\mathtt {c}})\subseteq (V^{2r}_v)_{\mathrm {reg}}$ for
$\operatorname {\mathrm {supp}}(\phi ^\infty _{1v}\otimes (\phi ^\infty _{2v})^{\mathtt {c}})\subseteq (V^{2r}_v)_{\mathrm {reg}}$ for  $v\in \mathtt {R}'$;
$v\in \mathtt {R}'$;• for
 $i=1,2$,
$i=1,2$,  $\mathrm {s}_i$ is a product of two elements in
$\mathrm {s}_i$ is a product of two elements in  $(\mathbb {S}^{\mathtt {R}}_{\mathbb {Q}^{\mathrm {ac}}})^{\langle \ell \rangle }_{L_{\mathtt {R}}}$;
$(\mathbb {S}^{\mathtt {R}}_{\mathbb {Q}^{\mathrm {ac}}})^{\langle \ell \rangle }_{L_{\mathtt {R}}}$;• for
 $i=1,2$,
$i=1,2$,  $g_i$ is an element in
$g_i$ is an element in  $G_r(\mathbb {A}_F^{\mathtt {R}'})$.
$G_r(\mathbb {A}_F^{\mathtt {R}'})$.
For an ![]() $(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple
$(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple ![]() $(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ and every pair
$(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ and every pair ![]() $(T_1,T_2)$ of elements in
$(T_1,T_2)$ of elements in ![]() $\mathrm {Herm}_r^\circ (F)^+$, we define
$\mathrm {Herm}_r^\circ (F)^+$, we define
(1) the global index
 $I_{T_1,T_2}(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)^\ell _L$ to be as an element in
$I_{T_1,T_2}(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)^\ell _L$ to be as an element in $$ \begin{align*} \langle\omega_{r,\infty}(g_{1\infty})\phi^0_\infty(T_1)\cdot\mathrm{s}_1^*Z_{T_1}(\omega_r^\infty(g_1^\infty)\phi^\infty_1)_L, \omega_{r,\infty}(g_{2\infty})\phi^0_\infty(T_2)\cdot\mathrm{s}_2^*Z_{T_2}(\omega_r^\infty(g_2^\infty)\phi^\infty_2)_L \rangle_{X_L,E}^\ell \end{align*} $$
$$ \begin{align*} \langle\omega_{r,\infty}(g_{1\infty})\phi^0_\infty(T_1)\cdot\mathrm{s}_1^*Z_{T_1}(\omega_r^\infty(g_1^\infty)\phi^\infty_1)_L, \omega_{r,\infty}(g_{2\infty})\phi^0_\infty(T_2)\cdot\mathrm{s}_2^*Z_{T_2}(\omega_r^\infty(g_2^\infty)\phi^\infty_2)_L \rangle_{X_L,E}^\ell \end{align*} $$ $\mathbb {C}\otimes _{\mathbb {Q}}\mathbb {Q}_\ell $, where we note that for
$\mathbb {C}\otimes _{\mathbb {Q}}\mathbb {Q}_\ell $, where we note that for  $i=1,2$,
$i=1,2$,  $\mathrm {s}_i^*Z_{T_i}(\omega _r^\infty (g_i^\infty )\phi ^\infty _i)_L$ belongs to
$\mathrm {s}_i^*Z_{T_i}(\omega _r^\infty (g_i^\infty )\phi ^\infty _i)_L$ belongs to  $\operatorname {\mathrm {CH}}^r(X_L)^{\langle \ell \rangle }_{\mathbb {C}}$ by Definition 4.14(2);
$\operatorname {\mathrm {CH}}^r(X_L)^{\langle \ell \rangle }_{\mathbb {C}}$ by Definition 4.14(2);(2) for every
 $u\in \mathtt {V}_E^{\mathrm {fin}}$, the local index
$u\in \mathtt {V}_E^{\mathrm {fin}}$, the local index  $I_{T_1,T_2}(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)^\ell _{L,u}$ to be as an element in
$I_{T_1,T_2}(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)^\ell _{L,u}$ to be as an element in $$ \begin{align*} \langle \omega_{r,\infty}(g_{1\infty})\phi^0_\infty(T_1)\cdot\mathrm{s}_1^*Z_{T_1}(\omega_r^\infty(g_1^\infty)\phi^\infty_1)_L, \omega_{r,\infty}(g_{2\infty})\phi^0_\infty(T_2)\cdot\mathrm{s}_2^*Z_{T_2}(\omega_r^\infty(g_2^\infty)\phi^\infty_2)_L \rangle_{X_{L,u},E_u}^\ell \end{align*} $$
$$ \begin{align*} \langle \omega_{r,\infty}(g_{1\infty})\phi^0_\infty(T_1)\cdot\mathrm{s}_1^*Z_{T_1}(\omega_r^\infty(g_1^\infty)\phi^\infty_1)_L, \omega_{r,\infty}(g_{2\infty})\phi^0_\infty(T_2)\cdot\mathrm{s}_2^*Z_{T_2}(\omega_r^\infty(g_2^\infty)\phi^\infty_2)_L \rangle_{X_{L,u},E_u}^\ell \end{align*} $$ $\mathbb {C}\otimes _{\mathbb {Q}}\mathbb {Q}_\ell $;
$\mathbb {C}\otimes _{\mathbb {Q}}\mathbb {Q}_\ell $;(3) for every
 $u\in \mathtt {V}_E^{(\infty )}$, the local index
$u\in \mathtt {V}_E^{(\infty )}$, the local index  $I_{T_1,T_2}(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)_{L,u}$ to be as an element in
$I_{T_1,T_2}(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)_{L,u}$ to be as an element in $$ \begin{align*} \langle \omega_{r,\infty}(g_{1\infty})\phi^0_\infty(T_1)\cdot\mathrm{s}_1^*Z_{T_1}(\omega_r^\infty(g_1^\infty)\phi^\infty_1)_L, \omega_{r,\infty}(g_{2\infty})\phi^0_\infty(T_2)\cdot\mathrm{s}_2^*Z_{T_2}(\omega_r^\infty(g_2^\infty)\phi^\infty_2)_L \rangle_{X_{L,u},E_u} \end{align*} $$
$$ \begin{align*} \langle \omega_{r,\infty}(g_{1\infty})\phi^0_\infty(T_1)\cdot\mathrm{s}_1^*Z_{T_1}(\omega_r^\infty(g_1^\infty)\phi^\infty_1)_L, \omega_{r,\infty}(g_{2\infty})\phi^0_\infty(T_2)\cdot\mathrm{s}_2^*Z_{T_2}(\omega_r^\infty(g_2^\infty)\phi^\infty_2)_L \rangle_{X_{L,u},E_u} \end{align*} $$ $\mathbb {C}$.
$\mathbb {C}$.
Let ![]() $(\pi ,\mathcal {V}_\pi )$ be as in Assumption 4.4 and assume Hypothesis 4.11 on the modularity of generating functions of codimension r.
$(\pi ,\mathcal {V}_\pi )$ be as in Assumption 4.4 and assume Hypothesis 4.11 on the modularity of generating functions of codimension r.
Remark 4.16. In the situation of Definition 4.12 (and suppose that ![]() $F\neq \mathbb {Q}$), suppose that L has the form
$F\neq \mathbb {Q}$), suppose that L has the form ![]() $L_{\mathtt {R}} L^{\mathtt {R}}$ where
$L_{\mathtt {R}} L^{\mathtt {R}}$ where ![]() $L^{\mathtt {R}}$ is defined in Notation 4.2(H8). We have, from [Reference Li and LiuLL21, Proposition 6.10], that for every
$L^{\mathtt {R}}$ is defined in Notation 4.2(H8). We have, from [Reference Li and LiuLL21, Proposition 6.10], that for every  $\varphi \in \mathcal {V}_\pi ^{[r]\mathtt {R}}$ and every
$\varphi \in \mathcal {V}_\pi ^{[r]\mathtt {R}}$ and every ![]() $\phi ^\infty \in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^L$,
$\phi ^\infty \in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^L$,
(1)
 $\mathrm {s}^*\Theta _{\phi ^\infty }(\varphi )_L=\chi ^{\mathtt {R}}_\pi (\mathrm {s})^{\mathtt {c}}\cdot \Theta _{\phi ^\infty }(\varphi )_L$ for every
$\mathrm {s}^*\Theta _{\phi ^\infty }(\varphi )_L=\chi ^{\mathtt {R}}_\pi (\mathrm {s})^{\mathtt {c}}\cdot \Theta _{\phi ^\infty }(\varphi )_L$ for every  $\mathrm {s}\in \mathbb {S}^{\mathtt {R}}_{\mathbb {Q}^{\mathrm {ac}}}$;
$\mathrm {s}\in \mathbb {S}^{\mathtt {R}}_{\mathbb {Q}^{\mathrm {ac}}}$;(2)
 $\Theta _{\phi ^\infty }(\varphi )_L\in \operatorname {\mathrm {CH}}^r(X_L)_{\mathbb {C}}^0$;
$\Theta _{\phi ^\infty }(\varphi )_L\in \operatorname {\mathrm {CH}}^r(X_L)_{\mathbb {C}}^0$;(3) under [Reference Li and LiuLL21, Hypothesis 6.6],
 $\Theta _{\phi ^\infty }(\varphi )_L\in \operatorname {\mathrm {CH}}^r(X_L)_{\mathbb {C}}^{\langle \ell \rangle }$ for every
$\Theta _{\phi ^\infty }(\varphi )_L\in \operatorname {\mathrm {CH}}^r(X_L)_{\mathbb {C}}^{\langle \ell \rangle }$ for every  $\mathtt {R}$-good rational prime
$\mathtt {R}$-good rational prime  $\ell $.
$\ell $.
We recall the normalised height pairing between the cycles ![]() $\Theta _{\phi ^\infty }(\varphi )$ in Definition 4.12, under [Reference Li and LiuLL21, Hypothesis 6.6].
$\Theta _{\phi ^\infty }(\varphi )$ in Definition 4.12, under [Reference Li and LiuLL21, Hypothesis 6.6].
Definition 4.17. Under [Reference Li and LiuLL21, Hypothesis 6.6], every collection of elements  $\varphi _1,\varphi _2\in \mathcal {V}_\pi ^{[r]}$ and
$\varphi _1,\varphi _2\in \mathcal {V}_\pi ^{[r]}$ and ![]() $\phi ^\infty _1,\phi ^\infty _2\in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )$, we define the normalised height pairing
$\phi ^\infty _1,\phi ^\infty _2\in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )$, we define the normalised height pairing
 $$ \begin{align*} \langle\Theta_{\phi^\infty_1}(\varphi_1),\Theta_{\phi^\infty_2}(\varphi_2)\rangle_{X,E}^\natural \in\mathbb{C}\otimes_{\mathbb{Q}}\mathbb{Q}_\ell \end{align*} $$
$$ \begin{align*} \langle\Theta_{\phi^\infty_1}(\varphi_1),\Theta_{\phi^\infty_2}(\varphi_2)\rangle_{X,E}^\natural \in\mathbb{C}\otimes_{\mathbb{Q}}\mathbb{Q}_\ell \end{align*} $$to be the unique element such that for every ![]() $L=L_{\mathtt {R}} L^{\mathtt {R}}$ as in Remark 4.16 (with
$L=L_{\mathtt {R}} L^{\mathtt {R}}$ as in Remark 4.16 (with ![]() $\mathtt {R}$ possibly enlarged) satisfying
$\mathtt {R}$ possibly enlarged) satisfying  $\varphi _1,\varphi _2\in \mathcal {V}_\pi ^{[r]\mathtt {R}}$,
$\varphi _1,\varphi _2\in \mathcal {V}_\pi ^{[r]\mathtt {R}}$,  $\phi ^\infty _1,\phi ^\infty _2\in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^L$ and that
$\phi ^\infty _1,\phi ^\infty _2\in \mathscr {S}(V^r\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^L$ and that ![]() $\ell $ is
$\ell $ is ![]() $\mathtt {R}$-good, we have
$\mathtt {R}$-good, we have
 $$ \begin{align*} \langle\Theta_{\phi^\infty_1}(\varphi_1),\Theta_{\phi^\infty_2}(\varphi_2)\rangle_{X,E}^\natural= \operatorname{\mathrm{vol}}^\natural(L)\cdot \langle\Theta_{\phi^\infty_1}(\varphi_1)_L,\Theta_{\phi^\infty_2}(\varphi_2)_L\rangle_{X_L,E}^\ell, \end{align*} $$
$$ \begin{align*} \langle\Theta_{\phi^\infty_1}(\varphi_1),\Theta_{\phi^\infty_2}(\varphi_2)\rangle_{X,E}^\natural= \operatorname{\mathrm{vol}}^\natural(L)\cdot \langle\Theta_{\phi^\infty_1}(\varphi_1)_L,\Theta_{\phi^\infty_2}(\varphi_2)_L\rangle_{X_L,E}^\ell, \end{align*} $$where ![]() $\operatorname {\mathrm {vol}}^\natural (L)$ is introduced in [Reference Li and LiuLL21, Definition 3.8] and
$\operatorname {\mathrm {vol}}^\natural (L)$ is introduced in [Reference Li and LiuLL21, Definition 3.8] and
 $$ \begin{align*} \langle\Theta_{\phi^\infty_1}(\varphi_1)_L,\Theta_{\phi^\infty_2}(\varphi_2)_L\rangle_{X_L,E}^\ell \end{align*} $$
$$ \begin{align*} \langle\Theta_{\phi^\infty_1}(\varphi_1)_L,\Theta_{\phi^\infty_2}(\varphi_2)_L\rangle_{X_L,E}^\ell \end{align*} $$is well-defined by Remark 4.16(3). Note that by the projection formula, the right-hand side of the above formula is independent of L.
Finally, we review the auxiliary Shimura variety that will only be used in the computation of local indices ![]() $I_{T_1,T_2}(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)_{L,u}$.
$I_{T_1,T_2}(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)_{L,u}$.
Notation 4.18. We denote by ![]() $\mathrm {T}_0$ the torus over
$\mathrm {T}_0$ the torus over ![]() $\mathbb {Q}$ such that for every commutative
$\mathbb {Q}$ such that for every commutative ![]() $\mathbb {Q}$-algebra R, we have
$\mathbb {Q}$-algebra R, we have ![]() $\mathrm {T}_0(R)=\{a\in E\otimes _{\mathbb {Q}} R\mathbin {|} \operatorname {\mathrm {Nm}}_{E/F}a \in R^\times \}$.
$\mathrm {T}_0(R)=\{a\in E\otimes _{\mathbb {Q}} R\mathbin {|} \operatorname {\mathrm {Nm}}_{E/F}a \in R^\times \}$.
We choose a CM type ![]() $\Phi $ of E containing
$\Phi $ of E containing ![]() $\boldsymbol {\iota }$ and denote by
$\boldsymbol {\iota }$ and denote by ![]() $E'$ the subfield of
$E'$ the subfield of ![]() $\mathbb {C}$ generated by E and the reflex field of
$\mathbb {C}$ generated by E and the reflex field of ![]() $\Phi $. We also choose a skew-hermitian space W over E of rank
$\Phi $. We also choose a skew-hermitian space W over E of rank ![]() $1$, whose group of rational similitude is canonically
$1$, whose group of rational similitude is canonically ![]() $\mathrm {T}_0$. For a (sufficiently small) open compact subgroup
$\mathrm {T}_0$. For a (sufficiently small) open compact subgroup ![]() $L_0$ of
$L_0$ of ![]() $\mathrm {T}_0(\mathbb {A}^\infty )$, we have the PEL type moduli scheme Y of CM abelian varieties with CM type
$\mathrm {T}_0(\mathbb {A}^\infty )$, we have the PEL type moduli scheme Y of CM abelian varieties with CM type ![]() $\Phi $ and level
$\Phi $ and level ![]() $L_0$, which is a smooth projective scheme over
$L_0$, which is a smooth projective scheme over ![]() $E'$ of dimension
$E'$ of dimension ![]() $0$ (see, for example, [Reference KottwitzKot92]). In what follows, when we invoke this construction, the data
$0$ (see, for example, [Reference KottwitzKot92]). In what follows, when we invoke this construction, the data ![]() $\Phi $, W and
$\Phi $, W and ![]() $L_0$ will be fixed and hence will not be carried into the notation
$L_0$ will be fixed and hence will not be carried into the notation ![]() $E'$ and Y. For every open compact subgroup
$E'$ and Y. For every open compact subgroup ![]() $L\subseteq H(\mathbb {A}_F^\infty )$, we put
$L\subseteq H(\mathbb {A}_F^\infty )$, we put
as a scheme over ![]() $E'$.
$E'$.
The following notation is parallel to [Reference Li and LiuLL21, Notation 5.6].
Notation 4.19. In Subsections 4.3, 4.4 and 4.5, we will consider a place  $u\in \mathtt {V}_E^{\mathrm {fin}}\setminus \mathtt {V}_F^\heartsuit $ (Definition 1.1). Let p be the underlying rational prime of u. We will fix an isomorphism
$u\in \mathtt {V}_E^{\mathrm {fin}}\setminus \mathtt {V}_F^\heartsuit $ (Definition 1.1). Let p be the underlying rational prime of u. We will fix an isomorphism  $\mathbb {C}\xrightarrow \sim \overline {\mathbb {Q}}_p$ under which
$\mathbb {C}\xrightarrow \sim \overline {\mathbb {Q}}_p$ under which ![]() $\boldsymbol {\iota }$ induces the place u. In particular, we may identify
$\boldsymbol {\iota }$ induces the place u. In particular, we may identify ![]() $\Phi $ as a subset of
$\Phi $ as a subset of  $\operatorname {\mathrm {Hom}}(E,\overline {\mathbb {Q}}_p)$.
$\operatorname {\mathrm {Hom}}(E,\overline {\mathbb {Q}}_p)$.
We further require that ![]() $\Phi $ in Notation 4.18 be admissible in the following sense: if
$\Phi $ in Notation 4.18 be admissible in the following sense: if ![]() $\Phi _v\subseteq \Phi $ denotes the subset inducing the place v for every
$\Phi _v\subseteq \Phi $ denotes the subset inducing the place v for every  $v\in \mathtt {V}_F^{(p)}$, then it satisfies
$v\in \mathtt {V}_F^{(p)}$, then it satisfies
(1) when
 $v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {spl}}$,
$v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {spl}}$,  $\Phi _v$ induces the same place of E above v;
$\Phi _v$ induces the same place of E above v;(2) when
 $v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {int}}$,
$v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {int}}$,  $\Phi _v$ is the pullback of a CM type of the maximal subfield of
$\Phi _v$ is the pullback of a CM type of the maximal subfield of  $E_v$ unramified over
$E_v$ unramified over  $\mathbb {Q}_p$;
$\mathbb {Q}_p$;(3) when
 $v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {ram}}$, the subfield of
$v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {ram}}$, the subfield of  $\overline {\mathbb {Q}}_p$ generated by
$\overline {\mathbb {Q}}_p$ generated by  $E_u$ and the reflex field of
$E_u$ and the reflex field of  $\Phi _v$ is unramified over
$\Phi _v$ is unramified over  $E_u$.
$E_u$.
To release the burden of notation, we denote by K the subfield of  $\overline {\mathbb {Q}}_p$ generated by
$\overline {\mathbb {Q}}_p$ generated by ![]() $E_u$ and the reflex field of
$E_u$ and the reflex field of ![]() $\Phi $, by k its residue field and by
$\Phi $, by k its residue field and by ![]() $\breve {K}$ the completion of the maximal unramified extension of K in
$\breve {K}$ the completion of the maximal unramified extension of K in  $\overline {\mathbb {Q}}_p$ with the residue field
$\overline {\mathbb {Q}}_p$ with the residue field ![]() $\overline {\mathbb {F}}_p$. It is clear that admissible CM type always exists for
$\overline {\mathbb {F}}_p$. It is clear that admissible CM type always exists for  $u\in \mathtt {V}_E^{\mathrm {fin}}\setminus \mathtt {V}_F^\heartsuit $ and that K is unramified over
$u\in \mathtt {V}_E^{\mathrm {fin}}\setminus \mathtt {V}_F^\heartsuit $ and that K is unramified over ![]() $E_u$.
$E_u$.
We also choose a (sufficiently small) open compact subgroup ![]() $L_0$ of
$L_0$ of ![]() $\mathrm {T}_0(\mathbb {A}^\infty )$ such that
$\mathrm {T}_0(\mathbb {A}^\infty )$ such that ![]() $L_{0,p}$ is maximal compact. We denote by
$L_{0,p}$ is maximal compact. We denote by ![]() $\mathcal {Y}$ the integral model of Y over
$\mathcal {Y}$ the integral model of Y over ![]() $O_K$ such that for every
$O_K$ such that for every  $S\in \operatorname {\mathrm {Sch}}^{\prime }_{/O_K}$,
$S\in \operatorname {\mathrm {Sch}}^{\prime }_{/O_K}$, ![]() $\mathcal {Y}(S)$ is the set of equivalence classes of quadruples
$\mathcal {Y}(S)$ is the set of equivalence classes of quadruples  $(A_0,\iota _{A_0},\lambda _{A_0},\eta _{A_0}^p)$ where
$(A_0,\iota _{A_0},\lambda _{A_0},\eta _{A_0}^p)$ where
•
 $(A_0,\iota _{A_0},\lambda _{A_0})$ is a unitary
$(A_0,\iota _{A_0},\lambda _{A_0})$ is a unitary  $O_E$-abelian scheme over S of signature type
$O_E$-abelian scheme over S of signature type  $\Phi $ (see [Reference Liu, Tian, Xiao, Zhang and ZhuLTXZZ, Definition 3.4.2 & Definition 3.4.3])Footnote 17 such that
$\Phi $ (see [Reference Liu, Tian, Xiao, Zhang and ZhuLTXZZ, Definition 3.4.2 & Definition 3.4.3])Footnote 17 such that  $\lambda _{A_0}$ is p-principal;
$\lambda _{A_0}$ is p-principal;•
 $\eta _{A_0}^p$ is an
$\eta _{A_0}^p$ is an  $L_0^p$-level structure (see [Reference Liu, Tian, Xiao, Zhang and ZhuLTXZZ, Definition 4.2.2] for more details).
$L_0^p$-level structure (see [Reference Liu, Tian, Xiao, Zhang and ZhuLTXZZ, Definition 4.2.2] for more details).
By [Reference HowardHow12, Proposition 3.1.2], ![]() $\mathcal {Y}$ is finite and étale over
$\mathcal {Y}$ is finite and étale over ![]() $O_K$.
$O_K$.
4.3 Local indices at split places
In this subsection, we compute local indices at almost all places in  $\mathtt {V}_E^{\mathrm {spl}}$. Our goal is to prove the following proposition.
$\mathtt {V}_E^{\mathrm {spl}}$. Our goal is to prove the following proposition.
Proposition 4.20. Let ![]() $\mathtt {R}$,
$\mathtt {R}$, ![]() $\mathtt {R}'$,
$\mathtt {R}'$, ![]() $\ell $ and L be as in Definition 4.15 such that the cardinality of
$\ell $ and L be as in Definition 4.15 such that the cardinality of ![]() $\mathtt {R}'$ is at least
$\mathtt {R}'$ is at least ![]() $2$. Let
$2$. Let ![]() $(\pi ,\mathcal {V}_\pi )$ be as in Assumption 4.4. For every
$(\pi ,\mathcal {V}_\pi )$ be as in Assumption 4.4. For every  $u\in \mathtt {V}_E^{\mathrm {spl}}$ satisfying
$u\in \mathtt {V}_E^{\mathrm {spl}}$ satisfying ![]() $\underline {u}\not \in \mathtt {R}\setminus \mathtt {V}_F^\heartsuit $ and
$\underline {u}\not \in \mathtt {R}\setminus \mathtt {V}_F^\heartsuit $ and  $\mathtt {V}_F^{(p)}\cap \mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$ where p is the underlying rational prime of u, there exist elements
$\mathtt {V}_F^{(p)}\cap \mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$ where p is the underlying rational prime of u, there exist elements  $\mathrm {s}_1^u,\mathrm {s}_2^u\in \mathbb {S}_{\mathbb {Q}^{\mathrm {ac}}}^{\mathtt {R}}\setminus \mathfrak {m}_\pi ^{\mathtt {R}}$ such that
$\mathrm {s}_1^u,\mathrm {s}_2^u\in \mathbb {S}_{\mathbb {Q}^{\mathrm {ac}}}^{\mathtt {R}}\setminus \mathfrak {m}_\pi ^{\mathtt {R}}$ such that
 $$ \begin{align*} I_{T_1,T_2}(\phi^\infty_1,\phi^\infty_2,\mathrm{s}_1^u\mathrm{s}_1,\mathrm{s}_2^u\mathrm{s}_2,g_1,g_2)^\ell_{L,u}=0 \end{align*} $$
$$ \begin{align*} I_{T_1,T_2}(\phi^\infty_1,\phi^\infty_2,\mathrm{s}_1^u\mathrm{s}_1,\mathrm{s}_2^u\mathrm{s}_2,g_1,g_2)^\ell_{L,u}=0 \end{align*} $$for every ![]() $(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple
$(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple ![]() $(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ and every pair
$(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ and every pair ![]() $(T_1,T_2)$ in
$(T_1,T_2)$ in ![]() $\mathrm {Herm}_r^\circ (F)^+$. Moreover, we may take
$\mathrm {Herm}_r^\circ (F)^+$. Moreover, we may take ![]() $\mathrm {s}_1^u=\mathrm {s}_2^u=1$ if
$\mathrm {s}_1^u=\mathrm {s}_2^u=1$ if ![]() $\underline {u}\not \in \mathtt {R}$.
$\underline {u}\not \in \mathtt {R}$.
Proof. This is simply [Reference Li and LiuLL21, Proposition 7.1] but without the assumption that ![]() $\pi _{\underline {u}}$ is a (tempered) principal series and without relying on [Reference Li and LiuLL21, Hypothesis 6.6]. The proof is the same, after we slightly generalise the construction of the integral model
$\pi _{\underline {u}}$ is a (tempered) principal series and without relying on [Reference Li and LiuLL21, Hypothesis 6.6]. The proof is the same, after we slightly generalise the construction of the integral model ![]() $\mathcal {X}_m$ to take care of places in
$\mathcal {X}_m$ to take care of places in  $\mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {ram}}$ and use Theorem 4.21, which generalises [Reference Li and LiuLL21, Lemma 7.3].
$\mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {ram}}$ and use Theorem 4.21, which generalises [Reference Li and LiuLL21, Lemma 7.3].
From now to the end of this section, we assume  $\mathtt {V}_F^{(p)}\cap \mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$. We also assume
$\mathtt {V}_F^{(p)}\cap \mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$. We also assume ![]() $\underline {u}\in \mathtt {V}_F^\heartsuit $ and when we need
$\underline {u}\in \mathtt {V}_F^\heartsuit $ and when we need ![]() $m\geqslant 1$ below. We invoke Notation 4.18 together with Notation 4.19. The isomorphism
$m\geqslant 1$ below. We invoke Notation 4.18 together with Notation 4.19. The isomorphism  $\mathbb {C}\xrightarrow \sim \overline {\mathbb {Q}}_p$ in Notation 4.19 identifies
$\mathbb {C}\xrightarrow \sim \overline {\mathbb {Q}}_p$ in Notation 4.19 identifies ![]() $\operatorname {\mathrm {Hom}}(E,\mathbb {C})$ with
$\operatorname {\mathrm {Hom}}(E,\mathbb {C})$ with ![]() $\operatorname {\mathrm {Hom}}(E,\mathbb {C}_p)$. For every
$\operatorname {\mathrm {Hom}}(E,\mathbb {C}_p)$. For every  $v\in \mathtt {V}_F^{(p)}$, let
$v\in \mathtt {V}_F^{(p)}$, let ![]() $\Phi _v$ be the subset of
$\Phi _v$ be the subset of ![]() $\Phi $, regarded as a subset of
$\Phi $, regarded as a subset of ![]() $\operatorname {\mathrm {Hom}}(E,\mathbb {C}_p)$, of elements that induce the place v of F.
$\operatorname {\mathrm {Hom}}(E,\mathbb {C}_p)$, of elements that induce the place v of F.
For every integer ![]() $m\geqslant 0$, we define a moduli functor
$m\geqslant 0$, we define a moduli functor ![]() $\mathcal {X}_m$ over
$\mathcal {X}_m$ over ![]() $O_K$ as follows: For every
$O_K$ as follows: For every  $S\in \operatorname {\mathrm {Sch}}^{\prime }_{/O_K}$,
$S\in \operatorname {\mathrm {Sch}}^{\prime }_{/O_K}$, ![]() $\mathcal {X}_m(S)$ is the set of equivalence classes of tuples
$\mathcal {X}_m(S)$ is the set of equivalence classes of tuples
 $$ \begin{align*} (A_0,\iota_{A_0},\lambda_{A_0},\eta_{A_0}^p;A,\iota_A,\lambda_A,\eta_A^p, \{\eta_{A,v}\}_{v\in\mathtt{V}_F^{(p)}\cap\mathtt{V}_F^{\mathrm{spl}}\setminus\{\underline{u}\}},\eta_{A,u,m}) \end{align*} $$
$$ \begin{align*} (A_0,\iota_{A_0},\lambda_{A_0},\eta_{A_0}^p;A,\iota_A,\lambda_A,\eta_A^p, \{\eta_{A,v}\}_{v\in\mathtt{V}_F^{(p)}\cap\mathtt{V}_F^{\mathrm{spl}}\setminus\{\underline{u}\}},\eta_{A,u,m}) \end{align*} $$where
•
 $(A_0,\iota _{A_0},\lambda _{A_0},\eta _{A_0}^p)$ is an element in
$(A_0,\iota _{A_0},\lambda _{A_0},\eta _{A_0}^p)$ is an element in  $\mathcal {Y}(S)$;
$\mathcal {Y}(S)$;•
 $(A,\iota _A,\lambda _A)$ is a unitary
$(A,\iota _A,\lambda _A)$ is a unitary  $O_E$-abelian scheme of signature type
$O_E$-abelian scheme of signature type  $n\Phi -\iota _w+\iota _w^{\mathtt {c}}$ over S, such that
$n\Phi -\iota _w+\iota _w^{\mathtt {c}}$ over S, such that– for every
 $v\in \mathtt {V}_F^{(p)}\setminus \mathtt {V}_F^{\mathrm {ram}}$,
$v\in \mathtt {V}_F^{(p)}\setminus \mathtt {V}_F^{\mathrm {ram}}$,  $\lambda _A[v^\infty ]$ is an isogeny whose kernel has order
$\lambda _A[v^\infty ]$ is an isogeny whose kernel has order  $q_v^{1-\epsilon _v}$;
$q_v^{1-\epsilon _v}$;–
 $\operatorname {\mathrm {Lie}}(A[u^{\mathtt {c},\infty }])$ is of rank
$\operatorname {\mathrm {Lie}}(A[u^{\mathtt {c},\infty }])$ is of rank  $1$ on which the action of
$1$ on which the action of  $O_E$ is given by the embedding
$O_E$ is given by the embedding  $\iota _w^{\mathtt {c}}$;
$\iota _w^{\mathtt {c}}$;– for every
 $v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {ram}}$, the triple
$v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {ram}}$, the triple  $(A_0[v^\infty ],\iota _{A_0}[v^\infty ],\lambda _{A_0}[v^\infty ])\otimes _{O_K}O_{\breve {K}}$ is an object of
$(A_0[v^\infty ],\iota _{A_0}[v^\infty ],\lambda _{A_0}[v^\infty ])\otimes _{O_K}O_{\breve {K}}$ is an object of  $\mathrm {Exo}_{(n,0)}^{\Phi _v}(S\otimes _{O_K}O_{\breve {K}})$ (Remark 2.67, with
$\mathrm {Exo}_{(n,0)}^{\Phi _v}(S\otimes _{O_K}O_{\breve {K}})$ (Remark 2.67, with  $E=E_v$,
$E=E_v$,  $F=F_v$ and
$F=F_v$ and  $\breve {E}=\breve {K}$)Footnote 18 ;
$\breve {E}=\breve {K}$)Footnote 18 ;
•
 $\eta _A^p$ is an
$\eta _A^p$ is an  $L^p$-level structure;
$L^p$-level structure;• for every
 $v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {spl}}\setminus \{\underline {u}\}$,
$v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {spl}}\setminus \{\underline {u}\}$,  $\eta _{A,v}$ is an
$\eta _{A,v}$ is an  $L_v$-level structure;
$L_v$-level structure;•
 $\eta _{A,u,m}$ is a Drinfeld level-m structure.
$\eta _{A,u,m}$ is a Drinfeld level-m structure.
See [Reference Li and LiuLL21, Section 7] for more details for the last three items. By [Reference Rapoport and ZinkRSZ20, Theorem 4.5], for every ![]() $m\geqslant 0$,
$m\geqslant 0$, ![]() $\mathcal {X}_m$ is a regular scheme, flat (smooth, if
$\mathcal {X}_m$ is a regular scheme, flat (smooth, if ![]() $m=0$) and projective over
$m=0$) and projective over ![]() $O_K$ and admits a canonical isomorphism
$O_K$ and admits a canonical isomorphism
 $$ \begin{align*} \mathcal{X}_m\otimes_{O_K}K\simeq X^{\prime}_{L_{\underline{u},m}L^{\underline{u}}}\otimes_{E'}K \end{align*} $$
$$ \begin{align*} \mathcal{X}_m\otimes_{O_K}K\simeq X^{\prime}_{L_{\underline{u},m}L^{\underline{u}}}\otimes_{E'}K \end{align*} $$of schemes over K. Note that for every integer ![]() $m\geqslant 0$,
$m\geqslant 0$, ![]() $\mathbb {S}^{\mathtt {R}\cup \mathtt {V}_F^{(p)}}$ naturally gives a ring of étale correspondences of
$\mathbb {S}^{\mathtt {R}\cup \mathtt {V}_F^{(p)}}$ naturally gives a ring of étale correspondences of ![]() $\mathcal {X}_m$.Footnote 19
$\mathcal {X}_m$.Footnote 19
The following theorem confirms the conjecture proposed in [Reference Li and LiuLL21, Remark 7.4], and the rest of this subsection will be devoted to its proof. It is worth mentioning that even in the situation of [Reference Li and LiuLL21, Lemma 7.3], the argument below is slightly improved so that [Reference Li and LiuLL21, Hypothesis 6.6] is not relied on anymore.
Theorem 4.21. Let the situation be as in Proposition 4.20 and assume ![]() $\underline {u}\in \mathtt {V}_F^\heartsuit $ and
$\underline {u}\in \mathtt {V}_F^\heartsuit $ and ![]() $p\neq \ell $. For every integer
$p\neq \ell $. For every integer ![]() $m\geqslant 0$,
$m\geqslant 0$,
 $$ \begin{align*} \left(\mathrm{H}^{2r}(\mathcal{X}_m,\mathbb{Q}_\ell(r))\otimes_{\mathbb{Q}}\mathbb{Q}^{\mathrm{ac}}\right)_{\mathfrak{m}}=0 \end{align*} $$
$$ \begin{align*} \left(\mathrm{H}^{2r}(\mathcal{X}_m,\mathbb{Q}_\ell(r))\otimes_{\mathbb{Q}}\mathbb{Q}^{\mathrm{ac}}\right)_{\mathfrak{m}}=0 \end{align*} $$holds, where  $\mathfrak {m} := \mathfrak {m}_\pi ^{\mathtt {R}}\cap \mathbb {S}^{\mathtt {R}\cup \mathtt {V}_F^{(p)}}_{\mathbb {Q}^{\mathrm {ac}}}$.
$\mathfrak {m} := \mathfrak {m}_\pi ^{\mathtt {R}}\cap \mathbb {S}^{\mathtt {R}\cup \mathtt {V}_F^{(p)}}_{\mathbb {Q}^{\mathrm {ac}}}$.
We temporarily allow n to be an arbitrary positive integer, not necessarily even. Put ![]() $Y_m := \mathcal {X}_m\otimes _{O_K}k$. For every point
$Y_m := \mathcal {X}_m\otimes _{O_K}k$. For every point  $x\in Y_m(\overline {\mathbb {F}}_p)$, we know that
$x\in Y_m(\overline {\mathbb {F}}_p)$, we know that ![]() $A_x[u^{\mathtt {c},\infty }]$ is a 1-dimensional
$A_x[u^{\mathtt {c},\infty }]$ is a 1-dimensional ![]() $O_{F_{\underline {u}}}$-divisible group of (relative) height n and we let
$O_{F_{\underline {u}}}$-divisible group of (relative) height n and we let ![]() $0\leqslant h(x)\leqslant n-1$ be the height of its étale part. For
$0\leqslant h(x)\leqslant n-1$ be the height of its étale part. For ![]() $0\leqslant h\leqslant n-1$, let
$0\leqslant h\leqslant n-1$, let  $Y_m^{[h]}$ be the locus where
$Y_m^{[h]}$ be the locus where ![]() $h(x)\leqslant h$, which is Zariski closed and hence will be endowed with the reduced induced scheme structure, and put
$h(x)\leqslant h$, which is Zariski closed and hence will be endowed with the reduced induced scheme structure, and put  $Y_m^{(h)} := Y_m^{[h]}-Y_m^{[h-1]}$ (
$Y_m^{(h)} := Y_m^{[h]}-Y_m^{[h-1]}$ ( $Y_m^{[-1]}=\emptyset $). It is known that
$Y_m^{[-1]}=\emptyset $). It is known that  $Y_m^{(h)}$ is smooth over k of pure dimension h.
$Y_m^{(h)}$ is smooth over k of pure dimension h.
Now we suppose that ![]() $m\geqslant 1$. Let
$m\geqslant 1$. Let ![]() $\mathfrak {S}_m^h$ be the set of free
$\mathfrak {S}_m^h$ be the set of free ![]() $O_{F_{\underline {u}}}/\mathfrak {p}_{\underline {u}}^m$-submodules of
$O_{F_{\underline {u}}}/\mathfrak {p}_{\underline {u}}^m$-submodules of ![]() $(\mathfrak {p}_{\underline {u}}^{-m}/O_{F_{\underline {u}}})^n$ of rank
$(\mathfrak {p}_{\underline {u}}^{-m}/O_{F_{\underline {u}}})^n$ of rank ![]() $n-h$ and put
$n-h$ and put  $\mathfrak {S}_m := \bigcup _{h=0}^{n-1}\mathfrak {S}_m^h$. For every
$\mathfrak {S}_m := \bigcup _{h=0}^{n-1}\mathfrak {S}_m^h$. For every ![]() $M\in \mathfrak {S}_m^h$, we denote by
$M\in \mathfrak {S}_m^h$, we denote by  $Y_m^{(M)}\subseteq Y_m^{(h)}$ the (open and closed) locus where the kernel of the Drinfeld level-m structure is M. Then we have
$Y_m^{(M)}\subseteq Y_m^{(h)}$ the (open and closed) locus where the kernel of the Drinfeld level-m structure is M. Then we have
 $$ \begin{align*} Y_m^{(h)}=\coprod_{M\in\mathfrak{S}_m^h}Y_m^{(M)} \end{align*} $$
$$ \begin{align*} Y_m^{(h)}=\coprod_{M\in\mathfrak{S}_m^h}Y_m^{(M)} \end{align*} $$for every ![]() $0\leqslant h\leqslant n-1$. Let
$0\leqslant h\leqslant n-1$. Let  $Y_m^{[M]}$ be the scheme-theoretic closure of
$Y_m^{[M]}$ be the scheme-theoretic closure of  $Y_m^{(M)}$ inside
$Y_m^{(M)}$ inside ![]() $Y_m$. Then we have
$Y_m$. Then we have
 $$ \begin{align} Y_m^{[M]}=\bigcup_{\substack{M'\in\mathfrak{S}_m \\ M\subseteq M'}}Y_m^{(M')} \end{align} $$
$$ \begin{align} Y_m^{[M]}=\bigcup_{\substack{M'\in\mathfrak{S}_m \\ M\subseteq M'}}Y_m^{(M')} \end{align} $$as a disjoint union of strata. Note that Hecke operators away from ![]() $\underline {u}$ (of level
$\underline {u}$ (of level ![]() $L^{\underline {u}}$) preserve
$L^{\underline {u}}$) preserve  $Y_m^{(M)}$ and hence
$Y_m^{(M)}$ and hence  $Y_m^{[M]}$ for every
$Y_m^{[M]}$ for every ![]() $M\in \mathfrak {S}_m$.
$M\in \mathfrak {S}_m$.
We need some general notation. For a sequence ![]() $(g_1,\dots ,g_t)$ of nonnegative integers with
$(g_1,\dots ,g_t)$ of nonnegative integers with ![]() $g=g_1+\cdots +g_t$, we denote by
$g=g_1+\cdots +g_t$, we denote by ![]() $\mathrm {P}_{g_1,\dots ,g_t}$ the standard upper triangular parabolic subgroup of
$\mathrm {P}_{g_1,\dots ,g_t}$ the standard upper triangular parabolic subgroup of ![]() $\operatorname {\mathrm {GL}}_g$ of block sizes
$\operatorname {\mathrm {GL}}_g$ of block sizes ![]() $g_1,\dots ,g_t$ and
$g_1,\dots ,g_t$ and ![]() $\mathrm {M}_{g_1,\dots ,g_t}$ its standard diagonal Levi subgroup. Moreover, we denote by
$\mathrm {M}_{g_1,\dots ,g_t}$ its standard diagonal Levi subgroup. Moreover, we denote by ![]() $C_m^{g_1,\dots ,g_t}$ the cardinality of
$C_m^{g_1,\dots ,g_t}$ the cardinality of
which depends only on the partition ![]() $g=g_1+\cdots +g_t$. We also put
$g=g_1+\cdots +g_t$. We also put
 $$ \begin{align*} L_{\underline{u},m}^g := \ker\left(\operatorname{\mathrm{GL}}_g(O_{F_{\underline{u}}})\to\operatorname{\mathrm{GL}}_g(O_{F_{\underline{u}}}/\mathfrak{p}_{\underline{u}}^m)\right). \end{align*} $$
$$ \begin{align*} L_{\underline{u},m}^g := \ker\left(\operatorname{\mathrm{GL}}_g(O_{F_{\underline{u}}})\to\operatorname{\mathrm{GL}}_g(O_{F_{\underline{u}}}/\mathfrak{p}_{\underline{u}}^m)\right). \end{align*} $$Lemma 4.22. For ![]() $(g_1,\dots ,g_t)$ with
$(g_1,\dots ,g_t)$ with ![]() $g=g_1+\cdots +g_t$ as above and another integer
$g=g_1+\cdots +g_t$ as above and another integer ![]() $g'\geqslant g$, we have
$g'\geqslant g$, we have
 $$ \begin{align*} C_m^{g'-g,g} C_m^{g_1,\dots,g_t}=C_m^{g'-g+g_1,g_2,\dots,g_t}. \end{align*} $$
$$ \begin{align*} C_m^{g'-g,g} C_m^{g_1,\dots,g_t}=C_m^{g'-g+g_1,g_2,\dots,g_t}. \end{align*} $$Proof. It follows from the isomorphism
Lemma 4.23. Suppose that ![]() $m\geqslant 1$. Take a sequence
$m\geqslant 1$. Take a sequence ![]() $(g_1,\dots ,g_t)$ of nonnegative integers with
$(g_1,\dots ,g_t)$ of nonnegative integers with ![]() $g=g_1+\cdots +g_t$. Let
$g=g_1+\cdots +g_t$. Let ![]() $\pi _1\boxtimes \cdots \boxtimes \pi _t$ be an admissible representation of
$\pi _1\boxtimes \cdots \boxtimes \pi _t$ be an admissible representation of ![]() $\mathrm {M}_{g_1,\dots ,g_t}(F_{\underline {u}})$. Then we have
$\mathrm {M}_{g_1,\dots ,g_t}(F_{\underline {u}})$. Then we have
 $$ \begin{align*} \dim\left(\operatorname{\mathrm{Ind}}_{\mathrm{P}_{g_1,\dots,g_t}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_g(F_{\underline{u}})}\pi_1\boxtimes\cdots\boxtimes\pi_t\right)^{L_{\underline{u},m}^g} =C_m^{g_1,\dots,g_t}\prod_{i=1}^t\dim\pi_i^{L_{\underline{u},m}^{g_i}}. \end{align*} $$
$$ \begin{align*} \dim\left(\operatorname{\mathrm{Ind}}_{\mathrm{P}_{g_1,\dots,g_t}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_g(F_{\underline{u}})}\pi_1\boxtimes\cdots\boxtimes\pi_t\right)^{L_{\underline{u},m}^g} =C_m^{g_1,\dots,g_t}\prod_{i=1}^t\dim\pi_i^{L_{\underline{u},m}^{g_i}}. \end{align*} $$Proof. Pick a set X of representatives of the double coset
 $$ \begin{align*} \mathrm{P}_{g_1,\dots,g_t}(F_{\underline{u}})\backslash \operatorname{\mathrm{GL}}_g(F_{\underline{u}}) / L_{\underline{u},m}^g \end{align*} $$
$$ \begin{align*} \mathrm{P}_{g_1,\dots,g_t}(F_{\underline{u}})\backslash \operatorname{\mathrm{GL}}_g(F_{\underline{u}}) / L_{\underline{u},m}^g \end{align*} $$contained in ![]() $\operatorname {\mathrm {GL}}_g(O_{F_{\underline {u}}})$, which is possible by the Iwasawa decomposition. Then an element
$\operatorname {\mathrm {GL}}_g(O_{F_{\underline {u}}})$, which is possible by the Iwasawa decomposition. Then an element
 $$ \begin{align*} f\in\left(\operatorname{\mathrm{Ind}}_{\mathrm{P}_{g_1,\dots,g_t}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_g(F_{\underline{u}})}\pi_1\boxtimes\cdots\boxtimes\pi_t\right)^{L_{\underline{u},m}^g} \end{align*} $$
$$ \begin{align*} f\in\left(\operatorname{\mathrm{Ind}}_{\mathrm{P}_{g_1,\dots,g_t}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_g(F_{\underline{u}})}\pi_1\boxtimes\cdots\boxtimes\pi_t\right)^{L_{\underline{u},m}^g} \end{align*} $$is determined by ![]() $f\mathbin {|}_X$. Since
$f\mathbin {|}_X$. Since ![]() $\operatorname {\mathrm {GL}}_g(O_{F_{\underline {u}}})$ normalises
$\operatorname {\mathrm {GL}}_g(O_{F_{\underline {u}}})$ normalises  $L_{\underline {u},m}^g$, a function
$L_{\underline {u},m}^g$, a function ![]() $f'$ on X is of the form
$f'$ on X is of the form ![]() $f'=f\mathbin {|}_X$ if and only if
$f'=f\mathbin {|}_X$ if and only if ![]() $f'$ takes values in
$f'$ takes values in  $\bigotimes _{i=1}^t\pi _i^{L_{\underline {u},m}^{g_i}}$. As
$\bigotimes _{i=1}^t\pi _i^{L_{\underline {u},m}^{g_i}}$. As ![]() $|X|=C_m^{g_1,\dots ,g_t}$, the lemma follows.
$|X|=C_m^{g_1,\dots ,g_t}$, the lemma follows.
For an irreducible supercuspidal representation ![]() $\pi $ of
$\pi $ of ![]() $\operatorname {\mathrm {GL}}_g(F_{\underline {u}})$ and a positive integer s, we have the representation
$\operatorname {\mathrm {GL}}_g(F_{\underline {u}})$ and a positive integer s, we have the representation ![]() $\operatorname {\mathrm {Sp}}_s(\pi )$ of
$\operatorname {\mathrm {Sp}}_s(\pi )$ of ![]() $\operatorname {\mathrm {GL}}_{sg}(F_{\underline {u}})$ defined in [Reference Harris and TaylorHT01, Section I.3]. In particular, when
$\operatorname {\mathrm {GL}}_{sg}(F_{\underline {u}})$ defined in [Reference Harris and TaylorHT01, Section I.3]. In particular, when ![]() $\phi $ is an unramified character of
$\phi $ is an unramified character of ![]() $F_{\underline {u}}^\times $,
$F_{\underline {u}}^\times $, ![]() $\operatorname {\mathrm {Sp}}_s(\phi )$ is the Steinberg representation of
$\operatorname {\mathrm {Sp}}_s(\phi )$ is the Steinberg representation of ![]() $\operatorname {\mathrm {GL}}_s(F_{\underline {u}})$ twisted by
$\operatorname {\mathrm {GL}}_s(F_{\underline {u}})$ twisted by  $\phi |\;|_{\underline {u}}^{\frac {s-1}{2}}$.
$\phi |\;|_{\underline {u}}^{\frac {s-1}{2}}$.
Lemma 4.24. Suppose that ![]() $m\geqslant 1$. For every positive integer g and every unramified character
$m\geqslant 1$. For every positive integer g and every unramified character ![]() $\phi $ of
$\phi $ of ![]() $F_{\underline {u}}^\times $, we have
$F_{\underline {u}}^\times $, we have
 $$ \begin{align*} \sum_{h=0}^g(-1)^h C_m^{g-h,h}\dim\operatorname{\mathrm{Sp}}_h(\phi)^{L_{\underline{u},m}^h}=0. \end{align*} $$
$$ \begin{align*} \sum_{h=0}^g(-1)^h C_m^{g-h,h}\dim\operatorname{\mathrm{Sp}}_h(\phi)^{L_{\underline{u},m}^h}=0. \end{align*} $$Proof. We claim the identity
 $$ \begin{align} \sum_{h=0}^g(-1)^h \left[\operatorname{\mathrm{Ind}}_{\mathrm{P}_{h,g-h}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_g(F_{\underline{u}})}\operatorname{\mathrm{Sp}}_h(\phi)\boxtimes\left(\phi|\;|_{\underline{u}}^{\frac{g+h-1}{2}}\circ\mathrm{det}_{g-h}\right)\right]=0 \end{align} $$
$$ \begin{align} \sum_{h=0}^g(-1)^h \left[\operatorname{\mathrm{Ind}}_{\mathrm{P}_{h,g-h}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_g(F_{\underline{u}})}\operatorname{\mathrm{Sp}}_h(\phi)\boxtimes\left(\phi|\;|_{\underline{u}}^{\frac{g+h-1}{2}}\circ\mathrm{det}_{g-h}\right)\right]=0 \end{align} $$in ![]() $\mathrm {Groth}(\operatorname {\mathrm {GL}}_g(F_{\underline {u}}))$. Assuming it, we have
$\mathrm {Groth}(\operatorname {\mathrm {GL}}_g(F_{\underline {u}}))$. Assuming it, we have
 $$ \begin{align*} \sum_{h=0}^g(-1)^h\dim\left(\operatorname{\mathrm{Ind}}_{\mathrm{P}_{h,g-h}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_g(F_{\underline{u}})} \operatorname{\mathrm{Sp}}_h(\phi)\boxtimes\left(\phi|\;|_{\underline{u}}^{\frac{g+h-1}{2}}\circ\mathrm{det}_{g-h}\right)\right)^{L_{\underline{u},m}^g}=0. \end{align*} $$
$$ \begin{align*} \sum_{h=0}^g(-1)^h\dim\left(\operatorname{\mathrm{Ind}}_{\mathrm{P}_{h,g-h}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_g(F_{\underline{u}})} \operatorname{\mathrm{Sp}}_h(\phi)\boxtimes\left(\phi|\;|_{\underline{u}}^{\frac{g+h-1}{2}}\circ\mathrm{det}_{g-h}\right)\right)^{L_{\underline{u},m}^g}=0. \end{align*} $$By Lemma 4.23, the lemma follows.
For the claim, put
 $$ \begin{align*} \mathrm{I}(\phi) := \operatorname{\mathrm{Ind}}_{\mathrm{P}_{1,\dots,1}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_g(F_{\underline{u}})} \phi\boxtimes\phi|\;|_{\underline{u}}\boxtimes\cdots\boxtimes\phi|\;|_{\underline{u}}^{g-1}. \end{align*} $$
$$ \begin{align*} \mathrm{I}(\phi) := \operatorname{\mathrm{Ind}}_{\mathrm{P}_{1,\dots,1}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_g(F_{\underline{u}})} \phi\boxtimes\phi|\;|_{\underline{u}}\boxtimes\cdots\boxtimes\phi|\;|_{\underline{u}}^{g-1}. \end{align*} $$By the transitivity of (normalised) parabolic induction, every irreducible constituent of
 $$ \begin{align*} \mathrm{I}(\phi)^{h,g-h} := \operatorname{\mathrm{Ind}}_{\mathrm{P}_{h,g-h}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_g(F_{\underline{u}})} \operatorname{\mathrm{Sp}}_h(\phi)\boxtimes\left(\phi|\;|_{\underline{u}}^{\frac{g+h-1}{2}}\circ\mathrm{det}_{g-h}\right) \end{align*} $$
$$ \begin{align*} \mathrm{I}(\phi)^{h,g-h} := \operatorname{\mathrm{Ind}}_{\mathrm{P}_{h,g-h}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_g(F_{\underline{u}})} \operatorname{\mathrm{Sp}}_h(\phi)\boxtimes\left(\phi|\;|_{\underline{u}}^{\frac{g+h-1}{2}}\circ\mathrm{det}_{g-h}\right) \end{align*} $$is a constituent of ![]() $\mathrm {I}(\phi )$. By [Reference ZelevinskyZel80], there is a bijection between the set of irreducible subquotients of
$\mathrm {I}(\phi )$. By [Reference ZelevinskyZel80], there is a bijection between the set of irreducible subquotients of ![]() $\mathrm {I}(\phi )$ and the set of sequences of signs of length
$\mathrm {I}(\phi )$ and the set of sequences of signs of length ![]() $g-1$. For such a sequence
$g-1$. For such a sequence ![]() $\sigma $, we denote by
$\sigma $, we denote by ![]() $\mathrm {I}(\phi )_\sigma $ the corresponding irreducible subquotient. For
$\mathrm {I}(\phi )_\sigma $ the corresponding irreducible subquotient. For ![]() $0\leqslant h\leqslant g-1$, we denote by
$0\leqslant h\leqslant g-1$, we denote by ![]() $\sigma (i)$ the sequence starting from h negative signs followed by
$\sigma (i)$ the sequence starting from h negative signs followed by ![]() $g-1-h$ positive signs. In particular,
$g-1-h$ positive signs. In particular,
 $$ \begin{align*} \mathrm{I}(\phi)_{\sigma(g-1)}=\operatorname{\mathrm{Sp}}_g(\phi)=\mathrm{I}(\phi)^{g,0},\qquad \mathrm{I}(\phi)_{\sigma(0)}=\phi|\;|_{\underline{u}}^{\frac{2g-1}{2}}\circ\mathrm{det}_g=\mathrm{I}(\phi)^{0,g}. \end{align*} $$
$$ \begin{align*} \mathrm{I}(\phi)_{\sigma(g-1)}=\operatorname{\mathrm{Sp}}_g(\phi)=\mathrm{I}(\phi)^{g,0},\qquad \mathrm{I}(\phi)_{\sigma(0)}=\phi|\;|_{\underline{u}}^{\frac{2g-1}{2}}\circ\mathrm{det}_g=\mathrm{I}(\phi)^{0,g}. \end{align*} $$By [Reference Harris and TaylorHT01, Lemma I.3.2], we have
 $$ \begin{align*} [\mathrm{I}(\phi)^{h,g-h}]=[\mathrm{I}(\phi)_{\sigma(h)}]+[\mathrm{I}(\phi)_{\sigma(h-1)}] \end{align*} $$
$$ \begin{align*} [\mathrm{I}(\phi)^{h,g-h}]=[\mathrm{I}(\phi)_{\sigma(h)}]+[\mathrm{I}(\phi)_{\sigma(h-1)}] \end{align*} $$in ![]() $\mathrm {Groth}(\operatorname {\mathrm {GL}}_g(F_{\underline {u}}))$ for
$\mathrm {Groth}(\operatorname {\mathrm {GL}}_g(F_{\underline {u}}))$ for ![]() $0<h<g$. Thus, (4.2) follows.
$0<h<g$. Thus, (4.2) follows.
Proposition 4.25. Fix an isomorphism ![]() $\overline {\mathbb {Q}}_\ell \simeq \mathbb {C}$. Suppose that
$\overline {\mathbb {Q}}_\ell \simeq \mathbb {C}$. Suppose that ![]() $m\geqslant 1$. For every
$m\geqslant 1$. For every ![]() $0\leqslant h\leqslant n-1$ and
$0\leqslant h\leqslant n-1$ and ![]() $M\in \mathfrak {S}_m^h$, we have
$M\in \mathfrak {S}_m^h$, we have
 $$ \begin{align*} \mathrm{H}^j(Y_m^{[M]}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)_{\mathfrak{m}}=0 \end{align*} $$
$$ \begin{align*} \mathrm{H}^j(Y_m^{[M]}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)_{\mathfrak{m}}=0 \end{align*} $$for every ![]() $j\neq h$.
$j\neq h$.
This is an extension of [Reference Taylor and YoshidaTY07, Proposition 4.4]. However, we allow arbitrary principal level structure at ![]() $\underline {u}$ and our case involves endoscopy.
$\underline {u}$ and our case involves endoscopy.
Proof. In what follows, h will always denote an integer satisfying ![]() $0\leqslant h\leqslant n-1$. Denote by
$0\leqslant h\leqslant n-1$. Denote by ![]() $\mathrm {D}_{n-h}$ the division algebra over
$\mathrm {D}_{n-h}$ the division algebra over ![]() $F_{\underline {u}}$ of Hasse invariant
$F_{\underline {u}}$ of Hasse invariant  $\tfrac {1}{n-h}$, with the maximal order
$\tfrac {1}{n-h}$, with the maximal order ![]() $O_{\mathrm {D}_{n-h}}$.
$O_{\mathrm {D}_{n-h}}$.
For a ![]() $\mathfrak {T}$-scheme Y of finite type over k and a (finite) character
$\mathfrak {T}$-scheme Y of finite type over k and a (finite) character  $\chi \colon \mathrm {T}_0(\mathbb {Q})\backslash \mathrm {T}_0(\mathbb {A}^\infty )/L_0\to \overline {\mathbb {Q}}_\ell ^\times $, we put
$\chi \colon \mathrm {T}_0(\mathbb {Q})\backslash \mathrm {T}_0(\mathbb {A}^\infty )/L_0\to \overline {\mathbb {Q}}_\ell ^\times $, we put
 $$ \begin{align*} [\mathrm{H}_{?,\chi}(Y,\overline{\mathbb{Q}}_\ell)] := \sum_{j\in\mathbb{Z}}(-1)^j\mathrm{H}^j_?(Y\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)[\chi] \end{align*} $$
$$ \begin{align*} [\mathrm{H}_{?,\chi}(Y,\overline{\mathbb{Q}}_\ell)] := \sum_{j\in\mathbb{Z}}(-1)^j\mathrm{H}^j_?(Y\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)[\chi] \end{align*} $$as an element in  $\mathrm {Groth}(\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_p/k))$ for
$\mathrm {Groth}(\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_p/k))$ for ![]() $?\in \{\;,c\}$.
$?\in \{\;,c\}$.
Let ![]() $I^h_m$ be the Igusa variety (of the first kind) introduced in [Reference Harris and TaylorHT01, Section IV.1] so that
$I^h_m$ be the Igusa variety (of the first kind) introduced in [Reference Harris and TaylorHT01, Section IV.1] so that ![]() $I^h_m$ is isomorphic to
$I^h_m$ is isomorphic to  $Y_m^{(M)}$ for every
$Y_m^{(M)}$ for every ![]() $M\in \mathfrak {S}_m^h$ as schemes over k (but not as schemes over
$M\in \mathfrak {S}_m^h$ as schemes over k (but not as schemes over  $Y_0^{(h)}$). Combining with (4.1), we obtain the identity
$Y_0^{(h)}$). Combining with (4.1), we obtain the identity
 $$ \begin{align} [\mathrm{H}_\chi(Y_m^{[M]},\overline{\mathbb{Q}}_\ell)] &=\sum_{h'=0}^h\sum_{\substack{M'\in\mathfrak{S}_m^{h'} \\ M\subseteq M'}}(-1)^{h-h'}[\mathrm{H}_{c,\chi}(Y_m^{(M')},\overline{\mathbb{Q}}_\ell)] \\ &=\sum_{h'=0}^h(-1)^{h-h'}\cdot\left|\{M'\in\mathfrak{S}_m^{h'} \mathbin{|} M\subseteq M'\}\right|\cdot [\mathrm{H}_{c,\chi}(I_m^{h'},\overline{\mathbb{Q}}_\ell)] \notag \\ &=\sum_{h'=0}^h(-1)^{h-h'}C_m^{h-h',h'}\cdot [\mathrm{H}_{c,\chi}(I_m^{h'},\overline{\mathbb{Q}}_\ell)] \notag \end{align} $$
$$ \begin{align} [\mathrm{H}_\chi(Y_m^{[M]},\overline{\mathbb{Q}}_\ell)] &=\sum_{h'=0}^h\sum_{\substack{M'\in\mathfrak{S}_m^{h'} \\ M\subseteq M'}}(-1)^{h-h'}[\mathrm{H}_{c,\chi}(Y_m^{(M')},\overline{\mathbb{Q}}_\ell)] \\ &=\sum_{h'=0}^h(-1)^{h-h'}\cdot\left|\{M'\in\mathfrak{S}_m^{h'} \mathbin{|} M\subseteq M'\}\right|\cdot [\mathrm{H}_{c,\chi}(I_m^{h'},\overline{\mathbb{Q}}_\ell)] \notag \\ &=\sum_{h'=0}^h(-1)^{h-h'}C_m^{h-h',h'}\cdot [\mathrm{H}_{c,\chi}(I_m^{h'},\overline{\mathbb{Q}}_\ell)] \notag \end{align} $$in  $\mathrm {Groth}(\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_p/k))$.
$\mathrm {Groth}(\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_p/k))$.
Now to compute  $[\mathrm {H}_\chi (I_m^{h'},\overline {\mathbb {Q}}_\ell )]$, we use [Reference Caraiani and ScholzeCS17, Lemma 5.5.1] in which the corresponding
$[\mathrm {H}_\chi (I_m^{h'},\overline {\mathbb {Q}}_\ell )]$, we use [Reference Caraiani and ScholzeCS17, Lemma 5.5.1] in which the corresponding ![]() $J_b(\mathbb {Q}_p)$ is
$J_b(\mathbb {Q}_p)$ is ![]() $\mathrm {D}_{n-h'}\times \operatorname {\mathrm {GL}}_{h'}(F_{\underline {u}})$, and we take
$\mathrm {D}_{n-h'}\times \operatorname {\mathrm {GL}}_{h'}(F_{\underline {u}})$, and we take ![]() $\phi =\phi ^{\underline {u}}\phi _{\underline {u}}$ where
$\phi =\phi ^{\underline {u}}\phi _{\underline {u}}$ where ![]() $\phi ^{\underline {u}}$ is the characteristic function of
$\phi ^{\underline {u}}$ is the characteristic function of ![]() $L^{\underline {u}}$ and
$L^{\underline {u}}$ and ![]() $\phi _{\underline {u}}$ is the characteristic function of
$\phi _{\underline {u}}$ is the characteristic function of  $O_{\mathrm {D}_{n-h'}}^\times \times L_{\underline {u},m}^{h'}$. Then we have the identity
$O_{\mathrm {D}_{n-h'}}^\times \times L_{\underline {u},m}^{h'}$. Then we have the identity
 $$ \begin{align} [\mathrm{H}_{c,\chi}(I_m^{h'},\overline{\mathbb{Q}}_\ell)]=\sum_{\boldsymbol{n}}\sum_{\Pi^{\boldsymbol{n}}}c(\boldsymbol{n},\Pi^{\boldsymbol{n}})\cdot \mathrm{Red}^{h'}_{\boldsymbol{n}}(\pi^{\boldsymbol{n}}_{\underline{u}})^{O_{\mathrm{D}_{n-h'}}^\times\times L_{\underline{u},m}^{h'}} \end{align} $$
$$ \begin{align} [\mathrm{H}_{c,\chi}(I_m^{h'},\overline{\mathbb{Q}}_\ell)]=\sum_{\boldsymbol{n}}\sum_{\Pi^{\boldsymbol{n}}}c(\boldsymbol{n},\Pi^{\boldsymbol{n}})\cdot \mathrm{Red}^{h'}_{\boldsymbol{n}}(\pi^{\boldsymbol{n}}_{\underline{u}})^{O_{\mathrm{D}_{n-h'}}^\times\times L_{\underline{u},m}^{h'}} \end{align} $$in  $\mathrm {Groth}(\mathrm {D}_{n-h'}^\times /O_{\mathrm {D}_{n-h'}}^\times )$, where
$\mathrm {Groth}(\mathrm {D}_{n-h'}^\times /O_{\mathrm {D}_{n-h'}}^\times )$, where
•
 $\boldsymbol {n}$ runs through ordered pairs
$\boldsymbol {n}$ runs through ordered pairs  $(n_1,n_2)$ of nonnegative integers such that
$(n_1,n_2)$ of nonnegative integers such that  $n_1+n_2=n$, which gives an elliptic endoscopic group
$n_1+n_2=n$, which gives an elliptic endoscopic group  $G_{\boldsymbol {n}}$ of
$G_{\boldsymbol {n}}$ of  ;
;•
 $\Pi ^{\boldsymbol {n}}$ runs through a finite set of certain isobaric irreducible cohomological (with respect to the trivial algebraic representation) automorphic representations of
$\Pi ^{\boldsymbol {n}}$ runs through a finite set of certain isobaric irreducible cohomological (with respect to the trivial algebraic representation) automorphic representations of  $\mathbb {G}_{\boldsymbol {n}}(\mathbb {A}_F)$, with
$\mathbb {G}_{\boldsymbol {n}}(\mathbb {A}_F)$, with  $\pi ^{\boldsymbol {n}}_{\underline {u}}$ the descent of
$\pi ^{\boldsymbol {n}}_{\underline {u}}$ the descent of  $\Pi ^{\boldsymbol {n}}_{\underline {u}}$ to
$\Pi ^{\boldsymbol {n}}_{\underline {u}}$ to  $G_{\boldsymbol {n}}(F_{\underline {u}})\simeq \mathrm {M}_{n_1,n_2}(F_{\underline {u}})$;
$G_{\boldsymbol {n}}(F_{\underline {u}})\simeq \mathrm {M}_{n_1,n_2}(F_{\underline {u}})$;•
 $c(\boldsymbol {n},\Pi ^{\boldsymbol {n}})$ is a constant depending only on
$c(\boldsymbol {n},\Pi ^{\boldsymbol {n}})$ is a constant depending only on  $\boldsymbol {n}$ and
$\boldsymbol {n}$ and  $\Pi ^{\boldsymbol {n}}$ but not on
$\Pi ^{\boldsymbol {n}}$ but not on  $h'$;
$h'$;•
 $\mathrm {Red}^{h'}_{\boldsymbol {n}}\colon \mathrm {Groth}(\mathrm {M}_{n_1,n_2}(F_{\underline {u}}))\to \mathrm {Groth}(\mathrm {D}_{n-h'}^\times \times \operatorname {\mathrm {GL}}_{h'}(F_{\underline {u}}))$ is the zero map if
$\mathrm {Red}^{h'}_{\boldsymbol {n}}\colon \mathrm {Groth}(\mathrm {M}_{n_1,n_2}(F_{\underline {u}}))\to \mathrm {Groth}(\mathrm {D}_{n-h'}^\times \times \operatorname {\mathrm {GL}}_{h'}(F_{\underline {u}}))$ is the zero map if  $h'<n_2$ and otherwise is the composition of
$h'<n_2$ and otherwise is the composition of– the normalised Jacquet functor
 $$ \begin{align*} \mathrm{Groth}(\mathrm{M}_{n_1,n_2}(F_{\underline{u}}))\to\mathrm{Groth}(\mathrm{M}_{n-h',h'-n_2,n_2}(F_{\underline{u}})), \end{align*} $$
$$ \begin{align*} \mathrm{Groth}(\mathrm{M}_{n_1,n_2}(F_{\underline{u}}))\to\mathrm{Groth}(\mathrm{M}_{n-h',h'-n_2,n_2}(F_{\underline{u}})), \end{align*} $$– the normalised parabolic induction
 $$ \begin{align*} \mathrm{Groth}(\mathrm{M}_{n-h',h'-n_2,n_2}(F_{\underline{u}}))\to\mathrm{Groth}(\mathrm{M}_{n-h',h'}(F_{\underline{u}})), \end{align*} $$
$$ \begin{align*} \mathrm{Groth}(\mathrm{M}_{n-h',h'-n_2,n_2}(F_{\underline{u}}))\to\mathrm{Groth}(\mathrm{M}_{n-h',h'}(F_{\underline{u}})), \end{align*} $$– the Langlands–Jacquet map (on the first factor)
 $$ \begin{align*} \mathrm{Groth}(\mathrm{M}_{n-h',h'}(F_{\underline{u}}))\to\mathrm{Groth}(\mathrm{D}_{n-h'}^\times\times\operatorname{\mathrm{GL}}_{h'}(F_{\underline{u}})). \end{align*} $$
$$ \begin{align*} \mathrm{Groth}(\mathrm{M}_{n-h',h'}(F_{\underline{u}}))\to\mathrm{Groth}(\mathrm{D}_{n-h'}^\times\times\operatorname{\mathrm{GL}}_{h'}(F_{\underline{u}})). \end{align*} $$
The image of  $[\mathrm {H}_{c,\chi }(I_m^{h'},\overline {\mathbb {Q}}_\ell )]$ in
$[\mathrm {H}_{c,\chi }(I_m^{h'},\overline {\mathbb {Q}}_\ell )]$ in  $\mathrm {Groth}(\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_p/k))$ is given by the map
$\mathrm {Groth}(\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_p/k))$ is given by the map
 $$ \begin{align*} \mathrm{Groth}(\mathrm{D}_{n-h'}^\times/O_{\mathrm{D}_{n-h'}}^\times)\to\mathrm{Groth}(\operatorname{\mathrm{Gal}}(\overline{\mathbb{F}}_p/k)) \end{align*} $$
$$ \begin{align*} \mathrm{Groth}(\mathrm{D}_{n-h'}^\times/O_{\mathrm{D}_{n-h'}}^\times)\to\mathrm{Groth}(\operatorname{\mathrm{Gal}}(\overline{\mathbb{F}}_p/k)) \end{align*} $$sending an (unramified) character  $\phi \circ \operatorname {\mathrm {Nm}}_{\mathrm {D}_{n-h'}^\times }$ to
$\phi \circ \operatorname {\mathrm {Nm}}_{\mathrm {D}_{n-h'}^\times }$ to ![]() $\mathrm {rec}(\phi ^{-1})\cdot \breve \chi $, where
$\mathrm {rec}(\phi ^{-1})\cdot \breve \chi $, where ![]() $\breve \chi $ is a finite character of
$\breve \chi $ is a finite character of  $\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_p/k)$ determined by
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_p/k)$ determined by ![]() $\chi $. In what follows, we will regard
$\chi $. In what follows, we will regard
 $$ \begin{align*} \mathrm{Red}^{h'}_{\boldsymbol{n}}(\pi^{\boldsymbol{n}}_{\underline{u}})^{O_{\mathrm{D}_{n-h'}}^\times\times L_{\underline{u},m}^{h'}} \end{align*} $$
$$ \begin{align*} \mathrm{Red}^{h'}_{\boldsymbol{n}}(\pi^{\boldsymbol{n}}_{\underline{u}})^{O_{\mathrm{D}_{n-h'}}^\times\times L_{\underline{u},m}^{h'}} \end{align*} $$as an element of  $\mathrm {Groth}(\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_p/k))$ via the above map.
$\mathrm {Groth}(\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_p/k))$ via the above map.
Now let us compute for each ![]() $\boldsymbol {n}=(n_1,n_2)$,
$\boldsymbol {n}=(n_1,n_2)$,
 $$ \begin{align} \sum_{h'=0}^h(-1)^{h-h'}C_m^{h-h',h'}\cdot\mathrm{Red}^{h'}_{\boldsymbol{n}}(\pi^{\boldsymbol{n}}_{\underline{u}})^{O_{\mathrm{D}_{n-h'}}^\times\times L_{\underline{u},m}^{h'}} \end{align} $$
$$ \begin{align} \sum_{h'=0}^h(-1)^{h-h'}C_m^{h-h',h'}\cdot\mathrm{Red}^{h'}_{\boldsymbol{n}}(\pi^{\boldsymbol{n}}_{\underline{u}})^{O_{\mathrm{D}_{n-h'}}^\times\times L_{\underline{u},m}^{h'}} \end{align} $$in  $\mathrm {Groth}(\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_p/k))$, when
$\mathrm {Groth}(\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_p/k))$, when ![]() $\pi ^{\boldsymbol {n}}_{\underline {u}}$ is tempered. Write
$\pi ^{\boldsymbol {n}}_{\underline {u}}$ is tempered. Write  $\pi ^{\boldsymbol {n}}_{\underline {u}}=\pi ^1\boxtimes \pi ^2$ where
$\pi ^{\boldsymbol {n}}_{\underline {u}}=\pi ^1\boxtimes \pi ^2$ where ![]() $\pi ^\alpha $ is an tempered irreducible admissible representation of
$\pi ^\alpha $ is an tempered irreducible admissible representation of ![]() $\operatorname {\mathrm {GL}}_{n_\alpha }(F_{\underline {u}})$. In particular,
$\operatorname {\mathrm {GL}}_{n_\alpha }(F_{\underline {u}})$. In particular, ![]() $\pi ^1$ is a full induction of the form
$\pi ^1$ is a full induction of the form
 $$ \begin{align*} \operatorname{\mathrm{Ind}}_{\mathrm{P}_{s_1g_1,\dots,s_tg_t}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_{n_1}(F_{\underline{u}})}\operatorname{\mathrm{Sp}}_{s_1}(\pi_1^1)\boxtimes\cdots\boxtimes\operatorname{\mathrm{Sp}}_{s_t}(\pi_t^1), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ind}}_{\mathrm{P}_{s_1g_1,\dots,s_tg_t}(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_{n_1}(F_{\underline{u}})}\operatorname{\mathrm{Sp}}_{s_1}(\pi_1^1)\boxtimes\cdots\boxtimes\operatorname{\mathrm{Sp}}_{s_t}(\pi_t^1), \end{align*} $$where ![]() $s_1,\dots ,s_t$ and
$s_1,\dots ,s_t$ and ![]() $g_1,\dots ,g_t$ are positive integers satisfying
$g_1,\dots ,g_t$ are positive integers satisfying ![]() $s_1g_1+\cdots +s_tg_t=n_1$, and for
$s_1g_1+\cdots +s_tg_t=n_1$, and for ![]() $1\leqslant i\leqslant t$,
$1\leqslant i\leqslant t$, ![]() $\pi _i^1$ is an irreducible supercuspidal representation of
$\pi _i^1$ is an irreducible supercuspidal representation of ![]() $\operatorname {\mathrm {GL}}_{g_i}(F_{\underline {u}})$ such that
$\operatorname {\mathrm {GL}}_{g_i}(F_{\underline {u}})$ such that  $\operatorname {\mathrm {Sp}}_{s_i}(\pi _i^1)$ is unitary. Let
$\operatorname {\mathrm {Sp}}_{s_i}(\pi _i^1)$ is unitary. Let ![]() $\mathbb {I}$ be the subset of
$\mathbb {I}$ be the subset of ![]() $\{1,\dots ,t\}$ such that
$\{1,\dots ,t\}$ such that ![]() $\pi _i^1$ is an unramified character (hence
$\pi _i^1$ is an unramified character (hence ![]() $g_i=1$) and
$g_i=1$) and ![]() $s_i\geqslant n-h$. Then we have for
$s_i\geqslant n-h$. Then we have for ![]() $h'\geqslant n_2$,
$h'\geqslant n_2$,
 $$ \begin{align} &\mathrm{Red}^{h'}_{\boldsymbol{n}}(\pi^{\boldsymbol{n}}_{\underline{u}})^{O_{\mathrm{D}_{n-h'}}^\times\times L_{\underline{u},m}^{h'}} \\ &=\sum_{\substack{i\in\mathbb{I} \\ s_i\geqslant n-h'}}\dim\left(\operatorname{\mathrm{Ind}}_{\mathrm{P}_?(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_{h'}(F_{\underline{u}})}\operatorname{\mathrm{Sp}}_{s_i+h'-n}(\pi_i^1)\boxtimes \left(\boxtimes_{j\neq i}\operatorname{\mathrm{Sp}}_{s_j}(\pi_j^1)\right)\boxtimes\pi^2\right)^{L_{\underline{u},m}^{h'}} \cdot[\mathrm{rec}((\pi_i^1)^{-1}|\;|_{\underline{u}}^{\frac{1-n}{2}})\cdot\breve\chi] \notag \end{align} $$
$$ \begin{align} &\mathrm{Red}^{h'}_{\boldsymbol{n}}(\pi^{\boldsymbol{n}}_{\underline{u}})^{O_{\mathrm{D}_{n-h'}}^\times\times L_{\underline{u},m}^{h'}} \\ &=\sum_{\substack{i\in\mathbb{I} \\ s_i\geqslant n-h'}}\dim\left(\operatorname{\mathrm{Ind}}_{\mathrm{P}_?(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_{h'}(F_{\underline{u}})}\operatorname{\mathrm{Sp}}_{s_i+h'-n}(\pi_i^1)\boxtimes \left(\boxtimes_{j\neq i}\operatorname{\mathrm{Sp}}_{s_j}(\pi_j^1)\right)\boxtimes\pi^2\right)^{L_{\underline{u},m}^{h'}} \cdot[\mathrm{rec}((\pi_i^1)^{-1}|\;|_{\underline{u}}^{\frac{1-n}{2}})\cdot\breve\chi] \notag \end{align} $$in which the suppressed subscript in ![]() $\mathrm {P}_?$ is
$\mathrm {P}_?$ is ![]() $(s_i+h'-n,s_1g_1,\dots ,\widehat {s_ig_i},\dots ,s_tg_t,n_2)$.
$(s_i+h'-n,s_1g_1,\dots ,\widehat {s_ig_i},\dots ,s_tg_t,n_2)$.
We claim that for each ![]() $i\in \mathbb {I}$,
$i\in \mathbb {I}$,
 $$ \begin{align} \sum_{h'=n-s_i}^h(-1)^{h-h'}C_m^{h-h',h'} \cdot\dim\left(\operatorname{\mathrm{Ind}}_{\mathrm{P}_?(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_{h'}(F_{\underline{u}})}\operatorname{\mathrm{Sp}}_{s_i+h'-n}(\pi_i^1)\boxtimes \left(\boxtimes_{j\neq i}\operatorname{\mathrm{Sp}}_{s_j}(\pi_j^1)\right)\boxtimes\pi^2\right)^{L_{\underline{u},m}^{h'}}=0 \end{align} $$
$$ \begin{align} \sum_{h'=n-s_i}^h(-1)^{h-h'}C_m^{h-h',h'} \cdot\dim\left(\operatorname{\mathrm{Ind}}_{\mathrm{P}_?(F_{\underline{u}})}^{\operatorname{\mathrm{GL}}_{h'}(F_{\underline{u}})}\operatorname{\mathrm{Sp}}_{s_i+h'-n}(\pi_i^1)\boxtimes \left(\boxtimes_{j\neq i}\operatorname{\mathrm{Sp}}_{s_j}(\pi_j^1)\right)\boxtimes\pi^2\right)^{L_{\underline{u},m}^{h'}}=0 \end{align} $$if ![]() $s_i>n-h$. In fact, by Lemma 4.23, there is a nonnegative integer D independent of
$s_i>n-h$. In fact, by Lemma 4.23, there is a nonnegative integer D independent of ![]() $h'$ such that the left-hand side of (4.7) equals
$h'$ such that the left-hand side of (4.7) equals
 $$ \begin{align*} &\sum_{h'=n-s_i}^h(-1)^{h-h'}C_m^{h-h',h'}\cdot C_m^{s_i+h'-n,s_1g_1,\dots,\widehat{s_ig_i},\dots,s_tg_t,n_2}\cdot D\cdot \dim\operatorname{\mathrm{Sp}}_{s_i+h'-n}(\pi_i^1)^{L_{\underline{u},m}^{s_i+h'-n}} \\ &=\sum_{h'=n-s_i}^h(-1)^{h-h'}C_m^{h-h',s_i+h'-n,s_1g_1,\dots,\widehat{s_ig_i},\dots,s_tg_t,n_2}\cdot D\cdot \dim\operatorname{\mathrm{Sp}}_{s_i+h'-n}(\pi_i^1)^{L_{\underline{u},m}^{s_i+h'-n}} \\ &=\sum_{h'=0}^{h+s_i-n}(-1)^{h-h'}C_m^{h+s_i-n-h',h',s_1g_1,\dots,\widehat{s_ig_i},\dots,s_tg_t,n_2}\cdot D\cdot \dim\operatorname{\mathrm{Sp}}_{h'}(\pi_i^1)^{L_{\underline{u},m}^{h'}} \\ &=(-1)^hC_m^{h+s_i-n,s_1g_1,\dots,\widehat{s_ig_i},\dots,s_tg_t,n_2}\cdot D\sum_{h'=0}^{h+s_i-n}(-1)^{h'} C_m^{h+s_i-n-h',h'}\cdot\dim\operatorname{\mathrm{Sp}}_{h'}(\pi_i^1)^{L_{\underline{u},m}^{h'}} \end{align*} $$
$$ \begin{align*} &\sum_{h'=n-s_i}^h(-1)^{h-h'}C_m^{h-h',h'}\cdot C_m^{s_i+h'-n,s_1g_1,\dots,\widehat{s_ig_i},\dots,s_tg_t,n_2}\cdot D\cdot \dim\operatorname{\mathrm{Sp}}_{s_i+h'-n}(\pi_i^1)^{L_{\underline{u},m}^{s_i+h'-n}} \\ &=\sum_{h'=n-s_i}^h(-1)^{h-h'}C_m^{h-h',s_i+h'-n,s_1g_1,\dots,\widehat{s_ig_i},\dots,s_tg_t,n_2}\cdot D\cdot \dim\operatorname{\mathrm{Sp}}_{s_i+h'-n}(\pi_i^1)^{L_{\underline{u},m}^{s_i+h'-n}} \\ &=\sum_{h'=0}^{h+s_i-n}(-1)^{h-h'}C_m^{h+s_i-n-h',h',s_1g_1,\dots,\widehat{s_ig_i},\dots,s_tg_t,n_2}\cdot D\cdot \dim\operatorname{\mathrm{Sp}}_{h'}(\pi_i^1)^{L_{\underline{u},m}^{h'}} \\ &=(-1)^hC_m^{h+s_i-n,s_1g_1,\dots,\widehat{s_ig_i},\dots,s_tg_t,n_2}\cdot D\sum_{h'=0}^{h+s_i-n}(-1)^{h'} C_m^{h+s_i-n-h',h'}\cdot\dim\operatorname{\mathrm{Sp}}_{h'}(\pi_i^1)^{L_{\underline{u},m}^{h'}} \end{align*} $$in which the last summation vanishes by applying Lemma 4.24 with ![]() $g=h+s_i-n>0$. Here, we have used Lemma 4.22 twice.
$g=h+s_i-n>0$. Here, we have used Lemma 4.22 twice.
By (4.6) and (4.7), we know that (4.5) is a linear combination of  $[\mathrm {rec}((\pi _i^1)^{-1}|\;|_{\underline {u}}^{\frac {1-n}{2}})\cdot \breve \chi ]$ with
$[\mathrm {rec}((\pi _i^1)^{-1}|\;|_{\underline {u}}^{\frac {1-n}{2}})\cdot \breve \chi ]$ with ![]() $i\in \mathbb {I}$ satisfying
$i\in \mathbb {I}$ satisfying ![]() $s_i=n-h$. Thus, (4.5) is strictly pure of weight h since
$s_i=n-h$. Thus, (4.5) is strictly pure of weight h since  $\operatorname {\mathrm {Sp}}_{s_i}(\pi _i^1)$ is unitary. By (4.3), (4.4) and the fact that localisation at
$\operatorname {\mathrm {Sp}}_{s_i}(\pi _i^1)$ is unitary. By (4.3), (4.4) and the fact that localisation at ![]() $\mathfrak {m}$ annihilates all terms in (4.4) with
$\mathfrak {m}$ annihilates all terms in (4.4) with ![]() $\pi ^{\boldsymbol {n}}_{\underline {u}}$ not tempered, we know that
$\pi ^{\boldsymbol {n}}_{\underline {u}}$ not tempered, we know that  $[\mathrm {H}_\chi (Y_m^{[M]},\overline {\mathbb {Q}}_\ell )]_{\mathfrak {m}}$ is strictly pure of weight h. Finally, by [Reference MantovanMan08, Proposition 12], we know that
$[\mathrm {H}_\chi (Y_m^{[M]},\overline {\mathbb {Q}}_\ell )]_{\mathfrak {m}}$ is strictly pure of weight h. Finally, by [Reference MantovanMan08, Proposition 12], we know that  $Y_m^{[M]}$ is smooth over k of pure dimension h. Since
$Y_m^{[M]}$ is smooth over k of pure dimension h. Since  $Y_m^{[M]}$ is also proper, we have
$Y_m^{[M]}$ is also proper, we have
 $$ \begin{align*} \mathrm{H}^j(Y_m^{[M]}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)[\chi]_{\mathfrak{m}}=0 \end{align*} $$
$$ \begin{align*} \mathrm{H}^j(Y_m^{[M]}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)[\chi]_{\mathfrak{m}}=0 \end{align*} $$for every ![]() $j\neq h$ and every character
$j\neq h$ and every character  $\chi \colon \mathrm {T}_0(\mathbb {Q})\backslash \mathrm {T}_0(\mathbb {A}^\infty )/L_0\to \overline {\mathbb {Q}}_\ell ^\times $ from the Weil conjecture. Then the proposition follows.
$\chi \colon \mathrm {T}_0(\mathbb {Q})\backslash \mathrm {T}_0(\mathbb {A}^\infty )/L_0\to \overline {\mathbb {Q}}_\ell ^\times $ from the Weil conjecture. Then the proposition follows.
Proof of Theorem 4.21.
Recall that ![]() $n=2r$ is even. We may assume
$n=2r$ is even. We may assume ![]() $m\geqslant 1$ since the morphism
$m\geqslant 1$ since the morphism ![]() $\mathcal {X}_m\to \mathcal {X}_0$ is finite and flat. In what follows, h is always an integer satisfying
$\mathcal {X}_m\to \mathcal {X}_0$ is finite and flat. In what follows, h is always an integer satisfying ![]() $0\leqslant h\leqslant n-1=2r-1$. For a subset
$0\leqslant h\leqslant n-1=2r-1$. For a subset ![]() $\Sigma \subset \mathfrak {S}_m^h$, we put
$\Sigma \subset \mathfrak {S}_m^h$, we put
 $$ \begin{align*} Y_m^{(\Sigma)} := \bigcup_{M\in\Sigma}Y_m^{(M)}, \qquad Y_m^{[\Sigma]} := \bigcup_{M\in\Sigma}Y_m^{[M]} \end{align*} $$
$$ \begin{align*} Y_m^{(\Sigma)} := \bigcup_{M\in\Sigma}Y_m^{(M)}, \qquad Y_m^{[\Sigma]} := \bigcup_{M\in\Sigma}Y_m^{[M]} \end{align*} $$in which the first union is disjoint. If ![]() $h\geqslant 1$, we also denote by
$h\geqslant 1$, we also denote by ![]() $\Sigma ^\dagger $ the subset of
$\Sigma ^\dagger $ the subset of ![]() $\mathfrak {S}_m^{h-1}$ consisting of
$\mathfrak {S}_m^{h-1}$ consisting of ![]() $M'$ that contains an element in
$M'$ that contains an element in ![]() $\Sigma $.
$\Sigma $.
Fix an arbitrary isomorphism ![]() $\overline {\mathbb {Q}}_\ell \simeq \mathbb {C}$. We claim
$\overline {\mathbb {Q}}_\ell \simeq \mathbb {C}$. We claim
(*) For every
 $0\leqslant h\leqslant 2r-1$ and every
$0\leqslant h\leqslant 2r-1$ and every  $\Sigma \subset \mathfrak {S}_m^h$, holds when
$\Sigma \subset \mathfrak {S}_m^h$, holds when $$ \begin{align*} \mathrm{H}^j_c(Y_m^{(\Sigma)}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)_{\mathfrak{m}}= \mathrm{H}^j(Y_m^{[\Sigma]}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)_{\mathfrak{m}}=0 \end{align*} $$
$$ \begin{align*} \mathrm{H}^j_c(Y_m^{(\Sigma)}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)_{\mathfrak{m}}= \mathrm{H}^j(Y_m^{[\Sigma]}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)_{\mathfrak{m}}=0 \end{align*} $$ $j>h$.
$j>h$.
Assuming the claim, we prove ![]() $\mathrm {H}^{2r}(\mathcal {X}_m,\overline {\mathbb {Q}}_\ell (r))_{\mathfrak {m}}=0$. By the proper base change theorem and the fact that taking global sections on
$\mathrm {H}^{2r}(\mathcal {X}_m,\overline {\mathbb {Q}}_\ell (r))_{\mathfrak {m}}=0$. By the proper base change theorem and the fact that taking global sections on ![]() $\operatorname {\mathrm {Spec}} O_K$ is the same as restricting to
$\operatorname {\mathrm {Spec}} O_K$ is the same as restricting to ![]() $\operatorname {\mathrm {Spec}} k$ and then taking global sections, the natural map
$\operatorname {\mathrm {Spec}} k$ and then taking global sections, the natural map ![]() $\mathrm {H}^{2r}(\mathcal {X}_m,\overline {\mathbb {Q}}_\ell (r))\to \mathrm {H}^{2r}(Y_m,\overline {\mathbb {Q}}_\ell (r))$ is an isomorphism. Thus, it suffices to show that
$\mathrm {H}^{2r}(\mathcal {X}_m,\overline {\mathbb {Q}}_\ell (r))\to \mathrm {H}^{2r}(Y_m,\overline {\mathbb {Q}}_\ell (r))$ is an isomorphism. Thus, it suffices to show that
 $$ \begin{align*} \mathrm{H}^0(k,\mathrm{H}^{2r}(Y_m\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell(r)))_{\mathfrak{m}}= \mathrm{H}^1(k,\mathrm{H}^{2r-1}(Y_m\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell(r)))_{\mathfrak{m}}=0. \end{align*} $$
$$ \begin{align*} \mathrm{H}^0(k,\mathrm{H}^{2r}(Y_m\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell(r)))_{\mathfrak{m}}= \mathrm{H}^1(k,\mathrm{H}^{2r-1}(Y_m\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell(r)))_{\mathfrak{m}}=0. \end{align*} $$The vanishing of  $\mathrm {H}^0(k,\mathrm {H}^{2r}(Y_m\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell (r)))_{\mathfrak {m}}$ already follows from (
$\mathrm {H}^0(k,\mathrm {H}^{2r}(Y_m\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell (r)))_{\mathfrak {m}}$ already follows from (![]() $*$) as
$*$) as  $Y_m=Y_m^{[2r-1]}$. Now we consider
$Y_m=Y_m^{[2r-1]}$. Now we consider  $\mathrm {H}^1(k,\mathrm {H}^{2r-1}(Y_m\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell (r)))_{\mathfrak {m}}$. Again by (
$\mathrm {H}^1(k,\mathrm {H}^{2r-1}(Y_m\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell (r)))_{\mathfrak {m}}$. Again by (![]() $*$), we have
$*$), we have  $\mathrm {H}^{2r-1}(Y_m^{[2r-2]}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell )_{\mathfrak {m}}=0$; hence, the natural map
$\mathrm {H}^{2r-1}(Y_m^{[2r-2]}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell )_{\mathfrak {m}}=0$; hence, the natural map
 $$ \begin{align*} \mathrm{H}^{2r-1}_c(Y_m^{(2r-1)}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)_{\mathfrak{m}}\to\mathrm{H}^{2r-1}(Y_m\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)_{\mathfrak{m}} \end{align*} $$
$$ \begin{align*} \mathrm{H}^{2r-1}_c(Y_m^{(2r-1)}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)_{\mathfrak{m}}\to\mathrm{H}^{2r-1}(Y_m\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell)_{\mathfrak{m}} \end{align*} $$is surjective. It suffices to show that  $\mathrm {H}^1(k,\mathrm {H}^{2r-1}_c(Y_m^{(2r-1)}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell (r)))_{\mathfrak {m}}=0$. Now we prove by induction on
$\mathrm {H}^1(k,\mathrm {H}^{2r-1}_c(Y_m^{(2r-1)}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell (r)))_{\mathfrak {m}}=0$. Now we prove by induction on ![]() $0\leqslant h\leqslant 2r-1$ that for every
$0\leqslant h\leqslant 2r-1$ that for every ![]() $M\in \mathfrak {S}_m^h$,
$M\in \mathfrak {S}_m^h$,  $\mathrm {H}^1(k,\mathrm {H}^h_c(Y_m^{(M)}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell (r)))_{\mathfrak {m}}=0$.
$\mathrm {H}^1(k,\mathrm {H}^h_c(Y_m^{(M)}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell (r)))_{\mathfrak {m}}=0$.
The case ![]() $h=0$ is trivial. Consider
$h=0$ is trivial. Consider ![]() $h>0$ and
$h>0$ and ![]() $M\in \mathfrak {S}_m^h$. Since
$M\in \mathfrak {S}_m^h$. Since  $Y_m^{[M]}$ is proper smooth over k by [Reference MantovanMan08, Proposition 12], we have
$Y_m^{[M]}$ is proper smooth over k by [Reference MantovanMan08, Proposition 12], we have  $\mathrm {H}^1(k,\mathrm {H}^h(Y_m^{[M]}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell (r)))_{\mathfrak {m}}=0$ by the Weil conjecture. By (
$\mathrm {H}^1(k,\mathrm {H}^h(Y_m^{[M]}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell (r)))_{\mathfrak {m}}=0$ by the Weil conjecture. By (![]() $*$), we have
$*$), we have  $\mathrm {H}^h(Y_m^{[\{M\}^\dagger ]}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell )_{\mathfrak {m}}=0$. Thus, it suffices to show that
$\mathrm {H}^h(Y_m^{[\{M\}^\dagger ]}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell )_{\mathfrak {m}}=0$. Thus, it suffices to show that  $\mathrm {H}^1(k,\mathrm {H}^{h-1}(Y_m^{[\{M\}^\dagger ]}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell (r)))_{\mathfrak {m}}=0$. By (
$\mathrm {H}^1(k,\mathrm {H}^{h-1}(Y_m^{[\{M\}^\dagger ]}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell (r)))_{\mathfrak {m}}=0$. By (![]() $*$) again, we have
$*$) again, we have  $\mathrm {H}^{h-1}(Y_m^{[\{M\}^{\dagger \dagger }]}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell )_{\mathfrak {m}}=0$. Thus, the desired vanishing property follows from
$\mathrm {H}^{h-1}(Y_m^{[\{M\}^{\dagger \dagger }]}\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell )_{\mathfrak {m}}=0$. Thus, the desired vanishing property follows from
 $$ \begin{align*} \mathrm{H}^1(k,\mathrm{H}^{h-1}_c(Y_m^{(\{M\}^\dagger)}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell(r)))_{\mathfrak{m}} =\bigoplus_{M'\in\{M\}^\dagger}\mathrm{H}^1(k,\mathrm{H}^{h-1}_c(Y_m^{(M')}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell(r)))_{\mathfrak{m}}=0, \end{align*} $$
$$ \begin{align*} \mathrm{H}^1(k,\mathrm{H}^{h-1}_c(Y_m^{(\{M\}^\dagger)}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell(r)))_{\mathfrak{m}} =\bigoplus_{M'\in\{M\}^\dagger}\mathrm{H}^1(k,\mathrm{H}^{h-1}_c(Y_m^{(M')}\otimes_k\overline{\mathbb{F}}_p,\overline{\mathbb{Q}}_\ell(r)))_{\mathfrak{m}}=0, \end{align*} $$which holds by the induction hypothesis. We have now proved ![]() $\mathrm {H}^{2r}(\mathcal {X}_m,\overline {\mathbb {Q}}_\ell (r))_{\mathfrak {m}}=0$ assuming (
$\mathrm {H}^{2r}(\mathcal {X}_m,\overline {\mathbb {Q}}_\ell (r))_{\mathfrak {m}}=0$ assuming (![]() $*$).
$*$).
To show the claim (![]() $*$), we use induction on h. To ease notation, we simply write
$*$), we use induction on h. To ease notation, we simply write ![]() $\mathrm {H}^\bullet _?(-)$ for
$\mathrm {H}^\bullet _?(-)$ for  $\mathrm {H}^\bullet _?(-\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell )_{\mathfrak {m}}$ for
$\mathrm {H}^\bullet _?(-\otimes _k\overline {\mathbb {F}}_p,\overline {\mathbb {Q}}_\ell )_{\mathfrak {m}}$ for ![]() $?\in \{\;,c\}$. The case for
$?\in \{\;,c\}$. The case for ![]() $h=0$ is trivial. Suppose that we know (
$h=0$ is trivial. Suppose that we know (![]() $*$) for
$*$) for ![]() $h-1$ for some
$h-1$ for some ![]() $h\geqslant 1$. For every
$h\geqslant 1$. For every ![]() $M\in \mathfrak {S}_m^h$, we have the exact sequence
$M\in \mathfrak {S}_m^h$, we have the exact sequence
 $$ \begin{align*} \cdots\to\mathrm{H}^{j-1}(Y^{[\{M\}^\dagger]}_m)\to\mathrm{H}^j_c(Y^{(M)}_m)\to\mathrm{H}^j(Y^{[M]}_m)\to\cdots \end{align*} $$
$$ \begin{align*} \cdots\to\mathrm{H}^{j-1}(Y^{[\{M\}^\dagger]}_m)\to\mathrm{H}^j_c(Y^{(M)}_m)\to\mathrm{H}^j(Y^{[M]}_m)\to\cdots \end{align*} $$By Proposition 4.25 and the induction hypothesis, we have  $\mathrm {H}^j_c(Y^{(M)}_m)=0$ for
$\mathrm {H}^j_c(Y^{(M)}_m)=0$ for ![]() $j>h$. Now take a subset
$j>h$. Now take a subset ![]() $\Sigma $ of
$\Sigma $ of ![]() $\mathfrak {S}_m^h$. Then we have
$\mathfrak {S}_m^h$. Then we have  $\mathrm {H}^j_c(Y^{(\Sigma )}_m)=\bigoplus _{M\in \Sigma }\mathrm {H}^j_c(Y^{(M)}_m)=0$ for
$\mathrm {H}^j_c(Y^{(\Sigma )}_m)=\bigoplus _{M\in \Sigma }\mathrm {H}^j_c(Y^{(M)}_m)=0$ for ![]() $j> h$. By the exact sequence
$j> h$. By the exact sequence
 $$ \begin{align*} \cdots\to\mathrm{H}^j_c(Y^{(\Sigma)}_m)\to\mathrm{H}^j(Y^{[\Sigma]}_m)\to\mathrm{H}^j(Y^{[\Sigma^\dagger]}_m)\to\cdots \end{align*} $$
$$ \begin{align*} \cdots\to\mathrm{H}^j_c(Y^{(\Sigma)}_m)\to\mathrm{H}^j(Y^{[\Sigma]}_m)\to\mathrm{H}^j(Y^{[\Sigma^\dagger]}_m)\to\cdots \end{align*} $$and the induction hypothesis, we have  $\mathrm {H}^j(Y^{[\Sigma ]}_m)=0$ for
$\mathrm {H}^j(Y^{[\Sigma ]}_m)=0$ for ![]() $j>h$. Thus, (
$j>h$. Thus, (![]() $*$) holds for h.
$*$) holds for h.
The theorem is proved.
Remark 4.26. In fact, our proof of Theorem 4.21 shows that for general n (not necessarily even),
 $$ \begin{align*} \left(\mathrm{H}^{n'}(\mathcal{X}_m,\mathbb{Q}_\ell(r'))\otimes_{\mathbb{Q}}\mathbb{Q}^{\mathrm{ac}}\right)_{\mathfrak{m}}=0 \end{align*} $$
$$ \begin{align*} \left(\mathrm{H}^{n'}(\mathcal{X}_m,\mathbb{Q}_\ell(r'))\otimes_{\mathbb{Q}}\mathbb{Q}^{\mathrm{ac}}\right)_{\mathfrak{m}}=0 \end{align*} $$as long as ![]() $n\leqslant n'\leqslant 2r'$, where
$n\leqslant n'\leqslant 2r'$, where ![]() $\mathfrak {m}$ is the maximal ideal of a suitable spherical Hecke algebra associated to a tempered cuspidal automorphic representation of the corresponding unitary group.
$\mathfrak {m}$ is the maximal ideal of a suitable spherical Hecke algebra associated to a tempered cuspidal automorphic representation of the corresponding unitary group.
4.4 Local indices at inert places
In this subsection, we compute local indices at places in  $\mathtt {V}_E^{\mathrm {int}}$ not above
$\mathtt {V}_E^{\mathrm {int}}$ not above ![]() $\mathtt {R}$.
$\mathtt {R}$.
Proposition 4.27. Let ![]() $\mathtt {R}$,
$\mathtt {R}$, ![]() $\mathtt {R}'$,
$\mathtt {R}'$, ![]() $\ell $ and L be as in Definition 4.15. Take an element
$\ell $ and L be as in Definition 4.15. Take an element  $u\in \mathtt {V}_E^{\mathrm {int}}$ such that its underlying rational prime p is odd and satisfies
$u\in \mathtt {V}_E^{\mathrm {int}}$ such that its underlying rational prime p is odd and satisfies  $\mathtt {V}_F^{(p)}\cap \mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$.
$\mathtt {V}_F^{(p)}\cap \mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$.
(1) Suppose that
 $\underline {u}\not \in \mathtt {S}$. Then we have for every
$\underline {u}\not \in \mathtt {S}$. Then we have for every $$ \begin{align*} \log q_u\cdot \operatorname{\mathrm{vol}}^\natural(L)\cdot I_{T_1,T_2}(\phi^\infty_1,\phi^\infty_2,\mathrm{s}_1,\mathrm{s}_2,g_1,g_2)^\ell_{L,u} =\mathfrak{E}_{T_1,T_2}((g_1,g_2),\Phi_\infty^0\otimes(\mathrm{s}_1\phi^\infty_1\otimes(\mathrm{s}_2\phi^\infty_2)^{\mathtt{c}}))_u \end{align*} $$
$$ \begin{align*} \log q_u\cdot \operatorname{\mathrm{vol}}^\natural(L)\cdot I_{T_1,T_2}(\phi^\infty_1,\phi^\infty_2,\mathrm{s}_1,\mathrm{s}_2,g_1,g_2)^\ell_{L,u} =\mathfrak{E}_{T_1,T_2}((g_1,g_2),\Phi_\infty^0\otimes(\mathrm{s}_1\phi^\infty_1\otimes(\mathrm{s}_2\phi^\infty_2)^{\mathtt{c}}))_u \end{align*} $$ $(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple
$(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple  $(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ and every pair
$(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ and every pair  $(T_1,T_2)$ in
$(T_1,T_2)$ in  $\mathrm {Herm}_r^\circ (F)^+$.
$\mathrm {Herm}_r^\circ (F)^+$.(2) Suppose that
 $\underline {u}\in \mathtt {S}\cap \mathtt {V}_F^\heartsuit $ and is unramified over
$\underline {u}\in \mathtt {S}\cap \mathtt {V}_F^\heartsuit $ and is unramified over  $\mathbb {Q}$. Recall that we have fixed a u-nearby space
$\mathbb {Q}$. Recall that we have fixed a u-nearby space  and an isomorphism
and an isomorphism  from Notation 4.2(H9). We also fix a
from Notation 4.2(H9). We also fix a  $\psi _{E,\underline {u}}$-self-dual lattice
$\psi _{E,\underline {u}}$-self-dual lattice  $\Lambda ^\star _{\underline {u}}$ of
$\Lambda ^\star _{\underline {u}}$ of  . Then there exist elements
. Then there exist elements  $\mathrm {s}_1^u,\mathrm {s}_2^u\in \mathbb {S}_{\mathbb {Q}^{\mathrm {ac}}}^{\mathtt {R}}\setminus \mathfrak {m}_\pi ^{\mathtt {R}}$ such that for every
$\mathrm {s}_1^u,\mathrm {s}_2^u\in \mathbb {S}_{\mathbb {Q}^{\mathrm {ac}}}^{\mathtt {R}}\setminus \mathfrak {m}_\pi ^{\mathtt {R}}$ such that for every
 $(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple
$(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple  $(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ and every pair
$(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ and every pair  $(T_1,T_2)$ in
$(T_1,T_2)$ in  $\mathrm {Herm}_r^\circ (F)^+$.
$\mathrm {Herm}_r^\circ (F)^+$.
In both cases, the right-hand side is defined in Definition 4.10 with the Gaussian function ![]() $\Phi _\infty ^0\in \mathscr {S}(V^{2r}\otimes _{\mathbb {A}_F}F_\infty )$ (Notation 4.2(H3)) and
$\Phi _\infty ^0\in \mathscr {S}(V^{2r}\otimes _{\mathbb {A}_F}F_\infty )$ (Notation 4.2(H3)) and ![]() $\operatorname {\mathrm {vol}}^\natural (L)$ is defined in [Reference Li and LiuLL21, Definition 3.8].
$\operatorname {\mathrm {vol}}^\natural (L)$ is defined in [Reference Li and LiuLL21, Definition 3.8].
Proof. Part (1) is proved in the same way as [Reference Li and LiuLL21, Proposition 8.1]. Part (2) is proved in the same way as [Reference Li and LiuLL21, Proposition 9.1]. Note that we need to extend the definition of the integral model due to the presence of places in  $\mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {ram}}$, as we do in the previous subsection. The requirement that
$\mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {ram}}$, as we do in the previous subsection. The requirement that ![]() $\underline {u}\in \mathtt {V}_F^\heartsuit $ in (2) is to ensure that K is unramified over
$\underline {u}\in \mathtt {V}_F^\heartsuit $ in (2) is to ensure that K is unramified over ![]() $E_u$ (see Notation 4.19).
$E_u$ (see Notation 4.19).
4.5 Local indices at ramified places
In this subsection, we compute local indices at places in ![]() $\mathtt {V}_E^{\mathrm {ram}}$ not above
$\mathtt {V}_E^{\mathrm {ram}}$ not above ![]() $\mathtt {R}$.
$\mathtt {R}$.
Proposition 4.28. Let ![]() $\mathtt {R}$,
$\mathtt {R}$, ![]() $\mathtt {R}'$,
$\mathtt {R}'$, ![]() $\ell $ and L be as in Definition 4.15. Take an element
$\ell $ and L be as in Definition 4.15. Take an element ![]() $u\in \mathtt {V}_E^{\mathrm {ram}}$ such that its underlying rational prime p satisfies
$u\in \mathtt {V}_E^{\mathrm {ram}}$ such that its underlying rational prime p satisfies  $\mathtt {V}_F^{(p)}\cap \mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$. Then we have
$\mathtt {V}_F^{(p)}\cap \mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$. Then we have
 $$ \begin{align*} \log q_u\cdot \operatorname{\mathrm{vol}}^\natural(L)\cdot I_{T_1,T_2}(\phi^\infty_1,\phi^\infty_2,\mathrm{s}_1,\mathrm{s}_2,g_1,g_2)^\ell_{L,u} =\mathfrak{E}_{T_1,T_2}((g_1,g_2),\Phi_\infty^0\otimes(\mathrm{s}_1\phi^\infty_1\otimes(\mathrm{s}_2\phi^\infty_2)^{\mathtt{c}}))_u \end{align*} $$
$$ \begin{align*} \log q_u\cdot \operatorname{\mathrm{vol}}^\natural(L)\cdot I_{T_1,T_2}(\phi^\infty_1,\phi^\infty_2,\mathrm{s}_1,\mathrm{s}_2,g_1,g_2)^\ell_{L,u} =\mathfrak{E}_{T_1,T_2}((g_1,g_2),\Phi_\infty^0\otimes(\mathrm{s}_1\phi^\infty_1\otimes(\mathrm{s}_2\phi^\infty_2)^{\mathtt{c}}))_u \end{align*} $$for every ![]() $(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple
$(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple ![]() $(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ and every pair
$(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ and every pair ![]() $(T_1,T_2)$ in
$(T_1,T_2)$ in ![]() $\mathrm {Herm}_r^\circ (F)^+$, where the right-hand side is defined in Definition 4.10 with the Gaussian function
$\mathrm {Herm}_r^\circ (F)^+$, where the right-hand side is defined in Definition 4.10 with the Gaussian function ![]() $\Phi _\infty ^0\in \mathscr {S}(V^{2r}\otimes _{\mathbb {A}_F}F_\infty )$ (Notation 4.2(H3)) and
$\Phi _\infty ^0\in \mathscr {S}(V^{2r}\otimes _{\mathbb {A}_F}F_\infty )$ (Notation 4.2(H3)) and ![]() $\operatorname {\mathrm {vol}}^\natural (L)$ is defined in [Reference Li and LiuLL21, Definition 3.8].
$\operatorname {\mathrm {vol}}^\natural (L)$ is defined in [Reference Li and LiuLL21, Definition 3.8].
Proof. The proof of the proposition follows the same line as in [Reference Li and LiuLL21, Proposition 8.1], as long as we accomplish the following three tasks. We invoke Notation 4.18 together with Notation 4.19.
(1) Construct a good integral model
 $\mathcal {X}_{\tilde {L}}$ for
$\mathcal {X}_{\tilde {L}}$ for  $X_{\tilde {L}}$ over
$X_{\tilde {L}}$ over  $O_K$ for open compact subgroups
$O_K$ for open compact subgroups  $\tilde {L}\subseteq L$ satisfying
$\tilde {L}\subseteq L$ satisfying  $\tilde {L}_v=L_v$ for
$\tilde {L}_v=L_v$ for  $v\in \mathtt {V}_F^{(p)}\setminus \mathtt {V}_F^{\mathrm {spl}}$, which is provided after the proof.
$v\in \mathtt {V}_F^{(p)}\setminus \mathtt {V}_F^{\mathrm {spl}}$, which is provided after the proof.(2) Establish the non-Archimedean uniformisation of
 $\mathcal {X}_{\tilde {L}}$ along the supersingular locus using the relative Rapoport–Zink space
$\mathcal {X}_{\tilde {L}}$ along the supersingular locus using the relative Rapoport–Zink space  $\mathcal {N}$ from Definition 2.3, analogous to [Reference Li and LiuLL21, (8.2)], and compare special divisors. This is done in Proposition 4.30.
$\mathcal {N}$ from Definition 2.3, analogous to [Reference Li and LiuLL21, (8.2)], and compare special divisors. This is done in Proposition 4.30.(3) Show that for
 with
with  $T(x)\in \mathrm {Herm}_{2r}^\circ (F_{\underline {u}})$, we have if
$T(x)\in \mathrm {Herm}_{2r}^\circ (F_{\underline {u}})$, we have if
 $T(x)=T^\Box $. In fact, this follows from Theorem 2.7, Remark 2.18 and the identity
$T(x)=T^\Box $. In fact, this follows from Theorem 2.7, Remark 2.18 and the identity  $$ \begin{align*} b_{2r,\underline{u}}(0)=\prod_{i=1}^r(1-q_u^{-2i}). \end{align*} $$
$$ \begin{align*} b_{2r,\underline{u}}(0)=\prod_{i=1}^r(1-q_u^{-2i}). \end{align*} $$
The proposition is proved.
Let the situation be as in Proposition 4.28. The isomorphism  $\mathbb {C}\xrightarrow \sim \overline {\mathbb {Q}}_p$ in Notation 4.19 identifies
$\mathbb {C}\xrightarrow \sim \overline {\mathbb {Q}}_p$ in Notation 4.19 identifies ![]() $\operatorname {\mathrm {Hom}}(E,\mathbb {C})$ with
$\operatorname {\mathrm {Hom}}(E,\mathbb {C})$ with ![]() $\operatorname {\mathrm {Hom}}(E,\mathbb {C}_p)$. For every
$\operatorname {\mathrm {Hom}}(E,\mathbb {C}_p)$. For every  $v\in \mathtt {V}_F^{(p)}$, let
$v\in \mathtt {V}_F^{(p)}$, let ![]() $\Phi _v$ be the subset of
$\Phi _v$ be the subset of ![]() $\Phi $, regarded as a subset of
$\Phi $, regarded as a subset of ![]() $\operatorname {\mathrm {Hom}}(E,\mathbb {C}_p)$, of elements that induce the place v of F.
$\operatorname {\mathrm {Hom}}(E,\mathbb {C}_p)$, of elements that induce the place v of F.
To ease notation, put
 $$ \begin{align*} \mathtt{U} := \{v\in\mathtt{V}_F^{(p)}\setminus\mathtt{V}_F^{\mathrm{spl}}\mathbin{|} v\neq\underline{u}\}. \end{align*} $$
$$ \begin{align*} \mathtt{U} := \{v\in\mathtt{V}_F^{(p)}\setminus\mathtt{V}_F^{\mathrm{spl}}\mathbin{|} v\neq\underline{u}\}. \end{align*} $$In particular, ![]() $\mathtt {U}\cap \mathtt {R}=\emptyset $.
$\mathtt {U}\cap \mathtt {R}=\emptyset $.
There is a projective system ![]() $\{\mathcal {X}_{\tilde {L}}\}$, for open compact subgroups
$\{\mathcal {X}_{\tilde {L}}\}$, for open compact subgroups ![]() $\tilde {L}\subseteq L$ satisfying
$\tilde {L}\subseteq L$ satisfying ![]() $\tilde {L}_v=L_v$ for
$\tilde {L}_v=L_v$ for  $v\in \mathtt {V}_F^{(p)}\setminus \mathtt {V}_F^{\mathrm {spl}}$, of smooth projective schemes over
$v\in \mathtt {V}_F^{(p)}\setminus \mathtt {V}_F^{\mathrm {spl}}$, of smooth projective schemes over ![]() $O_K$ (see [Reference Rapoport and ZinkRSZ20, Theorem 4.7, AT type (2)]) with
$O_K$ (see [Reference Rapoport and ZinkRSZ20, Theorem 4.7, AT type (2)]) with
 $$ \begin{align*} \mathcal{X}_{\tilde{L}}\otimes_{O_K}K=X^{\prime}_{\tilde{L}}\otimes_{E'}K =\left(X_{\tilde{L}}\otimes_{E}Y\right)\otimes_{E'}K \end{align*} $$
$$ \begin{align*} \mathcal{X}_{\tilde{L}}\otimes_{O_K}K=X^{\prime}_{\tilde{L}}\otimes_{E'}K =\left(X_{\tilde{L}}\otimes_{E}Y\right)\otimes_{E'}K \end{align*} $$and finite étale transition morphisms such that for every  $S\in \operatorname {\mathrm {Sch}}^{\prime }_{/O_K}$,
$S\in \operatorname {\mathrm {Sch}}^{\prime }_{/O_K}$, ![]() $\mathcal {X}_{\tilde {L}}(S)$ is the set of equivalence classes of tuples
$\mathcal {X}_{\tilde {L}}(S)$ is the set of equivalence classes of tuples
 $$ \begin{align*} (A_0,\iota_{A_0},\lambda_{A_0},\eta_{A_0}^p;A,\iota_A,\lambda_A,\eta_A^p,\{\eta_{A,v}\}_{v\in\mathtt{V}_F^{(p)}\cap\mathtt{V}_F^{\mathrm{spl}}}) \end{align*} $$
$$ \begin{align*} (A_0,\iota_{A_0},\lambda_{A_0},\eta_{A_0}^p;A,\iota_A,\lambda_A,\eta_A^p,\{\eta_{A,v}\}_{v\in\mathtt{V}_F^{(p)}\cap\mathtt{V}_F^{\mathrm{spl}}}) \end{align*} $$where
•
 $(A_0,\iota _{A_0},\lambda _{A_0},\eta _{A_0}^p)$ is an element in
$(A_0,\iota _{A_0},\lambda _{A_0},\eta _{A_0}^p)$ is an element in  $\mathcal {Y}(S)$;
$\mathcal {Y}(S)$;•
 $(A,\iota _A,\lambda _A)$ is a unitary
$(A,\iota _A,\lambda _A)$ is a unitary  $O_E$-abelian scheme of signature type
$O_E$-abelian scheme of signature type  $n\Phi -\iota _w+\iota _w^{\mathtt {c}}$ over S, such that
$n\Phi -\iota _w+\iota _w^{\mathtt {c}}$ over S, such that– for every
 $v\in \mathtt {V}_F^{(p)}\setminus \mathtt {V}_F^{\mathrm {ram}}$,
$v\in \mathtt {V}_F^{(p)}\setminus \mathtt {V}_F^{\mathrm {ram}}$,  $\lambda _A[v^\infty ]$ is an isogeny whose kernel has order
$\lambda _A[v^\infty ]$ is an isogeny whose kernel has order  $q_v^{1-\epsilon _v}$;
$q_v^{1-\epsilon _v}$;– for every
 $v\in \mathtt {U}\cap \mathtt {V}_F^{\mathrm {ram}}$, the triple
$v\in \mathtt {U}\cap \mathtt {V}_F^{\mathrm {ram}}$, the triple  $(A_0[v^\infty ],\iota _{A_0}[v^\infty ],\lambda _{A_0}[v^\infty ])\otimes _{O_K}O_{\breve {K}}$ is an object of
$(A_0[v^\infty ],\iota _{A_0}[v^\infty ],\lambda _{A_0}[v^\infty ])\otimes _{O_K}O_{\breve {K}}$ is an object of  $\mathrm {Exo}_{(n,0)}^{\Phi _v}(S\otimes _{O_K}O_{\breve {K}})$ (Remark 2.67, with
$\mathrm {Exo}_{(n,0)}^{\Phi _v}(S\otimes _{O_K}O_{\breve {K}})$ (Remark 2.67, with  $E=E_v$,
$E=E_v$,  $F=F_v$ and
$F=F_v$ and  $\breve {E}=\breve {K}$);
$\breve {E}=\breve {K}$);– for
 $v=\underline {u}$, the triple
$v=\underline {u}$, the triple  $(A_0[v^\infty ],\iota _{A_0}[v^\infty ],\lambda _{A_0}[v^\infty ])\otimes _{O_K}O_{\breve {K}}$ is an object of
$(A_0[v^\infty ],\iota _{A_0}[v^\infty ],\lambda _{A_0}[v^\infty ])\otimes _{O_K}O_{\breve {K}}$ is an object of  $\mathrm {Exo}_{(n-1,1)}^{\Phi _v}(S\otimes _{O_K}O_{\breve {K}})$ (Definition 2.59, with
$\mathrm {Exo}_{(n-1,1)}^{\Phi _v}(S\otimes _{O_K}O_{\breve {K}})$ (Definition 2.59, with  $E=E_v$,
$E=E_v$,  $F=F_v$ and
$F=F_v$ and  $\breve {E}=\breve {K}$);
$\breve {E}=\breve {K}$);
•
 $\eta _A^p$ is an
$\eta _A^p$ is an  $\tilde {L}^p$-level structure;
$\tilde {L}^p$-level structure;• for every
 $v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {spl}}$,
$v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {spl}}$,  $\eta _{A,v}$ is an
$\eta _{A,v}$ is an  $\tilde {L}_v$-level structure.
$\tilde {L}_v$-level structure.
In particular, ![]() $\mathbb {S}^{\mathtt {R}}$ is naturally a ring of étale correspondences of
$\mathbb {S}^{\mathtt {R}}$ is naturally a ring of étale correspondences of ![]() $\mathcal {X}_L$.
$\mathcal {X}_L$.
Let  $\phi ^\infty \in \mathscr {S}(V\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^{\tilde {L}}$ be a p-basic element [Reference Li and LiuLL21, Definition 6.5]. For every element
$\phi ^\infty \in \mathscr {S}(V\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^{\tilde {L}}$ be a p-basic element [Reference Li and LiuLL21, Definition 6.5]. For every element ![]() $t\in F$ that is totally positive, we have a cycle
$t\in F$ that is totally positive, we have a cycle ![]() $\mathcal {Z}_t(\phi ^\infty )_{\tilde {L}}\in \mathrm {Z}^1(\mathcal {X}_{\tilde {L}})$ extending the restriction of
$\mathcal {Z}_t(\phi ^\infty )_{\tilde {L}}\in \mathrm {Z}^1(\mathcal {X}_{\tilde {L}})$ extending the restriction of ![]() $Z_t(\phi ^\infty )$ to
$Z_t(\phi ^\infty )$ to ![]() $X^{\prime }_{\tilde {L}}$, defined similarly as in [Reference Li and ZhangLZa, Section 13.3].
$X^{\prime }_{\tilde {L}}$, defined similarly as in [Reference Li and ZhangLZa, Section 13.3].
Now we study the non-Archimedean uniformisation of ![]() $\mathcal {X}_{\tilde {L}}$ along the supersingular locus. Fix a point
$\mathcal {X}_{\tilde {L}}$ along the supersingular locus. Fix a point  $P_0 := (A_0,\iota _{A_0},\lambda _{A_0},\eta _{A_0}^p)\in \mathcal {Y}(O_{\breve {K}})$. Put
$P_0 := (A_0,\iota _{A_0},\lambda _{A_0},\eta _{A_0}^p)\in \mathcal {Y}(O_{\breve {K}})$. Put
 $$ \begin{align*} \mathcal{X} := \varprojlim_{\tilde{L}}\mathcal{X}_{\tilde{L}} \end{align*} $$
$$ \begin{align*} \mathcal{X} := \varprojlim_{\tilde{L}}\mathcal{X}_{\tilde{L}} \end{align*} $$and denote by ![]() $\mathcal {X}_0$ the fibre of
$\mathcal {X}_0$ the fibre of ![]() $P_0$ along the natural projection
$P_0$ along the natural projection ![]() $\mathcal {X}\to \mathcal {Y}$. Let
$\mathcal {X}\to \mathcal {Y}$. Let ![]() $\mathcal {X}_0^\wedge $ be the completion along the (closed) locus where
$\mathcal {X}_0^\wedge $ be the completion along the (closed) locus where ![]() $A[u^\infty ]$ is supersingular, as a formal scheme over
$A[u^\infty ]$ is supersingular, as a formal scheme over ![]() $\operatorname {\mathrm {Spf}} O_K$. We also fix a point
$\operatorname {\mathrm {Spf}} O_K$. We also fix a point  $\boldsymbol {P}\in \mathcal {X}_0^\wedge (\overline {\mathbb {F}}_p)$ represented by
$\boldsymbol {P}\in \mathcal {X}_0^\wedge (\overline {\mathbb {F}}_p)$ represented by  $(P_0\otimes _{O_{\breve {K}}}\overline {\mathbb {F}}_p;\boldsymbol {A},\iota _{\boldsymbol {A}},\lambda _{\boldsymbol {A}},\eta _{\boldsymbol {A}}^p,\{\eta _{\boldsymbol {A},v}\}_{v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {spl}}})$.
$(P_0\otimes _{O_{\breve {K}}}\overline {\mathbb {F}}_p;\boldsymbol {A},\iota _{\boldsymbol {A}},\lambda _{\boldsymbol {A}},\eta _{\boldsymbol {A}}^p,\{\eta _{\boldsymbol {A},v}\}_{v\in \mathtt {V}_F^{(p)}\cap \mathtt {V}_F^{\mathrm {spl}}})$.
Put  $\boldsymbol {V} := \operatorname {\mathrm {Hom}}_{O_E}(A_0\otimes _{O_{\breve {E}}}\overline {\mathbb {F}}_p,\boldsymbol {A})\otimes \mathbb {Q}$. Fixing an element
$\boldsymbol {V} := \operatorname {\mathrm {Hom}}_{O_E}(A_0\otimes _{O_{\breve {E}}}\overline {\mathbb {F}}_p,\boldsymbol {A})\otimes \mathbb {Q}$. Fixing an element ![]() $\varpi \in O_F$ that has valuation
$\varpi \in O_F$ that has valuation ![]() $0$ (respectively
$0$ (respectively ![]() $1$) at places in
$1$) at places in  $\mathtt {U}\cap \mathtt {V}_F^{\mathrm {int}}$ (respectively,
$\mathtt {U}\cap \mathtt {V}_F^{\mathrm {int}}$ (respectively, ![]() $\mathtt {U}\cap \mathtt {V}_F^{\mathrm {ram}}$), we have a pairing
$\mathtt {U}\cap \mathtt {V}_F^{\mathrm {ram}}$), we have a pairing
sending ![]() $(x,y)\in \boldsymbol {V}^2$ to the composition of quasi-homomorphisms
$(x,y)\in \boldsymbol {V}^2$ to the composition of quasi-homomorphisms
 $$ \begin{align*} A_0\xrightarrow{x}\boldsymbol{X}\xrightarrow{\lambda_{\boldsymbol{A}}}\boldsymbol{A}^\vee\xrightarrow{y^\vee}A_0^\vee\xrightarrow{\varpi^{-1}\lambda_{A_0}^{-1}}A_0 \end{align*} $$
$$ \begin{align*} A_0\xrightarrow{x}\boldsymbol{X}\xrightarrow{\lambda_{\boldsymbol{A}}}\boldsymbol{A}^\vee\xrightarrow{y^\vee}A_0^\vee\xrightarrow{\varpi^{-1}\lambda_{A_0}^{-1}}A_0 \end{align*} $$as an element in ![]() $\operatorname {\mathrm {End}}_{O_E}(A_0)\otimes \mathbb {Q}$ and hence in E via
$\operatorname {\mathrm {End}}_{O_E}(A_0)\otimes \mathbb {Q}$ and hence in E via ![]() $\iota _{A_0}^{-1}$. We have the following properties concerning
$\iota _{A_0}^{-1}$. We have the following properties concerning ![]() $\boldsymbol {V}$:
$\boldsymbol {V}$:
•
 $\boldsymbol {V},(\,,\,)_{\boldsymbol {V}}$ is a totally positive definite hermitian space over E of rank n;
$\boldsymbol {V},(\,,\,)_{\boldsymbol {V}}$ is a totally positive definite hermitian space over E of rank n;• for every
 $v\in \mathtt {V}_F^{\mathrm {fin}}\setminus (\mathtt {V}_F^{(p)}\setminus \mathtt {V}_F^{\mathrm {spl}})$, we have a canonical isometry
$v\in \mathtt {V}_F^{\mathrm {fin}}\setminus (\mathtt {V}_F^{(p)}\setminus \mathtt {V}_F^{\mathrm {spl}})$, we have a canonical isometry  $\boldsymbol {V}\otimes _FF_v\simeq V\otimes _FF_v$ of hermitian spaces;
$\boldsymbol {V}\otimes _FF_v\simeq V\otimes _FF_v$ of hermitian spaces;• for every
 $v\in \mathtt {U}$, the
$v\in \mathtt {U}$, the  $O_{E_v}$-lattice
$O_{E_v}$-lattice  $\boldsymbol {\Lambda }_v := \operatorname {\mathrm {Hom}}_{O_E}(A_0\otimes _{O_{\breve {E}}}\overline {\mathbb {F}}_p,\boldsymbol {A})\otimes _{O_F}O_{F_v}$ is
$\boldsymbol {\Lambda }_v := \operatorname {\mathrm {Hom}}_{O_E}(A_0\otimes _{O_{\breve {E}}}\overline {\mathbb {F}}_p,\boldsymbol {A})\otimes _{O_F}O_{F_v}$ is– self-dual if
 $v\in \mathtt {U}\cap \mathtt {V}_F^{\mathrm {int}}$ and
$v\in \mathtt {U}\cap \mathtt {V}_F^{\mathrm {int}}$ and  $\epsilon _v=1$,
$\epsilon _v=1$,– almost self-dual if
 $v\in \mathtt {U}\cap \mathtt {V}_F^{\mathrm {int}}$ and
$v\in \mathtt {U}\cap \mathtt {V}_F^{\mathrm {int}}$ and  $\epsilon _v=-1$,
$\epsilon _v=-1$,– self-dual if
 $v\in \mathtt {U}\cap \mathtt {V}_F^{\mathrm {ram}}$;
$v\in \mathtt {U}\cap \mathtt {V}_F^{\mathrm {ram}}$;
•
 $\boldsymbol {V}\otimes _FF_{\underline {u}}$ is nonsplit and we have a canonical isomorphism of hermitian spaces over
$\boldsymbol {V}\otimes _FF_{\underline {u}}$ is nonsplit and we have a canonical isomorphism of hermitian spaces over $$ \begin{align*} \boldsymbol{V}\otimes_FF_{\underline{u}}\simeq\operatorname{\mathrm{Hom}}_{O_{E_u}}(A_0[u^\infty]\otimes_{O_{\breve{K}}}\overline{\mathbb{F}}_p,\boldsymbol{A}[u^\infty])\otimes\mathbb{Q} \end{align*} $$
$$ \begin{align*} \boldsymbol{V}\otimes_FF_{\underline{u}}\simeq\operatorname{\mathrm{Hom}}_{O_{E_u}}(A_0[u^\infty]\otimes_{O_{\breve{K}}}\overline{\mathbb{F}}_p,\boldsymbol{A}[u^\infty])\otimes\mathbb{Q} \end{align*} $$ $E_u$.
$E_u$.
We have a Rapoport–Zink space ![]() $\mathcal {N}$ (Definition 2.3, with
$\mathcal {N}$ (Definition 2.3, with ![]() $E=E_u$,
$E=E_u$, ![]() $F=F_{\underline {u}}$,
$F=F_{\underline {u}}$, ![]() $\breve {E}=\breve {K}$ and
$\breve {E}=\breve {K}$ and ![]() $\varphi _0$ the natural embedding) with respect to the object
$\varphi _0$ the natural embedding) with respect to the object
 $$ \begin{align*} (\boldsymbol{X},\iota_{\boldsymbol{X}},\lambda_{\boldsymbol{X}}) := (\boldsymbol{A}[u^\infty],\iota_{\boldsymbol{A}}[u^\infty],\lambda_{\boldsymbol{A}}[u^\infty])^{\mathrm{rel}} \in\mathrm{Exo}_{(n-1,1)}^{\mathrm{b}}(\overline{\mathbb{F}}_p), \end{align*} $$
$$ \begin{align*} (\boldsymbol{X},\iota_{\boldsymbol{X}},\lambda_{\boldsymbol{X}}) := (\boldsymbol{A}[u^\infty],\iota_{\boldsymbol{A}}[u^\infty],\lambda_{\boldsymbol{A}}[u^\infty])^{\mathrm{rel}} \in\mathrm{Exo}_{(n-1,1)}^{\mathrm{b}}(\overline{\mathbb{F}}_p), \end{align*} $$where ![]() $-^{\mathrm {rel}}$ is the morphism (2.22). We now construct a morphism
$-^{\mathrm {rel}}$ is the morphism (2.22). We now construct a morphism
 $$ \begin{align} \Upsilon^{\mathrm{rel}}\colon\mathcal{X}_0^\wedge\to\mathrm{U}(\boldsymbol{V})(F)\backslash\left(\mathcal{N}\times\mathrm{U}(\boldsymbol{V})(\mathbb{A}_F^{\infty,\underline{u}})/\prod_{v\in\mathtt{U}}\boldsymbol{L}_v\right) \end{align} $$
$$ \begin{align} \Upsilon^{\mathrm{rel}}\colon\mathcal{X}_0^\wedge\to\mathrm{U}(\boldsymbol{V})(F)\backslash\left(\mathcal{N}\times\mathrm{U}(\boldsymbol{V})(\mathbb{A}_F^{\infty,\underline{u}})/\prod_{v\in\mathtt{U}}\boldsymbol{L}_v\right) \end{align} $$of formal schemes over ![]() $\operatorname {\mathrm {Spf}} O_{\breve {K}}$, where
$\operatorname {\mathrm {Spf}} O_{\breve {K}}$, where ![]() $\boldsymbol {L}_v$ is the stabiliser of
$\boldsymbol {L}_v$ is the stabiliser of ![]() $\boldsymbol {\Lambda }_v$ in
$\boldsymbol {\Lambda }_v$ in ![]() $\mathrm {U}(\boldsymbol {V})(F_v)$, as follows.
$\mathrm {U}(\boldsymbol {V})(F_v)$, as follows.
We have the Rapoport–Zink space  $\mathcal {N}^{\Phi _u}=\mathcal {N}^{\Phi _u}_{(\boldsymbol {A}[u^\infty ],\iota _{\boldsymbol {A}}[u^\infty ],\lambda _{\boldsymbol {A}}[u^\infty ])}$ from Definition 2.64. We first define a morphism
$\mathcal {N}^{\Phi _u}=\mathcal {N}^{\Phi _u}_{(\boldsymbol {A}[u^\infty ],\iota _{\boldsymbol {A}}[u^\infty ],\lambda _{\boldsymbol {A}}[u^\infty ])}$ from Definition 2.64. We first define a morphism
 $$ \begin{align*} \Upsilon\colon\mathcal{X}_0^\wedge\to\mathrm{U}(\boldsymbol{V})(F)\backslash\left(\mathcal{N}^{\Phi_u}\times\mathrm{U}(\boldsymbol{V})(\mathbb{A}_F^{\infty,\underline{u}})/\prod_{v\in\mathtt{U}}\boldsymbol{L}_v\right) \end{align*} $$
$$ \begin{align*} \Upsilon\colon\mathcal{X}_0^\wedge\to\mathrm{U}(\boldsymbol{V})(F)\backslash\left(\mathcal{N}^{\Phi_u}\times\mathrm{U}(\boldsymbol{V})(\mathbb{A}_F^{\infty,\underline{u}})/\prod_{v\in\mathtt{U}}\boldsymbol{L}_v\right) \end{align*} $$and then define ![]() $\Upsilon ^{\mathrm {rel}}$ as the composition of
$\Upsilon ^{\mathrm {rel}}$ as the composition of ![]() $\Upsilon $ with the morphism in Corollary 2.65. To construct
$\Upsilon $ with the morphism in Corollary 2.65. To construct ![]() $\Upsilon $, we take a point
$\Upsilon $, we take a point
 $$ \begin{align*} P=(P_0\otimes_{O_{\breve{K}}}S;A,\iota_A,\lambda_A,\eta_A^p,\{\eta_{A,v}\}_{v\in\mathtt{V}_F^{(p)}\cap\mathtt{V}_F^{\mathrm{spl}}})\in\mathcal{X}_0^\wedge(S) \end{align*} $$
$$ \begin{align*} P=(P_0\otimes_{O_{\breve{K}}}S;A,\iota_A,\lambda_A,\eta_A^p,\{\eta_{A,v}\}_{v\in\mathtt{V}_F^{(p)}\cap\mathtt{V}_F^{\mathrm{spl}}})\in\mathcal{X}_0^\wedge(S) \end{align*} $$ for a connected scheme S in  $\operatorname {\mathrm {Sch}}^{\prime }_{/O_{\breve {K}}}\cap \operatorname {\mathrm {Sch}}_{/O_{\breve {K}}}^{\mathrm {v}}$ with a geometric point s. In particular,
$\operatorname {\mathrm {Sch}}^{\prime }_{/O_{\breve {K}}}\cap \operatorname {\mathrm {Sch}}_{/O_{\breve {K}}}^{\mathrm {v}}$ with a geometric point s. In particular, ![]() $A[p^\infty ]$ is supersingular. By [Reference Rapoport, Smithling and ZhangRZ96, Proposition 6.29], we can choose an
$A[p^\infty ]$ is supersingular. By [Reference Rapoport, Smithling and ZhangRZ96, Proposition 6.29], we can choose an ![]() $O_E$-linear quasi-isogeny
$O_E$-linear quasi-isogeny
 $$ \begin{align*} \rho\colon A\times_S(S\otimes_{O_{\breve{K}}}\overline{\mathbb{F}}_p)\to\boldsymbol{A}\otimes_{\overline{\mathbb{F}}_p}(S\otimes_{O_{\breve{K}}}\overline{\mathbb{F}}_p) \end{align*} $$
$$ \begin{align*} \rho\colon A\times_S(S\otimes_{O_{\breve{K}}}\overline{\mathbb{F}}_p)\to\boldsymbol{A}\otimes_{\overline{\mathbb{F}}_p}(S\otimes_{O_{\breve{K}}}\overline{\mathbb{F}}_p) \end{align*} $$of height zero such that  $\rho ^*\lambda _{\boldsymbol {A}}\otimes _{\overline {\mathbb {F}}_p}(S\otimes _{O_{\breve {K}}}\overline {\mathbb {F}}_p)=\lambda _A\times _S(S\otimes _{O_{\breve {K}}}\overline {\mathbb {F}}_p)$. We have
$\rho ^*\lambda _{\boldsymbol {A}}\otimes _{\overline {\mathbb {F}}_p}(S\otimes _{O_{\breve {K}}}\overline {\mathbb {F}}_p)=\lambda _A\times _S(S\otimes _{O_{\breve {K}}}\overline {\mathbb {F}}_p)$. We have
•
 $(A[u^\infty ],\iota _A[u^\infty ],\lambda _A[u^\infty ];\rho [u^\infty ])$ is an element in
$(A[u^\infty ],\iota _A[u^\infty ],\lambda _A[u^\infty ];\rho [u^\infty ])$ is an element in  $\mathcal {N}^{\Phi _u}(S)$;
$\mathcal {N}^{\Phi _u}(S)$;• the composite map
is an isometry, which gives rise to an element $$ \begin{align*} \boldsymbol{V}\otimes_{\mathbb{Q}}\mathbb{A}^{\infty,p}&\xrightarrow{\sim}V\otimes_{\mathbb{Q}}\mathbb{A}^{\infty,p}\xrightarrow{\eta_A^p} \operatorname{\mathrm{Hom}}_{E\otimes_{\mathbb{Q}}\mathbb{A}^{\infty,p}}(\mathrm{H}_1(A_{0,s},\mathbb{A}^{\infty,p}),\mathrm{H}_1(A_s,\mathbb{A}^{\infty,p})) \\ &\xrightarrow{\rho_{s*}\circ}\operatorname{\mathrm{Hom}}_{E\otimes_{\mathbb{Q}}\mathbb{A}^{\infty,p}}(\mathrm{H}_1(A_{0,s},\mathbb{A}^{\infty,p}),\mathrm{H}_1(\boldsymbol{A}_s,\mathbb{A}^{\infty,p})) =\boldsymbol{V}\otimes_{\mathbb{Q}}\mathbb{A}^{\infty,p} \end{align*} $$
$$ \begin{align*} \boldsymbol{V}\otimes_{\mathbb{Q}}\mathbb{A}^{\infty,p}&\xrightarrow{\sim}V\otimes_{\mathbb{Q}}\mathbb{A}^{\infty,p}\xrightarrow{\eta_A^p} \operatorname{\mathrm{Hom}}_{E\otimes_{\mathbb{Q}}\mathbb{A}^{\infty,p}}(\mathrm{H}_1(A_{0,s},\mathbb{A}^{\infty,p}),\mathrm{H}_1(A_s,\mathbb{A}^{\infty,p})) \\ &\xrightarrow{\rho_{s*}\circ}\operatorname{\mathrm{Hom}}_{E\otimes_{\mathbb{Q}}\mathbb{A}^{\infty,p}}(\mathrm{H}_1(A_{0,s},\mathbb{A}^{\infty,p}),\mathrm{H}_1(\boldsymbol{A}_s,\mathbb{A}^{\infty,p})) =\boldsymbol{V}\otimes_{\mathbb{Q}}\mathbb{A}^{\infty,p} \end{align*} $$ $h^p\in \mathrm {U}(\boldsymbol {V})(\mathbb {A}_F^{\infty ,p})$;
$h^p\in \mathrm {U}(\boldsymbol {V})(\mathbb {A}_F^{\infty ,p})$;• the same process as above will produce an element
 $$ \begin{align*} h_p^{\mathrm{spl}}\in\prod_{v\in\mathtt{V}_F^{(p)}\cap\mathtt{V}_F^{\mathrm{spl}}}\mathrm{U}(\boldsymbol{V})(F_v); \end{align*} $$
$$ \begin{align*} h_p^{\mathrm{spl}}\in\prod_{v\in\mathtt{V}_F^{(p)}\cap\mathtt{V}_F^{\mathrm{spl}}}\mathrm{U}(\boldsymbol{V})(F_v); \end{align*} $$• for every
 $v\in \mathtt {U}$, the image of the map is an
$v\in \mathtt {U}$, the image of the map is an $$ \begin{align*} \rho_{s*}\circ\colon\operatorname{\mathrm{Hom}}_{O_{E_v}}(A_{0,s}[v^\infty],A_s[v^\infty])\to\operatorname{\mathrm{Hom}}_{O_{E_v}}(A_{0,s}[v^\infty],\boldsymbol{A}_s[v^\infty])\otimes\mathbb{Q} =\boldsymbol{V}\otimes_FF_v \end{align*} $$
$$ \begin{align*} \rho_{s*}\circ\colon\operatorname{\mathrm{Hom}}_{O_{E_v}}(A_{0,s}[v^\infty],A_s[v^\infty])\to\operatorname{\mathrm{Hom}}_{O_{E_v}}(A_{0,s}[v^\infty],\boldsymbol{A}_s[v^\infty])\otimes\mathbb{Q} =\boldsymbol{V}\otimes_FF_v \end{align*} $$ $O_{E_v}$-lattice in the same
$O_{E_v}$-lattice in the same  $\mathrm {U}(\boldsymbol {V})(F_v)$-orbit of
$\mathrm {U}(\boldsymbol {V})(F_v)$-orbit of  $\boldsymbol {\Lambda }_v$, which gives rise to an element
$\boldsymbol {\Lambda }_v$, which gives rise to an element  $h_v\in \mathrm {U}(\boldsymbol {V})(F_v)/\boldsymbol {L}_v$.
$h_v\in \mathrm {U}(\boldsymbol {V})(F_v)/\boldsymbol {L}_v$.
Together, we obtain an element
 $$ \begin{align*} \left((A[u^\infty],\iota_A[u^\infty],\lambda_A[u^\infty];\rho[u^\infty]),(h^p,h_p^{\mathrm{spl}},\{h_v\}_{v\in\mathtt{U}})\right) \in\mathcal{N}^{\Phi_u}(S)\times\mathrm{U}(\boldsymbol{V})(\mathbb{A}_F^{\infty,\underline{u}})/\prod_{v\in\mathtt{U}}\boldsymbol{L}_v, \end{align*} $$
$$ \begin{align*} \left((A[u^\infty],\iota_A[u^\infty],\lambda_A[u^\infty];\rho[u^\infty]),(h^p,h_p^{\mathrm{spl}},\{h_v\}_{v\in\mathtt{U}})\right) \in\mathcal{N}^{\Phi_u}(S)\times\mathrm{U}(\boldsymbol{V})(\mathbb{A}_F^{\infty,\underline{u}})/\prod_{v\in\mathtt{U}}\boldsymbol{L}_v, \end{align*} $$and we define ![]() $\Upsilon (P)$ to be its image in the quotient, which is independent of the choice of
$\Upsilon (P)$ to be its image in the quotient, which is independent of the choice of ![]() $\rho $.
$\rho $.
Remark 4.29. Both ![]() $\boldsymbol {V}$ and
$\boldsymbol {V}$ and ![]() $\Upsilon ^{\mathrm {rel}}$ depend on the choice of
$\Upsilon ^{\mathrm {rel}}$ depend on the choice of ![]() $\boldsymbol {P}$, while the isometry class of
$\boldsymbol {P}$, while the isometry class of ![]() $\boldsymbol {V}$ does not.
$\boldsymbol {V}$ does not.
Proposition 4.30. The morphism ![]() $\Upsilon ^{\mathrm {rel}}$ (4.8) is an isomorphism. Moreover, for every p-basic element
$\Upsilon ^{\mathrm {rel}}$ (4.8) is an isomorphism. Moreover, for every p-basic element  $\phi ^\infty \in \mathscr {S}(V\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^{\tilde {L}}$ and every
$\phi ^\infty \in \mathscr {S}(V\otimes _{\mathbb {A}_F}\mathbb {A}_F^\infty )^{\tilde {L}}$ and every ![]() $t\in F$ that is totally positive, we have
$t\in F$ that is totally positive, we have
 $$ \begin{align} \Upsilon^{\mathrm{rel}}\left(\mathcal{Z}_t(\phi^\infty)_{\tilde{L}}\mathbin{|}_{\mathcal{X}_0^\wedge}\right) =\sum_{\substack{x\in\mathrm{U}(\boldsymbol{V})(F)\backslash\boldsymbol{V} \\ (x,x)_{\boldsymbol{V}}=t}} \sum_{h\in\mathrm{U}(\boldsymbol{V}^x)(F)\backslash\mathrm{U}(\boldsymbol{V})(\mathbb{A}_F^{\infty,\underline{u}})/\prod_{v\in\mathtt{U}}\boldsymbol{L}_v}\boldsymbol{\phi}(h^{-1}x)\cdot (\mathcal{N}(x^{\mathrm{rel}}),h), \end{align} $$
$$ \begin{align} \Upsilon^{\mathrm{rel}}\left(\mathcal{Z}_t(\phi^\infty)_{\tilde{L}}\mathbin{|}_{\mathcal{X}_0^\wedge}\right) =\sum_{\substack{x\in\mathrm{U}(\boldsymbol{V})(F)\backslash\boldsymbol{V} \\ (x,x)_{\boldsymbol{V}}=t}} \sum_{h\in\mathrm{U}(\boldsymbol{V}^x)(F)\backslash\mathrm{U}(\boldsymbol{V})(\mathbb{A}_F^{\infty,\underline{u}})/\prod_{v\in\mathtt{U}}\boldsymbol{L}_v}\boldsymbol{\phi}(h^{-1}x)\cdot (\mathcal{N}(x^{\mathrm{rel}}),h), \end{align} $$where
•
 $\boldsymbol {V}^x$ denotes the orthogonal complement of x in
$\boldsymbol {V}^x$ denotes the orthogonal complement of x in  $\boldsymbol {V}$;
$\boldsymbol {V}$;•
 $\boldsymbol {\phi }$ is a Schwartz function on
$\boldsymbol {\phi }$ is a Schwartz function on  $\boldsymbol {V}\otimes _F\mathbb {A}_F^{\infty ,\underline {u}}$ such that
$\boldsymbol {V}\otimes _F\mathbb {A}_F^{\infty ,\underline {u}}$ such that  $\boldsymbol {\phi }_v=\phi ^\infty _v$ for
$\boldsymbol {\phi }_v=\phi ^\infty _v$ for  $v\in \mathtt {V}_F^{\mathrm {fin}}\setminus (\mathtt {V}_F^{(p)}\setminus \mathtt {V}_F^{\mathrm {spl}})$ and
$v\in \mathtt {V}_F^{\mathrm {fin}}\setminus (\mathtt {V}_F^{(p)}\setminus \mathtt {V}_F^{\mathrm {spl}})$ and  for
for  $v\in \mathtt {U}$;
$v\in \mathtt {U}$;•
 $x^{\mathrm {rel}}$ is defined in (2.26); and
$x^{\mathrm {rel}}$ is defined in (2.26); and•
 $(\mathcal {N}(x^{\mathrm {rel}}),h)$ denotes the corresponding double coset in (4.8).
$(\mathcal {N}(x^{\mathrm {rel}}),h)$ denotes the corresponding double coset in (4.8).
Proof. By a similar argument for [Reference Rapoport, Smithling and ZhangRZ96, Theorem 6.30], the morphism ![]() $\Upsilon $ is an isomorphism. Thus,
$\Upsilon $ is an isomorphism. Thus, ![]() $\Upsilon ^{\mathrm {rel}}$ is an isomorphism as well by Corollary 2.65.
$\Upsilon ^{\mathrm {rel}}$ is an isomorphism as well by Corollary 2.65.
For (4.9), by a similar argument for [Reference LiuLiu21, Theorem 5.22], the identity holds with ![]() $\mathcal {N}(x^{\mathrm {rel}})$ replaced by
$\mathcal {N}(x^{\mathrm {rel}})$ replaced by ![]() $\mathcal {N}^{\Phi _u}(x)$. Then it follows by Corollary 2.66.
$\mathcal {N}^{\Phi _u}(x)$. Then it follows by Corollary 2.66.
The proposition is proved.
4.6 Local indices at Archimedean places
In this subsection, we compute local indices at places in  $\mathtt {V}_E^{(\infty )}$.
$\mathtt {V}_E^{(\infty )}$.
Proposition 4.31. Let ![]() $\mathtt {R}$,
$\mathtt {R}$, ![]() $\mathtt {R}'$,
$\mathtt {R}'$, ![]() $\ell $ and L be as in Definition 4.15. Let
$\ell $ and L be as in Definition 4.15. Let ![]() $(\pi ,\mathcal {V}_\pi )$ be as in Assumption 4.4. Take an element
$(\pi ,\mathcal {V}_\pi )$ be as in Assumption 4.4. Take an element  $u\in \mathtt {V}_E^{(\infty )}$. Consider an
$u\in \mathtt {V}_E^{(\infty )}$. Consider an ![]() $(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple
$(\mathtt {R},\mathtt {R}',\ell ,L)$-admissible sextuple ![]() $(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ and an element
$(\phi ^\infty _1,\phi ^\infty _2,\mathrm {s}_1,\mathrm {s}_2,g_1,g_2)$ and an element  $\varphi _1\in \mathcal {V}_\pi ^{[r]\mathtt {R}}$. Let
$\varphi _1\in \mathcal {V}_\pi ^{[r]\mathtt {R}}$. Let ![]() $K_1\subseteq G_r(\mathbb {A}_F^\infty )$ be an open compact subgroup that fixes both
$K_1\subseteq G_r(\mathbb {A}_F^\infty )$ be an open compact subgroup that fixes both ![]() $\phi ^\infty _1$ and
$\phi ^\infty _1$ and ![]() $\varphi _1$ and
$\varphi _1$ and ![]() $\mathfrak {F}_1\subseteq G_r(F_\infty )$ a Siegel fundamental domain for the congruence subgroup
$\mathfrak {F}_1\subseteq G_r(F_\infty )$ a Siegel fundamental domain for the congruence subgroup  $G_r(F)\cap g_1^\infty K_1 (g_1^\infty )^{-1}$. Then for every
$G_r(F)\cap g_1^\infty K_1 (g_1^\infty )^{-1}$. Then for every ![]() $T_2\in \mathrm {Herm}_r^\circ (F)^+$, we have
$T_2\in \mathrm {Herm}_r^\circ (F)^+$, we have
 $$ \begin{align*} &\operatorname{\mathrm{vol}}^\natural(L)\cdot\int_{\mathfrak{F}_1}\varphi^{\mathtt{c}}(\tau_1g_1) \sum_{T_1\in\mathrm{Herm}_r^\circ(F)^+}I_{T_1,T_2}(\phi^\infty_1,\phi^\infty_2,\mathrm{s}_1,\mathrm{s}_2,\tau_1g_1,g_2)_{L,u}\,\mathrm{d}\tau_1 \\ &=\frac{1}{2}\int_{\mathfrak{F}_1}\varphi^{\mathtt{c}}(\tau_1g_1)\sum_{T_1\in\mathrm{Herm}_r^\circ(F)^+} \mathfrak{E}_{T_1,T_2}((\tau_1g_1,g_2),\Phi_\infty^0\otimes(\mathrm{s}_1\phi^\infty_1\otimes(\mathrm{s}_2\phi^\infty_2)^{\mathtt{c}}))_u\,\mathrm{d}\tau_1, \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{vol}}^\natural(L)\cdot\int_{\mathfrak{F}_1}\varphi^{\mathtt{c}}(\tau_1g_1) \sum_{T_1\in\mathrm{Herm}_r^\circ(F)^+}I_{T_1,T_2}(\phi^\infty_1,\phi^\infty_2,\mathrm{s}_1,\mathrm{s}_2,\tau_1g_1,g_2)_{L,u}\,\mathrm{d}\tau_1 \\ &=\frac{1}{2}\int_{\mathfrak{F}_1}\varphi^{\mathtt{c}}(\tau_1g_1)\sum_{T_1\in\mathrm{Herm}_r^\circ(F)^+} \mathfrak{E}_{T_1,T_2}((\tau_1g_1,g_2),\Phi_\infty^0\otimes(\mathrm{s}_1\phi^\infty_1\otimes(\mathrm{s}_2\phi^\infty_2)^{\mathtt{c}}))_u\,\mathrm{d}\tau_1, \end{align*} $$in which both sides are absolutely convergent. Here, the term ![]() $\mathfrak {E}_{T_1,T_2}$ is defined in Definition 4.10 with the Gaussian function
$\mathfrak {E}_{T_1,T_2}$ is defined in Definition 4.10 with the Gaussian function ![]() $\Phi _\infty ^0\in \mathscr {S}(V^{2r}\otimes _{\mathbb {A}_F}F_\infty )$ (Notation 4.2(H3)) and
$\Phi _\infty ^0\in \mathscr {S}(V^{2r}\otimes _{\mathbb {A}_F}F_\infty )$ (Notation 4.2(H3)) and ![]() $\operatorname {\mathrm {vol}}^\natural (L)$ is defined in [Reference Li and LiuLL21, Definition 3.8].
$\operatorname {\mathrm {vol}}^\natural (L)$ is defined in [Reference Li and LiuLL21, Definition 3.8].
Proof. This is simply [Reference Li and LiuLL21, Proposition 10.1].
4.7 Proof of main results
The proofs of Theorem 1.4, Theorem 1.5 and Corollary 1.7 follow from the same lines as for [Reference Li and LiuLL21, Theorem 1.5], [Reference Li and LiuLL21, Theorem 1.7] and [Reference Li and LiuLL21, Corollary 1.9], respectively, written in [Reference Li and LiuLL21, Section 11]. However, we need to take ![]() $\mathtt {R}$ to be a finite subset of
$\mathtt {R}$ to be a finite subset of  $\mathtt {V}_F^{\mathrm {spl}}\cap \mathtt {V}_F^\heartsuit $ containing
$\mathtt {V}_F^{\mathrm {spl}}\cap \mathtt {V}_F^\heartsuit $ containing ![]() $\mathtt {R}_\pi $ and of cardinality at least
$\mathtt {R}_\pi $ and of cardinality at least ![]() $2$ and modify the reference according to the table below.
$2$ and modify the reference according to the table below.

Remark 4.32. When ![]() $\mathtt {S}_\pi =\emptyset $, Theorem 1.4, Theorem 1.5 and Corollary 1.7 can all be proved without [Reference Li and LiuLL21, Hypothesis 6.6]. In fact, besides Proposition 4.27(2) (which we do not need as
$\mathtt {S}_\pi =\emptyset $, Theorem 1.4, Theorem 1.5 and Corollary 1.7 can all be proved without [Reference Li and LiuLL21, Hypothesis 6.6]. In fact, besides Proposition 4.27(2) (which we do not need as ![]() $\mathtt {S}_\pi =\emptyset $), the only place where [Reference Li and LiuLL21, Hypothesis 6.6] is used is [Reference Li and LiuLL21, Proposition 6.9(2)]. However, we can slightly modify the definition of
$\mathtt {S}_\pi =\emptyset $), the only place where [Reference Li and LiuLL21, Hypothesis 6.6] is used is [Reference Li and LiuLL21, Proposition 6.9(2)]. However, we can slightly modify the definition of  $(\mathbb {S}^{\mathtt {R}}_{\mathbb {L}})^{\langle \ell \rangle }_{L_{\mathtt {R}}}$ in Definition 4.14(2) such that it is the ideal of
$(\mathbb {S}^{\mathtt {R}}_{\mathbb {L}})^{\langle \ell \rangle }_{L_{\mathtt {R}}}$ in Definition 4.14(2) such that it is the ideal of ![]() $\mathbb {S}^{\mathtt {R}}_{\mathbb {L}}$ of elements that annihilate
$\mathbb {S}^{\mathtt {R}}_{\mathbb {L}}$ of elements that annihilate
 $$ \begin{align*} \bigoplus_{u\in\mathtt{V}_E^{\mathrm{fin}}\setminus\mathtt{V}_E^{(\ell)}}\mathrm{H}^{2r}_\dagger(X_{L_{\mathtt{R}} L^{\mathtt{R}},u},\mathbb{Q}_\ell(r))\otimes_{\mathbb{Q}}\mathbb{L}, \end{align*} $$
$$ \begin{align*} \bigoplus_{u\in\mathtt{V}_E^{\mathrm{fin}}\setminus\mathtt{V}_E^{(\ell)}}\mathrm{H}^{2r}_\dagger(X_{L_{\mathtt{R}} L^{\mathtt{R}},u},\mathbb{Q}_\ell(r))\otimes_{\mathbb{Q}}\mathbb{L}, \end{align*} $$where  $\mathrm {H}^{2r}_\dagger (X_{L_{\mathtt {R}} L^{\mathtt {R}},u},\mathbb {Q}_\ell (r))\otimes _{\mathbb {Q}}\mathbb {L}$ is the
$\mathrm {H}^{2r}_\dagger (X_{L_{\mathtt {R}} L^{\mathtt {R}},u},\mathbb {Q}_\ell (r))\otimes _{\mathbb {Q}}\mathbb {L}$ is the ![]() $\mathbb {Q}_\ell \otimes _{\mathbb {Q}}\mathbb {L}$-submodule of
$\mathbb {Q}_\ell \otimes _{\mathbb {Q}}\mathbb {L}$-submodule of ![]() $\mathrm {H}^{2r}(X_{L_{\mathtt {R}} L^{\mathtt {R}},u},\mathbb {Q}_\ell (r))\otimes _{\mathbb {Q}}\mathbb {L}$ generated by the image of the cycle class map
$\mathrm {H}^{2r}(X_{L_{\mathtt {R}} L^{\mathtt {R}},u},\mathbb {Q}_\ell (r))\otimes _{\mathbb {Q}}\mathbb {L}$ generated by the image of the cycle class map ![]() $\operatorname {\mathrm {CH}}^r(X_{L_{\mathtt {R}} L^{\mathtt {R}},u})\to \mathrm {H}^{2r}(X_{L_{\mathtt {R}} L^{\mathtt {R}},u},\mathbb {Q}_\ell (r))\otimes _{\mathbb {Q}}\mathbb {L}$.
$\operatorname {\mathrm {CH}}^r(X_{L_{\mathtt {R}} L^{\mathtt {R}},u})\to \mathrm {H}^{2r}(X_{L_{\mathtt {R}} L^{\mathtt {R}},u},\mathbb {Q}_\ell (r))\otimes _{\mathbb {Q}}\mathbb {L}$.
Theorem 4.21 implies that when u satisfies  $\underline {u}\in \mathtt {R}\cap \mathtt {V}_F^{\mathrm {spl}}\cap \mathtt {V}_F^\heartsuit $ and
$\underline {u}\in \mathtt {R}\cap \mathtt {V}_F^{\mathrm {spl}}\cap \mathtt {V}_F^\heartsuit $ and  $\mathtt {V}_F^{(p)}\cap \mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$ where p is the underlying rational prime of u, there exists an element in
$\mathtt {V}_F^{(p)}\cap \mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}$ where p is the underlying rational prime of u, there exists an element in  $(\mathbb {S}^{\mathtt {R}}_{\mathbb {Q}^{\mathrm {ac}}})^{\langle \ell \rangle }_{L_{\mathtt {R}}}\setminus \mathfrak {m}_\pi ^{\mathtt {R}}$ that annihilates
$(\mathbb {S}^{\mathtt {R}}_{\mathbb {Q}^{\mathrm {ac}}})^{\langle \ell \rangle }_{L_{\mathtt {R}}}\setminus \mathfrak {m}_\pi ^{\mathtt {R}}$ that annihilates  $\mathrm {H}^{2r}_\dagger (X_{L_{\mathtt {R}} L^{\mathtt {R}},u},\mathbb {Q}_\ell (r))\otimes _{\mathbb {Q}}\mathbb {Q}^{\mathrm {ac}}$. Indeed, we have a commutative diagram (in the context of the proof of Proposition 4.20)
$\mathrm {H}^{2r}_\dagger (X_{L_{\mathtt {R}} L^{\mathtt {R}},u},\mathbb {Q}_\ell (r))\otimes _{\mathbb {Q}}\mathbb {Q}^{\mathrm {ac}}$. Indeed, we have a commutative diagram (in the context of the proof of Proposition 4.20)

in which the left vertical arrow is surjective, implying that  $\mathrm {H}^{2r}_\dagger (X_{L_{\mathtt {R}} L^{\mathtt {R}},u},\mathbb {Q}_\ell (r))$ is a quotient of
$\mathrm {H}^{2r}_\dagger (X_{L_{\mathtt {R}} L^{\mathtt {R}},u},\mathbb {Q}_\ell (r))$ is a quotient of ![]() $\mathrm {H}^{2r}(\mathcal {X}_m,\mathbb {Q}_\ell (r))$.
$\mathrm {H}^{2r}(\mathcal {X}_m,\mathbb {Q}_\ell (r))$.
It follows that with this new definition of  $(\mathbb {S}^{\mathtt {R}}_{\mathbb {L}})^{\langle \ell \rangle }_{L_{\mathtt {R}}}$, [Reference Li and LiuLL21, Proposition 6.9(2)] holds when
$(\mathbb {S}^{\mathtt {R}}_{\mathbb {L}})^{\langle \ell \rangle }_{L_{\mathtt {R}}}$, [Reference Li and LiuLL21, Proposition 6.9(2)] holds when  $\mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}\cap \mathtt {V}_F^\heartsuit $ without assuming [Reference Li and LiuLL21, Hypothesis 6.6].
$\mathtt {R}\subseteq \mathtt {V}_F^{\mathrm {spl}}\cap \mathtt {V}_F^\heartsuit $ without assuming [Reference Li and LiuLL21, Hypothesis 6.6].
Remark 4.33. Finally, we explain the main difficulty on lifting the restriction ![]() $F\neq \mathbb {Q}$ (when
$F\neq \mathbb {Q}$ (when ![]() $r\geqslant 2$). Suppose that
$r\geqslant 2$). Suppose that ![]() $F=\mathbb {Q}$ and
$F=\mathbb {Q}$ and ![]() $r\geqslant 2$. Then the Shimura variety
$r\geqslant 2$. Then the Shimura variety ![]() $X_L$ from Subsection 4.2 is never proper over the base field. Nevertheless, it is well-known that
$X_L$ from Subsection 4.2 is never proper over the base field. Nevertheless, it is well-known that ![]() $X_L$ admits a canonical toroidal compactification, which is smooth. However, to run our argument, we need suitable compactification of their integral models at every finite place u of E as well. As far as we can see, the main obstacle is the compactification of integral models using Drinfeld level structures when u splits over F, together with a vanishing result like Theorem 4.21.
$X_L$ admits a canonical toroidal compactification, which is smooth. However, to run our argument, we need suitable compactification of their integral models at every finite place u of E as well. As far as we can see, the main obstacle is the compactification of integral models using Drinfeld level structures when u splits over F, together with a vanishing result like Theorem 4.21.
Acknowledgements
We thank Xuhua He and Yichao Tian for helpful discussion and Benedict Gross for useful comments. We also thank the anonymous referees for their careful reading and useful suggestions and comments. The research of C. L. is partially supported by NSF grants DMS-1802269 and DMS-2101157. The research of Y. L. is partially supported by NSF grant DMS-2000533.
Conflict of Interest:
None.