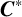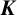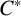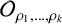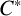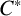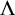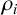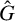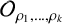1 Introduction
The study of graph
![]() $C^*$
-algebras was motivated, among other reasons, by the Doplicher–Roberts algebra
$C^*$
-algebras was motivated, among other reasons, by the Doplicher–Roberts algebra
![]() $\mathcal {O}_\rho $
associated to a group representation
$\mathcal {O}_\rho $
associated to a group representation
![]() $\rho $
(see [Reference Kajiwara, Pinzari and Watatani19, Reference Mann, Raeburn and Sutherland22]). It is natural to imagine that a rank k graph is related to a fixed set of k representations
$\rho $
(see [Reference Kajiwara, Pinzari and Watatani19, Reference Mann, Raeburn and Sutherland22]). It is natural to imagine that a rank k graph is related to a fixed set of k representations
![]() $\rho _1,\ldots ,\rho _k$
satisfying certain properties.
$\rho _1,\ldots ,\rho _k$
satisfying certain properties.
Given a compact group G and k finite-dimensional unitary representations
![]() $\rho _i$
on Hilbert spaces
$\rho _i$
on Hilbert spaces
![]() $\mathcal H_i$
of dimensions
$\mathcal H_i$
of dimensions
![]() $d_i$
for
$d_i$
for
![]() $i=1,\ldots ,k$
, we first construct a product system
$i=1,\ldots ,k$
, we first construct a product system
![]() $\mathcal E$
indexed by the semigroup
$\mathcal E$
indexed by the semigroup
![]() $(\mathbb {N}^k,+)$
with fibers
$(\mathbb {N}^k,+)$
with fibers
![]() $\mathcal E_{n}=\mathcal H_1^{\otimes n_1}\otimes \cdots \otimes \mathcal H_k^{\otimes n_k}$
for
$\mathcal E_{n}=\mathcal H_1^{\otimes n_1}\otimes \cdots \otimes \mathcal H_k^{\otimes n_k}$
for
![]() $n=(n_1,\ldots ,n_k)\in \mathbb {N}^k$
. Using the representations
$n=(n_1,\ldots ,n_k)\in \mathbb {N}^k$
. Using the representations
![]() $\rho _i$
, the group G acts on each fiber of
$\rho _i$
, the group G acts on each fiber of
![]() $\mathcal {E}$
in a compatible way, so we obtain an action of G on the Cuntz–Pimsner algebra
$\mathcal {E}$
in a compatible way, so we obtain an action of G on the Cuntz–Pimsner algebra
![]() $\mathcal {O}(\mathcal {E})$
. This action determines the crossed product
$\mathcal {O}(\mathcal {E})$
. This action determines the crossed product
![]() $\mathcal {O}(\mathcal {E})\rtimes G$
and the fixed point algebra
$\mathcal {O}(\mathcal {E})\rtimes G$
and the fixed point algebra
![]() $\mathcal {O}(\mathcal {E})^G$
.
$\mathcal {O}(\mathcal {E})^G$
.
Inspired by Section 7 of [Reference Kajiwara, Pinzari and Watatani19] and Section 3.3 of [Reference Albandik and Meyer1], we define a higher rank Doplicher–Roberts algebra
![]() $\mathcal O_{\rho _1,\ldots ,\rho _k}$
associated to the representations
$\mathcal O_{\rho _1,\ldots ,\rho _k}$
associated to the representations
![]() $\rho _1,\ldots ,\rho _k$
. This algebra is constructed from intertwiners
$\rho _1,\ldots ,\rho _k$
. This algebra is constructed from intertwiners
![]() $Hom (\rho ^n, \rho ^m)$
, where
$Hom (\rho ^n, \rho ^m)$
, where
![]() $\rho ^n=\rho _1^{\otimes n_1}\otimes \cdots \otimes \rho _k^{\otimes n_k}$
is acting on
$\rho ^n=\rho _1^{\otimes n_1}\otimes \cdots \otimes \rho _k^{\otimes n_k}$
is acting on
![]() $\mathcal {H}^n=\mathcal H_1^{\otimes n_1}\otimes \cdots \otimes \mathcal H_k^{\otimes n_k}$
for
$\mathcal {H}^n=\mathcal H_1^{\otimes n_1}\otimes \cdots \otimes \mathcal H_k^{\otimes n_k}$
for
![]() $n=(n_1,\ldots ,n_k)\in \mathbb N^k$
. We show that
$n=(n_1,\ldots ,n_k)\in \mathbb N^k$
. We show that
![]() $\mathcal O_{\rho _1,\ldots ,\rho _k}$
is isomorphic to
$\mathcal O_{\rho _1,\ldots ,\rho _k}$
is isomorphic to
![]() $\mathcal {O}(\mathcal {E})^G$
.
$\mathcal {O}(\mathcal {E})^G$
.
If the representations
![]() $\rho _1,\ldots ,\rho _k$
satisfy some mild conditions, we construct a k-colored graph
$\rho _1,\ldots ,\rho _k$
satisfy some mild conditions, we construct a k-colored graph
![]() $\Lambda $
with vertex space
$\Lambda $
with vertex space
![]() $\Lambda ^0=\hat {G}$
, and with edges
$\Lambda ^0=\hat {G}$
, and with edges
![]() $\Lambda ^{\varepsilon _i}$
given by some matrices
$\Lambda ^{\varepsilon _i}$
given by some matrices
![]() $M_i$
indexed by
$M_i$
indexed by
![]() $\hat {G}$
. Here
$\hat {G}$
. Here
![]() $\varepsilon _i=(0,\ldots ,1,\ldots ,0)\in \mathbb {N}^k$
with
$\varepsilon _i=(0,\ldots ,1,\ldots ,0)\in \mathbb {N}^k$
with
![]() $1$
in position i are the canonical generators. For
$1$
in position i are the canonical generators. For
![]() $v,w\in \hat {G}$
, the matrices
$v,w\in \hat {G}$
, the matrices
![]() $M_i$
have entries
$M_i$
have entries
which is the multiplicity of v in
![]() $w\otimes \rho _i$
for
$w\otimes \rho _i$
for
![]() $i=1,\ldots ,k$
. Note that the matrices
$i=1,\ldots ,k$
. Note that the matrices
![]() $M_i$
commute because
$M_i$
commute because
![]() $\rho _i\otimes \rho _j\cong \rho _j\otimes \rho _i$
for all
$\rho _i\otimes \rho _j\cong \rho _j\otimes \rho _i$
for all
![]() $i,j=1,\ldots ,k$
and therefore
$i,j=1,\ldots ,k$
and therefore
By a particular choice of isometric intertwiners in
![]() $Hom(v,w\otimes \rho _i)$
for each
$Hom(v,w\otimes \rho _i)$
for each
![]() $v,w\in \hat {G}$
and for each i, we can choose bijections
$v,w\in \hat {G}$
and for each i, we can choose bijections
obtaining a set of commuting squares for
![]() $\Lambda $
. For
$\Lambda $
. For
![]() $k\ge 3$
, we need to check the associativity of the commuting squares, that is,
$k\ge 3$
, we need to check the associativity of the commuting squares, that is,
as bijections from
![]() $\Lambda ^{\varepsilon _i}\times _{\Lambda ^0}\Lambda ^{\varepsilon _j}\times _{\Lambda ^0}\Lambda ^{\varepsilon _\ell }$
to
$\Lambda ^{\varepsilon _i}\times _{\Lambda ^0}\Lambda ^{\varepsilon _j}\times _{\Lambda ^0}\Lambda ^{\varepsilon _\ell }$
to
![]() $\Lambda ^{\varepsilon _\ell }\times _{\Lambda ^0}\Lambda ^{\varepsilon _j}\times _{\Lambda ^0}\Lambda ^{\varepsilon _i}$
for all
$\Lambda ^{\varepsilon _\ell }\times _{\Lambda ^0}\Lambda ^{\varepsilon _j}\times _{\Lambda ^0}\Lambda ^{\varepsilon _i}$
for all
![]() $i<j<\ell $
(see [Reference Fowler and Sims14]). If these conditions are satisfied, we obtain a rank k graph
$i<j<\ell $
(see [Reference Fowler and Sims14]). If these conditions are satisfied, we obtain a rank k graph
![]() $\Lambda $
, which is row-finite with no sources but, in general, is not unique.
$\Lambda $
, which is row-finite with no sources but, in general, is not unique.
In many situations,
![]() $\Lambda $
is cofinal and it satisfies the aperiodicity condition, so
$\Lambda $
is cofinal and it satisfies the aperiodicity condition, so
![]() $C^*(\Lambda )$
is simple. For
$C^*(\Lambda )$
is simple. For
![]() $k=2$
, the
$k=2$
, the
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C^*(\Lambda )$
is unique when it is simple and purely infinite, because its K-theory depends only on the matrices
$C^*(\Lambda )$
is unique when it is simple and purely infinite, because its K-theory depends only on the matrices
![]() $M_1, M_2$
. It is an open question what happens for
$M_1, M_2$
. It is an open question what happens for
![]() $k\ge 3$
.
$k\ge 3$
.
Assuming that the representations
![]() $\rho _1,\ldots ,\rho _k$
determine a rank k graph
$\rho _1,\ldots ,\rho _k$
determine a rank k graph
![]() $\Lambda $
, we prove that the Doplicher–Roberts algebra
$\Lambda $
, we prove that the Doplicher–Roberts algebra
![]() $\mathcal O_{\rho _1,\ldots ,\rho _k}$
is isomorphic to a corner of
$\mathcal O_{\rho _1,\ldots ,\rho _k}$
is isomorphic to a corner of
![]() $C^*(\Lambda )$
, so if
$C^*(\Lambda )$
, so if
![]() $C^*(\Lambda )$
is simple, then
$C^*(\Lambda )$
is simple, then
![]() $\mathcal O_{\rho _1,\ldots ,\rho _k}$
is Morita equivalent to
$\mathcal O_{\rho _1,\ldots ,\rho _k}$
is Morita equivalent to
![]() $C^*(\Lambda )$
. In particular cases, we can compute its K-theory using results from [Reference Evans11].
$C^*(\Lambda )$
. In particular cases, we can compute its K-theory using results from [Reference Evans11].
2 The product system
Product systems over arbitrary semigroups were introduced by Fowler [Reference Fowler13], inspired by work of Arveson, and studied by several authors (see [Reference Albandik and Meyer1, Reference Carlsen, Larsen, Sims and Vittadello4, Reference Sims and Yeend26]). In this paper, we are mostly interested in product systems
![]() $\mathcal {E}$
indexed by
$\mathcal {E}$
indexed by
![]() $( \mathbb {N}^k , +)$
, associated to some representations
$( \mathbb {N}^k , +)$
, associated to some representations
![]() $\rho _1,\ldots ,\rho _k$
of a compact group G. We remind the reader of some general definitions and constructions with product systems, but we restrict our attention to the Cuntz–Pimsner algebra
$\rho _1,\ldots ,\rho _k$
of a compact group G. We remind the reader of some general definitions and constructions with product systems, but we restrict our attention to the Cuntz–Pimsner algebra
![]() $\mathcal {O}(\mathcal {E})$
and we mention some properties in particular cases only (see Example 2.3 for
$\mathcal {O}(\mathcal {E})$
and we mention some properties in particular cases only (see Example 2.3 for
![]() $P=\mathbb {N}^k$
).
$P=\mathbb {N}^k$
).
Definition 2.1. Let
![]() $(P, \cdot )$
be a discrete semigroup with identity e and let A be a
$(P, \cdot )$
be a discrete semigroup with identity e and let A be a
![]() $C^*$
-algebra. A product system of
$C^*$
-algebra. A product system of
![]() $C^*$
-correspondences over A indexed by P is a semigroup
$C^*$
-correspondences over A indexed by P is a semigroup
![]() $\mathcal {E}=\bigsqcup _{p\in P}\mathcal {E}_p$
and a map
$\mathcal {E}=\bigsqcup _{p\in P}\mathcal {E}_p$
and a map
![]() $\mathcal {E}\to P$
such that:
$\mathcal {E}\to P$
such that:
-
• for each
 $p\in P$
, the fiber
$p\in P$
, the fiber
 $\mathcal {E}_p\subset \mathcal {E}$
is a
$\mathcal {E}_p\subset \mathcal {E}$
is a
 $C^*$
-correspondence over A with inner product
$C^*$
-correspondence over A with inner product
 $\langle \cdot ,\cdot \rangle _p$
;
$\langle \cdot ,\cdot \rangle _p$
; -
• the identity fiber
 $\mathcal {E}_e$
is A viewed as a
$\mathcal {E}_e$
is A viewed as a
 $C^*$
-correspondence over itself;
$C^*$
-correspondence over itself; -
• for
 $p,q\in P\setminus \{e\}$
, the multiplication map induces an isomorphism
$p,q\in P\setminus \{e\}$
, the multiplication map induces an isomorphism $$ \begin{align*}\mathcal{M}_{p,q}:\mathcal{E}_p\times \mathcal{E}_q\to \mathcal{E}_{pq},\;\; \mathcal{M}_{p,q}(x,y)= xy\end{align*} $$
$$ \begin{align*}\mathcal{M}_{p,q}:\mathcal{E}_p\times \mathcal{E}_q\to \mathcal{E}_{pq},\;\; \mathcal{M}_{p,q}(x,y)= xy\end{align*} $$
 $\mathcal {M}_{p,q}:\mathcal {E}_p\otimes _A \mathcal {E}_q\to \mathcal {E}_{pq}$
; and
$\mathcal {M}_{p,q}:\mathcal {E}_p\otimes _A \mathcal {E}_q\to \mathcal {E}_{pq}$
; and
-
• multiplication in
 $\mathcal {E}$
by elements of
$\mathcal {E}$
by elements of
 $\mathcal {E}_e=A$
implements the right and left actions of A on each
$\mathcal {E}_e=A$
implements the right and left actions of A on each
 $\mathcal {E}_p$
. In particular,
$\mathcal {E}_p$
. In particular,
 $\mathcal {M}_{p,e}$
is an isomorphism.
$\mathcal {M}_{p,e}$
is an isomorphism.
Let
![]() $\phi _p:A\to \mathcal {L}(\mathcal {E}_p)$
be the homomorphism implementing the left action. The product system
$\phi _p:A\to \mathcal {L}(\mathcal {E}_p)$
be the homomorphism implementing the left action. The product system
![]() $\mathcal {E}$
is said to be essential if each
$\mathcal {E}$
is said to be essential if each
![]() $\mathcal {E}_p$
is an essential correspondence, that is, if the span of
$\mathcal {E}_p$
is an essential correspondence, that is, if the span of
![]() $\phi _p(A)\mathcal {E}_p$
is dense in
$\phi _p(A)\mathcal {E}_p$
is dense in
![]() $\mathcal {E}_p$
for all
$\mathcal {E}_p$
for all
![]() $p\in P$
. In this case, the map
$p\in P$
. In this case, the map
![]() $\mathcal {M}_{e,p}$
is also an isomorphism.
$\mathcal {M}_{e,p}$
is also an isomorphism.
If the maps
![]() $\phi _p$
take values in
$\phi _p$
take values in
![]() $\mathcal {K}(\mathcal {E}_p)$
, then the product system is called row-finite or proper. If all maps
$\mathcal {K}(\mathcal {E}_p)$
, then the product system is called row-finite or proper. If all maps
![]() $\phi _p$
are injective, then
$\phi _p$
are injective, then
![]() $\mathcal {E}$
is called faithful.
$\mathcal {E}$
is called faithful.
Definition 2.2. Given a product system
![]() $\mathcal {E}\to P$
over A and a
$\mathcal {E}\to P$
over A and a
![]() $C^*$
-algebra B, a map
$C^*$
-algebra B, a map
![]() $\psi :\mathcal {E}\to B$
is called a Toeplitz representation of
$\psi :\mathcal {E}\to B$
is called a Toeplitz representation of
![]() $\mathcal {E}$
if:
$\mathcal {E}$
if:
-
• denoting
 $\psi _p:=\psi |_{\mathcal {E}_p}$
, each
$\psi _p:=\psi |_{\mathcal {E}_p}$
, each
 $\psi _p:\mathcal {E}_p\to B$
is linear,
$\psi _p:\mathcal {E}_p\to B$
is linear,
 $\psi _e:A\to B$
is a
$\psi _e:A\to B$
is a
 $*$
-homomorphism, and for all
$*$
-homomorphism, and for all $$ \begin{align*}\psi_e(\langle x,y\rangle_p)=\psi_p(x)^*\psi_p(y)\end{align*} $$
$$ \begin{align*}\psi_e(\langle x,y\rangle_p)=\psi_p(x)^*\psi_p(y)\end{align*} $$
 $x,y\in \mathcal {E}_p$
; and
$x,y\in \mathcal {E}_p$
; and
-
•
 $\psi _p(x)\psi _q(y)=\psi _{pq}(xy)$
for all
$\psi _p(x)\psi _q(y)=\psi _{pq}(xy)$
for all
 $p,q\in P, x\in \mathcal {E}_p, y\in \mathcal {E}_q$
.
$p,q\in P, x\in \mathcal {E}_p, y\in \mathcal {E}_q$
.
For each
![]() $p\in P$
, we write
$p\in P$
, we write
![]() $\psi ^{(p)}$
for the homomorphism
$\psi ^{(p)}$
for the homomorphism
![]() $\mathcal {K}(\mathcal {E}_p)\to B$
obtained by extending the map
$\mathcal {K}(\mathcal {E}_p)\to B$
obtained by extending the map
![]() $\theta _{\xi , \eta }\mapsto \psi _p(\xi )\psi _p(\eta )^*$
, where
$\theta _{\xi , \eta }\mapsto \psi _p(\xi )\psi _p(\eta )^*$
, where
The Toeplitz representation
![]() $\psi :\mathcal {E}\to B$
is Cuntz–Pimsner covariant if
$\psi :\mathcal {E}\to B$
is Cuntz–Pimsner covariant if
![]() $\psi ^{(p)}(\phi _p(a))=\psi _e(a)$
for all
$\psi ^{(p)}(\phi _p(a))=\psi _e(a)$
for all
![]() $p\in P$
and all
$p\in P$
and all
![]() $a\in A$
such that
$a\in A$
such that
![]() $\phi _p(a)\in \mathcal {K}(\mathcal {E}_p)$
.
$\phi _p(a)\in \mathcal {K}(\mathcal {E}_p)$
.
There is a
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal {T}_A(\mathcal {E})$
called the Toeplitz algebra of
$\mathcal {T}_A(\mathcal {E})$
called the Toeplitz algebra of
![]() $\mathcal {E}$
and a representation
$\mathcal {E}$
and a representation
![]() $i_{\mathcal {E}}:\mathcal {E}\to \mathcal {T}_A(\mathcal {E})$
which is universal in the following sense:
$i_{\mathcal {E}}:\mathcal {E}\to \mathcal {T}_A(\mathcal {E})$
which is universal in the following sense:
![]() $\mathcal {T}_A(\mathcal {E})$
is generated by
$\mathcal {T}_A(\mathcal {E})$
is generated by
![]() $i_{\mathcal {E}}(\mathcal {E})$
and, for any representation
$i_{\mathcal {E}}(\mathcal {E})$
and, for any representation
![]() $\psi :\mathcal {E}\to B$
, there is a homomorphism
$\psi :\mathcal {E}\to B$
, there is a homomorphism
![]() $\psi _*:\mathcal {T}_A(\mathcal {E})\to B$
such that
$\psi _*:\mathcal {T}_A(\mathcal {E})\to B$
such that
![]() $\psi _*\circ i_{\mathcal {E}}=\psi $
.
$\psi _*\circ i_{\mathcal {E}}=\psi $
.
The Cuntz–Pimsner algebra
![]() $\mathcal {O}_A(\mathcal {E})$
of a product system
$\mathcal {O}_A(\mathcal {E})$
of a product system
![]() $\mathcal {E}\to P$
is universal for Cuntz–Pimsner covariant representations.
$\mathcal {E}\to P$
is universal for Cuntz–Pimsner covariant representations.
There are various extra conditions on a product system
![]() $\mathcal {E}\to P$
and several other notions of covariance besides the Cuntz–Pimsner covariance from Definition 2.2, which allow one to define the Cuntz–Pimsner algebra
$\mathcal {E}\to P$
and several other notions of covariance besides the Cuntz–Pimsner covariance from Definition 2.2, which allow one to define the Cuntz–Pimsner algebra
![]() $\mathcal {O}_A(\mathcal {E})$
or the Cuntz–Nica–Pimsner algebra
$\mathcal {O}_A(\mathcal {E})$
or the Cuntz–Nica–Pimsner algebra
![]() $\mathcal {N}\mathcal {O}_A(\mathcal {E})$
satisfying certain properties (see [Reference Albandik and Meyer1, Reference Carlsen, Larsen, Sims and Vittadello4, Reference Dor-On and Kakariadis10, Reference Fowler13, Reference Sims and Yeend26], among others). We mention that
$\mathcal {N}\mathcal {O}_A(\mathcal {E})$
satisfying certain properties (see [Reference Albandik and Meyer1, Reference Carlsen, Larsen, Sims and Vittadello4, Reference Dor-On and Kakariadis10, Reference Fowler13, Reference Sims and Yeend26], among others). We mention that
![]() $\mathcal {O}_A(\mathcal {E})$
(or
$\mathcal {O}_A(\mathcal {E})$
(or
![]() $\mathcal {N}\mathcal {O}_A(\mathcal {E})$
) comes with a covariant representation
$\mathcal {N}\mathcal {O}_A(\mathcal {E})$
) comes with a covariant representation
![]() $j_{\mathcal {E}}:\mathcal {E}\to \mathcal {O}_A(\mathcal {E})$
and is universal in the following sense:
$j_{\mathcal {E}}:\mathcal {E}\to \mathcal {O}_A(\mathcal {E})$
and is universal in the following sense:
![]() $\mathcal {O}_A(\mathcal {E})$
is generated by
$\mathcal {O}_A(\mathcal {E})$
is generated by
![]() $j_{\mathcal {E}}(\mathcal {E})$
and, for any covariant representation
$j_{\mathcal {E}}(\mathcal {E})$
and, for any covariant representation
![]() $\psi :\mathcal {E}\to B$
, there is a homomorphism
$\psi :\mathcal {E}\to B$
, there is a homomorphism
![]() $\psi _*:\mathcal {O}_A(\mathcal {E})\to B$
such that
$\psi _*:\mathcal {O}_A(\mathcal {E})\to B$
such that
![]() $\psi _*\circ j_{\mathcal {E}}=\psi $
. Under certain conditions,
$\psi _*\circ j_{\mathcal {E}}=\psi $
. Under certain conditions,
![]() $\mathcal {O}_A(\mathcal {E})$
satisfies a gauge invariant uniqueness theorem.
$\mathcal {O}_A(\mathcal {E})$
satisfies a gauge invariant uniqueness theorem.
Example 2.3. For a product system
![]() $\mathcal {E}\to P$
with fibers
$\mathcal {E}\to P$
with fibers
![]() $\mathcal {E}_p$
that are nonzero finite-dimensional Hilbert spaces, and, in particular,
$\mathcal {E}_p$
that are nonzero finite-dimensional Hilbert spaces, and, in particular,
![]() $A=\mathcal {E}_e=\mathbb {C}$
, let us fix an orthonormal basis
$A=\mathcal {E}_e=\mathbb {C}$
, let us fix an orthonormal basis
![]() $\mathcal {B}_p$
in
$\mathcal {B}_p$
in
![]() $\mathcal {E}_p$
. Then a Toeplitz representation
$\mathcal {E}_p$
. Then a Toeplitz representation
![]() $\psi :\mathcal {E}\to B$
gives rise to a family of isometries
$\psi :\mathcal {E}\to B$
gives rise to a family of isometries
![]() $\{\psi (\xi ): \xi \in \mathcal {B}_p\}_{p\in P}$
with mutually orthogonal range projections. In this case,
$\{\psi (\xi ): \xi \in \mathcal {B}_p\}_{p\in P}$
with mutually orthogonal range projections. In this case,
![]() $\mathcal {T}(\mathcal {E})=\mathcal {T}_{\mathbb {C}}(\mathcal {E})$
is generated by a collection of Cuntz–Toeplitz algebras which interact according to the multiplication maps
$\mathcal {T}(\mathcal {E})=\mathcal {T}_{\mathbb {C}}(\mathcal {E})$
is generated by a collection of Cuntz–Toeplitz algebras which interact according to the multiplication maps
![]() $\mathcal {M}_{p,q}$
in
$\mathcal {M}_{p,q}$
in
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
A representation
![]() $\psi :\mathcal {E}\to B$
is Cuntz–Pimsner covariant if
$\psi :\mathcal {E}\to B$
is Cuntz–Pimsner covariant if
 $$ \begin{align*} \sum_{\xi\in \mathcal{B}_p}\psi(\xi)\psi(\xi)^*=\psi(1)\end{align*} $$
$$ \begin{align*} \sum_{\xi\in \mathcal{B}_p}\psi(\xi)\psi(\xi)^*=\psi(1)\end{align*} $$
for all
![]() $p\in P$
. The Cuntz–Pimsner algebra
$p\in P$
. The Cuntz–Pimsner algebra
![]() $\mathcal {O}(\mathcal {E})=\mathcal {O}_{\mathbb {C}}(\mathcal {E})$
is generated by a collection of Cuntz algebras, so it could be thought of as a multidimensional Cuntz algebra. Fowler proved in [Reference Fowler12] that if the function
$\mathcal {O}(\mathcal {E})=\mathcal {O}_{\mathbb {C}}(\mathcal {E})$
is generated by a collection of Cuntz algebras, so it could be thought of as a multidimensional Cuntz algebra. Fowler proved in [Reference Fowler12] that if the function
![]() $p\mapsto \dim \mathcal {E}_p$
is injective, then the algebra
$p\mapsto \dim \mathcal {E}_p$
is injective, then the algebra
![]() ${\mathcal O}(\mathcal {E})$
is simple and purely infinite. For other examples of multidimensional Cuntz algebras, see [Reference Burgstaller3].
${\mathcal O}(\mathcal {E})$
is simple and purely infinite. For other examples of multidimensional Cuntz algebras, see [Reference Burgstaller3].
Example 2.4. A row-finite k-graph with no sources
![]() $\Lambda $
(see [Reference Kumjian, Pask, Raeburn and Renault18]) determines a product system
$\Lambda $
(see [Reference Kumjian, Pask, Raeburn and Renault18]) determines a product system
![]() $\mathcal {E}\to \mathbb {N}^k$
with
$\mathcal {E}\to \mathbb {N}^k$
with
![]() $\mathcal {E}_0=A=C_0(\Lambda ^0)$
and
$\mathcal {E}_0=A=C_0(\Lambda ^0)$
and
![]() $\mathcal {E}_n=\overline {C_c(\Lambda ^n)}$
for
$\mathcal {E}_n=\overline {C_c(\Lambda ^n)}$
for
![]() $n\neq 0$
such that we have a
$n\neq 0$
such that we have a
![]() $\mathbb {T}^k$
-equivariant isomorphism
$\mathbb {T}^k$
-equivariant isomorphism
![]() $\mathcal {O}_A(\mathcal {E})\cong C^*(\Lambda )$
. Recall that, for product systems indexed by
$\mathcal {O}_A(\mathcal {E})\cong C^*(\Lambda )$
. Recall that, for product systems indexed by
![]() $\mathbb {N}^k$
, the universal property induces a gauge action on
$\mathbb {N}^k$
, the universal property induces a gauge action on
![]() $\mathcal {O}_A(\mathcal {E})$
defined by
$\mathcal {O}_A(\mathcal {E})$
defined by
![]() $\gamma _z(j_{\mathcal {E}}(\xi ))=z^nj_{\mathcal {E}}(\xi )$
for
$\gamma _z(j_{\mathcal {E}}(\xi ))=z^nj_{\mathcal {E}}(\xi )$
for
![]() $z\in \mathbb {T}^k$
and
$z\in \mathbb {T}^k$
and
![]() $\xi \in \mathcal {E}_n$
.
$\xi \in \mathcal {E}_n$
.
The following two definitions and two results are taken from [Reference Deaconu, Huang and Sims7]; see also [Reference Hao and Ng15, Reference Kumjian and Pask17].
Definition 2.5. An action
![]() $ \beta $
of a locally compact group
$ \beta $
of a locally compact group
![]() $ G $
on a product system
$ G $
on a product system
![]() $ \mathcal {E} \to P $
over A is a family
$ \mathcal {E} \to P $
over A is a family
![]() $ (\beta ^{p})_{p \in P} $
such that
$ (\beta ^{p})_{p \in P} $
such that
![]() $ \beta ^{p} $
is an action of
$ \beta ^{p} $
is an action of
![]() $ G $
on each fiber
$ G $
on each fiber
![]() $\mathcal {E}_{p} $
compatible with the action
$\mathcal {E}_{p} $
compatible with the action
![]() $\alpha =\beta ^e$
on A, and, furthermore, the actions
$\alpha =\beta ^e$
on A, and, furthermore, the actions
![]() $(\beta ^p)_{p\in P}$
are compatible with the multiplication maps
$(\beta ^p)_{p\in P}$
are compatible with the multiplication maps
![]() $\mathcal {M}_{p,q}$
in the sense that
$\mathcal {M}_{p,q}$
in the sense that
for all
![]() $ g \in G $
,
$ g \in G $
,
![]() $ x \in \mathcal {E}_{p} $
and
$ x \in \mathcal {E}_{p} $
and
![]() $ y \in \mathcal {E}_{q} $
.
$ y \in \mathcal {E}_{q} $
.
Definition 2.6. If
![]() $ \beta $
is an action of
$ \beta $
is an action of
![]() $ G $
on the product system
$ G $
on the product system
![]() $\mathcal {E} \to P $
, we define the crossed product
$\mathcal {E} \to P $
, we define the crossed product
![]() $\mathcal {E} \rtimes _{\beta } G $
as the product system indexed by
$\mathcal {E} \rtimes _{\beta } G $
as the product system indexed by
![]() $ P $
with fibers
$ P $
with fibers
![]() $ \mathcal {E}_{p} \rtimes _{\beta ^{p}} G $
, which are
$ \mathcal {E}_{p} \rtimes _{\beta ^{p}} G $
, which are
![]() $ C^{\ast } $
-correspondences over
$ C^{\ast } $
-correspondences over
![]() $ A \rtimes _{\alpha } G $
. For
$ A \rtimes _{\alpha } G $
. For
![]() $ \zeta \in C_c(G,\mathcal {E}_{p}) $
and
$ \zeta \in C_c(G,\mathcal {E}_{p}) $
and
![]() $ \eta \in C_c(G,\mathcal {E}_{q}) $
, the product
$ \eta \in C_c(G,\mathcal {E}_{q}) $
, the product
![]() $ \zeta \eta \in C_c(G,\mathcal {E}_{p q}) $
is defined by
$ \zeta \eta \in C_c(G,\mathcal {E}_{p q}) $
is defined by
 $$ \begin{align*}(\zeta \eta)(s) = \int_G\mathcal{M}_{p,q}(\zeta(t) \otimes \beta^{q}_t(\eta(t^{- 1} s)))\,dt. \end{align*} $$
$$ \begin{align*}(\zeta \eta)(s) = \int_G\mathcal{M}_{p,q}(\zeta(t) \otimes \beta^{q}_t(\eta(t^{- 1} s)))\,dt. \end{align*} $$
Proposition 2.7. The set
![]() $ \mathcal {E} \rtimes _{\beta } G = \bigsqcup _{p \in P} \mathcal {E}_{p} \rtimes _{\beta ^{p}} G $
with the above multiplication satisfies all the properties of a product system of
$ \mathcal {E} \rtimes _{\beta } G = \bigsqcup _{p \in P} \mathcal {E}_{p} \rtimes _{\beta ^{p}} G $
with the above multiplication satisfies all the properties of a product system of
![]() $ C^{\ast } $
-correspondences over
$ C^{\ast } $
-correspondences over
![]() $ A \rtimes _{\alpha } G $
.
$ A \rtimes _{\alpha } G $
.
Proposition 2.8. Suppose that a locally compact group
![]() $ G $
acts on a row-finite and faithful product system
$ G $
acts on a row-finite and faithful product system
![]() $ \mathcal {E} $
indexed by
$ \mathcal {E} $
indexed by
![]() $ P = (\mathbb {N}^{k},+) $
via automorphisms
$ P = (\mathbb {N}^{k},+) $
via automorphisms
![]() $ \beta ^{p}_{g} $
. Then
$ \beta ^{p}_{g} $
. Then
![]() $ G $
acts on the Cuntz–Pimsner algebra
$ G $
acts on the Cuntz–Pimsner algebra
![]() $\mathcal {O}_{A}(\mathcal {E}) $
via automorphisms denoted by
$\mathcal {O}_{A}(\mathcal {E}) $
via automorphisms denoted by
![]() $ \gamma _{g} $
. Moreover, if
$ \gamma _{g} $
. Moreover, if
![]() $ G $
is amenable, then
$ G $
is amenable, then
![]() $ \mathcal {E} \rtimes _{\beta } G $
is row-finite and faithful, and
$ \mathcal {E} \rtimes _{\beta } G $
is row-finite and faithful, and
Now we define the product system associated to k representations of a compact group G. We limit ourselves to finite-dimensional unitary representations, even though the definition makes sense in greater generality.
Definition 2.9. Given a compact group G and k finite-dimensional unitary representations
![]() $\rho _i$
of G on Hilbert spaces
$\rho _i$
of G on Hilbert spaces
![]() $\mathcal H_i$
for
$\mathcal H_i$
for
![]() $i=1,\ldots ,k$
, we construct the product system
$i=1,\ldots ,k$
, we construct the product system
![]() $\mathcal {E}=\mathcal {E}(\rho _1,\ldots ,\rho _k)$
indexed by the commutative monoid
$\mathcal {E}=\mathcal {E}(\rho _1,\ldots ,\rho _k)$
indexed by the commutative monoid
![]() $(\mathbb N^k,+)$
, with fibers
$(\mathbb N^k,+)$
, with fibers
for
![]() $n=(n_1,\ldots ,n_k)\in \mathbb {N}^k$
; in particular,
$n=(n_1,\ldots ,n_k)\in \mathbb {N}^k$
; in particular,
![]() $A=\mathcal E_0=\mathbb C$
. The multiplication maps
$A=\mathcal E_0=\mathbb C$
. The multiplication maps
in
![]() $\mathcal {E}$
are defined by using the standard isomorphisms
$\mathcal {E}$
are defined by using the standard isomorphisms
![]() $\rho _i\otimes \rho _j\cong \rho _j\otimes \rho _i$
for all
$\rho _i\otimes \rho _j\cong \rho _j\otimes \rho _i$
for all
![]() $i<j$
. The associativity in
$i<j$
. The associativity in
![]() $\mathcal {E}$
follows from the fact that
$\mathcal {E}$
follows from the fact that
as maps from
![]() $\mathcal {E}_n\times \mathcal {E}_m\times \mathcal {E}_p$
to
$\mathcal {E}_n\times \mathcal {E}_m\times \mathcal {E}_p$
to
![]() $\mathcal {E}_{n+m+p}.$
Then
$\mathcal {E}_{n+m+p}.$
Then
![]() $\mathcal {E}=\mathcal {E}(\rho _1,\ldots ,\rho _k)$
is called the product system of the representations
$\mathcal {E}=\mathcal {E}(\rho _1,\ldots ,\rho _k)$
is called the product system of the representations
![]() $\rho _1,\ldots ,\rho _k$
.
$\rho _1,\ldots ,\rho _k$
.
Remark 2.10. Similarly, a semigroup P of unitary representations of a group G determines a product system
![]() $\mathcal {E}\to P$
.
$\mathcal {E}\to P$
.
Proposition 2.11. With notation as in Definition 2.9, assume that
![]() $d_i=\dim \mathcal {H}_i\ge 2$
. Then the Cuntz–Pimsner algebra
$d_i=\dim \mathcal {H}_i\ge 2$
. Then the Cuntz–Pimsner algebra
![]() $\mathcal {O}(\mathcal {E})$
associated to the product system
$\mathcal {O}(\mathcal {E})$
associated to the product system
![]() $\mathcal {E}\to \mathbb {N}^k$
described above is isomorphic with the
$\mathcal {E}\to \mathbb {N}^k$
described above is isomorphic with the
![]() $C^*$
-algebra of a rank k graph
$C^*$
-algebra of a rank k graph
![]() $\Gamma $
with a single vertex and with
$\Gamma $
with a single vertex and with
![]() $|\Gamma ^{\varepsilon _i}|=d_i$
. This isomorphism is equivariant for the gauge action. Moreover,
$|\Gamma ^{\varepsilon _i}|=d_i$
. This isomorphism is equivariant for the gauge action. Moreover,
where
![]() $\mathcal O_n$
is the Cuntz algebra.
$\mathcal O_n$
is the Cuntz algebra.
Proof. Indeed, by choosing a basis in each
![]() $\mathcal {H}_i$
, we get the edges
$\mathcal {H}_i$
, we get the edges
![]() $\Gamma ^{\varepsilon _i}$
in a k-colored graph
$\Gamma ^{\varepsilon _i}$
in a k-colored graph
![]() $\Gamma $
with a single vertex. The isomorphisms
$\Gamma $
with a single vertex. The isomorphisms
![]() $\rho _i\otimes \rho _j\cong \rho _j\otimes \rho _i$
determine the factorization rules of the form
$\rho _i\otimes \rho _j\cong \rho _j\otimes \rho _i$
determine the factorization rules of the form
![]() $ef=fe$
for
$ef=fe$
for
![]() $e\in \Gamma ^{\varepsilon _i}$
and
$e\in \Gamma ^{\varepsilon _i}$
and
![]() $f\in \Gamma ^{\varepsilon _j}$
, which obviously satisfy the associativity condition. In particular, the corresponding isometries in
$f\in \Gamma ^{\varepsilon _j}$
, which obviously satisfy the associativity condition. In particular, the corresponding isometries in
![]() $C^*(\Gamma )$
commute and determine, by the universal property, a surjective homomorphism
$C^*(\Gamma )$
commute and determine, by the universal property, a surjective homomorphism
![]() $\varphi $
onto
$\varphi $
onto
![]() $\mathcal {O}(\mathcal {E})$
, preserving the gauge action. Using the gauge invariant uniqueness theorem for k-graph algebras, the map
$\mathcal {O}(\mathcal {E})$
, preserving the gauge action. Using the gauge invariant uniqueness theorem for k-graph algebras, the map
![]() $\varphi $
is an isomorphism. In particular,
$\varphi $
is an isomorphism. In particular,
![]() $\mathcal {O}(\mathcal {E})\cong \mathcal O_{d_1}\otimes \cdots \otimes \mathcal O_{d_k}$
.
$\mathcal {O}(\mathcal {E})\cong \mathcal O_{d_1}\otimes \cdots \otimes \mathcal O_{d_k}$
.
Remark 2.12. For
![]() $d_i\ge 2$
, the
$d_i\ge 2$
, the
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal {O}(\mathcal {E})\cong C^*(\Gamma )$
is always simple and purely infinite since it is a tensor product of simple and purely infinite
$\mathcal {O}(\mathcal {E})\cong C^*(\Gamma )$
is always simple and purely infinite since it is a tensor product of simple and purely infinite
![]() $C^*$
-algebras. If
$C^*$
-algebras. If
![]() $d_i=1$
for some i, then the isomorphism in Proposition 2.11 still holds, but
$d_i=1$
for some i, then the isomorphism in Proposition 2.11 still holds, but
![]() $C^*(\Gamma )\cong \mathcal {O}(\mathcal {E})$
contains a copy of
$C^*(\Gamma )\cong \mathcal {O}(\mathcal {E})$
contains a copy of
![]() $C(\mathbb {T})$
, so it is not simple. Of course, if
$C(\mathbb {T})$
, so it is not simple. Of course, if
![]() $d_i=1$
for all i, then
$d_i=1$
for all i, then
![]() $\mathcal {O}(\mathcal {E})\cong C(\mathbb {T}^k)$
. For more on single vertex rank k graphs, see [Reference Davidson and Yang5, Reference Davidson and Yang6].
$\mathcal {O}(\mathcal {E})\cong C(\mathbb {T}^k)$
. For more on single vertex rank k graphs, see [Reference Davidson and Yang5, Reference Davidson and Yang6].
Proposition 2.13. The compact group G acts on each fiber
![]() $\mathcal {E}_n$
of the product system
$\mathcal {E}_n$
of the product system
![]() $\mathcal E$
via the representation
$\mathcal E$
via the representation
![]() $\rho ^n=\rho _1^{\otimes n_1}\otimes \cdots \otimes \rho _k^{\otimes n_k}$
. This action is compatible with the multiplication maps and commutes with the gauge action of
$\rho ^n=\rho _1^{\otimes n_1}\otimes \cdots \otimes \rho _k^{\otimes n_k}$
. This action is compatible with the multiplication maps and commutes with the gauge action of
![]() $\mathbb {T}^k$
. The crossed product
$\mathbb {T}^k$
. The crossed product
![]() $\mathcal E\rtimes G$
becomes a row-finite and faithful product system indexed by
$\mathcal E\rtimes G$
becomes a row-finite and faithful product system indexed by
![]() $\mathbb N^k$
over the group
$\mathbb N^k$
over the group
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C^*(G)$
. Moreover,
$C^*(G)$
. Moreover,
Proof. Indeed, for
![]() $g\in G$
and
$g\in G$
and
![]() $\xi \in \mathcal {E}_n=\mathcal {H}^n$
, we define
$\xi \in \mathcal {E}_n=\mathcal {H}^n$
, we define
![]() $g\cdot \xi =\rho ^n(g)(\xi )$
, and since
$g\cdot \xi =\rho ^n(g)(\xi )$
, and since
![]() $\rho _i\otimes \rho _j\cong \rho _j\otimes \rho _i$
, we have
$\rho _i\otimes \rho _j\cong \rho _j\otimes \rho _i$
, we have
![]() $g\cdot (\xi \otimes \eta )=g\cdot \xi \otimes g\cdot \eta $
for
$g\cdot (\xi \otimes \eta )=g\cdot \xi \otimes g\cdot \eta $
for
![]() $\xi \in \mathcal {E}_n, \eta \in \mathcal {E}_m$
. Clearly,
$\xi \in \mathcal {E}_n, \eta \in \mathcal {E}_m$
. Clearly,
so the action of G commutes with the gauge action. Using Proposition 2.7,
![]() $\mathcal E\rtimes G$
becomes a product system indexed by
$\mathcal E\rtimes G$
becomes a product system indexed by
![]() $\mathbb N^k$
over
$\mathbb N^k$
over
![]() $C^*(G)\cong \mathbb {C}\rtimes G$
with fibers
$C^*(G)\cong \mathbb {C}\rtimes G$
with fibers
![]() $\mathcal {E}_n\rtimes G$
. The isomorphism
$\mathcal {E}_n\rtimes G$
. The isomorphism
![]() $\mathcal {O}(\mathcal {E}) \rtimes G \cong \mathcal {O}_{C^*(G)}(\mathcal {E} \rtimes G)$
follows from Proposition 2.8.
$\mathcal {O}(\mathcal {E}) \rtimes G \cong \mathcal {O}_{C^*(G)}(\mathcal {E} \rtimes G)$
follows from Proposition 2.8.
Corollary 2.14. Since the action of G commutes with the gauge action, the group G acts on the core algebra
![]() $\mathcal {F}=\mathcal {O}(\mathcal {E})^{\mathbb {T}^k}$
.
$\mathcal {F}=\mathcal {O}(\mathcal {E})^{\mathbb {T}^k}$
.
Remark 2.15. In some cases,
![]() $\mathcal {O}(\mathcal {E})\rtimes G$
is isomorphic to the self-similar k-graph
$\mathcal {O}(\mathcal {E})\rtimes G$
is isomorphic to the self-similar k-graph
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $\mathcal {O}_{G,\Lambda }$
introduced in [Reference Li and Yang21]. Moreover, for a self-similar k-graph
$\mathcal {O}_{G,\Lambda }$
introduced in [Reference Li and Yang21]. Moreover, for a self-similar k-graph
![]() $(G,\Lambda )$
with
$(G,\Lambda )$
with
![]() $|\Lambda ^0|=1$
, we have
$|\Lambda ^0|=1$
, we have
![]() $\mathcal {O}_{G,\Lambda }\cong \mathcal {Q}(\Lambda \bowtie G)$
, where
$\mathcal {O}_{G,\Lambda }\cong \mathcal {Q}(\Lambda \bowtie G)$
, where
![]() $\Lambda \bowtie G$
is a Zappa–Szép product and
$\Lambda \bowtie G$
is a Zappa–Szép product and
![]() $\mathcal {Q}(\Lambda \bowtie G)$
is its boundary quotient
$\mathcal {Q}(\Lambda \bowtie G)$
is its boundary quotient
![]() $C^*$
-algebra (see Example 3.10(4) in [Reference Li and Yang21] and Theorem 3.3 in [Reference Li and Yang20]). I thank the referee for bringing this relationship to my attention.
$C^*$
-algebra (see Example 3.10(4) in [Reference Li and Yang21] and Theorem 3.3 in [Reference Li and Yang20]). I thank the referee for bringing this relationship to my attention.
3 The Doplicher–Roberts algebra
The Doplicher–Roberts algebras
![]() $\mathcal {O}_\rho $
, denoted by
$\mathcal {O}_\rho $
, denoted by
![]() ${\mathcal O}_G$
in [Reference Doplicher and Roberts8], were introduced to construct a new duality theory for compact Lie groups G that strengthens the Tannaka–Krein duality. Here
${\mathcal O}_G$
in [Reference Doplicher and Roberts8], were introduced to construct a new duality theory for compact Lie groups G that strengthens the Tannaka–Krein duality. Here
![]() $\rho $
is the n-dimensional representation of G defined by the inclusion
$\rho $
is the n-dimensional representation of G defined by the inclusion
![]() $G\subseteq U(n)$
in some unitary group
$G\subseteq U(n)$
in some unitary group
![]() $U(n)$
. Let
$U(n)$
. Let
![]() ${\mathcal T}_G$
denote the representation category whose objects are tensor powers
${\mathcal T}_G$
denote the representation category whose objects are tensor powers
![]() $\rho ^p=\rho ^{\otimes p}$
for
$\rho ^p=\rho ^{\otimes p}$
for
![]() $p\ge 0$
, and whose arrows are the intertwiners
$p\ge 0$
, and whose arrows are the intertwiners
![]() $Hom(\rho ^p, \rho ^q)$
. The group G acts via
$Hom(\rho ^p, \rho ^q)$
. The group G acts via
![]() $\rho $
on the Cuntz algebra
$\rho $
on the Cuntz algebra
![]() ${\mathcal O}_n$
and
${\mathcal O}_n$
and
![]() ${\mathcal O}_G={\mathcal O}_\rho $
is identified in [Reference Doplicher and Roberts8] with the fixed point algebra
${\mathcal O}_G={\mathcal O}_\rho $
is identified in [Reference Doplicher and Roberts8] with the fixed point algebra
![]() ${\mathcal O}_n^G$
. If
${\mathcal O}_n^G$
. If
![]() $\sigma $
denotes the restriction to
$\sigma $
denotes the restriction to
![]() ${\mathcal O}_\rho $
of the canonical endomorphism of
${\mathcal O}_\rho $
of the canonical endomorphism of
![]() $\mathcal {O}_n$
, then
$\mathcal {O}_n$
, then
![]() ${\mathcal T}_G$
can be reconstructed from the pair
${\mathcal T}_G$
can be reconstructed from the pair
![]() $({\mathcal O}_\rho ,\sigma )$
. Subsequently, Doplicher–Roberts algebras were associated to any object
$({\mathcal O}_\rho ,\sigma )$
. Subsequently, Doplicher–Roberts algebras were associated to any object
![]() $\rho $
in a strict tensor
$\rho $
in a strict tensor
![]() $C^*$
-category (see [Reference Doplicher and Roberts9]).
$C^*$
-category (see [Reference Doplicher and Roberts9]).
Given finite-dimensional unitary representations
![]() $\rho _1,\ldots ,\rho _k$
of a compact group G on Hilbert spaces
$\rho _1,\ldots ,\rho _k$
of a compact group G on Hilbert spaces
![]() $\mathcal H_1,\ldots , \mathcal H_k$
, we construct a Doplicher–Roberts algebra
$\mathcal H_1,\ldots , \mathcal H_k$
, we construct a Doplicher–Roberts algebra
![]() $\mathcal O_{\rho _1,\ldots ,\rho _k}$
from intertwiners
$\mathcal O_{\rho _1,\ldots ,\rho _k}$
from intertwiners
where, for
![]() $n=(n_1,\ldots ,n_k)\in \mathbb N^k$
, the representation
$n=(n_1,\ldots ,n_k)\in \mathbb N^k$
, the representation
![]() $\rho ^n=\rho _1^{\otimes n_1}\otimes \cdots \otimes \rho _k^{\otimes n_k}$
acts on
$\rho ^n=\rho _1^{\otimes n_1}\otimes \cdots \otimes \rho _k^{\otimes n_k}$
acts on
![]() $\mathcal {H}^n=\mathcal H_1^{\otimes n_1}\otimes \cdots \otimes \mathcal H_k^{\otimes n_k}$
. Note that
$\mathcal {H}^n=\mathcal H_1^{\otimes n_1}\otimes \cdots \otimes \mathcal H_k^{\otimes n_k}$
. Note that
![]() $\rho ^0=\iota $
is the trivial representation of G, acting on
$\rho ^0=\iota $
is the trivial representation of G, acting on
![]() $\mathcal {H}^0=\mathbb {C}$
. This Doplicher–Roberts algebra is a subalgebra of
$\mathcal {H}^0=\mathbb {C}$
. This Doplicher–Roberts algebra is a subalgebra of
![]() $\mathcal {O}(\mathcal {E})$
for the product system
$\mathcal {O}(\mathcal {E})$
for the product system
![]() $\mathcal {E}$
, as in Definition 2.9.
$\mathcal {E}$
, as in Definition 2.9.
Lemma 3.1. Consider
 $$ \begin{align*} \mathcal{A}_0=\bigcup_{m,n\in \mathbb{N}^k}\mathcal{L}(\mathcal H^n,\mathcal H^m).\end{align*} $$
$$ \begin{align*} \mathcal{A}_0=\bigcup_{m,n\in \mathbb{N}^k}\mathcal{L}(\mathcal H^n,\mathcal H^m).\end{align*} $$
Then the linear span of
![]() $\mathcal {A}_0$
becomes a
$\mathcal {A}_0$
becomes a
![]() $*$
-algebra
$*$
-algebra
![]() $\mathcal {A}$
with appropriate multiplication and involution. This algebra has a natural
$\mathcal {A}$
with appropriate multiplication and involution. This algebra has a natural
![]() $\mathbb {Z}^k$
-grading coming from a gauge action of
$\mathbb {Z}^k$
-grading coming from a gauge action of
![]() $\mathbb {T}^k$
. Moreover, the Cuntz–Pimsner algebra
$\mathbb {T}^k$
. Moreover, the Cuntz–Pimsner algebra
![]() $\mathcal {O}(\mathcal {E})$
of the product system
$\mathcal {O}(\mathcal {E})$
of the product system
![]() $\mathcal {E}=\mathcal {E}(\rho _1,\ldots ,\rho _k)$
is equivariantly isomorphic to the
$\mathcal {E}=\mathcal {E}(\rho _1,\ldots ,\rho _k)$
is equivariantly isomorphic to the
![]() $C^*$
-closure of
$C^*$
-closure of
![]() $\mathcal {A}$
in the unique
$\mathcal {A}$
in the unique
![]() $C^*$
-norm for which the gauge action is isometric.
$C^*$
-norm for which the gauge action is isometric.
Proof. Recall that the Cuntz algebra
![]() $\mathcal {O}_n$
contains a canonical Hilbert space
$\mathcal {O}_n$
contains a canonical Hilbert space
![]() $\mathcal {H}$
of dimension n and it can be constructed as the closure of the linear span of
$\mathcal {H}$
of dimension n and it can be constructed as the closure of the linear span of
![]() $ \bigcup _{p,q\in \mathbb {N}}\mathcal {L}(\mathcal H^p,\mathcal H^q)$
using embeddings
$ \bigcup _{p,q\in \mathbb {N}}\mathcal {L}(\mathcal H^p,\mathcal H^q)$
using embeddings
where
![]() $\mathcal {H}^p=\mathcal H^{\otimes p}$
and
$\mathcal {H}^p=\mathcal H^{\otimes p}$
and
![]() $I:\mathcal {H}\to \mathcal {H}$
is the identity map. This linear span becomes a
$I:\mathcal {H}\to \mathcal {H}$
is the identity map. This linear span becomes a
![]() $*$
-algebra with a multiplication given by composition and an involution (see [Reference Doplicher and Roberts8] and Proposition 2.5 in [Reference Katsoulis16]).
$*$
-algebra with a multiplication given by composition and an involution (see [Reference Doplicher and Roberts8] and Proposition 2.5 in [Reference Katsoulis16]).
Similarly, for all
![]() $r\in \mathbb {N}^k$
, we consider embeddings
$r\in \mathbb {N}^k$
, we consider embeddings
![]() $\mathcal {L}(\mathcal {H}^n,\mathcal {H}^m)\subseteq \mathcal {L}(\mathcal {H}^{n+r},\mathcal {H}^{m+r})$
given by
$\mathcal {L}(\mathcal {H}^n,\mathcal {H}^m)\subseteq \mathcal {L}(\mathcal {H}^{n+r},\mathcal {H}^{m+r})$
given by
![]() $T\mapsto T\otimes I_r$
, where
$T\mapsto T\otimes I_r$
, where
![]() $I_r:{\mathcal H}^r\to {\mathcal H}^r$
is the identity map, and we endow
$I_r:{\mathcal H}^r\to {\mathcal H}^r$
is the identity map, and we endow
![]() $\mathcal {A}$
with a multiplication given by composition and an involution. More precisely, if
$\mathcal {A}$
with a multiplication given by composition and an involution. More precisely, if
![]() $S\in \mathcal {L}(\mathcal {H}^n,\mathcal {H}^m)$
and
$S\in \mathcal {L}(\mathcal {H}^n,\mathcal {H}^m)$
and
![]() $T\in \mathcal {L}(\mathcal {H}^q,\mathcal {H}^p)$
, then the product
$T\in \mathcal {L}(\mathcal {H}^q,\mathcal {H}^p)$
, then the product
![]() $ST$
is
$ST$
is
where we write
![]() $p\vee n$
for the coordinatewise maximum. This multiplication is well defined in
$p\vee n$
for the coordinatewise maximum. This multiplication is well defined in
![]() $\mathcal {A}$
and is associative. The adjoint of
$\mathcal {A}$
and is associative. The adjoint of
![]() $T\in \mathcal {L}(\mathcal {H}^n,\mathcal {H}^m)$
is
$T\in \mathcal {L}(\mathcal {H}^n,\mathcal {H}^m)$
is
![]() $T^*\in \mathcal {L}(\mathcal {H}^m,\mathcal {H}^n)$
.
$T^*\in \mathcal {L}(\mathcal {H}^m,\mathcal {H}^n)$
.
There is a natural
![]() $\mathbb Z^k$
-grading on
$\mathbb Z^k$
-grading on
![]() $\mathcal {A}$
given by the gauge action
$\mathcal {A}$
given by the gauge action
![]() $\gamma $
of
$\gamma $
of
![]() $\mathbb {T}^k$
, where, for
$\mathbb {T}^k$
, where, for
![]() $z=(z_1,\ldots ,z_k)\in \mathbb {T}^k$
and
$z=(z_1,\ldots ,z_k)\in \mathbb {T}^k$
and
![]() $T\in \mathcal {L}(\mathcal {H}^n,\mathcal {H}^m)$
, we define
$T\in \mathcal {L}(\mathcal {H}^n,\mathcal {H}^m)$
, we define
Adapting the argument in Theorem 4.2 in [Reference Doplicher and Roberts9] for
![]() $\mathbb {Z}^k$
-graded
$\mathbb {Z}^k$
-graded
![]() $C^*$
-algebras, the
$C^*$
-algebras, the
![]() $C^*$
-closure of
$C^*$
-closure of
![]() $\mathcal {A}$
in the unique
$\mathcal {A}$
in the unique
![]() $C^*$
-norm for which
$C^*$
-norm for which
![]() $\gamma _z$
is isometric is well defined. The map
$\gamma _z$
is isometric is well defined. The map
where
for
![]() $T_i\in \mathcal {L}(\mathcal H_i^{n_i},\mathcal H_i^{m_i})$
for
$T_i\in \mathcal {L}(\mathcal H_i^{n_i},\mathcal H_i^{m_i})$
for
![]() $i=1,\ldots ,k$
preserves the gauge action and it can be extended to an equivariant isomorphism from
$i=1,\ldots ,k$
preserves the gauge action and it can be extended to an equivariant isomorphism from
![]() $\mathcal {O}(\mathcal {E})\cong \mathcal {O}_{d_1}\otimes \cdots \otimes \mathcal {O}_{d_k}$
to the
$\mathcal {O}(\mathcal {E})\cong \mathcal {O}_{d_1}\otimes \cdots \otimes \mathcal {O}_{d_k}$
to the
![]() $C^*$
-closure of
$C^*$
-closure of
![]() $\mathcal {A}$
. Note that the closure of
$\mathcal {A}$
. Note that the closure of
![]() $ \bigcup _{n\in \mathbb {N}^k}\mathcal {L}(\mathcal H^n,\mathcal H^n)$
is isomorphic to the core
$ \bigcup _{n\in \mathbb {N}^k}\mathcal {L}(\mathcal H^n,\mathcal H^n)$
is isomorphic to the core
![]() $\mathcal {F}=\mathcal {O}(\mathcal {E})^{\mathbb {T}^k}$
, that is the fixed point algebra under the gauge action, which is a UHF-algebra.
$\mathcal {F}=\mathcal {O}(\mathcal {E})^{\mathbb {T}^k}$
, that is the fixed point algebra under the gauge action, which is a UHF-algebra.
To define the Doplicher–Roberts algebra
![]() $\mathcal O_{\rho _1,\ldots ,\rho _k}$
, we again identify
$\mathcal O_{\rho _1,\ldots ,\rho _k}$
, we again identify
![]() $Hom(\rho ^n,\rho ^m)$
with a subset of
$Hom(\rho ^n,\rho ^m)$
with a subset of
![]() $Hom(\rho ^{n+r},\rho ^{m+r})$
for each
$Hom(\rho ^{n+r},\rho ^{m+r})$
for each
![]() $r\in \mathbb N^k$
, via
$r\in \mathbb N^k$
, via
![]() $T\mapsto T\otimes I_r$
. After this identification, it follows that the linear span
$T\mapsto T\otimes I_r$
. After this identification, it follows that the linear span
![]() ${}^0{\mathcal O}_{\rho _1,\ldots , \rho _k}$
of
${}^0{\mathcal O}_{\rho _1,\ldots , \rho _k}$
of
![]() $ \bigcup _{m,n\in \mathbb {N}^k}Hom(\rho ^n, \rho ^m)\subseteq \mathcal {A}_0$
has a natural multiplication and involution inherited from
$ \bigcup _{m,n\in \mathbb {N}^k}Hom(\rho ^n, \rho ^m)\subseteq \mathcal {A}_0$
has a natural multiplication and involution inherited from
![]() $\mathcal {A}$
. Indeed, a computation shows that if
$\mathcal {A}$
. Indeed, a computation shows that if
![]() $S\in Hom(\rho ^n, \rho ^m)$
and
$S\in Hom(\rho ^n, \rho ^m)$
and
![]() $T\in Hom(\rho ^q,\rho ^p)$
, then
$T\in Hom(\rho ^q,\rho ^p)$
, then
![]() $S^*\in Hom(\rho ^m, \rho ^n)$
and
$S^*\in Hom(\rho ^m, \rho ^n)$
and
 $$ \begin{align*} &((S\otimes I_{p\vee n-n})\circ (T\otimes I_{p\vee n-p}))\rho^{q+p\vee n-p}(g)\\ &\quad=\rho^{m+p\vee n-n}(g)((S\otimes I_{p\vee n-n})\circ (T\otimes I_{p\vee n-p})),\end{align*} $$
$$ \begin{align*} &((S\otimes I_{p\vee n-n})\circ (T\otimes I_{p\vee n-p}))\rho^{q+p\vee n-p}(g)\\ &\quad=\rho^{m+p\vee n-n}(g)((S\otimes I_{p\vee n-n})\circ (T\otimes I_{p\vee n-p})),\end{align*} $$
so
![]() $(S\otimes I_{p\vee n-n})\circ (T\otimes I_{p\vee n-p})\in Hom(\rho ^{q+p\vee n-p}, \rho ^{m+p\vee n-n})$
and
$(S\otimes I_{p\vee n-n})\circ (T\otimes I_{p\vee n-p})\in Hom(\rho ^{q+p\vee n-p}, \rho ^{m+p\vee n-n})$
and
![]() ${}^0{\mathcal O}_{\rho _1,\ldots , \rho _k}$
is closed under these operations. Since the action of G commutes with the gauge action, there is a natural
${}^0{\mathcal O}_{\rho _1,\ldots , \rho _k}$
is closed under these operations. Since the action of G commutes with the gauge action, there is a natural
![]() $\mathbb Z^k$
-grading of
$\mathbb Z^k$
-grading of
![]() ${}^0{\mathcal O}_{\rho _1,\ldots ,\rho _k}$
given by the gauge action
${}^0{\mathcal O}_{\rho _1,\ldots ,\rho _k}$
given by the gauge action
![]() $\gamma $
of
$\gamma $
of
![]() $\mathbb {T}^k$
on
$\mathbb {T}^k$
on
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
It follows that the closure
![]() ${\mathcal O}_{\rho _1,\ldots , \rho _k}$
of
${\mathcal O}_{\rho _1,\ldots , \rho _k}$
of
![]() ${}^0{\mathcal O}_{\rho _1,\ldots ,\rho _k}$
in
${}^0{\mathcal O}_{\rho _1,\ldots ,\rho _k}$
in
![]() $\mathcal {O}(\mathcal {E})$
is well defined, obtaining the Doplicher–Roberts algebra associated to the representations
$\mathcal {O}(\mathcal {E})$
is well defined, obtaining the Doplicher–Roberts algebra associated to the representations
![]() $\rho _1,\ldots ,\rho _k$
. This
$\rho _1,\ldots ,\rho _k$
. This
![]() $C^*$
-algebra also has a
$C^*$
-algebra also has a
![]() $\mathbb Z^k$
-grading and a gauge action of
$\mathbb Z^k$
-grading and a gauge action of
![]() $\mathbb {T}^k$
. By construction,
$\mathbb {T}^k$
. By construction,
![]() ${\mathcal O}_{\rho _1,\ldots , \rho _k}\subseteq \mathcal {O}(\mathcal {E})$
.
${\mathcal O}_{\rho _1,\ldots , \rho _k}\subseteq \mathcal {O}(\mathcal {E})$
.
Remark 3.2. For a compact Lie group G, our Doplicher–Roberts algebra
![]() ${\mathcal O}_{\rho _1,\ldots , \rho _k}$
is Morita equivalent with the higher rank Doplicher–Roberts algebra
${\mathcal O}_{\rho _1,\ldots , \rho _k}$
is Morita equivalent with the higher rank Doplicher–Roberts algebra
![]() $\mathcal {D}$
defined in [Reference Albandik and Meyer1]. It is also the section
$\mathcal {D}$
defined in [Reference Albandik and Meyer1]. It is also the section
![]() $C^*$
-algebra of a Fell bundle over
$C^*$
-algebra of a Fell bundle over
![]() $\mathbb {Z}^k$
.
$\mathbb {Z}^k$
.
Theorem 3.3. Let
![]() $\rho _i$
be finite-dimensional unitary representations of a compact group G on Hilbert spaces
$\rho _i$
be finite-dimensional unitary representations of a compact group G on Hilbert spaces
![]() $\mathcal H_i$
of dimensions
$\mathcal H_i$
of dimensions
![]() $d_i\ge 2$
for
$d_i\ge 2$
for
![]() $i=1,\ldots ,k$
. Then the Doplicher–Roberts algebra
$i=1,\ldots ,k$
. Then the Doplicher–Roberts algebra
![]() ${\mathcal O}_{\rho _1,\ldots ,\rho _k}$
is isomorphic to the fixed point algebra
${\mathcal O}_{\rho _1,\ldots ,\rho _k}$
is isomorphic to the fixed point algebra
![]() ${\mathcal O}(\mathcal {E})^G\cong (\mathcal O_{d_1}\otimes \cdots \otimes \mathcal O_{d_k})^G$
, where
${\mathcal O}(\mathcal {E})^G\cong (\mathcal O_{d_1}\otimes \cdots \otimes \mathcal O_{d_k})^G$
, where
![]() $\mathcal {E}=\mathcal {E}(\rho _1,\ldots ,\rho _k)$
is the product system described in Definition 2.9.
$\mathcal {E}=\mathcal {E}(\rho _1,\ldots ,\rho _k)$
is the product system described in Definition 2.9.
Proof. We know from Lemma 3.1 that
![]() ${\mathcal O}(\mathcal {E})$
is isomorphic to the
${\mathcal O}(\mathcal {E})$
is isomorphic to the
![]() $C^*$
-algebra generated by the linear span of
$C^*$
-algebra generated by the linear span of
![]() $ \mathcal {A}_0= \bigcup _{m,n\in \mathbb {N}^k}\mathcal {L}({\mathcal H}^n, {\mathcal H}^m)$
. The group G acts on
$ \mathcal {A}_0= \bigcup _{m,n\in \mathbb {N}^k}\mathcal {L}({\mathcal H}^n, {\mathcal H}^m)$
. The group G acts on
![]() $\mathcal {L}({\mathcal H}^n, {\mathcal H}^m)$
by
$\mathcal {L}({\mathcal H}^n, {\mathcal H}^m)$
by
and the fixed point set is
![]() $Hom(\rho ^n, \rho ^m)$
. Indeed, we have
$Hom(\rho ^n, \rho ^m)$
. Indeed, we have
![]() $g\cdot T=T$
if and only if
$g\cdot T=T$
if and only if
![]() $T\rho ^n(g)=\rho ^m(g)T$
. This action is compatible with the embeddings and the operations, so it extends to the
$T\rho ^n(g)=\rho ^m(g)T$
. This action is compatible with the embeddings and the operations, so it extends to the
![]() $*$
-algebra
$*$
-algebra
![]() $\mathcal {A}$
and the fixed point algebra is the linear span of
$\mathcal {A}$
and the fixed point algebra is the linear span of
![]() $ \bigcup _{m,n\in \mathbb {N}^k}Hom(\rho ^n, \rho ^m)$
.
$ \bigcup _{m,n\in \mathbb {N}^k}Hom(\rho ^n, \rho ^m)$
.
It follows that
![]() ${}^0{\mathcal O}_{\rho _1,\ldots ,\rho _k}\subseteq {\mathcal O}(\mathcal {E})^G$
and therefore its closure
${}^0{\mathcal O}_{\rho _1,\ldots ,\rho _k}\subseteq {\mathcal O}(\mathcal {E})^G$
and therefore its closure
![]() ${\mathcal O}_{\rho _1,\ldots ,\rho _k}$
is isomorphic to a subalgebra of
${\mathcal O}_{\rho _1,\ldots ,\rho _k}$
is isomorphic to a subalgebra of
![]() ${\mathcal O}(\mathcal {E})^G$
. For the other inclusion, any element in
${\mathcal O}(\mathcal {E})^G$
. For the other inclusion, any element in
![]() ${\mathcal O}(\mathcal {E})^G$
can be approximated with an element from
${\mathcal O}(\mathcal {E})^G$
can be approximated with an element from
![]() ${}^0{\mathcal O}_{\rho _1,\ldots ,\rho _k}$
, and hence
${}^0{\mathcal O}_{\rho _1,\ldots ,\rho _k}$
, and hence
![]() ${\mathcal O}_{\rho _1,\ldots ,\rho _k}=\mathcal {O}(\mathcal {E})^G$
.
${\mathcal O}_{\rho _1,\ldots ,\rho _k}=\mathcal {O}(\mathcal {E})^G$
.
Remark 3.4. By left tensoring with
![]() $I_r$
for
$I_r$
for
![]() $r\in \mathbb {N}^k$
, we obtain some canonical unital endomorphisms
$r\in \mathbb {N}^k$
, we obtain some canonical unital endomorphisms
![]() $\sigma _r$
of
$\sigma _r$
of
![]() ${\mathcal O}_{\rho _1,\ldots ,\rho _k}$
.
${\mathcal O}_{\rho _1,\ldots ,\rho _k}$
.
In the next section, we show that, in many cases,
![]() $\mathcal O_{\rho _1,\ldots ,\rho _k}$
is isomorphic to a corner of
$\mathcal O_{\rho _1,\ldots ,\rho _k}$
is isomorphic to a corner of
![]() $C^*(\Lambda )$
for a rank k graph
$C^*(\Lambda )$
for a rank k graph
![]() $\Lambda $
, so, in some cases, we can compute its K-theory. It would be nice to express the K-theory of
$\Lambda $
, so, in some cases, we can compute its K-theory. It would be nice to express the K-theory of
![]() $\mathcal {O}_{\rho _1,\ldots ,\rho _k}$
in terms of the maps
$\mathcal {O}_{\rho _1,\ldots ,\rho _k}$
in terms of the maps
![]() $\pi \mapsto \pi \otimes \rho _i$
defined on the representation ring
$\pi \mapsto \pi \otimes \rho _i$
defined on the representation ring
![]() $\mathcal {R}(G)$
.
$\mathcal {R}(G)$
.
4 The rank k graphs
For convenience, we first collect some facts about higher rank graphs, introduced in [Reference Kumjian, Pask, Raeburn and Renault18]. A rank k graph or k-graph
![]() $(\Lambda , d)$
consists of a countable small category
$(\Lambda , d)$
consists of a countable small category
![]() $\Lambda $
with range and source maps r and s together with a functor
$\Lambda $
with range and source maps r and s together with a functor
![]() $d : \Lambda \rightarrow \mathbb {N}^k$
called the degree map, satisfying the factorization property: for every
$d : \Lambda \rightarrow \mathbb {N}^k$
called the degree map, satisfying the factorization property: for every
![]() $\lambda \in \Lambda $
and all
$\lambda \in \Lambda $
and all
![]() $m, n \in \mathbb {N}^k$
with
$m, n \in \mathbb {N}^k$
with
![]() $d( \lambda ) = m + n$
, there are unique elements
$d( \lambda ) = m + n$
, there are unique elements
![]() $\mu , \nu \in \Lambda $
such that
$\mu , \nu \in \Lambda $
such that
![]() $\lambda = \mu \nu $
and
$\lambda = \mu \nu $
and
![]() $d( \mu ) = m$
,
$d( \mu ) = m$
,
![]() $d( \nu ) = n$
. For
$d( \nu ) = n$
. For
![]() $n \in \mathbb {N}^k$
, we write
$n \in \mathbb {N}^k$
, we write
![]() $\Lambda ^n := d^{-1} (n)$
and call it the set of paths of degree n. For
$\Lambda ^n := d^{-1} (n)$
and call it the set of paths of degree n. For
![]() $\varepsilon _i=(0,\ldots ,1,\ldots ,0)$
with
$\varepsilon _i=(0,\ldots ,1,\ldots ,0)$
with
![]() $1$
in position i, the elements in
$1$
in position i, the elements in
![]() $\Lambda ^{\varepsilon _i}$
are called edges and the elements in
$\Lambda ^{\varepsilon _i}$
are called edges and the elements in
![]() $\Lambda ^0$
are called vertices.
$\Lambda ^0$
are called vertices.
A k-graph
![]() $\Lambda $
can be constructed from
$\Lambda $
can be constructed from
![]() $\Lambda ^0$
and from its k-colored skeleton
$\Lambda ^0$
and from its k-colored skeleton
![]() $\Lambda ^{\varepsilon _1}\cup \cdots \cup \Lambda ^{\varepsilon _k}$
using a complete and associative collection of commuting squares or factorization rules (see [Reference Sims25]).
$\Lambda ^{\varepsilon _1}\cup \cdots \cup \Lambda ^{\varepsilon _k}$
using a complete and associative collection of commuting squares or factorization rules (see [Reference Sims25]).
The k-graph
![]() $\Lambda $
is row-finite if, for all
$\Lambda $
is row-finite if, for all
![]() $n\in \mathbb {N}^k$
and all
$n\in \mathbb {N}^k$
and all
![]() $v\in \Lambda ^0$
, the set
$v\in \Lambda ^0$
, the set
![]() $v\Lambda ^n := \{\lambda \in \Lambda ^n : r(\lambda ) = v\}$
is finite. It has no sources if
$v\Lambda ^n := \{\lambda \in \Lambda ^n : r(\lambda ) = v\}$
is finite. It has no sources if
![]() $v\Lambda ^n\neq \emptyset $
for all
$v\Lambda ^n\neq \emptyset $
for all
![]() $v\in \Lambda ^0$
and
$v\in \Lambda ^0$
and
![]() $n\in \mathbb {N}^k$
. A k-graph
$n\in \mathbb {N}^k$
. A k-graph
![]() $\Lambda $
is said to be irreducible (or strongly connected) if, for every
$\Lambda $
is said to be irreducible (or strongly connected) if, for every
![]() $u,v\in \Lambda ^0$
, there is
$u,v\in \Lambda ^0$
, there is
![]() $\lambda \in \Lambda $
such that
$\lambda \in \Lambda $
such that
![]() $u = r(\lambda )$
and
$u = r(\lambda )$
and
![]() $v = s(\lambda )$
.
$v = s(\lambda )$
.
Recall that
![]() $C^*(\Lambda )$
is the universal
$C^*(\Lambda )$
is the universal
![]() $C^*$
-algebra generated by a family
$C^*$
-algebra generated by a family
![]() $\{S_\lambda : \lambda \in \Lambda \}$
of partial isometries satisfying:
$\{S_\lambda : \lambda \in \Lambda \}$
of partial isometries satisfying:
-
•
 $\{S_v:v\in \Lambda ^0\}$
is a family of mutually orthogonal projections;
$\{S_v:v\in \Lambda ^0\}$
is a family of mutually orthogonal projections; -
•
 $S_{\lambda \mu }=S_\lambda S_\mu $
for all
$S_{\lambda \mu }=S_\lambda S_\mu $
for all
 $\lambda , \mu \in \Lambda $
such that
$\lambda , \mu \in \Lambda $
such that
 $s(\lambda ) = r(\mu )$
;
$s(\lambda ) = r(\mu )$
; -
•
 $S_\lambda ^*S_\lambda = S_{s(\lambda )}$
for all
$S_\lambda ^*S_\lambda = S_{s(\lambda )}$
for all
 $\lambda \in \Lambda $
; and
$\lambda \in \Lambda $
; and -
• for all
 $v\in \Lambda ^0$
and
$v\in \Lambda ^0$
and
 $n\in \mathbb {N}^k$
,
$n\in \mathbb {N}^k$
,  $$ \begin{align*} S_v=\sum_{\lambda\in v\Lambda^n}S_\lambda S_\lambda^*.\end{align*} $$
$$ \begin{align*} S_v=\sum_{\lambda\in v\Lambda^n}S_\lambda S_\lambda^*.\end{align*} $$
A k-graph
![]() $\Lambda $
is said to satisfy the aperiodicity condition if, for every vertex
$\Lambda $
is said to satisfy the aperiodicity condition if, for every vertex
![]() $v\in \Lambda ^0$
, there is an infinite path
$v\in \Lambda ^0$
, there is an infinite path
![]() $x\in v\Lambda ^\infty $
such that
$x\in v\Lambda ^\infty $
such that
![]() $\sigma ^mx\neq \sigma ^nx$
for all
$\sigma ^mx\neq \sigma ^nx$
for all
![]() $m\neq n$
in
$m\neq n$
in
![]() $\mathbb {N}^k$
, where
$\mathbb {N}^k$
, where
![]() $\sigma ^m:\Lambda ^\infty \to \Lambda ^\infty $
are the shift maps. We say that
$\sigma ^m:\Lambda ^\infty \to \Lambda ^\infty $
are the shift maps. We say that
![]() $\Lambda $
is cofinal if, for every
$\Lambda $
is cofinal if, for every
![]() $x\in \Lambda ^\infty $
and
$x\in \Lambda ^\infty $
and
![]() $v\in \Lambda ^0$
, there is
$v\in \Lambda ^0$
, there is
![]() $\lambda \in \Lambda $
and
$\lambda \in \Lambda $
and
![]() $n\in \mathbb {N}^k$
such that
$n\in \mathbb {N}^k$
such that
![]() $s(\lambda )=x(n)$
and
$s(\lambda )=x(n)$
and
![]() $r(\lambda )=v$
.
$r(\lambda )=v$
.
Assume that
![]() $\Lambda $
is row-finite with no sources and that it satisfies the aperiodicity condition. Then
$\Lambda $
is row-finite with no sources and that it satisfies the aperiodicity condition. Then
![]() $C^*(\Lambda )$
is simple if and only if
$C^*(\Lambda )$
is simple if and only if
![]() $\Lambda $
is cofinal (see Proposition 4.8 in [Reference Kumjian, Pask, Raeburn and Renault18] and Theorem 3.4 in [Reference Robertson and Sims23]).
$\Lambda $
is cofinal (see Proposition 4.8 in [Reference Kumjian, Pask, Raeburn and Renault18] and Theorem 3.4 in [Reference Robertson and Sims23]).
We say that a path
![]() $\mu \in \Lambda $
is a loop with an entrance if
$\mu \in \Lambda $
is a loop with an entrance if
![]() $s(\mu )=r(\mu )$
, and there exists
$s(\mu )=r(\mu )$
, and there exists
![]() $\alpha \in s(\mu )\Lambda $
such that
$\alpha \in s(\mu )\Lambda $
such that
![]() $d(\mu )\ge d(\alpha )$
and there is no
$d(\mu )\ge d(\alpha )$
and there is no
![]() $\beta \in \Lambda $
with
$\beta \in \Lambda $
with
![]() $\mu = \alpha \beta $
. We say that every vertex connects to a loop with an entrance if, for every
$\mu = \alpha \beta $
. We say that every vertex connects to a loop with an entrance if, for every
![]() $v\in \Lambda ^0$
, there is a loop with an entrance
$v\in \Lambda ^0$
, there is a loop with an entrance
![]() $\mu \in \Lambda $
, and a path
$\mu \in \Lambda $
, and a path
![]() $\lambda \in \Lambda $
with
$\lambda \in \Lambda $
with
![]() $r(\lambda )=v$
and
$r(\lambda )=v$
and
![]() $s(\lambda )=r(\mu )=s(\mu )$
. If
$s(\lambda )=r(\mu )=s(\mu )$
. If
![]() $\Lambda $
satisfies the aperiodicity condition and every vertex connects to a loop with an entrance, then
$\Lambda $
satisfies the aperiodicity condition and every vertex connects to a loop with an entrance, then
![]() $C^*(\Lambda )$
is purely infinite (see Proposition 4.9 in [Reference Kumjian, Pask, Raeburn and Renault18] and Proposition 8.8 in [Reference Sims24]).
$C^*(\Lambda )$
is purely infinite (see Proposition 4.9 in [Reference Kumjian, Pask, Raeburn and Renault18] and Proposition 8.8 in [Reference Sims24]).
Given finite-dimensional unitary representations
![]() $\rho _i$
of a compact group G on Hilbert spaces
$\rho _i$
of a compact group G on Hilbert spaces
![]() $\mathcal H_i$
for
$\mathcal H_i$
for
![]() $i=1,\ldots ,k$
, we want to construct a rank k graph
$i=1,\ldots ,k$
, we want to construct a rank k graph
![]() $\Lambda =\Lambda (\rho _1,\ldots ,\rho _k)$
. Let R be the set of equivalence classes of irreducible summands
$\Lambda =\Lambda (\rho _1,\ldots ,\rho _k)$
. Let R be the set of equivalence classes of irreducible summands
![]() $\pi :G\to U(\mathcal {H}_\pi )$
which appear in the tensor powers
$\pi :G\to U(\mathcal {H}_\pi )$
which appear in the tensor powers
![]() $\rho ^n=\rho _1^{\otimes n_1}\otimes \cdots \otimes \rho _k^{\otimes n_k}$
for
$\rho ^n=\rho _1^{\otimes n_1}\otimes \cdots \otimes \rho _k^{\otimes n_k}$
for
![]() $n\in \mathbb {N}^k$
, as in [Reference Mann, Raeburn and Sutherland22]. Take
$n\in \mathbb {N}^k$
, as in [Reference Mann, Raeburn and Sutherland22]. Take
![]() $\Lambda ^0=R$
and, for each
$\Lambda ^0=R$
and, for each
![]() $i=1,\ldots ,k$
, consider the set of edges
$i=1,\ldots ,k$
, consider the set of edges
![]() $\Lambda ^{\varepsilon _i}$
which are uniquely determined by the matrices
$\Lambda ^{\varepsilon _i}$
which are uniquely determined by the matrices
![]() $M_i$
with entries
$M_i$
with entries
where
![]() $v,w\in R$
. The matrices
$v,w\in R$
. The matrices
![]() $M_i$
commute since
$M_i$
commute since
![]() $\rho _i\otimes \rho _j\cong \rho _j\otimes \rho _i$
and therefore
$\rho _i\otimes \rho _j\cong \rho _j\otimes \rho _i$
and therefore
for all
![]() $i<j$
. This allows us to fix some bijections
$i<j$
. This allows us to fix some bijections
for all
![]() $1\le i<j\le k$
, which determine the commuting squares of
$1\le i<j\le k$
, which determine the commuting squares of
![]() $\Lambda $
. As usual,
$\Lambda $
. As usual,
For
![]() $k\ge 3$
, we also need to verify that
$k\ge 3$
, we also need to verify that
![]() $\lambda _{ij}$
can be chosen to satisfy the associativity condition, that is,
$\lambda _{ij}$
can be chosen to satisfy the associativity condition, that is,
as bijections from
![]() $\Lambda ^{\varepsilon _i}\times _{\Lambda ^0}\Lambda ^{\varepsilon _j}\times _{\Lambda ^0}\Lambda ^{\varepsilon _\ell }$
to
$\Lambda ^{\varepsilon _i}\times _{\Lambda ^0}\Lambda ^{\varepsilon _j}\times _{\Lambda ^0}\Lambda ^{\varepsilon _\ell }$
to
![]() $\Lambda ^{\varepsilon _\ell }\times _{\Lambda ^0}\Lambda ^{\varepsilon _j}\times _{\Lambda ^0}\Lambda ^{\varepsilon _i}$
for all
$\Lambda ^{\varepsilon _\ell }\times _{\Lambda ^0}\Lambda ^{\varepsilon _j}\times _{\Lambda ^0}\Lambda ^{\varepsilon _i}$
for all
![]() $i<j<\ell $
.
$i<j<\ell $
.
Remark 4.1. Many times
![]() $R=\hat {G}$
, so
$R=\hat {G}$
, so
![]() $\Lambda ^0=\hat {G}$
, for example, if
$\Lambda ^0=\hat {G}$
, for example, if
![]() $\rho _i$
are faithful and
$\rho _i$
are faithful and
![]() $\rho _i(G)\subseteq SU(\mathcal {H}_i)$
or if G is finite,
$\rho _i(G)\subseteq SU(\mathcal {H}_i)$
or if G is finite,
![]() $\rho _i$
are faithful and
$\rho _i$
are faithful and
![]() $\dim \rho _i\ge 2$
for all
$\dim \rho _i\ge 2$
for all
![]() $i=1,\ldots ,k$
(see Lemma 7.2 and Remark 7.4 in [Reference Kajiwara, Pinzari and Watatani19]).
$i=1,\ldots ,k$
(see Lemma 7.2 and Remark 7.4 in [Reference Kajiwara, Pinzari and Watatani19]).
Proposition 4.2. Given representations
![]() $\rho _1,\ldots ,\rho _k$
as above, assume that
$\rho _1,\ldots ,\rho _k$
as above, assume that
![]() $\rho _i$
are faithful and that
$\rho _i$
are faithful and that
![]() $R=\hat {G}$
. Then each choice of bijections
$R=\hat {G}$
. Then each choice of bijections
![]() $\lambda _{ij}$
satisfying the associativity condition determines a rank k graph
$\lambda _{ij}$
satisfying the associativity condition determines a rank k graph
![]() $\Lambda $
which is cofinal and locally finite with no sources.
$\Lambda $
which is cofinal and locally finite with no sources.
Proof. Indeed, the sets
![]() $\Lambda ^{\varepsilon _i}$
are uniquely determined and the choice of bijections
$\Lambda ^{\varepsilon _i}$
are uniquely determined and the choice of bijections
![]() $\lambda _{ij}$
satisfying the associativity condition is enough to determine
$\lambda _{ij}$
satisfying the associativity condition is enough to determine
![]() $\Lambda $
. Since the entries of the matrices
$\Lambda $
. Since the entries of the matrices
![]() $M_i$
are finite and there are no zero rows, the graph is locally finite with no sources. To prove that
$M_i$
are finite and there are no zero rows, the graph is locally finite with no sources. To prove that
![]() $\Lambda $
is cofinal, fix a vertex
$\Lambda $
is cofinal, fix a vertex
![]() $v\in \Lambda ^0$
and an infinite path
$v\in \Lambda ^0$
and an infinite path
![]() $x\in \Lambda ^\infty $
. Arguing as in Lemma 7.2 in [Reference Kajiwara, Pinzari and Watatani19], any
$x\in \Lambda ^\infty $
. Arguing as in Lemma 7.2 in [Reference Kajiwara, Pinzari and Watatani19], any
![]() $w\in \Lambda ^0$
, in particular,
$w\in \Lambda ^0$
, in particular,
![]() $w=x(n)$
for a fixed n, can be joined by a path to v, so there is
$w=x(n)$
for a fixed n, can be joined by a path to v, so there is
![]() $\lambda \in \Lambda $
with
$\lambda \in \Lambda $
with
![]() $s(\lambda )=x(n)$
and
$s(\lambda )=x(n)$
and
![]() $r(\lambda )=v$
. See also Lemma 3.1 in [Reference Mann, Raeburn and Sutherland22].
$r(\lambda )=v$
. See also Lemma 3.1 in [Reference Mann, Raeburn and Sutherland22].
Remark 4.3. Note that the entry
![]() $M_i(w,v)$
is just the multiplicity of the irreducible representation v in
$M_i(w,v)$
is just the multiplicity of the irreducible representation v in
![]() $w\otimes \rho _i$
for
$w\otimes \rho _i$
for
![]() $i=1,\ldots ,k$
. If
$i=1,\ldots ,k$
. If
![]() $\rho _i^*=\rho _i$
, then the matrices
$\rho _i^*=\rho _i$
, then the matrices
![]() $M_i$
are symmetric since
$M_i$
are symmetric since
which implies
![]() $M_i(w; v) = M_i(v;w)$
. Here
$M_i(w; v) = M_i(v;w)$
. Here
![]() $\rho ^*_i$
denotes the dual representation defined by
$\rho ^*_i$
denotes the dual representation defined by
![]() $\rho _i^*(g)=\rho _i(g^{-1})^t$
and equal, in our case, to the conjugate representation
$\rho _i^*(g)=\rho _i(g^{-1})^t$
and equal, in our case, to the conjugate representation
![]() $\bar {\rho _i}$
.
$\bar {\rho _i}$
.
For G finite, these matrices are finite, and the entries
![]() $M_i(w,v)$
can be computed using the character table of G. For G infinite, the Clebsch–Gordan relations can be used to determine the numbers
$M_i(w,v)$
can be computed using the character table of G. For G infinite, the Clebsch–Gordan relations can be used to determine the numbers
![]() $M_i(w,v)$
. Since the bijections
$M_i(w,v)$
. Since the bijections
![]() $\lambda _{ij}$
are, in general, not unique, the rank k graph
$\lambda _{ij}$
are, in general, not unique, the rank k graph
![]() $\Lambda $
is not unique, as illustrated in some examples. It is an open question how the
$\Lambda $
is not unique, as illustrated in some examples. It is an open question how the
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C^*(\Lambda )$
depends, in general, on the factorization rules.
$C^*(\Lambda )$
depends, in general, on the factorization rules.
To relate the Doplicher–Roberts algebra
![]() $\mathcal {O}_{\rho _1,\ldots ,\rho _k}$
to a rank k graph
$\mathcal {O}_{\rho _1,\ldots ,\rho _k}$
to a rank k graph
![]() $\Lambda $
, we mimic the construction in [Reference Mann, Raeburn and Sutherland22]. For each edge
$\Lambda $
, we mimic the construction in [Reference Mann, Raeburn and Sutherland22]. For each edge
![]() $e\in \Lambda ^{\varepsilon _i}$
, choose an isometric intertwiner
$e\in \Lambda ^{\varepsilon _i}$
, choose an isometric intertwiner
in such a way that
for all
![]() $\pi \in \Lambda ^0$
, that is, the edges in
$\pi \in \Lambda ^0$
, that is, the edges in
![]() $\Lambda ^{\varepsilon _i}$
ending at
$\Lambda ^{\varepsilon _i}$
ending at
![]() $\pi $
give a specific decomposition of
$\pi $
give a specific decomposition of
![]() $\mathcal {H}_\pi \otimes \mathcal {H}_i$
into irreducibles. When
$\mathcal {H}_\pi \otimes \mathcal {H}_i$
into irreducibles. When
![]() $\dim Hom(s(e), r(e)\otimes \rho _i)\ge 2$
, we must choose a basis of isometric intertwiners with orthogonal ranges, so, in general,
$\dim Hom(s(e), r(e)\otimes \rho _i)\ge 2$
, we must choose a basis of isometric intertwiners with orthogonal ranges, so, in general,
![]() $T_e$
is not unique. In fact, specific choices for the isometric intertwiners
$T_e$
is not unique. In fact, specific choices for the isometric intertwiners
![]() $T_e$
determine the factorization rules in
$T_e$
determine the factorization rules in
![]() $\Lambda $
and whether or not they satisfy the associativity condition.
$\Lambda $
and whether or not they satisfy the associativity condition.
Given
![]() $e\in \Lambda ^{\varepsilon _i}$
and
$e\in \Lambda ^{\varepsilon _i}$
and
![]() $f\in \Lambda ^{\varepsilon _j}$
with
$f\in \Lambda ^{\varepsilon _j}$
with
![]() $r(f)=s(e)$
, we know how to multiply
$r(f)=s(e)$
, we know how to multiply
![]() $T_e\in Hom(s(e),r(e)\otimes \rho _i)$
with
$T_e\in Hom(s(e),r(e)\otimes \rho _i)$
with
![]() $T_f\in Hom(s(f),r(f)\otimes \rho _j)$
in the algebra
$T_f\in Hom(s(f),r(f)\otimes \rho _j)$
in the algebra
![]() $\mathcal {O}_{\rho _1,\ldots ,\rho _k}$
, by viewing
$\mathcal {O}_{\rho _1,\ldots ,\rho _k}$
, by viewing
![]() $Hom(s(e),r(e)\otimes \rho _i)$
as a subspace of
$Hom(s(e),r(e)\otimes \rho _i)$
as a subspace of
![]() $Hom(\rho ^n,\rho ^m)$
for some
$Hom(\rho ^n,\rho ^m)$
for some
![]() $m,n$
, and similarly for
$m,n$
, and similarly for
![]() $Hom(s(f),r(f)\otimes \rho _j)$
. We choose edges
$Hom(s(f),r(f)\otimes \rho _j)$
. We choose edges
![]() $e'\in \Lambda ^{\varepsilon _i}, f'\in \Lambda ^{\varepsilon _j}$
with
$e'\in \Lambda ^{\varepsilon _i}, f'\in \Lambda ^{\varepsilon _j}$
with
![]() $s(f)=s(e'), r(e)=r(f'), r(e')=s(f')$
such that
$s(f)=s(e'), r(e)=r(f'), r(e')=s(f')$
such that
![]() $T_eT_f=T_{f'}T_{e'}$
, where
$T_eT_f=T_{f'}T_{e'}$
, where
![]() $T_{f'}\in Hom(s(f'),r(f')\otimes \rho _j)$
and
$T_{f'}\in Hom(s(f'),r(f')\otimes \rho _j)$
and
![]() $T_{e'}\in Hom(s(e'),r(e')\otimes \rho _i)$
. This is possible since
$T_{e'}\in Hom(s(e'),r(e')\otimes \rho _i)$
. This is possible since
and
![]() $\rho _i\otimes \rho _j\cong \rho _j\otimes \rho _i$
. In this case, we declare that
$\rho _i\otimes \rho _j\cong \rho _j\otimes \rho _i$
. In this case, we declare that
![]() $ef=f'e'$
. Repeating this process, we obtain bijections
$ef=f'e'$
. Repeating this process, we obtain bijections
![]() $\lambda _{ij}:\Lambda ^{\varepsilon _i}\times _{\Lambda ^0}\Lambda ^{\varepsilon _j}\to \Lambda ^{\varepsilon _j}\times _{\Lambda ^0}\Lambda ^{\varepsilon _i}$
. Assuming that the associativity conditions are satisfied, we obtain a k-graph
$\lambda _{ij}:\Lambda ^{\varepsilon _i}\times _{\Lambda ^0}\Lambda ^{\varepsilon _j}\to \Lambda ^{\varepsilon _j}\times _{\Lambda ^0}\Lambda ^{\varepsilon _i}$
. Assuming that the associativity conditions are satisfied, we obtain a k-graph
![]() $\Lambda $
.
$\Lambda $
.
We write
![]() $T_{ef}=T_eT_f=T_{f'}T_{e'}=T_{f'e'}$
. A finite path
$T_{ef}=T_eT_f=T_{f'}T_{e'}=T_{f'e'}$
. A finite path
![]() $\lambda \in \Lambda ^n$
is a concatenation of edges and determines by composition a unique intertwiner
$\lambda \in \Lambda ^n$
is a concatenation of edges and determines by composition a unique intertwiner
Moreover, the paths
![]() $\lambda \in \Lambda ^n$
with
$\lambda \in \Lambda ^n$
with
![]() $r(\lambda )=\iota $
, the trivial representation, provide an explicit decomposition of
$r(\lambda )=\iota $
, the trivial representation, provide an explicit decomposition of
![]() $\mathcal {H}^n=\mathcal {H}_1^{\otimes n_1}\otimes \cdots \otimes \mathcal {H}_k^{\otimes n_k}$
into irreducibles, and hence
$\mathcal {H}^n=\mathcal {H}_1^{\otimes n_1}\otimes \cdots \otimes \mathcal {H}_k^{\otimes n_k}$
into irreducibles, and hence
Proposition 4.4. Assuming that the choices of isometric intertwiners
![]() $T_e$
, as above, determine a k-graph
$T_e$
, as above, determine a k-graph
![]() $\Lambda $
, the family
$\Lambda $
, the family
is a basis for
![]() $Hom(\rho ^n, \rho ^m)$
and each
$Hom(\rho ^n, \rho ^m)$
and each
![]() $T_\lambda T^*_\mu $
is a partial isometry.
$T_\lambda T^*_\mu $
is a partial isometry.
Proof. Each pair of paths
![]() $\lambda , \mu $
with
$\lambda , \mu $
with
![]() $d(\lambda )=m, d(\mu )=n$
and
$d(\lambda )=m, d(\mu )=n$
and
![]() $r(\lambda )=r(\mu )=\iota $
determines a pair of irreducible summands
$r(\lambda )=r(\mu )=\iota $
determines a pair of irreducible summands
![]() $T_\lambda (\mathcal {H}_{s(\lambda )}), T_\mu (\mathcal {H}_{s(\mu )})$
of
$T_\lambda (\mathcal {H}_{s(\lambda )}), T_\mu (\mathcal {H}_{s(\mu )})$
of
![]() $\mathcal {H}^m$
and
$\mathcal {H}^m$
and
![]() $ \mathcal {H}^n$
, respectively. By Schur’s lemma, the space of intertwiners of these representations is trivial unless
$ \mathcal {H}^n$
, respectively. By Schur’s lemma, the space of intertwiners of these representations is trivial unless
![]() $s(\lambda )=s(\mu )$
, in which case it is the one-dimensional space spanned by
$s(\lambda )=s(\mu )$
, in which case it is the one-dimensional space spanned by
![]() $T_\lambda T_\mu ^*$
. It follows that any element of
$T_\lambda T_\mu ^*$
. It follows that any element of
![]() $Hom(\rho ^n, \rho ^m)$
can be uniquely represented as a linear combination of elements
$Hom(\rho ^n, \rho ^m)$
can be uniquely represented as a linear combination of elements
![]() $T_\lambda T_\mu ^*$
, where
$T_\lambda T_\mu ^*$
, where
![]() $s(\lambda )=s(\mu )$
. Since
$s(\lambda )=s(\mu )$
. Since
![]() $T_\mu $
is isometric,
$T_\mu $
is isometric,
![]() $T_\mu ^*$
is a partial isometry with range
$T_\mu ^*$
is a partial isometry with range
![]() $\mathcal {H}_{s(\mu )}$
and hence
$\mathcal {H}_{s(\mu )}$
and hence
![]() $T_\lambda T_\mu ^*$
is also a partial isometry whenever
$T_\lambda T_\mu ^*$
is also a partial isometry whenever
![]() $s(\lambda )=s(\mu )$
.
$s(\lambda )=s(\mu )$
.
Theorem 4.5. Consider
![]() $\rho _1,\ldots , \rho _k$
finite-dimensional unitary representations of a compact group G and let
$\rho _1,\ldots , \rho _k$
finite-dimensional unitary representations of a compact group G and let
![]() $\Lambda $
be the k-colored graph with
$\Lambda $
be the k-colored graph with
![]() $\Lambda ^0=R\subseteq \hat {G}$
and edges
$\Lambda ^0=R\subseteq \hat {G}$
and edges
![]() $\Lambda ^{\varepsilon _i}$
determined by the incidence matrices
$\Lambda ^{\varepsilon _i}$
determined by the incidence matrices
![]() $M_i$
defined above. Assume that the factorization rules determined by the choices of
$M_i$
defined above. Assume that the factorization rules determined by the choices of
![]() $T_e\in Hom(s(e),r(e)\otimes \rho _i)$
for all edges
$T_e\in Hom(s(e),r(e)\otimes \rho _i)$
for all edges
![]() $e\in \Lambda ^{\varepsilon _i}$
satisfy the associativity condition, so
$e\in \Lambda ^{\varepsilon _i}$
satisfy the associativity condition, so
![]() $\Lambda $
becomes a rank k graph. If we consider
$\Lambda $
becomes a rank k graph. If we consider
![]() $P\in C^*(\Lambda )$
,
$P\in C^*(\Lambda )$
,
 $$ \begin{align*}P=\sum_{\lambda\in\iota \Lambda^{(1,\ldots,1)}}S_\lambda S_\lambda^*,\end{align*} $$
$$ \begin{align*}P=\sum_{\lambda\in\iota \Lambda^{(1,\ldots,1)}}S_\lambda S_\lambda^*,\end{align*} $$
where
![]() $\iota $
is the trivial representation, then there is a
$\iota $
is the trivial representation, then there is a
![]() $*$
-isomorphism of the Doplicher–Roberts algebra
$*$
-isomorphism of the Doplicher–Roberts algebra
![]() $\mathcal {O}_{\rho _1,\ldots ,\rho _k}$
onto the corner
$\mathcal {O}_{\rho _1,\ldots ,\rho _k}$
onto the corner
![]() $PC^*(\Lambda )P$
.
$PC^*(\Lambda )P$
.
Proof. Since
![]() $C^*(\Lambda )$
is generated by linear combinations of
$C^*(\Lambda )$
is generated by linear combinations of
![]() $S_\lambda S_\mu ^*$
with
$S_\lambda S_\mu ^*$
with
![]() $s(\lambda )=s(\mu )$
(see Lemma 3.1 in [Reference Kumjian, Pask, Raeburn and Renault18]), we first define the maps
$s(\lambda )=s(\mu )$
(see Lemma 3.1 in [Reference Kumjian, Pask, Raeburn and Renault18]), we first define the maps
where
![]() $s(\lambda )=s(\mu )$
and
$s(\lambda )=s(\mu )$
and
![]() $r(\lambda )=r(\mu )=\iota $
. Since
$r(\lambda )=r(\mu )=\iota $
. Since
![]() $S_\lambda S_\mu ^*=PS_\lambda S_\mu ^*P$
, the maps
$S_\lambda S_\mu ^*=PS_\lambda S_\mu ^*P$
, the maps
![]() $\phi _{n,m}$
take values in
$\phi _{n,m}$
take values in
![]() $PC^*(\Lambda )P$
. We claim that, for any
$PC^*(\Lambda )P$
. We claim that, for any
![]() $r\in \mathbb {N}^k$
,
$r\in \mathbb {N}^k$
,
This is because
 $$ \begin{align*}\mathcal{H}_{s(\lambda)}\otimes \mathcal{H}^r=\bigoplus_{\nu\in s(\lambda)\Lambda^r}T_\nu T_\nu^*(\mathcal{H}_{s(\lambda)}\otimes \mathcal{H}^r),\end{align*} $$
$$ \begin{align*}\mathcal{H}_{s(\lambda)}\otimes \mathcal{H}^r=\bigoplus_{\nu\in s(\lambda)\Lambda^r}T_\nu T_\nu^*(\mathcal{H}_{s(\lambda)}\otimes \mathcal{H}^r),\end{align*} $$
so that
 $$ \begin{align*}T_\lambda T_\mu^*\otimes I_r=\sum_{\nu\in s(\lambda)\Lambda^r}(T_\lambda\otimes I_r)(T_\nu T_\nu^*)(T_\mu^*\otimes I_r)=\sum_ {\nu\in s(\lambda)\Lambda^r} T_{\lambda\nu}T_{\mu\nu}^*\end{align*} $$
$$ \begin{align*}T_\lambda T_\mu^*\otimes I_r=\sum_{\nu\in s(\lambda)\Lambda^r}(T_\lambda\otimes I_r)(T_\nu T_\nu^*)(T_\mu^*\otimes I_r)=\sum_ {\nu\in s(\lambda)\Lambda^r} T_{\lambda\nu}T_{\mu\nu}^*\end{align*} $$
and
 $$ \begin{align*}S_\lambda S_\mu^*=\sum_{\nu\in s(\lambda)\Lambda^r}S_\lambda(S_\nu S_\nu^*)S_\mu^*=\sum_{\nu\in s(\lambda)\Lambda^r}S_{\lambda\nu}S_{\mu\nu}^*.\end{align*} $$
$$ \begin{align*}S_\lambda S_\mu^*=\sum_{\nu\in s(\lambda)\Lambda^r}S_\lambda(S_\nu S_\nu^*)S_\mu^*=\sum_{\nu\in s(\lambda)\Lambda^r}S_{\lambda\nu}S_{\mu\nu}^*.\end{align*} $$
The maps
![]() $\phi _{n,m}$
determine a map
$\phi _{n,m}$
determine a map
![]() $\phi : {}^0\mathcal {O}_{\rho _1,\ldots ,\rho _k}\to PC^*(\Lambda )P$
which is linear,
$\phi : {}^0\mathcal {O}_{\rho _1,\ldots ,\rho _k}\to PC^*(\Lambda )P$
which is linear,
![]() $*$
-preserving and multiplicative. Indeed,
$*$
-preserving and multiplicative. Indeed,
Consider now
![]() $T_\lambda T_\mu ^*\in Hom(\rho ^n, \rho ^m),\;\; T_\nu T_\omega ^*\in Hom (\rho ^q,\rho ^p)$
with
$T_\lambda T_\mu ^*\in Hom(\rho ^n, \rho ^m),\;\; T_\nu T_\omega ^*\in Hom (\rho ^q,\rho ^p)$
with
![]() $s(\lambda )=s(\mu ), s(\nu )=s(\omega ), r(\lambda )=r(\mu )=r(\nu )=r(\omega )=\iota $
. Since, for all
$s(\lambda )=s(\mu ), s(\nu )=s(\omega ), r(\lambda )=r(\mu )=r(\nu )=r(\omega )=\iota $
. Since, for all
![]() $n\in \mathbb {N}^k$
,
$n\in \mathbb {N}^k$
,
we get
 $$ \begin{align*}T_\mu^*T_\nu= \begin{cases} T_\beta^*\quad& \text{if } \mu=\nu\beta,\\ T_\alpha \quad& \text{if } \nu=\mu\alpha,\\0 \quad&\text{otherwise,}\end{cases}\end{align*} $$
$$ \begin{align*}T_\mu^*T_\nu= \begin{cases} T_\beta^*\quad& \text{if } \mu=\nu\beta,\\ T_\alpha \quad& \text{if } \nu=\mu\alpha,\\0 \quad&\text{otherwise,}\end{cases}\end{align*} $$
and hence
 $$ \begin{align*}\phi((T_\lambda T_\mu^*)(T_\nu T_\omega^*))=\begin{cases} \phi(T_\lambda T_{\omega\beta}^*)=S_\lambda S_{\omega\beta}^*\quad&\text{if } \mu=\nu\beta,\\ \phi(T_{\lambda\alpha}T_\omega^*)=S_{\lambda\alpha}S_\omega^*\quad&\text{if } \nu=\mu\alpha,\\0 \quad&\text{otherwise.}\end{cases}\end{align*} $$
$$ \begin{align*}\phi((T_\lambda T_\mu^*)(T_\nu T_\omega^*))=\begin{cases} \phi(T_\lambda T_{\omega\beta}^*)=S_\lambda S_{\omega\beta}^*\quad&\text{if } \mu=\nu\beta,\\ \phi(T_{\lambda\alpha}T_\omega^*)=S_{\lambda\alpha}S_\omega^*\quad&\text{if } \nu=\mu\alpha,\\0 \quad&\text{otherwise.}\end{cases}\end{align*} $$
On the other hand, from Lemma 3.1 in [Reference Kumjian, Pask, Raeburn and Renault18],
 $$ \begin{align*}S_\lambda S_\mu^* S_\nu S_{\omega}^*=\begin{cases} S_\lambda S_{\omega\beta}^*\quad&\text{if } \mu=\nu\beta,\\ S_{\lambda\alpha}S_\omega^*\quad&\text{if } \nu=\mu\alpha,\\0 \quad&\text{otherwise,}\end{cases}\end{align*} $$
$$ \begin{align*}S_\lambda S_\mu^* S_\nu S_{\omega}^*=\begin{cases} S_\lambda S_{\omega\beta}^*\quad&\text{if } \mu=\nu\beta,\\ S_{\lambda\alpha}S_\omega^*\quad&\text{if } \nu=\mu\alpha,\\0 \quad&\text{otherwise,}\end{cases}\end{align*} $$
and hence
Since
![]() $PS_\lambda S_\mu ^*P=\phi _{n,m}(T_\lambda T_\mu ^*)$
if
$PS_\lambda S_\mu ^*P=\phi _{n,m}(T_\lambda T_\mu ^*)$
if
![]() $r(\lambda )=r(\mu )=\iota $
and
$r(\lambda )=r(\mu )=\iota $
and
![]() $s(\lambda )=s(\mu )$
, it follows that
$s(\lambda )=s(\mu )$
, it follows that
![]() $\phi $
is surjective. Injectivity follows from the fact that
$\phi $
is surjective. Injectivity follows from the fact that
![]() $\phi $
is equivariant for the gauge action.
$\phi $
is equivariant for the gauge action.
Corollary 4.6. If the k-graph
![]() $\Lambda $
associated to
$\Lambda $
associated to
![]() $\rho _1,\ldots ,\rho _k$
is cofinal, satisfies the aperiodicity condition and every vertex connects to a loop with an entrance, then the Doplicher–Roberts algebra
$\rho _1,\ldots ,\rho _k$
is cofinal, satisfies the aperiodicity condition and every vertex connects to a loop with an entrance, then the Doplicher–Roberts algebra
![]() $\mathcal {O}_{\rho _1,\ldots ,\rho _k}$
is simple and purely infinite, and is Morita equivalent with
$\mathcal {O}_{\rho _1,\ldots ,\rho _k}$
is simple and purely infinite, and is Morita equivalent with
![]() $C^*(\Lambda )$
.
$C^*(\Lambda )$
.
Proof. This follows from the fact that
![]() $C^*(\Lambda )$
is simple and purely infinite and because
$C^*(\Lambda )$
is simple and purely infinite and because
![]() $PC^*(\Lambda )P$
is a full corner.
$PC^*(\Lambda )P$
is a full corner.
Remark 4.7. There is a groupoid
![]() $\mathcal {G}_\Lambda $
associated to a row-finite rank k graph
$\mathcal {G}_\Lambda $
associated to a row-finite rank k graph
![]() $\Lambda $
with no sources (see [Reference Kumjian, Pask, Raeburn and Renault18]). By taking the pointed groupoid
$\Lambda $
with no sources (see [Reference Kumjian, Pask, Raeburn and Renault18]). By taking the pointed groupoid
![]() $\mathcal {G}_\Lambda (\iota )$
, the reduction to the set of infinite paths with range
$\mathcal {G}_\Lambda (\iota )$
, the reduction to the set of infinite paths with range
![]() $\iota $
, under the same conditions as in Theorem 4.5, we get an isomorphism of the Doplicher–Roberts algebra
$\iota $
, under the same conditions as in Theorem 4.5, we get an isomorphism of the Doplicher–Roberts algebra
![]() $\mathcal {O}_{\rho _1,\ldots ,\rho _k}$
onto
$\mathcal {O}_{\rho _1,\ldots ,\rho _k}$
onto
![]() $C^*(\mathcal {G}_\Lambda (\iota ))$
.
$C^*(\mathcal {G}_\Lambda (\iota ))$
.
5 Examples
Example 5.1. Let
![]() $G=S_3$
be the symmetric group with
$G=S_3$
be the symmetric group with
![]() $\hat {G}=\{\iota , \epsilon , \sigma \}$
and character table
$\hat {G}=\{\iota , \epsilon , \sigma \}$
and character table

Here
![]() $\iota $
denotes the trivial representation,
$\iota $
denotes the trivial representation,
![]() $\epsilon $
is the sign representation and
$\epsilon $
is the sign representation and
![]() $\sigma $
is an irreducible
$\sigma $
is an irreducible
![]() $2$
-dimensional representation, for example,
$2$
-dimensional representation, for example,
 $$ \begin{align*}\sigma((12))=\left[\begin{array}{rr}-1&-1\\0&1\end{array}\right],\quad\sigma((123))=\left[\begin{array}{rr}-1&-1\\1&0\end{array}\right].\end{align*} $$
$$ \begin{align*}\sigma((12))=\left[\begin{array}{rr}-1&-1\\0&1\end{array}\right],\quad\sigma((123))=\left[\begin{array}{rr}-1&-1\\1&0\end{array}\right].\end{align*} $$
By choosing
![]() $\rho _1=\sigma $
on
$\rho _1=\sigma $
on
![]() $\mathcal {H}_1=\mathbb {C}^2$
and
$\mathcal {H}_1=\mathbb {C}^2$
and
![]() $\rho _2=\iota +\sigma $
on
$\rho _2=\iota +\sigma $
on
![]() $\mathcal {H}_2=\mathbb {C}^3$
, we get a product system
$\mathcal {H}_2=\mathbb {C}^3$
, we get a product system
![]() $\mathcal {E}\to \mathbb {N}^2$
and an action of
$\mathcal {E}\to \mathbb {N}^2$
and an action of
![]() $S_3$
on
$S_3$
on
![]() $\mathcal {O}(\mathcal {E})\cong \mathcal O_2\otimes \mathcal O_3$
with fixed point algebra
$\mathcal {O}(\mathcal {E})\cong \mathcal O_2\otimes \mathcal O_3$
with fixed point algebra
![]() $\mathcal {O}(\mathcal {E})^{S_3}\cong \mathcal {O}_{\rho _1,\rho _2}$
isomorphic to a corner of the
$\mathcal {O}(\mathcal {E})^{S_3}\cong \mathcal {O}_{\rho _1,\rho _2}$
isomorphic to a corner of the
![]() $C^*$
-algebra of a rank two graph
$C^*$
-algebra of a rank two graph
![]() $\Lambda $
. The set of vertices is
$\Lambda $
. The set of vertices is
![]() $\Lambda ^0=\{\iota ,\epsilon , \sigma \}$
and the edges are given by the incidence matrices
$\Lambda ^0=\{\iota ,\epsilon , \sigma \}$
and the edges are given by the incidence matrices
 $$ \begin{align*} M_1=\left[\begin{array}{ccc}0&0&1\\0&0&1\\1&1&1\end{array}\right], \quad M_2=\left[\begin{array}{ccc}1&0&1\\0&1&1\\1&1&2\end{array}\right].\end{align*} $$
$$ \begin{align*} M_1=\left[\begin{array}{ccc}0&0&1\\0&0&1\\1&1&1\end{array}\right], \quad M_2=\left[\begin{array}{ccc}1&0&1\\0&1&1\\1&1&2\end{array}\right].\end{align*} $$
This is because
We label the blue (solid) edges by
![]() $e_1,\ldots , e_5$
and the red (dashed) edges by
$e_1,\ldots , e_5$
and the red (dashed) edges by
![]() $f_1,\ldots ,f_8$
as in the figure below.
$f_1,\ldots ,f_8$
as in the figure below.

The isometric intertwiners are
such that
Here
![]() $I_\pi $
is the identity of
$I_\pi $
is the identity of
![]() $\mathcal {H}_\pi $
for
$\mathcal {H}_\pi $
for
![]() $\pi \in \hat {G}$
and
$\pi \in \hat {G}$
and
![]() $I_i$
is the identity of
$I_i$
is the identity of
![]() $\mathcal {H}_i$
for
$\mathcal {H}_i$
for
![]() $ i=1,2$
. Since
$ i=1,2$
. Since
 $$ \begin{align*}M_1M_2=\left[\begin{array}{ccc}1&1&2\\1&1&2\\2&2&4\end{array}\right]\end{align*} $$
$$ \begin{align*}M_1M_2=\left[\begin{array}{ccc}1&1&2\\1&1&2\\2&2&4\end{array}\right]\end{align*} $$
and
a possible choice of commuting squares is
This data is enough to determine a rank two graph
![]() $\Lambda $
associated to
$\Lambda $
associated to
![]() $\rho _1, \rho _2$
. But this is not the only choice, since, for example, we could have taken
$\rho _1, \rho _2$
. But this is not the only choice, since, for example, we could have taken
which determines a different
![]() $2$
-graph.
$2$
-graph.
A direct analysis using the definitions shows that, in each case, the
![]() $2$
-graph
$2$
-graph
![]() $\Lambda $
is cofinal, satisfies the aperiodicity condition and every vertex connects to a loop with an entrance. It follows that
$\Lambda $
is cofinal, satisfies the aperiodicity condition and every vertex connects to a loop with an entrance. It follows that
![]() $C^*(\Lambda )$
is simple and purely infinite and the Doplicher–Roberts algebra
$C^*(\Lambda )$
is simple and purely infinite and the Doplicher–Roberts algebra
![]() $\mathcal {O}_{\rho _1,\rho _2}$
is Morita equivalent with
$\mathcal {O}_{\rho _1,\rho _2}$
is Morita equivalent with
![]() $C^*(\Lambda )$
.
$C^*(\Lambda )$
.
The K-theory of
![]() $C^*(\Lambda )$
can be computed using Proposition 3.16 in [Reference Evans11] and it does not depend on the choice of factorization rules. We have
$C^*(\Lambda )$
can be computed using Proposition 3.16 in [Reference Evans11] and it does not depend on the choice of factorization rules. We have
 $$ \begin{align*}K_0(C^*(\Lambda))\cong\text{coker}[I-M_1^t\;\; I-M_2^t]\oplus\ker\left[\begin{array}{c}M_2^t-I\\I-M_1^t\end{array}\right]\cong \mathbb Z/2\mathbb Z,\end{align*} $$
$$ \begin{align*}K_0(C^*(\Lambda))\cong\text{coker}[I-M_1^t\;\; I-M_2^t]\oplus\ker\left[\begin{array}{c}M_2^t-I\\I-M_1^t\end{array}\right]\cong \mathbb Z/2\mathbb Z,\end{align*} $$
 $$ \begin{align*}K_1(C^*(\Lambda))\cong\ker[I-M_1^t\;\;I-M_2^t]/\text{im}\left[\begin{array}{c}M_2^t-I\\I-M_1^t\end{array}\right]\cong 0.\end{align*} $$
$$ \begin{align*}K_1(C^*(\Lambda))\cong\ker[I-M_1^t\;\;I-M_2^t]/\text{im}\left[\begin{array}{c}M_2^t-I\\I-M_1^t\end{array}\right]\cong 0.\end{align*} $$
In particular,
![]() $\mathcal {O}_{\rho _1,\rho _2}\cong \mathcal {O}_3$
.
$\mathcal {O}_{\rho _1,\rho _2}\cong \mathcal {O}_3$
.
On the other hand, since
![]() $\rho _1, \rho _2$
are faithful, both Doplicher–Roberts algebras
$\rho _1, \rho _2$
are faithful, both Doplicher–Roberts algebras
![]() $\mathcal {O}_{\rho _1}, \mathcal {O}_{\rho _2}$
are simple and purely infinite with
$\mathcal {O}_{\rho _1}, \mathcal {O}_{\rho _2}$
are simple and purely infinite with
so
![]() $\mathcal {O}_{\rho _1,\rho _2}\ncong \mathcal {O}_{\rho _1}\otimes \mathcal {O}_{\rho _2}$
.
$\mathcal {O}_{\rho _1,\rho _2}\ncong \mathcal {O}_{\rho _1}\otimes \mathcal {O}_{\rho _2}$
.
Example 5.2. With
![]() $G=S_3$
and
$G=S_3$
and
![]() $\rho _1=2\iota , \rho _2=\iota +\epsilon $
, then
$\rho _1=2\iota , \rho _2=\iota +\epsilon $
, then
![]() $R=\{\iota , \epsilon \}$
, so
$R=\{\iota , \epsilon \}$
, so
![]() $\Lambda $
has two vertices and incidence matrices
$\Lambda $
has two vertices and incidence matrices
 $$ \begin{align*}M_1=\left[\begin{array}{cc}2&0\\0&2\end{array}\right],\quad M_2=\left[\begin{array}{cc}1&1\\1&1\end{array}\right],\end{align*} $$
$$ \begin{align*}M_1=\left[\begin{array}{cc}2&0\\0&2\end{array}\right],\quad M_2=\left[\begin{array}{cc}1&1\\1&1\end{array}\right],\end{align*} $$
which give

Again, a corresponding choice of isometric intertwiners determines some factorization rules, for example,
Even though
![]() $\rho _1, \rho _2$
are not faithful, the obtained
$\rho _1, \rho _2$
are not faithful, the obtained
![]() $2$
-graph is cofinal, satisfies the aperiodicity condition and every vertex connects to a loop with an entrance, so
$2$
-graph is cofinal, satisfies the aperiodicity condition and every vertex connects to a loop with an entrance, so
![]() $\mathcal {O}_{\rho _1,\rho _2}$
is simple and purely infinite with trivial K-theory. In particular,
$\mathcal {O}_{\rho _1,\rho _2}$
is simple and purely infinite with trivial K-theory. In particular,
![]() $\mathcal {O}_{\rho _1,\rho _2}\cong \mathcal {O}_2$
.
$\mathcal {O}_{\rho _1,\rho _2}\cong \mathcal {O}_2$
.
Note that, since
![]() $\rho _1, \rho _2$
have kernel
$\rho _1, \rho _2$
have kernel
![]() $N=\langle (123)\rangle \cong \mathbb {Z}/3\mathbb {Z}$
, we could replace G by
$N=\langle (123)\rangle \cong \mathbb {Z}/3\mathbb {Z}$
, we could replace G by
![]() $G/N\cong \mathbb {Z}/2\mathbb {Z}$
and consider
$G/N\cong \mathbb {Z}/2\mathbb {Z}$
and consider
![]() $\rho _1,\rho _2$
as representations of
$\rho _1,\rho _2$
as representations of
![]() $\mathbb {Z}/2\mathbb {Z}$
.
$\mathbb {Z}/2\mathbb {Z}$
.
Example 5.3. Consider
![]() $G=\mathbb {Z}/2\mathbb {Z}=\{0,1\}$
with
$G=\mathbb {Z}/2\mathbb {Z}=\{0,1\}$
with
![]() $\hat {G}=\{\iota ,\chi \}$
and character table
$\hat {G}=\{\iota ,\chi \}$
and character table

Choose the
![]() $2$
-dimensional representations
$2$
-dimensional representations
which determine a product system
![]() $\mathcal {E}$
such that
$\mathcal {E}$
such that
![]() $\mathcal {O}(\mathcal {E})\cong \mathcal {O}_2\otimes \mathcal {O}_2\otimes \mathcal {O}_2$
and a Doplicher–Roberts algebra
$\mathcal {O}(\mathcal {E})\cong \mathcal {O}_2\otimes \mathcal {O}_2\otimes \mathcal {O}_2$
and a Doplicher–Roberts algebra
![]() $\mathcal {O}_{\rho _1,\rho _2,\rho _3}\cong \mathcal {O}(\mathcal {E})^{\mathbb {Z}/2\mathbb {Z}}$
.
$\mathcal {O}_{\rho _1,\rho _2,\rho _3}\cong \mathcal {O}(\mathcal {E})^{\mathbb {Z}/2\mathbb {Z}}$
.
An easy computation shows that the incidence matrices of the blue (solid), red (dashed) and green (dotted) graphs are
 $$ \begin{align*}M_1=\left[\begin{array}{cc}1&1\\1&1\end{array}\right],\quad M_2=\left[\begin{array}{cc}2&0\\0&2\end{array}\right],\quad M_3=\left[\begin{array}{cc}0&2\\2&0\end{array}\right].\end{align*} $$
$$ \begin{align*}M_1=\left[\begin{array}{cc}1&1\\1&1\end{array}\right],\quad M_2=\left[\begin{array}{cc}2&0\\0&2\end{array}\right],\quad M_3=\left[\begin{array}{cc}0&2\\2&0\end{array}\right].\end{align*} $$

With labels as in the figure, we choose the following factorization rules.
A tedious verification shows that all the following paths are well defined.
so the associativity property is satisfied and we get a rank three graph
![]() $\Lambda $
with two vertices. It is not difficult to check that
$\Lambda $
with two vertices. It is not difficult to check that
![]() $\Lambda $
is cofinal, satisfies the aperiodicity condition and every vertex connects to a loop with an entrance, so
$\Lambda $
is cofinal, satisfies the aperiodicity condition and every vertex connects to a loop with an entrance, so
![]() $C^*(\Lambda )$
is simple and purely infinite.
$C^*(\Lambda )$
is simple and purely infinite.
Since
![]() $\partial _1=[I-M_1^t\; I-M_2^t\; I-M_3^t]:\mathbb {Z}^6\to \mathbb {Z}^2$
is surjective, using Corollary 3.18 in [Reference Evans11], we obtain
$\partial _1=[I-M_1^t\; I-M_2^t\; I-M_3^t]:\mathbb {Z}^6\to \mathbb {Z}^2$
is surjective, using Corollary 3.18 in [Reference Evans11], we obtain
where
 $$ \begin{align*}\partial_2=\left[\begin{array}{ccc} M_2^t-I&M_3^t-I&0\\I-M_1^t&0&M_3^t-I\\0&I-M_1^t&I-M_2^t\end{array}\right],\quad\partial_3=\left[\begin{array}{c}I-M_3^t\\M_2^t-I\\I-M_1^t\end{array}\right],\end{align*} $$
$$ \begin{align*}\partial_2=\left[\begin{array}{ccc} M_2^t-I&M_3^t-I&0\\I-M_1^t&0&M_3^t-I\\0&I-M_1^t&I-M_2^t\end{array}\right],\quad\partial_3=\left[\begin{array}{c}I-M_3^t\\M_2^t-I\\I-M_1^t\end{array}\right],\end{align*} $$
and, in particular,
![]() $\mathcal {O}_{\rho _1,\rho _2,\rho _3}\cong \mathcal {O}_2$
.
$\mathcal {O}_{\rho _1,\rho _2,\rho _3}\cong \mathcal {O}_2$
.
Example 5.4. Let
![]() $G=\mathbb {T}$
. We have
$G=\mathbb {T}$
. We have
![]() $\hat {G}=\{\chi _k:k\in \mathbb {Z}\}$
, where
$\hat {G}=\{\chi _k:k\in \mathbb {Z}\}$
, where
![]() $\chi _k(z)=z^k$
and
$\chi _k(z)=z^k$
and
![]() $\chi _k\otimes \chi _\ell =\chi _{k+\ell }$
. The faithful representations
$\chi _k\otimes \chi _\ell =\chi _{k+\ell }$
. The faithful representations
of
![]() $\mathbb {T}$
determine a product system
$\mathbb {T}$
determine a product system
![]() $\mathcal {E}$
with
$\mathcal {E}$
with
![]() $\mathcal {O}(\mathcal {E})\cong \mathcal {O}_2\otimes \mathcal {O}_2$
and a Doplicher–Roberts algebra
$\mathcal {O}(\mathcal {E})\cong \mathcal {O}_2\otimes \mathcal {O}_2$
and a Doplicher–Roberts algebra
![]() $\mathcal {O}_{\rho _1,\rho _2}\cong \mathcal {O}(\mathcal {E})^{\mathbb {T}}$
isomorphic to a corner in the
$\mathcal {O}_{\rho _1,\rho _2}\cong \mathcal {O}(\mathcal {E})^{\mathbb {T}}$
isomorphic to a corner in the
![]() $C^*$
-algebra of a rank
$C^*$
-algebra of a rank
![]() $2$
graph
$2$
graph
![]() $\Lambda $
with
$\Lambda $
with
![]() $\Lambda ^0=\hat {G}$
and infinite incidence matrices, where
$\Lambda ^0=\hat {G}$
and infinite incidence matrices, where
 $$ \begin{align*}M_1(\chi_k,\chi_\ell)=\begin{cases}1 \quad&\text{if } \ell=k \;\text{or}\; \ell=k-1,\\0\quad& \text{otherwise,}\end{cases}\end{align*} $$
$$ \begin{align*}M_1(\chi_k,\chi_\ell)=\begin{cases}1 \quad&\text{if } \ell=k \;\text{or}\; \ell=k-1,\\0\quad& \text{otherwise,}\end{cases}\end{align*} $$
 $$ \begin{align*}M_2(\chi_k,\chi_\ell)=\begin{cases} 1 \quad&\text{if } \ell=k \;\text{or}\; \ell=k+1,\\0\quad& \text{otherwise.}\end{cases}\end{align*} $$
$$ \begin{align*}M_2(\chi_k,\chi_\ell)=\begin{cases} 1 \quad&\text{if } \ell=k \;\text{or}\; \ell=k+1,\\0\quad& \text{otherwise.}\end{cases}\end{align*} $$
The skeleton of
![]() $\Lambda $
looks like
$\Lambda $
looks like

and this
![]() $2$
-graph is cofinal, satisfies the aperiodicity condition and every vertex connects to a loop with an entrance, so
$2$
-graph is cofinal, satisfies the aperiodicity condition and every vertex connects to a loop with an entrance, so
![]() $C^*(\Lambda )$
is simple and purely infinite.
$C^*(\Lambda )$
is simple and purely infinite.
Example 5.5. Let
![]() $G=SU(2)$
. It is known (see page 84 in [Reference Bröcker and tom Dieck2]) that the elements in
$G=SU(2)$
. It is known (see page 84 in [Reference Bröcker and tom Dieck2]) that the elements in
![]() $\hat {G}$
are labeled by
$\hat {G}$
are labeled by
![]() $V_n$
for
$V_n$
for
![]() $n\ge 0$
, where
$n\ge 0$
, where
![]() $V_0=\iota $
is the trivial representation on
$V_0=\iota $
is the trivial representation on
![]() $\mathbb {C}$
,
$\mathbb {C}$
,
![]() $V_1$
is the standard representation of
$V_1$
is the standard representation of
![]() $SU(2)$
on
$SU(2)$
on
![]() $\mathbb {C}^2$
, and, for
$\mathbb {C}^2$
, and, for
![]() $n\ge 2$
,
$n\ge 2$
,
![]() $V_n=S^nV_1$
, the
$V_n=S^nV_1$
, the
![]() $n\, $
th symmetric power. In fact,
$n\, $
th symmetric power. In fact,
![]() $\dim V_n=n+1$
and
$\dim V_n=n+1$
and
![]() $V_n$
can be taken as the representation of
$V_n$
can be taken as the representation of
![]() $SU(2)$
on the space of homogeneous polynomials p of degree n in variables
$SU(2)$
on the space of homogeneous polynomials p of degree n in variables
![]() $z_1,z_2$
, where, for
$z_1,z_2$
, where, for
![]() $ g=\big [\begin {smallmatrix}a&b\\c&d\end {smallmatrix}\big ]\in SU(2)$
,
$ g=\big [\begin {smallmatrix}a&b\\c&d\end {smallmatrix}\big ]\in SU(2)$
,
The irreducible representations
![]() $V_n$
satisfy the Clebsch–Gordan formula
$V_n$
satisfy the Clebsch–Gordan formula
 $$ \begin{align*}V_k\otimes V_\ell=\bigoplus_{j=0}^qV_{k+\ell-2j},\; q=\min\{k,\ell\}.\end{align*} $$
$$ \begin{align*}V_k\otimes V_\ell=\bigoplus_{j=0}^qV_{k+\ell-2j},\; q=\min\{k,\ell\}.\end{align*} $$
If we choose
![]() $\rho _1=V_1, \rho _2=V_2$
, then we get a product system
$\rho _1=V_1, \rho _2=V_2$
, then we get a product system
![]() $\mathcal {E}$
with
$\mathcal {E}$
with
![]() $\mathcal {O}(\mathcal {E})\cong \mathcal {O}_2\otimes \mathcal {O}_3$
and a Doplicher–Roberts algebra
$\mathcal {O}(\mathcal {E})\cong \mathcal {O}_2\otimes \mathcal {O}_3$
and a Doplicher–Roberts algebra
![]() $\mathcal {O}_{\rho _1,\rho _2}\cong \mathcal {O}(\mathcal {E})^{SU(2)}$
isomorphic to a corner in the
$\mathcal {O}_{\rho _1,\rho _2}\cong \mathcal {O}(\mathcal {E})^{SU(2)}$
isomorphic to a corner in the
![]() $C^*$
-algebra of a rank two graph with
$C^*$
-algebra of a rank two graph with
![]() $\Lambda ^0=\hat {G}$
and edges given by the matrices
$\Lambda ^0=\hat {G}$
and edges given by the matrices
 $$ \begin{align*}M_1(V_k,V_\ell)=\begin{cases}1\quad&\text{if } k=0\;\text{and}\; \ell=1,\\ 1\quad& \text{if } k\ge 1\;\text{and}\; \ell \in\{k-1,k+1\},\\0\quad&\text{otherwise,}\end{cases}\end{align*} $$
$$ \begin{align*}M_1(V_k,V_\ell)=\begin{cases}1\quad&\text{if } k=0\;\text{and}\; \ell=1,\\ 1\quad& \text{if } k\ge 1\;\text{and}\; \ell \in\{k-1,k+1\},\\0\quad&\text{otherwise,}\end{cases}\end{align*} $$
 $$ \begin{align*}M_2(V_k, V_\ell)=\begin{cases} 1 \quad&\text{if } k=0\;\text{and}\; \ell=2,\\1\quad&\text{if } k=1\;\text{and}\; \ell\in \{1,3\},\\ 1\quad&\text{if } k\ge 2\;\text{and}\; \ell\in\{k-2,k,k+2\},\\0\quad&\text{otherwise.}\end{cases}\end{align*} $$
$$ \begin{align*}M_2(V_k, V_\ell)=\begin{cases} 1 \quad&\text{if } k=0\;\text{and}\; \ell=2,\\1\quad&\text{if } k=1\;\text{and}\; \ell\in \{1,3\},\\ 1\quad&\text{if } k\ge 2\;\text{and}\; \ell\in\{k-2,k,k+2\},\\0\quad&\text{otherwise.}\end{cases}\end{align*} $$
The skeleton looks like

and this
![]() $2$
-graph is cofinal, satisfies the aperiodicity condition and every vertex connects to a loop with an entrance; in particular,
$2$
-graph is cofinal, satisfies the aperiodicity condition and every vertex connects to a loop with an entrance; in particular,
![]() $\mathcal {O}_{\rho _1,\rho _2}$
is simple and purely infinite.
$\mathcal {O}_{\rho _1,\rho _2}$
is simple and purely infinite.