1 Introduction
What do people do when they do not know the answer to a problem and yet are willing to make a judgment? It is well known that people often use heuristics and make bounded rationality or satisficing decisions rather than more elaborately calculated decisions because of restrictions of cognitive processing capacity or ignorance (Reference Kahneman, Slovic and TverskyKahneman, Slovic & Tversky, 1982; Reference SimonSimon, 1959, 2000). Heuristics or simplifying cognitive rules make it possible for people to judge relationships which they understand very poorly or not at all, but the heuristics also lead to systematic biases (Reference Cohen, Dearnaley and HanselCohen, Dearnaley & Hansel, 1956; Reference Gilovich, Griffin and KahnemanGilovich, Griffin & Kahneman, 2002; Reference Kahneman, Slovic and TverskyKahneman & Tversky, 1982; Reference Johnson-LairdJohnson-Laird, 1999; Montibeller & von Winterfeldt, 2015; Reference Wagenaar and TimmersWagenaar & Timmers, 1979; Wikipedia, 2018). Detailed descriptions of the cognitive processes that generate a bias are scarce.Footnote 1 Therefore, we wanted to contribute some knowledge about the cognitive heuristic processes that generate a variety of biased driving judgments, e.g., time saving and braking capacity, that anyone driving a car is prone to make in or out of the car. The method of spectral analysis, used in the present study to identify different cognitive processes, is generic and can be applied to any kind of heuristics and biases.
Reference Stanovich and WestStanovich and West (1998) studied a set of cognitive biases and individual differences in cognitive abilities and found low to high covariances between the biases investigated (e.g., syllogism and overconfidence, r = −0.09; hindsight and overconfidence, r = 0.79). In a later study, Toplak, West and Stanowich (2016) investigated a number of heuristics (ratio bias, belief bias in syllogistic reasoning, reflection versus intuition, probabilistic and statistical reasoning, rational temporal discounting) and related them to real-world self-reported correlates including driving behavior.Footnote 2 The driving items were related to driving and safety but the internal consistency of this set of items was rather low (Cronbach’s α = 0.49), and there were no significant correlations between the composite driving variable and other heuristics.
Here, we take a more limited view of driving than that of Toplak et al. (2016), with the purpose of revealing a cognitive structure of the biases and, more importantly, different processes generating them. Different normative functions predict the correct judgments for the 5 different driving problems studied here, and we know from earlier studies that these problems are associated with biased judgments (Reference Svenson and ErikssonSvenson & Eriksson, 2017). The problems will be less disparate than the driving judgment problems used by Toplak et al. (2016) and we expect that this will increase the chance of finding interesting cognitive structures and consistencies of processes within and across problems. Spectral analysis of judgments will be used in the search for heuristic decision rules.
Most of the judgment biases, e.g., the time saving bias (Reference SvensonSvenson, 2008a), are not limited to driving but can also be found in other contexts, such as, consumer behavior (Reference De Langhe and PuntoniDe Langhe & Puntoni, 2016) and industrial production (Reference Svenson, Eriksson, Salo and PetersSvenson, 2011). Reference Svenson and ErikssonSvenson and Eriksson (2017) presented an overview of cognitive judgment biases in a driving context, and some of these will be explored in the present contribution and described next. The problems that we study concern driving when a person is not driving even though most of the biases seem to appear also when a person is driving a car, e.g., time saving when driving faster (Reference Eriksson, Svenson and ErikssonEriksson, Svenson & Eriksson, 2013) and stopping distance (Reference Colbourn, Brown and CopemanColbourn, Brown & Cooperman, 1978).
The first bias concerns mean speed judgments as a function of speeds on different parts of a trip (Reference Falk, Lann and ZamirFalk, Lann & Zamir, 2004; Reference Svenson and SaloSvenson & Salo, 2010). Most people misjudge mean speed because they do not weigh the speeds by time on each road segment (that is, compute the harmonic mean).
Reference Svenson and SaloSvenson and Salo (2010) used the following problem in their study of mean speed “On a 60 km long road you normally drive at a mean speed of 110 km/h. A temporary speed limit on 10 km of the distance slows down the mean speed there to 30 km/h. This means that the mean speed over the complete distance is changed to ___”. The average judgment was 82 km/h , an overestimation of the correct mean speed, 76 km/h.
In the following formal presentation, we will treat the mean speed over two road segments of a route with constant but different speeds on the road segments. The correct formula for mean speed over a distance with only two different speeds is described by equation (1).
where Vmean is the mean speed, T 1 and T 2 are the times that a vehicle travels with at each of the speeds V 1 and V 2. This is called the time weight model (Reference Falk, Lann and ZamirFalk, Lann & Zamir, 2004).
In most communications concerning speed and speed regulation, the information concerns different speeds on different road segments of a trip. Therefore, it is possible to assume that some people use the distances driven at the different speeds as weights when they judge mean speed. This was verified in earlier research (Reference Svenson and SaloSvenson & Salo, 2010; Reference Svenson, Eriksson, Salo and PetersSvenson et al., 2011) and parallels results reported by Reference Gamliel and PeerGamliel and Peer (2017) about fuel efficiency. Equation (2) shows how two distances D 1 and D 2 can be used to compute a weighted mean speed.
Finally, it is possible to use the simple mean of speeds as an estimate of mean speed.
Rules (1) and (2) are both weighted arithmetic means. In (1) it is necessary to estimate time, but in (2) the weight factor is given or apparent. Hence, rules (1), (2) and (3) form an hierarchy of cognitive complexity because (1) includes estimation of travel times not needed in the other rules and (2) includes a travel time weighed arithmetic meanwhile (3) uses the arithmetic mean only.
The second bias is associated with judgments about how fast it is possible to brake and decrease the speed of a car (Reference Svenson, Eriksson and GonzalezSvenson, Eriksson & Gonzalez, 2012; Reference Svenson, Eriksson and MertzSvenson, Eriksson & Mertz, 2013). In general, drivers judge that they can brake and decelerate much faster than possible at a higher speed compared to a lower speed. The following illustrates a braking problem instruction. We informed the participants about a dry and normal road surface and told them: “Imagine a car driving at 15 mph behind and past a bus standing at a bus stop. When the car passes the rear end of the bus a child runs out in the street, from behind the front of the bus. The driver brakes immediately and the car stops just in front of the child. Now imagine the same scenario, only this time the car is driving at 25 mph. At what speed would the car hit the child in this case?” The average judged speed was 13.6 mph in a study by Svenson, Eriksson and Gonzalez (2010). The correct speed is 23.4 mph.
In this case, a problem for unaided judgment is that a judge must be aware of the effect of driver and car braking reaction times on speed deceleration. Another problem for most people is to judge the non-linear reduction of speed over distance. Non-linear relationships are difficult to assess and both problems may contribute to the judgment bias.
In physical terms, equation (4) describes the remaining speed in a braking episode at a given moment in time t, after the driver has encountered a stop signal at time zero. V stands for velocity at a given time after the driver got a stop signal and t 0 for the driver’s and car’s braking reaction time. When we calculate correct speeds, we will use 1 sec reaction time. Equation (4) describes the speed after t 0 and at the distance D from the point where the driver first got a signal to stop. The constant g is a gravitational constant (9.81 m/sec2) and µ the friction between tires and the road surface (dry normal road surface = 0.8).
The third bias appears when people are asked to judge the time they save by increasing speed Reference SvensonSvenson (1970, 2008a). The time saving bias means that speed increases from a high speed (e.g., from 90 to 110 km/h) are judged to save more time than correct, and increases from a low speed (e.g., 20 to 30 km/h) are judged to save less time than correct over a given distance. The bias has been replicated a number of times also in other than driving contexts (Reference De Langhe and PuntoniDe Langhe & Puntoni, 2016; Reference Svenson, Eriksson, Salo and PetersSvenson, 2011; Reference TscharaktschiewTscharaktschiew, 2016; Tsiros & Chen, 2016). In the driving context, direct speed judgments Reference SvensonSvenson (1970), choice (Reference SvensonSvenson, 2008a) and matching speed judgments (Reference SvensonSvenson, 2008b) were used as dependent variables.
To illustrate, the time saved by increasing speed from 30 to 40 km/h is judged to save the same time as an increase from 60 to 73 km/h. However, the correct higher speed increase, matching the time saving from 30 to 40 km/h, is an increase from 60 to 110 km/h (Reference SvensonSvenson, 2008b).
The correct rule for calculating time savings is described by equation (5) in which, c is a constant D is distance, V 1 initial and V 2 increased mean speed.
Equation (6) describes another version of the same rule.
There is an uncertainty about which subjective judgment rules participants use when they make the time saving bias. To illustrate, Reference SvensonSvenson (1970, 2008) found evidence for proportional nonlinear rules, while Reference Peer and GamlielPeer and Gamliel (2012) reported the use of linear rules. A proportional rule is described by equation (7) in which β is a fitted constant. The rule describes the increase in speed as a proportion of the higher speed.
Reference SvensonSvenson (1970) and Reference Peer and GamlielPeer and Gamliel (2012) reported that the increase in proportion of the lower speed V 1 instead of V 2 was also a significant predictor of time saving judgments.
In a matching task the proportional rule and the rule in Equation (7) boil down to a ratio rule. Because equation (7) can be reformulated as follows, assuming constant distance and that a person judges a speed increase, J that gives the same time saving as a reference increase: ![]() .
.
A linear rule refers to the difference between the speeds expressed in equation (7) by a denominator that is constant = 1.0. The proportion rule uses computations of two ratios and is more complex than the linear rule. Hence, the two main rules that could explain judgments of time savings seem to be the difference and the proportion rules.
The fourth bias is associated with judgments of the increase in accident risk as a function of speed increase. A combination of physical and empirical facts determine the correct relationship. The physical fact is that the energy of a moving mass increases with the speed squared. Empirically, it has been found that speed is an important contributing factor to accidents (Reference Aarts and van SchagenAarts & Van Schagen, 2006; Reference Cameron and ElvikCameron & Elvik, 2010; Reference ElvikElvik, 2013; Reference NilssonNilsson, 2004). The conclusion from empirical facts — accident rates and fatal accident rates — is that accident risk increases approximately as a power function of the ratio between speeds (Reference ElvikElvik, 2013; Reference NilssonNilsson, 2004). The relationship between speed and risk of an accident is described in equation (8) with the exponent n = 2 (corresponding to the law that the energy of an object increases with the speed squared). For fatal accidents the increase in accident rate, R is described by an exponent n = 4 (Reference ElvikElvik, 2013).
The traffic environment can affect the exact size of the exponents, but in most environments they are close to these numbers (Reference Cameron and ElvikCameron & Elvik, 2010; Reference ElvikElvik, 2013; Reference NilssonNilsson, 2004). Reference SvensonSvenson (2008b) showed that the average driver underestimates the resulting increase of accident and fatal accident rates as a function of speed increase. To illustrate, an increase from 25 to 40 km/h was judged to increase the risk by 61%. The empirical risk increases by about 150% (Reference SvensonSvenson, 2008b).
The fifth bias concerns stopping distance increase as a function of speed increase. Stopping distance is the distance traveled from when a stop cue or signal first appears until the car has come to a complete standstill. Stopping distance, SD, is the most commonly used variable to describe the braking capacity of a car and it is often communicated to drivers and the public (University of Minnesota Traffic Safety Curriculum, 2012). The stopping distance increase from V 1 to V 2 increases with the ratio of the speeds squared, Equation (9).
Previous research lead us to assume that the increase in stopping distance following an increase in speed will be systematically underestimated.Footnote 3
We wanted to relate some individual cognitive differences to biases and the use of heuristics, because researchers have reported some relationships between cognitive abilities and decision making competence, for example, Reference Stanovich and WestStanowich and West (1998) and Reference Del Missier, Mäntylä and Bruin de BruineDel Missier, Mäntylä and Bruin de Bruine (2010, 2012). Therefore, in an exploratory way, we administered two items from the Berlin Numeracy Test (BNT; Reference Cokely, Galesic, Schulz, Ghazal and Garcia-RetameroCokeley et al., 2012) and a short version of the Cognitive Reflection test, CRT, originally developed by Reference FrederickFrederick (2005) and shortened by Primi and colleagues (Reference Primi, Morsanyi, Chiesi, Donati and HamiltonPrimi et al., 2016); the items can be found in the Appendix. People may differ in their judgmental biases not only for cognitive reasons but also because they are more or less impulsive and/or reflective. To test this assertion, we included the complete Barratt Impulsiveness Scale, BIS (Reference Stanford, Mathias, Dougherty, Lake, Anderson and PattonStanford et al., 2009). Finally, we added a few questions about self-rated driving skill and behavior (Reference SpolanderSpolander, 1983). On this scale most people rate themselves as more skilled and safe drivers than the average driver.
In summary, the aims of the present study are to find structural consistency across biases, to find consistencies in participants’ cognitive processes within a problem set and across problem sets, and to introduce spectral analysis into a judgment context.
2 Experiment
2.1 Method
2.1.1 Participants
A questionnaire was sent out to 132 Amazon Mechanical Turk respondents in the United States, aged between 20 and 66 years with a mean of 35.1 years. All but 2 participants had a driver’s license. There were 69 males and 53 females. A participant was paid $1.5 for participation. There were 9 participants who finished the study in 4 or minutes or less and all of their responses were excluded from further analysis, leaving 123 participants.
2.1.2 Procedure and material
The task was performed on individual computers, and Qualtrics was used to present the problems and register the responses. There were 4 problems in each of 5 groups of driving related problems and 4 problems about self-rated driving skills and risk. Based on earlier research, the problems were chosen so that most of the participants would make biased judgments. Each group of problems will be described below. The questionnaires also included the individual differences scales: the self-rating of driving behavior scale, BIS and 3 items of the short version of CRT and 2 of BNT (Appendix).
Mean speed.
Reference Svenson and SaloSvenson and Salo (2010) found that parts of a route driven at higher speeds were given too much weight in comparison with parts driven at a slower speed and we used their problems translated to English and mph when we selected problems for the present study. The instruction included the following: “When you drive slower over part of a distance the mean speed over the complete distance is reduced. Imagine that you drive on a 60 miles long road. There is a temporary speed limit of 10 miles on that road. The four questions below ask you to estimate the mean speed on the road after a temporary speed reduction on 10 miles of that road, please fill in the new mean speed.”
The speed combinations for the 4 problems were (1) normal speed; 55 mph, speed limit speed 20 mph, mean speed = ____, (2) 70 and 30 mph, (3) 55 and 10 mph and (4) 60 and 20 mph.
Braking speed.
We used problems studied by Svenson and colleagues (Reference Svenson, Eriksson and GonzalezSvenson, Eriksson & Gozalez, 2012; Reference Svenson, Eriksson and MertzSvenson, Eriksson & Mertz, 2013). We used the condition with a child to make the problem real and to engage the participants in the problem. One may argue that a corresponding affective component like the child was not present in the other problems, which could make it harder to find consistencies across problems. Hence, the consistencies reported later could have been stronger if there had been no affective component in this particular problem.
The instruction to the participant was the following: “When you drive faster, the stopping distance increases. Imagine that you are driving past a school at, for example, 15 mph and that you start to brake maximally when a child runs into the street in front of you. You are able to stop the car just before the child. You are an alert driver with a short reaction time. The condition on the road surface is good, dry with high friction. — Now assume that you had driven past the school at 25 mph and from the same position as before you see the child running out into the street at the same place in front of you as earlier. You react in the same way as before and hit the brakes at the moment you see the child. However, this time you will not be able to stop the car in time from the faster speed 25 mph and you will hit the child with your car. At what speed do you think that you will hit the child?”
The 4 problems of braking from different speeds were: (1) braking from 25 mph compared to successful braking at 15 mph, (2) from 30 mph compared to 20 mph, (3) from 45 mph compared to 30 mph, (4) from 70 mph compared to 45 mph.
Time saving.
The time saved by increasing speed is overestimated when the speed is high and underestimated when the speed is low. We presented two time saving problems that typically give underestimation and two that give overestimation of time savings (Reference SvensonSvenson, 2008b). This means that in a matching task with a low-reference-speed increase, the judged matching high speed increase will be too low. When the reference increase is in the high speed range, the judged matching increase of from a low speed be too high.
The participants were given the following instruction. “An important factor when new roads are planned and old roads are reconstructed, is the potential of saving travel time. Below you find two alternative improvements of roads, the road improvements are planned for roads with slower and faster average driving speeds. The roads are equally long and carry the same load of traffic. We will ask you to fill in a speed increase for the improvement of alternative road B that would give the same time saving as A.” The pairs of speed increases given to the participants were: (1) The time saved from a speed increase on road A from 20 to 25 mph matches the time saved after a B road increase from 35 mph to ___mph, (2) A: 25 to 30 mph and B: 50 to __mph, (3) A: 35 to 80 mph and B: 20 to ___mph (4) A: 35 to 70 mph and B: 20 to __mph.
Risk and speed.
We asked participants to judge the risk of a fatal accident as a function of speed increases and the instruction was the following. “When speed increases, the risk of an accident increases. Assume a road with a certain speed limit and that drivers on that road drive on average at this speed limit. Then, this would lead to 100 traffic fatalities per year. If they drove on average faster, there would be more fatalities and we will ask you to estimate the total average of fatalities at the higher speed.” The speed combinations were: (1) 100 fatalities at an average speed 30 mph if speed is 40 mph there will be ___ fatalities, (2) 100 at speed 30 mph higher speed 60 mph _____, (3) 100 at speed 50 mph higher speed 60 mph ____ and (4) 100 at speed 50 mph higher speed 70 mph ___.
Stopping distance.
This set of problems asked about stopping distances at different speeds. “When you drive faster the stopping distance increases. A very alert driver on a dry road, and with a good car may stop a car from 20 mph in 40 feet and we assume this road in the following items.” The problems were: (1) estimate the stopping distances when the same driver brakes in the same way at a speed of 30 mph, (2) 40 mph, (3) 50 mph and (4) 60 mph.
Driver skills.
The items were taken from Reference SpolanderSpolander (1983) with the instruction (translated from Swedish to English). “Please, compare yourself with the American driver in general. Try to decide if you are better, worse or just as good as those in the following abilities.” The abilities were (1) to be a skillful driver, (2) to be a safe driver, (3) to predict what will happen in traffic and (4) to drive smoothly. They were judged on response scales with the following steps, from left to right: (1) Much better, (2) Somewhat better, (3) Just as good, (4) Somewhat worse and (5) Much worse. A value smaller than 3 indicates a “better than average” effect.
Of the individual difference scales, the Barrat Impulsiveness Scale, BIS (Reference Stanford, Mathias, Dougherty, Lake, Anderson and PattonStanford et al., 2009) was given first followed by the driver skills scale. Then followed the bias judgment tasks in the order given in table 1. The remaining individual differences scales, the Cognitive Reflection Test, CRT (Reference Colbourn, Brown and CopemanFrederick, 2005) and the partial Berlin Numeracy Test (Reference Cokely, Galesic, Schulz, Ghazal and Garcia-RetameroCokely et al, 2012), BNT scale were presented last after all other items. The items of the two last scales can be found in the Appendix.
Table 1: Average judgments and differences between average judgments and correct values. Some participants’ judgments were not analyzed because of incomplete or unreasonable answers specified in the text.

Note:
** p<0.01
*** p< 0.001
indicate significant differences average judgment and correct value. For the driving skill scale a value significantly below 3.0 (better than average driver).
2.2 Results
In the following, we first present average judgments for the different problems and report average bias for each problem. Second, the biased judgments will be correlated pairwise in a search for a structure of biases across problems. Third, we will correlate the individual difference scales with the biases. Fourth, we will search for regularities in individual use of judgment rules.Footnote 4
2.2.1 Structural analyses of biases
Average judgments and biases.
Table 1 shows the average judgments and the correct values and differences from the correct values. The mean speed problems gave biased average judgments for only 2 problems (too high judgments when the slow speed was 10 mph — problem 3 — and a too small mean speed judgment when the slow speed was 30 mph — problem 2). All 4 braking problems produced too low speed judgments at collision. Time savings were biased in different directions as predicted: overestimated for high speeds (first 2 problems) and underestimated for low speeds (last 2 problems). Risk of fatal accident risk increased as a function of the ratio of the speeds but was generally underestimated. Stopping distance was underestimated and self-reported driving skills overestimated on average as predicted.
For each participant we computed one index value, a mean (judgment−correct) as a measure of that participant’s average bias. The mean speed judgments were biased in the predicted different direction for problems (2) and (3) and we used the absolute differences from the correct values when we computed the average bias across the 4 problems in each problem set for each person. The time saving bias predicts different biases for low and high speed increases. Therefore, we changed the signs of the differences for problems (3) and (4) to positive values so that a predicted bias always had a positive value. The mean judgments for the braking speed, accident risk and stopping distance problems all showed that risks of increasing speed were underestimated. Accident risk and stopping distance increase with a power function and the results showed that the exponent of the functions were underestimated. Greater negative values indicated greater bias for these three problems and we transformed the averages to positive values in the following correlation table. Hence, a greater value always indicates a greater bias. The internal consistency of the bias judgments within each set of problems was described by α for mean speed = 0.79, braking = 0.92, time saving = 0.53, fatal accidents = 0.84, stopping distance = 0.92 and driving skills = 0.87.
We computed pairwise product-moment correlations between the different biases. The analysis showed that no biases, except risk and stopping distance (r = 0.54, p<.01), were significantly correlated. Hence, this attempt at finding regularity across biases was not successful. Next, we examined the correlations between biases and the individual difference scales.Footnote 5 We added log of the time it took a participant to complete the study because it is possible to assume that time correlates negatively with bias, but there were no significant correlations between any bias and log time. Table 2 shows the relationships between the biases and the individual difference scales.
Table 2: Product-moment correlations between the size of a bias and individual difference scales.

Note: a correlation of 0.18 is significant at p<.05 (2 tailed), a correlation of 0.23 is significant at p<.01.
Table 2 shows a few significant relationships between biases and individual difference scales. The mean speed biases were significantly related to CRT and Numeracy and the correlations show that greater bias was associated with less cognitive capacity. Greater numeracy was associated with a smaller braking bias but not with time saving, stopping distance or risk. Those high in impulsiveness tended to make greater time saving biases.
To conclude, the structural analyses did not find any strong reliable consistencies of biases across problems except for the risk and stopping distances judgments. There were only few significant correlations between the cognitive scales and biases. Hence, the structural approach to consistency did not reveal any convincing results. Next, we turn to a search for consistency of cognitive processes that are used to judge different versions of the same problem in a problem set and across different problem sets.
2.2.2 Cognitive processes: Judgment rules
We applied a method that is a version of spectral analysis of the responses. We localized peaks in the frequency distribution of judgments over the number line for each problem. The peaks were used to infer the judgment rule that produced the judgments at the peak value. First, we analyzed the 4 problems in each problem set. We inspected the frequency of judgments on the response continuum for each problem in a search for possible rules that could explain the responses. This revealed clusters of judgments on the response continuum at a few locations. The largest cluster was around the mode. When the cluster of judgments around the mode was removed, we identified a new cluster of responses and a new mode and then a third if it summarized a significant number of responses. Then, each of the different mode judgments was coupled with a decision rule.
To illustrate, the first of the mean speed problems had one cluster of judgments centered on the mode 37 mph, another on the secondly derived mode 49 mph and still another on the third mode 43 mph. We inferred that these clusters indicate that several participants used the same judgment rule for the first mean speed problem. To specify, each cluster of judgments was linked to a judgment rule that was inferred from each of the cluster’s central value. In this particular example the rules are (a) average of the speeds = 37.50 mph, (b) average weighed by the distances driven at the speeds = 49.71 mph and (c) average weighed by the time driven at the speeds (correct rule) =42.58 mph. Judgments that did not fall into one of the main clusters were classified in a group of unknown rules except the few correct judgments that were included in the correct category. This procedure was repeated for each problem in each of the problem sets.
A cluster was defined to include judgments close to the judgment predicted by a rule (± 2.5 units) inferred from the mode. All judgments within that interval were classified as produced by the inferred rule corresponding to these judgments (e.g., mean rule). If two rules, e.g., a ratio and a difference rule predicted judgments closer than 5 units apart, we used the midpoint between the predictions to separate the clusters and corresponding rules. The four problems in each problem set showed approximately the same distributions of rules. This was the case for all the problem sets. Overall, then, we found no evidence for systematic changes of rules within each set.
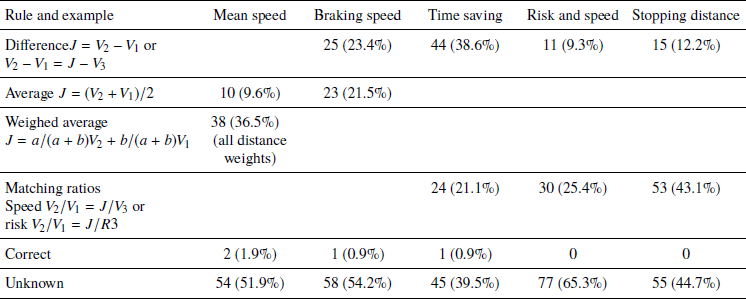
Table 3 gives the number of solutions described by different judgment rules. The rules are described in the left column in an order of increasing complexity. Complexity corresponds to the number of operations of a rule with the assumption that addition is simpler than multiplication and division. Some rules, e.g., the simple average rule, were identified for different sets of problems and others, e.g., the weighted average rule for only one problem set. The results show that the difference rule was used in almost all problem sets.
Table 3: Distribution of number of solutions across the 4 problems in each problem set. J is the judgment and the formulas describe the operations needed to arrive at a judgment.

Mean speed judgments were explained by 3 different rules. In all, 76% of the responses could be explained by the identified rules. The most frequently used rule was the distance weighed average rule with 43% of the judgments. The correct rule was used in only 11% of of the judgments. The braking speed judgments clustered around speeds predicted by the difference in speeds and the average rule. A total of 61% of the judgments were assigned to the rules: speed difference, speed average and correctly used information. The difference and average rules were about equally frequent. There were also judgments following unknown rules. In a special analysis of the unknown rule category we found a subgroup of 6 participants who gave the higher speed as a judgment for at least 3 of the 4 problems. This means that these participants thought that there would be no chance at all to decelerate the car before hitting the child.
The time saving judgments show that in all 77% of the judgments could be described by the difference and matching ratio (proportion) rules. The difference rule explained more judgments than the proportion rule, which supports the findings by Reference Peer and GamlielPeer and Gamliel (2012) who found that, for their data, a linear rule gave better predictions than a curvilinear one.
Risk and speed judgments concerned the risks of a fatal accident, which is approximately proportional to the speed raised to 4. Table 3 shows that many participants instead used the ratio with an exponent = 1.0 (matching ratios) or a difference rule. This was the most difficult set of judgments to describe by rules and there were 65.3% unclassified judgments.
Of the stopping distance judgments 69% of the judgments could be explained by 2 rules. The first rule increased the stopping distance with the same number of yards as the difference between the higher and lower speeds. To illustrate, an increase from 20 to 30 mph was judged to give a stopping distance increase from 40 yards to the response 50 yards. The second rule used the ratio between the speeds to predict the stopping distance, for instance, the speed increase from 20 to 30 mph gives 60 yards (20/30 = 40/60).
2.2.3 Consistency of rule within a problem set
Table 4 gives an overview of the rules used used in a consistent way (defined as 3 or more of the 4 problems in a set of problems solved by the same rule). The criteria for identifying the decision rules were the same as before. There were some participants in 4 of the 5 problems sets who had 2 or more missing values and they were excluded from the following analyses.Footnote 6 About 60% (44+24+1) of the participants used the same rules across problems in the time saving set. This contrasts with the lower consistency in the risk and speed judgments with only about 35% consistent rule-following participants. The results show that many of the participants used the same rule for all problems in a problem set, but we do not know whether there was any regularity from one set of problems to another.
Table 4: Consistency of rules applied (used in 3 or more of 4 problems in a problem set). Distribution of participants using a judgment rule consistently for each problem set. J is the judgment and the formulas describe the operations needed to arrive at a judgment.
2.2.4 Complexity of rules across problem sets
Because the rules in Table 4 are ordered in increasing complexity from top to bottom, we were able to explore regularities in the use of rules in terms of their complexity across problem sets. That is, we can find out to what extent a participant tended to use a more or less complex rules across two different problem sets. As before, a participant was classified as using one specific rule if it applied to 3 or 4 of the solutions of a problem set. Participants who could not be classified in this way were classified in the unknown category. A substantial minority of 27 participants used unknown rules in 4 or more of the 5 problem sets, and they were not included in the following analyses. We also excluded the 4 participants who made correct judgments. To illustrate the rank order complexity categorization with the mean speed problems, each person who used a rule consistently was given a number; if it was the simpler average rule it was 1 and if it was the more complex distance weighed rule, 2.
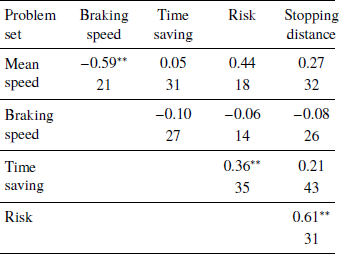
Table 5 shows the results of rank order correlations (Spearman’s ρ) between all pairs of problem sets across participants, describing the extent to which a person uses a more complex rule across each pair of problems sets. Most of the correlations are insignificant with 3 exceptions. A person who uses the distance weighed mean speed rule (complexity = 2) tends to use a difference rule (complexity = 1) rather than an average rule to judge braking speed (ρ = −0.59). Participants who used the matching difference rule for the time saving problems tended to use the same rule (matching differences) to judge risks after a speed increase (ρ = 0.36). Finally, the risk and stopping distance judgments were solved in quite similar ways (ρ = 0.61).
Table 5: Correlations in rule complexity (rank ordered from simpler to more complex) between problem sets. When a participant used the same rule in 3 out of 4 problems in a set, the participant was classified as a user of that rule and represented in the table. Unknown and correct rule participants were not included. Number of participants below each correlation.
Note:
** p= 0.01
significant two-tailed Spearman rho.
The time saving and risk correlation indicates a relationship between judgments that was not revealed in the correlation analysis of the biases. The table gives only consistency of rule complexity across pairs of problem sets and we were interested to see if participants used the same rules consistently across different problems sets. The difference rule was the only rule that could be traced over more than two problems sets. An analysis showed that the rule was used to judge 3 problem sets by 9 participants and 4 sets by 3 participants, who consistently used the rule across problem sets. This indicates that the participants may have adapted their rules to the different problems.Footnote 7
3 Discussion
In the introduction, we asked what people do when they do not know the answer to a problem and yet are willing to make judgments focused on driving problems. In response to this question, we first replicated a number of cognitive biases concerning the effects of speed and speed changes in driving. Second, the structure of the biases was described by pairwise correlations between the biases. Only two biases correlated significantly with each other, risk and stopping distance. Objective risk and stopping distance both increase with power functions of speed. The results showed that the participants underestimated the exponents in both power functions. In general, the structural analyses could not reveal any significant consistencies across probllems. The results support the conclusion of Reference Teovanović, Knežević and StankovTeovanović, Knežević and Stankov (2015) that there is no one-factor theory that can explain cognitive biases, and evidently not even in a limited driving context, as in the present study. However, higher values on the CRT and numeracy scales correlated positively with more accurate mean speed judgments.
A spectral analysis was used to analyze the judgments at the individual level. This method gives a more detailed analysis of judgment behavior than the statistical analyses that were based on averages and linear relationships. The spectral analyses showed that more than half of the participants used the same rule for the different versions of a problem. The rule(s) differed between participants for a specific problem set, but the different rules all produced the same bias (e.g., underestimation of braking capacity). Matching differences and ratios rules were the most frequently used rules.
Reference SvensonSvenson (2016) distinguished between three judgment strategies, associative strategies in which a judgment is retrieved directly from memory, computational strategies that use different algorithms to produce a judgment and analogue strategies including visual analogue representations and processing, e.g., anchoring and adjustment. The present study focused on computational strategies, acknowledging that few or no associative (correct) solutions would be elicited. The computational strategies explained about 70% of the judgment processes, but the remaining 30% unknown solutions were not explained. It is reasonable to assume that some of these judgments were random, but also that some were derived in analogue processes. The present design was unable to draw well motivated conclusions about complex analogue strategies (e.g., first computing an anchor in a computational strategy and then making an adjustment in an analogue process).
A detailed process study using verbal protocol analyses could reveal strategies not found in the present study and reduce the number of unknown strategies. A participant answering a questionnaire on line may be less motivated than a driver in a car to give correct answers and therefore the present results need to be validated in further studies. However, the structure and processes producing biased judgments generalize beyond driving to other contexts in which speed and speed changes are relevant. In many contexts they can lead to serious mistakes on both the personal and the societal level (Reference De Langhe and PuntoniDe Langhe & Puntoni, 2016; Reference Gamliel and PeerGamliel & Peer, 2017; Reference Larrick and SollLarrick & Soll, 2008; Reference Larrick, Soll and KeeneyLarrick, Soll & Keeney, 2015). The results show that if one wants to counteract or eliminate biased judgments it is important to understand that different rules have to be corrected for different persons. The main methodological finding of the present study, the capacity of a spectral analysis to identify decision rules, should be exploited in follow up studies.
Appendix
Short cognitive reflection test (Reference Primi, Morsanyi, Chiesi, Donati and HamiltonPrimi et al., 2016)
1. A bat and a ball cost £1.10 in total. The bat costs £1.00 more than the ball. How much does the ball cost?
[correct answer = 5 cents; heuristic answer = 10 cents]
2. If it takes 5 minutes for five machines to make five widgets, how long would it take for 100 machines to make 100 widgets?
[correct answer = 5 minutes; heuristic answer = 100 minutes]
3. In a lake, there is a patch of lily pads. Every day, the patch doubles in size. If it takes 48 days for the patch to cover the entire
lake, how long would it take for the patch to cover half of the lake?
[correct answer = 47 days; heuristic answer = 24 days]
From Berlin Numeracy test (Reference Cokely, Galesic, Schulz, Ghazal and Garcia-RetameroCokeley et al., 2012)
1. Out of 1,000 people in a small town 500 are members of a choir. Out of these 500 members in the choir 100 are men. Out of the 500 inhabitants that are not in the choir 300 are men. What is the probability that a randomly drawn man is a member of the choir? Please indicate the probability in percent.
2. In a forest 20% of mushrooms are red, 50% brown and 30% white. A red mushroom is poisonous with a probability of 20%. A mushroom that is not red is poisonous with a probability of 5%. What is the probability that a poisonous mushroom in the forest is red?







