1. Introduction

Accurate numerical modelling of the Antarctic ice sheet requires access to the best available datasets. In large-scale prognostic studies, in which ice thickness and ice-sheet extent are predicted forward in time, bedrock topography and accumulation rate represent the main input fields (e.g. Reference HuybrechtsHuybrechts, 1990). In particular, the position of the grounding line and the evolution of the ice shelves are very sensitive to bed elevation and the distribution of sea-bed shoals around the margin of the ice sheet. Similarly, mountain ranges have a strong effect on surface topography because they can dam the ice flow and act as nucleation sites in studies concentrating on the growth of the ice sheet in former geological times (Reference Barker, Barrett, Cooper and HuybrechtsBarker and others, 1999). The depth of troughs into which the ice is channelled at the margin is equally important as it determines the ice flux and therefore affects the configuration and surface topography of the catchment area. In addition, bedrock depth below the surface provides an important control for basal temperature because of the insulation effect of the ice, and thus regulates processes such as basal melting, basal sliding and basal-water flow.

In diagnostic studies, high accuracy is required for the key boundary conditions of surface elevation and ice thickness. On length scales an order of magnitude larger than ice thickness, driving stress is proportional to the product of surface slope and ice thickness. However, due to the non-linearity of the flow law, small errors in these are strongly amplified when calculating the locally defined "dynamics velocity" (e.g. Reference Bamber, Hardy, Huybrechts and JoughinBamber and others, 2000). Together with the accumulation rate, ice thickness and surface slope also determine the pattern of "balance velocity" which, compared with the model-derived "dynamics velocity", may help to constrain uncertainties introduced by the flow law, the ice viscosity (as a function of ice temperature and crystal properties) and/or basal sliding. Comparison of balance velocities with observations may also shed more light on the crucial problem of ice-sheet evolution and the response to global environmental changes.

So far, virtually all large-scale modelling studies of the Antarctic ice sheet relied on gridded versions of the Scott Polar Research Institute (SPRI) glaciological and geophysical folio (Reference DrewryDrewry, 1983), originally digitized by the Australian group (Reference Budd, Jenssen and SmithBudd and others, 1984) on a 20 × 20 km grid, and generalized on a 40 km grid with slight adaptations afterwards (Reference HuybrechtsHuybrechts, 1990; EISMINT Intercomparison Project, http://homepages.vub.ac.be/∼phuybrec/eismint/antarctica.html). However, as discussed in detail by Reference Bamber and HuybrechtsBamber and Huybrechts (1996), substantial deficiencies were found in these geometric datasets, due to combinations of errors and inconsistencies in the folio maps, errors in the digitization, and significant differences between the surface-elevation distribution of the SPRI map and a much improved elevation model derived from European Remote-sensing Satellite (ERS-1) radar-altimeter data. Perhaps most remarkably, the total ice volume mentioned in Reference DrewryDrewry and others (1983), and widely quoted since, was about 12% larger than the value derived from a direct digitization of the corresponding thickness map of the folio, which in turn differed from the distribution derived separately by subtracting bed elevation from surface elevation, as was done in the Budd digitization. An unequivocal explanation for these mismatches could not, however, be established, and definite answers should perhaps await the results of a future comprehensive recompilation of all Antarctic data as part of the BEDMAP Project (Reference VaughanVaughan, 1996; http://www.nerc-bas.ac.uk/public/aedc/bedmap/bedmap.html ).

The Reference Bamber and HuybrechtsBamber and Huybrechts (1996) grids were restricted to grounded ice only and excluded the Antarctic Peninsula, limiting the scope of their application. In this paper, we build further on these datasets and extend the grids beyond their current limits to include all of the continental shelf and surrounding ocean. At the same time, we develop a new gridded dataset for accumulation rate over the same model domain. The direct stimulus for undertaking this work is related to forthcoming detailed model studies of ice-sheet dynamics in Dronning Maud Land (DML), Antarctica, within the framework of the European Project for Ice Coring in Antarctica (EPICA) and the planned retrieval of a deep ice core. Therefore, special attention was devoted to incorporating all new data collected as part of the EPICA pre-site survey, most notably by the Alfred Wegener Institute (Reference Steinhage, Nixdorf, Meyer and MillerSteinhage and others, 1999; Reference Oerter, Graf, Wilhelms, Minikin and MillerOerter and others, 1999, Reference Oerter2000). Furthermore, it proved useful to reconsider data throughout Antarctica because the flow dynamics of DML is difficult to separate from changes occurring elsewhere on the ice sheet, especially when the interest is in the glacial cycles.

The consistency and quality of the new gridded datasets are demonstrated with a new assessment of the vertically integrated flow required for steady state (balance flow). In addition, an enlarged map of balance velocity over DML shows the flow activity of interest for siting a future ice core. At the same time, updated numbers on the size and the surface mass balance of the Antarctic ice sheet are provided.

2. Specifications for Modeling Purposes

The equations of the ice-sheet-ice-shelf model are solved with the finite-difference method. This requires the data to be specified on a Cartesian grid with rectangular boundaries. Because the ice sheet must be able to expand and retreat, the domain needs to cover all Antarctica and its surrounding continental shelf. In particular, the sea-bed elevation needs to be specified below the ice shelves and match the bed topography below the grounded ice sheet fluently. The most crucial area is close to the grounding line, where all three parameters, surface elevation, bed elevation, and ice thickness need to be consistent with a specified flotation criterion to predict regions of grounded and floating ice correctly. A further requirement is that the data need to be continuous over all the grid. In particular, there should be no gaps or nunataks sticking out of the ice sheet because these are difficult to handle, especially in dynamic situations.

For simplicity, we opted for the same 281 x281 grid with 20 km constant spacing of the Budd datasets. The map projection is polar stereographic with a standard parallel at 71 °S as adopted for the SPRI map folio. This projection conserves directions, but on the other hand is characterized by non-negligible areal distortions ranging from - 8 % at 60° S to +5.6% at the South Pole: more optimal alternatives exist, but were not attempted for reasons of consistency with previous datasets.

3. Data Sources

4. Data Manipulation

For interpolating the data, extensive use was made of the continuous-curvature spline-algorithm "surface" with a tension factor of zero (minimum curvature), available as part of the GMTsoftware (Reference Smith and WesselSmith and Wessel, 1990). This is equivalent to a low-pass filter with smoothing characteristics well suited to avoid numerical instabilities in the numerical model.

Updated subsets of ice-thickness and bed-topography data were merged within the main dataset by calculating the height offset at the common boundary and using this to weight the main dataset as a function of distance from this boundary. A distance-cubed weighting was found to provide smooth transitions and continuity of slope across the boundaries. Accumulation point measurements were given a weighting factor of 10, compared to the background Giovinetto data, to control the interpolation between the irregularly and sparsely distributed measurements. At the grid margin, a fixed value of 0.5 m a"¹ was adopted. This has no influence on values within the possible maximum extent of the Antarctic ice sheet, but ensures that the flow velocities in the surrounding ice shelf, which extends to the grid margin, do not give rise to numerical instabilities.

To satisfy the peculiarities of the numerical model and its parameterizations (Reference HuybrechtsHuybrechts, 1990), some small editing of the resulting datasets was necessary. These concerned local corrections that would not falsify any large-scale characteristics of the Antarctic ice sheet, but are required to avoid spurious, unwanted, or unrealistic effects in the model.

Manual intervention was needed to remove a rock barrier, running from Mawson Escarpment to the Prince Charles Mountains, which would have dammed the flow at the head of Lambert Glacier, but is in reality a collection of nunataks rather than a continuous mountain range. Editing of geometric data was also necessary in the Peninsula area to float the Larsen and George VI Ice Shelves. For these parts, no data existed on the SPRI thickness folio, justifying the manual intervention. Ice thickness was also set at the minimum value of 10 m over rock outcrops.

The treatment of the mass balance in the ice-sheet model assumes that the data for net surface mass balance, as a result of snowfall, hoarfrost, sublimation, melting, wind scouring, drift-snow deposition, etc., can be equated to precipitation. Runoff, or the fraction of precipitation falling as rain, if any, is derived in the model from the precipitation rate (Reference Huybrechts and de WoldeHuybrechts and de Wolde, 1999). Precipitation rates for different climates are then calculated as proportional to the gradient of the saturated water-vapor pressure at the temperature above the surface inversion layer (Reference RobinRobin, 1977). While probably being a reasonable first-order estimate, especially over most of the plateau area, the calculation requires positive input data. Zero or negative accumulation points have therefore been re-interpolated from surrounding positive gridpoints. The minimum value was set at 15 mma⁻¹. This effectively removed the blue-ice areas such as the area with negative mass balance at the head of Lambert Glacier, whose existence has otherwise been questioned (Reference Allison, Young and MedhurstAllison and others, 1985).

5. Results

Figure 1 shows the four new gridded datasets for bedrock elevation, ice thickness, surface elevation, and accumulation rate. Their principal feature is the complete coverage and improved detail in DML and on the Filchner-Ronne Ice Shelf as compared to the older SPRI maps. Over much of the continent, the geometric datasets are equivalent to those discussed by Reference Bamber and HuybrechtsBamber and Huybrechts (1996) and so are the improvements with respect to the Budd grids. Important new bedrock features, not seen on the SPRI map folio, include the deep subglacial troughs below Bailey Ice Stream and Slessor Glacier that extend well inland, as well as the rough mountainous terrain below DML (Reference Steinhage, Nixdorf, Meyer and MillerSteinhage and others, 1999). Improvements in the accumulation grid also involvemore detail in DML where the transition to a desertic precipitation regime (as defined by the 0.05 m a contour) is now more inland than in previous compilations.

Fig. 1. Contoured representations of the new datasets for ice-sheet modelling as developed in this study. Except for bed elevation, they are displayed within the area of the conterminous Antarctica, although all parameters are defined within the entire grid square. The bold line in the bedrock plot is for 0 m a.s.l.

A map of bed-elevation differences with the Budd grids summarizes some of the progress made in the last 15 years (Fig. 2). Over much of Wilkes Land, the bed is more than 500 m higher than in the Budd grids, which was attributed to a combination of errors in the surface-elevation data and the original digitization of the folio maps (Reference Bamber and HuybrechtsBamber and Huybrechts, 1996). In DML, the new bedrock topography is generally higher (and the ice thinner) east of the Greenwich meridian by up to 1000 m, while the reverse is evident in the western part of DML. Important differences can also be seen in the Filchner-Ronne basin, reflecting the vast increase in measurements since the SPRI folio was published in 1983.

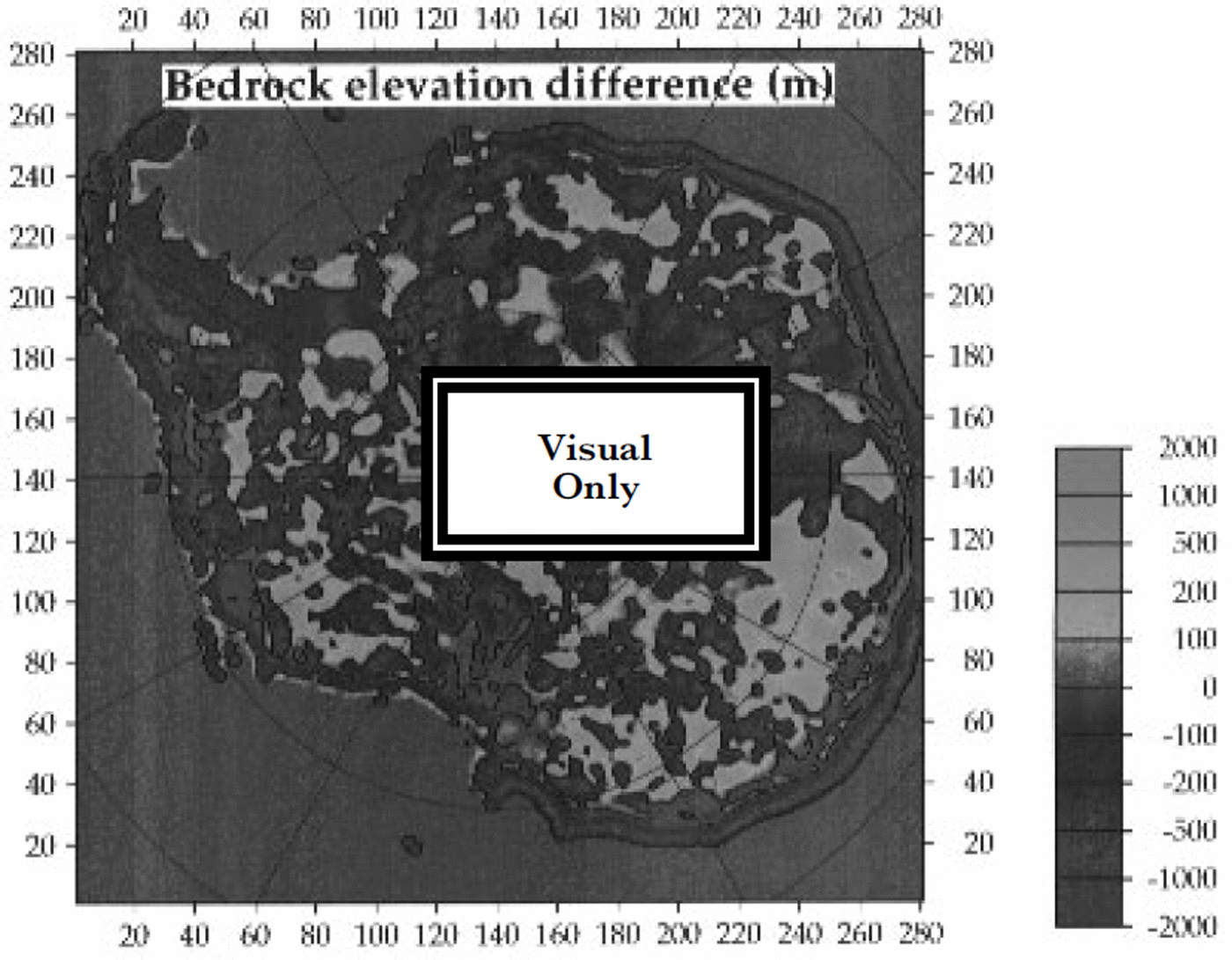
Fig. 2. Differences between the bedrock dataset of this paper and the bed grid digitized from the SPRI folio ( Reference DrewryDrewry, 1983) by Reference Budd, Jenssen and SmithBudd and others (1984). A negative difference means that the bed in the Budd dataset lies above ours. The 0 m contour is shown in bold.

A comparison of measured properties with earlier assessments of the Antarctic ice sheet is shown in Table 1. Most strikingly, the substantial reduction of ice volume by about 12% compared to the Reference Drewry, Jordan and JankowskiDrewry and others (1982) figure is confirmed. Despite the inclusion of the Antarctic Peninsula, the present value for total ice volume (ice sheet and ice shelves) of 26.37 × 10⁶km³ is about 1% lower than the value found in Reference Bamber and HuybrechtsBamber and Huybrechts (1996), which is mainly due to the higher topography of DML. On the other hand, we find comparably small differences with the Reference Drewry, Jordan and JankowskiDrewry and others (1982) figures for areal statistics. There is an even closer agreement (within 0.2%) with the Reference Fox and CooperFox and Cooper (1994) update based on the Scientific Committee on Antarctic Research ADD, though the position of the grounding line, especially along the Siple Coast and around Graham Land, is somewhat different. This is to be expected because of the difficulties of locating the grounding line at the mouth of ice streams where surface slopes are low and the usual strong break in slope is not well-developed. We find a reduction in the area of ice-free terrain to about a third of the Reference Drewry, Jordan and JankowskiDrewry and others (1982) figure, but our value is still three times larger than the figure derived in the Reference Fox and CooperFox and Cooper (1994) analysis. Our result here is biased by the minimum pixel size of 20 × 20 km and the absence of rock outcrops in the Antarctic Peninsula.

Table 1. Comparison of measured properties of the Antarctic ice sheet

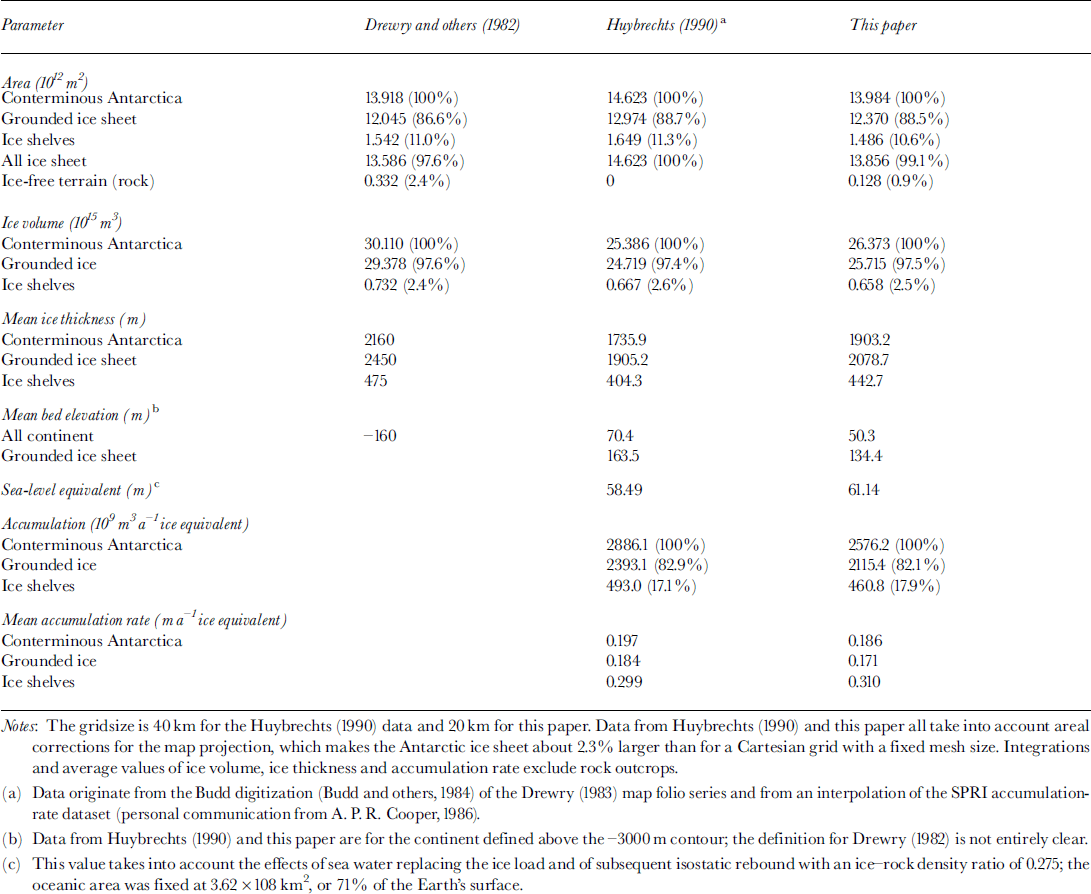
Total accumulation over the conterminous grounded ice sheet is more than 25% higher than the earlier Reference Giovinetto and BentleyGiovinetto and Bentley (1985) estimate. On the other hand, we find a value which is only slightly higher (+2.5%) than a recent independent compilation by Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others (1999) when including the ice shelves. This reduction in the spread of estimates seems to reflect the progress made towards a greater consensus on the total yearly mass input of the Antarctic ice sheet. Some of the differences with the Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others (1999) figure are likely due to a slightly different delineation of the ice sheet and a different control field, whereas the removal of ablation islands in our dataset hardly influences the result at all.

6. Balance Flow

A calculation of balance fluxes and balance velocities provides an excellent illustration of the quality of the datasets and, moreover, yields a good insight in the general flow pattern of the Antarctic ice sheet. While such a calculation only produces an estimate of the vertically averaged flow required to maintain continuity it shows very well where the flow is converging into streams and where ice divides and drainage boundaries are located.

The balance flow was calculated with the two-dimensional finite-difference method described by Reference Budd and WarnerBudd and Warner (1996), amended to take into account areal distortions introduced by the map projection. As input, surface-elevation, ice-thickness, and accumulation-rate data are required, which were supplemented by a mask file in order to exclude the ice-free land and the ice shelves. The main assumption underlying the method is that the flow is in the direction of steepest descent, as calculated over a representative distance of about 10 ice thicknesses. The method further requires that no surface hollows or exactly flat regions exist. Such areas were first removed by setting them equal to the average of the surrounding gridpoints. Corrections were necessary for about a thousand points, most of which were around rock outcrops or near to the grounding line. The only major depression in the surface data was found near Hercules Dome («86° S, 115° W). The correction procedure for calculating the balance flow involved elevation changes by a few hundred metres at most which were hardly detectable on the scale of the plots, but are excluded from the datasets in Figure 1.

The resulting balance flux is shown in Figure 3. A lot of fine detail can be seen, which primarily results from the elevation model, and to a lesser extent from the accumulation data. A dendritic pattern of major flow paths can be traced well inland. All major outlet glaciers and ice streams, in both East and West Antarctica, are clearly visible. That is particularly the case for the Siple Coast Ice Streams A to E, but Pine Island Glacier, Rutford Ice Stream, Foundation Ice Stream, Support Force Glacier, Recovery Glacier, Slessor Glacier, Jutulstraumen, Lambert and Byrd Glaciers also exhibit strongly convergent flow and fluxes in excess of 0.5 km² a⁻¹.

Fig. 3. The patternof ice balance flux over the grounded ice sheets in units of the transport quanitity km2 a-1.The pattern over the ice shelves is not shown because the flow is not necessarily parallel to the aspect as assumed by the method.

A clearly noticeable feature is Lake Vostok (≈78°S, 105° E), where the ice is predicted to be channelled in a southerly direction parallel to the maximum surface slope over the lake. This is, however, an area where the model assumptions are likely to break down. It is more probable that the flow over the lake is driven by ice velocities and strain rates around the lake margin rather than by the local surface slope, which trends north-south, or by the local strain rate which is similar to the dynamics of a confined ice shelf. Consequently, it is plausible that the general flow would not greatly change direction and magnitude over the lake and would be similar to the flow at its eastern and western sides (personal communication from C Mayer, 1999). Other subglacial lakes in East Antarctica are only a few kilometres in extent (Reference Siegert, Dowdeswell, Gorman and MclntyreSiegert and others, 1996) and therefore of subgrid scale and too small to disrupt the general flow pattern. A second unusual feature can be seen in the catchment areas of Foundation Ice Stream and Support Force Glacier, where flowline appear to run parallel over most of their route down from the South Pole. This apparently represents a poorly constrained ice divide. A distinct flow channel is also evident upstream of Recovery Glacier, which appears to skirt the 81.5° S boundary where the two surface datasets were matched, and therefore is possibly an artifact arising from the surface model. There is a maximum flux well inland, which suggests convergent flow followed by a strong divergence further downstream.

Comparing the pattern of balance flux with the earlier assessment presented in Reference Budd and WarnerBudd and Warner (1996) demonstrates the effect of the new datasets. The main aspects are a more concentrated flow, less continuous divides and new features such as Lake Vostok and Recovery Glacier. Also the pattern south of 80° S is quite different from the earlier calculation, though it is not clear to what extent the poorer data, derived from terrestrial, airborne, and TWERLE balloon measurements, could have played a role here.

Figure 4 shows the corresponding pattern of balance velocity. These are vertically averaged values, which need to be multiplied by the surface-to-column velocity ratio to obtain surface values. This ratio depends mainly on the temperature conditions in the basal layers, and can be shown to vary between about 1.15 for cold basal conditions to close to unity where the base is at the melting point and basal sliding takes place. Large flow velocities, generally in excess of 1 km a"¹, are predicted for the same outlets having large fluxes as mentioned above.

Fig. 4. Balance velocities over the Antarctic ice sheet obtained by dividing the balance flux shown in Figure 3 by the local ice thickness. The data allow for fine detail and resolve all of the major ice streams and outlet glaciers discharging from the grounded ice sheet.

A zoom on DML, where the input data reflect the most recent status of the observations, allows areas of active and stagnant flow of interest for siting the future EPIC A ice core to be distinguished (Fig. 5). In order to avoid important problems of interpretation of the climatic signal, in terms of the origin of the ice, it would be preferable to drill in an area where flow velocities are less than a few metres per year at most. Such conditions, for example, are provided in the region around 75° S and 0° W, a saddle area inland of Kottasberge, where ice thickness is 2000–3000 m and accumulation

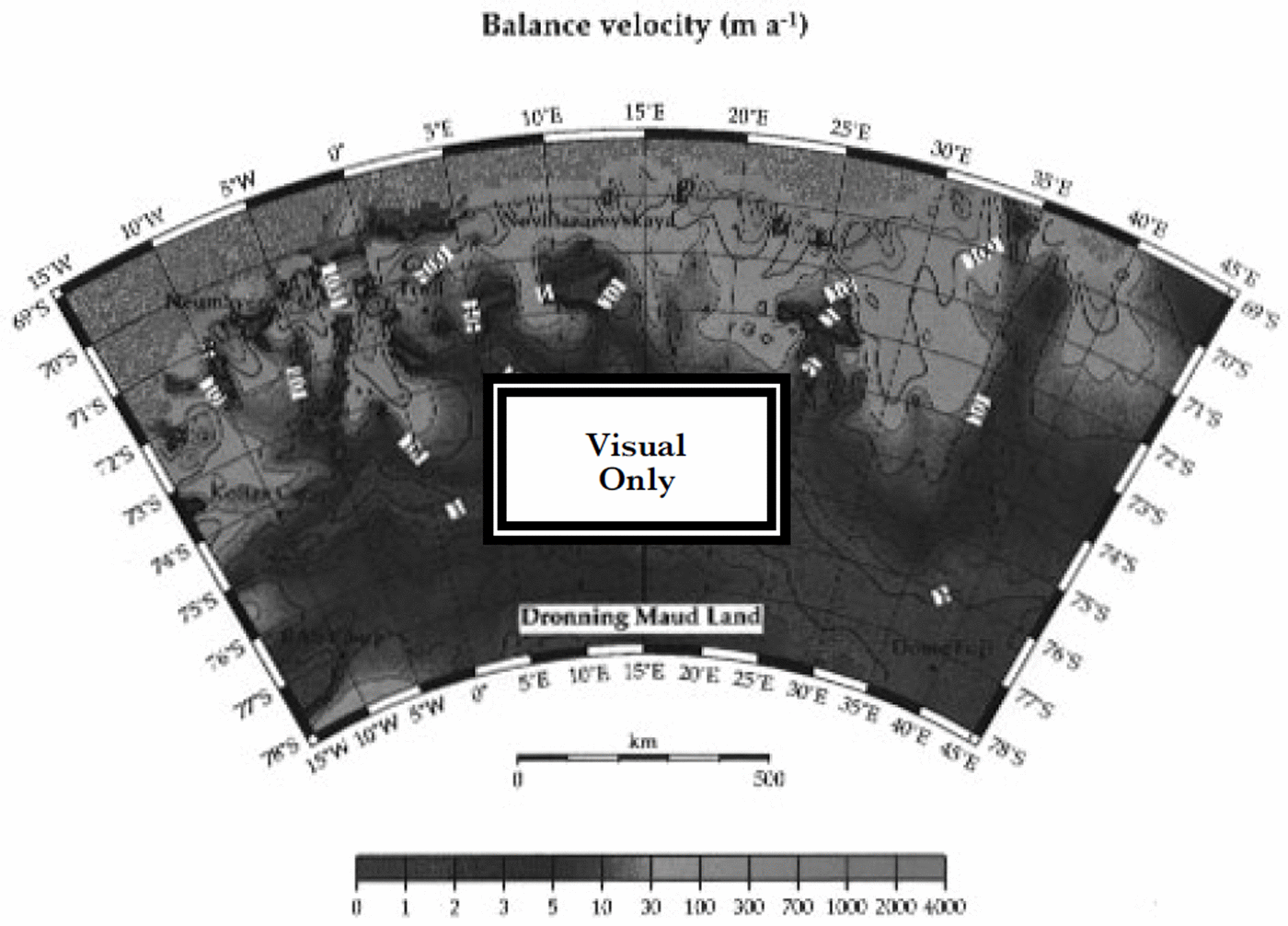
Fig. 5. Zoom of the balance-velocity pattern over Dronning Maud Land. These results represent column-averaged values, and should be multiplied by a factor between 1 and 1.15 for comparison with surface-velocity determinations. Bold lines are for the 1, 10,100, and 1000 ma⁻¹ contours.

Conclusions

New high-resolution datasets have been constructed for three-dimensional modelling of the Antarctic ice sheet. These data represent a significant improvement over the boundary conditions available so far as they cover the entire Antarctic continent and include the most up-to-date observations, in particular for Dronning Maud Land.

Here the datasets were used to calculate the balance flow over all the ice sheet, providing an excellent snapshot of the motion of the ice sheet in steady-state. The pattern of balance velocities yielded a surprising wealth of detail. Most remarkably, concentrated flow paths were found to extend well inland, throwing new light on the notion of "sheet flow-generally accepted for large continental ice sheets. Moreover, in many areas, it may be assumed that the balance velocities should be, after correction for the surface-to-column ratio, close to reality as the longer-term imbalance was found to be quite small and below 10% of the focal mass balance over most of the ice sheet (Reference Wingham, Ridout, Scharroo, Arthern and ShumWingham and others, 1998). Because the surface slopes are believed to be the most accurate, comparison with observed velocities may equally well point to deficiencies in the accumulation and ice-thickness data.

Balance velocities also provide initial conditions for dynamic ice-sheet models and are very useful for model validation. Comparison with model-derived dynamic velocities furthermore helps to constrain the uncertainties introduced by the flow law, basal sliding and the temperature regime of the ice sheet (Reference Bamber, Hardy, Huybrechts and JoughinBamber and others, 2000).

In addition, the balance flow helps guide measurements in the field. An enlargement over DML displayed the general flow pattern useful for locating the future EPICA deep ice core; thereby pointing to a favourable saddle location inland of Kottasberge. Dynamic model runs during the glacial cycles are now needed to investigate the stability of the flow characteristics over the anticipated age of the core. Such model runs would also yield the pattern of elevation changes and could help with dating the core, both in the planning phase and after the drilling.