1. INTRODUCTION
Recent studies of Greenland and Antarctic firn cores have suggested that certain impurities, such as Ca++, play a critical role in the densification of polar firn and also potentially in the creep of polycrystalline ice (Horhold and others, Reference Horhold2012; Freitag and others, Reference Freitag, Kipfstuhl and Laepple2013). Based on several firn core records from Greenland and Antarctica, Horhold and others (Reference Horhold2012) reported that there was a strong positive correlation between Ca++ concentration and firn densification. Although Horhold and others (Reference Horhold2012) acknowledge in their conclusions that this correlation does not provide conclusive evidence for causation or a physical link, they do postulate that local changes in density, not due to simple densification with depth, may be due to the presence of Ca++. Subsequent work by Freitag and others (Reference Freitag, Kipfstuhl and Laepple2013) gave a similar interpretation based on core-scale radioscopic imaging. Using one of the same firn cores as Horhold and others (Reference Horhold2012) (Antarctic firn core B32), the authors were able to increase the resolution of the density measurements. They also observed a positive correlation between Ca++ concentration and local changes in density, and suggested a physical link between Ca++ and densification.
In contrast to these two studies, Fujita and others (Reference Fujita2014) presented a detailed analysis of several Greenland firn cores from the North Eemian Ice Drilling (NEEM) camp, in which they also investigated the densification of polar firn. Using the measured dielectric permittivity and anisotropy as a surrogate for densification in their firn cores, Fujita and others (Reference Fujita2014) develop a correlation coefficient matrix for not only Ca++ but many additional impurities as well, including Na+, K+, Mg++, F−, Cl−, NO3 − and SO4 −−. In their analyses, in addition to the parameters of depth and density, Fujita and others (Reference Fujita2014) also included seasonal effects that could be relevant for local changes in density, such as the timing for when certain types of impurities are more likely to be deposited and when snow metamorphism may be seasonally enhanced due to larger temperature gradients. In their findings, they show that Ca++, Na+ and Mg++ are all correlated positively with deformation and local changes in density, but that there is not necessarily a physical causality for this correlation. Rather, they conclude that these correlations are superficial and caused by the seasonal synchronicity of the summer-to-autumn metamorphism of the snowpack and potentially also the presence of other anion concentrations that have already been shown to increase the ductility in ice single crystals such as F− and Cl− (Jones and Glen, Reference Jones and Glen1969; Nakamura and Jones, Reference Nakamura and Jones1970). Lastly, Fujita and others (Reference Fujita2014) also reference unpublished results from their current research at Dome Fuji, Antarctica, in which they report no correlation to exist between Ca++ concentration and densification. Although a more robust study, the results from Fujita and others (Reference Fujita2014) are still based only on empirical observations and correlations.
Observations from polar ice cores have shown that naturally formed polycrystalline ice can contain a wide variety of both chemical and physical impurities (Baker and Gerberich, Reference Baker and Gerberich1979; Lange and Ahrens, Reference Lange and Ahrens1983; Baker and others, Reference Baker, Cullen and Iliescu2003). While physical impurities, such as silt-sized soil particles, can become uniformly dispersed throughout the ice crystal microstructure, and have been shown to increase the strain rate and dislocation density of polycrystalline ice in laboratory testing (Song and others, Reference Song, Cole and Baker2005), higher concentrations of chemical impurities tend to preferentially reside in the grain boundaries and triple junctions of natural ice (Baker and others, Reference Baker, Cullen and Iliescu2003; Durand and others, Reference Durand2006; Obbard and Baker, Reference Obbard and Baker2007). This feature would presumably have some effect on the bulk mechanical properties of the ice, but it remains unclear in what way. As a first step in understanding the bulk mechanical effects of soluble impurities in polycrystalline ice, the effects of Ca++ are presented here.
2. EXPERIMENTAL
To test systematically how Ca++ affects the mechanical properties of polycrystalline ice, a series of mechanical tests were performed in the Dartmouth Ice Research Laboratory (IRL). Following Cole (Reference Cole1979), specimens of polycrystalline ice were created via a radial freezing technique, where seed grains were loaded into an aluminum mold, flooded with chilled and deaerated water, and then slowly frozen radially from the outside-inwards via a temperature controlled glycol wrap placed around the exterior of the mold. Following this approach, polycrystalline specimens of ice with a mean grain diameter of 1 mm and a gage aspect ratio of 3:1 were created. An example of the initial microstructure is shown in Figure 1, which displays a thin section taken from a right-cylindrical compression specimen photographed between crossed polarizing filters. Of note in this image, is that the initial microstructure consists of randomly oriented grains ranging from 0.8 to 1.2 mm in diameter. Following Cole (Reference Cole1979), this initial microstructure was found to be reproducible for all specimens.

Fig. 1. Initial microstructure of a cylindrical specimen prepared for mechanical testing as viewed through crossed polarizing filters. Mean grain diameters were typically of the order of 1 mm.
Two sets of specimens were created, a control set of undoped ice made from pure (Milli-Q 18.2 MΩ cm−1) water and a test set that had been doped with anhydrous CaSO4. For both the control and test specimen sets, right-cylindrical specimens, 3.8 cm in diameter by 11.4 cm in length, were made for loading in uniaxial compression under a constant strain rate and right-cylindrical dogbone-shaped specimens, 2.54 cm in diameter by 7.62 cm in gage width and length, respectively, were made for loading in uniaxial tension under a constant load. A schematic of the dogbone specimen is given in Figure 2. Compression tests were carried out using an MTS servo-hydraulic testing apparatus housed in a cold room in the IRL. Tension tests, designed to serve as high-temperature, low-stress creep tests, were carried out using a home-built apparatus also housed in a cold room in the IRL. This apparatus was designed such that undoped and doped dogbone specimens could be tested simultaneously, side-by-side, in order to limit any potential effects from temperature fluctuations during the twice-daily defrost cycles of the cold room. A schematic of this apparatus is given in Figure 3.

Fig. 2. ‘Dogbone’ shaped specimens of polycrystalline ice were made such that the gage height to diameter ratio would always be 3:1, with an average grain size of 1 mm.

Fig. 3. The constant load tension (creep) testing apparatus was designed such that doped and undoped specimens could be tested simultaneously side-by-side. Initial applied loads were 38 kg or ~0.75 MPa. The maximum measurable strain that can be achieved with this setup is ~30%.
Doping with 0.1 g L−1 CaSO4 led to test specimens with a Ca++ concentration of ~5 ppm, while doping with 0.34 g L−1 CaSO4 led to specimens with a Ca++ concentration of ~50 ppm. Both solutions were used as the Ca++ concentration could not be accurately measured until after the completion of each test, which showed a range of Ca++ concentrations between 5 and 50 ppm. The ionic compound CaSO4 was chosen as the dopant as it is found to exist in and be deposited on ice sheets and glaciers (Legrand and Mayewski, Reference Legrand and Mayewski1997; Obbard and Baker, Reference Obbard and Baker2007; Iizuka and others, Reference Iizuka2008). Furthermore, it was shown by Fujita and others (Reference Fujita2014) that SO4 −− was one of the least likely to contribute to firn densification and ice deformation, showing very poor correlations with densification, thereby also making CaSO4 a good candidate for studying the effects of Ca++.
Constant strain rates of 1 × 10−4, 1 × 10−5 and 1 × 10−6 s−1 were performed on cylindrical compression specimens at a temperature of −10°C (±0.2°C), while strain rates of 1 × 10−5 and 1 × 10−6 s−1 were applied at a temperature of −20°C (±0.2°C). All compression tests were terminated at an engineering strain of 5%.
Deformation tests in tension were performed on dogbone specimens at a constant load of 38 kg (0.75 MPa initial stress) and the resulting strain was measured with an Omega LD-320 displacement sensor (LVDT). All tests were conducted at −6°C (±0.2°C), which resulted in minimum strain rates of the order of 1 × 10−8 s−1. These tests took ~11–12 d to reach true strains of near 25%.
At the completion of each mechanical test, microstructural analysis was performed on thin cross-sectional sections (thin sections) taken from post-test compression and tension specimens. These thin sections were analyzed via crossed polarized light imaging and by scanning electron microscopy using a field emission gun FEI XL30 scanning electron microscope (SEM), equipped with a Gatan cryotransfer/cooling system. In the SEM, samples were kept between −60 and −120°C with a temperature controlled cold stage in low-vacuum (67 Pa) mode. An accelerating voltage of 15 kV was used and backscattered electron micrographs were collected. X-ray microchemical analysis was also performed via energy-dispersive spectroscopy (EDS) with an Edax light element Si(Li) detector.
3. RESULTS AND DISCUSSION
3.1. Compression tests
For all compression tests, a minimum of three tests were performed at each strain rate for each group of specimens (‘pure’ or ‘doped’). Over the course of these experiments, the mechanical behavior observed was found to be very reproducible, sometimes leading to data so closely overlapping that it could be difficult to discern the difference between two separate tests when plotted on a single plot. The only exception to performing three tests per strain rate, was for the tests conducted at −20°C and 1 × 10−6 s−1. For these tests and the tension (creep) tests conducted at −6°C, only two tests were performed for each pure and doped specimen, as time did not allow for any additional testing (tension tests were approximately 13 d per two experiments). However, the results from these tests were found to be generally in agreement and in support of all other experimental data and observations.
For compression tests conducted at −10°C, the Ca++ doping demonstrated either a strengthening effect or no effect on the observed peak stress (usually near 1% strain) and flow stress (taken always to be at 5% strain) depending on the strain rate, as shown in Figure 4. The strengthening effect was most pronounced at the highest strain rate applied, of 1 × 10−4 s−1 (Fig. 4a), but was also observable at 1 × 10−5 s−1 (Fig. 4b). For tests conducted at 1 × 10−6 s−1 (Fig. 4c), it is much more difficult to discern any effects of the Ca++, although there does seem to be a flattening of the Ca++ peak, a somewhat common feature among most tests.

Fig. 4. Results from all compression tests conducted at −10°C and constant strain rates of 1 × 10−4, 1 × 10−5 and 1 × 10−6 s−1.
Results for tests conducted at −20°C, as shown in Figure 5, demonstrate a much more discernable difference between the magnitudes of the peak stress and flow stress for the Ca++-doped specimens versus the undoped specimens. From results for 1 × 10−5 s−1 (Fig. 5a), a much higher peak stress and flow stress was observed for the Ca++-doped specimens than for the undoped specimens. For 1 × 10−6 s−1 (Fig. 5b), it is again difficult to discern a difference between the doped and pure specimens, although there does appear to be a distinctive flattening of the peak of Ca++-doped specimens. In both Figures 4, 5, small irregular bumps in the stress/strain curves (as very prevalent in Fig. 5b) are due to issues with the data acquisition software and were not caused by any known physical effect.

Fig. 5. Results from all compression tests conducted at −20°C and constant strain rates of 1 × 10−5 and 1 × 10−6 s−1.
3.2. Strain-rate sensitivity index
To compare the differences in the mean peak stress
![]() $\overline {\sigma _{{\rm ps}}} $
and mean flow stress
$\overline {\sigma _{{\rm ps}}} $
and mean flow stress
![]() $\overline {\sigma _{{\rm fs}}} $
from Figures 4, 5, which are summarized in Table 1, the strain-rate sensitivity index m can also be used to quantify the effects of Ca++ in the flow stress regime (Manley and Schulson, Reference Manley and Schulson1997). Provided that superplastic flow is responsible for the flow stress observed at 5% strain and an Arrhenius type of relationship is followed as given in Eqn (1) (Glen, Reference Glen1968):
$\overline {\sigma _{{\rm fs}}} $
from Figures 4, 5, which are summarized in Table 1, the strain-rate sensitivity index m can also be used to quantify the effects of Ca++ in the flow stress regime (Manley and Schulson, Reference Manley and Schulson1997). Provided that superplastic flow is responsible for the flow stress observed at 5% strain and an Arrhenius type of relationship is followed as given in Eqn (1) (Glen, Reference Glen1968):
where A is a material constant, σ is taken to be
![]() $\overline {\sigma _{{\rm fs}}} $
, T is the absolute temperature, R is the ideal gas constant, Q is the activation energy, and n is the stress exponent, then m (n = 1/m) can be solved for directly from Eqn (2) (Manley and Schulson, Reference Manley and Schulson1997; Smolej and others, Reference Smolej, Skaza and Fazarinc2009) for a given temperature
$\overline {\sigma _{{\rm fs}}} $
, T is the absolute temperature, R is the ideal gas constant, Q is the activation energy, and n is the stress exponent, then m (n = 1/m) can be solved for directly from Eqn (2) (Manley and Schulson, Reference Manley and Schulson1997; Smolej and others, Reference Smolej, Skaza and Fazarinc2009) for a given temperature
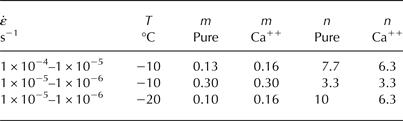
Table 1. Mean peak stress
![]() $\overline {\sigma _{{\rm ps}}} $
and mean flow stress
$\overline {\sigma _{{\rm ps}}} $
and mean flow stress
![]() $\overline {\sigma _{{\rm fs}}} $
from test results given in Figures 2, 3
$\overline {\sigma _{{\rm fs}}} $
from test results given in Figures 2, 3

The significance of m is that it quantifies the magnitude by which Ca++ may be acting to either enhance or retard the ice deformation rate.
For all compression tests,
![]() $\overline {\sigma _{{\rm fs}}} $
is plotted on a log/log scale in Figure 6 for tests conducted at −10°C (Fig. 6a) and −20°C (Fig. 6b). In these plots, the slope between points is representative of n and hence also m. Although it is not the point of this paper to make any broad statement about the most appropriate value of n, n and m values are reported in Table 2 to facilitate a more tangible discussion of the results. At −10°C (Fig. 6a), there is a distinct shift in the slopes between 1 × 10−5–1 × 10−6 s−1 and 1 × 10−5–1 × 10−4 s−1. This transition is generally thought to be due to a change from a purely plastic regime of deformation to a more ductile-to-brittle regime of deformation (e.g. Duval and others, Reference Duval, Ashby and Anderman1983; Schulson, Reference Schulson1990; Renshaw and Schulson, Reference Renshaw and Schulson2001; Schulson and Duval, Reference Schulson and Duval2009). This theory is supported by n-values for the region from 1 × 10−5 to 1 × 10−6 s−1 that are much closer to n = 3, which has been widely reported as the stress exponent commonly observed for creep in polycrystalline ice (Glen, Reference Glen1958), whereas n-values for the region from 1 × 10−5 to 1 × 10−4 s−1 are claimed by some (Barnes and others, Reference Barnes, Tabor and Walker1971; Weertman and others, Reference Weertman1983) to be much higher. At −20°C (Fig. 6b), n-values are again much higher than would be expected for purely plastic flow in polycrystalline ice, which would also suggest that a high-stress ductile-to-brittle regime of deformation is taking place as a result of the lowering of the temperature from −10 to −20°C. Although crack density was not a variable that was quantitatively measured in the post-test specimens, it was qualitatively quite clear at −20°C that there was a great deal more damage and microcracking that had been imparted to the specimens that had been tested at −20°C than for those tested at −10°C. An increase in the brittle behavior of a material with a decrease in its temperature is not particularly surprising, and is likely responsible for the rather high n-values observed at −20°C (n = 10; Table 2). It should be pointed out however, that for similar testing conditions, similar values of n were observed by Barnes and others (Reference Barnes, Tabor and Walker1971) (see their Fig. 2). More to the point of this study, however, is that m-values calculated for both possible deformation regimes show that the Ca++-doped specimens have generally either a higher or at least a non-differentiable strain-rate sensitivity index when compared with the m-values of the undoped ice. These results could be interpreted as either a lowering of the stress exponent and hence a reduction of the strain rate when in the ductile-to-brittle transition region of deformation, a possible strengthening effect, or as a non-differentiable effect when in a deformation regime of pure plastic flow.
$\overline {\sigma _{{\rm fs}}} $
is plotted on a log/log scale in Figure 6 for tests conducted at −10°C (Fig. 6a) and −20°C (Fig. 6b). In these plots, the slope between points is representative of n and hence also m. Although it is not the point of this paper to make any broad statement about the most appropriate value of n, n and m values are reported in Table 2 to facilitate a more tangible discussion of the results. At −10°C (Fig. 6a), there is a distinct shift in the slopes between 1 × 10−5–1 × 10−6 s−1 and 1 × 10−5–1 × 10−4 s−1. This transition is generally thought to be due to a change from a purely plastic regime of deformation to a more ductile-to-brittle regime of deformation (e.g. Duval and others, Reference Duval, Ashby and Anderman1983; Schulson, Reference Schulson1990; Renshaw and Schulson, Reference Renshaw and Schulson2001; Schulson and Duval, Reference Schulson and Duval2009). This theory is supported by n-values for the region from 1 × 10−5 to 1 × 10−6 s−1 that are much closer to n = 3, which has been widely reported as the stress exponent commonly observed for creep in polycrystalline ice (Glen, Reference Glen1958), whereas n-values for the region from 1 × 10−5 to 1 × 10−4 s−1 are claimed by some (Barnes and others, Reference Barnes, Tabor and Walker1971; Weertman and others, Reference Weertman1983) to be much higher. At −20°C (Fig. 6b), n-values are again much higher than would be expected for purely plastic flow in polycrystalline ice, which would also suggest that a high-stress ductile-to-brittle regime of deformation is taking place as a result of the lowering of the temperature from −10 to −20°C. Although crack density was not a variable that was quantitatively measured in the post-test specimens, it was qualitatively quite clear at −20°C that there was a great deal more damage and microcracking that had been imparted to the specimens that had been tested at −20°C than for those tested at −10°C. An increase in the brittle behavior of a material with a decrease in its temperature is not particularly surprising, and is likely responsible for the rather high n-values observed at −20°C (n = 10; Table 2). It should be pointed out however, that for similar testing conditions, similar values of n were observed by Barnes and others (Reference Barnes, Tabor and Walker1971) (see their Fig. 2). More to the point of this study, however, is that m-values calculated for both possible deformation regimes show that the Ca++-doped specimens have generally either a higher or at least a non-differentiable strain-rate sensitivity index when compared with the m-values of the undoped ice. These results could be interpreted as either a lowering of the stress exponent and hence a reduction of the strain rate when in the ductile-to-brittle transition region of deformation, a possible strengthening effect, or as a non-differentiable effect when in a deformation regime of pure plastic flow.

Fig. 6. Mean of flow stresses from all tests (at 5% strain) plotted as a function of the applied constant strain rate at temperatures of −10 and −20°C.
Table 2. Strain-rate sensitivity m and stress exponent n given as a function of
![]() $\overline {\sigma _{{\rm fs}}} $
(see Table 1)
$\overline {\sigma _{{\rm fs}}} $
(see Table 1)
3.3. Tension tests
Under a constant load, deformation tests in uniaxial tension were performed to further elucidate the possible effects of Ca++ in polycrystalline ice. A total of four tests were performed with two undoped specimens and two Ca++-doped specimens. The results, shown in Figure 7 as both strain versus time (Fig. 7a) and strain rate versus strain (Fig. 7b), demonstrate very little difference between the creep rates for undoped and doped specimens. These results would also seem to be in agreement with the former observations made in the above section with regards to pure plastic flow and compression testing at 1 × 10−6 s−1.

Fig. 7. Results from four creep tests conducted at −6°C showing little difference between pure ice and ice doped with Ca++ in (a) true strain as a function of time and (b) strain rate as a function of true strain.
3.4. Microstructure
For both the doped and undoped specimens, polarized light imaging was used to quantify the mean grain diameter as a function of strain rate for all constant strain-rate compression tests. Example images are shown in Figure 8. Although discernable by only visual inspection in this figure, the plot in Figure 9 shows that CaSO4-doped compression specimens tested at 1 × 10−6 s−1 had a much larger mean grain diameter at 5% strain than the undoped specimens. The mean grain diameter was calculated using the ASTM E1382 linear intercept length method (ASTM, 2004) in four evenly spaced (10 pixel increments) directions of 0°, 45°, 90° and 135° via an automated image analysis algorithm given by Lehto and others (Reference Lehto, Remes, Saukkonen, Hänninen and Romanoff2014). A minimum of 10 000 intercepts were measured in each direction for each binary image over the entire area of the thin section. The relative grain size dispersion d, as given in Eqn (3) (Lehto and others, Reference Lehto, Romanoff, Remes and Sarikka2016), was then used as a metric to quantify the approximate variance in grain size over the distribution of intercepts measured, where d
max and d
min are respectively the maximum and minimum distances found between two intercepts, d
avg is the mean grain diameter, and
![]() $P_{99\%} $
and
$P_{99\%} $
and
![]() $P_{1\%} $
are the 99 and 1% probability level grain sizes respectively.
$P_{1\%} $
are the 99 and 1% probability level grain sizes respectively.

Fig. 8. Post-test polarized light images of thin sections taken from specimens tested in uniaxial compression at constant strain rates of 1 × 10−4, 1 × 10−5 and 1 × 10−6 s−1. All tests were terminated at 5% strain.

Fig. 9. Comparison of mean grain diameter between compression-tested specimens at 5% strain following constant strain-rate compression tests of 1 × 10−4, 1 × 10−5 and 1 × 10−6 s−1.
To limit the effects of measurement uncertainty due to extrema occurring at the tails of the linear measured intercept (i.e. grain size) distribution, the maximum and minimum grain sizes are replaced with the 99 and 1% probability grain sizes, as calculated with a cumulative distribution function (Lehto and others, Reference Lehto, Remes, Saukkonen, Hänninen and Romanoff2014). The values of d calculated for the six thin section images shown in Figure 8 were nearly identical, with an average value of 4.56 and SD of only 0.09.
Thin sections from creep-tested specimens that had reached approximately 25% strain are shown in Figure 10. In these images, there is very little difference that can be discerned between the microstructures of the two specimens and little difference was found between the mean grain diameter for each specimen. Mean grain diameters for these doped and undoped thin sections were found to be 0.45 and 0.42 mm, respectively, with an average value of d of 4.6 ± 0.05.

Fig. 10. Polarized light images of thin sections taken from specimens tested in uniaxial tension under a constant load of 38 kg (0.75 MPa initial stress). Tests were terminated near 25% strain.
As mentioned above, microcracking was observed in all compression specimens at strain rates of 1 × 10−4 and 1 × 10−5 s−1, but was much more prominent at tests conducted at −20°C. At 1 × 10−6 s−1, microcracks were not observed, perhaps suggesting that deformation was only by pure plastic flow at this applied strain rate. The microcracks were characterized via scanning electron microscopy in backscattered electron mode. It was found that cracks had predominantly occurred along grain boundaries, suggesting intergranular fracture as the primary mode of failure.
3.5. Microchemical analysis
Using EDS in the SEM, creep-tested and compression-tested CaSO4-doped thin sections were analyzed to ascertain the local chemical compositions. C, O, Ca, S, Na and Cl could all be detected via EDS at grain boundaries and triple junctions. Based on the observation of predominantly Ca and S peaks from some precipitates, while Na and Cl peaks were observed from others, it is assumed that these precipitates consisted, respectively, of CaSO4 and NaCl. It is not clear whether or not these precipitates formed as a result of surface sublimation of the specimen while in the SEM or if they were already present (Cullen and Baker, Reference Cullen and Baker2000). In either case, it would seem that the impurities must have been concentrated at grain boundaries and triple junctions regardless of when the precipitation occurred. When sampling the ice crystal lattice away from the grain boundary, only O could be detected. Figure 11 shows a doped thin section from a compression test conducted at −10°C and a strain rate of 1 × 10−4 s−1, when the most significant cracking was observed. In this image, the black voids are cracks residing along grain boundaries and the precipitates sampled via EDS were primarily found to be NaCl. The NaCl was most likely present as an impurity of the original anhydrous CaSO4 that was used to create the doped specimens, which claimed an impurity concentration of 0.01% Cl. Figure 12 shows a doped thin section from a creep test conducted at −6°C, terminated at a final true strain of 25%. The precipitates in this thin section were found to primarily be CaSO4, as shown in the EDS spectra. Again when sampling the region away from the grain boundary, only an O peak could be detected via EDS.

Fig. 11. Image collected from a SEM in backscattered electron mode showing intergranular fracture and precipitation at grain boundaries in a compression-tested specimen taken to 5% strain under a constant strain rate of 1 × 10−4 s−1. Precipitates in this image were predominantly that of NaCl, as shown with the spectra (right) collected with EDS.

Fig. 12. Image collected from a SEM in backscattered electron mode showing precipitation at grain boundaries in a creep-tested specimen taken to 25% true strain under a constant load of 38 kg (0.75 MPa initial stress). Precipitates in this image were predominantly that of CaSO4, as shown with the spectra (right) collected with EDS, while only O could be detected in the inner matrix of the grain.
4. DISCUSSION
If sitting interstitially, it is thought that Ca++ would only act to inhibit the natural motion of dislocations along the basal plane, as Ca++ cannot aid the hydrogen bond reorientation that is requisite for the passage of dislocations in ice (Goodman and others, Reference Goodman, Frost and Ashby1981). Such thinking could also be extended to several other cations and anions present in natural ice, such as Na+, Mg++, NO3 − and SO4 −−, which would also be expected to manifest as interstitial defects. This theory would also support the findings from Fujita and others (Reference Fujita2014) described in the Introduction. If considering dislocation climb along the prismatic plane, the relative size (atomic radii) of Ca++ would suggest that it may be difficult for Ca++ to migrate from one interstitial site to another, which could affect dislocation climb. Such considerations would suggest that the presence of Ca++ in the crystal lattice should have either no effect on mechanical properties at low concentrations or perhaps a strengthening effect at higher concentrations.
If considering grain boundary mechanisms instead, from previous works (Baker and others, Reference Baker, Cullen and Iliescu2003; Durand and others, Reference Durand2006), it is thought that as creep occurs, Ca++ would become concentrated at the grain boundaries and triple junctions. This was also found to be true for the experiments presented here via EDS (see above section). Given that Ca++ and SO4 are concentrated at the grain boundaries, it is reasonable to think that grain boundary migration and potentially also dynamic recrystallization could be affected. This would generally be interpreted as a strengthening mechanism in most other materials (Arzt, Reference Arzt1998), particularly once precipitation has occurred. Prior to precipitation occurring at the grain boundaries, however, whether or not Ca++ may assist or inhibit with grain boundary sliding, dynamic recrystallization, or the generation of new dislocations is much more difficult to predict. It does seem though that the disparity in grain size between doped and undoped compression-tested specimens at 5% strain and strain rates of 1 × 10−6 s−1 would suggest that the presence of Ca++ and SO4 is having some effect on dynamic recrystallization within the polycrystal. If dynamic recrystallization is in fact being inhibited, then this too, could be perceived as a strengthening mechanism.
When compared with previous microstructural observations of natural ice from Vostok, Antarctica (Obbard and Baker, Reference Obbard and Baker2007), the findings of this study are only in partial agreement. Using ion chromatography and EDS, Obbard and Baker (Reference Obbard and Baker2007) also observed high Ca concentrations at grain boundaries, but could not determine if the impurity had originally manifested as CaSO4 or perhaps another naturally occurring ionic compound, such as CaCO3. As a general observation, Obbard and Baker (Reference Obbard and Baker2007) observed that Ca++ concentrations were higher in ice core layers made up of much finer grain sizes that had formed during glacial periods, as opposed to warmer interglacial periods (Lipenkov and others, Reference Lipenkov, Barkov, Duval and Pimienta1989), which were characterized by larger grain sizes and lower concentrations of Ca++. This correlation led Obbard and Baker (Reference Obbard and Baker2007) to conclude that Ca++ may have been acting to inhibit grain growth in these glacial layers. The apparent disparity between field and laboratory observations on this point suggests that perhaps some other soluble impurity may have been acting to inhibit grain growth observed during glacial periods in the Vostok ice core, or that the laboratory experiments presented here are not representative enough of natural conditions to produce the same effect. Alternatively, the observation of larger grains existing in laboratory specimens tested at relatively low constant strain rates may also be explained by a higher grown-in dislocation density in the laboratory-created ice, which may in turn act to increase the strain energy of the individual grains and thereby enhance grain boundary migration as a preferred mechanism of deformation. Because no difference in grain size was observed in tension-tested specimens at 25% strain, however, it remains difficult to assess the dominant mechanisms of deformation behavior as a function of soluble impurity.
Nonetheless, based on the laboratory experiments and results presented here, it would seem that Ca++ either slightly strengthens or has little effect on the mechanical properties of polycrystalline ice. Although this finding could potentially be extended to many other soluble ionic impurities known to exist in ice, such as Na+ and Mg++, additional experiments would need to be performed before making such assumptions.
5. CONCLUSIONS
When compared with undoped polycrystalline ice, it was found that Ca++ doping had either a small strengthening or little effect on the mechanical properties of ice. Our results show that CaSO4 slightly increases the strength of polycrystalline ice at higher strain rates and lower temperatures, but that the strengthening decreases with decreasing strain rate and/or increasing temperatures. Precipitates, which occurred primarily at grain boundaries and triple junctions, were found to include both Ca and S, indicating that higher concentrations of impurity must exist at these locations. From compression tests conducted at 1 × 10−6 s−1, mean grain diameters of the CaSO4-doped specimens were found to be larger than those in the undoped specimens at 5% strain. This effect diminished at higher strain rates and was not observed in the tension-tested specimens when measured at 25% strain.
ACKNOWLEDGEMENTS
This work was supported by National Science Foundation grant number PLR 1141411. The authors acknowledge the use of the Ice Research Laboratory (Director E.M. Schulson) at the Thayer School of Engineering. The authors also acknowledge Charles P. Daghlian for his assistance in the Dartmouth Electron Microscope Facility.
















