1. INTRODUCTION
Knowledge of underwater features and ocean bathymetry plays a significant role in coastal engineering and management, coastal resource exploitation, navigation, research on tide and biodiversity, planning for seawalls and wharves, offshore fisheries and aquaculture. Shallow water depth surveying is essential for the protection of vessels during navigation. Conventionally, depth charts are obtained by sonar measurements carried out from dedicated vessels, which are not only expensive and time consuming but may also be difficult in shallow water areas (Liang, Reference Liang1995; Calkoen et al., Reference Calkoen, Hesselmans, Wensink and Vogelzang2001). Remote sensing techniques may offer an alternative method that can be used to reduce the cost and labour needed for underwater topographic surveying and mapping.
Synthetic Aperture Radar (SAR) is an active remote sensor that is fairly weather-insensitive and has global coverage. It provides two-dimensional (2D) information on the ocean surface. Under favourable conditions, it has the ability to detect sea floor topographic features in shallow water areas (Jackson and Apel, Reference Jackson and Apel2004). The HJ-1C satellite (Huan Jing-1C; Huan Jing means environment in Chinese) was successfully launched on 19 November 2012. It operates from a sun-synchronous orbit at a height of 499·26 km and on a frequency of 3·2 GHz. The inclination of the orbit is 97·367° and the typical incidence angle for HJ-1C ranges between 25° and 47°. There are two different imaging modes, Strip mode and Scan mode, and two different spatial resolutions 5 m (single look) and 20 m (four looks).
Generally, there are two main kinds of shallow water depth detection methods that have been developed based on SAR imaging mechanisms and radar signature related to changes in water depth.
The first is based on variations of the SAR image intensity, which relies on the presence of a current, along with the presence of small-scale waves on the sea surface to provide the radar backscatter (Alpers and Hennings, Reference Alpers and Hennings1984; Stockdon and Holman., Reference Stockdon and Holman2000; Calkoen et al., Reference Calkoen, Hesselmans, Wensink and Vogelzang2001; Yang et al., Reference Yang, Zhang and Meng2010a; Reference Yang, Zhang and Meng2010b; Fan et al., Reference Fan, Huang, He, Fu and Gan2008b; Reference Fan, Huang, Lin, Pan, Fu and Gu2011; Reference Fan, Huang, Fu, Yu and Gu2012). The Bathymetry Assessment System (BAS) is typical of this method, and is based on the theory of imaging processes of underwater bottom topography by SAR as proposed by Alpers and Hennings (Alpers and Hennings, Reference Alpers and Hennings1984; Calkoen et al., Reference Calkoen, Hesselmans, Wensink and Vogelzang2001). Li et al. (Reference Li, Li, Xu and Pichel2009) showed that sand ridges parallel to tidal currents could also be imaged by SAR.
The second method is based on swell patterns in SAR images, which relies on the refraction of long surface gravity waves as they propagate shoreward. It requires the assumption that the same wave train exists throughout the image (Liu et al, Reference Liu, Yoon and Kirby1985; Wacherman et al., Reference Wacherman, Lyzenga, Ericson and Walker1998; Fan et al., Reference Fan, Huang, He, Zhang and Chen2008a; Brusch et al., Reference Brusch, Held, Lehner, Rosenthal and Pleskachevsky2011; Pleskachevsky et al., Reference Pleskachevsky, Lehner, Heege and Mott2011). Fan et al. (Reference Fan, Huang, He, Zhang and Chen2008a) proposed a wave-number spectrum technique to retrieve coastal water depth by means of ERS-2 SAR image of waves. Results show that this technique is suitable for coastal waters, especially for the near-shore regions with variable water depths. Brusch et al. (Reference Brusch, Held, Lehner, Rosenthal and Pleskachevsky2011) used TerraSAR-X data with high resolution and low cut-off wavelength to calculate water depth, and showed the general agreement of SAR-obtained depths and map depths (deviation less than 5 m for 72·2% of compared entries and less than 7 m for 89·2% of entries). Pleskachevsky et al. (Reference Pleskachevsky, Lehner, Heege and Mott2011) explored bathymetry by the synergetic use of multiple remote sensing data resources (radar data from TerraSAR-X and optical data from QuickBird satellite) for coastal areas. The SAR-based method covered the depth domain between 100 m and 10 m. The underwater topography is obtained with accuracy of 15% for depths between 60-20 m using the SAR-based method. Water depths less than 20 m are detected by the optical-based method using sunlight reflection analysis. The depths in the range of 20 m up to 10 m represent the domain where the synergy of data from both sources arises.
The aim of this study is to estimate shallow water depths in a coastal region where water depth is less than 10 m using HJ-1C SAR data in S band, whereas the majority of previous studies used SAR data in C band and X band to detect water depths ranging between 100 m and 10 m (Fan et al., Reference Fan, Huang, He, Zhang and Chen2008a; Brusch et al., Reference Brusch, Held, Lehner, Rosenthal and Pleskachevsky2011; Pleskachevsky et al., Reference Pleskachevsky, Lehner, Heege and Mott2011). When the waves propagate towards the shore, the wavelengths decrease as the water depths become shallow. Shoaling waves are tracked by ray tracing mode, fixed grid mode and integrated mode from the open sea to the shoreline. Wavelength and wave direction can be retrieved by means of Fast Fourier Transformation (FFT) computation. Therefore, shallow water depths can be estimated using the linear dispersion relation of ocean waves (Jackson and Apel, Reference Jackson and Apel2004). The details are presented in Section 5. The swell pattern based method is applied to one case study on the Fujian coastal region, China. The details and results are presented in Section 6. A discussion on the potential influence factors of the water depth detection by SAR imagery is presented at the end of this paper.
2. SAR OCEAN IMAGING
Waves are one of the most obvious surface features from SAR images taken over the ocean. SAR backscatter from the ocean is governed by the ocean surface roughness. With incidence angles between 20° to 60°, Bragg scattering is the dominant backscatter mechanism (Jackson and Apel, Reference Jackson and Apel2004; Brusch et al., Reference Brusch, Held, Lehner, Rosenthal and Pleskachevsky2011). Bragg scattering assumes that the brightness in the SAR image is determined strictly by the amplitude of the small-scale waves called Bragg waves, which are similar to the SAR wavelength. This is expressed by the following relation:
where λ B is the wavelength of the Bragg wave, λ r is the SAR wavelength, and θ i is the local incidence angle.
The combination of Bragg scattering with the two-scale assumption is used to describe the imaging process of long waves by SAR. It is useful for interpreting SAR signatures in a coastal region ( Hasselmann et al., Reference Hasselmann, Raney, Plant, Alpers, Shuchman, Lyzenga and Tucker1985; Romeiser and Alpers, Reference Romeiser and Alpers1997). The short Bragg waves are modified by long waves. It has three modulation mechanisms: title modulation, hydrodynamic modulation and velocity bunching modulation. Title modulation means that the longer waves change the local slope of the shorter wave fields. Hydrodynamic modulation means that the longer waves change the distribution of the shorter wave fields. Velocity bunching modulation means that the motion of the long waves alters the SAR imaging process. When long waves are propagating in a direction perpendicular to the SAR platform, title modulation and hydrodynamic modulation have the strongest effects on the SAR returns (Jackson and Apel, Reference Jackson and Apel2004; Zheng et al., Reference Zheng, Li, Guo, Ge, Zhu and Li2006).
SAR cannot sense ocean surface wave components that are shorter than the azimuth cut-off wavelength. While the orbital motion of longer ocean waves with an azimuth component allows the waves to be imaged through the velocity bunching mechanism, the random motions of the ocean surface caused by the short scale waves introduce random position shifts in the azimuth that in turn degrade the azimuth resolution. This limits the detectable ocean wavelengths (Jackson and Apel, Reference Jackson and Apel2004; Brusch et al., Reference Brusch, Held, Lehner, Rosenthal and Pleskachevsky2011). Even though the SAR image contains swell patterns, it may not be suitable for shallow water depth estimation. The cut-off wavelength Lmin can be estimated by a semi-empirical relationship:
where R is the slant range, V is the platform velocity, and H is the significant wave height. The lower the satellite orbit and the smaller the wave height, the smaller the shoaling waves that can be detected.
3. WAVE SHOALING AND REFRACTION
Shoaling and refraction of waves occur when the waves are in shallow water. If the water depth is less than half of the wavelength, then the wave is considered to be in shallow water. Shoaling occurs as the waves enter shallower water. If a long wave is propagating into shallow water, it will be decelerated, which causes the wavelength to shorten. Wave refraction is when waves start to turn towards the shore so that eventually the wave crests become parallel to the shoreline or the wave breaks regardless of the original direction in deeper water. This occurs due to the interaction between the waves and the shoaling topography.
4. STUDY AREA AND DATA SETS
4.1. Study Area
Xiapu County is located in the centre of China's Golden Coast, with the longest coast line along the western coast of the Taiwan Straits. It is abundant in resources and convenient in transportation. The study area is located in Xiapu, Fujian province, China where water depth is less than 12 m from ENC. Figure 1 displays the collected HJ-1C SAR image over the study area.

Figure 1. Spatial location of the study area of Xiapu, Fujian province, China. The red box corresponds to the sub image of the collected HJ-1C SAR image for shallow water estimation shown in Figure 2.

Figure 2. Depth map from the ENC. The red box shows the depth for the selected sub image from Figure 1.
4.2. SAR Data and Auxiliary Data
One scene of the HJ-1C SAR Strip mode data acquired at 6:02 on 14 December 2012 with single polarization (VV) and pixel size of 5 m was collected for shallow water depth estimation.
Two different datasets are used in this study. For depth information, an ENC (http://map.enclive.cn/) from the Navigation Guarantee Department (NGD) of the Chinese Navy Headquarter (CNH) is used for comparing and analysing the detected results. Figure 2 shows a water depth map from the ENC. For cut-off wavelength, wave and wind field forecasted results (http://www.fjmf.gov.cn) from Fujian Marine Forecasts in 3-hour steps are used (Figure 3).

Figure 3. Fujian Marine Forecasts numerical forecast of wave and wind field at 20:00 on 13 December 2012. The study area is outlined in red.
5. METHODOLOGY
In the near-shore region, surface waves mimic the ocean floor topography, causing changes in the wave's length and direction of wave propagation. Ray tracing mode, fixed grid mode and integrated mode from open sea to shoreline track shoaling waves. Wavelength and wave direction can be retrieved by means of FFT computation. Shallow water depth can be estimated due to the fact that SAR images are able to image long waves in the ocean and their wavelength can be connected to the local depth.
5.1. Wave Tracking Method
The long wave parameters for shallow water depth estimation are calculated by FFT computation. By means of the FFT for the selected sub image, a 2D image spectrum in wave number space is retrieved. The peak in the 2D spectrum marks wavelength and wave direction of all waves visible in the sub image. The wavelength and direction of a long wave can be estimated from the following formula (Collard et al., Reference Collard, Ardhuin and Chapron2005; Brusch et al., Reference Brusch, Held, Lehner, Rosenthal and Pleskachevsky2011):
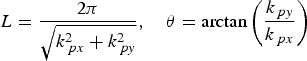 $$L = \displaystyle{{2\pi} \over {\sqrt {k_{\,px}^2 + k_{\,py}^2}}}\comma \quad \theta = {\rm arctan}\left( {\displaystyle{{k_{\,py}} \over {k_{\,px}}}} \right)$$
$$L = \displaystyle{{2\pi} \over {\sqrt {k_{\,px}^2 + k_{\,py}^2}}}\comma \quad \theta = {\rm arctan}\left( {\displaystyle{{k_{\,py}} \over {k_{\,px}}}} \right)$$where L is the peak wavelength, θ is the peak wave direction with respect to the sub image, k px and k py are the peak coordinates in the wave number space. The retrieved directions have an ambiguity of 180° due to the static nature of a SAR image (Brusch et al., Reference Brusch, Held, Lehner, Rosenthal and Pleskachevsky2011). This ambiguity can be solved with information from the cross spectrum or first guess information from other sources. In coastal areas where wave shoaling and refraction appear, the ambiguity problem can be solved by manual inspection.
All wavelengths can be implemented by wave tracking that contains three modes of operation: ray tracing, fixed grid and integrated mode. Ray tracing mode tracks the long wave in the wave direction with the distance related to the wavelength. The distance between the neighbouring wave rays is fixed. In this way, the wave can be tracked from the open sea to the shoreline and the change in wavelength and direction can be measured. Fixed grid mode tracks the long wave not in the wave direction but at a constant specified shift. In this way, the wave can also be tracked from the open sea to the shoreline uniformly and the change in wavelength can be measured. Integrated mode tracks the long wave by the two modes mentioned above.
Starting from the open ocean, the FFT-box (e.g. 512 × 512) is moved in the direction of the wave route by a multiple of the wavelength L (ray tracing mode: n × L) or a constant specified shift (fixed grid mode: dx and dy), then a new FFT is computed in the wave direction and a new FFT is shifted. The same process is repeated for fixed grid mode until the FFT-box reaches both the row edge and column edge of the image. For ray tracing mode, if one wave reaches row edge or column edge of the image another wave is tracked until this next wave is terminated within the image.
5.2. Linear Dispersion Relation
For freely propagating ocean waves, the wave number, wave frequency and water depth are not independent, but are linked by the wave dispersion relation. If the effect of the current can be neglected, the linear dispersion relation is given by:
where d is the water depth, ω is the angular wave frequency (ω = 2π/T with T being the wave period), g is the gravitational acceleration (9·8 m/s2), k is the wave number and is equal to k = 2π/L.
Water depth can be written as:
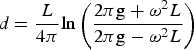 $$d = \displaystyle{L \over {4\pi}} {\rm ln}\left( {\displaystyle{{{\rm 2}\pi {\rm g} + \omega ^2 L} \over {{\rm 2}\pi {\rm g} - \omega ^2 L}}} \right)$$
$$d = \displaystyle{L \over {4\pi}} {\rm ln}\left( {\displaystyle{{{\rm 2}\pi {\rm g} + \omega ^2 L} \over {{\rm 2}\pi {\rm g} - \omega ^2 L}}} \right)$$5.3. Procedure of Shallow Water Depth Estimation
Estimation of shallow water depth from SAR image is divided into three steps:
(1) Estimation of angular wave frequency. The angular wave frequency is calculated from other sources or first guesses of initial water depth or wave period. Firstly, the collected SAR images are analysed. Only those that have obvious wave features over the shallow water will be used to estimate shallow water depth. Then the wavelength and direction of the long waves are calculated and analysed. Sub images over the isobaths are chosen for the initial angular wave frequency estimation, whereas sub images over different depths are chosen for swell patterns analysis. Finally, the angular wave frequency is calculated by the linear dispersion relation (Equation (4)) from the first guesses of the initial water depth or water depths from other resources. It can also be calculated by wave periods from other resources (such as buoys or weather services).
The threshold minimum peak period (T min) for the peak wavelength (L max) is obtained from the deep water relation:
(6)where g is the gravitational acceleration (9·8 m/s2). For water depth estimation, the wave period should be greater than the peak period. If the wave period is smaller than the peak period, the wave belongs to the deep-water domain. $$T_{\min} = \sqrt {2\pi L_{\max} /g} $$
$$T_{\min} = \sqrt {2\pi L_{\max} /g} $$(2) Obtaining a wave field map using wave tracking method. Starting from the open ocean, wavelength and wave direction can be retrieved by ray tracing mode, fixed grid mode or the integrated mode using FFT. In this paper, the integrated mode is used.
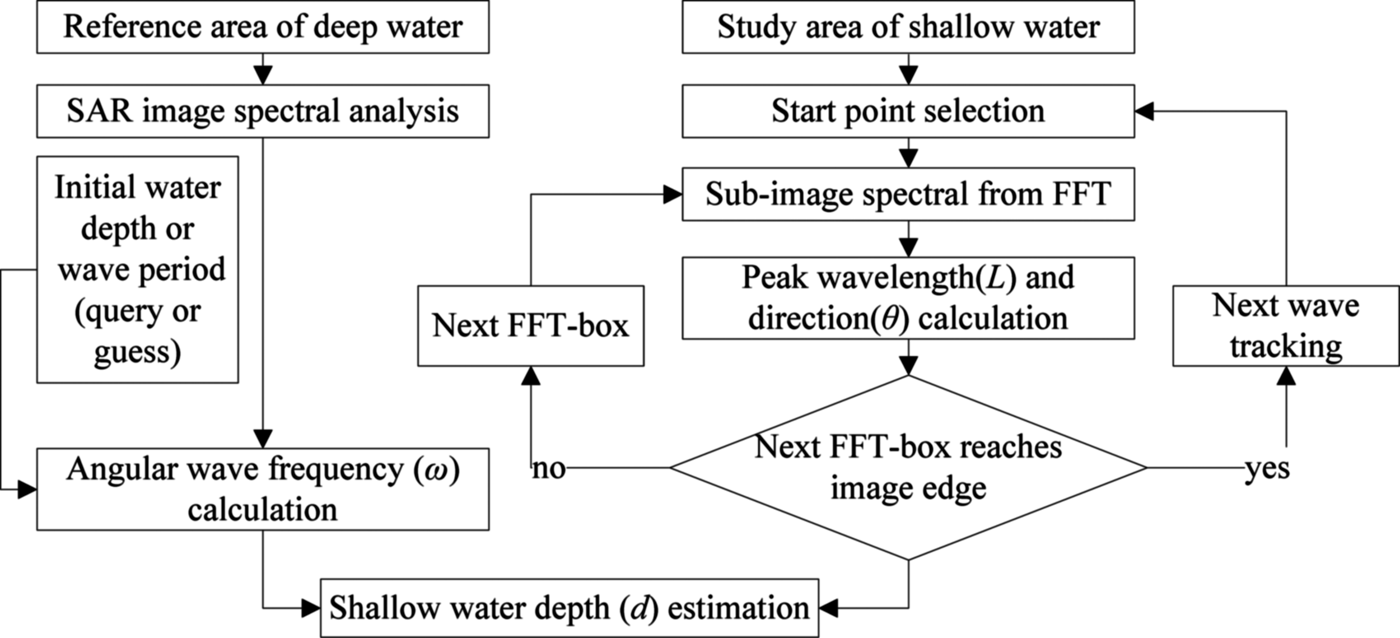
(3) Shallow water depth estimation. To estimate the shallow water depth from a SAR image, the linear dispersion relation for ocean gravity waves is used. In the end, all estimated shallow water depths are analysed and abnormal data (e.g. water depth over the land, water depth from the FFT-box image that has invisible swell patterns) will be removed. The flow chart of shallow water depth estimation from a SAR image is shown in Figure 4.

Figure 4. Flow chart of shallow water depth estimation from a SAR image.
6. APPLICATION IN A NEAR-SHORE AREA
In this section, the estimated results from the HJ-1C SAR image over the near-shore area of the Fujian province is presented. Before shallow water depth estimation, a Frost filter with 3 × 3 filter windows was used to remove the speckle noise from the SAR image. According to the procedure of detection, there are eight different subset areas (256 × 256 pixels, a to h) that are used for image spectrum analysis as shown in Figure 5.

Figure 5. HJ-1C (S-band, VV) SAR image (strip mode) of Xiapu, acquired at 6:02 on 14 December 2012. The sub image (2304 × 2048 pixels, pixel size is 5 m) covers 11520 m × 10240 m. Yellow square boxes (a to h) show locations of the sub image (256 × 256 pixels) for image spectrum analysis (middle). The corresponding wavelength and direction are on the right. Four regions (a-d) in relative deep water are used for wave frequency estimation and analysis and the others in different water depth are used for wave features analysis.
By computing the FFT, wavelength and propagation direction of these areas are estimated from the 2D spectrum (wavelength between 21·3 m and 128 m are kept and wind streaks are removed). Figure 5 shows the mean wavelength of regions labelled a to h where water depth is about 10·8 m (from Figure 2) and wavelength is about 75 m. The minimum peak period for the longest tracked wavelength (84·04 m in Figure 6) is 7·34 s, angular wave frequency computed by the dispersion relation is about 0·768 rad/s and the wave period is about 8·18 s, which is greater than minimum peak period (7·34 s). The ratio of water depth to wavelength is less than 0·15, which indicates that these areas are shallow water. The island and coastal line is to the left of the study area where the topography is relatively flat. Wavelength from locations h to e is decreasing (73·3 m to 56·74 m) and the corresponding water depth is becoming shallower. The waves are considered to be propagating towards the costal line.

Figure 6. Wave field maps prepared by wave tracking. (a) Wave field map prepared by ray tracing mode. (b) Wave field map prepared by fixed grid mode.
Both the ray tracing mode and fixed grid mode are used to map the wave fields of the study area according to the surface swell patterns. Every arrow indicates an FFT-box. Its length is twice that of the wavelength and direction indicates the propagating direction of the wave. Waves over or near the island are removed from the map. In ray tracing mode, the displacement from one FFT-box to the next in the same wave ray is set to twice that of wavelength and the distance of the next wave ray is set to 160 m (32 pixels). In fixed grid mode, the distance between the tracked FFT-boxes is set to 160 m. Wave shoaling and refraction features (the change in both wavelength and direction) are clearly visible in Figure 6 (a).
In Figure 6, wave-propagating direction is nearly perpendicular to the movement direction of the SAR platform. It means the bunching modulation has less of an effect on SAR imaging, therefore the SAR imaging mechanism can be simplified as linear (Jackson and Apel, Reference Jackson and Apel2004). Shallow water depths are estimated from the retrieved wavelengths by the linear dispersion relation (Equation (5)) based on the assumption of the presence of a single wave system in the SAR image. Figure 7(a) shows the results of SAR-based shallow water estimation (wave period is set to 8·2 s), which contains results from both ray tracing and fixed grid modes. Comparing Figure 2 to Figure 7(a), the estimated results agree well with the water depth map from the ENC, while the estimated results have a higher spatial resolution and more detailed underwater topography.

Figure 7. The estimated results from HJ-1C SAR image. (a) Water depth map by integrated mode. (b) Ratio map of estimated and map depth.
In order to validate the detected results, there are 175 pairs of the depths estimated from the SAR image (76 pairs from fixed grid mode and 99 pairs from ray tracing mode) and the nearest neighbour distance of the map depth selects depths from the ENC over the wave-tracked area from Figure 6. When the wave period is set to 8·2 s, the average absolute error is about 0·86 m and the average relative error is about 11·05%. Figure 7(b) shows the ratio of the estimated depth to the map depth in order to identify any deviations of the estimated depth with respect to the map depth. The light green points (55·43% of all points with relative errors of less than 10%) indicate that the datasets are in agreement, and the other points (84·4% of all points with relative errors of less than 20%) show that the relative errors of the overestimated or underestimated results are greater than 10%. The red points on the left suggest that water depths less than 5 m are overestimated, most likely due to the waves becoming nonlinear. Figure 8 shows the estimated three-dimensional (3D) underwater topography, where water depths equal −15 m indicates no data.

Figure 8. Three-dimensional of underwater topography. A depth of -15 m indicates no data in the area.
Figure 3 shows wave and wind field numerical forecast results from Fujian Marine Forecasts, respectively. The significant wave height H was less than 0·5 m and a wind speed 10 m over the water surface was less than 5·5 m/s. HJ-1C operates from a sun-synchronous orbit at a height of 499·26 km above the surface, and its platform velocity is 7·617 km/s. When the incidence angle is set to 30° and the significant wave height H is set to 0·3 m, the cut-off wavelength L min can be estimated as 41·45 m, which is less than the minimum of the detectable wavelengths (47·7 m), indicating that the estimated results are plausible.
7. DISCUSSION
The accuracy of the swell pattern-based method is mainly affected by initial input parameters (wave period or water depth) and wave tracking mode (wave direction and wavelength). Although the acquisition of the wave periods is easier than the acquisition of water depths, water depth data have higher spatial resolution (especially in shallow water) that is more suitable for water depth detection. Nautical charts, including ENCs, are a major source of water depth data. Earthquakes, volcanic activity, storms, estuary deposits and transports, coral reefs and human activities can readily modify underwater topography, therefore these charts can easily be incorrect. Furthermore, grid-based maps are made by mathematical interpolation between transects. There are potential errors in shallow water depth detection. The statistical analysis of input parameters and wave tracking mode will be given in the following part.
7.1. Input Parameters Analysis
In order to evaluate different input parameters for water depth estimated by the linear dispersion relation in order to observe how they affect the results in relative shallow water, the wavelengths derived from the SAR image, water depth and wave period are varied for this analysis.
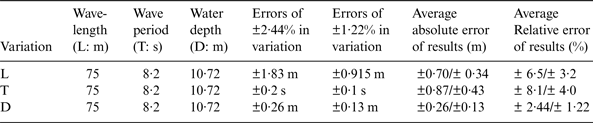
If the wave period is considered accurate, the estimated results are affected only by the wavelengths derived from the SAR image. When wave period is set to 8·2 s, errors of ±2·44 % and ±1·22 % in wavelengths (75 m) are assumed to estimate the initial wave period (Table 1, row 1). These variations lead to absolute errors of ±0·16 s and ±0·08 s in the wave period, respectively. Then, with a given wavelength (75 m), the absolute and relative errors of estimated water depth from different estimated initial wave periods are about ±0·7 m and±0·34 m,±6·5% and±3·2%, respectively.
Table 1. Errors of estimated water depth by different input parameters.

Likewise, if the derived wavelengths from SAR are not changed, the initial wave period or water depth affects the estimated results. When wavelength is set to 75 m, variations of ±2·44% and ±1·22% in a wave period (8·2 s) are assumed (Table 1, row 2) to estimate water depth. The absolute and relative errors of the estimated water depth from different wave periods are about ±0·87 m and ±0·43 m, ±8·1% and ±4%, respectively. For different initial water depths in a given wavelength (75 m) (Table 1, row 3), the absolute and relative errors of estimated water depths from different wave periods are about ±0·26 m and±0·13 m, ±2·44% and ±1·22%, respectively.
Thus, it can be concluded that initial input wave periods are more sensitive than initial water depths in order to estimate water depths in relatively shallow water. The sensitivity of the wavelength effect is between that of the water depth and wave period.
7.2. Wave Tracking Mode Analysis
The accuracy of the method to estimate water depth from swell patterns is evaluated. Average absolute errors and average relative errors of different wave tracking modes are presented in Table 2. They show that most average absolute errors and average relative errors of ray tracing mode are greater than fixed grid mode, but they are the same order of magnitude as reported by Pleskachevsky and Lehner's method (Brusch et al., Reference Brusch, Held, Lehner, Rosenthal and Pleskachevsky2011; Pleskachevsky et al., Reference Pleskachevsky, Lehner, Heege and Mott2011). For ray tracing mode as shown in Figure 6(a), it provides a clearly visible image of wave shoaling and refraction features in the SAR image and keeps the tracked wave ray within the same wave system. The fixed grid mode is simple and provides a uniform distribution of the region whereas the former method may not completely cover the area. Therefore, they are not independent but complementary in shallow water depth estimates.
Table 2. Errors of estimated water depth by different wave tracking modes.

The integrated mode keeps the tracked wave ray within the same wave system and provides more underwater topography. The errors (as shown in Table 2) of the integrated mode-based method are less than ray tracing and fixed grid mode when considered separately. Figure 9 shows the scatter plots for the estimated results and water depth from the map by different wave tracking modes. The R squared (R2) value of the integrated mode is greater than the ray tracing and fixed grid modes separately. In the study case, water depth estimated by integrated mode is better than ray tracing and fixed grid mode.

Figure 9. Scatter plot for the estimated results and water depths from the prepared maps.
8. CONCLUSIONS
In this paper, a practical method for shallow water depth estimation is presented based on swell patterns in SAR images with fewer initial input parameters. One scene of HJ-1C SAR image over the Fujian coastal region is chosen for investigation. The estimated water depths from the SAR image are compared with ENC, and the average absolute error is within 0·9 m with the average relative error less than 11·5%. This indicates that HJ-1C SAR is capable of detecting wave shoaling and refraction even in depths shallower than 10 m because of its low orbit and high resolution, and the method can be used for water depth with a resolution of 10 m to 5 m detection with good accuracy within the test area.
However, the swell pattern-based method is generally dependent on sea conditions (swell availability) and SAR acquisition quality (swell patterns). Although the introduced method may be not precisely accurate, it can provide general information about changes in the depth, especially in coastal areas where underwater topography could not be easily detected by other methods. In the future, this method will be applied to other test areas while testing different bands and polarization of SAR images in the same test areas in order to develop the method further. The improved method may be used for further underwater topographic mapping with higher temporal resolution and spatial resolution.
ACKNOWLEDGEMENTS
The authors would like to thank the Satellite Environment Center, Ministry of Environmental Protection of China for providing the HJ-1C SAR data. This study is jointly supported by the National Science Foundation of China under grant numbers 41301500, 41431174 and 61471358, and the opening foundation of Institute of Remote Sensing and Earth Sciences, Hangzhou Normal University, grant No. PDKF2012YG04. The authors would also like to thank the anonymous reviewers' comments to improve the manuscript.