No CrossRef data available.
Article contents
Dimension in team semantics
Published online by Cambridge University Press: 12 March 2024
Abstract
We introduce three measures of complexity for families of sets. Each of the three measures, which we call dimensions, is defined in terms of the minimal number of convex subfamilies that are needed for covering the given family. For upper dimension, the subfamilies are required to contain a unique maximal set, for dual upper dimension a unique minimal set, and for cylindrical dimension both a unique maximal and a unique minimal set. In addition to considering dimensions of particular families of sets, we study the behavior of dimensions under operators that map families of sets to new families of sets. We identify natural sufficient criteria for such operators to preserve the growth class of the dimensions. We apply the theory of our dimensions for proving new hierarchy results for logics with team semantics. To this end we associate each atom with a natural notion or arity. First, we show that the standard logical operators preserve the growth classes of the families arising from the semantics of formulas in such logics. Second, we show that the upper dimension of 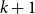 $k+1$-ary dependence, inclusion, independence, anonymity, and exclusion atoms is in a strictly higher growth class than that of any k-ary atoms, whence the
$k+1$-ary dependence, inclusion, independence, anonymity, and exclusion atoms is in a strictly higher growth class than that of any k-ary atoms, whence the 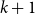 $k+1$-ary atoms are not definable in terms of any atoms of smaller arity.
$k+1$-ary atoms are not definable in terms of any atoms of smaller arity.
- Type
- Special Issue: Logic and Complexity
- Information
- Mathematical Structures in Computer Science , Volume 34 , Special Issue 5: Logic and Complexity , May 2024 , pp. 410 - 454
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
Footnotes
Supported by the Academy of Finland (grant No 322795) and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant No 101020762).



