Introduction
A modern approach to fracture toughness is to relate the resistance to fracture in materials to the stress-strain condition at a defect such as the tip of a crack when it begins to grow. The most serious problem of crack propagation is associated with the brittle behaviour of normally ductile materials, e.g. as has occurred in pressure vessels, ships, and pipe-lines. The stress field at the tip of a crack can be described with the aid of a parameter K called the stress intensity factor, i.e.
where r and θ are polar coordinates with the origin at the tip.
It can be shown that, in general,
for linear elastic materials. Here σ is the applied stress, a is the crack length, and γ is a geometric factor.
As stress increases, or as the crack grows, the value of K increases until a critical value K c is attained at which fracture occurs. The most unsafe situation occurs when a crack is in a constrained field that permits only minimal plastic deformation at the crack tip. This occurs under plane-strain conditions. The plane-strain fracture toughness of the material is a material property and is denoted by the symbol K IC . It is a function of environment, temperature, and loading rate. The suffix I refers to the tensile opening mode of crack extension whilst II and III symbolize shear and anti-plane-strain modes. An alternative approach in linear elastic fracture mechanics is to consider the energy release rate G. G can also be considered as the rate of strain-energy flux flowing toward a crack tip as the crack extends. Under plane-strain conditions
Griffith (1921) derived a relation for brittle fracture from the Inglis ( 1913) elastic solution for a cracked plate by equating G with the rate of increase in specific surface energy γ, and showed that the critical stress required to propagate the crack was given by
although Equation (2) and (3) would give

An extensive review of the elastic mechanics approach to fracture analysis is provided in a special issue of the Journal of Strain Analysis (1975), whilst recent extensions to fracture mechanics to account for energy losses due to crack-tip plasticity are given in a paper by Reference Kfouri and MillerKfouri and Miller (1976).
In the work of Kfouri and Miller, the fracture-toughness variation with temperature was related to changes in yield-stress variation and so it is worth noting that the tensile, compressive, and shear fracture strengths of fresh-water ice decrease rapidly as the test temperature increases towards the melting point (Reference PineginPinegin, 1923; Reference Vitman and ShandrikovVitman and Shandrikov, 1938; Reference ButkovichButkovich, 1954; Reference Kozitskiy and BybinKozitskiy and Bybin, 1967). On the other hand, it appears that the compressive strength of lake ice decreases as the stress and strain-rate increase (Reference KorzhavinKorzhavin, 1962; Reference Korzhavin and PtukhinKorzhavin and Ptukhin, 1966) although recent work indicates that more study is required (Reference GoldGold, 1977). For example, as the rate of stress application increases, the tensile strength at first increases but then passes through a maximum to attain a constant value (Reference JellinekJellinek, 1958).
Ice may be regarded as a brittle material and amenable to fracture analysis, even so, little work has been reported on K c measurements. Reference SmithSmith (1975), in an analysis to determine the depths of crevasses, assumed K c to be zero. Reference GoldGold (1963) studied crack formation caused by thermal shock in polycrystalline ice. The cracks were formed on the surface and propagated into the material. From the calculated thermal stress and crack size he estimated the values of the stress intensity factor for crack arrest. In the present study, the fracture toughness of fresh-water ice was measured at various temperatures between –1 and –46°C and at six loading rates. Finally, values of fracture toughness in the presence of water and the stress intensity factors at crack arrest were also measured.
Experimental procedure
Compact tension specimens of the geometry shown in Figure 1 were used for the fracture toughness tests. The initial slot was cut with a bandsaw and then a V-notch was formed with a very sharp blade at the bottom of the slot, to provide a notch-root radius of less than 0.002 5 mm. In order to maintain the notch tip geometry, the notch was coated with silicone grease to prevent sublimation. Some of the specimens were pre-cracked before the fracture toughness test. No significant difference could be detected between the measured fracture toughnesses of the notched and pre-cracked specimens. The 25.4 mm thickness of the specimens is considered sufficient to make valid KIc measurements of ice (Reference Brown and SrawleyBrown and Srawley, [c1966]).

Fig. 1. The compact tension specimen.
The specimens were prepared from fresh-water ice slabs, approximately 8 cm thick. These slabs were made from distilled water in an aluminium tank. To start the freezing, a layer, 4 mm thick, of seeded, small-grain ice was formed using a fine water spray directed to the bottom of the tank, pre-cooled water was then added. The four sides of the tank were insulated, and the air temperature above the water was kept at approximately 5°C. The tank was stored in a chamber at temperatures between —8 and —10°C. The ice froze from the bottom upwards, thereby forcing a large number of air bubbles to form at the ice-water interface. These bubbles were liberated by mechanical vibration. This technique produces ice with low bubble density and facilitates the production of specimens which have no bubbles in the region of the notch root.
The ice slabs are polycrystalline. The crystals are columnar with the long dimension of the crystals perpendicular to the c-axes, which are themselves in the plane of the tank (see also Reference Perey and PounderPerey and Pounder, 1958, and Reference Hobbs, Ketcham, Riehl, Riehl, Bullemer and EngelhardtHobbs and Ketcham, 1969). Specimens were made from 13 slabs in order to test the effects of temperature and loading rate on KIc.
Six loading rates were applied to specimens. The four fastest rates were controlled by the crosshead speeds of the test machine and were 58 cm/min, 5 cm/min, 1 cm/min, and 0.1 cm/min, The two slowest rates (0.06 cm/min and 0.005 cm/min) were load controlled.
Specimens were made from additional ice slabs in order to measure environmental effects, such as the addition of a mixture of water and antifreeze, on fracture toughness. Further details of the apparatus, specimens, and their manufacture will appear elsewhere.
Crack-arrest tests were also conducted to measure the values of the stress intensity factor at crack arrest K Ia . The experimental geometry is shown in Figure 2. The dimensions of the specimens are approximately 25 cm long, 12 cm wide and 2.5 cm thick with initial slot lengths from 6.2 cm to 7.8 cm. The V-notch at the end of the slot was formed by freezing a razor blade into the notch. The loading was applied with a 30° wedge, as shown in Figure 2, using a crosshead speed of 0.1 cm/min. A typical load-time recording is shown in Figure 3. As the load reached a critical level P I the crack started to grow. As the crack propagated, the load dropped, and the stress intensity factor decreased. When the stress intensity factor became low enough, the crack became arrested. The initial crack length and P 1 were used to calculate K Ic . The final load level P 2 and the final crack length were used to calculate K Ia. Values of K Ia were derived at three temperatures, viz. —12, —8, and —4°C. At test temperatures lower than —12°C, once cracking was initiated the specimens fractured completely without arrest.
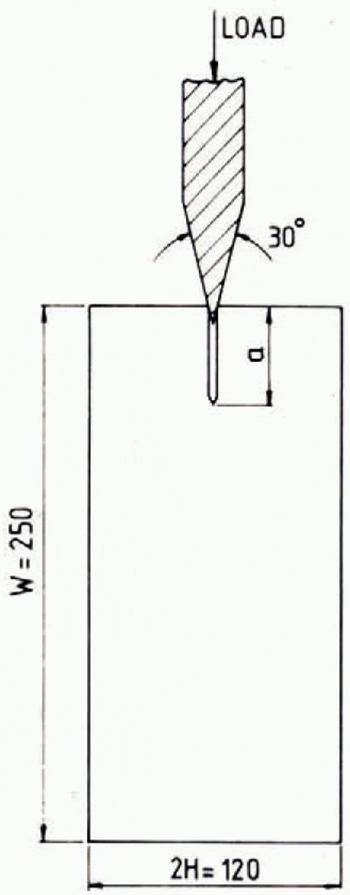
Fig. 2. The specimen and loading arrangement for measuring the fracture toughness at crack arrest.

Fig. 3. A typical load record for a crack arrest test.
Results
The values of K Ic , K (the time derivative of K), and test temperatures are shown in Table I. The ice slab from which each specimen was taken is also indicated. The average values of K Ic at each combination of test temperature and loading rate are plotted in Figure 4 as a function of temperature. The equivalent crosshead speeds of the two lowest rates are estimated from the average values of K of each of those two groups of specimens assuming that the compliances of these specimens are the same as those tested at loading rates of 10 mm/min and 1 mm/min.


Fig. 4. The effect of temperature and loading rate on the fracture toughness of fresh–water ice.
Values of fracture toughness were computed according to the equation
where P is the fracture load and a, B, and W are defined in Figure 1.
The equivalent factor Z for the specimen shown in Figure 1 is given by
For tests involving specimens of the type shown in Figure 2, the value of K Ic and K Ia were calculated from the equation derived by Kanninen (1973) namely,

where c= W—a, λ = 1.565H, and F is the force in the tensile opening mode perpendicular to the crack plane and is equal to 0.5P/tan 15° assuming frictionless contact. The values of K were computed from a knowledge of the loading rate.
Discussion
The data show considerable scatter. This is probably caused by variations in ice crystal properties between samples, particularly the variation of the grain size and the orientation of the small number of crystals near the crack tip (the grain size of the specimens was about 5 mm). Machine misalignment, the variation of K within each group of specimens at the same crosshead speed, the slight variations of temperature from one test to another, and notch shape may also contribute to the scatter. The variation of K at a given loading rate is primarily caused by the variation of crack lengths from one specimen to another. In view of the large scatter of the data, samples for a given test condition were often made from several ice slabs in an attempt to reduce these systematic errors.
The data clearly shows high fracture toughness at low testing temperatures and at slow loading rates. As a cracked specimen is loaded, the stresses in the vicinity of a crack tip are increased. When the local stress exceeds the cohesive strength of the ice crystals, fracture occurs. The fracture tests were carried out at temperatures very close to the melting point. At these relatively high temperatures, creep takes place and the crack tip stresses are relaxed. Furthermore, increased creep deformation and stress relaxation can take place at the slower loading rates. In other words, when the same applied K is reached by specimens loaded at various K, the crack tip stress of the specimen at the lower K is less because of stress relaxation. Therefore, the applied K (at a lower K) has to reach a higher level in order to reach the same level of fracture stress at the crack tip. As a consequence, the fracture toughness is higher at lower values of K. In terms of energy, one may say that stress relaxation reduces the available potential energy for crack extension.
It is well known that the fracture toughness of a truly brittle solid is directly related to its surface energy, see Equation (4). Reference FletcherFletcher (1970) has shown that a transition from a crystalline to a quasi-liquid surface exists at some temperature between —2 and —10°C. This thin liquid film, a few tens of ångstroms thick, will lower the total free energy of the ice surface. The smaller K Ic values at temperatures above — 10°C could be caused by this anomalous surface phenomenon.
The solid–vapour interface energy of ice is 10–5 J/mm2, whereas the solid-liquid interface energy is 2.2 X 10–6 J/mm2 (Reference FletcherFletcher, 1970). Therefore it is probable that ice fracture toughness will be reduced by the presence of water. Two separate batches A and B of ice specimens were prepared. The fracture toughnesses of both batches were measured both in air and in a mixture of water and antifreeze. The results are as shown in Table II. The fracture toughnesses ofice in water are almost half of the corresponding values in air. These results provide evidence that fracture toughness of ice is directly related to its surface energy.
Table II. Effect of water on fracture toughness of ice

The fracture toughnesses of Batch a ice are higher than those listed in Table I, whilst those of Batch b are lower. The real cause of this difference remains to be investigated. However, it was noticed that the freezing rate of Batch a ice was slower, while Batch b ice froze faster and contained considerably more air bubbles. However, in view of the fact that the differences between the fracture toughnesses, in air and in water, are almost the same as the range of scatter in data at a given test condition, additional effort is needed to substantiate these observations.
The values of K Ic , K Ia , and test temperatures are given in Table III. The values of K Ia vary from 125 to
Table III. Fracture toughness of ice at crack arrest

The wedge moved into the slot at a rate of 0.1 cm/min and so the relative opening displacement at the open end of the slot is approximately 0.05 cm/min. The cracks in these specimens are longer than those listed in Table I. Now, at a given rate of relative opening displacement, at the open end of the slot, a lower value of K results for the longer crack. Therefore, a longer crack is equivalent to a slower crosshead movement. It is estimated that the equivalent crosshead speed is 0.03 cm/min. The K Ic values of these specimens therefore agree quite well with the data in Figure 4.
Conclusions
The fracture toughness of fresh-water ice is increased by a decrease in test temperature and by a decrease in loading rate. Water reduces the fracture toughness of ice. The fracture toughness for crack arrest in ice is slightly lower than its static fracture toughness.
Acknowledgements
This work was conducted partly at the Cold Regions Research and Engineering Laboratory, U.S. Army, Hanover, New Hampshire, U.S.A. and partly at the Scott Polar Research Institute, University of Cambridge, Cambridge, U.K. The authors sincerely wish to acknowledge the assistance of the members of these two laboratories, particularly M. A. Wuori and Drs A. Assur and D. Drewry. One of the authors (H.W.L.) wishes to thank the members of the University Engineering Department of the University of Cambridge and the Science Research Council for their assistance. The authors wish to thank L. W. Loop of IBM Corporation (formerly of CRREL) and J. G. Larby, M. S. McGeown, C. M. Nickols, and M. R. H. Sheppard of the University of Cambridge for conducting some of the tests. Part of the work was performed as a final-year undergraduate research project at the University of Cambridge.








