Published online by Cambridge University Press: 31 October 2024
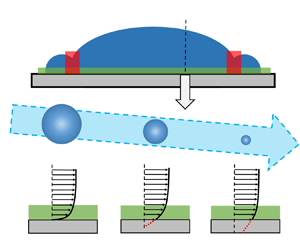
Recent studies of viscous dissipation mechanisms in impacting droplets have revealed distinct behaviours between the macroscale and nanoscale. However, the transition of these mechanisms from the macroscale to the nanoscale remains unexplored due to limited research at the microscale. This work addresses the gap using the many-body dissipative particle dynamics (MDPD) method. While the MDPD method omits specific atomic details, it retains crucial mesoscopic effects, making it suitable for investigating the impact dynamics at the microscale. Through the analysis of velocity contours within impacting droplets, the research identifies three primary contributors to viscous dissipation during spreading: boundary-layer viscous dissipation from shear flow; rim geometric head loss; and bulk viscous dissipation caused by droplet deformation. This prompts a re-evaluation of viscous dissipation mechanisms at both the macroscale and nanoscale. It reveals that the same three kinds of dissipation are present across all scales, differing only in their relative intensities at each scale. A model of the maximum spreading factor (βmax) incorporating all forms of viscous dissipation without adjustable parameters is developed to substantiate this insight. This model is validated against three distinct datasets representing the macroscale, microscale and nanoscale, encompassing a broad spectrum of Weber numbers, Ohnesorge numbers and contact angles. The satisfactory agreement between the model predictions and the data signifies a breakthrough in establishing a universal βmax model applicable across all scales. This model demonstrates the consistent nature of viscous dissipation mechanisms across different scales and underscores the importance of integrating microscale behaviours to understand macroscale and nanoscale phenomena.