1. INTRODUCTION
The BeiDou Satellite Navigation System (BDS) is developed, owned and operated by China. It has started providing its regional navigation and positioning service, which means that BDS has now become an important member of the Global Navigation Satellite System (GNSS) family (Wang, Reference Wang2010). Like other GNSS, the signal transmission of BeiDou is affected by the changes in the refractive index in the ionosphere, due to the movement of free electrons in the propagation medium. These refractive index changes affect the velocity of the waves, causing the well-known effects of first-order ionospheric phase advance and group delay (Hofmann et al., Reference Hofmann, Lichtenegger and Wasle2008). The contribution of ionospheric delay to the pseudo-range errors is significant due to not only its potential magnitude, but also its large variability (Mazzella et al., Reference Mazzella, Holland and Rao1996). Therefore it is one of the major error sources of satellite based navigation and positioning. Based on dispersive property of the ionospheric delay, about 99% of ionospheric error can be removed successfully by forming the “ionosphere free” linear combination (LC) (Xie and Han, Reference Xie and Han2000). On the other hand, the dispersive property also provides an opportunity to measure the ionospheric total electron content (TEC) directly (Klobuchar, Reference Klobuchar1985).
Scholars have carried out a wide range of studies on the characteristics of the ionosphere by using GPS observation data. Since the 1990s, GPS-based monitoring has become an ideal method to monitor the spatial variation of ionospheric TEC, and it can be widely used in detecting and studying the irregular ionospheric structure (Pi et al., Reference Pi, Mannucci, Lindwister and Ho1997), the influence of geomagnetic storms on the ionosphere (Ho et al., Reference Ho, Mannucci, Lindwister, Pi and Tsurutani1996; Reference Ho, Mannucci, Lindwister, Pi and Tsurutani1997), the ionospheric scintillation characteristics (Wang et al., Reference Wang, Wu, Zhang and Meng2004), etc. This article focuses on BeiDou-based ionosphere monitoring performance. In this paper, combined pseudo-range and carrier phase observations are utilized to estimate TEC, and the hardware delay deviation is also calculated. Using the observational data from five BeiDou CORSs situated at different latitudes in China, the TEC monitoring results based on both BeiDou and GPS were obtained at a single station. These results were compared with the Global Ionosphere Maps (GIM) which are generated on a daily basis at CODE (Center for Orbit Determination in Europe) using data from about 200 GPS/GLONASS sites of the IGS (International GNSS Service) and other institutions (Schaer, Reference Schaer1997). Finally, the performance using BDS measurements in the ionosphere monitoring is analysed.
2. FROM OBSERVATIONAL DATA TO TOTAL ELECTRON CONTENT
The total electron content (TEC) is the number of electrons in a column square extending from the observing station to the satellite. Generally, dual-frequency pseudo-range or carrier phase observation data can be used to estimate ionospheric TEC. Due to the fact that pseudo-range observations do not contain ambiguity parameters, this method is easy to implement. However, calculation of TEC from only pseudo-range measurements will produce a noisy result, so it is desirable to use the relative phase delay between the two carrier frequencies to obtain a more precise result. In the carrier phase measurements, the actual number of cycles of phase is not known; therefore the absolute TEC cannot be estimated (Zhao, Reference Zhao2003; Dautermann et al., Reference Dautermann, Calais, Haase and Garrison2007; Norsuzila et al., Reference Norsuzila, Mahamod and Mardina2007). Based on the above considerations, in this paper the single station TEC is estimated by using the combination of pseudo-range and carrier phase observations. The dual frequency pseudo-range observation equations can be expressed as follows (Klobuchar, Reference Klobuchar1985):
$$\matrix{ {P_1 = \rho _0 + c(t^S - t_R ) + I_1 + V_{trop}} \cr {P_2 = \rho _0 + c(t^S - t_R ) + I_2 + V_{trop}} \cr} $$where ρ 0 is the geometric range between the satellite and the receiver; tS, t R are the satellite and receiver clock offsets respectively; I 1, I 2 are the ionospheric corrections of the dual frequencies; and V trop is the tropospheric delay. A linear combination can be obtained from Equation (1) as
$$P_2 - P_1 = I_2 - I_1 = A*\displaystyle{{\,f_1^2 - f_2^2} \over {\,f_1^2 \; f_2^2}} *STEC$$Here Slant TEC (STEC) is a measure of the total electron content of the ionosphere, and can be written as (Dautermann et al., Reference Dautermann, Calais, Haase and Garrison2007)
$$STEC = P_G *\displaystyle{{\,f_1^2 \; f_2} \over {\,f_1^2 - f_2^2}} *\displaystyle{c \over A}$$Where 
$A = \displaystyle{{e^2} \over {8\pi ^2 \varepsilon _0 m_e}} \approx 40.3$ and 
$P_G = \displaystyle{{P_2 - P_1} \over {\lambda _2}} $. Values of physical constants are listed in the Table 1.
Table 1. Values of physical constants.
The phase observables can be modelled (in cycles) as follows:
$$\matrix{ {\phi _1 = \displaystyle{{\rho _0} \over {\lambda _1}} + f_1 (t^s - t_R ) - \displaystyle{{I_1} \over {\lambda _1}} + \displaystyle{{V_{trop}} \over {\lambda _1}} - N_1} \cr {\phi _2 = \displaystyle{{\rho _0} \over {\lambda _2}} + f_2 (t^s - t_R ) - \displaystyle{{I_2} \over {\lambda _2}} + \displaystyle{{V_{trop}} \over {\lambda _2}} - N_2} \cr} $$ A linear combination of the carrier phase measurements can be formed as, with 
$N = N_2 - \displaystyle{{\,f_2} \over {\,f_1}} N_1 $.
$$L_{GU} = \phi _2 - \displaystyle{{\,f_2} \over {\,f_1}} \phi _1 + N$$In the computation of absolute TEC, a non-negligible error source is introduced by the different travel times of the signal on the two separate frequencies through the analogue hardware of satellite and receiver, respectively, which produce a constant TEC bias. These differential biases must be estimated and removed from the measurements before an accurate estimation of the total electron content can be obtained (Coco et al., Reference Coco, Coker, Dahlke and Clynch1991). In order to improve the accuracy of TEC estimation, this paper takes the satellite hardware delay deviation timing group delay (TGD) and the receiver hardware delay deviation of inter-frequency bias (IFB) into consideration. Then the expression of LGU can be obtained from Equation (4)
$$\eqalign{L_{GU} &= L_G + N = \phi _2 - \displaystyle{{\,f_2} \over {\,f_1}} \phi _1 + N \cr &= f_2 t_{TGD} - f_2 t_{IFB} + \displaystyle{A \over c}*\displaystyle{{\,f_2^2 - f_1^2} \over {\,f_1^2 \; f_2^2}} *STEC} $$ The ambiguity constant N for each satellite pass can be calculated using the average difference between L G and P G over all available epochs as, 
$N = \displaystyle{1 \over m}\sum\limits_{i = 1}^m {(P_G - L_G )} $, where m is the number of epochs. Then Equation (6) can be altered to Equation (7) as follows:
$$\displaystyle{{L_{GU}} \over {\,f_2}} - t_{TGD} + t_{IFB} = \displaystyle{A \over c}*\displaystyle{{\,f_2^2 - f_1^2} \over {\,f_1^2 \; f_2^2}} *STEC$$In the above equation there are three undetermined parameters, which are STEC, satellite hardware delay deviation (t TGD) and receiver hardware delay deviation (t IFB). The t TGD can be obtained from the satellite broadcast navigation messages. Moving those known parameters to the right hand side of Equation (7), and denoting the individual satellites by an index j, the following equation can be obtained for each epoch and each observed satellite:
$$L_{GU}^i - f_2 t_{TGD} ^{\,j} = \displaystyle{K \over {E_\theta ^{\,j}}} VTEC^{\,j} - f_2 t_{IFB} $$Where 
$K = A\displaystyle{{\,f_1^2 - f_2^2} \over {cf_1^2\ \ f_2^2}} $,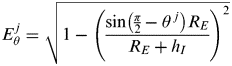 
$E_\theta ^{\,j} = \sqrt {1 - \left( {\displaystyle{{\sin \left( {{\textstyle{\pi \over 2}} - \theta ^{\,\,j}} \right)R_E} \over {R_E + h_I}}} \right)^2} $ is the elevation mapping function (Liu and Xie, Reference Liu and Xie2001), θ is the satellite elevation angle, R E is the average radius of the Earth and h I is the height of the main electron concentration in the ionosphere. Mapping the STEC to the vertical, each measurement from high elevation satellites should yield approximately the same TEC values assigned to the location above the site of the receiver. So we assume a single vertical total electron content (VTEC). An equation set can be obtained for each epoch:
$$L = Ax$$where the matrices of L, A, X are written as follows:
$$L = \left( {\matrix{ {L_{GU}^1 - f_2 t_{TGD} ^1} \cr {L_{GU}^2 - f_2 t_{TGD} ^2} \cr {L_{GU}^3 - f_2 t_{TGD} ^3} \cr { \vdots \quad \quad \quad \quad \vdots} \cr}} \right),\;A = \left( {\matrix{ {{\textstyle{K \over {E_\theta ^1}}} - f_2} \cr {{\textstyle{K \over {E_\theta ^2}}} - f_2} \cr {{\textstyle{K \over {E_\theta ^3}}} - f_2} \cr { \vdots \quad \quad \vdots} \cr}} \right),\;X = \left( {\matrix{ {VTEC} \cr {t_{IFB}} \cr}} \right).$$3. EXPERIMENTAL DATA AND RESULT ANALYSIS
3.1. Data selection
This paper mainly studies performance by using BDS measurements for ionosphere monitoring. Five stations with different latitudes were selected in Harbin, Lhasa, Wuhan, Guangzhou and Hong Kong in China that have been established by the GNSS Research Center of Wuhan University in China. Four data frequencies (BeiDou on B1, B2 and GPS on L1, L2) of dual system receivers were collected on 21 August 2012, as ionospheric activity is considered more active in summer. The TEC monitoring results from BeiDou and GPS systems were calculated separately. The sampling rate is 30 seconds, cut-off elevation angle is 15°. The height of the single-layer ionosphere is set to be 450 km to remain consistent with the Global Ionosphere Maps generated at CODE.
3.2. Comparison of TEC results
Single station TEC monitoring was carried out in the above mentioned five stations, using BDS or GPS systems separately. The results were compared with global ionospheric grid model interpolation. This paper presents the results in the order of Harbin (HARN), Lhasa (LASA), Wuhan (WUHN), Guangzhou (GDCH) and Hong Kong (HKTU). The figure for each station consists of two parts: the upper one shows computing results of BDS, GPS and GIM; the lower one displays the difference between BeiDou and GIM and the difference between GPS and GIM. The unit is TECU (1TECU=1016 el m−2), the horizontal coordinate is labelled as LT time, as shown in Figure 1.
Figure 1. The TEC values and differences of each station.
Figure 1 shows that the solution from the BeiDou system reflects the TEC diurnal variation trend at each station, with a certain level of consistency to the solutions from GPS and GIM. However, the BeiDou system currently has fewer in-orbit satellites than GPS, which resulted in worse satellite geometry at some stations, so the accuracy of ionospheric monitoring using BeiDou is lower than that of GPS. The calculation results of the BeiDou system are compared with that of GPS. The difference between the GIM interpolation result and the estimated TEC value from the BeiDou system is evaluated epoch by epoch, and the statistical average of the differences is calculated. The similar statistic was calculated for GPS as well. The results are listed in Table 2. In this table, it can be seen that the GPS results are closer to the GIM interpolation results when compared to the BeiDou result. The mean difference to the GIM model from the BeiDou solutions at a higher latitude is about four TECU while this mean value is about three TECU from the GPS solution; at a lower latitude it becomes six TECU for BeiDou and four TECU for GPS; at the lowest latitude for both systems the mean difference to GIM is about six TECU. With the latitude decreasing, the ionosphere becomes active. Therefore the monitoring performance of both systems is less accurate at low latitude than high latitude. Table 2 also reflects that the degradation trend of ionosphere monitoring performance of the BeiDou system is closer to that of GPS with the latitude decreasing.
Table 2. The TEC D-values of each station.
In order to get a better understanding of the above results, this research paper selected the representative stations in Lhasa, Guangzhou and Hong Kong and drew the sky charts of the GPS and BeiDou system for ionosphere monitoring, colour unit is TECU, as shown in Figures 2–4.
Figure 2. The TEC comparison of GPS and BeiDou at LASA station.
It can be seen from the figures that, because the BeiDou satellite navigation system has fewer in-orbit satellites than GPS and some of them are geostationary satellites (GEO), the number of ionosphere piercing points (IPP) is much less than in the GPS solutions, and they are unevenly distributed. Therefore the BeiDou system cannot reflect the changes of the ionosphere over the station, resulting in less accurate ionosphere monitoring than GPS. At the LASA station, the BeiDou satellites were mainly distributed to the east of the station, so the satellite geometry is worse than for GPS. At GDCH the distribution of BeiDou satellites was better, but it can be seen from the Figure 3 that the results from a particular satellite are poor as the estimated TEC values are larger than 120 TECU even at a high elevation angle. While at the HKTU station, the distribution of BeiDou satellites is good and all satellites are working normally. These details explain the results in Table 2: with the decreasing of latitude, the ionosphere becomes more active, and the monitoring performance of both systems is less accurate at low latitude than at high latitude. However, at middle and high latitudes, because of the worse geometry of the BeiDou satellites, the ionosphere monitoring performance of BeiDou is less accurate compared to GPS; while at low latitudes, the benefit from the better satellite distribution means the ionosphere monitoring performance of BeiDou is close to GPS.
Figure 3. The TEC comparison of GPS and BeiDou at GDCH station.
Figure 4. The TEC comparison of GPS and BeiDou at HKTU station.
Since the BeiDou Navigation Satellite System provided test run services from 27 December 2011, it has successfully launched six more satellites in four launches, expanded the system coverage, enhanced constellation robustness and improved system accuracy. Currently, all in-orbit satellites and ground systems run stably and system performance meets the design requirements through the testing and evaluation of various types of user terminals. From 27 December 2012, the BeiDou Navigation Satellite System officially started to provide continuous passive positioning, navigation and timing services for China and the surrounding area, as well as active positioning, two-way timing and short message communication services originally provided by the BeiDou Experimental Navigation Satellite System. With the increase in the number of in-orbit satellites of the BeiDou navigation system, three stations in the CORS system of HuBei province were used to study the current ionosphere monitoring performance with BeiDou. Using BDS or GPS systems separately, the single station TEC monitoring results were compared with global ionospheric grid model interpolation. We present here the results in the order of CENT, SY02 and XN06 on 2 February 2013.The figure of each station consists of two parts: the left part shows the TEC values and differences of each station, the right part shows the sky charts of the BeiDou system of each station. The unit is TECU, as shown in Figure 5.
Figure 5. The TEC values and differences of each station.
The difference between the GIM interpolation result and the estimated TEC value from the BeiDou system is evaluated epoch by epoch, and the statistical average of the differences is calculated. A similar statistic was calculated for GPS as well. The results are listed in Table 3. With the increased number of in-orbit satellites of BeiDou system, the satellite geometry becomes better than before, which can be seen from the right part of Figure 5. Because of the better satellite distribution, the ionosphere monitoring performance of BeiDou is close to GPS even at middle latitudes. This conclusion can be obtained from the left part of Figure 5 and also from Table 3. In spite of the increased number of in-orbit satellites, however, because part of the BeiDou system are geostationary satellites (GEO), the number of ionosphere piercing points (IPP) is still much less than in the GPS solutions, and they are unevenly distributed, resulting in less accurate ionosphere monitoring than GPS.
Table 3. The TEC D-values of each station.
3.3. Comparison of tIFB results
As claimed in Section 2, the tIFB could also be calculated, so in Table 4 one day's mean receiver hardware delay deviations at each station are listed in the second column named Method One. In order to check the estimates, the tIFB of each station is also computed by the method put forward by Jin which is based on the least squares method (Jin et al., Reference Jin, Jin and Feng2012) and is listed in the third column named Method Two. The two estimates show good agreement with a mean difference of less than 0·5 ns.
Table 4. The tIFB of each station.
3.4. Comparison of multi-day results
For better comparison, multi-day results were obtained. We present here the results in the order of HARN, LASA and HKTU from 1 to 3 August 2013 (DOY:213∼215). Using the comparison method as described above, the results are shown in Figure 6 and Table 5. The conclusions can be drawn that BeiDou system has the ability to detect the TEC diurnal variation trend that generally is in line with the results of GIM.
Figure 6. The TEC values and differences of each station for multi-day data.
Table 5. The TEC D-values of each station for multi-day data.
4. CONCLUSIONS
This paper focuses on the analysis of BeiDou-based ionosphere monitoring performance. In this paper, combined pseudo-range and carrier phase observations are used to estimate TEC, and the hardware delay deviation is also calculated. Based on the observation data from five BDS CORS in China and three BDS CORS in HuBei province in China, the TEC monitoring results on single station from BeiDou system and GPS system were analysed and compared. Through the measured data of reference stations the following conclusions can be drawn:
• The BeiDou system has the ability to detect the TEC diurnal variation trends that generally are in line with the results of GIM. The RMS difference between the results from BeiDou and the GIM model at a higher latitude in China is about four TECU, while the difference between the GPS and the GIM model is about three TECU; at a lower latitude in China this difference rises to six TECU for BeiDou and four TECU for GPS; at the station with the lowest latitude, the differences for both systems are about six TECU. With the latitude decreasing, the ionosphere becomes more active. Therefore the monitoring performance of both systems is less accurate at low latitude than high latitude because of its large variability.
• This paper also compared the ionosphere monitoring performance of BeiDou and GPS. The results demonstrated that the ionosphere monitoring performance of the BeiDou satellite system is closer to that of GPS with the decreasing of latitude mainly because of the better geometry of BeiDou satellites at low latitude.
• With the increased number of in-orbit BeiDou satellites and the better satellite distribution, ionosphere monitoring using the measurements of the BeiDou system can obtain a more precise result than before. However, because some of the BeiDou satellites are geostationary (GEO), the number of ionosphere piercing points (IPP) is still much less than in the GPS solutions, and they are unevenly distributed which resulted in less accurate ionosphere monitoring than GPS.
ACKNOWLEDGEMENTS
This work is partially sponsored by Natural Science Foundation of China (grant no. 41004014 and no.41304028), partially sponsored by National 863 Project of China (2012AA12A202), and partially supported by the Fundamental Research Funds for the Central Universities (No. 2012214020208).
