1. INTRODUCTION
With the rapid development of information technology, the precision strike capability of long-range weapon systems is gradually becoming more intelligent and efficient. One of the key techniques, which is also an impediment, is the development of a high-precision navigation system which can supply high-precision information on the motion states of modern aircraft and missiles. At present, integrated multi-navigation systems, which can take full advantage of different types of navigation systems that process integrated multi-sensors information, are the only way of achieving high precision navigation.
The developmental research of (Quan et al., Reference Quan, Liu, Gong and Fang2011; Mohinder et al., Reference Mohinder, Lawrence and Angus2007; Robert, Reference Robert2007) on integrated multi-sensor navigation systems has attracted worldwide attention. The integration of a Strapdown Inertial Navigation System (SINS) with a Global Positioning System (GPS) (Kim et al., Reference Kim, Jee and Lee1998; Kim et al., Reference Kim, Lee and Park2009; Francois et al., Reference Francois, Emmanuel, Denis and Philippe2006) has received much attention for providing this performance augmentation, but GPS receivers are vulnerable to the effects of jamming which can vary from complete loss of data, to reduced tracking performance and degraded navigational accuracy. Nevertheless, the performance objectives of navigation systems do not have to be vulnerable to dependence on GPS data. To overcome this possible problem, a Celestial Navigation System (CNS) has been integrated with the SINS/GPS (Leonid, Reference Leonid2007; Ali, Reference Ali and Fang2006; Xu and Fang, Reference Xu and Fang2008) to provide a high-performance autonomous mission capability. To achieve the long duration mission accuracy and reliability requirements necessary for navigation systems, the GPS and CNS measurements are fused with the SINS to provide a best estimate of the navigation information. This SINS/CNS/GPS integrated multi-sensor navigation system offers a more reliable, robust and possibly more accurate navigation solution than that provided by any single system (Wang et al, Reference Wang, Fang and Quan2004).
However, in practical applications, the noise model parameters of a SINS/CNS/GPS integrated multi-sensor navigation system will alter because of external destabilization and changes in the complex flight environment, which require the filtering capability of a complex nonlinear system (Wang et al., Reference Wang, Fang and Quan2004). Multi-sensor integrated navigation systems, which can deal with this problem effectively, have the potential of achieving high levels of accuracy and fault-tolerance. The presence of multiple data sources provides functional redundancy as well as greater observability of the desired navigation states. Multi-sensor integration techniques are used in many tracking and surveillance systems as well as in applications where the fidelity of the system is a foremost concern (Ali and Fang, Reference Ali and Fang2005b).
One method for the design of such systems is to make use of a number of sensors and to blend the information obtained from them in a central processor. The Kalman filter with a centralized structure in multi-sensor situations is relied on in many applications such as military surveillance, air traffic control and mobile robots. Target tracking using multiple sensors can offer improved functionality over a single sensor. Previous attempts to develop multi-sensor integration algorithms for a centralized architecture, in which measurements from all the sensors are sent to a central processor, have shown that significant gains in performance are possible.
However, if multi-sensor systems are to be able to process their data in real-time, the performance of a centralized Kalman filter needs to be improved. The Federated Kalman Filter (FKF) configuration was contemplated as another approach for data fusion in (Paik and Oh, Reference Paik and Oh2000). It is recognized that the FKFs have the advantages of simplicity and fault-tolerance over other decentralized filter techniques. The FKF method based on meticulous information-sharing principles makes available globally optimal or near-optimal estimation accuracy with a high degree of fault tolerance. The federated filter structure employs sensor-dedicated Local Filters (LFs) and a Master Filter (MF) to combine or fuse the LFs outputs. There are many methods for selecting and optimizing the information sharing coefficients of the FKF, such as the adaptive algorithm, neural network and Genetic Algorithm (GA). The adaptive algorithms have the advantages of simplicity and high efficiency, but are not highly adaptable to complicated surroundings. A neural network is usually used to build a model of an integrated navigation system, but is not suitable for optimization. The GA is a derivative-free stochastic optimization method based loosely on the concepts of natural selection in a parallel searching mechanism, which has high adaptability and is suitable for optimization.
In this study, the GA is adopted and improved. One of the main contributions of the study is the implementation of a multi-sensor navigation system using FKF with information sharing coefficients optimized by an improved GA. This improved GA algorithm avoids the premature convergence problem of a general GA by improving the fitness function, takes advantage of decimal-coding to improve both the speed and accuracy of calculation, and is used to build the FKF model through analysing the model parameters of the reference-system and local-filters.
The other main contribution of this study is that a solution and realization of a high performance SINS/CNS/GPS integrated multi-sensor navigation system is proposed using the design of hardware-functional modularization and software-flow integration. The experiment is performed using this improved FKF on the SINS/CNS/GPS integrated multi-sensor navigation system. In addition, an Unscented Kalman Filter (UKF) is used to deal with the nonlinearities of the integrated navigation system.
The experimental results show that, with the same experimental conditions, the estimated errors are very good when using the proposed method. The estimated 3-axis attitude errors are less than 2″, the estimated 3-axis position errors are less than 1 m and the estimated 3-axis velocity errors are approximately 0·04 m/s. These errors are 0·25, 0·4 and 0·5 times the corresponding errors estimated by the traditional FKF. When estimating the effect of the gyro errors and accelerometers biases, the fluctuating extent of the estimated value of the gyro errors is smaller than that of the traditional FKF and the rapidity of convergence to the estimated value is quicker. The estimated gyro errors are up to 0·02°/h using 140 s while the FKF only achieves 0·025°/h using about 280 s. When estimating the accelerometer biases, the two methods have the same level of convergence rapidity but the fluctuating extent of the estimated value is different.
In total, the FKF based on the improved GA not only significantly increases the navigation system's accuracy and reliability, but also has quick rapidity of convergence compared with the traditional FKF algorithm.
2. SINS/CNS/GNSS INTEGRATED NAVIGATION MODEL
2.1. Coordinate Frames
Definitions of the coordinate frames in the study are given as follows:
• The launch inertial frame (li-frame) has its origin at the launch point. Its x-axis is horizontal and perpendicular to the nominal launch plane, toward the right, its y-axis is horizontal and lies in the nominal launch plane; its z-axis is vertical upward and normal to the reference ellipsoid.
• The geocentric inertial frame (i-frame) has its origin at the centre of the Earth and is non-rotating with respect to the fixed stars. Its x-axis is in the equatorial plane and points the vernal equinox point, its z-axis is normal to that plane; its y-axis complements the right-handed system.
• The body frame (b-frame) has its origin at the centre of mass of the vehicle. Its x-axis points along the longitudinal axis of the vehicle, its z-axis is perpendicular to the longitudinal plane of symmetry; its y-axis complements the right-handed system.
2.2. Error Model (Quan et al., Reference Quan, Liu, Gong and Fang2011)
2.2.1. Attitude Error Model
Attitude error analysis establishes the relationship between different frames. Here, c and p refer to the computed and analytical platform frame. It is obvious that indirectly ‘c’ follows ‘li’, and ‘p’ follows ‘c’ and ‘li’. There is misalignment between the ‘li’ and ‘p’ frames which is expressed by the angles φ x, φy, φz. Therefore, the estimated attitude matrix C bp from the SINS is expressed as:
The attitude error in the space-stabilized SINS mechanization is the orthogonal transformation error between the b- and li-frames. In this perspective, the attitude error equation can be depicted as a nonlinear attitude error model of the SINS. For large attitude errors, the relationship between the p- and li-frames is obtained by three successive rotations of the li-frame using the misalignment angles φ x, φy, φz about the x, y and z axes expressed by:
The angular velocity of the mathematical p-frame relative to the i-frame is equal to the sum of the angular velocity of the li-frame relative to the i-frame and the angular velocity of the p-frame relative to the li-frame. This relationship is described by:
where 
represents the angular rate of the li-frame through the axes misalignment angles (i.e., 
. 
because the i- and li-frames are inertially fixed). Thus, 
.
In the above relationship, 
in which 
, where 
and 
represent the gyro's constant and random drifts. Thus:
2.2.2. Velocity Error and Position Error Model
The velocity error in the space-stabilized mechanization is given as:
where:
is the specific force measured by the accelerometer.- is a constant transformation matrix between the indicated frames.
- is the acceleration error caused by gravity.
- and represent the accelerometer constant and random biases, the subscript a stands for accelerometer, and×represents the cross product.
is the specific force measured by the accelerometer.
is a constant transformation matrix between the indicated frames.
is the acceleration error caused by gravity.
and 
represent the accelerometer constant and random biases, the subscript a stands for accelerometer, and×represents the cross product.While deriving an expression for the acceleration error caused by gravity, the inverse square gravity model is considered for the spherical Earth model. The gravity model used in the derivation of the error equation is given by:
where:
μ=(3·9860305±3×10−7)×1014[m 3/s 2].
- ; are components of the position vector.
J 2 is a second-order harmonic constant coefficient and its value is (1·08230±0·0002)×10−3.
r e is the Earth's equatorial radius which is equal to 6378137 m.
; 
are components of the position vector.The quantities μ, J 2 and r e are specific to the reference inertial frame for the SINS space-stabilized mechanization.
The gravity gradient 
for a two body gravity field can be formulated as follows:
where, g ij(i,j=1,2,3) is given in reference (Quan et al., Reference Quan, Liu, Gong and Fang2011).
The position error in rectangular coordinates is as follows:
3. DESIGN OF FKF BASED ON IMPROVED GA
3.1. FKF and Its Information Sharing
FKF is a partitioned estimation method that employs a two stage data processing architecture, in which the outputs of the sensor related LFs are subsequently combined by a large MF (Carlson and Berarducci, Reference Carlson and Berarducci1994). As indicated, each LF is dedicated to a separate sensor subsystem and uses data from the traditional reference SINS. The SINS acts as a fundamental sensor in the system and its data is the measurement input for the MF. The data from the GPS and the CNS are dedicated to the corresponding LFs, and after implementation, supply their resulting solutions to the MF for the master update, yielding a global solution (Gao et al., Reference Gao, Krakiwsky, Abousalem and Mclellan1993). The FKF avoids the theoretical and practical difficulties of standard Kalman filtering by means of a simple, yet effective, information sharing methodology. The advantages of information sharing implemented within the federated filter are increased data throughput by the parallel operation of the LFs, enhanced system fault-tolerance by retaining multiple component solutions, and improved accuracy and stability of cascaded filter operations (Carlson, Reference Carlson1990; Carlson, Reference Carlson1996). The basic concept of the information distribution approach in the FKF is to divide all the system information among the LFs, perform local time propagation and measurement processing, and then recombine the updated local information into a new total sum.
Applying the maxim of conservation to the estimated error covariance, results in information sharing between the filters. The information residing in the estimated error covariance can be construed to be the memory of the filter system. To remain optimal, the filter must combine the local estimation into a single estimate every cycle. After the combination step, at the start of the next cycle, the estimation or memory can be fed back to the LFs with the MF retaining part or none of the information. At this point, all the estimates in the system are equal and the information is distributed. If feedback is implemented, conservation of information simply dictates that the net sum of the information in the filter system before and after the feedback operation must remain the same. However, every feedback operation requires an adjustment of the covariance to reflect information sharing. In general, when the information is redistributed among the LFs and MFs, the sum of the LF and MF matrices after feedback must equal the MF information before feedback. In the FKF implementation, the system dynamic model is applied to each filter, but the statistical weight of the dynamics driving noise is distributed such that information is preserved. The individual LFs are considered sub-optimal for this reason. The LFs are then combined to give an optimal global estimate through the MF. Our aim is to find the optimal information sharing coefficients for the FKF. The GA is a robust, domain-independent mechanism for optimization and has a high probability of finding optimal solutions in large and complex nonlinear spaces. Consequently it is a good method for finding the optimal information sharing coefficients.
3.2. Improved Genetic Algorithm
The general GA is a derivative-free stochastic optimization method based loosely on the concepts of natural selection, which distinguish themselves from many other optimization methods by their parallel searching mechanism. They work with the coding of the parameter set, not the parameters themselves. The optimization process with a GA is depicted in (Yang, Reference Yang1999). First, to make it easier to evaluate and choose results, the GA constructed fitness function is based on all the requirements. Thereafter, the GA adopts a real-coded mode and selects a suitable initial individual. An individual structure is then created randomly. With that, each individual filter is evaluated. Secondly, they are operated by three main operators: reproduction, crossover, and mutation, to create a better individual filter. Each individual filter is assigned a ‘fitness score’ according to how good the solution is. Only individual filters that are competitive (according to their fitness values) get the chance to survive long enough to produce offspring by crossover and mutation and thus to transfer their genetic material to the next generation. If the termination criteria are not met, the individual filter is operated on by the above three operators and evaluated again. This procedure is continued until the termination criteria are met.Considering the slow executing speed and premature convergence problem in calculating the fitness of the general GA, the fitness function and the coding are improved in this study.
3.2.1. Improved Fitness Function
In general, GAs depend on a fitness function to simulate natural selection, which decides various genetic operations by calculating the fitness value for each individual filter. Therefore, the fitness function is closely related to convergence speed and accuracy of the GA. The practice of defining a fitness function can be thought of as follows: suppose that the population size is S, sample numbers are N, genetic generations are G, the algorithm calculates the summary of the variance between the theoretical and experimental values with individual K(i) (1<i<S) and takes it as the performance index B(i,t) of the individual filter K(i) in the 
th (1<t<G) generation.
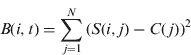
where:
S(i,j) is the theoretical value of sample j (1<j<N)with the individual filter K(i).
C(j) is the experimental value of sample j.
Based on the performance B(i,t), this study defines the fitness function of the GAs as:
To avoid premature convergence in calculating fitness, the performance index sum of all individual filters in the current generation T(t) is calculated as 
. With the individual filter size S, the algorithms then diverge and converge to the performance index of each individual filter in accordance with B′(i,t)=(S×B(i,t))/T(t). Finally, we have the eventual fitness function:
3.2.2. Real Number Coding
The two coding schemes for a general GA are binary and real number coding. Considering the conventional binary code, genetic algorithms must encode and decode in solving continuous optimization problems, so they have a definite influence upon computing speed and accuracy. Since in a physical world, most optimization problems involve real-valued parameters, it is better to manipulate them directly in the original real-valued space instead of the discretized space. Moreover, real-coded GAs not only cancel out the process of encoding and decoding but also improve the efficiency and stability of a general GA. A real-coded GA has a distinct advantage in parameter optimization.
3.3. FKF Based on the Improved GA for a SINS/CNS/GPS Integrated Multi-sensors Navigation System
The SINS/CNS/GPS integrated multi-sensor navigation system comprises one main system and two sub-systems. The SINS acts as a fundamental sensor (main system) in the system, and its data is the measurement input for the MF. The data from the GPS (sub system 1) and the CNS (sub system 2) is dedicated to corresponding LFs and, after implementation, supply their resulting solutions to the MF for a time update and optimization fusion (Li et al., Reference Li, Fang and Jia2002). The frame of the FKF based on the improved GA is shown in Figure 1.
Figure 1. FKF based on the improved GA configuration of a SINS/CNS/GPS integrated multi-sensors navigation system.
The primary sensor subsystems used in the integrated multi-sensor navigation system are the SINS, CNS and GPS. The SINS used in the simulation generates position, velocity and attitude information, the CNS provides attitude information, while the GPS outputs position and velocity solutions. The purpose of the integrated system is to achieve increased accuracy and improved estimates of the SINS error sources. The CNS provides the attitude of the vehicle that is combined with the SINS attitude information to output an observation to the LF1 (Unscented Kalman Filter1:UKF1). Velocity and position information available from the GPS in conjunction with the SINS yields observations to the LF2 (UKF2).
Suppose that the state and measurement equations of the main system are given by:
where W k−1 and V k are the uncorrelated Gaussian white noise sequences with the covariance as Q k, Rk.
The state and measurement equations of the subsystem are as follows:
where:
i represents the corresponding measurement sources for the LFs, i=1, 2 … N.
W i,k−1 and V i,k are the uncorrelated Gaussian white noise sequences with covariance Q i,k,R i,k.
Suppose that 
and LFs are uncorrelated. Then,
where:
P g is the covariance matrix of the global FKF.
P ii is the covariance matrix of the i th LF.
The covariance matrix and its propagation in time are vital in both describing and analysing physical test results and comparing them to theoretical predictions. This number is a significant indication of the overall performance of the system and is often employed as a ‘metric to minimize’ when making decisions about how to consider the navigation data. To solve state space system error equations, the covariance matrix is propagated continuously so that error estimates and covariance are available at the discrete time when the measurements transpire (Daniel, Reference Daniel1999).
The estimation of the LFs is correlated because they use a common dynamic system. To eliminate this correlation, the process noise and the state vector covariance are set to their upper bounds:
where β i(≥0) is an information sharing coefficient, and:
For the time update equations and the measurement update equations for the LFs refer to reference (Ali and Fang, Reference Ali and Fang2005b). The information sharing coefficients are selected by the estimated error covariance of the LFs. The information residing in the estimated error covariance can be construed to be the memory of the filter system. To remain optimal, the filter must combine the local estimates into a single estimate every cycle. After the combination step, at the start of the next cycle, the estimate or memory can be fed back to the LFs with the MF retaining a part or none of the information. At this point, all estimates in the system are equal and the information is distributed. If feedback is implemented, conservation of information simply dictates that the net sum of the information in the filter system before and after the feedback operation must remain the same. However, every feedback operation requires an adjustment of the covariance to reflect information sharing.
In general, when the information is redistributed about the LFs and MFs, the sum of the local and MF matrices after feedback must be equal to the MF information before feedback. The simplest form of parametric control is to choose parameters β i and β m with a summation of one, and set the error covariance of the individual filter and MFs after feedback equal to β i and β m times the MF covariance before feedback. In our real-coded GA, individual filters are directly composed of real type original variables of the regression model (β 1β 2 … β N) and have N chromosomes. Parameter N of the above content is set to 2. In this FKF based on the improved GA, a quaternion is obtained from the corrected attitude matrix and is fed back for attitude error compensation. Similarly, the estimated velocity and position error states are used for velocity and position error compensation. The effective method that improved the GA determines the optimized information sharing coefficients for the FKF to accomplish good navigation results.
Considering the SINS/CNS/GPS integrated multi-sensor navigation system, we suppose that the state vectors for the LFs are the same as the MF:
We select the information sharing coefficients using the improved GA. Using the fitness function, as follows:
where:
β 1+β 2+β m=1.
β t is the calculated information-sharing coefficient of the t th generation.
W 1, W 2 are the regulated power dependent on the Q and P.
The algorithms then set the evaluated fitness of each individual filter for the current generation in ascending order and the relative individual filter is correspondingly ordered. Consequently the improved GA determines the best fitness. If the best fitness satisfies the given conditions, the improved GA finds out the relative best individual filter and exports it as the optimum solution. After that, the calculation is ended and the present optimum solution becomes the final optimization result of the improved GA.
4. EXPERIMENTAL RESULTS
4.1. Hardware & Software Design for the SINS/CNS/GPS Integrated Multi-sensors Navigation System
Considering the versatility, agility and transportability of the algorithms, this FKF based on the improved GA for the SINS/CNS/GPS integrated multi-sensor navigation system should have the features of low cost and high efficiency, and also retain the design and realization ideas of hardware-function modularization and software-flow integration.
4.1.1. Hardware Design
Considering the integrated design, the whole hardware system is divided into the devices, component and system layers. Each layer integrates downward, and supplies testing and functional verification to the upper layer at the same time. The system is connected by multifunction ports between the layers. In this way, changing the elements in each layer, while ensuring the coherence of the interface protocol, will not affect the other layers, sequentially realizing the versatility of the hybrid simulation system. In addition, both the devices and components layers have pre-formed interfaces, which enhance the expandability of the system. The devices layer includes the elements of inertia measurement that consist of an Optical Fibre Gyro Accelerometer (OFGA), TFT Liquid Crystal Light Valve (LCLV) star atlas simulator (Roelfo and Van, Reference Roelof and Van1994; Quan and Fang, Reference Quan and Fang2005), Charge Coupled Device (CCD) star sensor device, GPS Receiver and a preformed interface. The components layer consists of a Trajectory Generator Module (TGM), Strapdown Inertial Navigation Module (SINM), Celestial Navigation Module (CNM), GPS Module (GPSM), Peripheral Processing Module (PPM) and a Preformed Interface Module (PIM).The system layer consists of an integrated multi-sensor navigation and performance testing system. The entire layers of the hardware system are shown in Figure 2.
Figure 2. Hardware for the SINS/CNS/GPS integrated multi-sensor navigation system.
4.1.2. Software Design
Considering the versatility, flexibility and portability of the hybrid simulation of a SINS/CNS/GPS integrated multi-sensor navigation system, the design of each part possesses its own characteristics as well as adopting a universal exploitation environment, which realizes the functional integrated design. In this way, the system can be exploited expediently and carried out with a hybrid simulation experiment. The flow diagram of the entire software system is show in Figure 3.
Figure 3. Flow diagram of a SINS/CNS/GPS integrated multi-sensor navigation system.
First, the hardware and software of the system are initialized, and performance-testing parameters are set for integrated multi-sensor navigation. Secondly, after obtaining data from the SINS, if it is available, the ‘proceed’ performance mode will be decided; otherwise the systems wait for the next SINS data. The next step determines whether it is in the‘integrated’ mode, which depends on whether CNS and GPS data have been received. The adaptive FKF together with the Improved GA module and the Strapdown Inertial Navigation (SIN) module are then performed to achieve integrated multi-sensor navigation and feedback compensation for the system; in the absence of CNS and GPS data, the fine strapdown algorithm is executed to achieve SIN. Thirdly, real-time performance testing of the navigation information of system is carried out to determine whether the CNS and GPS data have been received or not; if not, the system continues to receive the next set of SINS data. If successful, a Performance Testing Report (PTR) for the integrated multi-sensor navigation system is generated, and the software flow ends.
4.1.3. Construction of SINS/CNS/GPS Integrated Multi-Sensor Navigation System
To construct the SINS/CNS/GPS integrated multi-sensor navigation system in a laboratory, practical/actual devices and parts are used. Based on prior work (Quan et al., Reference Quan, Fang, Xu and Sheng2008), actual research development and engineering applications of all the various sub-systems, a synthesized approach is carried out on the design of the hardware and software of the system. The hybrid simulation system devices and parts for the experimental SINS/CNS/GPS integrated multi-sensor navigation system are shown in Figure 4.
Figure 4. SINS/CNS/GPS integrated multi-sensor navigation system.
4.2. Experimental Method
Based on the error model and SINS/CNS/GPS integrated multi-sensor navigation system as shown in Figure 4, some experiments were performed (Ali and Fang, Reference Ali and Fang2005a; Zhang et al., Reference Zhang, Li, Deng and Chen2004). At the same time, the experiment of the FKF based on the improved GA was performed on the integrated multi-sensor navigation system. The conditions for the experiment were:
• (1) For the improved GA: S=20, the chromosome number of an individual filter N=2, the genetic generation G=200, the crossover probability P c=0·1, the mutation probability P m=0·01, W 1=0·3, W 2=0·7.
• (2) Assuming a long flight-time unmanned plane as an example, the initial latitude was set at 39·984°, the initial longitude at 116·344°. The initial error angle for the head was set at 6′, for the pitch at 20″, and for the roll at 20″. The gyroscopic drift was 0·01°/h (1σ) and the accelerometer zero offset was 100 μg (1σ). The attitude precision of the CNS was 5″ (1σ), the position and velocity precision of the GPS were 5 m(1σ) and 0·1 m/s(1σ), and the filter period was 1 s.
We assumed the initial value 
of state vector xf is zero. P f (0) and Q are given by:
where:
Initial values of the information sharing coefficients are assumed to be β 1(0)=β 2(0)=0·49 and β m(0)=0·02. The LFs and the MF are initialized as:
The experimental results using the FKF and the proposed FKF based on the improved GA method for the SINS/CNS/GPS integrated system are depicted in Figures 5 to 7.
Figure 5. Attitude errors.
Figure 6. Position errors and velocity errors.
Figure 7. Gyros drift and accelerometers biases.
Using the UKF and improved GA for the selection of optimized information sharing coefficients, the FKF based on the improved GA can estimate the attitude errors, position errors, velocity errors, gyro drifts and accelerometer biases better than for the traditional FKF. Since gyro induced drift errors are the only error variables that contribute to the attitude errors, the CNS updates are effective in estimating and compensating for these drift errors, as well as the position and velocity errors that occur due to misalignments. Velocity and position updates from the GPS can estimate and compensate for velocity, position and accelerometer biases.
From Figures 5 and 6, it can be seen that the estimated attitude and position errors are minimal using the proposed method. The estimated 3-axis attitude errors are less than 2″, which is better than the 5″ using the traditional FKF. The estimated 3-axis position errors are less than 1 m, which is better than the 4 m using the traditional FKF. The estimated 3-axis velocity errors are much better than the traditional FKF, which are 0·04 m/s rather than 0·08 m/s.
From Figure 7, it can be seen that the gyro errors and accelerometer biases are estimated and compensated effectively using the proposed method. Compared with the FKF, the fluctuating extent of the estimated value of gyro errors and accelerometer biases is smaller, and the convergence of the estimated value is more rapid. The proposed method gives estimated gyro errors of up to 0·02°/h at about 140 s while for the FKF they are only up to 0·025°/h at about 280 s. For estimating the accelerometers biases, the two methods have the same effective convergence rapidity but the fluctuating extent for the estimated values is different.
5. CONCLUSIONS
In this study, the Strapdown Inertial Navigation System (SINS) / Celestial Navigation System (CNS) / Global Positioning System (GPS) multi-sensors integration using Federated Kalman Filter (FKF) based on the improved Genetic Algorithm (GA) for enhancing navigational performance is investigated. First, the information sharing coefficients of FKF for the multi-sensor navigation system were optimized using the improved GA, which improved the fitness function, avoiding the premature convergence problem of the general GA, while taking advantage of the decimal-coding to improve the speed and accuracy of calculation. Second, a solution and construction of a high performance SINS/CNS/GPS integrated navigation system was proposed using the design of functional modular hardware and software-flow integration. Third, the Unscented Kalman Filter (UKF) was used to deal with the nonlinearity of the integrated navigation system. The experimental results show that with the same experimental conditions, the estimated errors were minimal using the proposed method. These errors were 0·25, 0·4 and 0·5 times the corresponding errors estimated by the traditional FKF. The fluctuating extent for the estimated value of the gyro errors was smaller than that of the traditional FKF and the convergence of the estimated value was also quicker. When estimating the accelerometer biases, the two methods had the same rapidity of convergence but the fluctuating extent of estimated values was different. In total, compared with the traditional FKF, the proposed method not only greatly increased the accuracy and reliability of the navigation system, but also resulted in rapid convergence, which would be appropriate for a long flight-time unmanned plane or long-range ballistic missile. It has been applied in a project involving the cooperation of the Fifth Research Unit in Beihang University and the NO.2 Artillery Engineering College with considerable success.
ACKNOWLEDGEMENTS
The authors thank Professor Guo Lei for his helpful technical support. Support for this research was provided by The National Nature Science Foundation Grant (61004140, 60825305, 61104198, 60904093 and 61004129) and 973 Project (2009CB72400101C).
