No CrossRef data available.
Article contents
CANONICAL DECOMPOSITION AND QUIVER REPRESENTATIONS OF TYPE 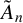 $\tilde {A}_n$ OVER FINITE FIELDS
$\tilde {A}_n$ OVER FINITE FIELDS
Published online by Cambridge University Press: 22 September 2022
Abstract
Let Q be a quiver of type
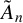 $\tilde {A}_n$
. Let
$\tilde {A}_n$
. Let
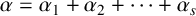 $\alpha =\alpha _1+\alpha _2+\cdots +\alpha _s$
be the canonical decomposition. For the polynomials
$\alpha =\alpha _1+\alpha _2+\cdots +\alpha _s$
be the canonical decomposition. For the polynomials
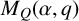 $M_Q(\alpha ,q)$
that count the number of isoclasses of representations of Q over
$M_Q(\alpha ,q)$
that count the number of isoclasses of representations of Q over
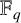 ${\mathbb F}_q$
with dimension vector
${\mathbb F}_q$
with dimension vector
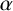 $\alpha $
, we obtain a precise relation between the degree of
$\alpha $
, we obtain a precise relation between the degree of
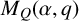 $M_Q(\alpha ,q)$
and that of
$M_Q(\alpha ,q)$
and that of
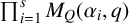 $\prod _{i=1}^{s} M_Q(\alpha _i,q)$
for an arbitrary dimension vector
$\prod _{i=1}^{s} M_Q(\alpha _i,q)$
for an arbitrary dimension vector
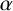 $\alpha $
.
$\alpha $
.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.



