1 Introduction
Collisionless plasma shock waves are important in numerous space and astrophysical phenomena (Caprioli, Blasi & Amato Reference Caprioli, Blasi and Amato2011; Karimabadi et al. Reference Karimabadi, Roytershteyn, Vu, Omelchenko, Scudder, Daughton, Dimmock, Nykyri, Wan and Sibeck2014) and in laboratory experiments (Romagnani et al. Reference Romagnani, Bulanov, Borghesi, Audebert, Gauthier, Löwenbrück, Mackinnon, Patel, Pretzler and Toncian2008). In particular, not only are they believed to be responsible for cosmic ray acceleration (Bell Reference Bell2013), but their ability to energize ions makes them a possible candidate for laser plasma based generation of high-energy ion beams with a narrow energy spectrum (Tikhonchuk et al. Reference Tikhonchuk, Andreev, Bochkarev and Bychenkov2005; Haberberger et al. Reference Haberberger, Tochitsky, Fiuza, Gong, Fonseca, Silva, Mori and Joshi2012). In practice, it is highly non-trivial to produce a quasi-monoenergetic peak in the ion energy spectrum that competes in total beam charge with the more robust target normal sheath acceleration mechanism. However, recent experimental results by Pak et al. (Reference Pak, Kerr, Lemos, Link, Patel, Albert, Divol, Pollock, Haberberger and Froula2018) demonstrate that a shock-accelerated quasi-monoenergetic beam with a high total charge can be achieved by optimizing plasma profiles.
Often, the Coulomb mean free paths of the plasma particles are much larger than the width of the shock front or its dynamically relevant vicinity. In this case, the abrupt change in plasma parameters between upstream and downstream is set up by some collisionless kinetic process (Tidman & Krall Reference Tidman and Krall1971; Marcowith et al. Reference Marcowith, Bret, Bykov, Dieckman, Drury, Lembége, Lemoine, Morlino, Murphy and Pelletier2016), such as ion reflection in the electrostatic shock potential (Moiseev & Sagdeev Reference Moiseev and Sagdeev1963) or electromagnetic turbulence (Bret et al. Reference Bret, Stockem, Fiuza, Ruyer, Gremillet, Narayan and Silva2013), and collisions do not play a significant role in the dynamics of the shock (Balogh & Treumann Reference Balogh and Treumann2013). In the other extreme, when the mean free paths are shorter than the spatial structures of the shock – with relevance to inertial confinement fusion (ICF) and other high-energy-density applications – the dynamics is very similar to fluid shocks, where the entropy generation of the shock is caused by binary collisions. The collisional limit is often studied by single-fluid hydrodynamic codes, while the collisionless limit is mostly studied by particle-in-cell (PIC) simulation codes.
The intermediate region of parameters where the physics is kinetic but collisions also play a role is, however, much less explored than the above mentioned extremes, although it can be relevant for laser plasma experiments. Approaching from the high collisionality direction, the ICF community has already started to explore this region using Fokker–Planck solvers (Thomas et al. Reference Thomas, Tzoufras, Robinson, Kingham, Ridgers, Sherlock and Bell2012; Keenan et al. Reference Keenan, Simakov, Taitano and Chacón2018). Other types of laser plasma experiments, such as those aimed at ion acceleration, do not compress the target but heat it considerably, which corresponds to small collisionalities. However, when lasers predominantly couple their energy to the electrons, and the target is of solid density and/or consists of a high charge number element, the ion collisionality need not be vanishingly small. Among the limited number of studies on the effect of a finite collisionality in electrostatic shocks relevant for ion acceleration experiments, Turrell, Sherlock & Rose (Reference Turrell, Sherlock and Rose2015) found that in multi-species plasmas the collisional friction between the different ion species can lead to very rapid heating.
In the field of laser plasmas – perhaps owing to the short time scales of the studied phenomena and that the systems considered are open – the fact that collisionality need not be order unity to significantly affect the dynamics of the system is somewhat overlooked. Meanwhile, there is a wealth of examples in the field of magnetic confinement fusion where weak but finite collisionality is essential. The ability to move particles across phase-space separatrices that divide regions with qualitatively different particle dynamics – e.g. a trapped–passing boundary, a boundary of a loss cone or the threshold of the runaway region – can make collisions important, even when they are rare (Dreicer Reference Dreicer1960; Chankin & McCracken Reference Chankin and McCracken1993; Nemov et al. Reference Nemov, Kasilov, Kernbichler and Heyn1999; Fülöp, Pusztai & Helander Reference Fülöp, Pusztai and Helander2008).
In this paper, we depart from the strictly collisionless limit, and investigate the effects of a weak but finite ion collisionality on kinetic electrostatic shocks. The process we focus on here, the collisional population of the originally empty trapped regions of the ion phase space, is a cumulative effect. Therefore, the relevant quantity is the collisional age, which can reach order-unity values during the lifetime of the shock, even if the collisionality is small. We consider laminar (i.e. non-turbulent) shocks that exist at low (i.e. order-unity) Mach numbers (Sagdeev Reference Sagdeev1966), and are relevant for plasma-based ion acceleration experiments (Haberberger et al. Reference Haberberger, Tochitsky, Fiuza, Gong, Fonseca, Silva, Mori and Joshi2012).
The paper is organized as follows. Section 2 starts by describing the assumptions of the model we use to calculate the effect of collisional scattering of ions across the phase-space separatrices in kinetic electrostatic shocks, and qualitatively explains the emerging physical picture. Then, in §§ 2.2 and 2.3, the perturbative orbit-averaged treatment of collisions and the reduction of the problem to a diffusion equation are detailed, respectively. Finally, we present the results in § 3, mostly concerning the development of the potential structure with collisional age for various Mach numbers and electron-to-ion temperature ratios.
2 The kinetic shock model
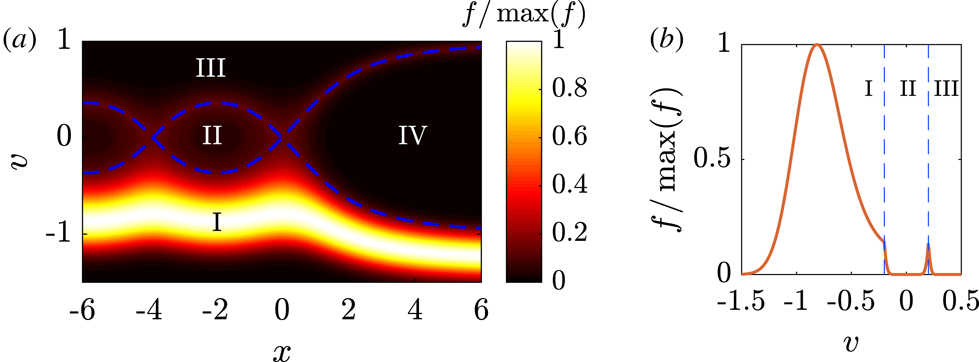
An important process in the physics of electrostatic shocks is the partial reflection of ions at the shock front. The electrostatic potential, see figure 1(a), ramps up from
![]() $\unicode[STIX]{x1D719}=0$
in the far upstream to a maximum of
$\unicode[STIX]{x1D719}=0$
in the far upstream to a maximum of
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
. The reflection of ions creates an asymmetry between the up- (
$\unicode[STIX]{x1D719}_{\text{max}}$
. The reflection of ions creates an asymmetry between the up- (
![]() $x\geqslant 0$
) and downstream (
$x\geqslant 0$
) and downstream (
![]() $x<0$
) regions of the shock. This asymmetry, together with the potential response of the ions and electrons, creates a downstream potential that oscillates between
$x<0$
) regions of the shock. This asymmetry, together with the potential response of the ions and electrons, creates a downstream potential that oscillates between
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
and
$\unicode[STIX]{x1D719}_{\text{max}}$
and
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
(Sagdeev Reference Sagdeev1966).
$\unicode[STIX]{x1D719}_{\text{min}}$
(Sagdeev Reference Sagdeev1966).

Figure 1. (a) Electrostatic potential,
![]() $\unicode[STIX]{x1D719}(x)$
, of a typical kinetic electrostatic shock propagating to the right. The shock has a ramp-up in potential, to a maximum of
$\unicode[STIX]{x1D719}(x)$
, of a typical kinetic electrostatic shock propagating to the right. The shock has a ramp-up in potential, to a maximum of
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
; behind that, the potential oscillates between
$\unicode[STIX]{x1D719}_{\text{max}}$
; behind that, the potential oscillates between
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
and
$\unicode[STIX]{x1D719}_{\text{min}}$
and
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
. (b) Phase-space diagram, showing constant energy contours in the frame of the shock. The dashed curves denote the upper and lower separatrices. Regions of phase space: I – passing, II – trapped, III – co-passing and IV – reflected.
$\unicode[STIX]{x1D719}_{\text{max}}$
. (b) Phase-space diagram, showing constant energy contours in the frame of the shock. The dashed curves denote the upper and lower separatrices. Regions of phase space: I – passing, II – trapped, III – co-passing and IV – reflected.
In this paper, we use the following normalization scheme: the velocity is normalized to the sound speed
![]() $c_{\text{s}}=\sqrt{ZT_{\text{e}}/m}$
defined with the far upstream electron temperature,Footnote
1
where the plasma is completely unaffected by the shock,
$c_{\text{s}}=\sqrt{ZT_{\text{e}}/m}$
defined with the far upstream electron temperature,Footnote
1
where the plasma is completely unaffected by the shock,
![]() $T_{\text{e}}$
;
$T_{\text{e}}$
;
![]() $m$
and
$m$
and
![]() $Ze$
denote the ion mass and charge, with
$Ze$
denote the ion mass and charge, with
![]() $e$
the elementary charge. In particular, the ion flow velocity becomes equal to minus the Mach number
$e$
the elementary charge. In particular, the ion flow velocity becomes equal to minus the Mach number
![]() ${\mathcal{M}}=V_{0}/c_{\text{s}}$
, where
${\mathcal{M}}=V_{0}/c_{\text{s}}$
, where
![]() $V_{0}$
is the shock speed with respect to the unperturbed upstream medium. The potential
$V_{0}$
is the shock speed with respect to the unperturbed upstream medium. The potential
![]() $\unicode[STIX]{x1D719}$
is normalized to
$\unicode[STIX]{x1D719}$
is normalized to
![]() $T_{\text{e}}/e$
, the configuration coordinate
$T_{\text{e}}/e$
, the configuration coordinate
![]() $x$
to the Debye length
$x$
to the Debye length
![]() $\unicode[STIX]{x1D706}_{\text{D}}=\sqrt{\unicode[STIX]{x1D716}_{0}T_{\text{e}}/(e^{2}n_{0})}$
and time
$\unicode[STIX]{x1D706}_{\text{D}}=\sqrt{\unicode[STIX]{x1D716}_{0}T_{\text{e}}/(e^{2}n_{0})}$
and time
![]() $t$
to
$t$
to
![]() $\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
; here
$\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
; here
![]() $n_{0}$
is the electron density far upstream, where the plasma is completely unperturbed by the shock, which we normalize to 1. All the calculations in this paper are done in the reference frame of the shock front.
$n_{0}$
is the electron density far upstream, where the plasma is completely unperturbed by the shock, which we normalize to 1. All the calculations in this paper are done in the reference frame of the shock front.
The one-dimensional (1-D) collisionless shock problem has a steady state solution, which has been considered by Pusztai et al. (Reference Pusztai, TenBarge, Csapó, Juno, Hakim, Yi and Fülöp2018); its solution, in the frame of the shock, is derived from the time-independent Vlasov–Poisson system,
where
![]() $n_{\text{i}}=\int _{-\infty }^{\infty }f_{\text{i}}\,\text{d}v$
. To keep the following discussion focused on collisional effects and avoid issues with inter-species collisions, the model considered in this paper only concerns single ion species distributions,
$n_{\text{i}}=\int _{-\infty }^{\infty }f_{\text{i}}\,\text{d}v$
. To keep the following discussion focused on collisional effects and avoid issues with inter-species collisions, the model considered in this paper only concerns single ion species distributions,
![]() $f_{\text{i}}\rightarrow f$
, and the electrons are assumed to be Maxwell–Boltzmann distributed, which results in
$f_{\text{i}}\rightarrow f$
, and the electrons are assumed to be Maxwell–Boltzmann distributed, which results in
![]() $n_{\text{e}}=n_{\text{e},1}\exp (\unicode[STIX]{x1D719})$
, where
$n_{\text{e}}=n_{\text{e},1}\exp (\unicode[STIX]{x1D719})$
, where
![]() $n_{\text{e},1}=Zn_{\text{i}}(\unicode[STIX]{x1D719}\rightarrow 0)$
is the electron density which balances both the incoming and reflected ions. Note that
$n_{\text{e},1}=Zn_{\text{i}}(\unicode[STIX]{x1D719}\rightarrow 0)$
is the electron density which balances both the incoming and reflected ions. Note that
![]() $n_{\text{e},1}\neq 1$
, because the normalized electron density only takes the value
$n_{\text{e},1}\neq 1$
, because the normalized electron density only takes the value
![]() $1$
in the unperturbed upstream plasma, i.e. where the reflected ion beam is not yet present.
$1$
in the unperturbed upstream plasma, i.e. where the reflected ion beam is not yet present.
The solution to (2.1) is given by
![]() $f(x,v)=f({\mathcal{E}})$
, where
$f(x,v)=f({\mathcal{E}})$
, where
![]() ${\mathcal{E}}=v^{2}/2+\unicode[STIX]{x1D719}(x)$
is the total ion energy; that is, ions stream along constant-energy contours in phase space, see figure 1(b). With the assumption that the incoming ions have a Maxwell–Boltzmann distribution, the ion distribution function in regions I and IV becomesFootnote
2
${\mathcal{E}}=v^{2}/2+\unicode[STIX]{x1D719}(x)$
is the total ion energy; that is, ions stream along constant-energy contours in phase space, see figure 1(b). With the assumption that the incoming ions have a Maxwell–Boltzmann distribution, the ion distribution function in regions I and IV becomesFootnote
2
where
![]() $\unicode[STIX]{x1D70F}\equiv ZT_{\text{e}}/T_{\text{i}}$
. We also divide up phase space into four different regions: passing, trapped, co-passing and reflected regions of phase space, which we denote by the roman numerals I, II, III and IV, respectively. In the collisionless case, regions II and III are completely empty, which consequently means that the ion distribution is discontinuous at the separatrix. The separatrix is marked out by the dashed line in figure 1(b), and it is given by
$\unicode[STIX]{x1D70F}\equiv ZT_{\text{e}}/T_{\text{i}}$
. We also divide up phase space into four different regions: passing, trapped, co-passing and reflected regions of phase space, which we denote by the roman numerals I, II, III and IV, respectively. In the collisionless case, regions II and III are completely empty, which consequently means that the ion distribution is discontinuous at the separatrix. The separatrix is marked out by the dashed line in figure 1(b), and it is given by
![]() $\pm v_{0}=\pm \sqrt{2(\unicode[STIX]{x1D719}_{\text{max}}-\unicode[STIX]{x1D719})}$
in the up- (
$\pm v_{0}=\pm \sqrt{2(\unicode[STIX]{x1D719}_{\text{max}}-\unicode[STIX]{x1D719})}$
in the up- (
![]() $+v_{0}$
) and downstream (
$+v_{0}$
) and downstream (
![]() $-v_{0}$
). It is this discontinuity of the distribution function to which we will turn our attention in the following sections.
$-v_{0}$
). It is this discontinuity of the distribution function to which we will turn our attention in the following sections.
2.1 Introducing collisions
In the following, we will describe the underlying assumptions of the collisional shock model. While the collisionless model has a steady-state solution with a discontinuity, that discontinuity can clearly not survive in the collisional problem. In this paper, we consider a model problem where this discontinuous
![]() $f$
is taken as the initial condition for the collisional problem, which has a time dependence resulting from collisions. We assume that the collision frequency is small; in particular, the collision time is much longer than the typical time for ions to stream through some finite vicinity of the shock front considered, i.e. across a few downstream oscillations.
$f$
is taken as the initial condition for the collisional problem, which has a time dependence resulting from collisions. We assume that the collision frequency is small; in particular, the collision time is much longer than the typical time for ions to stream through some finite vicinity of the shock front considered, i.e. across a few downstream oscillations.
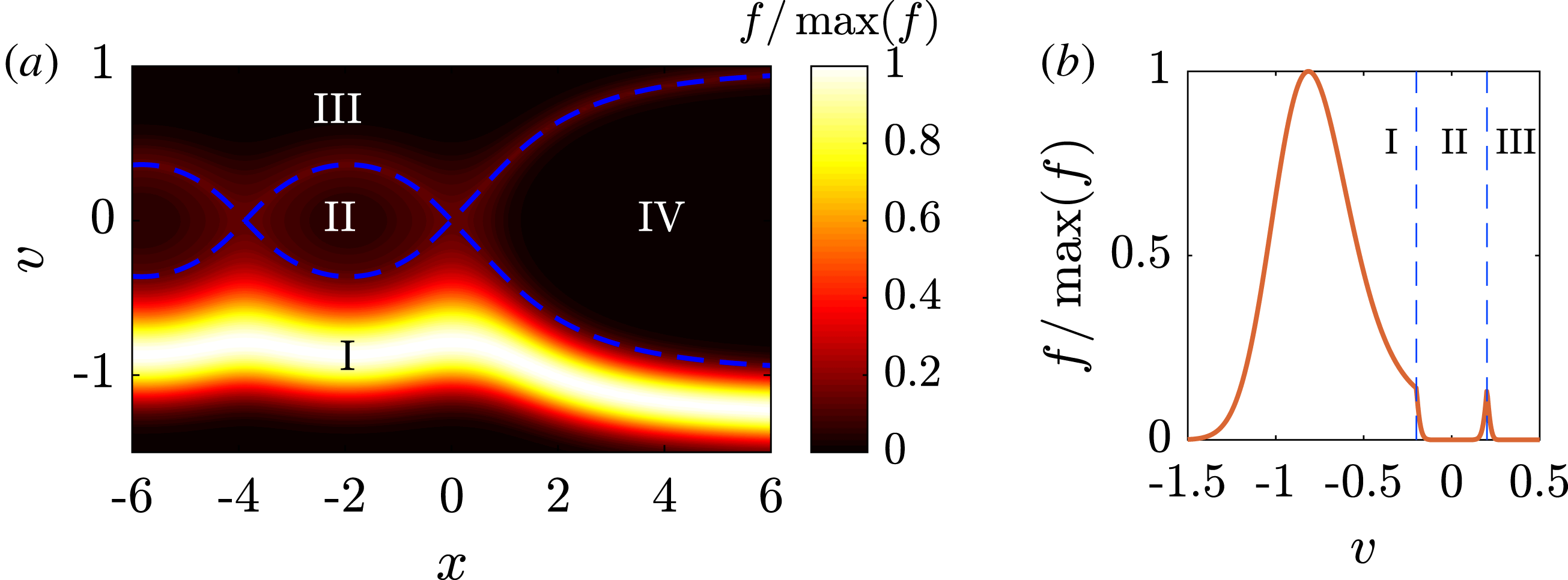
Figure 2. (a) Density plot of the ion distribution function at a collisional age of
![]() $\unicode[STIX]{x1D708}_{\ast }t=0.01$
, for the parameters
$\unicode[STIX]{x1D708}_{\ast }t=0.01$
, for the parameters
![]() $\unicode[STIX]{x1D70F}=50$
,
$\unicode[STIX]{x1D70F}=50$
,
![]() ${\mathcal{M}}=1.25$
(calculated using the model of § 2.2). Dashed curves: phase-space separatrices. Regions of phase space: I – passing, II – trapped, III – co-passing, IV – reflected. (b) The ion velocity distribution at
${\mathcal{M}}=1.25$
(calculated using the model of § 2.2). Dashed curves: phase-space separatrices. Regions of phase space: I – passing, II – trapped, III – co-passing, IV – reflected. (b) The ion velocity distribution at
![]() $x=-0.62$
, showing the counter and co-propagating populations of the trapped ions (region II).
$x=-0.62$
, showing the counter and co-propagating populations of the trapped ions (region II).
The collisions will, heuristically, act to smooth out the original discontinuity into a thin boundary layer. As ions are scattered into this boundary layer, they enter the trapped region (II), where they will orbit; a population of trapped ions will develop along both the upper and lower separatrices, as is illustrated in figure 2(a). A cut of the same distribution at a certain downstream location is shown in figure 2(b). There will also be scattering of ions near the upper separatrix into region III.
Far from the boundary layers, where the distribution function is not as sharp, the solution remains essentially unchanged. Thus, for
![]() $x\geqslant 0$
, we may assume
$x\geqslant 0$
, we may assume
![]() $f$
to be the collisionless solution in regions I and IV. There is, however, a boundary layer in region I, which is due to the depletion of ions near the separatrix in region I, but since this layer is very thin and almost static in time, we disregard it and focus on the thicker (but still thin compared to the thermal speed) and time varying boundary layer which develops in regions II and III. We therefore use the value of
$f$
to be the collisionless solution in regions I and IV. There is, however, a boundary layer in region I, which is due to the depletion of ions near the separatrix in region I, but since this layer is very thin and almost static in time, we disregard it and focus on the thicker (but still thin compared to the thermal speed) and time varying boundary layer which develops in regions II and III. We therefore use the value of
![]() $f^{\text{I,IV}}$
, from (2.3), on the separatrix,
$f^{\text{I,IV}}$
, from (2.3), on the separatrix,
![]() $v=-v_{0}$
, as a boundary condition for
$v=-v_{0}$
, as a boundary condition for
![]() $f$
in region II.
$f$
in region II.
For this problem, we would like to solve the ion kinetic equation, which in the 1-D electrostatic case reads
where
![]() $C$
is the collision operator. Since we consider the dynamics of a thin boundary layer, we only need to focus on the highest-order derivative term – the diffusion. Later, as we will introduce other phase-space coordinates, first-order derivatives will be systematically neglected, which will be justified a posteriori. For simplicity, we will also neglect the velocity dependence of the collision frequency. With these choices, it is sufficient to replace
$C$
is the collision operator. Since we consider the dynamics of a thin boundary layer, we only need to focus on the highest-order derivative term – the diffusion. Later, as we will introduce other phase-space coordinates, first-order derivatives will be systematically neglected, which will be justified a posteriori. For simplicity, we will also neglect the velocity dependence of the collision frequency. With these choices, it is sufficient to replace
![]() $C[f]$
by
$C[f]$
by
![]() $(\unicode[STIX]{x1D708}_{\ast }/\unicode[STIX]{x1D70F})\unicode[STIX]{x2202}_{vv}$
, where the collisionality is assumed to be small,
$(\unicode[STIX]{x1D708}_{\ast }/\unicode[STIX]{x1D70F})\unicode[STIX]{x2202}_{vv}$
, where the collisionality is assumed to be small,
![]() $\unicode[STIX]{x1D708}_{\ast }\ll 1$
. We have chosen to define the collisionality,
$\unicode[STIX]{x1D708}_{\ast }\ll 1$
. We have chosen to define the collisionality,
![]() $\unicode[STIX]{x1D708}_{\ast }=\unicode[STIX]{x1D708}(v_{\text{i},\text{th}})\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
, using the natural time normalization,
$\unicode[STIX]{x1D708}_{\ast }=\unicode[STIX]{x1D708}(v_{\text{i},\text{th}})\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
, using the natural time normalization,
![]() $\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
, and the collision frequency at the ion thermal velocity,
$\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
, and the collision frequency at the ion thermal velocity,
![]() $v_{\text{i},\text{th}}/c_{\text{s}}=\unicode[STIX]{x1D70F}^{-1/2}$
. This choice is the reason for the factor
$v_{\text{i},\text{th}}/c_{\text{s}}=\unicode[STIX]{x1D70F}^{-1/2}$
. This choice is the reason for the factor
![]() $1/\unicode[STIX]{x1D70F}$
in our model collision operator.
$1/\unicode[STIX]{x1D70F}$
in our model collision operator.
In our analytical model, we only consider the effects of collisions within the narrow boundary layer around the separatrices. This treatment of collisions effectively means that the collisionality between high-energy ions and the bulk is suppressed. We point this fact out since the shocks will have structures that are widely separated in velocity space, e.g. the incoming and the reflected ions. Consequently, any attempt at simulating collisional shocks must be done with a collision operator which accurately captures the diminishing collisional effect on particles with high relative velocities. In practice, this comment applies to any simulation with a strongly super-thermal population. We elaborate further on collisional simulations in appendix A, with a focus on the Lenard–Bernstein model collision operator.
2.2 Perturbative, orbit-averaged solution to the kinetic equation
To solve (2.4), we employ a perturbative scheme in the ordering
![]() $\unicode[STIX]{x1D708}_{\ast }\ll 1$
, and we assume that all explicit time dependence in the frame of the shock is due to collisions. As such, all dependencies on
$\unicode[STIX]{x1D708}_{\ast }\ll 1$
, and we assume that all explicit time dependence in the frame of the shock is due to collisions. As such, all dependencies on
![]() $t$
vary on much slower time scales than that of ions streaming past a few downstream oscillations. With
$t$
vary on much slower time scales than that of ions streaming past a few downstream oscillations. With
![]() $f(x,v,t)$
perturbatively expanded as
$f(x,v,t)$
perturbatively expanded as
![]() $f=f_{0}+f_{1}+\cdots$
, where
$f=f_{0}+f_{1}+\cdots$
, where
![]() $f_{k+1}/f_{k}$
is small in
$f_{k+1}/f_{k}$
is small in
![]() $\unicode[STIX]{x1D708}_{\ast }$
, the lowest-order equation becomes
$\unicode[STIX]{x1D708}_{\ast }$
, the lowest-order equation becomes
which recovers (2.1) used for the collisionless model. Analogously to the collisionless model, the solution to (2.5) is given here by
![]() $f_{0}(x,v,t)=f_{0}({\mathcal{E}},t)$
, again with
$f_{0}(x,v,t)=f_{0}({\mathcal{E}},t)$
, again with
![]() ${\mathcal{E}}=v^{2}/2+\unicode[STIX]{x1D719}$
. However, whereas the collisionless model was static and the energy dependence was derived from a Maxwellian ion distribution with the addition of reflected ions, the energy and time dependence of
${\mathcal{E}}=v^{2}/2+\unicode[STIX]{x1D719}$
. However, whereas the collisionless model was static and the energy dependence was derived from a Maxwellian ion distribution with the addition of reflected ions, the energy and time dependence of
![]() $f_{0}$
is as yet undetermined; to obtain an equation for that, we need to consider the next-order correction to the kinetic equation,
$f_{0}$
is as yet undetermined; to obtain an equation for that, we need to consider the next-order correction to the kinetic equation,
In analogy to gyrokinetics, a closed equation for
![]() $f_{0}$
is obtained by taking an appropriate orbit average of (2.6) that annihilates the
$f_{0}$
is obtained by taking an appropriate orbit average of (2.6) that annihilates the
![]() $f_{1}$
terms. We employ the following orbit average
$f_{1}$
terms. We employ the following orbit average
where the integrals are taken along constant
![]() ${\mathcal{E}}$
contours, over a bounce period for trapped particles and over a full oscillation period of the downstream potential for passing particles. For any
${\mathcal{E}}$
contours, over a bounce period for trapped particles and over a full oscillation period of the downstream potential for passing particles. For any
![]() $g$
that is periodic in these domains, we find that
$g$
that is periodic in these domains, we find that
We have found from (2.5) that
![]() $\text{d}f_{0}/\text{d}\unicode[STIX]{x1D703}=0$
and we assume
$\text{d}f_{0}/\text{d}\unicode[STIX]{x1D703}=0$
and we assume
![]() $f_{1}$
to have the required periodicity to make the
$f_{1}$
to have the required periodicity to make the
![]() $f_{1}$
terms in (2.6) vanish upon orbit averaging, which gives
$f_{1}$
terms in (2.6) vanish upon orbit averaging, which gives
where we have neglected all first-order derivative
![]() $\unicode[STIX]{x2202}_{{\mathcal{E}}}f_{0}$
terms against the second-order derivative term, due to the sharp variation of
$\unicode[STIX]{x2202}_{{\mathcal{E}}}f_{0}$
terms against the second-order derivative term, due to the sharp variation of
![]() $f_{0}$
across the boundary layer, and used that
$f_{0}$
across the boundary layer, and used that
![]() $\unicode[STIX]{x2202}_{{\mathcal{E}}{\mathcal{E}}}f_{0}$
is
$\unicode[STIX]{x2202}_{{\mathcal{E}}{\mathcal{E}}}f_{0}$
is
![]() $\unicode[STIX]{x1D703}$
-independent to pull it through the orbit average. We have hereby obtained an equation with only
$\unicode[STIX]{x1D703}$
-independent to pull it through the orbit average. We have hereby obtained an equation with only
![]() $f_{0}$
, which can be used to solve for the energy and time dependence of
$f_{0}$
, which can be used to solve for the energy and time dependence of
![]() $f_{0}$
.
$f_{0}$
.
In order to explicitly evaluate
![]() $\langle v^{2}\rangle _{{\mathcal{E}}}$
, we need to specify
$\langle v^{2}\rangle _{{\mathcal{E}}}$
, we need to specify
![]() $\unicode[STIX]{x1D719}(x)$
. Orbit averages defined by (2.7) for an arbitrary
$\unicode[STIX]{x1D719}(x)$
. Orbit averages defined by (2.7) for an arbitrary
![]() $\unicode[STIX]{x1D719}(x)$
would not lead to closed form expressions. To find the qualitative behaviour while keeping the problem analytically tractable, we assume a simple harmonic oscillation of the downstream potential, which can be justified in the low amplitude limit, where the downstream oscillations reduce to linear ion acoustic oscillations. We thus write
$\unicode[STIX]{x1D719}(x)$
would not lead to closed form expressions. To find the qualitative behaviour while keeping the problem analytically tractable, we assume a simple harmonic oscillation of the downstream potential, which can be justified in the low amplitude limit, where the downstream oscillations reduce to linear ion acoustic oscillations. We thus write
where
![]() $\unicode[STIX]{x1D706}$
is the wavelength of the downstream oscillation, and
$\unicode[STIX]{x1D706}$
is the wavelength of the downstream oscillation, and
![]() $\unicode[STIX]{x1D719}_{\text{A}}=\unicode[STIX]{x1D719}_{\text{max}}-\unicode[STIX]{x1D719}_{\text{min}}$
with
$\unicode[STIX]{x1D719}_{\text{A}}=\unicode[STIX]{x1D719}_{\text{max}}-\unicode[STIX]{x1D719}_{\text{min}}$
with
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
and
$\unicode[STIX]{x1D719}_{\text{max}}$
and
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
the maximum and minimum downstream values of
$\unicode[STIX]{x1D719}_{\text{min}}$
the maximum and minimum downstream values of
![]() $\unicode[STIX]{x1D719}$
, respectively. Note that while normally
$\unicode[STIX]{x1D719}$
, respectively. Note that while normally
![]() $x=0$
denotes the location of the first potential maximum, as in figure 1, when evaluating orbit averages we set
$x=0$
denotes the location of the first potential maximum, as in figure 1, when evaluating orbit averages we set
![]() $x=0$
at a downstream potential minimum.
$x=0$
at a downstream potential minimum.
We also introduce
![]() $k=\sqrt{({\mathcal{E}}-\unicode[STIX]{x1D719}_{\text{min}})/\unicode[STIX]{x1D719}_{\text{A}}}$
, for which
$k=\sqrt{({\mathcal{E}}-\unicode[STIX]{x1D719}_{\text{min}})/\unicode[STIX]{x1D719}_{\text{A}}}$
, for which
![]() $k<1$
in the trapped regions and
$k<1$
in the trapped regions and
![]() $k\geqslant 1$
outside. The integrals of the orbit average in the passing region can now be evaluated to:
$k\geqslant 1$
outside. The integrals of the orbit average in the passing region can now be evaluated to:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \oint _{{\mathcal{E}}}\,\text{d}\unicode[STIX]{x1D703}=\frac{1}{\sqrt{2}}\oint \frac{\text{d}x}{\sqrt{{\mathcal{E}}-\unicode[STIX]{x1D719}(x)}}=\frac{2\unicode[STIX]{x1D706}}{\sqrt{2\unicode[STIX]{x1D719}_{\text{A}}}\unicode[STIX]{x03C0}k}\mathop{\int }_{0}^{\unicode[STIX]{x03C0}/2}\frac{\text{d}y}{\sqrt{1-k^{-2}\sin ^{2}y}}=\frac{\sqrt{2}\unicode[STIX]{x1D706}}{\unicode[STIX]{x03C0}\sqrt{\unicode[STIX]{x1D719}_{\text{A}}}k}K(k^{-2}),\\ \begin{array}{@{}rcl@{}}\displaystyle \oint _{{\mathcal{E}}}v^{2}\,\text{d}\unicode[STIX]{x1D703}\ & =\ & \displaystyle \sqrt{2}\oint \sqrt{{\mathcal{E}}-\unicode[STIX]{x1D719}(x)}\,\text{d}x\\ \ & =\ & \displaystyle \frac{2\sqrt{2\unicode[STIX]{x1D719}_{\text{A}}}k\unicode[STIX]{x1D706}}{\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}/2}\sqrt{1-k^{-2}\sin ^{2}y}\,\text{d}y=\frac{2\sqrt{2\unicode[STIX]{x1D719}_{\text{A}}}k\unicode[STIX]{x1D706}}{\unicode[STIX]{x03C0}}E(k^{-2}),\end{array}\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \oint _{{\mathcal{E}}}\,\text{d}\unicode[STIX]{x1D703}=\frac{1}{\sqrt{2}}\oint \frac{\text{d}x}{\sqrt{{\mathcal{E}}-\unicode[STIX]{x1D719}(x)}}=\frac{2\unicode[STIX]{x1D706}}{\sqrt{2\unicode[STIX]{x1D719}_{\text{A}}}\unicode[STIX]{x03C0}k}\mathop{\int }_{0}^{\unicode[STIX]{x03C0}/2}\frac{\text{d}y}{\sqrt{1-k^{-2}\sin ^{2}y}}=\frac{\sqrt{2}\unicode[STIX]{x1D706}}{\unicode[STIX]{x03C0}\sqrt{\unicode[STIX]{x1D719}_{\text{A}}}k}K(k^{-2}),\\ \begin{array}{@{}rcl@{}}\displaystyle \oint _{{\mathcal{E}}}v^{2}\,\text{d}\unicode[STIX]{x1D703}\ & =\ & \displaystyle \sqrt{2}\oint \sqrt{{\mathcal{E}}-\unicode[STIX]{x1D719}(x)}\,\text{d}x\\ \ & =\ & \displaystyle \frac{2\sqrt{2\unicode[STIX]{x1D719}_{\text{A}}}k\unicode[STIX]{x1D706}}{\unicode[STIX]{x03C0}}\int _{0}^{\unicode[STIX]{x03C0}/2}\sqrt{1-k^{-2}\sin ^{2}y}\,\text{d}y=\frac{2\sqrt{2\unicode[STIX]{x1D719}_{\text{A}}}k\unicode[STIX]{x1D706}}{\unicode[STIX]{x03C0}}E(k^{-2}),\end{array}\end{array}\right\}\end{eqnarray}$$
where
![]() $K$
and
$K$
and
![]() $E$
denote the complete elliptic integrals of the first and second kind,
$E$
denote the complete elliptic integrals of the first and second kind,
![]() $y=\unicode[STIX]{x03C0}x/\unicode[STIX]{x1D706}$
, and we made use of the symmetry of the potential about the potential minimum. Thus, we have
$y=\unicode[STIX]{x03C0}x/\unicode[STIX]{x1D706}$
, and we made use of the symmetry of the potential about the potential minimum. Thus, we have
In the trapped region, the calculation is slightly more complicated, since the particle does not sample the entire
![]() $[-\unicode[STIX]{x1D706}/2,+\unicode[STIX]{x1D706}/2]$
region, only
$[-\unicode[STIX]{x1D706}/2,+\unicode[STIX]{x1D706}/2]$
region, only
![]() $[-\unicode[STIX]{x1D706}_{{\mathcal{E}}}/2,+\unicode[STIX]{x1D706}_{{\mathcal{E}}}/2]$
, where the limits
$[-\unicode[STIX]{x1D706}_{{\mathcal{E}}}/2,+\unicode[STIX]{x1D706}_{{\mathcal{E}}}/2]$
, where the limits
![]() $\pm \unicode[STIX]{x1D706}_{{\mathcal{E}}}/2$
depend on
$\pm \unicode[STIX]{x1D706}_{{\mathcal{E}}}/2$
depend on
![]() ${\mathcal{E}}$
. Introducing
${\mathcal{E}}$
. Introducing
![]() $z$
such that
$z$
such that
![]() $k\sin z=\sin y$
, we find
$k\sin z=\sin y$
, we find
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \oint _{{\mathcal{E}}}\,\text{d}\unicode[STIX]{x1D703}=\frac{2}{\sqrt{2}}\int _{-\unicode[STIX]{x1D706}_{{\mathcal{E}}}/2}^{\unicode[STIX]{x1D706}_{{\mathcal{E}}}/2}\frac{\text{d}x}{\sqrt{{\mathcal{E}}-\unicode[STIX]{x1D719}(x)}}=\frac{2\sqrt{2}\unicode[STIX]{x1D706}}{\sqrt{\unicode[STIX]{x1D719}_{\text{A}}}\unicode[STIX]{x03C0}k}\int _{0}^{\unicode[STIX]{x03C0}/2}\frac{\text{d}z}{\sqrt{1-k^{2}\sin ^{2}z}}=\frac{2\sqrt{2}\unicode[STIX]{x1D706}}{\unicode[STIX]{x03C0}\sqrt{\unicode[STIX]{x1D719}_{\text{A}}}}K(k^{2}),\\ \displaystyle \oint _{{\mathcal{E}}}v^{2}\,\text{d}\unicode[STIX]{x1D703}=2\sqrt{2}\int _{-\unicode[STIX]{x1D706}_{{\mathcal{E}}}/2}^{\unicode[STIX]{x1D706}_{{\mathcal{E}}}/2}\sqrt{{\mathcal{E}}-\unicode[STIX]{x1D719}(x)}\,\text{d}x=\frac{4\sqrt{2\unicode[STIX]{x1D719}_{\text{A}}}\unicode[STIX]{x1D706}}{\unicode[STIX]{x03C0}}[(k^{2}-1)K(k^{2})+E(k^{2})],\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \oint _{{\mathcal{E}}}\,\text{d}\unicode[STIX]{x1D703}=\frac{2}{\sqrt{2}}\int _{-\unicode[STIX]{x1D706}_{{\mathcal{E}}}/2}^{\unicode[STIX]{x1D706}_{{\mathcal{E}}}/2}\frac{\text{d}x}{\sqrt{{\mathcal{E}}-\unicode[STIX]{x1D719}(x)}}=\frac{2\sqrt{2}\unicode[STIX]{x1D706}}{\sqrt{\unicode[STIX]{x1D719}_{\text{A}}}\unicode[STIX]{x03C0}k}\int _{0}^{\unicode[STIX]{x03C0}/2}\frac{\text{d}z}{\sqrt{1-k^{2}\sin ^{2}z}}=\frac{2\sqrt{2}\unicode[STIX]{x1D706}}{\unicode[STIX]{x03C0}\sqrt{\unicode[STIX]{x1D719}_{\text{A}}}}K(k^{2}),\\ \displaystyle \oint _{{\mathcal{E}}}v^{2}\,\text{d}\unicode[STIX]{x1D703}=2\sqrt{2}\int _{-\unicode[STIX]{x1D706}_{{\mathcal{E}}}/2}^{\unicode[STIX]{x1D706}_{{\mathcal{E}}}/2}\sqrt{{\mathcal{E}}-\unicode[STIX]{x1D719}(x)}\,\text{d}x=\frac{4\sqrt{2\unicode[STIX]{x1D719}_{\text{A}}}\unicode[STIX]{x1D706}}{\unicode[STIX]{x03C0}}[(k^{2}-1)K(k^{2})+E(k^{2})],\end{array}\right\}\end{eqnarray}$$
which yields
With the explicitly evaluated orbit averages, (2.12) and (2.14), we can now express (2.9) as
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}t}=2\frac{\unicode[STIX]{x1D708}_{\ast }}{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D719}_{\text{A}}k^{2}F(k^{2})\frac{\unicode[STIX]{x2202}^{2}f_{0}}{\unicode[STIX]{x2202}{\mathcal{E}}^{2}},\quad F(k)=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{k^{2}}\left[\frac{E(k^{2})}{K(k^{2})}+k^{2}-1\right]\quad & \text{for}~k<1,\\ \displaystyle \frac{E(k^{-2})}{K(k^{-2})}\quad & \text{for}~k\geqslant 1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}t}=2\frac{\unicode[STIX]{x1D708}_{\ast }}{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D719}_{\text{A}}k^{2}F(k^{2})\frac{\unicode[STIX]{x2202}^{2}f_{0}}{\unicode[STIX]{x2202}{\mathcal{E}}^{2}},\quad F(k)=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{k^{2}}\left[\frac{E(k^{2})}{K(k^{2})}+k^{2}-1\right]\quad & \text{for}~k<1,\\ \displaystyle \frac{E(k^{-2})}{K(k^{-2})}\quad & \text{for}~k\geqslant 1.\end{array}\right.\end{eqnarray}$$
2.3 Transformation to a diffusion equation and solution
It is practical to rewrite (2.15) as a simple diffusion equation
where the approximations made are that only second-order derivatives are kept. The intermediary variable,
![]() $\unicode[STIX]{x1D716}=1-k$
, is positive in the trapped region and negative outside, and
$\unicode[STIX]{x1D716}=1-k$
, is positive in the trapped region and negative outside, and
![]() $w$
is defined by
$w$
is defined by
Thus, the stretched variable
![]() $w$
is defined to be order unity across the boundary layer, while
$w$
is defined to be order unity across the boundary layer, while
![]() $\unicode[STIX]{x1D716}\ll 1$
. Henceforth, the zero subscript of
$\unicode[STIX]{x1D716}\ll 1$
. Henceforth, the zero subscript of
![]() $f$
is dropped to streamline notation, as
$f$
is dropped to streamline notation, as
![]() $f_{1}$
is unimportant to this order in
$f_{1}$
is unimportant to this order in
![]() $\unicode[STIX]{x1D708}_{\ast }$
.
$\unicode[STIX]{x1D708}_{\ast }$
.
We use the collisionless distribution function, (2.3), as both the initial condition for this problem as well as the boundary condition on the separatrix between regions I and II, assuming that the collisionality is low enough that the shock has time to form on a much faster time scale. In region II,
![]() $f$
is solved for using
$f$
is solved for using
where we take the value of
![]() $f^{\text{I}}$
at the separatrix
$f^{\text{I}}$
at the separatrix
as a boundary condition and
![]() $v_{0}=\sqrt{2(\unicode[STIX]{x1D719}_{\text{max}}-\unicode[STIX]{x1D719})}$
is the magnitude of the velocity at the separatrix. We do this since region I is constantly replenished with new ions passing from the upstream.
$v_{0}=\sqrt{2(\unicode[STIX]{x1D719}_{\text{max}}-\unicode[STIX]{x1D719})}$
is the magnitude of the velocity at the separatrix. We do this since region I is constantly replenished with new ions passing from the upstream.
The solution to the diffusion equation (2.18) with the initial condition
![]() $f(t=0,w)=\unicode[STIX]{x1D6E9}(-w)$
, where
$f(t=0,w)=\unicode[STIX]{x1D6E9}(-w)$
, where
![]() $\unicode[STIX]{x1D6E9}$
denotes the Heaviside step function, together with the boundary conditions
$\unicode[STIX]{x1D6E9}$
denotes the Heaviside step function, together with the boundary conditions
![]() $f(w\rightarrow -\infty )=1$
and
$f(w\rightarrow -\infty )=1$
and
![]() $f(w\rightarrow +\infty )=0$
, is
$f(w\rightarrow +\infty )=0$
, is
![]() $f(w,t)=(1/2)\text{erfc}[w/(2\sqrt{t})]$
, where
$f(w,t)=(1/2)\text{erfc}[w/(2\sqrt{t})]$
, where
![]() $\text{erfc}$
is the complementary error function. This is easily shown employing the Green’s function
$\text{erfc}$
is the complementary error function. This is easily shown employing the Green’s function
![]() $G(t,w-w^{\prime })=(4\unicode[STIX]{x03C0}t)^{-1/2}\exp [-(w-w^{\prime })^{2}/(4t)]$
. Noting that for this
$G(t,w-w^{\prime })=(4\unicode[STIX]{x03C0}t)^{-1/2}\exp [-(w-w^{\prime })^{2}/(4t)]$
. Noting that for this
![]() $f(w,t)$
,
$f(w,t)$
,
![]() $f(w=0)=1/2$
for all times, it is clear that
$f(w=0)=1/2$
for all times, it is clear that
![]() $f$
can also be considered as the solution for the problem in the semi-infinite domain, where the boundary conditions are
$f$
can also be considered as the solution for the problem in the semi-infinite domain, where the boundary conditions are
![]() $f(w=0)=1/2$
,
$f(w=0)=1/2$
,
![]() $f(w\rightarrow +\infty )=0$
, and the initial condition is
$f(w\rightarrow +\infty )=0$
, and the initial condition is
![]() $f(w>0,t=0)=0$
. The boundary condition
$f(w>0,t=0)=0$
. The boundary condition
![]() $f(w=0)=1/2$
can only be sustained by a net influx of particles across the boundary. The particles streaming along the lower separatrix, coming from the upstream and keeping
$f(w=0)=1/2$
can only be sustained by a net influx of particles across the boundary. The particles streaming along the lower separatrix, coming from the upstream and keeping
![]() $f$
fixed in region I, represent a reservoir that provides this time-dependent influx into region II (with the slight difference that the value of
$f$
fixed in region I, represent a reservoir that provides this time-dependent influx into region II (with the slight difference that the value of
![]() $f$
at the separatrix is
$f$
at the separatrix is
![]() ${\mathcal{F}}$
instead of
${\mathcal{F}}$
instead of
![]() $1/2$
). The time scale separation between the streaming and the collisional processes guarantees that
$1/2$
). The time scale separation between the streaming and the collisional processes guarantees that
![]() $f$
is held fixed at the boundary, even though there is a net outflux to region III, on top of the random walk of particles away from the separatrix, deeper into II. The fact that, formally,
$f$
is held fixed at the boundary, even though there is a net outflux to region III, on top of the random walk of particles away from the separatrix, deeper into II. The fact that, formally,
![]() $w$
only has a finite range in region II is not a concern, since this range is large for a small value of our perturbation parameter
$w$
only has a finite range in region II is not a concern, since this range is large for a small value of our perturbation parameter
![]() $\unicode[STIX]{x1D708}_{\ast }$
, and
$\unicode[STIX]{x1D708}_{\ast }$
, and
![]() $\text{erfc}$
drops rapidly for an argument larger than unity. Hence the solution is
$\text{erfc}$
drops rapidly for an argument larger than unity. Hence the solution is
where the sign of the argument in region II (III) is
![]() $+$
(
$+$
(
![]() $-$
). Note that there is some ambiguity of
$-$
). Note that there is some ambiguity of
![]() $f$
in region III, as it depends on the behaviour of
$f$
in region III, as it depends on the behaviour of
![]() $f$
far downstream. This solution assumes an infinite downstream oscillation, and as such, it represents an upper bound to the density contribution from region III. We will find that the actual behaviour of
$f$
far downstream. This solution assumes an infinite downstream oscillation, and as such, it represents an upper bound to the density contribution from region III. We will find that the actual behaviour of
![]() $f$
in region III has only a minor effect:
$f$
in region III has only a minor effect:
![]() $f$
being finite in this region leads to a slight reduction of
$f$
being finite in this region leads to a slight reduction of
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
.
$\unicode[STIX]{x1D719}_{\text{max}}$
.
The resulting densities in regions II and III, due to (2.20), are
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle n^{\text{II}}=2\int _{0}^{v_{0}}f^{\text{II}}(v)\,\text{d}v=2{\mathcal{F}}\sqrt{2\unicode[STIX]{x1D719}_{\text{A}}}\int _{\unicode[STIX]{x1D705}}^{1}\text{erfc}\left(\frac{w(k)}{2\sqrt{t}}\right)\frac{k\,\text{d}k}{\sqrt{k^{2}-\unicode[STIX]{x1D705}^{2}}},\\ \displaystyle n^{\text{III}}=\int _{1}^{\infty }f^{\text{II}}(v)\,\text{d}v={\mathcal{F}}\sqrt{2\unicode[STIX]{x1D719}_{\text{A}}}\int _{1}^{\infty }\text{erfc}\left(-\frac{w(k)}{2\sqrt{t}}\right)\frac{k\,\text{d}k}{\sqrt{k^{2}-\unicode[STIX]{x1D705}^{2}}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle n^{\text{II}}=2\int _{0}^{v_{0}}f^{\text{II}}(v)\,\text{d}v=2{\mathcal{F}}\sqrt{2\unicode[STIX]{x1D719}_{\text{A}}}\int _{\unicode[STIX]{x1D705}}^{1}\text{erfc}\left(\frac{w(k)}{2\sqrt{t}}\right)\frac{k\,\text{d}k}{\sqrt{k^{2}-\unicode[STIX]{x1D705}^{2}}},\\ \displaystyle n^{\text{III}}=\int _{1}^{\infty }f^{\text{II}}(v)\,\text{d}v={\mathcal{F}}\sqrt{2\unicode[STIX]{x1D719}_{\text{A}}}\int _{1}^{\infty }\text{erfc}\left(-\frac{w(k)}{2\sqrt{t}}\right)\frac{k\,\text{d}k}{\sqrt{k^{2}-\unicode[STIX]{x1D705}^{2}}},\end{array}\right\}\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}(\unicode[STIX]{x1D719})=\sqrt{(\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{\text{min}})/\unicode[STIX]{x1D719}_{\text{A}}}$
; in region II, we used that
$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}(\unicode[STIX]{x1D719})=\sqrt{(\unicode[STIX]{x1D719}-\unicode[STIX]{x1D719}_{\text{min}})/\unicode[STIX]{x1D719}_{\text{A}}}$
; in region II, we used that
![]() $f$
is even in
$f$
is even in
![]() $v$
. The practical aspects of how these integrals are evaluated, along with further details on the numerical implementation of the model, are discussed in appendix B. These densities, together with the velocity integrals of
$v$
. The practical aspects of how these integrals are evaluated, along with further details on the numerical implementation of the model, are discussed in appendix B. These densities, together with the velocity integrals of
![]() $f^{\text{I}}$
and
$f^{\text{I}}$
and
![]() $f^{\text{IV}}$
(
$f^{\text{IV}}$
(
![]() $v$
from
$v$
from
![]() $-\infty$
to
$-\infty$
to
![]() $-v_{0}$
and
$-v_{0}$
and
![]() $v_{0}$
, respectively) given by (2.3), are used in Poisson’s equation (2.2) to calculate the potential.
$v_{0}$
, respectively) given by (2.3), are used in Poisson’s equation (2.2) to calculate the potential.
Since the ion distribution function implicitly depends on
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
and
$\unicode[STIX]{x1D719}_{\text{max}}$
and
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
, these need to be calculated before Poisson’s equation can be integrated to obtain
$\unicode[STIX]{x1D719}_{\text{min}}$
, these need to be calculated before Poisson’s equation can be integrated to obtain
![]() $\unicode[STIX]{x1D719}(x)$
. This is achieved by introducing the Sagdeev potential,
$\unicode[STIX]{x1D719}(x)$
. This is achieved by introducing the Sagdeev potential,
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D719};\unicode[STIX]{x1D719}_{\text{max}},\unicode[STIX]{x1D719}_{\text{min}})$
, with the property
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D719};\unicode[STIX]{x1D719}_{\text{max}},\unicode[STIX]{x1D719}_{\text{min}})$
, with the property
![]() $\text{d}\unicode[STIX]{x1D6F7}/\text{d}\unicode[STIX]{x1D719}=-\text{d}^{2}\unicode[STIX]{x1D719}/\text{d}x^{2}$
(Tidman & Krall Reference Tidman and Krall1971). Thus,
$\text{d}\unicode[STIX]{x1D6F7}/\text{d}\unicode[STIX]{x1D719}=-\text{d}^{2}\unicode[STIX]{x1D719}/\text{d}x^{2}$
(Tidman & Krall Reference Tidman and Krall1971). Thus,
in the upstream and
in the downstream region. Then the potential extrema can be found solving the system
![]() $\unicode[STIX]{x1D6F7}^{\text{u}}(\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{\text{max}};\unicode[STIX]{x1D719}_{\text{max}},\unicode[STIX]{x1D719}_{\text{min}})=0$
and
$\unicode[STIX]{x1D6F7}^{\text{u}}(\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{\text{max}};\unicode[STIX]{x1D719}_{\text{max}},\unicode[STIX]{x1D719}_{\text{min}})=0$
and
![]() $\unicode[STIX]{x1D6F7}^{\text{d}}(\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{\text{min}};\unicode[STIX]{x1D719}_{\text{max}},\unicode[STIX]{x1D719}_{\text{min}})=0$
simultaneously. Note that
$\unicode[STIX]{x1D6F7}^{\text{d}}(\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{\text{min}};\unicode[STIX]{x1D719}_{\text{max}},\unicode[STIX]{x1D719}_{\text{min}})=0$
simultaneously. Note that
![]() $\unicode[STIX]{x1D70C}^{\text{u}}$
and
$\unicode[STIX]{x1D70C}^{\text{u}}$
and
![]() $\unicode[STIX]{x1D70C}^{\text{d}}$
are slightly different due to the reflected ions, which indeed makes (2.22) and (2.23) two independent equations for the two unknowns
$\unicode[STIX]{x1D70C}^{\text{d}}$
are slightly different due to the reflected ions, which indeed makes (2.22) and (2.23) two independent equations for the two unknowns
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
and
$\unicode[STIX]{x1D719}_{\text{max}}$
and
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
. This completes the calculation of
$\unicode[STIX]{x1D719}_{\text{min}}$
. This completes the calculation of
![]() $\unicode[STIX]{x1D719}(x)$
for any given instance of time.
$\unicode[STIX]{x1D719}(x)$
for any given instance of time.
Before we start discussing the results, we revisit the practice of neglecting first-order derivatives across the boundary layer. If the first-order energy derivative was not neglected on the right-hand side of (2.9), we would get
The approximation to neglect the second term must break down in a certain vicinity of the separatrix, since
![]() $\langle v^{2}\rangle _{{\mathcal{E}}}$
vanishes at the separatrix. To estimate the size of this region, we balance the sizes of the two terms
$\langle v^{2}\rangle _{{\mathcal{E}}}$
vanishes at the separatrix. To estimate the size of this region, we balance the sizes of the two terms
where
![]() $\unicode[STIX]{x0394}$
refers to the size of the collisional boundary layer and
$\unicode[STIX]{x0394}$
refers to the size of the collisional boundary layer and
![]() $\unicode[STIX]{x1D6FF}$
to the size of the layer where the approximation breaks down. The width of the collisional layer in
$\unicode[STIX]{x1D6FF}$
to the size of the layer where the approximation breaks down. The width of the collisional layer in
![]() $\unicode[STIX]{x1D716}$
is
$\unicode[STIX]{x1D716}$
is
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D716}\sim \sqrt{t}/\unicode[STIX]{x1D6F6}\sim \sqrt{\unicode[STIX]{x1D708}_{\ast }t}\ll 1$
, since the width in
$\unicode[STIX]{x0394}\unicode[STIX]{x1D716}\sim \sqrt{t}/\unicode[STIX]{x1D6F6}\sim \sqrt{\unicode[STIX]{x1D708}_{\ast }t}\ll 1$
, since the width in
![]() $w$
is
$w$
is
![]() ${\sim}\sqrt{t}$
, and although
${\sim}\sqrt{t}$
, and although
![]() $\unicode[STIX]{x1D70F}$
is usually large, it is considered to be an order-unity quantity in our perturbation theory, as is
$\unicode[STIX]{x1D70F}$
is usually large, it is considered to be an order-unity quantity in our perturbation theory, as is
![]() $\unicode[STIX]{x1D719}_{\text{A}}$
. Thus, we also have
$\unicode[STIX]{x1D719}_{\text{A}}$
. Thus, we also have
![]() $\unicode[STIX]{x0394}{\mathcal{E}}=2\unicode[STIX]{x1D719}_{\text{A}}k\unicode[STIX]{x1D6FF}k\sim \sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
. Using the asymptotic behaviour of
$\unicode[STIX]{x0394}{\mathcal{E}}=2\unicode[STIX]{x1D719}_{\text{A}}k\unicode[STIX]{x1D6FF}k\sim \sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
. Using the asymptotic behaviour of
![]() $F(\unicode[STIX]{x1D716})\simeq 2/\ln (8/|\unicode[STIX]{x1D716}|)$
for
$F(\unicode[STIX]{x1D716})\simeq 2/\ln (8/|\unicode[STIX]{x1D716}|)$
for
![]() $\unicode[STIX]{x1D716}\rightarrow 0$
, equation (2.25) yields
$\unicode[STIX]{x1D716}\rightarrow 0$
, equation (2.25) yields
We therefore find that the layer where the approximation breaks down is exponentially small
and the accumulated contributions to
![]() $f_{0}$
form first-order derivatives are thus negligible.
$f_{0}$
form first-order derivatives are thus negligible.
As it is relevant to the present discussion, we note again that we have also neglected another small boundary layer around the separatrix of a time-independent width in
![]() $v$
of
$v$
of
![]() ${\sim}\sqrt{\unicode[STIX]{x1D708}_{\ast }}\ll 1$
.
${\sim}\sqrt{\unicode[STIX]{x1D708}_{\ast }}\ll 1$
.
To avoid significantly increasing the mathematical complexity of the problem, in deriving (2.9), we have also neglected the term
![]() $\langle \dot{{\mathcal{E}}}\unicode[STIX]{x2202}_{{\mathcal{E}}}f_{0}\rangle _{{\mathcal{E}}}=\langle \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D719}\rangle _{{\mathcal{E}}}\unicode[STIX]{x2202}_{{\mathcal{E}}}f_{0}$
, stemming from the coordinate transformation
$\langle \dot{{\mathcal{E}}}\unicode[STIX]{x2202}_{{\mathcal{E}}}f_{0}\rangle _{{\mathcal{E}}}=\langle \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D719}\rangle _{{\mathcal{E}}}\unicode[STIX]{x2202}_{{\mathcal{E}}}f_{0}$
, stemming from the coordinate transformation
![]() $\{x,v\}\rightarrow \{\unicode[STIX]{x1D703},{\mathcal{E}}\}$
. Due to the
$\{x,v\}\rightarrow \{\unicode[STIX]{x1D703},{\mathcal{E}}\}$
. Due to the
![]() $\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
time dependence of the downstream potential oscillations – as we shall find in § 3 – this term is formally of the same order as the collisional diffusion term that we keep. Physically, it describes adiabatic trapping of ions as their trapping region grows in time, and it speeds up the accumulation of ions in the trapping region. Although not changing the character of the solution, and importantly the
$\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
time dependence of the downstream potential oscillations – as we shall find in § 3 – this term is formally of the same order as the collisional diffusion term that we keep. Physically, it describes adiabatic trapping of ions as their trapping region grows in time, and it speeds up the accumulation of ions in the trapping region. Although not changing the character of the solution, and importantly the
![]() $\propto \sqrt{t}$
dependence of the potential variation (as confirmed by numerical solutions of the problem), it leads to a somewhat higher effective diffusion rate. Accordingly, our results represent a lower bound on the effect of collisions.
$\propto \sqrt{t}$
dependence of the potential variation (as confirmed by numerical solutions of the problem), it leads to a somewhat higher effective diffusion rate. Accordingly, our results represent a lower bound on the effect of collisions.
3 Results
The qualitative effect of the collisional diffusion of ions is the following: as the collisional boundary layer widens around the phase-space separatrices with time, the difference between the upstream and downstream densities decreases. Accordingly, the downstream behaviour of the potential becomes increasingly similar to that of the upstream, namely, the minimum of the potential
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
decreases, and the wavelength
$\unicode[STIX]{x1D719}_{\text{min}}$
decreases, and the wavelength
![]() $\unicode[STIX]{x1D706}$
increases. This behaviour is illustrated in figure 3, which shows the potential for three different values of the collisional age,
$\unicode[STIX]{x1D706}$
increases. This behaviour is illustrated in figure 3, which shows the potential for three different values of the collisional age,
![]() $\unicode[STIX]{x1D708}_{\ast }t$
. Unless the shock is terminated by some other mechanism, this process would continue until the width of the collisional layer becomes comparable to the ion thermal width, at which point the shock has developed into a symmetric, soliton-like structure. This stage of the evolution corresponds to
$\unicode[STIX]{x1D708}_{\ast }t$
. Unless the shock is terminated by some other mechanism, this process would continue until the width of the collisional layer becomes comparable to the ion thermal width, at which point the shock has developed into a symmetric, soliton-like structure. This stage of the evolution corresponds to
![]() $\unicode[STIX]{x1D708}_{\ast }t\sim 1$
; however, over that time scale, the assumption of neglecting collisional friction as compared to diffusion has already broken down. The maximum of the potential
$\unicode[STIX]{x1D708}_{\ast }t\sim 1$
; however, over that time scale, the assumption of neglecting collisional friction as compared to diffusion has already broken down. The maximum of the potential
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
is less affected; it only changes due to the distribution function becoming finite in region III. Indeed, if
$\unicode[STIX]{x1D719}_{\text{max}}$
is less affected; it only changes due to the distribution function becoming finite in region III. Indeed, if
![]() $f^{\text{III}}$
would be set to zero,
$f^{\text{III}}$
would be set to zero,
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
would stay constant in time, as it is only affected by the upstream distribution function.
$\unicode[STIX]{x1D719}_{\text{max}}$
would stay constant in time, as it is only affected by the upstream distribution function.

Figure 3. The variation of electrostatic potential over time due to collisions, for
![]() $\unicode[STIX]{x1D70F}=50$
,
$\unicode[STIX]{x1D70F}=50$
,
![]() ${\mathcal{M}}=1.15$
.
${\mathcal{M}}=1.15$
.
![]() $\unicode[STIX]{x1D719}(x)$
is plotted for the collisional ages
$\unicode[STIX]{x1D719}(x)$
is plotted for the collisional ages
![]() $\unicode[STIX]{x1D708}_{\ast }t=0$
(solid curve), 0.02 (dotted) and 0.2 (dashed).
$\unicode[STIX]{x1D708}_{\ast }t=0$
(solid curve), 0.02 (dotted) and 0.2 (dashed).

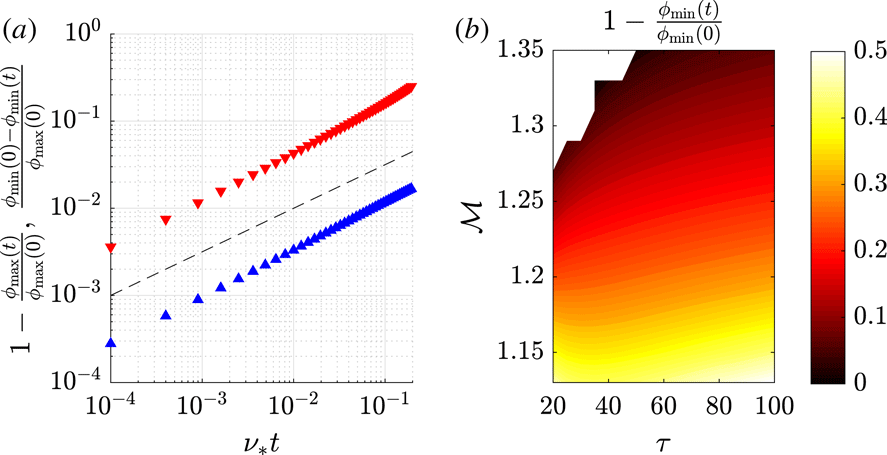
Figure 4. (a) Reduction in
![]() $\unicode[STIX]{x1D719}_{\text{max}}/\unicode[STIX]{x1D719}_{\text{max}}(t=0)$
(▴, blue) and
$\unicode[STIX]{x1D719}_{\text{max}}/\unicode[STIX]{x1D719}_{\text{max}}(t=0)$
(▴, blue) and
![]() $\unicode[STIX]{x1D719}_{\text{min}}/\unicode[STIX]{x1D719}_{\text{max}}(t=0)$
(▾, red) with collisional age, for
$\unicode[STIX]{x1D719}_{\text{min}}/\unicode[STIX]{x1D719}_{\text{max}}(t=0)$
(▾, red) with collisional age, for
![]() $\unicode[STIX]{x1D70F}=50$
, and
$\unicode[STIX]{x1D70F}=50$
, and
![]() ${\mathcal{M}}=1.15$
. For reference, the
${\mathcal{M}}=1.15$
. For reference, the
![]() $\propto \sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
dependence is indicated by the dashed line. (b) The
$\propto \sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
dependence is indicated by the dashed line. (b) The
![]() ${\mathcal{M}}$
and
${\mathcal{M}}$
and
![]() $\unicode[STIX]{x1D70F}$
dependence of
$\unicode[STIX]{x1D70F}$
dependence of
![]() $1-\unicode[STIX]{x1D719}_{\text{min}}(t)/\unicode[STIX]{x1D719}_{\text{min}}(t=0)$
at the collisional age
$1-\unicode[STIX]{x1D719}_{\text{min}}(t)/\unicode[STIX]{x1D719}_{\text{min}}(t=0)$
at the collisional age
![]() $\unicode[STIX]{x1D708}_{\ast }t=0.1$
.
$\unicode[STIX]{x1D708}_{\ast }t=0.1$
.
The changes of both the potential maximum and minimum with collisional age are both approximately proportional to
![]() $\sqrt{t}$
, although the effect on
$\sqrt{t}$
, although the effect on
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
is usually an order of magnitude smaller than that on
$\unicode[STIX]{x1D719}_{\text{max}}$
is usually an order of magnitude smaller than that on
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
. This result is illustrated in the log–log plot of figure 4(a), showing
$\unicode[STIX]{x1D719}_{\text{min}}$
. This result is illustrated in the log–log plot of figure 4(a), showing
![]() $[\unicode[STIX]{x1D719}_{\text{max}}(0)-\unicode[STIX]{x1D719}_{\text{max}}(t)]/\unicode[STIX]{x1D719}_{\text{max}}(0)$
and
$[\unicode[STIX]{x1D719}_{\text{max}}(0)-\unicode[STIX]{x1D719}_{\text{max}}(t)]/\unicode[STIX]{x1D719}_{\text{max}}(0)$
and
![]() $[\unicode[STIX]{x1D719}_{\text{min}}(0)-\unicode[STIX]{x1D719}_{\text{min}}(t)]/\unicode[STIX]{x1D719}_{\text{max}}(0)$
as functions of
$[\unicode[STIX]{x1D719}_{\text{min}}(0)-\unicode[STIX]{x1D719}_{\text{min}}(t)]/\unicode[STIX]{x1D719}_{\text{max}}(0)$
as functions of
![]() $\unicode[STIX]{x1D708}_{\ast }t$
, corresponding to the symbols ▴ and ▾, respectively. The
$\unicode[STIX]{x1D708}_{\ast }t$
, corresponding to the symbols ▴ and ▾, respectively. The
![]() $\sqrt{t}$
dependence is expected, since the width of the boundary layer is
$\sqrt{t}$
dependence is expected, since the width of the boundary layer is
![]() ${\sim}\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
. However, the actual dependence is slightly stronger than
${\sim}\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
. However, the actual dependence is slightly stronger than
![]() $\sqrt{t}$
, and it is not strictly a power law, due to the mapping of
$\sqrt{t}$
, and it is not strictly a power law, due to the mapping of
![]() $w$
to
$w$
to
![]() $v$
, and the nonlinear nature of the problem.
$v$
, and the nonlinear nature of the problem.
The importance of the collisional effects can be quantified by the relative reduction of
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
for a given finite collisional age. Figure 4(b) shows
$\unicode[STIX]{x1D719}_{\text{min}}$
for a given finite collisional age. Figure 4(b) shows
![]() $[\unicode[STIX]{x1D719}_{\text{min}}(0)-\unicode[STIX]{x1D719}_{\text{min}}(t)]/\unicode[STIX]{x1D719}_{\text{min}}(0)$
at
$[\unicode[STIX]{x1D719}_{\text{min}}(0)-\unicode[STIX]{x1D719}_{\text{min}}(t)]/\unicode[STIX]{x1D719}_{\text{min}}(0)$
at
![]() $\unicode[STIX]{x1D708}_{\ast }t=0.1$
as a function of
$\unicode[STIX]{x1D708}_{\ast }t=0.1$
as a function of
![]() ${\mathcal{M}}$
and
${\mathcal{M}}$
and
![]() $\unicode[STIX]{x1D70F}$
. We have chosen the normalization such that the solution would become soliton-like when this quantity would reach the value 1. Naturally, the importance of the collisions depends on the size of the ion trapped region at
$\unicode[STIX]{x1D70F}$
. We have chosen the normalization such that the solution would become soliton-like when this quantity would reach the value 1. Naturally, the importance of the collisions depends on the size of the ion trapped region at
![]() $t=0$
, and thus on the amplitude of the downstream potential oscillation, characterized by
$t=0$
, and thus on the amplitude of the downstream potential oscillation, characterized by
![]() $\unicode[STIX]{x1D719}_{\text{A}}$
. There is an upper limit in
$\unicode[STIX]{x1D719}_{\text{A}}$
. There is an upper limit in
![]() ${\mathcal{M}}$
for laminar electrostatic shock solutions to exist, see e.g. figure 2 of Cairns et al. (Reference Cairns, Bingham, Trines and Norreys2015), and that is the reason for the upper left corner of figure 4(b) being empty. At this limit,
${\mathcal{M}}$
for laminar electrostatic shock solutions to exist, see e.g. figure 2 of Cairns et al. (Reference Cairns, Bingham, Trines and Norreys2015), and that is the reason for the upper left corner of figure 4(b) being empty. At this limit,
![]() $\unicode[STIX]{x1D719}_{\text{A}}$
reduces to zero; therefore, the effect of collisions on
$\unicode[STIX]{x1D719}_{\text{A}}$
reduces to zero; therefore, the effect of collisions on
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
vanishes. Thus, the effectiveness of collisions decreases with increasing
$\unicode[STIX]{x1D719}_{\text{min}}$
vanishes. Thus, the effectiveness of collisions decreases with increasing
![]() ${\mathcal{M}}$
, as seen in figure 4(b). The effect of collisions mostly increases with
${\mathcal{M}}$
, as seen in figure 4(b). The effect of collisions mostly increases with
![]() $\unicode[STIX]{x1D70F}$
, for the same reason. Thus, for a fixed
$\unicode[STIX]{x1D70F}$
, for the same reason. Thus, for a fixed
![]() ${\mathcal{M}}$
, a higher
${\mathcal{M}}$
, a higher
![]() $\unicode[STIX]{x1D70F}$
corresponds to a larger relative downstream oscillation.
$\unicode[STIX]{x1D70F}$
corresponds to a larger relative downstream oscillation.
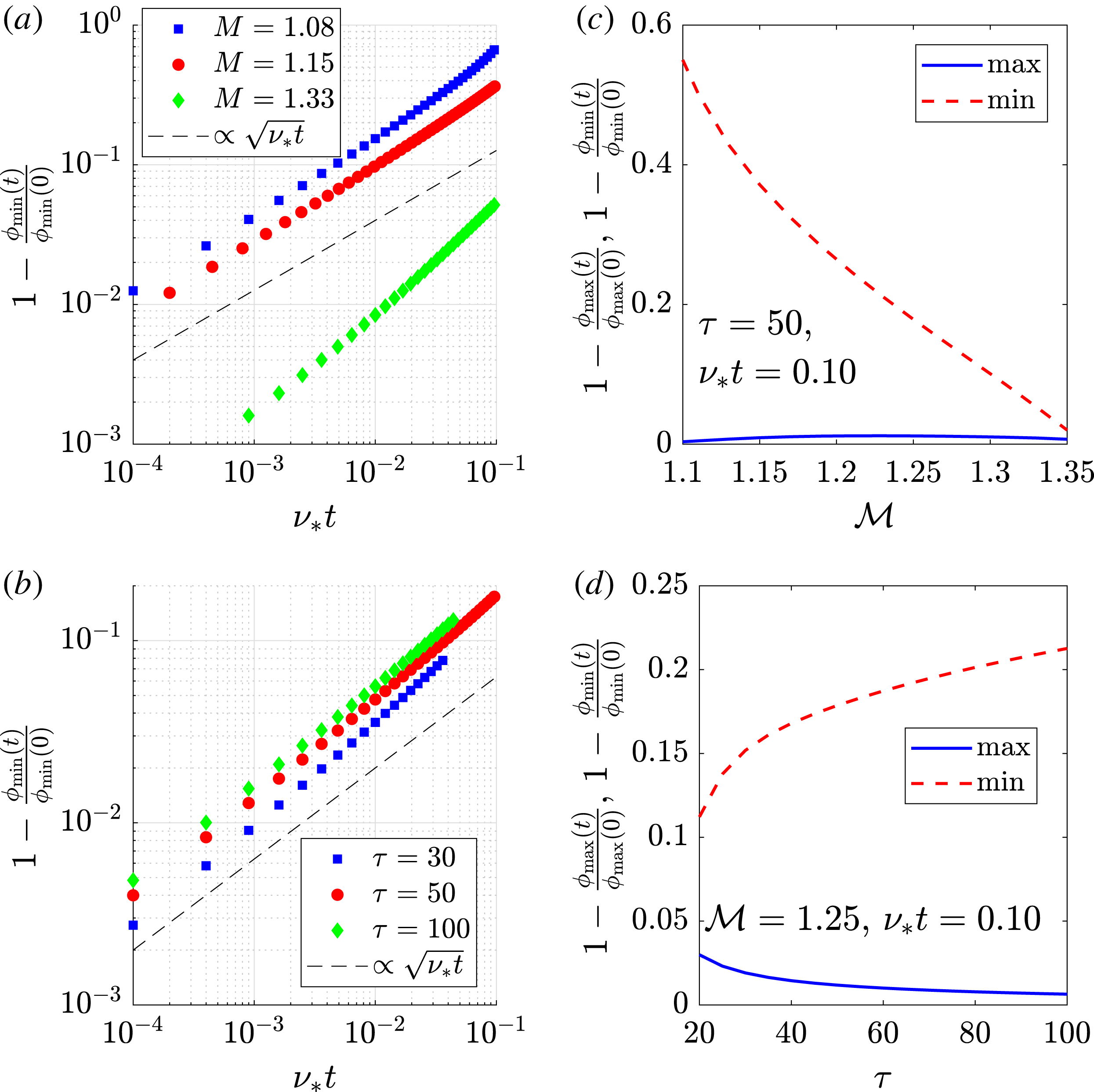
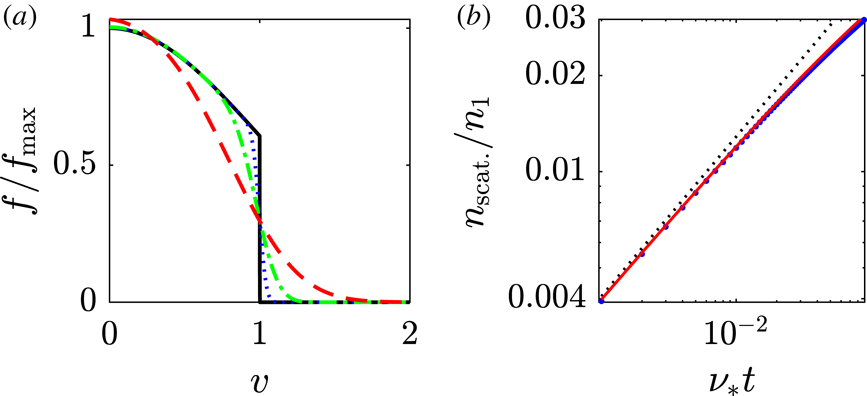
Figure 5. (a,b) Relative reduction of
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
with collisional age. (a) For
$\unicode[STIX]{x1D719}_{\text{min}}$
with collisional age. (a) For
![]() $\unicode[STIX]{x1D70F}=50$
;
$\unicode[STIX]{x1D70F}=50$
;
![]() ${\mathcal{M}}=1.08$
(square symbols), 1.15 (circles) and 1.33 (diamonds). (b) For
${\mathcal{M}}=1.08$
(square symbols), 1.15 (circles) and 1.33 (diamonds). (b) For
![]() ${\mathcal{M}}=1.25$
;
${\mathcal{M}}=1.25$
;
![]() $\unicode[STIX]{x1D70F}=30$
(squares), 50 (circles) and 100 (diamonds). For reference, the
$\unicode[STIX]{x1D70F}=30$
(squares), 50 (circles) and 100 (diamonds). For reference, the
![]() $\propto \sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
dependence is indicated by dashed lines. (c,d) Relative reduction of
$\propto \sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
dependence is indicated by dashed lines. (c,d) Relative reduction of
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
(dashed line) and
$\unicode[STIX]{x1D719}_{\text{min}}$
(dashed line) and
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
(solid), at
$\unicode[STIX]{x1D719}_{\text{max}}$
(solid), at
![]() $\unicode[STIX]{x1D708}_{\ast }t=0.1$
: (c)
$\unicode[STIX]{x1D708}_{\ast }t=0.1$
: (c)
![]() ${\mathcal{M}}$
scan for
${\mathcal{M}}$
scan for
![]() $\unicode[STIX]{x1D70F}=50$
. (d)
$\unicode[STIX]{x1D70F}=50$
. (d)
![]() $\unicode[STIX]{x1D70F}$
scan for
$\unicode[STIX]{x1D70F}$
scan for
![]() ${\mathcal{M}}=1.25$
.
${\mathcal{M}}=1.25$
.
The above parametric dependencies are analysed further in figure 5. We find that the scaling of
![]() $[\unicode[STIX]{x1D719}_{\text{min}}(0)-\unicode[STIX]{x1D719}_{\text{min}}(t)]/\unicode[STIX]{x1D719}_{\text{min}}(0)$
is close to the
$[\unicode[STIX]{x1D719}_{\text{min}}(0)-\unicode[STIX]{x1D719}_{\text{min}}(t)]/\unicode[STIX]{x1D719}_{\text{min}}(0)$
is close to the
![]() $\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
scaling observed for intermediate values of
$\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
scaling observed for intermediate values of
![]() ${\mathcal{M}}$
, as seen in figure 5(a). For high
${\mathcal{M}}$
, as seen in figure 5(a). For high
![]() ${\mathcal{M}}$
, where the trapped region of the collisionless solution is small, we find an overall stronger scaling. For low
${\mathcal{M}}$
, where the trapped region of the collisionless solution is small, we find an overall stronger scaling. For low
![]() ${\mathcal{M}}$
the scaling gets stronger at larger collisional ages when the effect of collisions on the potential becomes order unity, and the downstream oscillation becomes significantly non-sinusoidal. Besides showing the strong
${\mathcal{M}}$
the scaling gets stronger at larger collisional ages when the effect of collisions on the potential becomes order unity, and the downstream oscillation becomes significantly non-sinusoidal. Besides showing the strong
![]() ${\mathcal{M}}$
dependence of the collisional effects on
${\mathcal{M}}$
dependence of the collisional effects on
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
, figure 5(c) also illustrates that the effect on
$\unicode[STIX]{x1D719}_{\text{min}}$
, figure 5(c) also illustrates that the effect on
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
remains negligible for all
$\unicode[STIX]{x1D719}_{\text{max}}$
remains negligible for all
![]() ${\mathcal{M}}$
values. As seen in figure 5(b), getting further away from the limit of shock existence – as
${\mathcal{M}}$
values. As seen in figure 5(b), getting further away from the limit of shock existence – as
![]() $\unicode[STIX]{x1D70F}$
increases – also leads to a scaling closer to
$\unicode[STIX]{x1D70F}$
increases – also leads to a scaling closer to
![]() $\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
. We find that for lower values of
$\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
. We find that for lower values of
![]() $\unicode[STIX]{x1D70F}$
, collisional effects on
$\unicode[STIX]{x1D70F}$
, collisional effects on
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
increase, see figure 5(d). However, the corresponding changes on the reflected ion fraction are still weak, as discussed in appendix C.
$\unicode[STIX]{x1D719}_{\text{max}}$
increase, see figure 5(d). However, the corresponding changes on the reflected ion fraction are still weak, as discussed in appendix C.
4 Conclusions and discussion
We have studied the effect of a weak but finite collisionality on the dynamics of kinetic electrostatic shocks in one dimension. The electrostatic reflection of ions results in the trapped and co-passing regions of ion phase space being empty in the exact collisionless case. This depletion of certain phase-space regions corresponds to a discontinuity in the distribution function across the separatrix. In the presence of collisions, ions are scattered into the originally empty regions of phase space, leading to the development of collisional boundary layers around the separatrix. To focus on this process, we discuss only single ion species plasmas. We consider an initial value problem, initialized by the solution to the collisionless problem, and employ a perturbative, orbit-averaged treatment based on the smallness of the ion collisionality
![]() $\unicode[STIX]{x1D708}_{\ast }=\unicode[STIX]{x1D708}\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
.
$\unicode[STIX]{x1D708}_{\ast }=\unicode[STIX]{x1D708}\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
.
One might be tempted to neglect collisions when
![]() $\unicode[STIX]{x1D708}_{\ast }\ll 1$
; however, since particles keep accumulating in the ion trapped regions, the important quantity for the process is not
$\unicode[STIX]{x1D708}_{\ast }\ll 1$
; however, since particles keep accumulating in the ion trapped regions, the important quantity for the process is not
![]() $\unicode[STIX]{x1D708}_{\ast }$
, but rather the collisional age,
$\unicode[STIX]{x1D708}_{\ast }$
, but rather the collisional age,
![]() $\unicode[STIX]{x1D708}_{\ast }t$
. Even though
$\unicode[STIX]{x1D708}_{\ast }t$
. Even though
![]() $\unicode[STIX]{x1D708}_{\ast }\ll 1$
, the collisional age can become substantial during the lifetime of the shock. Furthermore, as expected from a diffusion problem, the width of the collisional boundary layer is approximately proportional to
$\unicode[STIX]{x1D708}_{\ast }\ll 1$
, the collisional age can become substantial during the lifetime of the shock. Furthermore, as expected from a diffusion problem, the width of the collisional boundary layer is approximately proportional to
![]() $\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
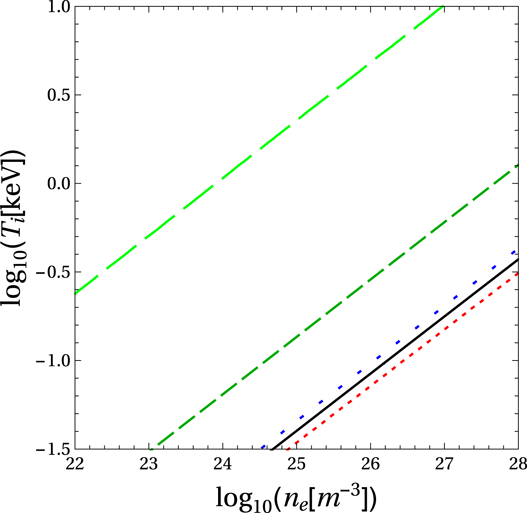
. For the effect of collisions to be non-negligible, low ion temperature and high electron density are required. Meanwhile, the collisional effects depend only weakly on the electron temperature. For a reference point, in a hydrogen plasma with
$\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
. For the effect of collisions to be non-negligible, low ion temperature and high electron density are required. Meanwhile, the collisional effects depend only weakly on the electron temperature. For a reference point, in a hydrogen plasma with
![]() $T_{\text{i}}=0.1~\text{keV}$
and
$T_{\text{i}}=0.1~\text{keV}$
and
![]() $n_{e}=10^{27}~\text{m}^{-3}$
,
$n_{e}=10^{27}~\text{m}^{-3}$
,
![]() $t\sim 30$
(in dimensional time,
$t\sim 30$
(in dimensional time,
![]() $30\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}\sim 0.7~\text{ns}$
) corresponds to an order unity
$30\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}\sim 0.7~\text{ns}$
) corresponds to an order unity
![]() $\unicode[STIX]{x1D708}_{\ast }t$
.
$\unicode[STIX]{x1D708}_{\ast }t$
.
While the effect of collisions on the shock potential
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
is small, as the trapped region gets populated by ions, the trapped regions become increasingly similar to the reflected region close to the shock. Accordingly, the minimum value of the downstream electrostatic potential,
$\unicode[STIX]{x1D719}_{\text{max}}$
is small, as the trapped region gets populated by ions, the trapped regions become increasingly similar to the reflected region close to the shock. Accordingly, the minimum value of the downstream electrostatic potential,
![]() $\unicode[STIX]{x1D719}_{\text{min}}$
, decreases towards the far upstream value of
$\unicode[STIX]{x1D719}_{\text{min}}$
, decreases towards the far upstream value of
![]() $\unicode[STIX]{x1D719}$
, which is zero in our choice of gauge, and the wavelength of the downstream oscillations increases. These effects can reach significant levels more rapidly when the trapped region in the initial state is larger, corresponding to smaller values of
$\unicode[STIX]{x1D719}$
, which is zero in our choice of gauge, and the wavelength of the downstream oscillations increases. These effects can reach significant levels more rapidly when the trapped region in the initial state is larger, corresponding to smaller values of
![]() ${\mathcal{M}}$
and higher values of
${\mathcal{M}}$
and higher values of
![]() $\unicode[STIX]{x1D70F}$
. When
$\unicode[STIX]{x1D70F}$
. When
![]() $\unicode[STIX]{x1D708}_{\ast }t$
becomes order unity, our mathematical model breaks down, but it is expected that the solution becomes somewhat similar to a train of solitary waves, each one becoming symmetric about its maximum.
$\unicode[STIX]{x1D708}_{\ast }t$
becomes order unity, our mathematical model breaks down, but it is expected that the solution becomes somewhat similar to a train of solitary waves, each one becoming symmetric about its maximum.
We would also predict, from the rather weak effect collisions have on
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
and the reflected ion population, that these types of shocks have the potential to be used as relatively long time stable high-energy ion sources – compared to other laser time scales. Even though the shock downstream might degenerate due to collisions, the upstream stays rather unaffected, both in terms of number of reflected ions and their energy.
$\unicode[STIX]{x1D719}_{\text{max}}$
and the reflected ion population, that these types of shocks have the potential to be used as relatively long time stable high-energy ion sources – compared to other laser time scales. Even though the shock downstream might degenerate due to collisions, the upstream stays rather unaffected, both in terms of number of reflected ions and their energy.
In more than one spatial dimensions ion–ion modes, beam-Weibel and temperature anisotropy driven Weibel instabilities can become unstable and represent limitations on the lifetime of the shock; see Kato & Takabe (Reference Kato and Takabe2010) and references therein. Considering scenarios where such instabilities develop and interfere with the collisional process considered here is outside the scope of our studies, but we presume that interesting synergistic effects from the growing trapped regions in the downstream and anisotropy driven instabilities may arise.
We have considered only the early development of electrostatic shocks under the influence of collisions. Realizing the similarity between the transport in phase space across trapped region and the transport around magnetic islands in a magnetic confinement fusion device, the long time asymptotic collisional behaviour of weakly collisional shocks could be studied employing methods similar to those used by Hazeltine, Helander & Catto (Reference Hazeltine, Helander and Catto1997). Another possibility to generalize the semi-analytical model of this paper would be to allow for multiple ion species, where collisional friction between the various species can become important (Turrell et al. Reference Turrell, Sherlock and Rose2015).
Acknowledgements
The authors are grateful for the fruitful discussions with I. G. Abel, L. Gremillet, J. Ferri, T. Fülöp and L. Yi. This work was supported by the European Research Council (ERC-2014-CoG grant 647121), the International Career Grant of Vetenskapsrådet (VR) (Dnr. 330-2014-6313) and Marie Skłodowska Curie Actions, Cofund, Project INCA 600398. J.J. was supported by a NASA Earth and Space Science Fellowship (grant no. 80NSSC17K0428); J.M.T. was support by NSF SHINE award (AGS-1622306). The development of the Gkeyll code is partly funded by the US Department of Energy under Contract No. DE-AC02-09CH11466 and by the Air Force Office of Scientific Research under grant number FA9550-15-1-0193. The simulations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at Chalmers Centre for Computational Science and Engineering (C3SE).
Appendix A. Kinetic simulations, limitations of the Lenard–Bernstein operator
Here, we first consider the collisional boundary layer formation in initially discontinuous distributions in kinetic simulations, then we discuss the limitations of the Lenard–Bernstein operator in the presence of energetic populations.
The development of a collisional boundary layer at a discontinuity of the distribution function was reproduced in simulations with the Vlasov–Maxwell solver in the open-source framework Gkeyll Footnote 3 (Juno et al. Reference Juno, Hakim, TenBarge, Shi and Dorland2018). While the implementation of a Fokker–Planck operator is ongoing, collisions are currently modelled through a generalized Lenard–Bernstein collision operator (LBO) (Lenard & Bernstein Reference Lenard and Bernstein1958), allowing a finite flow speed and inter-species collisions (with some restrictions to avoid negative entropy production). Here we only use the ion–ion collision part of the operator that, in one dimension, reads
where
![]() $V$
and
$V$
and
![]() $v_{\text{th}}$
represent the flow and thermal speed of
$v_{\text{th}}$
represent the flow and thermal speed of
![]() $f$
(the latter defined such that it is
$f$
(the latter defined such that it is
![]() $\sqrt{T/m}$
for a Maxwellian).
$\sqrt{T/m}$
for a Maxwellian).
Figure 6. (a) Simulated distribution function near a sharp cutoff, in an otherwise Maxwellian ion distribution, at collisional ages
![]() $\unicode[STIX]{x1D708}_{\ast }t=0$
(black line),
$\unicode[STIX]{x1D708}_{\ast }t=0$
(black line),
![]() $10^{-3}$
(blue dotted),
$10^{-3}$
(blue dotted),
![]() $10^{-2}$
(green dash-dotted) and
$10^{-2}$
(green dash-dotted) and
![]() $10^{-1}$
(red dashed). (b) The time evolution of the density of the ions which have been scattered out above the cutoff, simulated value (blue dots) compared to a theoretical estimate assuming only diffusion (red solid line), and the early time asymptotic behaviour
$10^{-1}$
(red dashed). (b) The time evolution of the density of the ions which have been scattered out above the cutoff, simulated value (blue dots) compared to a theoretical estimate assuming only diffusion (red solid line), and the early time asymptotic behaviour
![]() $\propto \sqrt{t}$
(black dotted).
$\propto \sqrt{t}$
(black dotted).
We first consider the time evolution of a spatially homogeneous distribution that is Maxwellian with no flow and unit thermal speed for
![]() $v<1$
, and 0 above. Note that this truncation means that
$v<1$
, and 0 above. Note that this truncation means that
![]() $V<0$
and
$V<0$
and
![]() $v_{\text{th}}<1$
for this distribution. The simulation uses 2048 cells in velocity spanning
$v_{\text{th}}<1$
for this distribution. The simulation uses 2048 cells in velocity spanning
![]() $[-4c_{\text{s}},2c_{\text{s}}]$
, and a polynomial order of 2; the electrons and the electric field were not evolved. The box is
$[-4c_{\text{s}},2c_{\text{s}}]$
, and a polynomial order of 2; the electrons and the electric field were not evolved. The box is
![]() $1\unicode[STIX]{x1D706}_{\text{D}}$
wide in configuration space, with 16 cells and periodic boundary conditions.
$1\unicode[STIX]{x1D706}_{\text{D}}$
wide in configuration space, with 16 cells and periodic boundary conditions.
The sharp drop in
![]() $f$
is quickly smoothed out, as seen in figure 6(a), showing
$f$
is quickly smoothed out, as seen in figure 6(a), showing
![]() $f$
at four instances of time. In figure 6(b), the density of ions scattered above the cutoff velocity,
$f$
at four instances of time. In figure 6(b), the density of ions scattered above the cutoff velocity,
![]() $n_{\text{scat.}}=\int _{1}^{\infty }f\,\text{d}v$
, is plotted against the collisional age
$n_{\text{scat.}}=\int _{1}^{\infty }f\,\text{d}v$
, is plotted against the collisional age
![]() $\unicode[STIX]{x1D708}_{\ast }t$
. For very low collisional age, the scattered density (blue dots) follows a
$\unicode[STIX]{x1D708}_{\ast }t$
. For very low collisional age, the scattered density (blue dots) follows a
![]() $\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
behaviour (black dotted line) very closely, but above
$\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
behaviour (black dotted line) very closely, but above
![]() $\unicode[STIX]{x1D708}_{\ast }t\sim 0.01$
it starts to deviate, growing more slowly than
$\unicode[STIX]{x1D708}_{\ast }t\sim 0.01$
it starts to deviate, growing more slowly than
![]() $\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
. This behaviour is well approximated by taking the integral
$\sqrt{\unicode[STIX]{x1D708}_{\ast }t}$
. This behaviour is well approximated by taking the integral
![]() $n_{\text{scat.}}^{(0)}=\int _{1}^{\infty }f_{0}\,\text{d}v$
, where
$n_{\text{scat.}}^{(0)}=\int _{1}^{\infty }f_{0}\,\text{d}v$
, where
which is plotted in the figure with red solid line. At later times, as the collisional drag becomes comparable with diffusion, the distribution will eventually evolve towards a new Maxwellian characterized by
![]() $V$
and
$V$
and
![]() $v_{\text{th}}$
. However, the good agreement with the theoretical estimate based on assuming a pure diffusion suggests that neglecting drag is reasonable, even up to a collisional age of
$v_{\text{th}}$
. However, the good agreement with the theoretical estimate based on assuming a pure diffusion suggests that neglecting drag is reasonable, even up to a collisional age of
![]() ${\sim}0.1$
.
${\sim}0.1$
.
The Lenard–Bernstein operator (LBO) (Lenard & Bernstein Reference Lenard and Bernstein1958) is often employed as a simple collision model that captures both collisional diffusion and drag, and importantly, because it is meaningful in one velocity dimension. By construction, the LBO has a velocity independent collision frequency, which drives the distribution towards a Maxwellian with density, flow speed and temperature determined by the first three velocity moments of the original distribution function. This construction is to ensure the conservation of particles, momentum and energy. However, the LBO is not well suited for situations when the distribution has a significant super-thermal population, as in our case.
The main contributor to the unphysical behaviour of the LBO is the large effect super-thermal structures can have on the moments of the distribution, especially on
![]() $v_{\text{th}}^{2}$
. Take, for instance, the collisional interaction between a high-energy beam and a bulk plasma – a situation which we have in the shock upstream. In reality (as in the Fokker–Planck operator), the collisionality between the particles in the beam and the bulk would decrease as
$v_{\text{th}}^{2}$
. Take, for instance, the collisional interaction between a high-energy beam and a bulk plasma – a situation which we have in the shock upstream. In reality (as in the Fokker–Planck operator), the collisionality between the particles in the beam and the bulk would decrease as
![]() $v^{-2}$
, which would mean that the collisional interaction between the beam and bulk would be virtually non-existent. However, the LBO has no such features, and the high energy of the beam significantly skews the energy and velocity moments; there will also be an artificially high drag due to the linear increase of the friction term. Consequently, the bulk plasma will also be noticeably affected, even when the beam only constitutes a very low fraction of the total density. In the case of our shock simulations, the reflected ions only made up approximately 1 % of the upstream plasma, but the artificially high collisional effects still render the simulation unusable for testing our analytical model.
$v^{-2}$
, which would mean that the collisional interaction between the beam and bulk would be virtually non-existent. However, the LBO has no such features, and the high energy of the beam significantly skews the energy and velocity moments; there will also be an artificially high drag due to the linear increase of the friction term. Consequently, the bulk plasma will also be noticeably affected, even when the beam only constitutes a very low fraction of the total density. In the case of our shock simulations, the reflected ions only made up approximately 1 % of the upstream plasma, but the artificially high collisional effects still render the simulation unusable for testing our analytical model.
Figure 7. (a–d) Ion distribution functions at different stages of numerical simulations of shocks with
![]() ${\mathcal{M}}=1.3$
and
${\mathcal{M}}=1.3$
and
![]() $\unicode[STIX]{x1D70F}=200$
. (a) All simulations were initialized with the collisionless ion distribution function calculated from the analytical model. (b) The time-evolved distribution function with no collisions. This shows that the shock is static, as is required in the model. (c,d) The time-evolved distribution function with the Lenard–Bernstein collision operator (LBO) acting on it. The unphysical collisional interaction between the high-energy reflected ions and the incoming bulk quickly destroys the shock structure.
$\unicode[STIX]{x1D70F}=200$
. (a) All simulations were initialized with the collisionless ion distribution function calculated from the analytical model. (b) The time-evolved distribution function with no collisions. This shows that the shock is static, as is required in the model. (c,d) The time-evolved distribution function with the Lenard–Bernstein collision operator (LBO) acting on it. The unphysical collisional interaction between the high-energy reflected ions and the incoming bulk quickly destroys the shock structure.
To illustrate this problem, we have performed collisional simulations of shocks in Gkeyll, using the LBO. The shock simulations were initiated with the collisionless shock ion distribution function. The initial condition was constructed by calculating
![]() $\unicode[STIX]{x1D719}(x)$
from our semi-analytical model, which was then used to initialize the ion distribution function according to (2.3) in regions I and IV. Above the separatrix, a rapid Gaussian cutoff was employed,
$\unicode[STIX]{x1D719}(x)$
from our semi-analytical model, which was then used to initialize the ion distribution function according to (2.3) in regions I and IV. Above the separatrix, a rapid Gaussian cutoff was employed,
where
![]() $\unicode[STIX]{x1D6FF}v$
is the simulation velocity grid size. This gradual cutoff at the separatrix makes the simulation discretization smoother, and thus also results in smoother simulation results. Furthermore, the electrons were initialized to be Maxwell–Boltzmann distributed with a flow velocity
$\unicode[STIX]{x1D6FF}v$
is the simulation velocity grid size. This gradual cutoff at the separatrix makes the simulation discretization smoother, and thus also results in smoother simulation results. Furthermore, the electrons were initialized to be Maxwell–Boltzmann distributed with a flow velocity
![]() $-{\mathcal{M}}$
, and the initial electric field was simply taken as
$-{\mathcal{M}}$
, and the initial electric field was simply taken as
![]() $-\text{d}\unicode[STIX]{x1D719}/\text{d}x$
. The simulations are done in the shock frame, with 640 cells in configuration space covering
$-\text{d}\unicode[STIX]{x1D719}/\text{d}x$
. The simulations are done in the shock frame, with 640 cells in configuration space covering
![]() $x=[-29,20]\unicode[STIX]{x1D706}_{\text{D}}$
and employ perfectly matched layer boundary conditions. The velocity space covers
$x=[-29,20]\unicode[STIX]{x1D706}_{\text{D}}$
and employ perfectly matched layer boundary conditions. The velocity space covers
![]() $v=[-3.5,3.5]c_{\text{s}}$
with 512 cells for ions, and
$v=[-3.5,3.5]c_{\text{s}}$
with 512 cells for ions, and
![]() $v=[-5,5]v_{e}=[-214,214]c_{\text{s}}$
with 256 cells for electrons, with the physical electron-to-proton mass ratio. A zero flux boundary condition is used in velocity. The polynomial order is 2.
$v=[-5,5]v_{e}=[-214,214]c_{\text{s}}$
with 256 cells for electrons, with the physical electron-to-proton mass ratio. A zero flux boundary condition is used in velocity. The polynomial order is 2.
In figure 7, we show the resulting ion distribution functions at various simulation times (measured in
![]() $\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
) after the time evolution in Gkeyll, both with (c,d) and without (b) collisions in the simulation. The initial ion distribution function for both simulation runs is shown in figure 7(a). From figure 7(b), we see that the shock is indeed static, as was expected and required by our semi-analytical model. The time evolution to
$\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
) after the time evolution in Gkeyll, both with (c,d) and without (b) collisions in the simulation. The initial ion distribution function for both simulation runs is shown in figure 7(a). From figure 7(b), we see that the shock is indeed static, as was expected and required by our semi-analytical model. The time evolution to
![]() $t=20$
, figure 7(b), required
$t=20$
, figure 7(b), required
![]() ${\sim}30\,000$
simulation time steps. This result demonstrates that the initial condition is faithfully imported and shows the numerical stability of the code.
${\sim}30\,000$
simulation time steps. This result demonstrates that the initial condition is faithfully imported and shows the numerical stability of the code.
However, the collisional simulation of the shock in figure 7(c,d) is clearly not static, and the collisional effects evolve at rates much faster than would have been expected from the relatively low collisionality of
![]() $\unicode[STIX]{x1D708}_{\ast }=0.01$
. We see that the collisional effects mostly originate upstream (
$\unicode[STIX]{x1D708}_{\ast }=0.01$
. We see that the collisional effects mostly originate upstream (
![]() $x>0$
) of the shock (c), and then they eventually propagate downstream of the shock (d). This result is precisely the expected behaviour of the LBO in a scenario with a high-energy beam interacting with the bulk plasma: the bulk heats up at an unphysical rate due to collisions with the high-energy beam.
$x>0$
) of the shock (c), and then they eventually propagate downstream of the shock (d). This result is precisely the expected behaviour of the LBO in a scenario with a high-energy beam interacting with the bulk plasma: the bulk heats up at an unphysical rate due to collisions with the high-energy beam.
Since the LBO is relatively simple, it is often the first choice of model collision operator to be implemented in a kinetic Eulerian simulation code. In some circumstances, where
![]() $f$
remains close to a Maxwellian, the above discussed artefacts of LBO will not arise. We would, however, point out the risk of using the LBO in simulations with more complex systems: distributions which are strongly non-Maxwellian and/or have high-energy structures will experience unphysical collisional effects due to artificially strong collisionality between particles with a large velocity separation.
$f$
remains close to a Maxwellian, the above discussed artefacts of LBO will not arise. We would, however, point out the risk of using the LBO in simulations with more complex systems: distributions which are strongly non-Maxwellian and/or have high-energy structures will experience unphysical collisional effects due to artificially strong collisionality between particles with a large velocity separation.
Appendix B. Numerical implementation of the analytical model
The solution for
![]() $f$
, equation (2.20), is given in terms of
$f$
, equation (2.20), is given in terms of
![]() $w$
, while the densities are more conveniently written in terms of
$w$
, while the densities are more conveniently written in terms of
![]() $k$
, equation (2.21). Thus
$k$
, equation (2.21). Thus
![]() $w(k)$
, or in practice
$w(k)$
, or in practice
![]() $w(\unicode[STIX]{x1D716})$
, needs to be evaluated. Note that the direct numerical integration of the equation that relates them, equation (2.17), is problematic, since
$w(\unicode[STIX]{x1D716})$
, needs to be evaluated. Note that the direct numerical integration of the equation that relates them, equation (2.17), is problematic, since
![]() $\text{d}w/\text{d}\unicode[STIX]{x1D716}$
is divergent at
$\text{d}w/\text{d}\unicode[STIX]{x1D716}$
is divergent at
![]() $\unicode[STIX]{x1D716}=0$
. For an accurate evaluation of
$\unicode[STIX]{x1D716}=0$
. For an accurate evaluation of
![]() $w(\unicode[STIX]{x1D716})$
, the numerical integration of (2.17) can be started at some finite
$w(\unicode[STIX]{x1D716})$
, the numerical integration of (2.17) can be started at some finite
![]() $\unicode[STIX]{x1D716}$
, where
$\unicode[STIX]{x1D716}$
, where
![]() $w$
is given by its small
$w$
is given by its small
![]() $\unicode[STIX]{x1D716}$
asymptotic value
$\unicode[STIX]{x1D716}$
asymptotic value
For a less accurate but significantly faster evaluation of
![]() $w(\unicode[STIX]{x1D716})$
, we use an approximation functionFootnote
4
$w(\unicode[STIX]{x1D716})$
, we use an approximation functionFootnote
4
![]() ${\hat{w}}(\unicode[STIX]{x1D716})$
that is defined in the following way. It takes the asymptotic value (B 1) for
${\hat{w}}(\unicode[STIX]{x1D716})$
that is defined in the following way. It takes the asymptotic value (B 1) for
![]() $0<\unicode[STIX]{x1D716}\leqslant 0.1$
, then for
$0<\unicode[STIX]{x1D716}\leqslant 0.1$
, then for
![]() $0.1<\unicode[STIX]{x1D716}\leqslant 1$
it is given by
$0.1<\unicode[STIX]{x1D716}\leqslant 1$
it is given by
which is obtained by integrating the
![]() $k\rightarrow 0$
asymptote
$k\rightarrow 0$
asymptote
and setting the constant of integration
![]() $C^{+}=1.4756$
by the numerically determined value of
$C^{+}=1.4756$
by the numerically determined value of
![]() $w(\unicode[STIX]{x1D716}=1)$
. For negative values of
$w(\unicode[STIX]{x1D716}=1)$
. For negative values of
![]() $\unicode[STIX]{x1D716}$
we use (B 1) for
$\unicode[STIX]{x1D716}$
we use (B 1) for
![]() $-0.5\leqslant \unicode[STIX]{x1D716}<0$
, and for
$-0.5\leqslant \unicode[STIX]{x1D716}<0$
, and for
![]() $\unicode[STIX]{x1D716}\leqslant -2$
we take
$\unicode[STIX]{x1D716}\leqslant -2$
we take
where in the
![]() $\unicode[STIX]{x1D716}\rightarrow -\infty$
limit,
$\unicode[STIX]{x1D716}\rightarrow -\infty$
limit,
![]() $\unicode[STIX]{x1D6F6}^{-1}\text{d}w/\text{d}\unicode[STIX]{x1D716}\simeq 1$
is integrated, and
$\unicode[STIX]{x1D6F6}^{-1}\text{d}w/\text{d}\unicode[STIX]{x1D716}\simeq 1$
is integrated, and
![]() $C^{-}=-0.3310$
is determined by evaluating
$C^{-}=-0.3310$
is determined by evaluating
![]() $w(\unicode[STIX]{x1D716})$
at some sufficiently large negative value of
$w(\unicode[STIX]{x1D716})$
at some sufficiently large negative value of
![]() $\unicode[STIX]{x1D716}$
, namely
$\unicode[STIX]{x1D716}$
, namely
![]() $w(\unicode[STIX]{x1D716}=-50)/\unicode[STIX]{x1D6F6}=-50.3310$
. For the region
$w(\unicode[STIX]{x1D716}=-50)/\unicode[STIX]{x1D6F6}=-50.3310$
. For the region
![]() $-2\leqslant \unicode[STIX]{x1D716}<-0.5$
a linear curve matching to the two asymptotes is used. The relative error
$-2\leqslant \unicode[STIX]{x1D716}<-0.5$
a linear curve matching to the two asymptotes is used. The relative error
![]() $|{\hat{w}}/w-1|$
of the above approximation stays below 5 % and it is asymptotically correct in the most important limit
$|{\hat{w}}/w-1|$
of the above approximation stays below 5 % and it is asymptotically correct in the most important limit
![]() $|\unicode[STIX]{x1D716}|\rightarrow 0$
.
$|\unicode[STIX]{x1D716}|\rightarrow 0$
.
Appendix C. Parameter region for relevance and reflected ion fraction
The importance of the fact that collisions act to populate ion trapped regions is that the effect of collisions accumulates with time. Therefore, even when
![]() $\unicode[STIX]{x1D708}_{\ast }\ll 1$
– tempting one to neglect collisions – if the lifetime of the shock corresponds to an order-unity collisional age, the shock will be significantly affected. As a rough estimate for when collisions are relevant, in figure 8 we plot
$\unicode[STIX]{x1D708}_{\ast }\ll 1$
– tempting one to neglect collisions – if the lifetime of the shock corresponds to an order-unity collisional age, the shock will be significantly affected. As a rough estimate for when collisions are relevant, in figure 8 we plot
![]() $\unicode[STIX]{x1D708}_{\ast }=0.01$
curves in the
$\unicode[STIX]{x1D708}_{\ast }=0.01$
curves in the
![]() $n_{e}$
–
$n_{e}$
–
![]() $T_{\text{i}}$
parameter space for various values of
$T_{\text{i}}$
parameter space for various values of
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $Z$
, which corresponds to
$Z$
, which corresponds to
![]() $\unicode[STIX]{x1D708}_{\ast }t=1$
for a reasonable shock lifetime of
$\unicode[STIX]{x1D708}_{\ast }t=1$
for a reasonable shock lifetime of
![]() ${\sim}100\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
. The
${\sim}100\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
. The
![]() $T_{\text{e}}$
dependences of
$T_{\text{e}}$
dependences of
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
and
$\unicode[STIX]{x1D706}_{\text{D}}$
and
![]() $c_{\text{s}}$
cancel, so only a very weak
$c_{\text{s}}$
cancel, so only a very weak
![]() $T_{\text{e}}$
dependence remains (see the dotted curves) due to that of the Coulomb logarithm. Also, the
$T_{\text{e}}$
dependence remains (see the dotted curves) due to that of the Coulomb logarithm. Also, the
![]() $m_{\text{i}}$
dependences of
$m_{\text{i}}$
dependences of
![]() $\unicode[STIX]{x1D708}_{\text{i}\text{i}}$
and
$\unicode[STIX]{x1D708}_{\text{i}\text{i}}$
and
![]() $c_{\text{s}}$
cancel, so it does not matter whether the charge-to-mass ratio is hydrogen or deuterium like. As expected, there is a rather strong dependence on
$c_{\text{s}}$
cancel, so it does not matter whether the charge-to-mass ratio is hydrogen or deuterium like. As expected, there is a rather strong dependence on
![]() $Z$
, which is relevant for non-hydrogen targets. For a concrete example, in a hydrogen plasma with the parameters
$Z$
, which is relevant for non-hydrogen targets. For a concrete example, in a hydrogen plasma with the parameters
![]() $n_{e}=10^{27}~\text{m}^{-3}$
,
$n_{e}=10^{27}~\text{m}^{-3}$
,
![]() $T_{\text{i}}=100~\text{eV}$
and
$T_{\text{i}}=100~\text{eV}$
and
![]() $T_{\text{e}}=1~\text{MeV}$
, a case with relevance to ion acceleration that was considered by Fiuza et al. (Reference Fiuza, Stockem, Boella, Fonseca, Silva, Haberberger, Tochitsky, Mori and Joshi2013),
$T_{\text{e}}=1~\text{MeV}$
, a case with relevance to ion acceleration that was considered by Fiuza et al. (Reference Fiuza, Stockem, Boella, Fonseca, Silva, Haberberger, Tochitsky, Mori and Joshi2013),
![]() $\unicode[STIX]{x1D708}_{\ast }t$
becomes 1 at time
$\unicode[STIX]{x1D708}_{\ast }t$
becomes 1 at time
![]() $31\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}\sim 0.7~\text{ns}$
, that is shorter than the lifetime of the shock.
$31\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}\sim 0.7~\text{ns}$
, that is shorter than the lifetime of the shock.

Figure 8. Approximate boundaries of the parameter regions where collisions qualitatively affect the dynamics of shocks. Below the lines
![]() $\unicode[STIX]{x1D708}_{\ast }>0.01$
, thus for shocks which live
$\unicode[STIX]{x1D708}_{\ast }>0.01$
, thus for shocks which live
![]() $100\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
the cumulative effect of collisions becomes order unity. Baseline parameters (corresponding to solid line):
$100\unicode[STIX]{x1D706}_{\text{D}}/c_{\text{s}}$
the cumulative effect of collisions becomes order unity. Baseline parameters (corresponding to solid line):
![]() $Z=1$
,
$Z=1$
,
![]() $\unicode[STIX]{x1D70F}=100$
. Dashed:
$\unicode[STIX]{x1D70F}=100$
. Dashed:
![]() $Z=2$
, long dashed:
$Z=2$
, long dashed:
![]() $Z=10$
, dotted:
$Z=10$
, dotted:
![]() $\unicode[STIX]{x1D70F}=1000$
, small dotted:
$\unicode[STIX]{x1D70F}=1000$
, small dotted:
![]() $\unicode[STIX]{x1D70F}=10$
.
$\unicode[STIX]{x1D70F}=10$
.
While
![]() $\unicode[STIX]{x1D708}_{\ast }t\ll 1$
, and so our model is valid, the shock properties do not change qualitatively, so the effect of collisions on
$\unicode[STIX]{x1D708}_{\ast }t\ll 1$
, and so our model is valid, the shock properties do not change qualitatively, so the effect of collisions on
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
is rather weak. The reflected ion fraction is
$\unicode[STIX]{x1D719}_{\text{max}}$
is rather weak. The reflected ion fraction is
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\frac{\displaystyle \int _{0}^{v_{0}}f(v,\unicode[STIX]{x1D719}=0)\,\text{d}v}{\displaystyle \int _{\infty }^{0}f(v,\unicode[STIX]{x1D719}=0)\,\text{d}v}=\frac{\displaystyle \text{erf}\left[\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D70F}}{2}}}{\mathcal{M}}\right]+\text{erf}\left[\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D70F}}{2}}}\left(\sqrt{2\unicode[STIX]{x1D719}_{\text{max}}}-{\mathcal{M}}\right)\right]}{1+\text{erf}\left[\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D70F}}{2}}}{\mathcal{M}}\right]},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\frac{\displaystyle \int _{0}^{v_{0}}f(v,\unicode[STIX]{x1D719}=0)\,\text{d}v}{\displaystyle \int _{\infty }^{0}f(v,\unicode[STIX]{x1D719}=0)\,\text{d}v}=\frac{\displaystyle \text{erf}\left[\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D70F}}{2}}}{\mathcal{M}}\right]+\text{erf}\left[\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D70F}}{2}}}\left(\sqrt{2\unicode[STIX]{x1D719}_{\text{max}}}-{\mathcal{M}}\right)\right]}{1+\text{erf}\left[\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D70F}}{2}}}{\mathcal{M}}\right]},\end{eqnarray}$$
where
![]() $f$
is the upstream distribution and
$f$
is the upstream distribution and
![]() $\text{erf}$
denotes the error function. For
$\text{erf}$
denotes the error function. For
![]() $\unicode[STIX]{x1D70F}\gg 1$
, this result reduces to
$\unicode[STIX]{x1D70F}\gg 1$
, this result reduces to
where
![]() $F=2\unicode[STIX]{x1D719}_{\text{max}}/{\mathcal{M}}^{2}$
and it takes values close to 1 for most cases of interest, as discussed by Pusztai et al. (Reference Pusztai, TenBarge, Csapó, Juno, Hakim, Yi and Fülöp2018).
$F=2\unicode[STIX]{x1D719}_{\text{max}}/{\mathcal{M}}^{2}$
and it takes values close to 1 for most cases of interest, as discussed by Pusztai et al. (Reference Pusztai, TenBarge, Csapó, Juno, Hakim, Yi and Fülöp2018).
Figure 9. (a) Reflected ion fraction plotted as
![]() $\log _{10}\unicode[STIX]{x1D6FC}(t=0)$
, as a function of
$\log _{10}\unicode[STIX]{x1D6FC}(t=0)$
, as a function of
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() ${\mathcal{M}}$
. (b) Relative reduction in the reflected ion fraction for a collisional age of
${\mathcal{M}}$
. (b) Relative reduction in the reflected ion fraction for a collisional age of
![]() $\unicode[STIX]{x1D708}_{\ast }t=0.1$
.
$\unicode[STIX]{x1D708}_{\ast }t=0.1$
.
We find that
![]() $\unicode[STIX]{x1D6FC}$
increases strongly with
$\unicode[STIX]{x1D6FC}$
increases strongly with
![]() ${\mathcal{M}}$
– as seen in figure 9(a) – since
${\mathcal{M}}$
– as seen in figure 9(a) – since
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
increases more strongly than
$\unicode[STIX]{x1D719}_{\text{max}}$
increases more strongly than
![]() ${\mathcal{M}}^{2}$
, corresponding to higher values of
${\mathcal{M}}^{2}$
, corresponding to higher values of
![]() $F$
. In turn,
$F$
. In turn,
![]() $\unicode[STIX]{x1D6FC}$
is exponentially sensitive to
$\unicode[STIX]{x1D6FC}$
is exponentially sensitive to
![]() $F$
. We have found that
$F$
. We have found that
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
is reduced by collisions, and we might expect that the exponential sensitivity to
$\unicode[STIX]{x1D719}_{\text{max}}$
is reduced by collisions, and we might expect that the exponential sensitivity to
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
can lead to significant changes in
$\unicode[STIX]{x1D719}_{\text{max}}$
can lead to significant changes in
![]() $\unicode[STIX]{x1D6FC}$
. However, the reduction in
$\unicode[STIX]{x1D6FC}$
. However, the reduction in
![]() $\unicode[STIX]{x1D719}_{\text{max}}$
is so weak that even for a collisional age of
$\unicode[STIX]{x1D719}_{\text{max}}$
is so weak that even for a collisional age of
![]() $\unicode[STIX]{x1D708}_{\ast }t=0.1$
, the maximum relative reduction in
$\unicode[STIX]{x1D708}_{\ast }t=0.1$
, the maximum relative reduction in
![]() $\unicode[STIX]{x1D6FC}$
is below 15 % in the region of parameter space shown in figure 9(b). This effect is even weaker for higher
$\unicode[STIX]{x1D6FC}$
is below 15 % in the region of parameter space shown in figure 9(b). This effect is even weaker for higher
![]() $\unicode[STIX]{x1D70F}$
, which is more relevant for ion acceleration experiments.
$\unicode[STIX]{x1D70F}$
, which is more relevant for ion acceleration experiments.