No CrossRef data available.
Article contents
A q-SUPERCONGRUENCE ARISING FROM ANDREWS’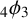 
$_4\phi _3$ IDENTITY
Published online by Cambridge University Press: 29 August 2024
Abstract
We establish a q-analogue of a supercongruence related to a supercongruence of Rodriguez-Villegas, which extends a q-congruence of Guo and Zeng [‘Some q-analogues of supercongruences of Rodriguez-Villegas’, J. Number Theory 145 (2014), 301–316]. The important ingredients in the proof include Andrews’ 
$_4\phi _3$ terminating identity.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by the National Natural Science Foundation of China (grant no. 12171370).
References
Chowla, S., Dwork, B. and Evans, R. J., ‘On the mod
${p}^2$
determination of
$\left(\frac{\left(p-1\right)/2}{\left(p-1\right)/4}\right)$
’, J. Number Theory 24 (1986), 188–196.CrossRefGoogle Scholar
${p}^2$
determination of
$\left(\frac{\left(p-1\right)/2}{\left(p-1\right)/4}\right)$
’, J. Number Theory 24 (1986), 188–196.CrossRefGoogle ScholarGasper, G. and Rahman, M., Basic Hypergeometric Series, 2nd edn, Encyclopedia of Mathematics and Its Applications, 96 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Guo, V. J. W. and Zeng, J., ‘Some
$q$
-analogues of supercongruences of Rodriguez-Villegas’, J. Number Theory 145 (2014), 301–316.CrossRefGoogle Scholar
$q$
-analogues of supercongruences of Rodriguez-Villegas’, J. Number Theory 145 (2014), 301–316.CrossRefGoogle ScholarMortenson, E., ‘A supercongruence conjecture of Rodriguez-Villegas for a certain truncated hypergeometric function’, J. Number Theory 99 (2003), 139–147.CrossRefGoogle Scholar
Rodriguez-Villegas, F., ‘Hypergeometric families of Calabi–Yau manifolds’, in: Calabi–Yau Varieties and Mirror Symmetry (Toronto, ON, 2001), Fields Institute Communications, 38 (eds. Yui, N. and Lewis, J. D.) (American Mathematical Society, Providence, RI, 2003), 223–231.Google Scholar
Sun, Z.-H., ‘Congruences concerning Legendre polynomials’, Proc. Amer. Math. Soc. 139 (2011), 1915–1929.CrossRefGoogle Scholar
Sun, Z.-W., ‘On congruences related to central binomial coefficients’, J. Number Theory 131 (2011), 2219–2238.CrossRefGoogle Scholar
Tauraso, R., ‘An elementary proof of a Rodriguez-Villegas supercongruence’, Preprint, 2009, arXiv:0911.4261v1.Google Scholar