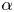1. Introduction
Consider a planar differential system
parameterized by $\alpha \in I$![]() (an interval of $\mathbb {R}$
(an interval of $\mathbb {R}$![]() ), and use $(P(x,y,\alpha ),Q(x,y,\alpha ))$
), and use $(P(x,y,\alpha ),Q(x,y,\alpha ))$![]() to present its vector field, where functions $P, Q, \partial P/\partial \alpha, \partial Q/\partial \alpha$
to present its vector field, where functions $P, Q, \partial P/\partial \alpha, \partial Q/\partial \alpha$![]() are Lipschitzian in $D\times I$
are Lipschitzian in $D\times I$![]() and $D\subset \mathbb {R}^2$
and $D\subset \mathbb {R}^2$![]() is a connected open set. The vector field $(P(x,y,\alpha ),Q(x,y,\alpha ))$
is a connected open set. The vector field $(P(x,y,\alpha ),Q(x,y,\alpha ))$![]() is called a complete family of rotated vector fields with a rotated parameter $\alpha$
is called a complete family of rotated vector fields with a rotated parameter $\alpha$![]() if the following conditions hold:
if the following conditions hold:
(D1) Equilibria fixed: The number and location of equilibria are fixed as $\alpha$
 varies.
varies.(D2) Direction fixed: $(P(x,y,\alpha ), Q(x,y,\alpha ))$
 rotates counter-clockwise at any regular point $(x,y)$
rotates counter-clockwise at any regular point $(x,y)$ as the rotated parameter $\alpha$
as the rotated parameter $\alpha$ increases.
increases.(D3) Symmetrically periodic: $P,Q$
 are periodic functions in $\alpha$
are periodic functions in $\alpha$ with minimum period $2\pi$
with minimum period $2\pi$ , and $(P(x,y,\alpha +\pi ), Q(x,y,\alpha +\pi ))=-(P(x,y,\alpha ), ~Q(x,y,\alpha ))$
, and $(P(x,y,\alpha +\pi ), Q(x,y,\alpha +\pi ))=-(P(x,y,\alpha ), ~Q(x,y,\alpha ))$ .
.
This concept, originated by Duff ([Reference Duff8]) in 1953, was proved to have the following properties: (DR1) the limit cycles $L(\alpha _1)$![]() and $L(\alpha _2)$
and $L(\alpha _2)$![]() of the vector fields with different $\alpha _1$
of the vector fields with different $\alpha _1$![]() and $\alpha _2$
and $\alpha _2$![]() respectively in the family do not intersect each other; (DR2) every simple limit cycle expands or contracts monotonically as $\alpha$
respectively in the family do not intersect each other; (DR2) every simple limit cycle expands or contracts monotonically as $\alpha$![]() varies monotonically; (DR3) every semi-stable limit cycle splits into a stable cycle and an unstable one when $\alpha$
varies monotonically; (DR3) every semi-stable limit cycle splits into a stable cycle and an unstable one when $\alpha$![]() increases or decreases, but disappears when $\alpha$
increases or decreases, but disappears when $\alpha$![]() varies in the opposite direction; (DR4) the outer boundary and the inner one of the annulus $\mathcal {R}$
varies in the opposite direction; (DR4) the outer boundary and the inner one of the annulus $\mathcal {R}$![]() covered by all limit cycles $L(\alpha )$
covered by all limit cycles $L(\alpha )$![]() , $\alpha \in I$
, $\alpha \in I$![]() , i.e., $\mathcal {R}:=\{(x,y)\in \mathbb {R}^2: (x,y)\in L(\alpha ), \alpha \in I\}$
, i.e., $\mathcal {R}:=\{(x,y)\in \mathbb {R}^2: (x,y)\in L(\alpha ), \alpha \in I\}$![]() , surround an equilibrium each. These properties attracted great attentions (see e.g. [Reference Cândido, Llibre and Valls3, Reference Dumortier and Li9, Reference Dumortier and Rousseau12, Reference Perko21, Reference Perko22, Reference Perko24, Reference Perko25, Reference Ye28–Reference Zhang, Ding, Huang and Dong30]) to rotated vector fields because they can be used to discuss the non-existence and the uniqueness of limit cycles as well as bifurcations of heteroclinic loops.
, surround an equilibrium each. These properties attracted great attentions (see e.g. [Reference Cândido, Llibre and Valls3, Reference Dumortier and Li9, Reference Dumortier and Rousseau12, Reference Perko21, Reference Perko22, Reference Perko24, Reference Perko25, Reference Ye28–Reference Zhang, Ding, Huang and Dong30]) to rotated vector fields because they can be used to discuss the non-existence and the uniqueness of limit cycles as well as bifurcations of heteroclinic loops.
Perko ([Reference Perko20, Reference Perko23]) weakened Duff's complete version to an uncomplete one, not requiring the symmetric periodicity but allowing the vector field not to rotate on an analytic curve $\Omega (x,y)=0$![]() not having a branch congruent to a limit cycle of (1.1). He called $(P(x,y,\alpha ), Q(x,y,\alpha ))$
not having a branch congruent to a limit cycle of (1.1). He called $(P(x,y,\alpha ), Q(x,y,\alpha ))$![]() a family of rotated vector fields (mod $\Omega =0$
a family of rotated vector fields (mod $\Omega =0$![]() ) with the rotated parameter $\alpha$
) with the rotated parameter $\alpha$![]() if the following conditions hold:
if the following conditions hold:
(P1) Equilibria fixed: the same as (D1).
(P2) Direction fixed: $(P(x,y,\alpha ), Q(x,y,\alpha ))$
 rotates counter-clockwise at any regular point $(x,y)$
rotates counter-clockwise at any regular point $(x,y)$ as the rotated parameter $\alpha$
as the rotated parameter $\alpha$ increases except on the curve $\Omega (x,y)=0$
increases except on the curve $\Omega (x,y)=0$ .
.
Assuming that the family of rotated vector fields is analytic in $(x,y,\alpha )$![]() , he proved in [Reference Perko23, Reference Perko26] the following results:
, he proved in [Reference Perko23, Reference Perko26] the following results:
• (PR1) If the rotated vector field with $\alpha =\alpha _0$
 exhibits a limit cycle $\Gamma _0$
exhibits a limit cycle $\Gamma _0$ of odd multiplicity then the cycle remains for $\alpha :=\alpha _0+\varepsilon$
of odd multiplicity then the cycle remains for $\alpha :=\alpha _0+\varepsilon$ with small enough $|\varepsilon |$
with small enough $|\varepsilon |$ and expands or contracts monotonically as $\varepsilon$
and expands or contracts monotonically as $\varepsilon$ increases (see [Reference Perko26, Theorem 1 of Section 6 of Chapter IV]).
increases (see [Reference Perko26, Theorem 1 of Section 6 of Chapter IV]).• (PR2) If the rotated vector field with $\alpha =\alpha _0$
 exhibits a limit cycle $\Gamma _0$
exhibits a limit cycle $\Gamma _0$ of even multiplicity then, as the parameter $\alpha$
of even multiplicity then, as the parameter $\alpha$ increases or decreases, $\Gamma _0$
increases or decreases, $\Gamma _0$ splits into two simple limit cycles $\Gamma _\alpha ^-$
splits into two simple limit cycles $\Gamma _\alpha ^-$ and $\Gamma _\alpha ^+$
and $\Gamma _\alpha ^+$ , where the inner one $\Gamma _\alpha ^-$
, where the inner one $\Gamma _\alpha ^-$ contracts and the outer one $\Gamma _\alpha ^+$
contracts and the outer one $\Gamma _\alpha ^+$ expands, but disappears as $\alpha$
expands, but disappears as $\alpha$ varies oppositely (see [Reference Perko26, Theorem 2 of Section 6 of Chapter IV]).
varies oppositely (see [Reference Perko26, Theorem 2 of Section 6 of Chapter IV]).• (PR3) If the origin $O$
 of the rotated vector field with $\alpha =\alpha _0$
of the rotated vector field with $\alpha =\alpha _0$ is a weak focus then a unique limit cycle occurs in a small neighbourhood of $O$
is a weak focus then a unique limit cycle occurs in a small neighbourhood of $O$ as $\alpha$
as $\alpha$ varies from $\alpha _0$
varies from $\alpha _0$ with the change of stability at $O$
with the change of stability at $O$ (see [Reference Perko26, Theorem 5 of Section 6 of Chapter IV]) and, moreover, the limit cycle is of the same stability as the weak focus at the origin when $\alpha =\alpha _0$
(see [Reference Perko26, Theorem 5 of Section 6 of Chapter IV]) and, moreover, the limit cycle is of the same stability as the weak focus at the origin when $\alpha =\alpha _0$ .
.• (PR4) If the rotated vector field with $\alpha =\alpha _0$
 has an isolated homoclinic loop $\Gamma _*$
has an isolated homoclinic loop $\Gamma _*$ then, as the parameter $\alpha$
then, as the parameter $\alpha$ increases or decreases, the loop disappears while a unique limit cycle $\Gamma _\alpha$
increases or decreases, the loop disappears while a unique limit cycle $\Gamma _\alpha$ with the same stability arises near $\Gamma _*$
with the same stability arises near $\Gamma _*$ , but no closed orbits arise as $\alpha$
, but no closed orbits arise as $\alpha$ varies oppositely (see [Reference Perko26, Theorem 3 of Section 6 of Chapter IV]).
varies oppositely (see [Reference Perko26, Theorem 3 of Section 6 of Chapter IV]).
However, the above properties (PR1)–(PR4) may not be true if the rotated vector field is not analytic. The two examples of piecewise-defined families given in § 2, which are smooth but not analytic and satisfy the rotated conditions, show that a limit cycle of odd multiplicity may produce new limit cycles and a limit cycle of even multiplicity may produce more than two limit cycles, which do not match (PR1) and (PR2) separately.
In this paper, we investigate rotated vector fields of piecewise analytic generalized Liénard form and see which one of results (PR1)–(PR4) remains true. For this purpose, we consider the family of generalized Liénard equations
with non-analytic functions $f$![]() and $g$
and $g$![]() in $x$
in $x$![]() or $\dot {x}$
or $\dot {x}$![]() such that its corresponding planar vector field is rotated with the parameter $\alpha \in I$
such that its corresponding planar vector field is rotated with the parameter $\alpha \in I$![]() . In § 2 we give our main results on the relation between variational exponent and multiplicity of hyperbolic limit cycles (which was not obtained for analytic rotated vector fields), non-hyperbolic limit cycles and semi-stable limit cycles of the vector field of (1.2) as $\alpha$
. In § 2 we give our main results on the relation between variational exponent and multiplicity of hyperbolic limit cycles (which was not obtained for analytic rotated vector fields), non-hyperbolic limit cycles and semi-stable limit cycles of the vector field of (1.2) as $\alpha$![]() varies and answer to the questions:
varies and answer to the questions:
(Q1) Can we find conditions such that the aforementioned results (PR1)–(PR4) still hold?
(Q2) Can we give an expanding (or contracting) rate for limit cycles in terms of the rotated parameter $\alpha$
 ?
?(Q3) Can we use the rotated rule to determine the number of bifurcated limit cycles for a class of non-analytic systems?
In § 3 we further investigate the number of limit cycles bifurcated from a weak focus or a homoclinic loop in rotated vector fields. In § 4 and 5 we apply our main results obtained in § 2 to an SD oscillator and a continuous piecewise linear differential system with three zones and asymmetry for the number of limit cycles, respectively.
2. Main results
Let us begin this section from the family
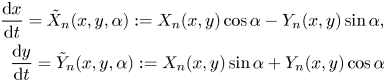
with the functions

or

where $r:=\sqrt {x^2+y^2}$![]() is near $r_0>0$
is near $r_0>0$![]() and $n$
and $n$![]() is a positive integer. Note that system (2.1) with (2.2) (resp. (2.3)) is continuous and even $\mathcal {C}^{n}$
is a positive integer. Note that system (2.1) with (2.2) (resp. (2.3)) is continuous and even $\mathcal {C}^{n}$![]() (resp. $\mathcal {C}^{n-1}$
(resp. $\mathcal {C}^{n-1}$![]() ) but not analytic because its derivative is $\mathcal {C}^{n-1}$
) but not analytic because its derivative is $\mathcal {C}^{n-1}$![]() (resp. $\mathcal {C}^{n-2}$
(resp. $\mathcal {C}^{n-2}$![]() ) by an inductive proof from $n=1$
) by an inductive proof from $n=1$![]() .
.
We first consider family (2.1) with (2.2), which is a Duff's complete family of rotated vector fields with the rotated parameter $\alpha \in [-\pi, \pi )$![]() and therefore a Perko's family because
and therefore a Perko's family because
and

at each regular point. For $\alpha =0$![]() , $\tilde X_n(x,y,0)=X_n(x,y)$
, $\tilde X_n(x,y,0)=X_n(x,y)$![]() and $\tilde Y_n(x,y,0)=Y_n(x,y)$
and $\tilde Y_n(x,y,0)=Y_n(x,y)$![]() . Then system (2.1) with (2.2) as $\alpha =0$
. Then system (2.1) with (2.2) as $\alpha =0$![]() , denoted by (E1), has a unique limit cycle $r=r_0$
, denoted by (E1), has a unique limit cycle $r=r_0$![]() , which is of multiplicity $2n+1$
, which is of multiplicity $2n+1$![]() , because the function $V(x,y):=x^2+y^2$
, because the function $V(x,y):=x^2+y^2$![]() satisfies
satisfies

for $r$![]() near $r_0$
near $r_0$![]() . On the other hand, for arbitrary $m\in \mathbb {Z}_+$
. On the other hand, for arbitrary $m\in \mathbb {Z}_+$![]() there exist $\alpha >0$
there exist $\alpha >0$![]() and three values $r_1=r_0+2/(5\pi +4m\pi )$
and three values $r_1=r_0+2/(5\pi +4m\pi )$![]() , $r_2=r_0+2/(\pi +4m\pi )$
, $r_2=r_0+2/(\pi +4m\pi )$![]() and $r_3=r_0+2/(-\pi +4m\pi )$
and $r_3=r_0+2/(-\pi +4m\pi )$![]() such that $3(r_1-r_0)^{2n+1}<\alpha <3(r_2-r_0)^{2n+1}<3(r_3-r_0)^{2n+1}$
such that $3(r_1-r_0)^{2n+1}<\alpha <3(r_2-r_0)^{2n+1}<3(r_3-r_0)^{2n+1}$![]() and $r_1< r_2< r_3$
and $r_1< r_2< r_3$![]() . Thus, it is not difficult to check that
. Thus, it is not difficult to check that

and

By the mean value theorem, ${\rm d}r/{\rm d}t$![]() has two zeros, one lies in $(r_1, r_2)$
has two zeros, one lies in $(r_1, r_2)$![]() and the other lies in $(r_2, r_3)$
and the other lies in $(r_2, r_3)$![]() , which implies that system (2.1) has at least two limit cycles in a small neighbourhood of $r=r_0$
, which implies that system (2.1) has at least two limit cycles in a small neighbourhood of $r=r_0$![]() if the positive integer $m$
if the positive integer $m$![]() is large enough, a result different from (PR1). This implies that for an arbitrary $\varepsilon$
is large enough, a result different from (PR1). This implies that for an arbitrary $\varepsilon$![]() -neighbourhood of the circle $r=r_0$
-neighbourhood of the circle $r=r_0$![]() there exists a number $N\in \mathbb {Z}_+$
there exists a number $N\in \mathbb {Z}_+$![]() such that the circle $r=r_i$
such that the circle $r=r_i$![]() for $i=1,2,3$
for $i=1,2,3$![]() lies in the $\varepsilon$
lies in the $\varepsilon$![]() -neighbourhood of $r=r_0$
-neighbourhood of $r=r_0$![]() if $m>N$
if $m>N$![]() .
.
Family (2.1) with (2.3) is also a Duff's complete family of rotated vector fields with the rotated parameter $\alpha \in [-\pi, \pi )$![]() and therefore a Perko's family because (2.4) and (2.5) hold for this system at each regular point. Then system (2.1) with (2.3) as $\alpha =0$
and therefore a Perko's family because (2.4) and (2.5) hold for this system at each regular point. Then system (2.1) with (2.3) as $\alpha =0$![]() , denoted by (E2), has a unique limit cycle $r=r_0$
, denoted by (E2), has a unique limit cycle $r=r_0$![]() , which is of multiplicity $2n$
, which is of multiplicity $2n$![]() and semi-stable, because
and semi-stable, because

for $r$![]() near $r_0$
near $r_0$![]() . On the other hand, for $\alpha \neq 0$
. On the other hand, for $\alpha \neq 0$![]() we have
we have

Since ${\rm d}r/{\rm d}t>0$![]() , there is no limit cycle as $\alpha <0$
, there is no limit cycle as $\alpha <0$![]() . For $\alpha =\varepsilon >0$
. For $\alpha =\varepsilon >0$![]() is small, we can obtain two limit cycles by a similar discussion as for system (2.1) with (2.2) in both cases $r>r_0$
is small, we can obtain two limit cycles by a similar discussion as for system (2.1) with (2.2) in both cases $r>r_0$![]() and $r< r_0$
and $r< r_0$![]() near $r=r_0$
near $r=r_0$![]() respectively, which implies that system (2.1) with (2.3) has at least four limit cycles in a small neighbourhood of $r=r_0$
respectively, which implies that system (2.1) with (2.3) has at least four limit cycles in a small neighbourhood of $r=r_0$![]() , a result different from (PR2).
, a result different from (PR2).
The above two examples show that the properties (PR1) and (PR2) do not always hold for some non-analytic rotated vector fields, which suggest considering some non-analytic rotated vector fields for those properties (PR1)–(PR4). In this paper, we discuss the generalized Liénard equation (1.2), which is equivalent to the following planar system
where $(x,y)\in D$![]() , a connected open set in $\mathbb {R}^2$
, a connected open set in $\mathbb {R}^2$![]() . The system defines the corresponding vector field $\mathcal {L}_\alpha :=(y, -g(x )-f(x,y,\alpha )y)$
. The system defines the corresponding vector field $\mathcal {L}_\alpha :=(y, -g(x )-f(x,y,\alpha )y)$![]() .
.
Let $a_1$![]() (resp. $a_2$
(resp. $a_2$![]() ) denote the minimum (resp. maximum) for abscissas of points in $D$
) denote the minimum (resp. maximum) for abscissas of points in $D$![]() , which may be $-\infty$
, which may be $-\infty$![]() (resp. $+\infty$
(resp. $+\infty$![]() ). We need the following hypotheses:
). We need the following hypotheses:
(H 1) Piecewise analytic : The function $g(x)$
 is piecewise analytic on $(a_1,x_1)\cup (x_1,x_2)\cup (x_2,x_3)\cup \ldots \cup (x_n,a_2)$
is piecewise analytic on $(a_1,x_1)\cup (x_1,x_2)\cup (x_2,x_3)\cup \ldots \cup (x_n,a_2)$ , and functions $f(x,y,\alpha )$
, and functions $f(x,y,\alpha )$ , $\partial f(x,y,\alpha )/\partial y$
, $\partial f(x,y,\alpha )/\partial y$ are piecewise analytic on $D_1\cup D_2\cup \ldots \cup D_{n+1}$
are piecewise analytic on $D_1\cup D_2\cup \ldots \cup D_{n+1}$ , where $D_1=\{(x,y)\in D: a_1< x< x_1\}$
, where $D_1=\{(x,y)\in D: a_1< x< x_1\}$ , $D_i=\{(x,y)\in D: x_{i-1}< x< x_{i} \}$
, $D_i=\{(x,y)\in D: x_{i-1}< x< x_{i} \}$ for $i=2,\ldots,n$
for $i=2,\ldots,n$ and $D_{n+1}=\{(x,y)\in D: x_n< x< a_2\}$
and $D_{n+1}=\{(x,y)\in D: x_n< x< a_2\}$ .
.(H 2) ($H_2$
 ) Rotated
(2.7)\begin{equation} \frac{\partial f(x,y, \alpha )}{\partial \alpha}\geq0~({\rm or}~\leq0) \end{equation}in $D$
) Rotated
(2.7)\begin{equation} \frac{\partial f(x,y, \alpha )}{\partial \alpha}\geq0~({\rm or}~\leq0) \end{equation}in $D$
 and the equality in (2.7) does not hold on an entire closed orbit of (2.6).
and the equality in (2.7) does not hold on an entire closed orbit of (2.6).
Note that $D= D_1\cup \bar D_2\cup \ldots \cup \bar D_n \cup D_{n+1}$![]() , where $\bar D_i$
, where $\bar D_i$![]() denotes the closure of $D_i$
denotes the closure of $D_i$![]() . Without loss of generality, in this paper we only consider the case ‘$\geq$
. Without loss of generality, in this paper we only consider the case ‘$\geq$![]() ’ in (2.7). Otherwise, we can make the transformation $(y,t)\to (-y,-t)$
’ in (2.7). Otherwise, we can make the transformation $(y,t)\to (-y,-t)$![]() . Inequality (2.7) is not very restrictive because, for example, one can easily check that the function $f(x,y,\alpha ):= \alpha x^{2m}y^{2n}+\hat f(x,y)$
. Inequality (2.7) is not very restrictive because, for example, one can easily check that the function $f(x,y,\alpha ):= \alpha x^{2m}y^{2n}+\hat f(x,y)$![]() with non-negative integers $m,n$
with non-negative integers $m,n$![]() and a piecewise analytic function $\hat f(x,y)$
and a piecewise analytic function $\hat f(x,y)$![]() satisfies $\frac {\partial f(x,y, \alpha )}{\partial \alpha }= x^{2m}y^{2n}\geq 0$
satisfies $\frac {\partial f(x,y, \alpha )}{\partial \alpha }= x^{2m}y^{2n}\geq 0$![]() , i.e. inequality (2.7). The following proposition indicates that the generalized Liénard system (2.6) is rotated if inequality (2.7) is satisfied.
, i.e. inequality (2.7). The following proposition indicates that the generalized Liénard system (2.6) is rotated if inequality (2.7) is satisfied.
Proposition 2.1 $\mathcal {L}_\alpha$![]() with the hypotheses ($H_1$
with the hypotheses ($H_1$![]() ) and ($H_2$
) and ($H_2$![]() ) satisfies conditions (P1) and (P2) in Perko's definition.
) satisfies conditions (P1) and (P2) in Perko's definition.
Proof. One can check that (P1) is true because all equilibria lie at the $x$![]() -axis and the abscissas of all equilibria are the roots of $g(x)=0$
-axis and the abscissas of all equilibria are the roots of $g(x)=0$![]() which are independent of $\alpha$
which are independent of $\alpha$![]() . In order to check (P2), let $\theta$
. In order to check (P2), let $\theta$![]() denote the angle from the $x$
denote the angle from the $x$![]() -axis to the vector $(X(x,y,\alpha ),Y(x,y,\alpha ))$
-axis to the vector $(X(x,y,\alpha ),Y(x,y,\alpha ))$![]() of system (1.1) in counter-clockwise direction. Then
of system (1.1) in counter-clockwise direction. Then

For $\mathcal {L}_\alpha$![]() , we have $X(x,y,\alpha )=y$
, we have $X(x,y,\alpha )=y$![]() and $Y(x,y,\alpha )=-g(x)-f(x,y,\alpha )y$
and $Y(x,y,\alpha )=-g(x)-f(x,y,\alpha )y$![]() . Then, it implies that the vector $(X(x,y,\alpha ), Y(x,y,\alpha ))$
. Then, it implies that the vector $(X(x,y,\alpha ), Y(x,y,\alpha ))$![]() rotates counter-clockwise at a regular point $P_0(x,y)$
rotates counter-clockwise at a regular point $P_0(x,y)$![]() as $\alpha$
as $\alpha$![]() varies since
varies since

at the regular point $P_0(x,y)$![]() for all $\alpha \in I$
for all $\alpha \in I$![]() except in the curves $\Omega (x,y):=\frac {\partial f(x,y, \alpha )}{\partial \alpha }y^2=0$
except in the curves $\Omega (x,y):=\frac {\partial f(x,y, \alpha )}{\partial \alpha }y^2=0$![]() . Thus, condition (P2) holds.
. Thus, condition (P2) holds.
As indicated in the theory of non-analytic dynamical systems ([Reference di Bernardo, Budd, Champneys and Kowalczyk1, Reference Kunze15]), limit cycles of piecewise analytic vector field $\mathcal {L}_\alpha$![]() are referred to the three types: crossing limit cycle (limit cycle intersecting a switching manifold transversely and only containing isolated crossing points of the switching manifold), grazing limit cycle (limit cycle tangent to a switching manifold) and sliding limit cycle (a curve segment of the limit cycle lies on a switching manifold). System (2.6) has no sliding limit cycles because only one point $\{(x_i, 0)\}$
are referred to the three types: crossing limit cycle (limit cycle intersecting a switching manifold transversely and only containing isolated crossing points of the switching manifold), grazing limit cycle (limit cycle tangent to a switching manifold) and sliding limit cycle (a curve segment of the limit cycle lies on a switching manifold). System (2.6) has no sliding limit cycles because only one point $\{(x_i, 0)\}$![]() lies in the sliding set of each switching line $x=x_i$
lies in the sliding set of each switching line $x=x_i$![]() . Thus, we only discuss crossing limit cycles and grazing limit cycles.
. Thus, we only discuss crossing limit cycles and grazing limit cycles.
The first equation of (2.6) shows that the $x$![]() -axis is a unique vertical isocline of the vector field $\mathcal {L}_\alpha$
-axis is a unique vertical isocline of the vector field $\mathcal {L}_\alpha$![]() . Then each limit cycle $\Gamma _\alpha$
. Then each limit cycle $\Gamma _\alpha$![]() of system (2.6) has exactly two intersection points with the $x$
of system (2.6) has exactly two intersection points with the $x$![]() -axis, denoted by $Q_0:(x_l,0)$
-axis, denoted by $Q_0:(x_l,0)$![]() and $P_0:(x_r,0)$
and $P_0:(x_r,0)$![]() with $x_l< x_r$
with $x_l< x_r$![]() . Without loss of generality, in what follows we assume that $\Gamma _\alpha$
. Without loss of generality, in what follows we assume that $\Gamma _\alpha$![]() is a crossing limit cycle; otherwise, we can research similarly because any small vicinity of the grazing limit cycle $\Gamma _\alpha$
is a crossing limit cycle; otherwise, we can research similarly because any small vicinity of the grazing limit cycle $\Gamma _\alpha$![]() (where $\Gamma _\alpha$
(where $\Gamma _\alpha$![]() is not included) only possibly contains the crossing points (see the definition in [Reference di Bernardo, Budd, Champneys and Kowalczyk1, Reference Kuznetsov, Rinaldi and Gragnani16]) of the switching line $x=x_i$
is not included) only possibly contains the crossing points (see the definition in [Reference di Bernardo, Budd, Champneys and Kowalczyk1, Reference Kuznetsov, Rinaldi and Gragnani16]) of the switching line $x=x_i$![]() for $i=1,\ldots,n$
for $i=1,\ldots,n$![]() . Since any small neighbourhood of the crossing limit cycle $\Gamma _\alpha$
. Since any small neighbourhood of the crossing limit cycle $\Gamma _\alpha$![]() only possibly contains the crossing points of the included switching lines, the solution of system (2.6) is Lipschitzian ([Reference di Bernardo, Budd, Champneys, Kowalczyk, Nordmark, Tost and Piiroinen2]). Then, the well-known existence and uniqueness theorem and the continuous dependence theorem of solutions remain true for system (2.6) in the small neighbourhood of $\Gamma _\alpha$
only possibly contains the crossing points of the included switching lines, the solution of system (2.6) is Lipschitzian ([Reference di Bernardo, Budd, Champneys, Kowalczyk, Nordmark, Tost and Piiroinen2]). Then, the well-known existence and uniqueness theorem and the continuous dependence theorem of solutions remain true for system (2.6) in the small neighbourhood of $\Gamma _\alpha$![]() . Obviously, the $x$
. Obviously, the $x$![]() -axis is the normal of $\Gamma _\alpha$
-axis is the normal of $\Gamma _\alpha$![]() at $P_0$
at $P_0$![]() and $Q_0$
and $Q_0$![]() . In this sense, we call the right-hand intersection point $P_0:(x_r(\alpha ),0)$
. In this sense, we call the right-hand intersection point $P_0:(x_r(\alpha ),0)$![]() the right-endpoint of the limit cycle $\Gamma _\alpha$
the right-endpoint of the limit cycle $\Gamma _\alpha$![]() and regard $x_r$
and regard $x_r$![]() , denoted by $x_r(\alpha )$
, denoted by $x_r(\alpha )$![]() for the dependence on the rotated parameter $\alpha$
for the dependence on the rotated parameter $\alpha$![]() , as the $x$
, as the $x$![]() -radius of the cycle. By a translation, we can assume that $x_r(\alpha )=0$
-radius of the cycle. By a translation, we can assume that $x_r(\alpha )=0$![]() without loss of generality. Thus, $g(0 )>0$
without loss of generality. Thus, $g(0 )>0$![]() and $g(x_l )<0$
and $g(x_l )<0$![]() . Consider variation $\varepsilon$
. Consider variation $\varepsilon$![]() of $\alpha$
of $\alpha$![]() and suppose that the vector field $\mathcal {L}_{\alpha +\varepsilon }$
and suppose that the vector field $\mathcal {L}_{\alpha +\varepsilon }$![]() has a limit cycle $\Gamma _{\alpha +\varepsilon }$
has a limit cycle $\Gamma _{\alpha +\varepsilon }$![]() with right-endpoint $\tilde {P}_0:(\tilde {x}_r(\alpha +\varepsilon ),0)$
with right-endpoint $\tilde {P}_0:(\tilde {x}_r(\alpha +\varepsilon ),0)$![]() . Then the difference between $x$
. Then the difference between $x$![]() -radii $\tilde {x}_r(\alpha +\varepsilon )$
-radii $\tilde {x}_r(\alpha +\varepsilon )$![]() and $x_r(\alpha )$
and $x_r(\alpha )$![]() depends on $\varepsilon$
depends on $\varepsilon$![]() , i.e. the function
, i.e. the function
has the same smoothness as $x_r(\alpha )$![]() or $\tilde {x}_r(\alpha )$
or $\tilde {x}_r(\alpha )$![]() . By the continuity, $\Delta _\alpha (\varepsilon )\to 0$
. By the continuity, $\Delta _\alpha (\varepsilon )\to 0$![]() as $\varepsilon \to 0$
as $\varepsilon \to 0$![]() . In the following theorem 2.3, we prove that
. In the following theorem 2.3, we prove that
for a certain $\ell \in \mathbb {R}^+$![]() . Clearly, the amplitude of the limit cycle $\Gamma _\alpha$
. Clearly, the amplitude of the limit cycle $\Gamma _\alpha$![]() expands outwards if $\zeta >0$
expands outwards if $\zeta >0$![]() or inwards (or say contracts) if $\zeta <0$
or inwards (or say contracts) if $\zeta <0$![]() with the variational exponent $\ell$
with the variational exponent $\ell$![]() .
.
On the other hand, we also consider those spiral orbits near limit cycles. Let $P$![]() denote $(x_0,0)$
denote $(x_0,0)$![]() , where $|x_0|<\delta$
, where $|x_0|<\delta$![]() and $\delta >0$
and $\delta >0$![]() is small. By the continuous dependence theorem, the orbit $\varphi (P, I^+)$
is small. By the continuous dependence theorem, the orbit $\varphi (P, I^+)$![]() starting from $P$
starting from $P$![]() intersects the $x$
intersects the $x$![]() -axis again for the first time at a point $P_1=(x_1,0)$
-axis again for the first time at a point $P_1=(x_1,0)$![]() , as shown in figure 1. Here, without loss of generality, we only show the case of the external neighbourhood of $\Gamma$
, as shown in figure 1. Here, without loss of generality, we only show the case of the external neighbourhood of $\Gamma$![]() in figure 1. Thus, we can define the map $\mathcal {P}:P\mapsto P_1$
in figure 1. Thus, we can define the map $\mathcal {P}:P\mapsto P_1$![]() (or $x_0\mapsto x_1$
(or $x_0\mapsto x_1$![]() equivalently) on the $x$
equivalently) on the $x$![]() -axis, called a Poincaré map, and the successive function $\varrho$
-axis, called a Poincaré map, and the successive function $\varrho$![]() between $P$
between $P$![]() and $\mathcal {P}(P)$
and $\mathcal {P}(P)$![]() , i.e.
, i.e.
As indicated in Definition 2 of [Reference Perko26, p.216] or Section 2 of [Reference Zhang, Ding, Huang and Dong30, Chapter 4], $\Gamma _\alpha$![]() is externally stable (resp. unstable) when there is a sufficiently small $\delta >0$
is externally stable (resp. unstable) when there is a sufficiently small $\delta >0$![]() such that $\varrho (x)<0$
such that $\varrho (x)<0$![]() (resp. $>0$
(resp. $>0$![]() ) for all $x\in (0,\delta )$
) for all $x\in (0,\delta )$![]() . Similarly, $\Gamma _\alpha$
. Similarly, $\Gamma _\alpha$![]() is internally stable (resp. unstable) if $\varrho (x)>0$
is internally stable (resp. unstable) if $\varrho (x)>0$![]() (resp. $<0$
(resp. $<0$![]() ) for all $x\in (-\delta,0)$
) for all $x\in (-\delta,0)$![]() . $\Gamma _\alpha$
. $\Gamma _\alpha$![]() is stable (resp. unstable) if it is both externally stable (resp. unstable) and internally stable (resp. unstable). Naturally, we have $\varrho (0)=0$
is stable (resp. unstable) if it is both externally stable (resp. unstable) and internally stable (resp. unstable). Naturally, we have $\varrho (0)=0$![]() and $\varrho (x)=x^kh(x)$
and $\varrho (x)=x^kh(x)$![]() , where $k>0$
, where $k>0$![]() is a real number and $h$
is a real number and $h$![]() is a continuous function such that $h(0)\neq 0$
is a continuous function such that $h(0)\neq 0$![]() . $\Gamma _\alpha$
. $\Gamma _\alpha$![]() is called a limit cycle of multiplicity $k$
is called a limit cycle of multiplicity $k$![]() (which may not be an integer) if
(which may not be an integer) if
In particular, if system (2.6) is smooth then $k\in \mathbb {Z}_+$![]() and condition (2.10) is equivalent to the following $\varrho (0)=\varrho '(0)=\cdots =\varrho ^{(k-1)}(0)=0~{\rm and}~\varrho ^{(k)}(0)\neq 0$
and condition (2.10) is equivalent to the following $\varrho (0)=\varrho '(0)=\cdots =\varrho ^{(k-1)}(0)=0~{\rm and}~\varrho ^{(k)}(0)\neq 0$![]() by [Reference Zhang, Ding, Huang and Dong30, Chapter 4.2, Definition 2.1]. Then, $\Gamma _\alpha$
by [Reference Zhang, Ding, Huang and Dong30, Chapter 4.2, Definition 2.1]. Then, $\Gamma _\alpha$![]() is called a simple or hyperbolic limit cycle for $k=1$
is called a simple or hyperbolic limit cycle for $k=1$![]() ; for odd $k$
; for odd $k$![]() , $\Gamma _\alpha$
, $\Gamma _\alpha$![]() is stable (resp. unstable) if $\varrho ^{(k)}(0)<0$
is stable (resp. unstable) if $\varrho ^{(k)}(0)<0$![]() or $c_k<0$
or $c_k<0$![]() (resp. $\varrho ^{(k)}(0)>0$
(resp. $\varrho ^{(k)}(0)>0$![]() or $c_k>0$
or $c_k>0$![]() ); for even $k$
); for even $k$![]() , $\Gamma _\alpha$
, $\Gamma _\alpha$![]() is semi-stable. The multiplicity $k$
is semi-stable. The multiplicity $k$![]() is an integer if the system is smooth (see Theorem 7.19 in [Reference Dumortier, Llibre and Artés11, p.196]), but may not be integer for piecewise analytic systems. For example, the following system
is an integer if the system is smooth (see Theorem 7.19 in [Reference Dumortier, Llibre and Artés11, p.196]), but may not be integer for piecewise analytic systems. For example, the following system
with an integer $p$![]() and an odd number $q$
and an odd number $q$![]() has the limit cycle $x^2+y^2=1$
has the limit cycle $x^2+y^2=1$![]() , which is of multiplicity $p/q$
, which is of multiplicity $p/q$![]() because one can reduce the system to the equation $\frac {{\rm d}r}{{\rm d}t}=-r(r^2-1)^{p/q},$
because one can reduce the system to the equation $\frac {{\rm d}r}{{\rm d}t}=-r(r^2-1)^{p/q},$![]() where $r=\sqrt {x^2+y^2}$
where $r=\sqrt {x^2+y^2}$![]() . For simplicity, let $p/q=5/3$
. For simplicity, let $p/q=5/3$![]() . Then, for an initial value $(r,\theta )=(1+\varepsilon,0)$
. Then, for an initial value $(r,\theta )=(1+\varepsilon,0)$![]() with arbitrarily small $|\varepsilon |$
with arbitrarily small $|\varepsilon |$![]() , near the cycle $r=1$
, near the cycle $r=1$![]() we can use the method of indeterminate coefficients to give the successive function
we can use the method of indeterminate coefficients to give the successive function
where $k=5/3$![]() and $c_k=- 2^{8/3}\pi$
and $c_k=- 2^{8/3}\pi$![]() .
.

Figure 1. The orbits close to limit cycle $\Gamma$![]() for $\varepsilon >0$
for $\varepsilon >0$![]() .
.
Unlike (2.10), $\Gamma _{\alpha }$![]() is called an externally (or internally) compound limit cycle (see [Reference Zhang, Ding, Huang and Dong30, Chapter 4.2]) if for arbitrarily given small $\delta >0$
is called an externally (or internally) compound limit cycle (see [Reference Zhang, Ding, Huang and Dong30, Chapter 4.2]) if for arbitrarily given small $\delta >0$![]() there are two points $x_0,\tilde x_0\in (0,\delta )$
there are two points $x_0,\tilde x_0\in (0,\delta )$![]() (or $\in (-\delta,0)$
(or $\in (-\delta,0)$![]() ) such that
) such that
i.e. near a side of $\Gamma _{\alpha }$![]() there is not a periodic annulus but there is a sequence of periodic solutions approaching the cycle $\Gamma _{\alpha }$
there is not a periodic annulus but there is a sequence of periodic solutions approaching the cycle $\Gamma _{\alpha }$![]() . Although any analytic system does not have a compound limit cycle ([Reference Zhang, Ding, Huang and Dong30, Theorem 2.1 of Chapter 4]), a piecewise analytic Liénard system may have. For example, consider system (2.6) with $g(x)=x$
. Although any analytic system does not have a compound limit cycle ([Reference Zhang, Ding, Huang and Dong30, Theorem 2.1 of Chapter 4]), a piecewise analytic Liénard system may have. For example, consider system (2.6) with $g(x)=x$![]() and
and

where $k$![]() is a positive integer. In the polar coordinates $(x,y)=(r\cos \theta, r\sin \theta ),$
is a positive integer. In the polar coordinates $(x,y)=(r\cos \theta, r\sin \theta ),$![]() we obtain
we obtain

It implies that system (2.6) with $g(x)=x$![]() and $f(x)$
and $f(x)$![]() exhibited in (2.11) has a compound limit cycle $x^2+y^2=1$
exhibited in (2.11) has a compound limit cycle $x^2+y^2=1$![]() because it has closed orbits $x^2+y^2=1\pm 2/n$
because it has closed orbits $x^2+y^2=1\pm 2/n$![]() for all integers $n\geq 3$
for all integers $n\geq 3$![]() , but for each $n\ge 3$
, but for each $n\ge 3$![]() in the annular regions $\sqrt {1+2/(n+1)}< r<\sqrt {1+2/n}$
in the annular regions $\sqrt {1+2/(n+1)}< r<\sqrt {1+2/n}$![]() and $\sqrt {1-2/n}< r<\sqrt {1-2/(n+1)}$
and $\sqrt {1-2/n}< r<\sqrt {1-2/(n+1)}$![]() system (2.6) with $g(x)=x$
system (2.6) with $g(x)=x$![]() and $f(x)$
and $f(x)$![]() exhibited in (2.11) has no closed orbits. Otherwise, integrating along a closed orbit $\gamma$
exhibited in (2.11) has no closed orbits. Otherwise, integrating along a closed orbit $\gamma$![]() (if exists in one of the annular region), we obtain a contradiction
(if exists in one of the annular region), we obtain a contradiction

because $\sin \frac {2\pi }{r^2-1}\ne 0$![]() and $1+\sin \theta \cos \theta (r^2-1)^k\sin \frac {2\pi }{r^2-1}>0$
and $1+\sin \theta \cos \theta (r^2-1)^k\sin \frac {2\pi }{r^2-1}>0$![]() .
.
The above two examples show that compound limit cycle and limit cycle of fractional multiplicity are both possible for piecewise analytic systems, but neither of them happens in a Liénard system (2.6) with the specific piecewise analyticity ($H_1$![]() ).
).
Lemma 2.2 Any limit cycle of the generalized Liénard system (2.6) with hypothesis ($H_1$![]() ) is neither compound nor of fractional multiplicity.
) is neither compound nor of fractional multiplicity.
Proof. Assume that system (2.6) with hypothesis ($H_1$![]() ) has a limit cycle $\Gamma$
) has a limit cycle $\Gamma$![]() , as shown in figure 2. For compound structure and fractional multiplicity, we need to consider a small annulus surrounding $\Gamma$
, as shown in figure 2. For compound structure and fractional multiplicity, we need to consider a small annulus surrounding $\Gamma$![]() . Since the function $g$
. Since the function $g$![]() is piecewise analytic on $(a_1,x_1)\cup (x_1,x_2)\cup (x_2,x_3)\cup \ldots \cup (x_n,a_2)$
is piecewise analytic on $(a_1,x_1)\cup (x_1,x_2)\cup (x_2,x_3)\cup \ldots \cup (x_n,a_2)$![]() , and functions $f(x,y,\alpha )$
, and functions $f(x,y,\alpha )$![]() , $\partial f(x,y,\alpha )/\partial y$
, $\partial f(x,y,\alpha )/\partial y$![]() are piecewise analytic on $D_1\cup D_2\cup \ldots \cup D_{n+1}$
are piecewise analytic on $D_1\cup D_2\cup \ldots \cup D_{n+1}$![]() , there is a small $\varepsilon >0$
, there is a small $\varepsilon >0$![]() such that each normal at any $P\in \Gamma$
such that each normal at any $P\in \Gamma$![]() restricted to the open annular neighbourhood $S(\Gamma,\varepsilon )$
restricted to the open annular neighbourhood $S(\Gamma,\varepsilon )$![]() of $\Gamma$
of $\Gamma$![]() with the radius $\varepsilon$
with the radius $\varepsilon$![]() is non-contact. Thus, we can set up curvilinear coordinates in the annulus $S(\Gamma,\varepsilon )$
is non-contact. Thus, we can set up curvilinear coordinates in the annulus $S(\Gamma,\varepsilon )$![]() . Each point $\underline {P}$
. Each point $\underline {P}$![]() in $S(\Gamma,\varepsilon )$
in $S(\Gamma,\varepsilon )$![]() has a corresponding point $P\in \Gamma$
has a corresponding point $P\in \Gamma$![]() such that $\underline {P}$
such that $\underline {P}$![]() lies on the normal at $P$
lies on the normal at $P$![]() .
.

Figure 2. The curvilinear coordinates in the annulus $S(\Gamma,\varepsilon )$![]() .
.
Note that a point on limit cycle $\Gamma$![]() can be written as
can be written as
where $s$![]() is the arclength (parameter) from $P$
is the arclength (parameter) from $P$![]() to a specified point in the clockwise direction. Let $p$
to a specified point in the clockwise direction. Let $p$![]() be the length from $P$
be the length from $P$![]() to $\underline {P}$
to $\underline {P}$![]() positively in the outward direction. Thus, as shown in [Reference Zhang, Ding, Huang and Dong30, Chapter 4.2], we can represent the point $\underline {P}: (x,y)$
positively in the outward direction. Thus, as shown in [Reference Zhang, Ding, Huang and Dong30, Chapter 4.2], we can represent the point $\underline {P}: (x,y)$![]() in the curvilinear coordinates $s$
in the curvilinear coordinates $s$![]() and $p$
and $p$![]() in each region $D_j$
in each region $D_j$![]() ($j=1,2,\ldots,n+1$
($j=1,2,\ldots,n+1$![]() ) as
) as
where

Therefore, we have

implying that
where

Having the above curvilinear coordinates, we first consider the case that $\Gamma$![]() does not intersect any switching line. Let $P_0:(0,p_0) \in \overline {P\underline {P}}$
does not intersect any switching line. Let $P_0:(0,p_0) \in \overline {P\underline {P}}$![]() and $p_0$
and $p_0$![]() be the length from $P$
be the length from $P$![]() to $P_0$
to $P_0$![]() positively in the outward direction, as shown in figure 2. It follows from (2.12) that the Poincaré map $\mathcal {P}$
positively in the outward direction, as shown in figure 2. It follows from (2.12) that the Poincaré map $\mathcal {P}$![]() satisfies
satisfies
where $l$![]() is the total arc length of $\Gamma$
is the total arc length of $\Gamma$![]() .
.
Second, consider the case that $\Gamma$![]() intersects only one switching line $x=x_j$
intersects only one switching line $x=x_j$![]() . It is clear that $\Gamma$
. It is clear that $\Gamma$![]() is divided by $x=x_j$
is divided by $x=x_j$![]() into two parts: left part and right part. Consider $P_0:(0,p_0)$
into two parts: left part and right part. Consider $P_0:(0,p_0)$![]() to be the initial point of the Poincaré map on $x=x_j$
to be the initial point of the Poincaré map on $x=x_j$![]() , and let $(l_1,p_1)$
, and let $(l_1,p_1)$![]() (resp. $(l_2,p_2)$
(resp. $(l_2,p_2)$![]() ) denote the first intersection point of the positive-(resp. negative-) half orbit with $x=x_j$
) denote the first intersection point of the positive-(resp. negative-) half orbit with $x=x_j$![]() . Without loss of generality, we can assume that the segment $\overline {PP_0}$
. Without loss of generality, we can assume that the segment $\overline {PP_0}$![]() on the switching line $x=x_j$
on the switching line $x=x_j$![]() is vertical to $\Gamma$
is vertical to $\Gamma$![]() . Otherwise, a rotation can achieve this because the switching line $x=x_j$
. Otherwise, a rotation can achieve this because the switching line $x=x_j$![]() is transversal to $\Gamma$
is transversal to $\Gamma$![]() . Then, we can obtain the two half Poincaré maps
. Then, we can obtain the two half Poincaré maps
and
as shown in figure 3. Notice that the denominator of the right-hand side of (2.12) does not equal zero since $X^2(\varphi (s),\phi (s),\alpha )+Y^2(\varphi (s),\phi (s),\alpha )\neq 0$![]() . Moreover, the vector field of system (2.6) is analytic for $x< x_j$
. Moreover, the vector field of system (2.6) is analytic for $x< x_j$![]() and $x>x_j$
and $x>x_j$![]() in $S(\Gamma,\varepsilon )$
in $S(\Gamma,\varepsilon )$![]() . Therefore,
. Therefore,

Thus, we obtain the following successive function

The coefficients $a_i-b_i$![]() in the above series have the two cases:
in the above series have the two cases:
(i) $a_i-b_i=0$
 for each positive integer $i\in \mathbb {Z}_+$
for each positive integer $i\in \mathbb {Z}_+$ ;
;(ii) there exists a positive integer $i_1$
 such that $a_{i_1}-b_{i_1}\ne 0$
such that $a_{i_1}-b_{i_1}\ne 0$ and $a_j-b_j= 0$
and $a_j-b_j= 0$ for all $1\le j< i_1$
for all $1\le j< i_1$ .
.
In case (i) we have a periodic annulus and no limit cycles exist. In case (ii), $\Gamma$![]() is a limit cycle of multiplicity $i_1\in \mathbb {Z}_+$
is a limit cycle of multiplicity $i_1\in \mathbb {Z}_+$![]() and there are at most $i_1$
and there are at most $i_1$![]() zeros of $\varrho (p_0)$
zeros of $\varrho (p_0)$![]() near the origin by the Malgrange preparation theorem ([Reference Chow and Hale6]). Consequently, limit cycle $\Gamma$
near the origin by the Malgrange preparation theorem ([Reference Chow and Hale6]). Consequently, limit cycle $\Gamma$![]() is not compound and has a multiplicity $i_1 \in \mathbb {Z}_+$
is not compound and has a multiplicity $i_1 \in \mathbb {Z}_+$![]() if $\Gamma$
if $\Gamma$![]() intersects only one switching line.
intersects only one switching line.

Figure 3. The successive function $\varrho (p_0)= \mathcal {P}_1(p_0)- \mathcal {P}_2(p_0)$![]() .
.
In addition, if the crossing limit cycle $\Gamma$![]() intersects two or more switching lines, we can prove our result similarly as we do for the case of only one switching line. Actually, if $\Gamma$
intersects two or more switching lines, we can prove our result similarly as we do for the case of only one switching line. Actually, if $\Gamma$![]() intersects $n$
intersects $n$![]() ($n>1$
($n>1$![]() ) switching lines, a small neighbourhood of the crossing limit cycle $\Gamma$
) switching lines, a small neighbourhood of the crossing limit cycle $\Gamma$![]() only possibly contains the crossing points of the switching lines. Thus, we can present the Poincaré map in $2n$
only possibly contains the crossing points of the switching lines. Thus, we can present the Poincaré map in $2n$![]() pieces, each of which is a map from a witching line to the next similar to (2.13). Since $\Gamma$
pieces, each of which is a map from a witching line to the next similar to (2.13). Since $\Gamma$![]() intersects transversally the switching lines, each piece of the Poincaré map is well defined and close to the corresponding segment of the orbit $\Gamma$
intersects transversally the switching lines, each piece of the Poincaré map is well defined and close to the corresponding segment of the orbit $\Gamma$![]() in the corresponding zone $D_i$
in the corresponding zone $D_i$![]() between the executive switching lines. In contrast, if $\Gamma$
between the executive switching lines. In contrast, if $\Gamma$![]() is a grazing limit cycle, there are at most two grazing points, at which $\Gamma$
is a grazing limit cycle, there are at most two grazing points, at which $\Gamma$![]() intersects two switching lines at the $x$
intersects two switching lines at the $x$![]() -axis. Therefore, any small vicinity of $\Gamma$
-axis. Therefore, any small vicinity of $\Gamma$![]() (where $\Gamma$
(where $\Gamma$![]() is not included) only possibly contains the crossing points of the switching lines and thus the successive function can be constructed similarly as we did above for the case that $\Gamma$
is not included) only possibly contains the crossing points of the switching lines and thus the successive function can be constructed similarly as we did above for the case that $\Gamma$![]() intersects only one switching line.
intersects only one switching line.
Having the above lemma, we are ready to prove the following theorem, which shows that properties (PR1) and (PR2), obtained by Perko ([Reference Perko23, Reference Perko26]) for analytic families of rotated vector field, remain true for Liénard system (2.6) with hypotheses ($H_1$![]() ) and ($H_2$
) and ($H_2$![]() ). Note that system (2.6) with hypotheses ($H_1$
). Note that system (2.6) with hypotheses ($H_1$![]() ) and ($H_2$
) and ($H_2$![]() ) is rotated in Perko's definition by proposition 2.1. Additionally, we give the relation between variational exponent and multiplicity of limit cycles.
) is rotated in Perko's definition by proposition 2.1. Additionally, we give the relation between variational exponent and multiplicity of limit cycles.
Theorem 2.3 Assume that system (2.6) satisfies hypotheses ($H_1$![]() ) and ($H_2$
) and ($H_2$![]() ) and has a limit cycle $\Gamma$
) and has a limit cycle $\Gamma$![]() of multiplicity $k$
of multiplicity $k$![]() for $\alpha =\alpha _0$
for $\alpha =\alpha _0$![]() . Then
. Then
(a) When $k$
 is odd, the cycle $\Gamma$
is odd, the cycle $\Gamma$ still exists, denoted by $\Gamma _{\alpha }$
still exists, denoted by $\Gamma _{\alpha }$ , and expands inwards (resp. outwards) monotonically as $\alpha :=\alpha _0+\varepsilon$
, and expands inwards (resp. outwards) monotonically as $\alpha :=\alpha _0+\varepsilon$ increases if $\Gamma$
increases if $\Gamma$ is stable (resp. unstable), where $\varepsilon >0$
is stable (resp. unstable), where $\varepsilon >0$ is sufficiently small. Moreover, the variational exponent of the cycle $\Gamma _{\alpha }$
is sufficiently small. Moreover, the variational exponent of the cycle $\Gamma _{\alpha }$ is $\varepsilon ^{2/k}$
is $\varepsilon ^{2/k}$ .
.(b) When $k$
 is even, $\Gamma$
is even, $\Gamma$ splits into exact two simple limit cycles $\Gamma _{\alpha }^\pm$
splits into exact two simple limit cycles $\Gamma _{\alpha }^\pm$ , one of which is stable but the other is unstable as the parameter $\alpha$
, one of which is stable but the other is unstable as the parameter $\alpha$ varies in one direction and $\Gamma$
varies in one direction and $\Gamma$ disappears as $\alpha$
disappears as $\alpha$ varies in the opposite direction. Moreover, the outer limit cycle $\Gamma _{\alpha }^+$
varies in the opposite direction. Moreover, the outer limit cycle $\Gamma _{\alpha }^+$ expands outwards and the inner one $\Gamma _{\alpha }^-$
expands outwards and the inner one $\Gamma _{\alpha }^-$ expands inwards as $\alpha$
expands inwards as $\alpha$ varies. Additionally, the variational exponent of the two cycles $\Gamma _{\alpha }^\pm$
varies. Additionally, the variational exponent of the two cycles $\Gamma _{\alpha }^\pm$ is $\varepsilon ^{2/k}$
is $\varepsilon ^{2/k}$ , where $\alpha =\alpha _0+\varepsilon$
, where $\alpha =\alpha _0+\varepsilon$ .
.
Proof. By lemma 2.2, $k$![]() is a positive integer. In the following, we discuss the distance between an orbit without perturbation and the orbit under perturbation near a limit cycle. From the distance we can further investigate zeros of successive function and the relation between variational exponent and multiplicity of limit cycles.
is a positive integer. In the following, we discuss the distance between an orbit without perturbation and the orbit under perturbation near a limit cycle. From the distance we can further investigate zeros of successive function and the relation between variational exponent and multiplicity of limit cycles.
Without loss of generality, we only discuss the case that the limit cycle $\Gamma$![]() is externally stable as $\alpha =\alpha _0$
is externally stable as $\alpha =\alpha _0$![]() , i.e. those points $P_0, P_1$
, i.e. those points $P_0, P_1$![]() and $P$
and $P$![]() defined by the Poincaré map and the successive function $\varrho$
defined by the Poincaré map and the successive function $\varrho$![]() (see (2.9) and figure 1) are ranked by $0< x_1< x_0$
(see (2.9) and figure 1) are ranked by $0< x_1< x_0$![]() . Otherwise, $\Gamma$
. Otherwise, $\Gamma$![]() is externally unstable, for which we make a time-rescaling $t\to -t$
is externally unstable, for which we make a time-rescaling $t\to -t$![]() , so that the limit cycle of the rescaled system is externally stable.
, so that the limit cycle of the rescaled system is externally stable.
We always let $Q:(x_Q, y_Q)$![]() be a general point $Q$
be a general point $Q$![]() . Notice that the closed orbit $\Gamma$
. Notice that the closed orbit $\Gamma$![]() has two intersection points $P_0$
has two intersection points $P_0$![]() and $Q_0$
and $Q_0$![]() with the $x$
with the $x$![]() -axis. Moreover, the orbit $\widehat {PQ_1P_1}$
-axis. Moreover, the orbit $\widehat {PQ_1P_1}$![]() starts from $P:(x_0,0)$
starts from $P:(x_0,0)$![]() , passes through $Q_1:(x_{Q_1},0)$
, passes through $Q_1:(x_{Q_1},0)$![]() and returns the positive $x$
and returns the positive $x$![]() -axis at $P_1:(x_1,0)$
-axis at $P_1:(x_1,0)$![]() such that $x_{Q_1}<0< x_{P_1}< x_P$
such that $x_{Q_1}<0< x_{P_1}< x_P$![]() , as shown in figure 1. We consider the perturbed system (2.6)$|_{\alpha =\alpha _0+\varepsilon }$
, as shown in figure 1. We consider the perturbed system (2.6)$|_{\alpha =\alpha _0+\varepsilon }$![]() and let $\widehat {Q_3Q_1Q_2}$
and let $\widehat {Q_3Q_1Q_2}$![]() be the orbit of system (2.6)$|_{\alpha =\alpha _0+\varepsilon }$
be the orbit of system (2.6)$|_{\alpha =\alpha _0+\varepsilon }$![]() crossing $Q_1$
crossing $Q_1$![]() and having two intersection points $Q_2$
and having two intersection points $Q_2$![]() and $Q_3$
and $Q_3$![]() with the positive $x$
with the positive $x$![]() -axis. For simplicity, let
-axis. For simplicity, let
For $x\in (x_{Q_1}, x_{12})$![]() , let
, let
where $y={\tilde y}_0(x)$![]() and $y={\tilde y}_{\varepsilon }(x)$
and $y={\tilde y}_{\varepsilon }(x)$![]() represent the orbit segments $\widehat {Q_1P_1}$
represent the orbit segments $\widehat {Q_1P_1}$![]() and $\widehat {Q_1Q_2}$
and $\widehat {Q_1Q_2}$![]() , respectively. For $x\in (x_{Q_1}, x_{03})$
, respectively. For $x\in (x_{Q_1}, x_{03})$![]() , let
, let
where $y={\hat y}_0(x)$![]() and $y={\hat y}_{\varepsilon }(x)$
and $y={\hat y}_{\varepsilon }(x)$![]() represent the orbit segments $\widehat {P Q_1}$
represent the orbit segments $\widehat {P Q_1}$![]() and $\widehat {Q_3 Q_1}$
and $\widehat {Q_3 Q_1}$![]() , respectively. Moreover, let
, respectively. Moreover, let
By the mean value theorem, we see from the equations ${\tilde y}_{\varepsilon }(x_{Q_1})={\tilde y}_0(x_{Q_1})=0$![]() that
that

where $\tilde y^*$![]() lies between $\tilde y_0$
lies between $\tilde y_0$![]() and $\tilde y_\varepsilon$
and $\tilde y_\varepsilon$![]() , $\varepsilon _1$
, $\varepsilon _1$![]() lies between $0$
lies between $0$![]() and $\varepsilon$
and $\varepsilon$![]() , and
, and

By (2.16),
indicating that the function $h_3(x):=\int ^x_{x_{Q_1}}z_1(\tau )h_2(\tau ){\rm d}\tau$![]() satisfies
satisfies
By the variation of constant formula, we get from (2.17) that
Since $h_1(x_{Q_1})=0$![]() , we see from (2.7), (2.16) and (2.18) that for all $x\in (x_{Q_1},x_{12})$
, we see from (2.7), (2.16) and (2.18) that for all $x\in (x_{Q_1},x_{12})$![]()

Similarly, for all $x\in (x_{Q_1},x_{03})$![]() we can obtain
we can obtain
where $\varepsilon _2\in (0, \varepsilon )$![]() and
and
for $\hat y^*$![]() lying between $\hat y_0$
lying between $\hat y_0$![]() and $\hat y_\varepsilon$
and $\hat y_\varepsilon$![]() .
.
Construct an energy function
Then
restricted on system (2.6). From (2.19) and (2.20) we see that the two points $P_2$![]() and $P_3$
and $P_3$![]() lie on the two orbit segments $\widehat {Q_1P_1}$
lie on the two orbit segments $\widehat {Q_1P_1}$![]() and $\widehat {Q_3Q_1}$
and $\widehat {Q_3Q_1}$![]() respectively, where $x_{P_2}=x_{Q_2}$
respectively, where $x_{P_2}=x_{Q_2}$![]() , $x_{P_3}=x_{P}$
, $x_{P_3}=x_{P}$![]() , $y_{P_2}>0$
, $y_{P_2}>0$![]() and $y_{P_3}<0$
and $y_{P_3}<0$![]() , as shown in figure 1. From (2.19)–(2.22), and $\int _{\widehat {P_2P_1}}{\rm d}E=E(P_1)-E(P_2)$
, as shown in figure 1. From (2.19)–(2.22), and $\int _{\widehat {P_2P_1}}{\rm d}E=E(P_1)-E(P_2)$![]() , we obtain
, we obtain

where $z_1(\cdot )$![]() is defined in (2.14). Thus, there exist $x^*\in [x_{Q_2},x_1]$
is defined in (2.14). Thus, there exist $x^*\in [x_{Q_2},x_1]$![]() and $y^*\in [0, -z_1(x_{Q_2})]$
and $y^*\in [0, -z_1(x_{Q_2})]$![]() such that
such that

by the mean value theorem for integrals. Thus,
because $g(x^*)=g(x_0)+O(\varepsilon )$![]() . From (2.19)–(2.22) and the equality
. From (2.19)–(2.22) and the equality
we obtain

where $z_2(\cdot )$![]() is defined in (2.15). It follows from equality (2.24) that
is defined in (2.15). It follows from equality (2.24) that
On the other hand, $\Gamma$![]() is a limit cycle of multiple $k$
is a limit cycle of multiple $k$![]() , i.e.
, i.e.
as seen in the definition of a limit cycle of multiple $k$![]() in [Reference Zhang, Ding, Huang and Dong30, Chapter 4.2]. Moreover, $\Gamma$
in [Reference Zhang, Ding, Huang and Dong30, Chapter 4.2]. Moreover, $\Gamma$![]() is externally stable, i.e. $a_k<0$
is externally stable, i.e. $a_k<0$![]() . It follows from (2.23)–(2.26) that
. It follows from (2.23)–(2.26) that
Since $\dot {y}=-g(x)<0$![]() on both the positive $x$
on both the positive $x$![]() -axis and the negative $x$
-axis and the negative $x$![]() -axis near the origin, we see that $g(x_0)>0$
-axis near the origin, we see that $g(x_0)>0$![]() .
.
Consider the case that $k$![]() is odd, i.e. $\Gamma$
is odd, i.e. $\Gamma$![]() is stable in both internal and external neighbourhoods of $\Gamma$
is stable in both internal and external neighbourhoods of $\Gamma$![]() . In the external neighbourhood of $\Gamma$
. In the external neighbourhood of $\Gamma$![]() , we can obtain that $x_{Q_3}-x_{Q_2}>0$
, we can obtain that $x_{Q_3}-x_{Q_2}>0$![]() by (2.27) and the inequalities $a_k<0$
by (2.27) and the inequalities $a_k<0$![]() , $g(x_0)>0$
, $g(x_0)>0$![]() and $x_1>0$
and $x_1>0$![]() , implying that no limit cycles exist in the external neighbourhood of $\Gamma$
, implying that no limit cycles exist in the external neighbourhood of $\Gamma$![]() when $\alpha$
when $\alpha$![]() increases. In the internal neighbourhood of $\Gamma$
increases. In the internal neighbourhood of $\Gamma$![]() , we can also obtain equality (2.27) and the inequalities $a_k<0$
, we can also obtain equality (2.27) and the inequalities $a_k<0$![]() , $g(x_0)>0$
, $g(x_0)>0$![]() but $x_1<0$
but $x_1<0$![]() from a similar discussion to the external neighbourhood of $\Gamma$
from a similar discussion to the external neighbourhood of $\Gamma$![]() . Since the solution of system (2.6) is Lipschitzian, the implicit function theorem is applicable. Thus, from (2.27) with $X_1:={x_1}^k$
. Since the solution of system (2.6) is Lipschitzian, the implicit function theorem is applicable. Thus, from (2.27) with $X_1:={x_1}^k$![]() , we see that equality $x_{Q_3}-x_{Q_2}=0$
, we see that equality $x_{Q_3}-x_{Q_2}=0$![]() has a unique root $X_1= (z_1^2(x_{Q_2})+z_2^2(x_0))/(2a_kg(x_0 )) +o(\varepsilon ^{2})<0$
has a unique root $X_1= (z_1^2(x_{Q_2})+z_2^2(x_0))/(2a_kg(x_0 )) +o(\varepsilon ^{2})<0$![]() , which is equivalent to
, which is equivalent to

It implies that system (2.6)$|_{\alpha =\alpha _0+\varepsilon }$![]() produces a stable limit cycle $\Gamma _{\alpha }$
produces a stable limit cycle $\Gamma _{\alpha }$![]() in the internal neighbourhood of $\Gamma$
in the internal neighbourhood of $\Gamma$![]() , where the bifurcated limit cycle $\Gamma _{\alpha }$
, where the bifurcated limit cycle $\Gamma _{\alpha }$![]() passes through the point $(x_1, 0)$
passes through the point $(x_1, 0)$![]() . Moreover, the stable limit cycle expands inwards (or contracts) monotonically as $\alpha$
. Moreover, the stable limit cycle expands inwards (or contracts) monotonically as $\alpha$![]() increases. From (2.8) and (2.28), we can obtain
increases. From (2.8) and (2.28), we can obtain
implying that the variational exponent is $2/k$![]() . This proves the results of statement (a).
. This proves the results of statement (a).
In the case that $k$![]() is even, i.e. $\Gamma$
is even, i.e. $\Gamma$![]() is semi-stable (externally stable but internally unstable), we obtain equality (2.27), $a_k<0$
is semi-stable (externally stable but internally unstable), we obtain equality (2.27), $a_k<0$![]() and $g(x_0)>0$
and $g(x_0)>0$![]() in the neighbourhood of $\Gamma$
in the neighbourhood of $\Gamma$![]() , implying that $x_{Q_3}-x_{Q_2}>0$
, implying that $x_{Q_3}-x_{Q_2}>0$![]() near the origin and then system (2.6) has no limit cycles in a neighbourhood of $\Gamma$
near the origin and then system (2.6) has no limit cycles in a neighbourhood of $\Gamma$![]() as $\alpha$
as $\alpha$![]() increases.
increases.
In order to completely investigate limit cycles bifurcating from semi-stable $\Gamma$![]() for even $k$
for even $k$![]() , we consider the case that $\alpha :=\alpha _0-\varepsilon$
, we consider the case that $\alpha :=\alpha _0-\varepsilon$![]() decreases. By a similar calculation to (2.27), we obtain
decreases. By a similar calculation to (2.27), we obtain
where $g(x_0)>0$![]() and $a_k<0$
and $a_k<0$![]() . Let $k:=2n$
. Let $k:=2n$![]() for $n\in \mathbb {Z}_+$
for $n\in \mathbb {Z}_+$![]() and $X_2:={x_1}^n$
and $X_2:={x_1}^n$![]() . By the implicit function theorem and (2.29), the equality $x_{Q_3}-x_{Q_2}=0$
. By the implicit function theorem and (2.29), the equality $x_{Q_3}-x_{Q_2}=0$![]() has exactly two roots
has exactly two roots
$X_2= \pm \sqrt { -(z_1^2(x_{P_2})+z_2^2(x_{Q_3}))/(2a_kg(x_0 ))}+o(\varepsilon ^{2})$![]() , which is equivalent to
, which is equivalent to

It follows that two simple limit cycles $\Gamma _{\alpha }^{\pm }$![]() of system (2.6)$|_{\alpha =\alpha _0-\varepsilon }$
of system (2.6)$|_{\alpha =\alpha _0-\varepsilon }$![]() exist in a neighbourhood of $\Gamma$
exist in a neighbourhood of $\Gamma$![]() , and the outer limit cycle $\Gamma _{\alpha }^+$
, and the outer limit cycle $\Gamma _{\alpha }^+$![]() is stable but the inner one $\Gamma _{\alpha }^-$
is stable but the inner one $\Gamma _{\alpha }^-$![]() is unstable. Moreover, $\Gamma _{\alpha }^+$
is unstable. Moreover, $\Gamma _{\alpha }^+$![]() expands outwards monotonically and $\Gamma _{\alpha }^-$
expands outwards monotonically and $\Gamma _{\alpha }^-$![]() expands inwards monotonically as $\alpha$
expands inwards monotonically as $\alpha$![]() decreases. From (2.8) and (2.30), we can obtain $\Delta _\alpha (\varepsilon ):=x_1-0=x_1$
decreases. From (2.8) and (2.30), we can obtain $\Delta _\alpha (\varepsilon ):=x_1-0=x_1$![]() , implying that the variational exponent is $2/k$
, implying that the variational exponent is $2/k$![]() . This proves the results of statement (b).
. This proves the results of statement (b).
In conclusion, for odd $k$![]() system (2.6) produces a stable (resp. unstable) limit cycle $\Gamma _{\alpha }$
system (2.6) produces a stable (resp. unstable) limit cycle $\Gamma _{\alpha }$![]() when $\Gamma$
when $\Gamma$![]() is stable (resp. unstable) in an internal (resp. external) neighbourhood of $\Gamma _{\alpha }$
is stable (resp. unstable) in an internal (resp. external) neighbourhood of $\Gamma _{\alpha }$![]() as $\alpha$
as $\alpha$![]() increases. On the other hand, for even $k$
increases. On the other hand, for even $k$![]() the externally stable and internally unstable (resp. externally stable and internally unstable) $\Gamma$
the externally stable and internally unstable (resp. externally stable and internally unstable) $\Gamma$![]() splits into exact two simple limit cycles $\Gamma _{\alpha }^{\pm }$
splits into exact two simple limit cycles $\Gamma _{\alpha }^{\pm }$![]() . Moreover, the outer limit cycle $\Gamma _{\alpha }^+$
. Moreover, the outer limit cycle $\Gamma _{\alpha }^+$![]() is stable (resp. unstable) and expands outwards, but the inner one $\Gamma _{\alpha }^-$
is stable (resp. unstable) and expands outwards, but the inner one $\Gamma _{\alpha }^-$![]() is unstable (resp. stable) and expands inwards as $\alpha$
is unstable (resp. stable) and expands inwards as $\alpha$![]() decreases (resp. increases). However, the limit cycle $\Gamma$
decreases (resp. increases). However, the limit cycle $\Gamma$![]() disappears as $\alpha$
disappears as $\alpha$![]() varies in the opposite direction. Furthermore, the variational exponent of the new limit cycle is $\varepsilon ^{2/k}$
varies in the opposite direction. Furthermore, the variational exponent of the new limit cycle is $\varepsilon ^{2/k}$![]() .
.
Theorem 2.3 shows how the limit cycle expands or bifurcates as the rotated parameter $\alpha$![]() varies, where the stable (or unstable) limit cycle may be hyperbolic or non-hyperbolic. Clearly, the results of theorem 2.3 are true for analytic rotated Liénard systems. Additionally, theorem 2.3 gives variational exponents to show the expanding rates of the limit cycles depending on the rotated parameter $\alpha$
varies, where the stable (or unstable) limit cycle may be hyperbolic or non-hyperbolic. Clearly, the results of theorem 2.3 are true for analytic rotated Liénard systems. Additionally, theorem 2.3 gives variational exponents to show the expanding rates of the limit cycles depending on the rotated parameter $\alpha$![]() , which was not discussed yet even for analytic rotated vector fields.
, which was not discussed yet even for analytic rotated vector fields.
3. Rotated Hopf bifurcation and rotated homoclinic bifurcation
In this section, we introduce results on homoclinic loops and Hopf bifurcation of the one-parameter family of rotated vector fields (2.6) with hypotheses ($H_1$![]() ) and ($H_2$
) and ($H_2$![]() ).
).
Theorem 3.1 Properties (PR3) and (PR4) in §$1$![]() are still true for system (2.6) with hypotheses ($H_1$
are still true for system (2.6) with hypotheses ($H_1$![]() ) and ($H_2$
) and ($H_2$![]() ).
).
Proof. First, we prove property (PR3). Without loss of generality, assume that the origin of system (2.6) is a weak focus as $\alpha =\alpha _0$![]() and the weak focus is stable, as shown in figure 4. When the vector field of system (2.6) is analytic in a small neighbourhood of the origin, the conclusion holds directly by [Reference Perko23]. Since the origin is a weak focus, we obtain that
and the weak focus is stable, as shown in figure 4. When the vector field of system (2.6) is analytic in a small neighbourhood of the origin, the conclusion holds directly by [Reference Perko23]. Since the origin is a weak focus, we obtain that
on the $x$![]() -axis, where $\mathcal {P}(x)$
-axis, where $\mathcal {P}(x)$![]() is the Poincaré map, $k$
is the Poincaré map, $k$![]() is a positive integer and ${x>0}$
is a positive integer and ${x>0}$![]() is small. As proven in theorem 2.3, (2.27) still holds, where $P, P_1, Q_1, Q_2, Q_3$
is small. As proven in theorem 2.3, (2.27) still holds, where $P, P_1, Q_1, Q_2, Q_3$![]() , $x_0,x_1, x_{Q_1}, x_{Q_2}, x_{Q_3}$
, $x_0,x_1, x_{Q_1}, x_{Q_2}, x_{Q_3}$![]() are defined similarly in figure 1 and the proof of theorem 2.3, as shown in figure 4. Then, $a_k<0$
are defined similarly in figure 1 and the proof of theorem 2.3, as shown in figure 4. Then, $a_k<0$![]() since the weak focus is stable. For positive integer $k$
since the weak focus is stable. For positive integer $k$![]() and $\alpha =\alpha _0-\varepsilon$
and $\alpha =\alpha _0-\varepsilon$![]() , the equality $x_{Q_3}-x_{Q_2}=0$
, the equality $x_{Q_3}-x_{Q_2}=0$![]() has a unique positive zero
has a unique positive zero

where $\varepsilon >0$![]() is small and $g(x_0)>0$
is small and $g(x_0)>0$![]() . When $\alpha =\alpha _0+\varepsilon$
. When $\alpha =\alpha _0+\varepsilon$![]() , for even $k$
, for even $k$![]() the equality $x_{Q_3}-x_{Q_2}=0$
the equality $x_{Q_3}-x_{Q_2}=0$![]() has no positive zeros. Thus, system (2.6)$|_{\alpha =\alpha _0-\varepsilon }$
has no positive zeros. Thus, system (2.6)$|_{\alpha =\alpha _0-\varepsilon }$![]() produces a new stable limit cycle in a small neighbourhood of the origin. Thus, property (PR3) still holds.
produces a new stable limit cycle in a small neighbourhood of the origin. Thus, property (PR3) still holds.

Figure 4. Poincaré map near $O$![]() in system (2.6).
in system (2.6).
Next, we prove property (PR4). Assume that system (2.6) exhibits a homoclinic loop $\Gamma _0$![]() as $\alpha =\alpha _0$
as $\alpha =\alpha _0$![]() . Without loss of generality, we consider that the saddle in the homoclinic loop is the origin and the homoclinic loop is stable. By the sign of the vector field $(y,-g(x)-f(x,y,\alpha )y)$
. Without loss of generality, we consider that the saddle in the homoclinic loop is the origin and the homoclinic loop is stable. By the sign of the vector field $(y,-g(x)-f(x,y,\alpha )y)$![]() near the saddle, in a small neighbourhood of the origin one side of the stable manifold and one side of the unstable manifold of the saddle lie in the left-half plane, but the other sides of the two manifolds lie in the right-half plane. Assume that $\Gamma _0$
near the saddle, in a small neighbourhood of the origin one side of the stable manifold and one side of the unstable manifold of the saddle lie in the left-half plane, but the other sides of the two manifolds lie in the right-half plane. Assume that $\Gamma _0$![]() intersects the positive (or negative) $y$
intersects the positive (or negative) $y$![]() -axis and surrounds neither one stable manifold nor one unstable manifold of the origin other than those in $\Gamma _0$
-axis and surrounds neither one stable manifold nor one unstable manifold of the origin other than those in $\Gamma _0$![]() , as shown in figures 5a, b. Notice that $\dot x=y>0$
, as shown in figures 5a, b. Notice that $\dot x=y>0$![]() in the positive $y$
in the positive $y$![]() -axis and $\dot x=y<0$
-axis and $\dot x=y<0$![]() in the negative $y$
in the negative $y$![]() -axis. However, in figures 5a, b the sign of $\dot x$
-axis. However, in figures 5a, b the sign of $\dot x$![]() at the intersection point $\Gamma _0$
at the intersection point $\Gamma _0$![]() and the $y$
and the $y$![]() -axis is opposite by the location of the stable and unstable manifolds of $\Gamma _0$
-axis is opposite by the location of the stable and unstable manifolds of $\Gamma _0$![]() . Thus, system (2.6) has no homoclinic loops which intersect the positive (or negative) $y$
. Thus, system (2.6) has no homoclinic loops which intersect the positive (or negative) $y$![]() -axis and do not surround the other stable and unstable manifolds. In other words, if system (2.6) has a homoclinic loop $\Gamma _0$
-axis and do not surround the other stable and unstable manifolds. In other words, if system (2.6) has a homoclinic loop $\Gamma _0$![]() which does not surround one stable and one unstable manifolds of $O$
which does not surround one stable and one unstable manifolds of $O$![]() other than those in $\Gamma _0$
other than those in $\Gamma _0$![]() , then $\Gamma _0$
, then $\Gamma _0$![]() lies in the left-half (or right-half) plane. It is similar to prove that system (2.6) has no homoclinic loops which intersect the positive and negative $y$
lies in the left-half (or right-half) plane. It is similar to prove that system (2.6) has no homoclinic loops which intersect the positive and negative $y$![]() -axes, and surround the other two manifolds, as shown in figures 5c, d. Therefore, it is sufficient to prove that the homoclinic loop has one of the configurations shown in figure 6. Otherwise, we apply the transformation $(x,y)\to (-x,-y)$
-axes, and surround the other two manifolds, as shown in figures 5c, d. Therefore, it is sufficient to prove that the homoclinic loop has one of the configurations shown in figure 6. Otherwise, we apply the transformation $(x,y)\to (-x,-y)$![]() . The case of figure 6b can be treated by a similar mean to the case of figure 6a, where the only difference is that the Poincaré map need to be considered in the outer neighbourhood of the homoclinic loop for the case of figure 6b. Therefore, we only need to discuss the case of figure 6a. Now, consider $\delta _0:=-f(0,0, \alpha _0)\neq 0$
. The case of figure 6b can be treated by a similar mean to the case of figure 6a, where the only difference is that the Poincaré map need to be considered in the outer neighbourhood of the homoclinic loop for the case of figure 6b. Therefore, we only need to discuss the case of figure 6a. Now, consider $\delta _0:=-f(0,0, \alpha _0)\neq 0$![]() . In other words, the sum of the two eigenvalues of the hyperbolic saddle is not equal to zero. Let
. In other words, the sum of the two eigenvalues of the hyperbolic saddle is not equal to zero. Let
where $(x,y)=(\varphi (t),\phi (t))$![]() represents the homoclinic loop. Consider the perturbed system of (2.6) for $\alpha =\alpha _0+\varepsilon$
represents the homoclinic loop. Consider the perturbed system of (2.6) for $\alpha =\alpha _0+\varepsilon$![]() with sufficiently small $|\varepsilon |$
with sufficiently small $|\varepsilon |$![]() . By Theorem 3.7 of [Reference Chow, Li and Wang7, Chapter 3], we have the following conclusions:
. By Theorem 3.7 of [Reference Chow, Li and Wang7, Chapter 3], we have the following conclusions:
(a) There is exactly one limit cycle bifurcating from the homoclinic loop of system (2.6) when $\delta _0\varepsilon \Delta >0$
 (resp. $<0$
(resp. $<0$ ), which is stable for $\delta _0<0$
), which is stable for $\delta _0<0$ and unstable for $\delta _0>0$
and unstable for $\delta _0>0$ , where
\[ \Delta:={-}\int_{-\infty}^{+\infty}e^{-\int_0^t \delta(s){\rm d}s} \frac{\partial f(\varphi(t),\phi(t),\alpha)}{\partial \alpha}|_{\alpha=\alpha_0} \phi^2(t){\rm d}t. \]
, where
\[ \Delta:={-}\int_{-\infty}^{+\infty}e^{-\int_0^t \delta(s){\rm d}s} \frac{\partial f(\varphi(t),\phi(t),\alpha)}{\partial \alpha}|_{\alpha=\alpha_0} \phi^2(t){\rm d}t. \]
(b) There are no limit cycles in a small neighbourhood of the homoclinic loop of system (2.6) when $\delta _0\varepsilon \Delta <0$
 (resp. $>0$
(resp. $>0$ ).
).

Figure 5. Impossible cases of homoclinic loops for system (2.6).

Figure 6. Classification of homoclinic loops for system (2.6).
We consider the case $\delta _0=0$![]() . In this case we cannot apply [Reference Chow, Li and Wang7, Theorem 3.7 of Chapter 3] directly, which only considers the case $\delta _0\ne 0$
. In this case we cannot apply [Reference Chow, Li and Wang7, Theorem 3.7 of Chapter 3] directly, which only considers the case $\delta _0\ne 0$![]() . We can obtain the Poincaré map again
. We can obtain the Poincaré map again
on the $x$![]() -axis, defined in an interior neighbourhood of any homoclinic loop, where $k$
-axis, defined in an interior neighbourhood of any homoclinic loop, where $k$![]() is a positive integer. As proven in theorem 2.3, (2.27) still holds, where $P$
is a positive integer. As proven in theorem 2.3, (2.27) still holds, where $P$![]() , $P_0$
, $P_0$![]() , $P_1$
, $P_1$![]() , $Q_1$
, $Q_1$![]() , $Q_2$
, $Q_2$![]() , $Q_3$
, $Q_3$![]() , $x_0,x_1, x_{Q_2}, x_{Q_3}$
, $x_0,x_1, x_{Q_2}, x_{Q_3}$![]() are defined similarly in the proof of theorem 2.3, as shown in figure 6. Then, $a_k>0$
are defined similarly in the proof of theorem 2.3, as shown in figure 6. Then, $a_k>0$![]() since the homoclinic loop is stable. For $\alpha =\alpha _0+\varepsilon$
since the homoclinic loop is stable. For $\alpha =\alpha _0+\varepsilon$![]() and positive integer $k$
and positive integer $k$![]() , the equality $x_{Q_3}-x_{Q_2}=0$
, the equality $x_{Q_3}-x_{Q_2}=0$![]() has a unique zero
has a unique zero

where $\tilde {x}_0$![]() is the abscissa of $P_0$
is the abscissa of $P_0$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() is small. When $\alpha =\alpha _0-\varepsilon$
is small. When $\alpha =\alpha _0-\varepsilon$![]() , for even $k$
, for even $k$![]() and small $\varepsilon _1>0$
and small $\varepsilon _1>0$![]() the equality $x_{Q_3}-x_{Q_2}=0$
the equality $x_{Q_3}-x_{Q_2}=0$![]() has no zeros in $(\tilde {x}_0-\varepsilon _1, \tilde {x}_0)$
has no zeros in $(\tilde {x}_0-\varepsilon _1, \tilde {x}_0)$![]() . Thus, the proof is completed.
. Thus, the proof is completed.
Note that theorems 2.3 and 3.1 give positive answers to questions (Q1) and (Q2) mentioned in the Introduction.
The following assumptions are needed for studying singular closed orbits (homoclinic loops or heteroclinic loops).
(H a) Assume that system (1.1) defines a family of analytic rotated vector fields. Let system (1.1) have a singular closed orbit $L_0\subset \bar {D}$
 for some $\lambda _0 \in I$
for some $\lambda _0 \in I$ such that the Poincaré map is well defined on one side of $L_0$
such that the Poincaré map is well defined on one side of $L_0$ , where $\bar {D}$
, where $\bar {D}$ is the closure of $D$
is the closure of $D$ .
.
For singular closed orbits in a family of analytic rotated vector fields, it was proved by Han in [Reference Han14, Theorem 2.4] that
(i) if $L_0$
 is non-isolated, system (1.1) has no closed orbits in a small neighbourhood of $L_0$
is non-isolated, system (1.1) has no closed orbits in a small neighbourhood of $L_0$ for $\lambda \in I\backslash \{\lambda _0\}$
for $\lambda \in I\backslash \{\lambda _0\}$ , and
, and(ii) if $L_0$
 is isolated, system (1.1) has at least one limit cycle near $L_0$
is isolated, system (1.1) has at least one limit cycle near $L_0$ as $\lambda$
as $\lambda$ varies in a suitable sense but no closed orbits near $L_0$
varies in a suitable sense but no closed orbits near $L_0$ as $\lambda$
as $\lambda$ varies in the opposite sense.
varies in the opposite sense.
Based on result (ii), a conjecture follows.
Conjecture of [Reference Han14]: There is at most one limit cycle near $L_0$![]() for $\lambda \in I$
for $\lambda \in I$![]() satisfying $0<|\lambda -\lambda _0|\ll 1$
satisfying $0<|\lambda -\lambda _0|\ll 1$![]() under the conditions of [Reference Han14, Theorem 2.4], i.e. under the assumptions ( $H_a$
under the conditions of [Reference Han14, Theorem 2.4], i.e. under the assumptions ( $H_a$![]() ) for the vector field of (1.1).
) for the vector field of (1.1).
The following theorem, indicating that two limit cycles can be bifurcated from a cuspidal loop, gives a negative answer to the above conjecture.
Theorem 3.2 Assume that system (2.6) with hypotheses ($H_1$![]() ) and ($H_2$
) and ($H_2$![]() ) has a cuspidal loop $\Gamma$
) has a cuspidal loop $\Gamma$![]() for $\alpha =\alpha _0$
for $\alpha =\alpha _0$![]() and the cusp persists if $|\alpha -\alpha _0|\ll 1$
and the cusp persists if $|\alpha -\alpha _0|\ll 1$![]() . Moreover, the vector field of system (2.6) is analytic in a small neighbourhood of the cusp. Then, we have the following conclusions:
. Moreover, the vector field of system (2.6) is analytic in a small neighbourhood of the cusp. Then, we have the following conclusions:
(i) If $\Gamma$
 is of odd multiplicity, system (2.6) has a unique limit cycle near $\Gamma$
is of odd multiplicity, system (2.6) has a unique limit cycle near $\Gamma$ for $\alpha \in I$
for $\alpha \in I$ with $0<|\alpha -\alpha _0|\ll 1$
with $0<|\alpha -\alpha _0|\ll 1$ .
.(ii) If $\Gamma$
 is of even multiplicity, system (2.6) has exactly two limit cycles near $\Gamma$
is of even multiplicity, system (2.6) has exactly two limit cycles near $\Gamma$ as $\alpha$
as $\alpha$ varies in a suitable sense and has no closed orbits near $\Gamma$
varies in a suitable sense and has no closed orbits near $\Gamma$ as $\alpha$
as $\alpha$ varies in the opposite sense.
varies in the opposite sense.
Proof. Without loss of generality, we can assume that the cusp is located at $(0,0)$![]() . Since the vector field of system (2.6) at the cusp is analytic, in a small neighbourhood of $(0,0)$
. Since the vector field of system (2.6) at the cusp is analytic, in a small neighbourhood of $(0,0)$![]() system (2.6) can be rewritten as
system (2.6) can be rewritten as

by [Reference Dumortier, Llibre and Artés11, Chapter 3] or [Reference Zhang, Ding, Huang and Dong30, Chapter 2], where integer $k\ge 2$![]() , integers $n,l$
, integers $n,l$![]() are positive, and functions $p_1(x)$
are positive, and functions $p_1(x)$![]() , $p_2(x)$
, $p_2(x)$![]() , $p_3(x,y)$
, $p_3(x,y)$![]() and $p_4(x,y,\alpha )$
and $p_4(x,y,\alpha )$![]() are analytic such that $p_1(0)=0$
are analytic such that $p_1(0)=0$![]() , $p_2(0)=0$
, $p_2(0)=0$![]() and $y^{l}p_4(x,y,\alpha )\geq 0$
and $y^{l}p_4(x,y,\alpha )\geq 0$![]() . By Theorem 3.5 of [Reference Dumortier, Llibre and Artés11, Chapter 3] or Theorem 7.3 of [Reference Zhang, Ding, Huang and Dong30, Chapter 2], the origin $(0,0)$
. By Theorem 3.5 of [Reference Dumortier, Llibre and Artés11, Chapter 3] or Theorem 7.3 of [Reference Zhang, Ding, Huang and Dong30, Chapter 2], the origin $(0,0)$![]() of system (3.1) is a cusp when one of the following statements holds:
of system (3.1) is a cusp when one of the following statements holds:
(a) $k=2\,m$
 ($m\ge 1$
($m\ge 1$ ), $l\geq 2$
), $l\geq 2$ and $b_n=0$
and $b_n=0$ .
.(b) $k=2\,m$
 ($m\ge 1$
($m\ge 1$ ), $n\geq m$
), $n\geq m$ , $l\geq 2$
, $l\geq 2$ and $b_n\neq 0$
and $b_n\neq 0$ .
.
Therefore, according to the conditions of this theorem, we can define the Poincaré map on both sides of $\Gamma _0$![]() when $|\alpha -\alpha _0|\ll 1$
when $|\alpha -\alpha _0|\ll 1$![]() . Moreover, system (3.1) is of the form of system (2.6), the remainder research is similar to the proof of theorem 2.3 and we omit it.
. Moreover, system (3.1) is of the form of system (2.6), the remainder research is similar to the proof of theorem 2.3 and we omit it.
Remark that in theorem 3.2 we provide a class of singular closed orbits in a family of rotated vector fields for system (1.1) and two limit cycles can be bifurcated from the singular closed orbit.
By theorems 2.3–3.2, we have the following further result.
Proposition 3.3 When system (2.6) has a singular closed orbit $L_0\subset \bar {D}$![]() for some $\lambda _0 \in I$
for some $\lambda _0 \in I$![]() such that the Poincaré map is well defined on only one side of $L_0$
such that the Poincaré map is well defined on only one side of $L_0$![]() , conjecture of [Reference Han14] is correct. Furthermore, when system (2.6) has a singular closed orbit $L_0\subset \bar {D}$
, conjecture of [Reference Han14] is correct. Furthermore, when system (2.6) has a singular closed orbit $L_0\subset \bar {D}$![]() with even multiplicity for some $\lambda _0 \in I$
with even multiplicity for some $\lambda _0 \in I$![]() such that the Poincaré map is well defined on both sides of $L_0$
such that the Poincaré map is well defined on both sides of $L_0$![]() , there can exist more than one limit cycle near $L_0$
, there can exist more than one limit cycle near $L_0$![]() for $0<|\lambda -\lambda _0|\ll 1$
for $0<|\lambda -\lambda _0|\ll 1$![]() , i.e. a negative answer to the conjecture of [Reference Han14].
, i.e. a negative answer to the conjecture of [Reference Han14].
For a specific example to proposition 3.3, consider the system
where $\delta$![]() is a perturbation parameter. For $\delta =0$
is a perturbation parameter. For $\delta =0$![]() system (3.2) is Hamiltonian and has a cuspidal loop $\Gamma _0$
system (3.2) is Hamiltonian and has a cuspidal loop $\Gamma _0$![]() . As indicated in the main theorem on page 211 of [Reference Dumortier and Li10], limit cycles of system (3.2) have been researched by computing Abelian integrals. Let $\alpha _1:=\delta \alpha$
. As indicated in the main theorem on page 211 of [Reference Dumortier and Li10], limit cycles of system (3.2) have been researched by computing Abelian integrals. Let $\alpha _1:=\delta \alpha$![]() . Then the vector field of (3.2) is rotated with the rotated parameter $\alpha _1$
. Then the vector field of (3.2) is rotated with the rotated parameter $\alpha _1$![]() . Thus, system (3.2) can have two limit cycles near $\Gamma _0$
. Thus, system (3.2) can have two limit cycles near $\Gamma _0$![]() with even multiplicity for $0<|\alpha _1|$
with even multiplicity for $0<|\alpha _1|$![]() as the rotated parameter $\alpha _1$
as the rotated parameter $\alpha _1$![]() varies and $(\alpha _1, \beta )$
varies and $(\alpha _1, \beta )$![]() is near the point $C_2:(0,14 / 15)$
is near the point $C_2:(0,14 / 15)$![]() .
.
4. Application to SD oscillator
The main results in § 2 can be applied to the problem of limit cycles for the SD oscillator. In other words, we will use our theorems to give a positive answer to question (Q3), mentioned in the Introduction for this differential system.
The authors of [Reference Chen, Llibre and Tang4] studied the global bifurcation diagram and all phase portraits of the SD oscillator
where $(a,b,\xi )\in \mathbb {R}^+\times \mathbb {R}\times \mathbb {R}^+$![]() . It is shown in [Reference Chen, Llibre and Tang4] that system (4.1) has three equilibria
. It is shown in [Reference Chen, Llibre and Tang4] that system (4.1) has three equilibria

if $a<1$![]() , and only $E_0$
, and only $E_0$![]() exists if $a\ge 1$
exists if $a\ge 1$![]() . Large limit cycles represent the ones surrounding all three equilibria and small limit cycles the ones surrounding a single equilibrium. However, the maximum number of small limit cycles of system (4.1) are not proven as parameters belong to the region
. Large limit cycles represent the ones surrounding all three equilibria and small limit cycles the ones surrounding a single equilibrium. However, the maximum number of small limit cycles of system (4.1) are not proven as parameters belong to the region

where $b=\varphi (a,\xi )$![]() is the homoclinic bifurcation surface and $2\sqrt {3}a-4<\varphi (a,\xi )< a^2-1$
is the homoclinic bifurcation surface and $2\sqrt {3}a-4<\varphi (a,\xi )< a^2-1$![]() . By the symmetry of system (4.1), we only need to study the maximum number of small limit cycles surrounding $E_R$
. By the symmetry of system (4.1), we only need to study the maximum number of small limit cycles surrounding $E_R$![]() . Moreover, the authors of [Reference Chen, Llibre and Tang4] conjectured that system (4.1) has at most two small limit cycles surrounding $E_R$
. Moreover, the authors of [Reference Chen, Llibre and Tang4] conjectured that system (4.1) has at most two small limit cycles surrounding $E_R$![]() . In other words, the bifurcation surface of double limit cycle can be expressed as a function $b=\phi (a,\xi )$
. In other words, the bifurcation surface of double limit cycle can be expressed as a function $b=\phi (a,\xi )$![]() , continuous in $a\in (0,\sqrt {3}/3)$
, continuous in $a\in (0,\sqrt {3}/3)$![]() , such that $2\sqrt {3}a-4 <\phi (a,\xi )<\min \{\varphi (a,\xi ),3a^2-3\}$
, such that $2\sqrt {3}a-4 <\phi (a,\xi )<\min \{\varphi (a,\xi ),3a^2-3\}$![]() , $\phi (1/\sqrt {3},\xi )=-2$
, $\phi (1/\sqrt {3},\xi )=-2$![]() and $\phi (0,\xi )=\varphi (0,\xi )$
and $\phi (0,\xi )=\varphi (0,\xi )$![]() .
.
Recently, Liu and Sun ([Reference Sun and Liu27]) proved that the conjecture is true in $\mathcal {G}$![]() for small $\xi$
for small $\xi$![]() by computing Abelian integrals. However, the approach of Abelian integrals is not available for general (large) $\xi$
by computing Abelian integrals. However, the approach of Abelian integrals is not available for general (large) $\xi$![]() because system (4.1) is no longer near-Hamiltonian. In this paper, we use theorem 2.3 to prove that at most two small limit cycles surround equilibrium $E_R$
because system (4.1) is no longer near-Hamiltonian. In this paper, we use theorem 2.3 to prove that at most two small limit cycles surround equilibrium $E_R$![]() of system (4.1) as parameters lie in the region $\mathcal {G}$
of system (4.1) as parameters lie in the region $\mathcal {G}$![]() for general $\xi$
for general $\xi$![]() .
.
Theorem 4.1 System (4.1) has at most two small limit cycles surrounding $E_R$![]() for $(a,b,\xi )\in \mathcal {G}$
for $(a,b,\xi )\in \mathcal {G}$![]() with general $\xi$
with general $\xi$![]() . Specially, a path of a small semi-stable limit cycle can be presented by a function $b=\phi (a,\xi )$
. Specially, a path of a small semi-stable limit cycle can be presented by a function $b=\phi (a,\xi )$![]() , where $0< a<\sqrt {3}/3$
, where $0< a<\sqrt {3}/3$![]() , $2\sqrt {3}a-4 <\phi (a,\xi )<\min \{\varphi (a,\xi ),3a^2-3\}$
, $2\sqrt {3}a-4 <\phi (a,\xi )<\min \{\varphi (a,\xi ),3a^2-3\}$![]() , $\phi (1/\sqrt {3},\xi )=-2$
, $\phi (1/\sqrt {3},\xi )=-2$![]() and $\phi (0,\xi )=\varphi (0,\xi )$
and $\phi (0,\xi )=\varphi (0,\xi )$![]() .
.
Proof. Let $\tilde b=b\xi$![]() and take $(a, \tilde b, \xi )$
and take $(a, \tilde b, \xi )$![]() as new parameter. With the transformation $(x,y)\to (x, y+\tilde bx+\xi x^3)$
as new parameter. With the transformation $(x,y)\to (x, y+\tilde bx+\xi x^3)$![]() , system (4.1) can be changed into the following form
, system (4.1) can be changed into the following form
We can check that $(y,-x(1-{1}/{\sqrt {x^2+a^2}})-(\tilde b+3\xi x^2)y)$![]() is a rotated vector field with respect to $\tilde b$
is a rotated vector field with respect to $\tilde b$![]() and $\xi$
and $\xi$![]() . Moreover, the parameter region $\mathcal {G}$
. Moreover, the parameter region $\mathcal {G}$![]() can be changed into
can be changed into

By theorem 2.3, unstable limit cycles of system (4.2) expand and stable limit cycles contract as either $\tilde b$![]() or $\xi$
or $\xi$![]() increases. Assume that system (4.2) has at least three limit cycles $\Gamma _1$
increases. Assume that system (4.2) has at least three limit cycles $\Gamma _1$![]() , $\Gamma _2$
, $\Gamma _2$![]() and $\Gamma _3$
and $\Gamma _3$![]() surrounding $E_R$
surrounding $E_R$![]() only. Without loss of generality, we assume that $\Gamma _1$
only. Without loss of generality, we assume that $\Gamma _1$![]() , $\Gamma _2$
, $\Gamma _2$![]() and $\Gamma _3$
and $\Gamma _3$![]() are innermost limit cycles and $\Gamma _i$
are innermost limit cycles and $\Gamma _i$![]() lies in the interior region surrounded by $\Gamma _{i+1}$
lies in the interior region surrounded by $\Gamma _{i+1}$![]() for $i=1,2$
for $i=1,2$![]() .
.
In the following we prove by reduction to absurdity that at most two small limit cycles surround $E_R$![]() only as the parameter belongs to region $\mathcal {G}_1$
only as the parameter belongs to region $\mathcal {G}_1$![]() . First, we exhibit the idea of the proof. We assume that there may exist three small limit cycles surrounding $E_R$
. First, we exhibit the idea of the proof. We assume that there may exist three small limit cycles surrounding $E_R$![]() only as the parameter belongs to region $\mathcal {G}_1$
only as the parameter belongs to region $\mathcal {G}_1$![]() . Then we enlarge or lessen those rotated parameters $\tilde b$
. Then we enlarge or lessen those rotated parameters $\tilde b$![]() and $\xi$
and $\xi$![]() in order, and the parameters lie in a region at last for such case the number of limit cycles has been obtained which is smaller than three. Thus, it induces a contradiction.
in order, and the parameters lie in a region at last for such case the number of limit cycles has been obtained which is smaller than three. Thus, it induces a contradiction.
By the instability of $E_R$![]() , we can consider the case that $\Gamma _1$
, we can consider the case that $\Gamma _1$![]() and $\Gamma _3$
and $\Gamma _3$![]() are stable and $\Gamma _2$
are stable and $\Gamma _2$![]() is unstable. Otherwise, we will vary the rotated parameters to obtain such case. Now we go on the following steps:
is unstable. Otherwise, we will vary the rotated parameters to obtain such case. Now we go on the following steps:
Step 1: Lessen $\xi =\xi _1<\xi _0$![]() till either $\Gamma _1$
till either $\Gamma _1$![]() and $\Gamma _2$
and $\Gamma _2$![]() coincidence or $\Gamma _3$
coincidence or $\Gamma _3$![]() becomes a homoclinic loop or $\Gamma _3$
becomes a homoclinic loop or $\Gamma _3$![]() becomes a semi-stable limit cycle for fixed $a=a_0$
becomes a semi-stable limit cycle for fixed $a=a_0$![]() and $\tilde b=\tilde b_0$
and $\tilde b=\tilde b_0$![]() . We claim that $(a,\tilde b, \xi )=(a_0,\tilde b_0, \xi _1)\in \mathcal {G}_1$
. We claim that $(a,\tilde b, \xi )=(a_0,\tilde b_0, \xi _1)\in \mathcal {G}_1$![]() . Otherwise, system (4.1) has at least three small limit cycles surrounding $E_R$
. Otherwise, system (4.1) has at least three small limit cycles surrounding $E_R$![]() as parameters lie in the other region except $\mathcal {G}_1$
as parameters lie in the other region except $\mathcal {G}_1$![]() by the rotated properties of vector fields. By theorem 1 of [Reference Chen, Llibre and Tang4], this is a contradiction. We also claim that $\xi _1$
by the rotated properties of vector fields. By theorem 1 of [Reference Chen, Llibre and Tang4], this is a contradiction. We also claim that $\xi _1$![]() is not small. By the results of [Reference Sun and Liu27], system (4.1) has at most two small limit cycles surrounding $E_R$
is not small. By the results of [Reference Sun and Liu27], system (4.1) has at most two small limit cycles surrounding $E_R$![]() for small $\xi _1$
for small $\xi _1$![]() , also implying a contradiction.
, also implying a contradiction.
Step 2: Enlarge $\tilde b=\tilde b_1>\tilde b_0$![]() . We can get three limit cycles, which are still denoted by $\Gamma _1, \Gamma _2$
. We can get three limit cycles, which are still denoted by $\Gamma _1, \Gamma _2$![]() and $\Gamma _3$
and $\Gamma _3$![]() by the rotated properties of vector fields. We continue to enlarge $\tilde b$
by the rotated properties of vector fields. We continue to enlarge $\tilde b$![]() till $\Gamma _2$
till $\Gamma _2$![]() and $\Gamma _3$
and $\Gamma _3$![]() coincide. In other words, we get a stable $\Gamma _1$
coincide. In other words, we get a stable $\Gamma _1$![]() and a semi-stable $\tilde \Gamma _{23}$
and a semi-stable $\tilde \Gamma _{23}$![]() . Moreover, $\tilde \Gamma _{23}$
. Moreover, $\tilde \Gamma _{23}$![]() is internally unstable and externally stable. We claim that $(a,\tilde b, \xi )=(a_0,\tilde b_1, \xi _1)\in \mathcal {G}_1$
is internally unstable and externally stable. We claim that $(a,\tilde b, \xi )=(a_0,\tilde b_1, \xi _1)\in \mathcal {G}_1$![]() and $\tilde b_1$
and $\tilde b_1$![]() is not small. Otherwise, we can similarly obtain a contradiction as tep 1.
is not small. Otherwise, we can similarly obtain a contradiction as tep 1.
Step 3: Repeat step 1, i.e. lessen $\xi =\xi _2<\xi _1$![]() till either $\Gamma _1$
till either $\Gamma _1$![]() and $\Gamma _2$
and $\Gamma _2$![]() coincide or $\Gamma _3$
coincide or $\Gamma _3$![]() becomes a homoclinic loop or $\Gamma _3$
becomes a homoclinic loop or $\Gamma _3$![]() becomes a semi-stable limit cycle for fixed $a=a_0$
becomes a semi-stable limit cycle for fixed $a=a_0$![]() and $\tilde b=\tilde b_1$
and $\tilde b=\tilde b_1$![]() . We also claim that $(a,\tilde b, \xi )=(a_0,\tilde b_1, \xi _2)\in \mathcal {G}_1$
. We also claim that $(a,\tilde b, \xi )=(a_0,\tilde b_1, \xi _2)\in \mathcal {G}_1$![]() and $\xi _2$
and $\xi _2$![]() is not small. Otherwise, we can obtain the similar contradiction as step 1. Then repeat step 2, step 1, step 2,…, up to $n$
is not small. Otherwise, we can obtain the similar contradiction as step 1. Then repeat step 2, step 1, step 2,…, up to $n$![]() times.
times.
On the other hand, by the proof of theorem 2.3, both the variations of $\tilde b$![]() and $\xi$
and $\xi$![]() in the aforementioned steps are not sufficiently small (i.e. there exists a positive $d_0$
in the aforementioned steps are not sufficiently small (i.e. there exists a positive $d_0$![]() such that the variations are larger than $d_0$
such that the variations are larger than $d_0$![]() ) because none of distances between any two of given $\Gamma _1, \Gamma _2$
) because none of distances between any two of given $\Gamma _1, \Gamma _2$![]() and $\Gamma _3$
and $\Gamma _3$![]() is sufficiently small. Thus, we stop the aforementioned process in finitely many steps when either $\xi$
is sufficiently small. Thus, we stop the aforementioned process in finitely many steps when either $\xi$![]() is sufficiently close to $0$
is sufficiently close to $0$![]() or $\tilde b\ge \min \{\xi \varphi (a,\xi ),(3a^2-3)\xi \}$
or $\tilde b\ge \min \{\xi \varphi (a,\xi ),(3a^2-3)\xi \}$![]() . Then there exists $n_0\in \mathbb {Z}_+$
. Then there exists $n_0\in \mathbb {Z}_+$![]() such that the number of limit cycles is larger than $2$
such that the number of limit cycles is larger than $2$![]() as $(a,\tilde b, \xi )=(a_0,\tilde b_n, \xi _n)$
as $(a,\tilde b, \xi )=(a_0,\tilde b_n, \xi _n)$![]() for $n>n_0$
for $n>n_0$![]() , contradicting the result ‘a unique limit cycle’ for $\tilde b=\min \{\xi \varphi (a,\xi ),(3a^2-3)\xi \}$
, contradicting the result ‘a unique limit cycle’ for $\tilde b=\min \{\xi \varphi (a,\xi ),(3a^2-3)\xi \}$![]() and the result ‘at most $2$
and the result ‘at most $2$![]() limit cycles’ for small $\xi$
limit cycles’ for small $\xi$![]() . This is a contradiction. Therefore, there are at most two small limit cycles only surrounding $E_R$
. This is a contradiction. Therefore, there are at most two small limit cycles only surrounding $E_R$![]() as the parameter belongs to region $\mathcal {G}$
as the parameter belongs to region $\mathcal {G}$![]() . By the instability of $E_0$
. By the instability of $E_0$![]() , the interior small limit cycle is stable and the outer one is unstable respectively if there exist exactly two small limit cycles surrounding $E_R$
, the interior small limit cycle is stable and the outer one is unstable respectively if there exist exactly two small limit cycles surrounding $E_R$![]() .
.
Remark that the global dynamics of system (4.1) can be presented completely by [Reference Chen, Llibre and Tang4, Theorem 1], results of [Reference Sun and Liu27] and theorem 4.1.
5. Application to switching system with three zones
The main results in § 2 can also be applied to the problem of limit cycles for piecewise linear differential system with three zones and asymmetry. Consider a piecewise linear differential system
with two parallel lines and asymmetry, which was introduced in [Reference Chen and Tang5, Reference Euzébio, Pazim and Ponce13, Reference Llibre, Ponce and Valls18, Reference Llibre, Ponce and Valls19], where

The plane is separated by two switching lines $\Gamma _L=\{(x,y): x=-u\}$![]() and $\Gamma _R=\{(x,y): x=v\}$
and $\Gamma _R=\{(x,y): x=v\}$![]() .
.
Llibre et al. [Reference Llibre, Ponce and Valls18] discussed system (5.1) in the parameter regions

and obtained the following results.
Proposition 5.1 [Reference Llibre, Ponce and Valls18, Theorems 7-10]
In the parameter region $\mathcal {G}_1$![]() (resp. $\mathcal {G}_2$
(resp. $\mathcal {G}_2$![]() , $\mathcal {G}_3$
, $\mathcal {G}_3$![]() , $\mathcal {G}_4$
, $\mathcal {G}_4$![]() ), the following statements hold.
), the following statements hold.
(a) When $0< t_c\leq t_r$
 (resp. $0< t_c\leq t_l$
(resp. $0< t_c\leq t_l$ , $t_r\leq t_c<0$
, $t_r\leq t_c<0$ , $t_l\leq t_c<0$
, $t_l\leq t_c<0$ ), system (5.1) has a unique limit cycle, which is stable (resp. stable, unstable, unstable).
), system (5.1) has a unique limit cycle, which is stable (resp. stable, unstable, unstable).(b) When $t_c=0$
 , the origin of system (5.1) is surrounded by a bounded period annulus. The most external periodic orbit of the period annulus, which is tangent to the line $x=v$
, the origin of system (5.1) is surrounded by a bounded period annulus. The most external periodic orbit of the period annulus, which is tangent to the line $x=v$ , is unstable (resp. unstable, stable, stable). There exists a stable (resp. stable, unstable, unstable) limit cycle surrounding such period annulus.
, is unstable (resp. unstable, stable, stable). There exists a stable (resp. stable, unstable, unstable) limit cycle surrounding such period annulus.(c) There exists small $\varepsilon >0$
 such that if $-\varepsilon < t_c<0$
such that if $-\varepsilon < t_c<0$ (resp. $-\varepsilon < t_c<0$
(resp. $-\varepsilon < t_c<0$ , $0< t_c<\varepsilon$
, $0< t_c<\varepsilon$ , $0< t_c<\varepsilon$
, $0< t_c<\varepsilon$ ), then the origin is surrounded by at least two limit cycles, where the smaller is unstable (resp. unstable, stable, stable) and the bigger is stable (resp. stable, unstable, unstable).
), then the origin is surrounded by at least two limit cycles, where the smaller is unstable (resp. unstable, stable, stable) and the bigger is stable (resp. stable, unstable, unstable).
In order to study the hyperbolicity and exact number of limit cycles obtained in theorem 5.1, we further recall the following results, where

Proposition 5.2 [Reference Chen and Tang5, Theorem 1.2]
When $0\le t_c\leq t_r$![]() (resp. $0\le t_c\leq t_l$
(resp. $0\le t_c\leq t_l$![]() , $t_r\leq t_c \le 0$
, $t_r\leq t_c \le 0$![]() , $t_l\leq t_c\le 0$
, $t_l\leq t_c\le 0$![]() ) and parameters lie in the region $\mathcal {G}_1$
) and parameters lie in the region $\mathcal {G}_1$![]() (resp. $\mathcal {G}_2$
(resp. $\mathcal {G}_2$![]() , $\mathcal {G}_3$
, $\mathcal {G}_3$![]() , $\mathcal {G}_4$
, $\mathcal {G}_4$![]() ), system (5.1) has a unique limit cycle, which is hyperbolic. Moreover, the limit cycle is stable in $\mathcal {G}_1$
), system (5.1) has a unique limit cycle, which is hyperbolic. Moreover, the limit cycle is stable in $\mathcal {G}_1$![]() , $\mathcal {G}_2$
, $\mathcal {G}_2$![]() and unstable in $\mathcal {G}_3$
and unstable in $\mathcal {G}_3$![]() , $\mathcal {G}_4$
, $\mathcal {G}_4$![]() .
.
Proposition 5.3 [Reference Chen and Tang5, Theorem 1.3]
In the parameter region $\mathcal {G}_1$![]() (resp. $\mathcal {G}_2$
(resp. $\mathcal {G}_2$![]() , $\mathcal {G}_3$
, $\mathcal {G}_3$![]() , $\mathcal {G}_4$
, $\mathcal {G}_4$![]() ), the following statements hold.
), the following statements hold.
(1) When $t_c\leq h_1 ~({\rm resp.} ~t_c\leq h_2, ~t_c\geq h_3, ~t_c\geq h_4),$
 system (5.1) exhibits no limit cycles.
system (5.1) exhibits no limit cycles.(2) When $-\varepsilon < t_c<0$
 (resp. $-\varepsilon < t_c<0$
(resp. $-\varepsilon < t_c<0$ , $0< t_c<\varepsilon$
, $0< t_c<\varepsilon$ , $0< t_c<\varepsilon$
, $0< t_c<\varepsilon$ ) for small $\varepsilon >0$
) for small $\varepsilon >0$ , system (5.1) exhibits exactly two limit cycles, where the inner limit cycle which only intersects $\Gamma _R$
, system (5.1) exhibits exactly two limit cycles, where the inner limit cycle which only intersects $\Gamma _R$ is hyperbolic and unstable (resp. unstable, stable, stable) and the outer one which intersects $\Gamma _L$
is hyperbolic and unstable (resp. unstable, stable, stable) and the outer one which intersects $\Gamma _L$ and $\Gamma _R$
and $\Gamma _R$ is hyperbolic and stable(resp. stable, unstable, unstable).
is hyperbolic and stable(resp. stable, unstable, unstable).
By propositions 5.2 and 5.3, we naturally have the following question:
(Q4) When $h_1< t_c<-\varepsilon$![]() (resp. $h_2< t_c<-\varepsilon$
(resp. $h_2< t_c<-\varepsilon$![]() , $\varepsilon < t_c< h_3$
, $\varepsilon < t_c< h_3$![]() , $\varepsilon < t_c< h_4$
, $\varepsilon < t_c< h_4$![]() ) for small $\varepsilon >0$
) for small $\varepsilon >0$![]() , how many limit cycles does system (5.1) exhibit?
, how many limit cycles does system (5.1) exhibit?
The following theorem can answer question (Q4).
Theorem 5.4 In the parameter region $\mathcal {G}_1$![]() (resp. $\mathcal {G}_2$
(resp. $\mathcal {G}_2$![]() , $\mathcal {G}_3$
, $\mathcal {G}_3$![]() , $\mathcal {G}_4$
, $\mathcal {G}_4$![]() ), there are four functions $t_c=\varphi _1(t_r)$
), there are four functions $t_c=\varphi _1(t_r)$![]() (resp. $\varphi _2(t_r)$
(resp. $\varphi _2(t_r)$![]() , $\varphi _3(t_l)$
, $\varphi _3(t_l)$![]() , $\varphi _4(t_l)$
, $\varphi _4(t_l)$![]() ) for any fixed ($t_l, l,r,u,v$
) for any fixed ($t_l, l,r,u,v$![]() ) (resp. ($t_l, l,r,u,v$
) (resp. ($t_l, l,r,u,v$![]() ), ($t_r, l,r,u,v$
), ($t_r, l,r,u,v$![]() ), ($t_r, l, r,u,v$
), ($t_r, l, r,u,v$![]() )) such that
)) such that
(1) system (5.1) has exactly two limit cycles when $\varphi _1(t_r)< t_c<0$
 (resp. $\varphi _2(t_r)< t_c<0$
(resp. $\varphi _2(t_r)< t_c<0$ , $0< t_c<\varphi _3(t_l)$
, $0< t_c<\varphi _3(t_l)$ , $0< t_c<\varphi _4(t_l)$
, $0< t_c<\varphi _4(t_l)$ ) for small $\varepsilon >0$
) for small $\varepsilon >0$ , where the inner limit cycle which only intersects $\Gamma _R$
, where the inner limit cycle which only intersects $\Gamma _R$ is unstable (resp. unstable, stable, stable) and the outer one which intersects $\Gamma _L$
is unstable (resp. unstable, stable, stable) and the outer one which intersects $\Gamma _L$ and $\Gamma _R$
and $\Gamma _R$ is stable (resp. stable, unstable, unstable);
is stable (resp. stable, unstable, unstable);(2) system (5.1) has exactly one semi-stable limit cycle when $t_c=\varphi _1(t_r)$
 (resp. $\varphi _2(t_r)$
(resp. $\varphi _2(t_r)$ , $\varphi _3(t_l)$
, $\varphi _3(t_l)$ , $\varphi _4(t_l)$
, $\varphi _4(t_l)$ ), where the limit cycle which intersects $\Gamma _L$
), where the limit cycle which intersects $\Gamma _L$ and $\Gamma _R$
and $\Gamma _R$ is externally stable (resp. stable, unstable, unstable);
is externally stable (resp. stable, unstable, unstable);(3) system (5.1) has no limit cycles when $t_c<\varphi _1(t_r)$
 (resp. $t_c<\varphi _2(t_r)$
(resp. $t_c<\varphi _2(t_r)$ , $t_c>\varphi _3(t_l)$
, $t_c>\varphi _3(t_l)$ , $t_c>\varphi _4(t_l)$
, $t_c>\varphi _4(t_l)$ ).
).
Proof. Without loss of generality, we only discuss $\mathcal {G}_1$![]() since the remainder cases $\mathcal {G}_2$
since the remainder cases $\mathcal {G}_2$![]() , $\mathcal {G}_3$
, $\mathcal {G}_3$![]() , $\mathcal {G}_4$
, $\mathcal {G}_4$![]() can be discussed similarly. With the transformation $(x,y)\to (x,y+F(x))$
can be discussed similarly. With the transformation $(x,y)\to (x,y+F(x))$![]() , system (5.1) is changed into the following discontinuous system
, system (5.1) is changed into the following discontinuous system
where

We can check that the vector field $(-y, g(x)+f(x)y)$![]() of system (5.2) is rotated about $t_c, t_l$
of system (5.2) is rotated about $t_c, t_l$![]() and $t_r$
and $t_r$![]() .
.
Assume that system (5.2) has at least three limit cycles as parameters lie in the region $\mathcal {G}_1$![]() and $(t_c,t_r)=(t_c^0, t_r^0)$
and $(t_c,t_r)=(t_c^0, t_r^0)$![]() for $h_1< t_c^0<-\varepsilon$
for $h_1< t_c^0<-\varepsilon$![]() and $0< t_r^0<2$
and $0< t_r^0<2$![]() , and $\Gamma _1$
, and $\Gamma _1$![]() , $\Gamma _2$
, $\Gamma _2$![]() and $\Gamma _3$
and $\Gamma _3$![]() are the three innermost limit cycles, where $\Gamma _2$
are the three innermost limit cycles, where $\Gamma _2$![]() lies in the annular region surrounded by inner boundary $\Gamma _1$
lies in the annular region surrounded by inner boundary $\Gamma _1$![]() and outer boundary $\Gamma _3$
and outer boundary $\Gamma _3$![]() . Without loss of generality, we can let $\Gamma _1, \Gamma _3$
. Without loss of generality, we can let $\Gamma _1, \Gamma _3$![]() be unstable and $\Gamma _2$
be unstable and $\Gamma _2$![]() be stable. By theorem 2.3, $\Gamma _1, \Gamma _3$
be stable. By theorem 2.3, $\Gamma _1, \Gamma _3$![]() contract and $\Gamma _2$
contract and $\Gamma _2$![]() expands when one of $t_c$
expands when one of $t_c$![]() , $t_l$
, $t_l$![]() , $t_r$
, $t_r$![]() increases. Now we make a similar process to the proof of theorem 4.1 as follows.
increases. Now we make a similar process to the proof of theorem 4.1 as follows.
Step 1: There is $t_c^1\in (t_c^0,0)$![]() such that $\Gamma _2, \Gamma _3$
such that $\Gamma _2, \Gamma _3$![]() coincide when the other parameters are fixed. We claim that $|t_c^1|$
coincide when the other parameters are fixed. We claim that $|t_c^1|$![]() is not small. Otherwise, system (5.2) has more than one limit cycle as $t_c=0$
is not small. Otherwise, system (5.2) has more than one limit cycle as $t_c=0$![]() by the rotated properties of vector fields. This contradicts proposition 5.2 and what we claimed is true.
by the rotated properties of vector fields. This contradicts proposition 5.2 and what we claimed is true.
Step 2: There is $t_r^1\in (0, t_r^0)$![]() such that $\Gamma _1, \Gamma _2$
such that $\Gamma _1, \Gamma _2$![]() coincide or $\Gamma _3$
coincide or $\Gamma _3$![]() becomes a semi-stable limit cycle when the other parameters are fixed. In this step, we claim that $t_r^1$
becomes a semi-stable limit cycle when the other parameters are fixed. In this step, we claim that $t_r^1$![]() is not small. Otherwise, system (5.2) has more than one limit cycle as $t_r=0$
is not small. Otherwise, system (5.2) has more than one limit cycle as $t_r=0$![]() . By [Reference Llibre, Ordóñez and Ponce17], system (5.2) has at most one limit cycle for $t_r=0$
. By [Reference Llibre, Ordóñez and Ponce17], system (5.2) has at most one limit cycle for $t_r=0$![]() . This is a contradiction. We claim that $t_c^1$
. This is a contradiction. We claim that $t_c^1$![]() keeps in $(h_1, -\varepsilon )$
keeps in $(h_1, -\varepsilon )$![]() . Otherwise, assume that $t_c^1\leq h_1$
. Otherwise, assume that $t_c^1\leq h_1$![]() . From proposition 5.3 system (5.2) has no limit cycles if $t_c^1\leq h_1$
. From proposition 5.3 system (5.2) has no limit cycles if $t_c^1\leq h_1$![]() . This is also a contradiction. Then, we turn to step 1 again.
. This is also a contradiction. Then, we turn to step 1 again.
Finally, for arbitrary small $\varepsilon >0$![]() there exists $n_0\in \mathbb {Z}_+$
there exists $n_0\in \mathbb {Z}_+$![]() such that $|t_c^n|<\varepsilon$
such that $|t_c^n|<\varepsilon$![]() or $t_r^n<\varepsilon$
or $t_r^n<\varepsilon$![]() as $n>n_0$
as $n>n_0$![]() step by step. We can find that system (5.2) still has at least three limit cycles as $|t_c^n|$
step by step. We can find that system (5.2) still has at least three limit cycles as $|t_c^n|$![]() or $t_r^n$
or $t_r^n$![]() is small, which contradicts proposition 5.3. Therefore, in the parameter region $\mathcal {G}_1$
is small, which contradicts proposition 5.3. Therefore, in the parameter region $\mathcal {G}_1$![]() for $h_1< t_c<-\varepsilon$
for $h_1< t_c<-\varepsilon$![]() system (5.1) has at most two limit cycles. Applying the rotated properties from theorem 2.3, the continuity of vector fields and propositions 5.1–5.3, there exists a function $t_c=\varphi _1(t_r)$
system (5.1) has at most two limit cycles. Applying the rotated properties from theorem 2.3, the continuity of vector fields and propositions 5.1–5.3, there exists a function $t_c=\varphi _1(t_r)$![]() such that system (5.1) has exactly two limit cycles when $\varphi _1(t_r)< t_c<0$
such that system (5.1) has exactly two limit cycles when $\varphi _1(t_r)< t_c<0$![]() , where the inner limit cycle which only intersects $\Gamma _R$
, where the inner limit cycle which only intersects $\Gamma _R$![]() is unstable and the outer one which intersects $\Gamma _L$
is unstable and the outer one which intersects $\Gamma _L$![]() and $\Gamma _R$
and $\Gamma _R$![]() is stable; system (5.1) has exactly one semi-stable limit cycle when $t_c=\varphi _1(t_r)$
is stable; system (5.1) has exactly one semi-stable limit cycle when $t_c=\varphi _1(t_r)$![]() , where the limit cycle which intersects $\Gamma _L$
, where the limit cycle which intersects $\Gamma _L$![]() and $\Gamma _R$
and $\Gamma _R$![]() is externally stable; and system (5.1) has no limit cycles when $t_c<\varphi _1(t_r)$
is externally stable; and system (5.1) has no limit cycles when $t_c<\varphi _1(t_r)$![]() . The proof is completed.
. The proof is completed.
Therefore, the exact number of limit cycles of system (5.1) can be obtained completely when parameters lie in regions $\mathcal {G}_1$![]() , $\mathcal {G}_2$
, $\mathcal {G}_2$![]() , $\mathcal {G}_3$
, $\mathcal {G}_3$![]() or $\mathcal {G}_4$
or $\mathcal {G}_4$![]() by propositions 5.1–5.3 and theorem 5.4.
by propositions 5.1–5.3 and theorem 5.4.
Acknowledgements
This work is financially supported by the National Key R&D Program of China (No. 2022YFA1005900). The first author is supported by the National Natural Science Foundation of China (Nos. 12322109, 12171485) and Science and Technology Innovation Program of Hunan Province (No. 2023RC3040). The second author is supported by the National Natural Science Foundations of China (Nos. 11931016, 12271355, 12161131001). The third author is supported by the National Natural Science Foundation of China (Nos. 12171336, 11831012).