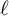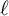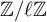1 Introduction
Let K be an algebraically closed complete non-archimedean field whose topology is given by a valuation
![]() $ \vert \cdot \vert \colon K \to {\mathbb R}_{\geq 0}$
of rank
$ \vert \cdot \vert \colon K \to {\mathbb R}_{\geq 0}$
of rank
![]() $1$
. Let
$1$
. Let
![]() ${\mathcal O}=K^{\circ }$
be the ring of integers of K. In this paper, we study local constancy of étale cohomology of rigid analytic varieties over K, or more precisely, of adic spaces of finite type over
${\mathcal O}=K^{\circ }$
be the ring of integers of K. In this paper, we study local constancy of étale cohomology of rigid analytic varieties over K, or more precisely, of adic spaces of finite type over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
.
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
.
1.1 A main result
The theory of étale cohomology for adic spaces was developed by Huber (see [Reference Huber14]). Huber obtained several finiteness results on étale cohomology of adic spaces in a series of papers [Reference Huber15, Reference Huber16, Reference Huber18]. Let us recall one of the main results of [Reference Huber16] (see [Reference Huber16, Theorem 3.6] for a more precise statement).
Theorem 1.1 (Huber [Reference Huber16, Theorem 3.6])
We assume that K is of characteristic zero. Let X be a separated adic space of finite type over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
and Z a closed adic subspace of X. Let n be a positive integer invertible in
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
and Z a closed adic subspace of X. Let n be a positive integer invertible in
![]() ${\mathcal O}$
. Then there exists an open subset V of X containing Z such that the restriction map
${\mathcal O}$
. Then there exists an open subset V of X containing Z such that the restriction map
on étale cohomology groups is an isomorphism for every integer i. Moreover, we can assume that V is quasicompact.
It is a natural question to ask whether we can take an open subset V as in Theorem 1.1 independent of n. In the present paper, we answer this question in the affirmative for adic spaces which arise from schemes of finite type over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
More precisely, we will prove the following theorem. For a scheme
![]() $\mathcal {X}$
of finite type over
$\mathcal {X}$
of finite type over
![]() ${\mathcal O}$
, let
${\mathcal O}$
, let
![]() $\widehat {\mathcal {X}}$
denote the
$\widehat {\mathcal {X}}$
denote the
![]() $\varpi $
-adic formal completion of
$\varpi $
-adic formal completion of
![]() $\mathcal {X}$
, where
$\mathcal {X}$
, where
![]() $\varpi \in K^{\times }$
is an element with
$\varpi \in K^{\times }$
is an element with
![]() $\vert \varpi \vert <1$
. The Raynaud generic fibre of
$\vert \varpi \vert <1$
. The Raynaud generic fibre of
![]() $\widehat {\mathcal {X}}$
is denoted by
$\widehat {\mathcal {X}}$
is denoted by
![]() $(\widehat {\mathcal {X}})^{\mathop {\mathrm {rig}}\nolimits }$
in this section, which is an adic space of finite type over
$(\widehat {\mathcal {X}})^{\mathop {\mathrm {rig}}\nolimits }$
in this section, which is an adic space of finite type over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
(it is denoted by
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
(it is denoted by
![]() $d(\widehat {\mathcal {X}})$
in [Reference Huber14] and in the main body of this paper).
$d(\widehat {\mathcal {X}})$
in [Reference Huber14] and in the main body of this paper).
Theorem 1.2 (Theorem 4.9)
Let
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
be a closed immersion of separated schemes of finite type over
$\mathcal {Z} \hookrightarrow \mathcal {X}$
be a closed immersion of separated schemes of finite type over
![]() ${\mathcal O}$
. We have a closed embedding
${\mathcal O}$
. We have a closed embedding
![]() $(\widehat {\mathcal {Z}})^{\mathop {\mathrm {rig}}\nolimits } \hookrightarrow (\widehat {\mathcal {X}})^{\mathop {\mathrm {rig}}\nolimits }$
. Then there exists an open subset V of
$(\widehat {\mathcal {Z}})^{\mathop {\mathrm {rig}}\nolimits } \hookrightarrow (\widehat {\mathcal {X}})^{\mathop {\mathrm {rig}}\nolimits }$
. Then there exists an open subset V of
![]() $(\widehat {\mathcal {X}})^{\mathop {\mathrm {rig}}\nolimits }$
containing
$(\widehat {\mathcal {X}})^{\mathop {\mathrm {rig}}\nolimits }$
containing
![]() $(\widehat {\mathcal {Z}})^{\mathop {\mathrm {rig}}\nolimits }$
such that, for every positive integer n invertible in
$(\widehat {\mathcal {Z}})^{\mathop {\mathrm {rig}}\nolimits }$
such that, for every positive integer n invertible in
![]() ${\mathcal O}$
, the restriction map
${\mathcal O}$
, the restriction map
on étale cohomology groups is an isomorphism for every integer i. Moreover, we can assume that V is quasicompact.
A more precise statement is given in Theorem 4.9. In this paper, we will use de Jong’s alterations in several ways. This is the main reason why we restrict ourselves to the case where adic spaces arise from schemes of finite type over
![]() ${\mathcal O}$
. We remark that, in our case, we need not impose any conditions on the characteristic of K. We will also prove an analogous statement for étale cohomology with compact support (see Theorem 4.8).
${\mathcal O}$
. We remark that, in our case, we need not impose any conditions on the characteristic of K. We will also prove an analogous statement for étale cohomology with compact support (see Theorem 4.8).
Remark 1.3. In [Reference Scholze29], Scholze proved the weight-monodromy conjecture for a projective smooth variety X over a non-archimedean local field L of mixed characteristic
![]() $(0, p)$
which is a set-theoretic complete intersection in a projective smooth toric variety, by reduction to the function field case proved by Deligne. In the proof, Scholze used Theorem 1.1 to construct, for a fixed prime number
$(0, p)$
which is a set-theoretic complete intersection in a projective smooth toric variety, by reduction to the function field case proved by Deligne. In the proof, Scholze used Theorem 1.1 to construct, for a fixed prime number
![]() $\ell \neq p$
, a projective smooth variety Y over a function field of characteristic p and an appropriate mapping from étale cohomology with
$\ell \neq p$
, a projective smooth variety Y over a function field of characteristic p and an appropriate mapping from étale cohomology with
![]() ${\mathbb Z}/\ell {\mathbb Z}$
-coefficients of X to that of Y. The initial motivation for the present study is, following the method of Scholze, to prove that an analogue of the weight-monodromy conjecture holds for étale cohomology with
${\mathbb Z}/\ell {\mathbb Z}$
-coefficients of X to that of Y. The initial motivation for the present study is, following the method of Scholze, to prove that an analogue of the weight-monodromy conjecture holds for étale cohomology with
![]() ${\mathbb Z}/\ell {\mathbb Z}$
-coefficients of such a variety X for all but finitely many
${\mathbb Z}/\ell {\mathbb Z}$
-coefficients of such a variety X for all but finitely many
![]() $\ell \neq p$
by reduction to an ultraproduct variant of Weil II established by Cadoret [Reference Cadoret5]. For this, we shall use Theorem 1.2 instead of Theorem 1.1. The details are given in [Reference Ito21].
$\ell \neq p$
by reduction to an ultraproduct variant of Weil II established by Cadoret [Reference Cadoret5]. For this, we shall use Theorem 1.2 instead of Theorem 1.1. The details are given in [Reference Ito21].
1.2 Local constancy of higher direct images with proper support
For the proof of Theorem 1.2, we need to investigate local constancy of higher direct images with proper support for an algebraizable morphism of adic spaces whose target is the unit disc. To see this, let us give an outline of the proof of Theorem 1.1.
Sketch of the proof of Theorem 1.1. We assume that K is of characteristic zero. For simplicity, we assume that the closed embedding
![]() $Z \hookrightarrow X$
is of the form
$Z \hookrightarrow X$
is of the form
![]() $(\widehat {\mathcal {Z}})^{\mathop {\mathrm {rig}}\nolimits } \hookrightarrow (\widehat {\mathcal {X}})^{\mathop {\mathrm {rig}}\nolimits }$
for a closed immersion of finite presentation
$(\widehat {\mathcal {Z}})^{\mathop {\mathrm {rig}}\nolimits } \hookrightarrow (\widehat {\mathcal {X}})^{\mathop {\mathrm {rig}}\nolimits }$
for a closed immersion of finite presentation
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
of separated schemes of finite type over
$\mathcal {Z} \hookrightarrow \mathcal {X}$
of separated schemes of finite type over
![]() ${\mathcal O}$
. By considering the blow-up of
${\mathcal O}$
. By considering the blow-up of
![]() $\mathcal {X}$
along
$\mathcal {X}$
along
![]() $\mathcal {Z}$
, we may assume further that the closed subscheme
$\mathcal {Z}$
, we may assume further that the closed subscheme
![]() $\mathcal {Z}$
is defined by one global function
$\mathcal {Z}$
is defined by one global function
![]() $f \in {\mathcal O}_{\mathcal {X}}(\mathcal {X})$
. Let
$f \in {\mathcal O}_{\mathcal {X}}(\mathcal {X})$
. Let
be the morphism defined by
![]() $T \mapsto f$
. The Raynaud generic fibre of the
$T \mapsto f$
. The Raynaud generic fibre of the
![]() $\varpi $
-adic formal completion of
$\varpi $
-adic formal completion of
![]() $\mathop {\mathrm {Spec}} {\mathcal O}[T]$
is the unit disc
$\mathop {\mathrm {Spec}} {\mathcal O}[T]$
is the unit disc
![]() $ \mathbb {B}(1) := \mathop {\mathrm {Spa}}\nolimits (K\langle T \rangle , {\mathcal O} \langle T \rangle ). $
The set of K-rational points of
$ \mathbb {B}(1) := \mathop {\mathrm {Spa}}\nolimits (K\langle T \rangle , {\mathcal O} \langle T \rangle ). $
The set of K-rational points of
![]() $\mathbb {B}(1)$
is identified with the set
$\mathbb {B}(1)$
is identified with the set
The morphism f induces the following morphism of adic spaces:
The inverse image
![]() $(f^{\mathop {\mathrm {rig}}\nolimits })^{-1}(0)$
of the origin
$(f^{\mathop {\mathrm {rig}}\nolimits })^{-1}(0)$
of the origin
![]() $0 \in \mathbb {B}(1)$
is the closed subspace
$0 \in \mathbb {B}(1)$
is the closed subspace
![]() $(\widehat {\mathcal {Z}})^{\mathop {\mathrm {rig}}\nolimits }$
.
$(\widehat {\mathcal {Z}})^{\mathop {\mathrm {rig}}\nolimits }$
.
We fix a positive integer n invertible in
![]() ${\mathcal O}$
. We want to take an open subset V in Theorem 1.1 as the inverse image
${\mathcal O}$
. We want to take an open subset V in Theorem 1.1 as the inverse image
of the disc
![]() $\mathbb {B}(\epsilon ) \subset \mathbb {B}(1)$
of radius
$\mathbb {B}(\epsilon ) \subset \mathbb {B}(1)$
of radius
![]() $\epsilon $
centred at
$\epsilon $
centred at
![]() $0$
for a small
$0$
for a small
![]() $\epsilon \in \vert K^{\times } \vert $
. Such a subset is called a tubular neighbourhood of
$\epsilon \in \vert K^{\times } \vert $
. Such a subset is called a tubular neighbourhood of
![]() $(\widehat {\mathcal {Z}})^{\mathop {\mathrm {rig}}\nolimits }$
. For this, we have to compute étale cohomology with
$(\widehat {\mathcal {Z}})^{\mathop {\mathrm {rig}}\nolimits }$
. For this, we have to compute étale cohomology with
![]() ${\mathbb Z}/n{\mathbb Z}$
-coefficients of
${\mathbb Z}/n{\mathbb Z}$
-coefficients of
![]() $(f^{\mathop {\mathrm {rig}}\nolimits })^{-1}(\mathbb {B}(\epsilon ))$
for a small
$(f^{\mathop {\mathrm {rig}}\nolimits })^{-1}(\mathbb {B}(\epsilon ))$
for a small
![]() $\epsilon \in \vert K^{\times } \vert $
. By the Leray spectral sequence for
$\epsilon \in \vert K^{\times } \vert $
. By the Leray spectral sequence for
![]() $f^{\mathop {\mathrm {rig}}\nolimits }$
, it suffices to compute the cohomology group
$f^{\mathop {\mathrm {rig}}\nolimits }$
, it suffices to compute the cohomology group
for all
![]() $i, j$
. The key steps are as follows.
$i, j$
. The key steps are as follows.
-
• By [Reference Huber16, Theorem 2.1], the étale sheaf
 $ R^jf^{\mathop {\mathrm {rig}}\nolimits }_*{\mathbb Z}/n{\mathbb Z} $
is an oc-quasiconstructible étale sheaf of
$ R^jf^{\mathop {\mathrm {rig}}\nolimits }_*{\mathbb Z}/n{\mathbb Z} $
is an oc-quasiconstructible étale sheaf of
 ${\mathbb Z}/n{\mathbb Z}$
-modules in the sense of [Reference Huber16, Definition 1.4]. It follows that there exists an element
${\mathbb Z}/n{\mathbb Z}$
-modules in the sense of [Reference Huber16, Definition 1.4]. It follows that there exists an element
 $\epsilon _1 \in \vert K^{\times } \vert $
such that the restriction
$\epsilon _1 \in \vert K^{\times } \vert $
such that the restriction
 $(R^jf^{\mathop {\mathrm {rig}}\nolimits }_*{\mathbb Z}/n{\mathbb Z})\vert _{\mathbb {B}(\epsilon _1) \backslash \{ 0 \}}$
is a locally constant
$(R^jf^{\mathop {\mathrm {rig}}\nolimits }_*{\mathbb Z}/n{\mathbb Z})\vert _{\mathbb {B}(\epsilon _1) \backslash \{ 0 \}}$
is a locally constant
 ${\mathbb Z}/n{\mathbb Z}$
-sheaf of finite type.
${\mathbb Z}/n{\mathbb Z}$
-sheaf of finite type. -
• By the p-adic Riemann existence theorem of Lütkebohmert [Reference Lütkebohmert22, Theorem 2.2], there exists an element
 $\epsilon _0 \in \vert K^{\times } \vert $
with
$\epsilon _0 \in \vert K^{\times } \vert $
with
 $\epsilon _0 \leq \epsilon _1$
such that
$\epsilon _0 \leq \epsilon _1$
such that
 $(R^jf^{\mathop {\mathrm {rig}}\nolimits }_*{\mathbb Z}/n{\mathbb Z})\vert _{\mathbb {B}(\epsilon _0) \backslash \{ 0 \}}$
is trivialized by a Kummer covering
$(R^jf^{\mathop {\mathrm {rig}}\nolimits }_*{\mathbb Z}/n{\mathbb Z})\vert _{\mathbb {B}(\epsilon _0) \backslash \{ 0 \}}$
is trivialized by a Kummer covering
 $\varphi _m \colon \mathbb {B}(\epsilon ^{1/m}_0) \backslash \{ 0 \} \to \mathbb {B}(\epsilon _0) \backslash \{ 0 \}$
defined by
$\varphi _m \colon \mathbb {B}(\epsilon ^{1/m}_0) \backslash \{ 0 \} \to \mathbb {B}(\epsilon _0) \backslash \{ 0 \}$
defined by
 $T \mapsto T^m$
.
$T \mapsto T^m$
.
Then the desired result can be obtained by explicit calculations.
![]() $\Box $
$\Box $
In our case, the problem is to show that
![]() $\epsilon _0$
and
$\epsilon _0$
and
![]() $\epsilon _1$
in the above argument can be taken independent of n. To overcome this problem, by de Jong’s alterations and by cohomological descent, we reduce to the case where there exists an element
$\epsilon _1$
in the above argument can be taken independent of n. To overcome this problem, by de Jong’s alterations and by cohomological descent, we reduce to the case where there exists an element
![]() $\epsilon \in \vert K^{\times } \vert $
with
$\epsilon \in \vert K^{\times } \vert $
with
![]() $\epsilon \leq 1$
such that the restriction
$\epsilon \leq 1$
such that the restriction
of
![]() $f^{\mathop {\mathrm {rig}}\nolimits }$
is smooth. In this case, we will analyse the higher direct image sheaf with proper support
$f^{\mathop {\mathrm {rig}}\nolimits }$
is smooth. In this case, we will analyse the higher direct image sheaf with proper support
on
![]() $\mathbb {B}(1)$
, which is defined in [Reference Huber14, Definition 5.4.4]. An important fact is that, since
$\mathbb {B}(1)$
, which is defined in [Reference Huber14, Definition 5.4.4]. An important fact is that, since
![]() $f^{\mathop {\mathrm {rig}}\nolimits }$
is smooth over
$f^{\mathop {\mathrm {rig}}\nolimits }$
is smooth over
![]() $\mathbb {B}(\epsilon ) \backslash \{ 0 \}$
, the restriction
$\mathbb {B}(\epsilon ) \backslash \{ 0 \}$
, the restriction
![]() $ (R^jf^{\mathop {\mathrm {rig}}\nolimits }_!{\mathbb Z}/n{\mathbb Z})\vert _{\mathbb {B}(\epsilon ) \backslash \{ 0 \}} $
is a constructible étale sheaf of
$ (R^jf^{\mathop {\mathrm {rig}}\nolimits }_!{\mathbb Z}/n{\mathbb Z})\vert _{\mathbb {B}(\epsilon ) \backslash \{ 0 \}} $
is a constructible étale sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules (in the sense of [Reference Huber14, Definition 2.7.2]) for every positive integer n invertible in
${\mathbb Z}/n{\mathbb Z}$
-modules (in the sense of [Reference Huber14, Definition 2.7.2]) for every positive integer n invertible in
![]() ${\mathcal O}$
by [Reference Huber14, Theorem 6.2.2].
${\mathcal O}$
by [Reference Huber14, Theorem 6.2.2].
The following theorem is the most fundamental result in this paper. We do not suppose that K is of characteristic zero. For elements
![]() $a, b \in \vert K^{\times } \vert $
with
$a, b \in \vert K^{\times } \vert $
with
![]() $a < b \leq 1$
, let
$a < b \leq 1$
, let
![]() $ \mathbb {B}(a, b) \subset \mathbb {B}(1) $
be the annulus with inner radius a and outer radius b centred at
$ \mathbb {B}(a, b) \subset \mathbb {B}(1) $
be the annulus with inner radius a and outer radius b centred at
![]() $0$
.
$0$
.
Theorem 1.4 (Proposition 6.6 and Theorem 6.10)
Let
![]() $f \colon \mathcal {X} \to \mathop {\mathrm {Spec}} {\mathcal O}[T]$
be a separated morphism of finite presentation. We assume that there exists an element
$f \colon \mathcal {X} \to \mathop {\mathrm {Spec}} {\mathcal O}[T]$
be a separated morphism of finite presentation. We assume that there exists an element
![]() $\epsilon \in \vert K^{\times } \vert $
with
$\epsilon \in \vert K^{\times } \vert $
with
![]() $\epsilon \leq 1$
such that the induced morphism
$\epsilon \leq 1$
such that the induced morphism
is smooth over
![]() $\mathbb {B}(\epsilon ) \backslash \{ 0 \}$
. Then there exists an element
$\mathbb {B}(\epsilon ) \backslash \{ 0 \}$
. Then there exists an element
![]() $\epsilon _0 \in \vert K^{\times } \vert $
with
$\epsilon _0 \in \vert K^{\times } \vert $
with
![]() $\epsilon _0 \leq \epsilon $
such that, for every positive integer n invertible in
$\epsilon _0 \leq \epsilon $
such that, for every positive integer n invertible in
![]() ${\mathcal O}$
, the following two assertions hold:
${\mathcal O}$
, the following two assertions hold:
-
(1) The restriction
 $ (R^if^{\mathop {\mathrm {rig}}\nolimits }_!{\mathbb Z}/n{\mathbb Z})\vert _{\mathbb {B}(\epsilon _0) \backslash \{ 0 \}} $
is a locally constant
$ (R^if^{\mathop {\mathrm {rig}}\nolimits }_!{\mathbb Z}/n{\mathbb Z})\vert _{\mathbb {B}(\epsilon _0) \backslash \{ 0 \}} $
is a locally constant
 ${\mathbb Z}/n{\mathbb Z}$
-sheaf of finite type for every i.
${\mathbb Z}/n{\mathbb Z}$
-sheaf of finite type for every i. -
(2) For elements
 $a, b \in \vert K^{\times } \vert $
with
$a, b \in \vert K^{\times } \vert $
with
 $a < b \leq \epsilon _0$
, there exists a composition
$a < b \leq \epsilon _0$
, there exists a composition  $$\begin{align*}h \colon \mathbb{B}(c^{1/m}, d^{1/m}) \overset{\varphi_m}{\longrightarrow} \mathbb{B}(c, d) \overset{g}{\longrightarrow} \mathbb{B}(a, b) \end{align*}$$
$$\begin{align*}h \colon \mathbb{B}(c^{1/m}, d^{1/m}) \overset{\varphi_m}{\longrightarrow} \mathbb{B}(c, d) \overset{g}{\longrightarrow} \mathbb{B}(a, b) \end{align*}$$
of a Kummer covering
 $ \varphi _m $
of degree m, where m is invertible in
$ \varphi _m $
of degree m, where m is invertible in
 ${\mathcal O}$
, with a finite Galois étale morphism g, such that
${\mathcal O}$
, with a finite Galois étale morphism g, such that
 $(R^if^{\mathop {\mathrm {rig}}\nolimits }_!{\mathbb Z}/n{\mathbb Z})\vert _{\mathbb {B}(a, b)}$
is trivialized by h for every i. If K is of characteristic zero, then we can take g as a Kummer covering (the morphism g can be taken independent of n although the integer m possibly depends on n).
$(R^if^{\mathop {\mathrm {rig}}\nolimits }_!{\mathbb Z}/n{\mathbb Z})\vert _{\mathbb {B}(a, b)}$
is trivialized by h for every i. If K is of characteristic zero, then we can take g as a Kummer covering (the morphism g can be taken independent of n although the integer m possibly depends on n).
Remark 1.5. For the proof of Theorem 1.4 (1), we need Huber’s result [Reference Huber14, Theorem 6.2.2]. However, our methods are different from the ones used in [Reference Huber15, Reference Huber16, Reference Huber18].
Remark 1.6. We will prove Theorem 1.4 in a slightly more general setting involving certain sheaves on
![]() $\mathcal {X}$
which are not necessary constant (see Section 6 for details).
$\mathcal {X}$
which are not necessary constant (see Section 6 for details).
Under the assumptions of Theorem 1.4, the same results hold for the higher direct image sheaf
![]() $R^if^{\mathop {\mathrm {rig}}\nolimits }_*{\mathbb Z}/n{\mathbb Z}$
by Poincaré duality [Reference Huber14, Corollary 7.5.5], which will imply Theorem 1.2.
$R^if^{\mathop {\mathrm {rig}}\nolimits }_*{\mathbb Z}/n{\mathbb Z}$
by Poincaré duality [Reference Huber14, Corollary 7.5.5], which will imply Theorem 1.2.
1.3 Nearby cycles over general bases
A key ingredient in the proof of Theorem 1.4 is the following uniform refinement of a theorem of Orgogozo [Reference Orgogozo25, Théorème 2.1] on the compatibility of the sliced nearby cycles functors with base change. We also obtain a result on uniform unipotency of the sliced nearby cycles functors (see Section 2.1 for the definition of the sliced nearby cycles functors, and see Definition 2.3 for the terminology used in the following theorem).
Theorem 1.7 (Corollary 2.9)
Let S be an excellent Noetherian scheme and
![]() $g \colon Y \to S$
a separated morphism of finite type. There exists an alteration
$g \colon Y \to S$
a separated morphism of finite type. There exists an alteration
![]() $S' \to S$
such that, for every positive integer n invertible on S, the following assertions hold:
$S' \to S$
such that, for every positive integer n invertible on S, the following assertions hold:
-
(1) The sliced nearby cycles complexes for the base change
 $g_{S'} \colon Y_{S'} \to S'$
of g and the constant sheaf
$g_{S'} \colon Y_{S'} \to S'$
of g and the constant sheaf
 ${\mathbb Z}/n{\mathbb Z}$
are compatible with any base change.
${\mathbb Z}/n{\mathbb Z}$
are compatible with any base change. -
(2) The sliced nearby cycles complexes for
 $g_{S'} \colon Y_{S'} \to S'$
and the constant sheaf
$g_{S'} \colon Y_{S'} \to S'$
and the constant sheaf
 ${\mathbb Z}/n{\mathbb Z}$
are unipotent.
${\mathbb Z}/n{\mathbb Z}$
are unipotent.
Theorem 1.7 is a corollary of a more general result (Theorem 2.8), which may be of independent interest. For the proof, we use a combination of the methods of [Reference Orgogozo25] and of [Reference Orgogozo26] and we need de Jong’s alteration.
By using a comparison theorem of Huber [Reference Huber14, Theorem 5.7.8], we will study the relation between higher direct images with proper support for morphisms of adic spaces and the sliced nearby cycles functors. Then we will deduce Theorem 1.4 from Theorem 1.7. Roughly speaking, Theorem 1.4 (1) can be deduced from Theorem 1.7 (1) by considering a specialization map from an adic space of finite type over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
to its reduction (see Section 5.3 and Section 6.2 for details). Theorem 1.4 (2) can be deduced from Theorem 1.7 (2) and some properties of the discriminant function
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
to its reduction (see Section 5.3 and Section 6.2 for details). Theorem 1.4 (2) can be deduced from Theorem 1.7 (2) and some properties of the discriminant function
![]() $ \delta _h \colon [0, \infty ) \to {\mathbb R}_{\geq 0} $
associated with a finite Galois étale covering
$ \delta _h \colon [0, \infty ) \to {\mathbb R}_{\geq 0} $
associated with a finite Galois étale covering
![]() $h \colon Y \to \mathbb {B}(1) \backslash \{ 0 \}$
defined in [Reference Lütkebohmert22, Reference Lütkebohmert and Schmechta23, Reference Ramero27] (see Section 6.1 and Appendix A for details). In the proofs of both parts of Theorem 1.4, points of rank
$h \colon Y \to \mathbb {B}(1) \backslash \{ 0 \}$
defined in [Reference Lütkebohmert22, Reference Lütkebohmert and Schmechta23, Reference Ramero27] (see Section 6.1 and Appendix A for details). In the proofs of both parts of Theorem 1.4, points of rank
![]() $2$
of (finite Galois étale coverings of)
$2$
of (finite Galois étale coverings of)
![]() $\mathbb {B}(1)$
play important roles.
$\mathbb {B}(1)$
play important roles.
1.4 The organisation of this paper
This paper is organised as follows. In Section 2, we first recall the definition of the sliced nearby cycles functors. Then we formulate our main result (Theorem 2.8) on the sliced nearby cycles functors. In Section 3, we prove Theorem 2.8.
In Section 4, we recall the definition of tubular neighbourhoods, and then we state our main results (Theorem 4.8 and Theorem 4.9) on étale cohomology of tubular neighbourhoods. In Section 5, we recall a comparison theorem of Huber and use it to study the relation between higher direct images with proper support for morphisms of adic spaces and the sliced nearby cycles functors. In Section 6, we prove Theorem 1.4 in a slightly more general setting. In Section 7, we prove Theorem 4.8 and Theorem 4.9 (and, hence, Theorem 1.2) by using Theorem 1.4.
Finally, in Appendix A, we prove two theorems (Theorem 6.2 and Theorem 6.3) on finite étale coverings of annuli, which basically follow from the results in [Reference Lütkebohmert22, Reference Lütkebohmert and Schmechta23, Reference Ramero27].
2 Nearby cycles over general bases
In this section, we formulate our main results on nearby cycles over general bases. We will use the following notation throughout this paper. Let
![]() $f \colon X \to S$
be a morphism of schemes. For a morphism
$f \colon X \to S$
be a morphism of schemes. For a morphism
![]() $T \to S$
of schemes, the base change
$T \to S$
of schemes, the base change
![]() $X \times _S T$
of X is denoted by
$X \times _S T$
of X is denoted by
![]() $X_T$
and the base change of f is denoted by
$X_T$
and the base change of f is denoted by
![]() $f_T \colon X_T \to T$
. For a commutative ring
$f_T \colon X_T \to T$
. For a commutative ring
![]() $\Lambda $
, let
$\Lambda $
, let
![]() $D^+(X, \Lambda )$
be the derived category of bounded below complexes of étale sheaves of
$D^+(X, \Lambda )$
be the derived category of bounded below complexes of étale sheaves of
![]() $\Lambda $
-modules on X. For a complex
$\Lambda $
-modules on X. For a complex
![]() $\mathcal {K} \in D^+(X, \Lambda )$
, the pullback of
$\mathcal {K} \in D^+(X, \Lambda )$
, the pullback of
![]() $\mathcal {K}$
to
$\mathcal {K}$
to
![]() $X_T$
is denoted by
$X_T$
is denoted by
![]() $\mathcal {K}_T$
. We often call an étale sheaf on X simply a sheaf on X.
$\mathcal {K}_T$
. We often call an étale sheaf on X simply a sheaf on X.
We will use the following terminology (see also [Reference Orgogozo26, 1.2.4]).
Definition 2.1. Let G be a group and X a scheme. We say that a sheaf
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $\Lambda $
-modules on X with a G-action is G-unipotent if
$\Lambda $
-modules on X with a G-action is G-unipotent if
![]() $\mathcal {F}$
has a finite filtration which is stable by the action of G such that the action of G on each successive quotient is trivial. We say that a complex
$\mathcal {F}$
has a finite filtration which is stable by the action of G such that the action of G on each successive quotient is trivial. We say that a complex
![]() $\mathcal {K} \in D^+(X, \Lambda )$
with a G-action is G-unipotent if its cohomology sheaves are G-unipotent.
$\mathcal {K} \in D^+(X, \Lambda )$
with a G-action is G-unipotent if its cohomology sheaves are G-unipotent.
Remark 2.2. Assume that
![]() $\mathcal {F}$
as above is G-unipotent. Then every subquotient of
$\mathcal {F}$
as above is G-unipotent. Then every subquotient of
![]() $\mathcal {F}$
(as a sheaf of
$\mathcal {F}$
(as a sheaf of
![]() $\Lambda $
-modules with a G-action) is G-unipotent. We also note that higher direct images of
$\Lambda $
-modules with a G-action) is G-unipotent. We also note that higher direct images of
![]() $\mathcal {F}$
(and, hence, of G-unipotent complexes) with induced G-actions are G-unipotent, and the same statements hold for higher direct images with proper support, pullbacks, etc.
$\mathcal {F}$
(and, hence, of G-unipotent complexes) with induced G-actions are G-unipotent, and the same statements hold for higher direct images with proper support, pullbacks, etc.
2.1 Sliced nearby cycles functor
In this paper, a scheme is called a strictly local scheme if it is isomorphic to an affine scheme
![]() $\mathop {\mathrm {Spec}} R$
where R is a strictly Henselian local ring. Let
$\mathop {\mathrm {Spec}} R$
where R is a strictly Henselian local ring. Let
![]() $f \colon X \to S$
be a morphism of schemes. Let
$f \colon X \to S$
be a morphism of schemes. Let
![]() $q \colon U \to S$
be a morphism from a strictly local scheme U. The closed point of U is denoted by u. Let
$q \colon U \to S$
be a morphism from a strictly local scheme U. The closed point of U is denoted by u. Let
![]() $\eta \in U$
be a point. Let
$\eta \in U$
be a point. Let
![]() $\overline {\eta } \to U$
be an algebraic geometric point lying above
$\overline {\eta } \to U$
be an algebraic geometric point lying above
![]() $\eta $
, that is, it is a geometric point lying above
$\eta $
, that is, it is a geometric point lying above
![]() $\eta $
such that the residue field
$\eta $
such that the residue field
![]() $\kappa (\overline {\eta })$
is a separable closure of the residue field
$\kappa (\overline {\eta })$
is a separable closure of the residue field
![]() $\kappa (\eta )$
of
$\kappa (\eta )$
of
![]() $\eta $
. The strict localization of U at
$\eta $
. The strict localization of U at
![]() $\overline {\eta } \to U$
is denoted by
$\overline {\eta } \to U$
is denoted by
![]() $U_{(\overline {\eta })}$
. We have the following commutative diagram:
$U_{(\overline {\eta })}$
. We have the following commutative diagram:

Let
![]() $\Lambda $
be a commutative ring. We have the following functor:
$\Lambda $
be a commutative ring. We have the following functor:
This functor is called the sliced nearby cycles functor in [Reference Illusie19]. For a complex
![]() $\mathcal {K} \in D^{+}(X_U, \Lambda )$
, we have an action of the absolute Galois group
$\mathcal {K} \in D^{+}(X_U, \Lambda )$
, we have an action of the absolute Galois group
![]() $\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
on
$\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
on
![]() $R\Psi _{f_U, \overline {\eta }}(\mathcal {K})$
via the canonical isomorphism
$R\Psi _{f_U, \overline {\eta }}(\mathcal {K})$
via the canonical isomorphism
Let
![]() $q \colon V \to U$
be a local morphism of strictly local schemes over S, that is, a morphism over S which sends the closed point v of V to the closed point u of U. Let
$q \colon V \to U$
be a local morphism of strictly local schemes over S, that is, a morphism over S which sends the closed point v of V to the closed point u of U. Let
![]() $\xi \in V$
be a point with image
$\xi \in V$
be a point with image
![]() $\eta =q(\xi ) \in U$
. For an algebraic geometric point
$\eta =q(\xi ) \in U$
. For an algebraic geometric point
![]() $\overline {\xi } \to V$
lying above
$\overline {\xi } \to V$
lying above
![]() $\xi $
, we have an algebraic geometric point
$\xi $
, we have an algebraic geometric point
![]() $\overline {\eta } \to U$
lying above
$\overline {\eta } \to U$
lying above
![]() $\eta $
by taking the separable closure of
$\eta $
by taking the separable closure of
![]() $\kappa (\eta )$
in
$\kappa (\eta )$
in
![]() $\kappa (\overline {\xi })$
. We call
$\kappa (\overline {\xi })$
. We call
![]() $\overline {\eta } \to U$
the image of
$\overline {\eta } \to U$
the image of
![]() $\overline {\xi } \to V$
under the morphism q. We have the following commutative diagram:
$\overline {\xi } \to V$
under the morphism q. We have the following commutative diagram:

where the vertical morphisms are induced by q. For a complex
![]() $\mathcal {K} \in D^{+}(X_U, \Lambda )$
, we have the following base change map:
$\mathcal {K} \in D^{+}(X_U, \Lambda )$
, we have the following base change map:
Definition 2.3. Let
![]() $f \colon X \to S$
be a morphism of schemes. Let
$f \colon X \to S$
be a morphism of schemes. Let
![]() $\Lambda $
be a commutative ring and
$\Lambda $
be a commutative ring and
![]() $\mathcal {K} \in D^{+}(X, \Lambda )$
a complex.
$\mathcal {K} \in D^{+}(X, \Lambda )$
a complex.
-
(1) We say that the sliced nearby cycles complexes for f and
 $\mathcal {K}$
are compatible with any base change (or simply that the nearby cycles for f and
$\mathcal {K}$
are compatible with any base change (or simply that the nearby cycles for f and
 $\mathcal {K}$
are compatible with any base change) if for every local morphism
$\mathcal {K}$
are compatible with any base change) if for every local morphism
 $q \colon V \to U$
of strictly local schemes over S and every algebraic geometric point
$q \colon V \to U$
of strictly local schemes over S and every algebraic geometric point
 $\overline {\xi } \to V$
with image
$\overline {\xi } \to V$
with image
 $\overline {\eta } \to U$
, the base change map is an isomorphism.
$\overline {\eta } \to U$
, the base change map is an isomorphism. $$\begin{align*}q^*R\Psi_{f_U, \overline{\eta}}(\mathcal{K}_U) \to R\Psi_{f_V, \overline{\xi}}(\mathcal{K}_V) \end{align*}$$
$$\begin{align*}q^*R\Psi_{f_U, \overline{\eta}}(\mathcal{K}_U) \to R\Psi_{f_V, \overline{\xi}}(\mathcal{K}_V) \end{align*}$$
-
(2) We say that the sliced nearby cycles complexes for f and
 $\mathcal {K}$
are unipotent (or simply that the nearby cycles for f and
$\mathcal {K}$
are unipotent (or simply that the nearby cycles for f and
 $\mathcal {K}$
are unipotent) if, for every morphism
$\mathcal {K}$
are unipotent) if, for every morphism
 $q \colon U \to S$
from a strictly local scheme U, a point
$q \colon U \to S$
from a strictly local scheme U, a point
 $\eta \in U$
and an algebraic geometric point
$\eta \in U$
and an algebraic geometric point
 $\overline {\eta } \to U$
lying above
$\overline {\eta } \to U$
lying above
 $\eta $
, the complex
$\eta $
, the complex
 $R\Psi _{f_{U}, \overline {\eta }}(\mathcal {K}_U)$
is
$R\Psi _{f_{U}, \overline {\eta }}(\mathcal {K}_U)$
is
 $\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent in the sense of Definition 2.1.
$\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent in the sense of Definition 2.1.
Remark 2.4. We can restate Definition 2.3 (1) in terms of vanishing topoi as follows. Let
![]() $f \colon X \to S$
be a morphism of schemes. Let
$f \colon X \to S$
be a morphism of schemes. Let
be the vanishing topos, where the étale topos of a scheme X is also denoted by X by abuse of notation. See [Reference Illusie19] for the definition and basic properties of the vanishing topos
![]() $X \overset {\leftarrow }{\times }_S S$
. Let
$X \overset {\leftarrow }{\times }_S S$
. Let
![]() $\Lambda $
be a commutative ring. We have a morphism of topoi
$\Lambda $
be a commutative ring. We have a morphism of topoi
![]() $\Psi _f \colon X \to X \overset {\leftarrow }{\times }_S S$
. The direct image functor
$\Psi _f \colon X \to X \overset {\leftarrow }{\times }_S S$
. The direct image functor
defined by
![]() $\Psi _f$
is called the nearby cycles functor. For a morphism
$\Psi _f$
is called the nearby cycles functor. For a morphism
![]() $q \colon T \to S$
of schemes, we have a morphism of topoi
$q \colon T \to S$
of schemes, we have a morphism of topoi
![]() $ {\overset {\leftarrow }{q}} \colon X_T \overset {\leftarrow }{\times }_T T \to X \overset {\leftarrow }{\times }_S S $
and a
$ {\overset {\leftarrow }{q}} \colon X_T \overset {\leftarrow }{\times }_T T \to X \overset {\leftarrow }{\times }_S S $
and a
![]() $2$
-commutative diagram
$2$
-commutative diagram

where
![]() $X_T \to X$
is the projection. For a complex
$X_T \to X$
is the projection. For a complex
![]() $\mathcal {K} \in D^{+}(X, \Lambda )$
, we have the base change map
$\mathcal {K} \in D^{+}(X, \Lambda )$
, we have the base change map
For a morphism
![]() $f \colon X \to S$
of schemes and a complex
$f \colon X \to S$
of schemes and a complex
![]() $\mathcal {K} \in D^{+}(X, \Lambda )$
, the sliced nearby cycles complexes for f and
$\mathcal {K} \in D^{+}(X, \Lambda )$
, the sliced nearby cycles complexes for f and
![]() $\mathcal {K}$
are compatible with any base change in the sense of Definition 2.3 (1) if and only if, for every morphism
$\mathcal {K}$
are compatible with any base change in the sense of Definition 2.3 (1) if and only if, for every morphism
![]() $q \colon T \to S$
of schemes, the base change map
$q \colon T \to S$
of schemes, the base change map
![]() $ c_{f, q}(\mathcal {K}) $
is an isomorphism (see also the proof of [Reference Orgogozo25, Lemme 4.1]). This follows from the following descriptions of the stalks of the nearby cycles functor and the sliced nearby cycles functors.
$ c_{f, q}(\mathcal {K}) $
is an isomorphism (see also the proof of [Reference Orgogozo25, Lemme 4.1]). This follows from the following descriptions of the stalks of the nearby cycles functor and the sliced nearby cycles functors.
Let
![]() $x \to X$
be a geometric point of X, and let
$x \to X$
be a geometric point of X, and let
![]() $s \to S$
denote the composition
$s \to S$
denote the composition
![]() $x \to X \to S$
. Let
$x \to X \to S$
. Let
![]() $t \to S$
be a geometric point with a specialization map
$t \to S$
be a geometric point with a specialization map
![]() $\alpha \colon t \to s$
, that is, an S-morphism
$\alpha \colon t \to s$
, that is, an S-morphism
![]() $\alpha \colon S_{(t)} \to S_{(s)}$
, where
$\alpha \colon S_{(t)} \to S_{(s)}$
, where
![]() $S_{(s)}$
(resp.
$S_{(s)}$
(resp.
![]() $S_{(t)}$
) is the strict localization of S at
$S_{(t)}$
) is the strict localization of S at
![]() $s \to S$
(resp.
$s \to S$
(resp.
![]() $t \to S$
). The triple
$t \to S$
). The triple
![]() $(x, t, \alpha )$
defines a point of the vanishing topos
$(x, t, \alpha )$
defines a point of the vanishing topos
![]() $X \overset {\leftarrow }{\times }_S S$
, and every point of
$X \overset {\leftarrow }{\times }_S S$
, and every point of
![]() $X \overset {\leftarrow }{\times }_S S$
is of this form (up to equivalence). The topos
$X \overset {\leftarrow }{\times }_S S$
is of this form (up to equivalence). The topos
![]() $X \overset {\leftarrow }{\times }_S S$
has enough points. For the stalk
$X \overset {\leftarrow }{\times }_S S$
has enough points. For the stalk
![]() $R\Psi _f(\mathcal {K})_{(x, t, \alpha )}$
of
$R\Psi _f(\mathcal {K})_{(x, t, \alpha )}$
of
![]() $R\Psi _f(\mathcal {K})$
at
$R\Psi _f(\mathcal {K})$
at
![]() $(x, t, \alpha )$
, we have an isomorphism
$(x, t, \alpha )$
, we have an isomorphism
(see [Reference Illusie19, (1.3.2)]). Here, the pullback of
![]() $\mathcal {K}$
to
$\mathcal {K}$
to
![]() $X_{(x)}\times _{S_{(s)}} S_{(t)}$
is also denoted by
$X_{(x)}\times _{S_{(s)}} S_{(t)}$
is also denoted by
![]() $\mathcal {K}$
(we will use this notation in this paper when there is no possibility of confusion).
$\mathcal {K}$
(we will use this notation in this paper when there is no possibility of confusion).
We have a similar description of the stalks of the sliced nearby cycles functors. More precisely, let
![]() $q \colon U \to S$
be a morphism from a strictly local scheme U and
$q \colon U \to S$
be a morphism from a strictly local scheme U and
![]() $\overline {\eta } \to U$
an algebraic geometric point. Let
$\overline {\eta } \to U$
an algebraic geometric point. Let
![]() $x \to X_u$
be a geometric point of the special fibre
$x \to X_u$
be a geometric point of the special fibre
![]() $X_u$
of
$X_u$
of
![]() $X_U$
. Then, since the morphism
$X_U$
. Then, since the morphism
![]() $X_{U_{(\overline {\eta })}} \to X_U$
is quasicompact and quasiseparated, we have
$X_{U_{(\overline {\eta })}} \to X_U$
is quasicompact and quasiseparated, we have
2.2 Main results on nearby cycles over general bases
A proper surjective morphism
![]() $f \colon X \to Y$
of Noetherian schemes is called an alteration if it sends every generic point of X to a generic point of Y and it is generically finite, that is, there exists a dense open subset
$f \colon X \to Y$
of Noetherian schemes is called an alteration if it sends every generic point of X to a generic point of Y and it is generically finite, that is, there exists a dense open subset
![]() $U \subset Y$
such that the restriction
$U \subset Y$
such that the restriction
![]() $f^{-1}(U) \to U$
is a finite morphism. If, furthermore, X and Y are integral schemes, then f is called an integral alteration. An alteration
$f^{-1}(U) \to U$
is a finite morphism. If, furthermore, X and Y are integral schemes, then f is called an integral alteration. An alteration
![]() $f \colon X \to Y$
is called a modification if there exists a dense open subset
$f \colon X \to Y$
is called a modification if there exists a dense open subset
![]() $U \subset Y$
such that the restriction
$U \subset Y$
such that the restriction
![]() $f^{-1}(U) \to U$
is an isomorphism.
$f^{-1}(U) \to U$
is an isomorphism.
Let
![]() $f \colon X \to S$
be a morphism of finite type of excellent Noetherian schemes. In [Reference Orgogozo25], Orgogozo proved the following result:
$f \colon X \to S$
be a morphism of finite type of excellent Noetherian schemes. In [Reference Orgogozo25], Orgogozo proved the following result:
Theorem 2.5 (Orgogozo [Reference Orgogozo25, Théorème 2.1])
For a positive integer n invertible on S and for a constructible sheaf
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on X, there exists a modification
${\mathbb Z}/n{\mathbb Z}$
-modules on X, there exists a modification
![]() $S' \to S$
such that the sliced nearby cycles complexes for
$S' \to S$
such that the sliced nearby cycles complexes for
![]() $f_{S'}$
and
$f_{S'}$
and
![]() $\mathcal {F}_{S'}$
are compatible with any base change in the sense of Definition 2.3 (1).
$\mathcal {F}_{S'}$
are compatible with any base change in the sense of Definition 2.3 (1).
Proof. See [Reference Orgogozo25, Théorème 2.1] for the proof and for a more general result (actually, Orgogozo formulated his results in terms of vanishing topoi, see Remark 2.4).
To prove Theorem 1.2, we need a uniform refinement of Theorem 2.5. More precisely, we need a modification (or an alteration)
![]() $S' \to S$
such that, for every positive integer n invertible on S, the sliced nearby cycles complexes for
$S' \to S$
such that, for every positive integer n invertible on S, the sliced nearby cycles complexes for
![]() $f_{S'}$
and the constant sheaf
$f_{S'}$
and the constant sheaf
![]() ${\mathbb Z}/n{\mathbb Z}$
are compatible with any base change.
${\mathbb Z}/n{\mathbb Z}$
are compatible with any base change.
In order to prove the existence of such a modification, we will use the methods developed in a recent paper [Reference Orgogozo26] of Orgogozo. In fact, by the same methods, we can also prove that there exists an alteration
![]() $S' \to S$
such that, for every positive integer n invertible on S, the sliced nearby cycles complexes for
$S' \to S$
such that, for every positive integer n invertible on S, the sliced nearby cycles complexes for
![]() $f_{S'}$
and the constant sheaf
$f_{S'}$
and the constant sheaf
![]() ${\mathbb Z}/n{\mathbb Z}$
are unipotent in the sense of Definition 2.3 (2). Such an alteration is also needed in the proof of Theorem 1.2.
${\mathbb Z}/n{\mathbb Z}$
are unipotent in the sense of Definition 2.3 (2). Such an alteration is also needed in the proof of Theorem 1.2.
We need to recall the definition of a locally unipotent sheaf on a Noetherian scheme from [Reference Orgogozo26]. Let X be a Noetherian scheme. In this paper, we call a finite set
![]() $\mathfrak {X}= \{ X_{\alpha } \}_{\alpha }$
of locally closed subsets of X a stratification if we have
$\mathfrak {X}= \{ X_{\alpha } \}_{\alpha }$
of locally closed subsets of X a stratification if we have
![]() $X=\coprod _{\alpha } X_{\alpha }$
(set theoretically).
$X=\coprod _{\alpha } X_{\alpha }$
(set theoretically).
Definition 2.6 (Orgogozo [Reference Orgogozo26, 1.2.1])
Let X be a Noetherian scheme and
![]() $\mathfrak {X}$
a stratification of X. We say that an abelian sheaf
$\mathfrak {X}$
a stratification of X. We say that an abelian sheaf
![]() $\mathcal {F}$
on X is locally unipotent along
$\mathcal {F}$
on X is locally unipotent along
![]() $\mathfrak {X}$
if, for every morphism
$\mathfrak {X}$
if, for every morphism
![]() $U \to X$
from a strictly local scheme U and every
$U \to X$
from a strictly local scheme U and every
![]() $X_{\alpha } \in \mathfrak {X}$
, the pullback of
$X_{\alpha } \in \mathfrak {X}$
, the pullback of
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $U \times _X X_{\alpha }$
has a finite filtration whose successive quotients are constant sheaves.
$U \times _X X_{\alpha }$
has a finite filtration whose successive quotients are constant sheaves.
Remark 2.7. If a constructible abelian sheaf
![]() $\mathcal {F}$
on a Noetherian scheme X is locally unipotent along a stratification
$\mathcal {F}$
on a Noetherian scheme X is locally unipotent along a stratification
![]() $\mathfrak {X}$
, then it is constructible along
$\mathfrak {X}$
, then it is constructible along
![]() $\mathfrak {X}$
, that is, for every
$\mathfrak {X}$
, that is, for every
![]() $X_{\alpha } \in \mathfrak {X}$
, the pullback of
$X_{\alpha } \in \mathfrak {X}$
, the pullback of
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $X_{\alpha }$
is locally constant (see [Reference Orgogozo26, 1.2.2]).
$X_{\alpha }$
is locally constant (see [Reference Orgogozo26, 1.2.2]).
Our main result on nearby cycles over general bases is as follows.
Theorem 2.8. Let S be an excellent Noetherian scheme. Let
![]() $f \colon X \to S$
be a proper morphism. Let
$f \colon X \to S$
be a proper morphism. Let
![]() $\mathfrak {X}$
be a stratification of X. Then there exists an alteration
$\mathfrak {X}$
be a stratification of X. Then there exists an alteration
![]() $S' \to S$
such that, for every positive integer n invertible on S and every complex
$S' \to S$
such that, for every positive integer n invertible on S and every complex
![]() $\mathcal {K} \in D^{+}(X, {\mathbb Z}/n{\mathbb Z})$
whose cohomology sheaves are constructible sheaves of
$\mathcal {K} \in D^{+}(X, {\mathbb Z}/n{\mathbb Z})$
whose cohomology sheaves are constructible sheaves of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules and are locally unipotent along
${\mathbb Z}/n{\mathbb Z}$
-modules and are locally unipotent along
![]() $\mathfrak {X}$
, the following two assertions hold.
$\mathfrak {X}$
, the following two assertions hold.
-
(1) The sliced nearby cycles complexes for
 $f_{S'} \colon X_{S'} \to S'$
and
$f_{S'} \colon X_{S'} \to S'$
and
 $\mathcal {K}_{S'}$
are compatible with any base change.
$\mathcal {K}_{S'}$
are compatible with any base change. -
(2) The sliced nearby cycles complexes for
 $f_{S'} \colon X_{S'} \to S'$
and
$f_{S'} \colon X_{S'} \to S'$
and
 $\mathcal {K}_{S'}$
are unipotent.
$\mathcal {K}_{S'}$
are unipotent.
For future reference, we state the following corollary.
Corollary 2.9. Let S be an excellent Noetherian scheme and
![]() $f \colon X \to S$
a separated morphism of finite type. There exists an alteration
$f \colon X \to S$
a separated morphism of finite type. There exists an alteration
![]() $S' \to S$
such that, for every positive integer n invertible on S, the sliced nearby cycles complexes for
$S' \to S$
such that, for every positive integer n invertible on S, the sliced nearby cycles complexes for
![]() $f_{S'} \colon X_{S'} \to S'$
and the constant sheaf
$f_{S'} \colon X_{S'} \to S'$
and the constant sheaf
![]() ${\mathbb Z}/n{\mathbb Z}$
are compatible with any base change and are unipotent.
${\mathbb Z}/n{\mathbb Z}$
are compatible with any base change and are unipotent.
Proof. This follows immediately from Theorem 2.8.
In fact, as in [Reference Orgogozo25], we can show a more precise result for the compatibility of the sliced nearby cycles functors with base change as a corollary of Theorem 2.8:
Corollary 2.10. Under the assumptions of Theorem 2.8, there exists a modification
![]() $S' \to S$
such that, for every positive integer n invertible on S and every complex
$S' \to S$
such that, for every positive integer n invertible on S and every complex
![]() $\mathcal {K} \in D^{+}(X, {\mathbb Z}/n{\mathbb Z})$
whose cohomology sheaves are constructible sheaves of
$\mathcal {K} \in D^{+}(X, {\mathbb Z}/n{\mathbb Z})$
whose cohomology sheaves are constructible sheaves of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules and are locally unipotent along
${\mathbb Z}/n{\mathbb Z}$
-modules and are locally unipotent along
![]() $\mathfrak {X}$
, the sliced nearby cycles complexes for
$\mathfrak {X}$
, the sliced nearby cycles complexes for
![]() $f_{S'} \colon X_{S'} \to S'$
and
$f_{S'} \colon X_{S'} \to S'$
and
![]() $\mathcal {K}_{S'}$
are compatible with any base change.
$\mathcal {K}_{S'}$
are compatible with any base change.
Proof. Theorem 2.8, together with [Reference Orgogozo25, Lemme 3.2 and Lemme 3.3], implies the result.
3 Proof of Theorem 2.8
3.1 Nodal curves
In this subsection, we recall some results on nodal curves from [Reference de Jong7, Reference Orgogozo26]. Let
![]() $f \colon X \to S$
be a morphism of Noetherian schemes. We say that f is a nodal curve if it is a flat projective morphism such that every geometric fibre of f is a connected reduced curve having at most ordinary double points as singularities. We say that f is a nodal curve adapted to a pair
$f \colon X \to S$
be a morphism of Noetherian schemes. We say that f is a nodal curve if it is a flat projective morphism such that every geometric fibre of f is a connected reduced curve having at most ordinary double points as singularities. We say that f is a nodal curve adapted to a pair
![]() $(X^{\circ }, S^{\circ })$
of dense open subsets
$(X^{\circ }, S^{\circ })$
of dense open subsets
![]() $X^{\circ }$
and
$X^{\circ }$
and
![]() $S^{\circ }$
of X and S, respectively, if the following conditions are satisfied:
$S^{\circ }$
of X and S, respectively, if the following conditions are satisfied:
-
• f is a nodal curve which is smooth over
 $S^{\circ }$
.
$S^{\circ }$
. -
• There is a closed subscheme D of X which is étale over S and is contained in the smooth locus of f. Moreover, we have
 $f^{-1}(S^{\circ }) \cap (X \backslash D)=X^{\circ }$
.
$f^{-1}(S^{\circ }) \cap (X \backslash D)=X^{\circ }$
.
The following proposition will be used in the proof of Theorem 2.8, which is one of the main reasons why we introduce the notion of locally unipotent sheaves.
Proposition 3.1 (Orgogozo [Reference Orgogozo26, Proposition 2.3.1])
Let S be a Noetherian scheme and
![]() $f \colon X \to S$
a nodal curve adapted to a pair
$f \colon X \to S$
a nodal curve adapted to a pair
![]() $(X^{\circ }, S^{\circ })$
of dense open subsets
$(X^{\circ }, S^{\circ })$
of dense open subsets
![]() $X^{\circ }$
and
$X^{\circ }$
and
![]() $S^{\circ }$
of X and S, respectively. Let
$S^{\circ }$
of X and S, respectively. Let
![]() $u \colon X^{\circ } \hookrightarrow X$
denote the open immersion. Assume that
$u \colon X^{\circ } \hookrightarrow X$
denote the open immersion. Assume that
![]() $S^{\circ }$
is normal. Then, for every positive integer n invertible on S and every locally constant constructible sheaf
$S^{\circ }$
is normal. Then, for every positive integer n invertible on S and every locally constant constructible sheaf
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
![]() $X^{\circ }$
such that
$X^{\circ }$
such that
![]() $u_{!}\mathcal {L}$
is locally unipotent along the stratification
$u_{!}\mathcal {L}$
is locally unipotent along the stratification
![]() $\mathfrak {X}=\{ X^{\circ }, X \backslash X^{\circ } \}$
of X, the sheaf
$\mathfrak {X}=\{ X^{\circ }, X \backslash X^{\circ } \}$
of X, the sheaf
is locally unipotent along the stratification
![]() $\mathfrak {S}=\{ S^{\circ }, S \backslash S^{\circ } \}$
of S for every i.
$\mathfrak {S}=\{ S^{\circ }, S \backslash S^{\circ } \}$
of S for every i.
Proof. See [Reference Orgogozo26, Proposition 2.3.1].
Remark 3.2. The proof of Theorem 2.8 is inspired by that of Proposition 3.1. In fact, we can show that, with the notation of Proposition 3.1, the nearby cycles for f and
![]() $u_! \mathcal {L}$
are compatible with any base change and unipotent. Since we will not use this fact in the proof of Theorem 2.8, we omit the proof of it.
$u_! \mathcal {L}$
are compatible with any base change and unipotent. Since we will not use this fact in the proof of Theorem 2.8, we omit the proof of it.
We say that a morphism
![]() $f \colon X \to S$
of Noetherian integral schemes is a pluri nodal curve adapted to a dense open subset
$f \colon X \to S$
of Noetherian integral schemes is a pluri nodal curve adapted to a dense open subset
![]() $X^{\circ } \subset X$
if there are an integer
$X^{\circ } \subset X$
if there are an integer
![]() $d \geq 0$
, a sequence
$d \geq 0$
, a sequence
of morphisms of Noetherian integral schemes and dense open subsets
![]() $X^{\circ }_i \subset X_i$
for every
$X^{\circ }_i \subset X_i$
for every
![]() $0 \leq i \leq d$
with
$0 \leq i \leq d$
with
![]() $X^{\circ }_d=X^{\circ }$
such that
$X^{\circ }_d=X^{\circ }$
such that
![]() $f_i \colon X_i \to X_{i-1}$
is a nodal curve adapted to the pair
$f_i \colon X_i \to X_{i-1}$
is a nodal curve adapted to the pair
![]() $(X^{\circ }_i, X^{\circ }_{i-1})$
for every
$(X^{\circ }_i, X^{\circ }_{i-1})$
for every
![]() $ 1 \leq i \leq d$
. If
$ 1 \leq i \leq d$
. If
![]() $d=0$
, by convention, it means that
$d=0$
, by convention, it means that
![]() $X=S$
and f is the identity map.
$X=S$
and f is the identity map.
The following theorem of de Jong plays an important role in the proof of Theorem 2.8.
Theorem 3.3 (de Jong [Reference de Jong7, Theorem 5.9])
Let
![]() $f \colon X \to S$
be a proper surjective morphism of excellent Noetherian integral schemes. Let
$f \colon X \to S$
be a proper surjective morphism of excellent Noetherian integral schemes. Let
![]() $X^{\circ } \subset X$
be a dense open subset. We assume that the geometric generic fibre of f is irreducible. Then there is the following commutative diagram:
$X^{\circ } \subset X$
be a dense open subset. We assume that the geometric generic fibre of f is irreducible. Then there is the following commutative diagram:

where the vertical maps are integral alterations and
![]() $f'$
is a pluri nodal curve adapted to a dense open subset
$f'$
is a pluri nodal curve adapted to a dense open subset
![]() $X^{\circ \circ }_0 \subset X_0$
which is contained in the inverse image of
$X^{\circ \circ }_0 \subset X_0$
which is contained in the inverse image of
![]() $X^{\circ } \subset X$
.
$X^{\circ } \subset X$
.
Proof. See [Reference de Jong7, Theorem 5.9] and the proof of [Reference de Jong7, Theorem 5.10]. We note that if the dimension of the generic fibre of f is zero, then f is an integral alteration. Hence, we can take
![]() $S'$
as X and take
$S'$
as X and take
![]() $f'$
as the identity map on X in this case.
$f'$
as the identity map on X in this case.
3.2 Preliminary lemmas
We shall give two lemmas, which will be used in the proof of Theorem 2.8.
We will need the following terminology.
Definition 3.4. Let
![]() $f \colon X \to S$
be a morphism of schemes. Let
$f \colon X \to S$
be a morphism of schemes. Let
![]() $\Lambda $
be a commutative ring and
$\Lambda $
be a commutative ring and
![]() $\mathcal {K} \in D^{+}(X, \Lambda )$
a complex. Let
$\mathcal {K} \in D^{+}(X, \Lambda )$
a complex. Let
![]() $\rho $
be an integer.
$\rho $
be an integer.
-
(1) We say that the sliced nearby cycles complexes for f and
 $\mathcal {K}$
are
$\mathcal {K}$
are
 $\rho $
-compatible with any base change (or simply that the nearby cycles for f and
$\rho $
-compatible with any base change (or simply that the nearby cycles for f and
 $\mathcal {K}$
are
$\mathcal {K}$
are
 $\rho $
-compatible with any base change) if for every local morphism
$\rho $
-compatible with any base change) if for every local morphism
 $q \colon V \to U$
of strictly local schemes over S and every algebraic geometric point
$q \colon V \to U$
of strictly local schemes over S and every algebraic geometric point
 $\overline {\xi } \to V$
with image
$\overline {\xi } \to V$
with image
 $\overline {\eta } \to U$
, we have
$\overline {\eta } \to U$
, we have
 $\tau _{\leq \rho } \Delta =0$
for the cone
$\tau _{\leq \rho } \Delta =0$
for the cone
 $\Delta $
of the base change map:
$\Delta $
of the base change map:  $$\begin{align*}q^*R\Psi_{f_U, \overline{\eta}}(\mathcal{K}_U) \to R\Psi_{f_V, \overline{\xi}}(\mathcal{K}_V) \to \Delta \to. \end{align*}$$
$$\begin{align*}q^*R\Psi_{f_U, \overline{\eta}}(\mathcal{K}_U) \to R\Psi_{f_V, \overline{\xi}}(\mathcal{K}_V) \to \Delta \to. \end{align*}$$
-
(2) We say that the sliced nearby cycles complexes for f and
 $\mathcal {K}$
are
$\mathcal {K}$
are
 $\rho $
-unipotent (or simply that the nearby cycles for f and
$\rho $
-unipotent (or simply that the nearby cycles for f and
 $\mathcal {K}$
are
$\mathcal {K}$
are
 $\rho $
-unipotent) if, for every morphism
$\rho $
-unipotent) if, for every morphism
 $q \colon U \to S$
from a strictly local scheme U, a point
$q \colon U \to S$
from a strictly local scheme U, a point
 $\eta \in U$
and an algebraic geometric point
$\eta \in U$
and an algebraic geometric point
 $\overline {\eta } \to U$
lying above
$\overline {\eta } \to U$
lying above
 $\eta $
, the complex
$\eta $
, the complex  $$\begin{align*}\tau_{\leq \rho}R\Psi_{f_{U}, \overline{\eta}}(\mathcal{K}_U) \end{align*}$$
$$\begin{align*}\tau_{\leq \rho}R\Psi_{f_{U}, \overline{\eta}}(\mathcal{K}_U) \end{align*}$$
is
 $\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent (in the sense of Definition 2.1).
$\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent (in the sense of Definition 2.1).
As in [Reference Orgogozo25], we need some results on cohomological descent (see [Reference Artin, Grothendieck and Verdier1, Exposé Vbis] and [Reference Deligne8, Section 5] for the terminology used here). Let
![]() $f \colon Y \to X$
be a morphism of schemes. Let
$f \colon Y \to X$
be a morphism of schemes. Let
be the augmented simplicial object in the category of schemes defined as in [Reference Deligne8, (5.1.4)], so
![]() $Y_m$
is the
$Y_m$
is the
![]() $(m+1)$
-times fibre product
$(m+1)$
-times fibre product
![]() $Y \times _X \cdots \times _X Y$
for
$Y \times _X \cdots \times _X Y$
for
![]() $m \geq 0$
. We can associate to the étale topoi of
$m \geq 0$
. We can associate to the étale topoi of
![]() $Y_m$
(
$Y_m$
(
![]() $m \geq 0$
) a topos
$m \geq 0$
) a topos
![]() $(Y_{\bullet })^{\sim }$
(see [Reference Deligne8, (5.1.6)–(5.1.8)]). Moreover, as in [Reference Deligne8, (5.1.11)], we have a morphism of topoi
$(Y_{\bullet })^{\sim }$
(see [Reference Deligne8, (5.1.6)–(5.1.8)]). Moreover, as in [Reference Deligne8, (5.1.11)], we have a morphism of topoi
from
![]() $(Y_{\bullet })^{\sim }$
to the étale topos
$(Y_{\bullet })^{\sim }$
to the étale topos
![]() $X^{\sim }_{\mathrm {\acute {e}t}}$
of X.
$X^{\sim }_{\mathrm {\acute {e}t}}$
of X.
Lemma 3.5. Let
![]() $f \colon X \to S$
be a morphism of schemes. Let
$f \colon X \to S$
be a morphism of schemes. Let
![]() $\beta _0 \colon Y \to X$
be a proper surjective morphism. We put
$\beta _0 \colon Y \to X$
be a proper surjective morphism. We put
![]() $\beta \colon Y_{\bullet }:=\mathop {\mathrm {cosq}}\nolimits _0(Y/X) \to X$
. Let
$\beta \colon Y_{\bullet }:=\mathop {\mathrm {cosq}}\nolimits _0(Y/X) \to X$
. Let
![]() $\mathcal {F}$
be a sheaf of
$\mathcal {F}$
be a sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on X and
${\mathbb Z}/n{\mathbb Z}$
-modules on X and
![]() $\mathcal {F}_m:=\beta _m^*\mathcal {F}$
the pullback of
$\mathcal {F}_m:=\beta _m^*\mathcal {F}$
the pullback of
![]() $\mathcal {F}$
by
$\mathcal {F}$
by
![]() $\beta _m \colon Y_m \to X$
. The composition
$\beta _m \colon Y_m \to X$
. The composition
![]() $f \circ \beta _m$
is denoted by
$f \circ \beta _m$
is denoted by
![]() $f_m$
. Let
$f_m$
. Let
![]() $\rho \geq -1$
be an integer.
$\rho \geq -1$
be an integer.
-
(1) If the nearby cycles for
 $f_m$
and
$f_m$
and
 $\mathcal {F}_m$
are
$\mathcal {F}_m$
are
 $(\rho -m)$
-compatible with any base change for every
$(\rho -m)$
-compatible with any base change for every
 $0 \leq m \leq \rho +1$
, then the nearby cycles for f and
$0 \leq m \leq \rho +1$
, then the nearby cycles for f and
 $\mathcal {F}$
are
$\mathcal {F}$
are
 $\rho $
-compatible with any base change.
$\rho $
-compatible with any base change. -
(2) If the nearby cycles for
 $f_m$
and
$f_m$
and
 $\mathcal {F}_m$
are
$\mathcal {F}_m$
are
 $(\rho -m)$
-unipotent for every
$(\rho -m)$
-unipotent for every
 $0 \leq m \leq \rho $
, then the nearby cycles for f and
$0 \leq m \leq \rho $
, then the nearby cycles for f and
 $\mathcal {F}$
are
$\mathcal {F}$
are
 $\rho $
-unipotent.
$\rho $
-unipotent.
Proof. The assertion (1) is [Reference Orgogozo25, Lemme 4.1] (see also Remark 2.4). Although it is stated for constant sheaves, the same proof works for sheaves of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules (or more generally, for torsion abelian sheaves).
${\mathbb Z}/n{\mathbb Z}$
-modules (or more generally, for torsion abelian sheaves).
The assertion (2) can be proved by the same arguments as in the proof of [Reference Orgogozo25, Lemme 4.1]. We shall give a sketch here. Let
![]() $q \colon U \to S$
be a morphism from a strictly local scheme U and
$q \colon U \to S$
be a morphism from a strictly local scheme U and
![]() $\overline {\eta } \to U$
an algebraic geometric point with image
$\overline {\eta } \to U$
an algebraic geometric point with image
![]() $\eta \in U$
. Let
$\eta \in U$
. Let
![]() $u \in U$
be the closed point. We have the following diagram:
$u \in U$
be the closed point. We have the following diagram:

where
![]() $\beta \colon (Y_{\bullet })_U \to X_U$
is the base change of
$\beta \colon (Y_{\bullet })_U \to X_U$
is the base change of
![]() $\beta $
, etc. By [Reference Artin, Grothendieck and Verdier1, Exposé Vbis, Proposition 4.3.2], the morphism
$\beta $
, etc. By [Reference Artin, Grothendieck and Verdier1, Exposé Vbis, Proposition 4.3.2], the morphism
![]() $\beta _0 \colon Y \to X$
is universally of cohomological descent, and, hence, we have
$\beta _0 \colon Y \to X$
is universally of cohomological descent, and, hence, we have
![]() $\mathcal {F}_U \cong R\beta _*\beta ^*\mathcal {F}_U$
. Using this isomorphism and the proper base change theorem, we obtain
$\mathcal {F}_U \cong R\beta _*\beta ^*\mathcal {F}_U$
. Using this isomorphism and the proper base change theorem, we obtain
The pullback of the complex
to
![]() $(Y_m)_u$
is isomorphic to
$(Y_m)_u$
is isomorphic to
![]() $R\Psi _{(f_m)_{U}, \overline {\eta }}((\mathcal {F}_m)_{U})$
for every
$R\Psi _{(f_m)_{U}, \overline {\eta }}((\mathcal {F}_m)_{U})$
for every
![]() $m \geq 0$
. Thus, we have the following spectral sequence:
$m \geq 0$
. Thus, we have the following spectral sequence:
(see [Reference Deligne8, (5.2.7.1)]). The assertion follows from this spectral sequence since our assumption implies that the sheaf
is
![]() $\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent if
$\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent if
![]() $k+l \leq \rho $
.
$k+l \leq \rho $
.
3.3 Proof of Theorem 2.8
In this subsection, we prove Theorem 2.8. Our main technique is a combination of the methods of [Reference Orgogozo25] and [Reference Orgogozo26].
In this section, we use the following terminology.
Definition 3.6. Let S be a Noetherian scheme and
![]() $f \colon X \to S$
a morphism of finite type. Let
$f \colon X \to S$
a morphism of finite type. Let
![]() $\rho $
be an integer.
$\rho $
be an integer.
-
(1) Let
 $\mathfrak {X}$
be a stratification of X. We say that an alteration
$\mathfrak {X}$
be a stratification of X. We say that an alteration
 $S' \to S$
is
$S' \to S$
is
 $\rho $
-adapted to the pair
$\rho $
-adapted to the pair
 $(f, \mathfrak {X})$
if, for every positive integer n invertible on S and every constructible sheaf
$(f, \mathfrak {X})$
if, for every positive integer n invertible on S and every constructible sheaf
 $\mathcal {F}$
of
$\mathcal {F}$
of
 ${\mathbb Z}/n{\mathbb Z}$
-modules on X which is locally unipotent along
${\mathbb Z}/n{\mathbb Z}$
-modules on X which is locally unipotent along
 $\mathfrak {X}$
, the nearby cycles for
$\mathfrak {X}$
, the nearby cycles for
 $f_{S'} \colon X_{S'} \to S'$
and
$f_{S'} \colon X_{S'} \to S'$
and
 $\mathcal {F}_{S'}$
are
$\mathcal {F}_{S'}$
are
 $\rho $
-compatible with any base change and
$\rho $
-compatible with any base change and
 $\rho $
-unipotent.
$\rho $
-unipotent. -
(2) Let
 $u \colon U \hookrightarrow X$
be an open immersion. We say that an alteration
$u \colon U \hookrightarrow X$
be an open immersion. We say that an alteration
 $S' \to S$
is
$S' \to S$
is
 $\rho $
-adapted to the pair
$\rho $
-adapted to the pair
 $(f, U)$
if, for every positive integer n invertible on S and every locally constant constructible sheaf
$(f, U)$
if, for every positive integer n invertible on S and every locally constant constructible sheaf
 $\mathcal {L}$
of
$\mathcal {L}$
of
 ${\mathbb Z}/n{\mathbb Z}$
-modules on U such that
${\mathbb Z}/n{\mathbb Z}$
-modules on U such that
 $u_!\mathcal {L}$
is locally unipotent along the stratification
$u_!\mathcal {L}$
is locally unipotent along the stratification
 $\{ U, X\backslash U \}$
, the nearby cycles for
$\{ U, X\backslash U \}$
, the nearby cycles for
 $f_{S'} \colon X_{S'} \to S'$
and
$f_{S'} \colon X_{S'} \to S'$
and
 $(u_!\mathcal {L})_{S'}$
are
$(u_!\mathcal {L})_{S'}$
are
 $\rho $
-compatible with any base change and
$\rho $
-compatible with any base change and
 $\rho $
-unipotent.
$\rho $
-unipotent.
Let S be an excellent Noetherian integral scheme. Let
![]() $\rho $
and d be two integers. We shall consider the following statement
$\rho $
and d be two integers. We shall consider the following statement
![]() $\textbf {P}(S, \rho , d)$
:
$\textbf {P}(S, \rho , d)$
:
-
 $\textbf {P}(S, \rho , d)$
: For every integral alteration
$\textbf {P}(S, \rho , d)$
: For every integral alteration
 $T \to S$
, for every proper morphism
$T \to S$
, for every proper morphism
 $f \colon Y \to T$
such that the dimension of the generic fibre of f is less than or equal to d and for any stratification
$f \colon Y \to T$
such that the dimension of the generic fibre of f is less than or equal to d and for any stratification
 $\mathfrak {Y}$
of Y, there exists an alteration
$\mathfrak {Y}$
of Y, there exists an alteration
 $T' \to T$
which is
$T' \to T$
which is
 $\rho $
-adapted to
$\rho $
-adapted to
 $(f, \mathfrak {Y})$
in the sense of Definition 3.6 (1).
$(f, \mathfrak {Y})$
in the sense of Definition 3.6 (1).
Remark 3.7.
-
(1)
 $\textbf {P}(S, -2, d)$
holds trivially for every excellent Noetherian integral scheme S and every integer d.
$\textbf {P}(S, -2, d)$
holds trivially for every excellent Noetherian integral scheme S and every integer d. -
(2) For an integral scheme T and a proper morphism
 $f \colon Y \to T$
, the condition that the dimension of the generic fibre is less than or equal to
$f \colon Y \to T$
, the condition that the dimension of the generic fibre is less than or equal to
 $-1$
means that f is not surjective. The statement
$-1$
means that f is not surjective. The statement
 $\textbf {P}(S, \rho , -1)$
is not trivial.
$\textbf {P}(S, \rho , -1)$
is not trivial.
Lemma 3.8. To prove Theorem 2.8, it is enough to show that the statement
![]() $\textbf {P}(S, \rho , d)$
holds for every triple
$\textbf {P}(S, \rho , d)$
holds for every triple
![]() $(S, \rho , d)$
.
$(S, \rho , d)$
.
Proof. The assertion can be proved by standard arguments, using the following fact proved in [Reference Orgogozo25, Proposition 3.1] (see also Remark 2.4): Let S be a Noetherian scheme and
![]() $f \colon X \to S$
a morphism of finite type. Let N be the supremum of dimensions of fibres of f. Let
$f \colon X \to S$
a morphism of finite type. Let N be the supremum of dimensions of fibres of f. Let
![]() $q \colon U \to S$
be a morphism from a strictly local scheme U and
$q \colon U \to S$
be a morphism from a strictly local scheme U and
![]() $\overline {\eta } \to U$
an algebraic geometric point. Then, for every sheaf
$\overline {\eta } \to U$
an algebraic geometric point. Then, for every sheaf
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on X, where n is a positive integer, we have
${\mathbb Z}/n{\mathbb Z}$
-modules on X, where n is a positive integer, we have
![]() $R^i\Psi _{f_U, \overline {\eta }}(\mathcal {F}_U)=0$
for
$R^i\Psi _{f_U, \overline {\eta }}(\mathcal {F}_U)=0$
for
![]() $i> 2N$
.
$i> 2N$
.
We will prove
![]() $\textbf {P}(S, \rho , d)$
by induction on the triples
$\textbf {P}(S, \rho , d)$
by induction on the triples
![]() $(S, \rho , d)$
. For two excellent Noetherian integral schemes S and
$(S, \rho , d)$
. For two excellent Noetherian integral schemes S and
![]() $S'$
, we denote
$S'$
, we denote
if
![]() $S'$
is isomorphic to a proper closed subscheme of an integral alteration of S. For an excellent Noetherian integral scheme S and an integer
$S'$
is isomorphic to a proper closed subscheme of an integral alteration of S. For an excellent Noetherian integral scheme S and an integer
![]() $\rho $
, we also consider the following statements.
$\rho $
, we also consider the following statements.
-
•
 $\textbf {P}(S, \rho , *)$
: The statement
$\textbf {P}(S, \rho , *)$
: The statement
 $\textbf {P}(S, \rho , d')$
holds for every integer
$\textbf {P}(S, \rho , d')$
holds for every integer
 $d'$
.
$d'$
. -
•
 $\textbf {P}(* \prec S, \rho , *)$
: The statement
$\textbf {P}(* \prec S, \rho , *)$
: The statement
 $\textbf {P}(S', \rho , d')$
holds for every excellent Noetherian integral scheme
$\textbf {P}(S', \rho , d')$
holds for every excellent Noetherian integral scheme
 $S'$
with
$S'$
with
 $S' \prec S$
and every integer
$S' \prec S$
and every integer
 $d'$
.
$d'$
.
We begin with the following lemma.
Lemma 3.9. Let S be an excellent Noetherian integral scheme and
![]() $\rho $
an integer. If
$\rho $
an integer. If
![]() $\textbf {P}(* \prec S, \rho , *)$
holds, then
$\textbf {P}(* \prec S, \rho , *)$
holds, then
![]() $\textbf {P}(S, \rho , -1)$
holds.
$\textbf {P}(S, \rho , -1)$
holds.
Proof. This lemma can be proved by the same arguments as in [Reference Orgogozo25, Section 4.2] by using [Reference Orgogozo26, Proposition 1.6.2] instead of [Reference Orgogozo25, Lemme 4.3].
Our next task is to show the following proposition, which is the most difficult part.
Proposition 3.10. Let
![]() $(S, \rho , d)$
be a triple of an excellent Noetherian integral scheme S and two integers
$(S, \rho , d)$
be a triple of an excellent Noetherian integral scheme S and two integers
![]() $\rho $
and d. Assume that
$\rho $
and d. Assume that
![]() $d \geq 0$
. If
$d \geq 0$
. If
![]() $\textbf {P}(S, \rho , d-1)$
,
$\textbf {P}(S, \rho , d-1)$
,
![]() $\textbf {P}(S, \rho -1, *)$
and
$\textbf {P}(S, \rho -1, *)$
and
![]() $\textbf {P}(* \prec S, \rho , *)$
hold, then
$\textbf {P}(* \prec S, \rho , *)$
hold, then
![]() $\textbf {P}(S, \rho , d)$
holds.
$\textbf {P}(S, \rho , d)$
holds.
The proof of Proposition 3.10 is divided into two steps. The first step is to reduce to the case of pluri nodal curves:
Lemma 3.11. We assume that
![]() $\textbf {P}(S, \rho , d-1)$
,
$\textbf {P}(S, \rho , d-1)$
,
![]() $\textbf {P}(S, \rho -1, *)$
and
$\textbf {P}(S, \rho -1, *)$
and
![]() $\textbf {P}(* \prec S, \rho , *)$
hold. Under this assumption, to prove
$\textbf {P}(* \prec S, \rho , *)$
hold. Under this assumption, to prove
![]() $\textbf {P}(S, \rho , d)$
, it suffices to prove the following statement
$\textbf {P}(S, \rho , d)$
, it suffices to prove the following statement
![]() $\textbf {P}_{\text {nd}}(S, \rho , d)$
:
$\textbf {P}_{\text {nd}}(S, \rho , d)$
:
-
 $\textbf {P}_{\text {nd}}(S, \rho , d)$
: For every integral alteration
$\textbf {P}_{\text {nd}}(S, \rho , d)$
: For every integral alteration
 $T \to S$
and for every pluri nodal curve
$T \to S$
and for every pluri nodal curve
 $f \colon Y \to T$
adapted to a dense open subset
$f \colon Y \to T$
adapted to a dense open subset
 $Y^{\circ } \subset Y$
such that the dimension of the generic fibre of f is less than or equal to d, there is an alteration
$Y^{\circ } \subset Y$
such that the dimension of the generic fibre of f is less than or equal to d, there is an alteration
 $T' \to T$
which is
$T' \to T$
which is
 $\rho $
-adapted to
$\rho $
-adapted to
 $(f, Y^{\circ })$
in the sense of Definition 3.6 (2).
$(f, Y^{\circ })$
in the sense of Definition 3.6 (2).
Proof. This lemma can be proved by an argument similar to that in the proof of [Reference Orgogozo26, Théorème 3.1.1] together with Theorem 3.3, Lemma 3.5, and Lemma 3.9 (see especially [Reference Orgogozo26, 3.5.2]).
Next, we prove
![]() $\textbf {P}_{\text {nd}}(S, \rho , d)$
in Lemma 3.11 under the assumptions:
$\textbf {P}_{\text {nd}}(S, \rho , d)$
in Lemma 3.11 under the assumptions:
Lemma 3.12. We assume that
![]() $\textbf {P}(S, \rho , d-1)$
,
$\textbf {P}(S, \rho , d-1)$
,
![]() $\textbf {P}(S, \rho -1, *)$
and
$\textbf {P}(S, \rho -1, *)$
and
![]() $\textbf {P}(* \prec S, \rho , *)$
hold. Then the statement
$\textbf {P}(* \prec S, \rho , *)$
hold. Then the statement
![]() $\textbf {P}_{\text {nd}}(S, \rho , d)$
in Lemma 3.11 is true.
$\textbf {P}_{\text {nd}}(S, \rho , d)$
in Lemma 3.11 is true.
Proof. Let
![]() $T \to S$
be an integral alteration and
$T \to S$
be an integral alteration and
![]() $f \colon Y \to T$
a pluri nodal curve adapted to a dense open subset
$f \colon Y \to T$
a pluri nodal curve adapted to a dense open subset
![]() $Y^{\circ } \subset Y$
such that the dimension of the generic fibre of f is less than or equal to d. Let
$Y^{\circ } \subset Y$
such that the dimension of the generic fibre of f is less than or equal to d. Let
![]() $u \colon Y^{\circ } \hookrightarrow Y$
denote the open immersion. If f is an isomorphism, then there is nothing to prove. Hence, we may assume that f is not an isomorphism, and, hence, there are a factorisation
$u \colon Y^{\circ } \hookrightarrow Y$
denote the open immersion. If f is an isomorphism, then there is nothing to prove. Hence, we may assume that f is not an isomorphism, and, hence, there are a factorisation

and a dense open subset
![]() $X^{\circ } \subset X$
such that
$X^{\circ } \subset X$
such that
![]() $h \colon Y \to X$
is a nodal curve adapted to the pair
$h \colon Y \to X$
is a nodal curve adapted to the pair
![]() $(Y^{\circ }, X^{\circ })$
and
$(Y^{\circ }, X^{\circ })$
and
![]() $g \colon X \to T$
is a pluri nodal curve adapted to
$g \colon X \to T$
is a pluri nodal curve adapted to
![]() $X^{\circ }$
. Since
$X^{\circ }$
. Since
![]() $\textbf {P}(S, \rho , d-1)$
holds, we may assume that the identity map
$\textbf {P}(S, \rho , d-1)$
holds, we may assume that the identity map
![]() $T \to T$
is
$T \to T$
is
![]() $\rho $
-adapted to the following two pairs
$\rho $
-adapted to the following two pairs
By replacing T with its normalization, we may assume that T is normal.
We claim that the identity map
![]() $T \to T$
is
$T \to T$
is
![]() $\rho $
-adapted to
$\rho $
-adapted to
![]() $(f, Y^{\circ })$
. The proof is divided into two parts. First, we prove the assertion after restricting to the smooth locus
$(f, Y^{\circ })$
. The proof is divided into two parts. First, we prove the assertion after restricting to the smooth locus
![]() $Y' \subset Y$
of h. Then, we prove our claim by using the results on the smooth locus
$Y' \subset Y$
of h. Then, we prove our claim by using the results on the smooth locus
![]() $Y'$
.
$Y'$
.
Claim 3.13. Let
![]() $a \colon Y' \to T$
denote the restriction of f to
$a \colon Y' \to T$
denote the restriction of f to
![]() $Y'$
. Let n be a positive integer invertible on T and
$Y'$
. Let n be a positive integer invertible on T and
![]() $\mathcal {L}$
a locally constant constructible sheaf of
$\mathcal {L}$
a locally constant constructible sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
![]() $Y^{\circ }$
such that
$Y^{\circ }$
such that
![]() $u_!\mathcal {L}$
is locally unipotent along the stratification
$u_!\mathcal {L}$
is locally unipotent along the stratification
![]() $\mathfrak {Y}:=\{ Y^{\circ }, Y\backslash Y^{\circ } \}$
. Let
$\mathfrak {Y}:=\{ Y^{\circ }, Y\backslash Y^{\circ } \}$
. Let
![]() $\mathcal {F}$
be the pullback of
$\mathcal {F}$
be the pullback of
![]() $u_!\mathcal {L}$
to
$u_!\mathcal {L}$
to
![]() $Y'$
. Then the following assertions hold:
$Y'$
. Then the following assertions hold:
-
(1) The nearby cycles for
 $a \colon Y' \to T$
and
$a \colon Y' \to T$
and
 $\mathcal {F}$
are
$\mathcal {F}$
are
 $\rho $
-compatible with any base change.
$\rho $
-compatible with any base change. -
(2) The nearby cycles for
 $a \colon Y' \to T$
and
$a \colon Y' \to T$
and
 $\mathcal {F}$
are
$\mathcal {F}$
are
 $\rho $
-unipotent.
$\rho $
-unipotent.
Proof. (1) We fix a local morphism
![]() $q \colon V \to U$
of strictly local schemes over T and an algebraic geometric point
$q \colon V \to U$
of strictly local schemes over T and an algebraic geometric point
![]() $\overline {\xi } \to V$
with image
$\overline {\xi } \to V$
with image
![]() $\overline {\eta } \to U$
. In the following, for a morphism
$\overline {\eta } \to U$
. In the following, for a morphism
![]() $\phi \colon Z \to T$
and a complex
$\phi \colon Z \to T$
and a complex
![]() $\mathcal {K} \in D^+(Z, {\mathbb Z}/n{\mathbb Z})$
, the cone of the base change map
$\mathcal {K} \in D^+(Z, {\mathbb Z}/n{\mathbb Z})$
, the cone of the base change map
is denoted by
![]() $\Delta (\phi , \mathcal {K})$
. For a morphism
$\Delta (\phi , \mathcal {K})$
. For a morphism
![]() $\psi \colon Z \to W$
of T-schemes and a T-scheme
$\psi \colon Z \to W$
of T-schemes and a T-scheme
![]() $T'$
, the base change
$T'$
, the base change
![]() $Z_{T'} \to W_{T'}$
is often denoted by the same letter
$Z_{T'} \to W_{T'}$
is often denoted by the same letter
![]() $\psi $
when there is no possibility of confusion.
$\psi $
when there is no possibility of confusion.
We want to show
![]() $\tau _{\leq \rho } \Delta (a, \mathcal {F})=0$
. It suffices to prove that
$\tau _{\leq \rho } \Delta (a, \mathcal {F})=0$
. It suffices to prove that
![]() $\tau _{\leq \rho } \Delta (a, \mathcal {F})_{x}=0$
at every geometric point
$\tau _{\leq \rho } \Delta (a, \mathcal {F})_{x}=0$
at every geometric point
![]() $x \to Y^{\prime }_s$
, where
$x \to Y^{\prime }_s$
, where
![]() $s \in V$
is the closed point. The morphism
$s \in V$
is the closed point. The morphism
on the stalks can be identified with the pullback map
(see also (2.1) in Remark 2.4).
In order to show
![]() $\tau _{\leq \rho } \Delta (a, \mathcal {F})_{x}=0$
, we can assume that
$\tau _{\leq \rho } \Delta (a, \mathcal {F})_{x}=0$
, we can assume that
![]() $\mathcal {L}$
is a constant sheaf on
$\mathcal {L}$
is a constant sheaf on
![]() $Y^{\circ }$
. Indeed, let
$Y^{\circ }$
. Indeed, let
![]() $\mathcal {L}'$
denote the pullback of
$\mathcal {L}'$
denote the pullback of
![]() $\mathcal {L}$
to
$\mathcal {L}$
to
![]() $(Y^{\prime }_U)_{(x)} \times _Y Y^{\circ }$
. It has a finite filtration
$(Y^{\prime }_U)_{(x)} \times _Y Y^{\circ }$
. It has a finite filtration
such that each successive quotient
![]() $\mathcal {L}^{\prime }_{i+1}/\mathcal {L}^{\prime }_i$
is a constant sheaf since
$\mathcal {L}^{\prime }_{i+1}/\mathcal {L}^{\prime }_i$
is a constant sheaf since
![]() $u_!\mathcal {L}$
is locally unipotent along
$u_!\mathcal {L}$
is locally unipotent along
![]() $\mathfrak {Y}=\{ Y^{\circ }, Y\backslash Y^{\circ } \}$
. The pullback of
$\mathfrak {Y}=\{ Y^{\circ }, Y\backslash Y^{\circ } \}$
. The pullback of
![]() $u_!\mathcal {L}$
to
$u_!\mathcal {L}$
to
![]() $(Y^{\prime }_U)_{(x)}$
is isomorphic to
$(Y^{\prime }_U)_{(x)}$
is isomorphic to
![]() $u^{\prime }_!\mathcal {L}'$
, where
$u^{\prime }_!\mathcal {L}'$
, where
![]() $u' \colon (Y^{\prime }_U)_{(x)} \times _Y Y^{\circ } \hookrightarrow (Y^{\prime }_U)_{(x)}$
denotes the open immersion. Let
$u' \colon (Y^{\prime }_U)_{(x)} \times _Y Y^{\circ } \hookrightarrow (Y^{\prime }_U)_{(x)}$
denotes the open immersion. Let
![]() $\Delta _i$
(resp.
$\Delta _i$
(resp.
![]() $\Delta _{i+1, i}$
) denote the cone of the map
$\Delta _{i+1, i}$
) denote the cone of the map
(resp.
We obtain a distinguished triangle
![]() $\Delta _i \to \Delta _{i+1} \to \Delta _{i+1, i} \to $
for each i. Thus, if we have shown
$\Delta _i \to \Delta _{i+1} \to \Delta _{i+1, i} \to $
for each i. Thus, if we have shown
![]() $\tau _{\leq \rho } \Delta _{i+1, i}=0$
for every i, then we can prove
$\tau _{\leq \rho } \Delta _{i+1, i}=0$
for every i, then we can prove
![]() $\tau _{\leq \rho } \Delta _{i}=0$
for every i inductively, which, in turn, implies
$\tau _{\leq \rho } \Delta _{i}=0$
for every i inductively, which, in turn, implies
![]() $\tau _{\leq \rho } \Delta (a, \mathcal {F})_{x}=0$
. Since
$\tau _{\leq \rho } \Delta (a, \mathcal {F})_{x}=0$
. Since
![]() $\mathcal {L}^{\prime }_{i+1}/\mathcal {L}^{\prime }_i$
is a constant sheaf (and, hence, is the pullback of a constant sheaf on
$\mathcal {L}^{\prime }_{i+1}/\mathcal {L}^{\prime }_i$
is a constant sheaf (and, hence, is the pullback of a constant sheaf on
![]() $Y^{\circ }$
), this means that it suffices to treat the case where
$Y^{\circ }$
), this means that it suffices to treat the case where
![]() $\mathcal {L}$
is a constant sheaf.
$\mathcal {L}$
is a constant sheaf.
Now we assume that
![]() $\mathcal {L}=\Lambda $
is a constant sheaf on
$\mathcal {L}=\Lambda $
is a constant sheaf on
![]() $Y^{\circ }$
. Note that
$Y^{\circ }$
. Note that
![]() $Y^{\circ }$
is contained in
$Y^{\circ }$
is contained in
![]() $Y'$
. Since we have the following exact sequence of sheaves on
$Y'$
. Since we have the following exact sequence of sheaves on
![]() $Y'$
$Y'$
where
![]() $v \colon Y' \backslash Y^{\circ } \hookrightarrow Y'$
is the closed immersion and we denote the open immersion
$v \colon Y' \backslash Y^{\circ } \hookrightarrow Y'$
is the closed immersion and we denote the open immersion
![]() $Y^{\circ } \hookrightarrow Y'$
by the same letter u, it suffices to prove that
$Y^{\circ } \hookrightarrow Y'$
by the same letter u, it suffices to prove that
![]() $\tau _{\leq \rho }\Delta (a, \Lambda )=0$
and
$\tau _{\leq \rho }\Delta (a, \Lambda )=0$
and
![]() $\tau _{\leq \rho }\Delta (a, v_*\Lambda )=0$
.
$\tau _{\leq \rho }\Delta (a, v_*\Lambda )=0$
.
It follows from the assumption on T that the nearby cycles for
![]() $a \circ v$
and the constant sheaf
$a \circ v$
and the constant sheaf
![]() $\Lambda $
are
$\Lambda $
are
![]() $\rho $
-compatible with any base change. Hence, we have
$\rho $
-compatible with any base change. Hence, we have
![]() $\tau _{\leq \rho }\Delta (a, v_*\Lambda )=0$
. By the assumption on T again, the nearby cycles for g and the constant sheaf
$\tau _{\leq \rho }\Delta (a, v_*\Lambda )=0$
. By the assumption on T again, the nearby cycles for g and the constant sheaf
![]() $\Lambda $
are
$\Lambda $
are
![]() $\rho $
-compatible with any base change. Since the composition
$\rho $
-compatible with any base change. Since the composition
![]() $b \colon Y' \hookrightarrow Y \to X$
is smooth, we have
$b \colon Y' \hookrightarrow Y \to X$
is smooth, we have
![]() $ \Delta (a, \Lambda ) \cong b^*\Delta (g, \Lambda ) $
by the smooth base change theorem. Hence, we obtain that
$ \Delta (a, \Lambda ) \cong b^*\Delta (g, \Lambda ) $
by the smooth base change theorem. Hence, we obtain that
(2) Let
![]() $q \colon U \to T$
be a morphism from a strictly local scheme U, a point
$q \colon U \to T$
be a morphism from a strictly local scheme U, a point
![]() $\eta \in U$
and an algebraic geometric point
$\eta \in U$
and an algebraic geometric point
![]() $\overline {\eta } \to U$
lying above
$\overline {\eta } \to U$
lying above
![]() $\eta $
. Let
$\eta $
. Let
![]() $s \in U$
be the closed point. We want to show that the complex
$s \in U$
be the closed point. We want to show that the complex
is
![]() $\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent.
$\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent.
We first claim that for every
![]() $i \leq \rho $
, the sheaf
$i \leq \rho $
, the sheaf
![]() $R^i\Psi _{a_{U}, \overline {\eta }}(\mathcal {F}_U)$
is constructible. Since we have already shown that the nearby cycles for a and
$R^i\Psi _{a_{U}, \overline {\eta }}(\mathcal {F}_U)$
is constructible. Since we have already shown that the nearby cycles for a and
![]() $\mathcal {F}$
are
$\mathcal {F}$
are
![]() $\rho $
-compatible with any base change, we may assume that U is the strict localization of T at
$\rho $
-compatible with any base change, we may assume that U is the strict localization of T at
![]() $s \to T$
, in particular, we may assume that U is Noetherian. Then, by using [Reference Grothendieck11, Proposition 7.1.9], we may assume that U is the spectrum of strictly Henselian discrete valuation ring, and in this case, the claim follows from [Reference Deligne9, Th. finitude, Théorème 3.2] (see also [Reference Orgogozo25, Section 8]). Now, it suffices to prove that, for every geometric point
$s \to T$
, in particular, we may assume that U is Noetherian. Then, by using [Reference Grothendieck11, Proposition 7.1.9], we may assume that U is the spectrum of strictly Henselian discrete valuation ring, and in this case, the claim follows from [Reference Deligne9, Th. finitude, Théorème 3.2] (see also [Reference Orgogozo25, Section 8]). Now, it suffices to prove that, for every geometric point
![]() $x \to Y^{\prime }_s$
, the complex
$x \to Y^{\prime }_s$
, the complex
is
![]() $\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent (see [Reference Orgogozo26, Lemme 1.2.5]). Since the sheaf
$\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent (see [Reference Orgogozo26, Lemme 1.2.5]). Since the sheaf
![]() $u_!\mathcal {L}$
is locally unipotent along
$u_!\mathcal {L}$
is locally unipotent along
![]() $\mathfrak {Y}=\{ Y^{\circ }, Y\backslash Y^{\circ } \}$
, we reduce to the case where
$\mathfrak {Y}=\{ Y^{\circ }, Y\backslash Y^{\circ } \}$
, we reduce to the case where
![]() $\mathcal {L}=\Lambda $
is a constant sheaf on
$\mathcal {L}=\Lambda $
is a constant sheaf on
![]() $Y^{\circ }$
as in the proof of (1).
$Y^{\circ }$
as in the proof of (1).
By the exact sequence
![]() $ 0 \to u_!\Lambda \to \Lambda \to v_*\Lambda \to 0, $
it suffices to prove that the nearby cycles for a and
$ 0 \to u_!\Lambda \to \Lambda \to v_*\Lambda \to 0, $
it suffices to prove that the nearby cycles for a and
![]() $v_*\Lambda $
and the nearby cycles for a and
$v_*\Lambda $
and the nearby cycles for a and
![]() $\Lambda $
are
$\Lambda $
are
![]() $\rho $
-unipotent. By using the assumption on T, we conclude by the same argument as in the proof of (1).
$\rho $
-unipotent. By using the assumption on T, we conclude by the same argument as in the proof of (1).
Claim 3.14. Let n be a positive integer invertible on T and
![]() $\mathcal {L}$
a locally constant constructible sheaf of
$\mathcal {L}$
a locally constant constructible sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
![]() $Y^{\circ }$
such that
$Y^{\circ }$
such that
![]() $\mathcal {F}:=u_!\mathcal {L}$
is locally unipotent along the stratification
$\mathcal {F}:=u_!\mathcal {L}$
is locally unipotent along the stratification
![]() $\mathfrak {Y}=\{ Y^{\circ }, Y\backslash Y^{\circ } \}$
. Then the following assertions hold:
$\mathfrak {Y}=\{ Y^{\circ }, Y\backslash Y^{\circ } \}$
. Then the following assertions hold:
-
(1) The nearby cycles for f and
 $\mathcal {F}$
are
$\mathcal {F}$
are
 $\rho $
-compatible with any base change.
$\rho $
-compatible with any base change. -
(2) The nearby cycles for f and
 $\mathcal {F}$
are
$\mathcal {F}$
are
 $\rho $
-unipotent.
$\rho $
-unipotent.
Proof. (1) We fix a local morphism
![]() $q \colon V \to U$
of strictly local schemes over T and an algebraic geometric point
$q \colon V \to U$
of strictly local schemes over T and an algebraic geometric point
![]() $\overline {\xi } \to V$
with image
$\overline {\xi } \to V$
with image
![]() $\overline {\eta } \to U$
. We retain the notation of the proof of Claim 3.13 (1). We write
$\overline {\eta } \to U$
. We retain the notation of the proof of Claim 3.13 (1). We write
![]() $\Delta :=\Delta (f, \mathcal {F})$
. We want to show
$\Delta :=\Delta (f, \mathcal {F})$
. We want to show
![]() $\tau _{\leq \rho } \Delta =0$
. Let
$\tau _{\leq \rho } \Delta =0$
. Let
![]() $c \colon Z \hookrightarrow Y$
be a closed immersion whose complement is the smooth locus
$c \colon Z \hookrightarrow Y$
be a closed immersion whose complement is the smooth locus
![]() $Y'$
of h. By Claim 3.13 (1), we have
$Y'$
of h. By Claim 3.13 (1), we have
and, hence, it suffices to show that
![]() $c^* \tau _{\leq \rho }\Delta =0$
. Since the composition
$c^* \tau _{\leq \rho }\Delta =0$
. Since the composition
![]() $d \colon Z \to Y \to X$
is a finite morphism, it is enough to prove that
$d \colon Z \to Y \to X$
is a finite morphism, it is enough to prove that
By using
![]() $\tau _{\leq \rho } \Delta \cong c_*c^* \tau _{\leq \rho }\Delta $
, we obtain an isomorphism
$\tau _{\leq \rho } \Delta \cong c_*c^* \tau _{\leq \rho }\Delta $
, we obtain an isomorphism
![]() $d_*c^* \tau _{\leq \rho }\Delta \cong \tau _{\leq \rho }Rh_*\Delta $
. By the proper base change theorem, we have
$d_*c^* \tau _{\leq \rho }\Delta \cong \tau _{\leq \rho }Rh_*\Delta $
. By the proper base change theorem, we have
![]() $Rh_*\Delta \cong \Delta (g, Rh_*\mathcal {F})$
. Note that
$Rh_*\Delta \cong \Delta (g, Rh_*\mathcal {F})$
. Note that
![]() $X^{\circ }$
is normal since T is normal. Hence, the cohomology sheaves of
$X^{\circ }$
is normal since T is normal. Hence, the cohomology sheaves of
![]() $Rh_*\mathcal {F}$
are locally unipotent along the stratification
$Rh_*\mathcal {F}$
are locally unipotent along the stratification
![]() $\{ X^{\circ }, X \backslash X^{\circ } \}$
by Proposition 3.1. By the assumption on T, we have
$\{ X^{\circ }, X \backslash X^{\circ } \}$
by Proposition 3.1. By the assumption on T, we have
![]() $ \tau _{\leq \rho }\Delta (g, R^{i}h_*\mathcal {F})=0 $
for every i. It follows that
$ \tau _{\leq \rho }\Delta (g, R^{i}h_*\mathcal {F})=0 $
for every i. It follows that
![]() $ \tau _{\leq \rho }\Delta (g, Rh_*\mathcal {F})=0. $
This completes the proof of (1).
$ \tau _{\leq \rho }\Delta (g, Rh_*\mathcal {F})=0. $
This completes the proof of (1).
(2) Let
![]() $q \colon U \to T$
be a morphism from a strictly local scheme U, a point
$q \colon U \to T$
be a morphism from a strictly local scheme U, a point
![]() $\eta \in U$
and an algebraic geometric point
$\eta \in U$
and an algebraic geometric point
![]() $\overline {\eta } \to U$
lying above
$\overline {\eta } \to U$
lying above
![]() $\eta $
. We write
$\eta $
. We write
![]() $\mathcal {K}:= R\Psi _{f_U, \overline {\eta }}(\mathcal {F}_U)$
. Let
$\mathcal {K}:= R\Psi _{f_U, \overline {\eta }}(\mathcal {F}_U)$
. Let
![]() $e \colon Y' \to Y$
denote the open immersion. We have the following distinguished triangle:
$e \colon Y' \to Y$
denote the open immersion. We have the following distinguished triangle:
By Claim 3.13 (2), it suffices to prove that
![]() $c^*\tau _{\leq \rho }\mathcal {K}$
is
$c^*\tau _{\leq \rho }\mathcal {K}$
is
![]() $\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent. Since d is a finite morphism, it suffices to prove that
$\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent. Since d is a finite morphism, it suffices to prove that
is
![]() $\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent. We have the following distinguished triangle:
$\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent. We have the following distinguished triangle:
Since the complex
![]() $Rh_*e_!e^*\tau _{\leq \rho }\mathcal {K}$
is
$Rh_*e_!e^*\tau _{\leq \rho }\mathcal {K}$
is
![]() $\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent by Claim 3.13 (2), it is enough to show that
$\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent by Claim 3.13 (2), it is enough to show that
![]() $ \tau _{\leq \rho }Rh_*\tau _{\leq \rho }\mathcal {K} \cong \tau _{\leq \rho }Rh_*\mathcal {K} $
is
$ \tau _{\leq \rho }Rh_*\tau _{\leq \rho }\mathcal {K} \cong \tau _{\leq \rho }Rh_*\mathcal {K} $
is
![]() $\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent. By the proper base change theorem, we have
$\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent. By the proper base change theorem, we have
As above, by Proposition 3.1 and the assumption on T, it follows that the complex
![]() $\tau _{\leq \rho }R\Psi _{g_{U}, \overline {\eta }}((Rh_*\mathcal {F})_U)$
is
$\tau _{\leq \rho }R\Psi _{g_{U}, \overline {\eta }}((Rh_*\mathcal {F})_U)$
is
![]() $\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent, whence, (2).
$\mathop {\mathrm {Gal}}\nolimits (\kappa (\overline {\eta })/\kappa (\eta ))$
-unipotent, whence, (2).
The proof of Lemma 3.12 is complete.
Now Proposition 3.10 follows from Lemma 3.11 and Lemma 3.12. Finally, we prove the following proposition which completes the proof Theorem 2.8.
Proposition 3.15. For every triple
![]() $(S, \rho , d)$
of an excellent Noetherian integral scheme S and two integers
$(S, \rho , d)$
of an excellent Noetherian integral scheme S and two integers
![]() $\rho $
and d, the statement
$\rho $
and d, the statement
![]() $\textbf {P}(S, \rho , d)$
holds.
$\textbf {P}(S, \rho , d)$
holds.
Proof. We assume that
![]() $\textbf {P}(S, \rho , d)$
does not hold. Then, by Lemma 3.9 and Proposition 3.10, we can find infinitely many triples
$\textbf {P}(S, \rho , d)$
does not hold. Then, by Lemma 3.9 and Proposition 3.10, we can find infinitely many triples
![]() $\{ (S_n, \rho _n, d_n) \}_{n \in {\mathbb Z}_{\geq 0}}$
with the following properties:
$\{ (S_n, \rho _n, d_n) \}_{n \in {\mathbb Z}_{\geq 0}}$
with the following properties:
-
(1)
 $\textbf {P}(S_n, \rho _n, d_n)$
does not hold for every
$\textbf {P}(S_n, \rho _n, d_n)$
does not hold for every
 $n \in {\mathbb Z}_{\geq 0}$
.
$n \in {\mathbb Z}_{\geq 0}$
. -
(2)
 $(S_0, \rho _0, d_0)=(S, \rho , d)$
.
$(S_0, \rho _0, d_0)=(S, \rho , d)$
. -
(3) For every
 $n \in {\mathbb Z}_{\geq 0}$
, we either have
$n \in {\mathbb Z}_{\geq 0}$
, we either have-
(a)
 $S_{n+1} \prec S_n$
,
$S_{n+1} \prec S_n$
, -
(b)
 $S_{n+1}=S_{n}$
,
$S_{n+1}=S_{n}$
,
 $\rho _{n+1}=\rho _n-1$
, and
$\rho _{n+1}=\rho _n-1$
, and
 $d_n \geq 0$
or
$d_n \geq 0$
or -
(c)
 $S_{n+1}=S_{n}$
,
$S_{n+1}=S_{n}$
,
 $\rho _{n+1}=\rho _n$
, and
$\rho _{n+1}=\rho _n$
, and
 $d_{n+1}=d_n-1 \geq -1$
.
$d_{n+1}=d_n-1 \geq -1$
.
-
By [Reference Orgogozo26, Lemme in 3.4.4], there is an integer
![]() $N \geq 0$
such that
$N \geq 0$
such that
![]() $S_{n+1}=S_n$
for every
$S_{n+1}=S_n$
for every
![]() $n \geq N$
. Since
$n \geq N$
. Since
![]() $\textbf {P}(S', -2, d')$
holds trivially for every excellent Noetherian integral scheme
$\textbf {P}(S', -2, d')$
holds trivially for every excellent Noetherian integral scheme
![]() $S'$
and every integer
$S'$
and every integer
![]() $d'$
, there is an integer
$d'$
, there is an integer
![]() $N' \geq N$
such that
$N' \geq N$
such that
![]() $d_{n+1}=d_n-1 \geq -1$
for every
$d_{n+1}=d_n-1 \geq -1$
for every
![]() $n \geq N'$
. This leads to a contradiction.
$n \geq N'$
. This leads to a contradiction.
4 Tubular neighbourhoods and main results
In this section, we will state our main results on étale cohomology of tubular neighbourhoods.
4.1 Adic spaces and pseudo-adic spaces
In this paper, we will freely use the theory of adic spaces and pseudo-adic spaces developed by Huber. Our basis references are [Reference Huber12, Reference Huber13, Reference Huber14]. We shall recall the definitions very roughly. We will use the terminology in [Reference Huber14, Section 1.1], such as a valuation of a ring, an affinoid ring, a Tate ring or a strongly Noetherian Tate ring.
An adic space is by definition a triple
where X is a topological space,
![]() ${\mathcal O}_X$
is a sheaf of topological rings on the topological space X and
${\mathcal O}_X$
is a sheaf of topological rings on the topological space X and
![]() $v_x$
is an equivalence class of valuations of the stalk
$v_x$
is an equivalence class of valuations of the stalk
![]() ${\mathcal O}_{X, x}$
at
${\mathcal O}_{X, x}$
at
![]() $x \in X$
which is locally isomorphic to the affinoid adic space
$x \in X$
which is locally isomorphic to the affinoid adic space
![]() $\mathop {\mathrm {Spa}}\nolimits (A, A^+)$
associated with an affinoid ring
$\mathop {\mathrm {Spa}}\nolimits (A, A^+)$
associated with an affinoid ring
![]() $(A, A^+)$
(see [Reference Huber14, Section 1.1] for details). In this paper, unless stated otherwise, we assume that every adic space is locally isomorphic to the affinoid adic space
$(A, A^+)$
(see [Reference Huber14, Section 1.1] for details). In this paper, unless stated otherwise, we assume that every adic space is locally isomorphic to the affinoid adic space
![]() $\mathop {\mathrm {Spa}}\nolimits (A, A^+)$
associated with an affinoid ring
$\mathop {\mathrm {Spa}}\nolimits (A, A^+)$
associated with an affinoid ring
![]() $(A, A^+)$
such that A is a strongly Noetherian Tate ring. So we can use the results in [Reference Huber14] (see [Reference Huber14, (1.1.1)]). In particular, we only treat analytic adic spaces (see [Reference Huber14, Section 1.1] for the definition of an analytic adic space).
$(A, A^+)$
such that A is a strongly Noetherian Tate ring. So we can use the results in [Reference Huber14] (see [Reference Huber14, (1.1.1)]). In particular, we only treat analytic adic spaces (see [Reference Huber14, Section 1.1] for the definition of an analytic adic space).
A pseudo-adic space is a pair
where X is an adic space and S is a subset of X satisfying certain conditions (see [Reference Huber14, Definition 1.10.3]). If X is an adic space and
![]() $S \subset X$
is a locally closed subset, then
$S \subset X$
is a locally closed subset, then
![]() $(X, S)$
is a pseudo-adic space. Almost all pseudo-adic spaces which appear in this paper are of this form. A morphism
$(X, S)$
is a pseudo-adic space. Almost all pseudo-adic spaces which appear in this paper are of this form. A morphism
![]() $f \colon (X, S) \to (X', S')$
of pseudo-adic spaces is by definition a morphism
$f \colon (X, S) \to (X', S')$
of pseudo-adic spaces is by definition a morphism
![]() $f \colon X \to X'$
of adic spaces with
$f \colon X \to X'$
of adic spaces with
![]() $f(S) \subset S'$
.
$f(S) \subset S'$
.
We have a functor
![]() $X \mapsto (X, X)$
from the category of adic spaces to the category of pseudo-adic spaces. We often consider an adic space as a pseudo-adic space via this functor.
$X \mapsto (X, X)$
from the category of adic spaces to the category of pseudo-adic spaces. We often consider an adic space as a pseudo-adic space via this functor.
A typical example of an adic space is the following. Let K be a non-archimedean field, that is, it is a topological field whose topology is induced by a valuation
![]() $ \vert \cdot \vert \colon K \to {\mathbb R}_{\geq 0}$
of rank
$ \vert \cdot \vert \colon K \to {\mathbb R}_{\geq 0}$
of rank
![]() $1$
. We assume that K is complete. Let
$1$
. We assume that K is complete. Let
![]() ${\mathcal O}=K^{\circ }$
be the valuation ring of
${\mathcal O}=K^{\circ }$
be the valuation ring of
![]() $\vert \cdot \vert $
. We call
$\vert \cdot \vert $
. We call
![]() ${\mathcal O}$
the ring of integers of K. Let
${\mathcal O}$
the ring of integers of K. Let
![]() $\varpi \in K^{\times }$
be an element with
$\varpi \in K^{\times }$
be an element with
![]() $\vert \varpi \vert < 1$
. Let
$\vert \varpi \vert < 1$
. Let
![]() $\mathcal {X}$
be a scheme of finite type over
$\mathcal {X}$
be a scheme of finite type over
![]() ${\mathcal O}$
. The
${\mathcal O}$
. The
![]() $\varpi $
-adic formal completion of
$\varpi $
-adic formal completion of
![]() $\mathcal {X}$
is denoted by
$\mathcal {X}$
is denoted by
![]() $\widehat {\mathcal {X}}$
or
$\widehat {\mathcal {X}}$
or
![]() $\mathcal {X}^{\wedge }$
. Following [Reference Huber14, Section 1.9], the Raynaud generic fibre of
$\mathcal {X}^{\wedge }$
. Following [Reference Huber14, Section 1.9], the Raynaud generic fibre of
![]() $\widehat {\mathcal {X}}$
is denoted by
$\widehat {\mathcal {X}}$
is denoted by
![]() $d(\widehat {\mathcal {X}})$
, which is an adic space of finite type over
$d(\widehat {\mathcal {X}})$
, which is an adic space of finite type over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. In particular,
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. In particular,
![]() $d(\widehat {\mathcal {X}})$
is quasicompact. For example, we have
$d(\widehat {\mathcal {X}})$
is quasicompact. For example, we have
We often identify
![]() $d((\mathop {\mathrm {Spec}} {\mathcal O}[T])^{\wedge })$
with
$d((\mathop {\mathrm {Spec}} {\mathcal O}[T])^{\wedge })$
with
![]() $\mathbb {B}(1)$
. For a morphism
$\mathbb {B}(1)$
. For a morphism
![]() $f \colon \mathcal {Y} \to \mathcal {X}$
of schemes of finite type over
$f \colon \mathcal {Y} \to \mathcal {X}$
of schemes of finite type over
![]() ${\mathcal O}$
, the induced morphism
${\mathcal O}$
, the induced morphism
![]() $d(\widehat {\mathcal {Y}}) \to d(\widehat {\mathcal {X}})$
is denoted by
$d(\widehat {\mathcal {Y}}) \to d(\widehat {\mathcal {X}})$
is denoted by
![]() $d(f)$
(rather than
$d(f)$
(rather than
![]() $d(\widehat {f})$
).
$d(\widehat {f})$
).
Important examples of pseudo-adic spaces for us are tubular neighbourhoods of adic spaces. In the next subsection, we will define them in the case where adic spaces arise from schemes of finite type over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
4.2 Tubular neighbourhoods
Let
![]() $X=(X, {\mathcal O}_X, \{ v_{x} \}_{x \in X})$
be an adic space. Let
$X=(X, {\mathcal O}_X, \{ v_{x} \}_{x \in X})$
be an adic space. Let
![]() $U \subset X$
be an open subset and
$U \subset X$
be an open subset and
![]() $g \in {\mathcal O}_X(U)$
an element. Following [Reference Huber14], for a point
$g \in {\mathcal O}_X(U)$
an element. Following [Reference Huber14], for a point
![]() $x \in U$
, we write
$x \in U$
, we write
![]() $\vert g(x) \vert :=v_x(g)$
(strictly speaking, we implicitly choose a valuation from the equivalence class
$\vert g(x) \vert :=v_x(g)$
(strictly speaking, we implicitly choose a valuation from the equivalence class
![]() $v_x$
).
$v_x$
).
As in the previous subsection, let K be a complete non-archimedean field with ring of integers
![]() ${\mathcal O}$
.
${\mathcal O}$
.
Proposition 4.1. Let
![]() $\mathcal {X}$
be a scheme of finite type over
$\mathcal {X}$
be a scheme of finite type over
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation. Let
$\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation. Let
![]() $\epsilon \in \vert K^{\times } \vert $
be an element.
$\epsilon \in \vert K^{\times } \vert $
be an element.
-
(1) There exist subsets
 $$\begin{align*}S(\mathcal{Z}, \epsilon) \subset d(\widehat{\mathcal{X}}) \quad \text{and} \quad T(\mathcal{Z}, \epsilon) \subset d(\widehat{\mathcal{X}}) \end{align*}$$
$$\begin{align*}S(\mathcal{Z}, \epsilon) \subset d(\widehat{\mathcal{X}}) \quad \text{and} \quad T(\mathcal{Z}, \epsilon) \subset d(\widehat{\mathcal{X}}) \end{align*}$$
satisfying the following properties; for any affine open subset
 $\mathcal {U} \subset \mathcal {X}$
and any set
$\mathcal {U} \subset \mathcal {X}$
and any set
 $\{ g_1, \dotsc , g_q \} \subset {\mathcal O}_{\mathcal {U}}(\mathcal {U})$
of elements defining the closed subscheme
$\{ g_1, \dotsc , g_q \} \subset {\mathcal O}_{\mathcal {U}}(\mathcal {U})$
of elements defining the closed subscheme
 $\mathcal {Z} \cap \mathcal {U}$
of
$\mathcal {Z} \cap \mathcal {U}$
of
 $\mathcal {U}$
, we have
$\mathcal {U}$
, we have  $$ \begin{align*} S(\mathcal{Z}, \epsilon) \cap d(\widehat{\mathcal{U}}) &= \{ x \in d(\widehat{\mathcal{U}}) \, \vert \, \vert g_i(x) \vert < \epsilon \ \text{for every } 1 \leq i \leq q \} \\ &:=\{ x \in d(\widehat{\mathcal{U}}) \, \vert \, \vert g_i(x) \vert < \vert \varpi(x) \vert \ \text{for every } 1 \leq i \leq q \} \end{align*} $$
$$ \begin{align*} S(\mathcal{Z}, \epsilon) \cap d(\widehat{\mathcal{U}}) &= \{ x \in d(\widehat{\mathcal{U}}) \, \vert \, \vert g_i(x) \vert < \epsilon \ \text{for every } 1 \leq i \leq q \} \\ &:=\{ x \in d(\widehat{\mathcal{U}}) \, \vert \, \vert g_i(x) \vert < \vert \varpi(x) \vert \ \text{for every } 1 \leq i \leq q \} \end{align*} $$
and
 $$ \begin{align*} T(\mathcal{Z}, \epsilon) \cap d(\widehat{\mathcal{U}}) &= \{ x \in d(\widehat{\mathcal{U}}) \, \vert \, \vert g_i(x) \vert \leq \epsilon \ \text{for every } 1 \leq i \leq q \} \\ &:= \{ x \in d(\widehat{\mathcal{U}}) \, \vert \, \vert g_i(x) \vert \leq \vert \varpi(x) \vert \ \text{for every } 1 \leq i \leq q \}, \end{align*} $$
$$ \begin{align*} T(\mathcal{Z}, \epsilon) \cap d(\widehat{\mathcal{U}}) &= \{ x \in d(\widehat{\mathcal{U}}) \, \vert \, \vert g_i(x) \vert \leq \epsilon \ \text{for every } 1 \leq i \leq q \} \\ &:= \{ x \in d(\widehat{\mathcal{U}}) \, \vert \, \vert g_i(x) \vert \leq \vert \varpi(x) \vert \ \text{for every } 1 \leq i \leq q \}, \end{align*} $$
where
 $\varpi \in K^{\times }$
is an element with
$\varpi \in K^{\times }$
is an element with
 $\epsilon = \vert \varpi \vert $
and the element of
$\epsilon = \vert \varpi \vert $
and the element of
 ${\mathcal O}_{d(\widehat {\mathcal {U}})}(d(\widehat {\mathcal {U}}))$
arising from
${\mathcal O}_{d(\widehat {\mathcal {U}})}(d(\widehat {\mathcal {U}}))$
arising from
 $g_i$
is denoted by the same letter. Moreover, they are characterised by the above properties.
$g_i$
is denoted by the same letter. Moreover, they are characterised by the above properties. -
(2) The subset
 $T(\mathcal {Z}, \epsilon )$
is a quasicompact open subset of
$T(\mathcal {Z}, \epsilon )$
is a quasicompact open subset of
 $d(\widehat {\mathcal {X}})$
. The subset
$d(\widehat {\mathcal {X}})$
. The subset
 $S(\mathcal {Z}, \epsilon )$
is closed and constructible in
$S(\mathcal {Z}, \epsilon )$
is closed and constructible in
 $d(\widehat {\mathcal {X}})$
(see [Reference Huber14, (1.1.13)] for the definition of a constructible subset).
$d(\widehat {\mathcal {X}})$
(see [Reference Huber14, (1.1.13)] for the definition of a constructible subset). -
(3) For a morphism
 $f \colon \mathcal {Y} \to \mathcal {X}$
of finite type, we have
$f \colon \mathcal {Y} \to \mathcal {X}$
of finite type, we have  $$\begin{align*}S(\mathcal{Z} \times_{\mathcal{X}} \mathcal{Y} , \epsilon)= d(f)^{-1}(S(\mathcal{Z}, \epsilon)) \quad \text{and} \quad T(\mathcal{Z} \times_{\mathcal{X}} \mathcal{Y} , \epsilon)= d(f)^{-1}(T(\mathcal{Z}, \epsilon)). \end{align*}$$
$$\begin{align*}S(\mathcal{Z} \times_{\mathcal{X}} \mathcal{Y} , \epsilon)= d(f)^{-1}(S(\mathcal{Z}, \epsilon)) \quad \text{and} \quad T(\mathcal{Z} \times_{\mathcal{X}} \mathcal{Y} , \epsilon)= d(f)^{-1}(T(\mathcal{Z}, \epsilon)). \end{align*}$$
Proof. (1) Let
![]() $\varpi \in K^{\times }$
be an element with
$\varpi \in K^{\times }$
be an element with
![]() $\epsilon = \vert \varpi \vert $
. Let
$\epsilon = \vert \varpi \vert $
. Let
![]() $\mathcal {U} \subset \mathcal {X}$
be an affine open subset. It suffices to show that the subsets
$\mathcal {U} \subset \mathcal {X}$
be an affine open subset. It suffices to show that the subsets
and
are independent of the choice of a set
![]() $\{ g_1, \dotsc , g_q \} \subset {\mathcal O}_{\mathcal {U}}(\mathcal {U})$
of elements defining the closed subscheme
$\{ g_1, \dotsc , g_q \} \subset {\mathcal O}_{\mathcal {U}}(\mathcal {U})$
of elements defining the closed subscheme
![]() $\mathcal {Z} \cap \mathcal {U}$
of
$\mathcal {Z} \cap \mathcal {U}$
of
![]() $\mathcal {U}$
. Let
$\mathcal {U}$
. Let
![]() $\{ h_1, \dotsc , h_r\} \subset {\mathcal O}_{\mathcal {U}}(\mathcal {U})$
be another set of such elements. Then, for every i, we have
$\{ h_1, \dotsc , h_r\} \subset {\mathcal O}_{\mathcal {U}}(\mathcal {U})$
be another set of such elements. Then, for every i, we have
for some elements
![]() $\{ s_{ij} \} \subset {\mathcal O}_{\mathcal {U}}(\mathcal {U})$
. Since we have
$\{ s_{ij} \} \subset {\mathcal O}_{\mathcal {U}}(\mathcal {U})$
. Since we have
![]() $\vert s_{ij}(x) \vert \leq 1$
for every
$\vert s_{ij}(x) \vert \leq 1$
for every
![]() $x \in d(\widehat {\mathcal {U}})$
and every
$x \in d(\widehat {\mathcal {U}})$
and every
![]() $s_{ij}$
, the assertion follows.
$s_{ij}$
, the assertion follows.
(2) We may assume that
![]() $\mathcal {X}$
is affine. The subset
$\mathcal {X}$
is affine. The subset
![]() $T(\mathcal {Z}, \epsilon )$
is a rational subset of the affinoid adic space
$T(\mathcal {Z}, \epsilon )$
is a rational subset of the affinoid adic space
![]() $d(\widehat {\mathcal {X}})$
, and, hence, it is open and quasicompact. The subset
$d(\widehat {\mathcal {X}})$
, and, hence, it is open and quasicompact. The subset
![]() $S(\mathcal {Z}, \epsilon )$
is the complement of the union of finitely many rational subsets. It follows that
$S(\mathcal {Z}, \epsilon )$
is the complement of the union of finitely many rational subsets. It follows that
![]() $S(\mathcal {Z}, \epsilon )$
is closed and constructible.
$S(\mathcal {Z}, \epsilon )$
is closed and constructible.
(3) We may assume that
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
are affine. Then the assertion follows from the descriptions given in (1).
$\mathcal {Y}$
are affine. Then the assertion follows from the descriptions given in (1).
The subsets
![]() $T(\mathcal {Z}, \epsilon )$
and
$T(\mathcal {Z}, \epsilon )$
and
![]() $S(\mathcal {Z}, \epsilon )$
in Proposition 4.1 are called an open tubular neighbourhood and a closed tubular neighbourhood of
$S(\mathcal {Z}, \epsilon )$
in Proposition 4.1 are called an open tubular neighbourhood and a closed tubular neighbourhood of
![]() $d(\widehat {\mathcal {Z}})$
in
$d(\widehat {\mathcal {Z}})$
in
![]() $d(\widehat {\mathcal {X}})$
, respectively. For an element
$d(\widehat {\mathcal {X}})$
, respectively. For an element
![]() $\epsilon \in \vert K^{\times } \vert $
, we also consider the following subsets:
$\epsilon \in \vert K^{\times } \vert $
, we also consider the following subsets:
This is a quasicompact open subset of
![]() $d(\widehat {\mathcal {X}})$
.
$d(\widehat {\mathcal {X}})$
.
For a locally closed subset S of an adic space X, the pseudo-adic space
![]() $(X, S)$
is often denoted by S for simplicity. For example, the pseudo-adic spaces
$(X, S)$
is often denoted by S for simplicity. For example, the pseudo-adic spaces
![]() $(d(\widehat {\mathcal {X}}), S(\mathcal {Z}, \epsilon ))$
and
$(d(\widehat {\mathcal {X}}), S(\mathcal {Z}, \epsilon ))$
and
![]() $(d(\widehat {\mathcal {X}}), T(\mathcal {Z}, \epsilon ))$
are denoted by
$(d(\widehat {\mathcal {X}}), T(\mathcal {Z}, \epsilon ))$
are denoted by
![]() $S(\mathcal {Z}, \epsilon )$
and
$S(\mathcal {Z}, \epsilon )$
and
![]() $T(\mathcal {Z}, \epsilon )$
, respectively.
$T(\mathcal {Z}, \epsilon )$
, respectively.
Remark 4.2. For a formal scheme
![]() $\mathscr {X}$
of finite type over
$\mathscr {X}$
of finite type over
![]() $\mathop {\mathrm {Spf}} {\mathcal O}$
and a closed immersion
$\mathop {\mathrm {Spf}} {\mathcal O}$
and a closed immersion
![]() $\mathscr {Z} \hookrightarrow \mathscr {X}$
of finite presentation (in the sense of [Reference Fujiwara and Kato10, Chapter I, Definition 2.2.1]), we can also define tubular neighbourhoods of
$\mathscr {Z} \hookrightarrow \mathscr {X}$
of finite presentation (in the sense of [Reference Fujiwara and Kato10, Chapter I, Definition 2.2.1]), we can also define tubular neighbourhoods of
![]() $d(\mathscr {Z})$
in
$d(\mathscr {Z})$
in
![]() $d(\mathscr {X})$
in the same way. However, we will always work with algebraizable formal schemes of finite type over
$d(\mathscr {X})$
in the same way. However, we will always work with algebraizable formal schemes of finite type over
![]() ${\mathcal O}$
in this paper.
${\mathcal O}$
in this paper.
We end this subsection with the following lemma.
Lemma 4.3. Let
![]() $\mathcal {X}$
be a scheme of finite type over
$\mathcal {X}$
be a scheme of finite type over
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation. For a constructible subset
$\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation. For a constructible subset
![]() $W \subset d(\widehat {\mathcal {X}})$
containing
$W \subset d(\widehat {\mathcal {X}})$
containing
![]() $d(\widehat {\mathcal {Z}})$
, there is an element
$d(\widehat {\mathcal {Z}})$
, there is an element
![]() $\epsilon \in \vert K^{\times } \vert $
such that
$\epsilon \in \vert K^{\times } \vert $
such that
![]() $T(\mathcal {Z}, \epsilon ) \subset W$
.
$T(\mathcal {Z}, \epsilon ) \subset W$
.
Proof. We may assume that
![]() $\mathcal {X}$
is affine. Then the underlying topological space of
$\mathcal {X}$
is affine. Then the underlying topological space of
![]() $d(\widehat {\mathcal {X}})$
is a spectral space. We have
$d(\widehat {\mathcal {X}})$
is a spectral space. We have
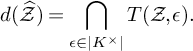 $$\begin{align*}d(\widehat{\mathcal{Z}})=\bigcap_{\epsilon \in \vert K^{\times} \vert} T(\mathcal{Z}, \epsilon). \end{align*}$$
$$\begin{align*}d(\widehat{\mathcal{Z}})=\bigcap_{\epsilon \in \vert K^{\times} \vert} T(\mathcal{Z}, \epsilon). \end{align*}$$
Hence, the intersection
 $$\begin{align*}\bigcap_{\epsilon \in \vert K^{\times} \vert} T(\mathcal{Z}, \epsilon) \cap (d(\widehat{\mathcal{X}}) \backslash W) \end{align*}$$
$$\begin{align*}\bigcap_{\epsilon \in \vert K^{\times} \vert} T(\mathcal{Z}, \epsilon) \cap (d(\widehat{\mathcal{X}}) \backslash W) \end{align*}$$
is empty. In the constructible topology, the subsets
![]() $T(\mathcal {Z}, \epsilon )$
and
$T(\mathcal {Z}, \epsilon )$
and
![]() $d(\widehat {\mathcal {X}}) \backslash W$
are closed and
$d(\widehat {\mathcal {X}}) \backslash W$
are closed and
![]() $d(\widehat {\mathcal {X}})$
is quasicompact. It follows that there is an element
$d(\widehat {\mathcal {X}})$
is quasicompact. It follows that there is an element
![]() $\epsilon \in \vert K^{\times } \vert $
such that the intersection
$\epsilon \in \vert K^{\times } \vert $
such that the intersection
![]() $T(\mathcal {Z}, \epsilon ) \cap d(\widehat {\mathcal {X}}) \backslash W$
is empty, whence
$T(\mathcal {Z}, \epsilon ) \cap d(\widehat {\mathcal {X}}) \backslash W$
is empty, whence
![]() $T(\mathcal {Z}, \epsilon ) \subset W$
.
$T(\mathcal {Z}, \epsilon ) \subset W$
.
4.3 Main results on tubular neighbourhoods
In this subsection, let K be an algebraically closed complete non-archimedean field with ring of integers
![]() ${\mathcal O}$
.
${\mathcal O}$
.
To state our main results on tubular neighbourhoods, we need étale cohomology and étale cohomology with proper support of pseudo-adic spaces (see [Reference Huber14, Section 2.3] for definition of the étale site of a pseudo-adic space). As shown in [Reference Huber14, Proposition 2.3.7], for an adic space X and an open subset
![]() $U \subset X$
, the étale topos of the adic space U is naturally equivalent to the étale topos of the pseudo-adic space
$U \subset X$
, the étale topos of the adic space U is naturally equivalent to the étale topos of the pseudo-adic space
![]() $(X, U)$
. For a commutative ring
$(X, U)$
. For a commutative ring
![]() $\Lambda $
, let
$\Lambda $
, let
![]() $D^+(X, \Lambda )$
denote the derived category of bounded below complexes of étale sheaves of
$D^+(X, \Lambda )$
denote the derived category of bounded below complexes of étale sheaves of
![]() $\Lambda $
-modules on a pseudo-adic space X.
$\Lambda $
-modules on a pseudo-adic space X.
Let
![]() $f \colon X \to Y$
be a morphism of analytic pseudo-adic spaces. We assume that f is separated, locally of finite type and taut (see [Reference Huber14, Definition 5.1.2] for the definitions of a taut pseudo-adic space and a taut morphism of pseudo-adic spaces; for example, if f is separated and quasicompact, then f is taut). For such a morphism f, the direct image functor with proper support
$f \colon X \to Y$
be a morphism of analytic pseudo-adic spaces. We assume that f is separated, locally of finite type and taut (see [Reference Huber14, Definition 5.1.2] for the definitions of a taut pseudo-adic space and a taut morphism of pseudo-adic spaces; for example, if f is separated and quasicompact, then f is taut). For such a morphism f, the direct image functor with proper support
is defined in [Reference Huber14, Definition 5.4.4], where
![]() $\Lambda $
is a torsion commutative ring. Moreover, if
$\Lambda $
is a torsion commutative ring. Moreover, if
![]() $Y=\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
, we obtain for a complex
$Y=\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
, we obtain for a complex
![]() $\mathcal {K} \in D^+(X, \Lambda )$
the cohomology group with proper support
$\mathcal {K} \in D^+(X, \Lambda )$
the cohomology group with proper support
Example 4.4. Let
![]() $\mathcal {X}$
be a separated scheme of finite type over
$\mathcal {X}$
be a separated scheme of finite type over
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation.
$\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation.
-
(1) The adic spaces
 $d(\widehat {\mathcal {Z}})$
and
$d(\widehat {\mathcal {Z}})$
and
 $d(\widehat {\mathcal {X}})$
are separated and of finite type over
$d(\widehat {\mathcal {X}})$
are separated and of finite type over
 $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. The morphism
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. The morphism
 $d(\widehat {\mathcal {X}}) \backslash d(\widehat {\mathcal {Z}}) \to \mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
is separated, locally of finite type and taut (see [Reference Huber14, Lemma 5.1.4]).
$d(\widehat {\mathcal {X}}) \backslash d(\widehat {\mathcal {Z}}) \to \mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
is separated, locally of finite type and taut (see [Reference Huber14, Lemma 5.1.4]). -
(2) The pseudo-adic spaces
 $S(\mathcal {Z}, \epsilon )$
,
$S(\mathcal {Z}, \epsilon )$
,
 $T(\mathcal {Z}, \epsilon )$
and
$T(\mathcal {Z}, \epsilon )$
and
 $Q(\mathcal {Z}, \epsilon )$
are separated and of finite type (and, hence, taut) over
$Q(\mathcal {Z}, \epsilon )$
are separated and of finite type (and, hence, taut) over
 $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
.
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. -
(3) For a subset S of an analytic adic space X, the interior of S in X is denoted by
 $S^{\circ }$
. The morphism
$S^{\circ }$
. The morphism
 $S(\mathcal {Z}, \epsilon )^{\circ } \to \mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
is separated, locally of finite type and taut [Reference Huber15, Lemma 1.3 iii)].
$S(\mathcal {Z}, \epsilon )^{\circ } \to \mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
is separated, locally of finite type and taut [Reference Huber15, Lemma 1.3 iii)].
Let us recall the following results due to Huber in our setting.
Theorem 4.5 (Huber [Reference Huber15, Theorem 2.5], [Reference Huber16, Theorem 3.6])
We assume that K is of characteristic zero. Let
![]() $\mathcal {X}$
be a separated scheme of finite type over
$\mathcal {X}$
be a separated scheme of finite type over
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation. Let n be a positive integer invertible in
$\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation. Let n be a positive integer invertible in
![]() ${\mathcal O}$
, and let
${\mathcal O}$
, and let
![]() $\mathcal {F}$
be a constructible étale sheaf of
$\mathcal {F}$
be a constructible étale sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
![]() $d(\widehat {\mathcal {X}})$
in the sense of [Reference Huber14, Definition 2.7.2].
$d(\widehat {\mathcal {X}})$
in the sense of [Reference Huber14, Definition 2.7.2].
-
(1) There exists an element
 $\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
$\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
 $\epsilon \in \vert K^{\times } \vert $
with
$\epsilon \in \vert K^{\times } \vert $
with
 $\epsilon \leq \epsilon _0$
, the following natural maps are isomorphisms for every i:
$\epsilon \leq \epsilon _0$
, the following natural maps are isomorphisms for every i:-
(a)
 $H^i_c(S(\mathcal {Z}, \epsilon ), \mathcal {F}\vert _{S(\mathcal {Z}, \epsilon )}) \overset {\cong }{\to } H^i_c(d(\widehat {\mathcal {Z}}), \mathcal {F}\vert _{d(\widehat {\mathcal {Z}})})$
.
$H^i_c(S(\mathcal {Z}, \epsilon ), \mathcal {F}\vert _{S(\mathcal {Z}, \epsilon )}) \overset {\cong }{\to } H^i_c(d(\widehat {\mathcal {Z}}), \mathcal {F}\vert _{d(\widehat {\mathcal {Z}})})$
. -
(b)
 $H^i_c(T(\mathcal {Z}, \epsilon ), \mathcal {F}) \overset {\cong }{\to } H^i_c(T(\mathcal {Z}, \epsilon _0), \mathcal {F})$
.
$H^i_c(T(\mathcal {Z}, \epsilon ), \mathcal {F}) \overset {\cong }{\to } H^i_c(T(\mathcal {Z}, \epsilon _0), \mathcal {F})$
. -
(c)
 $H^i_c(Q(\mathcal {Z}, \epsilon ), \mathcal {F}) \overset {\cong }{\to } H^i_c(d(\widehat {\mathcal {X}})\backslash d(\widehat {\mathcal {Z}}), \mathcal {F})$
.
$H^i_c(Q(\mathcal {Z}, \epsilon ), \mathcal {F}) \overset {\cong }{\to } H^i_c(d(\widehat {\mathcal {X}})\backslash d(\widehat {\mathcal {Z}}), \mathcal {F})$
.
-
-
(2) We assume further that
 $\mathcal {F}$
is locally constant. Then there exists an element
$\mathcal {F}$
is locally constant. Then there exists an element
 $\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
$\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
 $\epsilon \in \vert K^{\times } \vert $
with
$\epsilon \in \vert K^{\times } \vert $
with
 $\epsilon \leq \epsilon _0$
, the restriction maps on étale cohomology groups are isomorphisms for every i.
$\epsilon \leq \epsilon _0$
, the restriction maps on étale cohomology groups are isomorphisms for every i. $$\begin{align*}\begin{aligned} H^i(T(\mathcal{Z}, \epsilon), \mathcal{F}) &\overset{\cong}{\to} H^i(S(\mathcal{Z}, \epsilon), \mathcal{F}\vert_{S(\mathcal{Z}, \epsilon)}) \\ &\overset{\cong}{\to} H^i(S(\mathcal{Z}, \epsilon)^{\circ}, \mathcal{F}) \overset{\cong}{\to} H^i(d(\widehat{\mathcal{Z}}), \mathcal{F}\vert_{d(\widehat{\mathcal{Z}})}) \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} H^i(T(\mathcal{Z}, \epsilon), \mathcal{F}) &\overset{\cong}{\to} H^i(S(\mathcal{Z}, \epsilon), \mathcal{F}\vert_{S(\mathcal{Z}, \epsilon)}) \\ &\overset{\cong}{\to} H^i(S(\mathcal{Z}, \epsilon)^{\circ}, \mathcal{F}) \overset{\cong}{\to} H^i(d(\widehat{\mathcal{Z}}), \mathcal{F}\vert_{d(\widehat{\mathcal{Z}})}) \end{aligned} \end{align*}$$
Proof. See [Reference Huber15, Theorem 2.5] for the proof of (1) and a more general result; see [Reference Huber14, Remark 5.5.11] for the constructions of the natural maps. See [Reference Huber13, Theorem 3.6] for the proof (2) and a more general result.
Remark 4.6. For an algebraically closed complete non-archimedean field K of positive characteristic, an analogous statement to Theorem 4.5 (1) is proved in [Reference Huber18, Corollary 5.8].
Remark 4.7. If the residue field of
![]() ${\mathcal O}$
is of positive characteristic
${\mathcal O}$
is of positive characteristic
![]() $p>0$
, the assumption that n is invertible in
$p>0$
, the assumption that n is invertible in
![]() ${\mathcal O}$
in Theorem 4.5 is essential. For example, the étale cohomology group
${\mathcal O}$
in Theorem 4.5 is essential. For example, the étale cohomology group
![]() $H^1(\mathbb {B}(1), {\mathbb Z}/p{\mathbb Z})$
is an infinite dimensional
$H^1(\mathbb {B}(1), {\mathbb Z}/p{\mathbb Z})$
is an infinite dimensional
![]() ${\mathbb Z}/p{\mathbb Z}$
-vector space (see the computations in [Reference Berkovich2, Remark 6.4.2]). However, we have
${\mathbb Z}/p{\mathbb Z}$
-vector space (see the computations in [Reference Berkovich2, Remark 6.4.2]). However, we have
![]() $H^1(\{ 0 \}, {\mathbb Z}/p{\mathbb Z})=0$
for the origin
$H^1(\{ 0 \}, {\mathbb Z}/p{\mathbb Z})=0$
for the origin
![]() $0 \in \mathbb {B}(1)$
.
$0 \in \mathbb {B}(1)$
.
The main objective of this paper is to prove uniform variants of Theorem 4.5 for constant sheaves. Our main result on étale cohomology groups with proper support of tubular neighbourhoods is as follows.
Theorem 4.8. Let K be an algebraically closed complete non-archimedean field with ring of integers
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $\mathcal {X}$
be a separated scheme of finite type over
$\mathcal {X}$
be a separated scheme of finite type over
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation. Then there exists an element
$\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation. Then there exists an element
![]() $\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
$\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
![]() $\epsilon \in \vert K^{\times } \vert $
with
$\epsilon \in \vert K^{\times } \vert $
with
![]() $\epsilon \leq \epsilon _0$
and for every positive integer n invertible in
$\epsilon \leq \epsilon _0$
and for every positive integer n invertible in
![]() ${\mathcal O}$
, the following natural maps are isomorphisms for every i:
${\mathcal O}$
, the following natural maps are isomorphisms for every i:
-
(1)
 $H^i_c(S(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z}) \overset {\cong }{\to } H^i_c(d(\widehat {\mathcal {Z}}), {\mathbb Z}/n{\mathbb Z})$
.
$H^i_c(S(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z}) \overset {\cong }{\to } H^i_c(d(\widehat {\mathcal {Z}}), {\mathbb Z}/n{\mathbb Z})$
. -
(2)
 $H^i_c(T(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z}) \overset {\cong }{\to } H^i_c(T(\mathcal {Z}, \epsilon _0), {\mathbb Z}/n{\mathbb Z})$
.
$H^i_c(T(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z}) \overset {\cong }{\to } H^i_c(T(\mathcal {Z}, \epsilon _0), {\mathbb Z}/n{\mathbb Z})$
. -
(3)
 $H^i_c(Q(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z}) \overset {\cong }{\to } H^i_c(d(\widehat {\mathcal {X}})\backslash d(\widehat {\mathcal {Z}}), {\mathbb Z}/n{\mathbb Z})$
.
$H^i_c(Q(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z}) \overset {\cong }{\to } H^i_c(d(\widehat {\mathcal {X}})\backslash d(\widehat {\mathcal {Z}}), {\mathbb Z}/n{\mathbb Z})$
.
Our main result on étale cohomology groups of tubular neighbourhoods is as follows.
Theorem 4.9. Let K be an algebraically closed complete non-archimedean field with ring of integers
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $\mathcal {X}$
be a separated scheme of finite type over
$\mathcal {X}$
be a separated scheme of finite type over
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation. Then there exists an element
$\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation. Then there exists an element
![]() $\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
$\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
![]() $\epsilon \in \vert K^{\times } \vert $
with
$\epsilon \in \vert K^{\times } \vert $
with
![]() $\epsilon \leq \epsilon _0$
and for every positive integer n invertible in
$\epsilon \leq \epsilon _0$
and for every positive integer n invertible in
![]() ${\mathcal O}$
, the restriction maps
${\mathcal O}$
, the restriction maps
are isomorphisms for every i.
Theorem 1.2 follows from Theorem 4.9 (see also the following remark).
Remark 4.10. In Theorem 4.8 and Theorem 4.9, the assumption that the closed immersion
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
is of finite presentation is not important in practice. Indeed, if we are only interested in the adic spaces
$\mathcal {Z} \hookrightarrow \mathcal {X}$
is of finite presentation is not important in practice. Indeed, if we are only interested in the adic spaces
![]() $d(\widehat {\mathcal {Z}})$
and
$d(\widehat {\mathcal {Z}})$
and
![]() $d(\widehat {\mathcal {X}})$
, then by replacing
$d(\widehat {\mathcal {X}})$
, then by replacing
![]() $\mathcal {Z}$
with the closed subscheme
$\mathcal {Z}$
with the closed subscheme
![]() $\mathcal {Z}' \hookrightarrow \mathcal {Z}$
defined by the sections killed by a power of a nonzero element of the maximal ideal of
$\mathcal {Z}' \hookrightarrow \mathcal {Z}$
defined by the sections killed by a power of a nonzero element of the maximal ideal of
![]() ${\mathcal O}$
, we can reduce to the case where
${\mathcal O}$
, we can reduce to the case where
![]() $\mathcal {Z}$
is flat over
$\mathcal {Z}$
is flat over
![]() ${\mathcal O}$
without changing
${\mathcal O}$
without changing
![]() $d(\widehat {\mathcal {Z}})$
. Then
$d(\widehat {\mathcal {Z}})$
. Then
![]() $\mathcal {Z}$
is of finite presentation over
$\mathcal {Z}$
is of finite presentation over
![]() ${\mathcal O}$
by [Reference Raynaud and Gruson28, Première partie, Corollaire 3.4.7], and, hence,
${\mathcal O}$
by [Reference Raynaud and Gruson28, Première partie, Corollaire 3.4.7], and, hence,
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
is also of finite presentation.
$\mathcal {Z} \hookrightarrow \mathcal {X}$
is also of finite presentation.
The proofs of Theorem 4.8 and Theorem 4.9 will be given in Section 7. In the rest of this section, we will restate Theorem 4.9 for proper schemes over K.
Let
![]() $L \subset K$
be a subfield of K which is a complete non-archimedean field with the induced topology. Let
$L \subset K$
be a subfield of K which is a complete non-archimedean field with the induced topology. Let
![]() ${\mathcal O}_L$
be the ring of integers of L. For a scheme X of finite type over L, the adic space associated with X is denoted by
${\mathcal O}_L$
be the ring of integers of L. For a scheme X of finite type over L, the adic space associated with X is denoted by
(see [Reference Huber13, Proposition 3.8]). For an adic space Y locally of finite type over
![]() $\mathop {\mathrm {Spa}}\nolimits (L, {\mathcal O}_L)$
, we denote by
$\mathop {\mathrm {Spa}}\nolimits (L, {\mathcal O}_L)$
, we denote by
the base change of Y to
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
, which exists by [Reference Huber14, Proposition 1.2.2].
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
, which exists by [Reference Huber14, Proposition 1.2.2].
Corollary 4.11. Let X be a proper scheme over L and
![]() $Z \hookrightarrow X$
a closed immersion. We have a closed immersion
$Z \hookrightarrow X$
a closed immersion. We have a closed immersion
![]() $Z^{\mathrm {ad}} \hookrightarrow X^{\mathrm {ad}}$
of adic spaces over
$Z^{\mathrm {ad}} \hookrightarrow X^{\mathrm {ad}}$
of adic spaces over
![]() $\mathop {\mathrm {Spa}}\nolimits (L, {\mathcal O}_L)$
. Then, there is a quasicompact open subset V of
$\mathop {\mathrm {Spa}}\nolimits (L, {\mathcal O}_L)$
. Then, there is a quasicompact open subset V of
![]() $X^{\mathrm {ad}}$
containing
$X^{\mathrm {ad}}$
containing
![]() $Z^{\mathrm {ad}}$
such that, for every positive integer n invertible in
$Z^{\mathrm {ad}}$
such that, for every positive integer n invertible in
![]() ${\mathcal O}$
, the restriction map
${\mathcal O}$
, the restriction map
is an isomorphism for every i.
Proof. There exist a proper scheme
![]() $\mathcal {X}$
over
$\mathcal {X}$
over
![]() $\mathop {\mathrm {Spec}} {\mathcal O}_L$
and a closed immersion
$\mathop {\mathrm {Spec}} {\mathcal O}_L$
and a closed immersion
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
such that the base change of it to
$\mathcal {Z} \hookrightarrow \mathcal {X}$
such that the base change of it to
![]() $\mathop {\mathrm {Spec}} L$
is isomorphic to the closed immersion
$\mathop {\mathrm {Spec}} L$
is isomorphic to the closed immersion
![]() $Z \hookrightarrow X$
by Nagata’s compactification theorem (see [Reference Fujiwara and Kato10, Chapter II, Theorem F.1.1] for example). As in Remark 4.10, we may assume that
$Z \hookrightarrow X$
by Nagata’s compactification theorem (see [Reference Fujiwara and Kato10, Chapter II, Theorem F.1.1] for example). As in Remark 4.10, we may assume that
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
is of finite presentation. Let
$\mathcal {Z} \hookrightarrow \mathcal {X}$
is of finite presentation. Let
denote the fibre products. We have
![]() $ d(\widehat {\overline {\mathcal {Z}}}) \cong d(\widehat {\mathcal {Z}})_K $
and
$ d(\widehat {\overline {\mathcal {Z}}}) \cong d(\widehat {\mathcal {Z}})_K $
and
![]() $ d(\widehat {\overline {\mathcal {X}}}) \cong d(\widehat {\mathcal {X}})_K. $
For an element
$ d(\widehat {\overline {\mathcal {X}}}) \cong d(\widehat {\mathcal {X}})_K. $
For an element
![]() $\epsilon \in \vert L^{\times } \vert $
, we have
$\epsilon \in \vert L^{\times } \vert $
, we have
![]() $T(\mathcal {Z}, \epsilon )_K=T(\overline {\mathcal {Z}}, \epsilon )$
in
$T(\mathcal {Z}, \epsilon )_K=T(\overline {\mathcal {Z}}, \epsilon )$
in
![]() $d(\widehat {\overline {\mathcal {X}}})$
. By [Reference Huber14, Proposition 1.9.6], we have
$d(\widehat {\overline {\mathcal {X}}})$
. By [Reference Huber14, Proposition 1.9.6], we have
![]() $d(\widehat {\mathcal {Z}}) = Z^{\mathrm {ad}}$
and
$d(\widehat {\mathcal {Z}}) = Z^{\mathrm {ad}}$
and
![]() $d(\widehat {\mathcal {X}}) = X^{\mathrm {ad}}$
. Therefore, the assertion follows from Theorem 4.9.
$d(\widehat {\mathcal {X}}) = X^{\mathrm {ad}}$
. Therefore, the assertion follows from Theorem 4.9.
5 Étale cohomology with proper support of adic spaces and nearby cycles
In this section, we study the relation between the compatibility of the sliced nearby cycles functors with base change and the bijectivity of specialization maps on stalks of higher direct image sheaves with proper support for adic spaces by using a comparison theorem of Huber [Reference Huber14, Theorem 5.7.8].
5.1 Analytic adic spaces associated with formal schemes
In this subsection, we recall the functor
![]() $d(-)$
from a certain category of formal schemes to the category of analytic adic spaces defined in [Reference Huber14, Section 1.9].
$d(-)$
from a certain category of formal schemes to the category of analytic adic spaces defined in [Reference Huber14, Section 1.9].
Following [Reference Huber14], for a commutative ring A and an element
![]() $s \in A$
, let
$s \in A$
, let
denote the localization
![]() $A[1/s]$
equipped with the structure of a Tate ring such that the image
$A[1/s]$
equipped with the structure of a Tate ring such that the image
![]() $A_0$
of the map
$A_0$
of the map
![]() $A \to A[1/s]$
is a ring of definition and
$A \to A[1/s]$
is a ring of definition and
![]() $s A_0$
is an ideal of definition.
$s A_0$
is an ideal of definition.
We record the following well known results.
Lemma 5.1. Let A be a commutative ring endowed with the
![]() $\varpi $
-adic topology for an element
$\varpi $
-adic topology for an element
![]() $\varpi \in A$
satisfying the following two properties:
$\varpi \in A$
satisfying the following two properties:
-
(i) A is
 $\varpi $
-adically complete, that is, the following natural map is an isomorphism:
$\varpi $
-adically complete, that is, the following natural map is an isomorphism:  $$\begin{align*}A \to \widehat{A}:={\mathop{\varprojlim}\limits_{n}} A/\varpi^nA. \end{align*}$$
$$\begin{align*}A \to \widehat{A}:={\mathop{\varprojlim}\limits_{n}} A/\varpi^nA. \end{align*}$$
-
(ii) Let
 $A\langle X_1, \dotsc , X_n \rangle $
be the
$A\langle X_1, \dotsc , X_n \rangle $
be the
 $\varpi $
-adic completion of
$\varpi $
-adic completion of
 $A[X_1, \dotsc , X_n]$
, called the restricted formal power series ring. Then
$A[X_1, \dotsc , X_n]$
, called the restricted formal power series ring. Then
 $A\langle X_1, \dotsc , X_n \rangle [1/\varpi ]$
is Noetherian for every
$A\langle X_1, \dotsc , X_n \rangle [1/\varpi ]$
is Noetherian for every
 $n \geq 0$
.
$n \geq 0$
.
Then the following assertions hold:
-
(1) For every ideal
 $I \subset A\langle X_1, \dotsc , X_n \rangle $
, the quotient
$I \subset A\langle X_1, \dotsc , X_n \rangle $
, the quotient
 $ A\langle X_1, \dotsc , X_n \rangle /I $
is
$ A\langle X_1, \dotsc , X_n \rangle /I $
is
 $\varpi $
-adically complete.
$\varpi $
-adically complete. -
(2) Let B be an A-algebra such that the
 $\varpi $
-adic completion
$\varpi $
-adic completion
 $\widehat {B}$
of B is isomorphic to
$\widehat {B}$
of B is isomorphic to
 $A\langle X_1, \dotsc , X_n \rangle $
. Let
$A\langle X_1, \dotsc , X_n \rangle $
. Let
 $I \subset B$
be an ideal. Then, the
$I \subset B$
be an ideal. Then, the
 $\varpi $
-adic completion
$\varpi $
-adic completion
 $\widehat {B/I}$
of
$\widehat {B/I}$
of
 $B/I$
is isomorphic to
$B/I$
is isomorphic to
 $\widehat {B}/I\widehat {B}$
.
$\widehat {B}/I\widehat {B}$
. -
(3) The Tate ring
 $A(\varpi /\varpi )$
is complete, and we have for every
$A(\varpi /\varpi )$
is complete, and we have for every
 $n \geq 0$
Here,
$n \geq 0$
Here, $$\begin{align*}A \langle X_1, \dotsc, X_n \rangle[1/\varpi]\cong A(\varpi/\varpi)\langle X_1, \dotsc, X_n \rangle. \end{align*}$$
$$\begin{align*}A \langle X_1, \dotsc, X_n \rangle[1/\varpi]\cong A(\varpi/\varpi)\langle X_1, \dotsc, X_n \rangle. \end{align*}$$
 $A(\varpi /\varpi )\langle Y_1, \dotsc , Y_m \rangle $
is the ring defined in [Reference Huber14, Section 1.1] for the Tate ring
$A(\varpi /\varpi )\langle Y_1, \dotsc , Y_m \rangle $
is the ring defined in [Reference Huber14, Section 1.1] for the Tate ring
 $A(\varpi /\varpi )$
. In particular, the Tate ring
$A(\varpi /\varpi )$
. In particular, the Tate ring
 $A(\varpi /\varpi )$
is strongly Noetherian.
$A(\varpi /\varpi )$
is strongly Noetherian.
Proof. See [Reference Fujiwara and Kato10, Chapter 0, Proposition 8.4.4] for (1). The rest of the proposition is an immediate consequence of (1). We will sketch the proof for the reader’s convenience.
(2) By (1), the ring
![]() $\widehat {B}/I\widehat {B}$
is
$\widehat {B}/I\widehat {B}$
is
![]() $\varpi $
-adically complete. Hence, we have
$\varpi $
-adically complete. Hence, we have
(3) Let
![]() $A_0$
be the image of the map
$A_0$
be the image of the map
![]() $A \to A[1/\varpi ]$
. By (1), the ring
$A \to A[1/\varpi ]$
. By (1), the ring
![]() $A_0$
is
$A_0$
is
![]() $\varpi $
-adically complete, and, hence,
$\varpi $
-adically complete, and, hence,
![]() $A(\varpi /\varpi )$
is complete. It is clear from the definitions that
$A(\varpi /\varpi )$
is complete. It is clear from the definitions that
Let N be the kernel of the surjection
![]() $B:=A[X_1, \dotsc , X_n] \to A_0[X_1, \dotsc , X_n]$
. By using (2), we have the following exact sequence:
$B:=A[X_1, \dotsc , X_n] \to A_0[X_1, \dotsc , X_n]$
. By using (2), we have the following exact sequence:
Since
![]() $N[1/\varpi ]=0$
, we have
$N[1/\varpi ]=0$
, we have
![]() $(N\otimes _{B} \widehat {B})[1/\varpi ]=0$
, and, hence,
$(N\otimes _{B} \widehat {B})[1/\varpi ]=0$
, and, hence,
This completes the proof of (3).
Let
![]() $\mathcal {C}$
be the category whose objects are formal schemes which are locally isomorphic to
$\mathcal {C}$
be the category whose objects are formal schemes which are locally isomorphic to
![]() $\mathop {\mathrm {Spf}} A$
for an adic ring A with an ideal of definition
$\mathop {\mathrm {Spf}} A$
for an adic ring A with an ideal of definition
![]() $\varpi A$
such that the pair
$\varpi A$
such that the pair
![]() $(A, \varpi )$
satisfies the conditions in Lemma 5.1. The morphisms in
$(A, \varpi )$
satisfies the conditions in Lemma 5.1. The morphisms in
![]() $\mathcal {C}$
are the adic morphisms. A formal scheme in
$\mathcal {C}$
are the adic morphisms. A formal scheme in
![]() $\mathcal {C}$
satisfies the condition (S) in [Reference Huber14, Section 1.9] by Lemma 5.1 (3). In [Reference Huber14, Proposition 1.9.1], Huber defined a functor
$\mathcal {C}$
satisfies the condition (S) in [Reference Huber14, Section 1.9] by Lemma 5.1 (3). In [Reference Huber14, Proposition 1.9.1], Huber defined a functor
from
![]() $\mathcal {C}$
to the category of analytic adic spaces. For a formal scheme
$\mathcal {C}$
to the category of analytic adic spaces. For a formal scheme
![]() $\mathscr {X}$
in
$\mathscr {X}$
in
![]() $\mathcal {C}$
, the adic space
$\mathcal {C}$
, the adic space
![]() $d(\mathscr {X})$
is equipped with a morphism of ringed spaces
$d(\mathscr {X})$
is equipped with a morphism of ringed spaces
This map is called a specialization map. If A and
![]() $\varpi \in A$
satisfy the conditions in Lemma 5.1, then we have
$\varpi \in A$
satisfy the conditions in Lemma 5.1, then we have
where
![]() $A^+$
is the integral closure of A in
$A^+$
is the integral closure of A in
![]() $A(\varpi /\varpi )=A[1/\varpi ]$
. The map
$A(\varpi /\varpi )=A[1/\varpi ]$
. The map
![]() $\lambda \colon d(\mathop {\mathrm {Spf}} A) \to \mathop {\mathrm {Spf}} A$
sends
$\lambda \colon d(\mathop {\mathrm {Spf}} A) \to \mathop {\mathrm {Spf}} A$
sends
![]() $x \in d(\mathop {\mathrm {Spf}} A)$
to the prime ideal
$x \in d(\mathop {\mathrm {Spf}} A)$
to the prime ideal
![]() $ \{ a \in A \, \vert \, \vert a (x) \vert < 1 \} \subset A. $
If
$ \{ a \in A \, \vert \, \vert a (x) \vert < 1 \} \subset A. $
If
![]() $f \colon \mathscr {X} \to \mathscr {Y}$
is an adic morphism of formal schemes in
$f \colon \mathscr {X} \to \mathscr {Y}$
is an adic morphism of formal schemes in
![]() $\mathcal {C}$
, then the induced morphism
$\mathcal {C}$
, then the induced morphism
![]() $d(f) \colon d(\mathscr {X}) \to d(\mathscr {Y})$
fits into the following commutative diagram:
$d(f) \colon d(\mathscr {X}) \to d(\mathscr {Y})$
fits into the following commutative diagram:

For the sake of completeness, we include a proof of the following result on the compatibility of the functor
![]() $d(-)$
with fibre products.
$d(-)$
with fibre products.
Proposition 5.2. Let
![]() $f \colon \mathscr {X} \to \mathscr {Y}$
be a morphism locally of finite type of formal schemes in
$f \colon \mathscr {X} \to \mathscr {Y}$
be a morphism locally of finite type of formal schemes in
![]() $\mathcal {C}$
. Let
$\mathcal {C}$
. Let
![]() $\mathscr {Z} \to \mathscr {Y}$
be an adic morphism of formal schemes in
$\mathscr {Z} \to \mathscr {Y}$
be an adic morphism of formal schemes in
![]() $\mathcal {C}$
. Then the morphism
$\mathcal {C}$
. Then the morphism
induced by the universal property of the fibre product is an isomorphism.
Proof. First, we note that the fibre product
![]() $ d(\mathscr {X}) \times _{d(\mathscr {Y})} d(\mathscr {Z}) $
exists by [Reference Huber14, Proposition 1.2.2] since
$ d(\mathscr {X}) \times _{d(\mathscr {Y})} d(\mathscr {Z}) $
exists by [Reference Huber14, Proposition 1.2.2] since
![]() $d(f) \colon d(\mathscr {X}) \to d(\mathscr {Y})$
is locally of finite type.
$d(f) \colon d(\mathscr {X}) \to d(\mathscr {Y})$
is locally of finite type.
We may assume that
![]() $\mathscr {X}=\mathop {\mathrm {Spf}} A$
,
$\mathscr {X}=\mathop {\mathrm {Spf}} A$
,
![]() $\mathscr {Y}= \mathop {\mathrm {Spf}} B$
and
$\mathscr {Y}= \mathop {\mathrm {Spf}} B$
and
![]() $\mathscr {Z}= \mathop {\mathrm {Spf}} C$
are affine, where B and C satisfy the conditions in Lemma 5.1 for some element
$\mathscr {Z}= \mathop {\mathrm {Spf}} C$
are affine, where B and C satisfy the conditions in Lemma 5.1 for some element
![]() $\varpi \in B$
and for its image in C, respectively. We may assume further that A is of the form
$\varpi \in B$
and for its image in C, respectively. We may assume further that A is of the form
![]() $B\langle X_1, \dotsc , X_n \rangle /I$
. We write
$B\langle X_1, \dotsc , X_n \rangle /I$
. We write
![]() $ D:=A \otimes _B C$
. The source of the morphism in question is isomorphic to
$ D:=A \otimes _B C$
. The source of the morphism in question is isomorphic to
where
![]() $\widehat {D}$
is the
$\widehat {D}$
is the
![]() $\varpi $
-adic completion of D and
$\varpi $
-adic completion of D and
![]() $E^{+}$
is the integral closure of
$E^{+}$
is the integral closure of
![]() $\widehat {D}$
in
$\widehat {D}$
in
![]() $(\widehat {D})[1/\varpi ]$
. On the other hand, the target of the morphism in question is isomorphic to
$(\widehat {D})[1/\varpi ]$
. On the other hand, the target of the morphism in question is isomorphic to
where
![]() $F^+$
is the integral closure of D in
$F^+$
is the integral closure of D in
![]() $D[1/\varpi ]$
. Let
$D[1/\varpi ]$
. Let
![]() $D_0$
be the image of the map
$D_0$
be the image of the map
![]() $D \to D[1/\varpi ]$
. Clearly, the completion of
$D \to D[1/\varpi ]$
. Clearly, the completion of
![]() $D(\varpi /\varpi )$
is isomorphic to
$D(\varpi /\varpi )$
is isomorphic to
![]() $(\widehat {D}_0)(\varpi /\varpi )$
. By a similar argument as in the proof of Lemma 5.1 (3), we have
$(\widehat {D}_0)(\varpi /\varpi )$
. By a similar argument as in the proof of Lemma 5.1 (3), we have
![]() $(\widehat {D})(\varpi /\varpi ) \cong (\widehat {D}_0)(\varpi /\varpi )$
. This completes the proof of the proposition since the adic spaces associated with an affinoid ring and its completion are naturally isomorphic (see [Reference Huber13, Lemma 1.5]).
$(\widehat {D})(\varpi /\varpi ) \cong (\widehat {D}_0)(\varpi /\varpi )$
. This completes the proof of the proposition since the adic spaces associated with an affinoid ring and its completion are naturally isomorphic (see [Reference Huber13, Lemma 1.5]).
A valuation ring R is called a microbial valuation ring if the field of fractions L of R admits a topologically nilpotent unit
![]() $\varpi $
with respect to the valuation topology (see [Reference Huber14, Definition 1.1.4]). We equip R with the valuation topology unless explicitly mentioned otherwise. In this case, the element
$\varpi $
with respect to the valuation topology (see [Reference Huber14, Definition 1.1.4]). We equip R with the valuation topology unless explicitly mentioned otherwise. In this case, the element
![]() $\varpi $
is contained in R, the ideal
$\varpi $
is contained in R, the ideal
![]() $\varpi R$
is an ideal of definition of R and we have
$\varpi R$
is an ideal of definition of R and we have
![]() $L=R[1/\varpi ]$
. The completion
$L=R[1/\varpi ]$
. The completion
![]() $ \widehat {R} $
of R is also a microbial valuation ring.
$ \widehat {R} $
of R is also a microbial valuation ring.
Let R be a complete microbial valuation ring. It is well known that
is Noetherian for every
![]() $n \geq 0$
(see [Reference Bosch, Güntzer and Remmert3, 5.2.6, Theorem 1]). A formal scheme
$n \geq 0$
(see [Reference Bosch, Güntzer and Remmert3, 5.2.6, Theorem 1]). A formal scheme
![]() $\mathscr {X}$
locally of finite type over
$\mathscr {X}$
locally of finite type over
![]() $\mathop {\mathrm {Spf}} R$
is in the category
$\mathop {\mathrm {Spf}} R$
is in the category
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
5.2 Étale cohomology with proper support of adic spaces and nearby cycles
We shall recall a comparison theorem of Huber. To formulate his result, we need some preparations.
Let R be a microbial valuation ring with field of fractions L. We assume that R is a strictly Henselian local ring. Let
![]() $\varpi $
be a topologically nilpotent unit in L. Let
$\varpi $
be a topologically nilpotent unit in L. Let
![]() $\overline {L}$
be a separable closure of L, and let
$\overline {L}$
be a separable closure of L, and let
![]() $\overline {R}$
be the valuation ring of
$\overline {R}$
be the valuation ring of
![]() $\overline {L}$
which extends R.
$\overline {L}$
which extends R.
We will use the following notation. Let
![]() $\eta \in \mathop {\mathrm {Spec}} R$
and
$\eta \in \mathop {\mathrm {Spec}} R$
and
![]() $\overline {\eta } \in \mathop {\mathrm {Spec}} \overline {R}$
be the generic points. For a scheme
$\overline {\eta } \in \mathop {\mathrm {Spec}} \overline {R}$
be the generic points. For a scheme
![]() $\mathcal {X}$
over R, we write
$\mathcal {X}$
over R, we write
The
![]() $\varpi $
-adic formal completion of a scheme (or a ring)
$\varpi $
-adic formal completion of a scheme (or a ring)
![]() $\mathcal {X}$
over R is denoted by
$\mathcal {X}$
over R is denoted by
![]() $\widehat {\mathcal {X}}$
. Let
$\widehat {\mathcal {X}}$
. Let
![]() $s \in \mathop {\mathrm {Spec}} R$
be the closed point and
$s \in \mathop {\mathrm {Spec}} R$
be the closed point and
![]() $\mathcal {X}_s$
the special fibre of
$\mathcal {X}_s$
the special fibre of
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
We write
Let
![]() $t \in S$
and
$t \in S$
and
![]() $\overline {t} \in \overline {S}$
be the closed points corresponding to the valuation rings R and
$\overline {t} \in \overline {S}$
be the closed points corresponding to the valuation rings R and
![]() $\overline {R}$
, respectively. The pseudo-adic space
$\overline {R}$
, respectively. The pseudo-adic space
![]() $ (\overline {S}, \{ \overline {t} \}) $
is also denoted by
$ (\overline {S}, \{ \overline {t} \}) $
is also denoted by
![]() $\overline {t}$
. The natural morphism
$\overline {t}$
. The natural morphism
![]() $\xi \colon \overline {t} \to S$
is a geometric point with support
$\xi \colon \overline {t} \to S$
is a geometric point with support
![]() $t \in S$
in the sense of [Reference Huber14, Definition 2.5.1].
$t \in S$
in the sense of [Reference Huber14, Definition 2.5.1].
Let
![]() $f \colon \mathcal {X} \to \mathop {\mathrm {Spec}} R$
be a separated morphism of finite type of schemes. The induced morphism
$f \colon \mathcal {X} \to \mathop {\mathrm {Spec}} R$
be a separated morphism of finite type of schemes. The induced morphism
is separated and of finite type; the separatedness can be checked, for example, by using Proposition 5.2 (we often write
![]() $d(f)$
instead of
$d(f)$
instead of
![]() $d(\widehat {f})$
). There is a natural morphism
$d(\widehat {f})$
). There is a natural morphism
![]() $d(\widehat {\mathcal {X}}) \to \mathcal {X}_{\eta }$
of locally ringed spaces (see [Reference Huber14, (1.9.4)]). An étale morphism
$d(\widehat {\mathcal {X}}) \to \mathcal {X}_{\eta }$
of locally ringed spaces (see [Reference Huber14, (1.9.4)]). An étale morphism
![]() $Y \to \mathcal {X}_{\eta }$
defines an adic space
$Y \to \mathcal {X}_{\eta }$
defines an adic space
![]() $d(\widehat {\mathcal {X}}) \times _{\mathcal {X}_{\eta }} Y$
, which is étale over
$d(\widehat {\mathcal {X}}) \times _{\mathcal {X}_{\eta }} Y$
, which is étale over
![]() $d(\widehat {\mathcal {X}})$
(see [Reference Huber13, Proposition 3.8] and [Reference Huber14, Corollary 1.7.3 i)]). In this way, we get a morphism of étale sites
$d(\widehat {\mathcal {X}})$
(see [Reference Huber13, Proposition 3.8] and [Reference Huber14, Corollary 1.7.3 i)]). In this way, we get a morphism of étale sites
Let
![]() $\Lambda $
be a torsion commutative ring. Let
$\Lambda $
be a torsion commutative ring. Let
![]() $\mathcal {F}$
be an étale sheaf of
$\mathcal {F}$
be an étale sheaf of
![]() $\Lambda $
-modules on
$\Lambda $
-modules on
![]() $\mathcal {X}$
. Let
$\mathcal {X}$
. Let
![]() $ \mathcal {F}^a $
denote the pullback of
$ \mathcal {F}^a $
denote the pullback of
![]() $\mathcal {F}$
by the composition
$\mathcal {F}$
by the composition
Recall that we have the direct image functor with proper support
for
![]() $d(f)$
by [Reference Huber14, Definition 5.4.4]. We define
$d(f)$
by [Reference Huber14, Definition 5.4.4]. We define
![]() $ R^nd(f)_!\mathcal {F}^a:=H^n(Rd(f)_!\mathcal {F}^a). $
We will describe the stalk
$ R^nd(f)_!\mathcal {F}^a:=H^n(Rd(f)_!\mathcal {F}^a). $
We will describe the stalk
at the geometric point
![]() $\xi \colon \overline {t} \to S$
in terms of the sliced nearby cycles functor relative to f. We defined the sliced nearby cycles functor
$\xi \colon \overline {t} \to S$
in terms of the sliced nearby cycles functor relative to f. We defined the sliced nearby cycles functor
in Section 2. Here, we fix the notation by the following commutative diagram:

Now we can state the following result due to Huber:
Theorem 5.3 (Huber [Reference Huber14, Theorem 5.7.8])
There is an isomorphism
for every n. This isomorphism is compatible with the natural actions of
![]() $\mathop {\mathrm {Gal}}\nolimits (\overline {L}/L)$
on both sides.
$\mathop {\mathrm {Gal}}\nolimits (\overline {L}/L)$
on both sides.
Proof. See [Reference Huber14, Theorem 5.7.8]. The construction of the isomorphism shows that it is
![]() $\mathop {\mathrm {Gal}}\nolimits (\overline {L}/L)$
-equivariant.
$\mathop {\mathrm {Gal}}\nolimits (\overline {L}/L)$
-equivariant.
5.3 Specialization maps on the stalks of
 $Rd(f)_!$
$Rd(f)_!$
In this subsection, we work over a complete non-archimedean field K with ring of integers
![]() ${\mathcal O}$
for simplicity. We fix a topologically nilpotent unit
${\mathcal O}$
for simplicity. We fix a topologically nilpotent unit
![]() $\varpi $
in K.
$\varpi $
in K.
For an adic space X over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
, we will use the following notation. For a point
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
, we will use the following notation. For a point
![]() $x \in X$
, let
$x \in X$
, let
![]() $k(x)$
be the residue field of the local ring
$k(x)$
be the residue field of the local ring
![]() ${\mathcal O}_{X, x}$
and
${\mathcal O}_{X, x}$
and
![]() $k(x)^+$
the valuation ring corresponding to the valuation
$k(x)^+$
the valuation ring corresponding to the valuation
![]() $v_x$
. We note that
$v_x$
. We note that
![]() $k(x)^+$
is a microbial valuation ring and the image of
$k(x)^+$
is a microbial valuation ring and the image of
![]() $\varpi $
, also denoted by
$\varpi $
, also denoted by
![]() $\varpi $
, is a topologically nilpotent unit in
$\varpi $
, is a topologically nilpotent unit in
![]() $k(x)$
. For a geometric point
$k(x)$
. For a geometric point
![]() $\xi $
of X, let
$\xi $
of X, let
![]() $\mathop {\mathrm {Supp}}(\xi ) \in X$
denote the support of it.
$\mathop {\mathrm {Supp}}(\xi ) \in X$
denote the support of it.
We recall strict localizations of analytic adic spaces. Let
![]() $ \xi \colon s \to X $
be a geometric point. The strict localization
$ \xi \colon s \to X $
be a geometric point. The strict localization
of X at
![]() $\xi $
is defined in [Reference Huber14, Section 2.5.11]. It is an adic space over X with an X-morphism
$\xi $
is defined in [Reference Huber14, Section 2.5.11]. It is an adic space over X with an X-morphism
![]() $s \to X(\xi )$
. We write
$s \to X(\xi )$
. We write
![]() $x:=\mathop {\mathrm {Supp}}(\xi )$
. By [Reference Huber14, Proposition 2.5.13], the strict localization
$x:=\mathop {\mathrm {Supp}}(\xi )$
. By [Reference Huber14, Proposition 2.5.13], the strict localization
![]() $X(\xi )$
is isomorphic to
$X(\xi )$
is isomorphic to
over X, where
![]() $\overline {k}(x)$
is a separable closure of
$\overline {k}(x)$
is a separable closure of
![]() $k(x)$
and
$k(x)$
and
![]() $\overline {k}(x)^+$
is a valuation ring extending
$\overline {k}(x)^+$
is a valuation ring extending
![]() $k(x)^+$
. A specialization morphism
$k(x)^+$
. A specialization morphism
![]() $\xi _1 \to \xi _2$
of geometric points of X is by definition a morphism
$\xi _1 \to \xi _2$
of geometric points of X is by definition a morphism
![]() $X(\xi _1) \to X(\xi _2)$
over X, and such a morphism exists if and only if we have
$X(\xi _1) \to X(\xi _2)$
over X, and such a morphism exists if and only if we have
Let
![]() $\mathcal {F}$
be an abelian étale sheaf on X. A specialization morphism
$\mathcal {F}$
be an abelian étale sheaf on X. A specialization morphism
![]() $\xi _1 \to \xi _2$
of geometric points of X induces a mapping
$\xi _1 \to \xi _2$
of geometric points of X induces a mapping
on the stalks in the usual way (see [Reference Huber14, (2.5.16)]).
Definition 5.4. Let X be an adic space over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
(or, more generally, an analytic adic space). Let
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
(or, more generally, an analytic adic space). Let
![]() $\mathcal {F}$
be an abelian étale sheaf on X. For a subset
$\mathcal {F}$
be an abelian étale sheaf on X. For a subset
![]() $W \subset X$
, we say that
$W \subset X$
, we say that
![]() $\mathcal {F}$
is overconvergent on W if for every specialization morphism
$\mathcal {F}$
is overconvergent on W if for every specialization morphism
![]() $\xi _1 \to \xi _2$
of geometric points of X whose supports are contained in W, the induced map
$\xi _1 \to \xi _2$
of geometric points of X whose supports are contained in W, the induced map
![]() $ \mathcal {F}_{\xi _2} \to \mathcal {F}_{\xi _1} $
is bijective.
$ \mathcal {F}_{\xi _2} \to \mathcal {F}_{\xi _1} $
is bijective.
Let
![]() $\mathcal {X}$
be a scheme of finite type over
$\mathcal {X}$
be a scheme of finite type over
![]() $\mathop {\mathrm {Spec}} {\mathcal O}$
. We write
$\mathop {\mathrm {Spec}} {\mathcal O}$
. We write
![]() $ \mathcal {X}_{K}:=\mathcal {X} \times _{\mathop {\mathrm {Spec}} {\mathcal O}} \mathop {\mathrm {Spec}} K. $
For an étale sheaf
$ \mathcal {X}_{K}:=\mathcal {X} \times _{\mathop {\mathrm {Spec}} {\mathcal O}} \mathop {\mathrm {Spec}} K. $
For an étale sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\mathcal {X}$
, let
$\mathcal {X}$
, let
![]() $ \mathcal {F}^a $
denote the pullback of
$ \mathcal {F}^a $
denote the pullback of
![]() $\mathcal {F}$
by the composition
$\mathcal {F}$
by the composition
Let
![]() $\Lambda $
be a torsion commutative ring.
$\Lambda $
be a torsion commutative ring.
Proposition 5.5. Let
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
be separated schemes of finite type over
$\mathcal {Y}$
be separated schemes of finite type over
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $f \colon \mathcal {X} \to \mathcal {Y}$
be a morphism over
$f \colon \mathcal {X} \to \mathcal {Y}$
be a morphism over
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $\mathcal {F}$
be an étale sheaf of
$\mathcal {F}$
be an étale sheaf of
![]() $\Lambda $
-modules on
$\Lambda $
-modules on
![]() $\mathcal {X}$
. We assume that the sliced nearby cycles complexes for f and
$\mathcal {X}$
. We assume that the sliced nearby cycles complexes for f and
![]() $\mathcal {F}$
are compatible with any base change (see Definition 2.3 (1)). Let
$\mathcal {F}$
are compatible with any base change (see Definition 2.3 (1)). Let
![]() $s \in \widehat {\mathcal {Y}}$
be a point. We consider the inverse image
$s \in \widehat {\mathcal {Y}}$
be a point. We consider the inverse image
![]() $\lambda ^{-1}(s)$
under the specialization map
$\lambda ^{-1}(s)$
under the specialization map
Then, the sheaf
![]() $R^nd(f)_!\mathcal {F}^a$
is overconvergent on
$R^nd(f)_!\mathcal {F}^a$
is overconvergent on
![]() $\lambda ^{-1}(s)$
for every n.
$\lambda ^{-1}(s)$
for every n.
Proof. Let
![]() $\xi _1 \to \xi _2$
be a specialization morphism of geometric points of
$\xi _1 \to \xi _2$
be a specialization morphism of geometric points of
![]() $d(\widehat {\mathcal {Y}})$
whose supports are contained in
$d(\widehat {\mathcal {Y}})$
whose supports are contained in
![]() $\lambda ^{-1}(s)$
. We write
$\lambda ^{-1}(s)$
. We write
![]() $y_m:= \mathop {\mathrm {Supp}}(\xi _m)$
(
$y_m:= \mathop {\mathrm {Supp}}(\xi _m)$
(
![]() $m=1, 2$
). Let
$m=1, 2$
). Let
![]() $\overline {k}(y_m)$
be a separable closure of
$\overline {k}(y_m)$
be a separable closure of
![]() $k(y_m)$
, and let
$k(y_m)$
, and let
![]() $\overline {k}(y_m)^+$
be a valuation ring extending
$\overline {k}(y_m)^+$
be a valuation ring extending
![]() $k(y_m)^+$
. We identify
$k(y_m)^+$
. We identify
![]() $d(\widehat {\mathcal {Y}})(\xi _m)$
with
$d(\widehat {\mathcal {Y}})(\xi _m)$
with
![]() $\mathop {\mathrm {Spa}}\nolimits (\overline {k}(y_m), \overline {k}(y_m)^+)$
. Let
$\mathop {\mathrm {Spa}}\nolimits (\overline {k}(y_m), \overline {k}(y_m)^+)$
. Let
![]() $R_m$
be the completion of
$R_m$
be the completion of
![]() $\overline {k}(y_m)^+$
, and we put
$\overline {k}(y_m)^+$
, and we put
![]() $U_m:= \mathop {\mathrm {Spec}} R_m$
. The morphism
$U_m:= \mathop {\mathrm {Spec}} R_m$
. The morphism
![]() $\mathop {\mathrm {Spa}}\nolimits (\overline {k}(y_m), \overline {k}(y_m)^+) \to d(\widehat {\mathcal {Y}})$
induces a natural morphism
$\mathop {\mathrm {Spa}}\nolimits (\overline {k}(y_m), \overline {k}(y_m)^+) \to d(\widehat {\mathcal {Y}})$
induces a natural morphism
over
![]() $\mathop {\mathrm {Spec}} {\mathcal O}$
, and the specialization morphism
$\mathop {\mathrm {Spec}} {\mathcal O}$
, and the specialization morphism
![]() $d(\widehat {\mathcal {Y}})(\xi _1) \to d(\widehat {\mathcal {Y}})(\xi _2)$
induces a natural
$d(\widehat {\mathcal {Y}})(\xi _1) \to d(\widehat {\mathcal {Y}})(\xi _2)$
induces a natural
![]() $\mathcal {Y}$
-morphism
$\mathcal {Y}$
-morphism
By the assumption, we have
![]() $ q_m(s_m)=s $
for the closed point
$ q_m(s_m)=s $
for the closed point
![]() $s_m \in U_m$
, where the image of
$s_m \in U_m$
, where the image of
![]() $s \in \widehat {\mathcal {Y}}$
in
$s \in \widehat {\mathcal {Y}}$
in
![]() $\mathcal {Y}$
is denoted by the same letter. Let
$\mathcal {Y}$
is denoted by the same letter. Let
![]() $\overline {s} \to \mathcal {Y}$
be an algebraic geometric point lying above s, and let U be the strict localization of
$\overline {s} \to \mathcal {Y}$
be an algebraic geometric point lying above s, and let U be the strict localization of
![]() $\mathcal {Y}$
at
$\mathcal {Y}$
at
![]() $\overline {s}$
. There are local
$\overline {s}$
. There are local
![]() $\mathcal {Y}$
-morphisms
$\mathcal {Y}$
-morphisms
![]() $\widetilde {q}_m \colon U_m \to U \ (m=1, 2)$
such that the following diagram commutes:
$\widetilde {q}_m \colon U_m \to U \ (m=1, 2)$
such that the following diagram commutes:

We remark that r is not a local morphism if
![]() $y_1 \neq y_2$
. Let
$y_1 \neq y_2$
. Let
![]() $\eta _m$
be the generic point of
$\eta _m$
be the generic point of
![]() $U_m$
. Then we have
$U_m$
. Then we have
![]() $r(\eta _1)=\eta _2$
. We write
$r(\eta _1)=\eta _2$
. We write
![]() $\eta :=\widetilde {q}_1(\eta _1)=\widetilde {q}_2(\eta _2)$
. Let
$\eta :=\widetilde {q}_1(\eta _1)=\widetilde {q}_2(\eta _2)$
. Let
![]() $\overline {\eta } \to U$
denote the algebraic geometric point which is the image of
$\overline {\eta } \to U$
denote the algebraic geometric point which is the image of
![]() $\eta _2$
.
$\eta _2$
.
Let
![]() $\mathcal {F}_{m}$
be the pullback of
$\mathcal {F}_{m}$
be the pullback of
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $\mathcal {X} \times _{\mathcal {Y}} U_m$
and
$\mathcal {X} \times _{\mathcal {Y}} U_m$
and
![]() $\mathcal {F}_U$
the pullback of
$\mathcal {F}_U$
the pullback of
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $\mathcal {X} \times _{\mathcal {Y}} U$
. For
$\mathcal {X} \times _{\mathcal {Y}} U$
. For
![]() $m=1, 2$
, we have
$m=1, 2$
, we have
by Theorem 5.3. By our assumption that the sliced nearby cycles complexes for f and
![]() $\mathcal {F}$
are compatible with any base change, the map
$\mathcal {F}$
are compatible with any base change, the map
is bijective for both
![]() $m=1$
and
$m=1$
and
![]() $m=2$
. Hence, the proposition follows from the following commutative diagram:
$m=2$
. Hence, the proposition follows from the following commutative diagram:

The commutativity of the diagram can be verified by tracing the construction of the isomorphism in Theorem 5.3.
6 Local constancy of higher direct images with proper support
In this section, we study local constancy of higher direct images with proper support for generically smooth morphisms of adic spaces whose target is one dimensional. We will formulate and prove the results not only for constant sheaves but also for nonconstant sheaves satisfying certain conditions related to the sliced nearby cycles functors.
Throughout this section, we fix an algebraically closed complete non-archimedean field K with ring of integers
![]() ${\mathcal O}$
.
${\mathcal O}$
.
6.1 Tame sheaves on annuli
In this subsection, we recall two theorems on finite étale coverings on annuli and the punctured disc, which basically follow from the results in [Reference Lütkebohmert22, Reference Lütkebohmert and Schmechta23, Reference Ramero27]. We do not impose any conditions on the characteristic of K. Since we can not directly apply some results there and some results are only stated in the case where the base field is of characteristic zero, we give proofs of the theorems in Appendix A.
To state the two theorems, we need some preparations. Recall that we defined
![]() $\mathbb {B}(1)=\mathop {\mathrm {Spa}}\nolimits (K \langle T \rangle , {\mathcal O} \langle T \rangle )$
. Let
$\mathbb {B}(1)=\mathop {\mathrm {Spa}}\nolimits (K \langle T \rangle , {\mathcal O} \langle T \rangle )$
. Let
be the punctured disc, where
![]() $0 \in \mathbb {B}(1)$
is the K-rational point corresponding to
$0 \in \mathbb {B}(1)$
is the K-rational point corresponding to
![]() $0 \in K$
. It is an adic space locally of finite type over
$0 \in K$
. It is an adic space locally of finite type over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. We fix a valuation
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. We fix a valuation
![]() $ \vert \cdot \vert \colon K \to {\mathbb R}_{\geq 0}$
of rank
$ \vert \cdot \vert \colon K \to {\mathbb R}_{\geq 0}$
of rank
![]() $1$
such that the topology of K is induced by it. For elements
$1$
such that the topology of K is induced by it. For elements
![]() $a, b \in \vert K^{\times } \vert $
with
$a, b \in \vert K^{\times } \vert $
with
![]() $a \leq b \leq 1$
, we define
$a \leq b \leq 1$
, we define
 $$ \begin{align*} \mathbb{B}(a, b)&:= \{ x \in \mathbb{B}(1) \, \vert \, a \leq \vert T(x) \vert \leq b \} \\ &:= \{ x \in \mathbb{B}(1) \, \vert \, \vert \varpi_a(x) \vert \leq \vert T(x) \vert \leq \vert \varpi_b(x) \vert \}, \end{align*} $$
$$ \begin{align*} \mathbb{B}(a, b)&:= \{ x \in \mathbb{B}(1) \, \vert \, a \leq \vert T(x) \vert \leq b \} \\ &:= \{ x \in \mathbb{B}(1) \, \vert \, \vert \varpi_a(x) \vert \leq \vert T(x) \vert \leq \vert \varpi_b(x) \vert \}, \end{align*} $$
which is called an open annulus. Here,
![]() $\varpi _a, \varpi _b \in K^{\times }$
are elements such that
$\varpi _a, \varpi _b \in K^{\times }$
are elements such that
![]() $a=\vert \varpi _a \vert $
and
$a=\vert \varpi _a \vert $
and
![]() $b=\vert \varpi _b \vert $
. It is a rational subset of
$b=\vert \varpi _b \vert $
. It is a rational subset of
![]() $\mathbb {B}(1)$
, and, hence, it is an affinoid open subspace of
$\mathbb {B}(1)$
, and, hence, it is an affinoid open subspace of
![]() $\mathbb {B}(1)$
.
$\mathbb {B}(1)$
.
Let m be a positive integer invertible in K. The finite étale morphism
![]() $ \varphi _m \colon \mathbb {B}(1)^{*} \to \mathbb {B}(1)^{*} $
defined by
$ \varphi _m \colon \mathbb {B}(1)^{*} \to \mathbb {B}(1)^{*} $
defined by
![]() $T \mapsto T^m$
is called a Kummer covering of degree m. For elements
$T \mapsto T^m$
is called a Kummer covering of degree m. For elements
![]() $a, b \in \vert K^{\times } \vert $
with
$a, b \in \vert K^{\times } \vert $
with
![]() $a \leq b \leq 1$
, the restriction
$a \leq b \leq 1$
, the restriction
of
![]() $\varphi _m$
is also called a Kummer covering of degree m (we also call a morphism of affinoid adic spaces of finite type over
$\varphi _m$
is also called a Kummer covering of degree m (we also call a morphism of affinoid adic spaces of finite type over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
a Kummer covering if it is isomorphic to
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
a Kummer covering if it is isomorphic to
![]() $\varphi _m \colon \mathbb {B}(a^{1/m}, b^{1/m}) \to \mathbb {B}(a, b)$
for
$\varphi _m \colon \mathbb {B}(a^{1/m}, b^{1/m}) \to \mathbb {B}(a, b)$
for
![]() $a, b \in \vert K^{\times } \vert $
and some m with
$a, b \in \vert K^{\times } \vert $
and some m with
![]() $a \leq b \leq 1$
).
$a \leq b \leq 1$
).
In this paper, we use the following notion of tameness for étale sheaves on one-dimensional smooth adic spaces over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
.
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
.
Definition 6.1. Let X be a one-dimensional smooth adic space over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. Let
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. Let
![]() $x \in X$
be a point which has a proper generalization in X, that is, there exists a point
$x \in X$
be a point which has a proper generalization in X, that is, there exists a point
![]() $x' \in X$
with
$x' \in X$
with
![]() $x \in \overline {\{ x' \}}$
and
$x \in \overline {\{ x' \}}$
and
![]() $x \neq x'$
. Let
$x \neq x'$
. Let
be the Henselization of the completion of the valuation ring
![]() $k(x)^+$
of x. Let
$k(x)^+$
of x. Let
![]() $L(x)$
be a separable closure of the field of fractions
$L(x)$
be a separable closure of the field of fractions
![]() $k(x)^{\wedge h}$
of
$k(x)^{\wedge h}$
of
![]() $k(x)^{\wedge h+}$
. It induces a geometric point
$k(x)^{\wedge h+}$
. It induces a geometric point
![]() $\overline {x} \to X$
with support x. For an étale sheaf
$\overline {x} \to X$
with support x. For an étale sheaf
![]() $\mathcal {F}$
on X, we say that
$\mathcal {F}$
on X, we say that
![]() $\mathcal {F}$
is tame at
$\mathcal {F}$
is tame at
![]() $x \in X$
if the action of
$x \in X$
if the action of
on the stalk
![]() $ \mathcal {F}_{\overline {x}} $
at the geometric point
$ \mathcal {F}_{\overline {x}} $
at the geometric point
![]() $\overline {x}$
factors through a finite group G such that
$\overline {x}$
factors through a finite group G such that
![]() $\sharp \, G$
is invertible in
$\sharp \, G$
is invertible in
![]() ${\mathcal O}$
, where
${\mathcal O}$
, where
![]() $\sharp \, G$
denotes the cardinality of G.
$\sharp \, G$
denotes the cardinality of G.
Now we can formulate the results.
Theorem 6.2 ([Reference Lütkebohmert22, Theorem 2.2], [Reference Lütkebohmert and Schmechta23, Theorem 4.11], [Reference Ramero27, Theorem 2.4.3])
Let
![]() $f \colon X \to \mathbb {B}(1)^{*}$
be a finite étale morphism of adic spaces. There exists an element
$f \colon X \to \mathbb {B}(1)^{*}$
be a finite étale morphism of adic spaces. There exists an element
![]() $\epsilon \in \vert K^{\times } \vert $
with
$\epsilon \in \vert K^{\times } \vert $
with
![]() $\epsilon \leq 1$
such that, for all
$\epsilon \leq 1$
such that, for all
![]() $a, b \in \vert K^{\times } \vert $
with
$a, b \in \vert K^{\times } \vert $
with
![]() $a < b \leq \epsilon $
, we have
$a < b \leq \epsilon $
, we have
 $$\begin{align*}f^{-1}(\mathbb{B}(a, b)) \cong \coprod^{n}_{i=1} \mathbb{B}(c_i, d_i) \end{align*}$$
$$\begin{align*}f^{-1}(\mathbb{B}(a, b)) \cong \coprod^{n}_{i=1} \mathbb{B}(c_i, d_i) \end{align*}$$
for some elements
![]() $c_i, d_i \in \vert K^{\times } \vert $
with
$c_i, d_i \in \vert K^{\times } \vert $
with
![]() $c_i < d_i \leq 1$
(
$c_i < d_i \leq 1$
(
![]() $1 \leq i \leq n$
). If K is of characteristic zero, after replacing
$1 \leq i \leq n$
). If K is of characteristic zero, after replacing
![]() $\epsilon \in \vert K^{\times } \vert $
by a smaller one, the restriction
$\epsilon \in \vert K^{\times } \vert $
by a smaller one, the restriction
of f to every component
![]() $\mathbb {B}(c_i, d_i)$
appearing in the above decomposition becomes a Kummer covering.
$\mathbb {B}(c_i, d_i)$
appearing in the above decomposition becomes a Kummer covering.
Theorem 6.3. Let
![]() $a, b \in \vert K^{\times } \vert $
be elements with
$a, b \in \vert K^{\times } \vert $
be elements with
![]() $a < b \leq 1$
. Let
$a < b \leq 1$
. Let
![]() $\mathcal {F}$
be a locally constant étale sheaf with finite stalks on
$\mathcal {F}$
be a locally constant étale sheaf with finite stalks on
![]() $\mathbb {B}(a, b)$
. We assume that the sheaf
$\mathbb {B}(a, b)$
. We assume that the sheaf
![]() $\mathcal {F}$
is tame at every
$\mathcal {F}$
is tame at every
![]() $x \in \mathbb {B}(a, b)$
having a proper generalization in
$x \in \mathbb {B}(a, b)$
having a proper generalization in
![]() $\mathbb {B}(a, b)$
, in the sense of Definition 6.1. Let
$\mathbb {B}(a, b)$
, in the sense of Definition 6.1. Let
![]() $t \in \vert K^{\times } \vert $
be an element with
$t \in \vert K^{\times } \vert $
be an element with
![]() $a/b < t^2 < 1$
. Then the restriction
$a/b < t^2 < 1$
. Then the restriction
![]() $\mathcal {F} \vert _{\mathbb {B}(a/t, tb)}$
of
$\mathcal {F} \vert _{\mathbb {B}(a/t, tb)}$
of
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $\mathbb {B}(a/t, tb)$
is trivialized by a Kummer covering
$\mathbb {B}(a/t, tb)$
is trivialized by a Kummer covering
![]() $\varphi _m$
of degree m, that is, the pullback
$\varphi _m$
of degree m, that is, the pullback
is a constant sheaf. Moreover, we can assume that the degree m is invertible in
![]() ${\mathcal O}$
.
${\mathcal O}$
.
We prove Theorem 6.2 and Theorem 6.3 in Appendix A.
Remark 6.4. If K is of characteristic zero, then Theorem 6.2 is known as the p-adic Riemann existence theorem of Lütkebohmert [Reference Lütkebohmert22].
6.2 Local constancy of
 $R^id(f)_!$
for generic smooth morphisms
$R^id(f)_!$
for generic smooth morphisms
As in Section 5, we use the following notation. Let
![]() $\mathcal {X}$
be a scheme of finite type over
$\mathcal {X}$
be a scheme of finite type over
![]() ${\mathcal O}$
. We write
${\mathcal O}$
. We write
![]() $ \mathcal {X}_{K}:=\mathcal {X} \times _{\mathop {\mathrm {Spec}} {\mathcal O}} \mathop {\mathrm {Spec}} K. $
For an étale sheaf
$ \mathcal {X}_{K}:=\mathcal {X} \times _{\mathop {\mathrm {Spec}} {\mathcal O}} \mathop {\mathrm {Spec}} K. $
For an étale sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\mathcal {X}$
, we denote by
$\mathcal {X}$
, we denote by
![]() $ \mathcal {F}^a $
the pullback of
$ \mathcal {F}^a $
the pullback of
![]() $\mathcal {F}$
by the composition
$\mathcal {F}$
by the composition
![]() $ d(\widehat {\mathcal {X}})_{\mathrm {\acute {e}t}} \overset {a}{\to } (\mathcal {X}_{K})_{\mathrm {\acute {e}t}} \to \mathcal {X}_{\mathrm {\acute {e}t}} $
(see Section 5.2 for the morphism
$ d(\widehat {\mathcal {X}})_{\mathrm {\acute {e}t}} \overset {a}{\to } (\mathcal {X}_{K})_{\mathrm {\acute {e}t}} \to \mathcal {X}_{\mathrm {\acute {e}t}} $
(see Section 5.2 for the morphism
![]() $a \colon d(\widehat {\mathcal {X}})_{\mathrm {\acute {e}t}} \to (\mathcal {X}_{K})_{\mathrm {\acute {e}t}}$
).
$a \colon d(\widehat {\mathcal {X}})_{\mathrm {\acute {e}t}} \to (\mathcal {X}_{K})_{\mathrm {\acute {e}t}}$
).
Let us introduce the following slightly technical definition.
Definition 6.5. We consider the following diagram:

where
-
•
 $\mathcal {Y}=\mathop {\mathrm {Spec}} A$
is an integral affine scheme of finite type over
$\mathcal {Y}=\mathop {\mathrm {Spec}} A$
is an integral affine scheme of finite type over
 ${\mathcal O}$
such that
${\mathcal O}$
such that
 $\mathcal {Y}_K$
is one dimensional and smooth over K,
$\mathcal {Y}_K$
is one dimensional and smooth over K, -
•
 $f \colon \mathcal {X} \to \mathcal {Y}$
is a separated morphism of finite type and
$f \colon \mathcal {X} \to \mathcal {Y}$
is a separated morphism of finite type and -
•
 $\pi \colon \mathcal {Z} \to \mathcal {Y}$
is a proper surjective morphism such that
$\pi \colon \mathcal {Z} \to \mathcal {Y}$
is a proper surjective morphism such that
 $\mathcal {Z}$
is an integral scheme whose generic fibre
$\mathcal {Z}$
is an integral scheme whose generic fibre
 $\mathcal {Z}_K$
is smooth over K, and the base change
$\mathcal {Z}_K$
is smooth over K, and the base change
 $\pi _K \colon \mathcal {Z}_K \to \mathcal {Y}_K$
is a finite morphism.
$\pi _K \colon \mathcal {Z}_K \to \mathcal {Y}_K$
is a finite morphism.
Let n be a positive integer invertible in
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\mathcal {F}$
a sheaf of
$\mathcal {F}$
a sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
![]() $\mathcal {X}$
. We say that
$\mathcal {X}$
. We say that
![]() $\mathcal {F}$
is adapted to the pair
$\mathcal {F}$
is adapted to the pair
![]() $(f, \pi )$
if the following conditions are satisfied:
$(f, \pi )$
if the following conditions are satisfied:
-
(1) The étale sheaf
 $\mathcal {F}^a$
of
$\mathcal {F}^a$
of
 ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
 $d(\widehat {\mathcal {X}})$
is constructible in the sense of [Reference Huber14, Definition 2.7.2].
$d(\widehat {\mathcal {X}})$
is constructible in the sense of [Reference Huber14, Definition 2.7.2]. -
(2) The sliced nearby cycles complexes for
 $f_{\mathcal {Z}}$
and
$f_{\mathcal {Z}}$
and
 $\mathcal {F}_{\mathcal {Z}}$
are compatible with any base change.
$\mathcal {F}_{\mathcal {Z}}$
are compatible with any base change. -
(3) The sliced nearby cycles complexes for
 $f_{\mathcal {Z}}$
and
$f_{\mathcal {Z}}$
and
 $\mathcal {F}_{\mathcal {Z}}$
are unipotent.
$\mathcal {F}_{\mathcal {Z}}$
are unipotent.
See Definition 2.3 for the terminology used in the conditions (2) and (3). Here, we retain the notation of Section 2. For example,
![]() $f_{\mathcal {Z}}$
denotes the base change
$f_{\mathcal {Z}}$
denotes the base change
![]() $ f_{\mathcal {Z}} \colon \mathcal {X} \times _{\mathcal {Y}} \mathcal {Z} \to \mathcal {Z} $
of f and
$ f_{\mathcal {Z}} \colon \mathcal {X} \times _{\mathcal {Y}} \mathcal {Z} \to \mathcal {Z} $
of f and
![]() $\mathcal {F}_{\mathcal {Z}}$
denotes the pullback of the sheaf
$\mathcal {F}_{\mathcal {Z}}$
denotes the pullback of the sheaf
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $\mathcal {X} \times _{\mathcal {Y}} \mathcal {Z}$
.
$\mathcal {X} \times _{\mathcal {Y}} \mathcal {Z}$
.
We need the following proposition, which is a consequence of Corollary 2.9.
Proposition 6.6. Let
![]() $\mathcal {Y}=\mathop {\mathrm {Spec}} A$
be an integral affine scheme of finite type over
$\mathcal {Y}=\mathop {\mathrm {Spec}} A$
be an integral affine scheme of finite type over
![]() ${\mathcal O}$
such that
${\mathcal O}$
such that
![]() $\mathcal {Y}_K$
is one dimensional and smooth over K. Let
$\mathcal {Y}_K$
is one dimensional and smooth over K. Let
![]() $f \colon \mathcal {X} \to \mathcal {Y}$
be a separated morphism of finite presentation. Then, there exists a proper surjective morphism
$f \colon \mathcal {X} \to \mathcal {Y}$
be a separated morphism of finite presentation. Then, there exists a proper surjective morphism
![]() $\pi \colon \mathcal {Z} \to \mathcal {Y}$
as in Definition 6.5 such that, for every positive integer n invertible in
$\pi \colon \mathcal {Z} \to \mathcal {Y}$
as in Definition 6.5 such that, for every positive integer n invertible in
![]() ${\mathcal O}$
, the constant sheaf
${\mathcal O}$
, the constant sheaf
![]() ${\mathbb Z}/n{\mathbb Z}$
on
${\mathbb Z}/n{\mathbb Z}$
on
![]() $\mathcal {X}$
is adapted to
$\mathcal {X}$
is adapted to
![]() $(f, \pi )$
.
$(f, \pi )$
.
Proof. The assertion follows from Corollary 2.9 and a spreading out argument.
By using the results in Section 5, we prove the following proposition:
Proposition 6.7. Let
![]() $f \colon \mathcal {X} \to \mathcal {Y}$
and
$f \colon \mathcal {X} \to \mathcal {Y}$
and
![]() $\pi \colon \mathcal {Z} \to \mathcal {Y}$
be morphisms as in Definition 6.5. We have the following diagram:
$\pi \colon \mathcal {Z} \to \mathcal {Y}$
be morphisms as in Definition 6.5. We have the following diagram:

Then the following assertions hold:
-
(1) Let
 $\mathcal {F}$
be an étale sheaf of
$\mathcal {F}$
be an étale sheaf of
 ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
 $\mathcal {X}$
adapted to
$\mathcal {X}$
adapted to
 $(f, \pi )$
with
$(f, \pi )$
with
 $n \in {\mathcal O}^{\times }$
. For every i, the sheaf
$n \in {\mathcal O}^{\times }$
. For every i, the sheaf  $$\begin{align*}d(\pi)^*R^id(f)_!\mathcal{F}^a \end{align*}$$
$$\begin{align*}d(\pi)^*R^id(f)_!\mathcal{F}^a \end{align*}$$
on
 $d(\widehat {\mathcal {Z}})$
is tame at every
$d(\widehat {\mathcal {Z}})$
is tame at every
 $z \in d(\widehat {\mathcal {Z}})$
having a proper generalization in
$z \in d(\widehat {\mathcal {Z}})$
having a proper generalization in
 $d(\widehat {\mathcal {Z}})$
, in the sense of Definition 6.1.
$d(\widehat {\mathcal {Z}})$
, in the sense of Definition 6.1. -
(2) Let
 $y \in d(\widehat {\mathcal {Y}})$
be a K-rational point. There exists an open subset
$y \in d(\widehat {\mathcal {Y}})$
be a K-rational point. There exists an open subset
 $ V \subset d(\widehat {\mathcal {Y}}) $
containing y such that, for every étale sheaf
$ V \subset d(\widehat {\mathcal {Y}}) $
containing y such that, for every étale sheaf
 $\mathcal {F}$
of
$\mathcal {F}$
of
 ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
 $\mathcal {X}$
adapted to
$\mathcal {X}$
adapted to
 $(f, \pi )$
with
$(f, \pi )$
with
 $n \in {\mathcal O}^{\times }$
, the sheaf
$n \in {\mathcal O}^{\times }$
, the sheaf
 $ d(\pi )^*R^id(f)_!\mathcal {F}^a $
is overconvergent on
$ d(\pi )^*R^id(f)_!\mathcal {F}^a $
is overconvergent on
 $d(\pi )^{-1}(V)$
for every i.
$d(\pi )^{-1}(V)$
for every i.
Proof. For an étale sheaf
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
![]() $\mathcal {X}$
with
$\mathcal {X}$
with
![]() $n \in {\mathcal O}^{\times }$
, the pullback of
$n \in {\mathcal O}^{\times }$
, the pullback of
![]() $\mathcal {F}^a$
by
$\mathcal {F}^a$
by
![]() $d(\widehat {\mathcal {X}_{\mathcal {Z}}}) \to d(\widehat {\mathcal {X}})$
is isomorphic to
$d(\widehat {\mathcal {X}_{\mathcal {Z}}}) \to d(\widehat {\mathcal {X}})$
is isomorphic to
![]() $(\mathcal {F}_{\mathcal {Z}})^a$
, and, hence, by using the base change theorem [Reference Huber14, Theorem 5.4.6] for
$(\mathcal {F}_{\mathcal {Z}})^a$
, and, hence, by using the base change theorem [Reference Huber14, Theorem 5.4.6] for
![]() $Rd(f)_!$
, we have
$Rd(f)_!$
, we have
(1) This is an immediate consequence of Theorem 5.3. Indeed, let
![]() $z \in d(\widehat {\mathcal {Z}})$
be an element having a proper generalization in
$z \in d(\widehat {\mathcal {Z}})$
be an element having a proper generalization in
![]() $d(\widehat {\mathcal {Z}})$
. Let
$d(\widehat {\mathcal {Z}})$
. Let
be the Henselization of the completion of the valuation ring
![]() $k(z)^+$
of z. By [Reference Huber17, Corollary 5.4], the residue field of R is algebraically closed. We write
$k(z)^+$
of z. By [Reference Huber17, Corollary 5.4], the residue field of R is algebraically closed. We write
![]() $U:= \mathop {\mathrm {Spec}} R$
. Let L be the field of fractions of R. The composite
$U:= \mathop {\mathrm {Spec}} R$
. Let L be the field of fractions of R. The composite
is induced by a natural morphism
![]() $q \colon U \to \mathcal {Z}$
of schemes over
$q \colon U \to \mathcal {Z}$
of schemes over
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $\overline {L}$
be a separable closure of L, which induces a geometric point
$\overline {L}$
be a separable closure of L, which induces a geometric point
![]() $\overline {t} \to \mathop {\mathrm {Spa}}\nolimits (L, R)$
and a geometric point
$\overline {t} \to \mathop {\mathrm {Spa}}\nolimits (L, R)$
and a geometric point
![]() $\overline {z} \to d(\widehat {\mathcal {Z}})$
in the usual way.
$\overline {z} \to d(\widehat {\mathcal {Z}})$
in the usual way.
Let
![]() $\mathcal {F}$
be an étale sheaf of
$\mathcal {F}$
be an étale sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
![]() $\mathcal {X}$
adapted to
$\mathcal {X}$
adapted to
![]() $(f, \pi )$
with
$(f, \pi )$
with
![]() $n \in {\mathcal O}^{\times }$
. By applying Theorem 5.3 to
$n \in {\mathcal O}^{\times }$
. By applying Theorem 5.3 to
![]() $f_U \colon \mathcal {X}_U \to U$
, we have
$f_U \colon \mathcal {X}_U \to U$
, we have
![]() $\mathop {\mathrm {Gal}}\nolimits (\overline {L}/L)$
-equivariant isomorphisms
$\mathop {\mathrm {Gal}}\nolimits (\overline {L}/L)$
-equivariant isomorphisms
where
![]() $s \in U$
is the closed point and
$s \in U$
is the closed point and
![]() $\overline {\eta }=\mathop {\mathrm {Spec}} \overline {L} \to U$
is the algebraic geometric point. By [Reference Huber14, Corollary 5.4.8 and Proposition 6.2.1 i)], the left-hand side is a finitely generated
$\overline {\eta }=\mathop {\mathrm {Spec}} \overline {L} \to U$
is the algebraic geometric point. By [Reference Huber14, Corollary 5.4.8 and Proposition 6.2.1 i)], the left-hand side is a finitely generated
![]() ${\mathbb Z}/n{\mathbb Z}$
-module. Moreover, the action of
${\mathbb Z}/n{\mathbb Z}$
-module. Moreover, the action of
![]() $\mathop {\mathrm {Gal}}\nolimits (\overline {L}/L)$
on it factors through a finite group. Since the complex
$\mathop {\mathrm {Gal}}\nolimits (\overline {L}/L)$
on it factors through a finite group. Since the complex
![]() $ R\Psi _{f_{U}, \overline {\eta }}(\mathcal {F}_{U}) $
is
$ R\Psi _{f_{U}, \overline {\eta }}(\mathcal {F}_{U}) $
is
![]() $\mathop {\mathrm {Gal}}\nolimits (\overline {L}/L)$
-unipotent and the integer n is invertible in
$\mathop {\mathrm {Gal}}\nolimits (\overline {L}/L)$
-unipotent and the integer n is invertible in
![]() ${\mathcal O}$
, it follows that the action of
${\mathcal O}$
, it follows that the action of
![]() $\mathop {\mathrm {Gal}}\nolimits (\overline {L}/L)$
on the right-hand side factors through a finite group G such that
$\mathop {\mathrm {Gal}}\nolimits (\overline {L}/L)$
on the right-hand side factors through a finite group G such that
![]() $\sharp \, G$
is invertible in
$\sharp \, G$
is invertible in
![]() ${\mathcal O}$
. This proves (1).
${\mathcal O}$
. This proves (1).
(2) Since
![]() $\pi \colon \mathcal {Z} \to \mathcal {Y}$
is proper, by [Reference Huber14, Proposition 1.9.6], we have
$\pi \colon \mathcal {Z} \to \mathcal {Y}$
is proper, by [Reference Huber14, Proposition 1.9.6], we have
![]() $ {d(\widehat {\mathcal {Z}}) \cong d(\widehat {\mathcal {Y}}) \times _{\mathcal {Y}} \mathcal {Z},} $
where
$ {d(\widehat {\mathcal {Z}}) \cong d(\widehat {\mathcal {Y}}) \times _{\mathcal {Y}} \mathcal {Z},} $
where
![]() $d(\widehat {\mathcal {Y}}) \times _{\mathcal {Y}} \mathcal {Z}$
is the adic space over
$d(\widehat {\mathcal {Y}}) \times _{\mathcal {Y}} \mathcal {Z}$
is the adic space over
![]() $d(\widehat {\mathcal {Y}})$
associated with
$d(\widehat {\mathcal {Y}})$
associated with
![]() $ d(\widehat {\mathcal {Y}}) \to \mathcal {Y}_K \to \mathcal {Y} $
and
$ d(\widehat {\mathcal {Y}}) \to \mathcal {Y}_K \to \mathcal {Y} $
and
![]() ${\pi \colon \mathcal {Z} \to \mathcal {Y}}$
(see [Reference Huber13, Proposition 3.8]). Since
${\pi \colon \mathcal {Z} \to \mathcal {Y}}$
(see [Reference Huber13, Proposition 3.8]). Since
![]() $\pi _K \colon \mathcal {Z}_K \to \mathcal {Y}_K$
is a finite morphism, it follows that
$\pi _K \colon \mathcal {Z}_K \to \mathcal {Y}_K$
is a finite morphism, it follows that
is finite over
![]() $d(\widehat {\mathcal {Y}})$
. The inverse image
$d(\widehat {\mathcal {Y}})$
. The inverse image
of
![]() $y \in d(\widehat {\mathcal {Y}})$
consists of finitely many K-rational points. Let
$y \in d(\widehat {\mathcal {Y}})$
consists of finitely many K-rational points. Let
be the specialization map associated with the formal scheme
![]() $\widehat {\mathcal {Z}}$
. Since the inverse image
$\widehat {\mathcal {Z}}$
. Since the inverse image
![]() $\lambda ^{-1}(\lambda (z_j))$
of
$\lambda ^{-1}(\lambda (z_j))$
of
![]() $\lambda (z_j)$
is a closed constructible subset of
$\lambda (z_j)$
is a closed constructible subset of
![]() $d(\widehat {\mathcal {Z}})$
and
$d(\widehat {\mathcal {Z}})$
and
![]() $z_j$
is a K-rational point, there exists an open neighbourhood
$z_j$
is a K-rational point, there exists an open neighbourhood
![]() $ V_j \subset d(\widehat {\mathcal {Z}}) $
of
$ V_j \subset d(\widehat {\mathcal {Z}}) $
of
![]() $z_j$
with
$z_j$
with
for every j (see Lemma 4.3). Since
![]() $d(\pi )$
is a finite morphism, there is an open neighbourhood
$d(\pi )$
is a finite morphism, there is an open neighbourhood
![]() $ V \subset d(\widehat {\mathcal {Y}}) $
of y with
$ V \subset d(\widehat {\mathcal {Y}}) $
of y with
![]() $ d(\pi )^{-1}(V) \subset \cup _j V_j. $
By using Proposition 5.5, we see that, for every étale sheaf
$ d(\pi )^{-1}(V) \subset \cup _j V_j. $
By using Proposition 5.5, we see that, for every étale sheaf
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
![]() $\mathcal {X}$
adapted to
$\mathcal {X}$
adapted to
![]() $(f, \pi )$
with
$(f, \pi )$
with
![]() $n \in {\mathcal O}^{\times }$
, the sheaf
$n \in {\mathcal O}^{\times }$
, the sheaf
![]() $R^id(f_{\mathcal {Z}})_!(\mathcal {F}_{\mathcal {Z}})^a$
is overconvergent on
$R^id(f_{\mathcal {Z}})_!(\mathcal {F}_{\mathcal {Z}})^a$
is overconvergent on
![]() $d(\pi )^{-1}(V)$
.
$d(\pi )^{-1}(V)$
.
We need the following finiteness result due to Huber.
Theorem 6.8 (Huber [Reference Huber14, Theorem 6.2.2])
Let Y be an adic space over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. Let
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. Let
![]() $f \colon X \to Y$
be a morphism of adic spaces which is smooth, separated and quasicompact. Let
$f \colon X \to Y$
be a morphism of adic spaces which is smooth, separated and quasicompact. Let
![]() $\mathcal {F}$
be a constructible sheaf of
$\mathcal {F}$
be a constructible sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on X with
${\mathbb Z}/n{\mathbb Z}$
-modules on X with
![]() $n \in {\mathcal O}^{\times }$
. Then, the sheaf
$n \in {\mathcal O}^{\times }$
. Then, the sheaf
![]() $ R^if_!\mathcal {F} $
on Y is a constructible sheaf of
$ R^if_!\mathcal {F} $
on Y is a constructible sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules for every i.
${\mathbb Z}/n{\mathbb Z}$
-modules for every i.
Proof. See [Reference Huber14, Theorem 6.2.2].
Remark 6.9. The assertion of Theorem 6.8 can fail for nonsmooth morphisms. See the introduction of [Reference Huber15] for details (see also [Reference Huber18, Proposition 7.1] for a more general result for smooth, separated and quasicompact morphisms of analytic pseudo-adic spaces).
As in the previous sections, we write
![]() $\mathbb {B}(1)=\mathop {\mathrm {Spa}}\nolimits (K \langle T \rangle , {\mathcal O} \langle T \rangle )$
. For an element
$\mathbb {B}(1)=\mathop {\mathrm {Spa}}\nolimits (K \langle T \rangle , {\mathcal O} \langle T \rangle )$
. For an element
![]() $\epsilon \in \vert K^{\times } \vert $
with
$\epsilon \in \vert K^{\times } \vert $
with
![]() $\epsilon \leq 1$
, we define
$\epsilon \leq 1$
, we define
and
![]() $ \mathbb {B}(\epsilon )^* := \mathbb {B}(\epsilon ) \backslash \{ 0 \}. $
Let X be a one-dimensional adic space of finite type over
$ \mathbb {B}(\epsilon )^* := \mathbb {B}(\epsilon ) \backslash \{ 0 \}. $
Let X be a one-dimensional adic space of finite type over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. We define an open disc
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. We define an open disc
![]() $V \subset X$
as an open subset V of X equipped with an isomorphism
$V \subset X$
as an open subset V of X equipped with an isomorphism
over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. For an open disc
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
. For an open disc
![]() $V \subset X$
, we write
$V \subset X$
, we write
Similarly, we write
for an open annulus
![]() $\mathbb {B}(a, b) \subset \mathbb {B}(1)$
.
$\mathbb {B}(a, b) \subset \mathbb {B}(1)$
.
The main result of this section is the following theorem.
Theorem 6.10. Let
![]() $f \colon \mathcal {X} \to \mathcal {Y}$
and
$f \colon \mathcal {X} \to \mathcal {Y}$
and
![]() $\pi \colon \mathcal {Z} \to \mathcal {Y}$
be morphisms as in Definition 6.5. We assume that there is an open disc
$\pi \colon \mathcal {Z} \to \mathcal {Y}$
be morphisms as in Definition 6.5. We assume that there is an open disc
![]() $V \subset d(\widehat {\mathcal {Y}})$
such that
$V \subset d(\widehat {\mathcal {Y}})$
such that
is smooth over
![]() $V(1)^*$
. Then there exists an element
$V(1)^*$
. Then there exists an element
![]() $\epsilon _0 \in \vert K^{\times } \vert $
with
$\epsilon _0 \in \vert K^{\times } \vert $
with
![]() $\epsilon _0 \leq 1$
such that, for every étale sheaf
$\epsilon _0 \leq 1$
such that, for every étale sheaf
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
![]() $\mathcal {X}$
adapted to
$\mathcal {X}$
adapted to
![]() $(f, \pi )$
with
$(f, \pi )$
with
![]() $n \in {\mathcal O}^{\times }$
, the following two assertions hold:
$n \in {\mathcal O}^{\times }$
, the following two assertions hold:
-
(1) The restriction
 $$\begin{align*}(R^id(f)_!\mathcal{F}^a)\vert_{V(\epsilon_0)^*} \end{align*}$$
$$\begin{align*}(R^id(f)_!\mathcal{F}^a)\vert_{V(\epsilon_0)^*} \end{align*}$$
of
 $R^id(f)_!\mathcal {F}^a$
to
$R^id(f)_!\mathcal {F}^a$
to
 $V(\epsilon _0)^*$
is a locally constant constructible sheaf of
$V(\epsilon _0)^*$
is a locally constant constructible sheaf of
 ${\mathbb Z}/n{\mathbb Z}$
-modules for every i.
${\mathbb Z}/n{\mathbb Z}$
-modules for every i. -
(2) For elements
 $a, b \in \vert K^{\times } \vert $
with
$a, b \in \vert K^{\times } \vert $
with
 $a < b \leq \epsilon _0$
, there exists a composition
$a < b \leq \epsilon _0$
, there exists a composition  $$\begin{align*}h \colon \mathbb{B}(c^{1/m}, d^{1/m}) \overset{\varphi_m}{\longrightarrow} \mathbb{B}(c, d) \overset{g}{\longrightarrow} V(a, b) \end{align*}$$
$$\begin{align*}h \colon \mathbb{B}(c^{1/m}, d^{1/m}) \overset{\varphi_m}{\longrightarrow} \mathbb{B}(c, d) \overset{g}{\longrightarrow} V(a, b) \end{align*}$$
of a Kummer covering
 $ \varphi _m $
of degree m, where m is invertible in
$ \varphi _m $
of degree m, where m is invertible in
 ${\mathcal O}$
, with a finite Galois étale morphism g, such that the pullback
${\mathcal O}$
, with a finite Galois étale morphism g, such that the pullback  $$\begin{align*}h^{*}((R^id(f)_!\mathcal{F}^a)\vert_{V(a, b)}) \end{align*}$$
$$\begin{align*}h^{*}((R^id(f)_!\mathcal{F}^a)\vert_{V(a, b)}) \end{align*}$$
is a constant sheaf associated with a finitely generated
 ${\mathbb Z}/n{\mathbb Z}$
-module for every i. If K is of characteristic zero, then we can take g as a Kummer covering.
${\mathbb Z}/n{\mathbb Z}$
-module for every i. If K is of characteristic zero, then we can take g as a Kummer covering.
Proof. Clearly, the first assertion (1) follows from the second assertion (2). We shall prove (2).
Step 1. We may assume that, for the dominant morphism
![]() $\pi \colon \mathcal {Z} \to \mathcal {Y}$
, the separable closure
$\pi \colon \mathcal {Z} \to \mathcal {Y}$
, the separable closure
![]() $k(\mathcal {Y})^{\text {sep}}$
of the function field
$k(\mathcal {Y})^{\text {sep}}$
of the function field
![]() $k(\mathcal {Y})$
of
$k(\mathcal {Y})$
of
![]() $\mathcal {Y}$
in the function field of
$\mathcal {Y}$
in the function field of
![]() $\mathcal {Z}$
is Galois over
$\mathcal {Z}$
is Galois over
![]() $k(\mathcal {Y})$
.
$k(\mathcal {Y})$
.
Indeed, there is a finite surjective morphism
![]() $Z' \to \mathcal {Z}_K$
from an integral scheme
$Z' \to \mathcal {Z}_K$
from an integral scheme
![]() $Z'$
which is smooth over K such that the separable closure of the function field
$Z'$
which is smooth over K such that the separable closure of the function field
![]() $k(\mathcal {Y})$
of
$k(\mathcal {Y})$
of
![]() $\mathcal {Y}$
in the function field of
$\mathcal {Y}$
in the function field of
![]() $Z'$
is Galois over
$Z'$
is Galois over
![]() $k(\mathcal {Y})$
. There exists a proper surjective morphism
$k(\mathcal {Y})$
. There exists a proper surjective morphism
![]() $\mathcal {Z}' \to \mathcal {Z}$
such that
$\mathcal {Z}' \to \mathcal {Z}$
such that
![]() $\mathcal {Z}'$
is integral and the base change
$\mathcal {Z}'$
is integral and the base change
![]() $\mathcal {Z}^{\prime }_K \to \mathcal {Z}_K$
is isomorphic to
$\mathcal {Z}^{\prime }_K \to \mathcal {Z}_K$
is isomorphic to
![]() $Z' \to \mathcal {Z}_K$
. We define
$Z' \to \mathcal {Z}_K$
. We define
![]() $\pi '$
as the composition
$\pi '$
as the composition
![]() $\pi ' \colon \mathcal {Z}' \to \mathcal {Z} \to \mathcal {Y}$
. If a sheaf
$\pi ' \colon \mathcal {Z}' \to \mathcal {Z} \to \mathcal {Y}$
. If a sheaf
![]() $\mathcal {F}$
is adapted to
$\mathcal {F}$
is adapted to
![]() $(f, \pi )$
, then it is also adapted to
$(f, \pi )$
, then it is also adapted to
![]() $(f, \pi ')$
. Thus, it suffices to prove Theorem 6.10 for
$(f, \pi ')$
. Thus, it suffices to prove Theorem 6.10 for
![]() $(f, \pi ')$
.
$(f, \pi ')$
.
Step 2. We will choose an appropriate
![]() $\epsilon _0 \in \vert K^{\times } \vert $
.
$\epsilon _0 \in \vert K^{\times } \vert $
.
Let
![]() $W \to \mathcal {Y}_K$
be the normalization of
$W \to \mathcal {Y}_K$
be the normalization of
![]() $\mathcal {Y}_K$
in
$\mathcal {Y}_K$
in
![]() $k(\mathcal {Y})^{\text {sep}}$
. Then the induced morphism
$k(\mathcal {Y})^{\text {sep}}$
. Then the induced morphism
![]() $\mathcal {Z}_K \to W$
is finite, radicial and surjective and there is a dense open subset
$\mathcal {Z}_K \to W$
is finite, radicial and surjective and there is a dense open subset
![]() $U \subset \mathcal {Y}_K$
over which
$U \subset \mathcal {Y}_K$
over which
![]() $W \to \mathcal {Y}_K$
is a finite Galois étale morphism. Let
$W \to \mathcal {Y}_K$
is a finite Galois étale morphism. Let
be the adic space over
![]() $d(\widehat {\mathcal {Y}})$
associated with
$d(\widehat {\mathcal {Y}})$
associated with
![]() $ d(\widehat {\mathcal {Y}}) \to \mathcal {Y}_K $
and
$ d(\widehat {\mathcal {Y}}) \to \mathcal {Y}_K $
and
![]() $W \to \mathcal {Y}_K$
. Let
$W \to \mathcal {Y}_K$
. Let
![]() $ g \colon W' \to d(\widehat {\mathcal {Y}}) $
denote the structure morphism. The morphism
$ g \colon W' \to d(\widehat {\mathcal {Y}}) $
denote the structure morphism. The morphism
![]() $d(\pi )$
can be written as the composition of finite morphisms
$d(\pi )$
can be written as the composition of finite morphisms
Let
![]() $\epsilon _1 \in \vert K^{\times } \vert $
be an element with
$\epsilon _1 \in \vert K^{\times } \vert $
be an element with
![]() $\epsilon _1 \leq 1$
, such that
$\epsilon _1 \leq 1$
, such that
![]() $V(\epsilon _1)^* \subset d(\widehat {\mathcal {Y}})$
is mapped into U under the map
$V(\epsilon _1)^* \subset d(\widehat {\mathcal {Y}})$
is mapped into U under the map
![]() $d(\widehat {\mathcal {Y}}) \to \mathcal {Y}_K$
. Then the restriction
$d(\widehat {\mathcal {Y}}) \to \mathcal {Y}_K$
. Then the restriction
is finite and étale. By Theorem 6.2, there exists an element
![]() $\epsilon _2 \in \vert K^{\times } \vert $
with
$\epsilon _2 \in \vert K^{\times } \vert $
with
![]() $\epsilon _2 \leq \epsilon _1$
such that, for all
$\epsilon _2 \leq \epsilon _1$
such that, for all
![]() $a, b \in \vert K^{\times } \vert $
with
$a, b \in \vert K^{\times } \vert $
with
![]() $a < b \leq \epsilon _2$
, we have
$a < b \leq \epsilon _2$
, we have
 $$\begin{align*}g^{-1}(V(a, b)) \cong \coprod^{N}_{j=1} \mathbb{B}(c_j, d_j) \end{align*}$$
$$\begin{align*}g^{-1}(V(a, b)) \cong \coprod^{N}_{j=1} \mathbb{B}(c_j, d_j) \end{align*}$$
for some elements
![]() $c_j, d_j \in \vert K^{\times } \vert $
with
$c_j, d_j \in \vert K^{\times } \vert $
with
![]() $c_j < d_j \leq 1$
(
$c_j < d_j \leq 1$
(
![]() $1 \leq j \leq N$
). If K is of characteristic zero, after replacing
$1 \leq j \leq N$
). If K is of characteristic zero, after replacing
![]() $\epsilon _2 \in \vert K^{\times } \vert $
by a smaller one, the restriction
$\epsilon _2 \in \vert K^{\times } \vert $
by a smaller one, the restriction
of g to every component
![]() $\mathbb {B}(c_j, d_j)$
appearing in the above decomposition becomes a Kummer covering. By Proposition 6.7 (2), there exists an element
$\mathbb {B}(c_j, d_j)$
appearing in the above decomposition becomes a Kummer covering. By Proposition 6.7 (2), there exists an element
![]() $\epsilon _3 \in \vert K^{\times } \vert $
with
$\epsilon _3 \in \vert K^{\times } \vert $
with
![]() $\epsilon _3 \leq \epsilon _2$
such that, for every étale sheaf
$\epsilon _3 \leq \epsilon _2$
such that, for every étale sheaf
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
![]() $\mathcal {X}$
adapted to
$\mathcal {X}$
adapted to
![]() $(f, \pi )$
with
$(f, \pi )$
with
![]() $n \in {\mathcal O}^{\times }$
, the sheaf
$n \in {\mathcal O}^{\times }$
, the sheaf
![]() $ d(\pi )^*R^id(f)_!\mathcal {F}^a $
is overconvergent on
$ d(\pi )^*R^id(f)_!\mathcal {F}^a $
is overconvergent on
![]() $d(\pi )^{-1}(V(\epsilon _3))$
for every i. Let
$d(\pi )^{-1}(V(\epsilon _3))$
for every i. Let
![]() $t \in \vert K^{\times } \vert $
be an element with
$t \in \vert K^{\times } \vert $
be an element with
![]() $t < 1$
. Then we put
$t < 1$
. Then we put
![]() $\epsilon _0:=t\epsilon _3$
.
$\epsilon _0:=t\epsilon _3$
.
Step 3. We shall show that
![]() $\epsilon _0$
satisfies the condition.
$\epsilon _0$
satisfies the condition.
Indeed, let
![]() $\mathcal {F}$
be an étale sheaf of
$\mathcal {F}$
be an étale sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
![]() $\mathcal {X}$
adapted to
$\mathcal {X}$
adapted to
![]() $(f, \pi )$
with
$(f, \pi )$
with
![]() $n \in {\mathcal O}^{\times }$
. Let
$n \in {\mathcal O}^{\times }$
. Let
![]() $a, b \in \vert K^{\times } \vert $
be elements with
$a, b \in \vert K^{\times } \vert $
be elements with
![]() $a < b \leq \epsilon _0$
. We have
$a < b \leq \epsilon _0$
. We have
![]() $ g^{-1}(V(ta, b/t)) \cong \coprod ^{N}_{i=1} \mathbb {B}(c_j, d_j) $
for some elements
$ g^{-1}(V(ta, b/t)) \cong \coprod ^{N}_{i=1} \mathbb {B}(c_j, d_j) $
for some elements
![]() $c_j, d_j \in \vert K^{\times } \vert $
with
$c_j, d_j \in \vert K^{\times } \vert $
with
![]() $c_j < d_j \leq 1$
(
$c_j < d_j \leq 1$
(
![]() $1 \leq j \leq N$
). We take a component
$1 \leq j \leq N$
). We take a component
![]() $\mathbb {B}(c_1, d_1)$
of the decomposition. The restriction
$\mathbb {B}(c_1, d_1)$
of the decomposition. The restriction
of g is denoted by the same letter. By the construction, it is a finite Galois étale morphism.
We remark that, since the morphism
![]() $\mathcal {Z}_K \to W$
is finite, radicial and surjective, it follows that
$\mathcal {Z}_K \to W$
is finite, radicial and surjective, it follows that
![]() $ \alpha \colon d(\widehat {\mathcal {Z}}) \to W' $
is a homeomorphism and, for every
$ \alpha \colon d(\widehat {\mathcal {Z}}) \to W' $
is a homeomorphism and, for every
![]() $z \in d(\widehat {\mathcal {Z}})$
, the extension
$z \in d(\widehat {\mathcal {Z}})$
, the extension
![]() $k(\alpha (z))^{\wedge } \to k(z)^{\wedge }$
of the completions of the residue fields is a finite purely inseparable extension, and, hence, the extension
$k(\alpha (z))^{\wedge } \to k(z)^{\wedge }$
of the completions of the residue fields is a finite purely inseparable extension, and, hence, the extension
![]() $k(\alpha (z))^{\wedge h} \to k(z)^{\wedge h}$
of the Henselizations of these fields is also a finite purely inseparable extension.
$k(\alpha (z))^{\wedge h} \to k(z)^{\wedge h}$
of the Henselizations of these fields is also a finite purely inseparable extension.
Since
![]() $ d(f) \colon d(\widehat {\mathcal {X}}) \to d(\widehat {\mathcal {Y}}) $
is smooth over
$ d(f) \colon d(\widehat {\mathcal {X}}) \to d(\widehat {\mathcal {Y}}) $
is smooth over
![]() $V(1)^*$
, the sheaf of
$V(1)^*$
, the sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules
${\mathbb Z}/n{\mathbb Z}$
-modules
on
![]() $\mathbb {B}(c_1, d_1)$
is constructible by Theorem 6.8. By the construction, it is overconvergent on
$\mathbb {B}(c_1, d_1)$
is constructible by Theorem 6.8. By the construction, it is overconvergent on
![]() $\mathbb {B}(c_1, d_1)$
. Therefore, by [Reference Huber14, Lemma 2.7.11], the sheaf
$\mathbb {B}(c_1, d_1)$
. Therefore, by [Reference Huber14, Lemma 2.7.11], the sheaf
![]() $\mathcal {G}$
is locally constant. Moreover, by Proposition 6.7 (1) and the remark above, the sheaf
$\mathcal {G}$
is locally constant. Moreover, by Proposition 6.7 (1) and the remark above, the sheaf
![]() $ \mathcal {G} $
is tame at every
$ \mathcal {G} $
is tame at every
![]() $x \in \mathbb {B}(c_1, d_1)$
having a proper generalization in
$x \in \mathbb {B}(c_1, d_1)$
having a proper generalization in
![]() $\mathbb {B}(c_1, d_1)$
. We have
$\mathbb {B}(c_1, d_1)$
. We have
![]() $ g^{-1}(V(a, b))=\mathbb {B}(c, d) $
for some elements
$ g^{-1}(V(a, b))=\mathbb {B}(c, d) $
for some elements
![]() $c, d \in \vert K^{\times } \vert $
with
$c, d \in \vert K^{\times } \vert $
with
![]() $c_1 < c < d < d_1$
. Hence, by Theorem 6.3, we conclude that the restriction of
$c_1 < c < d < d_1$
. Hence, by Theorem 6.3, we conclude that the restriction of
![]() $\mathcal {G}$
to
$\mathcal {G}$
to
![]() $g^{-1}(V(a, b))=\mathbb {B}(c, d)$
is trivialized by a Kummer covering
$g^{-1}(V(a, b))=\mathbb {B}(c, d)$
is trivialized by a Kummer covering
![]() $\varphi _m \colon \mathbb {B}(c^{1/m}, d^{1/m}) \to \mathbb {B}(c, d)$
with
$\varphi _m \colon \mathbb {B}(c^{1/m}, d^{1/m}) \to \mathbb {B}(c, d)$
with
![]() $m \in {\mathcal O}^{\times }$
.
$m \in {\mathcal O}^{\times }$
.
The proof of Theorem 6.10 is now complete.
Remark 6.11. In Theorem 6.10, the morphism g can be taken independent of
![]() $\mathcal {F}$
, although the integer m possibly depends on
$\mathcal {F}$
, although the integer m possibly depends on
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
For an element
![]() $ \epsilon \in \vert K^{\times } \vert $
, we define
$ \epsilon \in \vert K^{\times } \vert $
, we define
This is a closed constructible subset of
![]() $\mathbb {B}(1)$
. For later use, we record the following results.
$\mathbb {B}(1)$
. For later use, we record the following results.
Lemma 6.12. Let n be a positive integer invertible in
![]() ${\mathcal O}$
.
${\mathcal O}$
.
-
(1) Let
 $a, b \in \vert K^{\times } \vert $
be elements with
$a, b \in \vert K^{\times } \vert $
be elements with
 $a < b \leq 1$
. Let
$a < b \leq 1$
. Let
 $\mathcal {F}$
be a locally constant constructible sheaf of
$\mathcal {F}$
be a locally constant constructible sheaf of
 ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
 $\mathbb {B}(a, b)$
. Assume that there exists a finite étale morphism
$\mathbb {B}(a, b)$
. Assume that there exists a finite étale morphism
 $ h \colon \mathbb {B}(c, d) \to \mathbb {B}(a, b) $
such that h is a composition of finite Galois étale morphisms and the pullback
$ h \colon \mathbb {B}(c, d) \to \mathbb {B}(a, b) $
such that h is a composition of finite Galois étale morphisms and the pullback
 $ h^{*}\mathcal {F} $
is a constant sheaf. Then the following assertions hold:
$ h^{*}\mathcal {F} $
is a constant sheaf. Then the following assertions hold:-
(a) We have
 $$\begin{align*}H^i_c(\mathbb{B}(b) \backslash \mathbb{B}(a), \mathcal{F}\vert_{\mathbb{B}(b) \backslash \mathbb{B}(a)})=0 \quad \text{and} \quad H^i_c(\mathbb{D}(b) \cap \mathbb{B}(a, b), \mathcal{F}\vert_{\mathbb{D}(b) \cap \mathbb{B}(a, b)})=0 \end{align*}$$
$$\begin{align*}H^i_c(\mathbb{B}(b) \backslash \mathbb{B}(a), \mathcal{F}\vert_{\mathbb{B}(b) \backslash \mathbb{B}(a)})=0 \quad \text{and} \quad H^i_c(\mathbb{D}(b) \cap \mathbb{B}(a, b), \mathcal{F}\vert_{\mathbb{D}(b) \cap \mathbb{B}(a, b)})=0 \end{align*}$$
for every i.
-
(b) The restriction map
 $$\begin{align*}H^i(\mathbb{B}(a, b), \mathcal{F}) \to H^i(\mathbb{D}(b)^{\circ} \cap \mathbb{B}(a, b), \mathcal{F}) \end{align*}$$
$$\begin{align*}H^i(\mathbb{B}(a, b), \mathcal{F}) \to H^i(\mathbb{D}(b)^{\circ} \cap \mathbb{B}(a, b), \mathcal{F}) \end{align*}$$
is an isomorphism for every i, where
 $\mathbb {D}(b)^{\circ }$
is the interior of
$\mathbb {D}(b)^{\circ }$
is the interior of
 $\mathbb {D}(b)$
in
$\mathbb {D}(b)$
in
 $\mathbb {B}(1)$
.
$\mathbb {B}(1)$
.
-
-
(2) Let
 $\mathcal {F}$
be a locally constant constructible sheaf of
$\mathcal {F}$
be a locally constant constructible sheaf of
 ${\mathbb Z}/n{\mathbb Z}$
-modules on
${\mathbb Z}/n{\mathbb Z}$
-modules on
 $\mathbb {B}(1)^*$
. Assume that for all
$\mathbb {B}(1)^*$
. Assume that for all
 $a, b \in \vert K^{\times } \vert $
with
$a, b \in \vert K^{\times } \vert $
with
 $a < b \leq 1$
, there exists a finite étale morphism
$a < b \leq 1$
, there exists a finite étale morphism
 $ h \colon \mathbb {B}(c, d) \to \mathbb {B}(a, b) $
such that h is a composition of finite Galois étale morphisms and the pullback
$ h \colon \mathbb {B}(c, d) \to \mathbb {B}(a, b) $
such that h is a composition of finite Galois étale morphisms and the pullback
 $ h^{*}(\mathcal {F}\vert _{\mathbb {B}(a, b)}) $
is a constant sheaf. Then we have for every i.
$ h^{*}(\mathcal {F}\vert _{\mathbb {B}(a, b)}) $
is a constant sheaf. Then we have for every i. $$\begin{align*}H^i_c(\mathbb{D}(1) \backslash \{ 0 \}, \mathcal{F}\vert_{\mathbb{D}(1) \backslash \{ 0 \}})=0 \end{align*}$$
$$\begin{align*}H^i_c(\mathbb{D}(1) \backslash \{ 0 \}, \mathcal{F}\vert_{\mathbb{D}(1) \backslash \{ 0 \}})=0 \end{align*}$$
Proof. (1) After possibly changing the coordinate function of
![]() $\mathbb {B}(c, d)$
, we may assume that
$\mathbb {B}(c, d)$
, we may assume that
![]() $ h^{-1}(\mathbb {B}(a, a)) = \mathbb {B}(c, c) $
and
$ h^{-1}(\mathbb {B}(a, a)) = \mathbb {B}(c, c) $
and
![]() $ h^{-1}(\mathbb {B}(b, b)) = \mathbb {B}(d, d). $
Then, we have
$ h^{-1}(\mathbb {B}(b, b)) = \mathbb {B}(d, d). $
Then, we have
We shall show the first equality of (a). By the spectral sequence in [Reference Huber15, 4.2 ii)] and the fact that h is a composition of finite Galois étale morphisms, it is enough to show that, for a constant sheaf M on
![]() $\mathbb {B}(d) \backslash \mathbb {B}(c)$
associated with a finitely generated
$\mathbb {B}(d) \backslash \mathbb {B}(c)$
associated with a finitely generated
![]() ${\mathbb Z}/n{\mathbb Z}$
-module, we have for every i
${\mathbb Z}/n{\mathbb Z}$
-module, we have for every i
This is proved in [Reference Huber15, (II) in the proof of Theorem 2.5] (although the characteristic of the base field is always assumed to be zero in [Reference Huber15], we need not assume that the characteristic of K is zero here).
We shall show the second equality of (a). Similarly as above, it suffices to show that, for a constant sheaf M on
![]() $\mathbb {D}(d) \cap \mathbb {B}(c, d)$
associated with a finitely generated
$\mathbb {D}(d) \cap \mathbb {B}(c, d)$
associated with a finitely generated
![]() ${\mathbb Z}/n{\mathbb Z}$
-module, we have
${\mathbb Z}/n{\mathbb Z}$
-module, we have
![]() $ H^i_c(\mathbb {D}(d) \cap \mathbb {B}(c, d), M)=0 $
for every i. But this follows from (6.1) since
$ H^i_c(\mathbb {D}(d) \cap \mathbb {B}(c, d), M)=0 $
for every i. But this follows from (6.1) since
![]() $\mathbb {D}(d) \cap \mathbb {B}(c, d)$
is isomorphic to
$\mathbb {D}(d) \cap \mathbb {B}(c, d)$
is isomorphic to
![]() $\mathbb {B}(d) \backslash \mathbb {B}(c)$
as a pseudo-adic space over
$\mathbb {B}(d) \backslash \mathbb {B}(c)$
as a pseudo-adic space over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
.
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
.
We shall prove (b). By the Čech-to-cohomology spectral sequences and by the fact that h is a composition of finite Galois étale morphisms, it is enough to show that, for a constant sheaf M on
![]() $\mathbb {B}(c, d)$
associated with a finitely generated
$\mathbb {B}(c, d)$
associated with a finitely generated
![]() ${\mathbb Z}/n{\mathbb Z}$
-module, the restriction map
${\mathbb Z}/n{\mathbb Z}$
-module, the restriction map
is an isomorphism for every i. Let
![]() $t \in \vert K^{\times } \vert $
be an element with
$t \in \vert K^{\times } \vert $
be an element with
![]() $t <1$
. Then we have
$t <1$
. Then we have
(see also [Reference Huber15, Lemma 1.3]). Moreover,
![]() $H^i(\mathbb {B}(c, t^{1/m} d), M)$
is a finite group for every i (see [Reference Huber14, Proposition 6.1.1]). Therefore, by [Reference Huber14, Lemma 3.9.2 i)], we obtain that
$H^i(\mathbb {B}(c, t^{1/m} d), M)$
is a finite group for every i (see [Reference Huber14, Proposition 6.1.1]). Therefore, by [Reference Huber14, Lemma 3.9.2 i)], we obtain that
for every i. Thus, it suffices to prove that, for every
![]() $m \in {\mathbb Z}_{>0}$
, the restriction map
$m \in {\mathbb Z}_{>0}$
, the restriction map
is an isomorphism for every i. By [Reference Huber14, Example 6.1.2], both sides vanish when
![]() $i \geq 2$
. For
$i \geq 2$
. For
![]() $i \leq 1$
, the assertion can be proved by using the Kummer sequence (see the last paragraph of the proof of Theorem 6.3 in Appendix A).
$i \leq 1$
, the assertion can be proved by using the Kummer sequence (see the last paragraph of the proof of Theorem 6.3 in Appendix A).
(2) Since
![]() $ \mathbb {D}(1) \backslash \{ 0 \} = \bigcup _{\epsilon \in \vert K^{\times } \vert , \, \epsilon < 1} \mathbb {D}(1) \cap \mathbb {B}(\epsilon , 1), $
we have
$ \mathbb {D}(1) \backslash \{ 0 \} = \bigcup _{\epsilon \in \vert K^{\times } \vert , \, \epsilon < 1} \mathbb {D}(1) \cap \mathbb {B}(\epsilon , 1), $
we have
by [Reference Huber14, Proposition 5.4.5 ii)]. Therefore, the assertion follows from (1).
7 Proofs of Theorem 4.8 and Theorem 4.9
In this section, we shall prove Theorem 4.8 and Theorem 4.9. Let K be an algebraically closed complete non-archimedean field with ring of integers
![]() ${\mathcal O}$
.
${\mathcal O}$
.
The main part of the proofs of Theorem 4.8 and Theorem 4.9 is contained in the following lemma.
Lemma 7.1. Let
![]() $\mathcal {X}$
be a separated scheme of finite type over
$\mathcal {X}$
be a separated scheme of finite type over
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion defined by one global section
$\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion defined by one global section
![]() $f \in {\mathcal O}_{\mathcal {X}}(\mathcal {X})$
. Let
$f \in {\mathcal O}_{\mathcal {X}}(\mathcal {X})$
. Let
![]() $ f \colon \mathcal {X} \to \mathop {\mathrm {Spec}} {\mathcal O}[T] $
be the morphism defined by
$ f \colon \mathcal {X} \to \mathop {\mathrm {Spec}} {\mathcal O}[T] $
be the morphism defined by
![]() $T \mapsto f$
, which is also denoted by f. We assume that there is an element
$T \mapsto f$
, which is also denoted by f. We assume that there is an element
![]() $\epsilon _1 \in \vert K^{\times } \vert $
with
$\epsilon _1 \in \vert K^{\times } \vert $
with
![]() $\epsilon _1 \leq 1$
such that
$\epsilon _1 \leq 1$
such that
is smooth over
![]() $\mathbb {B}(\epsilon _1)^*=\mathbb {B}(\epsilon _1) \backslash \{ 0 \}$
. Then, there exists an element
$\mathbb {B}(\epsilon _1)^*=\mathbb {B}(\epsilon _1) \backslash \{ 0 \}$
. Then, there exists an element
![]() $\epsilon _0 \in \vert K^{\times } \vert $
with
$\epsilon _0 \in \vert K^{\times } \vert $
with
![]() $\epsilon _0 \leq \epsilon _1$
such that the following assertions hold for every
$\epsilon _0 \leq \epsilon _1$
such that the following assertions hold for every
![]() $\epsilon \in \vert K^{\times } \vert $
with
$\epsilon \in \vert K^{\times } \vert $
with
![]() $\epsilon \leq \epsilon _0$
, every positive integer n invertible in
$\epsilon \leq \epsilon _0$
, every positive integer n invertible in
![]() ${\mathcal O}$
and every integer i.
${\mathcal O}$
and every integer i.
-
(1)
 $H^i_c(S(\mathcal {Z}, \epsilon )\backslash d(\widehat {\mathcal {Z}}), {\mathbb Z}/n{\mathbb Z})=0$
and
$H^i_c(S(\mathcal {Z}, \epsilon )\backslash d(\widehat {\mathcal {Z}}), {\mathbb Z}/n{\mathbb Z})=0$
and
 $H^i_c(T(\mathcal {Z}, \epsilon _0)\backslash T(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z})=0.$
$H^i_c(T(\mathcal {Z}, \epsilon _0)\backslash T(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z})=0.$
-
(2)
 $ H^i(T(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z}) \overset {\cong }{\to } H^i(S(\mathcal {Z}, \epsilon )^{\circ }, {\mathbb Z}/n{\mathbb Z}). $
$ H^i(T(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z}) \overset {\cong }{\to } H^i(S(\mathcal {Z}, \epsilon )^{\circ }, {\mathbb Z}/n{\mathbb Z}). $
-
(3)
 $ H^i(S(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z})\overset {\cong }{\to } H^i(d(\widehat {\mathcal {Z}}), {\mathbb Z}/n{\mathbb Z}). $
$ H^i(S(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z})\overset {\cong }{\to } H^i(d(\widehat {\mathcal {Z}}), {\mathbb Z}/n{\mathbb Z}). $
-
(4)
 $ H^i(S(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z}) \overset {\cong }{\to } H^i(S(\mathcal {Z}, \epsilon )^{\circ }, {\mathbb Z}/n{\mathbb Z}). $
$ H^i(S(\mathcal {Z}, \epsilon ), {\mathbb Z}/n{\mathbb Z}) \overset {\cong }{\to } H^i(S(\mathcal {Z}, \epsilon )^{\circ }, {\mathbb Z}/n{\mathbb Z}). $
We first deduce Theorem 4.8 and Theorem 4.9 from Lemma 7.1. We will prove Lemma 7.1 in Section 7.3.
7.1 Cohomological descent for analytic adic spaces
We will recall some results on cohomological descent for analytic pseudo-adic spaces. Our basic references are [Reference Artin, Grothendieck and Verdier1, Exposé Vbis] and [Reference Deligne8, Section 5] (see also [24, Section 3]).
Let
![]() $f \colon Y \to X$
be a morphism of finite type of analytic pseudo-adic spaces. Let
$f \colon Y \to X$
be a morphism of finite type of analytic pseudo-adic spaces. Let
be the augmented simplicial object in the category of analytic pseudo-adic spaces of finite type over X (this category has finite projective limits by [Reference Huber14, Proposition 1.10.6]) defined as in [Reference Deligne8, (5.1.4)]. So
![]() $Y_m$
is the
$Y_m$
is the
![]() $(m+1)$
-times fibre product
$(m+1)$
-times fibre product
![]() $Y \times _X \cdots \times _X Y$
for
$Y \times _X \cdots \times _X Y$
for
![]() $m \geq 0$
. As in [Reference Deligne8, (5.1.6)–(5.1.8)], one can associate to the étale topoi
$m \geq 0$
. As in [Reference Deligne8, (5.1.6)–(5.1.8)], one can associate to the étale topoi
![]() $(Y_m)^{\sim }_{\mathrm {\acute {e}t}}$
(
$(Y_m)^{\sim }_{\mathrm {\acute {e}t}}$
(
![]() $m \geq 0$
) a topos
$m \geq 0$
) a topos
![]() $(Y_{\bullet })^{\sim }$
. Moreover, as in [Reference Deligne8, (5.1.11)], we have a morphism of topoi
$(Y_{\bullet })^{\sim }$
. Moreover, as in [Reference Deligne8, (5.1.11)], we have a morphism of topoi
from
![]() $(Y_{\bullet })^{\sim }$
to the étale topos
$(Y_{\bullet })^{\sim }$
to the étale topos
![]() $X^{\sim }_{\mathrm {\acute {e}t}}$
of X. We say that
$X^{\sim }_{\mathrm {\acute {e}t}}$
of X. We say that
![]() $f \colon Y \to X$
is a morphism of cohomological descent for torsion abelian étale sheaves if, for every torsion abelian étale sheaf
$f \colon Y \to X$
is a morphism of cohomological descent for torsion abelian étale sheaves if, for every torsion abelian étale sheaf
![]() $\mathcal {F}$
on X, the natural morphism
$\mathcal {F}$
on X, the natural morphism
in the derived category
![]() $D^+(X^{\sim }_{\mathrm {\acute {e}t}})$
is an isomorphism (see [Reference Artin, Grothendieck and Verdier1, Exposé Vbis, Section 2] for details). As a consequence of the proper base change theorem for analytic pseudo-adic spaces [Reference Huber14, Theorem 4.4.1], we have the following proposition. We formulate it in the generality we need.
$D^+(X^{\sim }_{\mathrm {\acute {e}t}})$
is an isomorphism (see [Reference Artin, Grothendieck and Verdier1, Exposé Vbis, Section 2] for details). As a consequence of the proper base change theorem for analytic pseudo-adic spaces [Reference Huber14, Theorem 4.4.1], we have the following proposition. We formulate it in the generality we need.
Proposition 7.2. Let
![]() $f \colon Y \to X$
be a morphism of analytic adic spaces which is proper, of finite type and surjective. Then for every morphism
$f \colon Y \to X$
be a morphism of analytic adic spaces which is proper, of finite type and surjective. Then for every morphism
![]() $Z \to X$
of analytic pseudo-adic spaces, the base change
$Z \to X$
of analytic pseudo-adic spaces, the base change
![]() $f \colon Y \times _X Z \to Z$
is of cohomological descent for torsion abelian étale sheaves.
$f \colon Y \times _X Z \to Z$
is of cohomological descent for torsion abelian étale sheaves.
Proof. First, we note that the fibre product
![]() $Y \times _X Z \to Z$
exists by [Reference Huber14, Proposition 1.10.6]. By the proper base change theorem for analytic pseudo-adic spaces [Reference Huber14, Theorem 4.4.1 (b)], it suffices to prove that, for every geometric point
$Y \times _X Z \to Z$
exists by [Reference Huber14, Proposition 1.10.6]. By the proper base change theorem for analytic pseudo-adic spaces [Reference Huber14, Theorem 4.4.1 (b)], it suffices to prove that, for every geometric point
![]() $S \to X$
, the base change
$S \to X$
, the base change
![]() $Y \times _X S \to S$
is of cohomological descent for torsion abelian étale sheaves. It is enough to show that there exists a section
$Y \times _X S \to S$
is of cohomological descent for torsion abelian étale sheaves. It is enough to show that there exists a section
![]() $S \to Y \times _X S$
(see [SGA Reference Cadoret5 II, Exposé Vbis, Proposition 3.3.1] for example). The existence of a section can be easily proved in our case: By the properness of f and [Reference Huber14, Corollary 1.3.9], we may assume that S is of rank
$S \to Y \times _X S$
(see [SGA Reference Cadoret5 II, Exposé Vbis, Proposition 3.3.1] for example). The existence of a section can be easily proved in our case: By the properness of f and [Reference Huber14, Corollary 1.3.9], we may assume that S is of rank
![]() $1$
. Then it is well known.
$1$
. Then it is well known.
For future reference, we state the following corollaries of Proposition 7.2.
Corollary 7.3. Let
![]() $\mathcal {X}$
be a separated scheme of finite type over
$\mathcal {X}$
be a separated scheme of finite type over
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $\beta _0 \colon \mathcal {Y} \to \mathcal {X}$
be a proper surjective morphism. We put
$\beta _0 \colon \mathcal {Y} \to \mathcal {X}$
be a proper surjective morphism. We put
![]() $ \beta \colon \mathcal {Y}_{\bullet }=\mathop {\mathrm {cosq}}\nolimits _0(\mathcal {Y}/\mathcal {X}) \to \mathcal {X}. $
Let
$ \beta \colon \mathcal {Y}_{\bullet }=\mathop {\mathrm {cosq}}\nolimits _0(\mathcal {Y}/\mathcal {X}) \to \mathcal {X}. $
Let
![]() $Z \subset d(\widehat {\mathcal {X}})$
be a taut locally closed subset. Then we have the following spectral sequence:
$Z \subset d(\widehat {\mathcal {X}})$
be a taut locally closed subset. Then we have the following spectral sequence:
where
![]() $Z_i$
is the inverse image of Z under the morphism
$Z_i$
is the inverse image of Z under the morphism
![]() $d(\beta _i) \colon d(\widehat {\mathcal {Y}}_i) \to d(\widehat {\mathcal {X}})$
.
$d(\beta _i) \colon d(\widehat {\mathcal {Y}}_i) \to d(\widehat {\mathcal {X}})$
.
Proof. This is an immediate consequence of Proposition 7.2 and [Reference Artin, Grothendieck and Verdier1, Exposé Vbis, Proposition 2.5.5].
Corollary 7.4. Let
![]() $\beta _0 \colon Y \to X$
be a morphism of analytic adic spaces which is proper, of finite type and surjective. We put
$\beta _0 \colon Y \to X$
be a morphism of analytic adic spaces which is proper, of finite type and surjective. We put
![]() $\beta \colon Y_{\bullet }=\mathop {\mathrm {cosq}}\nolimits _0(Y/X) \to X$
. Let
$\beta \colon Y_{\bullet }=\mathop {\mathrm {cosq}}\nolimits _0(Y/X) \to X$
. Let
![]() $i \colon Z \hookrightarrow W$
be an inclusion of locally closed subsets of X. For
$i \colon Z \hookrightarrow W$
be an inclusion of locally closed subsets of X. For
![]() $m \geq 0$
, let
$m \geq 0$
, let
![]() $i_m \colon Z_m \hookrightarrow W_m$
be the pullback of i by
$i_m \colon Z_m \hookrightarrow W_m$
be the pullback of i by
![]() $\beta _m \colon Y_m \to X$
. Let
$\beta _m \colon Y_m \to X$
. Let
and
be distinguished triangles. Let
![]() $\rho \geq -1$
be an integer. If
$\rho \geq -1$
be an integer. If
![]() $\tau _{\leq (\rho -m)}\mathcal {K}_m = 0$
for every
$\tau _{\leq (\rho -m)}\mathcal {K}_m = 0$
for every
![]() $0 \leq m \leq \rho +1$
, then we have
$0 \leq m \leq \rho +1$
, then we have
![]() $\tau _{\leq \rho }\mathcal {K}=0$
.
$\tau _{\leq \rho }\mathcal {K}=0$
.
Proof. The assertion follows from Proposition 7.2 and an argument similar to that of the proof of [Reference Orgogozo25, Lemma 4.1] (see also the proof of Lemma 3.5).
7.2 Reduction to the key case
In this subsection, we deduce Theorem 4.8 and Theorem 4.9 from Lemma 7.1. A theorem of de Jong [Reference de Jong6, Theorem 4.1] will, again, play a key role.
Lemma 7.5. To prove Theorem 4.8, it suffices to prove the following statement
![]() $\textbf {P}_c(i)$
for every integer i.
$\textbf {P}_c(i)$
for every integer i.
-
 $\textbf {P}_c(i)$
: For every separated scheme
$\textbf {P}_c(i)$
: For every separated scheme
 $\mathcal {X}$
of finite type over
$\mathcal {X}$
of finite type over
 ${\mathcal O}$
and every closed immersion
${\mathcal O}$
and every closed immersion
 $\mathcal {Z} \hookrightarrow \mathcal {X}$
defined by one global section
$\mathcal {Z} \hookrightarrow \mathcal {X}$
defined by one global section
 $f \in {\mathcal O}_{\mathcal {X}}(\mathcal {X})$
, there exists an element
$f \in {\mathcal O}_{\mathcal {X}}(\mathcal {X})$
, there exists an element
 $\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
$\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
 $\epsilon \in \vert K^{\times } \vert $
with
$\epsilon \in \vert K^{\times } \vert $
with
 $\epsilon \leq \epsilon _0$
and every positive integer n invertible in
$\epsilon \leq \epsilon _0$
and every positive integer n invertible in
 ${\mathcal O}$
, we have for every
${\mathcal O}$
, we have for every $$\begin{align*}H^j_c(S(\mathcal{Z}, \epsilon)\backslash d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z})=0 \quad \text{and} \quad H^j_c(T(\mathcal{Z}, \epsilon_0)\backslash T(\mathcal{Z}, \epsilon), {\mathbb Z}/n{\mathbb Z})=0 \end{align*}$$
$$\begin{align*}H^j_c(S(\mathcal{Z}, \epsilon)\backslash d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z})=0 \quad \text{and} \quad H^j_c(T(\mathcal{Z}, \epsilon_0)\backslash T(\mathcal{Z}, \epsilon), {\mathbb Z}/n{\mathbb Z})=0 \end{align*}$$
 $j \leq i$
.
$j \leq i$
.
Proof.
Step 1. To prove Theorem 4.8, it suffices to prove the following statement
![]() $\textbf {P}^{\prime }_c(i)$
for every i.
$\textbf {P}^{\prime }_c(i)$
for every i.
-
 $\textbf {P}^{\prime }_c(i)$
: For every separated scheme
$\textbf {P}^{\prime }_c(i)$
: For every separated scheme
 $\mathcal {X}$
of finite type over
$\mathcal {X}$
of finite type over
 ${\mathcal O}$
and every closed immersion
${\mathcal O}$
and every closed immersion
 $\mathcal {Z} \hookrightarrow \mathcal {X}$
of finite presentation, there exists an element
$\mathcal {Z} \hookrightarrow \mathcal {X}$
of finite presentation, there exists an element
 $\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
$\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
 $\epsilon \in \vert K^{\times } \vert $
with
$\epsilon \in \vert K^{\times } \vert $
with
 $\epsilon \leq \epsilon _0$
and every positive integer n invertible in
$\epsilon \leq \epsilon _0$
and every positive integer n invertible in
 ${\mathcal O}$
, we have for every
${\mathcal O}$
, we have for every $$\begin{align*}H^j_c(S(\mathcal{Z}, \epsilon)\backslash d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z})=0 \quad \text{and} \quad H^j_c(T(\mathcal{Z}, \epsilon_0)\backslash T(\mathcal{Z}, \epsilon), {\mathbb Z}/n{\mathbb Z})=0 \end{align*}$$
$$\begin{align*}H^j_c(S(\mathcal{Z}, \epsilon)\backslash d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z})=0 \quad \text{and} \quad H^j_c(T(\mathcal{Z}, \epsilon_0)\backslash T(\mathcal{Z}, \epsilon), {\mathbb Z}/n{\mathbb Z})=0 \end{align*}$$
 $j \leq i$
.
$j \leq i$
.
Indeed, let
![]() $\mathcal {X}$
be a separated scheme of finite type over
$\mathcal {X}$
be a separated scheme of finite type over
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation. By applying [Reference Huber14, Remark 5.5.11 iv)] to the following diagram
$\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion of finite presentation. By applying [Reference Huber14, Remark 5.5.11 iv)] to the following diagram
we have the following long exact sequence:
 $$\begin{align*}\begin{aligned} \cdots \to H^i_c(S(\mathcal{Z}, \epsilon)\backslash d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z}) \to\ & H^i_c(S(\mathcal{Z}, \epsilon), {\mathbb Z}/n{\mathbb Z}) \\ \to H^i_c(d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z}) \to\ & H^{i+1}_c(S(\mathcal{Z}, \epsilon)\backslash d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z}) \to \cdots. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \cdots \to H^i_c(S(\mathcal{Z}, \epsilon)\backslash d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z}) \to\ & H^i_c(S(\mathcal{Z}, \epsilon), {\mathbb Z}/n{\mathbb Z}) \\ \to H^i_c(d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z}) \to\ & H^{i+1}_c(S(\mathcal{Z}, \epsilon)\backslash d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z}) \to \cdots. \end{aligned} \end{align*}$$
We note that
![]() $ S(\mathcal {Z}, \epsilon )\backslash d(\widehat {\mathcal {Z}}) = (d(\widehat {\mathcal {X}})\backslash d(\widehat {\mathcal {Z}}))\backslash Q(\mathcal {Z}, \epsilon ). $
Hence, we have a similar spectral sequence for the diagram
$ S(\mathcal {Z}, \epsilon )\backslash d(\widehat {\mathcal {Z}}) = (d(\widehat {\mathcal {X}})\backslash d(\widehat {\mathcal {Z}}))\backslash Q(\mathcal {Z}, \epsilon ). $
Hence, we have a similar spectral sequence for the diagram
Moreover, for elements
![]() $\epsilon , \epsilon ' \in \vert K^{\times } \vert $
with
$\epsilon , \epsilon ' \in \vert K^{\times } \vert $
with
![]() $\epsilon \leq \epsilon '$
, we have a similar spectral sequence for the diagram
$\epsilon \leq \epsilon '$
, we have a similar spectral sequence for the diagram
By [Reference Huber14, Proposition 5.5.8], there exists an integer N, which is independent of n and
![]() $\epsilon , \epsilon ' \in \vert K^{\times } \vert $
, such that we have
$\epsilon , \epsilon ' \in \vert K^{\times } \vert $
, such that we have
for every
![]() $i \geq N$
. Our claim follows from these results.
$i \geq N$
. Our claim follows from these results.
Step 2. We suppose that
![]() $\textbf {P}_c(i)$
holds for every i. We will prove
$\textbf {P}_c(i)$
holds for every i. We will prove
![]() $\textbf {P}^{\prime }_c(i)$
by induction on i. The assertion holds trivially for
$\textbf {P}^{\prime }_c(i)$
by induction on i. The assertion holds trivially for
![]() $i=-1$
. We assume that
$i=-1$
. We assume that
![]() $\textbf {P}^{\prime }_c(i_0-1)$
holds. First, we claim that, to prove
$\textbf {P}^{\prime }_c(i_0-1)$
holds. First, we claim that, to prove
![]() $\textbf {P}^{\prime }_c(i_0)$
, we may assume that
$\textbf {P}^{\prime }_c(i_0)$
, we may assume that
![]() $\mathcal {X}$
is integral.
$\mathcal {X}$
is integral.
We may assume that
![]() $\mathcal {X}$
is flat over
$\mathcal {X}$
is flat over
![]() ${\mathcal O}$
. Then every irreducible component of
${\mathcal O}$
. Then every irreducible component of
![]() $\mathcal {X}$
dominates
$\mathcal {X}$
dominates
![]() $\mathop {\mathrm {Spec}} {\mathcal O}$
, and, hence,
$\mathop {\mathrm {Spec}} {\mathcal O}$
, and, hence,
![]() $\mathcal {X}$
has finitely many irreducible components. Let
$\mathcal {X}$
has finitely many irreducible components. Let
![]() $\mathcal {X}'$
be the disjoint union of the irreducible components of
$\mathcal {X}'$
be the disjoint union of the irreducible components of
![]() $\mathcal {X}$
. Then
$\mathcal {X}$
. Then
![]() $\mathcal {X}' \to \mathcal {X}$
is proper and surjective. By
$\mathcal {X}' \to \mathcal {X}$
is proper and surjective. By
![]() $\textbf {P}^{\prime }_c(i_0-1)$
and Corollary 7.3, it suffices to prove
$\textbf {P}^{\prime }_c(i_0-1)$
and Corollary 7.3, it suffices to prove
![]() $\textbf {P}^{\prime }_c(i_0)$
for
$\textbf {P}^{\prime }_c(i_0)$
for
![]() $\mathcal {X}'$
and
$\mathcal {X}'$
and
![]() $\mathcal {Z} \times _{\mathcal {X}} \mathcal {X}'$
. By considering each component of
$\mathcal {Z} \times _{\mathcal {X}} \mathcal {X}'$
. By considering each component of
![]() $\mathcal {X}'$
separately, our claim follows.
$\mathcal {X}'$
separately, our claim follows.
Step 3. We assume that
![]() $\mathcal {X}$
is integral. We may assume further that
$\mathcal {X}$
is integral. We may assume further that
![]() $\mathcal {Z}$
is not equal to
$\mathcal {Z}$
is not equal to
![]() $\mathcal {X}$
. Let
$\mathcal {X}$
. Let
![]() $\mathcal {Y} \to \mathcal {X}$
be the blow-up of
$\mathcal {Y} \to \mathcal {X}$
be the blow-up of
![]() $\mathcal {X}$
along
$\mathcal {X}$
along
![]() $\mathcal {Z}$
, which is proper and surjective. By
$\mathcal {Z}$
, which is proper and surjective. By
![]() $\textbf {P}^{\prime }_c(i_0-1)$
and Corollary 7.3, it suffices to prove
$\textbf {P}^{\prime }_c(i_0-1)$
and Corollary 7.3, it suffices to prove
![]() $\textbf {P}^{\prime }_c(i_0)$
for
$\textbf {P}^{\prime }_c(i_0)$
for
![]() $\mathcal {Y}$
and
$\mathcal {Y}$
and
![]() $\mathcal {Z} \times _{\mathcal {X}} \mathcal {Y}$
. Consequently, to prove
$\mathcal {Z} \times _{\mathcal {X}} \mathcal {Y}$
. Consequently, to prove
![]() $\textbf {P}^{\prime }_c(i_0)$
, we may assume further that
$\textbf {P}^{\prime }_c(i_0)$
, we may assume further that
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
is locally defined by one function.
$\mathcal {Z} \hookrightarrow \mathcal {X}$
is locally defined by one function.
Finally, let
![]() $\mathcal {X}=\bigcup _{\alpha \in I} \mathcal {U}_{\alpha }$
be a finite affine covering such that
$\mathcal {X}=\bigcup _{\alpha \in I} \mathcal {U}_{\alpha }$
be a finite affine covering such that
![]() $\mathcal {Z} \cap \mathcal {U}_{\alpha } \hookrightarrow \mathcal {U}_{\alpha }$
is defined by one global section in
$\mathcal {Z} \cap \mathcal {U}_{\alpha } \hookrightarrow \mathcal {U}_{\alpha }$
is defined by one global section in
![]() ${\mathcal O}_{\mathcal {X}}(\mathcal {U}_{\alpha })$
for every
${\mathcal O}_{\mathcal {X}}(\mathcal {U}_{\alpha })$
for every
![]() $\alpha \in I$
. We have the following spectral sequence by [Reference Huber14, Remark 5.5.12 iii)]:
$\alpha \in I$
. We have the following spectral sequence by [Reference Huber14, Remark 5.5.12 iii)]:
 $$\begin{align*}E^{i, j}_{1}=\bigoplus_{J \subset I, \, \sharp J = -i+1} H^j_c(S(\mathcal{Z}_J, \epsilon) \backslash d(\widehat{\mathcal{Z}}_J), {\mathbb Z}/n{\mathbb Z}) \Rightarrow H^{i+j}_c(S(\mathcal{Z}, \epsilon) \backslash d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z}). \end{align*}$$
$$\begin{align*}E^{i, j}_{1}=\bigoplus_{J \subset I, \, \sharp J = -i+1} H^j_c(S(\mathcal{Z}_J, \epsilon) \backslash d(\widehat{\mathcal{Z}}_J), {\mathbb Z}/n{\mathbb Z}) \Rightarrow H^{i+j}_c(S(\mathcal{Z}, \epsilon) \backslash d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z}). \end{align*}$$
Here, we write
![]() $\mathcal {U}_J:= \cap _{\alpha \in J}\mathcal {U}_{\alpha }$
and
$\mathcal {U}_J:= \cap _{\alpha \in J}\mathcal {U}_{\alpha }$
and
![]() $\mathcal {Z}_J := \mathcal {Z} \times _{\mathcal {X}} \mathcal {U}_J \hookrightarrow \mathcal {U}_J$
. We have a similar spectral sequence for
$\mathcal {Z}_J := \mathcal {Z} \times _{\mathcal {X}} \mathcal {U}_J \hookrightarrow \mathcal {U}_J$
. We have a similar spectral sequence for
![]() $T(\mathcal {Z}, \epsilon ')\backslash T(\mathcal {Z}, \epsilon )$
. Since
$T(\mathcal {Z}, \epsilon ')\backslash T(\mathcal {Z}, \epsilon )$
. Since
![]() $\textbf {P}_c(i)$
holds for every i by hypothesis, it follows that
$\textbf {P}_c(i)$
holds for every i by hypothesis, it follows that
![]() $\textbf {P}^{\prime }_c(i_0)$
holds for
$\textbf {P}^{\prime }_c(i_0)$
holds for
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
.
$\mathcal {Z} \hookrightarrow \mathcal {X}$
.
Lemma 7.6. To prove Theorem 4.9, it suffices to prove the following statement
![]() $\textbf {P}(i)$
for every integer i.
$\textbf {P}(i)$
for every integer i.
-
 $\textbf {P}(i)$
: For a separated scheme
$\textbf {P}(i)$
: For a separated scheme
 $\mathcal {X}$
of finite type over
$\mathcal {X}$
of finite type over
 ${\mathcal O}$
and a closed immersion
${\mathcal O}$
and a closed immersion
 $\mathcal {Z} \hookrightarrow \mathcal {X}$
defined by one global section
$\mathcal {Z} \hookrightarrow \mathcal {X}$
defined by one global section
 $f \in {\mathcal O}_{\mathcal {X}}(\mathcal {X})$
, we consider the following distinguished triangles:
$f \in {\mathcal O}_{\mathcal {X}}(\mathcal {X})$
, we consider the following distinguished triangles:  $$\begin{align*}R\Gamma(T(\mathcal{Z}, \epsilon), {\mathbb Z}/n{\mathbb Z}) \to R\Gamma(S(\mathcal{Z}, \epsilon)^{\circ}, {\mathbb Z}/n{\mathbb Z}) \to \mathcal{K}_1(\epsilon, n) \to, \end{align*}$$
$$\begin{align*}R\Gamma(T(\mathcal{Z}, \epsilon), {\mathbb Z}/n{\mathbb Z}) \to R\Gamma(S(\mathcal{Z}, \epsilon)^{\circ}, {\mathbb Z}/n{\mathbb Z}) \to \mathcal{K}_1(\epsilon, n) \to, \end{align*}$$
 $$\begin{align*}R\Gamma(S(\mathcal{Z}, \epsilon), {\mathbb Z}/n{\mathbb Z}) \to R\Gamma(d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z}) \to \mathcal{K}_2(\epsilon, n) \to, \end{align*}$$
For every
$$\begin{align*}R\Gamma(S(\mathcal{Z}, \epsilon), {\mathbb Z}/n{\mathbb Z}) \to R\Gamma(d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z}) \to \mathcal{K}_2(\epsilon, n) \to, \end{align*}$$
For every $$\begin{align*}R\Gamma(S(\mathcal{Z}, \epsilon), {\mathbb Z}/n{\mathbb Z}) \to R\Gamma(S(\mathcal{Z}, \epsilon)^{\circ}, {\mathbb Z}/n{\mathbb Z}) \to \mathcal{K}_3(\epsilon, n) \to. \end{align*}$$
$$\begin{align*}R\Gamma(S(\mathcal{Z}, \epsilon), {\mathbb Z}/n{\mathbb Z}) \to R\Gamma(S(\mathcal{Z}, \epsilon)^{\circ}, {\mathbb Z}/n{\mathbb Z}) \to \mathcal{K}_3(\epsilon, n) \to. \end{align*}$$
 $\mathcal {X}$
and
$\mathcal {X}$
and
 $\mathcal {Z} \hookrightarrow \mathcal {X}$
as above, there exists an element
$\mathcal {Z} \hookrightarrow \mathcal {X}$
as above, there exists an element
 $\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
$\epsilon _0 \in \vert K^{\times } \vert $
such that, for every
 $\epsilon \in \vert K^{\times } \vert $
with
$\epsilon \in \vert K^{\times } \vert $
with
 $\epsilon \leq \epsilon _0$
and every positive integer n invertible in
$\epsilon \leq \epsilon _0$
and every positive integer n invertible in
 ${\mathcal O}$
, we have
${\mathcal O}$
, we have
 $ \tau _{\leq i}\mathcal {K}_m(\epsilon , n)=0 $
for every
$ \tau _{\leq i}\mathcal {K}_m(\epsilon , n)=0 $
for every
 $m \in \{ 1, 2, 3 \}$
.
$m \in \{ 1, 2, 3 \}$
.
Proof. The assertion can be proved by a similar argument as in the proof of Lemma 7.5.
We will now prove the desired statement:
Proof. We suppose that Lemma 7.1 holds. By Lemma 7.5 and Lemma 7.6, it suffices to prove that
![]() $\textbf {P}_c(i)$
and
$\textbf {P}_c(i)$
and
![]() $\textbf {P}(i)$
hold for every i. Let us show the assertions by induction on i. The assertions
$\textbf {P}(i)$
hold for every i. Let us show the assertions by induction on i. The assertions
![]() $\textbf {P}_c(-1)$
and
$\textbf {P}_c(-1)$
and
![]() $\textbf {P}(-2)$
hold trivially. Assume that
$\textbf {P}(-2)$
hold trivially. Assume that
![]() $\textbf {P}_c(i-1)$
and
$\textbf {P}_c(i-1)$
and
![]() $\textbf {P}(i-1)$
hold. Let
$\textbf {P}(i-1)$
hold. Let
![]() $\mathcal {X}$
be a separated scheme of finite type over
$\mathcal {X}$
be a separated scheme of finite type over
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion defined by one global section
$\mathcal {Z} \hookrightarrow \mathcal {X}$
a closed immersion defined by one global section
![]() $f \in {\mathcal O}_{\mathcal {X}}(\mathcal {X})$
. We shall show that
$f \in {\mathcal O}_{\mathcal {X}}(\mathcal {X})$
. We shall show that
![]() $\textbf {P}_c(i)$
and
$\textbf {P}_c(i)$
and
![]() $\textbf {P}(i)$
hold for
$\textbf {P}(i)$
hold for
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Z}$
. As in the proof of Lemma 7.5, we may assume that
$\mathcal {Z}$
. As in the proof of Lemma 7.5, we may assume that
![]() $\mathcal {X}$
is integral. First, we prove the assertions in the case where K is of characteristic zero. By [Reference de Jong6, Theorem 4.1], there is an integral alteration
$\mathcal {X}$
is integral. First, we prove the assertions in the case where K is of characteristic zero. By [Reference de Jong6, Theorem 4.1], there is an integral alteration
![]() $Y \to \mathcal {X}_K$
such that Y is smooth over K. By Nagata’s compactification theorem, there is a proper surjective morphism
$Y \to \mathcal {X}_K$
such that Y is smooth over K. By Nagata’s compactification theorem, there is a proper surjective morphism
![]() $\mathcal {Y} \to \mathcal {X}$
such that
$\mathcal {Y} \to \mathcal {X}$
such that
![]() $\mathcal {Y}_K \cong Y$
over
$\mathcal {Y}_K \cong Y$
over
![]() $\mathcal {X}_K$
and
$\mathcal {X}_K$
and
![]() $\mathcal {Y}$
is integral. By the induction hypothesis, Corollary 7.3, and Corollary 7.4, it suffices to prove
$\mathcal {Y}$
is integral. By the induction hypothesis, Corollary 7.3, and Corollary 7.4, it suffices to prove
![]() $\textbf {P}_c(i)$
and
$\textbf {P}_c(i)$
and
![]() $\textbf {P}(i)$
for
$\textbf {P}(i)$
for
![]() $\mathcal {Y}$
and
$\mathcal {Y}$
and
![]() $\mathcal {Z} \times _{\mathcal {X}} \mathcal {Y}$
. Therefore, we may assume that
$\mathcal {Z} \times _{\mathcal {X}} \mathcal {Y}$
. Therefore, we may assume that
![]() $\mathcal {X}_K$
is smooth over K. Let
$\mathcal {X}_K$
is smooth over K. Let
be the morphism defined by
![]() $T \mapsto f$
. Since K is of characteristic zero, there is an open dense subset
$T \mapsto f$
. Since K is of characteristic zero, there is an open dense subset
![]() $W \subset \mathop {\mathrm {Spec}} K[T]$
such that
$W \subset \mathop {\mathrm {Spec}} K[T]$
such that
![]() $f_K$
is smooth over W. It follows from [Reference Huber14, Proposition 1.9.6] that there exists an open subset
$f_K$
is smooth over W. It follows from [Reference Huber14, Proposition 1.9.6] that there exists an open subset
![]() $V \subset \mathbb {B}(1)$
whose complement consists of finitely many K-rational points of
$V \subset \mathbb {B}(1)$
whose complement consists of finitely many K-rational points of
![]() $\mathbb {B}(1)$
such that
$\mathbb {B}(1)$
such that
![]() $d(f) \colon d(\widehat {\mathcal {X}}) \to \mathbb {B}(1)$
is smooth over V. Thus,
$d(f) \colon d(\widehat {\mathcal {X}}) \to \mathbb {B}(1)$
is smooth over V. Thus,
![]() $\textbf {P}_c(i)$
and
$\textbf {P}_c(i)$
and
![]() $\textbf {P}(i)$
hold for
$\textbf {P}(i)$
hold for
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Z}$
since we suppose that Lemma 7.1 holds.
$\mathcal {Z}$
since we suppose that Lemma 7.1 holds.
Let us now suppose that K is of characteristic
![]() $p>0$
. As above, let
$p>0$
. As above, let
![]() $ f \colon \mathcal {X} \to \mathop {\mathrm {Spec}} {\mathcal O}[T] $
be the morphism defined by
$ f \colon \mathcal {X} \to \mathop {\mathrm {Spec}} {\mathcal O}[T] $
be the morphism defined by
![]() $T \mapsto f$
. If f is not dominant, then
$T \mapsto f$
. If f is not dominant, then
![]() $\textbf {P}_c(i)$
and
$\textbf {P}_c(i)$
and
![]() $\textbf {P}(i)$
hold trivially for
$\textbf {P}(i)$
hold trivially for
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Z}$
. Thus, we may assume that f is dominant. By applying [Reference de Jong6, Theorem 4.1] to the underlying reduced subscheme of
$\mathcal {Z}$
. Thus, we may assume that f is dominant. By applying [Reference de Jong6, Theorem 4.1] to the underlying reduced subscheme of
![]() $ \mathcal {X} \times _{\mathop {\mathrm {Spec}} {\mathcal O}[T]} \mathop {\mathrm {Spec}} K(T^{1/p^{\infty }}), $
where
$ \mathcal {X} \times _{\mathop {\mathrm {Spec}} {\mathcal O}[T]} \mathop {\mathrm {Spec}} K(T^{1/p^{\infty }}), $
where
![]() $K(T^{1/p^{\infty }})$
is the perfection of
$K(T^{1/p^{\infty }})$
is the perfection of
![]() $K(T)$
, we find an alteration
$K(T)$
, we find an alteration
such that Y is integral and smooth over
![]() $K(T^{1/p^{N}})$
for some integer
$K(T^{1/p^{N}})$
for some integer
![]() $N \geq 0$
. By Nagata’s compactification theorem, there is a proper surjective morphism
$N \geq 0$
. By Nagata’s compactification theorem, there is a proper surjective morphism
whose base change to
![]() $\mathop {\mathrm {Spec}} K(T^{1/p^{N}})$
is isomorphic to
$\mathop {\mathrm {Spec}} K(T^{1/p^{N}})$
is isomorphic to
![]() $g_K$
. As above, it suffices to prove
$g_K$
. As above, it suffices to prove
![]() $\textbf {P}_c(i)$
and
$\textbf {P}_c(i)$
and
![]() $\textbf {P}(i)$
for
$\textbf {P}(i)$
for
![]() $\mathcal {Y}$
and
$\mathcal {Y}$
and
![]() $\mathcal {Z} \times _{\mathcal {X}} \mathcal {Y}$
.
$\mathcal {Z} \times _{\mathcal {X}} \mathcal {Y}$
.
Let
![]() $f'$
be the image of
$f'$
be the image of
![]() $T^{1/p^{N}} \in {\mathcal O}[T^{1/p^{N}}]$
in
$T^{1/p^{N}} \in {\mathcal O}[T^{1/p^{N}}]$
in
![]() ${\mathcal O}_{\mathcal {Y}}(\mathcal {Y})$
, and let
${\mathcal O}_{\mathcal {Y}}(\mathcal {Y})$
, and let
![]() $\mathcal {Z}' \hookrightarrow \mathcal {Y}$
be the closed subscheme defined by
$\mathcal {Z}' \hookrightarrow \mathcal {Y}$
be the closed subscheme defined by
![]() $f'$
. Then we have
$f'$
. Then we have
![]() $(f')^{p^N}=f$
, where the image of f in
$(f')^{p^N}=f$
, where the image of f in
![]() ${\mathcal O}_{\mathcal {Y}}(\mathcal {Y})$
is also denoted by f. Hence, the closed immersion
${\mathcal O}_{\mathcal {Y}}(\mathcal {Y})$
is also denoted by f. Hence, the closed immersion
![]() $ d(\widehat {\mathcal {Z}}') \hookrightarrow d((\mathcal {Z} \times _{\mathcal {X}} \mathcal {Y})^{\wedge }) $
is a homeomorphism and we have
$ d(\widehat {\mathcal {Z}}') \hookrightarrow d((\mathcal {Z} \times _{\mathcal {X}} \mathcal {Y})^{\wedge }) $
is a homeomorphism and we have
for every
![]() $\epsilon \in \vert K^{\times } \vert $
. Thus, it suffices to prove that
$\epsilon \in \vert K^{\times } \vert $
. Thus, it suffices to prove that
![]() $\textbf {P}_c(i)$
and
$\textbf {P}_c(i)$
and
![]() $\textbf {P}(i)$
hold for
$\textbf {P}(i)$
hold for
![]() $\mathcal {Y}$
and
$\mathcal {Y}$
and
![]() $\mathcal {Z}'$
(see [Reference Huber14, Proposition 2.3.7]). By the construction, the generic fibre of the morphism
$\mathcal {Z}'$
(see [Reference Huber14, Proposition 2.3.7]). By the construction, the generic fibre of the morphism
![]() $ \mathcal {Y} \to \mathop {\mathrm {Spec}} {\mathcal O}[T] $
defined by
$ \mathcal {Y} \to \mathop {\mathrm {Spec}} {\mathcal O}[T] $
defined by
![]() $T \mapsto f'$
is smooth over
$T \mapsto f'$
is smooth over
![]() $K(T)$
. Therefore, as in the case of characteristic zero, Lemma 7.1 implies
$K(T)$
. Therefore, as in the case of characteristic zero, Lemma 7.1 implies
![]() $\textbf {P}_c(i)$
and
$\textbf {P}_c(i)$
and
![]() $\textbf {P}(i)$
for
$\textbf {P}(i)$
for
![]() $\mathcal {Y}$
and
$\mathcal {Y}$
and
![]() $\mathcal {Z}'$
.
$\mathcal {Z}'$
.
The proof of Lemma 7.7 is complete.
7.3 Proof of the key case
In this subsection, we prove Lemma 7.1 and finish the proofs of Theorem 4.8 and Theorem 4.9.
Proof of Lemma 7.1
We may assume that
![]() $\mathcal {X}$
is flat over
$\mathcal {X}$
is flat over
![]() $\mathop {\mathrm {Spec}} {\mathcal O}$
. Then
$\mathop {\mathrm {Spec}} {\mathcal O}$
. Then
![]() $\mathcal {X}$
is of finite presentation over
$\mathcal {X}$
is of finite presentation over
![]() $\mathop {\mathrm {Spec}} {\mathcal O}$
by [Reference Raynaud and Gruson28, Première partie, Corollaire 3.4.7]. By Proposition 6.6 and Theorem 6.10, there exists an element
$\mathop {\mathrm {Spec}} {\mathcal O}$
by [Reference Raynaud and Gruson28, Première partie, Corollaire 3.4.7]. By Proposition 6.6 and Theorem 6.10, there exists an element
![]() $\epsilon _0 \in \vert K^{\times } \vert $
with
$\epsilon _0 \in \vert K^{\times } \vert $
with
![]() $\epsilon _0 \leq \epsilon _1$
such that, for all
$\epsilon _0 \leq \epsilon _1$
such that, for all
![]() $a, b \in \vert K^{\times } \vert $
with
$a, b \in \vert K^{\times } \vert $
with
![]() $a < b \leq \epsilon _0$
and every positive integer n invertible in
$a < b \leq \epsilon _0$
and every positive integer n invertible in
![]() ${\mathcal O}^{\times }$
, there exists a finite étale morphism
${\mathcal O}^{\times }$
, there exists a finite étale morphism
such that h is a composition of finite Galois étale morphisms and the pullback
is a constant sheaf associated with a finitely generated
![]() ${\mathbb Z}/n{\mathbb Z}$
-module for every i. We shall show that
${\mathbb Z}/n{\mathbb Z}$
-module for every i. We shall show that
![]() $\epsilon _0$
satisfies the desired properties. Let n be a positive integer invertible in
$\epsilon _0$
satisfies the desired properties. Let n be a positive integer invertible in
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\epsilon \in \vert K^{\times } \vert $
an element with
$\epsilon \in \vert K^{\times } \vert $
an element with
![]() $\epsilon \leq \epsilon _0$
.
$\epsilon \leq \epsilon _0$
.
(1) We have
Keeping the base change theorem [Reference Huber14, Theorem 5.4.6] for
![]() $Rd(f)_!$
in mind, we have the following spectral sequences by [Reference Huber14, Remark 5.5.12 i)]:
$Rd(f)_!$
in mind, we have the following spectral sequences by [Reference Huber14, Remark 5.5.12 i)]:
Hence, the assertion (1) follows from Lemma 6.12.
(2) We have
By the Leray spectral sequences, it suffices to prove that the restriction map
is an isomorphism for all
![]() $i, j$
. Let
$i, j$
. Let
![]() $\epsilon ' \in \vert K^{\times } \vert $
be an element with
$\epsilon ' \in \vert K^{\times } \vert $
be an element with
![]() $\epsilon ' < \epsilon $
. Then
$\epsilon ' < \epsilon $
. Then
![]() $ \{ \mathbb {B}(\epsilon ', \epsilon ), \mathbb {D}(\epsilon )^{\circ } \} $
is an open covering of
$ \{ \mathbb {B}(\epsilon ', \epsilon ), \mathbb {D}(\epsilon )^{\circ } \} $
is an open covering of
![]() $\mathbb {B}(\epsilon )$
. By the Čech-to-cohomology spectral sequences, it is enough to prove that the restriction map
$\mathbb {B}(\epsilon )$
. By the Čech-to-cohomology spectral sequences, it is enough to prove that the restriction map
is an isomorphism for all
![]() $i, j$
.
$i, j$
.
The inverse image
![]() $d(f)^{-1}(\mathbb {B}(\epsilon ', \epsilon ))$
has finitely many connected components. It is enough to show that, for every connected component
$d(f)^{-1}(\mathbb {B}(\epsilon ', \epsilon ))$
has finitely many connected components. It is enough to show that, for every connected component
![]() $W \subset d(f)^{-1}(\mathbb {B}(\epsilon ', \epsilon ))$
and the restriction
$W \subset d(f)^{-1}(\mathbb {B}(\epsilon ', \epsilon ))$
and the restriction
![]() $ g \colon W \to \mathbb {B}(\epsilon ', \epsilon ) $
of
$ g \colon W \to \mathbb {B}(\epsilon ', \epsilon ) $
of
![]() $d(f)$
, the restriction map
$d(f)$
, the restriction map
is an isomorphism for all
![]() $i, j$
. The morphism g is of pure dimension N for some integer
$i, j$
. The morphism g is of pure dimension N for some integer
![]() $N \geq 0$
(see [Reference Huber14, Section 1.8] for the definition of the dimension of a morphism of adic spaces). Since g is smooth and
$N \geq 0$
(see [Reference Huber14, Section 1.8] for the definition of the dimension of a morphism of adic spaces). Since g is smooth and
![]() $R^ig_!{\mathbb Z}/n{\mathbb Z}$
is a locally constant constructible sheaf of
$R^ig_!{\mathbb Z}/n{\mathbb Z}$
is a locally constant constructible sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules, Poincaré duality [Reference Huber14, Corollary 7.5.5] implies that
${\mathbb Z}/n{\mathbb Z}$
-modules, Poincaré duality [Reference Huber14, Corollary 7.5.5] implies that
for every j, where
![]() $(N)$
denotes the Tate twist and
$(N)$
denotes the Tate twist and
![]() $()^{\vee }$
denotes the
$()^{\vee }$
denotes the
![]() ${\mathbb Z}/n{\mathbb Z}$
-dual (here, we use the fact that
${\mathbb Z}/n{\mathbb Z}$
-dual (here, we use the fact that
![]() ${\mathbb Z}/n{\mathbb Z}$
is an injective
${\mathbb Z}/n{\mathbb Z}$
is an injective
![]() ${\mathbb Z}/n{\mathbb Z}$
-module). The right-hand side satisfies the assumption of Lemma 6.12 (1), and, hence, the assertion follows from the lemma.
${\mathbb Z}/n{\mathbb Z}$
-module). The right-hand side satisfies the assumption of Lemma 6.12 (1), and, hence, the assertion follows from the lemma.
(3) We have
![]() $S(\mathcal {Z}, \epsilon )=d(f)^{-1}(\mathbb {D}(\epsilon ))$
. Let
$S(\mathcal {Z}, \epsilon )=d(f)^{-1}(\mathbb {D}(\epsilon ))$
. Let
be the base change of
![]() $d(f)$
to
$d(f)$
to
![]() $\mathbb {D}(\epsilon )$
. We write
$\mathbb {D}(\epsilon )$
. We write
We claim that restriction map
![]() $ H^i(\mathbb {D}(\epsilon ), \mathcal {F}_j) \to H^i(\{ 0 \}, \mathcal {F}_j\vert _{ \{ 0 \}}) $
is an isomorphism for all
$ H^i(\mathbb {D}(\epsilon ), \mathcal {F}_j) \to H^i(\{ 0 \}, \mathcal {F}_j\vert _{ \{ 0 \}}) $
is an isomorphism for all
![]() $i, j$
. Since we have by [Reference Huber14, Example 2.6.2]
$i, j$
. Since we have by [Reference Huber14, Example 2.6.2]
 $$\begin{align*}H^i(\{ 0 \}, \mathcal{F}_j\vert_{ \{ 0 \}})= \begin{cases} H^j(d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z}) \quad &(i=0) \\ 0 \quad &(i \neq 0), \end{cases} \end{align*}$$
$$\begin{align*}H^i(\{ 0 \}, \mathcal{F}_j\vert_{ \{ 0 \}})= \begin{cases} H^j(d(\widehat{\mathcal{Z}}), {\mathbb Z}/n{\mathbb Z}) \quad &(i=0) \\ 0 \quad &(i \neq 0), \end{cases} \end{align*}$$
the claim and the Leray spectral sequence for
![]() $d(f)'$
imply the assertion (3). We prove the claim. Since
$d(f)'$
imply the assertion (3). We prove the claim. Since
![]() $\mathbb {D}(\epsilon )$
and
$\mathbb {D}(\epsilon )$
and
![]() $\{ 0 \}$
are proper over
$\{ 0 \}$
are proper over
![]() $\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
, we have
$\mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O})$
, we have
and, hence, it suffices to prove that
![]() $ H^i_c(\mathbb {D}(\epsilon )\backslash \{ 0 \}, \mathcal {F}_j\vert _{\mathbb {D}(\epsilon )\backslash \{ 0 \}}) = 0 $
for all
$ H^i_c(\mathbb {D}(\epsilon )\backslash \{ 0 \}, \mathcal {F}_j\vert _{\mathbb {D}(\epsilon )\backslash \{ 0 \}}) = 0 $
for all
![]() $i, j$
. Moreover, by [Reference Huber14, Proposition 5.4.5 ii)], it suffices to prove that, for any
$i, j$
. Moreover, by [Reference Huber14, Proposition 5.4.5 ii)], it suffices to prove that, for any
![]() $\epsilon ' \in \vert K^{\times } \vert $
with
$\epsilon ' \in \vert K^{\times } \vert $
with
![]() $\epsilon ' < \epsilon $
, we have
$\epsilon ' < \epsilon $
, we have
![]() $ H^i_c(\mathbb {D}(\epsilon )\cap \mathbb {B}(\epsilon ', \epsilon ), \mathcal {F}_j\vert _{\mathbb {D}(\epsilon )\cap \mathbb {B}(\epsilon ', \epsilon )}) = 0 $
for all
$ H^i_c(\mathbb {D}(\epsilon )\cap \mathbb {B}(\epsilon ', \epsilon ), \mathcal {F}_j\vert _{\mathbb {D}(\epsilon )\cap \mathbb {B}(\epsilon ', \epsilon )}) = 0 $
for all
![]() $i, j$
.
$i, j$
.
Let
![]() $\epsilon ' \in \vert K^{\times } \vert $
be an element with
$\epsilon ' \in \vert K^{\times } \vert $
be an element with
![]() $\epsilon ' < \epsilon $
. Let W and g be as in the proof of (2). Let
$\epsilon ' < \epsilon $
. Let W and g be as in the proof of (2). Let
be the base change of g. It suffices to prove that
![]() $ H^i_c(\mathbb {D}(\epsilon )\cap \mathbb {B}(\epsilon ', \epsilon ), R^jg^{\prime }_*{\mathbb Z}/n{\mathbb Z}) = 0 $
for all
$ H^i_c(\mathbb {D}(\epsilon )\cap \mathbb {B}(\epsilon ', \epsilon ), R^jg^{\prime }_*{\mathbb Z}/n{\mathbb Z}) = 0 $
for all
![]() $i, j$
. By the base change theorem [Reference Huber14, Theorem 5.4.6] for
$i, j$
. By the base change theorem [Reference Huber14, Theorem 5.4.6] for
![]() $Rg_!$
, we have
$Rg_!$
, we have
In particular, the right-hand side is a locally constant constructible sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules. As in the proof of (2), Poincaré duality [Reference Huber14, Corollary 7.5.5] for
${\mathbb Z}/n{\mathbb Z}$
-modules. As in the proof of (2), Poincaré duality [Reference Huber14, Corollary 7.5.5] for
![]() $g'$
then implies that
$g'$
then implies that
and the assertion follows from Lemma 6.12 (1).
(4) Similarly as above, it suffices to prove that the restriction map
is an isomorphism for all
![]() $i, j$
. Let
$i, j$
. Let
![]() $\epsilon ' \in \vert K^{\times } \vert $
be an element with
$\epsilon ' \in \vert K^{\times } \vert $
be an element with
![]() $\epsilon ' < \epsilon $
. As in the proof of (2), it suffices to prove that the restriction map
$\epsilon ' < \epsilon $
. As in the proof of (2), it suffices to prove that the restriction map
is an isomorphism for all
![]() $i, j$
. By the proof of (3), the sheaf
$i, j$
. By the proof of (3), the sheaf
![]() $\mathcal {F}_j\vert _{\mathbb {D}(\epsilon ) \cap \mathbb {B}(\epsilon ', \epsilon )}$
is a locally constant constructible sheaf of
$\mathcal {F}_j\vert _{\mathbb {D}(\epsilon ) \cap \mathbb {B}(\epsilon ', \epsilon )}$
is a locally constant constructible sheaf of
![]() ${\mathbb Z}/n{\mathbb Z}$
-modules. Hence, the assertion follows from the proof of [Reference Huber16, Lemma 2.5] (in [Reference Huber16], the characteristic of the base field is always assumed to be zero; however, [Reference Huber16, Lemma 2.5] holds in positive characteristic without changing the proof).
${\mathbb Z}/n{\mathbb Z}$
-modules. Hence, the assertion follows from the proof of [Reference Huber16, Lemma 2.5] (in [Reference Huber16], the characteristic of the base field is always assumed to be zero; however, [Reference Huber16, Lemma 2.5] holds in positive characteristic without changing the proof).
The proof of Lemma 7.1 is complete.
Theorem 4.8 and Theorem 4.9 now follow from Lemma 7.1 and Lemma 7.7.
Appendix A. Finite étale coverings of annuli
In this appendix, we prove Theorem 6.2 and Theorem 6.3. We retain the notation of Section 6.1. In particular, we fix an algebraically closed complete non-archimedean field K with ring of integers
![]() ${\mathcal O}$
. We will follow the methods given in Ramero’s paper [Reference Ramero27].
${\mathcal O}$
. We will follow the methods given in Ramero’s paper [Reference Ramero27].
Following [Reference Ramero27], we will use the following notation in this appendix. Recall that for a morphism of finite type
![]() $ \mathop {\mathrm {Spa}}\nolimits (A, A^+) \to \mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O}), $
where
$ \mathop {\mathrm {Spa}}\nolimits (A, A^+) \to \mathop {\mathrm {Spa}}\nolimits (K, {\mathcal O}), $
where
![]() $(A, A^+)$
is a complete affinoid ring, the ring
$(A, A^+)$
is a complete affinoid ring, the ring
![]() $A^+$
coincides with the ring
$A^+$
coincides with the ring
![]() $A^{\circ }$
of power-bounded elements of A (see [Reference Huber13, Lemma 4.4] and [Reference Huber14, Section 1.2]). We often omit
$A^{\circ }$
of power-bounded elements of A (see [Reference Huber13, Lemma 4.4] and [Reference Huber14, Section 1.2]). We often omit
![]() $A^+$
and abbreviate
$A^+$
and abbreviate
![]() $\mathop {\mathrm {Spa}}\nolimits (A, A^+)$
to
$\mathop {\mathrm {Spa}}\nolimits (A, A^+)$
to
![]() $ \mathop {\mathrm {Spa}}\nolimits (A). $
If A is reduced, then
$ \mathop {\mathrm {Spa}}\nolimits (A). $
If A is reduced, then
![]() $A^{\circ }$
is topologically of finite type over
$A^{\circ }$
is topologically of finite type over
![]() ${\mathcal O}$
, that is,
${\mathcal O}$
, that is,
![]() $ A^{\circ }\cong {\mathcal O} \langle T_1, \dotsc , T_n \rangle /I $
for some ideal
$ A^{\circ }\cong {\mathcal O} \langle T_1, \dotsc , T_n \rangle /I $
for some ideal
![]() $I \subset {\mathcal O} \langle T_1, \dotsc , T_n \rangle $
by [Reference Bosch, Güntzer and Remmert3, 6.4.1, Corollary 4]. Let
$I \subset {\mathcal O} \langle T_1, \dotsc , T_n \rangle $
by [Reference Bosch, Güntzer and Remmert3, 6.4.1, Corollary 4]. Let
![]() $\mathfrak {m} \subset {\mathcal O}$
be the maximal ideal, and let
$\mathfrak {m} \subset {\mathcal O}$
be the maximal ideal, and let
![]() $\kappa :={\mathcal O}/\mathfrak {m}$
be the residue field. The quotient
$\kappa :={\mathcal O}/\mathfrak {m}$
be the residue field. The quotient
is a finitely generated algebra over
![]() $\kappa $
. We note that the ideal
$\kappa $
. We note that the ideal
![]() $\mathfrak {m}A^{\circ }$
coincides with the set of topologically nilpotent elements of A. In particular, the ring
$\mathfrak {m}A^{\circ }$
coincides with the set of topologically nilpotent elements of A. In particular, the ring
![]() $A^{\sim }$
is reduced.
$A^{\sim }$
is reduced.
A.1 Open annuli in the unit disc
In this subsection, we prepare some notation and recall some basic properties of open annuli in the unit disc
![]() $\mathbb {B}(1)=\mathop {\mathrm {Spa}}\nolimits (K \langle T \rangle )$
.
$\mathbb {B}(1)=\mathop {\mathrm {Spa}}\nolimits (K \langle T \rangle )$
.
Let
![]() $a, b \in \vert K^{\times } \vert $
be elements with
$a, b \in \vert K^{\times } \vert $
be elements with
![]() $a \leq b \leq 1$
. Recall that we defined
$a \leq b \leq 1$
. Recall that we defined
 $$ \begin{align*} \mathbb{B}(a, b)&:= \{ x \in \mathbb{B}(1) \, \vert \, a \leq \vert T(x) \vert \leq b \} \\ &:= \{ x \in \mathbb{B}(1) \, \vert \, \vert \varpi_a(x) \vert \leq \vert T(x) \vert \leq \vert \varpi_b(x) \vert \}, \end{align*} $$
$$ \begin{align*} \mathbb{B}(a, b)&:= \{ x \in \mathbb{B}(1) \, \vert \, a \leq \vert T(x) \vert \leq b \} \\ &:= \{ x \in \mathbb{B}(1) \, \vert \, \vert \varpi_a(x) \vert \leq \vert T(x) \vert \leq \vert \varpi_b(x) \vert \}, \end{align*} $$
where
![]() $\varpi _a, \varpi _b \in K^{\times }$
are elements such that
$\varpi _a, \varpi _b \in K^{\times }$
are elements such that
![]() $a=\vert \varpi _a \vert $
and
$a=\vert \varpi _a \vert $
and
![]() $b=\vert \varpi _b \vert $
. We have
$b=\vert \varpi _b \vert $
. We have
as an adic space over
![]() $\mathbb {B}(1)$
. The adic space
$\mathbb {B}(1)$
. The adic space
![]() $\mathbb {B}(a, b)$
is isomorphic to
$\mathbb {B}(a, b)$
is isomorphic to
![]() $\mathbb {B}(a/b, 1)$
as an adic space over
$\mathbb {B}(a/b, 1)$
as an adic space over
![]() $\mathop {\mathrm {Spa}}\nolimits (K)$
. We write
$\mathop {\mathrm {Spa}}\nolimits (K)$
. We write
![]() $ A(a, b):={\mathcal O}_{\mathbb {B}(1)}(\mathbb {B}(a, b)). $
$ A(a, b):={\mathcal O}_{\mathbb {B}(1)}(\mathbb {B}(a, b)). $
We will focus on the following points of the unit disc
![]() $\mathbb {B}(1)$
. Let
$\mathbb {B}(1)$
. Let
![]() $r \in \vert K^{\times } \vert $
be an element with
$r \in \vert K^{\times } \vert $
be an element with
![]() $r \leq 1$
.
$r \leq 1$
.
-
• Let
be the Gauss norm of radius r centred at $$\begin{align*}\eta(r)^{\flat} \colon K \langle T \rangle \to \vert K^{\times} \vert, \quad \sum_{i \geq 0}a_i T^i \mapsto \max_{i \geq 0}\{ \vert a_i \vert r^i \} \end{align*}$$
$$\begin{align*}\eta(r)^{\flat} \colon K \langle T \rangle \to \vert K^{\times} \vert, \quad \sum_{i \geq 0}a_i T^i \mapsto \max_{i \geq 0}\{ \vert a_i \vert r^i \} \end{align*}$$
 $0$
. The corresponding point
$0$
. The corresponding point
 $\eta (r)^{\flat } \in \mathbb {B}(1)$
is denoted by the same letter.
$\eta (r)^{\flat } \in \mathbb {B}(1)$
is denoted by the same letter.
-
• Let
 $\langle \delta \rangle $
be an infinite cyclic group with generator
$\langle \delta \rangle $
be an infinite cyclic group with generator
 $\delta $
. We equip
$\delta $
. We equip
 $\vert K^{\times } \vert \times \langle \delta \rangle $
with a total order such that So we have
$\vert K^{\times } \vert \times \langle \delta \rangle $
with a total order such that So we have $$\begin{align*}(s, \delta^m) < (t, \delta^n) \Longleftrightarrow s < t, \quad \text{or} \quad s=t \quad \text{and} \quad m>n. \end{align*}$$
$$\begin{align*}(s, \delta^m) < (t, \delta^n) \Longleftrightarrow s < t, \quad \text{or} \quad s=t \quad \text{and} \quad m>n. \end{align*}$$
 $(1, \delta )<(1, 1)$
and
$(1, \delta )<(1, 1)$
and
 $(s, 1) < (1, \delta )$
for every
$(s, 1) < (1, \delta )$
for every
 $s \in \vert K^{\times } \vert $
with
$s \in \vert K^{\times } \vert $
with
 $s < 1$
. We identify
$s < 1$
. We identify
 $\delta $
with
$\delta $
with
 $(1, \delta )$
and r with
$(1, \delta )$
and r with
 $(r, 1)$
. The valuation gives a point
$(r, 1)$
. The valuation gives a point $$\begin{align*}\eta(r) \colon K \langle T \rangle \to \vert K^{\times} \vert \times \langle \delta \rangle, \quad \sum_{i \geq 0}a_i T^i \mapsto \max_{i \geq 0}\{ \vert a_i \vert r^i\delta^i \} \end{align*}$$
$$\begin{align*}\eta(r) \colon K \langle T \rangle \to \vert K^{\times} \vert \times \langle \delta \rangle, \quad \sum_{i \geq 0}a_i T^i \mapsto \max_{i \geq 0}\{ \vert a_i \vert r^i\delta^i \} \end{align*}$$
 $\eta (r) \in \mathbb {B}(1)$
. The point
$\eta (r) \in \mathbb {B}(1)$
. The point
 $\eta (r)$
is a specialization of
$\eta (r)$
is a specialization of
 $\eta (r)^{\flat }$
, that is, we have
$\eta (r)^{\flat }$
, that is, we have  $$\begin{align*}\eta(r) \in \overline{\{ \eta(r)^{\flat} \}}. \end{align*}$$
$$\begin{align*}\eta(r) \in \overline{\{ \eta(r)^{\flat} \}}. \end{align*}$$
-
• Similarly, if
 $r < 1$
, the valuation gives a point
$r < 1$
, the valuation gives a point $$\begin{align*}\eta(r)' \colon K \langle T \rangle \to \vert K^{\times} \vert \times \langle \delta \rangle, \quad \sum_{i \geq 0}a_i T^i \mapsto \max_{i \geq 0}\{ \vert a_i \vert r^i\delta^{-i} \} \end{align*}$$
$$\begin{align*}\eta(r)' \colon K \langle T \rangle \to \vert K^{\times} \vert \times \langle \delta \rangle, \quad \sum_{i \geq 0}a_i T^i \mapsto \max_{i \geq 0}\{ \vert a_i \vert r^i\delta^{-i} \} \end{align*}$$
 $\eta (r)' \in \mathbb {B}(1)$
. The point
$\eta (r)' \in \mathbb {B}(1)$
. The point
 $\eta (r)'$
is a specialization of
$\eta (r)'$
is a specialization of
 $\eta (r)^{\flat }$
.
$\eta (r)^{\flat }$
.
We can use the points
![]() $\eta (r)$
and
$\eta (r)$
and
![]() $\eta (r)'$
to describe the closure of an annulus
$\eta (r)'$
to describe the closure of an annulus
![]() $\mathbb {B}(a, b)$
.
$\mathbb {B}(a, b)$
.
Example A.1. Let
![]() $a, b \in \vert K^{\times } \vert $
be elements with
$a, b \in \vert K^{\times } \vert $
be elements with
![]() $a \leq b \leq 1$
.
$a \leq b \leq 1$
.
-
(1) For an element
 $r \in \vert K^{\times } \vert $
with
$r \in \vert K^{\times } \vert $
with
 $a \leq r \leq b$
, we have
$a \leq r \leq b$
, we have
 $\eta (r)^{\flat } \in \mathbb {B}(a, b)$
. If
$\eta (r)^{\flat } \in \mathbb {B}(a, b)$
. If
 $a < r \leq b$
, we have
$a < r \leq b$
, we have
 $\eta (r) \in \mathbb {B}(a, b)$
. Similarly, if
$\eta (r) \in \mathbb {B}(a, b)$
. Similarly, if
 $a \leq r < b$
, we have
$a \leq r < b$
, we have
 $\eta (r)' \in \mathbb {B}(a, b)$
.
$\eta (r)' \in \mathbb {B}(a, b)$
. -
(2) We assume that
 $a \leq b < 1$
. Let
$a \leq b < 1$
. Let
 $\mathbb {B}(a, b)^c$
be the closure of
$\mathbb {B}(a, b)^c$
be the closure of
 $\mathbb {B}(a, b)$
in
$\mathbb {B}(a, b)$
in
 $\mathbb {B}(1)$
. Then we have
$\mathbb {B}(1)$
. Then we have
 $ \mathbb {B}(a, b)^c \backslash \mathbb {B}(a, b)= \{ \eta (a), \eta (b)' \}. $
In particular, the complement
$ \mathbb {B}(a, b)^c \backslash \mathbb {B}(a, b)= \{ \eta (a), \eta (b)' \}. $
In particular, the complement
 $\mathbb {B}(a, b)^c \backslash \mathbb {B}(a, b)$
consists of two points.
$\mathbb {B}(a, b)^c \backslash \mathbb {B}(a, b)$
consists of two points. -
(3) We have some kind of converse to (2). We define
 $ \mathbb {D}(1):=\{ x \in \mathbb {B}(1) \, \vert \, \vert T(x) \vert < 1 \}, $
which is a closed subset of
$ \mathbb {D}(1):=\{ x \in \mathbb {B}(1) \, \vert \, \vert T(x) \vert < 1 \}, $
which is a closed subset of
 $\mathbb {B}(1)$
. Let
$\mathbb {B}(1)$
. Let
 $X \subset \mathbb {B}(1)$
be a connected affinoid open subset contained in
$X \subset \mathbb {B}(1)$
be a connected affinoid open subset contained in
 $\mathbb {D}(1)$
. Let
$\mathbb {D}(1)$
. Let
 $X^c$
be the closure of X in
$X^c$
be the closure of X in
 $\mathbb {B}(1)$
. If the complement
$\mathbb {B}(1)$
. If the complement
 $X^c \backslash X$
consists of two points, then there exists an isomorphism
$X^c \backslash X$
consists of two points, then there exists an isomorphism  $$\begin{align*}X \cong \mathbb{B}(a, 1) \end{align*}$$
$$\begin{align*}X \cong \mathbb{B}(a, 1) \end{align*}$$
of adic spaces over
 $\mathop {\mathrm {Spa}}\nolimits (K)$
for some element
$\mathop {\mathrm {Spa}}\nolimits (K)$
for some element
 $a \in \vert K^{\times } \vert $
with
$a \in \vert K^{\times } \vert $
with
 $a \leq 1$
. This can be proved by using [Reference Bosch, Güntzer and Remmert3, 9.7.2, Theorem 2].
$a \leq 1$
. This can be proved by using [Reference Bosch, Güntzer and Remmert3, 9.7.2, Theorem 2].
We recall the following example from [Reference Ramero27], which is useful to study finite étale coverings of
![]() $\mathbb {B}(a, b)$
.
$\mathbb {B}(a, b)$
.
Example A.2 [Reference Ramero27, Example 2.1.12]
We assume that
![]() $a < b$
. Let
$a < b$
. Let
be the morphism over
![]() $\mathop {\mathrm {Spa}}\nolimits (K)$
defined by the following homomorphism
$\mathop {\mathrm {Spa}}\nolimits (K)$
defined by the following homomorphism
The homomorphism
![]() $\psi $
makes
$\psi $
makes
![]() $A(a, b)^{\circ }$
into a free
$A(a, b)^{\circ }$
into a free
![]() ${\mathcal O} \langle S \rangle $
-module of rank
${\mathcal O} \langle S \rangle $
-module of rank
![]() $2$
.
$2$
.
Remark A.3. In the rest of this section, we shall study finite étale coverings of
![]() $\mathbb {B}(a, b)$
. We recall that there is a natural equivalence between the category of adic spaces which are finite and étale over X and the category of schemes which are finite and étale over
$\mathbb {B}(a, b)$
. We recall that there is a natural equivalence between the category of adic spaces which are finite and étale over X and the category of schemes which are finite and étale over
![]() $\mathop {\mathrm {Spec}} {\mathcal O}_X(X)$
(see [Reference Huber14, Example 1.6.6 ii)]).
$\mathop {\mathrm {Spec}} {\mathcal O}_X(X)$
(see [Reference Huber14, Example 1.6.6 ii)]).
In the rest of this subsection, we give two lemmas about the connected components of a finite étale covering of
![]() $\mathbb {B}(a, b)$
.
$\mathbb {B}(a, b)$
.
Lemma A.4. We assume that
![]() $a < b$
. Let
$a < b$
. Let
![]() $f \colon X \to \mathbb {B}(a, b)$
be a finite étale morphism of adic spaces. For every
$f \colon X \to \mathbb {B}(a, b)$
be a finite étale morphism of adic spaces. For every
![]() $t \in \vert K^{\times } \vert $
with
$t \in \vert K^{\times } \vert $
with
![]() $a/b < t^2 <1$
, there exists an element
$a/b < t^2 <1$
, there exists an element
![]() $s_0 \in \vert K^{\times } \vert $
with
$s_0 \in \vert K^{\times } \vert $
with
![]() $t< s_0 \leq 1$
such that every connected component of
$t< s_0 \leq 1$
such that every connected component of
![]() $f^{-1}(\mathbb {B}(a/s_0, s_0 b))$
remains connected after restricting to
$f^{-1}(\mathbb {B}(a/s_0, s_0 b))$
remains connected after restricting to
![]() $\mathbb {B}(a/s, s b)$
for every
$\mathbb {B}(a/s, s b)$
for every
![]() $s \in \vert K^{\times } \vert $
with
$s \in \vert K^{\times } \vert $
with
![]() $t < s \leq s_0$
.
$t < s \leq s_0$
.
Proof. The number of the connected components of
![]() $f^{-1}(\mathbb {B}(a/s, s b))$
increases with decreasing s, and it is bounded above by the degree of f (that is, the rank of
$f^{-1}(\mathbb {B}(a/s, s b))$
increases with decreasing s, and it is bounded above by the degree of f (that is, the rank of
![]() ${\mathcal O}_X(X)$
as an
${\mathcal O}_X(X)$
as an
![]() $A(a, b)$
-module) for every
$A(a, b)$
-module) for every
![]() $s \in \vert K^{\times } \vert $
with
$s \in \vert K^{\times } \vert $
with
![]() $a/b < s^2 \leq 1$
. The assertion follows from these properties.
$a/b < s^2 \leq 1$
. The assertion follows from these properties.
Lemma A.5. We assume that
![]() $a < b$
. Let
$a < b$
. Let
![]() $f \colon X \to \mathbb {B}(a, b)$
be a finite étale morphism of adic spaces. We write
$f \colon X \to \mathbb {B}(a, b)$
be a finite étale morphism of adic spaces. We write
![]() $B:={\mathcal O}_X(X)$
and consider the composition
$B:={\mathcal O}_X(X)$
and consider the composition
where
![]() $\psi $
is the homomorphism defined in Example A.2 and the second homomorphism is the one induced by f. Let
$\psi $
is the homomorphism defined in Example A.2 and the second homomorphism is the one induced by f. Let
![]() $ \{ \mathfrak {q}_1, \dotsc , \mathfrak {q}_n \} \subset \mathop {\mathrm {Spec}} B^{\circ } $
be the set of the prime ideals of
$ \{ \mathfrak {q}_1, \dotsc , \mathfrak {q}_n \} \subset \mathop {\mathrm {Spec}} B^{\circ } $
be the set of the prime ideals of
![]() $B^{\circ }$
lying above the maximal ideal
$B^{\circ }$
lying above the maximal ideal
![]() $ \mathfrak {m}{\mathcal O} \langle S \rangle +S {\mathcal O} \langle S \rangle \subset {\mathcal O} \langle S \rangle. $
Then, for every
$ \mathfrak {m}{\mathcal O} \langle S \rangle +S {\mathcal O} \langle S \rangle \subset {\mathcal O} \langle S \rangle. $
Then, for every
![]() $t \in \vert K^{\times } \vert $
with
$t \in \vert K^{\times } \vert $
with
![]() $a/b < t^2 <1$
, the adic space
$a/b < t^2 <1$
, the adic space
![]() $f^{-1}(\mathbb {B}(a/t, t b))$
has at least n connected components.
$f^{-1}(\mathbb {B}(a/t, t b))$
has at least n connected components.
Proof. This lemma is proved in the proof of [Reference Ramero27, Theorem 2.4.3]. We recall the arguments for the reader’s convenience.
We define g as the composition
Let
![]() $t \in \vert K^{\times } \vert $
be an element with
$t \in \vert K^{\times } \vert $
be an element with
![]() $a/b < t^2 <1$
. We define
$a/b < t^2 <1$
. We define
![]() $ \mathbb {B}(t):= \{ x \in \mathbb {B}(1) \, \vert \, \vert S(x) \vert \leq t \}. $
Since
$ \mathbb {B}(t):= \{ x \in \mathbb {B}(1) \, \vert \, \vert S(x) \vert \leq t \}. $
Since
![]() $\Psi ^{-1}(\mathbb {B}(t))= \mathbb {B}(a/t, tb)$
, it is enough to show that
$\Psi ^{-1}(\mathbb {B}(t))= \mathbb {B}(a/t, tb)$
, it is enough to show that
![]() $g^{-1}(\mathbb {B}(t))$
has at least n connected components. The ring
$g^{-1}(\mathbb {B}(t))$
has at least n connected components. The ring
![]() ${\mathcal O}[[S]]$
is a Henselian local ring. Since
${\mathcal O}[[S]]$
is a Henselian local ring. Since
![]() $B^{\circ }$
is a free
$B^{\circ }$
is a free
![]() ${\mathcal O} \langle S \rangle $
-module of finite rank by [Reference Ramero27, Proposition 2.3.5], we have a decomposition
${\mathcal O} \langle S \rangle $
-module of finite rank by [Reference Ramero27, Proposition 2.3.5], we have a decomposition
where
![]() $R_1, \dotsc , R_n$
are local rings, which are free
$R_1, \dotsc , R_n$
are local rings, which are free
![]() ${\mathcal O}[[S]]$
-modules of finite rank. Since the natural homomorphism
${\mathcal O}[[S]]$
-modules of finite rank. Since the natural homomorphism
![]() $ {\mathcal O} \langle S \rangle ={\mathcal O}_{\mathbb {B}(1)}(\mathbb {B}(1))^{\circ } \to {\mathcal O}_{\mathbb {B}(t)}(\mathbb {B}(t))^{\circ } $
factors through
$ {\mathcal O} \langle S \rangle ={\mathcal O}_{\mathbb {B}(1)}(\mathbb {B}(1))^{\circ } \to {\mathcal O}_{\mathbb {B}(t)}(\mathbb {B}(t))^{\circ } $
factors through
![]() ${\mathcal O} \langle S \rangle \to {\mathcal O}[[S]]$
, we have
${\mathcal O} \langle S \rangle \to {\mathcal O}[[S]]$
, we have
where
![]() $B_i:=R_i \otimes _{{\mathcal O}[[S]]} {\mathcal O}_{\mathbb {B}(t)}(\mathbb {B}(t))$
. This proves our claim since
$B_i:=R_i \otimes _{{\mathcal O}[[S]]} {\mathcal O}_{\mathbb {B}(t)}(\mathbb {B}(t))$
. This proves our claim since
![]() $\mathop {\mathrm {Spa}}\nolimits (B_i)$
is nonempty for every
$\mathop {\mathrm {Spa}}\nolimits (B_i)$
is nonempty for every
![]() $1 \leq i \leq n$
.
$1 \leq i \leq n$
.
A.2 Discriminant functions and finite étale coverings of open annuli
In this subsection, we give some properties of the discriminant function of a finite étale covering of
![]() $ \mathbb {B}(a, b), $
and then we prove Theorem 6.2.
$ \mathbb {B}(a, b), $
and then we prove Theorem 6.2.
Let
![]() $a, b \in \vert K^{\times } \vert $
be elements with
$a, b \in \vert K^{\times } \vert $
be elements with
![]() $a < b \leq 1$
. Let
$a < b \leq 1$
. Let
![]() $ f \colon X \to \mathbb {B}(a, b) $
be a finite étale morphism of adic spaces. Let us briefly recall the definition of the discriminant function
$ f \colon X \to \mathbb {B}(a, b) $
be a finite étale morphism of adic spaces. Let us briefly recall the definition of the discriminant function
associated with f following [Reference Ramero27].
Let
![]() ${\mathcal O}^+_X$
be the subsheaf of
${\mathcal O}^+_X$
be the subsheaf of
![]() ${\mathcal O}_X$
defined by
${\mathcal O}_X$
defined by
for every open subset
![]() $U \subset X$
. For an element
$U \subset X$
. For an element
![]() $r \in \vert K^{\times } \vert $
with
$r \in \vert K^{\times } \vert $
with
![]() $a \leq r \leq b$
, let
$a \leq r \leq b$
, let
be the stalk of
![]() $f_* {\mathcal O}^+_X$
at the point
$f_* {\mathcal O}^+_X$
at the point
![]() $\eta (r)^{\flat }$
. The maximal ideal of the stalk
$\eta (r)^{\flat }$
. The maximal ideal of the stalk
![]() ${\mathcal O}_{\mathbb {B}(a, b), \eta (r)^{\flat }}$
at
${\mathcal O}_{\mathbb {B}(a, b), \eta (r)^{\flat }}$
at
![]() $\eta (r)^{\flat }$
is zero, in other words, we have
$\eta (r)^{\flat }$
is zero, in other words, we have
![]() $ {\mathcal O}_{\mathbb {B}(a, b), \eta (r)^{\flat }}=k(\eta (r)^{\flat }). $
Hence, there is a natural homomorphism
$ {\mathcal O}_{\mathbb {B}(a, b), \eta (r)^{\flat }}=k(\eta (r)^{\flat }). $
Hence, there is a natural homomorphism
![]() $ k(\eta (r)^{\flat })^+ \to \mathscr {A}(r)^{\flat }. $
By applying [Reference Ramero27, Proposition 2.3.5] to the restriction
$ k(\eta (r)^{\flat })^+ \to \mathscr {A}(r)^{\flat }. $
By applying [Reference Ramero27, Proposition 2.3.5] to the restriction
![]() $f^{-1}(\mathbb {B}(r, r)) \to \mathbb {B}(r, r)$
of f, we see that
$f^{-1}(\mathbb {B}(r, r)) \to \mathbb {B}(r, r)$
of f, we see that
![]() $\mathscr {A}(r)^{\flat }$
is a free
$\mathscr {A}(r)^{\flat }$
is a free
![]() $k(\eta (r)^{\flat })^+$
-module of finite rank. Then we can define the valuation
$k(\eta (r)^{\flat })^+$
-module of finite rank. Then we can define the valuation
of the discriminant
![]() $\mathfrak {d}^{\flat }_f(r) \in k(\eta (r)^{\flat })^+$
of
$\mathfrak {d}^{\flat }_f(r) \in k(\eta (r)^{\flat })^+$
of
![]() $\mathscr {A}(r)^{\flat }$
over
$\mathscr {A}(r)^{\flat }$
over
![]() $k(\eta (r)^{\flat })^+$
(in the sense of [Reference Ramero27, Section 2.1]), and we define
$k(\eta (r)^{\flat })^+$
(in the sense of [Reference Ramero27, Section 2.1]), and we define
(see [Reference Ramero27, 2.3.12] for details).
Theorem A.6 (Ramero [Reference Ramero27, Theorem 2.3.25])
The function
![]() $\delta _f$
extends uniquely to a continuous, piecewise linear and convex function
$\delta _f$
extends uniquely to a continuous, piecewise linear and convex function
Moreover, the slopes of
![]() $\delta _f$
are integers.
$\delta _f$
are integers.
Proof. See [Reference Ramero27, Theorem 2.3.25].
Many basic properties of the discriminant function
![]() $\delta _f$
were studied in detail in [Reference Ramero27]. Here, we are interested in the case where
$\delta _f$
were studied in detail in [Reference Ramero27]. Here, we are interested in the case where
![]() $\delta _f$
is linear.
$\delta _f$
is linear.
Proposition A.7 (Ramero [Reference Ramero27])
Let
![]() $ f \colon X=\mathop {\mathrm {Spa}}\nolimits (B, B^{\circ }) \to \mathbb {B}(a, b) $
be a finite étale morphism of adic spaces with a complete affinoid ring
$ f \colon X=\mathop {\mathrm {Spa}}\nolimits (B, B^{\circ }) \to \mathbb {B}(a, b) $
be a finite étale morphism of adic spaces with a complete affinoid ring
![]() $(B, B^{\circ })$
. Define g as the composition
$(B, B^{\circ })$
. Define g as the composition
where
![]() $\Psi $
is the morphism defined in Example A.2. The map g induces a homomorphism
$\Psi $
is the morphism defined in Example A.2. The map g induces a homomorphism
![]() $ {\mathcal O} \langle S \rangle \to B^{\circ }. $
Let us suppose that the following two conditions hold:
$ {\mathcal O} \langle S \rangle \to B^{\circ }. $
Let us suppose that the following two conditions hold:
-
• There is only one prime ideal
 $\mathfrak {q} \subset B^{\circ }$
lying above the maximal ideal
$\mathfrak {q} \subset B^{\circ }$
lying above the maximal ideal
 $ \mathfrak {m}{\mathcal O} \langle S \rangle +S {\mathcal O} \langle S \rangle \subset {\mathcal O} \langle S \rangle. $
$ \mathfrak {m}{\mathcal O} \langle S \rangle +S {\mathcal O} \langle S \rangle \subset {\mathcal O} \langle S \rangle. $
-
• The discriminant function
 $\delta _f$
is linear.
$\delta _f$
is linear.
Then the inverse image
![]() $g^{-1}(\eta (1))$
consists of two points, or equivalently, the inverse images
$g^{-1}(\eta (1))$
consists of two points, or equivalently, the inverse images
![]() $f^{-1}(\eta (a)')$
and
$f^{-1}(\eta (a)')$
and
![]() $f^{-1}(\eta (b))$
both consist of one point. Moreover, the closed point
$f^{-1}(\eta (b))$
both consist of one point. Moreover, the closed point
corresponding to the prime ideal
![]() $\mathfrak {q}$
is an ordinary double point.
$\mathfrak {q}$
is an ordinary double point.
Proof. The first assertion is a consequence of [Reference Ramero27, (2.4.4) in the proof of Theorem 2.4.3]. The assumption that the characteristic of the base field is zero in loc. cit. is not needed here. Moreover, the morphism f need not be Galois.
The second assertion is claimed in [Reference Ramero27, Remark 2.4.8] (at least when K is of characteristic zero) without proof. Indeed, the hard parts of the proof were already done in [Reference Ramero27]. We shall explain how to use the results in loc. cit. to deduce the second assertion.
Before giving the proof of the second assertion, let us prepare some notation. We write
![]() $A:= K \langle S \rangle $
. For the points
$A:= K \langle S \rangle $
. For the points
![]() $\eta (1), \eta (1)^{\flat } \in \mathbb {B}(1)$
, we write
$\eta (1), \eta (1)^{\flat } \in \mathbb {B}(1)$
, we write
Note that
![]() $ {\mathcal O}_{\mathbb {B}(1), \eta (1)}=k(1) $
and
$ {\mathcal O}_{\mathbb {B}(1), \eta (1)}=k(1) $
and
![]() $ {\mathcal O}_{\mathbb {B}(1), \eta (1)^{\flat }}=k(1^{\flat }). $
We have a natural inclusion
$ {\mathcal O}_{\mathbb {B}(1), \eta (1)^{\flat }}=k(1^{\flat }). $
We have a natural inclusion
The residue field
![]() $k(1^{\flat })^+/\mathfrak {m}k(1^{\flat })^+$
of
$k(1^{\flat })^+/\mathfrak {m}k(1^{\flat })^+$
of
![]() $k(1^{\flat })^+$
is naturally isomorphic to the field of fractions
$k(1^{\flat })^+$
is naturally isomorphic to the field of fractions
![]() $\kappa (S)$
of
$\kappa (S)$
of
![]() $\kappa [S]$
. The image of
$\kappa [S]$
. The image of
![]() $k(1)^+$
in
$k(1)^+$
in
![]() $\kappa (S)$
is the localization
$\kappa (S)$
is the localization
![]() $\kappa [S]_{(S)}$
of
$\kappa [S]_{(S)}$
of
![]() $\kappa [S]$
at the maximal ideal
$\kappa [S]$
at the maximal ideal
![]() $(S) \subset \kappa [S]$
. More precisely, we have the following commutative diagram:
$(S) \subset \kappa [S]$
. More precisely, we have the following commutative diagram:

Let
be the stalk of
![]() $g_* {\mathcal O}^+_X$
at the point
$g_* {\mathcal O}^+_X$
at the point
![]() $\eta (1) \in \mathbb {B}(1)$
. We have a map
$\eta (1) \in \mathbb {B}(1)$
. We have a map
The target and the source of i are both free
![]() $k(1)^+$
-modules of finite rank by [Reference Ramero27, Proposition 2.3.5 and Lemma 2.2.17], and clearly i becomes an isomorphism after tensoring with
$k(1)^+$
-modules of finite rank by [Reference Ramero27, Proposition 2.3.5 and Lemma 2.2.17], and clearly i becomes an isomorphism after tensoring with
![]() $k(1)$
. In particular, the map i is injective. By [Reference Ramero27, Proposition 2.3.5] again, it follows that i becomes an isomorphism after tensoring with
$k(1)$
. In particular, the map i is injective. By [Reference Ramero27, Proposition 2.3.5] again, it follows that i becomes an isomorphism after tensoring with
![]() $k(1^{\flat })^+$
. Consequently, we have inclusions
$k(1^{\flat })^+$
. Consequently, we have inclusions
 $$\begin{align*}B^{\circ}\otimes_{A^{\circ}}k(1)^+& \hookrightarrow \mathscr{B}(1)^{+} \hookrightarrow B^{\circ}\otimes_{A^{\circ}} k(1^{\flat})^+,\\B^{\circ}\otimes_{A^{\circ}}(k(1)^+/\mathfrak{m}k(1)^+) &\hookrightarrow \mathscr{B}(1)^{+}/\mathfrak{m}\mathscr{B}(1)^{+} \hookrightarrow B^{\circ}\otimes_{A^{\circ}} (k(1^{\flat})^+/\mathfrak{m}k(1^{\flat})^+). \end{align*}$$
$$\begin{align*}B^{\circ}\otimes_{A^{\circ}}k(1)^+& \hookrightarrow \mathscr{B}(1)^{+} \hookrightarrow B^{\circ}\otimes_{A^{\circ}} k(1^{\flat})^+,\\B^{\circ}\otimes_{A^{\circ}}(k(1)^+/\mathfrak{m}k(1)^+) &\hookrightarrow \mathscr{B}(1)^{+}/\mathfrak{m}\mathscr{B}(1)^{+} \hookrightarrow B^{\circ}\otimes_{A^{\circ}} (k(1^{\flat})^+/\mathfrak{m}k(1^{\flat})^+). \end{align*}$$
We shall now prove the second assertion. First, we prove that the ring
![]() $\mathscr {B}(1)^{+}/\mathfrak {m}\mathscr {B}(1)^{+}$
is integrally closed in
$\mathscr {B}(1)^{+}/\mathfrak {m}\mathscr {B}(1)^{+}$
is integrally closed in
![]() $B^{\circ }\otimes _{A^{\circ }} (k(1^{\flat })^+/\mathfrak {m}k(1^{\flat })^+)$
. Let
$B^{\circ }\otimes _{A^{\circ }} (k(1^{\flat })^+/\mathfrak {m}k(1^{\flat })^+)$
. Let
be the completions with respect to the valuation topologies. By [Reference Huber14, Lemma 1.1.10 iii)], we have
![]() $ k(1)^{\wedge } \overset {\cong }{\to } k(1^{\flat })^{\wedge }. $
We have the following commutative diagram:
$ k(1)^{\wedge } \overset {\cong }{\to } k(1^{\flat })^{\wedge }. $
We have the following commutative diagram:

where the vertical maps and the top horizontal map are injective. By using [Reference Ramero27, Proposition 1.3.2 (iii)], we see that
![]() $\mathscr {B}(1)^{+} \otimes _{k(1)^+} k(1)^{\wedge +}$
is integrally closed in
$\mathscr {B}(1)^{+} \otimes _{k(1)^+} k(1)^{\wedge +}$
is integrally closed in
![]() $\mathscr {B}(1)^{+} \otimes _{k(1)^+} k(1)^{\wedge }$
, and, hence, integrally closed in
$\mathscr {B}(1)^{+} \otimes _{k(1)^+} k(1)^{\wedge }$
, and, hence, integrally closed in
![]() $B^{\circ }\otimes _{A^{\circ }} k(1^{\flat })^{\wedge +}$
. This implies that
$B^{\circ }\otimes _{A^{\circ }} k(1^{\flat })^{\wedge +}$
. This implies that
![]() $\mathscr {B}(1)^{+}/\mathfrak {m}\mathscr {B}(1)^{+}$
is integrally closed in
$\mathscr {B}(1)^{+}/\mathfrak {m}\mathscr {B}(1)^{+}$
is integrally closed in
![]() $B^{\circ }\otimes _{A^{\circ }} (k(1^{\flat })^+/\mathfrak {m}k(1^{\flat })^+)$
.
$B^{\circ }\otimes _{A^{\circ }} (k(1^{\flat })^+/\mathfrak {m}k(1^{\flat })^+)$
.
By the assumptions, the ring
is the local ring of
![]() $\mathop {\mathrm {Spec}} B^{\sim }$
at the closed point
$\mathop {\mathrm {Spec}} B^{\sim }$
at the closed point
![]() $x \in \mathop {\mathrm {Spec}} B^{\sim }$
. Moreover, the ring
$x \in \mathop {\mathrm {Spec}} B^{\sim }$
. Moreover, the ring
is the total ring of fractions of R. Hence, the ring
![]() $\mathscr {B}(1)^{+}/\mathfrak {m}\mathscr {B}(1)^{+}$
is the normalization of R. By using [Reference Ramero27, (2.4.4) in the proof of Theorem 2.4.3], one can show that there are exactly two maximal ideals of
$\mathscr {B}(1)^{+}/\mathfrak {m}\mathscr {B}(1)^{+}$
is the normalization of R. By using [Reference Ramero27, (2.4.4) in the proof of Theorem 2.4.3], one can show that there are exactly two maximal ideals of
![]() $\mathscr {B}(1)^{+}/\mathfrak {m}\mathscr {B}(1)^{+}$
and the length of
$\mathscr {B}(1)^{+}/\mathfrak {m}\mathscr {B}(1)^{+}$
and the length of
![]() $\mathscr {B}(1)^{+}/\mathfrak {m}\mathscr {B}(1)^{+}$
as an R-module is one. In other words, the closed point x is an ordinary double point.
$\mathscr {B}(1)^{+}/\mathfrak {m}\mathscr {B}(1)^{+}$
as an R-module is one. In other words, the closed point x is an ordinary double point.
The proof of Proposition A.7 is complete.
We deduce the following result from Proposition A.7, which is used in the proof of Theorem 6.2.
Proposition A.8. Let
![]() $ f \colon X \to \mathbb {B}(a, b) $
be a finite étale morphism of adic spaces. We assume that the discriminant function
$ f \colon X \to \mathbb {B}(a, b) $
be a finite étale morphism of adic spaces. We assume that the discriminant function
![]() $\delta _f$
is linear. Let
$\delta _f$
is linear. Let
![]() $t \in \vert K^{\times } \vert $
be an element with
$t \in \vert K^{\times } \vert $
be an element with
![]() $a/b < t^2 <1$
. Then we have
$a/b < t^2 <1$
. Then we have
 $$\begin{align*}f^{-1}(\mathbb{B}(a/t, t b)) \cong \coprod^{n}_{i=1} \mathbb{B}(c_i, 1) \end{align*}$$
$$\begin{align*}f^{-1}(\mathbb{B}(a/t, t b)) \cong \coprod^{n}_{i=1} \mathbb{B}(c_i, 1) \end{align*}$$
for some elements
![]() $c_i \in \vert K^{\times } \vert $
with
$c_i \in \vert K^{\times } \vert $
with
![]() $c_i < 1$
(
$c_i < 1$
(
![]() $1 \leq i \leq n$
).
$1 \leq i \leq n$
).
Proof. By Lemma A.4, without loss of generality, we may assume that every connected component of X remains connected after restricting to
![]() $\mathbb {B}(a/s, s b)$
for every
$\mathbb {B}(a/s, s b)$
for every
![]() $s \in \vert K^{\times } \vert $
with
$s \in \vert K^{\times } \vert $
with
![]() $t < s \leq 1$
. Let
$t < s \leq 1$
. Let
![]() $X_1, \dotsc , X_m$
be the connected components of X, and let
$X_1, \dotsc , X_m$
be the connected components of X, and let
![]() $f_i \colon X_i \to \mathbb {B}(a, b)$
be the restriction of f. By Theorem A.6, each discriminant function
$f_i \colon X_i \to \mathbb {B}(a, b)$
be the restriction of f. By Theorem A.6, each discriminant function
![]() $\delta _{f_i}$
associated with
$\delta _{f_i}$
associated with
![]() $f_i$
is a continuous, piecewise linear and convex function. Since
$f_i$
is a continuous, piecewise linear and convex function. Since
![]() $ \delta _f= \sum ^m_{i=1} \delta _{f_i}, $
it follows that
$ \delta _f= \sum ^m_{i=1} \delta _{f_i}, $
it follows that
![]() $\delta _{f_i}$
is linear for every i. Thus, we may further assume that X is connected.
$\delta _{f_i}$
is linear for every i. Thus, we may further assume that X is connected.
Let
![]() $(B, B^{\circ })$
be a complete affinoid ring such that
$(B, B^{\circ })$
be a complete affinoid ring such that
![]() $X=\mathop {\mathrm {Spa}}\nolimits (B, B^{\circ })$
. Define g as the composition
$X=\mathop {\mathrm {Spa}}\nolimits (B, B^{\circ })$
. Define g as the composition
By Lemma A.5, there is only one prime ideal
![]() $\mathfrak {q} \subset B^{\circ }$
lying above the maximal ideal
$\mathfrak {q} \subset B^{\circ }$
lying above the maximal ideal
![]() $ \mathfrak {m}{\mathcal O} \langle S \rangle +S {\mathcal O} \langle S \rangle \subset {\mathcal O} \langle S \rangle. $
Let
$ \mathfrak {m}{\mathcal O} \langle S \rangle +S {\mathcal O} \langle S \rangle \subset {\mathcal O} \langle S \rangle. $
Let
![]() $ x \in \mathop {\mathrm {Spec}} B^{\sim } $
be the closed point corresponding to the prime ideal
$ x \in \mathop {\mathrm {Spec}} B^{\sim } $
be the closed point corresponding to the prime ideal
![]() $\mathfrak {q}$
, which is an ordinary double point by Proposition A.7. Let
$\mathfrak {q}$
, which is an ordinary double point by Proposition A.7. Let
be the specialization map associated with the formal scheme
![]() $\mathop {\mathrm {Spf}}(B^{\circ })$
(see Section 5.2). By the proof of [Reference Bosch and Lütkebohmert4, Proposition 2.3], the interior
$\mathop {\mathrm {Spf}}(B^{\circ })$
(see Section 5.2). By the proof of [Reference Bosch and Lütkebohmert4, Proposition 2.3], the interior
![]() $\lambda ^{-1}(x)^{\circ }$
of the inverse image
$\lambda ^{-1}(x)^{\circ }$
of the inverse image
![]() $\lambda ^{-1}(x)$
in X is isomorphic to the interior
$\lambda ^{-1}(x)$
in X is isomorphic to the interior
![]() $\mathbb {D}(d, 1)^{\circ }$
of
$\mathbb {D}(d, 1)^{\circ }$
of
![]() $\mathbb {D}(d, 1)$
in
$\mathbb {D}(d, 1)$
in
![]() $\mathbb {B}(1)$
for some element
$\mathbb {B}(1)$
for some element
![]() $d \in \vert K^{\times } \vert $
with
$d \in \vert K^{\times } \vert $
with
![]() $d < 1$
as an adic space over
$d < 1$
as an adic space over
![]() $\mathop {\mathrm {Spa}}\nolimits (K)$
, where
$\mathop {\mathrm {Spa}}\nolimits (K)$
, where
We fix such an isomorphism. For every
![]() $s \in \vert K^{\times } \vert $
with
$s \in \vert K^{\times } \vert $
with
![]() $t \leq s < 1$
, we have
$t \leq s < 1$
, we have
Thus, we may consider
![]() $f^{-1}(\mathbb {B}(a/s, sb))$
as a connected affinoid open subset of
$f^{-1}(\mathbb {B}(a/s, sb))$
as a connected affinoid open subset of
![]() $\mathbb {B}(1)$
.
$\mathbb {B}(1)$
.
We write
![]() $X_t:=f^{-1}(\mathbb {B}(a/t, tb))$
. Let
$X_t:=f^{-1}(\mathbb {B}(a/t, tb))$
. Let
![]() $X^c_t$
be the closure of
$X^c_t$
be the closure of
![]() $X_t$
in
$X_t$
in
![]() $\mathbb {B}(1)$
, which is contained in
$\mathbb {B}(1)$
, which is contained in
![]() $g^{-1}(\mathbb {D}(1)^{\circ })$
. In view of Example A.1 (3), to prove the assertion, it suffices to prove that the complement
$g^{-1}(\mathbb {D}(1)^{\circ })$
. In view of Example A.1 (3), to prove the assertion, it suffices to prove that the complement
![]() $ X^{c}_t \backslash X_t $
consists of exactly two points. The map f induces a map
$ X^{c}_t \backslash X_t $
consists of exactly two points. The map f induces a map
We prove that
![]() $f'$
is bijective. Since f is surjective and specialising by [Reference Huber14, Lemma 1.4.5 ii)], it follows that the map
$f'$
is bijective. Since f is surjective and specialising by [Reference Huber14, Lemma 1.4.5 ii)], it follows that the map
![]() $f'$
is surjective. To show that the map
$f'$
is surjective. To show that the map
![]() $f'$
is injective, it suffices to prove the following claim:
$f'$
is injective, it suffices to prove the following claim:
Claim A.9. The inverse images
![]() $f^{-1}(\eta (a/t))$
and
$f^{-1}(\eta (a/t))$
and
![]() $f^{-1}(\eta (t b)')$
both consist of one point.
$f^{-1}(\eta (t b)')$
both consist of one point.
Proof. Recall that we assume that X remains connected after restricting to
![]() $\mathbb {B}(a/s, s b)$
for every
$\mathbb {B}(a/s, s b)$
for every
![]() $s \in \vert K^{\times } \vert $
with
$s \in \vert K^{\times } \vert $
with
![]() $t < s \leq 1$
. Thus, by Lemma A.5 and Proposition A.7, the inverse images
$t < s \leq 1$
. Thus, by Lemma A.5 and Proposition A.7, the inverse images
![]() $f^{-1}(\eta (a/s)')$
and
$f^{-1}(\eta (a/s)')$
and
![]() $f^{-1}(\eta (s b))$
both consist of one point for every
$f^{-1}(\eta (s b))$
both consist of one point for every
![]() $s \in \vert K^{\times } \vert $
with
$s \in \vert K^{\times } \vert $
with
![]() $t < s \leq 1$
. This fact implies that
$t < s \leq 1$
. This fact implies that
is connected for every
![]() $s_1, s_2 \in \vert K^{\times } \vert $
with
$s_1, s_2 \in \vert K^{\times } \vert $
with
![]() $t \leq s_1 < s_2 \leq 1$
(indeed, if it is not connected, then there exist at least two points mapped to
$t \leq s_1 < s_2 \leq 1$
(indeed, if it is not connected, then there exist at least two points mapped to
![]() $\eta (s_2 b)$
). By applying Lemma A.5 and Proposition A.7 to
$\eta (s_2 b)$
). By applying Lemma A.5 and Proposition A.7 to
we see that
![]() $f^{-1}(\eta (tb)')$
consists of one point. The same arguments show that
$f^{-1}(\eta (tb)')$
consists of one point. The same arguments show that
![]() $f^{-1}(\eta (a/t))$
consists of one point.
$f^{-1}(\eta (a/t))$
consists of one point.
The proof of Proposition A.8 is complete.
Remark A.10. Here, we prove Proposition A.7 and Proposition A.8 in the context of adic spaces as in [Reference Ramero27]. It is probably possible to prove these results (in a more geometric way) by using the methods of [Reference Lütkebohmert22, Reference Lütkebohmert and Schmechta23].
We now give a proof of Theorem 6.2.
Proof of Theorem 6.2
Let
![]() $f \colon X \to \mathbb {B}(1)^{*}$
be a finite étale morphism. Clearly, the discriminant functions on open annuli constructed in Theorem A.6 can be glued to a continuous, piecewise linear and convex function
$f \colon X \to \mathbb {B}(1)^{*}$
be a finite étale morphism. Clearly, the discriminant functions on open annuli constructed in Theorem A.6 can be glued to a continuous, piecewise linear and convex function
Moreover, the slopes of
![]() $\delta _f$
are integers. By [Reference Ramero27, Lemma 2.1.10], the function
$\delta _f$
are integers. By [Reference Ramero27, Lemma 2.1.10], the function
![]() $\delta _f$
is bounded above by some positive real number (depending only on the degree of f). It follows that there exists an element
$\delta _f$
is bounded above by some positive real number (depending only on the degree of f). It follows that there exists an element
![]() $\epsilon _0 \in \vert K^{\times } \vert $
with
$\epsilon _0 \in \vert K^{\times } \vert $
with
![]() $\epsilon _0 \leq 1$
such that the restriction of
$\epsilon _0 \leq 1$
such that the restriction of
![]() $\delta _f$
to
$\delta _f$
to
![]() $[-\log \epsilon _0, \infty )$
is constant. Let
$[-\log \epsilon _0, \infty )$
is constant. Let
![]() $t \in \vert K^{\times } \vert $
be an element with
$t \in \vert K^{\times } \vert $
be an element with
![]() $t < 1$
. We put
$t < 1$
. We put
![]() $\epsilon := t\epsilon _0$
. Then, for elements
$\epsilon := t\epsilon _0$
. Then, for elements
![]() $a, b \in \vert K^{\times } \vert $
with
$a, b \in \vert K^{\times } \vert $
with
![]() $a < b \leq \epsilon $
, we have
$a < b \leq \epsilon $
, we have
 $$\begin{align*}f^{-1}(\mathbb{B}(a, b)) \cong \coprod^{n}_{i=1} \mathbb{B}(c_i, d_i) \end{align*}$$
$$\begin{align*}f^{-1}(\mathbb{B}(a, b)) \cong \coprod^{n}_{i=1} \mathbb{B}(c_i, d_i) \end{align*}$$
for some elements
![]() $c_i, d_i \in \vert K^{\times } \vert $
with
$c_i, d_i \in \vert K^{\times } \vert $
with
![]() $c_i < d_i \leq 1$
(
$c_i < d_i \leq 1$
(
![]() $1 \leq i \leq n$
) by Proposition A.8. If K is of characteristic zero, after replacing
$1 \leq i \leq n$
) by Proposition A.8. If K is of characteristic zero, after replacing
![]() $\epsilon $
by a smaller one, we can easily show that the restriction
$\epsilon $
by a smaller one, we can easily show that the restriction
![]() $ \mathbb {B}(c_i, d_i) \to \mathbb {B}(a, b) $
of f is a Kummer covering by using [Reference Ramero27, Claim 2.4.5] (see also the proofs of [Reference Lütkebohmert22, Theorem 2.2] and [Reference Ramero27, Theorem 2.4.3]).
$ \mathbb {B}(c_i, d_i) \to \mathbb {B}(a, b) $
of f is a Kummer covering by using [Reference Ramero27, Claim 2.4.5] (see also the proofs of [Reference Lütkebohmert22, Theorem 2.2] and [Reference Ramero27, Theorem 2.4.3]).
A.3 Galois coverings and discriminant functions
In this subsection, we prove Theorem 6.3.
Let
![]() $a, b \in \vert K^{\times } \vert $
be elements with
$a, b \in \vert K^{\times } \vert $
be elements with
![]() $a < b \leq 1$
. Let
$a < b \leq 1$
. Let
be a finite étale morphism of adic spaces with a complete affinoid ring
![]() $(B, B^{\circ })$
. Let
$(B, B^{\circ })$
. Let
be the opposite of the group of
![]() $\mathbb {B}(a, b)$
-automorphisms on X, or equivalently, the group of
$\mathbb {B}(a, b)$
-automorphisms on X, or equivalently, the group of
![]() $A(a, b)$
-automorphisms of B. We assume that f is Galois, that is,
$A(a, b)$
-automorphisms of B. We assume that f is Galois, that is,
![]() $A(a, b)$
coincides with the ring
$A(a, b)$
coincides with the ring
![]() $B^G$
of G-invariants (this is equivalent to saying that the finite étale morphism
$B^G$
of G-invariants (this is equivalent to saying that the finite étale morphism
![]() $\mathop {\mathrm {Spec}} B \to \mathop {\mathrm {Spec}} A(a, b)$
of schemes is Galois; see Remark A.3). In this case, we call G the Galois group of f.
$\mathop {\mathrm {Spec}} B \to \mathop {\mathrm {Spec}} A(a, b)$
of schemes is Galois; see Remark A.3). In this case, we call G the Galois group of f.
We assume that X is connected. Let
![]() $r \in \vert K^{\times } \vert $
be an element with
$r \in \vert K^{\times } \vert $
be an element with
![]() $a < r \leq b$
, and let
$a < r \leq b$
, and let
![]() $x \in f^{-1}(\eta (r))$
be an element. Let
$x \in f^{-1}(\eta (r))$
be an element. Let
be the stabiliser of x. Let
![]() $k(x)^{\wedge h +}$
(resp.
$k(x)^{\wedge h +}$
(resp.
![]() $k(r)^{\wedge h+}$
) be the Henselization of the completion of the valuation ring
$k(r)^{\wedge h+}$
) be the Henselization of the completion of the valuation ring
![]() $k(x)^{+}$
(resp.
$k(x)^{+}$
(resp.
![]() $k(\eta (r))^{+}$
). Let
$k(\eta (r))^{+}$
). Let
![]() $k(x)^{\wedge h}$
and
$k(x)^{\wedge h}$
and
![]() $k(r)^{\wedge h}$
be the fields of fractions of
$k(r)^{\wedge h}$
be the fields of fractions of
![]() $k(x)^{\wedge h +}$
and
$k(x)^{\wedge h +}$
and
![]() $k(r)^{\wedge h+}$
, respectively. Then by [Reference Huber17, 5.5], the extension of fields
$k(r)^{\wedge h+}$
, respectively. Then by [Reference Huber17, 5.5], the extension of fields
is finite and Galois, and we have a natural isomorphism
In [Reference Huber17], Huber defined higher ramification subgroups and the Swan character of the Galois group
![]() $\mathop {\mathrm {Gal}}\nolimits (k(x)^{\wedge h}/k(r)^{\wedge h})$
. In [Reference Ramero27], Ramero investigated the relation between the discriminant functions and the Swan characters. We are interested in the case where all higher ramification subgroups and the Swan character of
$\mathop {\mathrm {Gal}}\nolimits (k(x)^{\wedge h}/k(r)^{\wedge h})$
. In [Reference Ramero27], Ramero investigated the relation between the discriminant functions and the Swan characters. We are interested in the case where all higher ramification subgroups and the Swan character of
![]() $\mathop {\mathrm {Gal}}\nolimits (k(x)^{\wedge h}/k(r)^{\wedge h})$
are trivial. All we need is the following lemma:
$\mathop {\mathrm {Gal}}\nolimits (k(x)^{\wedge h}/k(r)^{\wedge h})$
are trivial. All we need is the following lemma:
Lemma A.11 ([Reference Ramero27, Lemma 3.3.10])
Let
![]() $ f \colon X \to \mathbb {B}(a, b) $
be a finite Galois étale morphism such that X is connected. We assume that
$ f \colon X \to \mathbb {B}(a, b) $
be a finite Galois étale morphism such that X is connected. We assume that
![]() $ \sharp \mathop {\mathrm {Stab}}\nolimits _x $
is invertible in
$ \sharp \mathop {\mathrm {Stab}}\nolimits _x $
is invertible in
![]() ${\mathcal O}$
for every
${\mathcal O}$
for every
![]() $r \in \vert K^{\times } \vert $
with
$r \in \vert K^{\times } \vert $
with
![]() $a < r \leq b$
and every
$a < r \leq b$
and every
![]() $x \in f^{-1}(\eta (r))$
. Then the discriminant function
$x \in f^{-1}(\eta (r))$
. Then the discriminant function
associated with f is constant.
Proof. This follows from the second equality of [Reference Ramero27, Lemma 3.3.10]. Indeed, under the assumption, we have
![]() $\mathrm {Sw}^{\natural }_x=0$
for the Swan character
$\mathrm {Sw}^{\natural }_x=0$
for the Swan character
![]() $\mathrm {Sw}^{\natural }_x$
attached to
$\mathrm {Sw}^{\natural }_x$
attached to
![]() $x \in f^{-1}(\eta (r))$
defined in [Reference Ramero27, Section 3.3].
$x \in f^{-1}(\eta (r))$
defined in [Reference Ramero27, Section 3.3].
Finally, we prove Theorem 6.3.
Proof of Theorem 6.3
In fact, we will show that if a locally constant étale sheaf
![]() $\mathcal {F}$
with finite stalks on
$\mathcal {F}$
with finite stalks on
![]() $\mathbb {B}(a, b)$
is tame at
$\mathbb {B}(a, b)$
is tame at
![]() $\eta (r) \in \mathbb {B}(a, b)$
for every
$\eta (r) \in \mathbb {B}(a, b)$
for every
![]() $r \in \vert K^{\times } \vert $
with
$r \in \vert K^{\times } \vert $
with
![]() $a < r \leq b$
, then, for every
$a < r \leq b$
, then, for every
![]() $t \in \vert K^{\times } \vert $
with
$t \in \vert K^{\times } \vert $
with
![]() $a/b < t^2 < 1$
, there exists an integer m invertible in
$a/b < t^2 < 1$
, there exists an integer m invertible in
![]() ${\mathcal O}$
such that the restriction
${\mathcal O}$
such that the restriction
![]() $\mathcal {F} \vert _{\mathbb {B}(a/t, tb)}$
is trivialized by a Kummer covering
$\mathcal {F} \vert _{\mathbb {B}(a/t, tb)}$
is trivialized by a Kummer covering
![]() $\varphi _m$
.
$\varphi _m$
.
There is a finite Galois étale morphism
![]() $f \colon X \to \mathbb {B}(a, b)$
such that X is connected and
$f \colon X \to \mathbb {B}(a, b)$
such that X is connected and
![]() $f^*\mathcal {F}$
is a constant sheaf. Let G be the Galois group of f. By replacing X by a quotient of it by a subgroup of G (this makes sense by Remark A.3), we may assume that the induced homomorphism
$f^*\mathcal {F}$
is a constant sheaf. Let G be the Galois group of f. By replacing X by a quotient of it by a subgroup of G (this makes sense by Remark A.3), we may assume that the induced homomorphism
is injective. Let
![]() $t \in \vert K^{\times } \vert $
be an element with
$t \in \vert K^{\times } \vert $
be an element with
![]() $a/b < t^2 < 1$
. By Lemma A.4, we may assume that X remains connected after restricting to
$a/b < t^2 < 1$
. By Lemma A.4, we may assume that X remains connected after restricting to
![]() $\mathbb {B}(a/s, s b)$
for every
$\mathbb {B}(a/s, s b)$
for every
![]() $s \in \vert K^{\times } \vert $
with
$s \in \vert K^{\times } \vert $
with
![]() $t < s \leq 1$
.
$t < s \leq 1$
.
We claim that
![]() $ \sharp \mathop {\mathrm {Stab}}\nolimits _x $
is invertible in
$ \sharp \mathop {\mathrm {Stab}}\nolimits _x $
is invertible in
![]() ${\mathcal O}$
for every
${\mathcal O}$
for every
![]() $r \in \vert K^{\times } \vert $
with
$r \in \vert K^{\times } \vert $
with
![]() $a < r \leq b$
and every
$a < r \leq b$
and every
![]() $x \in f^{-1}(\eta (r))$
. Let
$x \in f^{-1}(\eta (r))$
. Let
![]() $L(r)$
be a separable closure of
$L(r)$
be a separable closure of
![]() $k(x)^{\wedge h}$
. It induces a geometric point
$k(x)^{\wedge h}$
. It induces a geometric point
![]() $\overline {x} \to X$
with support x. Let
$\overline {x} \to X$
with support x. Let
![]() $\overline {r} \to \mathbb {B}(a, b)$
denote the composition
$\overline {r} \to \mathbb {B}(a, b)$
denote the composition
![]() $\overline {x} \to X \to \mathbb {B}(a, b)$
. Since
$\overline {x} \to X \to \mathbb {B}(a, b)$
. Since
![]() $f^*\mathcal {F}$
is a constant sheaf, we have the following identifications
$f^*\mathcal {F}$
is a constant sheaf, we have the following identifications
Recall that we have
![]() $ \mathop {\mathrm {Stab}}\nolimits _x \cong \mathop {\mathrm {Gal}}\nolimits (k(x)^{\wedge h}/k(r)^{\wedge h}). $
Via these identifications, the action of
$ \mathop {\mathrm {Stab}}\nolimits _x \cong \mathop {\mathrm {Gal}}\nolimits (k(x)^{\wedge h}/k(r)^{\wedge h}). $
Via these identifications, the action of
![]() $\mathop {\mathrm {Stab}}\nolimits _x \subset G$
on
$\mathop {\mathrm {Stab}}\nolimits _x \subset G$
on
![]() $\Gamma (X, f^*\mathcal {F})$
is compatible with the action of
$\Gamma (X, f^*\mathcal {F})$
is compatible with the action of
![]() $\mathop {\mathrm {Gal}}\nolimits (L(r)/k(r)^{\wedge h})$
on
$\mathop {\mathrm {Gal}}\nolimits (L(r)/k(r)^{\wedge h})$
on
![]() $\mathcal {F}_{\overline {r}}$
. Since
$\mathcal {F}_{\overline {r}}$
. Since
![]() $\mathcal {F}$
is tame at
$\mathcal {F}$
is tame at
![]() $\eta (r)$
and
$\eta (r)$
and
![]() $\rho $
is injective, it follows that
$\rho $
is injective, it follows that
![]() $ \sharp \mathop {\mathrm {Gal}}\nolimits (k(x)^{\wedge h}/k(r)^{\wedge h}) $
is invertible in
$ \sharp \mathop {\mathrm {Gal}}\nolimits (k(x)^{\wedge h}/k(r)^{\wedge h}) $
is invertible in
![]() ${\mathcal O}$
. This proves our claim.
${\mathcal O}$
. This proves our claim.
By Lemma A.11, it follows that the discriminant function
![]() $\delta _f$
is constant. By Lemma A.5 and Proposition A.7, there is exactly one point x in
$\delta _f$
is constant. By Lemma A.5 and Proposition A.7, there is exactly one point x in
![]() $f^{-1}(\eta (b))$
. Therefore, the Galois group G is isomorphic to
$f^{-1}(\eta (b))$
. Therefore, the Galois group G is isomorphic to
![]() $ \mathop {\mathrm {Stab}}\nolimits _x \cong \mathop {\mathrm {Gal}}\nolimits (k(x)^{\wedge h}/k(b)^{\wedge h}). $
$ \mathop {\mathrm {Stab}}\nolimits _x \cong \mathop {\mathrm {Gal}}\nolimits (k(x)^{\wedge h}/k(b)^{\wedge h}). $
Theorem 6.3 now follows from [Reference Lütkebohmert22, Theorem 2.11]. Alternatively, we can argue as follows. By [Reference Huber17, Proposition 2.5, Corollary 2.7, and Corollary 5.4], we see that G is a cyclic group. Let us write
![]() $G \cong {\mathbb Z}/m{\mathbb Z}$
. We consider
$G \cong {\mathbb Z}/m{\mathbb Z}$
. We consider
![]() $f \colon X \to \mathbb {B}(a, b)$
as a
$f \colon X \to \mathbb {B}(a, b)$
as a
![]() ${\mathbb Z}/m{\mathbb Z}$
-torsor. As in the proof of [Reference Ramero27, Theorem 2.4.3], since the Picard group of
${\mathbb Z}/m{\mathbb Z}$
-torsor. As in the proof of [Reference Ramero27, Theorem 2.4.3], since the Picard group of
![]() $\mathbb {B}(a, b)$
is trivial, the Kummer sequence gives an isomorphism
$\mathbb {B}(a, b)$
is trivial, the Kummer sequence gives an isomorphism
Since m is invertible in
![]() ${\mathcal O}$
, the left-hand side is a cyclic group of order m generated by the coordinate function
${\mathcal O}$
, the left-hand side is a cyclic group of order m generated by the coordinate function
![]() $T \in A(a, b)^{\times }$
. It follows that every
$T \in A(a, b)^{\times }$
. It follows that every
![]() ${\mathbb Z}/m{\mathbb Z}$
-torsor over
${\mathbb Z}/m{\mathbb Z}$
-torsor over
![]() $\mathbb {B}(a, b)$
is the disjoint union of Kummer coverings. This completes the proof of Theorem 6.3.
$\mathbb {B}(a, b)$
is the disjoint union of Kummer coverings. This completes the proof of Theorem 6.3.
Acknowledgments
The author would like to thank his adviser Tetsushi Ito for his support and guidance and for bringing the paper [Reference Lütkebohmert and Schmechta23] to the attention of the author. The author would like to thank Teruhisa Koshikawa for many helpful suggestions and useful conversations. The author learned a lot from him. The author would like to thank Yoichi Mieda for helpful comments. The author also would like to thank Ryota Mikami for useful discussions. Finally, the author also thanks the referee for helpful comments and suggestions. The work of the author was supported by JSPS Research Fellowships for Young Scientists KAKENHI grant number 18J22191.
Competing Interests
None.