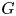1. Introduction
Let ![]() $p$ be a prime and let
$p$ be a prime and let ![]() $G$ be a connected reductive group over a finite extension
$G$ be a connected reductive group over a finite extension ![]() $F$ of
$F$ of ![]() $\mathbb {Q}_p$. We fix a conjugacy class of a minuscule cocharacter
$\mathbb {Q}_p$. We fix a conjugacy class of a minuscule cocharacter ![]() $\mu$ of
$\mu$ of ![]() $G_{\overline {F}}$, and denote by
$G_{\overline {F}}$, and denote by ![]() $E$ its field of definition, a finite extension of
$E$ its field of definition, a finite extension of ![]() $F$. Let
$F$. Let ![]() ${\mathcal {F}\ell }(G,\mu )$ be the associated flag variety, considered as an adic space over
${\mathcal {F}\ell }(G,\mu )$ be the associated flag variety, considered as an adic space over ![]() $\breve {E}$. Here
$\breve {E}$. Here ![]() $\breve {E}$ denotes the completion of the maximal unramified extension of
$\breve {E}$ denotes the completion of the maximal unramified extension of ![]() $E$.
$E$.
Let ![]() $b\in G(\breve {F})$. In [Reference Rapoport and ZinkRZ96], Rapoport and Zink define the weakly admissible locus
$b\in G(\breve {F})$. In [Reference Rapoport and ZinkRZ96], Rapoport and Zink define the weakly admissible locus ![]() ${\mathcal {F}\ell }(G,\mu,b)^{{\rm {wa}}}\subseteq {\mathcal {F}\ell }(G,\mu )$. It is an open adic subspace of
${\mathcal {F}\ell }(G,\mu,b)^{{\rm {wa}}}\subseteq {\mathcal {F}\ell }(G,\mu )$. It is an open adic subspace of ![]() ${\mathcal {F}\ell }(G,\mu )$ having an explicit description as the complement of a certain profinite union of linear subspaces. Its points are characterized by a semi-stability condition on the associated filtered isocrystals with additional structure.
${\mathcal {F}\ell }(G,\mu )$ having an explicit description as the complement of a certain profinite union of linear subspaces. Its points are characterized by a semi-stability condition on the associated filtered isocrystals with additional structure.
Let ![]() ${\mathcal {F}\ell }(G,\mu,b)^{{\rm a}}$ denote the admissible locus, an open adic subspace of
${\mathcal {F}\ell }(G,\mu,b)^{{\rm a}}$ denote the admissible locus, an open adic subspace of ![]() ${\mathcal {F}\ell }(G,\mu )$. The existence of the admissible locus has been conjectured by Rapoport and Zink, see [Reference Dat, Orlik and RapoportDOR10, Conjecture 11.4.4]. It is characterized by being a subspace of
${\mathcal {F}\ell }(G,\mu )$. The existence of the admissible locus has been conjectured by Rapoport and Zink, see [Reference Dat, Orlik and RapoportDOR10, Conjecture 11.4.4]. It is characterized by being a subspace of ![]() ${\mathcal {F}\ell }(G,\mu,b)^{{\rm {wa}}}$ having the same classical points and such that there exists a
${\mathcal {F}\ell }(G,\mu,b)^{{\rm {wa}}}$ having the same classical points and such that there exists a ![]() $p$-adic local system with additional structure over
$p$-adic local system with additional structure over ![]() ${\mathcal {F}\ell }(G,\mu,b)$ that interpolates the crystalline representations attached to all classical points. For
${\mathcal {F}\ell }(G,\mu,b)$ that interpolates the crystalline representations attached to all classical points. For ![]() $(G,\mu )$ of PEL type, Hartl [Reference HartlHar11] and Faltings [Reference FaltingsFal10] gave a construction using the Robba ring, respectively the crystalline period ring. In general, the admissible locus is constructed using modifications of
$(G,\mu )$ of PEL type, Hartl [Reference HartlHar11] and Faltings [Reference FaltingsFal10] gave a construction using the Robba ring, respectively the crystalline period ring. In general, the admissible locus is constructed using modifications of ![]() $G$-bundles on the Fargues–Fontaine curve, and based on the work of Fargues and Fontaine [Reference Fargues and FontaineFF18], Fargues [Reference FarguesFar20], Kedlaya and Liu [Reference Kedlaya and LiuKL15], and Scholze [Reference Scholze and WeinsteinSW20]. As was recently shown in [Reference Chen, Fargues and ShenCFS21], the admissible locus and the weakly admissible locus coincide only in exceptional cases.
$G$-bundles on the Fargues–Fontaine curve, and based on the work of Fargues and Fontaine [Reference Fargues and FontaineFF18], Fargues [Reference FarguesFar20], Kedlaya and Liu [Reference Kedlaya and LiuKL15], and Scholze [Reference Scholze and WeinsteinSW20]. As was recently shown in [Reference Chen, Fargues and ShenCFS21], the admissible locus and the weakly admissible locus coincide only in exceptional cases.
In order to understand the relation between these two subspaces, it is helpful to view them as part of a broader theory. The first generalization, carried out among others in the work of Fargues and Scholze, is to consider the adic Newton stratification instead of just the admissible locus (which is the unique open Newton stratum). The second step, and topic of this article, is then to establish a similar stratification whose unique open stratum is a variant of the weakly admissible locus. Let us begin by recalling the Newton stratification. To explain this, we also switch to the more general context of fixing any ![]() $G(\overline {F})$-conjugacy class
$G(\overline {F})$-conjugacy class ![]() $\{\mu \}$ of cocharacters of
$\{\mu \}$ of cocharacters of ![]() $G_{\overline {F}}$, and consider affine Schubert cells in the
$G_{\overline {F}}$, and consider affine Schubert cells in the ![]() ${B^+_{{\rm dR}}}$-Grassmannian instead of flag varieties.
${B^+_{{\rm dR}}}$-Grassmannian instead of flag varieties.
By ![]() ${\rm Gr}_G$ we denote the
${\rm Gr}_G$ we denote the ![]() $B_{{\rm dR}}^+$-Grassmannian as in [Reference Scholze and WeinsteinSW20, Definition 19.1.1]. Let
$B_{{\rm dR}}^+$-Grassmannian as in [Reference Scholze and WeinsteinSW20, Definition 19.1.1]. Let ![]() $C$ be a complete and algebraically closed field extension of
$C$ be a complete and algebraically closed field extension of ![]() $F$. Then the Cartan decomposition yields
$F$. Then the Cartan decomposition yields
where ![]() $\xi$ is a uniformizer of
$\xi$ is a uniformizer of ![]() $B_{{\rm dR}}^+(C)$ and where we take the union over all
$B_{{\rm dR}}^+(C)$ and where we take the union over all ![]() $G(\overline {F})$-conjugacy classes of cocharacters
$G(\overline {F})$-conjugacy classes of cocharacters ![]() $\mu$ of
$\mu$ of ![]() $G_{\overline {F}}$. We obtain an induced subdivision
$G_{\overline {F}}$. We obtain an induced subdivision ![]() ${\rm Gr}_G=\coprod {\rm Gr}_{G,\mu }$ into locally spacial sub-diamonds called affine Schubert cells, and also the closed affine Schubert cells
${\rm Gr}_G=\coprod {\rm Gr}_{G,\mu }$ into locally spacial sub-diamonds called affine Schubert cells, and also the closed affine Schubert cells ![]() ${\rm Gr}_{G,\leqslant \mu }=\coprod _{\mu '\leqslant \mu }{\rm Gr}_{G,\mu }$. For minuscule
${\rm Gr}_{G,\leqslant \mu }=\coprod _{\mu '\leqslant \mu }{\rm Gr}_{G,\mu }$. For minuscule ![]() $\mu$, the natural Bialynicki-Birula map
$\mu$, the natural Bialynicki-Birula map
is an isomorphism between the affine Schubert cell and the diamond associated with ![]() ${\mathcal {F}\ell }(G,\mu )$. In general, the Bialynicki-Birula map exists, but is not an isomorphism.
${\mathcal {F}\ell }(G,\mu )$. In general, the Bialynicki-Birula map exists, but is not an isomorphism.
Let ![]() $X$ be the Fargues–Fontaine curve over the tilt
$X$ be the Fargues–Fontaine curve over the tilt ![]() $C^{\flat }$ of
$C^{\flat }$ of ![]() $C$ and let
$C$ and let ![]() $\infty \in X$ be the point corresponding to its untilt
$\infty \in X$ be the point corresponding to its untilt ![]() $C$. By [Reference FarguesFar20] we have a bijection between the set of isomorphism classes of
$C$. By [Reference FarguesFar20] we have a bijection between the set of isomorphism classes of ![]() $G$-bundles on
$G$-bundles on ![]() $X$ and the Kottwitz set
$X$ and the Kottwitz set ![]() $B(G)$. Let
$B(G)$. Let ![]() ${\mathcal {E}}_b$ be the
${\mathcal {E}}_b$ be the ![]() $G$-bundle corresponding to the fixed element
$G$-bundle corresponding to the fixed element ![]() $b$. Using Beauville–Laszlo uniformization we have for every
$b$. Using Beauville–Laszlo uniformization we have for every ![]() $x\in {\rm Gr}(C)$ a
$x\in {\rm Gr}(C)$ a ![]() $G$-bundle
$G$-bundle ![]() ${\mathcal {E}}_{b,x}$ on
${\mathcal {E}}_{b,x}$ on ![]() $X$ that is obtained as a modification of
$X$ that is obtained as a modification of ![]() ${\mathcal {E}}_b$ at
${\mathcal {E}}_b$ at ![]() $\infty$, compare [Reference Fargues and ScholzeFS21, III.3]. Mapping
$\infty$, compare [Reference Fargues and ScholzeFS21, III.3]. Mapping ![]() $x$ to the isomorphism class of
$x$ to the isomorphism class of ![]() ${\mathcal {E}}_{b,x}$ one obtains a map
${\mathcal {E}}_{b,x}$ one obtains a map
to the stack of ![]() $G$-bundles on the Fargues–Fontaine curve. For
$G$-bundles on the Fargues–Fontaine curve. For ![]() $b=1$, the image of
$b=1$, the image of ![]() $|{\rm Gr}_{G,\mu }|$ or
$|{\rm Gr}_{G,\mu }|$ or ![]() $|{\rm Gr}_{G,\leqslant \mu }|$ consists of the finite set
$|{\rm Gr}_{G,\leqslant \mu }|$ consists of the finite set ![]() $B(G,-\mu )$. For any
$B(G,-\mu )$. For any ![]() $[b']\in B(G)$ we denote by
$[b']\in B(G)$ we denote by ![]() ${\rm Gr}_{G,\mu,b}^{[b']}$ the locally closed subspace of
${\rm Gr}_{G,\mu,b}^{[b']}$ the locally closed subspace of ![]() ${\rm Gr}_{G,\mu }$, and also the induced locally spatial sub-diamond, called the Newton stratum for
${\rm Gr}_{G,\mu }$, and also the induced locally spatial sub-diamond, called the Newton stratum for ![]() $[b']$ and
$[b']$ and ![]() $G,\mu,b$.
$G,\mu,b$.
By [Reference ViehmannVie21, § 4] there is also a generalization of the definition of the weakly admissible locus ![]() ${\rm Gr}_{G,\mu,b}^{{\rm {wa}}}\subset {\rm Gr}_{G,\mu }$ based on modifications of
${\rm Gr}_{G,\mu,b}^{{\rm {wa}}}\subset {\rm Gr}_{G,\mu }$ based on modifications of ![]() $G$-bundles on the Fargues–Fontaine curve. In the minuscule case it can be identified with the classical weakly admissible locus in
$G$-bundles on the Fargues–Fontaine curve. In the minuscule case it can be identified with the classical weakly admissible locus in ![]() ${\mathcal {F}\ell }(G,\mu )$ via the Bialynicki-Birula isomorphism. By [Reference ViehmannVie21, Theorem 1.3] the weakly admissible locus in a minuscule affine Schubert cell
${\mathcal {F}\ell }(G,\mu )$ via the Bialynicki-Birula isomorphism. By [Reference ViehmannVie21, Theorem 1.3] the weakly admissible locus in a minuscule affine Schubert cell ![]() ${\rm Gr}_{G,\mu }$ intersects all Newton strata that are Hodge–Newton indecomposable.
${\rm Gr}_{G,\mu }$ intersects all Newton strata that are Hodge–Newton indecomposable.
In this article, we embed the notion of weak admissibility in a broader theory by constructing a Harder–Narasimhan stratification of ![]() ${\rm Gr}_{G}$. Intersecting the semi-stable stratum with any
${\rm Gr}_{G}$. Intersecting the semi-stable stratum with any ![]() ${\rm Gr}_{G,\mu }$ one obtains the weakly admissible locus of [Reference ViehmannVie21]. We use a natural construction in terms of modifications of
${\rm Gr}_{G,\mu }$ one obtains the weakly admissible locus of [Reference ViehmannVie21]. We use a natural construction in terms of modifications of ![]() $G$-bundles on the curve that resembles the definition of Fargues and Fontaine's Harder–Narasimhan formalism that led to the Newton stratification. The main difference between the two theories is in the choice of the subbundles to define semi-stability. Fargues and Fontaine consider for a given vector bundle
$G$-bundles on the curve that resembles the definition of Fargues and Fontaine's Harder–Narasimhan formalism that led to the Newton stratification. The main difference between the two theories is in the choice of the subbundles to define semi-stability. Fargues and Fontaine consider for a given vector bundle ![]() ${\mathcal {E}}$ on
${\mathcal {E}}$ on ![]() $X$ all subbundles
$X$ all subbundles ![]() ${\mathcal {E}}'$ and their slopes. We consider vector bundles
${\mathcal {E}}'$ and their slopes. We consider vector bundles ![]() ${\mathcal {E}}={\mathcal {E}}_{b,x}$ obtained as a modification à la Beauville and Laszlo of some
${\mathcal {E}}={\mathcal {E}}_{b,x}$ obtained as a modification à la Beauville and Laszlo of some ![]() ${\mathcal {E}}_b$, and only those subbundles that correspond to direct summands of
${\mathcal {E}}_b$, and only those subbundles that correspond to direct summands of ![]() ${\mathcal {E}}_b$. The slope of such a subbundle of
${\mathcal {E}}_b$. The slope of such a subbundle of ![]() ${\mathcal {E}}_{b,x}$ is then the same as in the other theory. From this comparison one immediately obtains that the Harder–Narasimhan invariant is bounded above by (the opposite of) the Newton invariant. In particular, this yields the analog of the result that admissible implies weakly admissible.
${\mathcal {E}}_{b,x}$ is then the same as in the other theory. From this comparison one immediately obtains that the Harder–Narasimhan invariant is bounded above by (the opposite of) the Newton invariant. In particular, this yields the analog of the result that admissible implies weakly admissible.
To extend our theory to ![]() $G$-bundles for
$G$-bundles for ![]() $G$ other than
$G$ other than ![]() ${\rm GL}_n$ we then use the Tannakian formalism and a result of Cornut and Peche Irissarry [Reference Cornut and Peche IrissarryCPI19]. For this we have to restrict to modifications of the trivial bundle
${\rm GL}_n$ we then use the Tannakian formalism and a result of Cornut and Peche Irissarry [Reference Cornut and Peche IrissarryCPI19]. For this we have to restrict to modifications of the trivial bundle ![]() ${\mathcal {E}}_1$, which is, however, also the most relevant case for the consideration of Newton strata. Nevertheless it would be interesting to see if our theory can be generalized to all
${\mathcal {E}}_1$, which is, however, also the most relevant case for the consideration of Newton strata. Nevertheless it would be interesting to see if our theory can be generalized to all ![]() $G$ and
$G$ and ![]() $b$.
$b$.
In the past years, several closely related theories have been introduced. More precisely, our definition of the Harder–Narasimhan theory (or close variants of it) have been studied by several authors. However, most of the geometric and comparison properties that we establish are new. Let us comment in more detail.
In [Reference FarguesFar19, § 9.3], Fargues proved the existence of a Harder–Narasimhan filtration for pairs ![]() $(\mathcal {E}, x)$ when
$(\mathcal {E}, x)$ when ![]() $\mathcal {E}$ is the trivial bundle of rank
$\mathcal {E}$ is the trivial bundle of rank ![]() $n$ and
$n$ and ![]() $x \in {\rm Gr}_{n,\mu } (C)$ for some minuscule
$x \in {\rm Gr}_{n,\mu } (C)$ for some minuscule ![]() $\mu$. Our results extend this theory to the case where
$\mu$. Our results extend this theory to the case where ![]() $\mu$ is arbitrary and where
$\mu$ is arbitrary and where ![]() $G$ is any reductive group instead of
$G$ is any reductive group instead of ![]() ${\rm GL}_n$ or where the bundle
${\rm GL}_n$ or where the bundle ![]() ${\mathcal {E}}$ may be non-trivial. We also discuss the minuscule case of several of Fargues’ conjectures on the geometric properties of the Harder–Narasimhan strata that he stated in [Reference FarguesFar19, § 9.7].
${\mathcal {E}}$ may be non-trivial. We also discuss the minuscule case of several of Fargues’ conjectures on the geometric properties of the Harder–Narasimhan strata that he stated in [Reference FarguesFar19, § 9.7].
Cornut and Peche Irissarry [Reference Cornut and Peche IrissarryCPI19] generalized Fargues's theory by defining a Harder– Narasimhan theory for Breuil–Kisin–Fargues modules and call the resulting filtration the Fargues filtration. It coincides with the particular case for ![]() $b=1$ of our definition, and for general groups, we use their results.
$b=1$ of our definition, and for general groups, we use their results.
In [Reference Dat, Orlik and RapoportDOR10], Dat, Orlik and Rapoport use filtered isocrystals and define the weakly admissible locus in the flag variety ![]() ${\mathcal {F}\ell }(G,\mu )$ also for non-minuscule
${\mathcal {F}\ell }(G,\mu )$ also for non-minuscule ![]() $\mu$. They generalize this also to a Harder–Narasimhan stratification of the flag variety where again the weakly admissible locus is the semi-stable and unique open stratum. One can consider the inverse images of Dat, Orlik and Rapoport's Harder–Narasimhan strata under the Bialynicki-Birula map, which then define a decomposition of the affine Schubert cell
$\mu$. They generalize this also to a Harder–Narasimhan stratification of the flag variety where again the weakly admissible locus is the semi-stable and unique open stratum. One can consider the inverse images of Dat, Orlik and Rapoport's Harder–Narasimhan strata under the Bialynicki-Birula map, which then define a decomposition of the affine Schubert cell ![]() ${\rm Gr}_{G,\mu }$. This approach is taken by Shen in the first versions of [Reference ShenShe19]. This theory coincides with our Harder–Narasimhan stratification if
${\rm Gr}_{G,\mu }$. This approach is taken by Shen in the first versions of [Reference ShenShe19]. This theory coincides with our Harder–Narasimhan stratification if ![]() $\mu$ is minuscule. In general, already the notions of weak admissibility differ, compare [Reference ViehmannVie21, Example 4.10].
$\mu$ is minuscule. In general, already the notions of weak admissibility differ, compare [Reference ViehmannVie21, Example 4.10].
When we finished the present manuscript, Shen posted a new version of [Reference ShenShe19] on the arXiv, in which he changed his definition and adapted several of his arguments, so that part of his new version is in parallel to some of our results (the construction of the Harder–Narasimhan theory for ![]() $b=1$, as well as the proof that the strata are locally closed). Most of our geometric results of §§ 5–8 are independent of his work.
$b=1$, as well as the proof that the strata are locally closed). Most of our geometric results of §§ 5–8 are independent of his work.
Despite the fact that the Harder–Narasimhan theory that we study has been considered (at least in some form) by many people, very little was known about the properties of the associated decomposition of ![]() ${\rm Gr}_G$.
${\rm Gr}_G$.
In Proposition 3.13 we give a group-theoretic criterion for non-emptiness. Recall from [Reference RapoportRap18] that the set of non-empty Newton strata (for modifications of the trivial bundle) in ![]() ${\rm Gr}_{G,\mu }$ is indexed by the set
${\rm Gr}_{G,\mu }$ is indexed by the set ![]() $B(G,-\mu )$. In Proposition 3.13 we show that the set of non-empty Harder–Narasimhan strata in
$B(G,-\mu )$. In Proposition 3.13 we show that the set of non-empty Harder–Narasimhan strata in ![]() ${\rm Gr}_{G,\mu }$ is contained in a, in general strict, subset of
${\rm Gr}_{G,\mu }$ is contained in a, in general strict, subset of ![]() $B(G,\mu )$ that has an explicit description in terms of the involved Newton points. In [Reference OrlikOrl06], Orlik proves a non-emptiness criterion for the Dat–Orlik–Rapoport stratification for
$B(G,\mu )$ that has an explicit description in terms of the involved Newton points. In [Reference OrlikOrl06], Orlik proves a non-emptiness criterion for the Dat–Orlik–Rapoport stratification for ![]() $G={\rm GL}_n$ (and filtrations of an arbitrary isocrystal). As a byproduct of our theory, we generalize Orlik's description to the case of any
$G={\rm GL}_n$ (and filtrations of an arbitrary isocrystal). As a byproduct of our theory, we generalize Orlik's description to the case of any ![]() $G$, but the trivial
$G$, but the trivial ![]() $G$-isocrystal in Proposition 5.6.
$G$-isocrystal in Proposition 5.6.
From the definition of the two stratifications, one obtains the immediate estimate that the Harder–Narasimhan polygon is bounded by the Newton polygon. In § 6 we extend this comparison, showing that in Hodge–Newton decomposable cases, the Hodge–Newton decomposition also is a coarsening of the Harder–Narasimhan reduction. We use this to study cases where Newton strata and Harder–Narasimhan strata coincide. We continue in § 7 by giving an estimate for the dimension of Harder–Narasimhan strata in the minuscule case. It disproves [Reference FarguesFar19, Conjecture 2(2)], where Fargues conjectured that the dimension of a Harder–Narasimhan stratum for some ![]() $[b']\in B(G,\mu )$ should coincide with the dimension of the Newton stratum for some
$[b']\in B(G,\mu )$ should coincide with the dimension of the Newton stratum for some ![]() $[b']^*\in B(G,-\mu )$ where we refer to the next section for the notation. In Proposition 7.3 we prove that the dimension of a Newton stratum is an upper bound for the dimension of the corresponding Harder–Narasimhan stratum and determine the cases in which equality holds.
$[b']^*\in B(G,-\mu )$ where we refer to the next section for the notation. In Proposition 7.3 we prove that the dimension of a Newton stratum is an upper bound for the dimension of the corresponding Harder–Narasimhan stratum and determine the cases in which equality holds.
Notation
We use the following notation.
–
 $F$ is a finite degree extension of
$F$ is a finite degree extension of  $\mathbb {Q}_p$ and
$\mathbb {Q}_p$ and  $\pi$ is a uniformizer of
$\pi$ is a uniformizer of  $\mathcal {O}_F$. Let
$\mathcal {O}_F$. Let  $\overline {F}$ be an algebraic closure of
$\overline {F}$ be an algebraic closure of  $F$ and
$F$ and  $\Gamma = {\rm Gal}(\overline {F}|F)$.
$\Gamma = {\rm Gal}(\overline {F}|F)$.–
 $\breve {F}$ is the completion of the maximal unramified extension of
$\breve {F}$ is the completion of the maximal unramified extension of  $F$ with Frobenius
$F$ with Frobenius  $\sigma$.
$\sigma$.–
 $G$ is a connected reductive group over
$G$ is a connected reductive group over  $F$. Let
$F$. Let  $H$ be a quasi-split inner form of
$H$ be a quasi-split inner form of  $G$ and fix an inner twisting
$G$ and fix an inner twisting  $G_{\breve {F}} \overset {\sim }{\longrightarrow } H_{\breve {F}}$.
$G_{\breve {F}} \overset {\sim }{\longrightarrow } H_{\breve {F}}$.–
 $A \subseteq T \subseteq B$ where
$A \subseteq T \subseteq B$ where  $A$ is a maximal split torus,
$A$ is a maximal split torus,  $T = Z_H(A)$ is the centralizer of
$T = Z_H(A)$ is the centralizer of  $A$ in
$A$ in  $T$ and
$T$ and  $B$ is a Borel subgroup in
$B$ is a Borel subgroup in  $H$. Let
$H$. Let  $U$ be its unipotent radical.
$U$ be its unipotent radical.–
 $(X^*(T), \Phi, X_*(T), \Phi ^{\vee })$ is the absolute root datum of
$(X^*(T), \Phi, X_*(T), \Phi ^{\vee })$ is the absolute root datum of  $G$ with positive roots
$G$ with positive roots  $\Phi ^+$ and simple roots
$\Phi ^+$ and simple roots  $\Delta$ with respect to the choice of
$\Delta$ with respect to the choice of  $B$.
$B$.– Further,
 $(X^*(A), \Phi _0, X_*(A), \Phi ^{\vee }_0)$ denotes the relative root datum, with positive roots
$(X^*(A), \Phi _0, X_*(A), \Phi ^{\vee }_0)$ denotes the relative root datum, with positive roots  $\Phi ^+_0$ and simple roots
$\Phi ^+_0$ and simple roots  $\Delta _0$.
$\Delta _0$.– On
 $X_*(A)_{\mathbb {Q}}$, respectively
$X_*(A)_{\mathbb {Q}}$, respectively  $X_*(T)_{\mathbb {Q}}$, we consider the partial order given by
$X_*(T)_{\mathbb {Q}}$, we consider the partial order given by  $\nu \leqslant \nu '$ if
$\nu \leqslant \nu '$ if  $\nu ' - \nu$ is a non-negative rational linear combination of positive coroots, respectively of positive relative coroots.
$\nu ' - \nu$ is a non-negative rational linear combination of positive coroots, respectively of positive relative coroots.– Let
 $C | \overline {F}$ be an algebraically closed complete field. Let
$C | \overline {F}$ be an algebraically closed complete field. Let  $C^{\circ }$, respectively
$C^{\circ }$, respectively  $C^{\flat,\circ }$, be the subring of power-bounded elements of
$C^{\flat,\circ }$, be the subring of power-bounded elements of  $C$, respectively
$C$, respectively  $C^{\flat }$, and let
$C^{\flat }$, and let  $\xi$ be a generator of the kernel of the surjective map
$\xi$ be a generator of the kernel of the surjective map  $W(C^{\flat,\circ })\rightarrow C^{\circ }$. Let
$W(C^{\flat,\circ })\rightarrow C^{\circ }$. Let  ${B^+_{{\rm dR}}}:={B^+_{{\rm dR}}}(C)$ be the
${B^+_{{\rm dR}}}:={B^+_{{\rm dR}}}(C)$ be the  $\xi$-adic completion of
$\xi$-adic completion of  $W(C^{\flat,\circ })[1/p]$ and
$W(C^{\flat,\circ })[1/p]$ and  ${B_{{\rm dR}}}={B_{{\rm dR}}}(C)={B^+_{{\rm dR}}}[\xi ^{-1}]$. Then
${B_{{\rm dR}}}={B_{{\rm dR}}}(C)={B^+_{{\rm dR}}}[\xi ^{-1}]$. Then  ${B^+_{{\rm dR}}}\cong C[\![ \xi ]\!]$ and
${B^+_{{\rm dR}}}\cong C[\![ \xi ]\!]$ and  ${B_{{\rm dR}}}\cong C(\!( \xi )\!)$.
${B_{{\rm dR}}}\cong C(\!( \xi )\!)$.– Let
 $X$ be the schematic Fargues–Fontaine curve over
$X$ be the schematic Fargues–Fontaine curve over  $C^{\flat }$. The untilt
$C^{\flat }$. The untilt  $C$ of
$C$ of  $C^{\flat }$ corresponds to a point
$C^{\flat }$ corresponds to a point  $\infty \in |X|$ with residue field
$\infty \in |X|$ with residue field  $C$ and
$C$ and  $\widehat {\mathcal {O}}_{X, \infty }\cong {B^+_{{\rm dR}}}$.
$\widehat {\mathcal {O}}_{X, \infty }\cong {B^+_{{\rm dR}}}$.– The adic space
 $Y={\rm Spa} W_{{\mathcal {O}}_F}(C^{\circ })\setminus \{[\pi ]p=0\}$ is equipped with a Frobenius
$Y={\rm Spa} W_{{\mathcal {O}}_F}(C^{\circ })\setminus \{[\pi ]p=0\}$ is equipped with a Frobenius  $\varphi$. The quotient
$\varphi$. The quotient  $Y / \varphi ^{\mathbb {Z}} =: X^{{\rm {ad}}}$ is the adic Fargues–Fontaine curve. Recall that there is an equivalence between the categories of coherent sheaves over
$Y / \varphi ^{\mathbb {Z}} =: X^{{\rm {ad}}}$ is the adic Fargues–Fontaine curve. Recall that there is an equivalence between the categories of coherent sheaves over  $X$ and over
$X$ and over  $X^{{\rm {ad}}}$.
$X^{{\rm {ad}}}$.– Let
 $B(G)$ be the set of
$B(G)$ be the set of  $G(\breve {F})$-
$G(\breve {F})$- $\sigma$-conjugacy classes of elements of
$\sigma$-conjugacy classes of elements of  $G(\breve {F})$. By work of Kottwitz, elements
$G(\breve {F})$. By work of Kottwitz, elements  $[b]$ are classified by their Kottwitz point
$[b]$ are classified by their Kottwitz point  $\kappa _G(b)\in \pi _1(G)_{\Gamma }$ and their Newton point
$\kappa _G(b)\in \pi _1(G)_{\Gamma }$ and their Newton point  $\nu _b\in X_*(A)_{\mathbb {Q},{\rm dom}}$.
$\nu _b\in X_*(A)_{\mathbb {Q},{\rm dom}}$.– For a
 $G$-bundle
$G$-bundle  ${\mathcal {E}}$ on
${\mathcal {E}}$ on  $X$ let
$X$ let  $\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}})$ be the corresponding class in
$\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}})$ be the corresponding class in  $B(G)$.
$B(G)$.– Let
 $[b]\in B(G)$. Due to different sign conventions for Harder–Narasimhan polygons and Newton polygons, we write
$[b]\in B(G)$. Due to different sign conventions for Harder–Narasimhan polygons and Newton polygons, we write  $[b]^*$ for the unique element of
$[b]^*$ for the unique element of  $B(G)$ with
$B(G)$ with  $\kappa _G([b]^*)=-\kappa _G(b)$ and
$\kappa _G([b]^*)=-\kappa _G(b)$ and  $\nu _{[b]^*}=(-\nu _b)_{{\rm dom}}$. We have
$\nu _{[b]^*}=(-\nu _b)_{{\rm dom}}$. We have  $[b]^*\in B(G,-\mu )$ if and only if
$[b]^*\in B(G,-\mu )$ if and only if  $[b]\in B(G,\mu )$.
$[b]\in B(G,\mu )$.
2. The Harder–Narasimhan formalism for modifications of vector bundles
2.1 Generalities on vector bundles and gluing
Let ![]() ${\rm Bun} (X)$ denote the category of vector bundles on the Fargues–Fontaine curve
${\rm Bun} (X)$ denote the category of vector bundles on the Fargues–Fontaine curve ![]() $X$ and recall from [Reference Fargues and FontaineFF18] that every object in
$X$ and recall from [Reference Fargues and FontaineFF18] that every object in ![]() ${\rm Bun} (X)$ can be written as direct sum of simple objects which can be parametrized by
${\rm Bun} (X)$ can be written as direct sum of simple objects which can be parametrized by ![]() $\mathbb {Q}$. More precisely, the isomorphism classes of vector bundles of some rank
$\mathbb {Q}$. More precisely, the isomorphism classes of vector bundles of some rank ![]() $n$ on
$n$ on ![]() $X$ are in bijection with
$X$ are in bijection with ![]() $B({\rm GL}_n)$, the set of
$B({\rm GL}_n)$, the set of ![]() $\sigma$-conjugacy classes of elements
$\sigma$-conjugacy classes of elements ![]() $b \in {\rm GL}_n(\breve {F})$, or with isomorphism classes of
$b \in {\rm GL}_n(\breve {F})$, or with isomorphism classes of ![]() $\sigma$-isocrystals of rank
$\sigma$-isocrystals of rank ![]() $n$ over
$n$ over ![]() $\breve {F}$. Here, an isocrystal
$\breve {F}$. Here, an isocrystal ![]() $\mathcal {D} = (\breve {F}^n, \varphi _b := b \sigma )$ corresponds to the vector bundle
$\mathcal {D} = (\breve {F}^n, \varphi _b := b \sigma )$ corresponds to the vector bundle
over ![]() $X^{{\rm {ad}}}$, and to the corresponding bundle over
$X^{{\rm {ad}}}$, and to the corresponding bundle over ![]() $X$. Here, the automorphism
$X$. Here, the automorphism ![]() $\varphi$ on the left hand side acts via
$\varphi$ on the left hand side acts via ![]() $\varphi$ on
$\varphi$ on ![]() $Y$ and as
$Y$ and as ![]() $\varphi _b$ on
$\varphi _b$ on ![]() $\mathcal {D}$.
$\mathcal {D}$.
If ![]() $f : (\breve {F}^{n_1}, b_1 \sigma ) \longrightarrow (\breve {F}^{n_2}, b_2 \sigma )$ is a map of isocrystals, we obtain an induced morphism of vector bundles
$f : (\breve {F}^{n_1}, b_1 \sigma ) \longrightarrow (\breve {F}^{n_2}, b_2 \sigma )$ is a map of isocrystals, we obtain an induced morphism of vector bundles ![]() $\mathcal {E}(f) : \mathcal {E}_{b_1} \longrightarrow \mathcal {E}_{b_2}$. Be aware that the converse does not hold.
$\mathcal {E}(f) : \mathcal {E}_{b_1} \longrightarrow \mathcal {E}_{b_2}$. Be aware that the converse does not hold.
Recall that ![]() $X$ is the Fargues–Fontaine curve over
$X$ is the Fargues–Fontaine curve over ![]() $C^{\flat }$, which comes equipped with a point
$C^{\flat }$, which comes equipped with a point ![]() $\infty$ corresponding to
$\infty$ corresponding to ![]() $C$. By Beauville and Laszlo's gluing theorem [Reference Beauville and LaszloBL95] we have a bijective correspondence between vector bundles
$C$. By Beauville and Laszlo's gluing theorem [Reference Beauville and LaszloBL95] we have a bijective correspondence between vector bundles ![]() ${\mathcal {E}}$ on
${\mathcal {E}}$ on ![]() $X$ and triples
$X$ and triples ![]() $({\mathcal {E}}^e,{\mathcal {E}}_{{B^+_{{\rm dR}}}},\iota )$ where
$({\mathcal {E}}^e,{\mathcal {E}}_{{B^+_{{\rm dR}}}},\iota )$ where ![]() ${\mathcal {E}}^e$ is a vector bundle over
${\mathcal {E}}^e$ is a vector bundle over ![]() $X\setminus \{\infty \}$, where
$X\setminus \{\infty \}$, where ![]() ${\mathcal {E}}_{B^+_{\rm dR}}$ is a vector bundle on
${\mathcal {E}}_{B^+_{\rm dR}}$ is a vector bundle on ![]() $\mathop {\mathrm {Spec}}\nolimits ({B^+_{{\rm dR}}})$ and where
$\mathop {\mathrm {Spec}}\nolimits ({B^+_{{\rm dR}}})$ and where ![]() $\iota :\mathcal {E}^e \otimes _{B_e} {B_{{\rm dR}}}\rightarrow {\mathcal {E}}_{{B^+_{{\rm dR}}}}\otimes _{{B^+_{{\rm dR}}}}{B_{{\rm dR}}}$ is an isomorphism. Here, the triple corresponding to some
$\iota :\mathcal {E}^e \otimes _{B_e} {B_{{\rm dR}}}\rightarrow {\mathcal {E}}_{{B^+_{{\rm dR}}}}\otimes _{{B^+_{{\rm dR}}}}{B_{{\rm dR}}}$ is an isomorphism. Here, the triple corresponding to some ![]() ${\mathcal {E}}$ is given by the respective base changes of
${\mathcal {E}}$ is given by the respective base changes of ![]() ${\mathcal {E}}$ together with the induced isomorphism.
${\mathcal {E}}$ together with the induced isomorphism.
The pullback of a vector bundle ![]() ${\mathcal {E}}_b$ via
${\mathcal {E}}_b$ via ![]() $\mathop {\mathrm {Spec}}\nolimits ({B^+_{{\rm dR}}}) \longrightarrow X$ is trivial. Indeed, the inclusion
$\mathop {\mathrm {Spec}}\nolimits ({B^+_{{\rm dR}}}) \longrightarrow X$ is trivial. Indeed, the inclusion ![]() $F\hookrightarrow C\hookrightarrow {B^+_{{\rm dR}}}$ extends to an embedding of an algebraic closure
$F\hookrightarrow C\hookrightarrow {B^+_{{\rm dR}}}$ extends to an embedding of an algebraic closure ![]() $\bar F$ into
$\bar F$ into ![]() ${B^+_{{\rm dR}}}$. By Lang's theorem there is a
${B^+_{{\rm dR}}}$. By Lang's theorem there is a ![]() $g\in G(\bar F)$ with
$g\in G(\bar F)$ with ![]() $gb\sigma (g^{-1})=1$, which induces the desired trivialization. It is well defined up to the action of
$gb\sigma (g^{-1})=1$, which induces the desired trivialization. It is well defined up to the action of ![]() $G(F)$. The Beauville–Laszlo uniformization depends on the choice of such a trivialization. From now on we consider
$G(F)$. The Beauville–Laszlo uniformization depends on the choice of such a trivialization. From now on we consider ![]() ${\mathcal {E}}_b$ together with a trivialization of
${\mathcal {E}}_b$ together with a trivialization of ![]() ${\mathcal {E}}_{b,{B^+_{{\rm dR}}}}$, without explicitly mentioning it. If
${\mathcal {E}}_{b,{B^+_{{\rm dR}}}}$, without explicitly mentioning it. If ![]() $b=1$, we choose the natural trivialization. In all cases, the trivialization of
$b=1$, we choose the natural trivialization. In all cases, the trivialization of ![]() ${\mathcal {E}}_{b,{B^+_{{\rm dR}}}}$ induces a trivialization of
${\mathcal {E}}_{b,{B^+_{{\rm dR}}}}$ induces a trivialization of ![]() ${\mathcal {E}}_{b,{B^+_{{\rm dR}}}}\otimes _{{B^+_{{\rm dR}}}}{B_{{\rm dR}}}$ (i.e. an identification with
${\mathcal {E}}_{b,{B^+_{{\rm dR}}}}\otimes _{{B^+_{{\rm dR}}}}{B_{{\rm dR}}}$ (i.e. an identification with ![]() ${B_{{\rm dR}}}^n$ where
${B_{{\rm dR}}}^n$ where ![]() $n$ is the rank) identifying
$n$ is the rank) identifying ![]() ${\mathcal {E}}_{b,{B^+_{{\rm dR}}}}$ with the standard lattice
${\mathcal {E}}_{b,{B^+_{{\rm dR}}}}$ with the standard lattice ![]() $({B^+_{{\rm dR}}})^n$ in
$({B^+_{{\rm dR}}})^n$ in ![]() ${B_{{\rm dR}}}^n$.
${B_{{\rm dR}}}^n$.
For each ![]() $x \in {\rm Gr}_n (C)$ one can construct a modification
$x \in {\rm Gr}_n (C)$ one can construct a modification ![]() $\mathcal {E}_{b,x}$ of
$\mathcal {E}_{b,x}$ of ![]() $\mathcal {E}_b$ as follows. Using the trivialization of
$\mathcal {E}_b$ as follows. Using the trivialization of ![]() ${\mathcal {E}}_{b,{B^+_{{\rm dR}}}}$, we can write the triple corresponding to
${\mathcal {E}}_{b,{B^+_{{\rm dR}}}}$, we can write the triple corresponding to ![]() ${\mathcal {E}}_b$ as
${\mathcal {E}}_b$ as ![]() $(\mathcal {E}_{b | X \setminus \infty }, {\mathcal {E}}^{n,\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}},\iota )$ where
$(\mathcal {E}_{b | X \setminus \infty }, {\mathcal {E}}^{n,\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}},\iota )$ where ![]() ${\mathcal {E}}^{n,\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}}$ is the trivial bundle of rank
${\mathcal {E}}^{n,\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}}$ is the trivial bundle of rank ![]() $n$ on
$n$ on ![]() $\mathop {\mathrm {Spec}}\nolimits ({B^+_{{\rm dR}}})$. Then
$\mathop {\mathrm {Spec}}\nolimits ({B^+_{{\rm dR}}})$. Then ![]() ${\mathcal {E}}_{b,x}$ is given as the vector bundle corresponding to the triple
${\mathcal {E}}_{b,x}$ is given as the vector bundle corresponding to the triple ![]() $(\mathcal {E}_{b | X \setminus \infty }, {\mathcal {E}}^{n,\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}},\iota _x )$ where the isomorphism
$(\mathcal {E}_{b | X \setminus \infty }, {\mathcal {E}}^{n,\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}},\iota _x )$ where the isomorphism ![]() $\iota _x$ is given by the following commutative diagram.
$\iota _x$ is given by the following commutative diagram.

Here, ![]() $B_e = H^0(X \setminus \infty, \mathcal {O}_X)$ and the map
$B_e = H^0(X \setminus \infty, \mathcal {O}_X)$ and the map ![]() $x$ in the diagram is multiplication by a representative of
$x$ in the diagram is multiplication by a representative of ![]() $x$ on
$x$ on ![]() ${B_{{\rm dR}}}^n$. The isomorphism class of the triple only depends on the lattice
${B_{{\rm dR}}}^n$. The isomorphism class of the triple only depends on the lattice ![]() $x({\mathcal {E}}^{n,\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}})\subset {B_{{\rm dR}}}^n$ and is in particular independent of the choice of the representative.
$x({\mathcal {E}}^{n,\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}})\subset {B_{{\rm dR}}}^n$ and is in particular independent of the choice of the representative.
Write ![]() $\Lambda _{x} := x(\mathcal {E}^{n, \mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}})$ and
$\Lambda _{x} := x(\mathcal {E}^{n, \mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}})$ and ![]() $\mathcal {E}^{n, \mathop {\mathrm {tri}}\nolimits }_{{B_{{\rm dR}}}} := \mathcal {E}^{n, \mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}} \otimes _{{B^+_{{\rm dR}}}} {B_{{\rm dR}}}$. If
$\mathcal {E}^{n, \mathop {\mathrm {tri}}\nolimits }_{{B_{{\rm dR}}}} := \mathcal {E}^{n, \mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}} \otimes _{{B^+_{{\rm dR}}}} {B_{{\rm dR}}}$. If ![]() $(k_1,\dotsc,k_n)$ with
$(k_1,\dotsc,k_n)$ with ![]() $k_1\geqslant \dotsm \geqslant k_n$ is the relative position of
$k_1\geqslant \dotsm \geqslant k_n$ is the relative position of ![]() $\Lambda _x$ with respect to
$\Lambda _x$ with respect to ![]() $({B^+_{{\rm dR}}})^n$, we call
$({B^+_{{\rm dR}}})^n$, we call ![]() $(k_1, \dotsc, k_n)$ the type of
$(k_1, \dotsc, k_n)$ the type of ![]() $x$.
$x$.
2.2 The Harder–Narasimhan formalism
We want to define a Harder–Narasimhan filtration for each pair ![]() $(b, x)$ where
$(b, x)$ where ![]() $b \in {\rm GL}_n(\breve {F})$ and
$b \in {\rm GL}_n(\breve {F})$ and ![]() $x \in {\rm Gr}_{n}(C)={\rm Gr}_{{\rm GL}_n} (C)$ in such a way that it coincides with the Harder–Narasimhan filtration for the filtered isocrystal for
$x \in {\rm Gr}_{n}(C)={\rm Gr}_{{\rm GL}_n} (C)$ in such a way that it coincides with the Harder–Narasimhan filtration for the filtered isocrystal for ![]() $b$ with filtration induced by
$b$ with filtration induced by ![]() $x$ if
$x$ if ![]() $x$ is of minuscule type. We will use the general Harder–Narasimhan formalism as for example in [Reference AndréAnd09].
$x$ is of minuscule type. We will use the general Harder–Narasimhan formalism as for example in [Reference AndréAnd09].
Definition 2.1
(i) Let
 $\mathop {\mathrm {Isoc}}\nolimits$ be the category of
$\mathop {\mathrm {Isoc}}\nolimits$ be the category of  $\sigma$-isocrystals over
$\sigma$-isocrystals over  $\breve {F}$. Recall that each object is isomorphic to a pair
$\breve {F}$. Recall that each object is isomorphic to a pair  $({\breve {F}}^n, b\sigma )$ for some
$({\breve {F}}^n, b\sigma )$ for some  $n$. From now on we write
$n$. From now on we write  ${\mathcal {E}}_b$ for such a pair and identify it with the corresponding vector bundle on
${\mathcal {E}}_b$ for such a pair and identify it with the corresponding vector bundle on  $X$. However, for two vector bundles
$X$. However, for two vector bundles  $\mathcal {E}_{b_1}$ and
$\mathcal {E}_{b_1}$ and  $\mathcal {E}_{b_2}$ we set
the set of morphisms of isocrystals. In particular
$\mathcal {E}_{b_2}$ we set
the set of morphisms of isocrystals. In particular \[ {\rm Hom}_{\mathop{\mathrm{Isoc}}\nolimits} ( \mathcal{E}_{b_1}, \mathcal{E}_{b_2} ) = \{ \mathcal{E}(f) \mid f \in {\rm Hom} ( (\breve{F}^{n_1}, b_1 \sigma), (\breve{F}^{n_2}, b_2 \sigma )) \}, \]
\[ {\rm Hom}_{\mathop{\mathrm{Isoc}}\nolimits} ( \mathcal{E}_{b_1}, \mathcal{E}_{b_2} ) = \{ \mathcal{E}(f) \mid f \in {\rm Hom} ( (\breve{F}^{n_1}, b_1 \sigma), (\breve{F}^{n_2}, b_2 \sigma )) \}, \]
 $\mathop {\mathrm {Isoc}}\nolimits$ is abelian and every exact sequence splits.
$\mathop {\mathrm {Isoc}}\nolimits$ is abelian and every exact sequence splits.(ii) Let
 $\mathop {\mathrm {Isoc}}\nolimits ^{\bullet }$ be the category whose objects are pairs
$\mathop {\mathrm {Isoc}}\nolimits ^{\bullet }$ be the category whose objects are pairs  ${}^{\bullet } {\mathcal {E}}$ consisting of an element
${}^{\bullet } {\mathcal {E}}$ consisting of an element  $\mathcal {E}$ in
$\mathcal {E}$ in  $\mathop {\mathrm {Isoc}}\nolimits$ together with a filtration
$\mathop {\mathrm {Isoc}}\nolimits$ together with a filtration  $\mathop {\mathrm {Fil}}\nolimits ^{\bullet }\mathcal {E}$ in
$\mathop {\mathrm {Fil}}\nolimits ^{\bullet }\mathcal {E}$ in  $\mathop {\mathrm {Isoc}}\nolimits$ and whose morphisms are morphisms in
$\mathop {\mathrm {Isoc}}\nolimits$ and whose morphisms are morphisms in  $\mathop {\mathrm {Isoc}}\nolimits$ that are strictly compatible with the filtrations.
$\mathop {\mathrm {Isoc}}\nolimits$ that are strictly compatible with the filtrations.(iii) Let
 $\mathcal {E}_{b_1}$, respectively
$\mathcal {E}_{b_1}$, respectively  $\mathcal {E}_{b_2}$, be vector bundles of rank
$\mathcal {E}_{b_2}$, be vector bundles of rank  $n$, respectively
$n$, respectively  $m$, and let
$m$, and let  $f : \mathcal {E}_{b_1} \longrightarrow \mathcal {E}_{b_2}$ be a morphism in
$f : \mathcal {E}_{b_1} \longrightarrow \mathcal {E}_{b_2}$ be a morphism in  $\mathop {\mathrm {Isoc}}\nolimits$. Let
$\mathop {\mathrm {Isoc}}\nolimits$. Let  $x_1 \in {\rm Gr}_n (C)$ and
$x_1 \in {\rm Gr}_n (C)$ and  $x_2 \in {\rm Gr}_m (C)$. Then we have the associated
$x_2 \in {\rm Gr}_m (C)$. Then we have the associated  ${B^+_{{\rm dR}}}$-lattices
${B^+_{{\rm dR}}}$-lattices  $\Lambda _{x_1}$, respectively
$\Lambda _{x_1}$, respectively  $\Lambda _{x_2}$, of
$\Lambda _{x_2}$, of  $\mathcal {E}_{b_1}$, respectively
$\mathcal {E}_{b_1}$, respectively  $\mathcal {E}_{b_2}$. The morphism
$\mathcal {E}_{b_2}$. The morphism  $f$ is effective with respect to
$f$ is effective with respect to  $x_1$ and
$x_1$ and  $x_2$ if
$x_2$ if  $f( {\Lambda }_{x_1} ) \subset {\Lambda }_{x_2}$.
$f( {\Lambda }_{x_1} ) \subset {\Lambda }_{x_2}$.(iv) Using the same notation let
 $\tilde {\Lambda }_{x_2}$ be the intersection of
$\tilde {\Lambda }_{x_2}$ be the intersection of  $\Lambda _{x_2}$ with the isocrystal corresponding to
$\Lambda _{x_2}$ with the isocrystal corresponding to  $f(\mathcal {E}_{b_1})$. Then
$f(\mathcal {E}_{b_1})$. Then  $f$ is strict effective if
$f$ is strict effective if  $f( {\Lambda }_{x_1} ) = \tilde {\Lambda }_{x_2}$.
$f( {\Lambda }_{x_1} ) = \tilde {\Lambda }_{x_2}$.(v) We define a category
 $\mathcal {C}$ whose objects are pairs
$\mathcal {C}$ whose objects are pairs  $(\mathcal {E}, x)$ where
$(\mathcal {E}, x)$ where  $\mathcal {E}$ is a vector bundle on
$\mathcal {E}$ is a vector bundle on  $X$ of some rank
$X$ of some rank  $n$ and where
$n$ and where  $x \in {\rm Gr}_n (C)$. A morphism from
$x \in {\rm Gr}_n (C)$. A morphism from  $(\mathcal {E}_{b_1}, x_1)$ to
$(\mathcal {E}_{b_1}, x_1)$ to  $(\mathcal {E}_{b_2}, x_2)$ is a morphism
$(\mathcal {E}_{b_2}, x_2)$ is a morphism  $g \in {\rm Hom} _{\mathop {\mathrm {Isoc}}\nolimits } ( \mathcal {E}_{b_1}, \mathcal {E}_{b_2} )$ that is effective with respect to
$g \in {\rm Hom} _{\mathop {\mathrm {Isoc}}\nolimits } ( \mathcal {E}_{b_1}, \mathcal {E}_{b_2} )$ that is effective with respect to  $x_1$ and
$x_1$ and  $x_2$.
$x_2$.
Remark 2.2 The class of strict effective epimorphisms in ![]() $\mathcal {C}$ is stable under pull-backs in
$\mathcal {C}$ is stable under pull-backs in ![]() $\mathcal {C}$ and that of strict effective monomorphisms is stable under push-forward. Moreover the category
$\mathcal {C}$ and that of strict effective monomorphisms is stable under push-forward. Moreover the category ![]() $\mathcal {C}$ is additive and has kernels and cokernels. Indeed, let
$\mathcal {C}$ is additive and has kernels and cokernels. Indeed, let ![]() $g$ be in
$g$ be in ![]() ${\rm Hom} _{\mathcal {C}} ( (\mathcal {E}_{b_1}, x_1), (\mathcal {E}_{b_2}, x_2))$. Since the category
${\rm Hom} _{\mathcal {C}} ( (\mathcal {E}_{b_1}, x_1), (\mathcal {E}_{b_2}, x_2))$. Since the category ![]() $\mathop {\mathrm {Isoc}}\nolimits$ has kernels, there exists
$\mathop {\mathrm {Isoc}}\nolimits$ has kernels, there exists ![]() $(\mathcal {E}_{b'_1}, f)$, the kernel of
$(\mathcal {E}_{b'_1}, f)$, the kernel of ![]() $g$ in that category. Suppose that
$g$ in that category. Suppose that ![]() $\mathop {\mathrm {rank}}\nolimits (\mathcal {E}_{b'_1}) = \ell$ is not zero then
$\mathop {\mathrm {rank}}\nolimits (\mathcal {E}_{b'_1}) = \ell$ is not zero then ![]() $f$ induces an injective map
$f$ induces an injective map ![]() $\tilde {f} : \mathcal {E}_{b'_1}^e \otimes _{B_e} {B_{{\rm dR}}} \longrightarrow \mathcal {E}_{b_1}^e \otimes _{B_e} {B_{{\rm dR}}}$. Denote
$\tilde {f} : \mathcal {E}_{b'_1}^e \otimes _{B_e} {B_{{\rm dR}}} \longrightarrow \mathcal {E}_{b_1}^e \otimes _{B_e} {B_{{\rm dR}}}$. Denote ![]() $\Lambda _{x'_1} := \tilde {f}^{-1}(\Lambda _{x_1})$ for some
$\Lambda _{x'_1} := \tilde {f}^{-1}(\Lambda _{x_1})$ for some ![]() $x'_1 \in {\rm Gr}_{\ell }(C)$. Then
$x'_1 \in {\rm Gr}_{\ell }(C)$. Then ![]() $((\mathcal {E}_{b'_1}, x'_1), f)$ is the kernel of
$((\mathcal {E}_{b'_1}, x'_1), f)$ is the kernel of ![]() $g$ in
$g$ in ![]() $\mathcal {C}$. Similarly, the category
$\mathcal {C}$. Similarly, the category ![]() $\mathcal {C}$ also has cokernels. Therefore
$\mathcal {C}$ also has cokernels. Therefore ![]() $\mathcal {C}$ is an exact category whose exact sequences are exact sequences in
$\mathcal {C}$ is an exact category whose exact sequences are exact sequences in ![]() $\mathop {\mathrm {Isoc}}\nolimits$ with strict effective morphisms.
$\mathop {\mathrm {Isoc}}\nolimits$ with strict effective morphisms.
Remark 2.3 We consider the forgetful functor
It is clearly exact and faithful.
Consider an exact sequence
in ![]() $\mathcal {C}$. Let
$\mathcal {C}$. Let ![]() $\Lambda '$,
$\Lambda '$, ![]() $\Lambda$ and
$\Lambda$ and ![]() $\Lambda ''$ be the associated lattices. Then
$\Lambda ''$ be the associated lattices. Then ![]() $\Lambda '=\Lambda \cap {\mathcal {E}}^{'{\rm tri}}_{{B_{{\rm dR}}}}$ and
$\Lambda '=\Lambda \cap {\mathcal {E}}^{'{\rm tri}}_{{B_{{\rm dR}}}}$ and ![]() $\Lambda ''$ is the image of
$\Lambda ''$ is the image of ![]() $\Lambda$ in
$\Lambda$ in ![]() ${\mathcal {E}}^{''{\rm tri}}_{{B_{{\rm dR}}}}$. In particular, we obtain an exact sequence
${\mathcal {E}}^{''{\rm tri}}_{{B_{{\rm dR}}}}$. In particular, we obtain an exact sequence
of vector bundles on ![]() $X$. Notice that in general the morphisms are not morphisms of the associated isocrystals. This filtration of
$X$. Notice that in general the morphisms are not morphisms of the associated isocrystals. This filtration of ![]() ${\mathcal {E}}_x$ corresponds to the
${\mathcal {E}}_x$ corresponds to the ![]() $\mathcal {C}$-filtration
$\mathcal {C}$-filtration ![]() ${\mathcal {E}}'\hookrightarrow {\mathcal {E}}$ in the manner also explained in different terms in [Reference Chen, Fargues and ShenCFS21, Lemma 2.4].
${\mathcal {E}}'\hookrightarrow {\mathcal {E}}$ in the manner also explained in different terms in [Reference Chen, Fargues and ShenCFS21, Lemma 2.4].
The above consideration also shows that ![]() $\mathcal {F}ib$ induces a bijection between the strict subobjects of
$\mathcal {F}ib$ induces a bijection between the strict subobjects of ![]() $(\mathcal {E}_b, x)$ and the subobjects of
$(\mathcal {E}_b, x)$ and the subobjects of ![]() $\mathcal {E}_b$ in Isoc.
$\mathcal {E}_b$ in Isoc.
Definition 2.4 We consider the following rank, degree and slope functions on the category ![]() $\mathcal {C}$. For an object
$\mathcal {C}$. For an object ![]() $({\mathcal {E}},x)$ let
$({\mathcal {E}},x)$ let
 \begin{align*} {\rm rk\,} ( \mathcal{E}, x ) &= \mathop{\mathrm{rank}}\nolimits \mathcal{E}= \mathop{\mathrm{rank}}\nolimits {\mathcal{E}}_x, \\ \mathop{\mathrm{deg}}\nolimits ( \mathcal{E}, x ) &= \mathop{\mathrm{deg}}\nolimits\mathcal{E} - \mathop{\mathrm{deg}}\nolimits (x) =\mathop{\mathrm{deg}}\nolimits {\mathcal{E}}_x,\\ \mu ( \mathcal{E}, x ) &= \dfrac{\mathop{\mathrm{deg}}\nolimits ( \mathcal{E}, x )}{{\rm rk\,} ( \mathcal{E}, x )}, \end{align*}
\begin{align*} {\rm rk\,} ( \mathcal{E}, x ) &= \mathop{\mathrm{rank}}\nolimits \mathcal{E}= \mathop{\mathrm{rank}}\nolimits {\mathcal{E}}_x, \\ \mathop{\mathrm{deg}}\nolimits ( \mathcal{E}, x ) &= \mathop{\mathrm{deg}}\nolimits\mathcal{E} - \mathop{\mathrm{deg}}\nolimits (x) =\mathop{\mathrm{deg}}\nolimits {\mathcal{E}}_x,\\ \mu ( \mathcal{E}, x ) &= \dfrac{\mathop{\mathrm{deg}}\nolimits ( \mathcal{E}, x )}{{\rm rk\,} ( \mathcal{E}, x )}, \end{align*}
where ![]() $\mathop {\mathrm {deg}}\nolimits (x) =\mathop {\mathrm {val}}\nolimits _{\xi } (\mathop {\mathrm {det}}\nolimits ( \overline {x}))$ for any representative
$\mathop {\mathrm {deg}}\nolimits (x) =\mathop {\mathrm {val}}\nolimits _{\xi } (\mathop {\mathrm {det}}\nolimits ( \overline {x}))$ for any representative ![]() $\overline x$ of
$\overline x$ of ![]() $x$ in
$x$ in ![]() ${\rm GL}_n({B_{{\rm dR}}})$.
${\rm GL}_n({B_{{\rm dR}}})$.
Lemma 2.5 ![]() ${\rm rk\,} ( \mathcal {E}, x )$ and
${\rm rk\,} ( \mathcal {E}, x )$ and ![]() $\mathop {\mathrm {deg}}\nolimits ( \mathcal {E}, x )$ are additive on exact sequences in
$\mathop {\mathrm {deg}}\nolimits ( \mathcal {E}, x )$ are additive on exact sequences in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Proof. The functions ![]() ${\rm rk\,} {\mathcal {E}}$ and
${\rm rk\,} {\mathcal {E}}$ and ![]() $\mathop {\mathrm {deg}}\nolimits \mathcal {E}$ are additive for all exact sequences in the category of vector bundles on
$\mathop {\mathrm {deg}}\nolimits \mathcal {E}$ are additive for all exact sequences in the category of vector bundles on ![]() $X$, compare [Reference Fargues and FontaineFF18, § 5.5.2.1; Theorem 6.5.2]. Applying this to the exact sequence in (2.1), we also obtain additivity of the rank and degree function above.
$X$, compare [Reference Fargues and FontaineFF18, § 5.5.2.1; Theorem 6.5.2]. Applying this to the exact sequence in (2.1), we also obtain additivity of the rank and degree function above.
Remark 2.6 Suppose that there is a morphism ![]() $g : ( \mathcal {E}, x ) \longrightarrow ( \mathcal {E}', x' )$ such that
$g : ( \mathcal {E}, x ) \longrightarrow ( \mathcal {E}', x' )$ such that ![]() $\mathcal {F}ib ( g)$ is an isomorphism in
$\mathcal {F}ib ( g)$ is an isomorphism in ![]() $\mathop {\mathrm {Isoc}}\nolimits$. Then
$\mathop {\mathrm {Isoc}}\nolimits$. Then ![]() $\mathop {\mathrm {deg}}\nolimits \mathcal {E} = \mathop {\mathrm {deg}}\nolimits \mathcal {E}'$. Because
$\mathop {\mathrm {deg}}\nolimits \mathcal {E} = \mathop {\mathrm {deg}}\nolimits \mathcal {E}'$. Because ![]() $g$ is effective,
$g$ is effective, ![]() $\mathop {\mathrm {deg}}\nolimits (x) \geqslant \mathop {\mathrm {deg}}\nolimits (x')$, thus
$\mathop {\mathrm {deg}}\nolimits (x) \geqslant \mathop {\mathrm {deg}}\nolimits (x')$, thus ![]() $\mathop {\mathrm {deg}}\nolimits ( \mathcal {E}, x ) \leqslant \mathop {\mathrm {deg}}\nolimits ( \mathcal {E}', x' )$. Equality holds if and only if
$\mathop {\mathrm {deg}}\nolimits ( \mathcal {E}, x ) \leqslant \mathop {\mathrm {deg}}\nolimits ( \mathcal {E}', x' )$. Equality holds if and only if ![]() $g$ is strictly effective, in which case
$g$ is strictly effective, in which case ![]() $g^{-1}$ is also an effective morphism such that
$g^{-1}$ is also an effective morphism such that ![]() $\mathcal {F}ib ( g^{-1})$ is an isomorphism. In other words,
$\mathcal {F}ib ( g^{-1})$ is an isomorphism. In other words, ![]() $g$ is an isomorphism in
$g$ is an isomorphism in ![]() $\mathcal {C}$ if and only if it is strictly effective and
$\mathcal {C}$ if and only if it is strictly effective and ![]() $\mathcal {F}ib ( g)$ is an isomorphism in
$\mathcal {F}ib ( g)$ is an isomorphism in ![]() $\mathop {\mathrm {Isoc}}\nolimits$.
$\mathop {\mathrm {Isoc}}\nolimits$.
The above properties of the functor ![]() $\mathcal {F}ib$ and the functions
$\mathcal {F}ib$ and the functions ![]() $\mathop {\mathrm {deg}}\nolimits, {\rm rk}, \mu$ allows us to apply the Harder–Narasimhan formalism to the category
$\mathop {\mathrm {deg}}\nolimits, {\rm rk}, \mu$ allows us to apply the Harder–Narasimhan formalism to the category ![]() $\mathcal {C}$ [Reference AndréAnd09, Proposition 4.2.2], [Reference Fargues and FontaineFF18, § 5.5.1]. We thus immediately obtain the following results.
$\mathcal {C}$ [Reference AndréAnd09, Proposition 4.2.2], [Reference Fargues and FontaineFF18, § 5.5.1]. We thus immediately obtain the following results.
Recall that ![]() $Z=({\mathcal {E}},x)\in \mathcal {C}$ is called semi-stable if for every subobject
$Z=({\mathcal {E}},x)\in \mathcal {C}$ is called semi-stable if for every subobject ![]() $Z'=({\mathcal {E}}',x')$ we have
$Z'=({\mathcal {E}}',x')$ we have ![]() $\mu (Z')\leqslant \mu (Z)$.
$\mu (Z')\leqslant \mu (Z)$.
Proposition 2.7 Every object ![]() $Z$ has a unique filtration in
$Z$ has a unique filtration in ![]() $\mathcal {C}$
$\mathcal {C}$
such that:
•
 $Z_i / Z_{i-1}$ is semi-stable for each
$Z_i / Z_{i-1}$ is semi-stable for each  $1 \leqslant i \leqslant r$;
$1 \leqslant i \leqslant r$;• the sequence
 $(\mu ( Z_i / Z_{i-1} ))_{1 \leqslant i \leqslant r}$ is strictly decreasing.
$(\mu ( Z_i / Z_{i-1} ))_{1 \leqslant i \leqslant r}$ is strictly decreasing.
We call (2.2) the Harder–Narasimhan filtration of ![]() $Z$.
$Z$.
We write ![]() $Z^{\geqslant \lambda } := Z_m$ where
$Z^{\geqslant \lambda } := Z_m$ where ![]() $\mu ( Z_m / Z_{m-1} ) \geqslant \lambda > \mu ( Z_{m+1} / Z_m )$ and
$\mu ( Z_m / Z_{m-1} ) \geqslant \lambda > \mu ( Z_{m+1} / Z_m )$ and ![]() $Z^{> \lambda } := Z_k$ where
$Z^{> \lambda } := Z_k$ where ![]() $\mu ( Z_k / Z_{k-1} ) > \lambda \geqslant \mu ( Z_{k+1} / Z_k)$. Denote by
$\mu ( Z_k / Z_{k-1} ) > \lambda \geqslant \mu ( Z_{k+1} / Z_k)$. Denote by ![]() $\mathcal {C}_{\lambda }$ the full subcategory of
$\mathcal {C}_{\lambda }$ the full subcategory of ![]() $\mathcal {C}$ whose objects are semi-stable objects of slope
$\mathcal {C}$ whose objects are semi-stable objects of slope ![]() $\lambda$ in
$\lambda$ in ![]() $\mathcal {C}$. Then by the general properties of the Harder–Narasimhan formalism, this category is abelian and stable under extensions in
$\mathcal {C}$. Then by the general properties of the Harder–Narasimhan formalism, this category is abelian and stable under extensions in ![]() $\mathcal {C}$ [Reference Fargues and FontaineFF18, Theorem 5.5.4].
$\mathcal {C}$ [Reference Fargues and FontaineFF18, Theorem 5.5.4].
Definition 2.8 Let ![]() $Z \in \mathcal {C}$ and let
$Z \in \mathcal {C}$ and let ![]() $\mathcal {F}( Z ) : 0 = Z_0 \subsetneq Z_1 \subsetneq \cdots \subsetneq Z_r = Z$ be a filtration in
$\mathcal {F}( Z ) : 0 = Z_0 \subsetneq Z_1 \subsetneq \cdots \subsetneq Z_r = Z$ be a filtration in ![]() $\mathcal {C}$. The polygon
$\mathcal {C}$. The polygon ![]() $P\mathcal {F}( Z )$ attached to this filtration is the graph of the piecewise linear function defined on
$P\mathcal {F}( Z )$ attached to this filtration is the graph of the piecewise linear function defined on ![]() $[0, {\rm rk\,} Z]$ such that on the interval
$[0, {\rm rk\,} Z]$ such that on the interval ![]() $[{\rm rk\,} Z_i, {\rm rk\,} Z_{i+1}]$ for
$[{\rm rk\,} Z_i, {\rm rk\,} Z_{i+1}]$ for ![]() $i = 0, 1, \dotsc, r-1$, it is the linear function relating the points
$i = 0, 1, \dotsc, r-1$, it is the linear function relating the points
The Harder–Narasimhan polygon ![]() ${\rm HN}(Z)$ attached to an object
${\rm HN}(Z)$ attached to an object ![]() $Z$ is the polygon attached to the Harder–Narasimhan filtration of
$Z$ is the polygon attached to the Harder–Narasimhan filtration of ![]() $Z$.
$Z$.
We note that the set of points below the Harder–Narasimhan polygon ![]() ${\rm HN}(Z)$ is also the convex hull of the points with coordinates
${\rm HN}(Z)$ is also the convex hull of the points with coordinates ![]() $( {\rm rk\,} Z_i,\mathop {\mathrm {deg}}\nolimits Z_i )$. This does not hold for the polygon attached to an arbitrary filtration.
$( {\rm rk\,} Z_i,\mathop {\mathrm {deg}}\nolimits Z_i )$. This does not hold for the polygon attached to an arbitrary filtration.
We further have the following comparison theorem.
Proposition 2.9 [Reference AndréAnd09, Proposition 4.4.4]
Let ![]() $\mathcal{F}(Z) \!=\! ( 0 = Z_0 \subsetneq Z_1 \subsetneq \cdots \subsetneq Z_r \!=\! Z)$ be any filtration by strict subobjects in
$\mathcal{F}(Z) \!=\! ( 0 = Z_0 \subsetneq Z_1 \subsetneq \cdots \subsetneq Z_r \!=\! Z)$ be any filtration by strict subobjects in ![]() $\mathcal {C}$. Then
$\mathcal {C}$. Then ![]() $P\mathcal {F}( Z ) \leqslant {\rm HN}(Z)$. If equality occurs, then the filtration
$P\mathcal {F}( Z ) \leqslant {\rm HN}(Z)$. If equality occurs, then the filtration ![]() $\mathcal {F}( Z )$ is a refinement of the Harder–Narasimhan filtration of
$\mathcal {F}( Z )$ is a refinement of the Harder–Narasimhan filtration of ![]() $Z$ and
$Z$ and ![]() $Z_i / Z_{i-1}$ is semi-stable for each
$Z_i / Z_{i-1}$ is semi-stable for each ![]() $1 \leqslant i \leqslant r$.
$1 \leqslant i \leqslant r$.
Here the partial order on the polygons is as usual defined via Mazur's inequality. In other words, ![]() $P\mathcal {F}( Z )$ lies on or below
$P\mathcal {F}( Z )$ lies on or below ![]() ${\rm HN}(Z)$ with the same end points
${\rm HN}(Z)$ with the same end points ![]() $(0, 0)$ and
$(0, 0)$ and ![]() $({\rm rk\,} Z, \mathop {\mathrm {deg}}\nolimits Z)$.
$({\rm rk\,} Z, \mathop {\mathrm {deg}}\nolimits Z)$.
Proof. The first assertion is Proposition 4.4.4 in [Reference AndréAnd09]. Write the Harder–Narasimhan filtration of ![]() $Z$ as
$Z$ as ![]() $0 = Y_0 \subsetneq Y_1 \subsetneq \cdots \subsetneq Y_m = Z$ and
$0 = Y_0 \subsetneq Y_1 \subsetneq \cdots \subsetneq Y_m = Z$ and ![]() $P\mathcal {F}( Z ) = {\rm HN}(Z)$. Thus by definition of
$P\mathcal {F}( Z ) = {\rm HN}(Z)$. Thus by definition of ![]() $P\mathcal {F}( Z )$, there exist the indices
$P\mathcal {F}( Z )$, there exist the indices ![]() $0 < j_1 < \cdots < j_m \leqslant r$ such that
$0 < j_1 < \cdots < j_m \leqslant r$ such that ![]() ${\rm rk\,} Y_i = {\rm rk\,} Z_{j_i}$ and
${\rm rk\,} Y_i = {\rm rk\,} Z_{j_i}$ and ![]() $\mathop {\mathrm {deg}}\nolimits Y_i = \mathop {\mathrm {deg}}\nolimits Z_{j_i}$ for
$\mathop {\mathrm {deg}}\nolimits Y_i = \mathop {\mathrm {deg}}\nolimits Z_{j_i}$ for ![]() $0 < i \leqslant m$. In particular,
$0 < i \leqslant m$. In particular, ![]() $\mu (Z_{j_i} / Z_{j_{i-1}} ) = \mu ( Y_i / Y_{i-1} )$. Since the polygon
$\mu (Z_{j_i} / Z_{j_{i-1}} ) = \mu ( Y_i / Y_{i-1} )$. Since the polygon ![]() $P\mathcal {F}( Z )$ is maximal among the polygons associated with filtrations of
$P\mathcal {F}( Z )$ is maximal among the polygons associated with filtrations of ![]() $Z$, we see that
$Z$, we see that ![]() $Z_{j_i} / Z_{j_{i-1}}$ is semi-stable. Indeed, if this is not true then there exists a strict subobject
$Z_{j_i} / Z_{j_{i-1}}$ is semi-stable. Indeed, if this is not true then there exists a strict subobject ![]() $Y$ such that
$Y$ such that ![]() $\mu (Y / Z_{j_{i-1}}) > \mu (Z_{j_i} / Z_{j_{i-1}})$. Denote by
$\mu (Y / Z_{j_{i-1}}) > \mu (Z_{j_i} / Z_{j_{i-1}})$. Denote by ![]() $\mathcal {F}'(Z)$ the filtration
$\mathcal {F}'(Z)$ the filtration ![]() $0 = Z_0 \subsetneq Z_1 \subsetneq \cdots \subsetneq Z_{j_{i-1}} \subsetneq Y \subsetneq Z_{j_i} \subsetneq \cdots \subsetneq Z_r = Z$. Then the polygon
$0 = Z_0 \subsetneq Z_1 \subsetneq \cdots \subsetneq Z_{j_{i-1}} \subsetneq Y \subsetneq Z_{j_i} \subsetneq \cdots \subsetneq Z_r = Z$. Then the polygon ![]() $P\mathcal {F}'(Z)$ is strictly greater than
$P\mathcal {F}'(Z)$ is strictly greater than ![]() $P\mathcal {F}(Z)$, a contradiction. By the uniqueness of the Harder–Narasimhan filtration, we conclude that
$P\mathcal {F}(Z)$, a contradiction. By the uniqueness of the Harder–Narasimhan filtration, we conclude that ![]() $0 = Z_0 \subsetneq Z_{j_1} \subsetneq \cdots \subsetneq Z_{j_m} = Z$ is the Harder–Narasimhan filtration of
$0 = Z_0 \subsetneq Z_{j_1} \subsetneq \cdots \subsetneq Z_{j_m} = Z$ is the Harder–Narasimhan filtration of ![]() $Z$.
$Z$.
3. The Harder–Narasimhan formalism for modifications of  $G$-bundles
$G$-bundles
3.1 Construction
In this section we use the Tannaka formalism to extend the above Harder–Narasimhan theory to ![]() $G$-bundles for any reductive group
$G$-bundles for any reductive group ![]() $G$ over
$G$ over ![]() $F$, under the assumption that the bundle
$F$, under the assumption that the bundle ![]() ${\mathcal {E}}_b$ is trivial. In § 8, we explain how this implies the analogous theory for all semi-stable
${\mathcal {E}}_b$ is trivial. In § 8, we explain how this implies the analogous theory for all semi-stable ![]() $G$-bundles
$G$-bundles ![]() ${\mathcal {E}}_b$. For all applications, the case of modifications of the trivial (or a semi-stable)
${\mathcal {E}}_b$. For all applications, the case of modifications of the trivial (or a semi-stable) ![]() ${\mathcal {E}}_b$ is by far the most relevant one. Nevertheless, it is a natural question if one can extend the theory also to modifications of general
${\mathcal {E}}_b$ is by far the most relevant one. Nevertheless, it is a natural question if one can extend the theory also to modifications of general ![]() $G$-bundles
$G$-bundles ![]() ${\mathcal {E}}_b$.
${\mathcal {E}}_b$.
As a preparation and a main step in the proof, we first show that the Harder–Narasimhan filtration for modifications of vector bundles is compatible with direct sums and tensor products.
Denote by ![]() $\overline {\mathcal {C}}$ the full subcategory of
$\overline {\mathcal {C}}$ the full subcategory of ![]() $\mathcal {C}$ whose objects are pairs
$\mathcal {C}$ whose objects are pairs ![]() $(\mathcal {E}, x)$ where
$(\mathcal {E}, x)$ where ![]() $\mathcal {E}$ is the trivial vector bundle of some rank
$\mathcal {E}$ is the trivial vector bundle of some rank ![]() $n$ and where
$n$ and where ![]() $x\in {\rm Gr}_n(C)$. Note that if
$x\in {\rm Gr}_n(C)$. Note that if ![]() $(\mathcal {E}, x)$ is an object in
$(\mathcal {E}, x)$ is an object in ![]() $\overline {\mathcal {C}}$, then so are its subobjects. If
$\overline {\mathcal {C}}$, then so are its subobjects. If ![]() $( \mathcal {E}, x ), ( \mathcal {E}', x' )$ are objects in
$( \mathcal {E}, x ), ( \mathcal {E}', x' )$ are objects in ![]() $\overline {\mathcal {C}}$, then
$\overline {\mathcal {C}}$, then ![]() $(\mathcal {E} \oplus \mathcal {E}', x \oplus x')$ and
$(\mathcal {E} \oplus \mathcal {E}', x \oplus x')$ and ![]() $(\mathcal {E} \otimes \mathcal {E}', x \otimes x')$ are still objects in
$(\mathcal {E} \otimes \mathcal {E}', x \otimes x')$ are still objects in ![]() $\overline {\mathcal {C}}$.
$\overline {\mathcal {C}}$.
Proposition 3.1 Let ![]() $( \mathcal {E}, x ), ( \mathcal {E}', x' )\in \overline {\mathcal {C}}$. Then for all
$( \mathcal {E}, x ), ( \mathcal {E}', x' )\in \overline {\mathcal {C}}$. Then for all ![]() $\lambda \in \mathbb {Q}$ we have canonical functorial isomorphisms:
$\lambda \in \mathbb {Q}$ we have canonical functorial isomorphisms:
(i)
 $(\mathcal {E} \oplus \mathcal {E}', x \oplus x')^{\geqslant \lambda }\cong ( \mathcal {E}, x )^{\geqslant \lambda }\oplus ( \mathcal {E}', x' )^{\geqslant \lambda }$;
$(\mathcal {E} \oplus \mathcal {E}', x \oplus x')^{\geqslant \lambda }\cong ( \mathcal {E}, x )^{\geqslant \lambda }\oplus ( \mathcal {E}', x' )^{\geqslant \lambda }$;(ii)
 $\big ( (\mathcal {E}, x ) \otimes (\mathcal {E}', x')\big )^{\geqslant \lambda } \cong \sum _{\lambda _1 + \lambda _2 = \lambda } (\mathcal {E}, x)^{\geqslant \lambda _1} \otimes (\mathcal {E}', x')^{\geqslant \lambda _2}$.
$\big ( (\mathcal {E}, x ) \otimes (\mathcal {E}', x')\big )^{\geqslant \lambda } \cong \sum _{\lambda _1 + \lambda _2 = \lambda } (\mathcal {E}, x)^{\geqslant \lambda _1} \otimes (\mathcal {E}', x')^{\geqslant \lambda _2}$.
Proof. For every ![]() $\lambda$ the quotient
$\lambda$ the quotient ![]() $( \mathcal {E} \oplus \mathcal {E}', x \oplus x' )^{\geqslant {\lambda }} / ( \mathcal {E} \oplus \mathcal {E}', x \oplus x')^{ >{\lambda } } = (\mathcal {E}, x )^{ {\lambda } } \oplus (\mathcal {E}', x')^{{\lambda } }$ is semi-stable of slope
$( \mathcal {E} \oplus \mathcal {E}', x \oplus x' )^{\geqslant {\lambda }} / ( \mathcal {E} \oplus \mathcal {E}', x \oplus x')^{ >{\lambda } } = (\mathcal {E}, x )^{ {\lambda } } \oplus (\mathcal {E}', x')^{{\lambda } }$ is semi-stable of slope ![]() ${\lambda }$ (or trivial if both summands are trivial) since the category
${\lambda }$ (or trivial if both summands are trivial) since the category ![]() $\mathcal {C}_{\lambda }$ is abelian and stable under extensions in
$\mathcal {C}_{\lambda }$ is abelian and stable under extensions in ![]() $\mathcal {C}$. This implies (i).
$\mathcal {C}$. This implies (i).
It remains to prove (ii). By Theorem 9.1.3 in [Reference AndréAnd09], this property is equivalent to the following claim.
Claim. If ![]() $(\mathcal {E}, x)$, respectively
$(\mathcal {E}, x)$, respectively ![]() $(\mathcal {E}', x')$, are semi-stable objects of slopes
$(\mathcal {E}', x')$, are semi-stable objects of slopes ![]() $\lambda _1$, respectively
$\lambda _1$, respectively ![]() $\lambda _2$, then
$\lambda _2$, then ![]() $(\mathcal {E}, x) \otimes (\mathcal {E}', x')$ is semi-stable of slope
$(\mathcal {E}, x) \otimes (\mathcal {E}', x')$ is semi-stable of slope ![]() $\lambda _1 + \lambda _2$.
$\lambda _1 + \lambda _2$.
To prove this claim, we reduce it to results of Cornut [Reference CornutCor18] and Cornut and Peche Irissarry [Reference Cornut and Peche IrissarryCPI19], and Fargues's theorem [Reference Scholze and WeinsteinSW20, Theorem 14.1.1]. Consider the category ![]() ${\rm HT}^{{B_{{\rm dR}}}}$ of Hodge–Tate modules whose objects are pairs
${\rm HT}^{{B_{{\rm dR}}}}$ of Hodge–Tate modules whose objects are pairs ![]() $(V, \Xi )$ where
$(V, \Xi )$ where ![]() $V$ is a finite-dimensional
$V$ is a finite-dimensional ![]() $F$-vector space and where
$F$-vector space and where ![]() $\Xi \subset V \otimes _{F} {B_{{\rm dR}}}$ is a
$\Xi \subset V \otimes _{F} {B_{{\rm dR}}}$ is a ![]() ${B^+_{{\rm dR}}}$-lattice. A morphism
${B^+_{{\rm dR}}}$-lattice. A morphism ![]() $\mathcal {F} : (V, \Xi ) \longrightarrow (V', \Xi ')$ is an
$\mathcal {F} : (V, \Xi ) \longrightarrow (V', \Xi ')$ is an ![]() $F$-linear morphism
$F$-linear morphism ![]() $f : V \longrightarrow V'$ whose
$f : V \longrightarrow V'$ whose ![]() ${B_{{\rm dR}}}$-linear extension
${B_{{\rm dR}}}$-linear extension ![]() $f_{{B_{{\rm dR}}}} : V_{{B_{{\rm dR}}}} \longrightarrow V'_{{B_{{\rm dR}}}}$ satisfies
$f_{{B_{{\rm dR}}}} : V_{{B_{{\rm dR}}}} \longrightarrow V'_{{B_{{\rm dR}}}}$ satisfies ![]() $f_{{B_{{\rm dR}}}} (\Xi ) \subset \Xi '$.
$f_{{B_{{\rm dR}}}} (\Xi ) \subset \Xi '$.
Let ![]() $(\mathcal {E}, x) \in \overline {\mathcal {C}}$ and let
$(\mathcal {E}, x) \in \overline {\mathcal {C}}$ and let ![]() $(B^n_e, ({B^+_{{\rm dR}}})^n, \iota )$ be the triple corresponding to
$(B^n_e, ({B^+_{{\rm dR}}})^n, \iota )$ be the triple corresponding to ![]() ${\mathcal {E}}$ where
${\mathcal {E}}$ where ![]() $\iota : B^n_e \otimes _{B_e} {B_{{\rm dR}}} \overset {\sim }{\longrightarrow } ({B^+_{{\rm dR}}})^n \otimes _{{B^+_{{\rm dR}}}} {B_{{\rm dR}}}$ is the canonical isomorphism and
$\iota : B^n_e \otimes _{B_e} {B_{{\rm dR}}} \overset {\sim }{\longrightarrow } ({B^+_{{\rm dR}}})^n \otimes _{{B^+_{{\rm dR}}}} {B_{{\rm dR}}}$ is the canonical isomorphism and ![]() $n$ is some natural number. Moreover, let
$n$ is some natural number. Moreover, let ![]() $\Lambda _x =x({B^+_{{\rm dR}}})^n\subseteq ({B^+_{{\rm dR}}})^n \otimes _{{B^+_{{\rm dR}}}} {B_{{\rm dR}}}$ be the lattice associated with
$\Lambda _x =x({B^+_{{\rm dR}}})^n\subseteq ({B^+_{{\rm dR}}})^n \otimes _{{B^+_{{\rm dR}}}} {B_{{\rm dR}}}$ be the lattice associated with ![]() $x$. Furthermore,
$x$. Furthermore, ![]() $H^0 (\mathcal {E}) = V_{\mathcal {E}}$ is an
$H^0 (\mathcal {E}) = V_{\mathcal {E}}$ is an ![]() $n$-dimensional
$n$-dimensional ![]() $F$-vector space, see [Reference Fargues and FontaineFF18, § 8.2.1.1]. Thus, we can associate a pair
$F$-vector space, see [Reference Fargues and FontaineFF18, § 8.2.1.1]. Thus, we can associate a pair ![]() $(V_{\mathcal {E}}, \Lambda _x)$ with
$(V_{\mathcal {E}}, \Lambda _x)$ with ![]() $(\mathcal {E}, x)$.
$(\mathcal {E}, x)$.
By [Reference Cornut and Peche IrissarryCPI19, § 3.2.2], this induces an exact tensor equivalence between the tensor categories ![]() ${\rm HT}^{{B_{{\rm dR}}}}$ and
${\rm HT}^{{B_{{\rm dR}}}}$ and ![]() $\overline {\mathcal {C}}$. There are also degree and rank functions defined on the objects of the category
$\overline {\mathcal {C}}$. There are also degree and rank functions defined on the objects of the category ![]() ${\rm HT}^{{B_{{\rm dR}}}}$, compare [Reference Cornut and Peche IrissarryCPI19, § 3.2.2]. We claim that they agree with our functions rank and degree. Indeed,
${\rm HT}^{{B_{{\rm dR}}}}$, compare [Reference Cornut and Peche IrissarryCPI19, § 3.2.2]. We claim that they agree with our functions rank and degree. Indeed, ![]() ${\rm rk\,}(V_{\mathcal {E}}, \Lambda _x) := {\rm dim}\, (V_{\mathcal {E}}) = n = {\rm rk\,} (\mathcal {E}, x)$. Moreover, let
${\rm rk\,}(V_{\mathcal {E}}, \Lambda _x) := {\rm dim}\, (V_{\mathcal {E}}) = n = {\rm rk\,} (\mathcal {E}, x)$. Moreover, let ![]() $(k_1,\dotsc, k_n)$ be the relative position of
$(k_1,\dotsc, k_n)$ be the relative position of ![]() $\Lambda _x$ with respect to the standard lattice in
$\Lambda _x$ with respect to the standard lattice in ![]() ${B_{{\rm dR}}}^n$. Then,
${B_{{\rm dR}}}^n$. Then, ![]() $\mathop {\mathrm {deg}}\nolimits (\mathcal {E}, x) = - \sum _{i=1}^{n} k_i$ and by definition,
$\mathop {\mathrm {deg}}\nolimits (\mathcal {E}, x) = - \sum _{i=1}^{n} k_i$ and by definition, ![]() $\mathop {\mathrm {deg}}\nolimits (V_{\mathcal {E}}, \Lambda _x)$ is the degree of the filtration
$\mathop {\mathrm {deg}}\nolimits (V_{\mathcal {E}}, \Lambda _x)$ is the degree of the filtration ![]() $\mathcal {F}^{\bullet }$ of
$\mathcal {F}^{\bullet }$ of ![]() $V_C$ where for each
$V_C$ where for each ![]() $\lambda \in \mathbb {Z}$
$\lambda \in \mathbb {Z}$
 \[ \mathcal{F}^{\lambda} := \dfrac{({B^+_{{\rm dR}}})^n \cap \xi^{\lambda}\Lambda + (\xi {B^+_{{\rm dR}}})^n}{(\xi {B^+_{{\rm dR}}})^n} \quad \text{in} \ V_C = \dfrac{( {B^+_{{\rm dR}}})^n}{(\xi {B^+_{{\rm dR}}})^n}. \]
\[ \mathcal{F}^{\lambda} := \dfrac{({B^+_{{\rm dR}}})^n \cap \xi^{\lambda}\Lambda + (\xi {B^+_{{\rm dR}}})^n}{(\xi {B^+_{{\rm dR}}})^n} \quad \text{in} \ V_C = \dfrac{( {B^+_{{\rm dR}}})^n}{(\xi {B^+_{{\rm dR}}})^n}. \]
Hence, ![]() $\mathop {\mathrm {deg}}\nolimits (V_{\mathcal {E}}, \Lambda _x) = - \sum _{i=1}^{n} k_i=\mathop {\mathrm {deg}}\nolimits (\mathcal {E}, x)$. Therefore, the claim follows from the analogous assertion for
$\mathop {\mathrm {deg}}\nolimits (V_{\mathcal {E}}, \Lambda _x) = - \sum _{i=1}^{n} k_i=\mathop {\mathrm {deg}}\nolimits (\mathcal {E}, x)$. Therefore, the claim follows from the analogous assertion for ![]() ${\rm HT}^{{B_{{\rm dR}}}}$, which is shown in [Reference Cornut and Peche IrissarryCPI19, Proposition 44].
${\rm HT}^{{B_{{\rm dR}}}}$, which is shown in [Reference Cornut and Peche IrissarryCPI19, Proposition 44].
Let ![]() $G$ be a reductive group and consider a pair
$G$ be a reductive group and consider a pair ![]() $(\mathcal {E}, x)$ where
$(\mathcal {E}, x)$ where ![]() $\mathcal {E}$ is the trivial
$\mathcal {E}$ is the trivial ![]() $G$-bundle on
$G$-bundle on ![]() $X$ and
$X$ and ![]() $x \in {\rm Gr}_G (C)$. Here, we consider
$x \in {\rm Gr}_G (C)$. Here, we consider ![]() ${\mathcal {E}}$ as an exact tensor functor
${\mathcal {E}}$ as an exact tensor functor ![]() $P_{\mathcal {E}} : \mathop {\mathrm {Rep}}\nolimits _{F} G \longrightarrow {\rm Bun} (X)$ where
$P_{\mathcal {E}} : \mathop {\mathrm {Rep}}\nolimits _{F} G \longrightarrow {\rm Bun} (X)$ where ![]() $\mathop {\mathrm {Rep}}\nolimits _{F} G$ is the exact tensor category of algebraic representations of
$\mathop {\mathrm {Rep}}\nolimits _{F} G$ is the exact tensor category of algebraic representations of ![]() $G$ on finite-dimensional
$G$ on finite-dimensional ![]() $F$-vector spaces. Recall that for a finite-dimensional
$F$-vector spaces. Recall that for a finite-dimensional ![]() $F$-vector space
$F$-vector space ![]() $V$, elements of
$V$, elements of ![]() ${\rm Gr}_{{\rm GL}_V} (C)$ are in bijection with
${\rm Gr}_{{\rm GL}_V} (C)$ are in bijection with ![]() ${B^+_{{\rm dR}}}$-lattices in
${B^+_{{\rm dR}}}$-lattices in ![]() $V \otimes _{F} {B_{{\rm dR}}}$. Thus any representation
$V \otimes _{F} {B_{{\rm dR}}}$. Thus any representation ![]() $(V, \rho ) : \mathop {\mathrm {Rep}}\nolimits _{F} G \longrightarrow {\rm GL}_{V}$ gives rise to a
$(V, \rho ) : \mathop {\mathrm {Rep}}\nolimits _{F} G \longrightarrow {\rm GL}_{V}$ gives rise to a ![]() ${B^+_{{\rm dR}}}$-lattice
${B^+_{{\rm dR}}}$-lattice ![]() $(\rho \otimes _{F} {B_{{\rm dR}}}) (x)$ of
$(\rho \otimes _{F} {B_{{\rm dR}}}) (x)$ of ![]() $V \otimes _{F} {B_{{\rm dR}}}$.
$V \otimes _{F} {B_{{\rm dR}}}$.
Definition 3.2 Let ![]() $G$ be a reductive group.
$G$ be a reductive group.
(i) Let
 $K$ be a field extension of
$K$ be a field extension of  $F$. A
$F$. A  $G$-filtration of the category
$G$-filtration of the category  $\mathop {\mathrm {Vect}}\nolimits _{K}$ is the specification of a
$\mathop {\mathrm {Vect}}\nolimits _{K}$ is the specification of a  $K$-filtration on
$K$-filtration on  $V\otimes _{F} K$ of every object
$V\otimes _{F} K$ of every object  $(V, \rho ) \in \mathop {\mathrm {Rep}}\nolimits _{F} G$ satisfying the four conditions in [Reference Dat, Orlik and RapoportDOR10, Definition 4.2.6] (functoriality, compatibility with tensor products, normalization, and exactness of the associated functor to the category of graded
$(V, \rho ) \in \mathop {\mathrm {Rep}}\nolimits _{F} G$ satisfying the four conditions in [Reference Dat, Orlik and RapoportDOR10, Definition 4.2.6] (functoriality, compatibility with tensor products, normalization, and exactness of the associated functor to the category of graded  $K$-vector spaces).
$K$-vector spaces).(ii) Let
 $\mathcal {E}$ be a
$\mathcal {E}$ be a  $G$-bundle. An isoc-filtration of
$G$-bundle. An isoc-filtration of  $\mathcal {E}$ is a tensor functor
$\mathcal {E}$ is a tensor functor  $^{\bullet }{}{\mathcal {E}} : \mathop {\mathrm {Rep}}\nolimits _{F} G \longrightarrow \mathop {\mathrm {Isoc}}\nolimits ^{\bullet }$ such that:
$^{\bullet }{}{\mathcal {E}} : \mathop {\mathrm {Rep}}\nolimits _{F} G \longrightarrow \mathop {\mathrm {Isoc}}\nolimits ^{\bullet }$ such that:
(i)
 $\omega _{\text {fil}} \circ ^{\bullet }{}{\mathcal {E}} = P_{\mathcal {E}}$ where
$\omega _{\text {fil}} \circ ^{\bullet }{}{\mathcal {E}} = P_{\mathcal {E}}$ where  $\omega _{\text {fil}} : \mathop {\mathrm {Isoc}}\nolimits ^{\bullet }\longrightarrow \mathop {\mathrm {Isoc}}\nolimits$ forgets the filtration;
$\omega _{\text {fil}} : \mathop {\mathrm {Isoc}}\nolimits ^{\bullet }\longrightarrow \mathop {\mathrm {Isoc}}\nolimits$ forgets the filtration;(ii)
 $\omega _{\text {iso}} \circ ^{\bullet }{}{\mathcal {E}}$ is a
$\omega _{\text {iso}} \circ ^{\bullet }{}{\mathcal {E}}$ is a  $G$-filtration of
$G$-filtration of  $\mathop {\mathrm {Vect}}\nolimits _{{B_{{\rm dR}}}}$. Here
$\mathop {\mathrm {Vect}}\nolimits _{{B_{{\rm dR}}}}$. Here  $\omega _{\text {iso}} : \mathop {\mathrm {Isoc}}\nolimits ^{\bullet }\longrightarrow \mathop {\mathrm {FilVect}}\nolimits _{{B_{{\rm dR}}}}$ is the functor that maps a filtered vector bundle
$\omega _{\text {iso}} : \mathop {\mathrm {Isoc}}\nolimits ^{\bullet }\longrightarrow \mathop {\mathrm {FilVect}}\nolimits _{{B_{{\rm dR}}}}$ is the functor that maps a filtered vector bundle  $\mathcal {E}^1 \subset \cdots \subset \mathcal {E}^m$ to the corresponding filtered
$\mathcal {E}^1 \subset \cdots \subset \mathcal {E}^m$ to the corresponding filtered  ${B_{{\rm dR}}}$-vector space
${B_{{\rm dR}}}$-vector space  $\mathcal {E}^{1, \mathop {\mathrm {tri}}\nolimits }_{{B_{{\rm dR}}}} \subset \cdots \subset \mathcal {E}^{m, \mathop {\mathrm {tri}}\nolimits }_{{B_{{\rm dR}}}}$, an object of the category
$\mathcal {E}^{1, \mathop {\mathrm {tri}}\nolimits }_{{B_{{\rm dR}}}} \subset \cdots \subset \mathcal {E}^{m, \mathop {\mathrm {tri}}\nolimits }_{{B_{{\rm dR}}}}$, an object of the category  $\mathop {\mathrm {FilVect}}\nolimits _{{B_{{\rm dR}}}}$ of filtered
$\mathop {\mathrm {FilVect}}\nolimits _{{B_{{\rm dR}}}}$ of filtered  ${B_{{\rm dR}}}$-vector spaces.
${B_{{\rm dR}}}$-vector spaces.
Remark 3.3 If ![]() ${\mathcal {E}}$ is the trivial
${\mathcal {E}}$ is the trivial ![]() $G$-bundle, then for every
$G$-bundle, then for every ![]() $(V, \rho ) \in \mathop {\mathrm {Rep}}\nolimits _{F} G$, the vector bundle
$(V, \rho ) \in \mathop {\mathrm {Rep}}\nolimits _{F} G$, the vector bundle ![]() $P_{{\mathcal {E}}}(V, \rho )$ is trivial of rank
$P_{{\mathcal {E}}}(V, \rho )$ is trivial of rank ![]() ${\rm dim}\,_F V$. Furthermore, we denote
${\rm dim}\,_F V$. Furthermore, we denote ![]() $\omega ^F_{\text {iso}} : \mathop {\mathrm {Isoc}}\nolimits ^{\bullet }\longrightarrow \mathop {\mathrm {FilVect}}\nolimits _{F}$ the functor that maps a filtered vector bundle
$\omega ^F_{\text {iso}} : \mathop {\mathrm {Isoc}}\nolimits ^{\bullet }\longrightarrow \mathop {\mathrm {FilVect}}\nolimits _{F}$ the functor that maps a filtered vector bundle ![]() $\mathcal {E}^1 \subset \cdots \subset \mathcal {E}^m$ whose terms are trivial vector bundles to the corresponding filtered
$\mathcal {E}^1 \subset \cdots \subset \mathcal {E}^m$ whose terms are trivial vector bundles to the corresponding filtered ![]() $F$-vector space
$F$-vector space ![]() $H^0({\mathcal {E}}_1) \subset \cdots \subset H^0({\mathcal {E}}_m)$. Then
$H^0({\mathcal {E}}_1) \subset \cdots \subset H^0({\mathcal {E}}_m)$. Then ![]() $\omega ^F_{\text {iso}} \circ ^{\bullet }{}{\mathcal {E}}$ is a
$\omega ^F_{\text {iso}} \circ ^{\bullet }{}{\mathcal {E}}$ is a ![]() $G$-filtration of
$G$-filtration of ![]() $\mathop {\mathrm {Vect}}\nolimits _{F}$ and by [Reference Fargues and FontaineFF18, § 8.2.1.1], this functor factors through
$\mathop {\mathrm {Vect}}\nolimits _{F}$ and by [Reference Fargues and FontaineFF18, § 8.2.1.1], this functor factors through ![]() $\omega _{\text {iso}} \circ ^{\bullet }{}{\mathcal {E}}$ by the functor that sends a
$\omega _{\text {iso}} \circ ^{\bullet }{}{\mathcal {E}}$ by the functor that sends a ![]() ${B_{{\rm dR}}}$-vector space
${B_{{\rm dR}}}$-vector space ![]() $V_0$ to the
$V_0$ to the ![]() $F$-vector space
$F$-vector space ![]() $V_0^{{\rm Gal}({B_{{\rm dR}}} / F)}$.
$V_0^{{\rm Gal}({B_{{\rm dR}}} / F)}$.
Theorem 3.4 Let ![]() $G$ be a reductive group and let
$G$ be a reductive group and let ![]() $\mathcal {E}$ be the trivial
$\mathcal {E}$ be the trivial ![]() $G$-bundle. Let
$G$-bundle. Let ![]() $x \in {\rm Gr}_G (C)$. Then there is a unique isoc-filtration
$x \in {\rm Gr}_G (C)$. Then there is a unique isoc-filtration ![]() $^{\bullet (x)}{}{\mathcal {E}}$ of
$^{\bullet (x)}{}{\mathcal {E}}$ of ![]() $\mathcal {E}$ such that for any
$\mathcal {E}$ such that for any ![]() $(V , \rho ) \in \mathop {\mathrm {Rep}}\nolimits _{F} G$, the induced filtration
$(V , \rho ) \in \mathop {\mathrm {Rep}}\nolimits _{F} G$, the induced filtration ![]() $^{\bullet (x)}{}{\mathcal {E}}(V, \rho )$ on
$^{\bullet (x)}{}{\mathcal {E}}(V, \rho )$ on ![]() $P_{\mathcal {E}}(V, \rho )$ is the Harder–Narasimhan filtration of the pair
$P_{\mathcal {E}}(V, \rho )$ is the Harder–Narasimhan filtration of the pair ![]() $(P_{\mathcal {E}}(V, \rho ), P_x(V, \rho ))$ in the category
$(P_{\mathcal {E}}(V, \rho ), P_x(V, \rho ))$ in the category ![]() $\mathcal {C}$.
$\mathcal {C}$.
Proof. This result is proved as in the characteristic ![]() $0$ case of the proof of [Reference Dat, Orlik and RapoportDOR10, Theorem 5.3.1]. Indeed, for every object
$0$ case of the proof of [Reference Dat, Orlik and RapoportDOR10, Theorem 5.3.1]. Indeed, for every object ![]() $(V, \rho ) \in \mathop {\mathrm {Rep}}\nolimits _{F} G$, we have an object
$(V, \rho ) \in \mathop {\mathrm {Rep}}\nolimits _{F} G$, we have an object ![]() $Z:= ( P_{\mathcal {E}}(V, \rho ), P_x(V, \rho ) )$ in the category
$Z:= ( P_{\mathcal {E}}(V, \rho ), P_x(V, \rho ) )$ in the category ![]() $\overline { \mathcal {C}}$. Consider its Harder–Narasimhan filtration
$\overline { \mathcal {C}}$. Consider its Harder–Narasimhan filtration
where the sequence ![]() $\lambda _i := \mu (Z_i / Z_{i-1})$ is decreasing.
$\lambda _i := \mu (Z_i / Z_{i-1})$ is decreasing.
We then attach to this filtration the filtered vector bundle ![]() $0 = \mathcal {E}_0 \subset \mathcal {E}_{\lambda _1} \subset \cdots \subset \mathcal {E}_{\lambda _m} = P_{\mathcal {E}}(V, \rho )$ where
$0 = \mathcal {E}_0 \subset \mathcal {E}_{\lambda _1} \subset \cdots \subset \mathcal {E}_{\lambda _m} = P_{\mathcal {E}}(V, \rho )$ where ![]() $\mathcal {E}_{\lambda _i}$ is the underlying vector bundle of
$\mathcal {E}_{\lambda _i}$ is the underlying vector bundle of ![]() $Z_i$. In this way we get a functor
$Z_i$. In this way we get a functor ![]() $^{\bullet (x)}{}{\mathcal {E}} : \mathop {\mathrm {Rep}}\nolimits _{F} G \longrightarrow \mathop {\mathrm {Isoc}}\nolimits ^{\bullet }$. One checks that this functor satisfies the required properties in Definition 3.2. The key point is that the above Harder–Narasimhan formalism is compatible with tensor products and direct sums.
$^{\bullet (x)}{}{\mathcal {E}} : \mathop {\mathrm {Rep}}\nolimits _{F} G \longrightarrow \mathop {\mathrm {Isoc}}\nolimits ^{\bullet }$. One checks that this functor satisfies the required properties in Definition 3.2. The key point is that the above Harder–Narasimhan formalism is compatible with tensor products and direct sums.
3.2 Parabolic reductions
Let ![]() $\mathcal {E}$ be a
$\mathcal {E}$ be a ![]() $G$-bundle. For a parabolic subgroup
$G$-bundle. For a parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$, a reduction of
$G$, a reduction of ![]() ${\mathcal {E}}$ to
${\mathcal {E}}$ to ![]() $P$ is a
$P$ is a ![]() $P$-bundle
$P$-bundle ![]() ${\mathcal {E}}_P$ with an isomorphism
${\mathcal {E}}_P$ with an isomorphism ![]() ${\mathcal {E}}_P\times ^P G\rightarrow {\mathcal {E}}$.
${\mathcal {E}}_P\times ^P G\rightarrow {\mathcal {E}}$.
Construction 3.5 Let ![]() $^{\bullet }{}{\mathcal {E}}$ be an isoc-filtration of
$^{\bullet }{}{\mathcal {E}}$ be an isoc-filtration of ![]() $\mathcal {E}$. Then by [Reference Saavedra RivanoSR72, IV.2.2.5] the group
$\mathcal {E}$. Then by [Reference Saavedra RivanoSR72, IV.2.2.5] the group ![]() $P= P (^{\bullet }{}{\mathcal {E}}) = \underline {\mathrm{Aut}}^{\otimes } (\omega _{\text {iso}} \circ ^{\bullet }{}{\mathcal {E}})$ is a parabolic subgroup of
$P= P (^{\bullet }{}{\mathcal {E}}) = \underline {\mathrm{Aut}}^{\otimes } (\omega _{\text {iso}} \circ ^{\bullet }{}{\mathcal {E}})$ is a parabolic subgroup of ![]() $G$ defined over
$G$ defined over ![]() ${B_{{\rm dR}}}$. If
${B_{{\rm dR}}}$. If ![]() ${\mathcal {E}}$ is the trivial
${\mathcal {E}}$ is the trivial ![]() $G$-bundle then the functor
$G$-bundle then the functor ![]() $\omega ^F_{\text {iso}}$ is a fiber functor with value in the category
$\omega ^F_{\text {iso}}$ is a fiber functor with value in the category ![]() $\mathop {\mathrm {Vect}}\nolimits _F$ and
$\mathop {\mathrm {Vect}}\nolimits _F$ and ![]() $\omega _{\text {iso}}$ factors through
$\omega _{\text {iso}}$ factors through ![]() $\omega ^F_{\text {iso}}$. Thus, again by [Reference Saavedra RivanoSR72, IV.2.2.5], the group
$\omega ^F_{\text {iso}}$. Thus, again by [Reference Saavedra RivanoSR72, IV.2.2.5], the group ![]() $P_F = P (^{\bullet }{}{\mathcal {E}}) = \underline {\mathrm{Aut} }^{\otimes } (\omega ^F_{\text {iso}} \circ ^{\bullet }{}{\mathcal {E}})$ is a parabolic subgroup of
$P_F = P (^{\bullet }{}{\mathcal {E}}) = \underline {\mathrm{Aut} }^{\otimes } (\omega ^F_{\text {iso}} \circ ^{\bullet }{}{\mathcal {E}})$ is a parabolic subgroup of ![]() $G$ defined over
$G$ defined over ![]() $F$ and
$F$ and ![]() $P_F \otimes _F {B_{{\rm dR}}} = P$.
$P_F \otimes _F {B_{{\rm dR}}} = P$.
Consider the exact tensor functor assigning to ![]() $(V, \rho ) \in \mathop {\mathrm {Rep}}\nolimits _{F} G$ the pair
$(V, \rho ) \in \mathop {\mathrm {Rep}}\nolimits _{F} G$ the pair ![]() $(\mathcal {E}_0(V, \rho ),$
$(\mathcal {E}_0(V, \rho ),$ ![]() $\mathop {\mathrm {Fil}}\nolimits \mathcal {E}_0(V, \rho ) ) \in \mathop {\mathrm {Isoc}}\nolimits ^{\bullet }$ consisting of the trivial vector bundle of rank
$\mathop {\mathrm {Fil}}\nolimits \mathcal {E}_0(V, \rho ) ) \in \mathop {\mathrm {Isoc}}\nolimits ^{\bullet }$ consisting of the trivial vector bundle of rank ![]() ${\rm dim}\, V$ together with a filtration of trivial vector bundles such that we have
${\rm dim}\, V$ together with a filtration of trivial vector bundles such that we have ![]() $\omega _{\text {iso}} (^{\bullet }{}{\mathcal {E}} (V, \rho ) ) = \omega _{\text {iso}} ( \mathcal {E}_0(V, \rho ), \mathop {\mathrm {Fil}}\nolimits \mathcal {E}_0(V, \rho ) )$. In this way we get an isoc-filtration
$\omega _{\text {iso}} (^{\bullet }{}{\mathcal {E}} (V, \rho ) ) = \omega _{\text {iso}} ( \mathcal {E}_0(V, \rho ), \mathop {\mathrm {Fil}}\nolimits \mathcal {E}_0(V, \rho ) )$. In this way we get an isoc-filtration ![]() $^{\bullet }{}{\mathcal {E}}_0$ of
$^{\bullet }{}{\mathcal {E}}_0$ of ![]() $\mathcal {E}_0$ and moreover
$\mathcal {E}_0$ and moreover ![]() $P (^{\bullet }{}{\mathcal {E}}_0)=P$. We can also view
$P (^{\bullet }{}{\mathcal {E}}_0)=P$. We can also view ![]() $^{\bullet }{}{\mathcal {E}}_0$ as the functor corresponding to the trivial
$^{\bullet }{}{\mathcal {E}}_0$ as the functor corresponding to the trivial ![]() $P$-bundle on
$P$-bundle on ![]() $X$.
$X$.
Let ![]() $\mathcal {E}_P$ be the sheaf of local isomorphisms between
$\mathcal {E}_P$ be the sheaf of local isomorphisms between ![]() $^{\bullet }{}{\mathcal {E}}_0$ and
$^{\bullet }{}{\mathcal {E}}_0$ and ![]() $^{\bullet }{}{\mathcal {E}}$. Since we have an equivalence between the category of trivial vector bundles over
$^{\bullet }{}{\mathcal {E}}$. Since we have an equivalence between the category of trivial vector bundles over ![]() $X$ and the category of
$X$ and the category of ![]() $F$-vector spaces, the sheaf
$F$-vector spaces, the sheaf ![]() $\mathcal {E}_P$ has a structure of
$\mathcal {E}_P$ has a structure of ![]() $P$-torsor. The
$P$-torsor. The ![]() $G$-torsor
$G$-torsor ![]() $\mathcal {E}_P \times ^P G$ is indeed the sheaf of isomorphisms between
$\mathcal {E}_P \times ^P G$ is indeed the sheaf of isomorphisms between ![]() $\mathcal {E}_0$ and
$\mathcal {E}_0$ and ![]() $\mathcal {E}$ and thus it corresponds to the original
$\mathcal {E}$ and thus it corresponds to the original ![]() $G$-bundle
$G$-bundle ![]() $\mathcal {E}$. Therefore
$\mathcal {E}$. Therefore ![]() $\mathcal {E}_P$ is a
$\mathcal {E}_P$ is a ![]() $P$-reduction of the
$P$-reduction of the ![]() $G$-bundle
$G$-bundle ![]() $\mathcal {E}$.
$\mathcal {E}$.
By [Reference Saavedra RivanoSR72, IV.2.4], there is a cocharacter ![]() ${v} : \mathbb {G}_{m, F} \longrightarrow P$ that splits
${v} : \mathbb {G}_{m, F} \longrightarrow P$ that splits ![]() $\omega _{\text {iso}} \circ ^{\bullet }{}{\mathcal {E}}$. Further,
$\omega _{\text {iso}} \circ ^{\bullet }{}{\mathcal {E}}$. Further, ![]() $P$ is the parabolic subgroup associated with
$P$ is the parabolic subgroup associated with ![]() $v$, and thus
$v$, and thus ![]() $v$ can be seen as an element of
$v$ can be seen as an element of ![]() $X_*(Z_{M})_{\mathbb {Q}}^{\Gamma }$ where
$X_*(Z_{M})_{\mathbb {Q}}^{\Gamma }$ where ![]() $M$ is the Levi factor of
$M$ is the Levi factor of ![]() $P$ centralizing
$P$ centralizing ![]() $v$. In case that
$v$. In case that ![]() $G$ is quasi-split and that
$G$ is quasi-split and that ![]() $P$ is standard, we can also view
$P$ is standard, we can also view ![]() ${v}$ as a dominant element of
${v}$ as a dominant element of ![]() $X_*(T)_{\mathbb {Q}}^{\Gamma } = X_*(A)_{\mathbb {Q}}$ that is central in the standard Levi subgroup
$X_*(T)_{\mathbb {Q}}^{\Gamma } = X_*(A)_{\mathbb {Q}}$ that is central in the standard Levi subgroup ![]() $M$ of
$M$ of ![]() $P$.
$P$.
Definition 3.6 Let ![]() $\mathcal {E}$ be a
$\mathcal {E}$ be a ![]() $G$-bundle. Then for each
$G$-bundle. Then for each ![]() $x \in {\rm Gr}_G (C)$, there is a parabolic subgroup
$x \in {\rm Gr}_G (C)$, there is a parabolic subgroup ![]() $P_x := P (^{\bullet (x)}{}{\mathcal {E}})$ associated with the filtration
$P_x := P (^{\bullet (x)}{}{\mathcal {E}})$ associated with the filtration ![]() $\omega _{\text {iso}} \circ ^{\bullet (x)}{}{\mathcal {E}}$. Moreover, the cocharacter
$\omega _{\text {iso}} \circ ^{\bullet (x)}{}{\mathcal {E}}$. Moreover, the cocharacter ![]() ${v}_x:={\rm HN}({\mathcal {E}},x)$ that splits
${v}_x:={\rm HN}({\mathcal {E}},x)$ that splits ![]() $\omega _{\text {iso}} \circ ^{\bullet (x)}{}{\mathcal {E}}$ is called the Harder–Narasimhan vector of
$\omega _{\text {iso}} \circ ^{\bullet (x)}{}{\mathcal {E}}$ is called the Harder–Narasimhan vector of ![]() $x$.
$x$.
Remark 3.7 Let ![]() ${\mathcal {E}}$ be a
${\mathcal {E}}$ be a ![]() $G$-bundle on
$G$-bundle on ![]() $X$, let
$X$, let ![]() $P$ be a parabolic subgroup of
$P$ be a parabolic subgroup of ![]() $G$, and let
$G$, and let ![]() ${\mathcal {E}}_P$ be a reduction of
${\mathcal {E}}_P$ be a reduction of ![]() ${\mathcal {E}}$ to
${\mathcal {E}}$ to ![]() $P$. Consider the map
$P$. Consider the map
Let ![]() $M$ be the Levi quotient of
$M$ be the Levi quotient of ![]() $P$. Then we have a bijection
$P$. Then we have a bijection ![]() $X^*(P)\cong X^*(M^{{\rm ab}})$ where
$X^*(P)\cong X^*(M^{{\rm ab}})$ where ![]() $M^{{\rm ab}}$ is the maximal abelian quotient of
$M^{{\rm ab}}$ is the maximal abelian quotient of ![]() $M$ (or of
$M$ (or of ![]() $P$). Since the center of the derived group of
$P$). Since the center of the derived group of ![]() $P$ is finite it induces a bijection
$P$ is finite it induces a bijection ![]() $X^*(P)_{\mathbb {Q}}\cong X^*(Z_M)_{\mathbb {Q}}$. Hence
$X^*(P)_{\mathbb {Q}}\cong X^*(Z_M)_{\mathbb {Q}}$. Hence ![]() $v_P$ as above can be seen as an element
$v_P$ as above can be seen as an element ![]() $v_P$ of
$v_P$ of ![]() $X_*(Z_M)^{\Gamma }_{\mathbb {Q}}$. We call
$X_*(Z_M)^{\Gamma }_{\mathbb {Q}}$. We call ![]() $v_P$ the slope vector of
$v_P$ the slope vector of ![]() $\mathcal {E}_P$.
$\mathcal {E}_P$.
Recall that if ![]() ${\mathcal {E}}'$ is a modification of a
${\mathcal {E}}'$ is a modification of a ![]() $G$-bundle
$G$-bundle ![]() ${\mathcal {E}}$, then the isomorphism
${\mathcal {E}}$, then the isomorphism ![]() ${\mathcal {E}}'|_{X\setminus \{\infty \}}\cong {\mathcal {E}}|_{X\setminus \{\infty \}}$ induces a bijection between reductions of
${\mathcal {E}}'|_{X\setminus \{\infty \}}\cong {\mathcal {E}}|_{X\setminus \{\infty \}}$ induces a bijection between reductions of ![]() ${\mathcal {E}}$ to
${\mathcal {E}}$ to ![]() $P$ and reductions of
$P$ and reductions of ![]() ${\mathcal {E}}'$ to
${\mathcal {E}}'$ to ![]() $P$.
$P$.
Lemma 3.8 Let ![]() $x\in {\rm Gr}_G(C)$. Let
$x\in {\rm Gr}_G(C)$. Let ![]() $^{\bullet (x)}{}{\mathcal {E}}$ be the isoc-filtration of the trivial
$^{\bullet (x)}{}{\mathcal {E}}$ be the isoc-filtration of the trivial ![]() $G$-bundle
$G$-bundle ![]() $\mathcal {E}$ corresponding to the Harder–Narasimhan filtration of
$\mathcal {E}$ corresponding to the Harder–Narasimhan filtration of ![]() $({\mathcal {E}},x)$, and let
$({\mathcal {E}},x)$, and let ![]() $P\subseteq G$ be the associated parabolic subgroup of
$P\subseteq G$ be the associated parabolic subgroup of ![]() $G$ (defined over
$G$ (defined over ![]() $F$). Let
$F$). Let ![]() $v_1$ be the cocharacter associated with the filtration
$v_1$ be the cocharacter associated with the filtration ![]() $\omega _{\text {iso}} \circ ^{\bullet (x)}{}{\mathcal {E}}$. Let
$\omega _{\text {iso}} \circ ^{\bullet (x)}{}{\mathcal {E}}$. Let ![]() ${\mathcal {E}}_{x,P}$ be the reduction of
${\mathcal {E}}_{x,P}$ be the reduction of ![]() ${\mathcal {E}}_x$ to
${\mathcal {E}}_x$ to ![]() $P$ associated with the reduction of
$P$ associated with the reduction of ![]() ${\mathcal {E}}$ corresponding to
${\mathcal {E}}$ corresponding to ![]() $^{\bullet (x)}{}{\mathcal {E}}$. Then the associated cocharacter
$^{\bullet (x)}{}{\mathcal {E}}$. Then the associated cocharacter ![]() $v_P$ coincides with
$v_P$ coincides with ![]() $v_1$.
$v_1$.
Proof. One can compare the two slope vectors on representations of ![]() $G$, so we may assume that
$G$, so we may assume that ![]() $G={\rm GL}_n$. We consider the Harder–Narasimhan filtration of
$G={\rm GL}_n$. We consider the Harder–Narasimhan filtration of ![]() $({\mathcal {E}},x)$ where
$({\mathcal {E}},x)$ where ![]() ${\mathcal {E}}$ is the trivial vector bundle of rank
${\mathcal {E}}$ is the trivial vector bundle of rank ![]() $n$ on
$n$ on ![]() $X$. It induces a filtration in Isoc
$X$. It induces a filtration in Isoc ![]() ${\mathcal {E}}_0=(0)\subsetneq {\mathcal {E}}_1\subsetneq \dotsm \subsetneq {\mathcal {E}}_i$ of
${\mathcal {E}}_0=(0)\subsetneq {\mathcal {E}}_1\subsetneq \dotsm \subsetneq {\mathcal {E}}_i$ of ![]() ${\mathcal {E}}$. Let
${\mathcal {E}}$. Let ![]() $P$ be the stabilizer of this filtration, a parabolic subgroup of
$P$ be the stabilizer of this filtration, a parabolic subgroup of ![]() ${\rm GL}_n$ defined over
${\rm GL}_n$ defined over ![]() $F$. Its Levi quotient
$F$. Its Levi quotient ![]() $M$ is a product of
$M$ is a product of ![]() $i$ factors
$i$ factors ![]() ${\rm GL}_{n_j}$ with
${\rm GL}_{n_j}$ with ![]() $n_j={\rm rk\,} {\mathcal {E}}_j-{\rm rk\,} {\mathcal {E}}_{j-1}$.
$n_j={\rm rk\,} {\mathcal {E}}_j-{\rm rk\,} {\mathcal {E}}_{j-1}$.
The Harder–Narasimhan polygon of ![]() $({\mathcal {E}},x)$ is the convex hull of the points
$({\mathcal {E}},x)$ is the convex hull of the points ![]() $({\rm rk\,} {\mathcal {E}}_j,\mathop {\mathrm {deg}}\nolimits ({\mathcal {E}}_j)_x)$ for
$({\rm rk\,} {\mathcal {E}}_j,\mathop {\mathrm {deg}}\nolimits ({\mathcal {E}}_j)_x)$ for ![]() $j=0,\dotsc, i$ and where
$j=0,\dotsc, i$ and where ![]() $({\mathcal {E}}_j)_x$ is the
$({\mathcal {E}}_j)_x$ is the ![]() $j$th step of the filtration of
$j$th step of the filtration of ![]() ${\mathcal {E}}_x$ induced by the filtration of
${\mathcal {E}}_x$ induced by the filtration of ![]() ${\mathcal {E}}$. To compute
${\mathcal {E}}$. To compute ![]() $v_P$ we use that
$v_P$ we use that ![]() $X^*(P)_{\mathbb {Q}}\cong X^*(Z_M)_{\mathbb {Q}}\cong \mathbb {Z}^i$ with the
$X^*(P)_{\mathbb {Q}}\cong X^*(Z_M)_{\mathbb {Q}}\cong \mathbb {Z}^i$ with the ![]() $j$th factor being generated by the determinant on the
$j$th factor being generated by the determinant on the ![]() $j$th factor
$j$th factor ![]() ${\rm GL}_{n_j}$ of
${\rm GL}_{n_j}$ of ![]() $M$. Thus the inclusion
$M$. Thus the inclusion ![]() $X_*(Z_M)^{\Gamma }_{\mathbb {Q}}\hookrightarrow X_*(G)^{\Gamma }_{\mathbb {Q}}$ identifies
$X_*(Z_M)^{\Gamma }_{\mathbb {Q}}\hookrightarrow X_*(G)^{\Gamma }_{\mathbb {Q}}$ identifies ![]() $v_P$ with the Harder–Narasimhan polygon described above.
$v_P$ with the Harder–Narasimhan polygon described above.
Remark 3.9 (i) Suppose that ![]() $G = {\rm GL}_n$. Let
$G = {\rm GL}_n$. Let ![]() $x\in {\rm Gr}_G(C)$, let
$x\in {\rm Gr}_G(C)$, let ![]() $^{\bullet }{}{\mathcal {E}}$ be an arbitrary isoc-filtration of the trivial
$^{\bullet }{}{\mathcal {E}}$ be an arbitrary isoc-filtration of the trivial ![]() $G$-bundle
$G$-bundle ![]() ${\mathcal {E}}$ and let
${\mathcal {E}}$ and let ![]() $P \subset G$ be the associated parabolic subgroup of
$P \subset G$ be the associated parabolic subgroup of ![]() $G$ (defined over
$G$ (defined over ![]() $F$). As in the above lemma, we have a cocharacter
$F$). As in the above lemma, we have a cocharacter ![]() $v_P$ associated with the
$v_P$ associated with the ![]() $P$-reduction
$P$-reduction ![]() ${\mathcal {E}}_{x, P}$ corresponding to the
${\mathcal {E}}_{x, P}$ corresponding to the ![]() $P$-reduction of
$P$-reduction of ![]() ${\mathcal {E}}$ arising from
${\mathcal {E}}$ arising from ![]() $^{\bullet }{}{\mathcal {E}}$. Moreover, there is a polygon
$^{\bullet }{}{\mathcal {E}}$. Moreover, there is a polygon ![]() $P(^{\bullet }{}{\mathcal {E}})$, not necessarily convex, attached to
$P(^{\bullet }{}{\mathcal {E}})$, not necessarily convex, attached to ![]() $x$ and the isoc-filtration
$x$ and the isoc-filtration ![]() $^{\bullet }{}{\mathcal {E}}$ (Definition 2.8). Let
$^{\bullet }{}{\mathcal {E}}$ (Definition 2.8). Let ![]() $v_1$ be the cocharacter associated with this polygon. Since we can use the Iwasawa decomposition of
$v_1$ be the cocharacter associated with this polygon. Since we can use the Iwasawa decomposition of ![]() $x = p \cdot k$ (
$x = p \cdot k$ (![]() $p \in P({B_{{\rm dR}}}), k \in G({B^+_{{\rm dR}}})$) to calculate both
$p \in P({B_{{\rm dR}}}), k \in G({B^+_{{\rm dR}}})$) to calculate both ![]() $v_P$ and
$v_P$ and ![]() $v_1$, we see that they are equal.
$v_1$, we see that they are equal.
(ii) Let ![]() $G$ be a reductive group and let
$G$ be a reductive group and let ![]() $x, ^{\bullet }{}{\mathcal {E}}, P$ be as above. Hence we have a cocharacter
$x, ^{\bullet }{}{\mathcal {E}}, P$ be as above. Hence we have a cocharacter ![]() $v_P$. Let
$v_P$. Let ![]() $\rho : G \longrightarrow {\rm GL}(V)$ be a representation of
$\rho : G \longrightarrow {\rm GL}(V)$ be a representation of ![]() $G$ over
$G$ over ![]() $F$. Then
$F$. Then ![]() $\rho _*(^{\bullet }{}{\mathcal {E}})$ is an isoc-filtration of the trivial vector bundle
$\rho _*(^{\bullet }{}{\mathcal {E}})$ is an isoc-filtration of the trivial vector bundle ![]() $\rho _* \mathcal {E}$ and it gives rise to a cocharacter
$\rho _* \mathcal {E}$ and it gives rise to a cocharacter ![]() $v_{1, \rho }$. By the explanation above for the
$v_{1, \rho }$. By the explanation above for the ![]() ${\rm GL}_n$ case, we see that
${\rm GL}_n$ case, we see that ![]() $\rho \circ v_P = v_{1, \rho }$. Thus, we can understand the cocharacter
$\rho \circ v_P = v_{1, \rho }$. Thus, we can understand the cocharacter ![]() $v_P$ as the generalization of the polygon associated with an arbitrary isoc-filtration when
$v_P$ as the generalization of the polygon associated with an arbitrary isoc-filtration when ![]() $G$ is no longer
$G$ is no longer ![]() ${\rm GL}_n$.
${\rm GL}_n$.
Proposition 3.10 Let ![]() $x\in {\rm Gr}_G (C)$. Let
$x\in {\rm Gr}_G (C)$. Let ![]() ${\mathcal {E}}'={\mathcal {E}}_x$ be the associated modification of
${\mathcal {E}}'={\mathcal {E}}_x$ be the associated modification of ![]() ${\mathcal {E}}={\mathcal {E}}_1$. Then there is a unique parabolic subgroup
${\mathcal {E}}={\mathcal {E}}_1$. Then there is a unique parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$ such that the slope vector
$G$ such that the slope vector ![]() $v'_P$ of the reduction
$v'_P$ of the reduction ![]() ${\mathcal {E}}'_P$ corresponding to
${\mathcal {E}}'_P$ corresponding to ![]() ${\mathcal {E}}_{1}^P$ is maximal with respect to the partial order, and
${\mathcal {E}}_{1}^P$ is maximal with respect to the partial order, and ![]() $P$-regular. It coincides with the parabolic reduction corresponding (via Construction 3.5) to the Harder–Narasimhan filtration of
$P$-regular. It coincides with the parabolic reduction corresponding (via Construction 3.5) to the Harder–Narasimhan filtration of ![]() $({\mathcal {E}},x)$. Further,
$({\mathcal {E}},x)$. Further, ![]() $v'_P={\rm HN}({\mathcal {E}},x)$ is the Harder–Narasimhan vector as in Definition 3.6. We also call
$v'_P={\rm HN}({\mathcal {E}},x)$ is the Harder–Narasimhan vector as in Definition 3.6. We also call ![]() ${\mathcal {E}}'_P$ the canonical reduction of
${\mathcal {E}}'_P$ the canonical reduction of ![]() $({\mathcal {E}}_1,x)$.
$({\mathcal {E}}_1,x)$.
Remark 3.11 Here, we use the following partial order on the slope vectors (which should not be confused with the usual order on dominant representatives). Let ![]() $P,P'$ be two parabolic subgroups of
$P,P'$ be two parabolic subgroups of ![]() $G$ and let
$G$ and let ![]() $v_P:X^*(P)\rightarrow \mathbb {Z}$ and
$v_P:X^*(P)\rightarrow \mathbb {Z}$ and ![]() $v_{P'}:X^*(P')\rightarrow \mathbb {Z}$ be two slope vectors. Conjugating by a suitable element of
$v_{P'}:X^*(P')\rightarrow \mathbb {Z}$ be two slope vectors. Conjugating by a suitable element of ![]() $G$ we may assume that
$G$ we may assume that ![]() $P$ and
$P$ and ![]() $P'$ contain a joint parabolic subgroup
$P'$ contain a joint parabolic subgroup ![]() $P_0$. We view
$P_0$. We view ![]() $v_P$ and
$v_P$ and ![]() $v_{P'}$ as elements of
$v_{P'}$ as elements of ![]() $X_*(Z_M)_{\mathbb {Q}}$, respectively
$X_*(Z_M)_{\mathbb {Q}}$, respectively ![]() $X_*(Z_{M'})_{\mathbb {Q}}$, where
$X_*(Z_{M'})_{\mathbb {Q}}$, where ![]() $M$ and
$M$ and ![]() $M'$ are the Levi quotients of
$M'$ are the Levi quotients of ![]() $P$ and
$P$ and ![]() $P'$. Both sets of central cocharacters are subsets of
$P'$. Both sets of central cocharacters are subsets of ![]() $X_*(Z_{M_0})_{\mathbb {Q}}$ for the Levi quotient
$X_*(Z_{M_0})_{\mathbb {Q}}$ for the Levi quotient ![]() $M_0$ of
$M_0$ of ![]() $P_0$. Then
$P_0$. Then ![]() $v_P\leqslant v_{P'}$ if
$v_P\leqslant v_{P'}$ if ![]() $v_{P'}-v_P$ is a non-negative linear combination of coroots in the unipotent radical of
$v_{P'}-v_P$ is a non-negative linear combination of coroots in the unipotent radical of ![]() $P_0$. Since
$P_0$. Since ![]() $v_P$ and
$v_P$ and ![]() $v_{P'}$ are central in the respective Levi quotients, this last condition holds for some choice of conjugates and of
$v_{P'}$ are central in the respective Levi quotients, this last condition holds for some choice of conjugates and of ![]() $P_0$ if and only if it holds for every such choice.
$P_0$ if and only if it holds for every such choice.
For a quasi-split group ![]() $G$ with a fixed pinning
$G$ with a fixed pinning ![]() $B\supseteq T$, we may conjugate
$B\supseteq T$, we may conjugate ![]() $P$ and
$P$ and ![]() $P'$ to standard parabolics. This maps
$P'$ to standard parabolics. This maps ![]() $v_P$ and
$v_P$ and ![]() $v_{P'}$ to well-defined elements of
$v_{P'}$ to well-defined elements of ![]() $X_*(T)^{\Gamma }_{\mathbb {Q}}$, and the partial order then coincides with the usual partial order on coweights of
$X_*(T)^{\Gamma }_{\mathbb {Q}}$, and the partial order then coincides with the usual partial order on coweights of ![]() $T$ (but not with the one comparing dominant representatives).
$T$ (but not with the one comparing dominant representatives).
Proof of Proposition 3.10 By Theorem 3.4 and Construction 3.5, there exists a unique parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$ such that the parabolic reduction of
$G$ such that the parabolic reduction of ![]() ${\mathcal {E}}'$ corresponding to
${\mathcal {E}}'$ corresponding to ![]() ${\mathcal {E}}_1^P$ corresponds to the Harder–Narasimhan isoc-filtration of
${\mathcal {E}}_1^P$ corresponds to the Harder–Narasimhan isoc-filtration of ![]() $(\mathcal {E}, x)$. By definition, the associated slope vector is
$(\mathcal {E}, x)$. By definition, the associated slope vector is ![]() $P$-regular. It remains to show the claimed maximality.
$P$-regular. It remains to show the claimed maximality.
Let ![]() $Q$ be a parabolic subgroup of
$Q$ be a parabolic subgroup of ![]() $G$ and consider the parabolic reduction
$G$ and consider the parabolic reduction ![]() ${\mathcal {E}}^Q_{1,x}$ corresponding to
${\mathcal {E}}^Q_{1,x}$ corresponding to ![]() ${\mathcal {E}}_1^Q$. We have to show that the associated slope vector
${\mathcal {E}}_1^Q$. We have to show that the associated slope vector ![]() $v'_Q$ is bounded by
$v'_Q$ is bounded by ![]() $v'_P$. Possibly replacing
$v'_P$. Possibly replacing ![]() $Q$ by a larger parabolic subgroup
$Q$ by a larger parabolic subgroup ![]() $Q'$ and thus
$Q'$ and thus ![]() $v'_Q$ by the corresponding image in the rational cocharacters of the center of the Levi quotient of
$v'_Q$ by the corresponding image in the rational cocharacters of the center of the Levi quotient of ![]() $Q'$, we may assume that
$Q'$, we may assume that ![]() $v'_Q$ is
$v'_Q$ is ![]() $Q$-dominant and
$Q$-dominant and ![]() $Q$-regular, in other words that conjugation by
$Q$-regular, in other words that conjugation by ![]() $v'_Q$ on the unipotent radical of
$v'_Q$ on the unipotent radical of ![]() $Q$ has strictly positive weights. For the existence of such
$Q$ has strictly positive weights. For the existence of such ![]() $Q$ compare the claim in the proof of [Reference ViehmannVie21, Theorem 5.5].
$Q$ compare the claim in the proof of [Reference ViehmannVie21, Theorem 5.5].
We suppose first that ![]() $G = {\rm GL}_n$. The reduction
$G = {\rm GL}_n$. The reduction ![]() ${\mathcal {E}}_1^Q$ corresponds to an isoc-filtration
${\mathcal {E}}_1^Q$ corresponds to an isoc-filtration ![]() $\mathcal {F}(({\mathcal {E}}, x))$ of
$\mathcal {F}(({\mathcal {E}}, x))$ of ![]() $({\mathcal {E}}, x)$ in the category
$({\mathcal {E}}, x)$ in the category ![]() $\mathcal {C}$, which gives rise to a polygon
$\mathcal {C}$, which gives rise to a polygon ![]() $P\mathcal {F}(({\mathcal {E}}, x))$. In the same way as in the proof of Lemma 3.8, we can identify the slope vector
$P\mathcal {F}(({\mathcal {E}}, x))$. In the same way as in the proof of Lemma 3.8, we can identify the slope vector ![]() $v'_Q$ with the vector corresponding to
$v'_Q$ with the vector corresponding to ![]() $P\mathcal {F}(({\mathcal {E}}, x))$. Therefore from Proposition 2.9 we have
$P\mathcal {F}(({\mathcal {E}}, x))$. Therefore from Proposition 2.9 we have ![]() $v'_Q \leqslant v_x$ and
$v'_Q \leqslant v_x$ and ![]() $v_x = v'_P$.
$v_x = v'_P$.
Now consider general ![]() $G$ and let
$G$ and let ![]() $(V, \rho )$ be any algebraic representation of
$(V, \rho )$ be any algebraic representation of ![]() $G$. By the above
$G$. By the above ![]() ${\rm GL}_n$ case, we see that
${\rm GL}_n$ case, we see that ![]() $\rho (v'_Q) \leqslant \rho (v_x)$. Thus we have
$\rho (v'_Q) \leqslant \rho (v_x)$. Thus we have ![]() $v'_Q \leqslant v_x$.
$v'_Q \leqslant v_x$.
Remark 3.12 Let ![]() $P$ be a parabolic subgroup of
$P$ be a parabolic subgroup of ![]() $G$, let
$G$, let ![]() $N$ denote its unipotent radical and fix a Levi subgroup
$N$ denote its unipotent radical and fix a Levi subgroup ![]() $M$ of
$M$ of ![]() $P$. From the Iwasawa decomposition we obtain that
$P$. From the Iwasawa decomposition we obtain that
where the union is taken over all ![]() $P(\overline {F})$-conjugacy classes of cocharacters of
$P(\overline {F})$-conjugacy classes of cocharacters of ![]() $P_{\overline {F}}$, and where
$P_{\overline {F}}$, and where ![]() $\lambda$ denotes any fixed representative of its conjugacy class. Note that the decomposition into this disjoint union does not depend on the choice of
$\lambda$ denotes any fixed representative of its conjugacy class. Note that the decomposition into this disjoint union does not depend on the choice of ![]() $M$ or the representatives
$M$ or the representatives ![]() $\lambda$. For a similar construction, compare also [Reference ShenShe19, 6.6]
$\lambda$. For a similar construction, compare also [Reference ShenShe19, 6.6]
For ![]() $P=G$, the above decomposition coincides with the decomposition into affine Schubert cells, except that the piece for
$P=G$, the above decomposition coincides with the decomposition into affine Schubert cells, except that the piece for ![]() $\lambda$ corresponds to the affine Schubert cell for
$\lambda$ corresponds to the affine Schubert cell for ![]() $\lambda ^{-1}$. If
$\lambda ^{-1}$. If ![]() $P$ is a Borel subgroup, we obtain the decomposition into semi-infinite orbits à la Mirkovic and Vilonen. In the same way as in [Reference Fargues and ScholzeFS21, VI.3] we obtain that this decomposition induces a decomposition of
$P$ is a Borel subgroup, we obtain the decomposition into semi-infinite orbits à la Mirkovic and Vilonen. In the same way as in [Reference Fargues and ScholzeFS21, VI.3] we obtain that this decomposition induces a decomposition of ![]() ${\rm Gr}_G$ into locally closed sub-diamonds denoted
${\rm Gr}_G$ into locally closed sub-diamonds denoted ![]() $S_{\{\lambda \}_P,P}$.
$S_{\{\lambda \}_P,P}$.
Let ![]() $P'\supseteq M'$ be a second parabolic subgroup and Levi factor. Let
$P'\supseteq M'$ be a second parabolic subgroup and Levi factor. Let ![]() $\{\mu \}_M$ be an
$\{\mu \}_M$ be an ![]() $M(\overline {F})$-conjugacy class of cocharacters of
$M(\overline {F})$-conjugacy class of cocharacters of ![]() $M_{\overline {F}}$ and let
$M_{\overline {F}}$ and let ![]() $\{\mu '\}_{M'}$ be an
$\{\mu '\}_{M'}$ be an ![]() $M'(\overline {F})$-conjugacy class of cocharacters of
$M'(\overline {F})$-conjugacy class of cocharacters of ![]() $M'_{\overline {F}}$. Let
$M'_{\overline {F}}$. Let ![]() $B$ be a Borel subgroup of
$B$ be a Borel subgroup of ![]() $G_{\bar F}$ defined over an algebraic closure, and let
$G_{\bar F}$ defined over an algebraic closure, and let ![]() $T$ be a maximal torus of
$T$ be a maximal torus of ![]() $G_{\bar F}$ contained in
$G_{\bar F}$ contained in ![]() $B$. Then we write
$B$. Then we write ![]() $\mu _{{\rm dom}}\leqslant \mu '_{{\rm dom}}$ if the
$\mu _{{\rm dom}}\leqslant \mu '_{{\rm dom}}$ if the ![]() $B$-dominant representatives
$B$-dominant representatives ![]() $\mu _{{\rm dom}},\mu '_{{\rm dom}}\in X_*(T)$ satisfy the corresponding inequality. Notice that this does not depend on the choice of
$\mu _{{\rm dom}},\mu '_{{\rm dom}}\in X_*(T)$ satisfy the corresponding inequality. Notice that this does not depend on the choice of ![]() $B$ or
$B$ or ![]() $T$.
$T$.
As in [Reference Mirković and VilonenMV07, Theorem 3.2] one shows that ![]() $S_{\{\mu \}_P,P}\cap {\rm Gr}_{G,\mu '}\neq \emptyset$ implies that
$S_{\{\mu \}_P,P}\cap {\rm Gr}_{G,\mu '}\neq \emptyset$ implies that ![]() $\{\mu \}_P\cap \overline {{\rm Gr}_{G,\mu '}}\neq \emptyset$, and hence that
$\{\mu \}_P\cap \overline {{\rm Gr}_{G,\mu '}}\neq \emptyset$, and hence that ![]() $(-\mu )_{{\rm dom}}\leqslant \mu '_{{\rm dom}}$.
$(-\mu )_{{\rm dom}}\leqslant \mu '_{{\rm dom}}$.
Proposition 3.13
(i) Let
 $\{\mu \}$ be a conjugacy class of cocharacters of
$\{\mu \}$ be a conjugacy class of cocharacters of  $G_{\overline {F}}$ and let
$G_{\overline {F}}$ and let  $x\in {\rm Gr}_{G,\mu }(C)$. Then
$x\in {\rm Gr}_{G,\mu }(C)$. Then  ${\rm HN}({\mathcal {E}},x)=\nu _{b'}$ for some
${\rm HN}({\mathcal {E}},x)=\nu _{b'}$ for some  $[b']\in B(G,\mu )$ satisfying the following condition. Let
$[b']\in B(G,\mu )$ satisfying the following condition. Let  $P$ be the parabolic subgroup corresponding to the canonical reduction of
$P$ be the parabolic subgroup corresponding to the canonical reduction of  $({\mathcal {E}},x)$ and let
$({\mathcal {E}},x)$ and let  $M$ be a Levi subgroup. Then
$M$ be a Levi subgroup. Then  $[b']$ has a reduction
$[b']$ has a reduction  $b'_M$ to
$b'_M$ to  $M$ such that
$M$ such that  $P$ is the parabolic subgroup associated with the
$P$ is the parabolic subgroup associated with the  $M$-dominant Newton point
$M$-dominant Newton point  $\nu _{b'_M}^M$. Further, there is a
$\nu _{b'_M}^M$. Further, there is a  $\lambda \in X_*(M)$ with
$\lambda \in X_*(M)$ with  $(-\lambda )_{{\rm dom}}\leqslant \mu _{{\rm dom}}$ and
$(-\lambda )_{{\rm dom}}\leqslant \mu _{{\rm dom}}$ and  $\kappa _M(b'_M)=-\lambda ^{\sharp _M}\in \pi _1(M)$.
$\kappa _M(b'_M)=-\lambda ^{\sharp _M}\in \pi _1(M)$.(ii) Let
 $\lambda$ be as in (i), and assume in addition that
$\lambda$ be as in (i), and assume in addition that  $(-\lambda )_{{\rm dom}}=\mu _{{\rm dom}}$. Then the converse of (i) also holds. That is, for every
$(-\lambda )_{{\rm dom}}=\mu _{{\rm dom}}$. Then the converse of (i) also holds. That is, for every  $[b']\in B(G,\mu )$ as in (i) there is an
$[b']\in B(G,\mu )$ as in (i) there is an  $x\in {\rm Gr}_{G,\mu }(C)$ with
$x\in {\rm Gr}_{G,\mu }(C)$ with  ${\rm HN}({\mathcal {E}},x)=\nu _{b'}$. If
${\rm HN}({\mathcal {E}},x)=\nu _{b'}$. If  $\mu$ is minuscule, this can be applied to all
$\mu$ is minuscule, this can be applied to all  $\lambda$ as in (i).
$\lambda$ as in (i).(iii) For all
 $\lambda$ as in (i) there is an
$\lambda$ as in (i) there is an  $x\in {\rm Gr}_{G,\leqslant \mu }(C)$ with
$x\in {\rm Gr}_{G,\leqslant \mu }(C)$ with  ${\rm HN}({\mathcal {E}},x)=\nu _{b'}$.
${\rm HN}({\mathcal {E}},x)=\nu _{b'}$.
Definition 3.14 For ![]() $G$ and
$G$ and ![]() $\mu$ as above let
$\mu$ as above let ![]() $B(G,\mu )_{{\rm HN}}$ be the set of
$B(G,\mu )_{{\rm HN}}$ be the set of ![]() $[b']\in B(G)$ satisfying the condition of Proposition 3.13(i). Let
$[b']\in B(G)$ satisfying the condition of Proposition 3.13(i). Let ![]() $B(G)_{{\rm HN}}=\bigcup _{\mu }B(G,\mu )_{{\rm HN}}$, the set of
$B(G)_{{\rm HN}}=\bigcup _{\mu }B(G,\mu )_{{\rm HN}}$, the set of ![]() $[b']\in B(G)$ that have a reduction
$[b']\in B(G)$ that have a reduction ![]() $b'_M$ to a Levi subgroup
$b'_M$ to a Levi subgroup ![]() $M$ of some parabolic subgroup
$M$ of some parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$ such that
$G$ such that ![]() $[b'_M]_M\in B(M)$ is basic and the
$[b'_M]_M\in B(M)$ is basic and the ![]() $M$-dominant Newton point
$M$-dominant Newton point ![]() $\nu _{b'_M}$ of
$\nu _{b'_M}$ of ![]() $b'_M$ is
$b'_M$ is ![]() $P$-dominant
$P$-dominant ![]() $P$-regular in the sense that it satisfies
$P$-regular in the sense that it satisfies ![]() $\langle \alpha,\nu _{b'_M}\rangle >0$ for each root
$\langle \alpha,\nu _{b'_M}\rangle >0$ for each root ![]() $\alpha$ in the unipotent radical of
$\alpha$ in the unipotent radical of ![]() $P$.
$P$.
For ![]() $[b']\in B(G,\mu )_{{\rm HN}}$ we write
$[b']\in B(G,\mu )_{{\rm HN}}$ we write ![]() ${\rm Gr}_{G,\mu }(C)^{{\rm HN}=[b']}$ for the set of
${\rm Gr}_{G,\mu }(C)^{{\rm HN}=[b']}$ for the set of ![]() $x\in {\rm Gr}_{G,\mu }(C)$ with
$x\in {\rm Gr}_{G,\mu }(C)$ with ![]() ${\rm HN}({\mathcal {E}},x)=\nu _{b'}$.
${\rm HN}({\mathcal {E}},x)=\nu _{b'}$.
For such ![]() $x$ we also write
$x$ we also write ![]() ${\rm HN}({\mathcal {E}},x)=[b']$.
${\rm HN}({\mathcal {E}},x)=[b']$.
Remark 3.15 (i) It would be interesting to know if the converse of part (i) of the proposition also holds in general, without the additional assumption of part (ii).
(ii) By definition, ![]() $B(G,\mu )_{{\rm HN}}$ is a subset of
$B(G,\mu )_{{\rm HN}}$ is a subset of ![]() $B(G,\mu )$. In particular, it is finite. For
$B(G,\mu )$. In particular, it is finite. For ![]() $G$ quasi-split, one can show that
$G$ quasi-split, one can show that ![]() $B(G,\mu )=B(G,\mu )_{{\rm HN}}$.
$B(G,\mu )=B(G,\mu )_{{\rm HN}}$.
(iii) Let ![]() $[b']\in B(G)$. Then by part (iii) of the proposition, there is an
$[b']\in B(G)$. Then by part (iii) of the proposition, there is an ![]() $x\in {\rm Gr}_G(C)$ with
$x\in {\rm Gr}_G(C)$ with ![]() ${\rm HN}(x)=[b']$ if and only if
${\rm HN}(x)=[b']$ if and only if ![]() $[b']\in B(G)_{{\rm HN}}$.
$[b']\in B(G)_{{\rm HN}}$.
Proof of Proposition 3.13 Assume that ![]() $x\in {\rm Gr}_{G,\mu }(C)$ with
$x\in {\rm Gr}_{G,\mu }(C)$ with ![]() ${\rm HN}({\mathcal {E}},x)=v$. We consider the canonical reduction of
${\rm HN}({\mathcal {E}},x)=v$. We consider the canonical reduction of ![]() $({\mathcal {E}},x)$, which corresponds to a parabolic subgroup
$({\mathcal {E}},x)$, which corresponds to a parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$. Let
$G$. Let ![]() $\{\lambda \}_P$ be the
$\{\lambda \}_P$ be the ![]() $P(\overline {F})$-conjugacy class of cocharacters of
$P(\overline {F})$-conjugacy class of cocharacters of ![]() $P_{\overline {F}}$ with
$P_{\overline {F}}$ with ![]() $x\in S_{\{\lambda \}_P,P}(C)$. Non-emptiness of the intersection
$x\in S_{\{\lambda \}_P,P}(C)$. Non-emptiness of the intersection ![]() ${\rm Gr}_{G,\mu }(C)\cap S_{\{\lambda \}_P}(C)$ then implies that
${\rm Gr}_{G,\mu }(C)\cap S_{\{\lambda \}_P}(C)$ then implies that ![]() $(-\lambda )_{{\rm dom}}\leqslant \mu _{{\rm dom}}$.
$(-\lambda )_{{\rm dom}}\leqslant \mu _{{\rm dom}}$.
Let ![]() $M$ be a Levi subgroup of
$M$ be a Levi subgroup of ![]() $P$. By Lemma 3.8,
$P$. By Lemma 3.8, ![]() $v$ is the element of
$v$ is the element of ![]() $X_*(Z_M)_{\mathbb {Q}}^{\Gamma }$ corresponding to
$X_*(Z_M)_{\mathbb {Q}}^{\Gamma }$ corresponding to ![]() $-\lambda ^{\sharp _{M}}\in \pi _1(M)_{\Gamma }$. Let
$-\lambda ^{\sharp _{M}}\in \pi _1(M)_{\Gamma }$. Let ![]() $[b']\in B(M)$ be basic with
$[b']\in B(M)$ be basic with ![]() $\kappa _{M}(b')= -\lambda ^{\sharp _{M}}$. Then
$\kappa _{M}(b')= -\lambda ^{\sharp _{M}}$. Then ![]() $\nu _{b'}$ is central in
$\nu _{b'}$ is central in ![]() $M$ and
$M$ and ![]() $\kappa _{M}(b')=v^{\sharp _M}\in \pi _1(M)_{\Gamma,\mathbb {Q}}$. Thus
$\kappa _{M}(b')=v^{\sharp _M}\in \pi _1(M)_{\Gamma,\mathbb {Q}}$. Thus ![]() $v=\nu _{b'}$. Finally, we have
$v=\nu _{b'}$. Finally, we have ![]() $\nu _{b'}\leqslant (-\lambda )_{{\rm dom}}\leqslant \mu _{{\rm dom}}$, and
$\nu _{b'}\leqslant (-\lambda )_{{\rm dom}}\leqslant \mu _{{\rm dom}}$, and ![]() $\kappa _G(b')=-\lambda ^{\sharp _G}=\mu ^{\sharp _G}$, thus
$\kappa _G(b')=-\lambda ^{\sharp _G}=\mu ^{\sharp _G}$, thus ![]() $[b']\in B(G,\mu )$. This finishes the proof of (i).
$[b']\in B(G,\mu )$. This finishes the proof of (i).
Let ![]() $\lambda$ be as in (ii). By [Reference RapoportRap18, Corollary A.10] and our assumption
$\lambda$ be as in (ii). By [Reference RapoportRap18, Corollary A.10] and our assumption ![]() $\kappa _M(b'_M)=-\lambda ^{\sharp _M}$, the Newton stratum
$\kappa _M(b'_M)=-\lambda ^{\sharp _M}$, the Newton stratum ![]() ${\rm Gr}_{M,-\lambda,1}^{[b'_{M}]_M^*}$ is non-empty. Let
${\rm Gr}_{M,-\lambda,1}^{[b'_{M}]_M^*}$ is non-empty. Let ![]() $x_{M}\in {\rm Gr}_{M,-\lambda,1}^{[b'_{M}]_M^*}(C)$. Let
$x_{M}\in {\rm Gr}_{M,-\lambda,1}^{[b'_{M}]_M^*}(C)$. Let ![]() $x$ be its image under the natural inclusion
$x$ be its image under the natural inclusion ![]() ${\rm Gr}_{M}\rightarrow {\rm Gr}_G$. Since
${\rm Gr}_{M}\rightarrow {\rm Gr}_G$. Since ![]() $-\lambda \in \{\mu \}$, we have
$-\lambda \in \{\mu \}$, we have ![]() $x\in {\rm Gr}_{G,\mu,1}^{[b']^*}(C)$. By definition of
$x\in {\rm Gr}_{G,\mu,1}^{[b']^*}(C)$. By definition of ![]() $x$, the pair
$x$, the pair ![]() $({\mathcal {E}}_1,x)$ has a reduction to
$({\mathcal {E}}_1,x)$ has a reduction to ![]() $P$ of slope vector
$P$ of slope vector ![]() $\nu _{b'}$. By maximality of the Harder–Narasimhan reduction and by Lemma 6.1 we thus have
$\nu _{b'}$. By maximality of the Harder–Narasimhan reduction and by Lemma 6.1 we thus have ![]() $\nu _{b'}\leqslant {\rm HN}({\mathcal {E}}_1,x)\leqslant \nu _{b'}$, and hence
$\nu _{b'}\leqslant {\rm HN}({\mathcal {E}}_1,x)\leqslant \nu _{b'}$, and hence ![]() $x$ is a point in the claimed Harder–Narasimhan stratum. This proves (ii), and (iii) follows along the same lines.
$x$ is a point in the claimed Harder–Narasimhan stratum. This proves (ii), and (iii) follows along the same lines.
Let ![]() $G_{{\rm {ad}}}$ be the adjoint group of
$G_{{\rm {ad}}}$ be the adjoint group of ![]() $G$. By a subscript ad we denote the image of elements or subsets of
$G$. By a subscript ad we denote the image of elements or subsets of ![]() $G$ in
$G$ in ![]() $G_{{\rm {ad}}}$, and similarly for other invariants of elements.
$G_{{\rm {ad}}}$, and similarly for other invariants of elements.
Lemma 3.16 Let ![]() $\{\mu \}$ be a conjugacy class of cocharacters of
$\{\mu \}$ be a conjugacy class of cocharacters of ![]() $G_{\overline {F}}$, and let
$G_{\overline {F}}$, and let ![]() $x\in {\rm Gr}_{G,\mu }(C)$. Then
$x\in {\rm Gr}_{G,\mu }(C)$. Then ![]() ${\rm HN}_G(x)_{{\rm {ad}}}={\rm HN}_{G_{{\rm {ad}}}}(x_{{\rm {ad}}})$, and the canonical reduction of
${\rm HN}_G(x)_{{\rm {ad}}}={\rm HN}_{G_{{\rm {ad}}}}(x_{{\rm {ad}}})$, and the canonical reduction of ![]() $({\mathcal {E}}^{G_{{\rm {ad}}}}_1,x_{{\rm {ad}}})$ (to a parabolic subgroup
$({\mathcal {E}}^{G_{{\rm {ad}}}}_1,x_{{\rm {ad}}})$ (to a parabolic subgroup ![]() $P'$) is obtained from the canonical reduction of
$P'$) is obtained from the canonical reduction of ![]() $({\mathcal {E}}^G_1,x)$ (to a subgroup
$({\mathcal {E}}^G_1,x)$ (to a subgroup ![]() $P$) via the map
$P$) via the map ![]() $P\rightarrow P/Z(G)= P'\subseteq G_{{\rm {ad}}}$.
$P\rightarrow P/Z(G)= P'\subseteq G_{{\rm {ad}}}$.
Proof. The projection map ![]() $G\rightarrow G_{{\rm {ad}}}$ induces a bijection between parabolic
$G\rightarrow G_{{\rm {ad}}}$ induces a bijection between parabolic ![]() $F$-subgroups of
$F$-subgroups of ![]() $G$ and of
$G$ and of ![]() $G_{{\rm {ad}}}$, and also identifies all other data needed in the description of slope vectors of parabolic reductions of vector bundles, and in the criterion given in Proposition 3.10. Thus the proposition implies the lemma.
$G_{{\rm {ad}}}$, and also identifies all other data needed in the description of slope vectors of parabolic reductions of vector bundles, and in the criterion given in Proposition 3.10. Thus the proposition implies the lemma.
In the remainder of this section we introduce a second, finer invariant, called the Harder–Narasimhan type of a modification. It is along the lines of the notion of Harder– Narasimhan types in [Reference Dat, Orlik and RapoportDOR10], but differs from it if ![]() $\mu$ is not minuscule. Furthermore, our definition is less technical, due to our restriction to the case of modifications of the trivial bundle.
$\mu$ is not minuscule. Furthermore, our definition is less technical, due to our restriction to the case of modifications of the trivial bundle.
Definition 3.17
(i) A Harder–Narasimhan pair is a pair
 $(P,\{\lambda \}_P)$ consisting of a parabolic subgroup
$(P,\{\lambda \}_P)$ consisting of a parabolic subgroup  $P$ of
$P$ of  $G$ and a
$G$ and a  $P(\overline {F})$-conjugacy class
$P(\overline {F})$-conjugacy class  $\{\lambda \}$ of cocharacters of
$\{\lambda \}$ of cocharacters of  $P_{\overline {F}}$ satisfying the following property. Let
$P_{\overline {F}}$ satisfying the following property. Let  $M$ be a Levi factor of
$M$ be a Levi factor of  $P$ containing a representative
$P$ containing a representative  $\lambda$ of the given class. Then
$\lambda$ of the given class. Then  $P=P({\rm av}_M(-\lambda ))$ where
$P=P({\rm av}_M(-\lambda ))$ where  ${\rm av}_M(-\lambda )$ is the unique rational cocharacter of
${\rm av}_M(-\lambda )$ is the unique rational cocharacter of  $M$ that is central in
$M$ that is central in  $M$ and whose image in
$M$ and whose image in  $\pi _1(M)_{\Gamma }$ agrees with
$\pi _1(M)_{\Gamma }$ agrees with  $-\lambda ^{\sharp _M}$. Notice that this condition holds for all
$-\lambda ^{\sharp _M}$. Notice that this condition holds for all  $\lambda, M$ if it holds for one such pair.
$\lambda, M$ if it holds for one such pair.(ii) A Harder–Narasimhan type is a
 $G(F)$-conjugacy class of Harder–Narasimhan pairs.
$G(F)$-conjugacy class of Harder–Narasimhan pairs.(iii) For a conjugacy class
 $\{\mu \}\in X_*(G)/G$ and
$\{\mu \}\in X_*(G)/G$ and  $[b']\in B(G,\mu )_{{\rm HN}}$ let
$[b']\in B(G,\mu )_{{\rm HN}}$ let  $\Theta (\mu,[b'])$ be the set of Harder–Narasimhan types containing a pair
$\Theta (\mu,[b'])$ be the set of Harder–Narasimhan types containing a pair  $(P,\{\lambda \})$ such that
$(P,\{\lambda \})$ such that  $[b']$ has a reduction
$[b']$ has a reduction  $b'_M$ to some Levi factor
$b'_M$ to some Levi factor  $M$ of
$M$ of  $P$ that is basic in
$P$ that is basic in  $M$, such that
$M$, such that  $-\lambda ^{\sharp _M}=\kappa _M(b')\in \pi _1(M)_{\Gamma }$ and such that
$-\lambda ^{\sharp _M}=\kappa _M(b')\in \pi _1(M)_{\Gamma }$ and such that  $(-\lambda )_{G-{\rm dom}}\leqslant \mu _{G-{\rm dom}}$. Here,
$(-\lambda )_{G-{\rm dom}}\leqslant \mu _{G-{\rm dom}}$. Here,  $\lambda ^{\sharp _M}$ is the image of the projection of
$\lambda ^{\sharp _M}$ is the image of the projection of  $\lambda$ to
$\lambda$ to  $M$ in
$M$ in  $\pi _1(M)_{\Gamma }$.
$\pi _1(M)_{\Gamma }$.(iv) Let
 $x\in {\rm Gr}_{G,\mu }(C)$. Consider the canonical parabolic reduction of
$x\in {\rm Gr}_{G,\mu }(C)$. Consider the canonical parabolic reduction of  $({\mathcal {E}}_1,x)$, and let
$({\mathcal {E}}_1,x)$, and let  $P\subseteq G$ be the associated parabolic subgroup. Let
$P\subseteq G$ be the associated parabolic subgroup. Let  $\lambda \in X_*(P)$ with
$\lambda \in X_*(P)$ with  $x\in S_{\{\lambda \}_P,P}$. Then the
$x\in S_{\{\lambda \}_P,P}$. Then the  $G(F)$-conjugacy class of
$G(F)$-conjugacy class of  $(P,\{\lambda \}_P)$ is called the Harder–Narasimhan type of
$(P,\{\lambda \}_P)$ is called the Harder–Narasimhan type of  $({\mathcal {E}},x)$.
$({\mathcal {E}},x)$.
Remark 3.18 Parabolic subgroups of ![]() $G$ are
$G$ are ![]() $G(F)$-conjugate if and only if they are
$G(F)$-conjugate if and only if they are ![]() $G(\overline {F})$-conjugate. Furthermore, the conjugacy classes of parabolic subgroups of
$G(\overline {F})$-conjugate. Furthermore, the conjugacy classes of parabolic subgroups of ![]() $G$ are in bijection with subsets of the set of simple roots of
$G$ are in bijection with subsets of the set of simple roots of ![]() $G$ relative to
$G$ relative to ![]() $F$. In particular, for any given
$F$. In particular, for any given ![]() $G,\mu$ and
$G,\mu$ and ![]() $[b']\in B(G,\mu )_{{\rm HN}}$, the set
$[b']\in B(G,\mu )_{{\rm HN}}$, the set ![]() $\Theta (\mu,[b'])$ is finite. By definition of
$\Theta (\mu,[b'])$ is finite. By definition of ![]() $B(G,\mu )_{{\rm HN}}$, it is also non-empty.
$B(G,\mu )_{{\rm HN}}$, it is also non-empty.
It is easy to find examples where ![]() $\Theta (\mu,[b'])$ has more than one element. For example, let
$\Theta (\mu,[b'])$ has more than one element. For example, let ![]() $G={\rm GL}_5$, let
$G={\rm GL}_5$, let ![]() $\mu =(4,3,2,1,0)\in X_*(T)$ and let
$\mu =(4,3,2,1,0)\in X_*(T)$ and let ![]() $P$ be the standard parabolic subgroup obtained as stabilizer of
$P$ be the standard parabolic subgroup obtained as stabilizer of ![]() $\langle e_1,e_2\rangle \subseteq \breve {F}^5$. Then
$\langle e_1,e_2\rangle \subseteq \breve {F}^5$. Then ![]() $-\lambda _1=(1,4,0,2,3)$ and
$-\lambda _1=(1,4,0,2,3)$ and ![]() $-\lambda _2=(2,3,0,1,4)$ are two different cocharacters with
$-\lambda _2=(2,3,0,1,4)$ are two different cocharacters with ![]() $(P,\{\lambda _i\})\in \Theta (\mu,[b'])$ for
$(P,\{\lambda _i\})\in \Theta (\mu,[b'])$ for ![]() $[b']$ of Newton polygon
$[b']$ of Newton polygon ![]() $(\tfrac {5}{2}^{(2)},\tfrac {5}{3}^{(3)})$.
$(\tfrac {5}{2}^{(2)},\tfrac {5}{3}^{(3)})$.
Lemma 3.19 For ![]() $x\in {\rm Gr}_{G,\mu }(C)^{{\rm HN}=[b']}$, the Harder–Narasimhan type of
$x\in {\rm Gr}_{G,\mu }(C)^{{\rm HN}=[b']}$, the Harder–Narasimhan type of ![]() $({\mathcal {E}}_1,x)$ is a well-defined element of
$({\mathcal {E}}_1,x)$ is a well-defined element of ![]() $\Theta (\mu,[b'])$.
$\Theta (\mu,[b'])$.
Conversely, the Harder–Narasimhan type ![]() $(P,\{\lambda \}_P)$ of
$(P,\{\lambda \}_P)$ of ![]() $x$ determines
$x$ determines ![]() ${\rm HN}({\mathcal {E}},x)$ as being the unique class
${\rm HN}({\mathcal {E}},x)$ as being the unique class ![]() $[b']\in B(G,\mu )$ having a representative
$[b']\in B(G,\mu )$ having a representative ![]() $b'_M$ in a Levi factor
$b'_M$ in a Levi factor ![]() $M$ of
$M$ of ![]() $P$ that is basic in
$P$ that is basic in ![]() $M$ and with
$M$ and with ![]() $\kappa _M(b'_M)=(-\lambda )^{\sharp _M}$.
$\kappa _M(b'_M)=(-\lambda )^{\sharp _M}$.
Proof. The uniqueness of the canonical reduction implies that ![]() $P$ and
$P$ and ![]() $\lambda$ are uniquely determined. We have
$\lambda$ are uniquely determined. We have
Further, ![]() ${\rm av}_M(-\lambda )$ is the HNvector of
${\rm av}_M(-\lambda )$ is the HNvector of ![]() $({\mathcal {E}},x)$, hence the corresponding parabolic subgroup is indeed
$({\mathcal {E}},x)$, hence the corresponding parabolic subgroup is indeed ![]() $P$. Since
$P$. Since ![]() $x\in S_{\{\lambda \}_P}(C)\cap {\rm Gr}_{G,\mu }(C)$, we have
$x\in S_{\{\lambda \}_P}(C)\cap {\rm Gr}_{G,\mu }(C)$, we have ![]() $(-\lambda )_{{\rm dom}}\leqslant \mu _{{\rm dom}}$. Altogether, we have shown that the
$(-\lambda )_{{\rm dom}}\leqslant \mu _{{\rm dom}}$. Altogether, we have shown that the ![]() $G(F)$-conjugacy class of
$G(F)$-conjugacy class of ![]() $(P,\lambda )$ is an element of
$(P,\lambda )$ is an element of ![]() $\Theta (\mu,[b'])$.
$\Theta (\mu,[b'])$.
Because ![]() ${\rm HN}({\mathcal {E}}_b,x)$ is basic in
${\rm HN}({\mathcal {E}}_b,x)$ is basic in ![]() $M$, it is determined by its value of
$M$, it is determined by its value of ![]() $\kappa _M$. This then follows again from (3.1).
$\kappa _M$. This then follows again from (3.1).
In this article we are mainly concerned with the Harder–Narasimhan vector of a modification ![]() $({\mathcal {E}}_1,x)$.
$({\mathcal {E}}_1,x)$.
4. The Harder–Narasimhan stratification of the  $B_{{\rm {dR}}}^+$-Grassmannian
$B_{{\rm {dR}}}^+$-Grassmannian
Definition 4.1 We consider the (surjective) map
that maps any ![]() $x\in {\rm Gr}_{G}(C)$ to
$x\in {\rm Gr}_{G}(C)$ to ![]() ${\rm HN}({\mathcal {E}}_1,x)$, which by Proposition 3.13 is indeed an element of
${\rm HN}({\mathcal {E}}_1,x)$, which by Proposition 3.13 is indeed an element of ![]() $B(G)_{{\rm HN}}$. One can easily check that this is well defined in the sense that it is independent of the choice of
$B(G)_{{\rm HN}}$. One can easily check that this is well defined in the sense that it is independent of the choice of ![]() $C$ and only depends on the element of
$C$ and only depends on the element of ![]() $|{\rm Gr}_{G}|$ underlying the point
$|{\rm Gr}_{G}|$ underlying the point ![]() $x$.
$x$.
For ![]() $[b']\in B(G)_{{\rm HN}}$ let
$[b']\in B(G)_{{\rm HN}}$ let ![]() ${\rm Gr}_{G}(C)^{{\rm HN}\leqslant [b']}$ be the subset of all points with image
${\rm Gr}_{G}(C)^{{\rm HN}\leqslant [b']}$ be the subset of all points with image ![]() $[b'']$ for some
$[b'']$ for some ![]() $[b'']\leqslant [b']$ and likewise for
$[b'']\leqslant [b']$ and likewise for ![]() ${\rm Gr}_{G,\mu }(C)^{{\rm HN}\leqslant [b']}$,
${\rm Gr}_{G,\mu }(C)^{{\rm HN}\leqslant [b']}$, ![]() ${\rm Gr}_{G,\leqslant \mu }(C)^{{\rm HN}\leqslant [b']}$ and/or the subsets replacing
${\rm Gr}_{G,\leqslant \mu }(C)^{{\rm HN}\leqslant [b']}$ and/or the subsets replacing ![]() ${\rm HN}\leqslant [b']$ by
${\rm HN}\leqslant [b']$ by ![]() ${\rm HN}=[b']$.
${\rm HN}=[b']$.
Let ![]() $P$ be a parabolic subgroup of
$P$ be a parabolic subgroup of ![]() $G$ and let
$G$ and let ![]() $M$ be a Levi subgroup. Let
$M$ be a Levi subgroup. Let ![]() $\lambda \in X_*(P)$. Then
$\lambda \in X_*(P)$. Then ![]() $[v(\lambda )]$ is defined to be the element of
$[v(\lambda )]$ is defined to be the element of ![]() $B(G)$ corresponding to the unique basic element of
$B(G)$ corresponding to the unique basic element of ![]() $B(M)$ with
$B(M)$ with ![]() $\kappa _M(v(\lambda ))=\lambda ^{\sharp _M}$. It only depends on the
$\kappa _M(v(\lambda ))=\lambda ^{\sharp _M}$. It only depends on the ![]() $P(\overline {F})$-conjugacy class
$P(\overline {F})$-conjugacy class ![]() $\{\lambda \}_P$ and neither on the choice of
$\{\lambda \}_P$ and neither on the choice of ![]() $M$ nor of a representative
$M$ nor of a representative ![]() $\lambda$.
$\lambda$.
Theorem 4.2 Let ![]() $[b']\in B(G)_{{\rm HN}}$.
$[b']\in B(G)_{{\rm HN}}$.
(i) We have
(4.1)where the first union is taken over all parabolic subgroups of \begin{equation} {\rm Gr}_{G}(C)^{{\rm HN}\geqslant [b']}=\bigcup_{P\subseteq G} \bigcup_{\{\{\lambda\}_P\mid [v(\lambda)]\geqslant[b']\}}S_{\{\lambda\}_P,P}(C) \end{equation}
\begin{equation} {\rm Gr}_{G}(C)^{{\rm HN}\geqslant [b']}=\bigcup_{P\subseteq G} \bigcup_{\{\{\lambda\}_P\mid [v(\lambda)]\geqslant[b']\}}S_{\{\lambda\}_P,P}(C) \end{equation} $G$.
$G$.(ii)
 ${\rm Gr}_{G,\mu }(C)^{{\rm HN}\geqslant [b']}$, respectively
${\rm Gr}_{G,\mu }(C)^{{\rm HN}\geqslant [b']}$, respectively  ${\rm Gr}_{G,\mu }(C)^{{\rm HN}=[b']}$, are the sets of
${\rm Gr}_{G,\mu }(C)^{{\rm HN}=[b']}$, are the sets of  $C$-valued points of a closed, respectively a locally closed, subspace of
$C$-valued points of a closed, respectively a locally closed, subspace of  $|{\rm Gr}_{G,\mu }|$. They are invariant under the action of
$|{\rm Gr}_{G,\mu }|$. They are invariant under the action of  $G(F)$ on
$G(F)$ on  ${\rm Gr}_{G,\mu }$. Similarly,
${\rm Gr}_{G,\mu }$. Similarly,  ${\rm Gr}_{G,\leqslant \mu }(C)^{{\rm HN}=[b']}$ is the set of
${\rm Gr}_{G,\leqslant \mu }(C)^{{\rm HN}=[b']}$ is the set of  $C$-valued points of a locally closed subspace of
$C$-valued points of a locally closed subspace of  $|{\rm Gr}_{G,\leqslant \mu }|$, and
$|{\rm Gr}_{G,\leqslant \mu }|$, and  ${\rm Gr}_{G,\leqslant \mu }(C)^{{\rm HN}\leqslant [b']}$ is the set of
${\rm Gr}_{G,\leqslant \mu }(C)^{{\rm HN}\leqslant [b']}$ is the set of  $C$-valued points of a closed subspace of
$C$-valued points of a closed subspace of  $|{\rm Gr}_{G,\leqslant \mu }|$, and even of
$|{\rm Gr}_{G,\leqslant \mu }|$, and even of  $|{\rm Gr}_{G}|$.
$|{\rm Gr}_{G}|$.(iii)
 ${\rm HN}:|{\rm Gr}_{G}|\rightarrow B(G)_{{\rm HN}}$ is lower semi-continuous.
${\rm HN}:|{\rm Gr}_{G}|\rightarrow B(G)_{{\rm HN}}$ is lower semi-continuous.
Definition 4.3 Let ![]() ${\rm Gr}_{G,\mu }^{{\rm HN}\geqslant [b']}$ denote the closed, locally spatial subdiamond of
${\rm Gr}_{G,\mu }^{{\rm HN}\geqslant [b']}$ denote the closed, locally spatial subdiamond of ![]() ${\rm Gr}_{G,\mu }$ with
${\rm Gr}_{G,\mu }$ with ![]() ${\rm Gr}_{G,\mu }^{{\rm HN}\geqslant [b']}(C)={\rm Gr}_{G,\mu }(C)^{{\rm HN}\geqslant [b']}$. It is called the closed Harder–Narasimhan stratum for
${\rm Gr}_{G,\mu }^{{\rm HN}\geqslant [b']}(C)={\rm Gr}_{G,\mu }(C)^{{\rm HN}\geqslant [b']}$. It is called the closed Harder–Narasimhan stratum for ![]() $[b']$ in
$[b']$ in ![]() ${\rm Gr}_{G,\mu }$.
${\rm Gr}_{G,\mu }$.
Likewise, we define the Harder–Narasimhan stratum for ![]() $[b']$ to be the locally closed locally spatial subdiamond
$[b']$ to be the locally closed locally spatial subdiamond ![]() ${\rm Gr}_{G,\mu }^{{\rm HN}=[b']}\subseteq {\rm Gr}_{G,\mu }$ with
${\rm Gr}_{G,\mu }^{{\rm HN}=[b']}\subseteq {\rm Gr}_{G,\mu }$ with ![]() ${\rm Gr}_{G,\mu }^{{\rm HN}=[b']}(C)={\rm Gr}_{G,\mu }(C)^{{\rm HN}=[b']}$.
${\rm Gr}_{G,\mu }^{{\rm HN}=[b']}(C)={\rm Gr}_{G,\mu }(C)^{{\rm HN}=[b']}$.
We also use corresponding notions for ![]() ${\rm Gr}_{G,\leqslant \mu }$ instead of
${\rm Gr}_{G,\leqslant \mu }$ instead of ![]() ${\rm Gr}_{G,\mu }$.
${\rm Gr}_{G,\mu }$.
Proof of Theorem 4.2 For part (i) consider some ![]() $x\in {\rm Gr}_{G}(C)$ with
$x\in {\rm Gr}_{G}(C)$ with ![]() ${\rm HN}(x)=[b'']\geqslant [b']$. Let
${\rm HN}(x)=[b'']\geqslant [b']$. Let ![]() $P$ be the parabolic subgroup of
$P$ be the parabolic subgroup of ![]() $G$ corresponding to the canonical reduction of
$G$ corresponding to the canonical reduction of ![]() $({\mathcal {E}},x)$, and let
$({\mathcal {E}},x)$, and let ![]() $\{\lambda \}_P$ be such that
$\{\lambda \}_P$ be such that ![]() $x\in S_{\{\lambda \}_P,P}(C)$. Then by [Reference ViehmannVie21, Lemma 3.11(1)] the slope vector of the reduction
$x\in S_{\{\lambda \}_P,P}(C)$. Then by [Reference ViehmannVie21, Lemma 3.11(1)] the slope vector of the reduction ![]() $({\mathcal {E}}_{1,x})_P$ is equal to
$({\mathcal {E}}_{1,x})_P$ is equal to ![]() $[v(\lambda )]=[b'']\geqslant [b']$, which proves that the left hand side is contained in the right hand side of (4.1). Conversely, let
$[v(\lambda )]=[b'']\geqslant [b']$, which proves that the left hand side is contained in the right hand side of (4.1). Conversely, let ![]() $x\in S_{\{\lambda \}_P,P}(C)$ for some
$x\in S_{\{\lambda \}_P,P}(C)$ for some ![]() $P\subset G$ and some
$P\subset G$ and some ![]() $\{\lambda \}_P$. Then the slope vector of the parabolic reduction
$\{\lambda \}_P$. Then the slope vector of the parabolic reduction ![]() $({\mathcal {E}}_{1,x})_P$ corresponding to
$({\mathcal {E}}_{1,x})_P$ corresponding to ![]() ${\mathcal {E}}_1^P$ is (again by [Reference ViehmannVie21, Lemma 3.11(1)]) equal to
${\mathcal {E}}_1^P$ is (again by [Reference ViehmannVie21, Lemma 3.11(1)]) equal to ![]() $[v(\lambda )]\geqslant [b']$. By the maximality of the Harder–Narasimhan vector, this implies that
$[v(\lambda )]\geqslant [b']$. By the maximality of the Harder–Narasimhan vector, this implies that ![]() ${\rm HN}({\mathcal {E}},x)\geqslant [b']$.
${\rm HN}({\mathcal {E}},x)\geqslant [b']$.
Part (iii) follows immediately from part (ii), so it remains to prove part (ii). For this, it is enough to show that the intersection of ![]() ${\rm Gr}_{G,\leqslant \mu }$ with the right hand side of (4.1) is closed in
${\rm Gr}_{G,\leqslant \mu }$ with the right hand side of (4.1) is closed in ![]() ${\rm Gr}_{G,\leqslant \mu }$. Since
${\rm Gr}_{G,\leqslant \mu }$. Since ![]() $S_{\{\lambda \}_P,P}$ is a group orbit, its closure is a union of other
$S_{\{\lambda \}_P,P}$ is a group orbit, its closure is a union of other ![]() $S_{\{\lambda '\}_P,P}$ for the same
$S_{\{\lambda '\}_P,P}$ for the same ![]() $P$. For
$P$. For ![]() $x\in S_{\{\lambda \}_P,P}$ we have
$x\in S_{\{\lambda \}_P,P}$ we have ![]() $\kappa _M({\rm pr}_M(x))=\lambda ^{\sharp _M}\geqslant _P \kappa _M(b')$ where
$\kappa _M({\rm pr}_M(x))=\lambda ^{\sharp _M}\geqslant _P \kappa _M(b')$ where ![]() $a\geqslant _P a'$ for
$a\geqslant _P a'$ for ![]() $a,a'\in \pi _1(M)_{\Gamma }$ if
$a,a'\in \pi _1(M)_{\Gamma }$ if ![]() $a-a'$ is a non-negative linear combination of coroots for the unipotent radical of
$a-a'$ is a non-negative linear combination of coroots for the unipotent radical of ![]() $P$. The condition
$P$. The condition ![]() $\kappa _M({\rm pr}_M(x))\geqslant a$ for some fixed
$\kappa _M({\rm pr}_M(x))\geqslant a$ for some fixed ![]() $a$ being a closed condition, we see that also
$a$ being a closed condition, we see that also ![]() $(\lambda ')^{\sharp _M}\geqslant _P \kappa _M(b')$ for all
$(\lambda ')^{\sharp _M}\geqslant _P \kappa _M(b')$ for all ![]() $S_{\{\lambda '\}_P,P}\subseteq \overline {S_{\{\lambda \}_P,P}}$. In other words,
$S_{\{\lambda '\}_P,P}\subseteq \overline {S_{\{\lambda \}_P,P}}$. In other words, ![]() $[v(\lambda ')]\geqslant [b']$ for these
$[v(\lambda ')]\geqslant [b']$ for these ![]() $\lambda '$. In particular, for
$\lambda '$. In particular, for ![]() $P$ and
$P$ and ![]() $\{\lambda \}$ as on the right hand side of (4.1),
$\{\lambda \}$ as on the right hand side of (4.1), ![]() $\overline {S_{\{\lambda \}_{P},P}(C)}\cap {\rm Gr}_{G,\leqslant \mu }(C)$ is contained in the right hand side. Hence the intersection of
$\overline {S_{\{\lambda \}_{P},P}(C)}\cap {\rm Gr}_{G,\leqslant \mu }(C)$ is contained in the right hand side. Hence the intersection of ![]() ${\rm Gr}_{G,\leqslant \mu }$ with the right hand side of (4.1) is a finite union of subspaces of the form
${\rm Gr}_{G,\leqslant \mu }$ with the right hand side of (4.1) is a finite union of subspaces of the form
for some fixed parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$ and some fixed
$G$ and some fixed ![]() $\{\lambda \}_P$ with
$\{\lambda \}_P$ with ![]() $[v(\lambda )]\geqslant [b']$. It remains to show that (4.2) is a closed subspace. Furthermore, it is enough to take the union over all
$[v(\lambda )]\geqslant [b']$. It remains to show that (4.2) is a closed subspace. Furthermore, it is enough to take the union over all ![]() $g\in (G/P)(F)$.
$g\in (G/P)(F)$.
By the same argument as in the proof of [Reference Dat, Orlik and RapoportDOR10, Proposition 8.2.1], one proves that ![]() $(G/P)(F)$ is a compact subspace of
$(G/P)(F)$ is a compact subspace of ![]() $G/P$. Let
$G/P$. Let ![]() $x$ be a point in the closure of (4.2). Let
$x$ be a point in the closure of (4.2). Let ![]() $x_n$ be a sequence of elements of (4.2) converging towards
$x_n$ be a sequence of elements of (4.2) converging towards ![]() $x$ and let
$x$ and let ![]() $g_n\in (G/P)(F)$ with
$g_n\in (G/P)(F)$ with ![]() $x_n\in S_{\{g_n\lambda g_n^{-1}\}_{g_nPg_n^{-1}},g_nPg_n^{-1}}(C)\cap {\rm Gr}_{G,\leqslant \mu }(C)$. Since
$x_n\in S_{\{g_n\lambda g_n^{-1}\}_{g_nPg_n^{-1}},g_nPg_n^{-1}}(C)\cap {\rm Gr}_{G,\leqslant \mu }(C)$. Since ![]() $(G/P)(F)$ is compact, we may assume that the sequence
$(G/P)(F)$ is compact, we may assume that the sequence ![]() $g_n$ has a limit
$g_n$ has a limit ![]() $g$. The sequence
$g$. The sequence ![]() $g_n^{-1}x_n$ converges to
$g_n^{-1}x_n$ converges to ![]() $g^{-1}x$, and is contained in the closed subspace
$g^{-1}x$, and is contained in the closed subspace ![]() $\overline {S_{\{\lambda \}_{P},P}(C)}\cap {\rm Gr}_{G,\leqslant \mu }(C)$. Hence
$\overline {S_{\{\lambda \}_{P},P}(C)}\cap {\rm Gr}_{G,\leqslant \mu }(C)$. Hence ![]() $x\in \overline {S_{\{g\lambda g^{-1}\}_{gPg^{-1}},gPg^{-1}}(C)}\cap {\rm Gr}_{G,\leqslant \mu }(C)$.
$x\in \overline {S_{\{g\lambda g^{-1}\}_{gPg^{-1}},gPg^{-1}}(C)}\cap {\rm Gr}_{G,\leqslant \mu }(C)$.
Remark 4.4 Let ![]() $[b']\in B(G)_{{\rm HN}}$. Let
$[b']\in B(G)_{{\rm HN}}$. Let ![]() $P$,
$P$, ![]() $M$ and
$M$ and ![]() $b'_M$ be as in the definition of
$b'_M$ be as in the definition of ![]() $B(G)_{{\rm HN}}$. Using the same argument as at the beginning of the proof of Theorem 4.2, we also obtain that
$B(G)_{{\rm HN}}$. Using the same argument as at the beginning of the proof of Theorem 4.2, we also obtain that
where the first union is taken over all parabolic subgroups of ![]() $G$.
$G$.
By definition, for any ![]() $G$ and
$G$ and ![]() $\{\mu \}$, the semi-stable Harder–Narasimhan stratum in
$\{\mu \}$, the semi-stable Harder–Narasimhan stratum in ![]() ${\rm Gr}_{G,\mu }$ coincides with the weakly admissible locus
${\rm Gr}_{G,\mu }$ coincides with the weakly admissible locus ![]() ${\rm Gr}_{G,\mu,1}^{{\rm {wa}}}$ in the sense of [Reference ViehmannVie21, Definition 4.1]. Indeed, if
${\rm Gr}_{G,\mu,1}^{{\rm {wa}}}$ in the sense of [Reference ViehmannVie21, Definition 4.1]. Indeed, if ![]() $x$ is in the semi-stable Harder–Narasimhan stratum then
$x$ is in the semi-stable Harder–Narasimhan stratum then ![]() ${\rm HN}({\mathcal {E}}_{1}, x)(\chi ) = 0$ for any parabolic subgroup
${\rm HN}({\mathcal {E}}_{1}, x)(\chi ) = 0$ for any parabolic subgroup ![]() $P$ and any character
$P$ and any character ![]() $\chi \in X^*(P / Z_G)$. Moreover, if
$\chi \in X^*(P / Z_G)$. Moreover, if ![]() ${\rm HN}({\mathcal {E}}_{1}, x) - v(({\mathcal {E}}_{1,x})_P)$ is a non-negative rational linear combination of positive absolute roots then for any
${\rm HN}({\mathcal {E}}_{1}, x) - v(({\mathcal {E}}_{1,x})_P)$ is a non-negative rational linear combination of positive absolute roots then for any ![]() $P$-dominant character
$P$-dominant character ![]() $\chi \in X^*(P / Z_G)$, we have
$\chi \in X^*(P / Z_G)$, we have ![]() ${\rm HN}({\mathcal {E}}_{1}, x)(\chi ) - v(({\mathcal {E}}_{1,x})_P)(\chi ) \geqslant 0$ and hence
${\rm HN}({\mathcal {E}}_{1}, x)(\chi ) - v(({\mathcal {E}}_{1,x})_P)(\chi ) \geqslant 0$ and hence ![]() $v(({\mathcal {E}}_{1,x})_P)$ is non-positive.
$v(({\mathcal {E}}_{1,x})_P)$ is non-positive.
Furthermore, the theorem yields the following description of the complement of the weakly admissible locus.
Corollary 4.5 Let ![]() $b_0\in B(G,\mu )$ be the basic element. Then
$b_0\in B(G,\mu )$ be the basic element. Then
Remark 4.6 In general, ![]() ${\rm Gr}_{G,\mu }^{{\rm HN}\geqslant [b']}$ is not equal to the closure of
${\rm Gr}_{G,\mu }^{{\rm HN}\geqslant [b']}$ is not equal to the closure of ![]() ${\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$. Indeed, let
${\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$. Indeed, let ![]() $G={\rm GL}_7$, let
$G={\rm GL}_7$, let ![]() $B$ be the Borel subgroup of upper triangular matrices and let
$B$ be the Borel subgroup of upper triangular matrices and let ![]() $T$ be the diagonal torus. Let
$T$ be the diagonal torus. Let ![]() $\mu =(1,1,1,1,0,0,0)\in X_*(T)_{{\rm dom}}$. Since
$\mu =(1,1,1,1,0,0,0)\in X_*(T)_{{\rm dom}}$. Since ![]() $\mu$ is minuscule, we may use the Bialynicki-Birula isomorphism
$\mu$ is minuscule, we may use the Bialynicki-Birula isomorphism ![]() ${\rm BB}_{\mu }$ (compare (5.1)) to identify
${\rm BB}_{\mu }$ (compare (5.1)) to identify ![]() ${\rm Gr}_{G,\mu }$ with
${\rm Gr}_{G,\mu }$ with ![]() ${\mathcal {F}\ell }(G,\mu )^{\diamond }$, the diamond corresponding to the flag variety for
${\mathcal {F}\ell }(G,\mu )^{\diamond }$, the diamond corresponding to the flag variety for ![]() $G$ and
$G$ and ![]() $\mu$. Let
$\mu$. Let ![]() $[b']\in B(G,\mu )$ with Newton vector
$[b']\in B(G,\mu )$ with Newton vector ![]() $\bigl ({\tfrac {2}{3}}^{(3)},{\tfrac {1}{2}}^{(4)}\bigr )$ and let
$\bigl ({\tfrac {2}{3}}^{(3)},{\tfrac {1}{2}}^{(4)}\bigr )$ and let ![]() $[b'']\geqslant [b']$ with Newton vector
$[b'']\geqslant [b']$ with Newton vector ![]() $\bigl (1,{\tfrac {3}{5}}^{(5)},0\bigr )$. Since
$\bigl (1,{\tfrac {3}{5}}^{(5)},0\bigr )$. Since ![]() $G$ is split, both elements are in
$G$ is split, both elements are in ![]() $B(G)_{{\rm HN}}$. Consider the standard parabolic subgroup
$B(G)_{{\rm HN}}$. Consider the standard parabolic subgroup ![]() $P$ corresponding to
$P$ corresponding to ![]() $\nu _{b''}$ and its standard Levi subgroup
$\nu _{b''}$ and its standard Levi subgroup ![]() $M$, and let
$M$, and let ![]() $\lambda _0=(-1,0,0,-1,-1,-1,0)\in X_*(M)$. Then
$\lambda _0=(-1,0,0,-1,-1,-1,0)\in X_*(M)$. Then ![]() $\lambda _0=w.(-\mu )_{{\rm dom}}$ for some
$\lambda _0=w.(-\mu )_{{\rm dom}}$ for some ![]() $w\in S_7$ with
$w\in S_7$ with ![]() $\ell (w)=6$. We have
$\ell (w)=6$. We have ![]() $S_{\{\lambda _0\}_P,P}\cap {\rm Gr}_{G,\mu }\subseteq {\rm Gr}_{G,\mu }^{{\rm HN}\geqslant [b'']}$. Let
$S_{\{\lambda _0\}_P,P}\cap {\rm Gr}_{G,\mu }\subseteq {\rm Gr}_{G,\mu }^{{\rm HN}\geqslant [b'']}$. Let ![]() ${\mathcal {E}}_1$ be the trivial vector bundle of rank 7.
${\mathcal {E}}_1$ be the trivial vector bundle of rank 7.
We claim that on an open and dense subset ![]() $S'$ of
$S'$ of ![]() $S_{\{\lambda _0\}_P,P}\cap {\rm Gr}_{G,\mu }$, any sub-vector bundle of
$S_{\{\lambda _0\}_P,P}\cap {\rm Gr}_{G,\mu }$, any sub-vector bundle of ![]() ${\mathcal {E}}_{1,x}$ corresponding to a sub-isocrystal of
${\mathcal {E}}_{1,x}$ corresponding to a sub-isocrystal of ![]() ${\mathcal {E}}_1$ of rank 3 has degree
${\mathcal {E}}_1$ of rank 3 has degree ![]() $\leqslant 1$. Indeed,
$\leqslant 1$. Indeed, ![]() ${\rm BB}_{\mu }(S_{\{\lambda _0\}_P,P}\cap {\rm Gr}_{G,\mu })$ is the diamond associated with the Bruhat cell of
${\rm BB}_{\mu }(S_{\{\lambda _0\}_P,P}\cap {\rm Gr}_{G,\mu })$ is the diamond associated with the Bruhat cell of ![]() ${\mathcal {F}\ell }(G,\mu )$ for
${\mathcal {F}\ell }(G,\mu )$ for ![]() $w$, an irreducible subscheme of dimension
$w$, an irreducible subscheme of dimension ![]() $\langle 2\rho,\mu _{{\rm dom}}\rangle - \ell (w)=6$. Let
$\langle 2\rho,\mu _{{\rm dom}}\rangle - \ell (w)=6$. Let ![]() $({\breve {F}}^n,1\cdot \sigma )$ be the isocrystal corresponding to
$({\breve {F}}^n,1\cdot \sigma )$ be the isocrystal corresponding to ![]() ${\mathcal {E}}_1$, and let
${\mathcal {E}}_1$, and let ![]() $N'$ be the sub-isocrystal generated by the first three standard basis vectors. Then the sub-vector bundle of
$N'$ be the sub-isocrystal generated by the first three standard basis vectors. Then the sub-vector bundle of ![]() ${\mathcal {E}}_{1,x}$ corresponding to
${\mathcal {E}}_{1,x}$ corresponding to ![]() $N'$ has degree
$N'$ has degree ![]() $\geqslant 2$ if and only if
$\geqslant 2$ if and only if ![]() $x\in \overline {S_{\{\lambda _1\}_P,P}\cap {\rm Gr}_{G,\mu }}$ where
$x\in \overline {S_{\{\lambda _1\}_P,P}\cap {\rm Gr}_{G,\mu }}$ where ![]() $\lambda _1=(-1,-1,0,-1,-1,0,0)$. In the same way as for
$\lambda _1=(-1,-1,0,-1,-1,0,0)$. In the same way as for ![]() $\lambda _0$, one sees that
$\lambda _0$, one sees that ![]() $\overline {S_{\{\lambda _1\}_P,P}\cap {\rm Gr}_{G,\mu }}$ corresponds to a closed subscheme of
$\overline {S_{\{\lambda _1\}_P,P}\cap {\rm Gr}_{G,\mu }}$ corresponds to a closed subscheme of ![]() ${\mathcal {F}\ell }(G,\mu )$ of dimension 2. In particular, its intersection with the scheme associated with
${\mathcal {F}\ell }(G,\mu )$ of dimension 2. In particular, its intersection with the scheme associated with ![]() ${\rm BB}_{\mu }(S_{\{\lambda _0\}_P,P}\cap {\rm Gr}_{G,\mu })$ is a closed subscheme of the latter which is of smaller dimension. The condition that any sub-vector bundle of
${\rm BB}_{\mu }(S_{\{\lambda _0\}_P,P}\cap {\rm Gr}_{G,\mu })$ is a closed subscheme of the latter which is of smaller dimension. The condition that any sub-vector bundle of ![]() ${\mathcal {E}}_{1,x}$ corresponding to a sub-isocrystal of
${\mathcal {E}}_{1,x}$ corresponding to a sub-isocrystal of ![]() ${\mathcal {E}}_1$ of rank 3 has degree
${\mathcal {E}}_1$ of rank 3 has degree ![]() $\leqslant 1$ is satisfied if and only if
$\leqslant 1$ is satisfied if and only if ![]() $x$ is in the complement of
$x$ is in the complement of
In the same way as in the proof of Theorem 4.2 we then see that its complement in ![]() $S_{\{\lambda _0\}_P,P}\cap {\rm Gr}_{G,\mu }$ is open and dense in the latter, which proves the claim.
$S_{\{\lambda _0\}_P,P}\cap {\rm Gr}_{G,\mu }$ is open and dense in the latter, which proves the claim.
On the other hand, ![]() ${\rm Gr}_{G,\mu }^{{\rm HN}=[b']}\subset \bigcup _{P'\subseteq G}\bigcup _{\{\{\lambda \}_{P'}\mid [v(\lambda )]=[b']\}}S_{\{\lambda \}_{P'},{P'}}(C)\cap {\rm Gr}_{G,\mu }(C)$ where
${\rm Gr}_{G,\mu }^{{\rm HN}=[b']}\subset \bigcup _{P'\subseteq G}\bigcup _{\{\{\lambda \}_{P'}\mid [v(\lambda )]=[b']\}}S_{\{\lambda \}_{P'},{P'}}(C)\cap {\rm Gr}_{G,\mu }(C)$ where ![]() $P'$ runs through the
$P'$ runs through the ![]() $G(F)$-orbit of the standard parabolic corresponding to
$G(F)$-orbit of the standard parabolic corresponding to ![]() $\nu _{b'}$. From the proof of Theorem 4.2 we see that
$\nu _{b'}$. From the proof of Theorem 4.2 we see that ![]() ${\rm Gr}_{G,\mu }^{{\rm HN}=[b'']}\subseteq \overline {{\rm Gr}_{G,\mu }^{{\rm HN}=[b']}}$ can only hold if for every
${\rm Gr}_{G,\mu }^{{\rm HN}=[b'']}\subseteq \overline {{\rm Gr}_{G,\mu }^{{\rm HN}=[b']}}$ can only hold if for every ![]() $x\in {\rm Gr}_{G,\mu }^{{\rm HN}=[b'']}(C)$ there is a
$x\in {\rm Gr}_{G,\mu }^{{\rm HN}=[b'']}(C)$ there is a ![]() $P'$ and
$P'$ and ![]() $\lambda$ as above such that
$\lambda$ as above such that ![]() $x\in \overline {S_{\{\lambda \}_{P'},{P'}}\cap {\rm Gr}_{G,\mu }}$. Fix some such
$x\in \overline {S_{\{\lambda \}_{P'},{P'}}\cap {\rm Gr}_{G,\mu }}$. Fix some such ![]() $x$ and
$x$ and ![]() $P'$. Then
$P'$. Then ![]() $P'$ corresponds to a sub-vector bundle of
$P'$ corresponds to a sub-vector bundle of ![]() ${\mathcal {E}}_1$ of rank 3 which defines a filtration in
${\mathcal {E}}_1$ of rank 3 which defines a filtration in ![]() $\mathcal {C}$. Since
$\mathcal {C}$. Since ![]() $[v(\lambda )]=[b']$, for every
$[v(\lambda )]=[b']$, for every ![]() $x'\in S_{\{\lambda \}_{P'},{P'}}\cap {\rm Gr}_{G,\mu }$, the corresponding sub-vector bundle of
$x'\in S_{\{\lambda \}_{P'},{P'}}\cap {\rm Gr}_{G,\mu }$, the corresponding sub-vector bundle of ![]() ${\mathcal {E}}_{1,x'}$ is of degree 2. Thus the same holds for every
${\mathcal {E}}_{1,x'}$ is of degree 2. Thus the same holds for every ![]() $x$ in the closure. In particular, every
$x$ in the closure. In particular, every ![]() $x\in S'$ is not in the closure of
$x\in S'$ is not in the closure of ![]() ${\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$, but lies in
${\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$, but lies in ![]() $\overline {{\rm Gr}_{G,\mu }^{{\rm HN}=[b'']}}$.
$\overline {{\rm Gr}_{G,\mu }^{{\rm HN}=[b'']}}$.
One can also explicitly construct points ![]() $x\in {\rm Gr}_{G,\mu }^{{\rm HN}=[b'']}(C)$ that lie in the closure of
$x\in {\rm Gr}_{G,\mu }^{{\rm HN}=[b'']}(C)$ that lie in the closure of ![]() ${\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$. Thus the closure of a Harder–Narasimhan stratum is in general not a union of strata.
${\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$. Thus the closure of a Harder–Narasimhan stratum is in general not a union of strata.
A similar behavior is shown by the Harder–Narasimhan stratification of [Reference Dat, Orlik and RapoportDOR10]. However, we could not find an example of this for minuscule ![]() $\mu$ (and therefore applicable to our theory) in the literature.
$\mu$ (and therefore applicable to our theory) in the literature.
5. Harder–Narasimhan-strata in flag varieties, and classical points
Let ![]() $\{\mu \}$ be a conjugacy class of cocharacters of
$\{\mu \}$ be a conjugacy class of cocharacters of ![]() $G_{\overline {F}}$, and let
$G_{\overline {F}}$, and let ![]() $\mu$ be a representative. Let
$\mu$ be a representative. Let ![]() ${\mathcal {F}\ell }(G,\mu )$ be the flag variety for
${\mathcal {F}\ell }(G,\mu )$ be the flag variety for ![]() $G$ and
$G$ and ![]() $\{\mu \}$. In [Reference Dat, Orlik and RapoportDOR10, 9.6], Dat, Orlik and Rapoport introduce a Harder–Narasimhan stratification of
$\{\mu \}$. In [Reference Dat, Orlik and RapoportDOR10, 9.6], Dat, Orlik and Rapoport introduce a Harder–Narasimhan stratification of ![]() ${\mathcal {F}\ell }(G,\mu )$. Their semi-stable stratum coincides with the weakly admissible locus or period domain of Rapoport and Zink.
${\mathcal {F}\ell }(G,\mu )$. Their semi-stable stratum coincides with the weakly admissible locus or period domain of Rapoport and Zink.
By [Reference Scholze and WeinsteinSW20, Proposition 19.4.2] we have the natural Bialynicki-Birula map
to the diamond associated with ![]() ${\mathcal {F}\ell }(G,\mu )$. It is an isomorphism if
${\mathcal {F}\ell }(G,\mu )$. It is an isomorphism if ![]() $\mu$ is minuscule. On the level of
$\mu$ is minuscule. On the level of ![]() $C$-points,
$C$-points, ![]() ${\rm BB}_{\mu }$ has the following simple description. Write
${\rm BB}_{\mu }$ has the following simple description. Write ![]() $x\in {\rm Gr}_{G,\mu }(C)$ as
$x\in {\rm Gr}_{G,\mu }(C)$ as ![]() $x=g\mu (\xi ^{-1})G({B^+_{{\rm dR}}})/G({B^+_{{\rm dR}}})$ with
$x=g\mu (\xi ^{-1})G({B^+_{{\rm dR}}})/G({B^+_{{\rm dR}}})$ with ![]() $g\in G({B^+_{{\rm dR}}})$. Let
$g\in G({B^+_{{\rm dR}}})$. Let ![]() $\bar {g}\in G(C)$ be the image of
$\bar {g}\in G(C)$ be the image of ![]() $g$ under the natural projection
$g$ under the natural projection ![]() $G({B^+_{{\rm dR}}})\rightarrow G(C)$. Then
$G({B^+_{{\rm dR}}})\rightarrow G(C)$. Then ![]() ${\rm BB}_{\mu }(x)$ is the image of
${\rm BB}_{\mu }(x)$ is the image of ![]() $\bar g$ in
$\bar g$ in ![]() $\mathcal {F}\ell (G,\mu )$.
$\mathcal {F}\ell (G,\mu )$.
We fix any section ![]() $C\rightarrow {B^+_{{\rm dR}}}(C)$ of the reduction modulo
$C\rightarrow {B^+_{{\rm dR}}}(C)$ of the reduction modulo ![]() $\xi$, and thus consider
$\xi$, and thus consider ![]() $G(C)$ as a subset of
$G(C)$ as a subset of ![]() $G({B^+_{{\rm dR}}})$. Restricting to this subset, we obtain a natural bijection
$G({B^+_{{\rm dR}}})$. Restricting to this subset, we obtain a natural bijection
Theorem 5.1 Assume that:
(i)
 $x \in G(C) \mu (\xi ) G({B^+_{{\rm dR}}}) / G({B^+_{{\rm dR}}})$ for some section
$x \in G(C) \mu (\xi ) G({B^+_{{\rm dR}}}) / G({B^+_{{\rm dR}}})$ for some section  $C\rightarrow {B^+_{{\rm dR}}}(C)$; or
$C\rightarrow {B^+_{{\rm dR}}}(C)$; or(ii)
 $x \in {\rm Gr}_{G,\mu }(C)$ for some minuscule
$x \in {\rm Gr}_{G,\mu }(C)$ for some minuscule  $\mu$.
$\mu$.
Then the Harder–Narasimhan vector of ![]() $(\mathcal {E}_1, x)$ equals the Harder–Narasimhan vector of
$(\mathcal {E}_1, x)$ equals the Harder–Narasimhan vector of ![]() $(D, {\rm BB}_{\mu }(x))$ à la [Reference Dat, Orlik and RapoportDOR10] where
$(D, {\rm BB}_{\mu }(x))$ à la [Reference Dat, Orlik and RapoportDOR10] where ![]() $D$ is the isocrystal associated with
$D$ is the isocrystal associated with ![]() $1\in G(\breve {F})$. Furthermore, the Harder–Narasimhan filtrations correspond to the same parabolic subgroup of
$1\in G(\breve {F})$. Furthermore, the Harder–Narasimhan filtrations correspond to the same parabolic subgroup of ![]() $G$.
$G$.
Proof. We use the Tannakian formalism. Thus, suppose first that ![]() $G = {\rm GL}_n$ and that
$G = {\rm GL}_n$ and that ![]() $\mu$ is not necessary minuscule.
$\mu$ is not necessary minuscule.
Let ![]() $(\mathcal {E}, x)$ be an object in
$(\mathcal {E}, x)$ be an object in ![]() $\overline {\mathcal {C}}$ such that
$\overline {\mathcal {C}}$ such that ![]() ${\mathcal {E}}={\mathcal {E}}_1$ is the trivial vector bundle of rank
${\mathcal {E}}={\mathcal {E}}_1$ is the trivial vector bundle of rank ![]() $n$ and
$n$ and ![]() $x$ has a representative in
$x$ has a representative in ![]() ${\rm GL}_n(C) \mu (\xi ^{-1})$. It corresponds to the filtered isocrystal
${\rm GL}_n(C) \mu (\xi ^{-1})$. It corresponds to the filtered isocrystal ![]() $(\breve {F}^n, \mathop {\mathrm {Id}}\nolimits _{\breve {F}^n} \sigma, {\rm BB}_{\mu }(x))$ where we view
$(\breve {F}^n, \mathop {\mathrm {Id}}\nolimits _{\breve {F}^n} \sigma, {\rm BB}_{\mu }(x))$ where we view ![]() ${\rm BB}_{\mu }(x)$ as a filtration on
${\rm BB}_{\mu }(x)$ as a filtration on ![]() $\breve {F}^n$. Each sub-isocrystal
$\breve {F}^n$. Each sub-isocrystal ![]() $(V, \mathop {\mathrm {Id}}\nolimits _V\sigma )$ of
$(V, \mathop {\mathrm {Id}}\nolimits _V\sigma )$ of ![]() $(\breve {F}^n, \mathop {\mathrm {Id}}\nolimits _{\breve {F}^n} \sigma )$ gives rise to a sub-filtered isocrystal
$(\breve {F}^n, \mathop {\mathrm {Id}}\nolimits _{\breve {F}^n} \sigma )$ gives rise to a sub-filtered isocrystal ![]() $(V, \mathop {\mathrm {Id}}\nolimits _V \sigma, {\rm BB}_{\mu }(x) \cap V \otimes _{\breve {F}} C)$ of
$(V, \mathop {\mathrm {Id}}\nolimits _V \sigma, {\rm BB}_{\mu }(x) \cap V \otimes _{\breve {F}} C)$ of ![]() $(\breve {F}^n, \mathop {\mathrm {Id}}\nolimits _{\breve {F}^n} \sigma, {\rm BB}_{\mu }(x))$ and to a subobject
$(\breve {F}^n, \mathop {\mathrm {Id}}\nolimits _{\breve {F}^n} \sigma, {\rm BB}_{\mu }(x))$ and to a subobject ![]() $(\overline {\mathcal {E}}, \overline {x})$ of
$(\overline {\mathcal {E}}, \overline {x})$ of ![]() $(\mathcal {E}, x)$. More precisely,
$(\mathcal {E}, x)$. More precisely, ![]() $\overline {\mathcal {E}}$ is the trivial sub-vector bundle of
$\overline {\mathcal {E}}$ is the trivial sub-vector bundle of ![]() ${\mathcal {E}}$ of rank
${\mathcal {E}}$ of rank ![]() ${\rm dim}\,_{\breve {F}} V$ corresponding to the sub-isocrystal
${\rm dim}\,_{\breve {F}} V$ corresponding to the sub-isocrystal ![]() $(V,\mathop {\mathrm {Id}}\nolimits _V\sigma )$ of
$(V,\mathop {\mathrm {Id}}\nolimits _V\sigma )$ of ![]() $(\breve {F}^n, \mathop {\mathrm {Id}}\nolimits _{\breve {F}^n} \sigma )$. By Beauville–Laszlo's gluing theorem,
$(\breve {F}^n, \mathop {\mathrm {Id}}\nolimits _{\breve {F}^n} \sigma )$. By Beauville–Laszlo's gluing theorem, ![]() $\mathcal {E}^{\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}} \simeq \breve {F}^n \otimes _{\breve {F}} {B^+_{{\rm dR}}}$ and
$\mathcal {E}^{\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}} \simeq \breve {F}^n \otimes _{\breve {F}} {B^+_{{\rm dR}}}$ and ![]() $\overline {\mathcal {E}}^{\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}} \simeq V \otimes _{\breve {F}} {B^+_{{\rm dR}}}$. Then
$\overline {\mathcal {E}}^{\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}} \simeq V \otimes _{\breve {F}} {B^+_{{\rm dR}}}$. Then ![]() $\overline x$ is given by
$\overline x$ is given by ![]() $\overline {x} \cdot \overline {\mathcal {E}}^{\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}} = V \otimes _{\breve {F}} {B_{{\rm dR}}} \cap x\cdot ({B^+_{{\rm dR}}})^n.$
$\overline {x} \cdot \overline {\mathcal {E}}^{\mathop {\mathrm {tri}}\nolimits }_{{B^+_{{\rm dR}}}} = V \otimes _{\breve {F}} {B_{{\rm dR}}} \cap x\cdot ({B^+_{{\rm dR}}})^n.$
By definition we have that ![]() $\mathop {\mathrm {rank}}\nolimits (\overline {\mathcal {E}}, \overline {x}) = \mathop {\mathrm {rank}}\nolimits (V, \mathop {\mathrm {Id}}\nolimits _V \sigma, {\rm BB}_{\mu }(x) \cap V \otimes _{\breve {F}} C) = {\rm dim}\,_{\breve {F}} V$, that
$\mathop {\mathrm {rank}}\nolimits (\overline {\mathcal {E}}, \overline {x}) = \mathop {\mathrm {rank}}\nolimits (V, \mathop {\mathrm {Id}}\nolimits _V \sigma, {\rm BB}_{\mu }(x) \cap V \otimes _{\breve {F}} C) = {\rm dim}\,_{\breve {F}} V$, that ![]() $\mathop {\mathrm {deg}}\nolimits (\overline {\mathcal {E}}, \overline {x}) = -\mathop {\mathrm {deg}}\nolimits (\overline {x})$ and that
$\mathop {\mathrm {deg}}\nolimits (\overline {\mathcal {E}}, \overline {x}) = -\mathop {\mathrm {deg}}\nolimits (\overline {x})$ and that ![]() $\mathop {\mathrm {deg}}\nolimits (V, \mathop {\mathrm {Id}}\nolimits _V \sigma, {\rm BB}_{\mu }(x) \cap V \otimes _{\breve {F}} C) = \mathop {\mathrm {deg}}\nolimits ({\rm BB}_{\mu }(x) \cap V \otimes _{\breve {F}} C )$. It remains to show that
$\mathop {\mathrm {deg}}\nolimits (V, \mathop {\mathrm {Id}}\nolimits _V \sigma, {\rm BB}_{\mu }(x) \cap V \otimes _{\breve {F}} C) = \mathop {\mathrm {deg}}\nolimits ({\rm BB}_{\mu }(x) \cap V \otimes _{\breve {F}} C )$. It remains to show that
Let ![]() $P\subset G$ be the stabilizer of
$P\subset G$ be the stabilizer of ![]() $V$, a parabolic subgroup of
$V$, a parabolic subgroup of ![]() $G$. Because
$G$. Because ![]() $V$ is stable under
$V$ is stable under ![]() $\sigma$, the subgroup
$\sigma$, the subgroup ![]() $P$ is defined over
$P$ is defined over ![]() $F$. Its Levi quotient is
$F$. Its Levi quotient is ![]() $M={\rm GL}(V)\times {\rm GL}(\breve {F}^n/V)$. We consider a representative of
$M={\rm GL}(V)\times {\rm GL}(\breve {F}^n/V)$. We consider a representative of ![]() $x$ of the form
$x$ of the form ![]() $g\mu (\xi ^{-1})$ with
$g\mu (\xi ^{-1})$ with ![]() $g\in {\rm GL}_n(C)$. Using the Bruhat decomposition we can write
$g\in {\rm GL}_n(C)$. Using the Bruhat decomposition we can write ![]() $g=p_1wp_2$ with
$g=p_1wp_2$ with ![]() $p_1\in P(C)$,
$p_1\in P(C)$, ![]() $p_2\in P_{\mu }(C)$ and
$p_2\in P_{\mu }(C)$ and ![]() $w\in W$, the Weyl group of
$w\in W$, the Weyl group of ![]() $G$. Since
$G$. Since ![]() $\mu (\xi )p_2\mu (\xi ^{-1})\in G({B^+_{{\rm dR}}})$, we can replace the representative of
$\mu (\xi )p_2\mu (\xi ^{-1})\in G({B^+_{{\rm dR}}})$, we can replace the representative of ![]() $x$ by one of the form
$x$ by one of the form ![]() $p_1w\mu (\xi ^{-1})$, or
$p_1w\mu (\xi ^{-1})$, or ![]() $p_1{}^w\mu (\xi ^{-1})\in S_{\{{}^w\mu ^{-1}\}_{M}}$. From this last description we see that
$p_1{}^w\mu (\xi ^{-1})\in S_{\{{}^w\mu ^{-1}\}_{M}}$. From this last description we see that ![]() $\bar x$ is of the form
$\bar x$ is of the form ![]() $m_1({}^w\mu (\xi ^{-1}))_1$ where
$m_1({}^w\mu (\xi ^{-1}))_1$ where ![]() $m_1$ is the image of
$m_1$ is the image of ![]() $p_1$ in the first factor of
$p_1$ in the first factor of ![]() $M$, and
$M$, and ![]() $({}^w\mu (\xi ^{-1}))_1$ is the corresponding image of
$({}^w\mu (\xi ^{-1}))_1$ is the corresponding image of ![]() ${}^w\mu (\xi ^{-1})$. Its degree is the degree of
${}^w\mu (\xi ^{-1})$. Its degree is the degree of ![]() $({}^w\mu (\xi ^{-1}))_1$. On the other hand we have
$({}^w\mu (\xi ^{-1}))_1$. On the other hand we have ![]() ${\rm BB}_{\mu }(x)=p_1wP_{\mu }(C)/P_{\mu }(C)$. Again we obtain that
${\rm BB}_{\mu }(x)=p_1wP_{\mu }(C)/P_{\mu }(C)$. Again we obtain that ![]() ${\rm BB}_{\mu }(x)\cap V\otimes _{\breve {F}}C$ is the filtration corresponding to
${\rm BB}_{\mu }(x)\cap V\otimes _{\breve {F}}C$ is the filtration corresponding to ![]() $m_1({}^w\mu (\xi ^{-1}))_1$, hence the two degrees agree as claimed.
$m_1({}^w\mu (\xi ^{-1}))_1$, hence the two degrees agree as claimed.
Therefore our Harder–Narasimhan filtration of ![]() $(\mathcal {E}, x)$ and the Harder–Narasimhan filtration of
$(\mathcal {E}, x)$ and the Harder–Narasimhan filtration of ![]() $(\breve {F}^n, \mathop {\mathrm {Id}}\nolimits _{\breve {F}^n} \sigma, {\rm BB}_{\mu }(x))$ à la [Reference Dat, Orlik and RapoportDOR10] are identified by the map
$(\breve {F}^n, \mathop {\mathrm {Id}}\nolimits _{\breve {F}^n} \sigma, {\rm BB}_{\mu }(x))$ à la [Reference Dat, Orlik and RapoportDOR10] are identified by the map ![]() ${\rm BB}_{\mu }$.
${\rm BB}_{\mu }$.
The full subcategory of ![]() $\overline {\mathcal {C}}$ with objects
$\overline {\mathcal {C}}$ with objects ![]() $({\mathcal {E}},x)$ where
$({\mathcal {E}},x)$ where ![]() $x\in G(C)\mu (\xi ^{-1})$ for some
$x\in G(C)\mu (\xi ^{-1})$ for some ![]() $\mu$ is stable under tensor products and direct sums. Indeed, let
$\mu$ is stable under tensor products and direct sums. Indeed, let ![]() $(\mathcal {E}, x)$ and
$(\mathcal {E}, x)$ and ![]() $(\mathcal {E}', x')$ be objects in
$(\mathcal {E}', x')$ be objects in ![]() $\overline {\mathcal {C}}$ such that
$\overline {\mathcal {C}}$ such that ![]() $x = A \mu (\xi ^{-1})$, respectively
$x = A \mu (\xi ^{-1})$, respectively ![]() $x' = B \mu ' (\xi ^{-1})$, where
$x' = B \mu ' (\xi ^{-1})$, where ![]() $A \in {\rm GL}_n(C)$ respectively
$A \in {\rm GL}_n(C)$ respectively ![]() $B \in {\rm GL}_{n'}(C)$. Then
$B \in {\rm GL}_{n'}(C)$. Then ![]() $x \otimes x'$ is represented by the Kronecker product of matrices
$x \otimes x'$ is represented by the Kronecker product of matrices ![]() $A \mu (\xi ^{-1}) \otimes B \mu ' (\xi ^{-1}) = ( A \otimes B ) ( \mu (\xi ^{-1}) \otimes \mu '(\xi ^{-1}) )$. Similarly,
$A \mu (\xi ^{-1}) \otimes B \mu ' (\xi ^{-1}) = ( A \otimes B ) ( \mu (\xi ^{-1}) \otimes \mu '(\xi ^{-1}) )$. Similarly, ![]() $(\mathcal {E}, x) \oplus (\mathcal {E}', x') =({\mathcal {E}}\oplus {\mathcal {E}}', x\oplus x')$ with
$(\mathcal {E}, x) \oplus (\mathcal {E}', x') =({\mathcal {E}}\oplus {\mathcal {E}}', x\oplus x')$ with ![]() $x \oplus x' \in {\rm GL}_{n+n'}(C)\cdot (\mu (\xi ^{-1}), \mu ' (\xi ^{-1}) )$.
$x \oplus x' \in {\rm GL}_{n+n'}(C)\cdot (\mu (\xi ^{-1}), \mu ' (\xi ^{-1}) )$.
Granted the above properties, we consider the case where ![]() $G$ is any reductive group. Let
$G$ is any reductive group. Let ![]() $\mathcal {E}_1$ be the trivial
$\mathcal {E}_1$ be the trivial ![]() $G$-bundle and
$G$-bundle and ![]() $x \in G(C) \mu (\xi ^{-1})$. For every algebraic representation
$x \in G(C) \mu (\xi ^{-1})$. For every algebraic representation ![]() $\rho : G \longmapsto {\rm GL}_V \in \mathop {\mathrm {Rep}}\nolimits _{F}G$, the element
$\rho : G \longmapsto {\rm GL}_V \in \mathop {\mathrm {Rep}}\nolimits _{F}G$, the element ![]() $\rho (x)$ belongs to the subset
$\rho (x)$ belongs to the subset ![]() ${\rm GL}_V(C) \rho (\mu ) (\xi ^{-1})$. Hence the corresponding Harder–Narasimhan filtrations associated with
${\rm GL}_V(C) \rho (\mu ) (\xi ^{-1})$. Hence the corresponding Harder–Narasimhan filtrations associated with ![]() $(\rho (\mathcal {E}_1), \rho (x))$ à la [Reference Dat, Orlik and RapoportDOR10] and by our setting coincide. In other words, the Harder–Narasimhan filtrations of
$(\rho (\mathcal {E}_1), \rho (x))$ à la [Reference Dat, Orlik and RapoportDOR10] and by our setting coincide. In other words, the Harder–Narasimhan filtrations of ![]() $(\mathcal {E}_1, x)$ à la [Reference Dat, Orlik and RapoportDOR10] and by our setting coincide.
$(\mathcal {E}_1, x)$ à la [Reference Dat, Orlik and RapoportDOR10] and by our setting coincide.
Remark 5.2 This theorem crucially uses its assumptions (i) or (ii) and is not true in general. The key point is that under this assumption we can directly compare the Iwasawa decomposition and the Bruhat decomposition of the given element ![]() $g\mu (\xi ^{-1})$ to prove (5.3). For non-minuscule
$g\mu (\xi ^{-1})$ to prove (5.3). For non-minuscule ![]() $\mu$, even the weakly admissible locus in
$\mu$, even the weakly admissible locus in ![]() ${\rm Gr}_{G,\mu }$ (i.e. the semi-stable or basic Harder–Narasimhan stratum) does not coincide with the inverse image under
${\rm Gr}_{G,\mu }$ (i.e. the semi-stable or basic Harder–Narasimhan stratum) does not coincide with the inverse image under ![]() ${\rm BB}_{\mu }$ of the weakly admissible locus in
${\rm BB}_{\mu }$ of the weakly admissible locus in ![]() ${\mathcal {F}\ell }(G,\mu )$ as in [Reference Dat, Orlik and RapoportDOR10]. An explicit example for this is given in [Reference ViehmannVie21, Example 4.10].
${\mathcal {F}\ell }(G,\mu )$ as in [Reference Dat, Orlik and RapoportDOR10]. An explicit example for this is given in [Reference ViehmannVie21, Example 4.10].
We apply this to study classical points of ![]() ${\rm Gr}_{G,\mu }$, which are defined analogously to the usual notion of classical points on flag varieties.
${\rm Gr}_{G,\mu }$, which are defined analogously to the usual notion of classical points on flag varieties.
Definition 5.3 A classical point of ![]() ${\rm Gr}_G$ is a
${\rm Gr}_G$ is a ![]() $K$-valued point for some finite extension
$K$-valued point for some finite extension ![]() $K$ of
$K$ of ![]() $\breve {F}$.
$\breve {F}$.
Remark 5.4 Classical points are a particular case of the points we consider in Theorem 5.1. Indeed, let ![]() $K$ be a finite extension of
$K$ be a finite extension of ![]() $\breve {F}$. Then the
$\breve {F}$. Then the ![]() $K$-valued points of
$K$-valued points of ![]() ${\rm Gr}_{G}$ are
${\rm Gr}_{G}$ are ![]() $C$-valued points (for some algebraically closed complete extension of
$C$-valued points (for some algebraically closed complete extension of ![]() $K$) that are invariant under
$K$) that are invariant under ![]() ${\rm Gal}(C|K)$. Thus each such point has a representative in
${\rm Gal}(C|K)$. Thus each such point has a representative in ![]() $G(K)\mu (\xi )^{-1}$ for some choice of a Galois-equivariant section
$G(K)\mu (\xi )^{-1}$ for some choice of a Galois-equivariant section ![]() $K\rightarrow {B^+_{{\rm dR}}}(K)$. Notice that any such section identifies
$K\rightarrow {B^+_{{\rm dR}}}(K)$. Notice that any such section identifies ![]() $K$ with
$K$ with ![]() ${B^+_{{\rm dR}}}(C)^{{\rm Gal}(C|K)}\cong K$.
${B^+_{{\rm dR}}}(C)^{{\rm Gal}(C|K)}\cong K$.
Recall from (5.2) that for all ![]() $\mu$, the Bialynicki-Birula map induces a bijection
$\mu$, the Bialynicki-Birula map induces a bijection
We now prove a generalization of [Reference ViehmannVie21, Theorem 5.2], where a similar comparison was shown for basic ![]() $[b']$.
$[b']$.
Proposition 5.5 Let ![]() $x$ be a classical point of
$x$ be a classical point of ![]() ${\rm Gr}_{G,\mu }$. Then for
${\rm Gr}_{G,\mu }$. Then for ![]() $[b']\in B(G,\mu )$ the following are equivalent:
$[b']\in B(G,\mu )$ the following are equivalent:
(i)
 $x\in {\rm Gr}_{G,\mu }^{[b']^*}$;
$x\in {\rm Gr}_{G,\mu }^{[b']^*}$;(ii)
 $x\in {\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$;
$x\in {\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$;(iii) the Harder–Narasimhan vector of
 ${\rm BB}_{\mu }(x)\in {\mathcal {F}\ell }(G,\mu )$ in the sense of [Reference Dat, Orlik and RapoportDOR10] is equal to
${\rm BB}_{\mu }(x)\in {\mathcal {F}\ell }(G,\mu )$ in the sense of [Reference Dat, Orlik and RapoportDOR10] is equal to  $\nu _{b'}$.
$\nu _{b'}$.
Proof. We first prove equivalence of (i) and (ii). We consider the canonical reduction ![]() $({\mathcal {E}}_{1,x})_P$ of
$({\mathcal {E}}_{1,x})_P$ of ![]() $({\mathcal {E}}_1,x)$ where
$({\mathcal {E}}_1,x)$ where ![]() $P$ denotes the associated parabolic subgroup of
$P$ denotes the associated parabolic subgroup of ![]() $G$. Let
$G$. Let ![]() $[b']:={\rm HN}({\mathcal {E}}_1,x)\in B(G,\mu )$. Then we have to show that
$[b']:={\rm HN}({\mathcal {E}}_1,x)\in B(G,\mu )$. Then we have to show that ![]() ${\mathcal {E}}_{1,x}\cong {\mathcal {E}}_{[b']^*}$.
${\mathcal {E}}_{1,x}\cong {\mathcal {E}}_{[b']^*}$.
Let ![]() $M$ be a Levi subgroup of
$M$ be a Levi subgroup of ![]() $P$, and let
$P$, and let ![]() $b'$ be a representative of
$b'$ be a representative of ![]() $[b']$ in
$[b']$ in ![]() $M$ such that
$M$ such that ![]() $P$ is the parabolic subgroup associated with the Newton point of
$P$ is the parabolic subgroup associated with the Newton point of ![]() $b'$. Using the same argument as in the proof of (5.3), we obtain a representative of
$b'$. Using the same argument as in the proof of (5.3), we obtain a representative of ![]() $x$ of the form
$x$ of the form ![]() $p\mu (\xi ^{-1})$ with
$p\mu (\xi ^{-1})$ with ![]() $p\in P(K)$. Let
$p\in P(K)$. Let ![]() $m$ be the image of
$m$ be the image of ![]() $p$ in
$p$ in ![]() $M(K)$. By [Reference ViehmannVie21, Lemma 3.10] we have
$M(K)$. By [Reference ViehmannVie21, Lemma 3.10] we have ![]() $({\mathcal {E}}_{1,x})_P\times ^P M=(({\mathcal {E}}_{1}^P)\times ^P M)_{m}={\mathcal {E}}^M_{1,m}$. Isoc-filtrations of
$({\mathcal {E}}_{1,x})_P\times ^P M=(({\mathcal {E}}_{1}^P)\times ^P M)_{m}={\mathcal {E}}^M_{1,m}$. Isoc-filtrations of ![]() $({\mathcal {E}}_{1,x})_P\times ^P M$ (to parabolic subgroups of
$({\mathcal {E}}_{1,x})_P\times ^P M$ (to parabolic subgroups of ![]() $M$) induce isoc-filtrations of
$M$) induce isoc-filtrations of ![]() ${\mathcal {E}}_{1,x}$ to corresponding parabolic subgroups of
${\mathcal {E}}_{1,x}$ to corresponding parabolic subgroups of ![]() $G$ contained in
$G$ contained in ![]() $P$. From the maximality of
$P$. From the maximality of ![]() ${\rm HN}({\mathcal {E}}_1,x)$ we obtain that
${\rm HN}({\mathcal {E}}_1,x)$ we obtain that ![]() $({\mathcal {E}}_1^M,m)$ is semi-stable (i.e. weakly admissible). By [Reference ViehmannVie21, Theorem 5.2], it is also admissible. In other words,
$({\mathcal {E}}_1^M,m)$ is semi-stable (i.e. weakly admissible). By [Reference ViehmannVie21, Theorem 5.2], it is also admissible. In other words, ![]() $({\mathcal {E}}_{1,x})_P\times ^P M\cong {\mathcal {E}}_{[b']^*}^M$. The slope vector (in the sense of Fargues–Fontaine) of
$({\mathcal {E}}_{1,x})_P\times ^P M\cong {\mathcal {E}}_{[b']^*}^M$. The slope vector (in the sense of Fargues–Fontaine) of ![]() $({\mathcal {E}}_{1,x})_P\times ^P M$ equals
$({\mathcal {E}}_{1,x})_P\times ^P M$ equals ![]() ${\rm HN}({\mathcal {E}},x)$ and thus is dominant with respect to
${\rm HN}({\mathcal {E}},x)$ and thus is dominant with respect to ![]() $P$. By [Reference ChenChe19, Corollary 2.9, Theorem 2.7] this implies that
$P$. By [Reference ChenChe19, Corollary 2.9, Theorem 2.7] this implies that ![]() $({\mathcal {E}}_{1,x})_P\times ^P M$ is a reduction of
$({\mathcal {E}}_{1,x})_P\times ^P M$ is a reduction of ![]() ${\mathcal {E}}_{1,x}$ to
${\mathcal {E}}_{1,x}$ to ![]() $M$, that is
$M$, that is ![]() ${\mathcal {E}}_{1,x}\cong {\mathcal {E}}_{[b']^*}^G$.
${\mathcal {E}}_{1,x}\cong {\mathcal {E}}_{[b']^*}^G$.
The equivalence of (ii) and (iii) follows from Theorem 5.1.
As an application we can determine the non-emptiness pattern for Harder–Narasimhan strata in the sense of [Reference Dat, Orlik and RapoportDOR10], for the case that ![]() $b=1$.
$b=1$.
Proposition 5.6 Let ![]() $\{\mu \}$ be a conjugacy class of not necessary minuscule cocharacters of
$\{\mu \}$ be a conjugacy class of not necessary minuscule cocharacters of ![]() $G_{\overline {F}}$. Then the Harder–Narasimhan stratum for some Harder–Narasimhan vector
$G_{\overline {F}}$. Then the Harder–Narasimhan stratum for some Harder–Narasimhan vector ![]() $\nu$ in
$\nu$ in ![]() ${\mathcal {F}\ell }(G,\mu,1)$ in the sense of [Reference Dat, Orlik and RapoportDOR10] is non-empty if and only if
${\mathcal {F}\ell }(G,\mu,1)$ in the sense of [Reference Dat, Orlik and RapoportDOR10] is non-empty if and only if ![]() $\nu =\nu _{b'}$ for some
$\nu =\nu _{b'}$ for some ![]() $[b']\in B(G,\mu )$ satisfying the following condition. There is a parabolic subgroup
$[b']\in B(G,\mu )$ satisfying the following condition. There is a parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$ with a Levi subgroup
$G$ with a Levi subgroup ![]() $M$ such that
$M$ such that ![]() $[b']$ has a representative
$[b']$ has a representative ![]() $b'_M$ in
$b'_M$ in ![]() $M$ that is basic in
$M$ that is basic in ![]() $M$, and such that
$M$, and such that ![]() $P$ is the parabolic subgroup associated with
$P$ is the parabolic subgroup associated with ![]() $\nu _{b'_M}$. Furthermore, there is a
$\nu _{b'_M}$. Furthermore, there is a ![]() $\lambda \in X_*(P)$ in the conjugacy class of
$\lambda \in X_*(P)$ in the conjugacy class of ![]() $-\mu$ and such that
$-\mu$ and such that ![]() $\kappa _M(b'_M)=\lambda ^{\sharp _M}\in \pi _1(M)_{\Gamma }$.
$\kappa _M(b'_M)=\lambda ^{\sharp _M}\in \pi _1(M)_{\Gamma }$.
Remark 5.7 (i) In [Reference OrlikOrl06], Orlik gave an analogous non-emptiness criterion for Harder–Narasimhan strata in the sense of [Reference Dat, Orlik and RapoportDOR10] for ![]() $G={\rm GL}_n$, and arbitrary
$G={\rm GL}_n$, and arbitrary ![]() $b$.
$b$.
(ii) For minuscule ![]() $\mu$, Theorem 5.1 implies that
$\mu$, Theorem 5.1 implies that ![]() $B(G,\mu )_{{\rm HN}}$ consists of those
$B(G,\mu )_{{\rm HN}}$ consists of those ![]() $[b']$ that satisfy the condition of Proposition 5.5. We expect that for non-minuscule
$[b']$ that satisfy the condition of Proposition 5.5. We expect that for non-minuscule ![]() $\mu$, and already for
$\mu$, and already for ![]() $G={\rm GL}_n$, the set of non-empty Harder–Narasimhan strata in
$G={\rm GL}_n$, the set of non-empty Harder–Narasimhan strata in ![]() ${\rm Gr}_{G,\mu }$ in our sense strictly contains the one for
${\rm Gr}_{G,\mu }$ in our sense strictly contains the one for ![]() ${\mathcal {F}\ell }(G,\mu )$ in the sense of [Reference Dat, Orlik and RapoportDOR10].
${\mathcal {F}\ell }(G,\mu )$ in the sense of [Reference Dat, Orlik and RapoportDOR10].
Proof. Let ![]() $C = \widehat {\overline {F}}$ and consider the embedding
$C = \widehat {\overline {F}}$ and consider the embedding ![]() $C\rightarrow {B^+_{{\rm dR}}}$ induced by the inclusion
$C\rightarrow {B^+_{{\rm dR}}}$ induced by the inclusion ![]() $\overline {k} \hookrightarrow C^{\flat,\circ }$ where
$\overline {k} \hookrightarrow C^{\flat,\circ }$ where ![]() $\overline {k}$ is the residue field of
$\overline {k}$ is the residue field of ![]() $C$. Then we have a bijection
$C$. Then we have a bijection
and from the proof of (5.3) we see that for every parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$ we have
$G$ we have
Thus the necessity of the claimed condition follows from Proposition 3.13 and Theorem 5.1.
By [Reference Dat, Orlik and RapoportDOR10, 9.5.10], the semi-stable stratum in ![]() ${\mathcal {F}\ell }(M,-\lambda,1)$ is non-empty and open, and also has classical points. Let
${\mathcal {F}\ell }(M,-\lambda,1)$ is non-empty and open, and also has classical points. Let ![]() $x\in M(K)\lambda (\xi )M({B^+_{{\rm dR}}})/M({B^+_{{\rm dR}}})$ be the image of such a point, for some finite extension
$x\in M(K)\lambda (\xi )M({B^+_{{\rm dR}}})/M({B^+_{{\rm dR}}})$ be the image of such a point, for some finite extension ![]() $K$ of
$K$ of ![]() $\breve {F}$. Then by Proposition 5.5,
$\breve {F}$. Then by Proposition 5.5, ![]() $x$ is in the basic Newton stratum, which by
$x$ is in the basic Newton stratum, which by ![]() $\kappa _M(b'_M)=\lambda ^{\sharp _M}$ is the Newton stratum for
$\kappa _M(b'_M)=\lambda ^{\sharp _M}$ is the Newton stratum for ![]() $[b'_M]^{*_M}_M$. Its image in
$[b'_M]^{*_M}_M$. Its image in ![]() ${\rm Gr}_G$ is a classical point
${\rm Gr}_G$ is a classical point ![]() $x_G$ of
$x_G$ of ![]() ${\rm Gr}_G$. By definition of
${\rm Gr}_G$. By definition of ![]() $x_G$, the modified bundle
$x_G$, the modified bundle ![]() ${\mathcal {E}}_{1,x_G}$ has a reduction
${\mathcal {E}}_{1,x_G}$ has a reduction ![]() ${\mathcal {E}}_{1,x_G,P}$ to
${\mathcal {E}}_{1,x_G,P}$ to ![]() $P$ such that the associated slope vector
$P$ such that the associated slope vector ![]() $\nu _{b'_M}$ is
$\nu _{b'_M}$ is ![]() $P$-dominant and central in
$P$-dominant and central in ![]() $M$. Further,
$M$. Further, ![]() ${\mathcal {E}}_{1,x_G,P}\times ^P M={\mathcal {E}}^M_{1,x}$ is semi-stable. Thus it is a reduction of
${\mathcal {E}}_{1,x_G,P}\times ^P M={\mathcal {E}}^M_{1,x}$ is semi-stable. Thus it is a reduction of ![]() ${\mathcal {E}}_{1,x_G}$, which implies that
${\mathcal {E}}_{1,x_G}$, which implies that ![]() $x_G$ is a classical point in the Newton stratum for
$x_G$ is a classical point in the Newton stratum for ![]() $[b']^*$. Again by Proposition 5.5 this shows that
$[b']^*$. Again by Proposition 5.5 this shows that ![]() ${\rm BB}_{\mu }(x_G)$ is in the claimed Harder–Narasimhan stratum.
${\rm BB}_{\mu }(x_G)$ is in the claimed Harder–Narasimhan stratum.
6. Newton strata and the Hodge–Newton decomposition
Lemma 6.1 Let ![]() ${\mathcal {E}}$ be the trivial
${\mathcal {E}}$ be the trivial ![]() $G$-bundle on
$G$-bundle on ![]() $X$ and let
$X$ and let ![]() $x\in {\rm Gr}_{G,\mu }(C)$. Then
$x\in {\rm Gr}_{G,\mu }(C)$. Then
In particular, for any ![]() $[b']\in B(G,-\mu )$, we have the two containments
$[b']\in B(G,-\mu )$, we have the two containments
Proof. Recall that ![]() $\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{x})$ is defined via a different Harder–Narasimhan formalism, this time corresponding to all parabolic reductions of
$\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{x})$ is defined via a different Harder–Narasimhan formalism, this time corresponding to all parabolic reductions of ![]() ${\mathcal {E}}_{1,x}$ (not necessarily corresponding to an isoc-filtration of
${\mathcal {E}}_{1,x}$ (not necessarily corresponding to an isoc-filtration of ![]() ${\mathcal {E}}_1$), but for the same slope function. Thus the comparison theorem for this other Harder–Narasimhan theory implies (6.1), and the other two assertions are an immediate consequence.
${\mathcal {E}}_1$), but for the same slope function. Thus the comparison theorem for this other Harder–Narasimhan theory implies (6.1), and the other two assertions are an immediate consequence.
However, Newton strata and Harder–Narasimhan strata are in general far from being equal. For minuscule ![]() $\mu$, a description of the set of all Newton strata in
$\mu$, a description of the set of all Newton strata in ![]() ${\rm Gr}_{G,\mu }$ containing points that are semi-stable in the sense of our present Harder–Narasimhan formalism is given by [Reference ViehmannVie21, Theorem 1.3].
${\rm Gr}_{G,\mu }$ containing points that are semi-stable in the sense of our present Harder–Narasimhan formalism is given by [Reference ViehmannVie21, Theorem 1.3].
The following is an example of a non-basic Newton stratum in some ![]() ${\rm Gr}_{G,\mu }$ that is completely contained in the weakly admissible locus (i.e. in the basic or semi-stable Harder–Narasimhan stratum). This disproves an expectation expressed in [Reference FarguesFar19, 9.7.2(2)].
${\rm Gr}_{G,\mu }$ that is completely contained in the weakly admissible locus (i.e. in the basic or semi-stable Harder–Narasimhan stratum). This disproves an expectation expressed in [Reference FarguesFar19, 9.7.2(2)].
Example 6.2 Let ![]() $G_0={\rm GL}_5$, and
$G_0={\rm GL}_5$, and ![]() $[b]\in B(G_0)$ superbasic of slope
$[b]\in B(G_0)$ superbasic of slope ![]() $2/5$. Let
$2/5$. Let ![]() $G=G_b$ be the inner form of
$G=G_b$ be the inner form of ![]() $G_0$ corresponding to
$G_0$ corresponding to ![]() $b$. Then
$b$. Then ![]() $G$ does not have any proper parabolic subgroups. Thus the only non-empty Harder–Narasimhan stratum in any
$G$ does not have any proper parabolic subgroups. Thus the only non-empty Harder–Narasimhan stratum in any ![]() ${\rm Gr}_{G,\mu }$ is the weakly admissible locus, which then coincides with
${\rm Gr}_{G,\mu }$ is the weakly admissible locus, which then coincides with ![]() ${\rm Gr}_{G,\mu }$. However, there are in general many non-empty Newton strata. For example consider the minuscule cocharacter
${\rm Gr}_{G,\mu }$. However, there are in general many non-empty Newton strata. For example consider the minuscule cocharacter ![]() $\mu =(1,1,0,0,0)$. Then
$\mu =(1,1,0,0,0)$. Then ![]() $B(G,-\mu )=\{[b]^*,[b']\}$ where
$B(G,-\mu )=\{[b]^*,[b']\}$ where ![]() $[b']$ corresponds to the element of
$[b']$ corresponds to the element of ![]() $B({\rm GL}_5)$ with Newton slopes
$B({\rm GL}_5)$ with Newton slopes ![]() $-\tfrac {1}{3}$ and
$-\tfrac {1}{3}$ and ![]() $-\tfrac {1}{2}$ with multiplicities 3 and 2, respectively. Thus
$-\tfrac {1}{2}$ with multiplicities 3 and 2, respectively. Thus ![]() ${\rm Gr}_{G,\mu,1}^{[b']}$ is a non-basic and non-empty Newton stratum contained in the weakly admissible locus.
${\rm Gr}_{G,\mu,1}^{[b']}$ is a non-basic and non-empty Newton stratum contained in the weakly admissible locus.
More generally, let ![]() $G$ be a reductive group over
$G$ be a reductive group over ![]() $F$, let
$F$, let ![]() $\{\mu \}$ be a conjugacy class of cocharacters, and let
$\{\mu \}$ be a conjugacy class of cocharacters, and let ![]() $[b']\in B(G,-\mu )$. Assume that there is no non-basic
$[b']\in B(G,-\mu )$. Assume that there is no non-basic ![]() $[b'']\in B(G,\mu )_{{\rm HN}}$ with
$[b'']\in B(G,\mu )_{{\rm HN}}$ with ![]() $[b'']^*\leqslant [b']$. Then by (6.1), we obtain that
$[b'']^*\leqslant [b']$. Then by (6.1), we obtain that ![]() ${\rm Gr}_{G,\mu,1}^{[b']}$ is contained in the weakly admissible locus.
${\rm Gr}_{G,\mu,1}^{[b']}$ is contained in the weakly admissible locus.
Example 6.3 Let us give an example illustrating that the condition in the previous example is, however, not necessary for ![]() ${\rm Gr}_{G,\mu,1}^{[b']}$ to be contained in the weakly admissible locus. We use the compatibilities with inner twists explained in § 8. Let
${\rm Gr}_{G,\mu,1}^{[b']}$ to be contained in the weakly admissible locus. We use the compatibilities with inner twists explained in § 8. Let ![]() $G_0= {\rm GL}_{14}$, and let
$G_0= {\rm GL}_{14}$, and let ![]() $[b] \in B(G)$ such that
$[b] \in B(G)$ such that ![]() $\mathcal {E}_b = \mathcal {O}(\frac {5}{7}) \oplus \mathcal {O}(\frac {5}{7})$ where
$\mathcal {E}_b = \mathcal {O}(\frac {5}{7}) \oplus \mathcal {O}(\frac {5}{7})$ where ![]() $\mathcal {O}(\lambda )$ is the stable vector bundle of slope
$\mathcal {O}(\lambda )$ is the stable vector bundle of slope ![]() $\lambda$. Let
$\lambda$. Let ![]() $G=G_b$ be the inner form of
$G=G_b$ be the inner form of ![]() $G_0$ corresponding to
$G_0$ corresponding to ![]() $b$. Then the strict parabolic subgroups of
$b$. Then the strict parabolic subgroups of ![]() $G$ are all in one
$G$ are all in one ![]() $G(F)$-orbit, and the associated Levi quotient is the corresponding inner form of
$G(F)$-orbit, and the associated Levi quotient is the corresponding inner form of ![]() ${\rm GL}_7\times {\rm GL}_7$.
${\rm GL}_7\times {\rm GL}_7$.
Let ![]() $\mu = (1^{(4)}, 0^{(10)})$. We consider the weakly admissible locus
$\mu = (1^{(4)}, 0^{(10)})$. We consider the weakly admissible locus ![]() ${\rm Gr}_{G, \mu,1}^{\text {wa}}$. Let
${\rm Gr}_{G, \mu,1}^{\text {wa}}$. Let ![]() $[b'_1], [b'_2] \in B(G_b)$ such that
$[b'_1], [b'_2] \in B(G_b)$ such that ![]() $\mathcal {E}_{b'_1}$ and
$\mathcal {E}_{b'_1}$ and ![]() $\mathcal {E}_{b'_2}$ are the
$\mathcal {E}_{b'_2}$ are the ![]() $G_b$-bundles corresponding to the
$G_b$-bundles corresponding to the ![]() ${\rm GL}_{14}$-bundles
${\rm GL}_{14}$-bundles ![]() $\mathcal {O}(\frac {3}{2})^2 \oplus \mathcal {O}(\frac {4}{5})^2$ and
$\mathcal {O}(\frac {3}{2})^2 \oplus \mathcal {O}(\frac {4}{5})^2$ and ![]() $\mathcal {O}(\frac {8}{7}) \oplus \mathcal {O}(\frac {6}{7})$ via the inner twist. Then
$\mathcal {O}(\frac {8}{7}) \oplus \mathcal {O}(\frac {6}{7})$ via the inner twist. Then ![]() $[b'_1]>[b'_2]$ and
$[b'_1]>[b'_2]$ and ![]() ${\rm Gr}_{G,\mu,1}^{[b'_2]}$ is not totally contained in the weakly admissible locus (for example, one can construct a classical point in this Newton stratum, which then has Harder–Narasimhan vector
${\rm Gr}_{G,\mu,1}^{[b'_2]}$ is not totally contained in the weakly admissible locus (for example, one can construct a classical point in this Newton stratum, which then has Harder–Narasimhan vector ![]() $-\nu _{b'_2}$). We claim that
$-\nu _{b'_2}$). We claim that ![]() ${\rm Gr}_{G,\mu,1}^{[b'_1]}\subset {\rm Gr}_{G,\mu,1}^{{\rm {wa}}}$.
${\rm Gr}_{G,\mu,1}^{[b'_1]}\subset {\rm Gr}_{G,\mu,1}^{{\rm {wa}}}$.
Suppose that there exists an ![]() $x \in {\rm Gr}_{G,\mu,1}^{[b_1']}(C) \setminus {\rm Gr}_{G,\mu,1}^{{\rm {wa}}}(C)$. Using the inner twist between
$x \in {\rm Gr}_{G,\mu,1}^{[b_1']}(C) \setminus {\rm Gr}_{G,\mu,1}^{{\rm {wa}}}(C)$. Using the inner twist between ![]() $G$ and
$G$ and ![]() ${\rm GL}_{14}$ we obtain the following. Let
${\rm GL}_{14}$ we obtain the following. Let ![]() $P$ denote the standard parabolic subgroup of
$P$ denote the standard parabolic subgroup of ![]() ${\rm GL}_{14}$ whose standard Levi factor
${\rm GL}_{14}$ whose standard Levi factor ![]() $M$ is
$M$ is ![]() ${\rm GL}_7\times {\rm GL}_7$. Let
${\rm GL}_7\times {\rm GL}_7$. Let ![]() $[b_1]=[b'_1b]\in B({\rm GL}_{14})$ be the class corresponding to
$[b_1]=[b'_1b]\in B({\rm GL}_{14})$ be the class corresponding to ![]() $\mathcal {O}(\frac {3}{2})^2 \oplus \mathcal {O}(\frac {4}{5})^2$. Then there is a reduction of
$\mathcal {O}(\frac {3}{2})^2 \oplus \mathcal {O}(\frac {4}{5})^2$. Then there is a reduction of ![]() $b$ to
$b$ to ![]() $P(\breve {\mathbb {Q}}_p)$ such that the corresponding reduction of
$P(\breve {\mathbb {Q}}_p)$ such that the corresponding reduction of ![]() ${\mathcal {E}}_{b'_1}$ is violating the semi-stability condition.
${\mathcal {E}}_{b'_1}$ is violating the semi-stability condition.
We know that ![]() $(\mathcal {E}_b)_P \times ^P M \simeq \mathcal {O}(\frac {5}{7}) \times \mathcal {O}(\frac {5}{7})$ and
$(\mathcal {E}_b)_P \times ^P M \simeq \mathcal {O}(\frac {5}{7}) \times \mathcal {O}(\frac {5}{7})$ and ![]() $(\mathcal {E}_{b'_1})_P \times ^P M \simeq \mathcal {O}(\frac {5}{7})_{x_1} \times \mathcal {O}(\frac {5}{7})_{x_2}$ for some
$(\mathcal {E}_{b'_1})_P \times ^P M \simeq \mathcal {O}(\frac {5}{7})_{x_1} \times \mathcal {O}(\frac {5}{7})_{x_2}$ for some ![]() $x_i\in {\rm Gr}_{{\rm GL}_7,\mu _i}(C)$ where
$x_i\in {\rm Gr}_{{\rm GL}_7,\mu _i}(C)$ where ![]() $\mu _i = (1^{(n_i)}, 0^{(7 - n_i)})$ with
$\mu _i = (1^{(n_i)}, 0^{(7 - n_i)})$ with ![]() $n_1 + n_2 = 4$. Since the reduction contradicts weak admissibility, we have
$n_1 + n_2 = 4$. Since the reduction contradicts weak admissibility, we have ![]() $n_1 > 2$. Since
$n_1 > 2$. Since ![]() $\mathcal {O}(\frac {5}{7})_{x_1}$ is a sub-vector bundle of
$\mathcal {O}(\frac {5}{7})_{x_1}$ is a sub-vector bundle of ![]() $\mathcal {E}_{b_1}$, the biggest slope of
$\mathcal {E}_{b_1}$, the biggest slope of ![]() $\mathcal {O}(\frac {5}{7})_{x_1}$ is equal or smaller than
$\mathcal {O}(\frac {5}{7})_{x_1}$ is equal or smaller than ![]() $\frac {3}{2}$. Moreover, the comparison between the Harder–Narasimhan vector and the Newton polygon implies that
$\frac {3}{2}$. Moreover, the comparison between the Harder–Narasimhan vector and the Newton polygon implies that ![]() $n_1 < 4$, hence
$n_1 < 4$, hence ![]() $n_1 = 3$ and
$n_1 = 3$ and ![]() $n_2 = 1$.
$n_2 = 1$.
Since ![]() $\mathcal {O}(\frac {5}{7})_{x_1}$ can not contain
$\mathcal {O}(\frac {5}{7})_{x_1}$ can not contain ![]() $\mathcal {O}(\frac {3}{2})^2$, by [Reference ChenChe19, Corollary 2.9], the biggest slope of
$\mathcal {O}(\frac {3}{2})^2$, by [Reference ChenChe19, Corollary 2.9], the biggest slope of ![]() $\mathcal {O}(\frac {5}{7})_{x_2}$ is not smaller than
$\mathcal {O}(\frac {5}{7})_{x_2}$ is not smaller than ![]() $\frac {3}{2}$. However, this is not true since
$\frac {3}{2}$. However, this is not true since ![]() $\mu _2 = (1^{(1)}, 0^{(6)})$.
$\mu _2 = (1^{(1)}, 0^{(6)})$.
In the remainder of this section we consider the exceptional cases where certain Harder–Narasimhan strata and Newton strata coincide. This is closely related to the concept of Hodge–Newton decomposability, which we recall from [Reference ViehmannVie21, 7.1] and reformulate for our context. The signs we use here differ from those in [Reference ViehmannVie21] since our ![]() $[b']$ is such that
$[b']$ is such that ![]() $\nu _{b'}$ plays the role of a Harder–Narasimhan vector (either for our theory or the one of Fargues and Fontaine) whereas in [Reference ViehmannVie21],
$\nu _{b'}$ plays the role of a Harder–Narasimhan vector (either for our theory or the one of Fargues and Fontaine) whereas in [Reference ViehmannVie21], ![]() $\nu _{b'}$ is a Newton vector of a
$\nu _{b'}$ is a Newton vector of a ![]() $G$-bundle.
$G$-bundle.
To define the notion of Hodge–Newton decomposability, recall that the choice of an inner twisting between ![]() $G$ and a quasi-split inner form
$G$ and a quasi-split inner form ![]() $H$ allows to identify the Newton chamber of
$H$ allows to identify the Newton chamber of ![]() $G$ and
$G$ and ![]() $H$, where the Newton chamber is the set of Galois-invariant
$H$, where the Newton chamber is the set of Galois-invariant ![]() $G(\overline {F})$-conjugacy classes of homomorphisms
$G(\overline {F})$-conjugacy classes of homomorphisms ![]() $\mathbb {D}_{\overline {F}}\rightarrow G_{\overline {F}}$. Applying this to both
$\mathbb {D}_{\overline {F}}\rightarrow G_{\overline {F}}$. Applying this to both ![]() $\nu _{b'}$ and
$\nu _{b'}$ and ![]() $\mu ^{\diamond }$ (where
$\mu ^{\diamond }$ (where ![]() $\mu ^{\diamond }$ is the Galois average of
$\mu ^{\diamond }$ is the Galois average of ![]() $\mu$), a triple
$\mu$), a triple ![]() $(G,[b'],\mu )$ with
$(G,[b'],\mu )$ with ![]() $[b']\in B(G,\mu )$ is called Hodge–Newton decomposable if there is a proper standard Levi subgroup
$[b']\in B(G,\mu )$ is called Hodge–Newton decomposable if there is a proper standard Levi subgroup ![]() $M'$ of
$M'$ of ![]() $H$ that contains the centralizer of the dominant Newton point
$H$ that contains the centralizer of the dominant Newton point ![]() $\nu _{b'}$ of
$\nu _{b'}$ of ![]() $[b']$ and such that
$[b']$ and such that ![]() $\nu _{b',{\rm dom}}\leqslant _{M'} (\mu ^{\diamond })_{{\rm dom}}$, i.e.
$\nu _{b',{\rm dom}}\leqslant _{M'} (\mu ^{\diamond })_{{\rm dom}}$, i.e. ![]() $(\mu ^{\diamond })_{{\rm dom}}-(\nu _{b'})_{{\rm dom}}$ is a non-negative rational linear combination of positive coroots of
$(\mu ^{\diamond })_{{\rm dom}}-(\nu _{b'})_{{\rm dom}}$ is a non-negative rational linear combination of positive coroots of ![]() $M'$. If
$M'$. If ![]() $(G,\mu )$ is fixed, then we also say that
$(G,\mu )$ is fixed, then we also say that ![]() $[b']$ is Hodge–Newton decomposable.
$[b']$ is Hodge–Newton decomposable.
Let ![]() $M$ be a Levi subgroup of (a parabolic subgroup of)
$M$ be a Levi subgroup of (a parabolic subgroup of) ![]() $G$. From the Iwasawa decomposition we obtain a map
$G$. From the Iwasawa decomposition we obtain a map
mapping ![]() $x\in {\rm Gr}_G(C)$ to the unique element
$x\in {\rm Gr}_G(C)$ to the unique element ![]() $x_M$ with
$x_M$ with ![]() $x\in U({B_{{\rm dR}}})x_M$ where
$x\in U({B_{{\rm dR}}})x_M$ where ![]() $U({B_{{\rm dR}}})$ is the unipotent radical of
$U({B_{{\rm dR}}})$ is the unipotent radical of ![]() $P$. If
$P$. If ![]() $x\in S_{\{\lambda \}_P,P}$ for some cocharacter
$x\in S_{\{\lambda \}_P,P}$ for some cocharacter ![]() $\lambda$ of
$\lambda$ of ![]() $P$, then
$P$, then ![]() $x_M\in {\rm Gr}_{M,\lambda _{M}}$ where
$x_M\in {\rm Gr}_{M,\lambda _{M}}$ where ![]() $\lambda _{M}\in X_*(M)$ is a representative of the conjugacy class
$\lambda _{M}\in X_*(M)$ is a representative of the conjugacy class ![]() $\{\lambda \}_P$.
$\{\lambda \}_P$.
The following theorem is a variant of the Hodge–Newton decomposition, stated in terms of Harder–Narasimhan vectors, and generalized to not necessarily quasi-split groups.
Theorem 6.4 Let ![]() $(G,[b'],\mu )$ be Hodge–Newton decomposable with respect to some
$(G,[b'],\mu )$ be Hodge–Newton decomposable with respect to some ![]() $M'$.
$M'$.
(i) There is a parabolic subgroup
 $P$ of
$P$ of  $G$ with a Levi subgroup
$G$ with a Levi subgroup  $M$ both defined over
$M$ both defined over  $F$ and such that
$F$ and such that  $M$ is an inner form of
$M$ is an inner form of  $M'$. Further, there are representatives
$M'$. Further, there are representatives  $b'_M$ and
$b'_M$ and  $\mu _M$ of
$\mu _M$ of  $[b']$ and
$[b']$ and  $\{\mu \}$ such that conjugation by
$\{\mu \}$ such that conjugation by  $\mu _{M}$ on the unipotent radical of
$\mu _{M}$ on the unipotent radical of  $P$ has only non-negative weights and such that
$P$ has only non-negative weights and such that  $[b'_M]\in B(M, \mu _{M})$. Then the
$[b'_M]\in B(M, \mu _{M})$. Then the  $M$-dominant Newton point of
$M$-dominant Newton point of  $b'_M$ is also
$b'_M$ is also  $P$-dominant and
$P$-dominant and  $P$-regular, i.e. conjugation by
$P$-regular, i.e. conjugation by  $\nu _{b_M}$ on the unipotent radical of
$\nu _{b_M}$ on the unipotent radical of  $P$ has only positive weights.
$P$ has only positive weights.(ii) Let
 $x\in {\rm Gr}_{G,\mu,1}^{[b']^*}(C)$. Let
$x\in {\rm Gr}_{G,\mu,1}^{[b']^*}(C)$. Let  ${\mathcal {E}}_{1,x}^P$ be the reduction of
${\mathcal {E}}_{1,x}^P$ be the reduction of  ${\mathcal {E}}_{1,x}$ corresponding to
${\mathcal {E}}_{1,x}$ corresponding to  $b'_M\in M$. Then we have the following.
$b'_M\in M$. Then we have the following.
(a)
 ${\mathcal {E}}_{1,x_M}^M$ is a reduction of
${\mathcal {E}}_{1,x_M}^M$ is a reduction of  ${\mathcal {E}}_{1,x}$ to
${\mathcal {E}}_{1,x}$ to  $M$, and
$M$, and  $\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x_M}^M)=[b'_M]^*_M$.
$\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x_M}^M)=[b'_M]^*_M$.(b) Let
 ${\mathcal {E}}_1^P$ be the reduction to
${\mathcal {E}}_1^P$ be the reduction to  $P$ of
$P$ of  ${\mathcal {E}}_1$ that corresponds to
${\mathcal {E}}_1$ that corresponds to  ${\mathcal {E}}_{1,x}^P$. Then
${\mathcal {E}}_{1,x}^P$. Then  ${\mathcal {E}}_{1}^P\times ^P M$ is a reduction of
${\mathcal {E}}_{1}^P\times ^P M$ is a reduction of  ${\mathcal {E}}_{1}$ to
${\mathcal {E}}_{1}$ to  $M$. In particular,
$M$. In particular,  ${\rm HN}({\mathcal {E}}_1,x)\leqslant _M [b']$.
${\rm HN}({\mathcal {E}}_1,x)\leqslant _M [b']$.(c) Choose
 $P$ within its
$P$ within its  $G(F)$-conjugacy class in such a way that
$G(F)$-conjugacy class in such a way that  ${\mathcal {E}}_1^P$ as in (b) is the natural reduction to
${\mathcal {E}}_1^P$ as in (b) is the natural reduction to  $P$ of the trivial
$P$ of the trivial  $G$-bundle
$G$-bundle  ${\mathcal {E}}_1$. Then
${\mathcal {E}}_1$. Then  $x\in S_{\{\mu _M^{-1}\},P}(C)$. Let
$x\in S_{\{\mu _M^{-1}\},P}(C)$. Let  $x_M={\rm pr}_M(x)$. Then
$x_M={\rm pr}_M(x)$. Then  $x_M\in {\rm Gr}_{M,\mu _M,1}^{[b'_M]^*_M}$.
$x_M\in {\rm Gr}_{M,\mu _M,1}^{[b'_M]^*_M}$.(d)
 ${\rm HN}({\mathcal {E}}_1,x)$ is the image of
${\rm HN}({\mathcal {E}}_1,x)$ is the image of  ${\rm HN}({\mathcal {E}}_1^M,x_M)\in B(M,\mu _M)_{{\rm HN}}$ in
${\rm HN}({\mathcal {E}}_1^M,x_M)\in B(M,\mu _M)_{{\rm HN}}$ in  $B(G,\mu )$.
$B(G,\mu )$.(e)
 ${\rm pr}_M^{-1}(\{x_M\})\cap {\rm Gr}_{G,\mu,1}=\{x\}.$
${\rm pr}_M^{-1}(\{x_M\})\cap {\rm Gr}_{G,\mu,1}=\{x\}.$
Proof. Replacing ![]() $G$ by
$G$ by ![]() $G_{{\rm {ad}}}$ we may assume that
$G_{{\rm {ad}}}$ we may assume that ![]() $G$ is adjoint. Let
$G$ is adjoint. Let ![]() $b\in G(\breve {F})$ be a basic element such that the associated inner form
$b\in G(\breve {F})$ be a basic element such that the associated inner form ![]() $H=G_{b}$ is quasi-split. Let
$H=G_{b}$ is quasi-split. Let ![]() $[\tilde b']\in B(H)$ be the image of
$[\tilde b']\in B(H)$ be the image of ![]() $[b']$ under the induced isomorphism
$[b']$ under the induced isomorphism ![]() $B(G)\cong B(H)$. We choose a Borel subgroup and a maximal torus
$B(G)\cong B(H)$. We choose a Borel subgroup and a maximal torus ![]() $H\supseteq B\supseteq T$. Let
$H\supseteq B\supseteq T$. Let ![]() $\tilde M$ be the standard Levi subgroup of
$\tilde M$ be the standard Levi subgroup of ![]() $H$ from the definition of Hodge–Newton decomposability. It contains the centralizer of the dominant Newton point of
$H$ from the definition of Hodge–Newton decomposability. It contains the centralizer of the dominant Newton point of ![]() $[\tilde b']$, and is stable under the Frobenius
$[\tilde b']$, and is stable under the Frobenius ![]() $\sigma$. Let
$\sigma$. Let ![]() $\tilde b'\in \tilde M(\breve {F})\cap [\tilde b']$ be such that its
$\tilde b'\in \tilde M(\breve {F})\cap [\tilde b']$ be such that its ![]() $\tilde M$-dominant Newton point
$\tilde M$-dominant Newton point ![]() $\nu _{\tilde b'}$ is dominant. Let
$\nu _{\tilde b'}$ is dominant. Let ![]() $\tilde b\in \tilde M(\breve {F})$ with
$\tilde b\in \tilde M(\breve {F})$ with ![]() $\kappa _{\tilde M}(\tilde b)=\kappa _{\tilde M}(\tilde b')-\mu _{{\rm dom}}^{\sharp _{\tilde M}}$ and such that
$\kappa _{\tilde M}(\tilde b)=\kappa _{\tilde M}(\tilde b')-\mu _{{\rm dom}}^{\sharp _{\tilde M}}$ and such that ![]() $[\tilde b]_{\tilde M}\in B(\tilde M)$ is basic. We claim that
$[\tilde b]_{\tilde M}\in B(\tilde M)$ is basic. We claim that ![]() $[\tilde b]_H$ corresponds to
$[\tilde b]_H$ corresponds to ![]() $[1]_G$ under the isomorphism
$[1]_G$ under the isomorphism ![]() $B(G)\cong B(H)$. Let
$B(G)\cong B(H)$. Let ![]() $[b_0]_H\in B(H)$ be the image of
$[b_0]_H\in B(H)$ be the image of ![]() $[1]_G$. We have
$[1]_G$. We have ![]() $\kappa _G(b')=\mu ^{\sharp _G}$ and hence
$\kappa _G(b')=\mu ^{\sharp _G}$ and hence ![]() $\kappa _H(\tilde b)=\kappa _H(\tilde b')-\mu ^{\sharp _H}=\kappa _H(b_0).$ Further,
$\kappa _H(\tilde b)=\kappa _H(\tilde b')-\mu ^{\sharp _H}=\kappa _H(b_0).$ Further,
Since both ![]() $\nu _{\tilde {b}}$ and
$\nu _{\tilde {b}}$ and ![]() $\nu _{b_0}$ are central in
$\nu _{b_0}$ are central in ![]() $\tilde {M}$, they agree. Thus also
$\tilde {M}$, they agree. Thus also ![]() $[\tilde {b}]_{H}=[b_0]_H$.
$[\tilde {b}]_{H}=[b_0]_H$.
Let ![]() $G'=H_{b_0}$. Since
$G'=H_{b_0}$. Since ![]() $\tilde {M}$ and the corresponding parabolic subgroup
$\tilde {M}$ and the corresponding parabolic subgroup ![]() $\tilde {P}=\tilde {M} B$ are stable under
$\tilde {P}=\tilde {M} B$ are stable under ![]() $b_0$ and under
$b_0$ and under ![]() $\sigma$, the group
$\sigma$, the group ![]() $G'$ has a parabolic subgroup and Levi subgroup
$G'$ has a parabolic subgroup and Levi subgroup ![]() $P'=\tilde {P}_{b_0}\supseteq M'=\tilde {M}_{b_0}$ defined over
$P'=\tilde {P}_{b_0}\supseteq M'=\tilde {M}_{b_0}$ defined over ![]() $F$. Furthermore, the class in
$F$. Furthermore, the class in ![]() $B(G')$ corresponding to
$B(G')$ corresponding to ![]() $[\tilde {b}']_H$ has a representative in
$[\tilde {b}']_H$ has a representative in ![]() $M'$ with analogous properties as in (i). Using that
$M'$ with analogous properties as in (i). Using that ![]() $G'=G_{bb_0}\cong G$, we also obtain (i) for
$G'=G_{bb_0}\cong G$, we also obtain (i) for ![]() $G$.
$G$.
Now we prove (ii). Assertion (a) follows from the corresponding properties of the canonical reduction. Let ![]() ${\mathcal {E}}_1^P$ be the reduction to
${\mathcal {E}}_1^P$ be the reduction to ![]() $P$ of
$P$ of ![]() ${\mathcal {E}}_1$ that corresponds to
${\mathcal {E}}_1$ that corresponds to ![]() ${\mathcal {E}}_{1,x}^P$ and let
${\mathcal {E}}_{1,x}^P$ and let ![]() $v$ be the slope vector of
$v$ be the slope vector of ![]() ${\mathcal {E}}_1^P$. Since
${\mathcal {E}}_1^P$. Since ![]() ${\mathcal {E}}_1$ is semi-stable, we have
${\mathcal {E}}_1$ is semi-stable, we have ![]() $v\leqslant 0$ where
$v\leqslant 0$ where ![]() $0$ denotes the trivial slope vector. Let
$0$ denotes the trivial slope vector. Let ![]() $\{\tilde {\mu }\}_M$ be such that
$\{\tilde {\mu }\}_M$ be such that ![]() ${\rm pr}_M(x)\in {\rm Gr}_{M,\tilde {\mu }}$. Since
${\rm pr}_M(x)\in {\rm Gr}_{M,\tilde {\mu }}$. Since ![]() $x\in {\rm Gr}_{G,\mu }$ we have
$x\in {\rm Gr}_{G,\mu }$ we have ![]() $\tilde {\mu }_{{\rm dom}}\leqslant \mu _{{\rm dom}}$. By [Reference ViehmannVie21, Lemma 3.10] we have for the slope vector
$\tilde {\mu }_{{\rm dom}}\leqslant \mu _{{\rm dom}}$. By [Reference ViehmannVie21, Lemma 3.10] we have for the slope vector ![]() $v'$ of
$v'$ of ![]() ${\mathcal {E}}_{1,x}$ that
${\mathcal {E}}_{1,x}$ that
Thus equality holds at each step. This implies that ![]() $v^{\sharp _M}=0$. Hence
$v^{\sharp _M}=0$. Hence ![]() ${\mathcal {E}}_1^P\times ^P M$ is the trivial
${\mathcal {E}}_1^P\times ^P M$ is the trivial ![]() $M$-bundle, and a reduction of
$M$-bundle, and a reduction of ![]() ${\mathcal {E}}_1^G$ to
${\mathcal {E}}_1^G$ to ![]() $M$. In particular, the reduction
$M$. In particular, the reduction ![]() ${\mathcal {E}}_{1,x}^P$ also corresponds to a reduction of
${\mathcal {E}}_{1,x}^P$ also corresponds to a reduction of ![]() $({\mathcal {E}}_1,x)$ to
$({\mathcal {E}}_1,x)$ to ![]() $P$, hence
$P$, hence ![]() ${\rm HN}({\mathcal {E}}_1,x)^{\sharp _M}\geqslant \nu _{b'}^{\sharp _M}$. Comparison with the Newton point of
${\rm HN}({\mathcal {E}}_1,x)^{\sharp _M}\geqslant \nu _{b'}^{\sharp _M}$. Comparison with the Newton point of ![]() ${\mathcal {E}}_{1,x}$ also shows
${\mathcal {E}}_{1,x}$ also shows ![]() ${\rm HN}({\mathcal {E}}_1,x)^{\sharp _M}\leqslant \nu _{b'}^{\sharp _M}$, hence the last assertion of (b).
${\rm HN}({\mathcal {E}}_1,x)^{\sharp _M}\leqslant \nu _{b'}^{\sharp _M}$, hence the last assertion of (b).
For quasi-split groups, assertion (c) is shown in [Reference ViehmannVie21, Proposition 7.8]. The general case is shown analogously, using the existence of ![]() $M$ and
$M$ and ![]() $P$ we proved above. A main ingredient of this proof and our proof of assertion (e) below is [Reference ViehmannVie21, Lemma 7.9]. Since for this lemma, the reformulation in the non-quasi-split case is not obvious, we prove its generalization to our context as Lemma 6.5 below.
$P$ we proved above. A main ingredient of this proof and our proof of assertion (e) below is [Reference ViehmannVie21, Lemma 7.9]. Since for this lemma, the reformulation in the non-quasi-split case is not obvious, we prove its generalization to our context as Lemma 6.5 below.
Let ![]() $P_x$ be the parabolic subgroup of
$P_x$ be the parabolic subgroup of ![]() $G$ corresponding to the canonical reduction of
$G$ corresponding to the canonical reduction of ![]() $({\mathcal {E}}_1,x)$, and let
$({\mathcal {E}}_1,x)$, and let ![]() $P_0\supseteq P_x$ be such that
$P_0\supseteq P_x$ be such that ![]() $P_0$ is conjugate to
$P_0$ is conjugate to ![]() $P$. Let
$P$. Let ![]() $M_0$ be its Levi quotient. For assertion (d) we have to show that
$M_0$ be its Levi quotient. For assertion (d) we have to show that ![]() ${\mathcal {E}}_{1,x}^{P_0}={\mathcal {E}}_{1,x}^P$ as reductions of
${\mathcal {E}}_{1,x}^{P_0}={\mathcal {E}}_{1,x}^P$ as reductions of ![]() ${\mathcal {E}}_{1,x}$. The reduction
${\mathcal {E}}_{1,x}$. The reduction ![]() ${\mathcal {E}}_{1,x}^{P_0}$ has a slope vector
${\mathcal {E}}_{1,x}^{P_0}$ has a slope vector ![]() $v_0$ whose image in
$v_0$ whose image in ![]() $\pi _1(M_0)_{\Gamma }$ corresponds to
$\pi _1(M_0)_{\Gamma }$ corresponds to ![]() $\kappa _M({\rm HN}({\mathcal {E}}_1,x))=\kappa _M(b'_M)$. Since
$\kappa _M({\rm HN}({\mathcal {E}}_1,x))=\kappa _M(b'_M)$. Since ![]() $P_0$ and
$P_0$ and ![]() $P$ are conjugate, the proof of (i) shows that there is a
$P$ are conjugate, the proof of (i) shows that there is a ![]() $b\in P_0(\breve {F})$ such that
$b\in P_0(\breve {F})$ such that ![]() $[b]\in B(G)$ is basic and such that
$[b]\in B(G)$ is basic and such that ![]() $G_b$ is quasi-split. Let
$G_b$ is quasi-split. Let ![]() $\tilde {{\mathcal {E}}}_{P_{0,b}}$ be the
$\tilde {{\mathcal {E}}}_{P_{0,b}}$ be the ![]() $P_{0,b}$-bundle corresponding to
$P_{0,b}$-bundle corresponding to ![]() ${\mathcal {E}}_{1,x}^{P_0}$, a reduction of the
${\mathcal {E}}_{1,x}^{P_0}$, a reduction of the ![]() $G_b$-bundle
$G_b$-bundle ![]() $\tilde {\mathcal {E}}$ corresponding to
$\tilde {\mathcal {E}}$ corresponding to ![]() ${\mathcal {E}}_{1,x}$. The above condition on
${\mathcal {E}}_{1,x}$. The above condition on ![]() $v_0$ then translates into the condition that
$v_0$ then translates into the condition that ![]() $\tilde {{\mathcal {E}}}_{P_{0,b}}$ satisfies the assumption of Theorem A.5. Since
$\tilde {{\mathcal {E}}}_{P_{0,b}}$ satisfies the assumption of Theorem A.5. Since ![]() $M$ contains the centralizer of
$M$ contains the centralizer of ![]() $\nu _{b'}$, the Theorem implies that
$\nu _{b'}$, the Theorem implies that ![]() $\tilde {{\mathcal {E}}}_{P_{0,b}}$ is a coarsening of the canonical reduction of
$\tilde {{\mathcal {E}}}_{P_{0,b}}$ is a coarsening of the canonical reduction of ![]() $\tilde E$, and as such uniquely defined by its slope vector. Twisting back via
$\tilde E$, and as such uniquely defined by its slope vector. Twisting back via ![]() $b^{-1}$, we obtain that
$b^{-1}$, we obtain that ![]() ${\mathcal {E}}_{1,x}^{P_0}$ indeed agrees with
${\mathcal {E}}_{1,x}^{P_0}$ indeed agrees with ![]() ${\mathcal {E}}_{1,x}^P$ as reductions of
${\mathcal {E}}_{1,x}^P$ as reductions of ![]() ${\mathcal {E}}_{1,x}$, which proves assertion (d).
${\mathcal {E}}_{1,x}$, which proves assertion (d).
Assertion (e) follows from Lemma 6.5.
Lemma 6.5 Let ![]() $P\subseteq G$ be a parabolic subgroup of
$P\subseteq G$ be a parabolic subgroup of ![]() $G$ and let
$G$ and let ![]() $M$ be a Levi factor. Let
$M$ be a Levi factor. Let ![]() $\mu \in X_*(M)$ be
$\mu \in X_*(M)$ be ![]() $P$-dominant. Let
$P$-dominant. Let ![]() $U$ be the unipotent radical of
$U$ be the unipotent radical of ![]() $P$. Let
$P$. Let ![]() $\lambda \in X_*(M)$ with
$\lambda \in X_*(M)$ with ![]() $\lambda ^{\sharp _M}=\mu ^{\sharp _M}\in \pi _1(M)_{\Gamma }$. Then
$\lambda ^{\sharp _M}=\mu ^{\sharp _M}\in \pi _1(M)_{\Gamma }$. Then
This lemma and its proof are a generalization of corresponding results for unramified groups in [Reference KottwitzKot03].
Proof. The left hand side is empty unless ![]() $\lambda _{{\rm dom}}\leqslant \mu _{{\rm dom}}$, so we assume this.
$\lambda _{{\rm dom}}\leqslant \mu _{{\rm dom}}$, so we assume this.
Claim. We have ![]() $\lambda ^{\sharp _M}=\mu ^{\sharp _M}\in \pi _1(M)$, without taking coinvariants.
$\lambda ^{\sharp _M}=\mu ^{\sharp _M}\in \pi _1(M)$, without taking coinvariants.
We compute the fundamental groups with respect to a maximal torus of ![]() $M_{\overline {F}}$ and a Borel subgroup
$M_{\overline {F}}$ and a Borel subgroup ![]() $B\subseteq P_{\overline {F}}$. Let
$B\subseteq P_{\overline {F}}$. Let ![]() $\pi _1(G,M)$ be the kernel of the natural projection
$\pi _1(G,M)$ be the kernel of the natural projection ![]() $\pi _1(M)\rightarrow \pi _1(G)$. In other words, we have a short exact sequence
$\pi _1(M)\rightarrow \pi _1(G)$. In other words, we have a short exact sequence
Taking coinvariants, we get an exact sequence
The group ![]() $\pi _1(G,M)$ is a free abelian group generated by the images in
$\pi _1(G,M)$ is a free abelian group generated by the images in ![]() $\pi _1(M)$ of the simple roots of
$\pi _1(M)$ of the simple roots of ![]() $T$ in
$T$ in ![]() $U$. Since
$U$. Since ![]() $P$,
$P$, ![]() $M$ and
$M$ and ![]() $U$ are
$U$ are ![]() $\Gamma$-invariant,
$\Gamma$-invariant, ![]() $\pi _1(G,M)_{\Gamma }$ is a free abelian group generated by the set of
$\pi _1(G,M)_{\Gamma }$ is a free abelian group generated by the set of ![]() $\Gamma$-orbits on the above set of generators of
$\Gamma$-orbits on the above set of generators of ![]() $\pi _1(G,M)$, which are permuted under the action of
$\pi _1(G,M)$, which are permuted under the action of ![]() $\Gamma$. Thus
$\Gamma$. Thus ![]() $\pi _1(G,M)_{\Gamma }$ is torsion-free, and maps injectively to
$\pi _1(G,M)_{\Gamma }$ is torsion-free, and maps injectively to ![]() $\pi _1(M)_{\Gamma }$.
$\pi _1(M)_{\Gamma }$.
From ![]() $\lambda _{{\rm dom}}\leqslant \mu _{{\rm dom}}$ and the fact that
$\lambda _{{\rm dom}}\leqslant \mu _{{\rm dom}}$ and the fact that ![]() $\mu$ is
$\mu$ is ![]() $P$-dominant, we obtain that
$P$-dominant, we obtain that ![]() $(\mu -\lambda )^{\sharp _M}\in \pi _1(M)$ is the image of a non-negative linear combination of positive coroots. In particular, it lies in the subgroup
$(\mu -\lambda )^{\sharp _M}\in \pi _1(M)$ is the image of a non-negative linear combination of positive coroots. In particular, it lies in the subgroup ![]() $\pi _1(G,M)$. We consider its image in
$\pi _1(G,M)$. We consider its image in ![]() $\pi _1(G,M)_{\Gamma }$. Any non-negative linear combination of positive coroots in
$\pi _1(G,M)_{\Gamma }$. Any non-negative linear combination of positive coroots in ![]() $U$ is mapped to a similar linear combination in
$U$ is mapped to a similar linear combination in ![]() $\pi _1(G,M)_{\Gamma }$, and the image of
$\pi _1(G,M)_{\Gamma }$, and the image of ![]() $(\mu -\lambda )^{\sharp _M}$ vanishes if and only if
$(\mu -\lambda )^{\sharp _M}$ vanishes if and only if ![]() $(\mu -\lambda )^{\sharp _M}$ itself is
$(\mu -\lambda )^{\sharp _M}$ itself is ![]() $0$ in
$0$ in ![]() $\pi _1(G,M)$. We assumed that
$\pi _1(G,M)$. We assumed that ![]() $(\mu -\lambda )^{\sharp _M}$ is mapped to
$(\mu -\lambda )^{\sharp _M}$ is mapped to ![]() $0$ under
$0$ under ![]() $\pi _1(G,M)_{\Gamma }\hookrightarrow \pi _1(M)_{\Gamma }$. Hence
$\pi _1(G,M)_{\Gamma }\hookrightarrow \pi _1(M)_{\Gamma }$. Hence ![]() $(\mu -\lambda )^{\sharp _M}=0$ in
$(\mu -\lambda )^{\sharp _M}=0$ in ![]() $\pi _1(M)$. This finishes the proof of the claim.
$\pi _1(M)$. This finishes the proof of the claim.
The remainder of the assertion not involving a Galois action, we may base change to ![]() $\overline {F}$, and apply [Reference KottwitzKot03, Lemma 2.2] and its proof to conclude as in the case for split groups.
$\overline {F}$, and apply [Reference KottwitzKot03, Lemma 2.2] and its proof to conclude as in the case for split groups.
From the theorem we obtain that the inclusion ![]() $M\hookrightarrow G$ induces natural maps
$M\hookrightarrow G$ induces natural maps
and, for ![]() $[b'']_M={\rm HN}({\mathcal {E}}_1^M,x_M)$,
$[b'']_M={\rm HN}({\mathcal {E}}_1^M,x_M)$,
that are bijections, and that are sections of the corresponding restrictions of ![]() ${\rm pr}_{M}$.
${\rm pr}_{M}$.
Corollary 6.6 Let ![]() $x\in {\rm Gr}_{G,\mu }(C)$. Then
$x\in {\rm Gr}_{G,\mu }(C)$. Then ![]() $\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x})^*\in B(G,\mu )$ is Hodge–Newton decomposable for some Levi
$\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x})^*\in B(G,\mu )$ is Hodge–Newton decomposable for some Levi ![]() $M'$ if and only if
$M'$ if and only if ![]() ${\rm HN}({\mathcal {E}}_1,x)\in B(G,\mu )$ is Hodge–Newton decomposable for
${\rm HN}({\mathcal {E}}_1,x)\in B(G,\mu )$ is Hodge–Newton decomposable for ![]() $M'$.
$M'$.
Proof. Assume that ![]() ${\rm HN}({\mathcal {E}}_1,x)\in B(G,\mu )$ is Hodge–Newton decomposable for
${\rm HN}({\mathcal {E}}_1,x)\in B(G,\mu )$ is Hodge–Newton decomposable for ![]() $M'$. Then
$M'$. Then ![]() ${\rm HN}({\mathcal {E}}_1,x)\leqslant \mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x})^*\leqslant [\mu (\xi )]$ where the Newton point of
${\rm HN}({\mathcal {E}}_1,x)\leqslant \mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x})^*\leqslant [\mu (\xi )]$ where the Newton point of ![]() $\mu (\xi )$ is
$\mu (\xi )$ is ![]() $\mu ^{\diamond }$. In other words,
$\mu ^{\diamond }$. In other words, ![]() $\mu ^{\diamond }-{\rm HN}({\mathcal {E}}_1,x)$ is a non-negative rational linear combination of positive coroots of
$\mu ^{\diamond }-{\rm HN}({\mathcal {E}}_1,x)$ is a non-negative rational linear combination of positive coroots of ![]() $M'$. We have a decomposition of
$M'$. We have a decomposition of ![]() $\mu ^{\diamond }-{\rm HN}({\mathcal {E}}_1,x)$ into a sum of
$\mu ^{\diamond }-{\rm HN}({\mathcal {E}}_1,x)$ into a sum of ![]() $\mu ^{\diamond }-\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x})^*$ and
$\mu ^{\diamond }-\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x})^*$ and ![]() $\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x})^*-{\rm HN}({\mathcal {E}}_1,x)$, both of which are non-negative rational linear combinations of positive coroots of
$\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x})^*-{\rm HN}({\mathcal {E}}_1,x)$, both of which are non-negative rational linear combinations of positive coroots of ![]() $G$. Thus both summands are non-negative rational linear combinations of positive coroots of
$G$. Thus both summands are non-negative rational linear combinations of positive coroots of ![]() $M'$, which implies that
$M'$, which implies that ![]() $\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x})^*$ is also Hodge–Newton decomposable for
$\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x})^*$ is also Hodge–Newton decomposable for ![]() $M'$. The other direction follows from Theorem 6.4(ii)(b).
$M'$. The other direction follows from Theorem 6.4(ii)(b).
The following Corollary is a generalization of [Reference FarguesFar19, Conjecture 1(2)].
Corollary 6.7 Let ![]() $[b']\in B(G,\mu )$ be Hodge–Newton decomposable with respect to the Levi subgroup
$[b']\in B(G,\mu )$ be Hodge–Newton decomposable with respect to the Levi subgroup ![]() $M'$ that is the centralizer of
$M'$ that is the centralizer of ![]() $\nu _{b'}$ in the quasi-split inner form of
$\nu _{b'}$ in the quasi-split inner form of ![]() $G$. Then
$G$. Then
For the maximal element ![]() $[\mu (\xi )]$ of
$[\mu (\xi )]$ of ![]() $B(G,\mu )$, we have equality in (6.5).
$B(G,\mu )$, we have equality in (6.5).
Proof. Let ![]() $x\in {\rm Gr}_{G,\mu }^{[b']^*}(C).$ From the theorem we obtain a parabolic subgroup
$x\in {\rm Gr}_{G,\mu }^{[b']^*}(C).$ From the theorem we obtain a parabolic subgroup ![]() $P$ with Levi subgroup
$P$ with Levi subgroup ![]() $M$ such that
$M$ such that ![]() $M$ is an inner form of
$M$ is an inner form of ![]() $M'$ and
$M'$ and ![]() $x_M={\rm pr}_M(x)$ such that both
$x_M={\rm pr}_M(x)$ such that both ![]() ${\rm HN}({\mathcal {E}}_{1},x)$ and the Newton point of
${\rm HN}({\mathcal {E}}_{1},x)$ and the Newton point of ![]() ${\mathcal {E}}_{1,x}$ can be computed from the corresponding invariants for
${\mathcal {E}}_{1,x}$ can be computed from the corresponding invariants for ![]() $({\mathcal {E}}_1^M,x_M)$. Because
$({\mathcal {E}}_1^M,x_M)$. Because ![]() $M'$ is the centralizer of the Newton point of
$M'$ is the centralizer of the Newton point of ![]() $[b']$, we obtain that
$[b']$, we obtain that ![]() ${\mathcal {E}}_{1,x_M}^M$ is semi-stable, or in other words in the basic Newton stratum. Then by (6.1) together with minimality of the basic Newton point we obtain that
${\mathcal {E}}_{1,x_M}^M$ is semi-stable, or in other words in the basic Newton stratum. Then by (6.1) together with minimality of the basic Newton point we obtain that ![]() ${\rm HN}({\mathcal {E}}_1^M,x_M)=[b'_M]$, which finishes the proof of (6.5).
${\rm HN}({\mathcal {E}}_1^M,x_M)=[b'_M]$, which finishes the proof of (6.5).
Now let ![]() $[b']$ be maximal in
$[b']$ be maximal in ![]() $B(G,\mu )$. Then
$B(G,\mu )$. Then ![]() $[b']=[\mu (\xi )]$ clearly satisfies the assumption of the first assertion of the corollary. It remains to show that the reverse containment in (6.5) also holds for this
$[b']=[\mu (\xi )]$ clearly satisfies the assumption of the first assertion of the corollary. It remains to show that the reverse containment in (6.5) also holds for this ![]() $[b']$. But this follows immediately from (6.3) together with the maximality of
$[b']$. But this follows immediately from (6.3) together with the maximality of ![]() $[b']$.
$[b']$.
Our next result proves [Reference FarguesFar19, Conjecture 1(1)].
Proposition 6.8 The following are equivalent.
(i) The Newton stratification and the Harder–Narasimhan stratification on
 ${\rm Gr}_{G,\mu,1}$ coincide.
${\rm Gr}_{G,\mu,1}$ coincide.(ii) The basic Newton stratum in
 ${\rm Gr}_{G,\mu,1}$ agrees with the weakly admissible locus.
${\rm Gr}_{G,\mu,1}$ agrees with the weakly admissible locus.(iii)
 $(G,\mu )$ is fully Hodge–Newton decomposable in the sense of [Reference Görtz, He and NieGHN19, Definition 3.1].
$(G,\mu )$ is fully Hodge–Newton decomposable in the sense of [Reference Görtz, He and NieGHN19, Definition 3.1].
There are several characterizations of being fully Hodge–Newton decomposable. For example, ![]() $(G,\mu )$ is fully Hodge–Newton decomposable if and only if every non-basic
$(G,\mu )$ is fully Hodge–Newton decomposable if and only if every non-basic ![]() $[b']\in B(G,\mu )$ is Hodge–Newton decomposable.
$[b']\in B(G,\mu )$ is Hodge–Newton decomposable.
Proof. Clearly (i) implies (ii). The proof that (ii) implies (iii) is almost literally the same as in the minuscule case, compare [Reference Chen, Fargues and ShenCFS21, 6], the only difference being that one has to replace the flag varieties by affine Schubert cells in the ![]() ${B^+_{{\rm dR}}}$-Grassmannian. For more details, compare [Reference ShenShe19, 6.7].
${B^+_{{\rm dR}}}$-Grassmannian. For more details, compare [Reference ShenShe19, 6.7].
It remains to show that (iii) implies (ii).
Claim. If ![]() $(G,\mu )$ is fully Hodge–Newton decomposable, then every non-basic
$(G,\mu )$ is fully Hodge–Newton decomposable, then every non-basic ![]() $[b']\in B(G,\mu )$ is Hodge–Newton decomposable with respect to
$[b']\in B(G,\mu )$ is Hodge–Newton decomposable with respect to ![]() $M'$ where
$M'$ where ![]() $M'$ is equal to the centralizer of
$M'$ is equal to the centralizer of ![]() $\nu _{b'}$ in the quasi-split inner form
$\nu _{b'}$ in the quasi-split inner form ![]() $H$ of
$H$ of ![]() $G$.
$G$.
Since the claim is an assertion only involving the Newton points of elements of ![]() $B(G,\mu )$, we may replace
$B(G,\mu )$, we may replace ![]() $G$ by the quasi-split inner form of its adjoint group and thus assume that
$G$ by the quasi-split inner form of its adjoint group and thus assume that ![]() $G$ is quasi-split. Assume that there is some
$G$ is quasi-split. Assume that there is some ![]() $[b']\in B(G,\mu )$ that does not satisfy the assertion of the claim. Let
$[b']\in B(G,\mu )$ that does not satisfy the assertion of the claim. Let ![]() $M'$ be the centralizer of the dominant Newton point of
$M'$ be the centralizer of the dominant Newton point of ![]() $[b']$ and choose a corresponding representative
$[b']$ and choose a corresponding representative ![]() $b'\in M'(\breve {F})\cap [b']$. Then
$b'\in M'(\breve {F})\cap [b']$. Then ![]() $\mu _{{\rm dom}}-\nu _{b'}\notin \Phi _{M'}$. Let
$\mu _{{\rm dom}}-\nu _{b'}\notin \Phi _{M'}$. Let ![]() $\alpha$ be a simple root of
$\alpha$ be a simple root of ![]() $G$ such that
$G$ such that ![]() $\mu _{{\rm dom}}-\nu _{b'}\notin \Phi _{M_{\alpha }}$ where
$\mu _{{\rm dom}}-\nu _{b'}\notin \Phi _{M_{\alpha }}$ where ![]() $M_{\alpha }$ is the standard Levi subgroup of the maximal standard parabolic corresponding to
$M_{\alpha }$ is the standard Levi subgroup of the maximal standard parabolic corresponding to ![]() $\alpha$. Then
$\alpha$. Then ![]() $\kappa _{M_{\alpha }}(b')\neq \mu ^{\sharp _{M_{\alpha }}}$. Let
$\kappa _{M_{\alpha }}(b')\neq \mu ^{\sharp _{M_{\alpha }}}$. Let ![]() $b_0$ be basic in
$b_0$ be basic in ![]() $M_{\alpha }$ and with
$M_{\alpha }$ and with ![]() $\kappa _{M_{\alpha }}(b_0)=\kappa _{M_{\alpha }}(b')$. Then
$\kappa _{M_{\alpha }}(b_0)=\kappa _{M_{\alpha }}(b')$. Then ![]() $[b_0]\leqslant [b']$, hence
$[b_0]\leqslant [b']$, hence ![]() $b_0\in B(G,\mu )$. Furthermore,
$b_0\in B(G,\mu )$. Furthermore, ![]() $M_{\alpha }$ is the centralizer of
$M_{\alpha }$ is the centralizer of ![]() $\nu _{b_0}$. Because
$\nu _{b_0}$. Because ![]() $\kappa _{M_{\alpha }}(b_0)\neq \mu ^{\sharp _{M_{\alpha }}}$ and
$\kappa _{M_{\alpha }}(b_0)\neq \mu ^{\sharp _{M_{\alpha }}}$ and ![]() $M_{\alpha }$ is maximal, it is not Hodge–Newton decomposable. Thus
$M_{\alpha }$ is maximal, it is not Hodge–Newton decomposable. Thus ![]() $(G,\mu )$ is not fully Hodge–Newton decomposable, which finishes the proof of the claim.
$(G,\mu )$ is not fully Hodge–Newton decomposable, which finishes the proof of the claim.
From Corollary 6.7 we obtain that ![]() ${\rm Gr}_{G,\mu,1}^{[b']^*}\subseteq {\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$ for all
${\rm Gr}_{G,\mu,1}^{[b']^*}\subseteq {\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$ for all ![]() $[b']\in B(G,\mu )$. Thus we also have equality in these containments.
$[b']\in B(G,\mu )$. Thus we also have equality in these containments.
Our last result in this context classifies all ![]() $[b']$ for which the corresponding Newton stratum and Harder–Narasimhan stratum coincide.
$[b']$ for which the corresponding Newton stratum and Harder–Narasimhan stratum coincide.
Remark 6.9 Let ![]() $x\in {\rm Gr}_{G,\mu }(C)$. Recall from Corollary 6.6 that
$x\in {\rm Gr}_{G,\mu }(C)$. Recall from Corollary 6.6 that ![]() $(\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x}))^*$ is Hodge–Newton decomposable for some
$(\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x}))^*$ is Hodge–Newton decomposable for some ![]() $M'$ (with respect to
$M'$ (with respect to ![]() $(G,\mu )$) if and only if the same holds for
$(G,\mu )$) if and only if the same holds for ![]() ${\rm HN}({\mathcal {E}}_1,x)$. Let
${\rm HN}({\mathcal {E}}_1,x)$. Let ![]() $M'$ be the smallest Levi subgroup of the quasi-split inner form of
$M'$ be the smallest Levi subgroup of the quasi-split inner form of ![]() $G$ for which this is the case, and let
$G$ for which this is the case, and let ![]() $M$ and
$M$ and ![]() $x_M$ be as in Theorem 6.4. Then by the theorem,
$x_M$ be as in Theorem 6.4. Then by the theorem, ![]() $(\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x}))^*={\rm HN}({\mathcal {E}}_1,x)$ if and only if
$(\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x}))^*={\rm HN}({\mathcal {E}}_1,x)$ if and only if ![]() $\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x_M}^M)^*={\rm HN}({\mathcal {E}}_1^M,x_M)$. Thus, it is enough consider equality of Newton strata and Harder–Narasimhan strata for Hodge–Newton indecomposable
$\mathop {\mathrm {Newt}}\nolimits ({\mathcal {E}}_{1,x_M}^M)^*={\rm HN}({\mathcal {E}}_1^M,x_M)$. Thus, it is enough consider equality of Newton strata and Harder–Narasimhan strata for Hodge–Newton indecomposable ![]() $[b']$.
$[b']$.
Corollary 6.10 Let ![]() $[b']\in B(G,\mu )$. Assume that
$[b']\in B(G,\mu )$. Assume that ![]() $([b'],\mu )$ is Hodge–Newton indecomposable and that
$([b'],\mu )$ is Hodge–Newton indecomposable and that ![]() $\mu$ is minuscule. Then
$\mu$ is minuscule. Then ![]() ${\rm Gr}_{G,\mu }^{[b']^{*}}={\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$ if and only if
${\rm Gr}_{G,\mu }^{[b']^{*}}={\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$ if and only if ![]() $(G,\mu )$ is fully Hodge–Newton decomposable and
$(G,\mu )$ is fully Hodge–Newton decomposable and ![]() $[b']\in B(G,\mu )$ is the basic class.
$[b']\in B(G,\mu )$ is the basic class.
Proof. If ![]() $(G,\mu )$ is fully Hodge–Newton decomposable and
$(G,\mu )$ is fully Hodge–Newton decomposable and ![]() $[b']\in B(G,\mu )$ is the basic class, then
$[b']\in B(G,\mu )$ is the basic class, then ![]() ${\rm Gr}_{G,\mu }^{[b']^*}={\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$ by Proposition 6.8. Assume that
${\rm Gr}_{G,\mu }^{[b']^*}={\rm Gr}_{G,\mu }^{{\rm HN}=[b']}$ by Proposition 6.8. Assume that ![]() $(G,\mu )$ is not fully Hodge–Newton decomposable. Then by [Reference ViehmannVie21, Theorem 1.3], every Hodge–Newton indecomposable Newton stratum intersects the basic Harder–Narasimhan stratum, which proves the other implication.
$(G,\mu )$ is not fully Hodge–Newton decomposable. Then by [Reference ViehmannVie21, Theorem 1.3], every Hodge–Newton indecomposable Newton stratum intersects the basic Harder–Narasimhan stratum, which proves the other implication.
7. Dimensions of strata
For this section we assume that ![]() $\mu$ is minuscule. For this case, we have the comparison to the Harder–Narasimhan strata of [Reference Dat, Orlik and RapoportDOR10]. Since little is known about the geometric properties of the Harder–Narasimhan strata of [Reference Dat, Orlik and RapoportDOR10], our results also give new insight for this more classical theory.
$\mu$ is minuscule. For this case, we have the comparison to the Harder–Narasimhan strata of [Reference Dat, Orlik and RapoportDOR10]. Since little is known about the geometric properties of the Harder–Narasimhan strata of [Reference Dat, Orlik and RapoportDOR10], our results also give new insight for this more classical theory.
Proposition 7.1 Assume that ![]() $\mu$ is minuscule, and let
$\mu$ is minuscule, and let ![]() $[b']\in B(G,\mu )_{{\rm HN}}$. Then
$[b']\in B(G,\mu )_{{\rm HN}}$. Then
Here, we identify ![]() $\lambda$ with its
$\lambda$ with its ![]() $M_{b'}$-dominant representative in
$M_{b'}$-dominant representative in ![]() $X_*(T)$ and
$X_*(T)$ and ![]() $\mu$ is the representative in
$\mu$ is the representative in ![]() $X_*(T)_{{\rm dom}}$. Further,
$X_*(T)_{{\rm dom}}$. Further, ![]() $\rho$ is the half-sum of the positive roots of
$\rho$ is the half-sum of the positive roots of ![]() $T$ in
$T$ in ![]() $H$.
$H$.
Proof. From Remark 4.4 we obtain that
Since ![]() $\mu$ is minuscule,
$\mu$ is minuscule, ![]() $\lambda \in \{-\mu \}$. To compute the dimension of the right hand side we may base change to
$\lambda \in \{-\mu \}$. To compute the dimension of the right hand side we may base change to ![]() $\overline {F}$. The above claim is then obtained from the well-known formulas for the dimension of Bruhat cells in flag varieties.
$\overline {F}$. The above claim is then obtained from the well-known formulas for the dimension of Bruhat cells in flag varieties.
Remark 7.2 (i) So far, there is no formula for the dimension of intersections ![]() $S_{\lambda }\cap {\rm Gr}_{G,\mu }$ in the
$S_{\lambda }\cap {\rm Gr}_{G,\mu }$ in the ![]() ${B^+_{{\rm dR}}}$-Grassmannian. For the usual affine Grassmannian over
${B^+_{{\rm dR}}}$-Grassmannian. For the usual affine Grassmannian over ![]() $\mathbb {C}$, the analogous intersections (for
$\mathbb {C}$, the analogous intersections (for ![]() $P$ equal to a chosen Borel subgroup of
$P$ equal to a chosen Borel subgroup of ![]() $G$ and
$G$ and ![]() $\mu$ the dominant representative of
$\mu$ the dominant representative of ![]() $\{\mu \}$) are of dimension
$\{\mu \}$) are of dimension ![]() $\langle 2\rho, \mu +\lambda \rangle$. In view of this formula, we expect that if one can establish a similar dimension theory for the
$\langle 2\rho, \mu +\lambda \rangle$. In view of this formula, we expect that if one can establish a similar dimension theory for the ![]() ${B^+_{{\rm dR}}}$-Grassmannian, then also
${B^+_{{\rm dR}}}$-Grassmannian, then also ![]() ${\rm dim}\, {\rm Gr}_{G,\mu }^{{\rm HN}=[b']}\leqslant \max _{\lambda \in \Theta (\mu,[b'])}\langle 2\rho,\mu +\lambda \rangle$.
${\rm dim}\, {\rm Gr}_{G,\mu }^{{\rm HN}=[b']}\leqslant \max _{\lambda \in \Theta (\mu,[b'])}\langle 2\rho,\mu +\lambda \rangle$.
(ii) It would be interesting to know it equality holds in the above dimension estimate.
In [Reference FarguesFar19, Conjecture 2(2)], Fargues conjectured that the dimension of a Harder–Narasimhan stratum should agree with the dimension of the corresponding Newton stratum, which is by [Reference Fargues and ScholzeFS21, IV.1] given by ![]() $\langle 2\rho,\mu -\nu _{b'}\rangle$. Our next result is a classification of all
$\langle 2\rho,\mu -\nu _{b'}\rangle$. Our next result is a classification of all ![]() $[b']\in B(G,\mu )_{{\rm HN}}$ for which this is the case. In particular, we show that Fargues’ conjectural dimension formula only holds in exceptional cases.
$[b']\in B(G,\mu )_{{\rm HN}}$ for which this is the case. In particular, we show that Fargues’ conjectural dimension formula only holds in exceptional cases.
Proposition 7.3 Let ![]() $\mu$ be minuscule and
$\mu$ be minuscule and ![]() $[b']\in B(G,\mu )_{{\rm HN}}$. Then
$[b']\in B(G,\mu )_{{\rm HN}}$. Then
with equality if and only if ![]() $[b']$ is basic in the smallest Levi subgroup to which
$[b']$ is basic in the smallest Levi subgroup to which ![]() $(G,\mu,[b'])$ is Hodge–Newton decomposable.
$(G,\mu,[b'])$ is Hodge–Newton decomposable.
Proof. Let ![]() $M$ be the smallest standard Levi subgroup of
$M$ be the smallest standard Levi subgroup of ![]() $G$ such that
$G$ such that ![]() $(G,\mu,[b'])$ is Hodge–Newton decomposable with respect to
$(G,\mu,[b'])$ is Hodge–Newton decomposable with respect to ![]() $M$. By Remark 6.9, Theorem 6.4 and the Bialynicki-Birula isomorphism, the projection
$M$. By Remark 6.9, Theorem 6.4 and the Bialynicki-Birula isomorphism, the projection ![]() ${\mathcal {F}\ell }(G,\mu )\rightarrow {\mathcal {F}\ell }(M,\mu )$ induces bijections
${\mathcal {F}\ell }(G,\mu )\rightarrow {\mathcal {F}\ell }(M,\mu )$ induces bijections ![]() ${\mathcal {F}\ell }(G,\mu )^{[b']^*}(C)\rightarrow {\mathcal {F}\ell }(M,\mu )^{[b'_M]_M^{*}}(C)$ and
${\mathcal {F}\ell }(G,\mu )^{[b']^*}(C)\rightarrow {\mathcal {F}\ell }(M,\mu )^{[b'_M]_M^{*}}(C)$ and ![]() ${\mathcal {F}\ell }(G,\mu )^{{\rm HN}=[b']}(C)\rightarrow {\mathcal {F}\ell }(M,\mu )^{{\rm HN}=[b'_M]_M}(C)$. In particular, the dimensions of corresponding strata coincide. Thus we may assume that
${\mathcal {F}\ell }(G,\mu )^{{\rm HN}=[b']}(C)\rightarrow {\mathcal {F}\ell }(M,\mu )^{{\rm HN}=[b'_M]_M}(C)$. In particular, the dimensions of corresponding strata coincide. Thus we may assume that ![]() $M=G$ and that
$M=G$ and that ![]() $(G,\mu,[b'])$ is Hodge–Newton indecomposable.
$(G,\mu,[b'])$ is Hodge–Newton indecomposable.
If ![]() $[b']$ is basic, then
$[b']$ is basic, then ![]() ${\mathcal {F}\ell }(G,\mu )^{[b']^*}\subseteq {\mathcal {F}\ell }(G,\mu )^{{\rm HN}=[b']}\subseteq {\mathcal {F}\ell }(G,\mu )$. Since the dimension of the basic Newton stratum agrees with that of
${\mathcal {F}\ell }(G,\mu )^{[b']^*}\subseteq {\mathcal {F}\ell }(G,\mu )^{{\rm HN}=[b']}\subseteq {\mathcal {F}\ell }(G,\mu )$. Since the dimension of the basic Newton stratum agrees with that of ![]() ${\mathcal {F}\ell }(G,\mu )$, the same holds for the basic Harder–Narasimhan stratum.
${\mathcal {F}\ell }(G,\mu )$, the same holds for the basic Harder–Narasimhan stratum.
Now assume that ![]() $[b']$ is non-basic. Let
$[b']$ is non-basic. Let ![]() $M$ be the centralizer of its Newton point. From [Reference Fargues and ScholzeFS21, III.5] we obtain that
$M$ be the centralizer of its Newton point. From [Reference Fargues and ScholzeFS21, III.5] we obtain that ![]() ${\rm dim}\, {\mathcal {F}\ell }(G,\mu )^{[b']^*}=\langle 2\rho, \mu -\nu _{[b']^*,{\rm dom}}\rangle =\langle 2\rho, \mu -\nu _{b',{\rm dom}}\rangle$ where we write
${\rm dim}\, {\mathcal {F}\ell }(G,\mu )^{[b']^*}=\langle 2\rho, \mu -\nu _{[b']^*,{\rm dom}}\rangle =\langle 2\rho, \mu -\nu _{b',{\rm dom}}\rangle$ where we write ![]() $\mu$ for the representative of
$\mu$ for the representative of ![]() $\{\mu \}$ in
$\{\mu \}$ in ![]() $X_*(T)_{{\rm dom}}$. By the above proposition we have
$X_*(T)_{{\rm dom}}$. By the above proposition we have ![]() ${\rm dim}\, {\mathcal {F}\ell }(G,\mu )^{{\rm HN}=[b']}\leqslant \langle \rho, \mu +\lambda \rangle$ for some
${\rm dim}\, {\mathcal {F}\ell }(G,\mu )^{{\rm HN}=[b']}\leqslant \langle \rho, \mu +\lambda \rangle$ for some ![]() $\lambda \in \{-\mu \}$ with
$\lambda \in \{-\mu \}$ with ![]() $-\lambda \leqslant _{M} \nu _{b'}$ and
$-\lambda \leqslant _{M} \nu _{b'}$ and ![]() $\kappa _M(b')=-\lambda ^{\sharp _M}$. Using that
$\kappa _M(b')=-\lambda ^{\sharp _M}$. Using that ![]() $\nu _{b'}$ is central in
$\nu _{b'}$ is central in ![]() $M$ we obtain
$M$ we obtain
 \begin{align*} {\rm dim}\, {\mathcal{F}\ell}(G,\mu)^{[b']^*}-{\rm dim}\, {\mathcal{F}\ell}(G,\mu)^{{\rm HN}=[b']}&\geqslant\langle 2\rho, \mu-\nu_{b'}\rangle-\langle \rho, \mu+\lambda\rangle\\ &=\langle \rho, \mu-\nu_{b'}\rangle-\langle \rho, \lambda+\nu_{b'}\rangle\\ &=\langle \rho, \mu-\nu_{b'}\rangle-\langle \rho_M, \lambda+\nu_{b'}\rangle\\ &=\langle \rho, \mu-\nu_{b'}\rangle-\langle \rho_M, -w_{0,M}(\lambda)-\nu_{b'}\rangle\\ &=\langle \rho, \mu-\nu_{b'}\rangle-\langle \rho, -w_{0,M}(\lambda)-\nu_{b'}\rangle\\ &=\langle \rho, \mu-w_{0,M}(-\lambda)\rangle. \end{align*}
\begin{align*} {\rm dim}\, {\mathcal{F}\ell}(G,\mu)^{[b']^*}-{\rm dim}\, {\mathcal{F}\ell}(G,\mu)^{{\rm HN}=[b']}&\geqslant\langle 2\rho, \mu-\nu_{b'}\rangle-\langle \rho, \mu+\lambda\rangle\\ &=\langle \rho, \mu-\nu_{b'}\rangle-\langle \rho, \lambda+\nu_{b'}\rangle\\ &=\langle \rho, \mu-\nu_{b'}\rangle-\langle \rho_M, \lambda+\nu_{b'}\rangle\\ &=\langle \rho, \mu-\nu_{b'}\rangle-\langle \rho_M, -w_{0,M}(\lambda)-\nu_{b'}\rangle\\ &=\langle \rho, \mu-\nu_{b'}\rangle-\langle \rho, -w_{0,M}(\lambda)-\nu_{b'}\rangle\\ &=\langle \rho, \mu-w_{0,M}(-\lambda)\rangle. \end{align*}
Since ![]() $-\lambda \in W.\mu$, this pairing is non-negative with equality if and only if
$-\lambda \in W.\mu$, this pairing is non-negative with equality if and only if ![]() $w_{0,M}(-\lambda )=\mu$. However, this implies that
$w_{0,M}(-\lambda )=\mu$. However, this implies that ![]() $\kappa _M(b')=-\lambda ^{\sharp _M}=\mu ^{\sharp _M},$ in contradiction to the Hodge–Newton indecomposability of
$\kappa _M(b')=-\lambda ^{\sharp _M}=\mu ^{\sharp _M},$ in contradiction to the Hodge–Newton indecomposability of ![]() $(G,\mu,[b'])$.
$(G,\mu,[b'])$.
8. Compatibilities under inner twists
In this section we explain how to generalize our results to the case of modifications of a ![]() $G$-bundle
$G$-bundle ![]() ${\mathcal {E}}_b$ for some basic
${\mathcal {E}}_b$ for some basic ![]() $b\in G(\breve {F})$ instead of the trivial bundle
$b\in G(\breve {F})$ instead of the trivial bundle ![]() ${\mathcal {E}}_1$, and discuss the relation to inner twists of
${\mathcal {E}}_1$, and discuss the relation to inner twists of ![]() $G$.
$G$.
Recall from Lemma 3.16 that there is a direct comparison between the Harder–Narasimhan stratification of the ![]() ${B^+_{{\rm dR}}}$-Grassmannian for
${B^+_{{\rm dR}}}$-Grassmannian for ![]() $G$ and that for
$G$ and that for ![]() $G_{{\rm {ad}}}$. Replacing
$G_{{\rm {ad}}}$. Replacing ![]() $G$ by its adjoint group we obtain that each inner form of
$G$ by its adjoint group we obtain that each inner form of ![]() $G$ is an inner twist by some basic element
$G$ is an inner twist by some basic element ![]() $b\in G(\breve {F})$.
$b\in G(\breve {F})$.
Let ![]() $b\in G(\breve {F})$ be basic. By
$b\in G(\breve {F})$ be basic. By ![]() $G_b$ we denote corresponding the inner form of
$G_b$ we denote corresponding the inner form of ![]() $G$. We consider the isomorphism
$G$. We consider the isomorphism ![]() ${\rm Bun}_G\cong {\rm Bun}_{G_b}$ that maps any
${\rm Bun}_G\cong {\rm Bun}_{G_b}$ that maps any ![]() $G$-bundle
$G$-bundle ![]() ${\mathcal {E}}$ to the
${\mathcal {E}}$ to the ![]() $G_b$-bundle of isomorphisms
$G_b$-bundle of isomorphisms ![]() $\mathcal {I}som_{G}({\mathcal {E}}_b,{\mathcal {E}})$. Here,
$\mathcal {I}som_{G}({\mathcal {E}}_b,{\mathcal {E}})$. Here, ![]() ${\mathcal {E}}_b$ is the
${\mathcal {E}}_b$ is the ![]() $G$-bundle corresponding to
$G$-bundle corresponding to ![]() $b$. In particular, this identifies
$b$. In particular, this identifies ![]() ${\mathcal {E}}_b={\mathcal {E}}_b^{G}$ with the trivial
${\mathcal {E}}_b={\mathcal {E}}_b^{G}$ with the trivial ![]() $G_b$-bundle
$G_b$-bundle ![]() ${\mathcal {E}}_1^{G_b}$. For an explicit description in terms of
${\mathcal {E}}_1^{G_b}$. For an explicit description in terms of ![]() $B(G)$, see also [Reference ViehmannVie21, 3.2.2].
$B(G)$, see also [Reference ViehmannVie21, 3.2.2].
We consider the natural isomorphism ![]() $\varphi :{\rm Gr}_{G,\breve {F}}\rightarrow {\rm Gr}_{G_b,\breve {F}}$ induced by the identity map
$\varphi :{\rm Gr}_{G,\breve {F}}\rightarrow {\rm Gr}_{G_b,\breve {F}}$ induced by the identity map ![]() $G_{\breve {F}}\rightarrow G_{b,\breve {F}}$. It is compatible with Beauville–Laszlo uniformization in the sense that for
$G_{\breve {F}}\rightarrow G_{b,\breve {F}}$. It is compatible with Beauville–Laszlo uniformization in the sense that for ![]() $x\in {\rm Gr}_{G}(C)$ we have that
$x\in {\rm Gr}_{G}(C)$ we have that ![]() $({\mathcal {E}}_b^{G})_x$ is the
$({\mathcal {E}}_b^{G})_x$ is the ![]() $G$-bundle corresponding to
$G$-bundle corresponding to ![]() $({\mathcal {E}}_1^{G_b})_{\varphi (x)}$. In particular,
$({\mathcal {E}}_1^{G_b})_{\varphi (x)}$. In particular, ![]() $\varphi$ identifies corresponding Newton strata
$\varphi$ identifies corresponding Newton strata ![]() ${\rm Gr}_{G,\mu,b}^{[b']}$ and
${\rm Gr}_{G,\mu,b}^{[b']}$ and ![]() ${\rm Gr}_{G_b,\mu,1}^{[b'b^{-1}]}$. Here, a Newton stratum
${\rm Gr}_{G_b,\mu,1}^{[b'b^{-1}]}$. Here, a Newton stratum ![]() ${\rm Gr}_{G_b,\mu,1}^{[b'b^{-1}]}$ or
${\rm Gr}_{G_b,\mu,1}^{[b'b^{-1}]}$ or ![]() ${\rm Gr}_{G,\mu,b}^{[b']}$ is non-empty if and only if
${\rm Gr}_{G,\mu,b}^{[b']}$ is non-empty if and only if ![]() $[b'b^{-1}]\in B(G_b,-\mu )$. This motivates the notation
$[b'b^{-1}]\in B(G_b,-\mu )$. This motivates the notation
 \begin{align*} B(G,\mu,b)&=\{[b']\in B(G)\mid [b'b^{-1}]\in B(G_b,-\mu)\}\\ &=\{[b']\in B(G)\mid \kappa_G(b') =\kappa_G(b)-\mu^{\sharp_G}, \nu_{b'}\leqslant \nu_b(\mu^{-1,\diamond})_{{\rm dom}}\} \end{align*}
\begin{align*} B(G,\mu,b)&=\{[b']\in B(G)\mid [b'b^{-1}]\in B(G_b,-\mu)\}\\ &=\{[b']\in B(G)\mid \kappa_G(b') =\kappa_G(b)-\mu^{\sharp_G}, \nu_{b'}\leqslant \nu_b(\mu^{-1,\diamond})_{{\rm dom}}\} \end{align*}
where ![]() $\mu ^{-1,\diamond }$ is the Galois average of
$\mu ^{-1,\diamond }$ is the Galois average of ![]() $\mu ^{-1}$.
$\mu ^{-1}$.
Furthermore, the isomorphism ![]() $G_{\breve {F}}\rightarrow G_{b,\breve {F}}$ identifies parabolic subgroups of
$G_{\breve {F}}\rightarrow G_{b,\breve {F}}$ identifies parabolic subgroups of ![]() $G_b$ (defined over
$G_b$ (defined over ![]() $F$) with parabolic subgroups of
$F$) with parabolic subgroups of ![]() $G_{\breve {F}}$ that are stable under
$G_{\breve {F}}$ that are stable under ![]() $b\sigma$. We want to use these identifications to extend our definition of the Harder–Narasimhan formalism also to modifications of basic (but not necessarily trivial)
$b\sigma$. We want to use these identifications to extend our definition of the Harder–Narasimhan formalism also to modifications of basic (but not necessarily trivial) ![]() $G$-bundles for general
$G$-bundles for general ![]() $G$.
$G$.
Before that, we need to check compatibility with the Harder–Narasimhan formalism for any basic ![]() $b$ and
$b$ and ![]() $G={\rm GL}_n$ that we established in § 2.2.
$G={\rm GL}_n$ that we established in § 2.2.
Lemma 8.1 Let ![]() $G={\rm GL}_n$ and let
$G={\rm GL}_n$ and let ![]() $b\in G(\breve {F})$ be basic. Then the equivalence between vector bundles of rank
$b\in G(\breve {F})$ be basic. Then the equivalence between vector bundles of rank ![]() $n$ and
$n$ and ![]() $G_b$-bundles, together with its analog for vector bundles of rank
$G_b$-bundles, together with its analog for vector bundles of rank ![]() $n$ with a filtration in
$n$ with a filtration in ![]() $\mathcal {C}$ respectively
$\mathcal {C}$ respectively ![]() $P_b$-bundles (for parabolic subgroups
$P_b$-bundles (for parabolic subgroups ![]() $P_b$ of
$P_b$ of ![]() $G_b$) identifies the canonical filtration of
$G_b$) identifies the canonical filtration of ![]() $({\mathcal {E}}_b^{G},x)$ in the sense of § 2.2 with the canonical reduction of
$({\mathcal {E}}_b^{G},x)$ in the sense of § 2.2 with the canonical reduction of ![]() $({\mathcal {E}}_1^{G_b},\varphi (x))$.
$({\mathcal {E}}_1^{G_b},\varphi (x))$.
In particular, the bijection ![]() $B(G_b)\rightarrow B(G)$ identifies the Harder–Narasimhan vector of
$B(G_b)\rightarrow B(G)$ identifies the Harder–Narasimhan vector of ![]() $({\mathcal {E}}_b^{G},x)$ with the Harder–Narasimhan vector of
$({\mathcal {E}}_b^{G},x)$ with the Harder–Narasimhan vector of ![]() $({\mathcal {E}}_1^{G_b},\varphi (x))$.
$({\mathcal {E}}_1^{G_b},\varphi (x))$.
Proof. Let ![]() $P_b$ be a parabolic subgroup of
$P_b$ be a parabolic subgroup of ![]() $G_b$ and
$G_b$ and ![]() ${\mathcal {E}}_1^{P_b}$ be the corresponding
${\mathcal {E}}_1^{P_b}$ be the corresponding ![]() $P_b$-reduction of the trivial
$P_b$-reduction of the trivial ![]() $G_b$ bundle
$G_b$ bundle ![]() ${\mathcal {E}}_1^{G_b}$. Let
${\mathcal {E}}_1^{G_b}$. Let ![]() ${\mathcal {E}}_{1, \varphi (x)}^{P_b}$ be the corresponding
${\mathcal {E}}_{1, \varphi (x)}^{P_b}$ be the corresponding ![]() $P_b$-reduction of the modified
$P_b$-reduction of the modified ![]() $G_b$-bundle
$G_b$-bundle ![]() ${\mathcal {E}}_{1, \varphi (x)}^{G_b}$ and let
${\mathcal {E}}_{1, \varphi (x)}^{G_b}$ and let ![]() $v_{b, P_b}$ be the corresponding slope vector. By Proposition 3.10, the canonical reduction of
$v_{b, P_b}$ be the corresponding slope vector. By Proposition 3.10, the canonical reduction of ![]() $({\mathcal {E}}_1^{G_b},\varphi (x))$ is the unique reduction to a parabolic subgroup
$({\mathcal {E}}_1^{G_b},\varphi (x))$ is the unique reduction to a parabolic subgroup ![]() $P_b$ of
$P_b$ of ![]() $G_b$ such that
$G_b$ such that ![]() $v_{b, P_b}$ is maximal among the slope vectors for all possible parabolic subgroups of
$v_{b, P_b}$ is maximal among the slope vectors for all possible parabolic subgroups of ![]() $G_b$.
$G_b$.
On the other hand, we have a bijection between parabolic subgroups ![]() $P$ of
$P$ of ![]() $G_{\breve {F}}$ stable under
$G_{\breve {F}}$ stable under ![]() $b\sigma$ and filtrations
$b\sigma$ and filtrations ![]() $^{\bullet }{}{({\mathcal {E}}_b^{G},x)}$ of
$^{\bullet }{}{({\mathcal {E}}_b^{G},x)}$ of ![]() $({\mathcal {E}}_b^{G},x)$ in the category
$({\mathcal {E}}_b^{G},x)$ in the category ![]() $\mathcal {C}$. Hence for any
$\mathcal {C}$. Hence for any ![]() $P$ as above we have a corresponding slope vector
$P$ as above we have a corresponding slope vector ![]() $v_{1, P}$ by Definition 2.8. By Proposition 2.9, the canonical filtration of
$v_{1, P}$ by Definition 2.8. By Proposition 2.9, the canonical filtration of ![]() $({\mathcal {E}}_b^{G}, x)$ is the unique filtration such that
$({\mathcal {E}}_b^{G}, x)$ is the unique filtration such that ![]() $v_{1, P}$ is maximal among all the filtrations of
$v_{1, P}$ is maximal among all the filtrations of ![]() $({\mathcal {E}}_b^{G},x)$ in
$({\mathcal {E}}_b^{G},x)$ in ![]() $\mathcal {C}$.
$\mathcal {C}$.
There is a bijection between the set of parabolic subgroups of ![]() $G_b$ and parabolic subgroups of
$G_b$ and parabolic subgroups of ![]() $G$ being stable under
$G$ being stable under ![]() $b\sigma$. Thus if one denotes
$b\sigma$. Thus if one denotes ![]() $P \subset G$ the corresponding parabolic subgroup of
$P \subset G$ the corresponding parabolic subgroup of ![]() $P_b \subset G_b$ then it is enough to compare
$P_b \subset G_b$ then it is enough to compare ![]() $v_{b, P_b}$ and
$v_{b, P_b}$ and ![]() $v_{1, P}$. Let
$v_{1, P}$. Let ![]() $M$ be a Levi subgroup of
$M$ be a Levi subgroup of ![]() $P$ and let
$P$ and let ![]() $M_b$ be the corresponding Levi subgroup of
$M_b$ be the corresponding Levi subgroup of ![]() $P_b$. Then the map
$P_b$. Then the map ![]() $\varphi$ is compatible with the Iwasawa decomposition. More precisely, if
$\varphi$ is compatible with the Iwasawa decomposition. More precisely, if ![]() $x = x_P \cdot g$ where
$x = x_P \cdot g$ where ![]() $x_P \in P({B_{{\rm dR}}})$ and
$x_P \in P({B_{{\rm dR}}})$ and ![]() $g \in G({B^+_{{\rm dR}}})$ then
$g \in G({B^+_{{\rm dR}}})$ then ![]() $\varphi (x) = \varphi _{P}(x_P) \cdot g'$ where
$\varphi (x) = \varphi _{P}(x_P) \cdot g'$ where ![]() $\varphi _{P}(x_P) \in P_b$ and
$\varphi _{P}(x_P) \in P_b$ and ![]() $g' \in G_b({B^+_{{\rm dR}}})$.
$g' \in G_b({B^+_{{\rm dR}}})$.
By [Reference ViehmannVie21, Lemma 3.11], we see that ![]() $v_{b, P_b}$ is central in
$v_{b, P_b}$ is central in ![]() $X_*(M_b)_{\mathbb {Q}}$ and thus determined by its image in
$X_*(M_b)_{\mathbb {Q}}$ and thus determined by its image in ![]() $\pi _1(M_b)_{\Gamma }$, which equals
$\pi _1(M_b)_{\Gamma }$, which equals ![]() $- \kappa _{M_b}(\varphi (x_M))$, where
$- \kappa _{M_b}(\varphi (x_M))$, where ![]() $x_M$ is the image of
$x_M$ is the image of ![]() $x_P$ in
$x_P$ in ![]() $M({B_{{\rm dR}}})$. Similarly,
$M({B_{{\rm dR}}})$. Similarly, ![]() $v_{1, P}$ is central in
$v_{1, P}$ is central in ![]() $X_*(M)_{\mathbb {Q}}$ and equal to the difference of the
$X_*(M)_{\mathbb {Q}}$ and equal to the difference of the ![]() $G$-central element with image
$G$-central element with image ![]() $\kappa _G(b)$ in
$\kappa _G(b)$ in ![]() $\pi _1(G)_{\Gamma }$ and the element which is central in
$\pi _1(G)_{\Gamma }$ and the element which is central in ![]() $M$ and with image
$M$ and with image ![]() $\kappa _{M}(\varphi _M (x_{M}))$. By the argument at the end of the proof of [Reference Chen, Fargues and ShenCFS21, Proposition 5.2], these two vectors are the Newton points of corresponding elements of
$\kappa _{M}(\varphi _M (x_{M}))$. By the argument at the end of the proof of [Reference Chen, Fargues and ShenCFS21, Proposition 5.2], these two vectors are the Newton points of corresponding elements of ![]() $B(G_b)$, respectively
$B(G_b)$, respectively ![]() $B(G)$.
$B(G)$.
Remark 8.2 Let ![]() $G$ be a reductive group over
$G$ be a reductive group over ![]() $F$ and let
$F$ and let ![]() $b\in G(\breve {F})$ be basic.
$b\in G(\breve {F})$ be basic.
(i) We define the Harder–Narasimhan vector of ![]() $({\mathcal {E}}_b^G,x)$ for
$({\mathcal {E}}_b^G,x)$ for ![]() $x\in {\rm Gr}_{G,\mu }(C)$ to be the Harder–Narasimhan vector associated with
$x\in {\rm Gr}_{G,\mu }(C)$ to be the Harder–Narasimhan vector associated with ![]() $({\mathcal {E}}_1^{G_b},\varphi (x))$.
$({\mathcal {E}}_1^{G_b},\varphi (x))$.
(ii) Let ![]() $x\in {\rm Gr}_{G,\mu }(C)$ and consider the canonical reduction of
$x\in {\rm Gr}_{G,\mu }(C)$ and consider the canonical reduction of ![]() $({\mathcal {E}}_1^{G_b},\varphi (x))$. We obtain a parabolic subgroup
$({\mathcal {E}}_1^{G_b},\varphi (x))$. We obtain a parabolic subgroup ![]() $P'$ of
$P'$ of ![]() $G_b$, and a reduction
$G_b$, and a reduction ![]() $({\mathcal {E}}_{1,x}^{G_b})_{P'}$ of
$({\mathcal {E}}_{1,x}^{G_b})_{P'}$ of ![]() ${\mathcal {E}}_{1,x}$ induced by the reduction
${\mathcal {E}}_{1,x}$ induced by the reduction ![]() ${\mathcal {E}}_1^{P'}$. Then
${\mathcal {E}}_1^{P'}$. Then ![]() $P'$ corresponds to a parabolic subgroup
$P'$ corresponds to a parabolic subgroup ![]() $P$ of
$P$ of ![]() $G_{\breve {F}}$ stable under
$G_{\breve {F}}$ stable under ![]() $b\sigma$. Recall that the adic Fargues–Fontaine curve is defined as
$b\sigma$. Recall that the adic Fargues–Fontaine curve is defined as ![]() $X=Y/\phi ^{\mathbb {Z}}$ where for
$X=Y/\phi ^{\mathbb {Z}}$ where for ![]() $S={\rm Spa}(C^{\flat },C^{\flat,+})$, we have
$S={\rm Spa}(C^{\flat },C^{\flat,+})$, we have
Consider the pullback of ![]() ${\mathcal {E}}^{G_b}_{1,x}$ and
${\mathcal {E}}^{G_b}_{1,x}$ and ![]() $({\mathcal {E}}_{1,x}^{G_b})_{P'}$ to
$({\mathcal {E}}_{1,x}^{G_b})_{P'}$ to ![]() $Y$. They correspond to the pullback of
$Y$. They correspond to the pullback of ![]() $({\mathcal {E}}_b^G)_{\varphi (x)}$ to
$({\mathcal {E}}_b^G)_{\varphi (x)}$ to ![]() $Y$ and to a reduction to
$Y$ and to a reduction to ![]() $P$ of this bundle. Using descent via
$P$ of this bundle. Using descent via ![]() $b\sigma$ one obtains a bundle on
$b\sigma$ one obtains a bundle on ![]() $X$. However, one has to extend the definition of parabolic reductions of
$X$. However, one has to extend the definition of parabolic reductions of ![]() $G$-bundles on
$G$-bundles on ![]() $X$ to also include parabolic subgroups not defined over
$X$ to also include parabolic subgroups not defined over ![]() $F,$ but rather over
$F,$ but rather over ![]() $\breve {F}$ and stable under
$\breve {F}$ and stable under ![]() $b\sigma$.
$b\sigma$.
One can now reformulate all of our results in this new context. Since this translation is in each case easy to carry out, but makes the notation more involved, we leave it to the reader.
(iii) Notice that these remarks also apply to elements ![]() $b\in [1]\in B(G)$. For such an element, we have
$b\in [1]\in B(G)$. For such an element, we have ![]() $G\cong G_b$ and
$G\cong G_b$ and ![]() ${\mathcal {E}}_1\cong {\mathcal {E}}_b$. However, this identification leads to a different trivialization of the trivial bundle that we modify. Based on such a trivialization, all Harder–Narasimhan strata in some
${\mathcal {E}}_1\cong {\mathcal {E}}_b$. However, this identification leads to a different trivialization of the trivial bundle that we modify. Based on such a trivialization, all Harder–Narasimhan strata in some ![]() ${\rm Gr}_{G,\mu }$ get shifted by an element
${\rm Gr}_{G,\mu }$ get shifted by an element ![]() $g\in G(\breve {F})$ with
$g\in G(\breve {F})$ with ![]() $g^{-1}b\sigma (g)=1$.
$g^{-1}b\sigma (g)=1$.
Acknowledgements
The second author thanks Laurent Fargues and Michael Rapoport for helpful conversations. We thank Miaofen Chen and Ian Gleason for pointing out an error in a previous version.
Appendix A. A variant of Schieder's comparison theorem
In the first part of this appendix we study a much more classical situation, namely the canonical (or Harder–Narasimhan) reduction of ![]() $G$-bundles on a curve. The main result, a strengthening of Schieder's comparison theorem, seems to be unknown also in this case, and the proofs are completely parallel.
$G$-bundles on a curve. The main result, a strengthening of Schieder's comparison theorem, seems to be unknown also in this case, and the proofs are completely parallel.
Let ![]() $k$ be an algebraically closed field and let
$k$ be an algebraically closed field and let ![]() $X$ be a smooth complete curve over
$X$ be a smooth complete curve over ![]() $k$. Then by classical Harder–Narasimhan theory [Reference Harder and NarasimhanHN75], every vector bundle
$k$. Then by classical Harder–Narasimhan theory [Reference Harder and NarasimhanHN75], every vector bundle ![]() ${\mathcal {E}}$ on
${\mathcal {E}}$ on ![]() $X$ has a unique filtration
$X$ has a unique filtration ![]() $(0)={\mathcal {E}}_0\subsetneq {\mathcal {E}}_1\subsetneq \dotsm \subsetneq {\mathcal {E}}_r={\mathcal {E}}$, called the canonical filtration, such that the subquotients
$(0)={\mathcal {E}}_0\subsetneq {\mathcal {E}}_1\subsetneq \dotsm \subsetneq {\mathcal {E}}_r={\mathcal {E}}$, called the canonical filtration, such that the subquotients ![]() ${\mathcal {E}}_i/{\mathcal {E}}_{i-1}$ are semi-stable of some slopes
${\mathcal {E}}_i/{\mathcal {E}}_{i-1}$ are semi-stable of some slopes ![]() $\lambda _i\in \mathbb {Q}$ with
$\lambda _i\in \mathbb {Q}$ with ![]() $\lambda _i>\lambda _{i+1}$ for all
$\lambda _i>\lambda _{i+1}$ for all ![]() $i$. The vector
$i$. The vector ![]() $v_{{\mathcal {E}}}\in \mathbb {Q}^n_+$ where
$v_{{\mathcal {E}}}\in \mathbb {Q}^n_+$ where ![]() $n={\rm rk\,} {\mathcal {E}}$ and with components
$n={\rm rk\,} {\mathcal {E}}$ and with components ![]() $\lambda _1,\dotsc, \lambda _r$ with multiplicities
$\lambda _1,\dotsc, \lambda _r$ with multiplicities ![]() ${\rm rk\,}{\mathcal {E}}_i-{\rm rk\,} {\mathcal {E}}_{i-1}$ is called the Harder–Narasimhan polygon
${\rm rk\,}{\mathcal {E}}_i-{\rm rk\,} {\mathcal {E}}_{i-1}$ is called the Harder–Narasimhan polygon ![]() $HN({\mathcal {E}})$ of
$HN({\mathcal {E}})$ of ![]() ${\mathcal {E}}$. We also associate with it the convex polygon which is the graph of the piecewise linear continuous function
${\mathcal {E}}$. We also associate with it the convex polygon which is the graph of the piecewise linear continuous function ![]() $[0,n]\rightarrow \mathbb {R}$ mapping
$[0,n]\rightarrow \mathbb {R}$ mapping ![]() $0$ to
$0$ to ![]() $0$ and whose slope on
$0$ and whose slope on ![]() $[l-1,l]$ is equal to the
$[l-1,l]$ is equal to the ![]() $l$th component of
$l$th component of ![]() $HN({\mathcal {E}})$.
$HN({\mathcal {E}})$.
Furthermore, there is the following comparison theorem. Let ![]() ${\mathcal {E}}'$ be a sub-vector bundle of
${\mathcal {E}}'$ be a sub-vector bundle of ![]() ${\mathcal {E}}$. Then we have the following.
${\mathcal {E}}$. Then we have the following.
(i) The point
 $({\rm rk\,} {\mathcal {E}}',\mathop {\mathrm {deg}}\nolimits {\mathcal {E}}')$ lies under or on
$({\rm rk\,} {\mathcal {E}}',\mathop {\mathrm {deg}}\nolimits {\mathcal {E}}')$ lies under or on  $HN({\mathcal {E}})$.
$HN({\mathcal {E}})$.(ii) If it lies on
 $HN({\mathcal {E}})$, there is an
$HN({\mathcal {E}})$, there is an  $i$ with
$i$ with  ${\mathcal {E}}_i\subseteq {\mathcal {E}}'\subseteq {\mathcal {E}}_{i+1}$.
${\mathcal {E}}_i\subseteq {\mathcal {E}}'\subseteq {\mathcal {E}}_{i+1}$.
Now let ![]() $G$ be a reductive group over
$G$ be a reductive group over ![]() $k$. Generalizing the above theory there is for every
$k$. Generalizing the above theory there is for every ![]() $G$-bundle on
$G$-bundle on ![]() $X$ a canonical or Harder–Narasimhan reduction to a
$X$ a canonical or Harder–Narasimhan reduction to a ![]() $P$-bundle for some standard parabolic subgroup
$P$-bundle for some standard parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$; compare for example [Reference Biswas and HollaBH04, Reference BehrendBeh95]. In [Reference SchiederSch15, Theorem 4.1], Schieder generalizes the first part of the above comparison theorem to this context. The first goal of the present work, Theorem A.3 below, is to generalize (ii) above to the group-theoretic context. Schieder's comparison theorem also contains a second assertion concerning refinements of canonical reductions. It is the group-theoretic version of the following statement, which is implied by (ii) above. Assume that
$G$; compare for example [Reference Biswas and HollaBH04, Reference BehrendBeh95]. In [Reference SchiederSch15, Theorem 4.1], Schieder generalizes the first part of the above comparison theorem to this context. The first goal of the present work, Theorem A.3 below, is to generalize (ii) above to the group-theoretic context. Schieder's comparison theorem also contains a second assertion concerning refinements of canonical reductions. It is the group-theoretic version of the following statement, which is implied by (ii) above. Assume that ![]() $(0)={\mathcal {E}}'_0\subsetneq {\mathcal {E}}'_1\subsetneq \dotsm \subsetneq {\mathcal {E}}'_s={\mathcal {E}}$ is a second filtration of
$(0)={\mathcal {E}}'_0\subsetneq {\mathcal {E}}'_1\subsetneq \dotsm \subsetneq {\mathcal {E}}'_s={\mathcal {E}}$ is a second filtration of ![]() ${\mathcal {E}}$. Associate with it a similar polygon
${\mathcal {E}}$. Associate with it a similar polygon ![]() $v$ whose slopes are the slopes of the subquotients of this filtration with corresponding multiplicities. If
$v$ whose slopes are the slopes of the subquotients of this filtration with corresponding multiplicities. If ![]() $v=HN({\mathcal {E}})$, then this new filtration is a refinement of the canonical filtration of
$v=HN({\mathcal {E}})$, then this new filtration is a refinement of the canonical filtration of ![]() ${\mathcal {E}}$.
${\mathcal {E}}$.
Using the classification of ![]() $G$-bundles on the Fargues–Fontaine curve, we derive in § A.2 a variant of Theorem A.3 for this context.
$G$-bundles on the Fargues–Fontaine curve, we derive in § A.2 a variant of Theorem A.3 for this context.
A.1 Comparing reductions of  $G$-bundles
$G$-bundles
A.1.1 Canonical reductions
We recall some of the main notions regarding the canonical reduction for ![]() $G$-bundles on curves. We follow Schieder [Reference SchiederSch15, 2], but replace some of his notation. For more details and proofs compare [Reference Biswas and HollaBH04, Reference BehrendBeh95, Reference SchiederSch15].
$G$-bundles on curves. We follow Schieder [Reference SchiederSch15, 2], but replace some of his notation. For more details and proofs compare [Reference Biswas and HollaBH04, Reference BehrendBeh95, Reference SchiederSch15].
Let ![]() $k$ be an algebraically closed field of any characteristic, and let
$k$ be an algebraically closed field of any characteristic, and let ![]() $G$ be a reductive group over
$G$ be a reductive group over ![]() $k$. We fix a maximal torus
$k$. We fix a maximal torus ![]() $T$ and a Borel subgroup
$T$ and a Borel subgroup ![]() $B$ containing it. For a standard parabolic subgroup
$B$ containing it. For a standard parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$ we denote by
$G$ we denote by ![]() $M$ its Levi quotient. Let
$M$ its Levi quotient. Let ![]() $\Delta$ be the set of simple roots for our choice of
$\Delta$ be the set of simple roots for our choice of ![]() $B$ and
$B$ and ![]() $T$, and
$T$, and ![]() $\Delta _M$ correspondingly for
$\Delta _M$ correspondingly for ![]() $M$. We denote by
$M$. We denote by ![]() $\pi _1(G)$ the quotient of
$\pi _1(G)$ the quotient of ![]() $X_*(T)$ by the coroot lattice. For
$X_*(T)$ by the coroot lattice. For ![]() $v\in X_*(T)_{\mathbb {Q}}$ let
$v\in X_*(T)_{\mathbb {Q}}$ let ![]() $v^{\sharp _M}$ denote its image in
$v^{\sharp _M}$ denote its image in ![]() $\pi _1(M)_{\mathbb {Q}}$. We also write
$\pi _1(M)_{\mathbb {Q}}$. We also write ![]() $v^{\sharp }$ instead of
$v^{\sharp }$ instead of ![]() $v^{\sharp _G}$.
$v^{\sharp _G}$.
Let ![]() $X$ be a smooth and complete curve over
$X$ be a smooth and complete curve over ![]() $k$. As before,
$k$. As before, ![]() $G$-bundles on
$G$-bundles on ![]() $X$ can be viewed as
$X$ can be viewed as ![]() $G$-torsors on
$G$-torsors on ![]() $X$ that are locally trivial for the étale topology, or equivalently as exact tensor functors from the category
$X$ that are locally trivial for the étale topology, or equivalently as exact tensor functors from the category ![]() ${\rm Rep}_G$ of rational algebraic representations of
${\rm Rep}_G$ of rational algebraic representations of ![]() $G$ to the category
$G$ to the category ![]() ${\rm Bun}_X$ of vector bundles on
${\rm Bun}_X$ of vector bundles on ![]() $X$.
$X$.
We denote by ![]() ${\rm Bun}_G$ the moduli stack of
${\rm Bun}_G$ the moduli stack of ![]() $G$-bundles on
$G$-bundles on ![]() $X$, and similarly for other linear algebraic groups. For
$X$, and similarly for other linear algebraic groups. For ![]() $P$ and
$P$ and ![]() $M$ as above we have natural maps of stacks
$M$ as above we have natural maps of stacks
induced by the homomorphisms ![]() $P\hookrightarrow G$ and
$P\hookrightarrow G$ and ![]() $P\twoheadrightarrow M$.
$P\twoheadrightarrow M$.
We have ![]() $\pi _0({\rm Bun}_P)\cong \pi _1(M)$. For
$\pi _0({\rm Bun}_P)\cong \pi _1(M)$. For ![]() $\lambda \in \pi _1(M)$ we denote by
$\lambda \in \pi _1(M)$ we denote by ![]() ${\rm Bun}_{P,\lambda }$ the corresponding connected component of
${\rm Bun}_{P,\lambda }$ the corresponding connected component of ![]() ${\rm Bun}_P$.
${\rm Bun}_P$.
If ![]() $H\subseteq G$ is a subgroup and
$H\subseteq G$ is a subgroup and ![]() ${{\mathcal {E}}}\in {\rm Bun}_G$, a reduction of
${{\mathcal {E}}}\in {\rm Bun}_G$, a reduction of ![]() ${{\mathcal {E}}}$ to
${{\mathcal {E}}}$ to ![]() $H$ is an element
$H$ is an element ![]() ${{\mathcal {E}}}_H\in {\rm Bun}_H$ such that
${{\mathcal {E}}}_H\in {\rm Bun}_H$ such that ![]() ${{\mathcal {E}}}_H\times ^H G\cong {{\mathcal {E}}}$. Let
${{\mathcal {E}}}_H\times ^H G\cong {{\mathcal {E}}}$. Let ![]() ${{\mathcal {E}}}\in {\rm Bun}_G$ and let
${{\mathcal {E}}}\in {\rm Bun}_G$ and let ![]() ${{\mathcal {E}}}_P\in {\rm Bun}_P$ be a reduction to
${{\mathcal {E}}}_P\in {\rm Bun}_P$ be a reduction to ![]() $P$. We associate with
$P$. We associate with ![]() ${{\mathcal {E}}}_P$ the rational cocharacter
${{\mathcal {E}}}_P$ the rational cocharacter ![]() $v\in X_*(T)_{\mathbb {Q},{\rm dom}}$ defined via
$v\in X_*(T)_{\mathbb {Q},{\rm dom}}$ defined via
and such that ![]() $v$ is central in
$v$ is central in ![]() $M$. It is called the slope of
$M$. It is called the slope of ![]() ${{\mathcal {E}}}_P$.
${{\mathcal {E}}}_P$.
Remark A.1 A second description of ![]() $v$ (used in [Reference SchiederSch15]) is obtained by associating with
$v$ (used in [Reference SchiederSch15]) is obtained by associating with ![]() ${{\mathcal {E}}}_P$ the image
${{\mathcal {E}}}_P$ the image ![]() $\lambda _P=\lambda _P({{\mathcal {E}}}_P)\in \pi _1(M)$ under the composition
$\lambda _P=\lambda _P({{\mathcal {E}}}_P)\in \pi _1(M)$ under the composition ![]() ${\rm Bun}_P\rightarrow {\rm Bun}_M\rightarrow \pi _0({\rm Bun}_M)\cong \pi _1(M)$.
${\rm Bun}_P\rightarrow {\rm Bun}_M\rightarrow \pi _0({\rm Bun}_M)\cong \pi _1(M)$.
Then ![]() $v({{\mathcal {E}}}_P)\in X_*(T)_{\mathbb {Q},{\rm dom}}$ is the unique element that is central in
$v({{\mathcal {E}}}_P)\in X_*(T)_{\mathbb {Q},{\rm dom}}$ is the unique element that is central in ![]() $M$ and such that
$M$ and such that ![]() $v({{\mathcal {E}}}_P)^{\sharp _M}=\lambda _P({{\mathcal {E}}}_P)$ in
$v({{\mathcal {E}}}_P)^{\sharp _M}=\lambda _P({{\mathcal {E}}}_P)$ in ![]() $\pi _1(M)_{\mathbb {Q}}$. In other words, it is the image of
$\pi _1(M)_{\mathbb {Q}}$. In other words, it is the image of ![]() $\lambda _P({{\mathcal {E}}}_P)$ under
$\lambda _P({{\mathcal {E}}}_P)$ under
Conversely, ![]() $\lambda _P({{\mathcal {E}}}_P)$ is uniquely determined by its image in
$\lambda _P({{\mathcal {E}}}_P)$ is uniquely determined by its image in ![]() $\pi _1(G)$, which coincides with
$\pi _1(G)$, which coincides with ![]() $\lambda _G({{\mathcal {E}}})$, together with the image of
$\lambda _G({{\mathcal {E}}})$, together with the image of ![]() $\lambda _P({{\mathcal {E}}}_P)$ in
$\lambda _P({{\mathcal {E}}}_P)$ in ![]() $\pi _1(M)_{\mathbb {Q}}$, which coincides with
$\pi _1(M)_{\mathbb {Q}}$, which coincides with ![]() $v({{\mathcal {E}}}_P)^{\sharp _M}$. Indeed, this follows since the kernel of the projection map
$v({{\mathcal {E}}}_P)^{\sharp _M}$. Indeed, this follows since the kernel of the projection map ![]() $\pi _1(M)\rightarrow \pi _1(G)$ is torsion free.
$\pi _1(M)\rightarrow \pi _1(G)$ is torsion free.
For ![]() $\lambda,\lambda '\in X_*(T)_{\mathbb {Q}}$ we write
$\lambda,\lambda '\in X_*(T)_{\mathbb {Q}}$ we write ![]() $\lambda \preceq \lambda '$ if
$\lambda \preceq \lambda '$ if ![]() $\lambda '-\lambda$ is a non-negative linear combination of positive coroots. Notice that we do not assume
$\lambda '-\lambda$ is a non-negative linear combination of positive coroots. Notice that we do not assume ![]() $\lambda$ or
$\lambda$ or ![]() $\lambda '$ to be dominant.
$\lambda '$ to be dominant.
Definition A.2
(i) A
 $G$-bundle
$G$-bundle  ${{\mathcal {E}}}$ is called semi-stable if for every standard parabolic subgroup
${{\mathcal {E}}}$ is called semi-stable if for every standard parabolic subgroup  $P$ and every reduction
$P$ and every reduction  ${{\mathcal {E}}}_P$ of
${{\mathcal {E}}}_P$ of  ${{\mathcal {E}}}$ to
${{\mathcal {E}}}$ to  $P$ we have
$P$ we have  $v({{\mathcal {E}}}_P)\preceq v({{\mathcal {E}}})$. We denote the semi-stable locus in
$v({{\mathcal {E}}}_P)\preceq v({{\mathcal {E}}})$. We denote the semi-stable locus in  ${\rm Bun}_G$ by
${\rm Bun}_G$ by  ${\rm Bun}_G^{ss}$, and likewise for
${\rm Bun}_G^{ss}$, and likewise for  ${\rm Bun}_P^{ss}$,
${\rm Bun}_P^{ss}$,  ${\rm Bun}_{G,\lambda }^{ss}$ etc.
${\rm Bun}_{G,\lambda }^{ss}$ etc.(ii) Let
 $P$ be a standard parabolic subgroup of
$P$ be a standard parabolic subgroup of  $G$ and
$G$ and  $M$ its standard Levi factor. Then
$M$ its standard Levi factor. Then  $v\in X_*(T)_{\mathbb {Q},{\rm dom}}$ is called dominant
$v\in X_*(T)_{\mathbb {Q},{\rm dom}}$ is called dominant  $P$-regular if
$P$-regular if  $v$ is central in
$v$ is central in  $M$, and if
$M$, and if  $\langle v,\alpha \rangle >0$ for all simple roots
$\langle v,\alpha \rangle >0$ for all simple roots  $\alpha$ that are not in
$\alpha$ that are not in  $M$. Similarly,
$M$. Similarly,  $\lambda \in \pi _1(M)_{\mathbb {Q}}$ is called dominant
$\lambda \in \pi _1(M)_{\mathbb {Q}}$ is called dominant  $P$-regular if
$P$-regular if  $\phi _M(\lambda )$ is dominant
$\phi _M(\lambda )$ is dominant  $P$-regular.
$P$-regular.(iii) A reduction
 ${{\mathcal {E}}}_P$ of a
${{\mathcal {E}}}_P$ of a  $G$-bundle is called canonical, if
$G$-bundle is called canonical, if  ${{\mathcal {E}}}_P$ is semi-stable and
${{\mathcal {E}}}_P$ is semi-stable and  $v({{\mathcal {E}}}_P)$ is dominant
$v({{\mathcal {E}}}_P)$ is dominant  $P$-regular.
$P$-regular.
Then Harder–Narasimhan theory for ![]() $G$-bundles on
$G$-bundles on ![]() $X$ [Reference Biswas and HollaBH04, Reference BehrendBeh95] implies that for every
$X$ [Reference Biswas and HollaBH04, Reference BehrendBeh95] implies that for every ![]() $G$-bundle
$G$-bundle ![]() ${{\mathcal {E}}}$ on
${{\mathcal {E}}}$ on ![]() $X$ there is a unique standard parabolic subgroup
$X$ there is a unique standard parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$ such that there is a canonical reduction
$G$ such that there is a canonical reduction ![]() ${{\mathcal {E}}}_P$ of
${{\mathcal {E}}}_P$ of ![]() ${{\mathcal {E}}}$. This reduction is then also uniquely defined.
${{\mathcal {E}}}$. This reduction is then also uniquely defined.
A.1.2 The comparison theorem
Let ![]() $P_1,P_2$ be standard parabolic subgroups of
$P_1,P_2$ be standard parabolic subgroups of ![]() $G$ with standard Levi subgroups
$G$ with standard Levi subgroups ![]() $M_1,M_2$. Let
$M_1,M_2$. Let ![]() ${{\mathcal {E}}}_{P_1}\in {\rm Bun}_{P_1, \lambda _{P_1}}^{ss}$ and
${{\mathcal {E}}}_{P_1}\in {\rm Bun}_{P_1, \lambda _{P_1}}^{ss}$ and ![]() ${{\mathcal {E}}}_{P_2}\in {\rm Bun}_{P_2, \lambda _{P_2}}$ be reductions of the same
${{\mathcal {E}}}_{P_2}\in {\rm Bun}_{P_2, \lambda _{P_2}}$ be reductions of the same ![]() $G$-bundle
$G$-bundle ![]() ${{\mathcal {E}}}$ on the curve
${{\mathcal {E}}}$ on the curve ![]() $X$. Assume that
$X$. Assume that ![]() $\lambda _{P_1}=\lambda$ is dominant
$\lambda _{P_1}=\lambda$ is dominant ![]() $P_1$-regular, i.e.
$P_1$-regular, i.e. ![]() ${{\mathcal {E}}}_{P_1}$ is the canonical reduction of
${{\mathcal {E}}}_{P_1}$ is the canonical reduction of ![]() ${{\mathcal {E}}}$. Recall that by Remark A.1 we have
${{\mathcal {E}}}$. Recall that by Remark A.1 we have ![]() $v({{\mathcal {E}}}_{P_i})=\phi _{P_i}(\lambda _i)$. Then the first assertion of [Reference SchiederSch15, Theorem 4.1] shows
$v({{\mathcal {E}}}_{P_i})=\phi _{P_i}(\lambda _i)$. Then the first assertion of [Reference SchiederSch15, Theorem 4.1] shows ![]() $v({{\mathcal {E}}}_{P_2})\preceq v({{\mathcal {E}}}_{P_1})$. The aim of this section is to prove the following generalization of the second assertion of [Reference SchiederSch15, Theorem 4.1].
$v({{\mathcal {E}}}_{P_2})\preceq v({{\mathcal {E}}}_{P_1})$. The aim of this section is to prove the following generalization of the second assertion of [Reference SchiederSch15, Theorem 4.1].
Theorem A.3 In the above context assume that the images of ![]() $v({{\mathcal {E}}}_{P_1})$ and of
$v({{\mathcal {E}}}_{P_1})$ and of ![]() $v({{\mathcal {E}}}_{P_2})$ in
$v({{\mathcal {E}}}_{P_2})$ in ![]() $\pi _1(M_2)_{\mathbb {Q}}$ coincide. Let
$\pi _1(M_2)_{\mathbb {Q}}$ coincide. Let ![]() $Q=P_1\cap P_2$. Then there is a joint reduction
$Q=P_1\cap P_2$. Then there is a joint reduction ![]() ${{\mathcal {E}}}_Q\in {\rm Bun}_{Q}$ of
${{\mathcal {E}}}_Q\in {\rm Bun}_{Q}$ of ![]() ${{\mathcal {E}}}_{P_1}$ and
${{\mathcal {E}}}_{P_1}$ and ![]() ${{\mathcal {E}}}_{P_2}$.
${{\mathcal {E}}}_{P_2}$.
For the proof we need a lemma. Let ![]() $W_1, W_2$ be the Weyl groups of
$W_1, W_2$ be the Weyl groups of ![]() $M_1$ and
$M_1$ and ![]() $M_2$, respectively. By
$M_2$, respectively. By ![]() ${}^{M_1}W^{M_2}$ we denote the subset of
${}^{M_1}W^{M_2}$ we denote the subset of ![]() $W$ of elements
$W$ of elements ![]() $w$ which are shortest representatives of their double coset
$w$ which are shortest representatives of their double coset ![]() $W_1 wW_2$.
$W_1 wW_2$.
Lemma A.4 Let ![]() $P_1,P_2$ be standard parabolic subgroups of
$P_1,P_2$ be standard parabolic subgroups of ![]() $G$ with standard Levi factors
$G$ with standard Levi factors ![]() $M_1,M_2$ and unipotent radicals
$M_1,M_2$ and unipotent radicals ![]() $N_1,N_2$.
$N_1,N_2$.
(i) Let
 $\nu \in X_*(T)_{\mathbb {Q}}$ be dominant. For every
$\nu \in X_*(T)_{\mathbb {Q}}$ be dominant. For every  $w\in W,$
in
$w\in W,$
in \[ \nu\succeq w^{-1}(\nu) \]
\[ \nu\succeq w^{-1}(\nu) \]
 $X_*(T)_{\mathbb {Q}}$.
$X_*(T)_{\mathbb {Q}}$.(ii) Let
 $\nu \in X_*(T)_{\mathbb {Q}}$ be dominant
$\nu \in X_*(T)_{\mathbb {Q}}$ be dominant  $P_1$-regular. If
$P_1$-regular. If  $w\in {}^{M_1}W^{M_2}$ is such that the images of
$w\in {}^{M_1}W^{M_2}$ is such that the images of  $\nu$ and
$\nu$ and  $w^{-1}(\nu )$ in
$w^{-1}(\nu )$ in  $\pi _1(M_2)_{\mathbb {Q}}$ agree, then
$\pi _1(M_2)_{\mathbb {Q}}$ agree, then  $w=1$.
$w=1$.
Proof. Part (i) is shown in [Reference SchiederSch15, Lemma 4.8] and follows immediately from the assumption that ![]() $\nu$ is dominant. For (ii) we replace
$\nu$ is dominant. For (ii) we replace ![]() $\nu$ by a suitable multiple and may thus assume that
$\nu$ by a suitable multiple and may thus assume that ![]() $\nu \in X_*(T)$, and that the images of
$\nu \in X_*(T)$, and that the images of ![]() $\nu$ and
$\nu$ and ![]() $w^{-1}(\nu )$ in
$w^{-1}(\nu )$ in ![]() $\pi _1(M_2)$ agree. Let
$\pi _1(M_2)$ agree. Let ![]() $\nu '$ be the
$\nu '$ be the ![]() $M_2$-dominant representative in the
$M_2$-dominant representative in the ![]() $W_{M_2}$-orbit of
$W_{M_2}$-orbit of ![]() $w^{-1}(\nu )$. Since
$w^{-1}(\nu )$. Since ![]() $\nu,\nu '$ are in the same
$\nu,\nu '$ are in the same ![]() $W$-orbit and both
$W$-orbit and both ![]() $M_2$-dominant, there is no root hyperplane for
$M_2$-dominant, there is no root hyperplane for ![]() $M_2$ separating the two elements. Therefore,
$M_2$ separating the two elements. Therefore, ![]() $\nu -\nu '$ is a non-negative linear combination of coroots
$\nu -\nu '$ is a non-negative linear combination of coroots ![]() $\alpha ^{\vee }$ for roots
$\alpha ^{\vee }$ for roots ![]() $\alpha$ of
$\alpha$ of ![]() $T$ in
$T$ in ![]() $N_2$. Since
$N_2$. Since ![]() $\nu =\nu '$ in
$\nu =\nu '$ in ![]() $\pi _1(M_2)$, this implies that
$\pi _1(M_2)$, this implies that ![]() $\nu =\nu '$, hence
$\nu =\nu '$, hence ![]() $w^{-1}(\nu )\in W_{M_2}(\nu )$. Since
$w^{-1}(\nu )\in W_{M_2}(\nu )$. Since ![]() $w\in {}^{M_1}W^{M_2},$ this implies
$w\in {}^{M_1}W^{M_2},$ this implies ![]() $w=1$.
$w=1$.
Proof of Theorem A.3 By [Reference SchiederSch15, Lemma 4.1], there is a unique element ![]() $w\in {}^{M_1}W^{M_2}$ for which there is an open dense subset
$w\in {}^{M_1}W^{M_2}$ for which there is an open dense subset ![]() $U\subset X$ such that
$U\subset X$ such that ![]() ${{\mathcal {E}}}_{P_1}|_U$ is in relative position
${{\mathcal {E}}}_{P_1}|_U$ is in relative position ![]() $w$ with respect to
$w$ with respect to ![]() ${{\mathcal {E}}}_{P_2}|_U$.
${{\mathcal {E}}}_{P_2}|_U$.
By the proof of the first part of [Reference SchiederSch15, Theorem 4.1] we have
By assumption, the images of ![]() $v({{\mathcal {E}}}_{P_1})$ and
$v({{\mathcal {E}}}_{P_1})$ and ![]() $v({{\mathcal {E}}}_{P_2})$ in
$v({{\mathcal {E}}}_{P_2})$ in ![]() $\pi _1(M_2)_{\mathbb {Q}}$ agree. Hence they also coincide with the corresponding image of
$\pi _1(M_2)_{\mathbb {Q}}$ agree. Hence they also coincide with the corresponding image of ![]() $w^{-1}(v({{\mathcal {E}}}_{P_1}))$. By Lemma A.4, this implies
$w^{-1}(v({{\mathcal {E}}}_{P_1}))$. By Lemma A.4, this implies ![]() $w=1$.
$w=1$.
Since ![]() $w=1$, the substack
$w=1$, the substack
is closed. Thus ![]() ${{\mathcal {E}}}_{P_1}$ and
${{\mathcal {E}}}_{P_1}$ and ![]() ${{\mathcal {E}}}_{P_2}$ are in relative position
${{\mathcal {E}}}_{P_2}$ are in relative position ![]() $w=1$ not only generically, but on the entire curve
$w=1$ not only generically, but on the entire curve ![]() $X$.
$X$.
Furthermore, ![]() $Q=P_1\cap P_2$ is the parabolic subgroup corresponding to the set of simple roots
$Q=P_1\cap P_2$ is the parabolic subgroup corresponding to the set of simple roots
i.e. equal to both parabolic subgroups ![]() $Q_1,Q_2$ of [Reference SchiederSch15, Corollary 4.1]. Applying the corollary yields the desired reduction of
$Q_1,Q_2$ of [Reference SchiederSch15, Corollary 4.1]. Applying the corollary yields the desired reduction of ![]() ${{\mathcal {E}}}$ to
${{\mathcal {E}}}$ to ![]() $Q$.
$Q$.
A.2 The canonical reduction for  $G$-bundles on the Fargues–Fontaine curve
$G$-bundles on the Fargues–Fontaine curve
From now on we work use again the context and notation of the main part of the paper. Assume ![]() $G$ to be quasi-split. Let
$G$ to be quasi-split. Let ![]() $A$ be a maximal split torus,
$A$ be a maximal split torus, ![]() $T$ the centralizer of
$T$ the centralizer of ![]() $A$ and
$A$ and ![]() $B$ a Borel subgroup of
$B$ a Borel subgroup of ![]() $G$ containing
$G$ containing ![]() $T$.
$T$.
For bundles over the Fargues–Fontaine curve, the canonical reduction satisfies the following splitting property. Let ![]() ${{\mathcal {E}}}$ be a
${{\mathcal {E}}}$ be a ![]() $G$-bundle on
$G$-bundle on ![]() $X$ and let
$X$ and let ![]() ${{\mathcal {E}}}_P$ be its canonical reduction where
${{\mathcal {E}}}_P$ be its canonical reduction where ![]() $P$ is a standard parabolic subgroup of
$P$ is a standard parabolic subgroup of ![]() $G$. Let
$G$. Let ![]() $M$ be the standard Levi factor of
$M$ be the standard Levi factor of ![]() $P$. Then by [Reference FarguesFar20, Proposition 5.16],
$P$. Then by [Reference FarguesFar20, Proposition 5.16], ![]() ${{\mathcal {E}}}_P\times ^P M$ is a reduction of
${{\mathcal {E}}}_P\times ^P M$ is a reduction of ![]() ${{\mathcal {E}}}$ to
${{\mathcal {E}}}$ to ![]() $M$. In particular,
$M$. In particular, ![]() ${{\mathcal {E}}}$ has a semi-stable reduction to a Levi subgroup of
${{\mathcal {E}}}$ has a semi-stable reduction to a Levi subgroup of ![]() $G$.
$G$.
Theorem A.5 Let ![]() $P_1,P_2$ be standard parabolic subgroups of
$P_1,P_2$ be standard parabolic subgroups of ![]() $G$ with standard Levi subgroups
$G$ with standard Levi subgroups ![]() $M_1,M_2$. Let
$M_1,M_2$. Let ![]() ${{\mathcal {E}}}_{P_1}\in {\rm Bun}_{P_1}^{ss}$ and
${{\mathcal {E}}}_{P_1}\in {\rm Bun}_{P_1}^{ss}$ and ![]() ${{\mathcal {E}}}_{P_2}\in {\rm Bun}_{P_2}$ be reductions of the same
${{\mathcal {E}}}_{P_2}\in {\rm Bun}_{P_2}$ be reductions of the same ![]() $G$-bundle
$G$-bundle ![]() ${{\mathcal {E}}}$ on
${{\mathcal {E}}}$ on ![]() $X$. Assume that
$X$. Assume that ![]() ${{\mathcal {E}}}_{P_1}$ is the canonical reduction of
${{\mathcal {E}}}_{P_1}$ is the canonical reduction of ![]() ${{\mathcal {E}}}$. Then
${{\mathcal {E}}}$. Then
(i)
 $v({{\mathcal {E}}}_{P_2})\preceq v({{\mathcal {E}}}_{P_1})$.
$v({{\mathcal {E}}}_{P_2})\preceq v({{\mathcal {E}}}_{P_1})$.
Assume that the images of ![]() $v({{\mathcal {E}}}_{P_1})$ and of
$v({{\mathcal {E}}}_{P_1})$ and of ![]() $v({{\mathcal {E}}}_{P_2})$ in
$v({{\mathcal {E}}}_{P_2})$ in ![]() $\pi _1(M_2)_{\Gamma,\mathbb {Q}}$ coincide. Let
$\pi _1(M_2)_{\Gamma,\mathbb {Q}}$ coincide. Let ![]() $Q=P_1\cap P_2$.
$Q=P_1\cap P_2$.
(ii) There is a joint reduction
 ${{\mathcal {E}}}_Q\in {\rm Bun}_{Q}$ of
${{\mathcal {E}}}_Q\in {\rm Bun}_{Q}$ of  ${{\mathcal {E}}}_{P_1}$ and
${{\mathcal {E}}}_{P_1}$ and  ${{\mathcal {E}}}_{P_2}$.
${{\mathcal {E}}}_{P_2}$.(iii) Let
 $M$ be the standard Levi subgroup of
$M$ be the standard Levi subgroup of  $Q$. Then
$Q$. Then  ${{\mathcal {E}}}_Q\times ^Q M$ is a reduction of
${{\mathcal {E}}}_Q\times ^Q M$ is a reduction of  ${{\mathcal {E}}}$ to
${{\mathcal {E}}}$ to  $M$.
$M$.
Proof. Parts (i) and (ii) are the analogs of the first assertion of [Reference SchiederSch15, Theorem 4.1], respectively of the first assertion of Theorem A.3. The same arguments prove that they still hold in this context.
For the last assertion we use [Reference Chen, Fargues and ShenCFS21, Lemma 6.3] and its proof. Consider the parabolic subgroups ![]() $Q\subseteq P_1\subseteq G$ and their Levi subgroups
$Q\subseteq P_1\subseteq G$ and their Levi subgroups ![]() $M\subseteq M_1$. Then
$M\subseteq M_1$. Then ![]() $Q\cap M_1$ is a standard parabolic subgroup of
$Q\cap M_1$ is a standard parabolic subgroup of ![]() $M_1$ with standard Levi subgroup
$M_1$ with standard Levi subgroup ![]() $M$. Since
$M$. Since ![]() ${{\mathcal {E}}}_{P_1}$ is the canonical reduction,
${{\mathcal {E}}}_{P_1}$ is the canonical reduction, ![]() ${{\mathcal {E}}}_{P_1}\times ^{P_1}M_1$ is a reduction of
${{\mathcal {E}}}_{P_1}\times ^{P_1}M_1$ is a reduction of ![]() ${{\mathcal {E}}}$, and a semi-stable
${{\mathcal {E}}}$, and a semi-stable ![]() $M_1$-bundle. By the first part of the proof of [Reference Chen, Fargues and ShenCFS21, Lemma 6.3], the reduction
$M_1$-bundle. By the first part of the proof of [Reference Chen, Fargues and ShenCFS21, Lemma 6.3], the reduction ![]() ${{\mathcal {E}}}_Q$ corresponds to a unique reduction
${{\mathcal {E}}}_Q$ corresponds to a unique reduction ![]() $({{\mathcal {E}}}_{P_1}\times ^{P_1}M_1)_{M_1\cap Q}$ of
$({{\mathcal {E}}}_{P_1}\times ^{P_1}M_1)_{M_1\cap Q}$ of ![]() ${{\mathcal {E}}}_{P_1}\times ^{P_1}M_1$ to
${{\mathcal {E}}}_{P_1}\times ^{P_1}M_1$ to ![]() $M_1\cap Q$. Since
$M_1\cap Q$. Since ![]() ${{\mathcal {E}}}_{Q}$ is a reduction of
${{\mathcal {E}}}_{Q}$ is a reduction of ![]() ${{\mathcal {E}}}_{P_1}$, we have that
${{\mathcal {E}}}_{P_1}$, we have that ![]() $v({{\mathcal {E}}}_{P_1})-v({{\mathcal {E}}}_Q)$ is a linear combination of coroots in
$v({{\mathcal {E}}}_{P_1})-v({{\mathcal {E}}}_Q)$ is a linear combination of coroots in ![]() $M_1$. Since
$M_1$. Since ![]() ${{\mathcal {E}}}_Q$ is a reduction of
${{\mathcal {E}}}_Q$ is a reduction of ![]() ${{\mathcal {E}}}_{P_2}$, the image of
${{\mathcal {E}}}_{P_2}$, the image of ![]() $v({{\mathcal {E}}}_Q)$ in
$v({{\mathcal {E}}}_Q)$ in ![]() $\pi _1(M_2)_{\mathbb {Q}}$ coincides with the image of
$\pi _1(M_2)_{\mathbb {Q}}$ coincides with the image of ![]() $v({{\mathcal {E}}}_{P_2})$. By the assumption of the theorem this agrees with the image of
$v({{\mathcal {E}}}_{P_2})$. By the assumption of the theorem this agrees with the image of ![]() $v({{\mathcal {E}}}_{P_1})$. Thus
$v({{\mathcal {E}}}_{P_1})$. Thus ![]() $v({{\mathcal {E}}}_{P_1})-v({{\mathcal {E}}}_Q)$ is in fact a linear combination of coroots in
$v({{\mathcal {E}}}_{P_1})-v({{\mathcal {E}}}_Q)$ is in fact a linear combination of coroots in ![]() $M_1\cap M_2=M_Q$. Hence the assumption of [Reference Chen, Fargues and ShenCFS21, Lemma 6.3] is satisfied for the
$M_1\cap M_2=M_Q$. Hence the assumption of [Reference Chen, Fargues and ShenCFS21, Lemma 6.3] is satisfied for the ![]() $M_1$-bundle
$M_1$-bundle ![]() ${{\mathcal {E}}}_{P_1}\times ^{P_1}M_1$, and the lemma finishes the proof.
${{\mathcal {E}}}_{P_1}\times ^{P_1}M_1$, and the lemma finishes the proof.