2 Mathematical formulae

Consider the nonlinear interactions of two trains of progressive gravity waves with small amplitudes in deep water. Assume that the fluid is inviscid and incompressible, the flow is irrotational and the surface tension is neglected. The coordinate system $(x,y,z)$ is set on the free surface, with $z$ -axis positive vertically upwards. The velocity potential ${\it\varphi}(x,y,z,t)$ is governed by the Laplace equation

(2.1) $$\begin{eqnarray}\displaystyle {\rm\nabla}^{2}{\it\varphi}=0,\quad -\infty <z<{\it\eta}(x,y,t), & & \displaystyle\end{eqnarray}$$

subject to the kinematic and dynamic conditions on the unknown free surface $z={\it\eta}(x,y,t)$ :

(2.2) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial ^{2}{\it\varphi}}{\partial t^{2}}+g\frac{\partial {\it\varphi}}{\partial z}+\frac{\partial |\boldsymbol{{\rm\nabla}}{\it\varphi}|^{2}}{\partial t}+\boldsymbol{{\rm\nabla}}{\it\varphi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\left(\frac{1}{2}|\boldsymbol{{\rm\nabla}}{\it\varphi}|^{2}\right)=0, & \displaystyle\end{eqnarray}$$

(2.3) $$\begin{eqnarray}\displaystyle & \displaystyle g{\it\eta}+\frac{\partial {\it\varphi}}{\partial t}+\frac{1}{2}|\boldsymbol{{\rm\nabla}}{\it\varphi}|^{2}=0, & \displaystyle\end{eqnarray}$$

respectively, and the impermeable condition at the bottom:

(2.4) $$\begin{eqnarray}\displaystyle \lim _{z\rightarrow -\infty }\frac{\partial {\it\varphi}}{\partial z}=0, & & \displaystyle\end{eqnarray}$$

where ${\it\eta}(x,y,t)$ denotes the wave elevation, $t$ denotes the time and

(2.5) $$\begin{eqnarray}\displaystyle \boldsymbol{{\rm\nabla}}=\boldsymbol{i}\frac{\partial }{\partial x}+\boldsymbol{j}\frac{\partial }{\partial y}+\boldsymbol{k}\frac{\partial }{\partial z}, & & \displaystyle\end{eqnarray}$$

is a differential operator with $\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}$ denoting the unit vector in the $x,y,z$ direction, respectively.

Consider the nonlinear interaction of a steady-state wave system of two periodic travelling waves. Write

(2.6) $$\begin{eqnarray}\displaystyle {\it\xi}_{i}=\boldsymbol{k}_{i}\boldsymbol{\cdot }\boldsymbol{r}-{\it\sigma}_{i}\,t,\quad i=1,2, & & \displaystyle\end{eqnarray}$$

where $\boldsymbol{k}_{i}$ is the wavenumber, ${\it\sigma}_{i}$ denotes actual wave frequency and $\boldsymbol{r}=x\,\boldsymbol{i}+y\,\boldsymbol{j}$ , respectively. In this paper, we focus on the steady-state cases, say, all wavenumbers $\boldsymbol{k}_{i}$ and actual wave frequency ${\it\sigma}_{i}$ , where $i=1,2$ , are time-independent. Due to the nonlinearity, the actual wave frequency ${\it\sigma}_{i}$ is larger than the linear frequency ${\it\omega}_{i}=\sqrt{g|\boldsymbol{k}_{i}|}$ . Thus, the wave elevation can be expressed in the form

(2.7) $$\begin{eqnarray}\displaystyle {\it\eta}({\it\xi}_{1},{\it\xi}_{2})=\mathop{\sum }_{m=0}^{+\infty }\mathop{\sum }_{n=-\infty }^{+\infty }A_{m,n}\cos (m{\it\xi}_{1}+n{\it\xi}_{2}), & & \displaystyle\end{eqnarray}$$

where $A_{m,n}$ is a real number. Thus, $A_{m,n}^{2}$ versus $|m\boldsymbol{k}_{1}+n\boldsymbol{k}_{2}|$ gives a wave spectrum. Here,

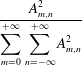(2.8) $$\begin{eqnarray}\frac{A_{m,n}^{2}}{\displaystyle \mathop{\sum }_{m=0}^{+\infty }\mathop{\sum }_{n=-\infty }^{+\infty }A_{m,n}^{2}}\end{eqnarray}$$

gives the percentage of wave energy of the wave component $\cos (m{\it\xi}_{1}+n{\it\xi}_{2})$ . As pointed out by Benney (Reference Benney1962), in a special case of exact resonance

(2.9a,b ) $$\begin{eqnarray}\boldsymbol{k}_{3}=2\boldsymbol{k}_{1}-\boldsymbol{k}_{2},\quad {\it\omega}_{3}=2{\it\omega}_{1}-{\it\omega}_{2},\end{eqnarray}$$

there exist periodic exchanges of wave energy between different wave components, i.e.  $A_{m,n}$ is time-dependent in general. In this case, the corresponding wave spectrum is time-dependent. Note that the wave spectrum is time-independent when $A_{m,n}$ , $\boldsymbol{k}_{i}$ and ${\it\sigma}_{i}$ are constants, corresponding to the so-called ‘steady-state waves’. In this paper, the wavenumber $\boldsymbol{k}_{i}$ and actual wave frequency ${\it\sigma}_{i}>{\it\omega}_{i}=\sqrt{g|\boldsymbol{k}_{i}|}$ , where $i=1,2$ , are given as constants, and the unknown, time-independent coefficient $A_{m,n}$ is determined in the way mentioned below. In addition, without loss of generality, we consider here only the so-called ‘nearly resonant’ case when (2.9) is nearly satisfied.

Since all of the wave amplitudes, the wavenumbers $\boldsymbol{k}_{i}$ and the actual wave frequencies ${\it\sigma}_{i}$ of the steady-state travelling waves are constant, i.e. independent of time, the original initial/boundary-value problem governed by (2.1)–(2.4) can be transformed into a boundary-value one by means of the new variables ${\it\xi}_{1}$ and ${\it\xi}_{2}$ . In the new coordinate system ( ${\it\xi}_{1},{\it\xi}_{2},z$ ), the Laplace equation (2.1) reads

(2.10) $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}\boldsymbol{k}_{i}\boldsymbol{\cdot }\boldsymbol{k}_{j}\frac{\partial ^{2}{\it\varphi}}{\partial {\it\xi}_{i}\partial {\it\xi}_{j}}+\frac{\partial ^{2}{\it\varphi}}{\partial z^{2}}=0,\quad -\infty <z<{\it\eta}({\it\xi}_{1},{\it\xi}_{2}) & & \displaystyle\end{eqnarray}$$

subject to the two boundary conditions on the unknown wave elevation $z={\it\eta}({\it\xi}_{1},{\it\xi}_{2})$ :

(2.11) $$\begin{eqnarray}\displaystyle \mathscr{N}_{1}[{\it\varphi}] & = & \displaystyle \mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}{\it\sigma}_{i}{\it\sigma}_{j}\frac{\partial ^{2}{\it\varphi}}{\partial {\it\xi}_{i}\partial {\it\xi}_{j}}+g\frac{\partial {\it\varphi}}{\partial z}-2\mathop{\sum }_{i=1}^{2}{\it\sigma}_{i}\frac{\partial f}{\partial {\it\xi}_{i}}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}\boldsymbol{k}_{i}\boldsymbol{\cdot }\boldsymbol{k}_{j}\frac{\partial {\it\varphi}}{\partial {\it\xi}_{i}}\frac{\partial f}{\partial {\it\xi}_{j}}+\frac{\partial {\it\varphi}}{\partial z}\frac{\partial f}{\partial z}=0,\quad \text{on }z={\it\eta}({\it\xi}_{1},{\it\xi}_{2}),\end{eqnarray}$$

(2.12) $$\begin{eqnarray}\mathscr{N}_{2}[{\it\varphi},{\it\eta}]={\it\eta}-\frac{1}{g}\left(\mathop{\sum }_{i=1}^{2}{\it\sigma}_{i}\frac{\partial {\it\varphi}}{\partial {\it\xi}_{i}}-f\right)=0,\quad \text{on }z={\it\eta}({\it\xi}_{1},{\it\xi}_{2}),\end{eqnarray}$$

and also the impermeable condition at the bottom

(2.13) $$\begin{eqnarray}\displaystyle \lim _{z\rightarrow -\infty }\frac{\partial {\it\varphi}}{\partial z}=0, & & \displaystyle\end{eqnarray}$$

where $\mathscr{N}_{1}$ and $\mathscr{N}_{2}$ are two nonlinear operators defined above, and

(2.14) $$\begin{eqnarray}\displaystyle f=\frac{1}{2}\left[\mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}\boldsymbol{k}_{i}\boldsymbol{\cdot }\boldsymbol{k}_{j}\frac{\partial {\it\varphi}}{\partial {\it\xi}_{i}}\frac{\partial {\it\varphi}}{\partial {\it\xi}_{j}}+\left(\frac{\partial {\it\varphi}}{\partial z}\right)^{2}\right]. & & \displaystyle\end{eqnarray}$$

For a steady-state wave system with time-independent spectrum, there is no exchange of wave energy between different wave components, i.e. all physical quantities (such as wave amplitude and frequency) are constant. Thus, the steady-state wave elevation ${\it\eta}$ reads

(2.15) $$\begin{eqnarray}\displaystyle {\it\eta}({\it\xi}_{1},{\it\xi}_{2})=\mathop{\sum }_{m=0}^{+\infty }\mathop{\sum }_{n=-\infty }^{+\infty }A_{m,n}\cos (m{\it\xi}_{1}+n{\it\xi}_{2}), & & \displaystyle\end{eqnarray}$$

where $A_{m,n}$ is a constant to be determined. Similarly, the velocity potential ${\it\varphi}({\it\xi}_{1},{\it\xi}_{2},z)$ should be in the form

(2.16) $$\begin{eqnarray}\displaystyle {\it\varphi}({\it\xi}_{1},{\it\xi}_{2},z)=\mathop{\sum }_{m=0}^{+\infty }\mathop{\sum }_{n=-\infty }^{+\infty }B_{m,n}{\it\Psi}_{m,n}({\it\xi}_{1},{\it\xi}_{2},z), & & \displaystyle\end{eqnarray}$$

with the definition

(2.17) $$\begin{eqnarray}\displaystyle {\it\Psi}_{m,n}({\it\xi}_{1},{\it\xi}_{2},z)=\sin (m{\it\xi}_{1}+n{\it\xi}_{2})\exp (|m\boldsymbol{k}_{1}+n\boldsymbol{k}_{2}|z), & & \displaystyle\end{eqnarray}$$

where $B_{m,n}$ is a constant to be determined. Note that the linear governing equation (2.10) and the bottom condition (2.13) are automatically satisfied by (2.16). So, the unknown coefficients $A_{m,n}$ and $B_{m,n}$ are determined by the two nonlinear boundary conditions (2.11) and (2.12).

In the special case (2.9) of the exact resonance, Liao (Reference Liao2011) successfully applied the HAM to gain the (numerically) convergent analytic approximation solutions of the full wave equations for the steady-state exactly resonant waves in deep water with time-independent spectrum. The same approach was further used by Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) to the full wave equations for the steady-state exactly resonant waves in finite water depth, and by Liu & Liao (Reference Liu and Liao2014) to the full wave equation for steady-state exactly resonant waves in deep water in more general cases. The steady-state nearly resonant waves can be obtained in a rather similar way, as shown below. Since almost all mathematical formulae are the same as those given by Liao (Reference Liao2011), we only describe here this approach briefly. For details, please refer to appendix A.

In the HAM-based approach (Liao Reference Liao2011), the velocity potential ${\it\varphi}({\it\xi}_{1},{\it\xi}_{2},z)$ and the free surface elevation ${\it\eta}({\it\xi}_{1},{\it\xi}_{2})$ are expressed by two infinite series

(2.18a,b ) $$\begin{eqnarray}\displaystyle {\it\varphi}({\it\xi}_{1},{\it\xi}_{2},z)={\it\varphi}_{0}({\it\xi}_{1},{\it\xi}_{2},z)+\mathop{\sum }_{m=1}^{+\infty }{\it\varphi}_{m}({\it\xi}_{1},{\it\xi}_{2},z),\quad {\it\eta}({\it\xi}_{1},{\it\xi}_{2})=\mathop{\sum }_{m=1}^{+\infty }{\it\eta}_{m}({\it\xi}_{1},{\it\xi}_{2}), & & \displaystyle\end{eqnarray}$$

where

(2.19) $$\begin{eqnarray}{\it\eta}_{m}=c_{0}\,{\it\Delta}_{m-1}^{{\it\eta}}+{\it\chi}_{m}\,{\it\eta}_{m-1},\quad \text{on }z=0,\end{eqnarray}$$

with the definition ${\it\chi}_{1}=0$ and ${\it\chi}_{m}=1$ for $m>1$ , ${\it\varphi}_{0}({\it\xi}_{1},{\it\xi}_{2},z)$ is an initial guess of the velocity potential, and ${\it\varphi}_{m}({\it\xi}_{1},{\it\xi}_{2},z)$ ( $m\geqslant 1$ ) is governed by the so-called $m$ th-order deformation equation

(2.20) $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}\boldsymbol{k}_{i}\boldsymbol{\cdot }\boldsymbol{k}_{j}\frac{\partial ^{2}{\it\varphi}_{m}}{\partial {\it\xi}_{i}\partial {\it\xi}_{j}}+\frac{\partial ^{2}{\it\varphi}_{m}}{\partial z^{2}}=0,\quad -\infty <z<0, & & \displaystyle\end{eqnarray}$$

subject to the linear boundary condition

(2.21) $$\begin{eqnarray}\mathscr{L}[{\it\varphi}_{m}]=c_{0}\,{\it\Delta}_{m-1}^{{\it\phi}}+{\it\chi}_{m}\,S_{m-1}-\bar{S}_{m},\quad \text{on }z=0,\end{eqnarray}$$

and the bed condition

(2.22) $$\begin{eqnarray}\frac{\partial {\it\varphi}_{m}}{\partial z}=0,\quad \text{as }z\rightarrow -\infty .\end{eqnarray}$$

Here, $\mathscr{L}$ is an auxiliary linear operator and $c_{0}$ is an auxiliary parameter, called ‘the convergence-control parameter’. In addition, all of the terms ${\it\Delta}_{m-1}^{{\it\eta}},{\it\Delta}_{m-1}^{{\it\phi}},S_{m-1},\bar{S}_{m}$ on the right-hand side are determined by the known previous approximations ${\it\eta}_{j}$ and ${\it\varphi}_{j}$ , where $j=0,1,2,\ldots ,m-1$ . For details, please refer to appendix A. Thus, as long as the initial guess ${\it\varphi}_{0}$ of the velocity potential, the auxiliary linear operator $\mathscr{L}$ and the convergence-control parameter $c_{0}$ are properly chosen, one can gain ${\it\eta}_{j}$ and ${\it\varphi}_{j}$ one by one.

It should be emphasized that, in the above-mentioned HAM-based approach (Liao Reference Liao2011), we have great freedom to choose the auxiliary linear operator ${\mathcal{L}}$ , the initial guesses ${\it\varphi}_{0}$ of the velocity potential and the convergence-control parameter $c_{0}$ . As mentioned by Liao (Reference Liao2011), Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) and Liu & Liao (Reference Liu and Liao2014), it is the freedom of the HAM on the choice of the initial guess that provides us a way to handle the singularity of the steady-state exactly resonant waves. In addition, although the so-called ‘convergence-control parameter’ $c_{0}$ in (2.19) and (2.21) has no physical meanings, it provides us a simple way to guarantee the convergence of the solution series (2.18), as illustrated by Liao (Reference Liao2011), Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) and Liu & Liao (Reference Liu and Liao2014) for the steady-state exactly resonant waves.

For the steady-state exactly resonant water waves satisfying the criterion (2.9), Liao (Reference Liao2011) chose the following auxiliary linear operator

(2.23) $$\begin{eqnarray}\mathscr{L}[{\it\varphi}]={\it\omega}_{1}^{2}\frac{\partial ^{2}{\it\varphi}}{\partial {\it\xi}_{1}^{2}}+2{\it\omega}_{1}\,{\it\omega}_{2}\frac{\partial ^{2}{\it\varphi}}{\partial {\it\xi}_{1}\partial {\it\xi}_{2}}+{\it\omega}_{2}^{2}\frac{\partial ^{2}{\it\varphi}}{\partial {\it\xi}_{2}^{2}}+g\frac{\partial {\it\varphi}}{\partial z},\quad -\infty <z<{\it\eta}({\it\xi}_{1},{\it\xi}_{2}),\end{eqnarray}$$

which has the property

(2.24) $$\begin{eqnarray}\mathscr{L}[{\it\Psi}_{m,n}({\it\xi}_{1},{\it\xi}_{2},z)]={\it\lambda}_{m,n}\,{\it\Psi}_{m,n}({\it\xi}_{1},{\it\xi}_{2},z),\quad -\infty <z<{\it\eta}({\it\xi}_{1},{\it\xi}_{2}),\end{eqnarray}$$

and

(2.25) $$\begin{eqnarray}\mathscr{L}^{-1}[{\it\Psi}_{m,n}({\it\xi}_{1},{\it\xi}_{2},z)]=\frac{{\it\Psi}_{m,n}({\it\xi}_{1},{\it\xi}_{2},z)}{{\it\lambda}_{m,n}},\quad -\infty <z<{\it\eta}({\it\xi}_{1},{\it\xi}_{2}),\end{eqnarray}$$

where $\mathscr{L}^{-1}$ is the inverse operator of $\mathscr{L}$ , ${\it\Psi}_{m,n}$ defined by (2.17) is the eigenfunction, and

(2.26) $$\begin{eqnarray}{\it\lambda}_{m,n}=g|m\boldsymbol{k}_{1}+n\boldsymbol{k}_{2}|-(m{\it\omega}_{1}+n{\it\omega}_{2})^{2}\end{eqnarray}$$

is an eigenvalue of ${\mathcal{L}}$ for arbitrary wavenumber $\boldsymbol{k}_{i}$ and the linear frequency ${\it\omega}_{i}=\sqrt{g|\boldsymbol{k}_{i}|}$ of the primary waves, where $i=1,2$ , with the property

(2.27) $$\begin{eqnarray}{\it\lambda}_{1,0}={\it\lambda}_{0,1}=0.\end{eqnarray}$$

In addition, in the case (2.9) for the exactly resonant waves, it holds

(2.28) $$\begin{eqnarray}{\it\lambda}_{2,-1}=0.\end{eqnarray}$$

So, from a mathematical viewpoint, the exactly resonant wave system (2.9) has three eigenvalues to be zero, i.e.

(2.29) $$\begin{eqnarray}{\it\lambda}_{1,0}={\it\lambda}_{0,1}={\it\lambda}_{2,-1}=0.\end{eqnarray}$$

Owing to (2.25), it is the additional zero eigenvalue (such as ${\it\lambda}_{2,-1}$ in the above-mentioned case) that brings singularity to the exactly resonant wave problems. Such kind of singularity is mathematically difficult to handle in the frame of perturbation methods, as mentioned by Madsen & Fuhrman (Reference Madsen and Fuhrman2012). However, it is easy to overcome in the frame of the HAM, as illustrated by Liao (Reference Liao2011), Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) and Liu & Liao (Reference Liu and Liao2014).

Write

(2.30) $$\begin{eqnarray}{\it\delta}_{m,n}=|{\it\lambda}_{m,n}|=|g|m\boldsymbol{k}_{1}+n\boldsymbol{k}_{2}|-(m{\it\omega}_{1}+n{\it\omega}_{2})^{2}|.\end{eqnarray}$$

Thus,

(2.31) $$\begin{eqnarray}{\it\lambda}_{m,n}=0,\quad m^{2}+n^{2}>1\end{eqnarray}$$

corresponds to the exact resonance. So, it is reasonable to define

(2.32) $$\begin{eqnarray}0<|{\it\lambda}_{m,n}|\leqslant 10^{-3},\quad m^{2}+n^{2}>1\end{eqnarray}$$

for the nearly resonant waves. Here $10^{-3}$ is a small number, which can be replaced by others such as $10^{-4}$ , but the conclusions given in this paper are qualitatively the same.

From a mathematical viewpoint, when the resonance criterion (2.9) is nearly satisfied, we have two zero eigenvalues ${\it\lambda}_{1.0}$ and ${\it\lambda}_{0,1}$ , and one eigenvalue ${\it\lambda}_{2,-1}$ very close to zero. In this case, the famous ‘small divisor problem’ (Poincaré Reference Poincaré1892; Yoccoz Reference Yoccoz1992) arises, and the above-mentioned HAM-based approach for steady-state exactly resonant waves (Liao Reference Liao2011; Xu et al. Reference Xu, Lin, Liao and Stiassnie2012; Liu & Liao Reference Liu and Liao2014) does not work, due to the same mathematical difficulties mentioned by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002) and Nicholls & Reitich (Reference Nicholls and Reitich2006) for three-dimensional periodic travelling waves.

How to overcome this ‘small divisor problem’ in the frame of the HAM?

Note that the HAM-based approach (Liao Reference Liao2011; Xu et al. Reference Xu, Lin, Liao and Stiassnie2012; Liu & Liao Reference Liu and Liao2014) works well for the steady-state exactly resonant waves that have more than two zero eigenvalues. Can we transfer the nearly resonant wave problems into exactly resonant ones? If yes, the nearly resonant wave problems can be solved almost in the same way as the exactly resonant ones.

It should be emphasized that the HAM-based approach (Liao Reference Liao2011; Xu et al. Reference Xu, Lin, Liao and Stiassnie2012; Liu & Liao Reference Liu and Liao2014) provides us great freedom to choose the auxiliary linear operator $\mathscr{L}$ . For the steady-state exactly resonant waves in case of (2.9), Liao (Reference Liao2011) simply chose the auxiliary linear operator (2.23), which is exactly the linear part of (2.11). However, if we choose the same auxiliary linear operator (2.23) for the nearly resonant waves, the small divisor ${\it\lambda}_{m,n}$ appears due to (2.25). Fortunately, in the frame of the HAM, it is not absolutely necessary to do so: the freedom provided by the HAM is so large that, for the steady-state nearly resonant waves, we can choose here such a new, generalized auxiliary linear operator

(2.33) $$\begin{eqnarray}\mathscr{L}[{\it\varphi}]={\it\omega}_{1}^{2}\frac{\partial ^{2}{\it\varphi}}{\partial {\it\xi}_{1}^{2}}+{\it\mu}\,{\it\omega}_{1}\,{\it\omega}_{2}\frac{\partial ^{2}{\it\varphi}}{\partial {\it\xi}_{1}\partial {\it\xi}_{2}}+{\it\omega}_{2}^{2}\frac{\partial ^{2}{\it\varphi}}{\partial {\it\xi}_{2}^{2}}+g\frac{\partial {\it\varphi}}{\partial z},\quad -\infty <z<{\it\eta}({\it\xi}_{1},{\it\xi}_{2}),\end{eqnarray}$$

where

(2.34) $$\begin{eqnarray}{\it\mu}=\frac{4{\it\omega}_{1}^{2}+{\it\omega}_{2}^{2}-g|2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}|}{2{\it\omega}_{1}{\it\omega}_{2}}\end{eqnarray}$$

is a constant in the case that (2.9) is nearly satisfied, with the property

(2.35) $$\begin{eqnarray}\mathscr{L}[{\it\Psi}_{m,n}({\it\xi}_{1},{\it\xi}_{2},z)]=\bar{{\it\lambda}}_{m,n}\,{\it\Psi}_{m,n}({\it\xi}_{1},{\it\xi}_{2},z),\quad -\infty <z<{\it\eta}({\it\xi}_{1},{\it\xi}_{2}),\end{eqnarray}$$

and

(2.36) $$\begin{eqnarray}\mathscr{L}^{-1}[{\it\Psi}_{m,n}({\it\xi}_{1},{\it\xi}_{2},0)]=\frac{{\it\Psi}_{m,n}({\it\xi}_{1},{\it\xi}_{2},z)}{\bar{{\it\lambda}}_{m,n}},\quad -\infty <z<{\it\eta}({\it\xi}_{1},{\it\xi}_{2}),\end{eqnarray}$$

in which ${\it\Psi}_{m,n}$ defined by (2.17) is the eigenfunction,

(2.37) $$\begin{eqnarray}\bar{{\it\lambda}}_{m,n}=g|m\boldsymbol{k}_{1}+n\boldsymbol{k}_{2}|-(m^{2}{\it\omega}_{1}^{2}+{\it\mu}mn{\it\omega}_{1}{\it\omega}_{2}+n^{2}{\it\omega}_{2}^{2})\end{eqnarray}$$

is an eigenvalue of the generalized auxiliary linear operator (2.33), respectively.

This is mainly because we have great freedom to choose the auxiliary linear operator in the frame of the HAM-based approach (Liao Reference Liao2011). Note that, for the nearly resonant waves with the small eigenvalue $0<|{\it\lambda}_{2,-1}|\leqslant 10^{-3}$ , there are only two zero eigenvalues ${\it\lambda}_{1,0}={\it\lambda}_{0,1}=0$ , where ${\it\lambda}_{m,n}$ defined by (2.26) is the eigenvalue of the auxiliary linear operator (2.23) that comes from the linear part of the original wave equations. However, using the generalized auxiliary linear operator (2.33), we have now three zero eigenvalues

(2.38) $$\begin{eqnarray}\bar{{\it\lambda}}_{1,0}=\bar{{\it\lambda}}_{0,1}=\bar{{\it\lambda}}_{2,-1}=0,\end{eqnarray}$$

where $\bar{{\it\lambda}}_{m,n}$ is the eigenvalue of (2.33), with the same eigenfunction ${\it\Psi}_{m,n}$ defined by (2.17). In this way, the small divisor (due to small eigenvalue such as ${\it\lambda}_{2,-1}$ ) at low frequency is avoided, or at least moved far away to rather high frequency with physically negligible wave energy, as illustrated below.

In the case (2.9) of the exactly resonant waves with ${\it\lambda}_{2,-1}=0$ , corresponding to

(2.39) $$\begin{eqnarray}4{\it\omega}_{1}{\it\omega}_{2}=4{\it\omega}_{1}^{2}+{\it\omega}_{2}^{2}-g|2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}|\end{eqnarray}$$

due to the definition (2.26), we have ${\it\mu}=2$ according to the definition (2.34). However, when (2.9) is nearly satisfied, ${\it\mu}$ deviates from 2 a little, so that the generalized auxiliary linear operator (2.33) is a little different from (2.23) used by Liao (Reference Liao2011) for the exactly resonant waves. Therefore, the auxiliary linear operator (2.33) works not only for the nearly resonant cases (such as $0<|{\it\lambda}_{2,-1}|\leqslant 10^{-3}$ ) but also for exactly resonant ones (such as ${\it\lambda}_{2,-1}=0$ ), since all other mathematical formulae are the same (Liao Reference Liao2011), as described in appendix A. In other words, the auxiliary linear operator (2.23) used by Liao (Reference Liao2011) for the exactly resonant waves is only a special case of the new auxiliary linear operator (2.33) for the nearly resonant ones. Thus, as long as the generalized auxiliary linear operator (2.33) is used, there always exist three zero eigenvalues

(2.40) $$\begin{eqnarray}\bar{{\it\lambda}}_{1,0}=\bar{{\it\lambda}}_{0,1}=\bar{{\it\lambda}}_{2,-1}=0,\end{eqnarray}$$

no matter whether the criterion (2.9) is either exactly or nearly satisfied. In other words, we can solve the steady-state nearly resonant waves almost in the same way as the exactly resonant ones. Therefore, from the viewpoints of the HAM, the steady-state nearly resonant water waves have nothing fundamentally different from the exactly resonant waves, except the more general definition (2.33) of the auxiliary linear operator $\mathscr{L}$ . We will illustrate this point in § 3 by means of a case study.

In summary, our strategy is to transfer the nearly resonant wave problem (with two zero eigenvalues $\bar{{\it\lambda}}_{1,0}=\bar{{\it\lambda}}_{0,1}=0$ and one small eigenvalue $\bar{{\it\lambda}}_{2,-1}$ that leads to small divisor problem) into the corresponding exactly resonant wave problem with three zero eigenvalues

(2.41) $$\begin{eqnarray}\bar{{\it\lambda}}_{1,0}=\bar{{\it\lambda}}_{0,1}=\bar{{\it\lambda}}_{2,-1}=0\end{eqnarray}$$

by means of choosing a generalized auxiliary linear operator (2.33) in the frame of the HAM. Note that the steady-state exactly resonant travelling waves in deep water and in finite depth governed by the full wave equations were successfully solved by means of the HAM (Liao Reference Liao2011; Xu et al. Reference Xu, Lin, Liao and Stiassnie2012; Liu & Liao Reference Liu and Liao2014), and also observed experimentally in a laboratory with good agreement between analytic approximation and experimental results (Liu et al. Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015). Here, it should be emphasized that, it is the HAM that provides us such kind of freedom to choose the generalized auxiliary linear operator (2.33), which is different from the linear part (2.23) of the original wave equations. This is quite different from perturbation methods (Madsen & Fuhrman Reference Madsen and Fuhrman2012) and the numerical approaches (Meiron et al. Reference Meiron, Saffman and Yuen1982; Craig & Nicholls Reference Craig and Nicholls2002; Nicholls & Reitich Reference Nicholls and Reitich2006), which always regard the linear part (2.23) of the original wave equations as a linear operator. As a result, perturbation methods and these numerical approaches had to directly handle the small divisor problem, which is mathematically very difficult to overcome, as pointed out by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002), Nicholls & Reitich (Reference Nicholls and Reitich2006) and Madsen & Fuhrman (Reference Madsen and Fuhrman2012). This is the novelty value of our HAM-based approach for the steady-state nearly resonant travelling waves.

3 A case study

Without loss of generality, we consider here such a case that the resonance criterion (2.9) is satisfied either exactly or nearly, which can be solved by means of the HAM-based approach (Liao Reference Liao2011) using the generalized auxiliary linear operator (2.33). Moreover, without loss of generality, we consider a special case

(3.1a-c ) $$\begin{eqnarray}{\it\alpha}=\frac{{\rm\pi}}{36},\quad \frac{{\it\sigma}_{1}}{{\it\omega}_{1}}=\frac{{\it\sigma}_{2}}{{\it\omega}_{2}}={\it\epsilon},\quad k_{2}=\frac{{\rm\pi}}{5},\quad 0.89\leqslant \frac{k_{2}}{k_{1}}\leqslant 0.895,\end{eqnarray}$$

where ${\it\alpha}$ denotes the angle between the wavenumbers $\boldsymbol{k}_{1}$ and $\boldsymbol{k}_{2}$ , ${\it\sigma}_{i}$ is the actual frequency, ${\it\omega}_{i}=\sqrt{gk_{i}}$ with $k_{i}=|\boldsymbol{k}_{i}|$ is the linear frequency and ${\it\epsilon}$ is a constant, respectively. Note that the resonance criterion (2.9) is exactly satisfied when $k_{2}/k_{1}=0.8925$ , a case studied by Liao (Reference Liao2011) in detail. Except the generalized auxiliary linear operator (2.33), all other formulae are exactly the same as those for the steady-state exactly resonant waves (Liao Reference Liao2011), as mentioned in appendix A. The (numerically) convergent analytic approximations of the steady-state wave systems for $0.89\leqslant k_{2}/k_{1}\leqslant 0.895$ in the case of (3.1) with ${\it\epsilon}=1.0003$ are obtained almost in the same way to that described by Liao (Reference Liao2011) for the steady-state exactly resonant waves. For details, please refer to appendix A.

We emphasize here that, unlike perturbation techniques and other analytic approximation methods, our HAM-based approach contains the so-called ‘convergence-control parameter’ $c_{0}$ , which has no physical meanings but can provide us a convenient way to guarantee the convergence of solution series. For example, in case of $k_{2}/k_{1}=0.8915$ (corresponding to a case of nearly resonant waves), the solution series converges (strictly speaking, here it is a kind of ‘numerical’ convergence, since we just numerically show the decrease of residual errors versus the order of approximation, which however is not a mathematical proof), rather quickly by means of $-1.25\leqslant c_{0}\leqslant -0.75$ , with the optimal value of $c_{0}$ near $-0.95$ , as shown in table 1. In fact, the numerical convergence of solution series given by the HAM for exactly resonant waves was generally guaranteed in the same way, as shown by Liao (Reference Liao2011), Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012), Liu & Liao (Reference Liu and Liao2014) and Liu et al. (Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015). Note that the numerically convergent analytic approximations for the steady-state exactly resonant waves in deep water given by the HAM-based approach agreed well with the experimental observation in a laboratory, as mentioned by Liu et al. (Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015).

Table 1. Averaged residual errors versus order of approximation for nearly resonant waves in case of ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}=1.0003$ and $k_{2}/k_{1}=0.8915$ by means of different values of the convergence-control parameter $c_{0}$ , with the corresponding distribution of wave energy 81.9 % (the first primary wave component), 9.7 % (the second primary one) and 8.2 % (the nearly resonant one). The angle between two wavenumbers $\boldsymbol{k}_{1}$ and $\boldsymbol{k}_{2}$ of the two primary waves is ${\rm\pi}/36$ . $\mathscr{E}_{{\it\phi}}$ and $\mathscr{E}_{{\it\eta}}$ denote the averaged residual errors of the two boundary conditions on the free surface.

Table 2. Energy distribution of the steady-state exactly or nearly resonant waves in the case of ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$ with various $k_{2}/k_{1}$ . The angle between two wavenumbers $\boldsymbol{k}_{1}$ and $\boldsymbol{k}_{2}$ of the two primary waves is ${\rm\pi}/36$ , and $^{\ast }$ denotes the exactly resonant wave.

In addition, unlike perturbation techniques, the HAM provides us great freedom to choose auxiliary linear operator $\mathscr{L}$ . The original linear operator (2.23) is widely used in perturbation approaches, which unfortunately leads to the so-called ‘small divisor problem’ at a low frequency (say, $m=2,n=-1$ , corresponding to the wave component $\cos (2{\it\xi}_{1}-{\it\xi}_{2})$ ) for the nearly resonant case considered in this paper. Such kind of ‘small divisor problem’ is very difficult to overcome in mathematics, as pointed out by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002), Nicholls & Reitich (Reference Nicholls and Reitich2006) and Madsen & Fuhrman (Reference Madsen and Fuhrman2012). However, by means of simply choosing a new auxiliary linear operator (2.33) in the frame of the HAM, such kind of ‘small divisor problem’ can be easily avoided: it is found that, in the case considered in table 1, the so-called ‘small divisor problem’, corresponding to ${\it\delta}_{m,n}<10^{-3}$ with the definition (2.30), does not occur at least for

(3.2) $$\begin{eqnarray}0<m\leqslant 10^{5},\quad |n|\leqslant 10^{5}\end{eqnarray}$$

by means of using the generalized auxiliary linear operator (2.33). From physical viewpoints, the kinetic energy of wave components with very high frequency, such as

(3.3) $$\begin{eqnarray}A_{m,n}\cos (m{\it\xi}_{1}+n{\it\xi}_{2}),\quad |m|>10^{5}\text{ and/or }|n|>10^{5},\end{eqnarray}$$

is rather small and thus can be ignored. Therefore, in the frame of the HAM, the small divisor problem does not appear even at the 1000th-order of approximations. Note that such high-order analytic approximations are unnecessary from numerical viewpoint, since the averaged residual errors of the two boundary conditions are at the level of $10^{-20}$ by means of the optimal convergence-control parameter $c_{0}=-0.95$ , as shown in table 1. In this way, the ‘small divisor’ at the low frequency of the steady-state nearly resonant waves is successfully moved far away to much higher frequencies, or even to infinity (although we cannot strictly prove this point right now for the considered case). This is mainly because the HAM is fundamentally different from other perturbation approaches, since it has nothing to do with any small physical parameters at all. Note that all other perturbation approaches cannot avoid such kind of ‘small divisor problems’. In other words, our HAM-based approach for the nearly resonant waves is novel, even only from the viewpoint that it can easily move the ‘small divisors’ at low frequency far away to rather high frequency by means of simply choosing the generalized auxiliary linear operator (2.33) that is different from the linear part (2.23) of the original wave equations.

Figure 1. Wave energy distribution (%) of the first primary wave of the steady-state exactly and nearly resonant wave system in the case of ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$ with various $k_{2}/k_{1}$ , when the angle between wavenumbers $\boldsymbol{k}_{1}$ and $\boldsymbol{k}_{2}$ of the two primary waves is ${\rm\pi}/36$ . The filled squares correspond to the exactly resonant wave.

Figure 2. Wave energy distribution (%) of the second primary wave of the steady-state exactly and nearly resonant wave system in the case of ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$ with various $k_{2}/k_{1}$ , when the angle between wavenumbers $\boldsymbol{k}_{1}$ and $\boldsymbol{k}_{2}$ of the two primary waves is ${\rm\pi}/36$ . The filled squares correspond to the exactly resonant wave.

Figure 3. Wave energy distribution (%) of the wave component $\boldsymbol{k}_{3}=2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}$ of the steady-state exactly and nearly resonant wave system in the case of ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$ with various $k_{2}/k_{1}$ , when the angle between wavenumbers $\boldsymbol{k}_{1}$ and $\boldsymbol{k}_{2}$ of the two primary waves is ${\rm\pi}/36$ . The filled squares correspond to the exactly resonant wave.

Here, we use another extraordinary advantage of the HAM, i.e. its freedom on choice of equation type for high-order approximations. In fact, such kind of advantage of the HAM has been successfully applied to many nonlinear problems, as illustrated by Liao & Tan (Reference Liao and Tan2007) who applied the HAM to successfully solve a second-order two-dimensional Gelfand equation even by means of a fourth-order auxiliary linear operator, and a second-order three-dimensional Gelfand equation even by means of a sixth-order auxiliary linear operator, respectively. In this paper, we further illustrate that, by means of simply choosing the generalized auxiliary linear operator (2.33) in the frame of the HAM, the so-called ‘small divisor’ can be easily moved far away from the low frequency to a very high one, where kinetic energy of wave components can be ignored from a physical viewpoint.

Given a value of $k_{2}/k_{1}$ , we search for the corresponding steady-state nearly (or exactly) resonant waves by means of the HAM-based approach mentioned above, and then gain the distribution of wave energy by means of (2.8). It is found that there exist multiple solutions in most cases, as shown in figures 1–3. The energy distribution (%) of the two primary waves (with the wavenumbers $\boldsymbol{k}_{1}$ and $\boldsymbol{k}_{2}$ ) and the nearly (or exactly) resonant wave component (with the wavenumber $\boldsymbol{k}_{3}=2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}$ ) is given in table 2.

Note that the resonance criterion (2.9) is exactly satisfied when $k_{2}/k_{1}=0.8925$ in the case of (3.1). The results of the exact resonance are marked by the filled squares in figures 1–3. It is very interesting that the exactly resonant results are not fundamentally different from other nearly resonant ones: from figures 1–3, one cannot distinguish the exactly resonant results from the nearly resonant ones. It suggests that, from physical viewpoints, nothing is fundamentally different between the steady-state exactly resonant waves and the steady-state nearly resonant ones. Note also that, mathematically speaking, both of the exactly and nearly resonant results are obtained in the same way by means of the same auxiliary linear operator (2.33) in the frame of the HAM. Therefore, from numerical viewpoints, nothing is fundamentally different between the exactly resonant waves and the nearly resonant ones either.

We studied many cases different from (3.1) in a similar way, and always obtained the corresponding steady-state nearly resonant waves. In all of our considered cases, the results of steady-state exactly resonant waves have nothing fundamentally different from those of nearly resonant ones. Thus, from physical viewpoints and in the frame of the HAM, nothing is fundamentally different between the steady-state exactly and nearly resonant waves.

All of our above-mentioned conclusions are based on the HAM-based approach for the full wave equations in deep water. Like Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012), we further numerically solve the Zakharov’s equation so as to verify the correctness of our above-mentioned conclusions. The numerical approach based on the Zakharov’s equation is described briefly in appendix B. For the same cases, numerical results given by the Zakharov’s equation are fundamentally the same as the analytical ones given by our HAM-based approach for the full wave equations, as shown in figures 4–6. In particular, from a physical viewpoint, the results of the steady-state exactly resonant waves (marked by the filled squares) have nothing fundamentally different from those of the nearly resonant ones either. This verifies the validity of the above-mentioned HAM-based approach and our analytic approximations gained from the full wave equations.

Figure 4. Wave energy distribution (%) obtained by Zakharov equation of the first primary wave of the steady-state exactly and nearly resonant wave system in the case of ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$ with various $k_{2}/k_{1}$ , when the angle between wavenumbers $\boldsymbol{k}_{1}$ and $\boldsymbol{k}_{2}$ of the two primary waves is ${\rm\pi}/36$ . The filled squares correspond to the exactly resonant wave.

Figure 5. Wave energy distribution (%) obtained by Zakharov equation of the second primary wave of the steady-state exactly and nearly resonant wave system in case of ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$ with various $k_{2}/k_{1}$ , when the angle between wavenumbers $\boldsymbol{k}_{1}$ and $\boldsymbol{k}_{2}$ of the two primary waves is ${\rm\pi}/36$ . The filled squares correspond to the exactly resonant wave.

Figure 6. Wave energy distribution (%) obtained by Zakharov equation of the wave component $\boldsymbol{k}_{3}=2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}$ of the steady-state exactly and nearly resonant wave system in the case of ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$ with various $k_{2}/k_{1}$ , when the angle between wavenumbers $\boldsymbol{k}_{1}$ and $\boldsymbol{k}_{2}$ of the two primary waves is ${\rm\pi}/36$ . The filled squares correspond to the exactly resonant wave.

4 Concluding remarks and discussions

In this paper, the HAM-based approach given by Liao (Reference Liao2011) for the steady-state exactly resonant waves is generalized for the steady-state nearly resonant waves by simply choosing the generalized auxiliary linear operator (2.33) but keeping all other formulae the same. In this way, we successfully gained, for the first time, the steady-state nearly resonant waves with time-independent spectrum in deep water. To the best of the authors’ knowledge, this kind of steady-state nearly resonant wave has not been obtained analytically from the full wave equations. Therefore, considering the published results about the steady-state exactly resonant waves (Liao Reference Liao2011; Xu et al. Reference Xu, Lin, Liao and Stiassnie2012, Reference Xu, Lin and Liao2015; Liu & Liao Reference Liu and Liao2014; Liu et al. Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015), steady-state gravity waves with time-independent amplitudes widely exist, no matter whether the resonance criterion is exactly or nearly satisfied.

Note that the HAM-based approach for the exactly resonant waves does not work for the nearly resonant ones, since the famous ‘small divisor problem’ appears. Even for numerical approaches, the small divisor problem is rather difficult to overcome in mathematics, as pointed out by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002) and Nicholls & Reitich (Reference Nicholls and Reitich2006). Our strategy is to mathematically transfer the steady-state nearly resonant wave problem into the corresponding exactly resonant ones by means of choosing a more general auxiliary linear operator (2.33) than the linear part (2.23) of the original wave equations. In this way, the ‘small divisor problem’ at low frequency is moved far away to rather high frequency with physically negligible wave energy, such as the wave component

(4.1) $$\begin{eqnarray}A_{m,n}\cos (m{\it\xi}_{1}+n{\it\xi}_{2}),\quad |m|>10^{5}\text{ and/or }|n|>10^{5},\end{eqnarray}$$

with a tiny wave amplitude $A_{m,n}$ much smaller than the small divisor, illustrated in a case study in § 3. Note that it is the HAM that provides us such kind of freedom to choose the generalized auxiliary linear operator (2.33): perturbation and numerical approaches often directly use the linear part (2.23) of the original wave equations, and thus had to directly handle the small divisor problems. So, our HAM-based analytic approximation approach is fundamentally different from other perturbation methods (Madsen & Fuhrman Reference Madsen and Fuhrman2012) and numerical approaches (Meiron et al. Reference Meiron, Saffman and Yuen1982; Craig & Nicholls Reference Craig and Nicholls2002; Nicholls & Reitich Reference Nicholls and Reitich2006). This also shows the novelty and originality of our approach for the steady-state nearly resonant travelling waves.

When the resonance criterion (2.9) is exactly satisfied, the general auxiliary linear operator (2.33) is the same (with ${\it\mu}=2$ ) as (2.23) for the exact resonance (Liao Reference Liao2011), with three eigenvalues being zero. However, using the more general auxiliary linear operator (2.33), we always have three eigenvalues being zero, even in the case of the nearly resonant waves. So, from the viewpoint of the HAM, nothing is fundamentally different between the steady-state exactly and nearly resonant waves. Moreover, from figures 1–3, one cannot distinguish the results of the exact resonance from all other near-resonances. So, from the physical viewpoint, the results of the steady-state exactly resonant waves also have nothing fundamentally different from the nearly resonant ones, either.

Therefore, from the physical viewpoints and in the frame of the HAM, nothing is fundamentally different between the steady-state exactly/nearly resonant waves with time-independent spectrum. Then, a question arises: why should we define the so-called ‘exactly resonant waves’? Let us consider such a thought experiment. Suppose that a person, who does not know Phillips’ criterion of wave resonance at all, applies the above-mentioned HAM-based approach to solve the steady-state travelling waves with time-independent spectrum. For them, the results in the case (2.9) at $k_{2}/k_{1}=0.8925$ have nothing special at all from physical viewpoints. In addition, in the frame of the HAM, all results are gained by using the same mathematical formulae with the same auxiliary linear operator (2.33). Thus, it seems unnecessary for them to define the special case $k_{2}/k_{1}=0.8925$ , which is traditionally called the ‘exactly resonant waves’ in the frame of perturbation methods. Note that the physics behind the same experimental observations should be independent of the used mathematical methods. So, this thought experiment suggests that the essence of the so-called ‘wave resonance’ should be reconsidered carefully from both physical and mathematical viewpoints.

The KP equation is a simplified model for water waves in shallow water. As pointed out by Hammack et al. (Reference Hammack, Scheffner and Segur1989, Reference Hammack, Henderson and Segur2005) and Dubrovin et al. (Reference Dubrovin, Flickinger and Segur1997), the KP equation has a closed-form solution with arbitrary two phase variables. Thus, there exist the steady-state exactly and nearly resonant waves of the KP equation in shallow water, although Hammack et al. (Reference Hammack, Scheffner and Segur1989, Reference Hammack, Henderson and Segur2005) and Dubrovin et al. (Reference Dubrovin, Flickinger and Segur1997) did not mention the wave resonance at all. However, the KP equation is only valid for waves in shallow water, and thus cannot describe waves in deep water. For example, Dubrovin et al. (Reference Dubrovin, Flickinger and Segur1997) gave closed-form analytic solutions of the KP equation with three phases for travelling waves in shallow water, and found that ‘almost every three-phase solution is time-dependent, in every coordinate system’. This conclusion is not correct for waves in deep water, since rather complicated steady-state exactly resonant waves in deep water are indeed found by Liu & Liao (Reference Liu and Liao2014) for the full wave equations. To the best of the authors’ knowledge, the steady-state nearly resonant waves in deep water with time-independent spectrum have never been obtained from the full wave equations in the form of analytic approximations. Neither have they been gained by other perturbation techniques (Madsen & Fuhrman Reference Madsen and Fuhrman2012) and numerical approaches due to the small divisor problem, as mentioned by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002) and Nicholls & Reitich (Reference Nicholls and Reitich2006).

Certainly, a lot of work should be done in future. Similarly, it is straightforward to gain the steady-state nearly resonant waves in a constant water depth and over a bottom with an infinite number of periodic ripples, in a similar manner to Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) and Xu et al. (Reference Xu, Lin and Liao2015) for the exactly resonant ones. In addition, it is quite possible to observe the steady-state nearly resonant waves in deep water experimentally (For this purpose, the steady-state nearly resonant water waves with large enough nonlinearity should be used.) in a basin, just like Liu et al. (Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015) did for the steady-state exactly resonant waves.

The HAM-based analytic approximation approach can successfully avoid the small-divisor problem (related to the nearly resonant wave propagation) by means of moving small divisor at low frequency far away to rather high frequencies with physically negligible wave energy. This is reasonable from physical and numerical viewpoints. However, from strictly mathematical viewpoints, the small divisor might be still an obstacle, since it is even unknown whether or not a solution exists mathematically (Craig & Nicholls (Reference Craig and Nicholls2000) gave a rigorous proof of an existence theorem for two- and three-dimensional travelling water waves in the presence of capillarity. No existence theorems have been strictly proved for water waves in general, to the best of the authors’ knowledge). This is similar to the famous Navier–Stokes equations, whose numerical solutions are widely used, but solution existence of the Navier–Stokes equations is not strictly proved mathematically in general.