2. Sequential parametrized topological complexity

Cohen, Farber and Weinberger introduced the notion of parametrized topological complexity in [Reference Cohen, Farber and Weinberger8] ,[Reference Cohen, Farber and Weinberger9]. This section briefly recalls some basic results related to this notion.

For a Hurewicz fibration $p:E\to B$, consider a subspace of the path space E^I, defined as follows:

\begin{align*}E^I_B:=\{\gamma\in E^I \mid p\circ \gamma(t)=b \text{ for some } b\in B \text{ and for all } t\in[0,1] \}.\end{align*}

The fibre product corresponding to $p:E\to B$ is defined by

\begin{align*}E^n_B:=\{(e_1,\dots,e_n)\in E^n \mid p(e_i)=p(e_j) \text{ for } 1\leq i,j\leq n\}.\end{align*}

Define a map $\Pi_n: E^I_B\to E^n_B$ by

(2)\begin{equation} \Pi_n(\gamma)= \left(\gamma(0), \gamma\left(\frac{1}{n-1}\right),\dots,\gamma\left(\frac{n-2}{n-1}\right),\gamma(1)\right). \end{equation}

It follows from the appendix of [Reference Cohen, Farber and Weinberger9] that $\Pi_n$ is a Hurewicz fibration. A section of $\Pi_n$ is called a sequential parametrized motion planning algorithm.

In their recent paper [Reference Farber and Kumar Paul23], Farber and Paul have established a theory for the sequential parametrized topological complexity, generalizing several results of the original parametrized topological complexity.

Definition 2.1. Let $p:E\to B$ be a fibration. The n-th sequential parametrized topological complexity of p is denoted by $\mathrm{TC}_n[p:E\to B]$, and defined as

\begin{align*}\mathrm{TC}_n[p:E\to B]:=\mathrm{secat}(\Pi_n).\end{align*}

It is observed in [Reference Farber and Kumar Paul23] that for a pullback fibration $q:E'\to B'$ along a map $f:B'\to B$ of $p:E\to B$, we have

\begin{align*}\mathrm{TC}_n[q:E'\to B']\leq \mathrm{TC}_n[p:E\to B].\end{align*}

In particular, for a fibration $p:E\to B$ with fibre F, we have

(3)\begin{equation} \mathrm{TC}_n(F)\leq \mathrm{TC}_n[p:E\to B]. \end{equation}

Various bounds have been established to estimate the parametrized topological complexity in [Reference Cohen, Farber and Weinberger8], and later, these were generalized in the sequential setting in [Reference Farber and Kumar Paul23]. For example, the cohomological lower bound for the parametrized topological complexity is given in [Reference Cohen, Farber and Weinberger8], and its sequential analogue is stated in [Reference Farber and Kumar Paul23]. We state the sequential version of the cohomological lower bound.

Theorem 2.2 ([Reference Farber and Kumar Paul23, proposition 6.3])

Let $p:E\to B$ be a fibration, $\triangle: E\to E^n_B$ be the diagonal map and $\triangle^{\ast}:H^{\ast}(E^n_B;R)\to H^{\ast}(E;R)$ be the corresponding induced homomorphism. Suppose there exists cohomology classes $u_i\in \ker(\triangle^{\ast}) $ for $1\leq i\leq r$ such that their cup product $u_1\cup \dots \cup u_r$ does not vanish. Then

\begin{align*}\mathrm{TC}_n[p:E\to B]\geq r+1.\end{align*}

In [Reference Farber and Kumar Paul23], Farber and Paul established a dimension-connectivity upper bound on the sequential parametrized topological complexity, generalizing the base case proved in [Reference Cohen, Farber and Weinberger8, proposition 7.1].

Theorem 2.3 [Reference Farber and Kumar Paul23, proposition 6.1]

Let $p:E\to B$ be a fibration with fibre F such that spaces E, B and F are CW-complexes. Suppose that for $m\geq 0$, F is m-connected. Then

\begin{align*}\mathrm{TC}_n[p:E\to B] \lt \frac{n\mathrm{dim}(F)+\mathrm{dim}(B)+1}{m+1}+1.\end{align*}

We now present the computations of the sequential parametrized topological complexity for some fibrations. Sarkar and Zvengrowski [Reference Sarkar and Zvengrowski39] introduced a class of topological spaces called generalized projective product spaces. We will now recall the definition of these spaces. Let M and N be CW-complexes with involutions $\tau \colon M \to M$ and $\sigma \colon N \to N$, where σ is fixed-point-free. The following identification space is called generalized projective product space

(4)\begin{equation} X(M, N) :=\displaystyle\frac{M \times N}{(x,y)\sim (\tau(x), \sigma(y))}. \end{equation}

Note that this class of manifolds includes all projective product spaces [Reference Davis17] and Dold manifolds [Reference Dold18]. The author and Soumen Sarkar studied the LS-category and topological complexity of generalized projective product spaces in [Reference Daundkar and Sarkar15].

Example 2.4.

Observe that there is a fibre bundle

(5)\begin{equation} M \hookrightarrow{} X(M, N) \stackrel{p}\longrightarrow N/\left \lt \sigma \right \gt , \end{equation}

defined by $p([(x,y)])=[y]$, where $N/\left \lt \sigma \right \gt $ is the orbit space of the group $\left \lt \sigma \right \gt $ action on N induced by the involution σ.

It follows from theorem 2.3 that

\begin{align*}\mathrm{TC}_n[p:X(M,N)\to N/\left \lt \sigma \right \gt ] \lt n\dim(M)+\dim(N)+2.\end{align*}

In particular,

\begin{align*}\mathrm{TC}_n[p:X(M,N)\to N/\left \lt \sigma \right \gt ]\leq n\dim(M)+\dim(N)+1.\end{align*}

Also, from (3), we have the following lower bound:

\begin{align*}\mathrm{TC}_n(M)\leq \mathrm{TC}_n[p:X(M,N)\to N/\left \lt \sigma \right \gt ].\end{align*}

Observe that if $N=S^0$ with free involution, then $N/\left \lt \sigma \right \gt $ is a singleton and $X(M,N)\cong M$. Thus, $\mathrm{TC}_n[p:X(M,S^0)\to S^0/\left \lt \sigma \right \gt ]=\mathrm{TC}_n(M)$.

Note that if $N=S^1$ with the antipodal involution and $\mathrm{TC}_n(M)=n\dim(M)+1$, then

\begin{align*}n\dim(M)+1\leq\mathrm{TC}_n[p:X(M,N)\to N/\left \lt \sigma \right \gt ]\leq n\dim(M)+2.\end{align*}

One example of spaces with involutions having maximal sequential topological complexity are orientable surfaces of positive genus. An orientable surface of genus $g\geq 1$ can be embedded in $\mathbb{R}^3$ to admit antipodal involution. It was proved in [Reference González, Gutiérrez, Gutiérrez and Lara29] that $\mathrm{TC}_n(\Sigma_g)=n\dim(\Sigma_g)+1=2n+1$.

In some cases, we can now compute the exact value of sequential parametrized topological complexity. Suppose for $d\geq 2$, consider $M=S^d$ with an involution τ obtained by reflecting S^d across the X-axis. Observe that $p:X(S^d,N)\to N/\left \lt \sigma \right \gt $ is a sphere bundle with structure group $\mathbb{Z}_2=\left \lt \tau \right \gt $. One can generalize [Reference Colman and Grant12, example 5.9] to obtain $\mathrm{TC}_{\mathbb{Z}_2,n}(S^d)=n+1$. Then it follows from [Reference Farber and Oprea25, theorem 3.4] that

\begin{align*}\mathrm{TC}_n[p:X(S^d,N)\to N/\left \lt \sigma \right \gt ]\leq \mathrm{TC}_{\mathbb{Z}_2,n}(S^d)=n+1.\end{align*}

From (3) we have $\mathrm{TC}_n(S^d)\leq \mathrm{TC}_n[p:X(S^d,N)\to N/\left \lt \sigma \right \gt ]$. Therefore, if d is even, we have $ \mathrm{TC}_n[p:X(S^d,N)\to N/\left \lt \sigma \right \gt ]=n+1$. If d is odd, then $\mathrm{TC}_n[p:X(S^d,N)\to N/\left \lt \sigma \right \gt ]\in\{n, n+1\}$.

Example 2.5.

In [Reference Milnor36], Milnor introduced a class of submanifolds of the products of real and complex projective spaces to define generators for the unoriented cobordism algebra. We define these manifolds as follows: Let r and s be integers such that $0\leq s\leq r$. A real Milnor manifold, denoted by $\mathbb{R}M_{r,s}$, is the submanifold of the product $\mathbb{R}P^r \times \mathbb{R}P^s$ of real projective spaces. It is defined as follows:

\begin{align*}\mathbb{R}M_{r,s}:=\Big\{\big([x_0: \dots: x_r], [y_0:\dots:y_s]\big) \in \mathbb{R}P^r \times \mathbb{R}P^s\mid x_0y_0 + \cdots + x_sy_s=0\Big\}.\end{align*}

The real Milnor manifold $\mathbb{R}M_{r,s}$ is an $(s+r-1)$-dimensional closed, smooth manifold. There is a fibre bundle:

(6)\begin{equation} \mathbb{R}P^{r-1} \stackrel{i}{\hookrightarrow} \mathbb{R}M_{r,s} \stackrel{p}{\longrightarrow} \mathbb{R}P^{s}. \end{equation}

A complex Milnor manifold, denoted by $\mathbb{C} M_{r,s}$, can be defined in a similar manner:

\begin{align*}\mathbb{C} M_{r,s}:=\Big\{\big([z_0:\dots:z_r],[w_0:\dots:w_s]\big)\in \mathbb{C} P^r \times \mathbb{C} P^s\mid z_0\overline{w}_0+\cdots+z_s\overline{w}_s=0\Big\}.\end{align*}

Note that $\mathbb{C} M_{r,s}$ is a closed, smooth manifold of dimension $2(s+r-1)$. Just as in the real case, $\mathbb{C} M_{r,s}$ is the total space of the fiber bundle:

(7)\begin{equation} \mathbb{C} P^{r-1} \stackrel{i}{\hookrightarrow} \mathbb{C} M_{r,s} \stackrel{q}{\longrightarrow} \mathbb{C} P^{s}. \end{equation}

The author and B. Singh [Reference Daundkar and Singh16] studied sequential topological complexity of $\mathbb{R} M_{r,s}$ and $\mathbb{C} M_{r,s}$, obtaining several sharp bounds and computing exact values in various cases.

Note that, using (3) and [Reference Farber and Kumar Paul23, proposition 6.1], we obtain

\begin{align*}\mathrm{TC}_n(\mathbb{R} P^{r-1})\leq\mathrm{TC}_n[p:\mathbb{R}M_{r,s} \stackrel{}{\longrightarrow} \mathbb{R}P^{s}]\leq n(r-1)+s+1.\end{align*}

The topological complexity of projective spaces has been studied in [Reference Farber, Tabachnikov and Yuzvinsky26] and the corresponding sequential analogue is discussed in [Reference Cadavid-Aguilar, González, Gutiérrez, Guzmán-Sáenz and Lara6].

If $r=2^m+1$, then it is known that $\mathrm{TC}_n(\mathbb{R} P^{r-1})=n(r-1)$. Thus, for $r=2^m+1$, we have

\begin{align*}n(r-1)\leq\mathrm{TC}_n[p:\mathbb{R}M_{r,s} \stackrel{}{\longrightarrow} \mathbb{R}P^{s}]\leq n(r-1)+s+1.\end{align*}

Since $\mathbb{C} M_{r,s}$ is simply connected, applying theorem 2.3 gives us

\begin{align*}\mathrm{TC}_n[q:\mathbb{C} M_{r,s} \stackrel{}{\longrightarrow} \mathbb{C} P^{s}]\leq n(r-1)+s+1.\end{align*}

Since $\mathrm{TC}_n(\mathbb{C} P^{r-1})=n(r-1)+1$, using (10) we obtain

\begin{align*}n(r-1)+1=\mathrm{TC}_n(\mathbb{C} P^{r-1})\leq \mathrm{TC}_n[q:\mathbb{C} M_{r,s} \stackrel{}{\longrightarrow} \mathbb{C} P^{s}].\end{align*}

Thus, if s = 1, then

\begin{align*}n(r-1)+1\leq \mathrm{TC}_{n}[\mathbb{C} M_{r,s} \stackrel{q}{\longrightarrow} \mathbb{C} P^1]\leq n(r-1)+2.\end{align*}

3. Equivariant sectional category

The sectional category of a Hurewicz fibration was introduced by Švarc in [Reference Švarc42]. Colman and Grant [Reference Colman and Grant12] generalized this notion and introduced the equivariant sectional category. Let G be a compact Lie group and $E, B$ be G-spaces such that $p\colon E \to B$ is a G-map. The symbol $\simeq_G$ denotes the G-homotopy equivalence. In this paper, when we refer to a group G, we mean a compact Lie group.

If no such k exists, we say $\mathrm{secat}_G(p)=\infty$. If G is a trivial group, then $\mathrm{secat}_G(p)$ is called the sectional category of p, denoted by $\mathrm{secat}(p)$.

Fadell [Reference Fadell19] introduced the notion of G-equivariant LS-category for G-spaces, and it was later studied by Marzantowicz in [Reference Marzantowicz35], Clapp and Puppe in [Reference Clapp and Puppe7], Colman [Reference Colman11], and Angel, Colman, Grant, and Oprea in [Reference Angel, Colman, Grant and Oprea1]. This homotopy invariant of a G-space X is denoted by $\mathrm{cat}_G(X)$. Before defining this notion, we recall the notion of G-categorical sets. An invariant open set U of a G-space X is called G-categorical if the inclusion $i_{U}:U\hookrightarrow X$ is G-homotopic to the map that takes values in a single orbit.

Let H be a closed subgroup of G and X be a G-space. The H-fixed point set of X is denoted by X^H and defined as

\begin{align*}X^H:=\{x\in X \mid hx=x \text{for all } h\in H\}.\end{align*}

It can be observed that if $x\in X$ is fixed point of a G-action and if X is a G-connected space, then for the inclusion map $i\colon \{x\} \to X$, $\mathrm{secat}_G(i\colon \{x\} \to X) = \mathrm{cat}_G(X)$; see [Reference Colman and Grant12, corollary 4.7]. Additionally, if G is trivial, then $\mathrm{cat}_G(X)=\mathrm{cat}(X)$.

We now recall the notion of sequential (higher) equivariant topological complexity introduced by Bayeh and Sarkar in [Reference Bayeh and Sarkar3]. This notion generalizes the equivariant topological complexity introduced by Colman and Grant in [Reference Colman and Grant12].

Let X be a G-space. Observe that the path space admits G-action via $(g\cdot \gamma)(t):=g\cdot \gamma(t)$. The product Xⁿ is also a G-space with the diagonal G-action. One can check that the fibration (1) is a G-fibration.

In the next section, we introduce sequential equivariant parametrized topological complexity, a special case of which is sequential equivariant topological complexity.

Several results from [Reference Colman and Grant12] are generalized by Bayeh and Sarkar in [Reference Bayeh and Sarkar3]. The following result is a sequential analogue of [Reference Colman and Grant12, corollary 5.8]. We couldn’t find this result in Bayeh and Sarkar’s paper [Reference Bayeh and Sarkar3]. Since the proof is fairly straightforward, we only include the statement.

Proposition 3.5. Let X be a G-space and H be a stabilizer of some $a\in X$. Then

\begin{align*}\mathrm{cat}_H(X^{n-1})\leq \mathrm{TC}_{G,n}(X).\end{align*}

The following result is also missed out in [Reference Bayeh and Sarkar3], which is a sequential analogue of [Reference Colman and Grant12, proposition 5.12]. Since the proof is almost identical to that of [Reference Colman and Grant12, proposition 5.12], we omit it here.

4. Equivariant parametrized topological complexity

This section introduces the concept of sequential equivariant parametrized topological complexity and examines its properties. We define fibrewise G-homotopy equivalent fibrations and prove one of the important results of this section which states that the sequential G-equivariant parametrized topological complexity of fibrewise G-homotopy equivalent fibrations coincides. Then, we obtain various bounds on sequential equivariant parametrized topological complexity, which generalize bounds on the equivariant topological complexity obtained by Colman and Grant in [Reference Colman and Grant12].

Let $p:E\to B$ be a G-fibration, and let $E^n_B$ be the corresponding fibre product. Define a G-action on $E^n_B$ as $g\cdot(e_1,\dots,e_n)=(ge_1,\dots,ge_n)$. Since p is G-map, we have $p(ge_i)=gp(g_i)=gp(e_j)=p(ge_j)$. Thus, this action is well-defined. The G-action on $E^I_B$ is defined as follows. Let $\gamma\in E^I_B$. Then define $(g\cdot \gamma)(t)=g\gamma(t)$. Note that $p(g\cdot \gamma)=gp(\gamma)$ and since $p(\gamma)$ is constant, $p(g\cdot \gamma)$ is also constant. Therefore, $E^I_B$ also admits a G-action. Observe that for $g\in G$ we have:

\begin{align*} \Pi_n(g\gamma)&= \left(g\gamma(0), g\gamma\left(\frac{1}{n-1}\right),\dots,g\gamma\left(\frac{n-2}{n-1}\right),g\gamma(1)\right)\\ &= g\cdot\left(\gamma(0), \gamma\left(\frac{1}{n-1}\right),\dots,\gamma\left(\frac{n-2}{n-1}\right),\gamma(1)\right) =g\cdot \Pi_n(\gamma). \end{align*}

Thus, $\Pi_n$ is G-equivariant.

Definition 4.1. The sequential equivariant parametrized topological complexity of a G-fibration $p:E\to B$, denoted by $\mathrm{TC}_{G,n}[p:E\to B]$, is defined as

\begin{align*}\mathrm{TC}_{G,n}[p:E\to B]:=\mathrm{secat}_G(\Pi_n:E^I_B\to E^n_B).\end{align*}

We recall that Colman and Grant observed in [Reference Colman and Grant12] that the fibration π_n is a G-fibration (also it follows from [Reference Grant30, proposition 2.5]). This can be proved using an equivariant analogue of [Reference Spanier40, theorem 2.8.2]. Cohen, Farber and Weinberger [Reference Cohen, Farber and Weinberger8, Appendix] have shown that the map $\Pi_n$ is a fibration. We want to prove an equivariant analogue of their result.

In [Reference İlhan31], an equivariant analogue of lifting function was defined and equivariant analogue of [Reference Spanier40, theorem 2.7.8] was proved (see [Reference İlhan31, § 2.1 and proposition 2.1.3]). We also refer the reader to [Reference Grant30, Reference İlhan32, Reference Waner43 § 2].

Let $p:E\to B$ be a G-fibration. Let X be a topological space with a trivial G-action. Consider the space $E^X_B=\{f:X\to E \mid p\circ f \text{is constant}\}$ with the compact open topology, on which the G-action is defined as $(gf)(x)=g(f(x))$. Let (K, L) be a pair of CW-complexes with trivial G-action, and $\Pi:E^K_B\to E^L_B$ be the restriction map defined by $\Pi(f)=f|_{L}$. Note that Π is a G map.

Proof. Since $p:E\to B$ is a G-fibration, it follow that (see [Reference İlhan31, proposition 2.1.3] or [Reference Grant30, lemma 2.2]), there exist a G-lifting function $\lambda: \bar{B}\to E^I$, where $\bar{B}=\{(e,\gamma)\in E\times B^I \mid p(e)=\gamma(0)\}$, such that $p\circ \lambda(e,\gamma)=\gamma$ and $\lambda(e,\gamma)(0)=e$. Consider the trivial action of G on L × I. An element h of $(E^L_B)^I$ can be considered as a map $h:L\times I\to E$ such that for any $t\in I$, the image $h(L\times \{t\})\subseteq E$ lies in a single fibre of p. Note that, we need to construct a G-lifting function $\Lambda: \bar{E}^L_B\to (E^K_B)^I$ for Π, where

\begin{align*}\bar{E}^L_B=\{(f,h)\in E^K_B\times (E^L_B)^I \mid f(x)=h(x,0) \text{for all} x\in L\}.\end{align*}

That is, Λ should satisfy the conditions: $\Lambda(f,h)(x,t)=h(x,t)$ for all $x\in L$ and $t\in I$, and $\Lambda(f,h)(x,0)=f(x)$ for $x\in K$. Note that $\bar{E}^L_B$ has the diagonal G-action.

Let $h\in (E^L_B)^I$. Define a path ω_h in B by $\omega_h(t)=p\circ h(x,t)$ for $x\in L$. Now define $\tilde{\Lambda}:\bar{E}^L_B\to (E^K_B)^I$ by $\tilde{\Lambda}(f,h)(x,t)=\lambda(f(x), \omega_h)(t)$. Note that for $g\in G$, we have $\tilde{\Lambda}(gf, gh)(x, t) =\lambda (gf(x), \omega_{gh})(t) = \lambda(gf(x), g\omega_h)(t) = g\lambda(f(x), \omega_h)(t)$. Thus, $\tilde{\Lambda}$ is a G-map. Observe that, $\tilde{\Lambda}(f,h)(x,0)=f(x)$ for $x\in K$. Thus $\tilde{\Lambda}$ satisfies the second condition of a G-lifting function. However, the condition $\tilde{\Lambda}(f,h)(x,t)=h(x,t)$ for all $x\in L$ is not guaranteed. Thus, we need a modification to $\tilde{\Lambda}$.

Define $\alpha_h:L\times I\times I\to E$ by

\begin{align*} \alpha_h(x,\tau,t)=\begin{cases} h(x,t),& 0\leq t\leq \tau,\\ \lambda(h(x,\tau), \omega_h^{[\tau,1]}(\frac{t-\tau}{1-\tau})),& \tau\leq t\leq 1, \end{cases} \end{align*}

where $\omega_h^{[\tau,1]}$ is a path defined by $\omega_h^{[\tau,1]}(s)=\omega_h(\tau+(1-\tau)s)$ for $s\in I$. Note that for $x\in L$, we have $p\circ \alpha_h(x,\tau,t)=\omega_h(t)$, $\alpha_h(x,0,t)=\lambda(h(x,0),\omega_h)(t)=\tilde{\Lambda}(f,h)(x,t)$, and $\alpha_h(x,1,t)=h(x,t)$.

We will now define

\begin{align*}\Lambda: \bar{E^L_B}\to (E^K_B)^I \text{ by } \Lambda(f,h)(x,t)=(\tilde{\Lambda}(f,h)\cup \alpha_h)(\rho(x,1),t),\end{align*}

where $\rho:K\times I\to K\times \{0\}\cup L\times I$ is a retraction. Here we have treated $\tilde{\Lambda}(f,g)$ as a function from $K\times \{0\}\times I\to E$. Since for $g\in G$, we have $g\alpha_h=\alpha_{gh}$ and $\tilde{\Lambda}$ is a G-map, we conclude that Λ is a G-map. One can check that $\Lambda(f,h)(x,t)=h(x,t)$ for all $x\in L$ and $\Lambda(f,h)(x,0)=f(x)$ for $x\in K$. Thus, Λ is a G-lifting function for Π.

The following proposition is a straightforward application of definition 4.1.

Proof. Parts (1) and (2) are obvious. We prove part (3) here. Let F and B be G-spaces and let $p: F\times B (=E)\to B$ be a trivial G-fibration. Then we have $E^n_B=F^n\times B$, $E^I_B=F^I\times B$ and $\Pi_n: E^I_B\to E^n_B$ becomes $\pi_n\times id: F^I\times B\to F^n\times B$. It is easy to see that $\mathrm{secat}_G(\pi_n\times id)=\mathrm{secat}_G(\pi_n)$. Thus we have

(8)\begin{equation} \mathrm{TC}_{G,n}[p:F\times B\to B]=\mathrm{TC}_{G,n}(F) . \end{equation}

In the following result, we establish an equivariant analogue of [Reference Daundkar14, lemma 2.4]. We also show that if the fixed point set of base space of a G-fibration is non-empty, then the sequential equivariant topological complexity of fibre is dominated by the sequential equivariant parametrized topological complexity.

Proposition 4.6. Let $p:E\to B$ be a G-fibration and let $\tilde{p}: \tilde{E}\to \tilde{B}$ be a pullback fibration corresponding to a G-map $\tilde{B}\to B$. Then,

(9)\begin{equation} \mathrm{TC}_{G,n}[\tilde{p}:\tilde{E}\to \tilde{B} ]\leq \mathrm{TC}_{G,n}[p:E\to B]. \end{equation}

Moreover, if $E^G\neq \emptyset$, then F admits G-action and

(10)\begin{equation} \mathrm{TC}_{G,n}(F)\leq \mathrm{TC}_{G,n}[p:E\to B]. \end{equation}

Proof. We consider the diagram of a pullback of G-fibrations

Note that f ^ʹ induces a G-map $\tilde{f'}: \tilde{E}^n_{\tilde{B}}\to E^n_B$ defined by $\tilde{f'}(e_1,\dots,e_n)=(f'(e_1),\dots,f'(e_n))$. The map $\tilde{f'}$ is well defined because of the commutativity of the above diagram. One can observe that the pullback of the G-fibration $\Pi_n: E^I_B\to E^n_B$ along $\tilde{f'}$ is isomorphic as a G-fibration to $\tilde{\Pi}_n:\tilde{E}^I_{\tilde{B}}\to \tilde{E}^n_{\tilde{B}}$. Thus,

\begin{align*}\mathrm{TC}_{G,n}[\tilde{p}:\tilde{E}\to \tilde{B}] = \mathrm{secat}_G(\tilde{\Pi}_n)\leq \mathrm{secat}_G(\Pi_n)=\mathrm{TC}_{G,n}[p: E\to B].\end{align*}

Since $E^G\neq \emptyset$, we have $B^G\neq \emptyset$. Then it is easy to see that, for $e\in E^G$, the fibre $F:=p^{-1}(p(e))$ admits a G-action. Then (10) follows from (9) by taking the pullback along the inclusion $\{b\}\hookrightarrow B$.

In the following result, we show that, under certain conditions, having a continuous G-equivariant parametrized motion planning algorithm for a G-fibration is equivalent to the fibre being G-contractible.

In [Reference tom Dieck41], tom Dieck introduced the notion of principal $(G,\alpha, A)$-bundles, where G and A are topological groups and G acts on A via a continuous homomorphism $\alpha:G\to \mathrm{Aut}(A)$. For more details, see [Reference Murayama and Shimakawa37]. We now define these bundles.

For such bundles we establish a relation between sequential equivariant parametrized topological complexity and the G-equivariant category of $A^{n-1}$. We observe that the latter coincides with the sequential G-equivariant topological complexity of A. The following result generalizes [Reference Farber and Kumar Paul23, proposition 3.3].

Theorem 4.9 Let $p:E\to B$ be a principal $(G,\alpha, A)$-bundle such that A is G-connected. Then,

\begin{align*}\mathrm{TC}_{G,n}[p:E\to B]=\mathrm{cat}_G(A^{n-1})=\mathrm{TC}_{G,n}(A).\end{align*}

Proof. Note that G acts on A via a continuous homomorphism $\alpha:G\to \mathrm{Aut}(A)$. Therefore, for the identity $e\in A$, we have $g\cdot e=\alpha(g)(e)=e$. Thus, e is a fixed point of the G-action on A. This allows the path space $P_0(A)=\{\gamma\in A^I \mid \gamma(0)=e\}$ to admit a G-action. Moreover, we have assumed that A is G-connected. Thus, it follows from [Reference Colman and Grant12, corollary 4.7] that $\mathrm{secat}_G(q:P_0(A)\to A^{n-1})=\mathrm{cat}_G(A^{n-1})$, where q is a G-map defined by $q(\gamma):=(\gamma(\frac{1}{n-1}),\dots,\gamma(\frac{n-2}{n-1}),\gamma(1))$.

We now use a similar idea which was used in [Reference Farber and Kumar Paul23, proposition 3.3]. Consider the following commutative diagram:

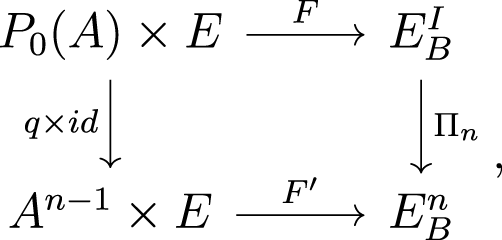
where F and F ^ʹ are defined such that

\begin{align*}F(\gamma,x)(t)=x \cdot \gamma(t) \text{and } F'(a_1,\dots,a_{n-1},x)=(x,x\cdot a_1,\dots,x\cdot a_{n-1}), \text{respectively} .\end{align*}

Note that F and F ^ʹ are homeomorphisms. We will verify that they are indeed G-maps. Let $g\in G$. Then we have $F(g\gamma,gx)(t)= gx \cdot g\gamma(t)= g (x \cdot \gamma(t))=gF(\gamma,x)(t)$ and

\begin{align*} F'(ga_1,\dots,ga_{n-1},gx) &= (gx, gx \cdot ga_1,\dots, gx\cdot ga_{n-1})\\ &= (gx, g(x\cdot a_1),\dots, g(x\cdot a_{n-1}))\\ &= g(x, x\cdot a_1,\dots,x\cdot a_{n-1})\\ &= gF'(a_1,\dots,a_{n-1},x). \end{align*}

Thus, F and F ^ʹ are G-equivariant homeomorphisms. Consequently, we get

\begin{align*}\mathrm{TC}_{G,n}[p:E\to B]=\mathrm{secat}_G(\Pi_n)=\mathrm{secat}_G(q\times id)=\mathrm{secat}_G(q)=\mathrm{cat}_{G}(A^{n-1}).\end{align*}

The equality $\mathrm{cat}_G(A^{n-1})=\mathrm{TC}_{G,n}(A)$ follows from proposition 3.6.

4.1. Fibrewise G-homotopy invariance

This subsection aims to achieve a fibrewise G-homotopy invariance of G-equivariant parametrized topological complexity. We begin by proving a lemma which plays a crucial role in showing that the sequential G-equivariant parametrized topological complexity of fibrewise G-homotopy equivalent fibrations coincide.

Lemma 4.10.

1. (1) Suppose $p:E\to B$ and $p':E'\to B$ are G-fibrations. If there is a continuous G-map $f:E\to E'$ which fits into the following commutative diagram

   

   then $\mathrm{secat}_G(p')\leq \mathrm{secat}_G(p)$.

2. (2) Suppose we have the following commutative diagram of G-maps:

   

   where $p:E\to B$ and $p':E'\to B'$ are G-fibrations. Suppose $f'\circ f\simeq_G id_B$. Then

   \begin{align*}\mathrm{secat}_G(p)\leq \mathrm{secat}_G(p').\end{align*}

Proof. For (1), consider a G-invariant open set U of B with a G-section s_U of p. Note that $f\circ s_U$ is a G-map, and due to the commutativity of the above diagram, it defines a G-section of p ^ʹ. Thus, we get the desired inequality in (1).

For (2), consider the pullback fibration $q:B\times_{B'} E'\to B$ of a G-fibration $p':E'\to B'$ along $f:B\to B'$. Then, from [Reference Colman and Grant12, proposition 4.3], we have:

(11)\begin{equation} \mathrm{secat}_{G}(q)\leq \mathrm{secat}_{G}(p'). \end{equation}

Let $\tilde{F}=F'\circ q'$, where $q':B\times_{B'} E'\to E'$ be the projection onto the second factor. Then, we have $p\circ\tilde{F}((b,x))=p\circ F'\circ q'((b,x))=f'\circ p'(x)$. Since $p'(x)=f(b)$, it follows that $p\circ\tilde{F}((b,x))=f'\circ f\circ q(b,x)$. In other words, $p\circ\tilde{F}=f'\circ f\circ q$. Since $f'\circ f\simeq_G id_B$, we have $p\circ\tilde{F}\simeq_G q$. Note that we have the following G-homotopy commutative diagram:

Now consider a G-homotopy $H_t:B\to B$ such that $H_0=f'\circ f$ and $H_1=id_B$. Using the G-homotopy lifting property, we obtain a G-homotopy $J_t:B\times_{B'} E'\to E$ such $J_0=\tilde{F}$, $p\circ J_t=H_t\circ q$ and $p\circ J_1=q$. Thus, from part (1), we get that $\mathrm{secat}_G(p)\leq \mathrm{secat}_G(q)$. We can now conclude the proof using (11).

We need the following definitions before introducing the equivariant analogue of fibrewise homotopy equivalent fibrations.

Definition 4.11. Let $p:E\to B$ and $q: E'\to B$ be G-fibrations. A fibrewise G-map from $p:E\to B$ to $q: E'\to B$ is a G-map $f:E\to E'$ such that $q\circ f=p$.

Definition 4.12. A fibrewise G-homotopy $F:E\times I\to E'$ is a G-map such that $q(F(-,t))=p$ for all $t\in I$. Thus, F is a G-homotopy between fibrewise G-maps $F(-,0)$ and $F(-,1)$.

Definition 4.13. Let $p:E\to B$ and $q: E'\to B$ be G-fibrations. Then p and q are said to be fibrewise G-homotopy equivalent if there exist fibrewise G-maps $f: E\to E'$ and $g:E'\to E$ such that there are fibrewise G-homotopies from $f\circ g$ to $Id_{E'}$ and from $g\circ f$ to Id_E.

Farber and Paul [Reference Farber and Kumar Paul23] show that the sequential parametrized topological complexity of fibrewise homotopy equivalent fibrations coincides. We now prove the equivariant analogue of their result.

Proposition 4.14. Suppose the G-fibrations $p:E\to B$ and $p:E'\to B$ are fibrewise G-homotopy equivalent. Then

\begin{align*}\mathrm{TC}_{G,n}[p:E\to B]=\mathrm{TC}_{G,n}[p':E'\to B].\end{align*}

Proof. The commutative diagram of G-maps given in the hypothesis induces the following two commutative diagrams of G-maps:

where $F^I(\gamma)(t)=F(\gamma(t))$ and $F'^I$ defined similarly. Since $f'\circ f$ and $f\circ f'$ are fibrewise G-homotopic to the identity maps id_E and $id_{E'}$, respectively, we have $f'^n\circ f^n\simeq_G id_{E^n_B}$ and $f^n\circ f'^n\simeq_G id_{E'^n_B}$. Thus, we obtain the desired equality using part (2) of lemma 4.10.

4.2. Bounds

In this subsection, we obtain various bounds on the sequential equivariant parametrized topological complexity. We note that the results in this subsection generalize the classical results of Farber [Reference Farber22, Reference Rudyak38] when we consider the trivial action of the group G, and the results of Colman-Grant [Reference Colman and Grant12] and Bayeh-Sarkar [Reference Bayeh and Sarkar3] when we consider the base space B to be a singleton.

We now establish the upper bound on the sequential equivariant parametrized topological complexity in terms of the equivariant category, and consequently, in terms of the dimension of the fibre product.

Proposition 4.15. Let $p:E\to B$ be a G-fibration with $E^G\neq \emptyset$ and $E^n_B$ is G-connected . Then

(12)\begin{equation} \mathrm{TC}_{G,n}[p:E\to B]\leq \mathrm{cat}_{G}(E^n_B)\leq \mathrm{dim}(E^n_B/G)+1. \end{equation}

Moreover, if G acts locally smoothly on E and F is the fibre of a smooth fibre bundle $p:E\to B$, then

(13)\begin{equation} \mathrm{TC}_{G,n}[p:E\to B]\leq n\mathrm{dim}(F)+\mathrm{dim}(B)-\mathrm{dim}(P)+1, \end{equation}

where P is the principal orbit (an orbit of maximal dimension) of the G-action on $E^n_B$.

Proof. One can observe that, since $E^G\neq \emptyset$, we have $(E^n_B)^G\neq \emptyset$. Consequently, $(E^I_B)^G\neq \emptyset$. Moreover, $E^n_B$ is G-connected, thus the first inequality of (12) follows from [Reference Colman and Grant12, proposition 4.4]. The right-most inequality of (12) follows from [Reference Marzantowicz35, corollary 1.12]. It follows from [Reference Bredon5, theorem IV.3.8] that $\mathrm{dim}(E^n_B/G)=\mathrm{dim}(E^n_B)-\mathrm{dim}(P)$. Then, the inequality in (13) follows from the fact that $\mathrm{dim}(E^n_B)\leq n\mathrm{dim}(F)+\mathrm{dim}(B)$.

Corollary 4.16. Suppose E admits a locally smooth, non-trivial and semi-free action of G, with $p:E\to B$ being a G-fibration such that $E^G\neq \emptyset$ and $E^n_B$ is G-connected. Then

(14)\begin{equation} \mathrm{TC}_{G,n}[p:E\to B]\leq n\mathrm{dim}(F)+\mathrm{dim}(B)-\mathrm{dim}(G)+1. \end{equation}

Proof. It follows that if the action is locally smooth, non-trivial, and semi-free, then the principal orbit’s dimension coincides with the group’s dimension. Thus, the conclusion follows from proposition 4.15.

Remark 4.17. Consider $p:E\to B$ a G-fibration. When $B= \{\ast\}$, the inequality (14) also appears in [Reference Daundkar and Singh16, proposition 3.1]. Since $\mathrm{TC}_n(X)\leq \mathrm{TC}_{G,n}(X)$, we can conclude that the inequality (14) generalizes [Reference Daundkar13, corollary 4.7].

Proposition 4.18. Let $p:E\to B$ be a G-fibration such that the fibre of $p|_{E^H}:E^H\to B^H$ is path connected for all closed subgroups H of G and let $E^n_B$ be G-connected. Then

\begin{align*}\mathrm{TC}_{G,n}[p:E\to B]\leq \mathrm{cat}_{G}(E^n_B).\end{align*}

Proof. Since $p|_{E^H}:E^H\to B^H$ is path connected for all closed subgroups H of G, the map $\Pi_n|_{(E^I_B)^H}:(E^I_B)^H\to (E^n_B)^H$ is surjective. Therefore, the conclusion follows from [Reference Colman and Grant12, proposition 4.5].

Proposition 4.19. Let $p:E\to B$ be a G-fibration. If E is G-contractible space, then

\begin{align*}\mathrm{cat}_G(E^n_B)\leq \mathrm{TC}_n[p:E\to B].\end{align*}

Proof. Let $x\in E$ and γ_x be a constant path at x. Then define $h:E\to E^I_B$ by $h(x)=\gamma_x$. Observe that h is a G-map since $h(gx)=\gamma_{gx}=g\cdot \gamma_x=g\cdot h(x)$. Notice that h has a G-homotopy inverse h ^ʹ, which sends a path to its initial point. This implies, $E\simeq_{G}E^I_B$. This implies $E^I_B$ is a G-contractible space. Therefore, we can apply [Reference Colman and Grant12, proposition 4.6] to the fibration $\Pi_n:E^I_B\to E^n_B$ to get the desired result.

Now, the following result is clear.

Corollary 4.20. Let $p:E\to B$ be a G-fibration and let E be a G-contractible space. If $E^n_B$ is G-connected and $E^G\neq \emptyset$, then

\begin{align*}\mathrm{TC}_n[p:E\to B]=\mathrm{cat}_G(E^n_B).\end{align*}

Theorem 4.21 Let $p:E\to B$ be a G fibration. Let H and K be any closed subgroups of G such that E^H is K-invariant. Then

\begin{align*}\mathrm{TC}_{K,n}[p:E^H\to B^H]\leq \mathrm{TC}_{G,n}[p:E\to B].\end{align*}

Proof. Let U be a G-invariant open set of $E^n_B$ on which we have a local G-section s of $\Pi_n:E^I_B\to E^n_B$. Let $V=U\cap (E^H)^n_B $. Then, observe that V is K-invariant. Note that for $x\in (E^H)^n_B$, we have $hs(x)=s(hx)=s(x)$. Therefore, $s(x)\in (E^I_B)^H$. But $(E^I_B)^H=(E^H)^I_{B^H}$. Thus, s restricts to V. Therefore, we have a K-section $s|_{V}:V\to (E^H)^I_B$. This concludes the result.

The following is an obvious consequence of theorem 4.21.

Corollary 4.22. Let $p:E\to B$ be a G-fibration. Then for any closed subgroups H and K of G we have:

1. (1) $\mathrm{TC}_n[p|_{E^H}:E^H\to B^H]\leq \mathrm{TC}_{G,n}[p:E\to B]$,

2. (2) $\mathrm{TC}_{K,n}[p:E\to B]\leq \mathrm{TC}_{G,n}[p:E\to B]$.

Remark 4.23. If B is a singleton, then theorem 4.21 generalizes [Reference Colman and Grant12, proposition 5.3] and [Reference Bayeh and Sarkar3, proposition 3.14].

In the following result, we establish the relation between sequential equivariant parametrized topological complexity of a G-fibration and the equivariant category of its fibre and the equivariant category of the corresponding fibre product. The proof is inspired by [Reference Colman and Grant12, proposition 5.7].

Theorem 4.24 Let $p:E\to B$ be a G-fibration such that $E^n_B$ is G-connected, and let H be a stabilizer of some $e\in E$. Then,

\begin{align*}\mathrm{cat}_H(F^{n-1})\leq \mathrm{TC}_{G,n}[p:E\to B] \leq \mathrm{cat}_G(E^n_B).\end{align*}

In particular, if $E^G\neq \emptyset$, then

\begin{align*}\mathrm{cat}_G(F^{n-1})\leq \mathrm{TC}_{G,n}[p:E\to B]\leq \mathrm{cat}_G(E^n_B).\end{align*}

Proof. Let $e\in E$ and $b=p(e)$. We consider $F=p^{-1}(b)$. Note that $b\in B^H$. Therefore, F admits an H-action. We now define a map $f:F^{n-1}\to E^n_B$ by $f(x_1,\dots,x_{n-1})=(e,x_1,\dots,x_{n-1})$. Note that f is a well-defined H-equivariant map. Now consider the following pullback diagram:

where $Y=\{\gamma\in E^I_B \mid \gamma(0)=e\}$. Note that Y is H-invariant and H-contractible. Therefore, $\mathrm{cat}_H(F^{n-1})\leq \mathrm{secat}_{H}(q)$. From [Reference Colman and Grant12, proposition 4.3], we have:

\begin{align*}\mathrm{secat}_H(q)\leq \mathrm{secat}_H(\Pi_n)=\mathrm{TC}_{H,n}[p:E\to B].\end{align*}

Now from corollary 4.22, we have $\mathrm{TC}_{H,n}[p:E\to B] \leq \mathrm{TC}_{G,n}[p:E\to B]$. This proves the desired inequality.

We will now obtain the cohomological lower bound on the equivariant parametrized topological complexity. Let X be a G-space, and $X^h_G=EG\times_{G} X$ be the homotopy orbit space of X. The Borel G-equivariant cohomology of X is defined as $H^{\ast}_G(X;R):=H^{\ast}(X^h_G;R)$, where R is any commutative ring.

Let $p:E\to B$ be a G-fibration and $E^n_B$ be the corresponding fibre product. Note that the diagonal map $\triangle: E\to E^n_B$ is G-equivariant. Therefore, it induces a map $\triangle_G: E^h_G\to (E^n_B)^h_G$.

Theorem 4.25 Let $\triangle_G^{\ast}:H^{\ast}_G(E^n_B)\to H^{\ast}_G(E)$ be the induced map from $\triangle_G: E^h_G\to (E^n_B)^h_G$. Suppose there exists cohomology classes $u_i\in \mathrm{ker}(\triangle_G^{\ast})$ for $1\leq i\leq r$ such that $u_1\cup \dots \cup u_r\neq 0$. Then

\begin{align*}\mathrm{TC}_{G,n}[p:E\to B] \gt r.\end{align*}

Proof. Consider the following commutative diagram:

where h is a G-homotopy equivalence. Suppose $\mathrm{TC}_{G,n}[p:E\to B]\leq r$. Consider a parametrized motion planning cover $\{U_1,\dots, U_r\}$. Since h is G-homotopy equivalence, the inclusion $i_{U_i}:U_i\to E^n_B$ factors through the diagonal $\triangle: E\to E^n_B$ up to G-homotopy. Therefore, $i_{U_i}^{\ast}(u_i)=0$ for $1\leq i\leq r$. Hence u_i’s are in the image of $H^{\ast}_G(E^n_B, U_i)\to H^{\ast}_G(E^n_B)$ for $1\leq i\leq r$. Since U_i covers $E^n_B$, we get that $u_1\cup\dots\cup u_r=0$ by the naturality of cup products. This completes the proof.

The upper bound on the equivariant sectional category of Serre G-fibrations has obtained in [Reference Grant30, theorem 3.5]. We now state this result with a slight modification.

Theorem 4.26 ([Reference Grant30, theorem 3.5])

Let $p:E\to B$ be a Serre G-fibration and let B be a G-CW complex with $\dim(B)\geq 2$. Suppose for all closed subgroups H of G, the fibre of $p^H:E^H\to B^H$ is $(m-1)$-connected. Then

\begin{align*}\mathrm{secat}_G(p) \lt \frac{\dim(B)+1}{m+1}+1.\end{align*}

We will now use theorem 4.26 to establish the upper bound on the equivariant parametrized topological complexity.

Theorem 4.27 Let $p:E\to B$ be a (Hurewicz) G-fibration and $E^n_B$ is a G-CW complex with $\mathrm{dim}(E^n_B)\geq 2$. Suppose for all subgroups H of G, the fibre of $p^H:E^H\to B^H$ is m-connected. Then

\begin{align*}\mathrm{TC}_{G,n}[p:E\to B] \lt \frac{n\mathrm{dim}(F)+\mathrm{dim}(B)+1}{m+1}+1.\end{align*}

Proof. Since $\Pi_n:E^I_B\to E^n_B$ is a (Hurewicz) G-fibration, it is also a Serre G-fibration. We can observe that $(E^I_B)^H=(E^H)^I_{B^H}$ and $(E^n_B)^H=(E^H)^n_{B^H}$ for any closed subgroup H of G. Thus, the fibration $(\Pi_n)^H:(E^I_B)^H\to (E^n_B)^H$ is, in fact, a sequential parametrized path fibration associated with the fibration $p^H:E^H\to B^H$. In other words, we have $(\Pi_n)^H:(E^H)^I_{B^H}\to (E^H)^n_{B^H}$. Let X_H denote the fibre of $p^H: E^H\to B^H$. Then, note that the fibre of $(\Pi_n)^H$ is $(\Omega X_H)^{n-1}$. Since X_H is m-connected and $\pi_i((\Omega X_H)^{n-1})=(\pi_i(\Omega X_H))^{n-1}=(\pi_{i+1}(X_H))^{n-1}$, it follows that $(\Omega X_H)^{n-1}$ is $(m-1)$-connected. Then from theorem 4.26, we obtain the following inequality:

(15)\begin{equation} \mathrm{TC}_{G,n}[p:E\to B] \lt \frac{\mathrm{dim}(E^n_B)+1}{m+1}+1. \end{equation}

It is well known that there is a locally trivial fibration $E^n_B\to B$ with fibre F ⁿ. Therefore, we have $\mathrm{dim}(E^n_B)\leq n\mathrm{dim}(F)+\mathrm{dim}(B)$. This completes the proof.

5. Examples

5.1. Equivariant Fadell–Neuwirth fibrations

In this subsection, we compute sequential equivariant parametrized topological complexity of Fadell–Neuwirth fibrations.

We start with recalling the definition of the ordered configuration space. The ordered configuration space of s points on $\mathbb{R}^d$ is denoted by $F(\mathbb{R}^d,s)$ and defined as

\begin{align*}F(\mathbb{R}^d,s)=\{(x_1,\dots,x_s)\in (\mathbb{R}^d)^s \mid x_i\neq x_j \text{for } i\neq j\}.\end{align*}

Definition 5.1 ([Reference Fadell and Neuwirth20])

The maps

\begin{align*}p: F(\mathbb{R}^d,s+t)\to F(\mathbb{R}^d,s) \text{ defined by } p(x_1,\dots,x_{s+t})=(x_1,\dots,x_s)\end{align*}

are called Fadell–Neuwirth fibrations.

The sequential parametrized topological complexity of these fibrations have been computed in [Reference Farber and Kumar Paul23] for odd $d\geq 3$ and in [Reference Farber and Kumar Paul24] for even $d\geq 2$. We now state their theorem.

Theorem 5.2 ([Reference Farber and Kumar Paul24, theorem 1.3])

Let $d\geq 2$ be an even integer, and $t\geq 1$, $s\geq 2$. Then

\begin{align*}\mathrm{TC}_n[p:F(\mathbb{R}^{d},s+t)\to F(\mathbb{R}^{d},s)]=nt+s-1.\end{align*}

Theorem 5.3 ([Reference Farber and Kumar Paul23, theorem 8.1])

Let $d\geq 3$ be an odd integer, and $s \geq 2$, $t \geq 1$. Then

\begin{align*}\mathrm{TC}_n[p:F(\mathbb{R}^{d},s+t)\to F(\mathbb{R}^{d},s)]=nt+s.\end{align*}

We now define an action of a permutation group $\Sigma_s$ (on s letters) on $F(\mathbb{R}^d,s+t)$. Let $\sigma\in \Sigma_s$. Define

\begin{align*}\sigma\cdot (x_1,\dots,x_s,y_1,\dots,y_t)=(x_{\sigma(1)},\dots,x_{\sigma(s)},y_1,\dots,y_t).\end{align*}

Also $\Sigma_s$ acts on $F(\mathbb{R}^d,s)$ by permuting coordinates. Observe that the map p in definition 5.1 satisfies

\begin{align*}p((x_{\sigma(1)},\dots,x_{\sigma(s)},y_1,\dots,y_t))=(x_{\sigma(1)},\dots,x_{\sigma(s)})=\sigma\cdot p((x_1,\dots,x_s,y_1,\dots,y_t)).\end{align*}

Thus, p is a $\Sigma_s$-equivariant map. We now show that p is indeed a $\Sigma_s$-fibration.

The local triviality of p was shown in [Reference Fadell and Husseini21, theorem 1.1], and we also refer the reader to [Reference Cohen10, theorem 3.3]. We will use the ideas from these results to show the $\Sigma_s$-equivariant local triviality of p. Consider a point $q=(q_1,\dots,q_s)\in F(\mathbb{R}^d,s)$ and mutually disjoint open discs D_i with centres q_i. Then consider the open set $V=\cup_{\sigma\in \Sigma_s}D_{\sigma(1)}\times \dots\times D_{\sigma(s)}$ containing q. Note that V is $\Sigma_s$-invariant and a disjoint union. Note that the fibre F_q of p at q is given by $F(\mathbb{R}^d\setminus \{q_1,\dots,q_s\},t)$. We identify F_q with the last t-coordinates of $F(\mathbb{R}^d,s+t)$ via $(y_1,\dots,y_t)\mapsto (q_1,\dots,q_s,y_1,\dots,y_t)$ and assume that $\Sigma_s$ acts trivially on F_q. We define a homeomorphism $\Phi_q:V\times F_q\to p^{-1}(V)$ in a similar way as it was defined in [Reference Fadell and Husseini21, theorem 1.1]. We fix the notation $\bar{y}=(y_1,\dots,y_t)$. Let $\bar{x}=(x_1,\dots,x_s)\in V$. That means $\bar{x}\in D_{\sigma(1)}\times \dots\times D_{\sigma(s)}$ for some $\sigma\in \Sigma_s$. Define

\begin{align*}\Phi_q(x_1,\dots,x_s,\bar{y})= \left(x_1,\dots,x_s,\left(\gamma_{\sigma(1)}^{-1}(x_1)\circ\dots\circ \gamma_{\sigma(s)}^{-1}(x_s)\right)(\bar{y})\right),\end{align*}

where functions $\gamma_i(x_i):\mathbb{R}^d\to \mathbb{R}^d$ are homeomorphisms defined as in the [Reference Fadell and Husseini21, corollary 1.1] for $1\leq i\leq s$ and we have denoted $(\gamma_{i}(x))^{-1}$ by $\gamma_i^{-1}(x)$. Recall that these functions have the following properties: for $x\in D_i$, we have $\gamma_i(x)(D_i)=D_i$, $\gamma_i(x)(x)=q_i$, and $\gamma_i(x)(y)=y$ for $y\in \mathbb{R}^d\setminus D_i$. Note that

\begin{align*}(\gamma_1^{-1}(x_1)\circ\dots\circ \gamma_s^{-1}(x_s))(\bar{y})& =((\gamma_1^{-1}(x_1)\circ\dots\circ \gamma_s^{-1}(x_s))(y_1),\dots,\\ & \quad \times (\gamma_1^{-1}(x_1)\circ\dots\circ \gamma_s^{-1}(x_s))(y_t)).\end{align*}

For $(x_1,\dots,x_s)\in D_1\times\dots\times D_s$, we note the important observation:

(16)\begin{equation} (\gamma_1^{-1}(x_1)\circ\dots\circ \gamma_s^{-1}(x_s))(y_i)=\begin{cases} \gamma_j^{-1}(x_j)(y_i),& \text{if } y_i\in D_j,\\ y_i,& \text{otherwise}. \end{cases} \end{equation}

We will now prove that $\Phi_q$ is $\Sigma_s$-equivariant. Let $\bar{x}\in D_{\sigma(1)}\times\dots\times D_{\sigma(s)}$ and $\rho\in\Sigma_s$. Note that $\rho\cdot \bar{x}\in D_{\sigma(\rho(1))}\times\dots\times D_{\sigma(\rho(s))}$. Then we have

\begin{align*}\Phi_q(\rho\cdot \bar{x},\bar{y})=(\rho\cdot \bar{x}, (\gamma_{\sigma(\rho(1))}^{-1}(x_{\rho(1)})\circ\dots\circ \gamma_{\sigma(\rho(s))}^{-1}(x_{\rho(s)}))(\bar{y})).\end{align*}

Observe that the sets $\{\gamma_{\sigma(r)}^{-1}(x_r) \mid 1\leq r\leq s\}$ and $\{\gamma_{\sigma(\rho(r))}^{-1}(x_{\rho(r)}) \mid 1\leq r\leq s\}$ coincides. Then using (16) we can see that

\begin{align*}(\gamma_{\sigma(\rho(1))}^{-1}(x_{\rho(1)})\circ\dots\circ \gamma_{\sigma(\rho(s))}^{-1}(x_{\rho(s)}))(y_i)=(\gamma_{\sigma(1)}^{-1}(x_1)\circ\dots\circ \gamma_{\sigma(s)}^{-1}(x_s))(y_i).\end{align*}

More precisely, if $y_i\in D_j$ for some $1\leq j \leq s$ and $\sigma(k)=j$, then we have

\begin{align*}(\gamma_{\sigma(1)}^{-1}(x_1)\circ\dots\circ \gamma_{\sigma(s)}^{-1}(x_s))(y_i)=\gamma^{-1}_{\sigma(k)}(x_k)(y_i).\end{align*}

Moreover, if $\sigma(\rho(r))=j$, then

\begin{align*}(\gamma_{\sigma(\rho(1))}^{-1}(x_{\rho(1)})\circ\dots\circ \gamma_{\sigma(\rho(s))}^{-1}(x_{\rho(s)}))(y_i)=\gamma^{-1}_{\sigma(\rho(r))}(x_{\rho(r)})(y_i).\end{align*}

Since $\rho(r)=k$, we get $\gamma^{-1}_{\sigma(k)}(x_k)(y_i)=\gamma^{-1}_{\sigma(\rho(r))}(x_{\rho(r)})(y_i)$. This gives us,

\begin{align*}\Phi_q(\rho\cdot \bar{x},\bar{y})& =(\rho\cdot \bar{x}, (\gamma_{\sigma(1)}^{-1}(x_1)\circ\dots\circ \gamma_{\sigma(s)}^{-1}(x_s))(\bar{y}))\nonumber\\ & \quad =\rho\cdot(\bar{x}, (\gamma_{\sigma(1)}^{-1}(x_1)\circ\dots\circ \gamma_{\sigma(s)}^{-1}(x_s))(\bar{y})).\end{align*}

This proves that $\Phi_q$ is $\Sigma_s$-equivariant.

Let $F=F(\mathbb{R}^d\setminus \{a_1,\dots,a_s\},t)$ be the fibre of p with $(a_1,\dots,a_s)\in F(\mathbb{R}^d,s)$ as chosen base point. We will now choose a stable homeomorphism (as in step-2 of [Reference Fadell and Husseini21, theorem 1.1]) $\alpha_q:F\to F_q$ and define $\Phi=\Phi_q\circ (id_V\times \alpha_q)$. Note that α_q is equivariant as $\Sigma_s$ acts trivially on both F and F_q. We conclude that $\Phi:V\times F\to p^{-1}(V)$ is $\Sigma_s$-equivariant local trivialization. Finally, using [Reference İlhan32, theorem 2.3], we conclude that the fibration p is a G-fibration.

We are going to use theorem 4.27 to obtain an upper bound on $\mathrm{TC}_{\Sigma_s,n}[p:F(\mathbb{R}^d,s+t)\to F(\mathbb{R}^d, s)]$. We denote the fibration $p:F(\mathbb{R}^d,s+t)\to F(\mathbb{R}^d, s)$ by $p:E\to B$. Note that F is $(d-2)$-connected. Since any closed subgroup H of $\Sigma_s$ acts freely on E and B, we only need to consider $p^H:E^H\to B^H$ when H is the trivial subgroup. In this case, $p^H=p$. Then from theorem 4.27, we get the following expression.

\begin{align*}\mathrm{TC}_{\Sigma_s,n}[p:E\to B] \lt \frac{(d-1)(nt+s-1) +1}{d-1}+1=nt+s + 1/(d-1).\end{align*}

This gives us

\begin{align*}\mathrm{TC}_{\Sigma_s,n}[p:F(\mathbb{R}^d,s+t)\to F(\mathbb{R}^d, s)]\leq nt+s.\end{align*}

Since we have

\begin{align*}\mathrm{TC}_n[p:F(\mathbb{R}^d,s+t)\to F(\mathbb{R}^d, s)]\leq \mathrm{TC}_{\Sigma_s,n}[p:F(\mathbb{R}^d,s+t)\to F(\mathbb{R}^d, s)],\end{align*}

we establish the following result.

Theorem 5.4

1. (1) Let $d\geq 3$ be an odd integer, and $s\geq 2$, $t\geq 1$. Then

   \begin{align*}\mathrm{TC}_{\Sigma_s,n}[p:F(\mathbb{R}^d,s+t)\to F(\mathbb{R}^d, s)]=nt+s.\end{align*}

2. (2) Let $d\geq 2$ be an even integer, and $t\geq 1$, $s\geq 2$. Then

   \begin{align*}\mathrm{TC}_{\Sigma_s,n}[p:F(\mathbb{R}^d,s+t)\to F(\mathbb{R}^d, s)]\in \{nt+s-1,nt+s\}.\end{align*}

5.2. Some generalized projective product spaces

Let τ be any involution on M. Consider the following generalized projective product space

\begin{align*} X(M, S^{2m+1}) :=\displaystyle\frac{M \times S^{2m+1}}{(x,y)\sim (\tau(x), -y)}. \end{align*}

We have a fibre bundle $p:X(M, S^{2m+1})\to \mathbb{R} P^{2m+1}$ with fibre M. We define a $\mathbb{Z}_2$-action on $X(M, S^{2m+1})$ by defining an involution

\begin{align*}\sigma([x,y]):=[x,\tilde{y}],\end{align*}

where $y=(y_0,y_1,\dots,y_{2m},y_{2m+1})$ and $\tilde{y}=(-y_1,y_0,\dots, -y_{2m+1},y_{2m})$. It can be observed that σ defines a free involution on $X(M, S^{2m+1})$. A $\mathbb{Z}_2$-action on $\mathbb{R} P^{2m+1}$ is defined by

\begin{align*}g\cdot [y_0:y_1:\dots:y_{2m}:y_{2m+1}]:=[-y_1:y_0:\dots: -y_{2m+1}:y_{2m}].\end{align*}

We now observe the following:

\begin{align*}& p([x,(-y_1,y_0,\dots, -y_{2m+1},y_{2m})])=[-y_1:y_0:\dots: -y_{2m+1}:y_{2m}] \nonumber\\ & \quad =g\cdot [y_0:y_1:\dots:y_{2m}:y_{2m+1}].\end{align*}

This shows that $p:X(M,S^{2m+1})\to \mathbb{R} P^{2m+1}$ is a $\mathbb{Z}_2$-equivariant map. One can also show that p is in fact a G-fibration. Observe that

\begin{align*}& X(M,S^{2m+1})^n_{\mathbb{R} P^{2m+1}}\nonumber\\ & \quad =\{([x_1,y_1],\dots,[x_n,y_n])\in X(M,S^{2m+1})^n \mid y_i=\pm y_j, 1\leq i,j\leq n\}.\end{align*}

Since $\mathbb{Z}_2$ acts freely on $X(M,S^{2m+1})$, we have free diagonal $\mathbb{Z}_2$-action on $X(M,S^{2m+1})^n_{\mathbb{R} P^{2m+1}}$. Thus $X(M,S^{2m+1})^n_{\mathbb{R} P^{2m+1}}$ is $\mathbb{Z}_2$-connected. Therefore using proposition 4.18 we get the following inequality:

\begin{align*}\mathrm{TC}_{\mathbb{Z}_2,n}[p:X(M,S^{2m+1})\to \mathbb{R} P^{2m+1}]\leq \mathrm{cat}_{\mathbb{Z}_2}(X(M,S^{2m+1})^n_{\mathbb{R} P^{2m+1}}).\end{align*}

From [Reference Colman and Grant12, proposition 3.5] we get $\mathrm{cat}_{\mathbb{Z}_2}(X(M,S^{2m+1})^n_{\mathbb{R} P^{2m+1}})=\mathrm{cat}(X(M,S^{2m+1})^n_{\mathbb{R} P^{2m+1}}/\mathbb{Z}_2)$. Using the dimensional inequality for category, we obtain

\begin{align*}\mathrm{TC}_{\mathbb{Z}_2,n}[p:X(M,S^{2m+1})\to \mathbb{R} P^{2m+1}]\leq n\dim(M)+2m+2.\end{align*}

In particular, if $M=\mathbb{R} P^k$ with any involution, then we have

\begin{align*}\mathrm{TC}_n(\mathbb{R} P^k)\leq \mathrm{TC}_{\mathbb{Z}_2,n}[p:X(\mathbb{R} P^k,S^{2m+1})\to \mathbb{R} P^{2m+1}]\leq nk+2m+2.\end{align*}

Suppose $k=2^r$, then using [Reference Farber, Tabachnikov and Yuzvinsky26, corollary 8.2], we have

\begin{align*}nk\leq \mathrm{TC}_{\mathbb{Z}_2,n}[p:X(\mathbb{R} P^k,S^{2m+1})\to \mathbb{R} P^{2m+1}]\leq nk+2m+2.\end{align*}