2.1. Energy Harvesting Principle

This study focuses on harvesting electromagnetic energy from overhead power lines. A soft magnetic rod core with a coil wound around is shown in Figure 1. The open circuit voltage of the coil (V _coil) can be found by Faraday’s law of magnetic induction:

(1) $\begin{array}{}{V}_{\text{coil}}=N\omega B_{\text{ex}}A{\mu }_{\text{eff}},\end{array}$

where N is the number of turns of the coil, ω is the angular frequency of transmission line current in rad/s, B _ex is the external magnetic flux density in T_rms, A is the effective cross-sectional area of core in m², and μ _eff is the effective permeability related to the shape and material properties of the core.

FIGURE 1: A coil harvesting electromagnetic energy from an alternating magnetic field.

The equivalent circuit of the harvesting coil with a load is shown in Figure 2. A compensating capacitor C = 1/(ω ² L _coil) is added to compensate for the inductance of the coil inductive L _coil. R _coil is the coil resistance that consists of copper wire resistance R _copper and the equivalent core resistance R _core. Based on the principle of maximum power transfer, a matching load should be equal to the coil resistance, and the max output power is as follows:

(2) $\begin{array}{}{P}_{\text{load}}=\frac{{\left(V_{\text{coil}}/2\right)}^2}{R_{\text{coil}}}.\end{array}$

FIGURE 2: The equivalent circuit of the harvesting coil with a matched load.

The power density of the energy harvester can be calculated by

(3) $\begin{array}{}{\rho }_{\text{power}}=\frac{\left(1/4\right)\left(V_{\text{coil}}^2/R_{\text{coil}}\right)}{\text{Vol}},\end{array}$

where Vol is the total volume of the energy harvester in m³.

2.2. Energy Harvester Design: I-Shaped

The open circuit voltage of coil V _coil is related to N, ω, B _ex, A, and μ _eff, where ω and B _ex are related to the external magnetic field environment which cannot be changed by changing the energy harvester. Assume that the length of the core and the winding number N are unchanged, and A and μ _eff are directly influenced by the energy harvester design. As the energy harvester does not form a closed loop, it results in a demagnetizing field. The effective permeability μ _eff is much lower than relative permeability μ _r for a uniform cylindrical core. The μ _eff can be derived as follows [Reference Ripka30]:

(4) $\begin{array}{}{\mu }_{\text{eff}}\approx \frac{{\mu }_r}{1+N_d{\mu }_r},\end{array}$

where N _d is the demagnetization factor related to the core shape, and the relative permeability μ _r is related to the core material. If uniform cylindrical core length l to diameter d ratio is m = l/d, N _d can be calculated using Stoner’s formula [Reference Ripka30]:

(5) $\begin{array}{}{N}_d=\frac{1}{m^2-1}\left(\frac{m}{\sqrt{m^2-1}}ln\left(m+\sqrt{m^2-1}\right)-1\right).\end{array}$

From (4) and (5), the effective permeability μ _eff is related to the relative permeability μ _r and core shape. Figure 3 shows the relationship between the μ _eff and m, μ _r .

FIGURE 3: The effective permeability of five different length-to-diameter ratios as a function of relative permeability.

Figure 3 shows the relationship between μ _eff and m, μ _r ; if m is given, on the increase of the relative permeability, the effective permeability surges and finally becomes stable with a knee point of μ _r . Given the relative permeability, the effective permeability increases with the growth of m. Actually, m is less than 15 due to the limit of size in practical application. Therefore, the relative permeability only needs to be above 1000 which can almost get a maximum value of effective permeability. For a long and thin rod core, the effective permeability is higher, but it occupies a greater space and is easily broken. In order to increase the effective permeability, this paper designs an I-shaped core that adds two big plates at both ends. As shown in Figure 4, it is mainly based on the following principles:

1. (1) Based on the Gauss theorem of the electromagnetic field, the magnetic flux from one end into the core is equal to the flux through the other end numerically. The core can guide more magnetic flux from the big plates at both ends and intensifies the magnetic field in the middle of the core.

2. (2) The big plates at both ends can separate the magnetic charge for the north and south poles and reduce the demagnetization field at the middle of the I-shaped core.

FIGURE 4: Schematic view of the magnetic flux guided by the I-shaped core (h is the plate thickness, D _out is the diameter of collector plates, and B _ex is the external magnetic flux density).

To verify the design,

1. (1) Figure 5 depicts two selective cores: one is a rod (a) without attachment and the other is an I-shaped core (b) with a pair of magnetic collector plates

2. (2) The core is an ideal material with a conductivity of zero and a relative permeability of 2000.

3. (3) The winding number N is 100 for all cores (the diameter of winding and the resistivity for the copper wire are 0.33 mm and 0.22 Ω/m, respectively)

4. (4) The core is placed in the same alternating magnetic field which is generated by the Helmholtz coil (6.5 μT_rms at 50 Hz)

FIGURE 5: (a) The conventional solenoid with D _in = 3.2 cm and L = 23 cm and (b) the I-shaped core with D _out = 10.5 cm, h = 2.5 cm, D _in = 3.2 cm, and L = 23 cm.

The conductivity of the core is set to be zero to eliminate the eddy current losses. The hysteresis losses are ignored due to a low-frequency electromagnetic field and low coercive force. Therefore, the magnetic properties of the two cores with different shapes can be researched. CST EM Studio is utilized to simulate the two cores: we first model the magnetic core, set it as a Mn-Zn ferrite material, and then add a copper coil.

A Helmholtz pair was used to generate the required magnetic field. The diameter of the Helmholtz coil is 1 m. The distance of the pair is 50 cm. Each coil has 30 turns of copper wire. The alternating current in the coil is 121 m to generate a uniform alternating magnetic field of 6.5 μT at 50 Hz. The harvester was placed in the middle of the Helmholtz pair. The load resistance R _load is the same as the coil resistance R _coil. A compensation capacitor as explained in Section 2.1 is then added in the circuit. This forms an energy harvesting loop. Then we measure the voltage V _coil on the load. The output power can be calculated using (2).

As depicted in Figure 6, the flux density in the middle of the proposed I-shaped core (b) (0.62 mT_rms) is relatively larger than the rod (a) (0.2 mT_rms), which verified the feasibility of the previous theoretical model (Figure 4).

FIGURE 6: The simulated magnetic flux density inside (a) the conventional solenoid and (b) the I-shaped core when an external magnetic field density of 6.5 μT_rms is applied.

As shown in Table 1, the resistance of the copper wire on the I-shaped core is the same as that on the rod, but the effective permeability of the I-shaped core is much greater. According to (2) and (3), its open circuit voltage and output power of the I-shaped core is 3 times and 9 times as much as that of the rod. Although the volume of the I-shaped core is larger than that of the rod core, its power density is still 3 times as much as that of the rod. Therefore, the I-shaped core shows a better performance than the rod one.

TABLE 1: The parameters of the two cores (μ _r = 2000 and N = 100).

In order to optimize the output power of the I-shaped core, a parametric study has been conducted on the magnetic flux collector plate with thickness h, inner rod length L, magnetic flux collector plate diameter D _out, and inner rod diameter D _in.

As shown in Figure 7, for a given D _out (10.5 cm) and D _in (3.2 cm), in theory, as L increases, the distance between the two magnetic poles gets further, making the demagnetization field weakened and the effective permeability increased significantly. When h increases, more magnetic flux can be guided into the core and the magnetic poles are formed at a further distance. It results in a decrease in the demagnetization field and an increase in the open circuit voltage. Thus, a longer inner rod and a pair of thicker magnetic flux collector plates can harvest more energy from the magnetic field. As shown in Figure 8, when h (2.5 cm) and L (23 cm) are given, as D _out increases, more magnetic flux can be guided into the core and enable the distribution of surface magnetic poles to become more discrete, which results in a significant increase in the open circuit voltage. As D _in decreases, the copper wire resistance becomes lower, leading to the increased output power. However, the volume of the I-shaped core increases significantly when a pair of bigger plates is used, which slowly increases the power density of the coil relative to the smaller plates. But the power density of the biggest plate remains the highest when D _in is larger than about 2.3 cm, as the results are shown in Figure 9.

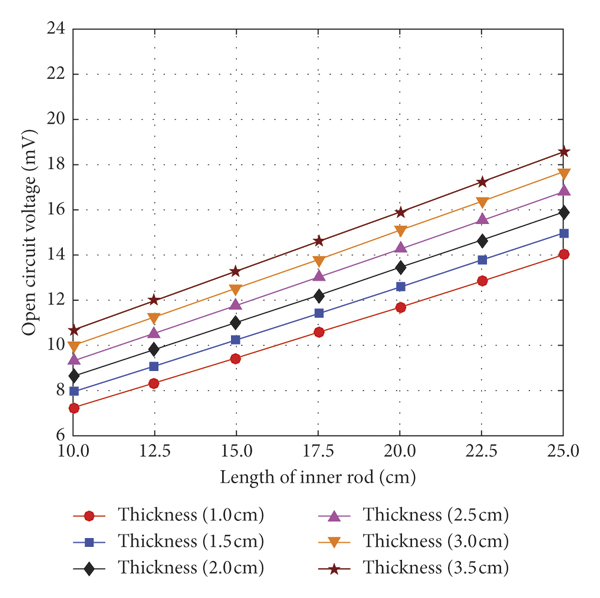
FIGURE 7: The open circuit voltage of the I-shaped coils with different lengths of the inner rod L as a function of the plate thickness h.

FIGURE 8: The output power of the I-shaped coils with different inner diameters D _in as a function of the plate diameter D _out.

FIGURE 9: The power density of the I-shaped coils with different inner diameters D _in as a function of the plate diameter D _out.

In summary, an I-shaped core which comprises a long and thin inner rod and a pair of thick and big magnetic collector plates can generate a greater output power. Keeping the h and L unchanged, a thinner inner rod which is above 2.3 cm and a pair of bigger plates can lead to an increase in both the output power and the power density.

2.3. Energy Harvester Design: Grid-Shaped

As shown in Figure 10, the field line (external magnetic flux) can be bent by high-permeability soft magnetic material. Although block (a) and block (b) have the same size, block (b) can guide more magnetic flux than block (a) due to its more discrete distribution. Block (b) and block (c) have the same sphere of guiding magnetic flux, but the volume of block (b) is smaller than that of block (c).

FIGURE 10: Schematic view of the field line bending by different sizes of high-permeability soft magnetic material. Volume (a) = volume (b) <volume (c).

Therefore, a more efficient grid-shaped energy harvester can be designed as shown in Figure 11. Compared with the I-shaped core shown in Figure 5(b), the magnetic collector plates of the grid-shaped core are hollow. Note that the grid-shaped core (a) and grid-shaped core (b) have the same outer diameter D _out with the I-shaped core, respectively.

FIGURE 11: The grid-shaped core (a) has the same D _out as the I-shaped core (D _out = 10.5 cm, h = 2.5 cm, and W = 1 cm); the grid-shaped core (b) has the same volume as the I-shaped (D _out = 18.5 cm, h = 2.5 cm, and W = 1 cm); (c) the schematic of the grid-shaped magnetic flux collector plate for both grid-shaped cores.

The grid-shaped coil is also simulated using CST EM Studio software. As depicted in Figure 12, the simulated environment is the same as the I-shaped coil described in Section 2.2. Due to that the hollow grid-shaped coil (a) has the same D _out as the solid I-shaped coil, both of them have almost the same sphere of guiding magnetic flux, making them have almost the same open circuit voltage. However, the volume of grid-shaped coil (a) is smaller than that of the I-shaped coil. As a result, the power density of the grid-shaped coil (a) is 44% higher. The calculated result is shown in Figure 13. The hollow grid-shaped coil (b) has the same volume Vol as the solid I-shaped coil, but the magnetic collector plates of the grid-shaped coil (b) are bigger than those of the I-shaped coil, allowing more magnetic flux to be guided, and a larger open circuit voltage (1.6 times that of the I-shaped coil when μ _r is 2000) can be acquired. As shown in Figure 13, the power density of the grid-shaped coil (b) can reach 2.6 times that of the I-shaped coil.

FIGURE 12: The simulated open circuit voltage of four coils when an external magnetic flux density of 6.5 μT_rms is applied.

FIGURE 13: The calculated power density of four coils when an external magnetic density of 6.5μT_rms is applied.

In summary, compared with the I-shaped coil, the weight of the grid-shaped coil is lighter and the power density is greater. If the I-shaped coil and the grid-shaped coil have the same weight (volume), the grid-shaped coil can guide more magnetic flux and achieve larger output power.

2.4. Core Material Selection

As seen in (2), the output power P depends on the open circuit voltage V _coil and coil resistance R _coil. V _coil can be influenced by the core material on the effective permeability μ _eff and the effective cross-sectional area A of the core. R _coil can be influenced by core equivalent resistance R _core.

The effective permeability of the core μ _eff is plotted in Figure 14 as a function of the relative permeability. The effective permeability increases with the increase of the relative permeability. The two curves become saturated as μ _r increased, and their knee point appears when μ _r is about 300 and 1000 for the rod core and I-shaped core, respectively. As a consequence, μ _r of the core material is at least approach 1000 which is more proper for the I-shaped core.

FIGURE 14: The effective permeability of two cores as a function of the relative permeability.

As a result of the skin effect occurred in the core and the magnetic flux tends to have a propagation along the surface of the path, it leads to reduced A. The skin depth can be derived as follows:

(6) $\begin{array}{}\delta =\sqrt{\frac{2\rho }{\omega {\mu }_0{\mu }_{\text{eff}}}},\end{array}$

where ρ is the material resistivity of the core in Ωm, ω is the angular frequency of transmission line current in rad/s, μ ₀ is the vacuum permeability which is equal to 4π × 10⁻⁷ H/m, and μ _eff is the effective permeability. As shown in (6), a greater ρ leads to a deeper skin depth. The μ _eff of the I-shaped core is about 100, and ω is set to 50 Hz. For the common soft magnetic material, ρ of iron-silicon alloy, amorphous and nanocrystalline alloy, nickel-iron alloy, and soft magnetic alloy material are all in the order of μΩm [31, 32]. Its maximum skin depth does not exceed 1 cm, which is less than the inner rod diameter D _in for the I-shaped core, and the skin effect cannot be ignored. The Mn-Zn soft ferrite belongs to nonmetallic materials and has been used as magnetic material widely, its ρ is extremely higher than those of silicon steel and soft magnetic alloy (usually in the magnitude of Ωm [33]), and the skin depth is far above the inner rod diameter range. As a consequence, the D _in can be considered as the diameter of the effective cross section and the skin effect can be ignored when we select Mn-Zn soft ferrite as core material. The following papers [Reference Van Schalkwyk and Hancke27–Reference Yuan, Huang, Zhou, Xu, Song and Yuan29] also used Mn-Zn cores for energy harvesting under power lines. In addition, the authors in [Reference Dyo, Ajmal, Allen, Jazani and Ivanov34, Reference Shirai, Mitamura and Arai35] used Mn-Zn for other energy harvesters.

For the core equivalent resistance R _core, there are three losses occurring in the soft magnetic core when it is placed in the alternating magnetic field, including eddy current losses, hysteresis losses, and residual losses. When using the soft magnetic material with low coercivity, the hysteresis losses and residual losses can be ignored in this application as it is placed in the extremely low-power frequency (50 Hz) and very weak magnetic field (usually in the magnitude of μT). The eddy current losses are mainly considered here, and the power consumption of the eddy current losses can be derived as follows:

(7) $\begin{array}{}{w}_{\text{eddy}}=\frac{S}{2k\rho }{\left(\frac{d{B}_{\text{in}}}{dt}\right)}^2,\end{array}$

where S is the cross-sectional area in m², ρ is the material resistivity of the core in Ωm, B _in is the inner magnetic flux density of core in T_rms, and k is the shape factor. When the I-shaped core is placed in an alternate magnetic field with 50 Hz, the W _eddy is inversely proportional to ρ. For the I-shaped core, set μ _r to be 2000, the material resistivity ρ is 1 μΩm (a typical value of ρ for the silicon steel and soft magnetic alloy material) and 6.5 Ωm (a typical value of ρ for the Mn-Zn soft ferrite), respectively. The simulation result of eddy current density in the cross section at the middle of I-shaped core is shown in Figure 15. At the edge of the core, the eddy current can be greater than 500 A/m² in Figure 15(a) and lower than 0.006 A/m² in Figure 15(b). The eddy current generates an opposite magnetic field which is against the external magnetic field and consumes electromagnetic energy in the form of heat. Compared with the ideal open circuit voltage V _coil of 15.8 mV when the ρ is infinite (the conductivity is zero), the simulation shows that the V _coil is reduced to 12.4 mV in Figure 15(a) but unchanged in Figure 15(b). As a consequence, the R _core can be ignored when the Mn-Zn soft ferrite is selected.

FIGURE 15: The eddy current density inside the core when μ _r = 2000. (a) The resistivity ρ is 1 μΩm and (b) the resistivity ρ is 6.5 Ωm.

In summary, the relative permeability of the Mn-Zn soft ferrite is about 2000 which is above the knee point of 1000, and the material resistivity is in the order of Ωm, and the skin effect and eddy current losses can be both ignored. Thus, the Mn-Zn soft ferrite is the most suitable material for the application and requirement.

3.1. Experiment Setup

While the rod core and the I-shaped core can be easily obtained from some magnetic materials factory, the grid-shaped core cannot be easily fabricated as it needs to be mold and cut. In this experiment, the concept of the I-shaped core was demonstrated by testing the I-shaped core and the rod core.

A pair of Helmholtz coils as shown in Figure 16 is made to generate a uniform alternating electromagnetic field to imitate the electromagnetic environment near the power line. The diameter of the Helmholtz coil is 1 m, winding 30 turns of copper wire. With 120 mA_rms alternating current which is outputted by a function generator (RIGOL, DG4162) passing through the Helmholtz coil, a magnetic flux density of 6.5 μT_rms can be generated.

FIGURE 16: A Helmholtz pair is made to generate a uniform alternating electromagnetic field in the laboratory.

The parameters of the rod core and I-shaped core are listed in Table 2. The rod core and a pair of magnetic collector plates are fabricated as shown in Figure 17. The I-shaped core can be combined with the rod core and plates. The dimensions of cores are the same as shown in Figure 5, and the Mn-Zn soft ferrite [36] is used as the core material (μ _r is 2300 ± 25% and material resistivity is 6.5 Ωm).

TABLE 2: Comparison of the rod and the I-shaped energy harvesters.

FIGURE 17: Overview of the rod core, a pair of magnetic collector plates, and three spools with a winding number of 10000, 20000, and 20000 from left to right, respectively.

In order to wind wire conveniently, three same spools are introduced. Their winding numbers are 10000, 20000, and 20000, respectively. The diameter of the winding and the resistivity for the copper wire are 0.33 mm and 0.22 Ω/m, respectively. The dimensions of the spool are shown in Figure 17. The core can be inserted into the spool that has a different combination to get different winding numbers.

3.2. Experiment Validations and Result

Two cores with an increasing winding number are put into the Helmholtz coil and the open circuit voltage is measured with a multimeter. As shown in Figure 18, the measured voltage values are in good agreement with the theoretical ones, and the measured voltage of I-shaped is 2.7 times that of the rod. It is noted that the experiment results of the rod core are a little higher than the simulation values. This should be mainly caused by the initial winding diameter (4 cm) which is slightly larger than the diameter of the core (3.2 cm), leading to more magnetic flux through the spool. However, for the I-shaped core, the loss of the core is not considered during simulation, also the collector plates are not fully in contact with both ends of the rod, and there are air gaps in every contact surface of the I-shaped core, leading to a slight reduction in the overall effective permeability and the lowered measured voltage than theory.

FIGURE 18: The open circuit voltage of the two coils as a function of the winding number.

The copper resistance R _copper can be considered as the coil resistance R _coil when the Mn-Zn soft ferrite is used. In theory, the copper wire can be winded from the diameter of the rod (3 cm), and the interval length is the length of the rod (23 cm). However, in practice, the copper wire is winded from the outer diameter of the spool (4 cm), and the interval length is the inner length of the spool (9.6 cm), resulting in increased copper resistance. As shown in Figure 19, the winding number 30000 is combined with 10000-turn spool and 20000-turn spool. The winding number 40000 is combined with two same 20000-turn spools. As a result, the R _copper is increased by 40.2%, 50.7%, 27.1%, and 20.7% for the winding number 10000, 20000, 30000, and 40000, respectively.

FIGURE 19: The copper resistance of the two coils as a function of the winding number.

The circuit with a compensating capacitor and a matched load is built to get the maximum output power for the harvesting coil. On the one hand, a perfect compensating capacitor could not be found in this experiment, which decreases the measured output power. On the other hand, from (2), the output power is directly proportional to the square of the open circuit voltage and is inversely proportional to the resistance of the coil. As shown in Figure 20, in this experiment, for the I-shaped core, the lower open circuit voltage and higher copper resistance relative to the theory can both reduce the output power. As a result, the output power reduces significantly. For the rod core, the higher open circuit voltage and higher copper resistance relative to the theory can offset the influence on the output power. It allows the measured output power to be in good agreement with the theoretical ones.

FIGURE 20: The output power of the two coils as a function of the winding number.

However, the output power of the I-shaped core is still higher than the conventional rod core. In this case, the measured output power of the I-shaped (4.5 mW) is 6.8 times that of the rod (665 μW) with 40000 turns. In addition, as shown in Figure 21, the power density of the I-shaped coil is 7.28 μW/cm³ with 40000 turns, which is double that of the rod coil under the same electromagnetic environment.

FIGURE 21: The power density of the two coils as a function of the winding number.

3.3. Circuit Design

In order to make the electromagnetic energy harvester drive a low energy load and verify the feature of self-powered I-shaped coil, as shown in Figure 22, a circuit [Reference Roscoe and Judd11, Reference Shirai, Mitamura and Arai35] is designed including storage circuit (part A), buffer circuit (part B), and load (part C).

FIGURE 22: Equivalent circuit of the complete free-standing electromagnetic energy harvester.

For the storage circuit (part A), C1 is the compensating capacitor, C2 is the storage capacitor (4700 μF), and D1 and D2 are the Schottky diodes, which constitute a double voltage rectification circuit. For the buffer circuit (part B), the Zener diode D3 provided a reference voltage to the negative input of the current comparator (LT1017). R2, R3, R4, R5, and R8 are reducing voltage resistors. R1, R6, and R7 are protecting resistors. Q1 and Q2 are MOSFET switches.

The test circuit is illustrated in Figure 23. The I-shaped coil with 40000 turns is used as the test harvester, and its maximum output power in the experiment is 4.5 mW. When the load is a high-power red LED light, it glowed periodically, the voltage of C2 increased from 2.1 V (U _L) to 4.0 V (U _H) after a period of 14 s, this corresponds to the energy E = 0.5C2 (U_H ² − H_L ²) = 27.2 mJ, and the time of the light glowed is about 0.2 s. Thus, the average power delivered can be up to 136 mW. This design can be used to power sensors which require high operating power. When the load is another low-power red LED light, it kept glowing and the voltage of C2 stabilized in 4.0 V (U _R) and the current of load stabilized in 0.6 mA (U _R), which is shown in Figure 19. Thus, the consumed power of the LED light is 2.4 mW, and the efficiency of the whole circuit is around 53%.

FIGURE 23: The real test circuit designed to drive a low-power red LED light, the multimeters (a) and (b) were used to measure the voltage and current of LED, respectively.