The concept of hierarchical structure in the domains of intelligence and personality, featuring a single general factor at the top, have been controversial ever since general factors were advocated early in the 20th century by Spearman (Reference Spearman1904) and Webb (Reference Webb1915). Spearman called the intelligence factor g, for general intelligence. Webb called the personality (or character) factor w, for will.
A general factor in the intelligence domain, whether labeled ‘g’ or ‘IQ’ has become assimilated into psychological thinking (e.g., Brody, Reference Brody1992; Carroll, Reference Carroll1993; Jensen, Reference Jensen1998), although in practice many prefer to work further down in the hierarchy of cognitive traits, and there has been controversy about how best to carve up the ability domain — fluid and crystallized abilities (Cattell, Reference Cattell1971); seven to nine Primary Mental Abilities (Thurstone, Reference Thurstone1938); v:ed and k:m (Vernon, Reference Vernon1951). In the personality domain, the postulation of a discrete set of traits at the highest level has been the typical approach: a set of five or six broad factors is currently most popular (e.g., Costa & McCrae, Reference Costa and McCrae1992; Goldberg, Reference Goldberg1990; Saucier, Reference Saucier2009).
Broad personality traits are often somewhat correlated empirically, and recent years have seen the re-emergence of the idea of a general factor of personality (GFP) at the top of a personality trait hierarchy (e.g., Musek, Reference Musek2007). Critics of this view have not necessarily denied the presence of a single higher-order factor, but have attributed it to measurement artifact (Bäckström et al. Reference Bäckström, Björklund and Larsson2009; Pettersson et al., Reference Pettersson, Turkheimer, Horn and Menatti2012) or declared it to be psychometrically weak (Revelle & Wilt, Reference Revelle and Wilt2013). However, in one study, partialing out self-esteem or social desirability measures did not greatly reduce a GFP (Erdle & Rushton, Reference Erdle and Rushton2011).
In defense of the substantive status of a GFP, twin studies have shown it to be substantially heritable (Loehlin & Martin, Reference Loehlin and Martin2011; Veselka et al., Reference Veselka, Schermer, Petrides and Vernon2009), and to show relationships with measures of social effectiveness and ratings of character and integrity (Dunkel & van der Linden, Reference Dunkel and van der Linden2014; van der Linden et al., Reference van der Linden, te Nijenhuis, Cremers, van de Ven and van der Heijden-Lek2014). Rushton et al. (Reference Rushton, Bons and Hur2008) proposed an evolutionary origin of the GFP: namely, that it was a result of selection on a set of traits contributing to social effectiveness and thus to reproductive success.
Evolutionary speculation has continued. On the cognitive side, Woodley (Reference Woodley2011) proposed what he called the ‘CD-IE’ hypothesis to account in evolutionary terms for the presence of both general and specialized intellectual ability. CD-IE stands for ‘Cognitive Differentiation-Integration Effort’. Woodley's hypothesis rests on the assumption that there are two basic dimensions underlying human development: one of general fitness and one of fast and slow life histories. On the cognitive side, general fitness takes the form of general intelligence (g). Woodley posits a genetic factor G1 underlying g that reflects mutation load: that is, an individual's general level of ability depends on the number of deleterious mutations he possesses (fewer such mutations = higher ability). Woodley suggests that an independent factor G2 underlies the differentiation of cognitive skills, and is related to fast or slow life history (the slower the life history, the greater the opportunity for and advantage of specialized skills). In evolutionary terms, fast or slow life histories reflect the predictability of environments: in unstable environments, fast life histories with an emphasis on reproduction predominate, whereas in stable environments slow life histories featuring fewer and better-cared-for offspring are the norm. The attributes of slow life histories are not limited to specialized cognitive skills. They may include, for example, general factors of health and of personality as aspects of a ‘Super-K’ factor (Figueredo et al., Reference Figueredo, Vásquez, Brumbach and Schneider2007). Woodley proposes that the relevant evolutionary processes for G2 include balancing and frequency-dependent selection, as opposed to the mutation-selection balance underlying G1.
Woodley carried out a meta-analysis of 10 studies in which measures of g and K (general intelligence and slow life history) were included. In eight of the 10, the correlation between the two was non-significant, with overall a near-zero correlation of 0.023. Based on this result and the theoretical assumptions sketched above, Woodley made a number of specific predictions, one of which was: ‘. . . heritable intelligence should show no genetic correlations with heritable life history indicators . . . when analyzed in a cross-twin cross-trait multivariate genetic analysis’ (p. 239).
Doubts may be raised about this prediction, even if personality is considered a life history indictor. For example, in a large study based on genotyped individuals rather than twins (Verweij et al., Reference Verweij, Yang, Lahti, Veijola, Hintsanen, Pulkki-Råback and Zeitsch2012), the authors concluded that personality variation appeared to be more consistent with the operation of mutation-selection balance involving rare alleles than with G2 genetic mechanisms of the sort suggested by Woodley. The absence of a phenotypic correlation may also be called into question. Two studies, in each of which Woodley was one of the co-authors, obtained an appreciable correlation between measures of g and GFP. One, based on the large data set of the 1960s U.S. Project Talent, reported appreciable correlations between general factors of personality and intelligence: r = 0.25 overall; and rs of 0.23, 0.33, and 0.16 within White (N = 147,355), Black (N = 6,533), and Asian (N = 999) subgroups, respectively (Dunkel et al., Reference Dunkel, Cabeza De Baca, Woodley and Fernandes2014a). The other, in a 1960s California prison sample (N = 2,622 to 2,668), obtained a correlation of 0.33 between an intelligence measure, the General Ability Test Battery, and a general personality factor from the California Psychological Inventory (Dunkel et al., Reference Dunkel, van der Linden, Beaver and Woodley2014b).
Nevertheless, even if a phenotypic correlation exists, it remains an empirical question whether a genetic one does. It is the testing of Woodley's prediction of a zero genetic correlation between general factors of personality and intelligence that is the subject of the present article.
Method
Twin Samples and Tests
Initially, data from two twin samples were analyzed, from Australia and the United States. The results were different enough to suggest the desirability of including additional samples, so data from three other existing twin studies were added to the design. These were studies in the Netherlands, Great Britain and Croatia, originally undertaken for various purposes, that had obtained measures of ability and personality at ages roughly comparable to those in the Australian and U.S. studies.
The Australian sample was part of a larger study in which twins, mostly recruited via South East Queensland schools, were tested at ages 12, 14, and 16 (Wright & Martin, Reference Wright and Martin2004). The present sample came from the age 16 testing, at which a cognitive test battery and the Junior Eysenck Personality Questionnaire (JEPQ) were administered to the twins. Scores from a set of cognitive tests, the Multidimensional Aptitude Battery (MAB) and the JEPQ, were available for 246 MZ and 154 same-sex DZ pairs. The general intelligence measure was obtained as the first principal factor from the five subtests of the MAB, and the personality factor from the four scales of the JEPQ. The Lie scale of the latter, although originally designed to detect faking, was included, since in a volunteer research population with no special motivation for impression management, the scale has been considered a measure of social conformity (e.g., Francis & Montgomery, Reference Francis and Montgomery1993; Tatalović Vorkapić, Reference Tatalović Vorkapić2012).
The second sample, from the United States, consisted of twin pairs identified from among the high school juniors who took the National Merit Scholarship Qualifying Test (NMSQT) in 1962 (Loehlin & Nichols, Reference Loehlin and Nichols1976). Those twins agreeing to participate in the research were mailed questionnaires, including the California Psychological Inventory (CPI). Scores from the CPI as well as the NMSQT were available for 490 MZ and 317 same-sex DZ pairs. General intelligence was obtained as the first factor from the five NMSQT subtests. The general personality factor was obtained from 13 of the 18 CPI scales. The five scales not used included three scales reflecting ability or achievement, Achievement via Conformity, Achievement via Independence, and Intellectual Efficiency, omitted to minimize the risk of an artifactual correlation of the personality composite with ability, and two response bias scales, Communality and Good Impression, omitted to avoid another possible artifactual source of correlation.
The third sample was from the Netherlands Twin Register (Van Beijsterveldt et al., Reference Van Beijsterveldt, Groen-Blokhuis, Hottenga, Franić, Hudziak, Lamb and Boomsma2013). From it, WAIS IQs and scores on the Dutch translation of a Five-Factor inventory (the NEO-FFI) were available (Bartels et al., Reference Bartels, van Weegen, Beijsterveldt, Carlier, Polderman, Hoekstra and Boomsma2012). The IQs were obtained at age 18, the personality measures at average ages of 20.7 and 29.0 for two subgroups. The IQ score was taken to represent the general intelligence factor, and a general personality factor was derived from the correlations among the five scales of the NEO. Intelligence and personality factors were available for both twins of 161 MZ and 112 same-sex DZ pairs.
The fourth sample was from the Twins’ Early Development Study in Great Britain (Haworth et al., Reference Haworth, Davis and Plomin2013). The general intelligence factor was derived from two cognitive tests administered to the twins at age 16, the Mill Hill vocabulary scale and Ravens Progressive Matrices; the personality factor was based on a Big Five inventory taken at the same age (details given in Krapohl et al., Reference Krapohl, Rimfeld, Shakeshaft, Trzaskowski, McMillan, Pingault and Plomin2014 — additional online material). There were 748 MZ and 633 same-sex DZ pairs for whom both general intelligence and general personality factors were available.
The fifth sample was from Croatia, from a twin study in which both an intelligence measure and a Big Five inventory were included (Bratko et al., Reference Bratko, Butkovic, Vukasovic, Chamorro-Premuzic and von Stumm2012). The intelligence measure was the verbal subtest of a Croatian version of the General Aptitude Test Battery (GATB); the personality measure a Croatian version of the NEO-FFI, from which a general factor was extracted. Intelligence and personality factors were available for both members of 103 MZ and 114 same-sex DZ pairs. Their ages ranged from 15 to 22, with a mean of 18.6 years.
Thus, the twin samples consisted of late adolescent to young adult twins, the majority in the 16- to 19-year age range. The personality measures in the Netherlands study were obtained when the twins were somewhat older, but would still be classified as young adults.
Analyses
General factors of intelligence and personality were obtained in all five samples, in the form of first principal factors from correlations among the relevant measures over all available individuals in the sample (including different-sex and unmatched twins, if present). In two of the samples, a single measure of ability was used as an index of g. Correlations among the general intelligence and personality factor scores of twin 1 and twin 2 were then obtained separately in MZ and same-sex DZ subsamples, and analyzed via structural equation modeling. If the individual correlations were based on differing numbers of cases, the median number was used for the model fitting.
In short, for each of the five studies two 4 × 4 correlation matrices were obtained, one for MZ and one for DZ twins. The four variables in each were the factor scores of the first and second twins of a pair on g and GFP, the general intelligence and personality factors.
The structural equation models represented in Figure 1 were fit to these correlation matrices, using LISREL 8.80. Degrees of freedom were adjusted for fitting to correlation matrices in multiple groups, as recommended by Neale and Cardon (Reference Neale and Cardon1992, p. 256). An ACE model (Additive genetic variance, Common or shared family environment, individual Environment plus error) or an ADE model (Additive genetic variance, genetic Dominance, individual Environment plus error) was fit, depending on whether the DZ correlation was greater or less than half the MZ correlation. In all five samples, the DZ correlation for intelligence exceeded half the MZ correlation, so an ACE model was fit. In two of the samples, Australia and the US, this was also the case for personality, but in the other three the DZ correlation for personality was less than half the MZ correlation, suggesting the presence of non-additive genetic variance, modeled as Dominance in an ADE model (e.g., van den Berg et al., Reference van den Berg, de Moor, McGue, Pettersson, Terracciano, Verweij and Boomsma2014).
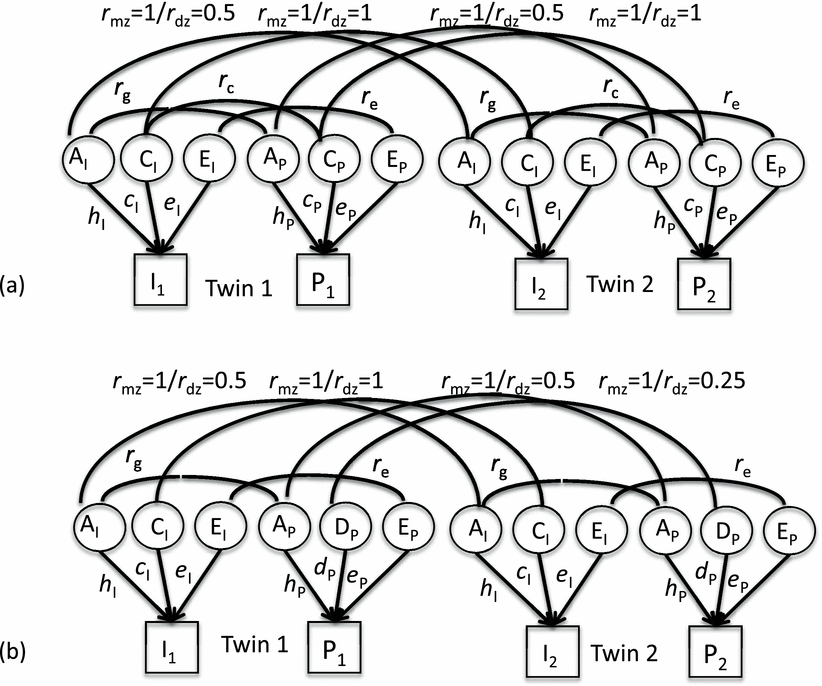
FIGURE 1. Structural equation model fitted in five twin samples: (a) ACE models for both intelligence and personality; (b) ACE model for intelligence, ADE model for personality. Note: Observed variables, in squares = general factors of intelligence (I) and personality (P) for Twin 1 and Twin 2. Latent variables, in circles = additive effects of genes (A), common environment of twin pair (C), dominance effects of genes (D), environment unique to each twin plus measurement error, etc. (E). Paths h, c, d, e = effects of latent on observed variables. Curved lines = correlations among latent variables: within each model, lower level curved lines represent within-individual correlations between intelligence and personality via genes (r g), common environment (r c), and non-shared environment (r e); upper level curved lines represent cross-twin correlations for the same traits. Not shown in figure: cross-twin, cross-trait correlations: equal to r g for MZ pairs, to 0.5*r g for DZ pairs, equal to r c for both types of pairs; equal to zero for r e. All latent and observed variables standardized.
In Figure 1, the upper circles represent latent variables capturing (respectively) genetic, shared environmental, and non-shared environmental sources of variation, with the downward arrows h, c, and e indicating the extent to which they influence the observed variables I1, P1, I2, and P2 in the squares below — the general intelligence and personality scores of the first and second twin. Figure 1(a) uses the ACE model for both traits. The squares of the h, c, and e paths represent the variances of the observed variables due to the three sets of causes, thus h 2 is the heritability of intelligence or personality, c 2 its dependence on environmental influences shared by the twins, and e 2 everything else — including the unique experiences of each twin and measurement error. An ADE model was used for personality in three of the samples; this is shown in Figure 1(b). D replaces C, a path d replaces the path c, and it is assumed the C of one trait is uncorrelated with the D of the other. In both models, the latent and observed variables are all standardized, that is, have variances of 1.0.
The curved lines at the top of the figures represent correlations among the latent variables that are assumed to underlie and explain the correlations among the observed variables. Thus, the correlation that Woodley hypothesizes to be zero, the genetic correlation between the intelligence and personality factors (r g), is represented by the curved line between the first and fourth circles (or, equivalently, that between the seventh and the tenth). The correlations between the intelligence and the personality factors due to the twins’ shared environments (r c) or to environmental factors that are not shared (r e) are also shown.
The correlations across the two twins for the same trait are assigned values specified by theory. For MZ twins, the genetic correlation is fixed at 1.0 — the twins, coming from the splitting of a single fertilized ovum, have the same genes. For DZ twins, who share on average one-half of their segregating genes, a value of 0.5 for the corresponding correlation was used. Shared environments of twins are by definition correlated 1.0, and unshared environments 0.0. Genetic dominance is correlated 0.25 across DZ twins. Correlations across twins across traits, not shown in the figure to avoid clutter, are related to the within-twin across-trait correlations r g and r c. For MZs, they are equal to r g and r c, since both genes and common environments are shared. The r g for DZs is assumed equal to one-half that for MZs, the r cs for both are equal, and the r es for both are zero — since non-shared environments, by definition, are not shared by the two twins. As noted earlier, the dominance deviations for one trait are assumed to be uncorrelated with the shared or unshared environment of the other.
Results
The loadings for the general intelligence and personality factors in the five samples are shown in Table 1, and the within- and cross-twin correlations between the two factors are shown in Table 2.
TABLE 1 Factor Loadings for General Factors of Intelligence and Personality in Five Countries

Numbers of individuals for the intelligence and personality factor analyses are given after country title.
TABLE 2 General Factor Score Correlations Within and Across Twin Pairs for Intelligence and Personality, to Which Models Were Fit
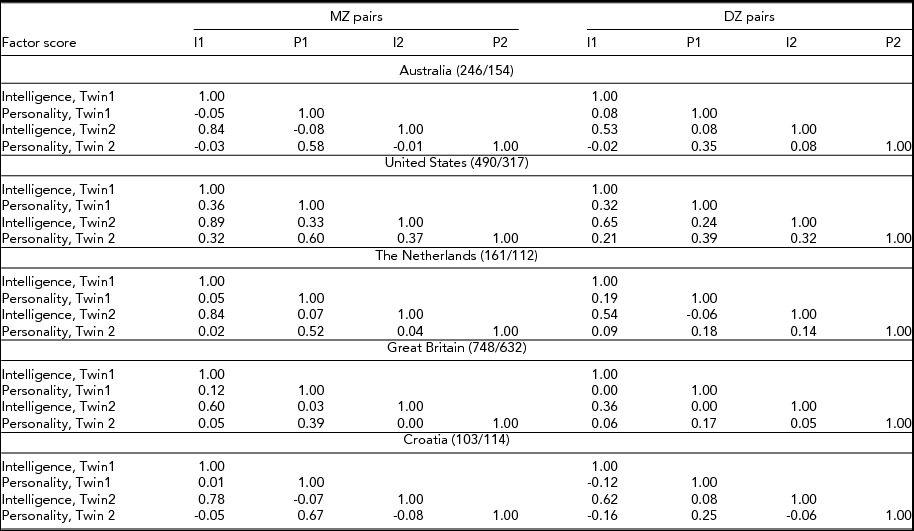
Numbers of MZ and DZ pairs given after country title. I1 = Intelligence, Twin 1; P1 = Personality, Twin 1; I2 = Intelligence, Twin 2; P2 = Personality, Twin 2.
A model constrained to have equal parameters across all the 10 matrices in Table 2 had a χ2 of 452.84 for 53 df, that is, was extremely improbable. A measure of departure from a perfect fit, the Root Mean Square Error of Approximation (RMSEA) was 0.152 (after correction for df), or almost twice the 0.08 considered to represent a reasonable fit by Browne and Cudeck (Reference Browne, Cudeck, Bollen and Long1993), and three times as large as the 0.05 they consider a close fit. However, the differences among the samples appeared to lie mainly in the paths from the latent to the observed variables, rather than the correlations. Woodley's hypothesis does not concern itself with the individual trait path values, only with the genetic correlation between the two composites. Permitting each of the five samples to have its own h, c or d, and e paths and fixing r g to zero resulted in a χ2 of 44.29 for 26 df, and an RMSEA of 0.046, a close fit, by the Browne/Cudeck criterion. Allowing r g to be free in the U.S. sample while remaining at zero in the other four resulted in a slightly but significantly better solution, with a χ2 of 39.71 for 25 df, RMSEA = 0.042. This is still a significant χ2(p < .05), meaning that the fit is less than perfect, but it is a good one, as judged by RMSEA. Parameters for the five samples in this solution are shown in Figure 2.
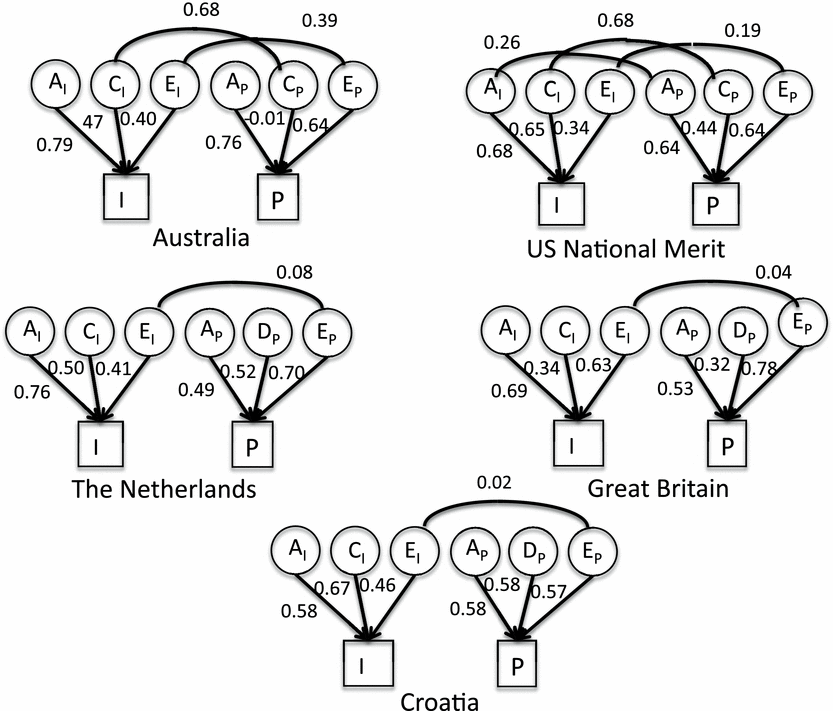
FIGURE 2. Parameters for models fit to twin data from five countries, with r g fixed to zero for all but U.S. sample.
As is evident from Figure 2, the three paths from the latent variables to the traits vary across the different samples, but they are typically all appreciable, with the exception of the near-zero c path for personality in the Australian sample. The r c correlation for the two samples from which this correlation is estimated is fairly large, 0.68, but it mostly depends on the U.S. sample — it is weakly determined in the Australian sample because of the near-zero c path — so its generality may be questionable. The correlations due to unshared environment vary. They are in the 0.02 to 0.08 range except for the U.S. and Australian samples, where they are 0.19 and 0.39, respectively.
Discussion
Fitting path models involving genetic and environmental correlations to data from five twin samples from the U.S., Europe and Australia gave results reasonably consistent with Woodley's hypothesis that the genetic correlation between general factors of intelligence and personality is zero.
Least consistent with the Woodley hypothesis was the U.S. National Merit sample. Allowing its r g parameter to be estimated separately from the other samples led to a modest but significant reduction in overall chi square. The National Merit sample was different from the other samples in several respects. It came from an earlier period — the data were gathered in the early 1960s, whereas the other samples were measured much more recently, in some cases nearly 50 years later. Its estimate of g came from a restricted range of ability, and to a greater degree reflected performance in areas of academic subject matter. The restriction in ability range ought to lower, rather than raise, the correlation with other measures (such as personality); the inclusion of academic achievement variance would have an uncertain effect — it might raise the correlation with conscientiousness, for example, but lower that with extraversion. There also conceivably could be a difference between twins in the U.S. and Europe/Australia. Two of these three alternatives are consistent with the substantial personality-intelligence correlation from the Project Talent data (Dunkel et al., Reference Dunkel, Cabeza De Baca, Woodley and Fernandes2014a) — based on a sample also from U.S. high schools and also from the 1960s, a sample much broader in ability range than the National Merit sample, as well as from a restricted-range California prison sample also from the U.S. and from the 1960s (Dunkel et al., Reference Dunkel, van der Linden, Beaver and Woodley2014b).
The parameters in the remaining four twin samples were clearly not identical, but the differences appeared to lie largely in the path values. That is, the samples differed in the paths from the genes and shared and unshared environments to the general factors rather than in the relations between the latter. This might partly reflect differences in the tests used, although differences for similar tests are notable — for example, Openness is related positively to the general personality factor in Great Britain, negatively in Croatia, and close to zero in the Netherlands. In a U.S. adult sample, general personality factors derived individually from seven different personality inventories had substantial loadings on a common general factor (ranging from 0.53 to 0.81; Loehlin, Reference Loehlin2012). These inventories included the NEO and the CPI used in the present study, although not the JEPQ. An eighth inventory, the HEXACO, had near-zero loadings on the common factor. This exception suggests that the common general factor was not simply a result of evaluative bias, or the like, which should apply equally to the HEXACO, but a matter of substance. The added Modesty/Humility dimension of the HEXACO apparently combined with Agreeableness to swing the first factor of this inventory away from the rest — with either of these two dimensions removed, the general factor of the HEXACO aligned with the others, with loadings of 0.62 or 0.67 on the common factor (Loehlin, Reference Loehlin2012).
As to samples, the present ones did not differ greatly in age, but were recruited in different ways, and were, of course, from different countries.
Lack of association between general factors does not rule out genetic and environmental correlations at the level of individual traits. For example, in the study from the Netherlands, genetic correlations between Agreeableness and IQ and Openness and IQ were present at the trait level (Bartels et al., Reference Bartels, van Weegen, Beijsterveldt, Carlier, Polderman, Hoekstra and Boomsma2012), although in the present analysis there was not a significant genetic contribution at the level of the general factor. There also were specific genetic associations between Openness and IQ and Extraversion and IQ in the Croatian sample (Bratko et al., Reference Bratko, Butkovic, Vukasovic, Chamorro-Premuzic and von Stumm2012).
One limitation of the present study is that the modeling involved only twins, so some confounding between shared environment and non-additive genetic variance may be present. More complex approaches, such as twin-family designs, could help discriminate these.
Although the present results are consistent with Woodley's prediction, how clearly do they support his distinction between general factors based on life history speed and on general fitness? Here, matters are a little murkier. The argument that slow life histories should lead to more differentiation of cognitive skills seems plausible, but one might wonder whether a similar argument might not apply to personality: that is, that slow life histories might lead to greater differentiation among personality traits, whereas general fitness might affect a general factor of personality. The absence of a substantial genetic correlation between the two general factors is one empirical argument against this view, but further clarification of the underlying theoretical relationships would seem desirable. For example, a particular evolutionary mechanism, mutation-selection balance, acting separately in two independent sets of genes, could leave the respective general factors uncorrelated unless selection on them occurred jointly.
In conclusion, it should be recognized that the finding of a zero (or near-zero) genetic correlation between general factors of intelligence and personality may be given various interpretations. One would be that general factors of intelligence and personality exist, but their evolutionary history and biological substrates are uncorrelated. Another would be that the GFP represents, at least in part, measurement biases such as self-esteem or halo effects, and, if the former, the genetic factors underlying these are uncorrelated with those underlying ability (not an altogether trivial assumption). Another view might be that the finding is not very interesting, because a more useful way of approaching personality (and perhaps ability as well) is at a level well below that of a single general factor — although to this third view one must surely add the qualification that the most useful level will depend upon one's purposes.
A fourth possibility is to take seriously the apparent phenotypic difference between the U.S. samples from the 1960s and more recent European and Australian samples, and postulate that some underlying process has changed. Not the effects of evolution, presumably, over such a short time span, but something in biology or culture or measurement affecting the relationship between general factors of intelligence and personality. The present data do not reveal what that something might be, but further investigation with other data sets spanning the period involved could clarify, first, whether the difference truly exists, and if it does, what changes underlie it.
Acknowledgments
We are grateful to Robert Plomin and Eva Krapohl for supplying the data from the Twins Early Development Study in Great Britain. For helpful comments on an earlier version of this article, we are grateful to David Buss, and also to Elliot Tucker-Drob, Paige Harden, and graduate students in their seminar — Frank Mann in particular.






