Cognition requires neuronal activity in a complex network of multiple spatially and functionally distinct brain areas that are interconnected via long axonal projections (Varela et al., Reference Varela, Lachaux, Rodriguez and Martinerie2001). Synchronization of neural activity yields functional connectivity, which has been studied extensively as a predictor of cognitive ability (Fries, Reference Fries2005; Varela et al., Reference Varela, Lachaux, Rodriguez and Martinerie2001). Functional connectivity is suggested to be reflective of underlying anatomical connectivity (Damoiseaux, Reference Damoiseaux2006; Honey et al., Reference Honey, Sporns, Cammoun, Gigandet, Thiran, Meuli and Hagmann2009; Johnston et al., Reference Johnston, Vaishnavi, Smyth, Zhang, He, Zempel and Raichle2008; Rykhlevskaia et al., Reference Rykhlevskaia, Gratton and Fabiani2008) and can be measured with a variety of methods, including blood-oxygen-level-dependent (BOLD) functional magnetic resonance imaging (fMRI), magnetoencephalography (MEG), and electroencephalography (EEG). In all these techniques, connectivity between brain areas is determined by identifying statistical interdependencies between the physiological time series recorded from different brain areas (Damoiseaux, Reference Damoiseaux2006; Fingelkurts et al., Reference Fingelkurts, Fingelkurts and Kahkonen2005; Salvador et al., Reference Salvador, Suckling, Coleman, Pickard, Menon and Bullmore2005).
EEG and MEG, because of their high time resolution, are considered especially useful measures for identifying synchronization in short-lived functional networks. Many measures have been constructed to quantify synchronization in EEG recordings. Coherence is the most widely used measure of the relation between pairs of signals as a function of frequency (Nunez et al., Reference Nunez, Srinivasan, Westdorp, Wijesinghe, Tucker, Silberstein and Cadusch1997). However, coherence is a biased measure for filtered signals, and is insensitive to non-linear coupling. To circumvent these limitations, measures derived from dynamical systems theory may be used (Pereda et al., Reference Pereda, Quiroga and Bhattacharya2005). Stam and van Dijk (Reference Stam and van Dijk2002) suggested a measure that captures both linear and non-linear dependencies: synchronization likelihood (SL). SL can deal with non-stationarity of EEG and shows no spurious connectivity between band pass filtered signals. This parameter measures the statistical interdependencies between two time series. SL has proven useful in clinical studies, showing increased connectivity during epileptic seizures, and a decrease in the alpha, beta, and gamma frequency bands in patients suffering from Alzheimer's disease (Pijnenburg et al., Reference Pijnenburg, vd Made, van Cappellen van Walsum, Knol, Scheltens and Stam2004; Ponten et al., Reference Ponten, Bartolomei and Stam2007; Stam & van Dijk, Reference Stam and van Dijk2002; Stam et al., Reference Stam, van der Made, Pijnenburg and Scheltens2003).
Building on the SL, graph theory has been used to show the efficiency of functional connectivity networks. Brains appear selected by evolution to minimize building costs with high densities of highly clustered short-range local connections, yet maximize integration of information between distant brain areas with a few long-range connections (Achard & Bullmore, Reference Achard and Bullmore2007; Bassett & Bullmore, Reference Bassett and Bullmore2006). Watts and Strogatz (Reference Watts and Strogatz1998) designated such networks as ‘small-world’ networks. In their groundbreaking article, they proposed two parameters to describe simplified networks. The clustering coefficient, CC, describes the amount of local connectivity. It takes a value between 0 and 1, indicating the proportion of neighboring nodes that are interconnected among each other. CC has been interpreted as a measure for cost and robustness against perturbations (Achard et al., Reference Achard, Salvador, Whitcher, Suckling and Bullmore2006). The second parameter describes the global interconnectedness and is called the average path length, L. This parameter represents the ability of a network to integrate information across distant sources.
Small-world networks are characterized with a high CC and a low L (high integration, low cost). It has been argued that small-world architecture may be optimal for synchronizing neural activity between different brain regions (Barahona & Pecora, Reference Barahona and Pecora2002; Lago-Fernandez et al., Reference Lago-Fernandez, Huerta, Corbacho and Siguenza2000; Latora & Marchiori, Reference Latora and Marchiori2001). Many EEG and MEG studies have since revealed a clear small-world topology in the resting healthy human brain (Bassett & Bullmore, Reference Bassett and Bullmore2006; Bassett et al., Reference Bassett, Meyer-Lindenberg, Achard, Duke and Bullmore2006; Micheloyannis et al., Reference Micheloyannis, Vourkas, Tsirka, Karakonstantaki, Kanatsouli and Stam2009; Stam, Reference Stam2004). Moreover, graph theoretical analysis can reveal abnormal patterns of the organization of functional connectivity. Recently, alterations in network architecture were found in patients with brain pathology such as Alzheimer's disease (Stam et al., Reference Stam, Jones, Nolte, Breakspear and Scheltens2007, Reference Stam, de Haan, Daffertshofer, Jones, Manshanden, van Cappellen van Walsum and Scheltens2009), epilepsy (Ponten et al., Reference Ponten, Bartolomei and Stam2007; Schindler et al., Reference Schindler, Bialonski, Horstmann, Elger and Lehnertz2008; Van Dellen et al., Reference Van Dellen, Douw, Baayen, Heimans, Ponten, Vandertop and Reijneveld2009), brain tumors (Bartolomei et al., Reference Bartolomei, Bosma, Klein, Baayen, Reijneveld, Postma and Stam2006; Bosma et al., Reference Bosma, Reijneveld, Klein, Douw, van Dijk, Heimans and Stam2009) and schizophrenia (Micheloyannis et al., Reference Micheloyannis, Pachou, Stam, Breakspear, Bitsios, Vourkas and Zervakis2006; Rubinov et al., Reference Rubinov, Knock, Stam, Micheloyannis, Harris, Williams and Breakspear2009).
Synchronization likelihood and its graph theoretical derivatives CC and L show large individual differences that can be partly explained by genetic factors. Studies by Posthuma et al. (Reference Posthuma, de Geus, Mulder, Smit, Boomsma and Stam2005) and Smit et al. (Reference Smit, Boersma, van Beijsterveldt, Posthuma, Boomsma, Stam and de Geus2010) in Dutch twin samples found that the main source of variance in SL between individuals can be explained by genetic factors: 33–82%, especially in the alpha frequency range (8–13 Hz). In the present study, CC and L were derived from the functional connectivity measure SL in EEG recordings from monozygotic (MZ) and dizygotic (DZ) twins and their siblings from a large population-based sample of Australian twins and their siblings. It was tested whether the heritability of CC, L, and SL could be replicated in this Australian sample, providing evidence that the genetic contribution to functional connectivity generalizes across populations.
Materials and Methods
Participants
Participants were adolescent twins recruited through South East Queensland secondary schools as part of an ongoing study on genetics of cognition (Wright et al., Reference Wright, de Geus, Ando, Luciano, Posthuma, Ono and Boomsma2001). Recording of EEG was a component of this study. Prior to testing, written informed consent was obtained from all participants and their parents or guardians. Ethics approval for the study was obtained from the Human Research Ethics Committee, Queensland Institute of Medical Research. Twin pairs were excluded from participation if parental report indicated that either twin had a history of head injury, neurological or psychiatric illness, substance abuse or dependence, or current use of medication with central nervous system effects. The full sample consisted of 533 females and 505 males between the ages of 15.4 and 18.2 (16.2 ± 0.3) years. After data cleaning, the final sample comprised 972 individuals and included six zygosity groups: 54 complete MZ female twin pairs (MZF; one pair with two siblings, 12 pairs with one sibling), 83 complete MZ male twin pairs (MZM; one pair with two siblings, nine pairs with one sibling), 53 complete DZ female twin pairs (DZF; one pair with two siblings, 11 pairs with one sibling), 52 complete DZ male twin pairs (DZM; one pair with two siblings, five pairs with one sibling), 48 complete DZ opposite sex twin pairs of which the female was born first (DOS FM; two pairs with two siblings, six pairs with one sibling), 58 complete DZ opposite sex twin pairs of which the male was born first (DOS MF; seven pairs with one sibling), and 14 incomplete twin pairs with one sibling. Zygosity was determined by typing nine independent polymorphic DNA markers using the AmpFLSTR Profile PCR Amplification Kit and cross-checking with ABO, MN and Rh blood groups and/or phenotypic information. Based on this, zygosity was assigned with an extremely low probability of error (less than 10−4). Subsequently, most of the sample was genotyped with the Illumina 610k array, further confirming zygosity assignment.
EEG Recordings
The resting state EEG was measured for 4 min. Participants were informed that the duration of the recording would be approximately 5 min and were asked to relax and sit quietly with their eyes closed, but stay awake and minimize eye and body movements. Recordings were taken in a semi-dark electrically shielded and sound-attenuated cubicle.
Electroencephalography was recorded from 15 scalp locations (Fp1, Fp2, Fz, F3, F4, F7, F8, Cz, C3, C4, Pz, P3, P4, O1, O2) using an electrode cap. The tin electrodes were arranged according to the International 10–20 System of Electrode Placement and referenced to physically linked ears, with the ear impedances matched at the beginning of the recording session. The ground lead was located just anterior to the Fz electrode. Ocular potentials (electro-oculogram or EOG) were recorded from single tin electrodes located on the outer canthus and the center of the supraorbital ridge above the left eye. Impedance readings were all below 5 kΩ. EOG, Fp1, and Fp2 were amplified with factor 5 K and all other channels with factor 20 K by Grass preamplifiers. Recordings were filtered with a band pass filter of 0.01 to 30 Hz and a 50-Hz notch filter. Software used for the recordings determined that the maximum length of the continuously recorded EEG was 12 s with a discontinuity of 2 s between successive 12-s blocks. Therefore, 20 12-s blocks were recorded.
EEG Data Processing
All available EEG was visually checked for bad channels such as absence of signal, hum, clipping, and external noise. Participants without the full set of 15 leads were excluded. The open source MATLAB toolbox EEGLAB was used to filter the data from 1 to 45 Hz. Subsequently, eye artifacts were removed using the ICA filtering technique of EEGLAB. Independent components were determined in the combined EEG/EOG data. Whenever a specific frontal loading and high correlations with one of the EOG channels was present (r > .7), these components were removed via backprojection of the component activations using only the remaining components. Next, data were cut into 8-s epochs of artifact-free signals. From these, 12 were randomly selected. Each epoch was filtered using alpha (7.0–13.0 Hz), beta (15.0–25.0 Hz), and theta (3.7–5 Hz) bandpass filters. Finally, the data were downsampled to 256 Hz.
Connectivity
Synchronization is a measure of coupling strength between two dynamical systems X and Y. If the state of one of the systems (the response system) can be mapped onto the state of other system (the driver system) via one-to-one continuous function F, that is, Y = F(X), then this is seen as an evidence for synchronization. Note that this relation does not require that X and Y are in the same state, merely that there exists a consistent mapping between states in X and Y. Synchronization is calculated as Synchronization Likelihood (SL) as follows. We determine the state of signal X at time i by creating a vector of signal values:
where l is the lag and m is the embedding dimension (Stam & van Dijk, Reference Stam and van Dijk2002). If signal X is in a certain state at time i then we may find a recurrence of that state at another time point j, where recurrences are defined as the Euclidian distance in an m-dimensional space at a predefined threshold. This threshold pref is chosen such that a fixed proportion of occurrences are near enough to be considered in the same state. Generally, pref is a small number ranging between 0.01 to 0.05; here we chose 0.02 but this choice is arbitrary (Smit et al., Reference Smit, Stam, Posthuma, Boomsma and de Geus2008). Next, the same comparison is made for response system Y at the time points i and j. A hit is recorded whenever this second signal Y is also in the same state at time points i and j. SL is then defined as the proportion of hits to the total number of recurrences in the X signal and is therefore a number between 0 and 1. Specific parameter settings for m, l, and pref depend on the frequency band analyzed and reflect similar choices from previous literature (Ponten et al., Reference Ponten, Bartolomei and Stam2007; Smit et al., Reference Smit, Stam, Posthuma, Boomsma and de Geus2008, Reference Smit, Boersma, van Beijsterveldt, Posthuma, Boomsma, Stam and de Geus2010). More details on SL calculation can be found in several other publications (Montez et al., Reference Montez, Linkenkaer-Hansen, van Dijk and Stam2006; Posthuma et al., Reference Posthuma, de Geus, Mulder, Smit, Boomsma and Stam2005; Stam and van Dijk, Reference Stam and van Dijk2002; Varela et al., Reference Varela, Lachaux, Rodriguez and Martinerie2001).
Graph Theory
Synchronization likelihood was computed between each pair of electrodes and for each epoch, resulting in twelve 15 × 15 connectivity matrices for each participant (15 is the number of EEG channels used in this study). The values in the diagonals were ignored. By applying a threshold such that the average number of edges per node (k) was fixed at k = 5, a binary graph was formed. This choice is somewhat arbitrary, but in this case was based on previous literature where comparable graphs were analyzed (Smit et al., Reference Smit, Stam, Posthuma, Boomsma and de Geus2008, Reference Smit, Boersma, van Beijsterveldt, Posthuma, Boomsma, Stam and de Geus2010).
Small-world networks are characterized by high CC and low L. The CC is the likelihood (a value between 0 and 1) that the neighbors of a vertex are also connected among each other, averaged over all vertices. L indicates the average number of steps required to go from a node to all others, taking the shortest route. In addition, the value of +∞ was assigned to the path length involving unconnected nodes and the harmonic mean was used to average the values obtained for path length across different nodes (Newman, Reference Newman2003). For each participant, the average CC and L over all epochs and electrodes were calculated. To be quantitatively defined as a small-world network, values of CC and L must be compared to their values for the equivalent random graph. By normalizing CC and L, we can quantify the extent of local and global efficiency of information transfer in a network. For each graph we created 1,000 randomized graphs by randomly reconnecting edges, preserving the symmetry of the matrix. Normalized CC is calculated by dividing the average CC of each subject by the average CC derived from these randomized graphs. Normalized L is calculated by dividing the average L by the average L derived from these random graphs. When it is found that L ≈ Lrandom and CC ≫ CCrandom the graph has a small-world organization (Latora & Marchiori, Reference Latora and Marchiori2001; Watts & Strogatz, Reference Watts and Strogatz1998). In the current paper, the normalized CC and L are used when referring to CC and L to describe the organization of networks.
Genetic Analyses
All genetic analyses were carried out using the statistical software package Mx (Neale et al., Reference Neale, Boker, Xie and Maes1999) using the raw data option, and this allow twins to be included without having data of their co-twin. First, a model that estimated all parameters freely (saturated model) was fitted to the data and then we tested whether twin correlations could be equated across sex within zygosity group. The variation in SL, CC, and L was decomposed into sources of additive genetic variance (A), dominant genetic variance (D) or common environmental variance (C), and unique environmental variance (E). C and D effects cannot be estimated simultaneously. The ratio of the MZ correlations to the DZ correlations can be used to determine which model (ACE or ADE) is most appropriate. In nearly all instances the DZ correlations were less than half the MZ correlations. Common environment factors were therefore not further considered as a source of variance. To calculate phenotypic and genetic correlations we used estimates from the AE decomposition. Significance of the components was tested by dropping the component from the model. Submodels were compared using the likelihood ratio test.
Results
Table 1 shows the descriptives for SL and CC and L. Median values are shown to define central tendency, since the distributions were in many cases skewed. CC is larger than unity for all frequencies. The parameter L is near 1, and concordant with a small-world architecture of functional connectivity.
TABLE 1 Medians and Interquartile Ranges for Synchronization Likelihood (SL), Cluster Coefficient (CC), and Path Length (L)

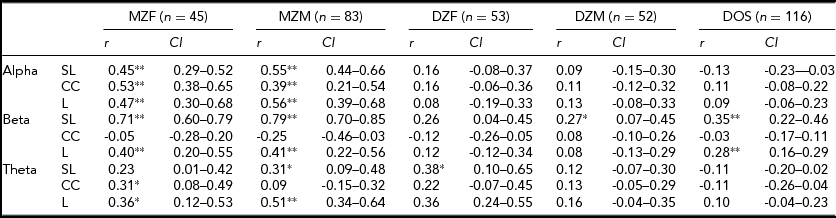
The MZ and DZ/sibling correlations of SL and the CC and L were estimated in the univariate saturated model, and are shown in Table 2. In nearly all instances the DZ correlations were less than half the MZ correlations. Common environment factors were therefore not further considered as a source of variance, and an ADE model was used throughout.
TABLE 2 Twin Correlations and the 95% Confidence Intervals From the Univariate Saturated Models in the Alpha, Beta, and Theta Frequency Bands for the Synchronization Likelihood (SL), Cluster Coefficient (CC), and Path Length (L)

*p < .01; **p < .001.
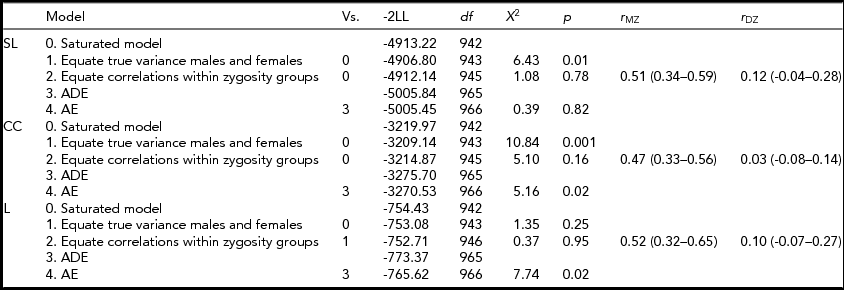
Table 3 shows the model specifications for alpha. First, we tested for differences in variances between the sexes. Furthermore, we tested for significant differences in correlations between the sexes in a 3-df test equating MZM and MZF correlations, and DZM, DZF, and DOS correlations. These same models were fitted for the beta and theta connectivity bands. Variances differed between the sexes only for SL and CC in the alpha band. Male variance in SL and CC was larger than female variance. For none of the variables a significant mean sex difference was found. In addition, no significant differences were found for twin and non-twin sibling correlations. Therefore, the MZM and MZF were combined into one MZ group and the DZM, DZF, and DOS into one DZ group. The resulting MZ and DZ correlations for SL, CC, and L in the alpha band are summarized in the last column of Table 3 with range of 0.47 to 0.52 for MZ twins and 0.03 to 0.12 for DZ twins. In the beta and theta frequency band, the MZ correlations range from -0.14 for CC to 0.75 for SL and from 0.20 to 0.43 respectively (see Supplementary Tables S1 and S2). The DZ correlations range from 0 for CC to 0.21 for L in the beta band and from 0.14 to 0.15 in the theta band (see Supplementary Tables S1 and S2; to view supplementary material for this paper, please visit http://dx.doi.org/).
TABLE 3 Model Fitting for the Synchronization Likelihood (SL), Cluster Coefficient (CC), and Path Length (L) in the Alpha Frequency Band

Vs. = versus; -2LL = -2 log likelihood; df = degrees of freedom; χ2 = chi-square test statistic; p = p-value.
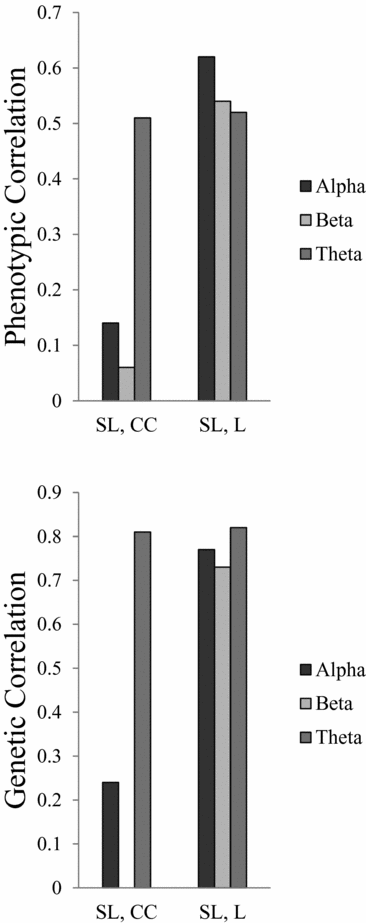
All heritability estimates and 95% confidence (95% CI) intervals are shown in Table 4. For SL, the heritability ranges from 0.74 for beta to 0.27 for theta. For L, the heritability was more consistent over all three frequency bands, ranging from 0.40 to 0.44. For CC the heritability for alpha and theta is 0.40 and 0.23 respectively, but no significant heritability was found for beta. Figure 1 shows the phenotypic and broad genetic correlations across the different connectivity parameters. The top panel shows the phenotypic correlations. SL and CC showed low (alpha band: r = .14; beta band: r = .06) to moderate (theta band: r = .51) correlations. The phenotypic correlations between SL and L are high and range from 0.52 in the theta band to 0.62 in the alpha band. The proportion of variance that SL and CC share due to common genetic sources was high for theta (0.81). The proportion of variance that SL and L share due to common genetic sources was high for all frequency bands, ranging from 0.73 for beta to 0.82 for theta.
TABLE 4 Heritability Estimates and 95% Confidence Intervals for the Synchronization Likelihood (SL), Cluster Coefficient (CC), and Path Length (L) Derived From the Univariate AE Model

*p < .001.

FIGURE 1 Phenotypic and genetic correlations between connectivity parameters synchronization likelihood (SL), cluster coefficient (CC), and path length (L).
Discussion
In a large Australian twin sample we successfully showed that genetic factors contribute significantly to functional connectivity measures obtained from a graph theoretical analysis of resting EEG signals. We found that connectivity measured by SL is most heritable in the alpha and beta frequency range (h2 = 40% and 74% respectively), consistent with the results from previous studies in Dutch twin samples (Posthuma et al., Reference Posthuma, de Geus, Mulder, Smit, Boomsma and Stam2005; Smit et al., Reference Smit, Stam, Posthuma, Boomsma and de Geus2008, Reference Smit, Boersma, van Beijsterveldt, Posthuma, Boomsma, Stam and de Geus2010). The heritability of graph parameter L in the alpha and beta frequency bands and CC in the alpha band ranged from 40% to 44%, which was consistent with the heritability for L in the Dutch sample with the same age ranges (age 16 years), where heritability varied from 29% to 58% (Smit et al., Reference Smit, Boersma, van Beijsterveldt, Posthuma, Boomsma, Stam and de Geus2010). However, Dutch heritability estimates for CC and L in the theta band were 50% and 89% respectively (Smit et al., Reference Smit, Stam, Posthuma, Boomsma and de Geus2008), whereas in the present sample these were lower at 23% and 40% respectively. The high genetic correlations between SL and average L confirm the sensitivity of L to the overall connectivity strength (Smit et al., Reference Smit, Boersma, van Beijsterveldt, Posthuma, Boomsma, Stam and de Geus2010). Note that this effect is found over and above the selection of a fixed degree k = 5, which effectively removes the effect of individual level of SL. The finding of dominance for CC and L in the alpha frequency band in this relatively small sample is interesting, and concurs with the findings of dominance by Smit et al. (Reference Smit, Boersma, van Beijsterveldt, Posthuma, Boomsma, Stam and de Geus2010). Although this may explain the low correlation between the DZ twins, this could also be caused by duplicate gene interactions (Eaves, Reference Eaves1988) and the contribution of D would be overestimated. Since genetic effects comprised both additive genetic and dominant genetic effects, we estimated r A from the AE model.
In the current paper unweighted graphs were used because these have proven useful in clinical studies (Bartolomei et al., Reference Bartolomei, Bosma, Klein, Baayen, Reijneveld, Postma and Stam2006). The application of a threshold to the SL connectivity matrices may have resulted in loss of valuable information and less precise estimates of phenotypic correlations. In addition, the choice of k, the average number of edges per node, is somewhat arbitrary. To construct more accurate models of neuronal networks, weights can be assigned to each of the edges of a graph, resulting in what is called weighted graphs (Latora & Marchiori, Reference Latora and Marchiori2001). However, weighted analysis also incorporates a great number of very weak connections in the entire network. It is an open question whether the use of weighted networks would reveal a different genetic architecture of the graph theoretical parameters.
All measurements of SL — and the network parameters CC and L that are derived from SL matrices — could be influenced by volume conduction. Time series recorded from electrodes in close proximity are likely to pick up activity from the same source, resulting in spurious connectivity for measures such as coherence and SL. Heritability estimates could therefore reflect individual variation in skull and scalp conductivity properties rather than functional differences in connectivity. In addition, spurious synchronicity between adjacent electrode pairs increases overall SL and may consequently increase CC and average L. However, in the present study, only 15 EEG channels were used to measure brain activity. In the International 10–20 system, the average inter-electrode distances are between 6 cm and 6.5 cm. Therefore, many combinations of electrodes were close to or further apart than 8 to 10 cm necessary to circumvent influences of volume conduction (Nunez & Srinivasan, Reference Nunez and Srinivasan2006; Srinivasan et al., Reference Srinivasan, Winter, Ding and Nunez2007). This suggests that the sparsely placed electrodes avoid a large influence of volume conduction and as a result it is unlikely that volume conduction has introduced much to the variation in functional connectivity in our recordings.
Within the last decade, neurophysiologists have progressed in terms of accuracy of measuring true synchronization between spatially and functionally distinct brain areas. SL and its graph theoretical derivatives CC and L have established themselves in several clinical studies as a useful tool for describing functional connectivity and capturing brain activity underlying behavioral traits and neurological disorders. These include differences in brain organization in schizophrenia (Micheloyannis et al., Reference Micheloyannis, Pachou, Stam, Breakspear, Bitsios, Vourkas and Zervakis2006) and Alzheimer's disease (de Haan et al., Reference de Haan, Pijnenburg, Strijers, van der Made, van der Flier, Scheltens and Stam2009). In normal development, both connectivity and graph parameters show marked changes from childhood to adulthood (Smit et al., Reference Smit, Boersma, Schnack, Micheloyannis, Boomsma, Hulshoff Pol and de Geus2012). Moreover, SL correlates with brain white matter volume (Smit et al., Reference Smit, Boersma, Schnack, Micheloyannis, Boomsma, Hulshoff Pol and de Geus2012). Many of these (pathological and non-pathological) traits are highly heritable. And since the brain-derived connectivity measures have shown to be heritable as well, we may conclude that SL and its graph theoretical derivatives are potential endophenotypes for these traits and neurological disorders.