Does eminence or extraordinary accomplishment owe more to ‘nature’ or ‘nurture’? This was the central question addressed by Francis Galton in his 1869 work Hereditary Genius. In doing so, Galton effectively created two fields, historiometrics (or historiometry) and behavior genetics. Historiometrics concerns itself with estimating the relative significance of a given cultural, political or scientific development, and the relative eminence of the individuals responsible for these developments, in addition to ascertaining their determinants (Simonton, Reference Simonton1984). This is accomplished using encyclopedias, biographies and other relatively neutral reference works as the basis for quantifying these properties (Simonton, Reference Simonton1984). Galton applied a crude form of historiometrics to the identification of extraordinary talent or eminence across a number of domains (science, industry, leadership and sports) within his own and in other notable British families — Galton believed that the assessment of individuals’ accomplishments by relevantly informed others offered the best basis for identifying eminence. Behavior genetics concerns itself with the measurement of the degree to which hereditary genetic and environmental factors (what Galton [Reference Galton1874] subsequently termed nature and nurture, respectively) influence variation with respect to a given behavioral or cognitive phenotype. In Hereditary Genius, Galton proposed that concentrations of eminence within pedigrees could be employed to demonstrate the contribution of hereditary factors to variation in this trait. Footnote 1 In tracking the prevalence of eminent individuals across multigenerational pedigrees (including his own), Galton concluded that the elements of eminence were indeed hereditary. However, he was unable to provide either a quantitative estimate of their heritability or adequately control for environmental confounds, a point made by Augustin de Candolle (Reference de Candolle1873) who was a major critic of Galton’s approach.
Modern historiometrics (much of the groundwork for which was laid by Dean Keith Simonton) allows for relatively rigorous Footnote 2 quantification of the eminence of prominent individuals — this is achieved by determining the degree to which various neutral reference works converge with one another with respect to their coverage of prospectively eminent individuals and their accomplishments. For example, a scientist whose name appears in one list of field-specific significant figures, but not in others, would be less eminent than one whose name appears in multiple independently compiled lists. Similarly, a scientist who features in general reference works (such as encyclopedias), in addition to field-specific ones, is more eminent than the one who has field-specific, but not general, prominence. In the extreme, the most accomplished and influential individuals will be sufficiently well known that they are household names, becoming known simply by their surnames (e.g., Darwin, Einstein, Freud, Marx, Mozart; Murray, Reference Murray2003). Footnote 3 Historiometrically defined eminence is necessarily a domain-general phenomenon — encompassing extraordinary achievement across many different areas of accomplishment (e.g., STEM, politics, arts, literature, and sport). The historiometric approach is nevertheless also informative about the domain-specific dispositions of eminent individuals, since relevant biographic data are often rich in details that are reflective of the cognitive, conative, and situational factors that incline such individuals toward specific degrees and domains of accomplishment (Simonton, Reference Simonton1984, Reference Simonton2009, Reference Simonton2018). Footnote 4
In terms of its broad determinants, Galton (Reference Galton1869) described eminence as the product of a ‘triple event, of ability, combined with zeal and with capacity for hard labor’ (p. 78). Johnson and Bouchard Jr. (Reference Johnson, Bouchard and Simonton2014) note that all of the elements comprising Galton’s ‘triple event’ are additively heritable; thus, it might be expected that historiometric eminence (presumably being a joint product of high levels of these elements) will itself be heritable. However, defining the phenotype of eminence for the purposes of behavior-genetic measurement models presents certain interesting challenges.
First, there is the problem of the sorts of historiometric thresholds that need to be met when identifying eminent individuals. Different researchers have different opinions on this matter. Charles Murray in his book Human Accomplishment (2003) employs a two-step procedure for identifying those whom he terms significant figures in the domains of science, technology, medicine, arts, literature, and philosophy (with such individuals being sourced from both Western and non-Western populations). Murray (Reference Murray2003) initially defines significant figures as those who are (a) featured in at minimum 50% of the various ‘qualified’ reference works that he consulted and (b) realized their accomplishments no later than 1950, so as to avoid ‘epochcentric’ or recency bias effects. Once this cutoff is achieved, such individuals can then be assigned an index score, which is a measure of their relative eminence based on that individual’s comparative prominence across the relevant reference works within a given inventory. This is essentially a function of the amount of text devoted to that individual across reference works (among which there is typically very high agreement), which is then normalized on a scale such that 1 is the lowest score and 100 is the highest score. This process resulted in the inclusion of 4002 significant figures in Human Accomplishment.
Yu and colleagues (Reference Yu, Ronen, Hu, Lu and Hidalgo2016) have generated an alternative global database of eminent individuals termed Pantheon, which is much broader than the one assembled by Murray, as it also includes politicians, economists, actors, and athletes among other categories, with no restrictions on year of accomplishment. As with Murray (Reference Murray2003), this dataset also employs a two-step inclusion criteria, with the first step being that for an individual to be included, they must have a Wikipedia page that has been translated into a minimum of (in the current version of the dataset) 15 languages. Earlier versions of the dataset had stricter inclusion rules (e.g., >25 languages in version 1.0; Yu et al., Reference Yu, Ronen, Hu, Lu and Hidalgo2016). The relaxation of this inclusion rule led to an increase in the number of eminent individuals (what Pantheon terms memorable people) from 11,341 (in the earliest version of the dataset) to 88,506 (in the current version). The second step involves assigning each individual a historical popularity index (HPI) value, which is a measure of biographic prominence generated by combining information on the number of languages in which an eminent individual’s Wikipedia biography is available, with page views, and the amount of time that has elapsed since the individual’s birth. Epochcentric bias is controlled by adjusting the HPI values of individuals who have been known for <70 years. Additional weights are used to compensate for English-language bias. As with Murray’s (Reference Murray2003) index score, the HPI is also normalized, such that 100 is the highest score and 1 is the lowest. The earliest version of Pantheon contained HPI values for 1570 individuals in the arts and sciences who overlapped with those included in Murray’s (Reference Murray2003) Human Accomplishment, which allowed Yu et al. (Reference Yu, Ronen, Hu, Lu and Hidalgo2016) to cross-validate their HPI values with respect to the latter’s index scores. They found that the two correlate modestly at .35 (95% C.I. [.31, .39]), which is consistent with the broader tendency noted by Murray (Reference Murray2003) for various neutral reference works to converge with one another in terms of their degree of coverage of eminent individuals.
The Murray (Reference Murray2003) and Yu et al. (Reference Yu, Ronen, Hu, Lu and Hidalgo2016) databases could, by virtue of the differential breadth of their respective inclusion criteria, be said to yield thin versus thick measures of eminence, respectively.
The second problem concerns the rarity of eminence. Families containing one or more eminent twins are doubtlessly very rare, making the most straightforward behavior-genetic approaches to estimating the heritability of this phenotype untenable. But as Galton (Reference Galton1869) noted, historiometric eminence seemed to run in his own family and other prominent families. As pedigree data can be used to estimate heritabilities, such data can be employed to quantify the heritability of eminence among related eminent individuals defined based on historiometric criteria.
Methods
Eminence Measure
As eminent individuals are relatively rare, it was decided that using individuals sourced from the latest (2020) release of the thicker Yu et al. (Reference Yu, Ronen, Hu, Lu and Hidalgo2016) Pantheon dataset (https://pantheon.world/data/datasets) would be best, as this would allow for the largest number of eminent individuals to be identified within the super-pedigree described below, thus increasing the power available to estimate heritability. In assigning eminent individuals to the super-pedigree, each individual is assigned their respective their HPI value (as estimated in the current release of Pantheon Footnote 5 ). Those who are noneminent are assigned values of 0, thus the model employed here is somewhat like a case–control design, in that a ‘liability threshold’ of biographic prominence has to be attained for an individual to get a nonzero degree of eminence; however, among the eminent, there is significant variation in terms of relative degree of eminence that provides the models used here with the variance necessary to establish stable heritability estimates. The possibility of using a strict case–control design to estimate heritability (i.e., where eminent individuals are assigned a value of 1 and noneminent individuals a value of 0) was also explored; however, the resultant model did not converge. This is consistent with the very low phenotypic variance associated with strict case–control designs that necessarily increases the error associated with parameter estimation. The use of a partial case–control model still has the benefit of bringing into sharp relief the most salient phenotypic difference, that is, whether the individual is eminent as measured by biographical prominence or not.
Super-Pedigree
Genealogical data were collected for a total of 301 individuals comprising a social (genealogical, nongenetic) super-pedigree involving four prominent and related British (and one British-Persian) families. The core of the super-pedigree was the Wedgwood–Darwin–Galton–Williams (henceforth Wedgwood–Darwin) pedigree, which includes three eminent Wedgwoods (Josiah Wedgwood I, Thomas Wedgwood, and Emma Wedgwood Footnote 6 ), six eminent Darwins (Erasmus Darwin, Robert Waring Darwin, Charles Robert Darwin, Charles Galton Darwin, George Howard Darwin, and Francis Darwin), in addition to Francis Galton and Ralph Vaughan Williams. The Wedgwood–Darwin pedigree employed here was compiled by Harry H. Laughlin in 1932, with the full data being republished in Berra et al. (Reference Berra, Alvarez and Shannon2010). Another prominent pedigree is the Arnold–Huxley–Collier (henceforth Arnold–Huxley) pedigree, the members of which are related to the Wedgwood–Darwin pedigree via two instances of cross-marriage. Footnote 7 This pedigree contains seven eminent individuals: Thomas Henry Huxley, Aldous Huxley, Julian Huxley, Andrew Huxley, Thomas Arnold the Elder, his son Matthew Arnold, and John Collier, who married two of Thomas Henry Huxley’s daughters. Data sourced from Wikipedia on the Darwin–Wedgwood and Arnold–Huxley family trees (Wikipedia, 2021a, 2021b) were used to enhance each pedigree and identify the linkages necessary for merger of both into a common super-pedigree. Another prominent family is the Keynes–Lopokova–Hill–Adrian–Baha’u’lláh (henceforth Keynes-Baha’u’lláh) pedigree, which is connected to the Wedgwood–Darwin pedigree via one instance of cross-marriage. Footnote 8 This pedigree contains seven eminent individuals, John Maynard Keynes, Alexander Skandar Keynes, Lydia Lopokova, Footnote 9 Archibald Hill (who married John Maynard Keynes’ sister, Margaret), Edgar Adrian, Baha’u’lláh, Footnote 10 his half-brother Subh-i-Azal, Footnote 11 his eldest son ‘Abd’u’l-Bahá, and his great-grandson Shoghi Effendi. As with the Arnold–Huxley pedigree, data permitting integration into the super-pedigree were obtained from the relevant significant figures’ Wikipedia pages. The final constituent family in the super-pedigree is the Benn–Rutherford pedigree. This pedigree contains three closely related eminent individuals (Anthony Wedgwood Benn, Hilary James Benn, and Margaret Rutherford), the first two whom are descended from the Wedgwood family via two distinct lines, both of which are collateral to the line of Josiah Wedgwood I. The precise nature of the connection between the Benn and Wedgwood families was ambiguous until recently, when the genealogist Maurice Frank was able to identify the relevant linkages (Frank, Reference Frank2021). In total, there are 30 eminent individuals out of 301 (9.97%) comprising the super-pedigree. These individuals, along with their birth and (where applicable) death years, coupled with their (current as of this writing) HPI values and accomplishment domains (from their Pantheon listings) are shown in Table 1. The super-pedigree is presented in Figure 1 along with a table containing the names of all entrants.
Table 1. Thirty eminent individuals sourced from Pantheon and contained within the super-pedigree, along with their birth and (where applicable) death years and accomplishment domains
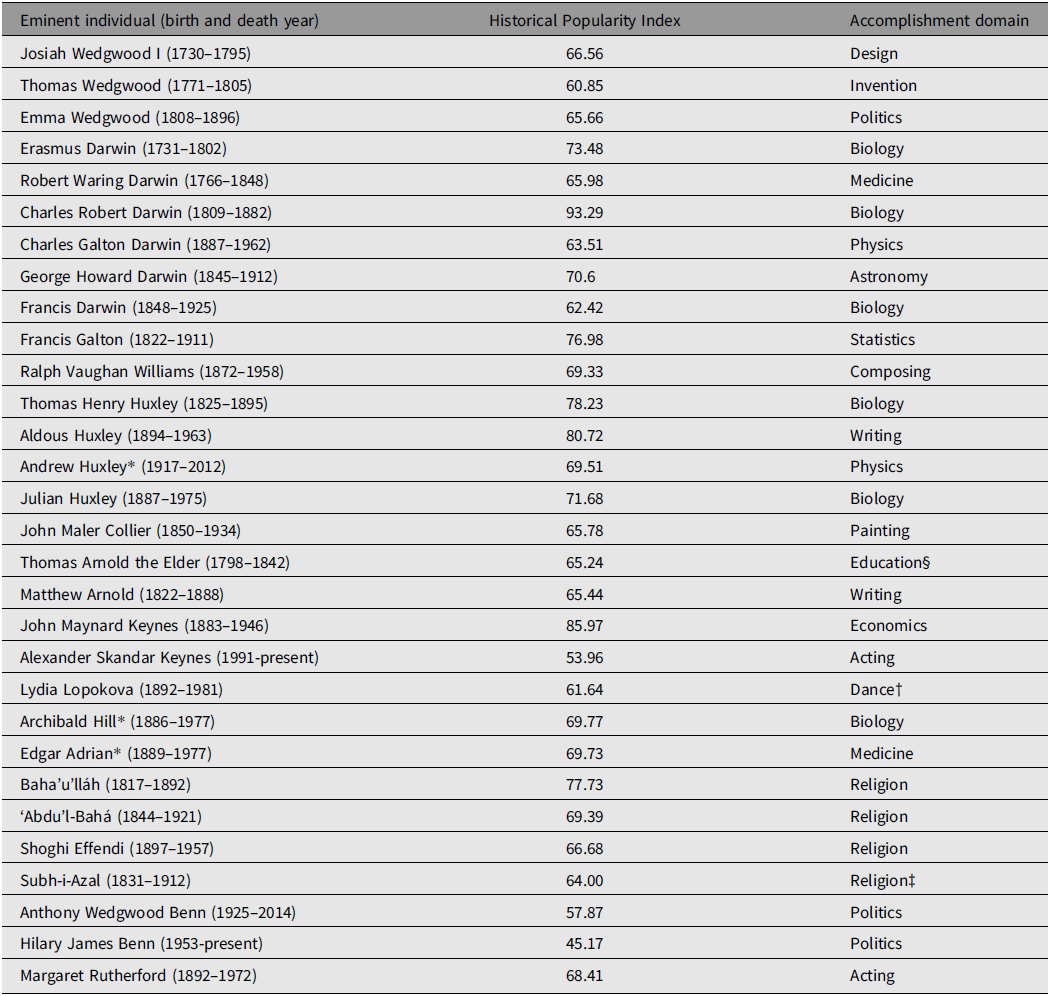
Note: *The individual won a Nobel Prize. †Pantheon (as of July 8, 2021) incorrectly lists Lopokova as a painter, when she was an eminent ballerina. ‡Pantheon incorrectly lists Subh-i-Azal as a writer, when he was a religious leader. §Pantheon incorrectly lists Thomas Arnold as a philosopher when he was a prominent educator.

Figure 1. The super-pedigree. Shaded entries correspond to eminent individuals. Double lines indicate the presence of intermarriage (specifically marriage involving individuals related to one another to the degree of third cousin or closer). Dashed lines indicate the presence of the same individual in different parts of the super-pedigree. For example, Josiah Wedgwood III (126) is the husband of Caroline Darwin (124) and also the brother of Emma Wedgwood (125), Hensleigh Wedgewood (128), and Henry Wedgwood (127)
Employing the thicker Pantheon database of eminent individuals yields both a more numerous and more diverse (in terms of accomplishment domains, nationality, and sex) sample of eminent individuals than does the thinner Human Accomplishment dataset. The latter contains only 8 eminent individuals, all of whom are male, British and whose accomplishments are restricted to science, mathematics, philosophy, literature, and the arts, Footnote 12 whereas the Pantheon-derived dataset contains data on 3 women (10% of the eminent sample) and 4 non-British (Persian) individuals (13.33% of the eminent sample), and spans 16 distinct accomplishment domains. Three of the individuals in the super-pedigree also won Nobel Prizes for scientific work (10% of the eminent sample).
Measurement Model
In addition to twin studies, geneticists have also adopted pedigree-based animal models to calculate heritability estimates. According to Wilson et al. (Reference Wilson, Reale, Clements, Morrissey, Postma, Walling, Kruuk and Nussey2010), an animal model operates as a linear mixed-effects model (LMM) where the breeding value (the additive effect of a subject’s genotype upon a trait compared to the population’s average phenotype) is added to the statistical equation as a random effect. This term is included as a random effect because researchers do not know the breeding value for each individual in the sample. Moreover, per Wilson et al. (Reference Wilson, Reale, Clements, Morrissey, Postma, Walling, Kruuk and Nussey2010), random effects enable researchers to infer the effects’ distribution in a larger population. The implementation of this value as a random effect allows, via the computation of variance components, the estimation of the additive genetic variance (A) and the environmental variance (E). Thus, by computing these components, it is possible to calculate the trait’s narrow-sense heritability. Although animal models can be estimated as LMMs, geneticists have gravitated toward Bayesian estimation in the past decade.
In this study, several Markov Chain Monte Carlo (MCMC) generalized linear mixed models were computed with the R package MCMCglmm (Hadfield, Reference Hadfield2015). This statistical procedure allows for the estimation of behavior-genetic variance components after accounting for the pedigree structure inherent in the data. Each model was computed using independent MCMC chains corresponding to 10,000,000 iterations, with sampling (thinning) occurring every 100 samples and a burnin period specified to disregard the first 300,000 iterations. The elimination of these initial iterations allowed the MCMC chain to explore and ascend through the likelihood landscape before sampling from the posterior distribution for the model’s parameters. Given the underlying skewedness of the variable’s residuals, a log-transformation was implemented to handle this issue. The model’s priors assumed that the G structure and the R structure were equivalent to the phenotypic variance divided by the number of V terms with the prior’s matrices following an order of N = 1. Thus, the observed phenotypic variance was divided between the informed priors (sourced from the meta-analysis of Polderman et al., Reference Polderman, Benyamin, De Leeuw, Sullivan, Van Bochoven, Visscher and Posthuma2015) corresponding to the model’s genetic (.49) and residual effects (.51).
After generating each model, variance components were extracted and used to estimate the trait’s narrow-sense heritability (h 2). These values were computed as the proportion between the additive genetic variance (A) and the total observed variance (A + E; where E is equivalent to the model’s residual variance). Heritability coefficients were also estimated with the function QGparams associated with the package QGglmm (Villemereuil et al., Reference de Villemereuil, Schielzeth, Nakagawa and Morrissey2016). In generating stable heritability values with pedigree data, the use of a minimum of 150 individuals is generally recommended (Perrier et al., Reference Perrier, Delahaie and Charmantier2018). The super-pedigree, therefore, exceeds this power requirement as it contains 301 individuals in total.
Concerning the estimation of fixed effects, the calculation of each parameter was accompanied by a significance test (pMCMC), evaluating whether the predictor was significantly different from zero. The models’ deviance information criterion (DIC) values were also extracted for subsequent model comparisons. Similar to other model fit indicators (e.g., Akaike’s information criteria [AIC], AIC second-order estimate [AICc], and Bayesian information criteria [BIC]), smaller (DIC) values indicate a better model fit. For a more accurate model appraisal, ΔDIC (the difference between the best model’s DIC and each of the competing model’s DIC values) and DIC weights (the relative probability that a particular model features the best statistical fit) were also computed. All statistical analyses were conducted with the statistical packages MCMCglmm (Hadfield, Reference Hadfield2015) and MuMin (Barton, Reference Bartoń2020) in R v 4.0.1.
Results
MCMCglmm Variance Components, Heritability Estimation, and Model Comparison
The analysis did not identify significant autocorrelations for the various variance components for lags above 100 samples. Table 2 features the MCMCglmm results, including the narrow-sense heritability estimates based on the models’ variance components. The A + E model tested here determined that the additive genetic component explained a sizeable proportion of the systematic variance. The analysis also revealed that the model’s intercept was significantly different from zero. Overall, the trait’s narrow-sense heritability is .510 (95% CI [.434, .579]) and the unshared environmentality is (1–h 2 ) .490. A similar pattern was found for an alternative model containing sex as a fixed effect. The trait’s narrow-sense heritability was slightly smaller (.507; 95% CI [.434, .578]). As reflected by Figure 2, the density function plot featured a normal distribution. In regard to the model’s fixed effect, males, scored significantly higher on the eminence scale (p = .0085). The best model was the one in which A was modeled as a random effect, and sex was included as a fixed effect. Table 3 features the results of a model comparison. The DIC weight of this model was .970, meaning that it had a 97% relative probability of being the best model.
Table 2. MCMCglmm evaluating the effects of sex on eminence

Note. pMCMC: Significance test evaluating whether the parameter is different from zero. Mu: In variance components analysis, Mu is equal to the model’s intercept. Although the pMCMC for Model 1’s Mu was nonsignificant (.3010), the Mu value for Model 2 did reach statistical significance (.0220). A: additive variance, Vp: phenotypic variance. QG: heritability coefficients computed with the function QGparams in R.
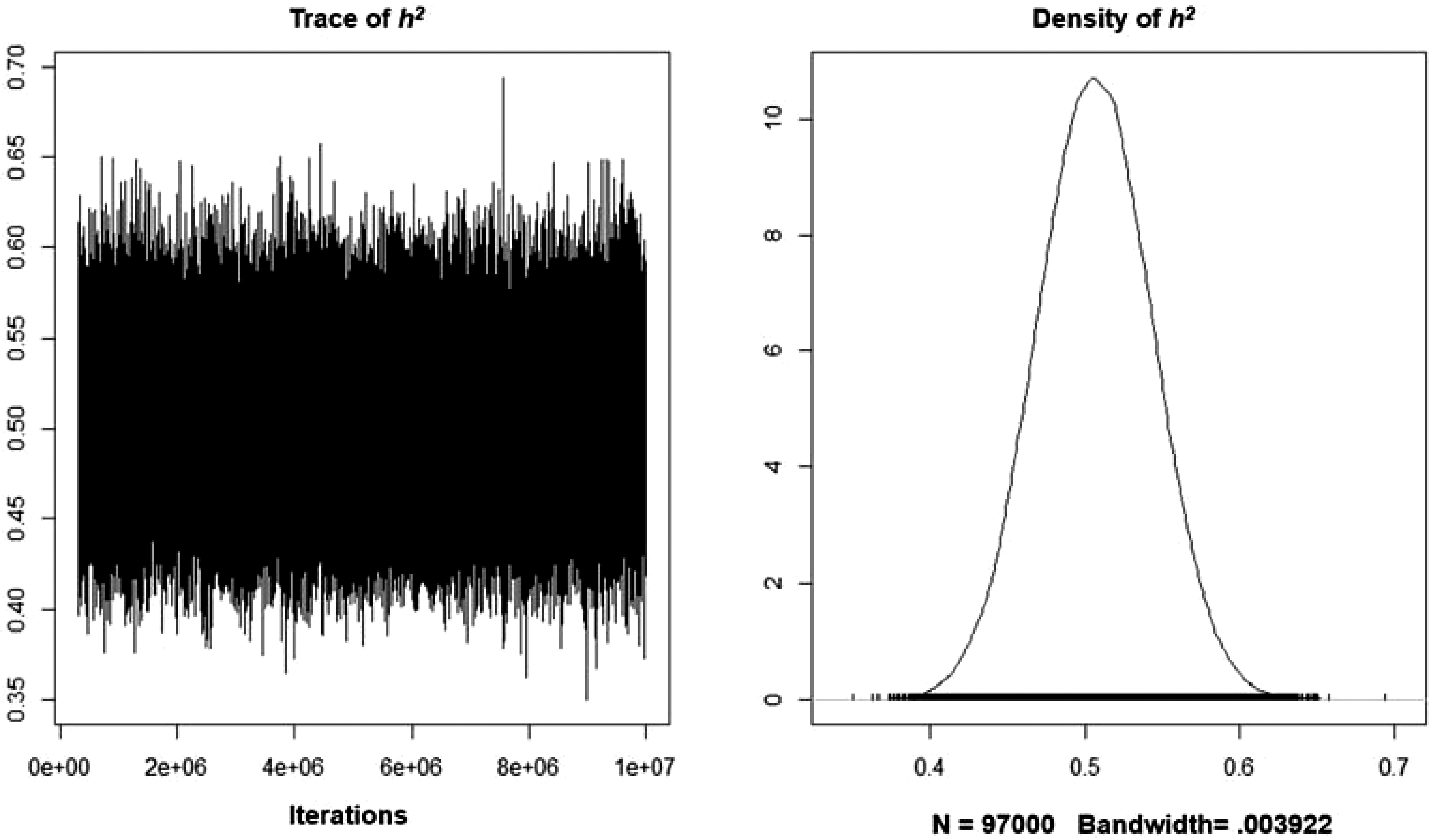
Figure 2. Trace and density plots representing the additive heritability estimate of eminence after controlling for sex
Table 3. MCMCglmm model comparison evaluating the effects of sex on eminence, ranked based on DIC weights

Note: DIC, deviance information criterion. Smaller DIC values indicate a better fit. DIC weights reflect the probability that a specific model is the best model.
Discussion
A and E behavior-genetic variance components were estimated using an informed prior, which was derived from the meta-analysis of heritability conducted by Polderman et al. (Reference Polderman, Benyamin, De Leeuw, Sullivan, Van Bochoven, Visscher and Posthuma2015). Two separate models were estimated and then compared, one without and one with sex modeled as a fixed effect. The best-fitting model (with a 97% probability) was the one that included sex. Based on this model, the additive (A) heritability (h 2) was estimated to be .507 (95% CI [.434, .578]) meaning that 50.7% of the variance in eminence can be attributed to genetic variants with additive effects on phenotypic variance. The nonshared environmentality (E) variance is .493. This variance component captures all contributions to trait variance that are not directly attributable to the action of additive genetic variance and would include error. This finding is broadly consistent with the high pedigree-based heritability estimate of social status in a large English lineage presented by Clark (Reference Clark2021).
The most straightforward interpretation of these results is that variation in eminence, much like the extremes of more conventionally measured dimensions of individual differences (such as IQ), is mostly influenced by additive genetic variation, which in turn is consistent with existing knowledge of the basis of normal-range phenotypic variance in many traits believed to contribute in part to eminence (again, such as IQ; Shakesharf et al., Reference Shakesharf, Trzaskowski, McMillan, Krapohl, Simpson, Reichenberg, Cederlöf, Larsson, Lichtenstein and Plomin2015). Congruent with this, Roeling et al. (Reference Roeling, Willemsen and Boomsma2016) estimated that the additive heritability of working in a creative profession (a potentially more normal-range manifestation of the sorts of phenotypes that contribute to ‘eminence’) is .70. Further, and interestingly, they found that the best-fitting model in their dataset was one estimating only A and E variances.
Visual inspection of the super-pedigree (Figure 1) yields clear indications of direct multiple generation-to-generation transmission of eminence. Erasmus Darwin was father to Robert Waring Darwin and grandfather to both Charles Robert Darwin (who was the son of Robert Waring Darwin) and Frances Galton. Josiah Wedgewood I was father to Thomas Wedgwood and grandfather to both Emma Wedgwood and Charles Robert Darwin. Josiah Wedgwood I and Erasmus Darwin were both great-grandfathers to George Howard Darwin, and Francis Darwin (both of whom were the children of Emma Wedgwood and Charles Robert Darwin), and great-great-grandfathers to Charles Galton Darwin (who was the son of George Howard Darwin). Anthony Wedgwood Benn was father to Hilary James Benn, Baha’u’lláh was father to ‘Abd’u’l-Bahá, who was grandfather to Shoghi Effendi, and Thomas Arnold the Elder was father to Matthew Arnold. Thomas Henry Huxley was a grandfather to Aldous, Andrew, and Julian Huxley. More indirect instances of vertical transmission are also present in the data. Josiah Wedgwood I (along with Erasmus Darwin, through Robert Waring Darwin) was a great-great-grandfather to Ralph Vaughn Williams and great-great-great-great-great-grandfather (along with Erasmus Darwin) to Alexander Skandar Keynes through Charles Robert Darwin and Emma Wedgwood, who were his great-great-great-grandparents. Baha’u’lláh was also great-great-great-grandfather to Alexander Skandar Keynes. One of the latter’s great-grandfathers was Edgar Adrian. Thomas Arnold the Elder was great grandfather to both Aldous and Julian Huxley.
There are alternative behavior-genetic models of extraordinary accomplishment that take into consideration nonadditive gene-by-gene interactions (genetic dominance and epistasis effects) and gene-by-environment interactions. An example of the former is emergenesis, which posits that extreme and rare phenotypes may primarily result from the action of rare nonadditive gene combinations (Eysenck, Reference Eysenck1995; Lykken et al., Reference Lykken, McGue, Tellegen and Bouchard1992; Jensen, Reference Jensen, Sternberg and Grigorenko1997; Simonton, Reference Simonton1999), with the resultant phenotype being effectively larger than the sum of its parts owing to the multiplicative, as opposed to additive, ways in which the relevant genetic variants interact. An example of the latter is the cosmobian hypothesis. Cosmobia is an old concept from developmental biology which holds that rare physiological deformity can exhibit a degree of variation that does not necessarily handicap the individual exhibiting such deformities. For example, individuals can exhibit severe deformities, such as the presence of just one, or more than two, eyes (these are termed primary deformities), but within this range of phenotypes there are far less pathological, but nevertheless quite rare, secondary deformities, such as having two pupils per eye. While such cosmobian variation might stem from genetic differences among individuals, in some cases, it may purely be a function of the capacity for a particular genotype to produce substantially different phenotypes, given special environmental conditions experienced during development (Johnson & Bouchard Jr., Reference Johnson, Bouchard and Simonton2014). Johnson and Bouchard Jr. (Reference Johnson, Bouchard and Simonton2014) have speculated that manifestations of extreme accomplishment (such as creative genius) might be another example of a cosmobian effect, with the possession of even extreme levels of the relevant dispositional traits being insufficient to bring about such a phenotype in the absence of certain unusual gene-by-environment correlations and resultant interactions. For discussion of models that similarly emphasize epigenetic and gene-by-environment interactions in the cultivation of extraordinary talent, see Papierno et al. (Reference Papierno, Ceci, Makel and Williams2005) and Simonton (Reference Simonton1999).
There exist statistical packages that allow for various gene-by-gene interactions to be estimated based on pedigree data; however, the author of one such package (Nadiv; Matthew Wolak) informed the authors that the super-pedigree has insufficient varieties of consanguineous mating (intermarriage) necessary for the reliable estimation of nonadditive effects, based on the results of simulations that were run on behalf of the authors. Four clear instances of intermarriage (involving individuals related to one another at the degree of third cousin or closer) are present in the super-pedigree: (1) Josiah Wedgewood I married his third cousin Sarah Wedgwood, (2) Josiah Wedgwood III married his first cousin Caroline Sarah Darwin, (3) Robert Barclay II married his first cousin Lucy Barclay, and (4) Charles Robert Darwin married his first cousin Emma Wedgwood. For the estimation of nonadditive effects, much more elaborate patterns of intermarriage are needed (such as those involving double-first cousins and half-cousins; Wolak, personal communication).
The cosmobia model could not be tested either, as it requires the estimation of gene-by-environment interactions, which cannot (currently) be done using the MCMCglmm software. Evidence of a substantial contribution to variance in eminence stemming from environmentality is nevertheless present, which might in part be reflective of factors such as the provisioning of ‘opportunities’ for the establishment of fortuitous gene-by-environment interactions via gene-by-environment correlation. Thus, it might be that eminence in this super-pedigree is a joint product of having high levels of additive genetic variants associated with the relevant dimensions of talent (e.g., high IQ, creativity, ambition, grit), in addition to having the rare opportunity to cultivate that talent to a truly extraordinary degree through access to unique environments (one such environment might the home of a highly accomplished family with rich stores of knowledge, which may in turn encourage and support one to work extraordinarily hard in order to live up to expectations). The sex difference in degree of eminence (favoring males) might also be a partial function of the rigidity of historical sex roles and associated stereotypes; however, this finding is also in line with the greater male variability hypothesis (which is robustly supported with respect to a large variety of neuroanatomical and behavioral measures: Thöni & Volk, Reference Thöni and Volk2021; Thöni et al., Reference Thöni, Volk and Cortina2021; Wierenga et al., Reference Wierenga, Doucet, Dimi, Agartz, Aghajani, Akudjedu, Albajes-Eizagirre, Alnæs, Alpert, Andreassen, Anticevic, Asherson, Banaschewski, Bargallo, Baumeister, Baur-Streubel, Bertolino, Bonvino and Tamnes2020). It should be furthermore noted that evidence of a significant impact of vertical nongenetic (i.e., cultural) transmission on trait variance is scant, especially when extended twin studies are used to properly control vertical transmission effects for genetic confounds (see Eaves et al., Reference Eaves, Heath, Martin, Maes, Neale, Kendler, Kirk and Corey1999; Kandler et al., Reference Kandler, Bleidorn and Riemann2012; Martin et al., Reference Martin, Eaves, Heath, Jardine, Feingold and Eysenck1986; Swagerman et al., Reference Swagerman, Van Bergen, Dolan, de Geus, Koenis, Pol and Boomsma2017). On this basis, it is not anticipated that these sorts of vertical transmission effects are (substantially) contributing to the patterns observed in these data. Footnote 13
The super-pedigree is unusual in that it contains so many historiometrically identified (based on biographic prominence) eminent individuals, given their extreme rarity, even when established using thicker inclusion criteria, as per Pantheon. Footnote 14 One possibility is that the members of this super-pedigree historically engaged in relatively high levels of intermarriage and assortative mating, which may have maintained at a high-frequency rarer genetic variants that predispose toward extraordinary accomplishment. Four instances of intermarriage involving individuals related to the degree of third cousin or closer have been noted in this super-pedigree, but it is possible that more cryptic forms of relatedness might also be present in this dataset (as an example of this, two separate Wedgwood lines, collateral to Josiah Wedgwood I, contributed to the Benn family via the marriage of William John Barker and Margaret Wedgwood who were fourth cousins). That many of the members of this super-pedigree may historically have been relatively highly interrelated is consistent with genomewide estimates of linkage disequilibrium among representatively sampled individuals from the population of the USA, which indicate that general levels of inbreeding were higher among older individuals (Nalls et al., Reference Nalls, Sanchez-Simon, Gibbs, Paisan-Ruiz, Bras, Tanaka, Matarin, Scholz, Weitz, Harris, Ferrucci, Hardy and Singleton2009). This would be consistent with historically more limited geographical dispersal among individuals (especially in the 19th and prior centuries) relative to their extended family members. Increased aggregate relatedness among partners would be expected to increase genomic linkage disequilibrium among offspring, raising trait heritability estimates. There may also be significant degrees of assortative mating in this super-pedigree, involving families who are similar with respect to specific talent-conferring genetic loci. Indeed, the merger through marriage of the Arnold–Huxley, Keynes-Baha’u’lláh, and Wedgwood–Darwin pedigrees could be evidence of this, as all three families were of equivalent social and intellectual standing (indeed Charles Robert Darwin and Thomas Henry Huxley were close scientific collaborators). Cryptic relatedness and assortative mating are difficult to estimate absent either genomic data or much more fine-grained and extensive social pedigree-based information.
There are some limitations in these data that need to be addressed. Chief among these is the social, as opposed to genetic, nature of the super-pedigree. It has been noted that ‘[h]eritability estimates …[are] slightly higher’ (Perrier et al., Reference Perrier, Delahaie and Charmantier2018, p. 863) when estimated using genetic, as opposed to social pedigree data. This discrepancy is attributed by Perrier et al. (Reference Perrier, Delahaie and Charmantier2018) ‘to incorrect pedigree links, including extra-pair paternity, and to lower information content’ (Perrier et al., Reference Perrier, Delahaie and Charmantier2018, p. 838). Therefore, the estimates of the additive heritability of eminence presented here are likely to be lower than would have been the case had corresponding genetic data for the super-pedigree been available, owing to error in identifying linkages, making these estimates likely somewhat conservative.
Another limitation concerns the use of the thicker Pantheon dataset, as opposed to a thinner, more selective dataset such as that of Human Accomplishment. It could be argued that some of the individuals counted as eminent might have had their historiometric bibliographic prominence inflated for relatively mundane reasons (such as in the case of those who are the offspring of someone eminent), or due to epochcentric effects (although the HPI values used here do attempt to correct for ‘recency bias’). The majority of the individuals that were included as ‘eminent’ are, however, clearly independently and (by world historical standards) significantly accomplished and therefore are eminent in their own right (such individuals include several unambiguous creative geniuses, three Nobelists, a major 18th century industrialist, and the founder of a significant world religion). Another advantage (beyond greater model power) of using the thicker Pantheon dataset is the breadth of domains covered. There are likely to be highly general genetic factors that predispose toward extraordinary achievement across multiple domains of accomplishment (including things as far afield as athletics and science), such as those contributing to individual differences in grit and achievement orientation. In the case of the present result, it is likely that the heritability estimated here for eminence is capturing the heritability of the relevant interactions among all of those dispositional factors in Galton’s ‘triple event’, therefore making the phenotype of eminence consistent with what has come to be termed the First Law of Behavior Genetics, specifically ‘all human behavioral traits are heritable’ (Turkheimer, Reference Turkheimer2000, p.160). Finally these findings potentially bring closure to the Galton-de Candolle debate, as eminence appears to be equal parts nature and nurture.
Conflict of interest
We the authors declare that there are no conflicts of interest.







