The basis of this Paper is the new method of graduation introduced by Professor E. T. Whittaker, and expressed in the equation
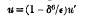
where δ indicates central differencing, so that δ6u′x=Δ6u′x−3;u′=the graduated and u the ungraduated values of a series of observations, and ∈ is a measure of the importance assigned in any particular case to adherence to the original data as against perfect smoothness in the graduated curve.
Certain terminal conditions attach to this equation, and it is suggested that if no attempt be made to carry the method to the extremes of the series of data, these terminal conditions may be disregarded.
By methods described in the Paper, different summation formulae of graduation are derived from the equation, giving ε various values. The results of test graduations of the a(f) and a(m) ultimate tables by certain of these formulae are shown, and compared with the results under the exact solutions obtained by Dr. A. C. Aitken. A graduation is also made of the Female Government Annuitants 1900-1920 Experience, and the results are compared with these produced by the methods suggested in Dr. Buchanan's recent paper (T.F.A., x., p. 289), and in the discussion thereon.
It is suggested that ε will prove of practical value as an aid to the selection and classification of graduation formulae, and that summation formulae obtained by the methods described have thus a practical advantage as well as one of theory.