Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T14:52:33.476Z Has data issue: false hasContentIssue false
  • English
  • Français

On Graduation by the General Formulae of Oscillatory Interpolation

Published online by Cambridge University Press:  07 November 2014

A. R. Reid  and
J. B. Dow
A. R. Reid
Affiliation:
Standard Life Assurance Company
J. B. Dow
Affiliation:
Standard Life Assurance Company
Get access

Synopsis

The paper is an attempt to bring out the exact relationship between what has been called the ‘modified osculatory process’ and the older formulae of osculatory interpolation. The conditions upon which the modified process is stated to be based are shown to be insufficient in themselves to produce a determinate formula even after the degree has been made as low as possible, and a general formula is derived which satisfies these conditions and of which the formulae hitherto employed are particular cases. The general formula contains, as might be expected, certain arbitrary constants which reflect the relaxation of certain of the conditions insisted on by the older formulae.

Illustrative graduations are performed by means of the general formulIllustrative graduations are performed by means of the general formula

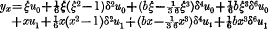
and the results are compared with previous graduations of the same data by Jenkins's fifth difference formula (which may be obtained by putting b=0 in the general formula), viz.:—

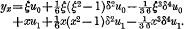
This is the particular case of the general formula which has hitherto been used in practice.

Type
Research Article
Information
Transactions of the Faculty of Actuaries , Volume 14 , Issue 1 , 1934 , pp. 185 - 220
Copyright
Copyright © Institute and Faculty of Actuaries 1934

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 185 note * T.F.A., xii. p. 117 et seq.

page 185 note † T.A.S.A., xxviii. p. 203 and xxxi. p. 24.

page 186 note * T.F.A., xi. pp. 22 and 23.

page 193 note * T.F.A., xii. pp. 142–4.

page 194 note * T.F.A. xii. p. 277 et seq.

page 196 note * T.A.S.A., xxviii. p. 208.

page 214 note * There is an obvious error in the printing of this formula in the paper which will no doubt be rectified in the final copy. [This has been done. —ED.]