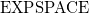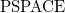1 Introduction
![]() ${\textrm{DatalogMTL}}$
(Brandt et al. Reference Brandt, Kalayc, Ryzhikov, Xiao and Zakharyaschev2018) extends positive Datalog (Abiteboul et al. Reference Abiteboul, Hull and Vianu1995) with operators from metric temporal logic (MTL) (Koymans Reference Koymans1990) interpreted over the rational or the integer timeline. For example, the following
${\textrm{DatalogMTL}}$
(Brandt et al. Reference Brandt, Kalayc, Ryzhikov, Xiao and Zakharyaschev2018) extends positive Datalog (Abiteboul et al. Reference Abiteboul, Hull and Vianu1995) with operators from metric temporal logic (MTL) (Koymans Reference Koymans1990) interpreted over the rational or the integer timeline. For example, the following
![]() ${\textrm{DatalogMTL}}$
rule can be used to state that a bus driver should not work for more than six months (i.e., half a year) in a row:
${\textrm{DatalogMTL}}$
rule can be used to state that a bus driver should not work for more than six months (i.e., half a year) in a row:
where the expression
![]() $\boxminus_{[0,0.5]} \textit{Working}(x)$
holds at time t if
$\boxminus_{[0,0.5]} \textit{Working}(x)$
holds at time t if
![]() $\textit{Working}(x)$
holds continuously in the time interval
$\textit{Working}(x)$
holds continuously in the time interval
![]() $[t-0.5, t]$
. Some other examples of expressions allowed in
$[t-0.5, t]$
. Some other examples of expressions allowed in
![]() ${\textrm{DatalogMTL}}$
are
${\textrm{DatalogMTL}}$
are ![]() , which holds at time t if
, which holds at time t if
![]() $\varphi$
holds at some instant within the time interval
$\varphi$
holds at some instant within the time interval
![]() $[t-t_2, t-t_1]$
, and
$[t-t_2, t-t_1]$
, and
![]() $\boxplus_{[t_1,t_2]} \varphi$
, which uses the “future-oriented” version of the operator
$\boxplus_{[t_1,t_2]} \varphi$
, which uses the “future-oriented” version of the operator
![]() $\boxminus$
and holds at time t if
$\boxminus$
and holds at time t if
![]() $\varphi$
holds continuously in the time interval
$\varphi$
holds continuously in the time interval
![]() $[t+t_1, t+t_2]$
. A
$[t+t_1, t+t_2]$
. A
![]() ${\textrm{DatalogMTL}}$
dataset consists of facts involving intervals, such as
${\textrm{DatalogMTL}}$
dataset consists of facts involving intervals, such as
![]() $Working(\mathit{alex})@[2022,2023]$
, stating that Alex was working continuously in the time interval [2022, 2023].
$Working(\mathit{alex})@[2022,2023]$
, stating that Alex was working continuously in the time interval [2022, 2023].
![]() ${\textrm{DatalogMTL}}$
is thus a very expressive language which allows a user to capture complex definitions, regulations, or events involving temporal intervals.
${\textrm{DatalogMTL}}$
is thus a very expressive language which allows a user to capture complex definitions, regulations, or events involving temporal intervals.
![]() ${\textrm{DatalogMTL}}$
is powerful enough to capture prominent temporal extensions of Datalog such as
${\textrm{DatalogMTL}}$
is powerful enough to capture prominent temporal extensions of Datalog such as
![]() $\mbox{Datalog}_{1S}$
(Chomicki and Imieliński 1988; 1989) and Templog (Abadi and Manna Reference Abadi and Manna1989), and ithas found applications in areas such as ontology-based data access (Brandt et al. Reference Brandt, Kalayc, Ryzhikov, Xiao and Zakharyaschev2018), stream reasoning (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019), and similar ideas were explored in logic programming (Brzoska Reference Brzoska1998). Reasoning in
$\mbox{Datalog}_{1S}$
(Chomicki and Imieliński 1988; 1989) and Templog (Abadi and Manna Reference Abadi and Manna1989), and ithas found applications in areas such as ontology-based data access (Brandt et al. Reference Brandt, Kalayc, Ryzhikov, Xiao and Zakharyaschev2018), stream reasoning (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019), and similar ideas were explored in logic programming (Brzoska Reference Brzoska1998). Reasoning in
![]() ${\textrm{DatalogMTL}}$
is known to be <monospace>PSpace</monospace>-complete in data complexity over both the rational (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019) and the integer timeline (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2020a).
${\textrm{DatalogMTL}}$
is known to be <monospace>PSpace</monospace>-complete in data complexity over both the rational (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019) and the integer timeline (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2020a).
Motivated by a range of applications, there has recently been a growing interest in logics that combine non-monotonic negation with temporal constructs (Cabalar and Vega Reference Cabalar and Vega2007; Aguado et al. Reference Aguado, Cabalar, Diéguez, Pérez and Vidal2013; Cabalar et al. 2018; Reference Cabalar, Dieguez, Schaub and Schuhmann2020; Beck et al. Reference Beck, Dao-Tran and Eiter2018; Zaniolo Reference Zaniolo2012). Recently, we have proposed an extension of
![]() ${\textrm{DatalogMTL}}$
over the rationals with stratified negation-as-failure, where rules can have negated atoms in the body, but there can be no recursion involving predicates mentioned in such atoms. With such an extension of
${\textrm{DatalogMTL}}$
over the rationals with stratified negation-as-failure, where rules can have negated atoms in the body, but there can be no recursion involving predicates mentioned in such atoms. With such an extension of
![]() ${\textrm{DatalogMTL}}$
, we can express, for example, a bus company’s policy that any vehicle older than 12 years must be decommissioned permanently unless it has passed a special inspection in the last year:
${\textrm{DatalogMTL}}$
, we can express, for example, a bus company’s policy that any vehicle older than 12 years must be decommissioned permanently unless it has passed a special inspection in the last year:
We also showed that the additional expressive power provided by this type of negation does not increase the complexity of reasoning regardless of whether we consider the rational or the integer timeline (Tena Cucala et al. Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021). The restriction to stratifiable programs, however, significantly limits the applicability
![]() ${\textrm{DatalogMTL}}$
to certain types of use cases.
${\textrm{DatalogMTL}}$
to certain types of use cases.
In this paper we take a further step in this direction and consider
![]() ${\textrm{DatalogMTL}}$
equipped with non-stratifiable negation interpreted under the stable model semantics (Gelfond and Lifschitz Reference Gelfond and Lifschitz1988; Brooks et al. Reference Brooks, Erdem, Erdogan, Minett and Ringe2007; Nogueira et al. Reference Nogueira, Balduccini, Gelfond, Watson and Barry2001). This extension paves the way for the use of
${\textrm{DatalogMTL}}$
equipped with non-stratifiable negation interpreted under the stable model semantics (Gelfond and Lifschitz Reference Gelfond and Lifschitz1988; Brooks et al. Reference Brooks, Erdem, Erdogan, Minett and Ringe2007; Nogueira et al. Reference Nogueira, Balduccini, Gelfond, Watson and Barry2001). This extension paves the way for the use of
![]() ${\textrm{DatalogMTL}}$
in applications where derived information can be retracted in light of new evidence, minimality of models is required, or temporal inertia rules need to be formalised. For instance, consider a bus company with the policy that vehicles that have been serviced at a given time t are automatically booked for a routine service in a year’s time (i.e., at time
${\textrm{DatalogMTL}}$
in applications where derived information can be retracted in light of new evidence, minimality of models is required, or temporal inertia rules need to be formalised. For instance, consider a bus company with the policy that vehicles that have been serviced at a given time t are automatically booked for a routine service in a year’s time (i.e., at time
![]() $t+1$
, represented by metric operator
$t+1$
, represented by metric operator
![]() $\boxplus_{[1,1]}$
), but this appointment must be cancelled if the bus is serviced again before then – that is, within the interval
$\boxplus_{[1,1]}$
), but this appointment must be cancelled if the bus is serviced again before then – that is, within the interval
![]() $(t + 0, t+1)$
, represented by
$(t + 0, t+1)$
, represented by ![]() . This policy can be written using the rule
. This policy can be written using the rule
which is not stratifiable as it involves recursion via negation.
Our setting is closely related to the recent research on combining answer set programming (ASP) with temporal logics. For example, temporal equilibrium logic (TEL) (Cabalar and Vega Reference Cabalar and Vega2007; Aguado et al. Reference Aguado, Cabalar, Diéguez, Pérez and Vidal2013; Cabalar et al. Reference Cabalar, Kaminski, Schaub and Schuhmann2018) combines ASP with linear temporal logic, and LARS combines ASP with window-based temporal constructs for stream reasoning (Beck et al. Reference Beck, Dao-Tran and Eiter2018). The logic recently proposed by Cabalar et al. (Reference Cabalar, Dieguez, Schaub and Schuhmann2020) is perhaps the closest to our work, as it combines stable model semantics with propositional MTL interpreted over the natural numbers; this logic, however, is rather different from
![]() ${\textrm{DatalogMTL}}$
, where the use of logical connectives and MTL operators is restricted in the spirit of Datalog to disallow disjunction and “existential” MTL operators (such as diamond, since, or until operators) in rule heads. As we show in our paper, considering a language with such restrictions can lead to favourable computational behaviour.
${\textrm{DatalogMTL}}$
, where the use of logical connectives and MTL operators is restricted in the spirit of Datalog to disallow disjunction and “existential” MTL operators (such as diamond, since, or until operators) in rule heads. As we show in our paper, considering a language with such restrictions can lead to favourable computational behaviour.
Our contributions in this paper are summarised as follows. In Section 3 we present our extension (
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
) of
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
) of
![]() ${\textrm{DatalogMTL}}$
with negation under stable model semantics. Our language is defined similarly to other temporal ASP formalisms; it extends both
${\textrm{DatalogMTL}}$
with negation under stable model semantics. Our language is defined similarly to other temporal ASP formalisms; it extends both
![]() ${\textrm{DatalogMTL}}$
with stratified negation and Datalog with stable model negation. To capture the semantics of stable models, we use interpretations similar to those of the here-and-there intuitionistic logic (Heyting Reference Heyting1930; Pearce Reference Pearce1996). The main reasoning problem we consider is the existence of a stable model for a program and a dataset. We show in Section 4 that, in this setting, reasoning over the rational timeline is undecidable; furthermore, undecidability holds even for propositional forward-propagating programs (where rules cannot propagate information towards past time points) and to data containing only bounded intervals (i.e., where endpoints of all intervals are rational numbers). To regain decidability, in Section 5 we focus on the integer timeline. We show in Section 5.1 that discreteness of the timeline has a crucial influence on the computational behaviour, as reasoning becomes decidable and in
${\textrm{DatalogMTL}}$
with stratified negation and Datalog with stable model negation. To capture the semantics of stable models, we use interpretations similar to those of the here-and-there intuitionistic logic (Heyting Reference Heyting1930; Pearce Reference Pearce1996). The main reasoning problem we consider is the existence of a stable model for a program and a dataset. We show in Section 4 that, in this setting, reasoning over the rational timeline is undecidable; furthermore, undecidability holds even for propositional forward-propagating programs (where rules cannot propagate information towards past time points) and to data containing only bounded intervals (i.e., where endpoints of all intervals are rational numbers). To regain decidability, in Section 5 we focus on the integer timeline. We show in Section 5.1 that discreteness of the timeline has a crucial influence on the computational behaviour, as reasoning becomes decidable and in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
in data complexity; this is shown by exploiting Büchi automata and their complements to find candidate stable models and verify their minimality. Then, in Section 5.2 we show that, when restricted to forward-propagating (or, dually, to backwards-propagating) programs and bounded datasets, reasoning becomes
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
in data complexity; this is shown by exploiting Büchi automata and their complements to find candidate stable models and verify their minimality. Then, in Section 5.2 we show that, when restricted to forward-propagating (or, dually, to backwards-propagating) programs and bounded datasets, reasoning becomes
![]() ${{\rm PS}{\small\rm PACE}}$
-complete and hence no harder than for negation-free
${{\rm PS}{\small\rm PACE}}$
-complete and hence no harder than for negation-free
![]() ${\textrm{DatalogMTL}}$
(Wałęga et al. 2019; Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2020a). This is in stark contrast with the undecidability of the same fragment over the rational numbers.
${\textrm{DatalogMTL}}$
(Wałęga et al. 2019; Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2020a). This is in stark contrast with the undecidability of the same fragment over the rational numbers.
2 Preliminaries
In this section we recapitulate the basics of temporal intervals over the integers or the rationals, and introduce the syntax and semantics of metric temporal operators.
2.1 Timelines and temporal intervals
A timeline
![]() $\mathbb{T}$
is either the set
$\mathbb{T}$
is either the set
![]() $\mathbb{Q}$
of rationals or the set
$\mathbb{Q}$
of rationals or the set
![]() $\mathbb{Z}$
of integers. A
$\mathbb{Z}$
of integers. A
![]() $\mathbb{T}$
-time point is an element of
$\mathbb{T}$
-time point is an element of
![]() $\mathbb{T}$
. A
$\mathbb{T}$
. A
![]() $\mathbb{T}$
-interval
$\mathbb{T}$
-interval
![]() $\varrho$
is a subset of
$\varrho$
is a subset of
![]() $\mathbb{T}$
satisfying both of the following properties:
$\mathbb{T}$
satisfying both of the following properties:
-
 $t \in\varrho$
for all
$t \in\varrho$
for all
 $t_1,t_2 \in \varrho$
and
$t_1,t_2 \in \varrho$
and
 $t \in \mathbb{T}$
such that
$t \in \mathbb{T}$
such that
 $t_1<t<t_2$
; and
$t_1<t<t_2$
; and -
the greatest lower bound
 $\varrho^-$
and the least upper bound
$\varrho^-$
and the least upper bound
 $\varrho^+$
of
$\varrho^+$
of
 $\varrho$
are both in
$\varrho$
are both in
 $\mathbb{T}\, \cup \{-\infty ,\infty\}$
.
$\mathbb{T}\, \cup \{-\infty ,\infty\}$
.
The bounds
![]() $\varrho^-$
and
$\varrho^-$
and
![]() $\varrho^+$
are called the left and right endpoints of
$\varrho^+$
are called the left and right endpoints of
![]() $\varrho$
, respectively. A
$\varrho$
, respectively. A
![]() $\mathbb{T}$
-interval is punctual if it contains exactly one
$\mathbb{T}$
-interval is punctual if it contains exactly one
![]() $\mathbb{T}$
-time point, it is non-negative if it contains no negative
$\mathbb{T}$
-time point, it is non-negative if it contains no negative
![]() $\mathbb{T}$
-time points, it is bounded if both its endpoints are in
$\mathbb{T}$
-time points, it is bounded if both its endpoints are in
![]() $\mathbb{T}$
, and it is closed if it includes both of its endpoints. In these and similar notions, we often omit the reference to
$\mathbb{T}$
, and it is closed if it includes both of its endpoints. In these and similar notions, we often omit the reference to
![]() $\mathbb{T}$
if it is clear from the context. We consider binary representations of integers and fractional representations of rationals, with an integer numerator and a positive integer denominator, encoded in binary. We use standard representations of the form
$\mathbb{T}$
if it is clear from the context. We consider binary representations of integers and fractional representations of rationals, with an integer numerator and a positive integer denominator, encoded in binary. We use standard representations of the form
![]() $\langle \varrho^-,\varrho^+ \rangle$
for a non-empty interval
$\langle \varrho^-,\varrho^+ \rangle$
for a non-empty interval
![]() $\varrho$
(i.e.,
$\varrho$
(i.e.,
![]() $\varrho \cap \mathbb{T} \neq \emptyset$
), where the left bracket
$\varrho \cap \mathbb{T} \neq \emptyset$
), where the left bracket
![]() $\langle$
is either [ or (, the right bracket
$\langle$
is either [ or (, the right bracket
![]() $\rangle$
is either ] or), and, if numeric, the endpoints
$\rangle$
is either ] or), and, if numeric, the endpoints
![]() $\varrho^-$
and
$\varrho^-$
and
![]() $\varrho^{+}$
are represented as explained above. Brackets [ and ] indicate that the endpoints are included in the interval, whereas (and) indicate that they are not included; note that, by this convention, [ and ] cannot be used with endpoints
$\varrho^{+}$
are represented as explained above. Brackets [ and ] indicate that the endpoints are included in the interval, whereas (and) indicate that they are not included; note that, by this convention, [ and ] cannot be used with endpoints
![]() $-\infty$
and
$-\infty$
and
![]() $\infty$
. We often abbreviate a punctual interval [t,t] as t. If it is clear from the context, we abuse notation and identify each interval representation with the interval it represents.
$\infty$
. We often abbreviate a punctual interval [t,t] as t. If it is clear from the context, we abuse notation and identify each interval representation with the interval it represents.
2.2 Syntax and semantics of metric temporal expressions
Assume a function-free first-order vocabulary and a timeline
![]() $\mathbb{T}$
. A relational atom is an expression of the form
$\mathbb{T}$
. A relational atom is an expression of the form
![]() $P(\mathbf{s})$
, where P is a predicate and
$P(\mathbf{s})$
, where P is a predicate and
![]() $\mathbf{s}$
is a tuple of constants and variables of the same arity as P. A metric atom is an expression given by the following grammar, where
$\mathbf{s}$
is a tuple of constants and variables of the same arity as P. A metric atom is an expression given by the following grammar, where
![]() $P(\mathbf{s})$
ranges over relational atoms and
$P(\mathbf{s})$
ranges over relational atoms and
![]() $\varrho$
over non-empty, non-negative intervals:
$\varrho$
over non-empty, non-negative intervals:
A metric atom is ground if it mentions no variables. A metric fact is an expression
![]() $M @ \varrho$
, with M a ground metric atom and
$M @ \varrho$
, with M a ground metric atom and
![]() $\varrho$
a non-empty
$\varrho$
a non-empty
![]() $\mathbb{T}$
-interval; it is relational if so is M. A dataset is a finite set of relational facts; it is bounded if so are all intervals it mentions. For a dataset
$\mathbb{T}$
-interval; it is relational if so is M. A dataset is a finite set of relational facts; it is bounded if so are all intervals it mentions. For a dataset
![]() $\mathcal{D}$
, we denote with
$\mathcal{D}$
, we denote with
![]() $t^{\min}_{\mathcal{D}}$
and
$t^{\min}_{\mathcal{D}}$
and
![]() $t^{\max}_{\mathcal{D}}$
the smallest and the largest numbers mentioned in
$t^{\max}_{\mathcal{D}}$
the smallest and the largest numbers mentioned in
![]() $\mathcal{D}$
; if
$\mathcal{D}$
; if
![]() $\mathcal{D}$
mentions no numbers, we let
$\mathcal{D}$
mentions no numbers, we let
![]() $t^{\min}_{\mathcal{D}}=t^{\max}_{\mathcal{D}}=0$
.
$t^{\min}_{\mathcal{D}}=t^{\max}_{\mathcal{D}}=0$
.
An interpretation
![]() $\mathfrak{I}$
is a function which assigns to each time point
$\mathfrak{I}$
is a function which assigns to each time point
![]() $t \in \mathbb{T}$
a set of ground relational atoms; if an atom
$t \in \mathbb{T}$
a set of ground relational atoms; if an atom
![]() $P(\mathbf{c})$
belongs to this set, we say that
$P(\mathbf{c})$
belongs to this set, we say that
![]() $P(\mathbf{c})$
is satisfied at t in
$P(\mathbf{c})$
is satisfied at t in
![]() $\mathfrak{I}$
and we write
$\mathfrak{I}$
and we write
![]() $\mathfrak{I},t \models_\mathbb{T} P(\mathbf{c})$
. This notion extends to other ground metric atoms as given in Table 1. Interpretation
$\mathfrak{I},t \models_\mathbb{T} P(\mathbf{c})$
. This notion extends to other ground metric atoms as given in Table 1. Interpretation
![]() $\mathfrak{I}$
is a model of a metric fact
$\mathfrak{I}$
is a model of a metric fact
![]() $M @ \varrho$
, written
$M @ \varrho$
, written
![]() $\mathfrak{I} \models_\mathbb{T} M @ \varrho$
, if
$\mathfrak{I} \models_\mathbb{T} M @ \varrho$
, if
![]() $\mathfrak{I},t \models M$
for all
$\mathfrak{I},t \models M$
for all
![]() $t \in \varrho$
; it is a model of a set
$t \in \varrho$
; it is a model of a set
![]() $\mathcal{M}$
of metric facts (e.g., a dataset) if it is a model of all facts in
$\mathcal{M}$
of metric facts (e.g., a dataset) if it is a model of all facts in
![]() $\mathcal{M}$
. Set
$\mathcal{M}$
. Set
![]() $\mathcal{M}$
entails a set
$\mathcal{M}$
entails a set
![]() $\mathcal{M}'$
of metric facts, written
$\mathcal{M}'$
of metric facts, written
![]() $\mathcal{M} \models \mathcal{M}'$
, if every model of
$\mathcal{M} \models \mathcal{M}'$
, if every model of
![]() $\mathcal{M}$
is a model of
$\mathcal{M}$
is a model of
![]() $\mathcal{M}'$
. An interpretation
$\mathcal{M}'$
. An interpretation
![]() $\mathfrak{I}$
contains an interpretation
$\mathfrak{I}$
contains an interpretation
![]() $\mathfrak{I}'$
, written
$\mathfrak{I}'$
, written
![]() $\mathfrak{I}' \subseteq \mathfrak{I}$
, if for each ground relational atom
$\mathfrak{I}' \subseteq \mathfrak{I}$
, if for each ground relational atom
![]() $P(\mathbf{c})$
and each time point
$P(\mathbf{c})$
and each time point
![]() $t \in \mathbb{T}$
, having
$t \in \mathbb{T}$
, having
![]() $\mathfrak{I}',t \models_\mathbb{T} P(\mathbf{c})$
implies
$\mathfrak{I}',t \models_\mathbb{T} P(\mathbf{c})$
implies
![]() $\mathfrak{I},t \models_\mathbb{T} P(\mathbf{c})$
. Furthermore,
$\mathfrak{I},t \models_\mathbb{T} P(\mathbf{c})$
. Furthermore,
![]() $\mathfrak{I}$
is the least interpretation in a set X of interpretations, if
$\mathfrak{I}$
is the least interpretation in a set X of interpretations, if
![]() $\mathfrak{I} \subseteq \mathfrak{I}'$
for every
$\mathfrak{I} \subseteq \mathfrak{I}'$
for every
![]() $\mathfrak{I}' \in X$
.
$\mathfrak{I}' \in X$
.
Table 1. Semantics of ground metric atoms

3 DatalogMTL with negation under stable model semantics
In this section we propose
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
, which extends
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
, which extends
![]() ${\textrm{DatalogMTL}}$
with stratified negation as defined by Tena Cucala et al. (Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021), to support unstratified use of negation in rules interpreted under stable model semantics.
${\textrm{DatalogMTL}}$
with stratified negation as defined by Tena Cucala et al. (Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021), to support unstratified use of negation in rules interpreted under stable model semantics.
The syntax of
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
is the natural extension of the positive case: rule bodies are conjunctions of atoms and negated atoms, whereas rule heads are defined as in
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
is the natural extension of the positive case: rule bodies are conjunctions of atoms and negated atoms, whereas rule heads are defined as in
![]() ${\textrm{DatalogMTL}}$
. Forward-propagating
${\textrm{DatalogMTL}}$
. Forward-propagating
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
programs are also defined analogously to the positive case (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019), by requiring that rule bodies and heads do not mention metric operators referring to the future and to the past, respectively.
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
programs are also defined analogously to the positive case (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019), by requiring that rule bodies and heads do not mention metric operators referring to the future and to the past, respectively.
Definition 3.1 A rule r is an expression of the form
where each
![]() $M_i$
is a metric atom, and M is a metric atom specified by the following grammar, where
$M_i$
is a metric atom, and M is a metric atom specified by the following grammar, where
![]() $P(\mathbf{s})$
ranges over relational atoms and
$P(\mathbf{s})$
ranges over relational atoms and
![]() $\varrho$
over non-empty non-negative intervals:
$\varrho$
over non-empty non-negative intervals:
The head of r is the consequent M and the body is the conjunction in the antecedent, where
![]() ${M_1, \ldots, M_k}$
are its positive body atoms, and
${M_1, \ldots, M_k}$
are its positive body atoms, and
![]() ${M_{k+1}, \ldots, M_{m}}$
are its negated body atoms. A rule is safe if each variable it mentions in the head occurs in some positive body atom in a position other than a left operand of
${M_{k+1}, \ldots, M_{m}}$
are its negated body atoms. A rule is safe if each variable it mentions in the head occurs in some positive body atom in a position other than a left operand of
![]() $\mathcal{S}$
or
$\mathcal{S}$
or
![]() $\mathcal{U}$
. A rule is ground if it has no variables, and it is positive if it has no negated body atoms. A (
$\mathcal{U}$
. A rule is ground if it has no variables, and it is positive if it has no negated body atoms. A (
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
) program is a finite set of safe rules; it is ground or positive if all its rules are. For a program
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
) program is a finite set of safe rules; it is ground or positive if all its rules are. For a program
![]() $\Pi$
, we let
$\Pi$
, we let
![]() $\mathsf{ground}({\Pi})$
be the set of all ground rules that can be obtained by replacing variables in
$\mathsf{ground}({\Pi})$
be the set of all ground rules that can be obtained by replacing variables in
![]() $\Pi$
with constants. A program is forward-propagating (
$\Pi$
with constants. A program is forward-propagating (
![]() ${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
) if it is
${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
) if it is
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
but does not mention the operators
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
but does not mention the operators ![]() ,
,
![]() $\boxplus$
, and
$\boxplus$
, and
![]() $\mathcal{U}$
in rule bodies, or the operator
$\mathcal{U}$
in rule bodies, or the operator
![]() $\boxminus$
in rule heads.
$\boxminus$
in rule heads.
The definitionf stable models for Datalog with negation relies on the reduct construction by Gelfond and Lifschitz (Reference Gelfond and Lifschitz1988), which has been adapted to various extensions of ASP (Faber et al. Reference Faber, Leone and Pfeifer2004). Such reduct constructions, however, do not have a natural equivalent in
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
, where interpretations may satisfy a fact at some, but not all points of the infinite timeline, and it is thus unclear which rules or atoms should be included in the reduct.
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
, where interpretations may satisfy a fact at some, but not all points of the infinite timeline, and it is thus unclear which rules or atoms should be included in the reduct.
Following the approach of Cabalar and Vega (Reference Cabalar and Vega2007) and Cabalar et al. (Reference Cabalar, Dieguez, Schaub and Schuhmann2020), we define stable models for
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
analogously to the models of equilibrium logic (Pearce Reference Pearce1996), which in turn are defined in terms of interpretations for the here-and-there intuitionistic logic (Heyting Reference Heyting1930). In this logic, each interpretation is an ordered pair (H,T) of sets H (“here”) and T (“there”) of relational propositional (i.e. using only predicates of arity 0) atoms such that
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
analogously to the models of equilibrium logic (Pearce Reference Pearce1996), which in turn are defined in terms of interpretations for the here-and-there intuitionistic logic (Heyting Reference Heyting1930). In this logic, each interpretation is an ordered pair (H,T) of sets H (“here”) and T (“there”) of relational propositional (i.e. using only predicates of arity 0) atoms such that
![]() $H \subseteq T$
. We therefore start by generalising such interpretations to the context of
$H \subseteq T$
. We therefore start by generalising such interpretations to the context of
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
. For the remainder of this section, we fix a timeline
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
. For the remainder of this section, we fix a timeline
![]() $\mathbb{T}$
, which will be implicit in all our definitions and technical results.
$\mathbb{T}$
, which will be implicit in all our definitions and technical results.
Definition 3.2 An HT-interpretation is a pair
![]() $( \mathfrak{H}, \mathfrak{T} )$
of interpretations such that
$( \mathfrak{H}, \mathfrak{T} )$
of interpretations such that
![]() $\mathfrak{H} \subseteq \mathfrak{T}$
. An HT-interpretation
$\mathfrak{H} \subseteq \mathfrak{T}$
. An HT-interpretation
![]() $( \mathfrak{H}, \mathfrak{T} )$
is an HT-model of a dataset
$( \mathfrak{H}, \mathfrak{T} )$
is an HT-model of a dataset
![]() $\mathcal{D}$
if
$\mathcal{D}$
if
![]() $\mathfrak{H}$
is a model of
$\mathfrak{H}$
is a model of
![]() $\mathcal{D}$
; furthermore, it is an HT-model of a rule r if, for each rule of Form (1) in
$\mathcal{D}$
; furthermore, it is an HT-model of a rule r if, for each rule of Form (1) in
![]() $\mathsf{ground}(\Pi)$
and for each
$\mathsf{ground}(\Pi)$
and for each
![]() $t\in\mathbb{T}$
, the following hold:
$t\in\mathbb{T}$
, the following hold:
-
1. If
 $\mathfrak{H} ,t \models_\mathbb{T} M_i$
for all
$\mathfrak{H} ,t \models_\mathbb{T} M_i$
for all
 $i \in \{1, \ldots, k\}$
and
$i \in \{1, \ldots, k\}$
and
 ${\mathfrak{T} ,t \not\models_\mathbb{T} M_j}$
for all
${\mathfrak{T} ,t \not\models_\mathbb{T} M_j}$
for all
 $j \in \{k+1, \ldots, m\}$
, then
$j \in \{k+1, \ldots, m\}$
, then
 ${\mathfrak{H} ,t \models_\mathbb{T} M}$
.
${\mathfrak{H} ,t \models_\mathbb{T} M}$
. -
2. If
 $\mathfrak{T} ,t \models_\mathbb{T} M_i$
for all
$\mathfrak{T} ,t \models_\mathbb{T} M_i$
for all
 $i \in \{1,\ldots, k\}$
and
$i \in \{1,\ldots, k\}$
and
 ${\mathfrak{T} ,t \not\models_\mathbb{T} M_j}$
for all
${\mathfrak{T} ,t \not\models_\mathbb{T} M_j}$
for all
 $j \in \{k+1, \ldots, m\}$
, then
$j \in \{k+1, \ldots, m\}$
, then
 ${\mathfrak{T} ,t \models_\mathbb{T} M}$
.
${\mathfrak{T} ,t \models_\mathbb{T} M}$
.
Finally,
![]() $( \mathfrak{H}, \mathfrak{T} )$
is an HT-model of a program if it is an HT-model of all its rules.
$( \mathfrak{H}, \mathfrak{T} )$
is an HT-model of a program if it is an HT-model of all its rules.
An HT-interpretation is, therefore, a pair
![]() $( \mathfrak{H}, \mathfrak{T} )$
of standard interpretations. Interpretation
$( \mathfrak{H}, \mathfrak{T} )$
of standard interpretations. Interpretation
![]() $\mathfrak{H}$
is contained in
$\mathfrak{H}$
is contained in
![]() $\mathfrak{T}$
and determines whether a dataset is satisfied. Although both interpretations are used to evaluate rules, it is
$\mathfrak{T}$
and determines whether a dataset is satisfied. Although both interpretations are used to evaluate rules, it is
![]() $\mathfrak{T}$
which evaluates negated body atoms and thus determines when a rule with negation can be “triggered”. When this happens, the rule ensures that if any of
$\mathfrak{T}$
which evaluates negated body atoms and thus determines when a rule with negation can be “triggered”. When this happens, the rule ensures that if any of
![]() $\mathfrak{H}$
or
$\mathfrak{H}$
or
![]() $\mathfrak{T}$
satisfies the positive body atoms, then it will also satisfy the head. Since
$\mathfrak{T}$
satisfies the positive body atoms, then it will also satisfy the head. Since
![]() $\mathfrak{H} \subseteq \mathfrak{T}$
in an HT-interpretation, all relational facts entailed by
$\mathfrak{H} \subseteq \mathfrak{T}$
in an HT-interpretation, all relational facts entailed by
![]() $\mathfrak{H}$
are also entailed by
$\mathfrak{H}$
are also entailed by
![]() $\mathfrak{T}$
. We show next that this property can be generalised to arbitrary metric facts.
$\mathfrak{T}$
. We show next that this property can be generalised to arbitrary metric facts.
Proposition 3.3 For every HT-interpretation
![]() $( \mathfrak{H}, \mathfrak{T} )$
, metric atom M, and time point t, if
$( \mathfrak{H}, \mathfrak{T} )$
, metric atom M, and time point t, if
![]() $\mathfrak{H} ,t \models M$
then
$\mathfrak{H} ,t \models M$
then
![]() $\mathfrak{T} ,t \models M$
.
$\mathfrak{T} ,t \models M$
.
Proof. We proceed by induction on the structure of M. If M is
![]() $\top$
or
$\top$
or
![]() $\bot$
, the claim holds trivially, and if M is a relational atom, then the claim holds by
$\bot$
, the claim holds trivially, and if M is a relational atom, then the claim holds by
![]() $\mathfrak{H} \subseteq \mathfrak{T}$
. For the inductive step it suffices to consider the cases when M is of the form
$\mathfrak{H} \subseteq \mathfrak{T}$
. For the inductive step it suffices to consider the cases when M is of the form
![]() $\boxminus_{\varrho} M_1$
or
$\boxminus_{\varrho} M_1$
or
![]() $M_1\mathcal{S}_{\varrho} M_2$
, for some interval
$M_1\mathcal{S}_{\varrho} M_2$
, for some interval
![]() $\varrho$
and metric atoms
$\varrho$
and metric atoms
![]() $M_1$
and
$M_1$
and
![]() $M_2$
. Indeed, if M is of the form
$M_2$
. Indeed, if M is of the form ![]() or
or ![]() , then it is equivalent to
, then it is equivalent to
![]() $\top\mathcal{S}_{\varrho} M_1$
or
$\top\mathcal{S}_{\varrho} M_1$
or
![]() $\top \mathcal{U}_{\varrho}M_1$
, respectively, while the cases when M is of the form
$\top \mathcal{U}_{\varrho}M_1$
, respectively, while the cases when M is of the form
![]() $\boxplus_{\varrho} M_1$
or
$\boxplus_{\varrho} M_1$
or
![]() $M_1 \mathcal{U}_{\varrho} M_2$
are symmetric to the cases of
$M_1 \mathcal{U}_{\varrho} M_2$
are symmetric to the cases of
![]() $\boxminus_{\varrho} M_1$
or
$\boxminus_{\varrho} M_1$
or
![]() $M_1\mathcal{S}_{\varrho} M_2$
, respectively.
$M_1\mathcal{S}_{\varrho} M_2$
, respectively.
If M is
![]() $\boxminus_{\varrho } M_1$
, then
$\boxminus_{\varrho } M_1$
, then
![]() $\mathfrak{H}, t \models M$
implies that
$\mathfrak{H}, t \models M$
implies that
![]() $\mathfrak{H}, t' \models M_1$
, for all t’ such that
$\mathfrak{H}, t' \models M_1$
, for all t’ such that
![]() $t-t'\in\varrho$
. Hence, by the inductive hypothesis,
$t-t'\in\varrho$
. Hence, by the inductive hypothesis,
![]() $\mathfrak{T}, t' \models M_1$
for all t’ such that
$\mathfrak{T}, t' \models M_1$
for all t’ such that
![]() $t-t'\in\varrho$
, and so,
$t-t'\in\varrho$
, and so,
![]() $\mathfrak{T}, t \models \boxminus_{\varrho } M_1$
. Similarly, if M is
$\mathfrak{T}, t \models \boxminus_{\varrho } M_1$
. Similarly, if M is
![]() $M_1\mathcal{S}_{\varrho} M_2$
, then there is t’ with
$M_1\mathcal{S}_{\varrho} M_2$
, then there is t’ with
![]() $t-t'\in\varrho$
such that
$t-t'\in\varrho$
such that
![]() $\mathfrak{H}, t' \models M_2$
and
$\mathfrak{H}, t' \models M_2$
and
![]() $\mathfrak{H}, t'' \models M_1$
, for all
$\mathfrak{H}, t'' \models M_1$
, for all
![]() $t'' \in (t',t)$
. By the inductive hypothesis we obtain that
$t'' \in (t',t)$
. By the inductive hypothesis we obtain that
![]() $\mathfrak{T}, t' \models M_2$
and
$\mathfrak{T}, t' \models M_2$
and
![]() $\mathfrak{T}, t'' \models M_1$
, for all
$\mathfrak{T}, t'' \models M_1$
, for all
![]() $t'' \in (t',t)$
, so
$t'' \in (t',t)$
, so
![]() $\mathfrak{T}, t \models M_1\mathcal{S}_{\varrho} M_2$
.
$\mathfrak{T}, t \models M_1\mathcal{S}_{\varrho} M_2$
.
Although theonverse statement does not always hold, we can nonetheless prove the following result, which will underpin our definition of stable models.
Theorem 3.4 Let
![]() $(\mathfrak{T},\mathfrak{T})$
be an HT-model of a program
$(\mathfrak{T},\mathfrak{T})$
be an HT-model of a program
![]() $\Pi$
and a dataset
$\Pi$
and a dataset
![]() $\mathcal{D}$
. Then the set of interpretations
$\mathcal{D}$
. Then the set of interpretations
![]() $\{ \mathfrak{H} \mid (\mathfrak{H},\mathfrak{T}) \text{ is an HT-model of } \Pi \text{ and } \mathcal{D} \}$
contains a unique least interpretation.
$\{ \mathfrak{H} \mid (\mathfrak{H},\mathfrak{T}) \text{ is an HT-model of } \Pi \text{ and } \mathcal{D} \}$
contains a unique least interpretation.
Proof. We use transfinite induction to construct a sequence of interpretations
![]() $\mathfrak{H}_0$
,
$\mathfrak{H}_0$
,
![]() $\mathfrak{H}_1$
,
$\mathfrak{H}_1$
,
![]() $\dots$
, where each interpretation is contained in
$\dots$
, where each interpretation is contained in
![]() $\mathfrak{T}$
. We will then show that
$\mathfrak{T}$
. We will then show that
![]() $\mathfrak{H}_{\omega_1}$
, where
$\mathfrak{H}_{\omega_1}$
, where
![]() $\omega_1$
is the first uncountable ordinal, is the least amongst all interpretations
$\omega_1$
is the first uncountable ordinal, is the least amongst all interpretations
![]() $\mathfrak{H}$
such that
$\mathfrak{H}$
such that
![]() $(\mathfrak{H},\mathfrak{T})$
is an HT-model of
$(\mathfrak{H},\mathfrak{T})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
.
$\mathcal{D}$
.
Let
![]() $\mathfrak{H}_0$
be the least model of
$\mathfrak{H}_0$
be the least model of
![]() $\mathcal{D}$
. Then, for each successor ordinal
$\mathcal{D}$
. Then, for each successor ordinal
![]() $\alpha$
, let
$\alpha$
, let
![]() $\mathfrak{H}_{\alpha}$
be the least interpretation satisfying the following property: for each rule of Form (1) in
$\mathfrak{H}_{\alpha}$
be the least interpretation satisfying the following property: for each rule of Form (1) in
![]() $\mathsf{ground}(\Pi)$
, and for each time point t, if
$\mathsf{ground}(\Pi)$
, and for each time point t, if
![]() ${\mathfrak{H}_{\alpha-1},t \models M_i}$
for each
${\mathfrak{H}_{\alpha-1},t \models M_i}$
for each
![]() $1 \leq i \leq k$
and
$1 \leq i \leq k$
and
![]() ${\mathfrak{T},t \not\models M_j}$
for each
${\mathfrak{T},t \not\models M_j}$
for each
![]() $k+1 \leq j \leq m$
, then
$k+1 \leq j \leq m$
, then
![]() ${\mathfrak{H}_{\alpha},t \models M}$
. Moreover, for each limit ordinal
${\mathfrak{H}_{\alpha},t \models M}$
. Moreover, for each limit ordinal
![]() $\alpha$
, we define
$\alpha$
, we define
![]() $\mathfrak{H}_{\alpha}$
as
$\mathfrak{H}_{\alpha}$
as
![]() $\bigcup_{\beta < \alpha}\mathfrak{H}_\beta$
. By induction on ordinals
$\bigcup_{\beta < \alpha}\mathfrak{H}_\beta$
. By induction on ordinals
![]() $\alpha$
we can show simultaneously that
$\alpha$
we can show simultaneously that
![]() $\mathfrak{H}_{\alpha}$
is well-defined and that
$\mathfrak{H}_{\alpha}$
is well-defined and that
![]() $\mathfrak{H}_\alpha \subseteq \mathfrak{T}$
. For the basis of the induction, we recall that
$\mathfrak{H}_\alpha \subseteq \mathfrak{T}$
. For the basis of the induction, we recall that
![]() $\mathfrak{H}_0$
is the least model of
$\mathfrak{H}_0$
is the least model of
![]() $\mathcal{D}$
, so
$\mathcal{D}$
, so
![]() $\mathfrak{H}_0 $
is well-defined. Moreover, since
$\mathfrak{H}_0 $
is well-defined. Moreover, since
![]() $(\mathfrak{T},\mathfrak{T})$
is an HT-model of
$(\mathfrak{T},\mathfrak{T})$
is an HT-model of
![]() $\mathcal{D}$
, we obtain that
$\mathcal{D}$
, we obtain that
![]() $\mathfrak{H}_0 \subseteq \mathfrak{T}$
. Now, consider the inductive step for a successor ordinal
$\mathfrak{H}_0 \subseteq \mathfrak{T}$
. Now, consider the inductive step for a successor ordinal
![]() $\alpha$
. To show that
$\alpha$
. To show that
![]() $\mathfrak{H}_{\alpha}$
is well-defined it suffices to show that for each rule of Form (1) in
$\mathfrak{H}_{\alpha}$
is well-defined it suffices to show that for each rule of Form (1) in
![]() $\mathsf{ground}(\Pi)$
, and for each time point t, if
$\mathsf{ground}(\Pi)$
, and for each time point t, if
![]() ${\mathfrak{H}_{\alpha-1},t \models M_i}$
for each
${\mathfrak{H}_{\alpha-1},t \models M_i}$
for each
![]() $1 \leq i \leq k$
and
$1 \leq i \leq k$
and
![]() ${\mathfrak{T},t \not\models M_j}$
for each
${\mathfrak{T},t \not\models M_j}$
for each
![]() $k+1 \leq j \leq m$
, then M is not
$k+1 \leq j \leq m$
, then M is not
![]() $\bot$
. Indeed, by the inductive assumption we have
$\bot$
. Indeed, by the inductive assumption we have
![]() $\mathfrak{H}_{\alpha-1} \subseteq \mathfrak{T}$
, so if M is
$\mathfrak{H}_{\alpha-1} \subseteq \mathfrak{T}$
, so if M is
![]() $\bot$
, then
$\bot$
, then
![]() $\mathfrak{T},t \models \bot$
, which contradicts the assumption that
$\mathfrak{T},t \models \bot$
, which contradicts the assumption that
![]() $(\mathfrak{T},\mathfrak{T})$
is an HT-model of
$(\mathfrak{T},\mathfrak{T})$
is an HT-model of
![]() $\Pi$
. Moreover, since
$\Pi$
. Moreover, since
![]() $\mathfrak{H}_{\alpha-1} \subseteq \mathfrak{T}$
and
$\mathfrak{H}_{\alpha-1} \subseteq \mathfrak{T}$
and
![]() $(\mathfrak{T},\mathfrak{T})$
is an HT-model of
$(\mathfrak{T},\mathfrak{T})$
is an HT-model of
![]() $\Pi$
, we need to have
$\Pi$
, we need to have
![]() $\mathfrak{T},t \models M$
, so
$\mathfrak{T},t \models M$
, so
![]() $\mathfrak{H}_\alpha \subseteq \mathfrak{T}$
. The inductive step for a limit ordinal
$\mathfrak{H}_\alpha \subseteq \mathfrak{T}$
. The inductive step for a limit ordinal
![]() $\alpha$
holds trivially, since
$\alpha$
holds trivially, since
![]() $\mathfrak{H}_{\alpha}$
is defined as
$\mathfrak{H}_{\alpha}$
is defined as
![]() $\bigcup_{\beta < \alpha}\mathfrak{H}_\beta$
.
$\bigcup_{\beta < \alpha}\mathfrak{H}_\beta$
.
We thus obtainhat
![]() $\mathfrak{H}_{\omega_1} \subseteq \mathfrak{T}$
, and so,
$\mathfrak{H}_{\omega_1} \subseteq \mathfrak{T}$
, and so,
![]() $(\mathfrak{H}_{\omega_1},\mathfrak{T})$
is an HT-interpretation. By construction,
$(\mathfrak{H}_{\omega_1},\mathfrak{T})$
is an HT-interpretation. By construction,
![]() $\mathfrak{H}_{\omega_1}$
contains
$\mathfrak{H}_{\omega_1}$
contains
![]() $\mathfrak{H}_0$
and therefore
$\mathfrak{H}_0$
and therefore
![]() $(\mathfrak{H}_{\omega_1},\mathfrak{T})$
is an HT-model of
$(\mathfrak{H}_{\omega_1},\mathfrak{T})$
is an HT-model of
![]() $\mathcal{D}$
. It is also an HT-model of
$\mathcal{D}$
. It is also an HT-model of
![]() $\Pi$
, since
$\Pi$
, since
![]() $\omega_1$
rounds of rule applications are enough to ensure that
$\omega_1$
rounds of rule applications are enough to ensure that
![]() $\mathfrak{H}_{\omega_1}$
is a fixpoint with respect to the application of the rules of
$\mathfrak{H}_{\omega_1}$
is a fixpoint with respect to the application of the rules of
![]() $\Pi$
(Brandt et al. Reference Brandt, Kontchakov, Ryzhikov, Xiao and Zakharyaschev2017). Finally, to show that
$\Pi$
(Brandt et al. Reference Brandt, Kontchakov, Ryzhikov, Xiao and Zakharyaschev2017). Finally, to show that
![]() $\mathfrak{H}_{\omega_1}$
is the least among interpretations
$\mathfrak{H}_{\omega_1}$
is the least among interpretations
![]() $\mathfrak{H}$
such that
$\mathfrak{H}$
such that
![]() $(\mathfrak{H},\mathfrak{T})$
is an HT-model of
$(\mathfrak{H},\mathfrak{T})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, consider any such
$\mathcal{D}$
, consider any such
![]() $\mathfrak{H}$
. Using transfinite induction in a way similar to the previous paragraph, one can show that
$\mathfrak{H}$
. Using transfinite induction in a way similar to the previous paragraph, one can show that
![]() $\mathfrak{H}_{\alpha} \subseteq \mathfrak{H}$
for each ordinal
$\mathfrak{H}_{\alpha} \subseteq \mathfrak{H}$
for each ordinal
![]() $\alpha$
, and thus
$\alpha$
, and thus
![]() $\mathfrak{H}_{\omega_1} \subseteq \mathfrak{H}$
.
$\mathfrak{H}_{\omega_1} \subseteq \mathfrak{H}$
.
Given a program
![]() $\Pi$
, a dataset
$\Pi$
, a dataset
![]() $\mathcal{D}$
, and an interpretation
$\mathcal{D}$
, and an interpretation
![]() $\mathfrak{T}$
such that
$\mathfrak{T}$
such that
![]() $(\mathfrak{T},\mathfrak{T})$
is an HT-model of
$(\mathfrak{T},\mathfrak{T})$
is an HT-model of
![]() $\Pi$
, we let
$\Pi$
, we let
![]() $\mathfrak{H}^\mathfrak{T}_{\Pi,\mathcal{D}}$
denote the least interpretation whose existence is guaranteed by Theorem 3.4.
$\mathfrak{H}^\mathfrak{T}_{\Pi,\mathcal{D}}$
denote the least interpretation whose existence is guaranteed by Theorem 3.4.
In equilibrium logic, a model of a program is a set T of relational propositional atoms that satisfies the rules of the program and for which there exists no set
![]() $H \subsetneq T$
such that (H,T) is a model of the program in here-and-there logic. This ensures that equilibrium logic implements a kind of minimal model reasoning. We next generalise this notion to
$H \subsetneq T$
such that (H,T) is a model of the program in here-and-there logic. This ensures that equilibrium logic implements a kind of minimal model reasoning. We next generalise this notion to
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
by building on our previous definition of the least interpretation
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
by building on our previous definition of the least interpretation
![]() $\mathfrak{H}^\mathfrak{T}_{\Pi,\mathcal{D}}$
.
$\mathfrak{H}^\mathfrak{T}_{\Pi,\mathcal{D}}$
.
Definition 3.5 An interpretation
![]() $\mathfrak{T}$
is a stable model of a program
$\mathfrak{T}$
is a stable model of a program
![]() $\Pi$
and a dataset
$\Pi$
and a dataset
![]() $\mathcal{D}$
if and only if
$\mathcal{D}$
if and only if
![]() $(\mathfrak{T},\mathfrak{T})$
is an HT-model of
$(\mathfrak{T},\mathfrak{T})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, and
$\mathcal{D}$
, and
![]() ${\mathfrak{H}^\mathfrak{T}_{\Pi,\mathcal{D}} = \mathfrak{T}}$
.
${\mathfrak{H}^\mathfrak{T}_{\Pi,\mathcal{D}} = \mathfrak{T}}$
.
Example 3.6 Consider a dataset with a single fact
![]() $P@[0,1]$
and a propositional
$P@[0,1]$
and a propositional
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program consisting of a single rule
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program consisting of a single rule ![]() . In this setting, there is just a single stable model, namely the interpretation where P holds at all time points from [0,1], R holds at all time points from [1,2], and no relational atoms are satisfied anywhere else.
. In this setting, there is just a single stable model, namely the interpretation where P holds at all time points from [0,1], R holds at all time points from [1,2], and no relational atoms are satisfied anywhere else.
Next, consider a dataset with facts
![]() $P@0$
and
$P@0$
and
![]() $Q@1$
, together with a propositional
$Q@1$
, together with a propositional
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program that consists of two rules
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program that consists of two rules ![]() and
and ![]() . This dataset and program have two stable models. In the first model, P and R hold at 0, whereas Q holds at 1. In the second model, P holds at 0, whereas Q and R hold at 1.
. This dataset and program have two stable models. In the first model, P and R hold at 0, whereas Q holds at 1. In the second model, P holds at 0, whereas Q and R hold at 1.
Finally, let us consider the empty dataset and a program consisting of rules
![]() $Q \gets \mathsf{not}\!\mathop{}\nolimits P$
and
$Q \gets \mathsf{not}\!\mathop{}\nolimits P$
and
![]() ${P \gets \mathsf{not}\!\mathop{}\nolimits Q}$
. Syntactically, this is not only apropositional
${P \gets \mathsf{not}\!\mathop{}\nolimits Q}$
. Syntactically, this is not only apropositional
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program, but also a standard ASP. According to our temporal semantics, this program and dataset admit infinitely many stable models: for each set X of time points, there is a stable model in which P holds at each time point in X and Q holds at all other time points. In contrast, the same program under the standard ASP semantics has only two stable models, namely
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program, but also a standard ASP. According to our temporal semantics, this program and dataset admit infinitely many stable models: for each set X of time points, there is a stable model in which P holds at each time point in X and Q holds at all other time points. In contrast, the same program under the standard ASP semantics has only two stable models, namely
![]() $\{ P \}$
and
$\{ P \}$
and
![]() $ \{ Q \}$
.
$ \{ Q \}$
.
We next show that our semantics for
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
also generalises the semantics of (positive)
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
also generalises the semantics of (positive)
![]() ${\textrm{DatalogMTL}}$
programs. If a
${\textrm{DatalogMTL}}$
programs. If a
![]() ${\textrm{DatalogMTL}}$
program
${\textrm{DatalogMTL}}$
program
![]() $\Pi$
and a dataset
$\Pi$
and a dataset
![]() $\mathcal{D}$
have a model, they also admit a least model (Brandt et al. Reference Brandt, Kontchakov, Ryzhikov, Xiao and Zakharyaschev2017). This can be equivalently reformulated by stating that if the set of all interpretations
$\mathcal{D}$
have a model, they also admit a least model (Brandt et al. Reference Brandt, Kontchakov, Ryzhikov, Xiao and Zakharyaschev2017). This can be equivalently reformulated by stating that if the set of all interpretations
![]() $\{ \mathfrak{I} \mid (\mathfrak{I},\mathfrak{I}) \text{ is an HT-model of } \Pi \text{ and } \mathcal{D}\}$
is not empty, then this set contains a unique least interpretation.
$\{ \mathfrak{I} \mid (\mathfrak{I},\mathfrak{I}) \text{ is an HT-model of } \Pi \text{ and } \mathcal{D}\}$
is not empty, then this set contains a unique least interpretation.
Theorem 3.7 Let
![]() $\Pi$
be a positive program and let
$\Pi$
be a positive program and let
![]() $\mathcal{D}$
be a dataset. An interpretation
$\mathcal{D}$
be a dataset. An interpretation
![]() $\mathfrak{I}$
is a stable model of
$\mathfrak{I}$
is a stable model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
if and only if
$\mathcal{D}$
if and only if
![]() $\mathfrak{I}$
is their least model.
$\mathfrak{I}$
is their least model.
Proof. We can first use the fact that
![]() $\Pi$
is positive to show that if
$\Pi$
is positive to show that if
![]() $(\mathfrak{I},\mathfrak{I})$
is an HT-model of
$(\mathfrak{I},\mathfrak{I})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, then
$\mathcal{D}$
, then
![]() $\mathfrak{H}^\mathfrak{I}_{\Pi,\mathcal{D}}$
is the least model of
$\mathfrak{H}^\mathfrak{I}_{\Pi,\mathcal{D}}$
is the least model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. Indeed, if
$\mathcal{D}$
. Indeed, if
![]() $(\mathfrak{I},\mathfrak{I})$
is an HT-model of
$(\mathfrak{I},\mathfrak{I})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, we can define the sequence
$\mathcal{D}$
, we can define the sequence
![]() $\mathfrak{H}_0$
,
$\mathfrak{H}_0$
,
![]() $\mathfrak{H}_1$
,
$\mathfrak{H}_1$
,
![]() $\dots$
of interpretations contained in
$\dots$
of interpretations contained in
![]() $\mathfrak{I}$
as in the proof of Theorem 3.4, which satisfies
$\mathfrak{I}$
as in the proof of Theorem 3.4, which satisfies
![]() $\mathfrak{H}_{\omega_1} = \mathfrak{H}^\mathfrak{I}_{\Pi,\mathcal{D}} $
. Furthermore, since
$\mathfrak{H}_{\omega_1} = \mathfrak{H}^\mathfrak{I}_{\Pi,\mathcal{D}} $
. Furthermore, since
![]() $\Pi$
is positive, we can observe that, for every ordinal
$\Pi$
is positive, we can observe that, for every ordinal
![]() $\alpha$
, it holds that
$\alpha$
, it holds that
![]() $ { \mathfrak{H}_\alpha = T_\Pi^\alpha(\mathfrak{I}_\mathcal{D}) }$
, where
$ { \mathfrak{H}_\alpha = T_\Pi^\alpha(\mathfrak{I}_\mathcal{D}) }$
, where
![]() $T_\Pi^\alpha(\mathfrak{I}_\mathcal{D})$
is the result of applying
$T_\Pi^\alpha(\mathfrak{I}_\mathcal{D})$
is the result of applying
![]() $\alpha$
times the immediate consequence operator of a positive program
$\alpha$
times the immediate consequence operator of a positive program
![]() $\Pi$
to an interpretation
$\Pi$
to an interpretation
![]() $\mathfrak{I}_\mathcal{D}$
represented by
$\mathfrak{I}_\mathcal{D}$
represented by
![]() $\mathcal{D}$
. In particular,
$\mathcal{D}$
. In particular,
![]() $ { \mathfrak{H}_{\omega_1} = T_\Pi^{\omega_1}(\mathfrak{I}_\mathcal{D}) }$
, which is the least model of
$ { \mathfrak{H}_{\omega_1} = T_\Pi^{\omega_1}(\mathfrak{I}_\mathcal{D}) }$
, which is the least model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
(Wałęga et al. Reference Wałęga, Tena Cucala, Kostylev and Cuenca Grau2021; Brandt et al. Reference Brandt, Kontchakov, Ryzhikov, Xiao and Zakharyaschev2017). Hence,
$\mathcal{D}$
(Wałęga et al. Reference Wałęga, Tena Cucala, Kostylev and Cuenca Grau2021; Brandt et al. Reference Brandt, Kontchakov, Ryzhikov, Xiao and Zakharyaschev2017). Hence,
![]() $\mathfrak{H}^\mathfrak{I}_{\Pi,\mathcal{D}}$
is the least model of
$\mathfrak{H}^\mathfrak{I}_{\Pi,\mathcal{D}}$
is the least model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
.
$\mathcal{D}$
.
Now, if
![]() $\mathfrak{I}$
is a stable model of
$\mathfrak{I}$
is a stable model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, then
$\mathcal{D}$
, then
![]() $(\mathfrak{I},\mathfrak{I})$
is an HT-model of
$(\mathfrak{I},\mathfrak{I})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
; as shown in the previous paragraph, this implies that
$\mathcal{D}$
; as shown in the previous paragraph, this implies that
![]() $\mathfrak{H}^\mathfrak{I}_{\Pi,\mathcal{D}}$
is the least model of
$\mathfrak{H}^\mathfrak{I}_{\Pi,\mathcal{D}}$
is the least model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. However, since
$\mathcal{D}$
. However, since
![]() $\mathfrak{I}$
is a stable model of
$\mathfrak{I}$
is a stable model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, we have
$\mathcal{D}$
, we have
![]() $\mathfrak{I} = \mathfrak{H}^\mathfrak{I}_{\Pi,\mathcal{D}}$
, and thus
$\mathfrak{I} = \mathfrak{H}^\mathfrak{I}_{\Pi,\mathcal{D}}$
, and thus
![]() $\mathfrak{I}$
is also the least model of
$\mathfrak{I}$
is also the least model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. Conversely, if
$\mathcal{D}$
. Conversely, if
![]() $\mathfrak{I}$
is the least model of
$\mathfrak{I}$
is the least model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, then
$\mathcal{D}$
, then
![]() $(\mathfrak{I},\mathfrak{I})$
is an HT-model of
$(\mathfrak{I},\mathfrak{I})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
; then, as shown in the previous paragraph,
$\mathcal{D}$
; then, as shown in the previous paragraph,
![]() $\mathfrak{I} = \mathfrak{H}^\mathfrak{I}_{\Pi,\mathcal{D}}$
, and so
$\mathfrak{I} = \mathfrak{H}^\mathfrak{I}_{\Pi,\mathcal{D}}$
, and so
![]() $\mathfrak{I}$
is a stable model of
$\mathfrak{I}$
is a stable model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
.
$\mathcal{D}$
.
It follows that, if a positive program and a dataset have a model, then they have a stable model. Note, however, that this is not the case for other temporal logics with stable model semantics (Cabalar and Demri Reference Cabalar and Demri2011; Bozzelli and Pearce Reference Bozzelli and Pearce2015), and the reason why this property holds in our setting is given by Theorem 3.4.
Finally, our semantics also generalises that of stratifiable
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
programs (Tena Cucala et al. Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021), where rules do not have cyclic dependencies via negation and can be organised in strata. Each such a stratifiable,
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
programs (Tena Cucala et al. Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021), where rules do not have cyclic dependencies via negation and can be organised in strata. Each such a stratifiable,
![]() $\bot$
-free program
$\bot$
-free program
![]() $\Pi$
and dataset
$\Pi$
and dataset
![]() $\mathcal{D}$
have a single least model constructed by applying to
$\mathcal{D}$
have a single least model constructed by applying to
![]() $\mathcal{D}$
rules of
$\mathcal{D}$
rules of
![]() $\Pi$
stratum by stratum in a minimal way (Tena Cucala et al. Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021). As in the case of positive programs, we can show that such least model corresponds to the single stable model of
$\Pi$
stratum by stratum in a minimal way (Tena Cucala et al. Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021). As in the case of positive programs, we can show that such least model corresponds to the single stable model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. Hence, analogously to the case of plain Datalog, positive and stratifiable
$\mathcal{D}$
. Hence, analogously to the case of plain Datalog, positive and stratifiable
![]() ${\textrm{DatalogMTL}}$
programs cannot have multiple stable models. Arbitrary programs, however, can have any number of stable models, which is witnessed by Example 3.6.
${\textrm{DatalogMTL}}$
programs cannot have multiple stable models. Arbitrary programs, however, can have any number of stable models, which is witnessed by Example 3.6.
In the rest of the paper we study decidability and complexity of reasoning, which is (in the context of this paper) the problem of checking if a
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program
![]() $\Pi$
and a dataset
$\Pi$
and a dataset
![]() $\mathcal{D}$
have a stable model. We focus on data complexity – that is, we assume that
$\mathcal{D}$
have a stable model. We focus on data complexity – that is, we assume that
![]() $\Pi$
is fixed and only
$\Pi$
is fixed and only
![]() $\mathcal{D}$
forms the input – which is the most relevant measure if complexity in data intensive applications.
$\mathcal{D}$
forms the input – which is the most relevant measure if complexity in data intensive applications.
Before we close this section, however, it is worth pointing out the connections between the problem of checking existence of a stable model and the related problem of fact entailment, as defined next. Following the standard conventions of non-monotonic logics and ASP (Eiter et al. Reference Eiter, Ianni and Krennwallner2009), we say that a
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program
![]() $\Pi$
and a dataset
$\Pi$
and a dataset
![]() $\mathcal{D}$
bravely entail a relational fact
$\mathcal{D}$
bravely entail a relational fact
![]() $P(\mathbf{c})@\varrho$
if
$P(\mathbf{c})@\varrho$
if
![]() $\mathfrak{I} \models_\mathbb{T} P(\mathbf{c})@\varrho$
for some stable model
$\mathfrak{I} \models_\mathbb{T} P(\mathbf{c})@\varrho$
for some stable model
![]() $\mathfrak{I}$
of
$\mathfrak{I}$
of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, and we say that
$\mathcal{D}$
, and we say that
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
cautiously entail
$\mathcal{D}$
cautiously entail
![]() $P(\mathbf{c})@\varrho$
if
$P(\mathbf{c})@\varrho$
if
![]() $\mathfrak{I} \models_\mathbb{T} P(\mathbf{c})@\varrho$
for all stable models
$\mathfrak{I} \models_\mathbb{T} P(\mathbf{c})@\varrho$
for all stable models
![]() $\mathfrak{I}$
of
$\mathfrak{I}$
of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. The problem of brave (resp. cautious) fact entailment consists in deciding whether a
$\mathcal{D}$
. The problem of brave (resp. cautious) fact entailment consists in deciding whether a
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program and a dataset bravely (resp. cautiously) entail a given relational fact. As we show next, both variants of the problem are inter-reducible with checking existence (or non-existence) of a stable model. Moreover, we argue that these reductions allow us to transfer bounds for data complexity which, for fact entailment, refers to the setting where both the program
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program and a dataset bravely (resp. cautiously) entail a given relational fact. As we show next, both variants of the problem are inter-reducible with checking existence (or non-existence) of a stable model. Moreover, we argue that these reductions allow us to transfer bounds for data complexity which, for fact entailment, refers to the setting where both the program
![]() $\Pi$
and the fact
$\Pi$
and the fact
![]() $P(\mathbf{c})@\varrho$
are fixed, and only the dataset
$P(\mathbf{c})@\varrho$
are fixed, and only the dataset
![]() $\mathcal{D}$
constitutes the input.
$\mathcal{D}$
constitutes the input.
Proposition 3.8 In
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
, existence of a stable model can be reduced in
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
, existence of a stable model can be reduced in
![]() ${{\small\rm AC}}^0$
to (i) brave fact entailment, and to (ii) the complement of cautious fact entailment, and vice versa. Furthermore, the reductions involved do not depend on the input dataset.
${{\small\rm AC}}^0$
to (i) brave fact entailment, and to (ii) the complement of cautious fact entailment, and vice versa. Furthermore, the reductions involved do not depend on the input dataset.
Proof. We start by showing Statement (i). To check if a
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program
![]() $\Pi$
and a dataset
$\Pi$
and a dataset
![]() $\mathcal{D}$
have a stable model, it suffices to add to
$\mathcal{D}$
have a stable model, it suffices to add to
![]() $\mathcal{D}$
a fact
$\mathcal{D}$
a fact
![]() $P@0$
with a fresh proposition P and check whether
$P@0$
with a fresh proposition P and check whether
![]() $\Pi$
and the extended dataset bravely entail
$\Pi$
and the extended dataset bravely entail
![]() $P@0$
. To check if
$P@0$
. To check if
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
bravely entail a relation fact
$\mathcal{D}$
bravely entail a relation fact
![]() $P(\mathbf{c}) @ \varrho$
, it suffices to verify that the following program
$P(\mathbf{c}) @ \varrho$
, it suffices to verify that the following program
![]() $\Pi'$
and dataset
$\Pi'$
and dataset
![]() $\mathcal{D}'$
have a stable model:
$\mathcal{D}'$
have a stable model:
where P’ is a fresh predicate of the same arity as P,
![]() $\mathbf{x}$
is a tuple of distinct variables, t is an arbitrary time point belonging to
$\mathbf{x}$
is a tuple of distinct variables, t is an arbitrary time point belonging to
![]() $\varrho$
, whereas
$\varrho$
, whereas
![]() $\varrho_1$
and
$\varrho_1$
and
![]() $\varrho_2$
depend on both
$\varrho_2$
depend on both
![]() $\varrho$
and t; for example, if
$\varrho$
and t; for example, if
![]() $\varrho =[ t_1,t_2 )$
, then
$\varrho =[ t_1,t_2 )$
, then
![]() $\varrho_1=[0,t-t_1]$
and
$\varrho_1=[0,t-t_1]$
and
![]() $\varrho_2=[0,t_2-t)$
, where if
$\varrho_2=[0,t_2-t)$
, where if
![]() $t_2= \infty$
, then
$t_2= \infty$
, then
![]() $t_2-t$
stands for
$t_2-t$
stands for
![]() $\infty$
.
$\infty$
.
Next, we show Statement (ii). To check if
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
have a stable model, it suffices to check if they do not cautiously entail a fact
$\mathcal{D}$
have a stable model, it suffices to check if they do not cautiously entail a fact
![]() $P@0$
, where P is a fresh proposition (Brandt et al. Reference Brandt, Kalayc, Ryzhikov, Xiao and Zakharyaschev2018, Proposition 3). On the other hand, to check if
$P@0$
, where P is a fresh proposition (Brandt et al. Reference Brandt, Kalayc, Ryzhikov, Xiao and Zakharyaschev2018, Proposition 3). On the other hand, to check if
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
do not cautiously entail a relational fact
$\mathcal{D}$
do not cautiously entail a relational fact
![]() $P(\mathbf{c}) @ \varrho$
, it suffices to verify that the following program
$P(\mathbf{c}) @ \varrho$
, it suffices to verify that the following program
![]() $\Pi''$
and dataset
$\Pi''$
and dataset
![]() $\mathcal{D}''$
have a stable model:
$\mathcal{D}''$
have a stable model:
where P’,
![]() $\mathbf{x}$
, t,
$\mathbf{x}$
, t,
![]() $\varrho_1$
, and
$\varrho_1$
, and
![]() $\varrho_2$
are as in the proof of Statement (i).
$\varrho_2$
are as in the proof of Statement (i).
Finally, we observe that all the above reductions can be performed in
![]() ${{\small\rm AC}}^0$
. Moreover, they allow us to transfer data complexity bounds, since the programs and facts we construct in the reductions do not depend on input datasets.
${{\small\rm AC}}^0$
. Moreover, they allow us to transfer data complexity bounds, since the programs and facts we construct in the reductions do not depend on input datasets.
4 Undecidability over the rational timeline
In this section we focus on the rational timeline, so let us fix
![]() $\mathbb{T} = \mathbb{Q}$
. In this setting, standard reasoning problems are
$\mathbb{T} = \mathbb{Q}$
. In this setting, standard reasoning problems are
![]() ${{\rm PS}{\small\rm PACE}}$
-complete in data complexity for positive programs (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019), as well as for programs with negation, if they are stratified (Tena Cucala et al. Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021).
${{\rm PS}{\small\rm PACE}}$
-complete in data complexity for positive programs (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019), as well as for programs with negation, if they are stratified (Tena Cucala et al. Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021).
We next show that, in stark contrast with the positive case, reasoning in
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
is undecidable. Furthermore, undecidability holds even for programs that are propositional, forward-propagating and considered to be fixed, and even if the input datasets are bounded.
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
is undecidable. Furthermore, undecidability holds even for programs that are propositional, forward-propagating and considered to be fixed, and even if the input datasets are bounded.
Theorem 4.1 Checking whether a propositional
![]() ${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
and a bounded dataset have a stable model over the rational timeline is undecidable with respect to data complexity.
${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
and a bounded dataset have a stable model over the rational timeline is undecidable with respect to data complexity.
Proof. Let ![]() be a deterministic Turing machine with
be a deterministic Turing machine with
![]() $\Sigma$
the input alphabet,
$\Sigma$
the input alphabet,
![]() $\mathcal{Q}$
the set of states,
$\mathcal{Q}$
the set of states, ![]() the transition function for
the transition function for
![]() $\Sigma_\sqcup = \Sigma \cup \{\sqcup\}$
and blank symbol
$\Sigma_\sqcup = \Sigma \cup \{\sqcup\}$
and blank symbol
![]() $\sqcup$
,
$\sqcup$
,
![]() $\mathsf{L}$
and
$\mathsf{L}$
and
![]() $\mathsf{R}$
the symbols indicating the head movements, and
$\mathsf{R}$
the symbols indicating the head movements, and ![]() the initial and halting states. Without loss of generality, we assume that
the initial and halting states. Without loss of generality, we assume that
![]() $\mathfrak{M}$
never tries to move to the left of the left-most cell of the tape.
$\mathfrak{M}$
never tries to move to the left of the left-most cell of the tape.
We construct a propositional
![]() ${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
program
${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
program
![]() $\Pi_\mathfrak{M}$
and then reduce (in
$\Pi_\mathfrak{M}$
and then reduce (in
![]() ${{{{\small\rm AC}^0}}}$
) every input word w to a dataset
${{{{\small\rm AC}^0}}}$
) every input word w to a dataset
![]() $\mathcal{D}_w$
with only bounded intervals so that
$\mathcal{D}_w$
with only bounded intervals so that
![]() $\mathfrak{M}$
halts on w if and only if
$\mathfrak{M}$
halts on w if and only if
![]() $\Pi_\mathfrak{M}$
and
$\Pi_\mathfrak{M}$
and
![]() $\mathcal{D}_w$
do not have a stable model.
$\mathcal{D}_w$
do not have a stable model.
We represent, for each
![]() $i \geq 1$
, the ith configuration in the computation of
$i \geq 1$
, the ith configuration in the computation of
![]() $\mathfrak{M}$
on input w within the interval
$\mathfrak{M}$
on input w within the interval
![]() $[2i,2i+2)$
, as illustrated in Figure 1, where we assume that in the configuration the state is q, the head is over the jth cell, and the contents of the first
$[2i,2i+2)$
, as illustrated in Figure 1, where we assume that in the configuration the state is q, the head is over the jth cell, and the contents of the first
![]() $|w| + i$
cells of the tape are symbols
$|w| + i$
cells of the tape are symbols
![]() $s_1, \dots, s_{|w|+i}$
(in the ith configuration, only the first
$s_1, \dots, s_{|w|+i}$
(in the ith configuration, only the first
![]() $|w|+i$
cells can be non-empty). The state is encoded within the first half
$|w|+i$
cells can be non-empty). The state is encoded within the first half
![]() $[2i, 2i+1]$
of the interval: a proposition
$[2i, 2i+1]$
of the interval: a proposition
![]() $S_{q}$
holds at some time point within
$S_{q}$
holds at some time point within
![]() $[2i,2i+1]$
. The contents of the tape and the head position are encoded within the second half
$[2i,2i+1]$
. The contents of the tape and the head position are encoded within the second half
![]() $(2i+1,2i+2)$
of the interval; in particular,
$(2i+1,2i+2)$
of the interval; in particular,
![]() $|w|+i$
time points
$|w|+i$
time points
![]() ${t^i_1 < \cdots < t^i_{|w|+i}}$
in
${t^i_1 < \cdots < t^i_{|w|+i}}$
in
![]() $(2i+1,2i+2)$
are used so that, for each
$(2i+1,2i+2)$
are used so that, for each
![]() $j \in\{1, \dots, |w| +i\}$
, proposition
$j \in\{1, \dots, |w| +i\}$
, proposition
![]() $C_{s_j}$
holds at
$C_{s_j}$
holds at
![]() $t^i_{j}$
, encoding the fact that
$t^i_{j}$
, encoding the fact that
![]() $s_j$
are the contents of the jth cell in the configuration, and proposition H holds at
$s_j$
are the contents of the jth cell in the configuration, and proposition H holds at
![]() $t^i_j$
, encoding the fact that the head is over the jth cell in the configuration. We also use additional propositions: S, which holds all through
$t^i_j$
, encoding the fact that the head is over the jth cell in the configuration. We also use additional propositions: S, which holds all through
![]() $[2i,2i+1]$
and ensures that these intervals are only used to encode states; N, which holds at a single new time point in
$[2i,2i+1]$
and ensures that these intervals are only used to encode states; N, which holds at a single new time point in
![]() $(2i+1,2i+2)$
beyond
$(2i+1,2i+2)$
beyond
![]() $t^i_{|w|+i}$
and will allow us to increase the number of time points encoding cells;
$t^i_{|w|+i}$
and will allow us to increase the number of time points encoding cells;
![]() $\overline{N}$
and
$\overline{N}$
and
![]() $\overline{H}$
, which simulate negations of N and H, respectively;
$\overline{H}$
, which simulate negations of N and H, respectively;
![]() $\overline{C}$
, which marks points not used to encode the tape contents, and L, used for encoding left-moving transitions.
$\overline{C}$
, which marks points not used to encode the tape contents, and L, used for encoding left-moving transitions.

Fig. 1. Encoding of the ith configuration.
The first block of rules in
![]() $\Pi_\mathfrak{M}$
consists of the following rules, for each
$\Pi_\mathfrak{M}$
consists of the following rules, for each
![]() $X \in \{N,H \}$
and
$X \in \{N,H \}$
and
![]() $s \in \Sigma_\sqcup$
:
$s \in \Sigma_\sqcup$
:

The first three rules state that, at each time point, either X or
![]() $\overline{X}$
holds. The fourth rule states that X cannot hold twice in an open interval of length 1. By the fifth rule, X and S cannot hold at the same time point. The sixth rule states that
$\overline{X}$
holds. The fourth rule states that X cannot hold twice in an open interval of length 1. By the fifth rule, X and S cannot hold at the same time point. The sixth rule states that
![]() $\overline{N}$
holds in all time points encoding cells. The second to last rule states that H does not hold in time points that do not encode cells. The last rule ensures that after time point
$\overline{N}$
holds in all time points encoding cells. The second to last rule states that H does not hold in time points that do not encode cells. The last rule ensures that after time point
![]() $t^i_{|w|+i}$
encoding the last relevant cell in the ith configuration, there is another time point within
$t^i_{|w|+i}$
encoding the last relevant cell in the ith configuration, there is another time point within
![]() $(2i+1,2i+2)$
where N holds. Note that the last rule uses conjunction within a metric operator, which is not syntactically allowed, but can be easily simulated by replacing
$(2i+1,2i+2)$
where N holds. Note that the last rule uses conjunction within a metric operator, which is not syntactically allowed, but can be easily simulated by replacing
![]() $\overline{C} \land \overline{N}$
with a fresh proposition P and adding a rule
$\overline{C} \land \overline{N}$
with a fresh proposition P and adding a rule
![]() $P \gets \overline{C} \land \overline{N}$
; this abbreviation will be useful for simplifying other formulas used later on in the reduction.
$P \gets \overline{C} \land \overline{N}$
; this abbreviation will be useful for simplifying other formulas used later on in the reduction.
The second block consists of the following rules, propagating propositions to the interval encoding the consequent configuration, for every
![]() $s \in \Sigma_\sqcup$
:
$s \in \Sigma_\sqcup$
:
By the first rule, S is always propagated into the future from t to
![]() $t+2$
. The second rule states that, if t does not encode a cell and
$t+2$
. The second rule states that, if t does not encode a cell and
![]() $\overline{N}$
holds therein, then
$\overline{N}$
holds therein, then
![]() $t+2$
does not encode a cell either. By the third rule, if N holds at t and this t is to the right of the time point encoding the initial state, then
$t+2$
does not encode a cell either. By the third rule, if N holds at t and this t is to the right of the time point encoding the initial state, then
![]() $t+2$
encodes an empty cell. The last rule states that, if t encodes a cell with contents s and the head is not on this cell, then
$t+2$
encodes an empty cell. The last rule states that, if t encodes a cell with contents s and the head is not on this cell, then
![]() $t+2$
also encodes a cell with contents s.
$t+2$
also encodes a cell with contents s.
We next encode the left-moving transitions. Proposition L is used to indicate a time point encoding a cell such that the head was on it in the previous configuration and then moved to the left. Program
![]() $\Pi_\mathfrak{M}$
contains the following rules for every
$\Pi_\mathfrak{M}$
contains the following rules for every
![]() $s \in \Sigma$
and
$s \in \Sigma$
and
![]() $q \in \mathcal{Q}$
with transition
$q \in \mathcal{Q}$
with transition
![]() $\delta(s,q)=(s',q',\mathsf{L})$
, and every
$\delta(s,q)=(s',q',\mathsf{L})$
, and every
![]() $s^* \in \Sigma$
:
$s^* \in \Sigma$
:

The first ruleimulates the transition: H holds as intended, the state is changed from q to q’, and the contents of the cell under the head change from s to s’ (the conjunction in the head is used for brevity and can be simulated by several rules). The last two rules encode the position of the head in the consequent configuration, by stating that H holds at the first time point encoding a cell to the left of the time point with L.
Similarly, for each transition
![]() ${\delta(s,q)=(s',q',\mathsf{R})}$
moving the head to the right and any
${\delta(s,q)=(s',q',\mathsf{R})}$
moving the head to the right and any
![]() $s^* \in \Sigma$
, program
$s^* \in \Sigma$
, program
![]() $\Pi_\mathfrak{M}$
has the rules
$\Pi_\mathfrak{M}$
has the rules

Here, the first rule encodes the change of the state and the contents of the cell above which the head is. The last two rules simulate the change of the position of the head. Finally,
![]() $\Pi_\mathfrak{M}$
contains rule
$\Pi_\mathfrak{M}$
contains rule ![]() , which yields an inconsistency when the halting state is reached.
, which yields an inconsistency when the halting state is reached.
We next reduce an input word
![]() $w=s_1 \dots s_{|w|}$
to a dataset
$w=s_1 \dots s_{|w|}$
to a dataset
![]() $\mathcal{D}_{w}$
. Assuming that w is non-empty, we let
$\mathcal{D}_{w}$
. Assuming that w is non-empty, we let
![]() ${t_k = 1 + \frac{k}{|w|+1}}$
for each
${t_k = 1 + \frac{k}{|w|+1}}$
for each
![]() $k \in \{1,\dots, |w|\}$
(it is only important here that
$k \in \{1,\dots, |w|\}$
(it is only important here that
![]() ${1 < t_1< \dots < t_{|w|} < 2}$
); then,
${1 < t_1< \dots < t_{|w|} < 2}$
); then,
![]() $\mathcal{D}_{w}$
contains the facts:
$\mathcal{D}_{w}$
contains the facts:

Intuitively,
![]() $\mathcal{D}_{w}$
describes the initial configuration of
$\mathcal{D}_{w}$
describes the initial configuration of
![]() $\mathfrak{M}$
on w within [0,2); the initial state is encoded in 1 and
$\mathfrak{M}$
on w within [0,2); the initial state is encoded in 1 and
![]() $t_1, \dots, t_{|w|}$
encode the first
$t_1, \dots, t_{|w|}$
encode the first
![]() $|w|$
cells of
$|w|$
cells of
![]() $\mathfrak{M}$
. Moreover,
$\mathfrak{M}$
. Moreover,
![]() $\overline{C}$
holds in all other time points in (1,2), whereas
$\overline{C}$
holds in all other time points in (1,2), whereas
![]() $\overline{N}$
and
$\overline{N}$
and
![]() $\overline{H}$
hold in [0,1].
$\overline{H}$
hold in [0,1].
We next showhat
![]() $\Pi_\mathfrak{M}$
and
$\Pi_\mathfrak{M}$
and
![]() $\mathcal{D}_{w}$
have a stable model if and only if
$\mathcal{D}_{w}$
have a stable model if and only if
![]() $\mathfrak{M}$
does not halt on w. Assume that
$\mathfrak{M}$
does not halt on w. Assume that
![]() $\mathfrak{T}$
is a stable model of
$\mathfrak{T}$
is a stable model of
![]() $\Pi_{\mathfrak{M}}$
and
$\Pi_{\mathfrak{M}}$
and
![]() $\mathcal{D}_{w}$
. Then, using induction over
$\mathcal{D}_{w}$
. Then, using induction over
![]() $i \in \mathbb{N}$
, we can prove that the ith configuration in the computation of
$i \in \mathbb{N}$
, we can prove that the ith configuration in the computation of
![]() $\mathfrak{M}$
on w is encoded as discussed above. In particular, if q is the state of
$\mathfrak{M}$
on w is encoded as discussed above. In particular, if q is the state of
![]() $\mathfrak{M}$
in the ith configuration, then
$\mathfrak{M}$
in the ith configuration, then
![]() $\mathfrak{T},t \models S_q$
for some
$\mathfrak{T},t \models S_q$
for some
![]() $t \in [2i, 2i+1]$
. Since
$t \in [2i, 2i+1]$
. Since
![]() $\mathfrak{T}$
is a model of
$\mathfrak{T}$
is a model of
![]() $\Pi_{\mathfrak{M}}$
, however, it satisfies the rule
$\Pi_{\mathfrak{M}}$
, however, it satisfies the rule ![]() ; therefore, the state
; therefore, the state ![]() cannot occur in any configuration in the computation of
cannot occur in any configuration in the computation of
![]() $\mathfrak{M}$
on w, and so
$\mathfrak{M}$
on w, and so
![]() $\mathfrak{M}$
does not halt on w.
$\mathfrak{M}$
does not halt on w.
For the opposite direction assume that
![]() $\mathfrak{M}$
does not halt on w. Then, we let
$\mathfrak{M}$
does not halt on w. Then, we let
![]() $\mathfrak{T}$
be the minimal interpretation which satisfies
$\mathfrak{T}$
be the minimal interpretation which satisfies
![]() $\mathcal{D}_{w}$
and the following statements, for every positive integer i, where we let
$\mathcal{D}_{w}$
and the following statements, for every positive integer i, where we let
![]() $t^{i}_j = 2i + 1+ \sum_{k=1}^j \frac{1}{2^k}$
for each
$t^{i}_j = 2i + 1+ \sum_{k=1}^j \frac{1}{2^k}$
for each
![]() $j \in \mathbb{N}$
(this definition ensures that there are infinitely many time points of the form
$j \in \mathbb{N}$
(this definition ensures that there are infinitely many time points of the form
![]() $t_j^i$
in interval
$t_j^i$
in interval
![]() $(2i+1,2i+2)$
):
$(2i+1,2i+2)$
):
-
 $\mathfrak{T} \models S @ [2i,2i+1]$
,
$\mathfrak{T} \models S @ [2i,2i+1]$
, -
 $\mathfrak{T}, t_j^i \models C_s$
, whenever s are the contents of the jth cell of
$\mathfrak{T}, t_j^i \models C_s$
, whenever s are the contents of the jth cell of
 $\mathfrak{M}$
in the ith step of computation on w, for
$\mathfrak{M}$
in the ith step of computation on w, for
 $j \in \{1, \dots, |w|+i\}$
,
$j \in \{1, \dots, |w|+i\}$
, -
 $\mathfrak{T},t \models \overline{C}$
, for each
$\mathfrak{T},t \models \overline{C}$
, for each
 $t \in (2i,2i+1) \setminus \{t^{i}_1, \dots, t^{i}_{|w|+i}\}$
,
$t \in (2i,2i+1) \setminus \{t^{i}_1, \dots, t^{i}_{|w|+i}\}$
, -
 $\mathfrak{T}, t_{|w|+i+1}^{i} \models N$
and
$\mathfrak{T}, t_{|w|+i+1}^{i} \models N$
and
 $\mathfrak{T}, t' \models \overline{N}$
for each
$\mathfrak{T}, t' \models \overline{N}$
for each
 $t' \in [2i,2i+2) \setminus \{ t_{|w|+i+1}^{i} \}$
,
$t' \in [2i,2i+2) \setminus \{ t_{|w|+i+1}^{i} \}$
, -
 $\mathfrak{T}, t^i_j \models H$
if the head of
$\mathfrak{T}, t^i_j \models H$
if the head of
 $\mathfrak{M}$
is above the jth cell in the ith step of its computation on w,
$\mathfrak{M}$
is above the jth cell in the ith step of its computation on w, -
 $\mathfrak{T}, t \models \overline{H}$
for each
$\mathfrak{T}, t \models \overline{H}$
for each
 $t \in [2i,2i+2) \backslash \{t^i_j\}$
, for j such that the head of
$t \in [2i,2i+2) \backslash \{t^i_j\}$
, for j such that the head of
 $\mathfrak{M}$
is above the jth cell in the ith step of its computation on w,
$\mathfrak{M}$
is above the jth cell in the ith step of its computation on w, -
 $\mathfrak{T}, t^{i+1}_j \models L$
if the head of
$\mathfrak{T}, t^{i+1}_j \models L$
if the head of
 $\mathfrak{M}$
is above the jth cell in the ith step of its computation on w,
$\mathfrak{M}$
is above the jth cell in the ith step of its computation on w, -
 $\mathfrak{T}, t^i_j +1 \models S_q$
if
$\mathfrak{T}, t^i_j +1 \models S_q$
if
 $\mathfrak{T}, t^i_j \models H$
and
$\mathfrak{T}, t^i_j \models H$
and
 $\mathfrak{M}$
is in the state q in the
$\mathfrak{M}$
is in the state q in the
 $i+1$
th step of computation on w.
$i+1$
th step of computation on w.
Clearly,
![]() $(\mathfrak{T},\mathfrak{T})$
is an HT-model of
$(\mathfrak{T},\mathfrak{T})$
is an HT-model of
![]() $\mathcal{D}_{w}$
, and it can be also verified, by inspecting the rules in
$\mathcal{D}_{w}$
, and it can be also verified, by inspecting the rules in
![]() $\Pi_{\mathfrak{M}}$
, that
$\Pi_{\mathfrak{M}}$
, that
![]() $(\mathfrak{T},\mathfrak{T})$
is an HT-model of
$(\mathfrak{T},\mathfrak{T})$
is an HT-model of
![]() $\Pi_{\mathfrak{M}}$
. Finally, to show that
$\Pi_{\mathfrak{M}}$
. Finally, to show that
![]() $(\mathfrak{T},\mathfrak{T})$
is a stable model of
$(\mathfrak{T},\mathfrak{T})$
is a stable model of
![]() $\Pi_{\mathfrak{M}}$
and
$\Pi_{\mathfrak{M}}$
and
![]() $\mathcal{D}_{w}$
, we need to show that
$\mathcal{D}_{w}$
, we need to show that
![]() $\mathfrak{T} = \mathfrak{H}^{\mathfrak{T}}_{\Pi_{\mathfrak{M}},\mathcal{D}_{w}}$
. Towards this goal, we first construct the sequence
$\mathfrak{T} = \mathfrak{H}^{\mathfrak{T}}_{\Pi_{\mathfrak{M}},\mathcal{D}_{w}}$
. Towards this goal, we first construct the sequence
![]() $\mathfrak{H}_0$
,
$\mathfrak{H}_0$
,
![]() $\mathfrak{H}_1$
of interpretations as in the proof of Theorem 3.4, for which it holds that
$\mathfrak{H}_1$
of interpretations as in the proof of Theorem 3.4, for which it holds that
![]() ${\mathfrak{H}_{\omega_1} = \mathfrak{H}^{\mathfrak{T}}_{\Pi_{\mathfrak{M}},\mathcal{D}_{w}}}$
. Then we can easily show, using transfinite induction, that for each
${\mathfrak{H}_{\omega_1} = \mathfrak{H}^{\mathfrak{T}}_{\Pi_{\mathfrak{M}},\mathcal{D}_{w}}}$
. Then we can easily show, using transfinite induction, that for each
![]() $i \in \mathbb{N}$
and each relational fact
$i \in \mathbb{N}$
and each relational fact
![]() $M@t$
with
$M@t$
with
![]() $t \in [2i,2i+2)$
,
$t \in [2i,2i+2)$
,
![]() $\mathfrak{T} \models M@t$
if and only if
$\mathfrak{T} \models M@t$
if and only if
![]() $\mathfrak{H}_i \models M@t$
, and also that
$\mathfrak{H}_i \models M@t$
, and also that
![]() ${\mathfrak{H}_i \models M@t}$
if and only if
${\mathfrak{H}_i \models M@t}$
if and only if
![]() $\mathfrak{H}^{\mathfrak{T}}_{\Pi_{\mathfrak{M}},\mathcal{D}_{w}} \models M@t$
, which together imply
$\mathfrak{H}^{\mathfrak{T}}_{\Pi_{\mathfrak{M}},\mathcal{D}_{w}} \models M@t$
, which together imply
![]() $\mathfrak{T} = \mathfrak{H}^{\mathfrak{T}}_{\Pi_{\mathfrak{M}},\mathcal{D}_{w}}$
.
$\mathfrak{T} = \mathfrak{H}^{\mathfrak{T}}_{\Pi_{\mathfrak{M}},\mathcal{D}_{w}}$
.
Observe that the reduction above shows undecidability of reasoning in
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
over the rational timeline, even if we restrict our attention to fixed propositional programs in the forward-propagating fragment, and we consider only bounded datasets. In the next section, we turn our attention to the integer timeline and show that reasoning becomes decidable.
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
over the rational timeline, even if we restrict our attention to fixed propositional programs in the forward-propagating fragment, and we consider only bounded datasets. In the next section, we turn our attention to the integer timeline and show that reasoning becomes decidable.
5 Decidability over the integer timeline
In this section we consider the integer timeline and thus we fix
![]() $\mathbb{T} = \mathbb{Z}$
. We will show that, in this case, reasoning becomes decidable in
$\mathbb{T} = \mathbb{Z}$
. We will show that, in this case, reasoning becomes decidable in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
with respect to data complexity; furthermore, complexity drops to
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
with respect to data complexity; furthermore, complexity drops to
![]() ${{\rm PS}{\small\rm PACE}}$
if we restrict our attention to forward-propagating programs and datasets mentioning only bounded intervals – a setting well-suited for stream reasoning (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019; Ronca et al. Reference Ronca, Kaminski, Cuenca Grau and Horrocks2018). In this setting, the additional expressive power provided by stable models comes at no computational cost since reasoning in the corresponding positive fragment is already
${{\rm PS}{\small\rm PACE}}$
if we restrict our attention to forward-propagating programs and datasets mentioning only bounded intervals – a setting well-suited for stream reasoning (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019; Ronca et al. Reference Ronca, Kaminski, Cuenca Grau and Horrocks2018). In this setting, the additional expressive power provided by stable models comes at no computational cost since reasoning in the corresponding positive fragment is already
![]() ${{\rm PS}{\small\rm PACE}}$
-complete (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2020a; 2019).
${{\rm PS}{\small\rm PACE}}$
-complete (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2020a; 2019).
In prior work on positive and stratifiable programs, upper bounds for reasoning have been established by constructing generalised Büchi automata that accept (words describing) models of a given program and dataset (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2020a; Tena Cucala et al. Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021). Checking existence of a stable model is more demanding, as we additionally need to ensure model minimality as in Definition 3.5; this requirement is non-trivial, and we will handle it differently for the cases of arbitrary and forward-propagating programs.
In the general case (Section 5.1), we construct two kinds of left- and right-moving automata: the first kind allows us to check existence of an HT-model of the form
![]() $(\mathfrak{T},\mathfrak{T})$
, while the second kind allows us to check existence of an HT-model of the form
$(\mathfrak{T},\mathfrak{T})$
, while the second kind allows us to check existence of an HT-model of the form
![]() $(\mathfrak{H},\mathfrak{T})$
with
$(\mathfrak{H},\mathfrak{T})$
with
![]() $\mathfrak{H} \neq \mathfrak{T}$
. Then, a pair of words
$\mathfrak{H} \neq \mathfrak{T}$
. Then, a pair of words
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() ${{{\overrightarrow{w}}}}$
that are accepted, respectively, by a pair of left- and right-moving automata of the first kind, but not by any pair of left and right-moving automata of the second kind, represents a stable model. This construction is conceptually similar to that of Cabalar and Demri (Reference Cabalar and Demri2011) for a logic with linear temporal operators and involves complementing nondeterministic automata, which leads to an exponential blowup. Consequently, we obtain an
${{{\overrightarrow{w}}}}$
that are accepted, respectively, by a pair of left- and right-moving automata of the first kind, but not by any pair of left and right-moving automata of the second kind, represents a stable model. This construction is conceptually similar to that of Cabalar and Demri (Reference Cabalar and Demri2011) for a logic with linear temporal operators and involves complementing nondeterministic automata, which leads to an exponential blowup. Consequently, we obtain an
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
upper bound and thus an exponential gap in data complexity with respect to positive programs (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2020a). In the case of forward-propagating programs (Section 5.2) we propose a different construction exploiting the fact that rules propagate information in a single temporal direction. This allows us to build automata that guarantee model minimality without complementation. As a result, we can establish a tight
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
upper bound and thus an exponential gap in data complexity with respect to positive programs (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2020a). In the case of forward-propagating programs (Section 5.2) we propose a different construction exploiting the fact that rules propagate information in a single temporal direction. This allows us to build automata that guarantee model minimality without complementation. As a result, we can establish a tight
![]() ${{\rm PS}{\small\rm PACE}}$
bound in data complexity.
${{\rm PS}{\small\rm PACE}}$
bound in data complexity.
5.1 General programs
It will be convenient for our presentation to assume that programs are in a normal form analogous to that by Tena Cucala et al. (Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021) for stratifiable programs: in each normalised rule the head is a relational atom or
![]() $\bot$
, there is neither nesting of metric operators nor occurrences of
$\bot$
, there is neither nesting of metric operators nor occurrences of ![]() or
or ![]() in rule bodies, and the only unbounded interval allowed is
in rule bodies, and the only unbounded interval allowed is
![]() $[0, \infty)$
.
$[0, \infty)$
.
Proposition 5.1 Each program
![]() $\Pi$
can be normalised in polynomial time into a program
$\Pi$
can be normalised in polynomial time into a program
![]() $\Pi'$
such that, for each dataset
$\Pi'$
such that, for each dataset
![]() $\mathcal{D}$
, program
$\mathcal{D}$
, program
![]() $\Pi$
and dataset
$\Pi$
and dataset
![]() $\mathcal{D}$
have a stable model if and only if so do
$\mathcal{D}$
have a stable model if and only if so do
![]() $\Pi'$
and
$\Pi'$
and
![]() $\mathcal{D}$
.
$\mathcal{D}$
.
Proof. To construct
![]() $\Pi'$
we first delete all (trivial) rules having
$\Pi'$
we first delete all (trivial) rules having
![]() $\top$
as the head. Then, we eliminate from the remaining rule heads metric operators (i.e., boxes). To this end, we replace each rule of the form
$\top$
as the head. Then, we eliminate from the remaining rule heads metric operators (i.e., boxes). To this end, we replace each rule of the form
![]() ${ \Box^1_{\varrho_1} \dots \Box^n_{\varrho_n} P(\mathbf{s}) \gets B}$
, where
${ \Box^1_{\varrho_1} \dots \Box^n_{\varrho_n} P(\mathbf{s}) \gets B}$
, where
![]() $n\geq 0$
, each
$n\geq 0$
, each
![]() $\Box^i$
is either
$\Box^i$
is either
![]() $\boxminus$
or
$\boxminus$
or
![]() $\boxplus$
, and B is the body of the rule, with rules
$\boxplus$
, and B is the body of the rule, with rules
![]() $P'(\mathbf{s}) \gets B$
and
$P'(\mathbf{s}) \gets B$
and ![]() , where
, where ![]() if
if
![]() $\Box^i = \boxminus$
and otherwise
$\Box^i = \boxminus$
and otherwise ![]() , and P’ is a fresh predicate of the same arity as P.
, and P’ is a fresh predicate of the same arity as P.
Second, we iteratively eliminate nested temporal operators from rule bodies. To this end, consider a rule r whose body has an occurrence M of a metric atom that mentions only one temporal operator and which is in the scope of some other temporal operator. If M is of one of the forms ![]() ,
, ![]() ,
,
![]() $\boxminus_\varrho P(\mathbf{s})$
, or
$\boxminus_\varrho P(\mathbf{s})$
, or
![]() $\boxplus_\varrho P(\mathbf{s})$
, then we replace it with
$\boxplus_\varrho P(\mathbf{s})$
, then we replace it with
![]() $P'(\mathbf{s})$
and add a rule
$P'(\mathbf{s})$
and add a rule
![]() $P'(\mathbf{s}) \gets M$
, where P’ is a fresh predicate of the same arity as P. If M mentions
$P'(\mathbf{s}) \gets M$
, where P’ is a fresh predicate of the same arity as P. If M mentions
![]() $\mathcal{S}$
or
$\mathcal{S}$
or
![]() $\mathcal{U}$
, we need to proceed in a special way to ensure safety of the new rules. If M is of the form
$\mathcal{U}$
, we need to proceed in a special way to ensure safety of the new rules. If M is of the form
![]() $P_1(\mathbf{s}_1) \mathcal{S}_{\varrho} P_2(\mathbf{s}_2)$
, we remove r and proceed as follows (note that the conditions below are not exclusive):
$P_1(\mathbf{s}_1) \mathcal{S}_{\varrho} P_2(\mathbf{s}_2)$
, we remove r and proceed as follows (note that the conditions below are not exclusive):
-
if
 $0 \in \varrho$
, we add the rule obtained by replacing M in r with
$0 \in \varrho$
, we add the rule obtained by replacing M in r with
 $P_2(\mathbf{s}_2)$
,
$P_2(\mathbf{s}_2)$
, -
if
 $1 \in \varrho$
, we add the rule obtained by replacing M in r with
$1 \in \varrho$
, we add the rule obtained by replacing M in r with
 $\boxminus_1 P_2(\mathbf{s}_2)$
,
$\boxminus_1 P_2(\mathbf{s}_2)$
, -
we add the rule
 and the rule obtained by replacing M in r with
and the rule obtained by replacing M in r with
 $P'(\mathbf{s}_1, \mathbf{s}_2)$
, where P’ is a fresh predicate whose arity equals the sum of arities of
$P'(\mathbf{s}_1, \mathbf{s}_2)$
, where P’ is a fresh predicate whose arity equals the sum of arities of
 $P_1$
and
$P_1$
and
 $P_2$
.
$P_2$
.
If M is of the form
![]() $P_1(\mathbf{s}_1) \mathcal{U}_{\varrho} P_2(\mathbf{s}_2)$
, we proceed analogously to the case when M is of the form
$P_1(\mathbf{s}_1) \mathcal{U}_{\varrho} P_2(\mathbf{s}_2)$
, we proceed analogously to the case when M is of the form
![]() $P_1(\mathbf{s}_1) \mathcal{S}_{\varrho} P_2(\mathbf{s}_2)$
, but instead of
$P_1(\mathbf{s}_1) \mathcal{S}_{\varrho} P_2(\mathbf{s}_2)$
, but instead of
![]() $\boxminus$
and
$\boxminus$
and ![]() we use, respectively,
we use, respectively,
![]() $\boxplus$
and
$\boxplus$
and ![]() in the new rules. Moreover, if M mentions
in the new rules. Moreover, if M mentions
![]() $\top$
or
$\top$
or
![]() $\bot$
, we treat these symbols as nullary predicates and proceed as before.
$\bot$
, we treat these symbols as nullary predicates and proceed as before.
Next, weliminate diamond operators by replacing ![]() and
and ![]() with, respectively,
with, respectively,
![]() $\top \mathcal{S}_\varrho M$
and
$\top \mathcal{S}_\varrho M$
and
![]() $\top \mathcal{U}_\varrho M$
. Finally, we eliminate unbounded intervals
$\top \mathcal{U}_\varrho M$
. Finally, we eliminate unbounded intervals
![]() $\varrho$
different from
$\varrho$
different from
![]() $[0,\infty)$
as follows. If a rule r mentions
$[0,\infty)$
as follows. If a rule r mentions
![]() $\Box_{\varrho} P(\mathbf{s})$
, we replace this
$\Box_{\varrho} P(\mathbf{s})$
, we replace this
![]() $\Box_{\varrho} P(\mathbf{s})$
with
$\Box_{\varrho} P(\mathbf{s})$
with
![]() $\Box_{t} P(\mathbf{s})$
and add a rule
$\Box_{t} P(\mathbf{s})$
and add a rule
![]() ${P'(\mathbf{s}) \gets \Box_{[0,\infty) }P(\mathbf{s})}$
, where
${P'(\mathbf{s}) \gets \Box_{[0,\infty) }P(\mathbf{s})}$
, where
![]() $\Box$
is either
$\Box$
is either
![]() $\boxminus$
or
$\boxminus$
or
![]() $\boxplus$
, t is the least natural number in
$\boxplus$
, t is the least natural number in
![]() $\varrho$
(so
$\varrho$
(so
![]() $t \geq 1$
), and P’ is a fresh predicate of the same arity as P. In the case of operators
$t \geq 1$
), and P’ is a fresh predicate of the same arity as P. In the case of operators
![]() $\mathcal{S}$
and
$\mathcal{S}$
and
![]() $\mathcal{U}$
we need to pay special attention to ensure that the new rules are safe. Assume that a rule r mentions
$\mathcal{U}$
we need to pay special attention to ensure that the new rules are safe. Assume that a rule r mentions
![]() ${M = P_1(\mathbf{s}_1) \mathcal{S}_{\varrho} P_2(\mathbf{s}_2) }$
with an unbounded
${M = P_1(\mathbf{s}_1) \mathcal{S}_{\varrho} P_2(\mathbf{s}_2) }$
with an unbounded
![]() $\varrho \neq [0,\infty)$
. We remove r and proceed as follows, for t the least natural number belonging to
$\varrho \neq [0,\infty)$
. We remove r and proceed as follows, for t the least natural number belonging to
![]() $\varrho$
:
$\varrho$
:
-
if
 $1 \in \varrho$
, we add the rule obtained by replacing M in r with
$1 \in \varrho$
, we add the rule obtained by replacing M in r with
 $\boxminus_1 P_2(\mathbf{s}_2)$
,
$\boxminus_1 P_2(\mathbf{s}_2)$
, -
if
 $1 \not\in \varrho$
, we add the rule obtained by replacing M in r with
$1 \not\in \varrho$
, we add the rule obtained by replacing M in r with
 $ \boxminus_{ t} P_2(\mathbf{s}_2) \land \boxminus_{(0,t)} P_1(\mathbf{s}_1)$
$ \boxminus_{ t} P_2(\mathbf{s}_2) \land \boxminus_{(0,t)} P_1(\mathbf{s}_1)$
-
we add the rule
 , and the rule obtained by replacing M in r with
, and the rule obtained by replacing M in r with
 $\boxminus_{ t } P'(\mathbf{s}_1, \mathbf{s}_2) \land \boxminus_{(0,t]} P_1(\mathbf{s}_1)$
, where P’ is a fresh predicate whose arity equals the sum of arities of
$\boxminus_{ t } P'(\mathbf{s}_1, \mathbf{s}_2) \land \boxminus_{(0,t]} P_1(\mathbf{s}_1)$
, where P’ is a fresh predicate whose arity equals the sum of arities of
 $P_1$
and
$P_1$
and
 $P_2$
.
$P_2$
.
In the case of atoms mentioning
![]() $\mathcal{U}$
, as well as
$\mathcal{U}$
, as well as
![]() $\top$
or
$\top$
or
![]() $\bot$
, we proceed analogously.
$\bot$
, we proceed analogously.
In the remainder of this section, we fix a normalised program
![]() $\Pi$
and a dataset
$\Pi$
and a dataset
![]() $\mathcal{D}$
, and let
$\mathcal{D}$
, and let
![]() $\mathsf{ground}(\Pi,\mathcal{D})$
be the subset of
$\mathsf{ground}(\Pi,\mathcal{D})$
be the subset of
![]() $\mathsf{ground}(\Pi)$
mentioning only constants from
$\mathsf{ground}(\Pi)$
mentioning only constants from
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. Then,
$\mathcal{D}$
. Then,
![]() $\mathsf{at}(\Pi, \mathcal{D})$
is the set consisting of all relational atoms in
$\mathsf{at}(\Pi, \mathcal{D})$
is the set consisting of all relational atoms in
![]() $\mathcal{D}$
, all metric atoms in
$\mathcal{D}$
, all metric atoms in
![]() $\mathsf{ground}(\Pi,\mathcal{D})$
, and all metric atoms of the forms
$\mathsf{ground}(\Pi,\mathcal{D})$
, and all metric atoms of the forms
![]() $\boxminus_{ [ 0,\infty)} M$
and
$\boxminus_{ [ 0,\infty)} M$
and
![]() $\boxplus_{ [ 0,\infty)} M$
, with M a relational atom mentioned in
$\boxplus_{ [ 0,\infty)} M$
, with M a relational atom mentioned in
![]() $\mathsf{ground}(\Pi,\mathcal{D})$
.
$\mathsf{ground}(\Pi,\mathcal{D})$
.
We next define the notion of a window – a fragment of an HT-interpretation over a particular interval; such windows will serve as states of our automata.
Definition 5.2 A window is a tuple
![]() $(\varrho, H,T,b)$
, where
$(\varrho, H,T,b)$
, where
![]() $\varrho$
is a closed (and hence bounded) interval,
$\varrho$
is a closed (and hence bounded) interval,
![]() $b \in \{ 0,1\}$
, and H and T are sets of metric facts of the form
$b \in \{ 0,1\}$
, and H and T are sets of metric facts of the form
![]() $M @ t$
satisfying the following conditions:
$M @ t$
satisfying the following conditions:
-
 $M \in\mathsf{at}(\Pi,\mathcal{D})$
,
$M \in\mathsf{at}(\Pi,\mathcal{D})$
,
 $t \in\varrho$
, and
$t \in\varrho$
, and
 $H \subseteq T$
;
$H \subseteq T$
; -
there exist interpretations
 $\mathfrak{H}$
and
$\mathfrak{H}$
and
 $\mathfrak{T}$
such that, for each
$\mathfrak{T}$
such that, for each
 ${M \in \mathsf{at}(\Pi,\mathcal{D})}$
and
${M \in \mathsf{at}(\Pi,\mathcal{D})}$
and
 $t \in \varrho$
,
$t \in \varrho$
, -
 ${M @ t \in H}$
if and only if
${M @ t \in H}$
if and only if
 $\mathfrak{H} \models M@t $
, and
$\mathfrak{H} \models M@t $
, and -
 ${M @ t \in T}$
if and only if
${M @ t \in T}$
if and only if
 $\mathfrak{T} \models M@t $
.
$\mathfrak{T} \models M@t $
.
The window’s length is the length of
![]() $\varrho$
. Finally, we say that a window is initial if either
$\varrho$
. Finally, we say that a window is initial if either
![]() $H=T$
and
$H=T$
and
![]() $b=0$
, or
$b=0$
, or
![]() $H \neq T$
and
$H \neq T$
and
![]() $b=1$
.
$b=1$
.
Intuitively, a window
![]() $(\varrho, H,T,b)$
is a fragment of an HT-interpretation
$(\varrho, H,T,b)$
is a fragment of an HT-interpretation
![]() $(\mathfrak{H},\mathfrak{T})$
restricted to
$(\mathfrak{H},\mathfrak{T})$
restricted to
![]() $\varrho$
, where H and T describe facts holding within
$\varrho$
, where H and T describe facts holding within
![]() $\varrho$
in
$\varrho$
in
![]() $\mathfrak{H}$
and
$\mathfrak{H}$
and
![]() $\mathfrak{T}$
, respectively. Windows will serve as states of the automata recognising word representations of specific HT-interpretations, and in this process the flag b is used to distinguish between stable and non-stable models; in particular, our automata will ensure that flag b is set to 1 in each state
$\mathfrak{T}$
, respectively. Windows will serve as states of the automata recognising word representations of specific HT-interpretations, and in this process the flag b is used to distinguish between stable and non-stable models; in particular, our automata will ensure that flag b is set to 1 in each state
![]() $\mathcal{W}$
of a run such that
$\mathcal{W}$
of a run such that
![]() $H \neq T$
in either
$H \neq T$
in either
![]() $\mathcal{W}$
or in some previous state of this run.
$\mathcal{W}$
or in some previous state of this run.
By definition, a window can be extended to an HT-interpretation. This HT-interpretation can be an HT-model of
![]() $\Pi$
only if the window locally satisfies
$\Pi$
only if the window locally satisfies
![]() $\Pi$
, which we define next.
$\Pi$
, which we define next.
Definition 5.3 A window
![]() $(\varrho, H,T,b)$
locally satisfies
$(\varrho, H,T,b)$
locally satisfies
![]() $\Pi$
if, for each rule of Form (1) in
$\Pi$
if, for each rule of Form (1) in
![]() $\mathsf{ground}(\Pi)$
and each
$\mathsf{ground}(\Pi)$
and each
![]() $t \in \varrho$
, both of the following hold:
$t \in \varrho$
, both of the following hold:
-
 $M@ t \in H$
if
$M@ t \in H$
if
 $ M_i @ t \in H$
for each
$ M_i @ t \in H$
for each
 $i \in \{1, \ldots, k\}$
and
$i \in \{1, \ldots, k\}$
and
 $M_j @ t \notin T$
for each
$M_j @ t \notin T$
for each
 $j \in \{k+1, \ldots, m\}$
,
$j \in \{k+1, \ldots, m\}$
, -
 $M@ t \in T$
if
$M@ t \in T$
if
 $ M_i @ t \in T$
for each
$ M_i @ t \in T$
for each
 $i \in \{1, \ldots, k\}$
and
$i \in \{1, \ldots, k\}$
and
 $M_j @ t \notin T$
for each
$M_j @ t \notin T$
for each
 $j \in \{k+1, \ldots, m\}$
.
$j \in \{k+1, \ldots, m\}$
.
Next, given an initial window
![]() $\mathcal{W}_0$
, we define automata
$\mathcal{W}_0$
, we define automata
![]() $\mathcal{A}_{\mathcal{W}_0}^\leftarrow$
and
$\mathcal{A}_{\mathcal{W}_0}^\leftarrow$
and
![]() $\mathcal{A}_{\mathcal{W}_0}^\rightarrow$
, which will allow us to recognise HT-models of
$\mathcal{A}_{\mathcal{W}_0}^\rightarrow$
, which will allow us to recognise HT-models of
![]() $\Pi$
that extend
$\Pi$
that extend
![]() $\mathcal{W}_0$
. In particular, if
$\mathcal{W}_0$
. In particular, if
![]() $\mathcal{A}_{\mathcal{W}_0}^\leftarrow$
and
$\mathcal{A}_{\mathcal{W}_0}^\leftarrow$
and
![]() $\mathcal{A}_{\mathcal{W}_0}^\rightarrow$
accept words
$\mathcal{A}_{\mathcal{W}_0}^\rightarrow$
accept words
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() ${{{\overrightarrow{w}}}}$
respectively, then we will be able to construct an HT-model extending
${{{\overrightarrow{w}}}}$
respectively, then we will be able to construct an HT-model extending
![]() $\mathcal{W}_0$
, for which the part located to the left of
$\mathcal{W}_0$
, for which the part located to the left of
![]() $\mathcal{W}_0$
is described by
$\mathcal{W}_0$
is described by
![]() ${{{\overleftarrow{w}}}}$
, and the part to the right of
${{{\overleftarrow{w}}}}$
, and the part to the right of
![]() $\mathcal{W}_0$
by
$\mathcal{W}_0$
by
![]() ${{{\overrightarrow{w}}}}$
.
${{{\overrightarrow{w}}}}$
.
Definition 5.4 Let
![]() ${ \mathcal{W}_0=(\varrho_0,H_0,T_0,b_0 ) }$
be an initial window locally satisfying
${ \mathcal{W}_0=(\varrho_0,H_0,T_0,b_0 ) }$
be an initial window locally satisfying
![]() $\Pi$
. Then,
$\Pi$
. Then,
![]() $\mathcal{A}_{\mathcal{W}_0}^\leftarrow = (\mathcal{Q}, \Sigma, \delta, q_0,F)$
is the generalised nondeterministic Büchi automaton with the following components:
$\mathcal{A}_{\mathcal{W}_0}^\leftarrow = (\mathcal{Q}, \Sigma, \delta, q_0,F)$
is the generalised nondeterministic Büchi automaton with the following components:
-
1. the states
 $\mathcal{Q}$
consist of all windows of the the same length as
$\mathcal{Q}$
consist of all windows of the the same length as
 $\mathcal{W}_0$
locally satisfying
$\mathcal{W}_0$
locally satisfying
 $\Pi$
;
$\Pi$
; -
2. the alphabet
 $\Sigma$
is the set of all
$\Sigma$
is the set of all
 $\sigma \subseteq \mathsf{at}(\Pi, {\mathcal{D}})$
;
$\sigma \subseteq \mathsf{at}(\Pi, {\mathcal{D}})$
; -
3. the transition function
 $\delta : \mathcal{Q} \times \Sigma \to 2^\mathcal{Q}$
is such that
$\delta : \mathcal{Q} \times \Sigma \to 2^\mathcal{Q}$
is such that
 ${(\varrho',H',T',b') \in \delta \big( (\varrho,H,T,b), \sigma \big)}$
if
${(\varrho',H',T',b') \in \delta \big( (\varrho,H,T,b), \sigma \big)}$
if-
–
 ${\varrho'=[\varrho^- -1,\varrho^+ -1]}$
,
${\varrho'=[\varrho^- -1,\varrho^+ -1]}$
, -
–
 $M @ t \in H'$
if and only if
$M @ t \in H'$
if and only if
 $M @ t \in H$
, for every
$M @ t \in H$
, for every
 ${M \in \mathsf{at}(\Pi,\mathcal{D})}$
and
${M \in \mathsf{at}(\Pi,\mathcal{D})}$
and
 $t\in \varrho' \cap \varrho$
,
$t\in \varrho' \cap \varrho$
, -
–
 $T' = \{ M @ t' \in T \mid t' \in \varrho'\} \cup \{ M @ (\varrho^{-}{-}\,1) \mid M \in \sigma \}$
, and
$T' = \{ M @ t' \in T \mid t' \in \varrho'\} \cup \{ M @ (\varrho^{-}{-}\,1) \mid M \in \sigma \}$
, and -
–
 $b'=1$
whenever
$b'=1$
whenever
 $b=1$
or
$b=1$
or
 $H' \neq T'$
, and
$H' \neq T'$
, and
 $b'=0$
otherwise;
$b'=0$
otherwise;
-
-
4. the initial state
 $q_0$
is
$q_0$
is
 $\mathcal{W}_0$
;
$\mathcal{W}_0$
; -
5. the accepting condition F is the family of sets of states which contains, for every atom
 ${\boxminus_{[0,\infty)} M \in \mathsf{at}(\Pi,\mathcal{D})}$
, the sets and, for each
${\boxminus_{[0,\infty)} M \in \mathsf{at}(\Pi,\mathcal{D})}$
, the sets and, for each \begin{align*}\{(\varrho,H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho \text{ such that }\boxminus_{[0,\infty)} M @ t \in H \text{ or } M @ t \notin H \},\\\{(\varrho,H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho \text{ such that }\boxminus_{[0,\infty)} M @ t \in T \text{ or } M @ t \notin T \},\end{align*}
\begin{align*}\{(\varrho,H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho \text{ such that }\boxminus_{[0,\infty)} M @ t \in H \text{ or } M @ t \notin H \},\\\{(\varrho,H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho \text{ such that }\boxminus_{[0,\infty)} M @ t \in T \text{ or } M @ t \notin T \},\end{align*}
 $M_1 \mathcal{S}_{[0,\infty)} M_2 \in \mathsf{at}(\Pi,\mathcal{D})$
, the sets
$M_1 \mathcal{S}_{[0,\infty)} M_2 \in \mathsf{at}(\Pi,\mathcal{D})$
, the sets  \begin{align*}\{ (\varrho,H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho \text{ such that } M_1 \mathcal{S}_{[0,\infty)} M_2 @ t \notin H \text{ or } M_2 @ t \in H \},\\\{ (\varrho,H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho \text{ such that } M_1 \mathcal{S}_{[0,\infty)} M_2 @ t \notin T \text{ or } M_2 @ t \in T \}.\end{align*}
\begin{align*}\{ (\varrho,H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho \text{ such that } M_1 \mathcal{S}_{[0,\infty)} M_2 @ t \notin H \text{ or } M_2 @ t \in H \},\\\{ (\varrho,H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho \text{ such that } M_1 \mathcal{S}_{[0,\infty)} M_2 @ t \notin T \text{ or } M_2 @ t \in T \}.\end{align*}
The automaton
![]() $\mathcal{A}_{\mathcal{W}_0}^\to$
is defined analogously, except that we let
$\mathcal{A}_{\mathcal{W}_0}^\to$
is defined analogously, except that we let
![]() ${\varrho'= [\varrho^- +1, \varrho^+ +1] }$
, in the definition of T’ we replace
${\varrho'= [\varrho^- +1, \varrho^+ +1] }$
, in the definition of T’ we replace
![]() $\varrho^-{-}1$
with
$\varrho^-{-}1$
with
![]() $\varrho^+ {+} 1$
, and in the definition of F we use
$\varrho^+ {+} 1$
, and in the definition of F we use
![]() $\boxplus$
and
$\boxplus$
and
![]() $\mathcal{U}$
instead of
$\mathcal{U}$
instead of
![]() $\boxminus$
and
$\boxminus$
and
![]() $\mathcal{S}$
, respectively.
$\mathcal{S}$
, respectively.
Accepting runs of these automata will correspond to HT-interpretations. Indeed, as we will show next, each HT-interpretation can be decomposed into an infinite sequence of windows
![]() $ \dots , \mathcal{W}_{-1}, \mathcal{W}_0, \mathcal{W}_1,\dots$
such that
$ \dots , \mathcal{W}_{-1}, \mathcal{W}_0, \mathcal{W}_1,\dots$
such that
![]() $\mathcal{W}_{0},\mathcal{W}_{-1}, \dots$
and
$\mathcal{W}_{0},\mathcal{W}_{-1}, \dots$
and
![]() $\mathcal{W}_0, \mathcal{W}_1,\dots$
are accepting runs of
$\mathcal{W}_0, \mathcal{W}_1,\dots$
are accepting runs of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
and
$\mathcal{A}_{\mathcal{W}_0}^\gets$
and
![]() $\mathcal{A}_{\mathcal{W}_0}^\to$
, respectively. We define the decomposition of an HT-interpretation as follows.
$\mathcal{A}_{\mathcal{W}_0}^\to$
, respectively. We define the decomposition of an HT-interpretation as follows.
Definition 5.5 We define the
![]() $\varrho$
-decomposition of an HT-interpretation
$\varrho$
-decomposition of an HT-interpretation
![]() $(\mathfrak{H}, \mathfrak{T})$
, for a bounded interval
$(\mathfrak{H}, \mathfrak{T})$
, for a bounded interval
![]() $\varrho$
, as the sequence of tuples
$\varrho$
, as the sequence of tuples
![]() ${\mathcal{W}_i= (\varrho_i, H_i, T_i, b_i)}$
, for
${\mathcal{W}_i= (\varrho_i, H_i, T_i, b_i)}$
, for
![]() $i\in\mathbb{Z}$
, such that the following hold:
$i\in\mathbb{Z}$
, such that the following hold:
-
 ${\varrho_i = [\varrho^- +i, \varrho^+ +i]}$
,
${\varrho_i = [\varrho^- +i, \varrho^+ +i]}$
, -
 $H_i$
is the set of all facts
$H_i$
is the set of all facts
 $M @ t$
such that
$M @ t$
such that
 $M \in \mathsf{at}(\Pi,\mathcal{D})$
,
$M \in \mathsf{at}(\Pi,\mathcal{D})$
,
 $t \in \varrho_i$
, and
$t \in \varrho_i$
, and
 ${\mathfrak{H} \models M @ t}$
,
${\mathfrak{H} \models M @ t}$
, -
 $T_i$
is the set of all facts
$T_i$
is the set of all facts
 $M @ t$
such that
$M @ t$
such that
 $M \in \mathsf{at}(\Pi,\mathcal{D})$
,
$M \in \mathsf{at}(\Pi,\mathcal{D})$
,
 $t \in \varrho_i$
, and
$t \in \varrho_i$
, and
 ${\mathfrak{T} \models M @ t}$
,
${\mathfrak{T} \models M @ t}$
, -
 $b_i=1$
if there exists
$b_i=1$
if there exists
 $j \in \{0, \dots, i \} $
such that
$j \in \{0, \dots, i \} $
such that
 $H_j \neq T_j$
; otherwise,
$H_j \neq T_j$
; otherwise,
 $b_i=0$
.
$b_i=0$
.
Lemma 5.6 Let
![]() $\varrho$
be a bounded interval, let a sequence of tuples
$\varrho$
be a bounded interval, let a sequence of tuples
![]() ${\mathcal{W}_i= (\varrho_i, H_i, T_i, b_i)}$
, with
${\mathcal{W}_i= (\varrho_i, H_i, T_i, b_i)}$
, with
![]() $i \in \mathbb{Z}$
, be a
$i \in \mathbb{Z}$
, be a
![]() $\varrho$
-decomposition of an HT-model
$\varrho$
-decomposition of an HT-model
![]() $(\mathfrak{H}, \mathfrak{T})$
of
$(\mathfrak{H}, \mathfrak{T})$
of
![]() $\Pi$
, and let
$\Pi$
, and let
![]() ${{{{\overleftarrow{w}}}}= \sigma_{-1} \sigma_{-2} \cdots }$
and
${{{{\overleftarrow{w}}}}= \sigma_{-1} \sigma_{-2} \cdots }$
and
![]() ${{{{\overrightarrow{w}}}}= \sigma_{1} \sigma_{2} \cdots}$
be the words such that
${{{{\overrightarrow{w}}}}= \sigma_{1} \sigma_{2} \cdots}$
be the words such that
![]() $\sigma_k = T_k \setminus T_{k+1}$
for
$\sigma_k = T_k \setminus T_{k+1}$
for
![]() $k<0$
and
$k<0$
and
![]() $\sigma_k=T_k \setminus T_{k-1} $
for
$\sigma_k=T_k \setminus T_{k-1} $
for
![]() ${k>0}$
. Then the following hold:
${k>0}$
. Then the following hold:
-
1. each
 $\mathcal{W}_i$
is a window locally satisfying
$\mathcal{W}_i$
is a window locally satisfying
 $\Pi$
,
$\Pi$
, -
2.
 $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
 $\mathcal{A}_{\mathcal{W}_0}^\gets$
on
$\mathcal{A}_{\mathcal{W}_0}^\gets$
on
 ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and -
3.
 $\mathcal{W}_0, \mathcal{W}_{1}, \dots$
is an accepting run of
$\mathcal{W}_0, \mathcal{W}_{1}, \dots$
is an accepting run of
 $\mathcal{A}_{\mathcal{W}_0}^\to$
on
$\mathcal{A}_{\mathcal{W}_0}^\to$
on
 ${{{\overrightarrow{w}}}}$
.
${{{\overrightarrow{w}}}}$
.
Proof. To show that Statement 1 holds, we start by observing that each
![]() $\mathcal{W}_i$
satisfies all the conditions from Definition 5.2 of a window. Indeed, by Definition 5.5,
$\mathcal{W}_i$
satisfies all the conditions from Definition 5.2 of a window. Indeed, by Definition 5.5,
![]() $H_i$
and
$H_i$
and
![]() $T_i$
are sets of metric facts
$T_i$
are sets of metric facts
![]() $M @ t$
with
$M @ t$
with
![]() $M \in\mathsf{at}(\Pi,\mathcal{D})$
and
$M \in\mathsf{at}(\Pi,\mathcal{D})$
and
![]() $t \in\varrho_i$
such that
$t \in\varrho_i$
such that
![]() $H_i \subseteq T_i$
, whereas
$H_i \subseteq T_i$
, whereas
![]() $b_i \in \{0,1 \}$
; moreover,
$b_i \in \{0,1 \}$
; moreover,
![]() $\mathfrak{H}$
and
$\mathfrak{H}$
and
![]() $\mathfrak{T}$
witness existence of the interpretations required in Definition 5.5. Furthermore, since
$\mathfrak{T}$
witness existence of the interpretations required in Definition 5.5. Furthermore, since
![]() $(\mathfrak{H}, \mathfrak{T})$
is an HT-model of
$(\mathfrak{H}, \mathfrak{T})$
is an HT-model of
![]() $\Pi$
, each
$\Pi$
, each
![]() $\mathcal{W}_i$
locally satisfies
$\mathcal{W}_i$
locally satisfies
![]() $\Pi$
.
$\Pi$
.
To prove that Statement 2, we observe that
![]() $\mathcal{W}_0$
is an initial window by construction, so the automaton
$\mathcal{W}_0$
is an initial window by construction, so the automaton
![]() $\mathcal{A}_{\mathcal{W}_0}^\leftarrow = (\mathcal{Q}, \Sigma, \delta, q_0,F)$
is well-defined. By the definition of the transition function
$\mathcal{A}_{\mathcal{W}_0}^\leftarrow = (\mathcal{Q}, \Sigma, \delta, q_0,F)$
is well-defined. By the definition of the transition function
![]() $\delta$
of
$\delta$
of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
(see Definition 5.4) as well as by the construction of
$\mathcal{A}_{\mathcal{W}_0}^\gets$
(see Definition 5.4) as well as by the construction of
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
and
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
and
![]() ${{{\overleftarrow{w}}}} = \sigma_{-1} \sigma_{-2} \dots$
, we get that
${{{\overleftarrow{w}}}} = \sigma_{-1} \sigma_{-2} \dots$
, we get that
![]() ${\mathcal{W}_{i-1} \in \delta(\mathcal{W}_i, \sigma_{i-1})}$
, for each integer
${\mathcal{W}_{i-1} \in \delta(\mathcal{W}_i, \sigma_{i-1})}$
, for each integer
![]() $i \leq 0$
. Thus,
$i \leq 0$
. Thus,
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is a run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is a run of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
on
$\mathcal{A}_{\mathcal{W}_0}^\gets$
on
![]() ${{{\overleftarrow{w}}}}$
. It remains to show that this run is accepting, that is, for every set S in the accepting condition F, there are infinitely many integers
${{{\overleftarrow{w}}}}$
. It remains to show that this run is accepting, that is, for every set S in the accepting condition F, there are infinitely many integers
![]() $i < 0$
such that
$i < 0$
such that
![]() $\mathcal{W}_i \in S$
. Towards a contradiction suppose that there exists
$\mathcal{W}_i \in S$
. Towards a contradiction suppose that there exists
![]() $S \in F$
which does not satisfy this property. Thus, there exists
$S \in F$
which does not satisfy this property. Thus, there exists
![]() $i \leq 0$
such that
$i \leq 0$
such that
![]() $\mathcal{W}_j \notin S$
, for all
$\mathcal{W}_j \notin S$
, for all
![]() $j \leq i$
. Assume first that S is of one of the following forms
$j \leq i$
. Assume first that S is of one of the following forms
 \begin{align*}\{(\varrho',H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho' \text{ such that }\boxminus_{[0,\infty)} M @ t \in H \text{ or } M @ t \notin H \}, \text{ or}\\\{(\varrho',H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho' \text{ such that }\boxminus_{[0,\infty)} M @ t \in T \text{ or } M @ t \notin T \},\end{align*}
\begin{align*}\{(\varrho',H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho' \text{ such that }\boxminus_{[0,\infty)} M @ t \in H \text{ or } M @ t \notin H \}, \text{ or}\\\{(\varrho',H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho' \text{ such that }\boxminus_{[0,\infty)} M @ t \in T \text{ or } M @ t \notin T \},\end{align*}
for some
![]() ${\boxminus_{[0,\infty)} M \in \mathsf{at}(\Pi,\mathcal{D})}$
. As a result,
${\boxminus_{[0,\infty)} M \in \mathsf{at}(\Pi,\mathcal{D})}$
. As a result,
![]() $\mathfrak{I} \not\models \boxminus_{[0,\infty)} M @ t $
and
$\mathfrak{I} \not\models \boxminus_{[0,\infty)} M @ t $
and
![]() $\mathfrak{I} \models M @ t $
, for each
$\mathfrak{I} \models M @ t $
, for each
![]() $t \leq \varrho_i^-$
, where the interpretation
$t \leq \varrho_i^-$
, where the interpretation
![]() $\mathfrak{I}$
is either
$\mathfrak{I}$
is either
![]() $\mathfrak{H}$
or
$\mathfrak{H}$
or
![]() $\mathfrak{T}$
, depending whether S is of the first or the second form presented above. This, however, contradicts the semantics of
$\mathfrak{T}$
, depending whether S is of the first or the second form presented above. This, however, contradicts the semantics of
![]() $\boxminus_{[0,\infty)}$
. It remains to consider the case where S is of one of the following forms
$\boxminus_{[0,\infty)}$
. It remains to consider the case where S is of one of the following forms
 \begin{align*}\{ (\varrho',H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho' \text{ such that } M_1 \mathcal{S}_{[0,\infty)} M_2 @ t \notin H \text{ or } M_2 @ t \in H \}, \text{ or}\\\{ (\varrho',H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho' \text{ such that } M_1 \mathcal{S}_{[0,\infty)} M_2 @ t \notin T \text{ or } M_2 @ t \in T \},\end{align*}
\begin{align*}\{ (\varrho',H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho' \text{ such that } M_1 \mathcal{S}_{[0,\infty)} M_2 @ t \notin H \text{ or } M_2 @ t \in H \}, \text{ or}\\\{ (\varrho',H, T,b) \in \mathcal{Q}& \mid \text{there exists } t \in \varrho' \text{ such that } M_1 \mathcal{S}_{[0,\infty)} M_2 @ t \notin T \text{ or } M_2 @ t \in T \},\end{align*}
for some
![]() $M_1 \mathcal{S}_{[0,\infty)} M_2 \in \mathsf{at}(\Pi,\mathcal{D})$
. Then,
$M_1 \mathcal{S}_{[0,\infty)} M_2 \in \mathsf{at}(\Pi,\mathcal{D})$
. Then,
![]() $\mathfrak{I} \models M_1 \mathcal{S}_{[0,\infty)} M_2 @ t $
and
$\mathfrak{I} \models M_1 \mathcal{S}_{[0,\infty)} M_2 @ t $
and
![]() ${\mathfrak{I} \not\models M_2 @ t }$
, for each
${\mathfrak{I} \not\models M_2 @ t }$
, for each
![]() $t \leq \varrho_i^-$
, where
$t \leq \varrho_i^-$
, where
![]() $\mathfrak{I}$
is either
$\mathfrak{I}$
is either
![]() $\mathfrak{H}$
or
$\mathfrak{H}$
or
![]() $\mathfrak{T}$
, depending whether S is of the first or the second form presented above. This directly contradicts the semantics of
$\mathfrak{T}$
, depending whether S is of the first or the second form presented above. This directly contradicts the semantics of
![]() $\mathcal{S}_{[0,\infty)}$
. Consequently,
$\mathcal{S}_{[0,\infty)}$
. Consequently,
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
needs to be an accepting run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
needs to be an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
on
$\mathcal{A}_{\mathcal{W}_0}^\gets$
on
![]() ${{{\overleftarrow{w}}}}$
.
${{{\overleftarrow{w}}}}$
.
The proof of Statement 3 is analogous to the proof of Statement 2, due to the symmetry between the automata
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
and
$\mathcal{A}_{\mathcal{W}_0}^\gets$
and
![]() $\mathcal{A}_{\mathcal{W}_0}^\to$
.
$\mathcal{A}_{\mathcal{W}_0}^\to$
.
To check existence of a stable model, however, we require automata that recognise HT-models
![]() $(\mathfrak{H},\mathfrak{T})$
with
$(\mathfrak{H},\mathfrak{T})$
with
![]() $\mathfrak{H}=\mathfrak{T}$
, and automata that recognise HT-models
$\mathfrak{H}=\mathfrak{T}$
, and automata that recognise HT-models
![]() $(\mathfrak{H},\mathfrak{T})$
with
$(\mathfrak{H},\mathfrak{T})$
with
![]() $\mathfrak{H} \subsetneq \mathfrak{T}$
. The intersection of the former with the complement of the latter allows us to recognise stable models – that is, essentially, HT-models
$\mathfrak{H} \subsetneq \mathfrak{T}$
. The intersection of the former with the complement of the latter allows us to recognise stable models – that is, essentially, HT-models
![]() $(\mathfrak{T},\mathfrak{T})$
for which there are no models
$(\mathfrak{T},\mathfrak{T})$
for which there are no models
![]() $(\mathfrak{H},\mathfrak{T})$
with
$(\mathfrak{H},\mathfrak{T})$
with
![]() $\mathfrak{H} \subsetneq \mathfrak{T}$
. To this end, we define two more types of automata as follows:
$\mathfrak{H} \subsetneq \mathfrak{T}$
. To this end, we define two more types of automata as follows:
Definition 5.7 Let
![]() $\mathcal{W}_0=(\varrho_0,H_0,T_0,b_0)$
be an initial window locally satisfying
$\mathcal{W}_0=(\varrho_0,H_0,T_0,b_0)$
be an initial window locally satisfying
![]() $\Pi$
. We define non-deterministic generalised Büchi automata
$\Pi$
. We define non-deterministic generalised Büchi automata
![]() $\mathcal{B}_{\mathcal{W}_0}^\leftarrow$
,
$\mathcal{B}_{\mathcal{W}_0}^\leftarrow$
,
![]() $\mathcal{B}_{\mathcal{W}_0}^\rightarrow$
and
$\mathcal{B}_{\mathcal{W}_0}^\rightarrow$
and
![]() $\mathcal{C}_{\mathcal{W}_0}^\leftarrow$
,
$\mathcal{C}_{\mathcal{W}_0}^\leftarrow$
,
![]() $\mathcal{C}_{\mathcal{W}_0}^\rightarrow$
as follows:
$\mathcal{C}_{\mathcal{W}_0}^\rightarrow$
as follows:
-
if
 $H_0 = T_0$
and
$H_0 = T_0$
and
 $b_0 = 0$
, the automata
$b_0 = 0$
, the automata
 $\mathcal{B}_{\mathcal{W}_0}^\leftarrow$
and
$\mathcal{B}_{\mathcal{W}_0}^\leftarrow$
and
 $\mathcal{B}_{\mathcal{W}_0}^\rightarrow$
are defined as
$\mathcal{B}_{\mathcal{W}_0}^\rightarrow$
are defined as
 $\mathcal{A}_{\mathcal{W}_0}^\leftarrow$
and
$\mathcal{A}_{\mathcal{W}_0}^\leftarrow$
and
 $\mathcal{A}_{\mathcal{W}_0}^\rightarrow$
, respectively, except that for a window
$\mathcal{A}_{\mathcal{W}_0}^\rightarrow$
, respectively, except that for a window
 $(\varrho,H,T,b)$
to be a state we additionally require that
$(\varrho,H,T,b)$
to be a state we additionally require that
 $H=T$
,
$H=T$
, -
the automata
 $\mathcal{C}_{\mathcal{W}_0}^\leftarrow$
and
$\mathcal{C}_{\mathcal{W}_0}^\leftarrow$
and
 $\mathcal{C}_{\mathcal{W}_0}^\rightarrow$
are defined as
$\mathcal{C}_{\mathcal{W}_0}^\rightarrow$
are defined as
 $\mathcal{A}_{\mathcal{W}_0}^\leftarrow$
and
$\mathcal{A}_{\mathcal{W}_0}^\leftarrow$
and
 $\mathcal{A}_{\mathcal{W}_0}^\rightarrow$
, respectively, except that we add to the accepting condition the set
$\mathcal{A}_{\mathcal{W}_0}^\rightarrow$
, respectively, except that we add to the accepting condition the set
 $\{ (\varrho,H, T,b) \in \mathcal{Q} \mid b=1\}$
.
$\{ (\varrho,H, T,b) \in \mathcal{Q} \mid b=1\}$
.
Intuitively, if
![]() $\mathcal{W}_0$
satisfies
$\mathcal{W}_0$
satisfies
![]() $\mathcal{D}$
, then the automata
$\mathcal{D}$
, then the automata
![]() $\mathcal{B}_{\mathcal{W}_0}^\gets$
and
$\mathcal{B}_{\mathcal{W}_0}^\gets$
and
![]() $\mathcal{B}_{\mathcal{W}_0}^\to$
recognise interpretations
$\mathcal{B}_{\mathcal{W}_0}^\to$
recognise interpretations
![]() $\mathfrak{T}$
such that
$\mathfrak{T}$
such that
![]() $(\mathfrak{T},\mathfrak{T})$
is an HT-model of
$(\mathfrak{T},\mathfrak{T})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. Furthermore, interpretations
$\mathcal{D}$
. Furthermore, interpretations
![]() $\mathfrak{T}$
accepted by
$\mathfrak{T}$
accepted by
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
and
$\mathcal{A}_{\mathcal{W}_0}^\gets$
and
![]() $\mathcal{C}_{\mathcal{W}_0}^\to$
, or by
$\mathcal{C}_{\mathcal{W}_0}^\to$
, or by
![]() $\mathcal{C}_{\mathcal{W}_0}^\gets$
and
$\mathcal{C}_{\mathcal{W}_0}^\gets$
and
![]() $\mathcal{A}_{\mathcal{W}_0}^\to$
are such that
$\mathcal{A}_{\mathcal{W}_0}^\to$
are such that
![]() $(\mathfrak{H},\mathfrak{T})$
is an HT-model of
$(\mathfrak{H},\mathfrak{T})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, for some
$\mathcal{D}$
, for some
![]() $\mathfrak{H} \subsetneq \mathfrak{T}$
. Hence, as we show next, we can use these automata to recognise stable models. This, however, requires the additional assumption that the windows in the automata are long enough to allow for capturing the semantics of metric operators occurring in a program. To this end, we will use windows of the same length as the interval
$\mathfrak{H} \subsetneq \mathfrak{T}$
. Hence, as we show next, we can use these automata to recognise stable models. This, however, requires the additional assumption that the windows in the automata are long enough to allow for capturing the semantics of metric operators occurring in a program. To this end, we will use windows of the same length as the interval
![]() ${\varrho_{(\Pi,\mathcal{D})} = [t^{\min}_{\mathcal{D}},t^{\max}_{\mathcal{D}}+t_{\Pi}]}$
. If the length of an initial window
${\varrho_{(\Pi,\mathcal{D})} = [t^{\min}_{\mathcal{D}},t^{\max}_{\mathcal{D}}+t_{\Pi}]}$
. If the length of an initial window
![]() $\mathcal{W}_0$
is as required, then we can reduce checking existence of a stable model to checking particular properties of our automata, as stated next.
$\mathcal{W}_0$
is as required, then we can reduce checking existence of a stable model to checking particular properties of our automata, as stated next.
Theorem 5.8 Program
![]() $\Pi$
and dataset
$\Pi$
and dataset
![]() $\mathcal{D}$
have a stable model if and only if there exists an initial window
$\mathcal{D}$
have a stable model if and only if there exists an initial window
![]() ${\mathcal{W}_0=(\varrho_0,T_0, T_0, 0)}$
locally satisfying
${\mathcal{W}_0=(\varrho_0,T_0, T_0, 0)}$
locally satisfying
![]() $\Pi$
with
$\Pi$
with
![]() ${\varrho_0 = \varrho_{(\Pi,\mathcal{D})}}$
and
${\varrho_0 = \varrho_{(\Pi,\mathcal{D})}}$
and
![]() $T_0 \models \mathcal{D}$
, and there exist words
$T_0 \models \mathcal{D}$
, and there exist words
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() ${{{\overrightarrow{w}}}}$
over
${{{\overrightarrow{w}}}}$
over
![]() $2^{\mathsf{at}(\Pi, {\mathcal{D}})}$
such that both of the following hold:
$2^{\mathsf{at}(\Pi, {\mathcal{D}})}$
such that both of the following hold:
-
1.
 ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
 ${{{\overrightarrow{w}}}}$
are accepted by
${{{\overrightarrow{w}}}}$
are accepted by
 $\mathcal{B}_{\mathcal{W}_0}^\gets$
and
$\mathcal{B}_{\mathcal{W}_0}^\gets$
and
 $\mathcal{B}_{\mathcal{W}_0}^\to$
, respectively,
$\mathcal{B}_{\mathcal{W}_0}^\to$
, respectively, -
2. there is no initial window
 ${\mathcal{W}'_0=(\varrho_0,H_0, T_0, b_0)}$
locally satisfying
${\mathcal{W}'_0=(\varrho_0,H_0, T_0, b_0)}$
locally satisfying
 $\Pi$
such that
$\Pi$
such that
 $H_0 \models \mathcal{D}$
, and
$H_0 \models \mathcal{D}$
, and
 ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
 ${{{\overrightarrow{w}}}}$
are accepted either by
${{{\overrightarrow{w}}}}$
are accepted either by
 $\mathcal{C}_{\mathcal{W}'_0}^\gets$
and
$\mathcal{C}_{\mathcal{W}'_0}^\gets$
and
 $\mathcal{A}_{\mathcal{W}'_0}^\to$
, respectively, or by
$\mathcal{A}_{\mathcal{W}'_0}^\to$
, respectively, or by
 $\mathcal{A}_{\mathcal{W}'_0}^\gets$
and
$\mathcal{A}_{\mathcal{W}'_0}^\gets$
and
 $\mathcal{C}_{\mathcal{W}'_0}^\to$
, respectively.
$\mathcal{C}_{\mathcal{W}'_0}^\to$
, respectively.
Proof. Assume that
![]() $\mathfrak{T}$
is a stable model of
$\mathfrak{T}$
is a stable model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. We will show how to construct the required
$\mathcal{D}$
. We will show how to construct the required
![]() $\mathcal{W}_0$
,
$\mathcal{W}_0$
,
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() ${{{\overrightarrow{w}}}}$
. To this end, let
${{{\overrightarrow{w}}}}$
. To this end, let
![]() $\dots, \mathcal{W}_{-1}, \mathcal{W}_0, \mathcal{W}_1, \dots$
be the
$\dots, \mathcal{W}_{-1}, \mathcal{W}_0, \mathcal{W}_1, \dots$
be the
![]() $\varrho_{(\Pi,\mathcal{D})}$
-decomposition of
$\varrho_{(\Pi,\mathcal{D})}$
-decomposition of
![]() $(\mathfrak{T}, \mathfrak{T})$
with
$(\mathfrak{T}, \mathfrak{T})$
with
![]() ${\mathcal{W}_i= (\varrho_i, H_i, T_i, b_i)}$
, for each
${\mathcal{W}_i= (\varrho_i, H_i, T_i, b_i)}$
, for each
![]() $i\in\mathbb{Z}$
. By Definition Definition 5.5, we obtain that
$i\in\mathbb{Z}$
. By Definition Definition 5.5, we obtain that
![]() $H_i=T_i$
and
$H_i=T_i$
and
![]() $b_i=0$
, for all
$b_i=0$
, for all
![]() $i \in \mathbb{Z}$
; furthermore,
$i \in \mathbb{Z}$
; furthermore,
![]() $\mathcal{W}_0$
locally satisfies
$\mathcal{W}_0$
locally satisfies
![]() $\Pi$
by Lemma 5.6. Finally, we have
$\Pi$
by Lemma 5.6. Finally, we have
![]() ${\varrho_0 = \varrho_{(\Pi,\mathcal{D})}}$
, which ensures
${\varrho_0 = \varrho_{(\Pi,\mathcal{D})}}$
, which ensures
![]() $T_0 \models \mathcal{D}$
, so
$T_0 \models \mathcal{D}$
, so
![]() $\mathcal{W}_0$
satisfies the initial requirements from the theorem. Next, let
$\mathcal{W}_0$
satisfies the initial requirements from the theorem. Next, let
![]() ${{{{\overleftarrow{w}}}}= \sigma_{-1} \sigma_{-2} \cdots}$
and
${{{{\overleftarrow{w}}}}= \sigma_{-1} \sigma_{-2} \cdots}$
and
![]() ${{{\overrightarrow{w}}}}= \sigma_{1} \sigma_{2} \cdots$
be the words such that
${{{\overrightarrow{w}}}}= \sigma_{1} \sigma_{2} \cdots$
be the words such that
![]() $\sigma_k=T_k \setminus T_{k+1}$
if
$\sigma_k=T_k \setminus T_{k+1}$
if
![]() $k<0$
, and
$k<0$
, and
![]() $\sigma_k=T_k \setminus T_{k-1} $
if
$\sigma_k=T_k \setminus T_{k-1} $
if
![]() ${k>0}$
. It remains to show that
${k>0}$
. It remains to show that
![]() $\mathcal{W}_0$
,
$\mathcal{W}_0$
,
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() ${{{\overrightarrow{w}}}}$
satisfy Conditions 1 and 2 from the theorem.
${{{\overrightarrow{w}}}}$
satisfy Conditions 1 and 2 from the theorem.
To show that Condition 1 holds, we observe that, by Lemma 5.6,
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
on
$\mathcal{A}_{\mathcal{W}_0}^\gets$
on
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() $\mathcal{W}_0, \mathcal{W}_{1}, \dots$
is an accepting run of
$\mathcal{W}_0, \mathcal{W}_{1}, \dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_0}^\to$
on
$\mathcal{A}_{\mathcal{W}_0}^\to$
on
![]() ${{{\overrightarrow{w}}}}$
. Moreover, since
${{{\overrightarrow{w}}}}$
. Moreover, since
![]() $H_i=T_i$
and
$H_i=T_i$
and
![]() $b_i = 0$
for all
$b_i = 0$
for all
![]() $i \in \mathbb{Z}$
, we obtain that
$i \in \mathbb{Z}$
, we obtain that
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
![]() $\mathcal{B}_{\mathcal{W}_0}^\gets$
on
$\mathcal{B}_{\mathcal{W}_0}^\gets$
on
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() $\mathcal{W}_0, \mathcal{W}_{1}, \dots$
is an accepting run of
$\mathcal{W}_0, \mathcal{W}_{1}, \dots$
is an accepting run of
![]() $\mathcal{B}_{\mathcal{W}_0}^\to$
on
$\mathcal{B}_{\mathcal{W}_0}^\to$
on
![]() ${{{\overrightarrow{w}}}}$
.
${{{\overrightarrow{w}}}}$
.
Next, let us suppose towards a contradiction that there exists
![]() ${\mathcal{W}_0' =(\varrho_0',H_0', T_0', b_0') }$
witnessing a violation of Condition 2. Hence,
${\mathcal{W}_0' =(\varrho_0',H_0', T_0', b_0') }$
witnessing a violation of Condition 2. Hence,
![]() $\mathcal{W}_0'$
is an initial window locally satisfying
$\mathcal{W}_0'$
is an initial window locally satisfying
![]() $\Pi$
such that
$\Pi$
such that
![]() $\varrho_0'=\varrho_0$
,
$\varrho_0'=\varrho_0$
,
![]() $T_0' = T_0$
, and
$T_0' = T_0$
, and
![]() $H_0' \models \mathcal{D}$
. Moreover, we assume that
$H_0' \models \mathcal{D}$
. Moreover, we assume that
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() ${{{\overrightarrow{w}}}}$
are accepted by
${{{\overrightarrow{w}}}}$
are accepted by
![]() $\mathcal{C}_{\mathcal{W}'_0}^\gets$
and
$\mathcal{C}_{\mathcal{W}'_0}^\gets$
and
![]() $\mathcal{A}_{\mathcal{W}'_0}^\to$
, respectively. Hence,
$\mathcal{A}_{\mathcal{W}'_0}^\to$
, respectively. Hence,
![]() $\mathcal{C}_{\mathcal{W}'_0}^\gets$
has an accepting run
$\mathcal{C}_{\mathcal{W}'_0}^\gets$
has an accepting run
![]() $\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
on
$\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
on
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() $\mathcal{A}_{\mathcal{W}'_0}^\to$
has an accepting run
$\mathcal{A}_{\mathcal{W}'_0}^\to$
has an accepting run
![]() $\mathcal{W}'_0, \mathcal{W}'_{1}, \dots$
on
$\mathcal{W}'_0, \mathcal{W}'_{1}, \dots$
on
![]() ${{{\overrightarrow{w}}}}$
, where we let
${{{\overrightarrow{w}}}}$
, where we let
![]() ${\mathcal{W}'_i= (\varrho_i', H_i', T_i', b_i')}$
, for all
${\mathcal{W}'_i= (\varrho_i', H_i', T_i', b_i')}$
, for all
![]() $i \in \mathbb{Z}$
. Clearly,
$i \in \mathbb{Z}$
. Clearly,
![]() $\varrho_i' = \varrho_i$
, for all
$\varrho_i' = \varrho_i$
, for all
![]() $i \in \mathbb{Z}$
. Moreover, by the definition of the transition functions of the automata and the construction of
$i \in \mathbb{Z}$
. Moreover, by the definition of the transition functions of the automata and the construction of
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() ${{{\overrightarrow{w}}}}$
, we obtain that
${{{\overrightarrow{w}}}}$
, we obtain that
![]() $T_i' = T_i$
, for all
$T_i' = T_i$
, for all
![]() $i \in \mathbb{Z}$
. Therefore,
$i \in \mathbb{Z}$
. Therefore,
![]() $\mathfrak{T}$
is the least model of all relational facts in
$\mathfrak{T}$
is the least model of all relational facts in
![]() $\bigcup_{i\in \mathbb{Z}}T'_i$
. We let
$\bigcup_{i\in \mathbb{Z}}T'_i$
. We let
![]() $\mathfrak{H}$
be the least model of all relational facts in
$\mathfrak{H}$
be the least model of all relational facts in
![]() $\bigcup_{i\in \mathbb{Z}}H_i$
; we will show that
$\bigcup_{i\in \mathbb{Z}}H_i$
; we will show that
![]() $(\mathfrak{H}, \mathfrak{T})$
is an HT-model of
$(\mathfrak{H}, \mathfrak{T})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
.
$\mathcal{D}$
.
Since
![]() $H_i' \subseteq T_i'$
, for all
$H_i' \subseteq T_i'$
, for all
![]() $i \in \mathbb{Z}$
, we obtain that
$i \in \mathbb{Z}$
, we obtain that
![]() $\mathfrak{H} \subseteq \mathfrak{T}$
, and so
$\mathfrak{H} \subseteq \mathfrak{T}$
, and so
![]() $(\mathfrak{H}, \mathfrak{T})$
is an HT-interpretation. Moreover,
$(\mathfrak{H}, \mathfrak{T})$
is an HT-interpretation. Moreover,
![]() $(\mathfrak{H}, \mathfrak{T})$
is an HT-model of
$(\mathfrak{H}, \mathfrak{T})$
is an HT-model of
![]() $\mathcal{D}$
, as
$\mathcal{D}$
, as
![]() $H_0' \models \mathcal{D}$
. Next we will show that
$H_0' \models \mathcal{D}$
. Next we will show that
![]() $(\mathfrak{H}, \mathfrak{T})$
is an HT-model of
$(\mathfrak{H}, \mathfrak{T})$
is an HT-model of
![]() $\Pi$
. Since each
$\Pi$
. Since each
![]() $\mathcal{W}_i'$
is a window of length
$\mathcal{W}_i'$
is a window of length
![]() $[t^{\min}_{\mathcal{D}},t^{\max}_{\mathcal{D}}+t_{\Pi}]$
(which is the length of
$[t^{\min}_{\mathcal{D}},t^{\max}_{\mathcal{D}}+t_{\Pi}]$
(which is the length of
![]() $\varrho_{(\Pi,\mathcal{D})}$
), it holds that
$\varrho_{(\Pi,\mathcal{D})}$
), it holds that
![]() $\mathfrak{H} \models M@t $
if and only if
$\mathfrak{H} \models M@t $
if and only if
![]() $M@t \in H_i'$
; as well as
$M@t \in H_i'$
; as well as
![]() $\mathfrak{T} \models M@t $
if and only if
$\mathfrak{T} \models M@t $
if and only if
![]() $M@t \in T_i'$
, for any
$M@t \in T_i'$
, for any
![]() $M \in \mathsf{at}(\Pi,\mathcal{D})$
and
$M \in \mathsf{at}(\Pi,\mathcal{D})$
and
![]() $t \in \varrho_i'$
. Indeed, we have shown an analogous statement for positive (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019, Lemma 9) and stratifiable programs (Tena Cucala et al. Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021), and the same argument applies here. Now, to show that
$t \in \varrho_i'$
. Indeed, we have shown an analogous statement for positive (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019, Lemma 9) and stratifiable programs (Tena Cucala et al. Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021), and the same argument applies here. Now, to show that
![]() $(\mathfrak{H},\mathfrak{T})$
is a model of
$(\mathfrak{H},\mathfrak{T})$
is a model of
![]() $\Pi$
, we fix a ground rule from
$\Pi$
, we fix a ground rule from
![]() $\mathsf{ground}(\Pi,\mathcal{D})$
of Form (1) and a time point t. If
$\mathsf{ground}(\Pi,\mathcal{D})$
of Form (1) and a time point t. If
![]() $\mathfrak{H} ,t \models M_i$
for all
$\mathfrak{H} ,t \models M_i$
for all
![]() ${i \in \{1, \ldots, k\} }$
and
${i \in \{1, \ldots, k\} }$
and
![]() ${\mathfrak{T} ,t \not\models M_j}$
for all
${\mathfrak{T} ,t \not\models M_j}$
for all
![]() ${j \in \{k+1, \ldots, m\} }$
, then
${j \in \{k+1, \ldots, m\} }$
, then
![]() $M_i@t \in H_n'$
for all
$M_i@t \in H_n'$
for all
![]() $i \in \{1, \ldots, k\}$
and
$i \in \{1, \ldots, k\}$
and
![]() $M_j@t \notin T_n$
for all
$M_j@t \notin T_n$
for all
![]() $j \in \{k+1, \ldots, m\}$
, for each n such that
$j \in \{k+1, \ldots, m\}$
, for each n such that
![]() $t \in \varrho_n'$
. Since
$t \in \varrho_n'$
. Since
![]() $\mathcal{W}_n'$
is a window locally satisfying
$\mathcal{W}_n'$
is a window locally satisfying
![]() $\Pi$
, we obtain that
$\Pi$
, we obtain that
![]() $M@t \in H_n$
(where M is the head of r), which implies
$M@t \in H_n$
(where M is the head of r), which implies
![]() $\mathfrak{H} ,t \models M$
by definition of
$\mathfrak{H} ,t \models M$
by definition of
![]() $\mathfrak{H}$
and the fact that
$\mathfrak{H}$
and the fact that
![]() $\Pi$
is in normal form so M is a relational atom. Similarly, if
$\Pi$
is in normal form so M is a relational atom. Similarly, if
![]() $\mathfrak{T} ,t \models M_i$
for all
$\mathfrak{T} ,t \models M_i$
for all
![]() $i \in \{1, \ldots, k\}$
and
$i \in \{1, \ldots, k\}$
and
![]() ${\mathfrak{T} ,t \not\models M_j}$
for all
${\mathfrak{T} ,t \not\models M_j}$
for all
![]() $j \in \{k+1, \ldots, m\}$
, then we obtain that
$j \in \{k+1, \ldots, m\}$
, then we obtain that
![]() $\mathfrak{T} ,t \models M$
. Hence,
$\mathfrak{T} ,t \models M$
. Hence,
![]() $(\mathfrak{H},\mathfrak{T})$
is indeed an HT-model of
$(\mathfrak{H},\mathfrak{T})$
is indeed an HT-model of
![]() $\Pi$
.
$\Pi$
.
However, the accepting condition of
![]() $\mathcal{C}_{\mathcal{W}'_0}^\gets$
guarantees that
$\mathcal{C}_{\mathcal{W}'_0}^\gets$
guarantees that
![]() $b'_i=1$
, for some
$b'_i=1$
, for some
![]() $i \leq 0$
, and so
$i \leq 0$
, and so
![]() ${H_i' \subsetneq T_i' }$
. Therefore,
${H_i' \subsetneq T_i' }$
. Therefore,
![]() $\mathfrak{H} \subsetneq \mathfrak{T}$
, and so
$\mathfrak{H} \subsetneq \mathfrak{T}$
, and so
![]() $\mathfrak{T}$
is not a stable model, which rises a contradiction. If
$\mathfrak{T}$
is not a stable model, which rises a contradiction. If
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() ${{{\overrightarrow{w}}}}$
are accepted by
${{{\overrightarrow{w}}}}$
are accepted by
![]() $\mathcal{A}_{\mathcal{W}'_0}^\gets$
and
$\mathcal{A}_{\mathcal{W}'_0}^\gets$
and
![]() $\mathcal{C}_{\mathcal{W}'_0}^\to$
, respectively, then we construct in an analogous way a run
$\mathcal{C}_{\mathcal{W}'_0}^\to$
, respectively, then we construct in an analogous way a run
![]() $\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
of
$\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
of
![]() $\mathcal{A}_{\mathcal{W}'_0}^\gets$
and a run
$\mathcal{A}_{\mathcal{W}'_0}^\gets$
and a run
![]() $\mathcal{W}'_0, \mathcal{W}'_{1}, \dots$
of
$\mathcal{W}'_0, \mathcal{W}'_{1}, \dots$
of
![]() $\mathcal{C}_{\mathcal{W}'_0}^\to$
. Repeating the argumentation above, we construct an HT-model
$\mathcal{C}_{\mathcal{W}'_0}^\to$
. Repeating the argumentation above, we construct an HT-model
![]() $(\mathfrak{H},\mathfrak{T})$
of
$(\mathfrak{H},\mathfrak{T})$
of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, and then, we show that there exists
$\mathcal{D}$
, and then, we show that there exists
![]() $i\geq 0$
such that
$i\geq 0$
such that
![]() $b'_i=1$
. Thus,
$b'_i=1$
. Thus,
![]() $H_i' \subsetneq T_i'$
, so
$H_i' \subsetneq T_i'$
, so
![]() $\mathfrak{H} \subsetneq \mathfrak{T}$
, and consequently,
$\mathfrak{H} \subsetneq \mathfrak{T}$
, and consequently,
![]() $\mathfrak{T}$
is not a stable model, raising again a contradiction. Thus, Condition 2 holds.
$\mathfrak{T}$
is not a stable model, raising again a contradiction. Thus, Condition 2 holds.
For the converse implication, assume that there exist
![]() $\mathcal{W}_0$
,
$\mathcal{W}_0$
,
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() ${{{\overrightarrow{w}}}}$
as described in the statement of the theorem. By Condition 1, there is an accepting run
${{{\overrightarrow{w}}}}$
as described in the statement of the theorem. By Condition 1, there is an accepting run
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
of
![]() $\mathcal{B}_{\mathcal{W}_0}^\gets$
on
$\mathcal{B}_{\mathcal{W}_0}^\gets$
on
![]() ${{{\overleftarrow{w}}}}$
, and an accepting run
${{{\overleftarrow{w}}}}$
, and an accepting run
![]() $\mathcal{W}_0, \mathcal{W}_1, \dots$
of
$\mathcal{W}_0, \mathcal{W}_1, \dots$
of
![]() $\mathcal{B}_{\mathcal{W}_0}^\to$
on
$\mathcal{B}_{\mathcal{W}_0}^\to$
on
![]() ${{{\overrightarrow{w}}}}$
, where
${{{\overrightarrow{w}}}}$
, where
![]() ${\mathcal{W}_i= (\varrho_i, T_i, T_i, 0)}$
. We argue that the least model
${\mathcal{W}_i= (\varrho_i, T_i, T_i, 0)}$
. We argue that the least model
![]() $\mathfrak{T}$
of relational facts in
$\mathfrak{T}$
of relational facts in
![]() $\bigcup_{i\in\mathbb{Z}} T_i$
is a stable model of
$\bigcup_{i\in\mathbb{Z}} T_i$
is a stable model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. By an argument analogous to the second to last paragraph above,
$\mathcal{D}$
. By an argument analogous to the second to last paragraph above,
![]() $(\mathfrak{T},\mathfrak{T})$
is an HT-model of
$(\mathfrak{T},\mathfrak{T})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. Suppose for contradiction that
$\mathcal{D}$
. Suppose for contradiction that
![]() $\mathfrak{T}$
is not stable, so there exists
$\mathfrak{T}$
is not stable, so there exists
![]() $\mathfrak{H} \subsetneq \mathfrak{T}$
such that
$\mathfrak{H} \subsetneq \mathfrak{T}$
such that
![]() $(\mathfrak{H}, \mathfrak{T})$
is an HT-model of
$(\mathfrak{H}, \mathfrak{T})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. Let
$\mathcal{D}$
. Let
![]() $\dots, \mathcal{W}'_{-1}, \mathcal{W}'_0, \mathcal{W}'_1, \dots$
be the
$\dots, \mathcal{W}'_{-1}, \mathcal{W}'_0, \mathcal{W}'_1, \dots$
be the
![]() $\varrho_{(\Pi,\mathcal{D})}$
-decomposition of
$\varrho_{(\Pi,\mathcal{D})}$
-decomposition of
![]() $(\mathfrak{H},\mathfrak{T})$
, with
$(\mathfrak{H},\mathfrak{T})$
, with
![]() ${\mathcal{W}_i'= (\varrho_i', H_i', T_i', b_i')}$
, and observe that
${\mathcal{W}_i'= (\varrho_i', H_i', T_i', b_i')}$
, and observe that
![]() $\mathcal{W}'_0$
is an initial window. By Lemma 5.6,
$\mathcal{W}'_0$
is an initial window. By Lemma 5.6,
![]() $\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
is an accepting run of
$\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}'_0}^\gets$
on
$\mathcal{A}_{\mathcal{W}'_0}^\gets$
on
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() $\mathcal{W}'_0, \mathcal{W}'_{1}, \dots$
is an accepting run of
$\mathcal{W}'_0, \mathcal{W}'_{1}, \dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}'_0}^\to$
on
$\mathcal{A}_{\mathcal{W}'_0}^\to$
on
![]() ${{{\overrightarrow{w}}}}$
. Moreover, since
${{{\overrightarrow{w}}}}$
. Moreover, since
![]() $\mathfrak{H} \subsetneq \mathfrak{T}$
, there is
$\mathfrak{H} \subsetneq \mathfrak{T}$
, there is
![]() $i \in \mathbb{Z}$
such that
$i \in \mathbb{Z}$
such that
![]() $H_i' \neq T_i'$
, and so
$H_i' \neq T_i'$
, and so
![]() $b_i'=1$
. If
$b_i'=1$
. If
![]() $i \leq 0$
, then
$i \leq 0$
, then
![]() $b_j' =1$
for all
$b_j' =1$
for all
![]() $j \leq i$
, and so
$j \leq i$
, and so
![]() $\mathcal{C}_{\mathcal{W}'_0}^\gets$
accepts
$\mathcal{C}_{\mathcal{W}'_0}^\gets$
accepts
![]() ${{{\overleftarrow{w}}}}$
; analogously, if
${{{\overleftarrow{w}}}}$
; analogously, if
![]() $i \geq 0$
, then
$i \geq 0$
, then
![]() $\mathcal{C}_{\mathcal{W}'_0}^\to$
accepts
$\mathcal{C}_{\mathcal{W}'_0}^\to$
accepts
![]() ${{{\overrightarrow{w}}}}$
. Thus, Condition 2 does not hold, leading to a contradiction.
${{{\overrightarrow{w}}}}$
. Thus, Condition 2 does not hold, leading to a contradiction.
Theorem 5.8 reduces checking existence of a stable model to checking specific properties of our automata. We aim at showing that the latter is feasible in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
. The main obstacle, however, is the size of states in the automata:
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
. The main obstacle, however, is the size of states in the automata:
![]() $\mathcal{W}_0$
is exponential in size with respect to
$\mathcal{W}_0$
is exponential in size with respect to
![]() $\mathcal{D}$
, and states of the automata from Theorem 5.8 can be arbitrarily large since time points in windows can be arbitrary integers. To remedy the first issue, we let
$\mathcal{D}$
, and states of the automata from Theorem 5.8 can be arbitrarily large since time points in windows can be arbitrary integers. To remedy the first issue, we let
![]() $t_\Pi$
be the largest positive number mentioned in
$t_\Pi$
be the largest positive number mentioned in
![]() $\Pi$
, and we let
$\Pi$
, and we let
![]() $t_{\Pi}=1$
if
$t_{\Pi}=1$
if
![]() $\Pi$
mentions no positive numbers – this choice of value is arbitrary since in this case we only need
$\Pi$
mentions no positive numbers – this choice of value is arbitrary since in this case we only need
![]() $t_\Pi$
to be a positive number in the timeline. Then, we show in Lemma 5.10 that it suffices to consider automata with states (i.e., windows) of length
$t_\Pi$
to be a positive number in the timeline. Then, we show in Lemma 5.10 that it suffices to consider automata with states (i.e., windows) of length
![]() $t_\Pi$
, which does not depend on
$t_\Pi$
, which does not depend on
![]() $\mathcal{D}$
. The second issue is addressed by Lemma 5.13 which tells us that, rather than considering automata with states of unbounded size (each of length
$\mathcal{D}$
. The second issue is addressed by Lemma 5.13 which tells us that, rather than considering automata with states of unbounded size (each of length
![]() ${t_\Pi}$
), we can construct equivalent automata with polynomial-size states instead.
${t_\Pi}$
), we can construct equivalent automata with polynomial-size states instead.
To state Lemma 5.10, we define the left-most and right-most fragments of length
![]() $t_\Pi$
of a window as follows.
$t_\Pi$
of a window as follows.
Definition 5.9 For a window
![]() ${\mathcal{W}=(\varrho,H,T,b)}$
of length at least
${\mathcal{W}=(\varrho,H,T,b)}$
of length at least
![]() $t_{\Pi}$
, we define
$t_{\Pi}$
, we define
![]() $\mathcal{W}^{L}=( \varrho^L, H^L,T^L, b^L )$
, where
$\mathcal{W}^{L}=( \varrho^L, H^L,T^L, b^L )$
, where
-
 ${\varrho^L=[\varrho^-,\varrho^- + t_\Pi]}$
,
${\varrho^L=[\varrho^-,\varrho^- + t_\Pi]}$
, -
 ${H^L = \{M@t \in H \mid t \in \varrho^L \} }$
,
${H^L = \{M@t \in H \mid t \in \varrho^L \} }$
, -
 ${T^L = \{M@t \in T \mid t \in \varrho^L \} }$
,
${T^L = \{M@t \in T \mid t \in \varrho^L \} }$
, -
 $b^L = 1$
if
$b^L = 1$
if
 ${H^L \neq T^L}$
; otherwise,
${H^L \neq T^L}$
; otherwise,
 $b^L = 0$
.
$b^L = 0$
.
Analogously, we let
![]() $\mathcal{W}^{R}=( \varrho^R, H^R,T^R, b^R )$
, where
$\mathcal{W}^{R}=( \varrho^R, H^R,T^R, b^R )$
, where
-
 ${\varrho^R=[\varrho^+ - t_\Pi, \varrho^+] }$
,
${\varrho^R=[\varrho^+ - t_\Pi, \varrho^+] }$
, -
 ${H^R = \{M@t \in H \mid t \in \varrho^R \} }$
,
${H^R = \{M@t \in H \mid t \in \varrho^R \} }$
, -
 ${T^R = \{M@t \in T \mid t \in \varrho^R \} }$
,
${T^R = \{M@t \in T \mid t \in \varrho^R \} }$
, -
 $b^R = 1$
if
$b^R = 1$
if
 ${H^R \neq T^R}$
; otherwise,
${H^R \neq T^R}$
; otherwise,
 $b^R = 0$
.
$b^R = 0$
.
We observe that if
![]() $\mathcal{W}$
is a window locally satisfying
$\mathcal{W}$
is a window locally satisfying
![]() $\Pi$
, then
$\Pi$
, then
![]() $\mathcal{W}^L$
and
$\mathcal{W}^L$
and
![]() $\mathcal{W}^R$
(which are “fragments” of
$\mathcal{W}^R$
(which are “fragments” of
![]() $\mathcal{W}$
) also are windows locally satisfying
$\mathcal{W}$
) also are windows locally satisfying
![]() $\Pi$
. Furthermore, both
$\Pi$
. Furthermore, both
![]() $\mathcal{W}^L$
and
$\mathcal{W}^L$
and
![]() $\mathcal{W}^R$
are initial windows by definition. Thus, if
$\mathcal{W}^R$
are initial windows by definition. Thus, if
![]() $\mathcal{W}_0$
is such that
$\mathcal{W}_0$
is such that
![]() $X_{\mathcal{W}_0}^\gets$
and
$X_{\mathcal{W}_0}^\gets$
and
![]() $X_{\mathcal{W}_0}^\to$
are well-defined automata, for some
$X_{\mathcal{W}_0}^\to$
are well-defined automata, for some
![]() $X \in \{ \mathcal{A},\mathcal{B},\mathcal{C} \}$
, then
$X \in \{ \mathcal{A},\mathcal{B},\mathcal{C} \}$
, then
![]() $X_{\mathcal{W}_0^{L}}^\gets$
and
$X_{\mathcal{W}_0^{L}}^\gets$
and
![]() $X_{\mathcal{W}_0^{R}}^\to$
are also well-defined automata. Moreover, we can show several equivalences between these automata.
$X_{\mathcal{W}_0^{R}}^\to$
are also well-defined automata. Moreover, we can show several equivalences between these automata.
Lemma 5.10 Let
![]() $X \in \{ \mathcal{A},\mathcal{B},\mathcal{C} \}$
and let
$X \in \{ \mathcal{A},\mathcal{B},\mathcal{C} \}$
and let
![]() $\mathcal{W}_0 = (\varrho_0,H_0,T_0,b_0)$
be a window such that
$\mathcal{W}_0 = (\varrho_0,H_0,T_0,b_0)$
be a window such that
![]() $X_{\mathcal{W}_0}^\gets$
and
$X_{\mathcal{W}_0}^\gets$
and
![]() $X_{\mathcal{W}_0}^\to$
are well-defined. Then, the following statements hold:
$X_{\mathcal{W}_0}^\to$
are well-defined. Then, the following statements hold:
-
1. If
 $X \in \{\mathcal{A}, \mathcal{B}\}$
, then
$X \in \{\mathcal{A}, \mathcal{B}\}$
, then
 $X_{\mathcal{W}_0}^\gets$
and
$X_{\mathcal{W}_0}^\gets$
and
 $X_{\mathcal{W}_0}^\to$
are equivalent to
$X_{\mathcal{W}_0}^\to$
are equivalent to
 $X_{\mathcal{W}_0^{L}}^\gets$
and
$X_{\mathcal{W}_0^{L}}^\gets$
and
 $X_{\mathcal{W}_0^{R}}^\to$
, respectively.
$X_{\mathcal{W}_0^{R}}^\to$
, respectively. -
2. If
 $X = \mathcal{C}$
and
$X = \mathcal{C}$
and
 $H_0 = T_0$
, then
$H_0 = T_0$
, then
 $X_{\mathcal{W}_0}^\gets$
and
$X_{\mathcal{W}_0}^\gets$
and
 $X_{\mathcal{W}_0}^\to$
are equivalent to
$X_{\mathcal{W}_0}^\to$
are equivalent to
 $X_{\mathcal{W}_0^{L}}^\gets$
and
$X_{\mathcal{W}_0^{L}}^\gets$
and
 $X_{\mathcal{W}_0^{R}}^\to$
, respectively.
$X_{\mathcal{W}_0^{R}}^\to$
, respectively. -
3. If
 $X = \mathcal{C}$
and
$X = \mathcal{C}$
and
 $H_0 \neq T_0$
, then
$H_0 \neq T_0$
, then
 $X_{\mathcal{W}_0}^\gets$
and
$X_{\mathcal{W}_0}^\gets$
and
 $X_{\mathcal{W}_0}^\to$
are equivalent to
$X_{\mathcal{W}_0}^\to$
are equivalent to
 $\mathcal{A}_{\mathcal{W}_0^{L}}^\gets$
and
$\mathcal{A}_{\mathcal{W}_0^{L}}^\gets$
and
 $\mathcal{A}_{\mathcal{W}_0^{R}}^\to$
, respectively.
$\mathcal{A}_{\mathcal{W}_0^{R}}^\to$
, respectively.
Proof. First, we show Statement 1 for
![]() $X = \mathcal{A}$
. Assume that
$X = \mathcal{A}$
. Assume that
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
on a word
$\mathcal{A}_{\mathcal{W}_0}^\gets$
on a word
![]() $w =\sigma_{-1},\sigma_{-2},\dots$
. We will show that there is an accepting run
$w =\sigma_{-1},\sigma_{-2},\dots$
. We will show that there is an accepting run
![]() $\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
of
$\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
of
![]() $\mathcal{A}_{\mathcal{W}^L_0}^\gets$
on the same word. To define this run, for each integer
$\mathcal{A}_{\mathcal{W}^L_0}^\gets$
on the same word. To define this run, for each integer
![]() $i \leq 0$
, we let
$i \leq 0$
, we let
![]() ${\mathcal{W}^L_i= (\varrho_i,H_i,T_i,b_i)}$
, and we define
${\mathcal{W}^L_i= (\varrho_i,H_i,T_i,b_i)}$
, and we define
![]() $\mathcal{W}'_i = (\varrho_i, H_i,T_i,b'_i)$
, where
$\mathcal{W}'_i = (\varrho_i, H_i,T_i,b'_i)$
, where
![]() $b'_i = 1$
if there exists
$b'_i = 1$
if there exists
![]() $j \in \{0, \dots, i \}$
such that
$j \in \{0, \dots, i \}$
such that
![]() $H_i \neq T_i$
, and otherwise
$H_i \neq T_i$
, and otherwise
![]() $b'_i=0$
. In particular,
$b'_i=0$
. In particular,
![]() $\mathcal{W}_0' = \mathcal{W}_0^L$
. Now, we will show that
$\mathcal{W}_0' = \mathcal{W}_0^L$
. Now, we will show that
![]() $\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
is an accepting run of
$\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_0^L}^\gets$
on w. We start by observing that since each
$\mathcal{A}_{\mathcal{W}_0^L}^\gets$
on w. We start by observing that since each
![]() $\mathcal{W}_i$
is a window locally satisfying
$\mathcal{W}_i$
is a window locally satisfying
![]() $\Pi$
and since
$\Pi$
and since
![]() $\mathcal{W}_i^L$
is a “fragment” of
$\mathcal{W}_i^L$
is a “fragment” of
![]() $\mathcal{W}_i$
, then
$\mathcal{W}_i$
, then
![]() $\mathcal{W}'_i$
is also a window locally satisfying
$\mathcal{W}'_i$
is also a window locally satisfying
![]() $\Pi$
. Thus,
$\Pi$
. Thus,
![]() $\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
are states of
$\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
are states of
![]() $\mathcal{A}_{\mathcal{W}_0^L}^\gets$
. To show that they constitute a run of
$\mathcal{A}_{\mathcal{W}_0^L}^\gets$
. To show that they constitute a run of
![]() $\mathcal{A}_{\mathcal{W}_0^L}^\gets$
on w, we observe that the transition functions
$\mathcal{A}_{\mathcal{W}_0^L}^\gets$
on w, we observe that the transition functions
![]() $\delta$
of
$\delta$
of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
and
$\mathcal{A}_{\mathcal{W}_0}^\gets$
and
![]() $\delta^L$
of
$\delta^L$
of
![]() $\mathcal{A}_{\mathcal{W}_0^L}^\gets$
are the same modulo definition of states. This observation and our definition of
$\mathcal{A}_{\mathcal{W}_0^L}^\gets$
are the same modulo definition of states. This observation and our definition of
![]() $b'_i$
, ensure that
$b'_i$
, ensure that
![]() $\mathcal{W}_{i-1} \in \delta(\mathcal{W}_i,\sigma_{i-1})$
implies
$\mathcal{W}_{i-1} \in \delta(\mathcal{W}_i,\sigma_{i-1})$
implies
![]() $\mathcal{W}'_{i-1} \in \delta^L(\mathcal{W}'_i,\sigma_{i-1})$
, for any integer
$\mathcal{W}'_{i-1} \in \delta^L(\mathcal{W}'_i,\sigma_{i-1})$
, for any integer
![]() $i \leq 0$
. It remains to show that
$i \leq 0$
. It remains to show that
![]() $\mathcal{A}_{\mathcal{W}_0^L}^\gets$
accepts the run
$\mathcal{A}_{\mathcal{W}_0^L}^\gets$
accepts the run
![]() $\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
. For this, we observe that
$\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
. For this, we observe that
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
and
$\mathcal{A}_{\mathcal{W}_0}^\gets$
and
![]() $\mathcal{A}_{\mathcal{W}_0^L}^\gets$
have the same accepting conditions modulo the definition of states. Next, let k be the difference between lengths of windows
$\mathcal{A}_{\mathcal{W}_0^L}^\gets$
have the same accepting conditions modulo the definition of states. Next, let k be the difference between lengths of windows
![]() $\mathcal{W}_0$
and
$\mathcal{W}_0$
and
![]() $\mathcal{W}^L_0$
. Observe that for any integer
$\mathcal{W}^L_0$
. Observe that for any integer
![]() $i \leq -k$
, if
$i \leq -k$
, if
![]() $\mathcal{W}_i$
belongs to some set S from the accepting condition of
$\mathcal{W}_i$
belongs to some set S from the accepting condition of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
, then there exists
$\mathcal{A}_{\mathcal{W}_0}^\gets$
, then there exists
![]() $j \in [i,i+k]$
such that
$j \in [i,i+k]$
such that
![]() $\mathcal{W}'_j$
belongs to a set from the accepting condition of
$\mathcal{W}'_j$
belongs to a set from the accepting condition of
![]() $\mathcal{A}_{\mathcal{W}_0^L}^\gets$
that corresponds to S. Since each set in the accepting condition of
$\mathcal{A}_{\mathcal{W}_0^L}^\gets$
that corresponds to S. Since each set in the accepting condition of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
is visited infinitely often by the states in the run
$\mathcal{A}_{\mathcal{W}_0}^\gets$
is visited infinitely often by the states in the run
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
, each set in the accepting condition of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
, each set in the accepting condition of
![]() $\mathcal{A}_{\mathcal{W}_0^L}^\gets$
is also visited infinitely often by the states in the run
$\mathcal{A}_{\mathcal{W}_0^L}^\gets$
is also visited infinitely often by the states in the run
![]() $\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
. Thus, the latter is an accepting run of
$\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
. Thus, the latter is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_0^L}^\gets$
. The case of
$\mathcal{A}_{\mathcal{W}_0^L}^\gets$
. The case of
![]() $\mathcal{A}_{\mathcal{W}_0^R}^\to$
is symmetric so, by an analogous argumentation, we obtain that if
$\mathcal{A}_{\mathcal{W}_0^R}^\to$
is symmetric so, by an analogous argumentation, we obtain that if
![]() $\mathcal{A}_{\mathcal{W}_0}^\to$
accepts a word w, then so does
$\mathcal{A}_{\mathcal{W}_0}^\to$
accepts a word w, then so does
![]() $\mathcal{A}_{\mathcal{W}_0^R}^\to$
.
$\mathcal{A}_{\mathcal{W}_0^R}^\to$
.
For the opposite direction of Statement 1, let us assume that
![]() $\mathcal{A}_{\mathcal{W}_{0}^L}^\gets$
has an accepting run
$\mathcal{A}_{\mathcal{W}_{0}^L}^\gets$
has an accepting run
![]() $\mathcal{W}_{0}^L, \mathcal{W}_{-1}', \mathcal{W}_{-2}',\dots$
on a word
$\mathcal{W}_{0}^L, \mathcal{W}_{-1}', \mathcal{W}_{-2}',\dots$
on a word
![]() $w = \sigma_{-1},\sigma_{-2},\dots$
; we will show that
$w = \sigma_{-1},\sigma_{-2},\dots$
; we will show that
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
has an accepting run on w. To facilitate the definition of this run, we divide
$\mathcal{A}_{\mathcal{W}_0}^\gets$
has an accepting run on w. To facilitate the definition of this run, we divide
![]() $\mathcal{W}_0 = (\varrho_0,H_0,T_0,b_0)$
into tuples
$\mathcal{W}_0 = (\varrho_0,H_0,T_0,b_0)$
into tuples
![]() $\mathcal{W}_{0}', \dots, \mathcal{W}_{k}'$
, where k is the difference between the lengths of
$\mathcal{W}_{0}', \dots, \mathcal{W}_{k}'$
, where k is the difference between the lengths of
![]() $\mathcal{W}_0$
and
$\mathcal{W}_0$
and
![]() $\mathcal{W}_0^L$
. In particular, for each
$\mathcal{W}_0^L$
. In particular, for each
![]() $i \in \{0, \dots, k \}$
, we define
$i \in \{0, \dots, k \}$
, we define
![]() ${\mathcal{W}_{i}' = (\varrho_i',H_i',T_i',b_i') }$
, such that
${\mathcal{W}_{i}' = (\varrho_i',H_i',T_i',b_i') }$
, such that
![]() ${\varrho_i'=[\varrho_0^- + k , \varrho_0^- +t_{\Pi} + k ]}$
,
${\varrho_i'=[\varrho_0^- + k , \varrho_0^- +t_{\Pi} + k ]}$
,
![]() ${H_i' = \{M@t \in H_0 \mid t \in \varrho_i' \} }$
,
${H_i' = \{M@t \in H_0 \mid t \in \varrho_i' \} }$
,
![]() ${T_i' = \{M@t \in T_0 \mid t \in \varrho_i' \} }$
, whereas
${T_i' = \{M@t \in T_0 \mid t \in \varrho_i' \} }$
, whereas
![]() $b_i' = 1$
if
$b_i' = 1$
if
![]() $H'_i \neq T'_i$
and
$H'_i \neq T'_i$
and
![]() $b'_i=0$
if
$b'_i=0$
if
![]() $H'_i = T'_i$
. Recall that since
$H'_i = T'_i$
. Recall that since
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
is well-defined,
$\mathcal{A}_{\mathcal{W}_0}^\gets$
is well-defined,
![]() $\mathcal{W}_0$
is an initial window locally satisfying
$\mathcal{W}_0$
is an initial window locally satisfying
![]() $\Pi$
, and as we already mentioned, by fragmenting windows locally satisfying
$\Pi$
, and as we already mentioned, by fragmenting windows locally satisfying
![]() $\Pi$
we obtain windows which also locally satisfy
$\Pi$
we obtain windows which also locally satisfy
![]() $\Pi$
. Hence all of
$\Pi$
. Hence all of
![]() $\mathcal{W}_{0}', \dots, \mathcal{W}_k'$
locally satisfy
$\mathcal{W}_{0}', \dots, \mathcal{W}_k'$
locally satisfy
![]() $\Pi$
. Furthermore, observe that
$\Pi$
. Furthermore, observe that
![]() $\mathcal{W}_{0}' = \mathcal{W}_{0}^L$
. Next, we show how to merge the windows
$\mathcal{W}_{0}' = \mathcal{W}_{0}^L$
. Next, we show how to merge the windows
![]() $\mathcal{W}_k', \dots, \mathcal{W}_0', \mathcal{W}_{-1}',\dots$
to obtain an accepting run of
$\mathcal{W}_k', \dots, \mathcal{W}_0', \mathcal{W}_{-1}',\dots$
to obtain an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_{0}}^\gets$
on w. To this end, for arbitrary windows
$\mathcal{A}_{\mathcal{W}_{0}}^\gets$
on w. To this end, for arbitrary windows
![]() $\mathcal{W} = ( \varrho, H,T, b )$
and
$\mathcal{W} = ( \varrho, H,T, b )$
and
![]() ${\mathcal{W}' =( \varrho', H',T', b' )}$
such that
${\mathcal{W}' =( \varrho', H',T', b' )}$
such that
![]() $\varrho \cap \varrho' \neq \emptyset$
, we define their union, written as
$\varrho \cap \varrho' \neq \emptyset$
, we define their union, written as
![]() $\mathcal{W} \cup \mathcal{W}'$
, as the tuple
$\mathcal{W} \cup \mathcal{W}'$
, as the tuple
![]() ${(\varrho \cup \varrho', H \cup H', T \cup T', \max(b,b'))}$
. We can then establish the following claim:
${(\varrho \cup \varrho', H \cup H', T \cup T', \max(b,b'))}$
. We can then establish the following claim:
Claim 5.11 Let
![]() $\mathcal{W} = (\varrho, H, T, b)$
and
$\mathcal{W} = (\varrho, H, T, b)$
and
![]() $\mathcal{W}' = (\varrho',H', T', b')$
be windows such that the left and right endpoints of
$\mathcal{W}' = (\varrho',H', T', b')$
be windows such that the left and right endpoints of
![]() $\varrho'$
succeed those of
$\varrho'$
succeed those of
![]() $\varrho$
, and for each
$\varrho$
, and for each
![]() $t \in \varrho \cap \varrho'$
and each
$t \in \varrho \cap \varrho'$
and each
![]() $X \in \{H,T\}$
,
$X \in \{H,T\}$
,
![]() $M@t \in X$
if and only if
$M@t \in X$
if and only if
![]() $M@t \in X'$
. If both
$M@t \in X'$
. If both
![]() $\mathcal{W}$
and
$\mathcal{W}$
and
![]() $\mathcal{W}'$
are of length at least
$\mathcal{W}'$
are of length at least
![]() $t_{\Pi}$
and locally satisfy
$t_{\Pi}$
and locally satisfy
![]() $\Pi$
, then
$\Pi$
, then
![]() $\mathcal{W} \cup \mathcal{W}'$
is a window locally satisfying
$\mathcal{W} \cup \mathcal{W}'$
is a window locally satisfying
![]() $\Pi$
.
$\Pi$
.
Proof of Claim 5.11
Let
![]() $\mathcal{W}'' = \mathcal{W} \cup \mathcal{W}' = (\varrho'', H'', T'', b'')$
. If
$\mathcal{W}'' = \mathcal{W} \cup \mathcal{W}' = (\varrho'', H'', T'', b'')$
. If
![]() $\mathcal{W}$
and
$\mathcal{W}$
and
![]() $\mathcal{W}'$
locally satisfy
$\mathcal{W}'$
locally satisfy
![]() $\Pi$
, then clearly
$\Pi$
, then clearly
![]() $\mathcal{W}''$
also locally satisfies
$\mathcal{W}''$
also locally satisfies
![]() $\Pi$
. It remains to show that
$\Pi$
. It remains to show that
![]() $\mathcal{W}''$
is a window. To this end, for
$\mathcal{W}''$
is a window. To this end, for
![]() $\mathfrak{I}$
an interpretation,
$\mathfrak{I}$
an interpretation,
![]() $\varrho_b$
a closed interval, and J a set of metric facts
$\varrho_b$
a closed interval, and J a set of metric facts
![]() $M@t$
with
$M@t$
with
![]() $M \in \mathsf{at}(\Pi,\mathcal{D})$
and
$M \in \mathsf{at}(\Pi,\mathcal{D})$
and
![]() $t \in \varrho_b$
, we say that
$t \in \varrho_b$
, we say that
![]() $\mathfrak{I}$
corresponds to J over
$\mathfrak{I}$
corresponds to J over
![]() $\varrho_b$
if, for every
$\varrho_b$
if, for every
![]() $t \in \varrho_b$
and
$t \in \varrho_b$
and
![]() $M \in \mathsf{at}(\Pi,\mathcal{D})$
, it holds that
$M \in \mathsf{at}(\Pi,\mathcal{D})$
, it holds that
![]() $\mathfrak{I} \models M@t$
if and only if
$\mathfrak{I} \models M@t$
if and only if
![]() $M@t \in J$
. To show that
$M@t \in J$
. To show that
![]() $\mathcal{W}''$
is a window, the only non-trivial condition that needs to be verified is that there exist two interpretations that correspond, respectively, to H” and T” over
$\mathcal{W}''$
is a window, the only non-trivial condition that needs to be verified is that there exist two interpretations that correspond, respectively, to H” and T” over
![]() $\varrho''$
. We show this for H” only, as the argument for T” is analogous. Let
$\varrho''$
. We show this for H” only, as the argument for T” is analogous. Let
![]() $\mathfrak{H}$
(resp.
$\mathfrak{H}$
(resp.
![]() $\mathfrak{H}'$
) be an interpretation corresponding to H over
$\mathfrak{H}'$
) be an interpretation corresponding to H over
![]() $\varrho$
(resp. H’ over
$\varrho$
(resp. H’ over
![]() $\varrho'$
); such an interpretation exists, since
$\varrho'$
); such an interpretation exists, since
![]() $\mathcal{W}$
(resp.
$\mathcal{W}$
(resp.
![]() $\mathcal{W}'$
) is a window. Let
$\mathcal{W}'$
) is a window. Let
![]() $\mathfrak{H}''$
be an arbitrary interpretation that coincides with
$\mathfrak{H}''$
be an arbitrary interpretation that coincides with
![]() $\mathfrak{H}$
over
$\mathfrak{H}$
over
![]() $\varrho$
and all time points to its left, and with
$\varrho$
and all time points to its left, and with
![]() $\mathfrak{H}'$
over
$\mathfrak{H}'$
over
![]() $\varrho'$
and all time points to its right. Note that
$\varrho'$
and all time points to its right. Note that
![]() $\mathfrak{H}$
and
$\mathfrak{H}$
and
![]() $\mathfrak{H}'$
agree over
$\mathfrak{H}'$
agree over
![]() $\varrho \cap \varrho'$
since, by assumption,
$\varrho \cap \varrho'$
since, by assumption,
![]() $M@t \in H$
if and only if
$M@t \in H$
if and only if
![]() $M@t \in H'$
for all
$M@t \in H'$
for all
![]() $t \in \varrho \cap \varrho'$
; thus,
$t \in \varrho \cap \varrho'$
; thus,
![]() $\mathfrak{H}''$
is well-defined. It remains to show that
$\mathfrak{H}''$
is well-defined. It remains to show that
![]() $\mathfrak{H}''$
corresponds to H” over
$\mathfrak{H}''$
corresponds to H” over
![]() $\varrho''$
– that is, for each
$\varrho''$
– that is, for each
![]() $M@t$
with
$M@t$
with
![]() $M \in \mathsf{at}(\Pi,\mathcal{D})$
and
$M \in \mathsf{at}(\Pi,\mathcal{D})$
and
![]() $t \in \varrho''$
, we must show that
$t \in \varrho''$
, we must show that
![]() $\mathfrak{H}'' \models M @ t$
if and only if
$\mathfrak{H}'' \models M @ t$
if and only if
![]() $M @ t \in H''$
. We show this explicitly for the case where M is of the form
$M @ t \in H''$
. We show this explicitly for the case where M is of the form
![]() $\boxminus_{\varrho_b} P$
, for
$\boxminus_{\varrho_b} P$
, for
![]() $\varrho_b$
a bounded interval and P a relational atom; the remaining cases can be proved in a similar way; see Wałęga et al. (Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019), Lemma 7. Suppose that
$\varrho_b$
a bounded interval and P a relational atom; the remaining cases can be proved in a similar way; see Wałęga et al. (Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019), Lemma 7. Suppose that
![]() $t \in \varrho$
. Since
$t \in \varrho$
. Since
![]() $\mathfrak{H}''$
and
$\mathfrak{H}''$
and
![]() $\mathfrak{H}$
coincide over
$\mathfrak{H}$
coincide over
![]() $\varrho$
and all time points to its left, we have that
$\varrho$
and all time points to its left, we have that
![]() $\mathfrak{H}'' \models \boxminus_{\varrho_b} P @t$
if and only if
$\mathfrak{H}'' \models \boxminus_{\varrho_b} P @t$
if and only if
![]() $\mathfrak{H} \models \boxminus_{\varrho_b} P@t$
. Then, since
$\mathfrak{H} \models \boxminus_{\varrho_b} P@t$
. Then, since
![]() $\mathfrak{H}$
corresponds to H over
$\mathfrak{H}$
corresponds to H over
![]() $\varrho$
, it holds that
$\varrho$
, it holds that
![]() $\mathfrak{H} \models \boxminus_{\varrho_b} P @ t$
if and only if
$\mathfrak{H} \models \boxminus_{\varrho_b} P @ t$
if and only if
![]() $\boxminus_{\varrho_b} P @t \in H$
. Finally, since H and H” coincide over
$\boxminus_{\varrho_b} P @t \in H$
. Finally, since H and H” coincide over
![]() $\varrho$
,
$\varrho$
,
![]() $\boxminus_{\varrho_b} P @t\in H$
if and only if
$\boxminus_{\varrho_b} P @t\in H$
if and only if
![]() $\boxminus_{\varrho_b} P @ t \in H''$
. Thus, by chaining together these double implications, we have that
$\boxminus_{\varrho_b} P @ t \in H''$
. Thus, by chaining together these double implications, we have that
![]() $\mathfrak{H}'' \models \boxminus_{\varrho_b} P @t$
if and only if
$\mathfrak{H}'' \models \boxminus_{\varrho_b} P @t$
if and only if
![]() $\boxminus_{\varrho_b} P @ t \in H''$
, which is the target equivalence. Suppose now that
$\boxminus_{\varrho_b} P @ t \in H''$
, which is the target equivalence. Suppose now that
![]() $t \notin \varrho$
, so t is the right endpoint of
$t \notin \varrho$
, so t is the right endpoint of
![]() $\varrho'$
. By the semantics of metric atoms,
$\varrho'$
. By the semantics of metric atoms,
![]() $\mathfrak{H}'' \models \boxminus_{\varrho_b} P @ t$
if and only if
$\mathfrak{H}'' \models \boxminus_{\varrho_b} P @ t$
if and only if
![]() $\mathfrak{H}'' \models P @ t-t'$
for each
$\mathfrak{H}'' \models P @ t-t'$
for each
![]() $t' \in \varrho_b$
. Since the length of
$t' \in \varrho_b$
. Since the length of
![]() $\varrho'$
is at least
$\varrho'$
is at least
![]() $t_{\Pi}$
, we have
$t_{\Pi}$
, we have
![]() $t - t' \in \varrho'$
for each
$t - t' \in \varrho'$
for each
![]() $t' \in \varrho_b$
. Hence, since
$t' \in \varrho_b$
. Hence, since
![]() $\mathfrak{H}''$
and
$\mathfrak{H}''$
and
![]() $\mathfrak{H}'$
coincide over
$\mathfrak{H}'$
coincide over
![]() $\varrho'$
,
$\varrho'$
,
![]() $\mathfrak{H}'' \models\boxminus_{\varrho_b} P$
if and only if
$\mathfrak{H}'' \models\boxminus_{\varrho_b} P$
if and only if
![]() $\mathfrak{H}' \models\boxminus_{\varrho_b} P$
, and the rest follows by an argument analogous to the previous case, finishing the proof of Claim 5.11.
$\mathfrak{H}' \models\boxminus_{\varrho_b} P$
, and the rest follows by an argument analogous to the previous case, finishing the proof of Claim 5.11.
We resume the proof of Lemma 5.10. Now, we construct an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
on w as follows. For each integer
$\mathcal{A}_{\mathcal{W}_0}^\gets$
on w as follows. For each integer
![]() $ i < 0$
, we let
$ i < 0$
, we let
![]() $\mathcal{W}_i = (\varrho_i,H_i,T_i,b_i)$
be
$\mathcal{W}_i = (\varrho_i,H_i,T_i,b_i)$
be
![]() $\mathcal{W}_i' \cup \dots \cup \mathcal{W}_{i+k}'$
with the exception that
$\mathcal{W}_i' \cup \dots \cup \mathcal{W}_{i+k}'$
with the exception that
![]() $b_i =1$
if there exists
$b_i =1$
if there exists
![]() $j \in \{i, \dots, k \}$
such that
$j \in \{i, \dots, k \}$
such that
![]() $H'_i \neq T'_i$
and
$H'_i \neq T'_i$
and
![]() $b_i =0$
otherwise.
$b_i =0$
otherwise.
Now, we will show that
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is indeed an accepting run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is indeed an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
on w. To this end, we observe that each
$\mathcal{A}_{\mathcal{W}_0}^\gets$
on w. To this end, we observe that each
![]() $\mathcal{W}_{i}$
is a window locally satisfying
$\mathcal{W}_{i}$
is a window locally satisfying
![]() $\Pi$
, since so is
$\Pi$
, since so is
![]() ${ \mathcal{W}_i' \cup \dots \cup \mathcal{W}_{i+k}' }$
by Claim 5.11; furthermore, each
${ \mathcal{W}_i' \cup \dots \cup \mathcal{W}_{i+k}' }$
by Claim 5.11; furthermore, each
![]() $\mathcal{W}_i$
it is of the same length as
$\mathcal{W}_i$
it is of the same length as
![]() $\mathcal{W}_0$
. Therefore, each
$\mathcal{W}_0$
. Therefore, each
![]() $\mathcal{W}_i$
is a state of the automaton
$\mathcal{W}_i$
is a state of the automaton
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
. Moreover, the definition of
$\mathcal{A}_{\mathcal{W}_0}^\gets$
. Moreover, the definition of
![]() $\mathcal{W}_i$
ensures that if there exists a transition on
$\mathcal{W}_i$
ensures that if there exists a transition on
![]() $\sigma_{i-1}$
from
$\sigma_{i-1}$
from
![]() $\mathcal{W}_i'$
to
$\mathcal{W}_i'$
to
![]() $\mathcal{W}_{i-1}'$
in
$\mathcal{W}_{i-1}'$
in
![]() $\mathcal{A}_{\mathcal{W}_0^L}^\gets$
, then there exists a transition on
$\mathcal{A}_{\mathcal{W}_0^L}^\gets$
, then there exists a transition on
![]() $\sigma_{i-1}$
from
$\sigma_{i-1}$
from
![]() $\mathcal{W}_i$
to
$\mathcal{W}_i$
to
![]() $\mathcal{W}_{i-1}$
in
$\mathcal{W}_{i-1}$
in
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
, so
$\mathcal{A}_{\mathcal{W}_0}^\gets$
, so
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is a run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is a run of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
on w. Furthermore, if
$\mathcal{A}_{\mathcal{W}_0}^\gets$
on w. Furthermore, if
![]() $\mathcal{W}_i'$
belongs to some set S in the accepting condition of
$\mathcal{W}_i'$
belongs to some set S in the accepting condition of
![]() $\mathcal{A}_{\mathcal{W}_0^L}^\gets$
, then the bigger window
$\mathcal{A}_{\mathcal{W}_0^L}^\gets$
, then the bigger window
![]() $\mathcal{W}_i$
belongs to the set corresponding to S in the accepting condition of
$\mathcal{W}_i$
belongs to the set corresponding to S in the accepting condition of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
. Hence,
$\mathcal{A}_{\mathcal{W}_0}^\gets$
. Hence,
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
accepts the run
$\mathcal{A}_{\mathcal{W}_0}^\gets$
accepts the run
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
. The case of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
. The case of
![]() $\mathcal{A}_{\mathcal{W}_0}^\to$
is symmetric, so we obtain that if
$\mathcal{A}_{\mathcal{W}_0}^\to$
is symmetric, so we obtain that if
![]() $\mathcal{A}_{\mathcal{W}_0^R}^\to$
accepts a word w, then so does
$\mathcal{A}_{\mathcal{W}_0^R}^\to$
accepts a word w, then so does
![]() $\mathcal{A}_{\mathcal{W}_0}^\to$
.
$\mathcal{A}_{\mathcal{W}_0}^\to$
.
To finish the proof of Statement 1, it remains to consider the case
![]() $X =\mathcal{B}$
. Recall that the only difference between the automata of the types
$X =\mathcal{B}$
. Recall that the only difference between the automata of the types
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
is that the latter impose additional requirement on the windows to be states (see Definition 5.7), namely for a window
$\mathcal{B}$
is that the latter impose additional requirement on the windows to be states (see Definition 5.7), namely for a window
![]() $\mathcal{W}=(\varrho,H,T,b)$
to be a state, it is required that
$\mathcal{W}=(\varrho,H,T,b)$
to be a state, it is required that
![]() $H=T$
. This, however, does not affect our argumentation above, and so, we obtain that
$H=T$
. This, however, does not affect our argumentation above, and so, we obtain that
![]() $\mathcal{B}_{\mathcal{W}_0}^\gets$
and
$\mathcal{B}_{\mathcal{W}_0}^\gets$
and
![]() $\mathcal{B}_{\mathcal{W}_0}^\to$
accept the same words as
$\mathcal{B}_{\mathcal{W}_0}^\to$
accept the same words as
![]() $\mathcal{B}_{\mathcal{W}_0^{L}}^\gets$
and
$\mathcal{B}_{\mathcal{W}_0^{L}}^\gets$
and
![]() $\mathcal{B}_{\mathcal{W}_0^{R}}^\to$
, respectively.
$\mathcal{B}_{\mathcal{W}_0^{R}}^\to$
, respectively.
To show that Statements 2 and 3 hold, we recall that the automata
![]() $\mathcal{C}$
differ from automata
$\mathcal{C}$
differ from automata
![]() $\mathcal{A}$
only in the existence of an additional set
$\mathcal{A}$
only in the existence of an additional set
![]() $S = \{ (\varrho,H, T,b) \in \mathcal{Q} \mid b=1\}$
in their accepting conditions (see Definition 5.7). If
$S = \{ (\varrho,H, T,b) \in \mathcal{Q} \mid b=1\}$
in their accepting conditions (see Definition 5.7). If
![]() $\mathcal{W}_0 = (\varrho_0,H_0,T_0,b_0)$
is such that
$\mathcal{W}_0 = (\varrho_0,H_0,T_0,b_0)$
is such that
![]() $H_0 = T_0$
, then we can show that
$H_0 = T_0$
, then we can show that
![]() $\mathcal{C}_{\mathcal{W}_0}^\gets$
and
$\mathcal{C}_{\mathcal{W}_0}^\gets$
and
![]() $\mathcal{C}_{\mathcal{W}_0}^\to$
accept the same words as
$\mathcal{C}_{\mathcal{W}_0}^\to$
accept the same words as
![]() $\mathcal{C}_{\mathcal{W}_0^{L}}^\gets$
and
$\mathcal{C}_{\mathcal{W}_0^{L}}^\gets$
and
![]() $\mathcal{C}_{\mathcal{W}_0^{R}}^\to$
, respectively, using the same argumentation as in the proof of Statement 1, except for the following difference. We use the fact that
$\mathcal{C}_{\mathcal{W}_0^{R}}^\to$
, respectively, using the same argumentation as in the proof of Statement 1, except for the following difference. We use the fact that
![]() $H_0 = T_0$
to ensure that in an arbitrary accepting run of
$H_0 = T_0$
to ensure that in an arbitrary accepting run of
![]() $\mathcal{C}_{\mathcal{W}_0}^\gets$
for some word, there exists a window
$\mathcal{C}_{\mathcal{W}_0}^\gets$
for some word, there exists a window
![]() $\mathcal{W}_i=(\varrho_i,H_i,T_i,b_i)$
to the left of
$\mathcal{W}_i=(\varrho_i,H_i,T_i,b_i)$
to the left of
![]() $\mathcal{W}_0$
with
$\mathcal{W}_0$
with
![]() $H_i \neq T_i$
, which in turn allows us to ensure that the corresponding run that we define for
$H_i \neq T_i$
, which in turn allows us to ensure that the corresponding run that we define for
![]() $\mathcal{C}_{\mathcal{W}^L_0}^\gets$
contains a “fragment”
$\mathcal{C}_{\mathcal{W}^L_0}^\gets$
contains a “fragment”
![]() $\mathcal{W}'_j=(\varrho'_j,H'_j,T'_j,b'_j)$
of
$\mathcal{W}'_j=(\varrho'_j,H'_j,T'_j,b'_j)$
of
![]() $\mathcal{W}_i$
with
$\mathcal{W}_i$
with
![]() $H'_j\neq T'_j$
, and hence the run is accepting. An analogous argument applies to
$H'_j\neq T'_j$
, and hence the run is accepting. An analogous argument applies to
![]() $\mathcal{C}_{\mathcal{W}_0}^\to$
. Thus, Statement 2 holds.
$\mathcal{C}_{\mathcal{W}_0}^\to$
. Thus, Statement 2 holds.
However, if
![]() $\mathcal{W}_0 = (\varrho_0,H_0,T_0,b_0)$
is such that
$\mathcal{W}_0 = (\varrho_0,H_0,T_0,b_0)$
is such that
![]() $H_0 \neq T_0$
– as in Statement 3 – then
$H_0 \neq T_0$
– as in Statement 3 – then
![]() $b_0=1$
since
$b_0=1$
since
![]() $\mathcal{W}_0$
is initial, and so, each window in any run of the automata
$\mathcal{W}_0$
is initial, and so, each window in any run of the automata
![]() $\mathcal{C}_{\mathcal{W}_0}^\gets$
and
$\mathcal{C}_{\mathcal{W}_0}^\gets$
and
![]() $\mathcal{C}_{\mathcal{W}_0}^\to$
will belong to the additional set
$\mathcal{C}_{\mathcal{W}_0}^\to$
will belong to the additional set
![]() ${ \{ (\varrho,H, T,b) \in \mathcal{Q} \mid b=1\} }$
from the accepting condition. Hence, this additional condition is trivially satisfied by any infinite run, so
${ \{ (\varrho,H, T,b) \in \mathcal{Q} \mid b=1\} }$
from the accepting condition. Hence, this additional condition is trivially satisfied by any infinite run, so
![]() $\mathcal{C}_{\mathcal{W}_0}^\gets$
and
$\mathcal{C}_{\mathcal{W}_0}^\gets$
and
![]() $\mathcal{C}_{\mathcal{W}_0}^\to$
are equivalent to
$\mathcal{C}_{\mathcal{W}_0}^\to$
are equivalent to
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
and
$\mathcal{A}_{\mathcal{W}_0}^\gets$
and
![]() $\mathcal{A}_{\mathcal{W}_0}^\to$
, respectively. Therefore, by Statement 1, we obtain that
$\mathcal{A}_{\mathcal{W}_0}^\to$
, respectively. Therefore, by Statement 1, we obtain that
![]() $\mathcal{C}_{\mathcal{W}_0}^\gets$
and
$\mathcal{C}_{\mathcal{W}_0}^\gets$
and
![]() $\mathcal{C}_{\mathcal{W}_0}^\to$
are also equivalent to
$\mathcal{C}_{\mathcal{W}_0}^\to$
are also equivalent to
![]() $\mathcal{A}_{\mathcal{W}_0^{L}}^\gets$
and
$\mathcal{A}_{\mathcal{W}_0^{L}}^\gets$
and
![]() $\mathcal{A}_{\mathcal{W}_0^{R}}^\to$
, respectively, which proves Statement 3.
$\mathcal{A}_{\mathcal{W}_0^{R}}^\to$
, respectively, which proves Statement 3.
Lemma 5.10 allows us to restrict our attention to automata with windows of polynomial length, but representations of such windows can still be unbounded, because arbitrarily large integers may occur in them. However, we will show in Lemma 5.13 that we can construct equivalent automata with states that can be represented in polynomial space, by merging “similar” states in the original automata. We use a notion of similarity given by the relation
![]() $\sim$
defined next:
$\sim$
defined next:
Definition 5.12 Let
![]() $\sim$
be the equivalence relation on windows such that
$\sim$
be the equivalence relation on windows such that
![]() $\mathcal{W} \sim \mathcal{W}'$
if and only if
$\mathcal{W} \sim \mathcal{W}'$
if and only if
![]() $\mathcal{W}'$
is obtained by increasing all time points mentioned in
$\mathcal{W}'$
is obtained by increasing all time points mentioned in
![]() $\mathcal{W}$
by some integer c. Let
$\mathcal{W}$
by some integer c. Let
![]() $[\mathcal{W}]_\sim$
be the equivalence class of
$[\mathcal{W}]_\sim$
be the equivalence class of
![]() $\mathcal{W}$
with respect to
$\mathcal{W}$
with respect to
![]() $\sim$
. Then, for any
$\sim$
. Then, for any
![]() ${X \in \{ \mathcal{A},\mathcal{B},\mathcal{C} \}}$
and any initial window
${X \in \{ \mathcal{A},\mathcal{B},\mathcal{C} \}}$
and any initial window
![]() $\mathcal{W}_0$
, if automaton
$\mathcal{W}_0$
, if automaton
![]() ${X_{\mathcal{W}_0^L}^\gets = (\mathcal{Q}, \Sigma, \delta, q_0,F)}$
is well-defined, then
${X_{\mathcal{W}_0^L}^\gets = (\mathcal{Q}, \Sigma, \delta, q_0,F)}$
is well-defined, then
![]() ${\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets = (\widetilde{\mathcal{Q}},\widetilde{\Sigma}, \widetilde{\delta}, \widetilde{q_0},\widetilde{F})}$
is the nondeterministic Büchi automaton defined as follows:
${\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets = (\widetilde{\mathcal{Q}},\widetilde{\Sigma}, \widetilde{\delta}, \widetilde{q_0},\widetilde{F})}$
is the nondeterministic Büchi automaton defined as follows:
-
1.
 $\widetilde{\mathcal{Q}}$
is the quotient set of
$\widetilde{\mathcal{Q}}$
is the quotient set of
 $\mathcal{Q}$
by the relation
$\mathcal{Q}$
by the relation
 $\sim$
,
$\sim$
, -
2.
 $\widetilde{\Sigma} = \Sigma$
,
$\widetilde{\Sigma} = \Sigma$
, -
3.
 $\widetilde{\delta}$
is such that, for any
$\widetilde{\delta}$
is such that, for any
 $q,q' \in \widetilde{\mathcal{Q}}$
and
$q,q' \in \widetilde{\mathcal{Q}}$
and
 $\sigma \in \Sigma$
, it holds that
$\sigma \in \Sigma$
, it holds that
 $q' \in \widetilde{\delta}(q,\sigma)$
if and only if there exist
$q' \in \widetilde{\delta}(q,\sigma)$
if and only if there exist
 $\mathcal{W},\mathcal{W}' \in \mathcal{Q}$
such that
$\mathcal{W},\mathcal{W}' \in \mathcal{Q}$
such that
 $[\mathcal{W}]_\sim = q$
,
$[\mathcal{W}]_\sim = q$
,
 $[\mathcal{W}']_\sim = q'$
, and
$[\mathcal{W}']_\sim = q'$
, and
 $q' \in \delta(q,\sigma)$
,
$q' \in \delta(q,\sigma)$
, -
4.
 $\widetilde{q_0} = [q_0]_\sim$
,
$\widetilde{q_0} = [q_0]_\sim$
, -
5.
 $\widetilde{F}=\{ S_1', \dots, S_n' \}$
is a family of subsets of
$\widetilde{F}=\{ S_1', \dots, S_n' \}$
is a family of subsets of
 $\widetilde{\mathcal{Q}}$
such that
$\widetilde{\mathcal{Q}}$
such that
 $q \in S_i'$
if and only if there exists
$q \in S_i'$
if and only if there exists
 $\mathcal{W} \in S_i$
such that
$\mathcal{W} \in S_i$
such that
 $[\mathcal{W}]_\sim = q$
; and if
$[\mathcal{W}]_\sim = q$
; and if
 ${X_{\mathcal{W}_0^R}^\to = (\mathcal{Q}, \Sigma, \delta, q_0,F)}$
is well-defined, then automaton
${X_{\mathcal{W}_0^R}^\to = (\mathcal{Q}, \Sigma, \delta, q_0,F)}$
is well-defined, then automaton
 $\widetilde{X}_{[\mathcal{W}_0^{R}]_\sim}^\to$
is defined analogously.
$\widetilde{X}_{[\mathcal{W}_0^{R}]_\sim}^\to$
is defined analogously.
Now we show that the new automata
![]() ${\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets }$
and
${\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets }$
and
![]() ${\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\to }$
are equivalent to the previously defined automata
${\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\to }$
are equivalent to the previously defined automata
![]() $X_{\mathcal{W}_0^L}^\gets$
an
$X_{\mathcal{W}_0^L}^\gets$
an
![]() $X_{\mathcal{W}_0^L}^\to$
, respectively.
$X_{\mathcal{W}_0^L}^\to$
, respectively.
Lemma 5.13 Let
![]() $X \in \{ \mathcal{A},\mathcal{B},\mathcal{C} \}$
and let
$X \in \{ \mathcal{A},\mathcal{B},\mathcal{C} \}$
and let
![]() $\mathcal{W}_0 = (\varrho_0,H_0,T_0,b_0)$
be an initial window locally satisfying
$\mathcal{W}_0 = (\varrho_0,H_0,T_0,b_0)$
be an initial window locally satisfying
![]() $\Pi$
such that
$\Pi$
such that
![]() $X_{\mathcal{W}_0}^\gets$
and
$X_{\mathcal{W}_0}^\gets$
and
![]() $X_{\mathcal{W}_0}^\to$
are well-defined. Then,
$X_{\mathcal{W}_0}^\to$
are well-defined. Then,
![]() $X_{\mathcal{W}_0^{L}}^\gets$
and
$X_{\mathcal{W}_0^{L}}^\gets$
and
![]() $X_{\mathcal{W}_0^{R}}^\to$
are equivalent to
$X_{\mathcal{W}_0^{R}}^\to$
are equivalent to
![]() $\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
and
$\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
and
![]() $\widetilde{X}_{[\mathcal{W}_0^{R}]_\sim}^\to$
, respectively.
$\widetilde{X}_{[\mathcal{W}_0^{R}]_\sim}^\to$
, respectively.
Proof. Assume that
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
![]() $X_{\mathcal{W}_0^L}^\gets$
on a word w. Then, by Definition 5.12,
$X_{\mathcal{W}_0^L}^\gets$
on a word w. Then, by Definition 5.12,
![]() $[\mathcal{W}_0]_\sim, [\mathcal{W}_{-1}]_\sim, \dots$
are states of
$[\mathcal{W}_0]_\sim, [\mathcal{W}_{-1}]_\sim, \dots$
are states of
![]() $\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
and
$\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
and
![]() $[\mathcal{W}_0]_\sim = [\mathcal{W}_0^{L}]_\sim$
. Moreover, by the definition of the transition function and the accepting conditions of
$[\mathcal{W}_0]_\sim = [\mathcal{W}_0^{L}]_\sim$
. Moreover, by the definition of the transition function and the accepting conditions of
![]() $\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
, the fact that
$\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
, the fact that
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
![]() $X_{\mathcal{W}_0^L}^\gets$
on w implies that
$X_{\mathcal{W}_0^L}^\gets$
on w implies that
![]() $[\mathcal{W}_0]_\sim, [\mathcal{W}_{-1}]_\sim, \dots$
is an accepting run of
$[\mathcal{W}_0]_\sim, [\mathcal{W}_{-1}]_\sim, \dots$
is an accepting run of
![]() $\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
on the same word w. Similarly, we can show that if
$\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
on the same word w. Similarly, we can show that if
![]() $X_{\mathcal{W}_0^R}^\to$
accepts w, then so does
$X_{\mathcal{W}_0^R}^\to$
accepts w, then so does
![]() $\widetilde{X}_{[\mathcal{W}_0^{R}]_\sim}^\to$
.
$\widetilde{X}_{[\mathcal{W}_0^{R}]_\sim}^\to$
.
For the opposite direction, let us assume that
![]() $q_0, q_{-1}, \dots$
is an accepting run of
$q_0, q_{-1}, \dots$
is an accepting run of
![]() $\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
on a word w. For each integer
$\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
on a word w. For each integer
![]() $i < 0$
, we let
$i < 0$
, we let
![]() $\mathcal{W}_i = (\varrho_i,H_i,T_i,b_i)$
be a state of
$\mathcal{W}_i = (\varrho_i,H_i,T_i,b_i)$
be a state of
![]() $X_{\mathcal{W}_0^L}^\gets$
such that
$X_{\mathcal{W}_0^L}^\gets$
such that
![]() $[\mathcal{W}_i]_\sim = q_i$
and
$[\mathcal{W}_i]_\sim = q_i$
and
![]() ${\varrho_i = [\varrho_0^- + i, \varrho_0^+ + i]}$
; such states are guaranteed to exist by definition of
${\varrho_i = [\varrho_0^- + i, \varrho_0^+ + i]}$
; such states are guaranteed to exist by definition of
![]() $X_{[\mathcal{W}_0^L]_{\sim}}^\gets$
. We show that
$X_{[\mathcal{W}_0^L]_{\sim}}^\gets$
. We show that
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
![]() $X_{\mathcal{W}_0^L}^\gets$
on w. To this end, we will show that for every integer
$X_{\mathcal{W}_0^L}^\gets$
on w. To this end, we will show that for every integer
![]() $i \leq 0$
and every symbol
$i \leq 0$
and every symbol
![]() $\sigma$
, if
$\sigma$
, if
![]() $q_{i-1} \in \widetilde{\delta}(q_i,\sigma)$
, then
$q_{i-1} \in \widetilde{\delta}(q_i,\sigma)$
, then
![]() $\mathcal{W}_{i-1} \in \delta (\mathcal{W}_i, \sigma)$
, where
$\mathcal{W}_{i-1} \in \delta (\mathcal{W}_i, \sigma)$
, where
![]() $\widetilde{\delta}$
and
$\widetilde{\delta}$
and
![]() $\delta$
are the transition functions of
$\delta$
are the transition functions of
![]() $\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
and
$\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
and
![]() $X_{\mathcal{W}_0^L}^\gets$
, respectively. Indeed, by definition, if
$X_{\mathcal{W}_0^L}^\gets$
, respectively. Indeed, by definition, if
![]() ${ q_{i-1} \in \widetilde{\delta}(q_i,\sigma) }$
, then there are states
${ q_{i-1} \in \widetilde{\delta}(q_i,\sigma) }$
, then there are states
![]() $\mathcal{W}$
and
$\mathcal{W}$
and
![]() $ \mathcal{W}' $
of
$ \mathcal{W}' $
of
![]() $X_{\mathcal{W}_0^L}^\gets$
such that
$X_{\mathcal{W}_0^L}^\gets$
such that
![]() $[\mathcal{W}]_\sim = q_i$
,
$[\mathcal{W}]_\sim = q_i$
,
![]() $[\mathcal{W}']_\sim = q_{i-1}$
, and
$[\mathcal{W}']_\sim = q_{i-1}$
, and
![]() $\mathcal{W}' \in \delta (\mathcal{W}, \sigma)$
. Hence,
$\mathcal{W}' \in \delta (\mathcal{W}, \sigma)$
. Hence,
![]() $\mathcal{W}_i \sim \mathcal{W}$
and
$\mathcal{W}_i \sim \mathcal{W}$
and
![]() $\mathcal{W}_{i-1} \sim \mathcal{W}'$
. This, by the definition of
$\mathcal{W}_{i-1} \sim \mathcal{W}'$
. This, by the definition of
![]() $\sim$
and the fact that
$\sim$
and the fact that
![]() $\mathcal{W}' \in \delta (\mathcal{W}, \sigma)$
, implies that
$\mathcal{W}' \in \delta (\mathcal{W}, \sigma)$
, implies that
![]() $\mathcal{W}_{i-1} \in \delta (\mathcal{W}_i, \sigma)$
. Therefore,
$\mathcal{W}_{i-1} \in \delta (\mathcal{W}_i, \sigma)$
. Therefore,
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is a run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is a run of
![]() $X_{\mathcal{W}_0^L}^\gets$
on w. Finally, since
$X_{\mathcal{W}_0^L}^\gets$
on w. Finally, since
![]() $q_0, q_{-1}, \dots$
is an accepting run of
$q_0, q_{-1}, \dots$
is an accepting run of
![]() $\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
, by the definition of accepting conditions, we obtain that
$\widetilde{X}_{[\mathcal{W}_0^{L}]_\sim}^\gets$
, by the definition of accepting conditions, we obtain that
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
is an accepting run of
![]() $X_{\mathcal{W}_0^L}^\gets$
. The same argumentation shows that if
$X_{\mathcal{W}_0^L}^\gets$
. The same argumentation shows that if
![]() $\widetilde{X}_{[\mathcal{W}_0^{R}]_\sim}^\to$
accepts w, then
$\widetilde{X}_{[\mathcal{W}_0^{R}]_\sim}^\to$
accepts w, then
![]() $X_{\mathcal{W}_0^R}^\to$
also does so.
$X_{\mathcal{W}_0^R}^\to$
also does so.
We are now ready to show
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
data complexity of reasoning in
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
data complexity of reasoning in
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
over
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
over
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
Theorem 5.14 Checking whether a
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program and a dataset have a stable model over the integer timeline is in
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program and a dataset have a stable model over the integer timeline is in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
with respect to data complexity.
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
with respect to data complexity.
Proof. It suffices to show that checking existence of
![]() $\mathcal{W}_0$
,
$\mathcal{W}_0$
,
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() ${{{\overrightarrow{w}}}}$
Theorem 5.8 is feasible in
${{{\overrightarrow{w}}}}$
Theorem 5.8 is feasible in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
in the size of (the representation of)
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
in the size of (the representation of)
![]() $\mathcal{D}$
. First, we observe that the length of
$\mathcal{D}$
. First, we observe that the length of
![]() $\varrho_{(\Pi,\mathcal{D})}$
is exponential, and so is the representation of windows over
$\varrho_{(\Pi,\mathcal{D})}$
is exponential, and so is the representation of windows over
![]() $\varrho_0 = \varrho_{(\Pi,\mathcal{D})}$
. Thus, it is feasible in
$\varrho_0 = \varrho_{(\Pi,\mathcal{D})}$
. Thus, it is feasible in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
to guess a tuple
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
to guess a tuple
![]() ${\mathcal{W}_0=(\varrho_0,T_0, T_0, 0)}$
as well as to verify that it is an initial window locally satisfying
${\mathcal{W}_0=(\varrho_0,T_0, T_0, 0)}$
as well as to verify that it is an initial window locally satisfying
![]() $\Pi$
and such that
$\Pi$
and such that
![]() ${T_0 \models \mathcal{D}}$
, as required in Theorem 5.8.
${T_0 \models \mathcal{D}}$
, as required in Theorem 5.8.
Thus, it remains to check existence of
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() ${{{\overrightarrow{w}}}}$
satisfying Conditions 1 and 2 from Theorem 5.8. To this end, we will treat a candidate pair of words
${{{\overrightarrow{w}}}}$
satisfying Conditions 1 and 2 from Theorem 5.8. To this end, we will treat a candidate pair of words
![]() ${w_1=\sigma_{-1} \sigma_{-2} \cdots}$
and
${w_1=\sigma_{-1} \sigma_{-2} \cdots}$
and
![]() ${w_2=\sigma_1 \sigma_2 \cdots}$
as a single word
${w_2=\sigma_1 \sigma_2 \cdots}$
as a single word
![]() $w_1w_2 = {(\sigma_{-1}, \sigma_{1}) ( \sigma_{-2}, \sigma_2) \cdots}$
and combine pairs of corresponding automata so that they accept combined words. In particular, for automata X and Y, we let XY be an automaton which on a word
$w_1w_2 = {(\sigma_{-1}, \sigma_{1}) ( \sigma_{-2}, \sigma_2) \cdots}$
and combine pairs of corresponding automata so that they accept combined words. In particular, for automata X and Y, we let XY be an automaton which on a word
![]() $w_1w_2$
simulates the run of X on
$w_1w_2$
simulates the run of X on
![]() $w_1$
and the run of Y on
$w_1$
and the run of Y on
![]() $w_2$
, simultaneously. Such an automaton XY is polynomially bigger than X and Y as its states are pairs consisting of a state of X and a state of Y. Thus, checking existence of
$w_2$
, simultaneously. Such an automaton XY is polynomially bigger than X and Y as its states are pairs consisting of a state of X and a state of Y. Thus, checking existence of
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() ${{{\overrightarrow{w}}}}$
from Theorem 5.8. reduces to checking existence of
${{{\overrightarrow{w}}}}$
from Theorem 5.8. reduces to checking existence of
![]() ${{{\overleftarrow{w}}}}{{{\overrightarrow{w}}}}$
such that
${{{\overleftarrow{w}}}}{{{\overrightarrow{w}}}}$
such that
-
(i)
 ${{{\overleftarrow{w}}}}{{{\overrightarrow{w}}}}$
is accepted by
${{{\overleftarrow{w}}}}{{{\overrightarrow{w}}}}$
is accepted by
 $\mathcal{B}^\gets_{\mathcal{W}_0} \mathcal{B}^\to_{\mathcal{W}_0}$
(Condition 1) and
$\mathcal{B}^\gets_{\mathcal{W}_0} \mathcal{B}^\to_{\mathcal{W}_0}$
(Condition 1) and -
(ii) there exists no
 $\mathcal{W}_0'$
(satisfying properties from Condition 2) such that
$\mathcal{W}_0'$
(satisfying properties from Condition 2) such that
 ${{{\overleftarrow{w}}}}{{{\overrightarrow{w}}}}$
is accepted by
${{{\overleftarrow{w}}}}{{{\overrightarrow{w}}}}$
is accepted by
 $\mathcal{C}^\gets_{\mathcal{W}_0'} \mathcal{A}^\to_{\mathcal{W}_0'}$
or by
$\mathcal{C}^\gets_{\mathcal{W}_0'} \mathcal{A}^\to_{\mathcal{W}_0'}$
or by
 $\mathcal{A}^\gets_{\mathcal{W}_0'} \mathcal{C}^\to_{\mathcal{W}_0'}$
.
$\mathcal{A}^\gets_{\mathcal{W}_0'} \mathcal{C}^\to_{\mathcal{W}_0'}$
.
By Lemmas 5.10 and 5.13, Item (i) reduces to checking if
![]() ${{{\overleftarrow{w}}}}{{{\overrightarrow{w}}}}$
is accepted by
${{{\overleftarrow{w}}}}{{{\overrightarrow{w}}}}$
is accepted by
![]() $\widetilde{\mathcal{B}}_{[\mathcal{W}_0^{L}]_\sim}^\gets \widetilde{\mathcal{B}}_{[\mathcal{W}_0^{R}]_\sim}^\to$
and Item (ii) reduces to checking non-existence of
$\widetilde{\mathcal{B}}_{[\mathcal{W}_0^{L}]_\sim}^\gets \widetilde{\mathcal{B}}_{[\mathcal{W}_0^{R}]_\sim}^\to$
and Item (ii) reduces to checking non-existence of
![]() $\mathcal{W}_0'=(\varrho_0,H_0,T_0,b)$
(satisfying properties from Condition 2) such that
$\mathcal{W}_0'=(\varrho_0,H_0,T_0,b)$
(satisfying properties from Condition 2) such that
![]() ${{{\overleftarrow{w}}}}{{{\overrightarrow{w}}}}$
is accepted by the union of the automata
${{{\overleftarrow{w}}}}{{{\overrightarrow{w}}}}$
is accepted by the union of the automata
![]() $\widetilde{\mathcal{C}}_{[(\mathcal{W}_0')^{L}]_\sim}^\gets \widetilde{\mathcal{A}}_{[(\mathcal{W}_0)'^{R}]_\sim}^\to$
and
$\widetilde{\mathcal{C}}_{[(\mathcal{W}_0')^{L}]_\sim}^\gets \widetilde{\mathcal{A}}_{[(\mathcal{W}_0)'^{R}]_\sim}^\to$
and
![]() $\widetilde{\mathcal{C}}_{[(\mathcal{W}_0)'^{L}]_\sim}^\gets \widetilde{\mathcal{A}}_{[(\mathcal{W}_0')^{R}]_\sim}^\to$
, if
$\widetilde{\mathcal{C}}_{[(\mathcal{W}_0)'^{L}]_\sim}^\gets \widetilde{\mathcal{A}}_{[(\mathcal{W}_0')^{R}]_\sim}^\to$
, if
![]() $H_0=T_0$
; or by the automaton
$H_0=T_0$
; or by the automaton
![]() $\widetilde{\mathcal{A}}_{[(\mathcal{W}_0')^{L}]_\sim}^\gets \widetilde{\mathcal{A}}_{[(\mathcal{W}_0')^{R}]_\sim}^\to$
, if
$\widetilde{\mathcal{A}}_{[(\mathcal{W}_0')^{L}]_\sim}^\gets \widetilde{\mathcal{A}}_{[(\mathcal{W}_0')^{R}]_\sim}^\to$
, if
![]() $H_0 \neq T_0$
.
$H_0 \neq T_0$
.
To perform these checks in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
, we will characterise each initial window of the form
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
, we will characterise each initial window of the form
![]() ${\mathcal{W}'_0=(\varrho_0,H_0, T_0, b_0)}$
locally satisfying
${\mathcal{W}'_0=(\varrho_0,H_0, T_0, b_0)}$
locally satisfying
![]() $\Pi$
and such that
$\Pi$
and such that
![]() $H_0 \models \mathcal{D}$
– as mentioned in Condition 2 of Theorem 5.8 – by a triple consisting of two initial windows
$H_0 \models \mathcal{D}$
– as mentioned in Condition 2 of Theorem 5.8 – by a triple consisting of two initial windows
![]() $(\mathcal{W}'_{0})^L$
,
$(\mathcal{W}'_{0})^L$
,
![]() $(\mathcal{W}'_{0})^R$
, and a flag
$(\mathcal{W}'_{0})^R$
, and a flag
![]() ${b \in \{0,1\}}$
such that
${b \in \{0,1\}}$
such that
![]() $b=1$
if and only if
$b=1$
if and only if
![]() $H_0 \neq T_0$
(so several windows can be characterised by the same triple). Now, we will show that a set
$H_0 \neq T_0$
(so several windows can be characterised by the same triple). Now, we will show that a set
![]() $\mathcal{T}$
of all triples characterising all such windows
$\mathcal{T}$
of all triples characterising all such windows
![]() $\mathcal{W}_0'$
can be constructed in
$\mathcal{W}_0'$
can be constructed in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
. We observe that all
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
. We observe that all
![]() $(\mathcal{W}'_{0})^L$
are over the same interval
$(\mathcal{W}'_{0})^L$
are over the same interval
![]() $\varrho^L$
, which is independent from the choice of the window
$\varrho^L$
, which is independent from the choice of the window
![]() $\mathcal{W}_0'$
, since all
$\mathcal{W}_0'$
, since all
![]() $\mathcal{W}_0'$
are over the same interval
$\mathcal{W}_0'$
are over the same interval
![]() $\varrho_{(\Pi,\mathcal{D})}$
. Similarly,
$\varrho_{(\Pi,\mathcal{D})}$
. Similarly,
![]() $(\mathcal{W}'_{0})^R$
are over the same interval
$(\mathcal{W}'_{0})^R$
are over the same interval
![]() $\varrho^R$
, which is independent from the choice of
$\varrho^R$
, which is independent from the choice of
![]() $\mathcal{W}_0'$
. Moreover, these
$\mathcal{W}_0'$
. Moreover, these
![]() $\varrho^L$
and
$\varrho^L$
and
![]() $\varrho^R$
are polynomially long, and so, each
$\varrho^R$
are polynomially long, and so, each
![]() $(\mathcal{W}'_{0})^L$
and
$(\mathcal{W}'_{0})^L$
and
![]() $(\mathcal{W}'_{0})^R$
has a polynomial representation. Thus, there are exponentially many triples
$(\mathcal{W}'_{0})^R$
has a polynomial representation. Thus, there are exponentially many triples
![]() $(\mathcal{W}_1,\mathcal{W}_2,b)$
which need to be checked for membership in
$(\mathcal{W}_1,\mathcal{W}_2,b)$
which need to be checked for membership in
![]() $\mathcal{T}$
. Our
$\mathcal{T}$
. Our
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
procedure iterates through all these triples. For each triple
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
procedure iterates through all these triples. For each triple
![]() $(\mathcal{W}_1,\mathcal{W}_2,b)$
, the procedure checks if there exists an initial window
$(\mathcal{W}_1,\mathcal{W}_2,b)$
, the procedure checks if there exists an initial window
![]() ${\mathcal{W}'_0=(\varrho_0,H_0, T_0, b_0)}$
locally satisfying
${\mathcal{W}'_0=(\varrho_0,H_0, T_0, b_0)}$
locally satisfying
![]() $\Pi$
such that
$\Pi$
such that
![]() $H_0 \models \mathcal{D}$
,
$H_0 \models \mathcal{D}$
,
![]() $(\mathcal{W}'_{0})^L=\mathcal{W}_1$
,
$(\mathcal{W}'_{0})^L=\mathcal{W}_1$
,
![]() $(\mathcal{W}'_{0})^R=\mathcal{W}_2$
, and
$(\mathcal{W}'_{0})^R=\mathcal{W}_2$
, and
![]() $b=1$
if and only if
$b=1$
if and only if
![]() $H_0 \neq T_0$
. All these checks are feasible in
$H_0 \neq T_0$
. All these checks are feasible in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
, and if they yield positive answers, then
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
, and if they yield positive answers, then
![]() $(\mathcal{W}_1,\mathcal{W}_2,b) \in \mathcal{T}$
.
$(\mathcal{W}_1,\mathcal{W}_2,b) \in \mathcal{T}$
.
We observe that checking Items (i) and (ii) reduces to checking non-emptiness of an automaton obtained by intersecting
![]() $\widetilde{\mathcal{B}}_{[\mathcal{W}_0^{L}]_\sim}^\gets \widetilde{\mathcal{B}}_{[\mathcal{W}_0^{R}]_\sim}^\to$
with complements of all the automata corresponding to triples from
$\widetilde{\mathcal{B}}_{[\mathcal{W}_0^{L}]_\sim}^\gets \widetilde{\mathcal{B}}_{[\mathcal{W}_0^{R}]_\sim}^\to$
with complements of all the automata corresponding to triples from
![]() $\mathcal{T}$
, where we say that a triple
$\mathcal{T}$
, where we say that a triple
![]() ${( (\mathcal{W}'_{0})^L, (\mathcal{W}'_{0})^R, b) \in \mathcal{T}}$
corresponds to the automaton which is the intersection of
${( (\mathcal{W}'_{0})^L, (\mathcal{W}'_{0})^R, b) \in \mathcal{T}}$
corresponds to the automaton which is the intersection of
![]() $\widetilde{\mathcal{C}}_{[(\mathcal{W}_0')^{L}]_\sim}^\gets \widetilde{\mathcal{A}}_{[(\mathcal{W}_0)'^{R}]_\sim}^\to$
and
$\widetilde{\mathcal{C}}_{[(\mathcal{W}_0')^{L}]_\sim}^\gets \widetilde{\mathcal{A}}_{[(\mathcal{W}_0)'^{R}]_\sim}^\to$
and
![]() $\widetilde{\mathcal{C}}_{[(\mathcal{W}_0)'^{L}]_\sim}^\gets \widetilde{\mathcal{A}}_{[(\mathcal{W}_0')^{R}]_\sim}^\to$
, if
$\widetilde{\mathcal{C}}_{[(\mathcal{W}_0)'^{L}]_\sim}^\gets \widetilde{\mathcal{A}}_{[(\mathcal{W}_0')^{R}]_\sim}^\to$
, if
![]() $b=0$
; and which is
$b=0$
; and which is
![]() $\widetilde{\mathcal{A}}_{[(\mathcal{W}_0')^{L}]_\sim}^\gets \widetilde{\mathcal{A}}_{[(\mathcal{W}_0')^{R}]_\sim}^\to$
, if
$\widetilde{\mathcal{A}}_{[(\mathcal{W}_0')^{L}]_\sim}^\gets \widetilde{\mathcal{A}}_{[(\mathcal{W}_0')^{R}]_\sim}^\to$
, if
![]() $b=1$
. To conclude, we show that this check is feasible in
$b=1$
. To conclude, we show that this check is feasible in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
. Indeed, by construction, all automata mentioned above have states that can be represented in polynomial space. However, since these automata are nondeterministic, their complements have states of exponential size. To intersect the exponentially many such complemented automata, we construct an automaton whose states are exponentially long tuples, whose ith element is a state of the ith complemented automata. Such an exponentially long tuple of exponentially large states is itself exponentially representable. Thus, the obtained automaton has exponentially big states. Checking non-emptiness of this automaton is feasible in
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
. Indeed, by construction, all automata mentioned above have states that can be represented in polynomial space. However, since these automata are nondeterministic, their complements have states of exponential size. To intersect the exponentially many such complemented automata, we construct an automaton whose states are exponentially long tuples, whose ith element is a state of the ith complemented automata. Such an exponentially long tuple of exponentially large states is itself exponentially representable. Thus, the obtained automaton has exponentially big states. Checking non-emptiness of this automaton is feasible in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
using the standard on-the-fly approach, where states are guessed one-by-one (Baier and Katoen Reference Baier and Katoen2008).
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
using the standard on-the-fly approach, where states are guessed one-by-one (Baier and Katoen Reference Baier and Katoen2008).
The procedure outlined in the proof of the theorem shows that reasoning in
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
over the integer timeline is in
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
over the integer timeline is in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
in data complexity. In the next section, we show how restricting the form of
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
in data complexity. In the next section, we show how restricting the form of
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
programs to the forward-propagating fragment allows us to establish a tight
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
programs to the forward-propagating fragment allows us to establish a tight
![]() ${{\rm PS}{\small\rm PACE}}$
bound for data complexity.
${{\rm PS}{\small\rm PACE}}$
bound for data complexity.
5.2 Forward-propagating programs
In this section, we consider reasoning with forward-propagating programs (see Definition 3.1) and bounded datasets. This setting has already been studied in the context of stream reasoning (Ronca et al. Reference Ronca, Kaminski, Cuenca Grau and Horrocks2018; Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019).
The normalisation of a
![]() ${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
program, as defined in Section 5.1, results also in a
${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
program, as defined in Section 5.1, results also in a
![]() ${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
program; thus, for the remainder of this section, we let
${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
program; thus, for the remainder of this section, we let
![]() $\Pi$
be a fixed (but arbitrary)
$\Pi$
be a fixed (but arbitrary)
![]() ${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
program in normal form and let
${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
program in normal form and let
![]() $\mathcal{D}$
be a bounded dataset.
$\mathcal{D}$
be a bounded dataset.
Restricting ourselves to forward-propagating programs and bounded datasets will enable a simplification of the procedure in Section 5.1, where we check existence of a stable model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
by looking for an initial window
$\mathcal{D}$
by looking for an initial window
![]() $\mathcal{W}_0$
and a pair of words
$\mathcal{W}_0$
and a pair of words
![]() ${{{\overleftarrow{w}}}}$
,
${{{\overleftarrow{w}}}}$
,
![]() ${{{\overrightarrow{w}}}}$
satisfying the conditions in Theorem 5.8. Towards this goal, we first show in Lemma 5.16 that we can guess the initial window
${{{\overrightarrow{w}}}}$
satisfying the conditions in Theorem 5.8. Towards this goal, we first show in Lemma 5.16 that we can guess the initial window
![]() $\mathcal{W}_0$
over an interval located to the left of all intervals in
$\mathcal{W}_0$
over an interval located to the left of all intervals in
![]() $\mathcal{D}$
, instead of
$\mathcal{D}$
, instead of
![]() $\varrho_{(\Pi,\mathcal{D})}$
as in the previous section. Furthermore, we can use the fact that
$\varrho_{(\Pi,\mathcal{D})}$
as in the previous section. Furthermore, we can use the fact that
![]() $\Pi$
is forward-propagating to show that checking existence of word
$\Pi$
is forward-propagating to show that checking existence of word
![]() ${{{\overleftarrow{w}}}}$
can be done independently of
${{{\overleftarrow{w}}}}$
can be done independently of
![]() $\mathcal{D}$
. Finally, to check existence of word
$\mathcal{D}$
. Finally, to check existence of word
![]() ${{{\overrightarrow{w}}}}$
, we define a new family of automata of the form
${{{\overrightarrow{w}}}}$
, we define a new family of automata of the form
![]() $\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
, which can be used instead of
$\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
, which can be used instead of
![]() $X_{\mathcal{W}_0}^\rightarrow$
, for
$X_{\mathcal{W}_0}^\rightarrow$
, for
![]() $X \in \{\mathcal{A},\mathcal{B},\mathcal{C}\}$
; doing so requires no complementation, and thus we avoid the exponential blowup. As a result, the procedure becomes feasible in polynomial space.
$X \in \{\mathcal{A},\mathcal{B},\mathcal{C}\}$
; doing so requires no complementation, and thus we avoid the exponential blowup. As a result, the procedure becomes feasible in polynomial space.
We next define a new automaton
![]() $\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
as a refinement of
$\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
as a refinement of
![]() $\mathcal{B}_{\mathcal{W}_0}^\rightarrow$
. Furthermore, we impose an additional restriction on states of
$\mathcal{B}_{\mathcal{W}_0}^\rightarrow$
. Furthermore, we impose an additional restriction on states of
![]() $\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
to guarantee their minimality, as described below.
$\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
to guarantee their minimality, as described below.
Definition 5.15 We say that a window
![]() $(\varrho,H,T,b)$
locally satisfies
$(\varrho,H,T,b)$
locally satisfies
![]() $\mathcal{D}$
if
$\mathcal{D}$
if
![]() $M @ t \in H$
for each
$M @ t \in H$
for each
![]() ${M \in \mathsf{at}(\Pi,\mathcal{D})}$
and each
${M \in \mathsf{at}(\Pi,\mathcal{D})}$
and each
![]() $t \in \varrho$
such that
$t \in \varrho$
such that
![]() ${\mathcal{D} \models M@t}$
. Let
${\mathcal{D} \models M@t}$
. Let
![]() $\mathcal{W}_0=(\varrho_0,T_0,T_0,0)$
be an initial window locally satisfying
$\mathcal{W}_0=(\varrho_0,T_0,T_0,0)$
be an initial window locally satisfying
![]() $\Pi$
(see Definition 5.3) and
$\Pi$
(see Definition 5.3) and
![]() $\mathcal{D}$
. We define the generalised Büchi automaton
$\mathcal{D}$
. We define the generalised Büchi automaton
![]() $\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
analogously to the automaton
$\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
analogously to the automaton
![]() $\mathcal{B}_{\mathcal{W}_0}^\rightarrow$
in Definition 5.7, except that:
$\mathcal{B}_{\mathcal{W}_0}^\rightarrow$
in Definition 5.7, except that:
-
states in
 $\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
are additionally required to locally satisfy
$\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
are additionally required to locally satisfy
 $\mathcal{D}$
, and
$\mathcal{D}$
, and -
the transition function is additionally restricted so that transitions to a window
 $(\varrho,T,T,0)$
are only allowed if there exists no window
$(\varrho,T,T,0)$
are only allowed if there exists no window
 $(\varrho,H,T,1)$
locally satisfying
$(\varrho,H,T,1)$
locally satisfying
 $\Pi$
and
$\Pi$
and
 $\mathcal{D}$
such that H and T coincide over
$\mathcal{D}$
such that H and T coincide over
 $[\varrho^{-},\varrho^{+}-1]$
and
$[\varrho^{-},\varrho^{+}-1]$
and
 $M@\varrho^+ \in T \backslash H$
for some relational atom M.
$M@\varrho^+ \in T \backslash H$
for some relational atom M.
Note that
![]() $\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
is essentially deterministic since
$\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
is essentially deterministic since
![]() $\delta(\mathcal{W},\sigma)$
contains at most one window for every state
$\delta(\mathcal{W},\sigma)$
contains at most one window for every state
![]() $\mathcal{W}$
and
$\mathcal{W}$
and
![]() $\sigma \in \Sigma$
. The following lemma provides the result analogous to Theorem 5.8 for the setting considered in this section.
$\sigma \in \Sigma$
. The following lemma provides the result analogous to Theorem 5.8 for the setting considered in this section.
Lemma 5.16 Program
![]() $\Pi$
and dataset
$\Pi$
and dataset
![]() $\mathcal{D}$
have a stable model if and only if there exists an initial window
$\mathcal{D}$
have a stable model if and only if there exists an initial window
![]() ${\mathcal{W}_0=(\varrho_0,T_0, T_0, 0)}$
locally satisfying
${\mathcal{W}_0=(\varrho_0,T_0, T_0, 0)}$
locally satisfying
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
with
$\mathcal{D}$
with
![]() $\varrho_0= [t^{\min}_{\mathcal{D}}- (t_\Pi +1), t^{\min}_{\mathcal{D}}-1]$
, which mentions only constants and predicates from
$\varrho_0= [t^{\min}_{\mathcal{D}}- (t_\Pi +1), t^{\min}_{\mathcal{D}}-1]$
, which mentions only constants and predicates from
![]() $\Pi$
, and there exist words
$\Pi$
, and there exist words
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() ${{{\overrightarrow{w}}}}$
over
${{{\overrightarrow{w}}}}$
over
![]() $2^{\mathsf{at}(\Pi, {\mathcal{D}})}$
such that all of the following conditions hold:
$2^{\mathsf{at}(\Pi, {\mathcal{D}})}$
such that all of the following conditions hold:
-
1.
 ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
 ${{{\overrightarrow{w}}}}$
are accepted by
${{{\overrightarrow{w}}}}$
are accepted by
 $\mathcal{B}_{\mathcal{W}_0}^\gets$
and
$\mathcal{B}_{\mathcal{W}_0}^\gets$
and
 $\mathcal{F}_{\mathcal{W}_0}^\to$
, respectively,
$\mathcal{F}_{\mathcal{W}_0}^\to$
, respectively, -
2. there is no initial window
 ${\mathcal{W}'_0=(\varrho_0,H_0, T_0, b_0)}$
locally satisfying
${\mathcal{W}'_0=(\varrho_0,H_0, T_0, b_0)}$
locally satisfying
 $\Pi$
and
$\Pi$
and
 $\mathcal{D}$
such that
$\mathcal{D}$
such that
 ${{{\overleftarrow{w}}}}$
is accepted by
${{{\overleftarrow{w}}}}$
is accepted by
 $\mathcal{C}_{\mathcal{W}'_0}^\gets$
,
$\mathcal{C}_{\mathcal{W}'_0}^\gets$
, -
3.
 ${{{\overleftarrow{w}}}}$
mentions only constants and predicates from
${{{\overleftarrow{w}}}}$
mentions only constants and predicates from
 $\Pi$
.
$\Pi$
.
Proof. Assume that
![]() $\mathfrak{T}$
is a stable model of
$\mathfrak{T}$
is a stable model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. To construct the required
$\mathcal{D}$
. To construct the required
![]() $\mathcal{W}_0$
,
$\mathcal{W}_0$
,
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() ${{{\overrightarrow{w}}}}$
, we let
${{{\overrightarrow{w}}}}$
, we let
![]() $\dots, \mathcal{W}_{-1}, \mathcal{W}_0, \mathcal{W}_1, \dots$
be the
$\dots, \mathcal{W}_{-1}, \mathcal{W}_0, \mathcal{W}_1, \dots$
be the
![]() ${[t^{\min}_{\mathcal{D}} - (t_\Pi +1), t^{\min}_{\mathcal{D}}-1]}$
-decomposition of HT-interpretation
${[t^{\min}_{\mathcal{D}} - (t_\Pi +1), t^{\min}_{\mathcal{D}}-1]}$
-decomposition of HT-interpretation
![]() $(\mathfrak{T},\mathfrak{T})$
, and we let
$(\mathfrak{T},\mathfrak{T})$
, and we let
![]() ${\mathcal{W}_i= (\varrho_i, H_i, T_i, b_i)}$
. Moreover, we let
${\mathcal{W}_i= (\varrho_i, H_i, T_i, b_i)}$
. Moreover, we let
![]() ${{{{\overleftarrow{w}}}}= \sigma_{-1} \sigma_{-2} \cdots}$
and
${{{{\overleftarrow{w}}}}= \sigma_{-1} \sigma_{-2} \cdots}$
and
![]() ${{{{\overrightarrow{w}}}}= \sigma_{1} \sigma_{2} \cdots}$
be the words such that
${{{{\overrightarrow{w}}}}= \sigma_{1} \sigma_{2} \cdots}$
be the words such that
![]() $\sigma_k = T_k \setminus T_{k+1}$
if
$\sigma_k = T_k \setminus T_{k+1}$
if
![]() $k<0$
, and
$k<0$
, and
![]() $T_k \setminus T_{k-1} $
if
$T_k \setminus T_{k-1} $
if
![]() ${k>0}$
. In what follows, we will show that the above defined
${k>0}$
. In what follows, we will show that the above defined
![]() $\mathcal{W}_0$
,
$\mathcal{W}_0$
,
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() ${{{\overrightarrow{w}}}}$
satisfy the requirements from the lemma. First, we observe that
${{{\overrightarrow{w}}}}$
satisfy the requirements from the lemma. First, we observe that
![]() $H_i=T_i$
and
$H_i=T_i$
and
![]() $b_i=0$
, for each
$b_i=0$
, for each
![]() $i \in \mathbb{Z}$
. Furthermore, by Lemma 5.6, each
$i \in \mathbb{Z}$
. Furthermore, by Lemma 5.6, each
![]() $\mathcal{W}_i$
is a window locally satisfying
$\mathcal{W}_i$
is a window locally satisfying
![]() $\Pi$
and, since
$\Pi$
and, since
![]() $\mathfrak{T}$
is a stable model of
$\mathfrak{T}$
is a stable model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, we obtain that each
$\mathcal{D}$
, we obtain that each
![]() $\mathcal{W}_i$
locally satisfies
$\mathcal{W}_i$
locally satisfies
![]() $\mathcal{D}$
. Therefore, as required in the lemma,
$\mathcal{D}$
. Therefore, as required in the lemma,
![]() $\mathcal{W}_0$
is an initial window of the form
$\mathcal{W}_0$
is an initial window of the form
![]() $(\varrho_0,T_0, T_0, 0)$
with
$(\varrho_0,T_0, T_0, 0)$
with
![]() $\varrho_0= [t^{\min}_{\mathcal{D}}- (t_\Pi +1), t^{\min}_{\mathcal{D}}- 1]$
, and it locally satisfies
$\varrho_0= [t^{\min}_{\mathcal{D}}- (t_\Pi +1), t^{\min}_{\mathcal{D}}- 1]$
, and it locally satisfies
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. Thus, it remains to show that
$\mathcal{D}$
. Thus, it remains to show that
![]() $\mathcal{W}_0$
mentions only constants and predicates from
$\mathcal{W}_0$
mentions only constants and predicates from
![]() $\Pi$
and that
$\Pi$
and that
![]() $\mathcal{W}_0$
,
$\mathcal{W}_0$
,
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() ${{{\overrightarrow{w}}}}$
satisfy Conditions 1–3.
${{{\overrightarrow{w}}}}$
satisfy Conditions 1–3.
To show that Condition 1 holds, we observe that, by Lemma 5.6,
![]() $\mathcal{W}_0,\mathcal{W}_{-1},\dots$
is an accepting run of
$\mathcal{W}_0,\mathcal{W}_{-1},\dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
; moreover, since
$\mathcal{A}_{\mathcal{W}_0}^\gets$
; moreover, since
![]() $H_i=T_i$
and
$H_i=T_i$
and
![]() $b_i=0$
for all integers
$b_i=0$
for all integers
![]() $i \leq 0$
, this run is also accepting for
$i \leq 0$
, this run is also accepting for
![]() $\mathcal{B}_{\mathcal{W}_0}^\gets$
. Analogously,
$\mathcal{B}_{\mathcal{W}_0}^\gets$
. Analogously,
![]() $\mathcal{W}_0,\mathcal{W}_{1},\dots$
is an accepting run of
$\mathcal{W}_0,\mathcal{W}_{1},\dots$
is an accepting run of
![]() $\mathcal{B}_{\mathcal{W}_0}^\to$
. Now, suppose towards a contradiction that
$\mathcal{B}_{\mathcal{W}_0}^\to$
. Now, suppose towards a contradiction that
![]() $\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
does not accept
$\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
does not accept
![]() ${{{\overrightarrow{w}}}}$
. Then, by Definition 5.15, there exists a smallest integer
${{{\overrightarrow{w}}}}$
. Then, by Definition 5.15, there exists a smallest integer
![]() $i > 0$
such that
$i > 0$
such that
![]() $\mathcal{W}_0, \dots , \mathcal{W}_{i-1}$
is a run of
$\mathcal{W}_0, \dots , \mathcal{W}_{i-1}$
is a run of
![]() $\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
on
$\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
on
![]() $\sigma_1 \cdots \sigma_{i-1}$
(where this word is empty if
$\sigma_1 \cdots \sigma_{i-1}$
(where this word is empty if
![]() $i=1$
), but
$i=1$
), but
![]() $\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
does not have a transition from
$\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
does not have a transition from
![]() $\mathcal{W}_{i-1}$
to
$\mathcal{W}_{i-1}$
to
![]() $\mathcal{W}_{i}$
on
$\mathcal{W}_{i}$
on
![]() $\sigma_{i}$
. Next, we will show how to define windows
$\sigma_{i}$
. Next, we will show how to define windows
![]() $\mathcal{W}'_i,\mathcal{W}'_{i+1}, \dots$
such that
$\mathcal{W}'_i,\mathcal{W}'_{i+1}, \dots$
such that
![]() $\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is an accepting run of
$\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is an accepting run of
![]() $\mathcal{C}_{\mathcal{W}_0}^{\to}$
on
$\mathcal{C}_{\mathcal{W}_0}^{\to}$
on
![]() ${{{\overrightarrow{w}}}}$
, which will allow us to raise a contradiction.
${{{\overrightarrow{w}}}}$
, which will allow us to raise a contradiction.
Claim 5.17 There exist windows
![]() $\mathcal{W}'_i,\mathcal{W}'_{i+1}, \dots$
locally satisfying
$\mathcal{W}'_i,\mathcal{W}'_{i+1}, \dots$
locally satisfying
![]() $\mathcal{D}$
such that
$\mathcal{D}$
such that
![]() $\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is an accepting run of
$\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is an accepting run of
![]() $\mathcal{C}_{\mathcal{W}_0}^{\to}$
on
$\mathcal{C}_{\mathcal{W}_0}^{\to}$
on
![]() ${{{\overrightarrow{w}}}}$
.
${{{\overrightarrow{w}}}}$
.
Proof of Claim 5.17
Recall that
![]() $\mathcal{W}_{i} = (\varrho_i,T_i,T_i,0)$
. Since
$\mathcal{W}_{i} = (\varrho_i,T_i,T_i,0)$
. Since
![]() $\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
does not have a transition from
$\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
does not have a transition from
![]() $\mathcal{W}_{i-1}$
to
$\mathcal{W}_{i-1}$
to
![]() $\mathcal{W}_{i}$
on
$\mathcal{W}_{i}$
on
![]() $\sigma_{i}$
, there exists a window
$\sigma_{i}$
, there exists a window
![]() ${\mathcal{W}' =(\varrho_i,H',T_i,1)}$
locally satisfying
${\mathcal{W}' =(\varrho_i,H',T_i,1)}$
locally satisfying
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
such that H’ coincides with
$\mathcal{D}$
such that H’ coincides with
![]() $T_i$
over
$T_i$
over
![]() $[\varrho^-_i,\varrho^+_{i-1}]$
, and there exists an atom
$[\varrho^-_i,\varrho^+_{i-1}]$
, and there exists an atom
![]() $M' \in \mathsf{at}{(\Pi,\mathcal{D})}$
satisfying
$M' \in \mathsf{at}{(\Pi,\mathcal{D})}$
satisfying
![]() ${M'@\varrho_i^+ \in T_i \backslash H' }$
. We note also that since
${M'@\varrho_i^+ \in T_i \backslash H' }$
. We note also that since
![]() $\mathcal{W}'$
is a window and
$\mathcal{W}'$
is a window and
![]() $H' \subseteq T_i$
, there exists an interpretation
$H' \subseteq T_i$
, there exists an interpretation
![]() $\mathfrak{H}'$
such that
$\mathfrak{H}'$
such that
![]() $\mathfrak{H}' \subseteq \mathfrak{T}$
and both items from Definition 5.2 hold. We will use
$\mathfrak{H}' \subseteq \mathfrak{T}$
and both items from Definition 5.2 hold. We will use
![]() $\mathfrak{H}'$
to define
$\mathfrak{H}'$
to define
![]() $\mathcal{W}'_i,\mathcal{W}'_{i+1}, \dots$
. To this end, we will say that an HT-interpretation
$\mathcal{W}'_i,\mathcal{W}'_{i+1}, \dots$
. To this end, we will say that an HT-interpretation
![]() $(\mathfrak{H}^*,\mathfrak{T}^*)$
satisfies a dataset
$(\mathfrak{H}^*,\mathfrak{T}^*)$
satisfies a dataset
![]() $\mathcal{D}$
and program
$\mathcal{D}$
and program
![]() $\Pi$
over an interval
$\Pi$
over an interval
![]() $\varrho^*$
if and only if
$\varrho^*$
if and only if
-
for every
 $M@\varrho \in \mathcal{D}$
and
$M@\varrho \in \mathcal{D}$
and
 $t \in \varrho \cap \varrho^*$
we have
$t \in \varrho \cap \varrho^*$
we have
 $\mathfrak{H}^*,t \models M$
, and
$\mathfrak{H}^*,t \models M$
, and -
 $(\mathfrak{H}^*,\mathfrak{T}^*)$
satisfy the conditions of Definition 3.2 for each
$(\mathfrak{H}^*,\mathfrak{T}^*)$
satisfy the conditions of Definition 3.2 for each
 $t \in \varrho^*$
.
$t \in \varrho^*$
.
We can use a construction similar to that in the proof of Theorem 3.4 to define the least interpretation
![]() $\mathfrak{H}$
such that
$\mathfrak{H}$
such that
![]() $\mathfrak{H}' \subseteq \mathfrak{H} \subseteq \mathfrak{T}$
,
$\mathfrak{H}' \subseteq \mathfrak{H} \subseteq \mathfrak{T}$
,
![]() $\mathfrak{H}$
coincides with
$\mathfrak{H}$
coincides with
![]() $\mathfrak{H}'$
over
$\mathfrak{H}'$
over
![]() $(-\infty,\varrho_i^-)$
, and
$(-\infty,\varrho_i^-)$
, and
![]() $(\mathfrak{H},\mathfrak{T})$
satisfies
$(\mathfrak{H},\mathfrak{T})$
satisfies
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\Pi$
over
$\Pi$
over
![]() $[\varrho_i^{-}, \infty)$
. An important observation is that since
$[\varrho_i^{-}, \infty)$
. An important observation is that since
![]() $\Pi$
is forward-propagating and
$\Pi$
is forward-propagating and
![]() $\mathcal{W}'$
locally satisfies
$\mathcal{W}'$
locally satisfies
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, interpretations
$\mathcal{D}$
, interpretations
![]() $\mathfrak{H}'$
and
$\mathfrak{H}'$
and
![]() $\mathfrak{H}$
also coincide over the interval
$\mathfrak{H}$
also coincide over the interval
![]() $\varrho_i$
.
$\varrho_i$
.
Now, we let
![]() $\dots, \mathcal{W}'_{-1}, \mathcal{W}'_0, \mathcal{W}'_1, \dots$
, with
$\dots, \mathcal{W}'_{-1}, \mathcal{W}'_0, \mathcal{W}'_1, \dots$
, with
![]() $\mathcal{W}'_j = (\varrho'_j,H'_j,T'_j,b'_j)$
, be the
$\mathcal{W}'_j = (\varrho'_j,H'_j,T'_j,b'_j)$
, be the
![]() $\varrho_0$
-decomposition of
$\varrho_0$
-decomposition of
![]() $(\mathfrak{H},\mathfrak{T})$
; hence,
$(\mathfrak{H},\mathfrak{T})$
; hence,
![]() $\varrho'_j = \varrho_j$
and
$\varrho'_j = \varrho_j$
and
![]() $T'_j = T_j$
, for each j. We observe also that since
$T'_j = T_j$
, for each j. We observe also that since
![]() $\mathfrak{H}$
coincides with
$\mathfrak{H}$
coincides with
![]() $\mathfrak{H}'$
over
$\mathfrak{H}'$
over
![]() $(-\infty,\varrho_i^+]$
,
$(-\infty,\varrho_i^+]$
,
![]() $H'_i$
agrees with H’ on all relational atoms over
$H'_i$
agrees with H’ on all relational atoms over
![]() $(-\infty,\varrho_i^+]$
, so
$(-\infty,\varrho_i^+]$
, so
![]() $M'@t \in T_i \backslash H'_i$
, and hence
$M'@t \in T_i \backslash H'_i$
, and hence
![]() $b'_j=1$
for each
$b'_j=1$
for each
![]() $j \geq i$
.
$j \geq i$
.
We will show that
![]() $\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is an accepting run of
$\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_0}^{\to}$
on
$\mathcal{A}_{\mathcal{W}_0}^{\to}$
on
![]() ${{{\overrightarrow{w}}}}$
where all windows locally satisfy
${{{\overrightarrow{w}}}}$
where all windows locally satisfy
![]() $\mathcal{D}$
, and then, we will show that this run is also accepted by
$\mathcal{D}$
, and then, we will show that this run is also accepted by
![]() $\mathcal{C}_{\mathcal{W}_0}^{\to}$
. To this end, we observe that since
$\mathcal{C}_{\mathcal{W}_0}^{\to}$
. To this end, we observe that since
![]() $\mathcal{W}_0, \dots , \mathcal{W}_{i-1}$
is a run of
$\mathcal{W}_0, \dots , \mathcal{W}_{i-1}$
is a run of
![]() $\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
on
$\mathcal{F}_{\mathcal{W}_0}^\rightarrow$
on
![]() $\sigma_1 \cdots \sigma_{i-1}$
, it is also a run of
$\sigma_1 \cdots \sigma_{i-1}$
, it is also a run of
![]() $\mathcal{A}_{\mathcal{W}_0}^\rightarrow$
on
$\mathcal{A}_{\mathcal{W}_0}^\rightarrow$
on
![]() $\sigma_1 \cdots \sigma_{i-1}$
. Moreover,
$\sigma_1 \cdots \sigma_{i-1}$
. Moreover,
![]() $\mathcal{W}'_i$
is an initial window, (since
$\mathcal{W}'_i$
is an initial window, (since
![]() $H'_i \neq T_i$
and
$H'_i \neq T_i$
and
![]() $b'_i=1$
) and, by an argument analogous to the proof of Lemma 5.6, each
$b'_i=1$
) and, by an argument analogous to the proof of Lemma 5.6, each
![]() $\mathcal{W}'_j$
for
$\mathcal{W}'_j$
for
![]() $j \geq i$
locally satisfies
$j \geq i$
locally satisfies
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, and
$\mathcal{D}$
, and
![]() $\mathcal{W}'_j , \mathcal{W}'_{j+1}, \dots$
is an accepting run of
$\mathcal{W}'_j , \mathcal{W}'_{j+1}, \dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}'_i}^{\to}$
on
$\mathcal{A}_{\mathcal{W}'_i}^{\to}$
on
![]() $\sigma_{i+1}, \sigma_{i+2}, \dots$
. Hence, to show that
$\sigma_{i+1}, \sigma_{i+2}, \dots$
. Hence, to show that
![]() $\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is an accepting run of
$\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is an accepting run of
![]() $\mathcal{A}^{\to}_{\mathcal{W}_0}$
, it remains to show that
$\mathcal{A}^{\to}_{\mathcal{W}_0}$
, it remains to show that
![]() $\mathcal{A}^{\to}_{\mathcal{W}_{0}}$
has a transition on
$\mathcal{A}^{\to}_{\mathcal{W}_{0}}$
has a transition on
![]() $\sigma_{i}$
from
$\sigma_{i}$
from
![]() $\mathcal{W}_{i-1}$
to
$\mathcal{W}_{i-1}$
to
![]() $\mathcal{W}'_i$
. To do this, we first show that
$\mathcal{W}'_i$
. To do this, we first show that
![]() $H'_i$
coincides with H’ over
$H'_i$
coincides with H’ over
![]() $[\varrho_i^{-},\varrho_{i-1}^{+}]$
. Indeed, consider an arbitrary fact
$[\varrho_i^{-},\varrho_{i-1}^{+}]$
. Indeed, consider an arbitrary fact
![]() $M@t$
with
$M@t$
with
![]() $M \in \mathsf{at}{(\Pi,\mathcal{D})}$
and
$M \in \mathsf{at}{(\Pi,\mathcal{D})}$
and
![]() $t \in [\varrho_i^{-},\varrho_{i-1}^{+}]$
; we will show that
$t \in [\varrho_i^{-},\varrho_{i-1}^{+}]$
; we will show that
![]() $M@t \in H'_i$
if and only if
$M@t \in H'_i$
if and only if
![]() $M@t \in H'$
. Note that since
$M@t \in H'$
. Note that since
![]() $\Pi$
is forward-propagating, any atom
$\Pi$
is forward-propagating, any atom
![]() $M \in \mathsf{at}{(\Pi,\mathcal{D})}$
is either of the form
$M \in \mathsf{at}{(\Pi,\mathcal{D})}$
is either of the form
![]() $\boxplus_{[0,\infty)} P(\mathbf{c})$
for some relational fact
$\boxplus_{[0,\infty)} P(\mathbf{c})$
for some relational fact
![]() $P(\mathbf{c})$
, or it does not mention future operators. Thus, if M does not mention future operators, the biconditional holds because
$P(\mathbf{c})$
, or it does not mention future operators. Thus, if M does not mention future operators, the biconditional holds because
![]() $\mathfrak{H}$
and
$\mathfrak{H}$
and
![]() $\mathfrak{H}'$
coincide over the interval
$\mathfrak{H}'$
coincide over the interval
![]() $(-\infty,\varrho_i^+]$
. Now, suppose M is of the form
$(-\infty,\varrho_i^+]$
. Now, suppose M is of the form
![]() $\boxplus_{[0,\infty)} P(\mathbf{c})$
. If
$\boxplus_{[0,\infty)} P(\mathbf{c})$
. If
![]() $\boxplus_{[0,\infty)} P(\mathbf{c}) @ t \in H'$
, then
$\boxplus_{[0,\infty)} P(\mathbf{c}) @ t \in H'$
, then
![]() $\boxplus_{[0,\infty)} P(\mathbf{c}) @ t \in H'_i$
since
$\boxplus_{[0,\infty)} P(\mathbf{c}) @ t \in H'_i$
since
![]() $H'\subseteq H'_i$
by construction of
$H'\subseteq H'_i$
by construction of
![]() $H'_i$
. Conversely, if
$H'_i$
. Conversely, if
![]() $\boxplus_{[0,\infty)} P(\mathbf{c}) @ t \in H'_i$
, we have that
$\boxplus_{[0,\infty)} P(\mathbf{c}) @ t \in H'_i$
, we have that
![]() $\mathfrak{H},t \models \boxplus_{[0,\infty)} P(\mathbf{c}) $
, and since
$\mathfrak{H},t \models \boxplus_{[0,\infty)} P(\mathbf{c}) $
, and since
![]() $\mathfrak{H} \subseteq \mathfrak{T}$
, we have
$\mathfrak{H} \subseteq \mathfrak{T}$
, we have
![]() $\mathfrak{T},t \models \boxplus_{[0,\infty)} P(\mathbf{c}) $
, so
$\mathfrak{T},t \models \boxplus_{[0,\infty)} P(\mathbf{c}) $
, so
![]() $\boxplus_{[0,\infty)} P(\mathbf{c}) @ t \in T_i$
. Then, since H’ agrees with
$\boxplus_{[0,\infty)} P(\mathbf{c}) @ t \in T_i$
. Then, since H’ agrees with
![]() $T_i$
over
$T_i$
over
![]() $[\varrho_i^{-},\varrho_{i-1}^{+}]$
, we conclude that
$[\varrho_i^{-},\varrho_{i-1}^{+}]$
, we conclude that
![]() $\boxplus_{[0,\infty)} P(\mathbf{c}) @ t \in H'$
. Thus, the biconditional also holds in this case. With the above result, we can show that there is a transition in
$\boxplus_{[0,\infty)} P(\mathbf{c}) @ t \in H'$
. Thus, the biconditional also holds in this case. With the above result, we can show that there is a transition in
![]() $\mathcal{A}^{\to}_{\mathcal{W}_{0}}$
from
$\mathcal{A}^{\to}_{\mathcal{W}_{0}}$
from
![]() $\mathcal{W}_{i-1}$
to
$\mathcal{W}_{i-1}$
to
![]() $\mathcal{W}'_i$
; we can see this by checking that all the four conditions from Item 3 in Definition 5.4 hold. The first, third, and fourth conditions hold directly by the definition of
$\mathcal{W}'_i$
; we can see this by checking that all the four conditions from Item 3 in Definition 5.4 hold. The first, third, and fourth conditions hold directly by the definition of
![]() $\mathcal{W}'_i$
and the fact that
$\mathcal{W}'_i$
and the fact that
![]() $\varrho'_i = \varrho_i$
,
$\varrho'_i = \varrho_i$
,
![]() $T'_i = T_i$
, and
$T'_i = T_i$
, and
![]() $b'_i=1$
. The second condition states that
$b'_i=1$
. The second condition states that
![]() $H'_i$
and
$H'_i$
and
![]() $H_{i-1}$
must coincide over the interval
$H_{i-1}$
must coincide over the interval
![]() $\varrho_{i-1} \cap \varrho_i$
. To see this, recall that
$\varrho_{i-1} \cap \varrho_i$
. To see this, recall that
![]() $H'_i$
coincides with H’ over this interval. In turn, H’ coincides with
$H'_i$
coincides with H’ over this interval. In turn, H’ coincides with
![]() $T_i$
over this interval by definition, and
$T_i$
over this interval by definition, and
![]() $T_i$
coincides with
$T_i$
coincides with
![]() $T_{i-1}$
over this interval by construction, but
$T_{i-1}$
over this interval by construction, but
![]() $T_{i-1}=H_{i-1}$
, so
$T_{i-1}=H_{i-1}$
, so
![]() $H'_i$
coincides with
$H'_i$
coincides with
![]() $H_{i-1}$
and the condition holds. Therefore,
$H_{i-1}$
and the condition holds. Therefore,
![]() $\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is an accepting run of
$\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_0}^{\to}$
on
$\mathcal{A}_{\mathcal{W}_0}^{\to}$
on
![]() ${{{\overrightarrow{w}}}}$
where all windows locally satisfy
${{{\overrightarrow{w}}}}$
where all windows locally satisfy
![]() $\mathcal{D}$
.
$\mathcal{D}$
.
Furthermore,
![]() $\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is also an accepting run of
$\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is also an accepting run of
![]() $\mathcal{C}_{\mathcal{W}_0}^{\to}$
on
$\mathcal{C}_{\mathcal{W}_0}^{\to}$
on
![]() ${{{\overrightarrow{w}}}}$
, since every window in the run after
${{{\overrightarrow{w}}}}$
, since every window in the run after
![]() $\mathcal{W}'_i$
has 1 as its fourth component, and so the additional accepting condition of
$\mathcal{W}'_i$
has 1 as its fourth component, and so the additional accepting condition of
![]() $\mathcal{C}_{\mathcal{W}_0}^{\to}$
is satisfied. This concludes the proof of Claim 5.17.
$\mathcal{C}_{\mathcal{W}_0}^{\to}$
is satisfied. This concludes the proof of Claim 5.17.
Having proved the claim, we resume the proof of Lemma 5.16. Recall that
![]() $\mathcal{W}_0,\mathcal{W}_{-1},\dots$
is an accepting run of
$\mathcal{W}_0,\mathcal{W}_{-1},\dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}_0}^\gets$
on
$\mathcal{A}_{\mathcal{W}_0}^\gets$
on
![]() ${{{\overleftarrow{w}}}}$
and, as we showed in the claim above,
${{{\overleftarrow{w}}}}$
and, as we showed in the claim above,
![]() $\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is an accepting run of
$\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
is an accepting run of
![]() $\mathcal{C}_{\mathcal{W}_0}^{\to}$
on
$\mathcal{C}_{\mathcal{W}_0}^{\to}$
on
![]() ${{{\overrightarrow{w}}}}$
. Hence, as in the proof of Theorem 5.8, we can use these runs to construct an HT-model
${{{\overrightarrow{w}}}}$
. Hence, as in the proof of Theorem 5.8, we can use these runs to construct an HT-model
![]() $(\mathfrak{H}'',\mathfrak{T})$
of
$(\mathfrak{H}'',\mathfrak{T})$
of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
such that
$\mathcal{D}$
such that
![]() $\mathfrak{H}'' \subsetneq \mathfrak{T}$
; in particular,
$\mathfrak{H}'' \subsetneq \mathfrak{T}$
; in particular,
![]() $\mathfrak{H}'' \models \mathcal{D}$
, as
$\mathfrak{H}'' \models \mathcal{D}$
, as
![]() $\varrho_0^{-}$
is to the left of any integer mentioned in
$\varrho_0^{-}$
is to the left of any integer mentioned in
![]() $\mathcal{D}$
and each window in the run
$\mathcal{D}$
and each window in the run
![]() $\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
locally satisfies
$\mathcal{W}_0, \dots, \mathcal{W}_{i-1}, \mathcal{W}'_i, \mathcal{W}'_{i+1}, \dots$
locally satisfies
![]() $\mathcal{D}$
. This, however, means that
$\mathcal{D}$
. This, however, means that
![]() $\mathfrak{T}$
is not a stable model of
$\mathfrak{T}$
is not a stable model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, which raises a contradiction.
$\mathcal{D}$
, which raises a contradiction.
To prove Condition 2, suppose towards a contradiction that there exists an initial window
![]() ${\mathcal{W}'_0=(\varrho_0, H_0,T_0,b_0)}$
which locally satisfies
${\mathcal{W}'_0=(\varrho_0, H_0,T_0,b_0)}$
which locally satisfies
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, and such that there exits an accepting run
$\mathcal{D}$
, and such that there exits an accepting run
![]() $\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
of
$\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
of
![]() $\mathcal{C}_{\mathcal{W}'_0}^{\gets}$
on
$\mathcal{C}_{\mathcal{W}'_0}^{\gets}$
on
![]() ${{{\overleftarrow{w}}}}$
. We observe that, by definition of
${{{\overleftarrow{w}}}}$
. We observe that, by definition of
![]() ${{{\overleftarrow{w}}}}$
, each
${{{\overleftarrow{w}}}}$
, each
![]() $\mathcal{W}'_i$
is of the form
$\mathcal{W}'_i$
is of the form
![]() $(\varrho_i,H_i,T_i,b_i)$
, for some set
$(\varrho_i,H_i,T_i,b_i)$
, for some set
![]() $H_i$
of metric atoms and
$H_i$
of metric atoms and
![]() $b_i \in \{0,1\}$
. We consider the least model
$b_i \in \{0,1\}$
. We consider the least model
![]() $\mathfrak{H}'$
of all relational facts in
$\mathfrak{H}'$
of all relational facts in
![]() $\bigcup_{i \leq 0} H_i$
. The accepting conditions of
$\bigcup_{i \leq 0} H_i$
. The accepting conditions of
![]() $\mathcal{C}_{\mathcal{W}'_0}^{\gets}$
ensure that there is an atom
$\mathcal{C}_{\mathcal{W}'_0}^{\gets}$
ensure that there is an atom
![]() $P(\mathbf{c})$
and a time point
$P(\mathbf{c})$
and a time point
![]() $t \in (-\infty,\varrho_0^+]$
such that
$t \in (-\infty,\varrho_0^+]$
such that
![]() $\mathfrak{H}' ,t \not \models P(\mathbf{c})$
but
$\mathfrak{H}' ,t \not \models P(\mathbf{c})$
but
![]() $\mathfrak{T} ,t \models P(\mathbf{c})$
. By an argument analogous to that in the proof of Theorem 5.8, and using the facts that
$\mathfrak{T} ,t \models P(\mathbf{c})$
. By an argument analogous to that in the proof of Theorem 5.8, and using the facts that
![]() $\mathcal{W}'_0$
locally satisfies
$\mathcal{W}'_0$
locally satisfies
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\mathcal{W}'_i$
locally satisfies
$\mathcal{W}'_i$
locally satisfies
![]() $\Pi$
for each
$\Pi$
for each
![]() $i \leq 0$
, we obtain that
$i \leq 0$
, we obtain that
![]() $(\mathfrak{H}',\mathfrak{T})$
satisfies
$(\mathfrak{H}',\mathfrak{T})$
satisfies
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\Pi$
over
$\Pi$
over
![]() $(-\infty,\varrho_0^+]$
. Then, using a construction similar to that in the proof of Theorem 3.4, we can extend
$(-\infty,\varrho_0^+]$
. Then, using a construction similar to that in the proof of Theorem 3.4, we can extend
![]() $\mathfrak{H}'$
to the minimal interpretation
$\mathfrak{H}'$
to the minimal interpretation
![]() $\mathfrak{H}$
such that
$\mathfrak{H}$
such that
![]() $(\mathfrak{H},\mathfrak{T})$
is an HT-model of
$(\mathfrak{H},\mathfrak{T})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. Since
$\mathcal{D}$
. Since
![]() $\Pi$
is forward-propagating, and
$\Pi$
is forward-propagating, and
![]() $(\mathfrak{H}',\mathfrak{T})$
already satisfies
$(\mathfrak{H}',\mathfrak{T})$
already satisfies
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $\Pi$
over
$\Pi$
over
![]() $(-\infty,\varrho_0^+]$
, we have that
$(-\infty,\varrho_0^+]$
, we have that
![]() $\mathfrak{H}$
and
$\mathfrak{H}$
and
![]() $\mathfrak{H}'$
agree over
$\mathfrak{H}'$
agree over
![]() $(-\infty,\varrho_0^+]$
. But then,
$(-\infty,\varrho_0^+]$
. But then,
![]() $\mathfrak{H} \subsetneq \mathfrak{T}$
since, as we have shown, there is
$\mathfrak{H} \subsetneq \mathfrak{T}$
since, as we have shown, there is
![]() $t \in (-\infty,\varrho_0^+]$
such that
$t \in (-\infty,\varrho_0^+]$
such that
![]() ${ \mathfrak{H}' ,t \not \models P(\mathbf{c}) }$
but
${ \mathfrak{H}' ,t \not \models P(\mathbf{c}) }$
but
![]() ${ \mathfrak{T} ,t \models P(\mathbf{c}) }$
. Thus,
${ \mathfrak{T} ,t \models P(\mathbf{c}) }$
. Thus,
![]() $\mathfrak{T}$
is not stable, which raises a contradiction.
$\mathfrak{T}$
is not stable, which raises a contradiction.
To prove Condition 3, we define a sequence
![]() $\mathfrak{H}_0, \mathfrak{H}_1,\dots$
of interpretations as follows:
$\mathfrak{H}_0, \mathfrak{H}_1,\dots$
of interpretations as follows:
-
 $\mathfrak{H}_0$
is the least model of
$\mathfrak{H}_0$
is the least model of
 $\mathcal{D}$
,
$\mathcal{D}$
, -
 $\mathfrak{H}_\alpha$
, for a successor ordinal
$\mathfrak{H}_\alpha$
, for a successor ordinal
 $\alpha$
, is the least interpretation such that for each rule of Form (1) in
$\alpha$
, is the least interpretation such that for each rule of Form (1) in
 $\mathsf{ground}(\Pi)$
, and for each time point t, if
$\mathsf{ground}(\Pi)$
, and for each time point t, if
 ${\mathfrak{H}_{\alpha-1},t \models M_i}$
for each
${\mathfrak{H}_{\alpha-1},t \models M_i}$
for each
 $1 \leq i \leq k$
and
$1 \leq i \leq k$
and
 ${\mathfrak{T},t \not\models M_j}$
for each
${\mathfrak{T},t \not\models M_j}$
for each
 $k+1 \leq j \leq m$
, then
$k+1 \leq j \leq m$
, then
 ${\mathfrak{H}_{\alpha},t \models M}$
,
${\mathfrak{H}_{\alpha},t \models M}$
, -
 $\mathfrak{H}_{\alpha} $
, for a limit ordinal
$\mathfrak{H}_{\alpha} $
, for a limit ordinal
 $\alpha$
, is
$\alpha$
, is
 $\bigcup_{\beta < \alpha}\mathfrak{H}_\beta$
.
$\bigcup_{\beta < \alpha}\mathfrak{H}_\beta$
.
By the proof of Theorem 3.4, each
![]() $\mathfrak{H}_\alpha$
is well defined and
$\mathfrak{H}_\alpha$
is well defined and
![]() $\mathfrak{T} = \mathfrak{H}_{\omega_1}$
. Hence, to prove Condition 3, it suffices to show by transfinite induction that, for every ordinal
$\mathfrak{T} = \mathfrak{H}_{\omega_1}$
. Hence, to prove Condition 3, it suffices to show by transfinite induction that, for every ordinal
![]() $\alpha$
, if
$\alpha$
, if
![]() $\mathfrak{H}_\alpha,t \models P(\mathbf{c})$
for some relational atom
$\mathfrak{H}_\alpha,t \models P(\mathbf{c})$
for some relational atom
![]() $P(\mathbf{c})$
and
$P(\mathbf{c})$
and
![]() $t < t^{\min}_{\mathcal{D}}$
, then P and all constants in
$t < t^{\min}_{\mathcal{D}}$
, then P and all constants in
![]() $\mathbf{c}$
occur in
$\mathbf{c}$
occur in
![]() $\Pi$
. In the base case
$\Pi$
. In the base case
![]() $\mathfrak{H}_0$
is the least model of
$\mathfrak{H}_0$
is the least model of
![]() $\mathcal{D}$
. Since
$\mathcal{D}$
. Since
![]() $\mathcal{D}$
is bounded, all the facts it mentions are over intervals contained in
$\mathcal{D}$
is bounded, all the facts it mentions are over intervals contained in
![]() $[t^{\min}_{\mathcal{D}}, \infty)$
, and so, the statement holds. In the inductive step for a successor ordinal
$[t^{\min}_{\mathcal{D}}, \infty)$
, and so, the statement holds. In the inductive step for a successor ordinal
![]() $\alpha$
, we suppose towards a contradiction that
$\alpha$
, we suppose towards a contradiction that
![]() $\mathfrak{H}_\alpha, t \models P(\mathbf{c})$
and
$\mathfrak{H}_\alpha, t \models P(\mathbf{c})$
and
![]() $\mathfrak{H}_{\alpha-1}, t \not\models P(\mathbf{c})$
, for some relational atom
$\mathfrak{H}_{\alpha-1}, t \not\models P(\mathbf{c})$
, for some relational atom
![]() $P(\mathbf{c})$
and
$P(\mathbf{c})$
and
![]() $t < t^{\min}_{\mathcal{D}}$
, such that P or some constant in
$t < t^{\min}_{\mathcal{D}}$
, such that P or some constant in
![]() $\mathbf{c}$
does not occur in
$\mathbf{c}$
does not occur in
![]() $\Pi$
. Hence, there exists a rule r in
$\Pi$
. Hence, there exists a rule r in
![]() $\mathsf{ground}(\Pi,\mathcal{D})$
whose head is
$\mathsf{ground}(\Pi,\mathcal{D})$
whose head is
![]() $P(\mathbf{c})$
, whose positive body atoms are satisfied by
$P(\mathbf{c})$
, whose positive body atoms are satisfied by
![]() $\mathfrak{H}_{\alpha-1}$
at t, and whose negated body atoms are satisfied by
$\mathfrak{H}_{\alpha-1}$
at t, and whose negated body atoms are satisfied by
![]() $\mathfrak{T}$
at t. Thus, P appears in
$\mathfrak{T}$
at t. Thus, P appears in
![]() $\Pi$
, so there exists a constant c in
$\Pi$
, so there exists a constant c in
![]() $\mathbf{c}$
which does not appear in
$\mathbf{c}$
which does not appear in
![]() $\Pi$
. By the safety and the normal form of r, the constant c needs to occur in a relational atom M such that either M or
$\Pi$
. By the safety and the normal form of r, the constant c needs to occur in a relational atom M such that either M or
![]() $\boxminus_\varrho M$
, or
$\boxminus_\varrho M$
, or
![]() $M' \mathcal{S}_\varrho M$
is a positive body atom in r. Each of these cases, however, implies that
$M' \mathcal{S}_\varrho M$
is a positive body atom in r. Each of these cases, however, implies that
![]() $\mathfrak{H}_{\alpha-1}, t' \models M$
, for some
$\mathfrak{H}_{\alpha-1}, t' \models M$
, for some
![]() $t' \leq t$
, which violates the induction hypothesis. In the inductive step for a limit ordinal
$t' \leq t$
, which violates the induction hypothesis. In the inductive step for a limit ordinal
![]() $\alpha$
, we have
$\alpha$
, we have
![]() $\mathfrak{H}_{\alpha} = \bigcup_{\beta < \alpha}\mathfrak{H}_\beta$
; since the claim holds for each
$\mathfrak{H}_{\alpha} = \bigcup_{\beta < \alpha}\mathfrak{H}_\beta$
; since the claim holds for each
![]() $\mathfrak{H}_\beta$
by induction hypothesis, it holds also for
$\mathfrak{H}_\beta$
by induction hypothesis, it holds also for
![]() $\mathfrak{H}_{\alpha}$
.
$\mathfrak{H}_{\alpha}$
.
We observe that the above result not only shows that Condition 3 holds, but also that
![]() $\mathcal{W}_0$
mentions only constants and predicates from
$\mathcal{W}_0$
mentions only constants and predicates from
![]() $\Pi$
, which completes the proof of the first implication from the lemma.
$\Pi$
, which completes the proof of the first implication from the lemma.
To show the reverse implication from Lemma 5.16, let
![]() $\mathcal{W}_0 = (\varrho_0,T_0,T_0,0)$
,
$\mathcal{W}_0 = (\varrho_0,T_0,T_0,0)$
,
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() ${{{\overrightarrow{w}}}}$
be as described in Lemma 5.16. In particular, by Condition 2,
${{{\overrightarrow{w}}}}$
be as described in Lemma 5.16. In particular, by Condition 2,
![]() $\mathcal{B}_{\mathcal{W}_0}^\gets$
has an accepting run
$\mathcal{B}_{\mathcal{W}_0}^\gets$
has an accepting run
![]() $\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
on
$\mathcal{W}_0, \mathcal{W}_{-1}, \dots$
on
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() $\mathcal{F}_{\mathcal{W}_0}^\to$
has an accepting run
$\mathcal{F}_{\mathcal{W}_0}^\to$
has an accepting run
![]() $\mathcal{W}_0, \mathcal{W}_{1}, \dots$
on
$\mathcal{W}_0, \mathcal{W}_{1}, \dots$
on
![]() ${{{\overrightarrow{w}}}}$
, where we let
${{{\overrightarrow{w}}}}$
, where we let
![]() ${\mathcal{W}_i= (\varrho_i, T_i, T_i, 0)}$
. We will show that the least model
${\mathcal{W}_i= (\varrho_i, T_i, T_i, 0)}$
. We will show that the least model
![]() $\mathfrak{T}$
of relational facts in
$\mathfrak{T}$
of relational facts in
![]() $\bigcup_{i \in \mathbb{Z}} T_i$
is a stable model of
$\bigcup_{i \in \mathbb{Z}} T_i$
is a stable model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. Using an argument analogous to the proof of Theorem 5.8, we obtain that
$\mathcal{D}$
. Using an argument analogous to the proof of Theorem 5.8, we obtain that
![]() $(\mathfrak{T},\mathfrak{T})$
is an HT-model of
$(\mathfrak{T},\mathfrak{T})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. Now, suppose towards a contradiction that
$\mathcal{D}$
. Now, suppose towards a contradiction that
![]() $\mathfrak{T}$
is not a stable model, so there is an interpretation
$\mathfrak{T}$
is not a stable model, so there is an interpretation
![]() ${\mathfrak{H} \subsetneq \mathfrak{T}}$
such that
${\mathfrak{H} \subsetneq \mathfrak{T}}$
such that
![]() $(\mathfrak{H}, \mathfrak{T})$
is an HT-model of
$(\mathfrak{H}, \mathfrak{T})$
is an HT-model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
. We let
$\mathcal{D}$
. We let
![]() $\dots, \mathcal{W}'_{-1}, \mathcal{W}'_0, \mathcal{W}'_1, \dots$
be the
$\dots, \mathcal{W}'_{-1}, \mathcal{W}'_0, \mathcal{W}'_1, \dots$
be the
![]() ${[t^{\min}_{\mathcal{D}}- (t_\Pi +1), t^{\min}_{\mathcal{D}}-1]}$
-decomposition of
${[t^{\min}_{\mathcal{D}}- (t_\Pi +1), t^{\min}_{\mathcal{D}}-1]}$
-decomposition of
![]() $(\mathfrak{H},\mathfrak{T})$
, where we let
$(\mathfrak{H},\mathfrak{T})$
, where we let
![]() ${\mathcal{W}_i'= (\varrho_i', H_i', T_i', b_i')}$
. By construction,
${\mathcal{W}_i'= (\varrho_i', H_i', T_i', b_i')}$
. By construction,
![]() $\varrho'_i = \varrho_i$
and
$\varrho'_i = \varrho_i$
and
![]() $T'_i=T_i$
. Moreover, by Definition 5.5,
$T'_i=T_i$
. Moreover, by Definition 5.5,
![]() $\mathcal{W}'_0$
is an initial window, and it is straightforward to verify that
$\mathcal{W}'_0$
is an initial window, and it is straightforward to verify that
![]() $\mathcal{W}_i'$
locally satisfies
$\mathcal{W}_i'$
locally satisfies
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, for each
$\mathcal{D}$
, for each
![]() $i \in \mathbb{Z}$
. Now, by Lemma 5.6,
$i \in \mathbb{Z}$
. Now, by Lemma 5.6,
![]() $\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
is an accepting run of
$\mathcal{W}'_0, \mathcal{W}'_{-1}, \dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}'_0}^\gets$
on
$\mathcal{A}_{\mathcal{W}'_0}^\gets$
on
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() $\mathcal{W}'_0, \mathcal{W}'_{1}, \dots$
is an accepting run of
$\mathcal{W}'_0, \mathcal{W}'_{1}, \dots$
is an accepting run of
![]() $\mathcal{A}_{\mathcal{W}'_0}^\to$
on
$\mathcal{A}_{\mathcal{W}'_0}^\to$
on
![]() ${{{\overrightarrow{w}}}}$
. Since
${{{\overrightarrow{w}}}}$
. Since
![]() $\mathfrak{H} \subsetneq \mathfrak{T}$
, there exists
$\mathfrak{H} \subsetneq \mathfrak{T}$
, there exists
![]() $i \in \mathbb{Z}$
such that
$i \in \mathbb{Z}$
such that
![]() $\mathfrak{T}, \varrho_i^+ \models M$
but
$\mathfrak{T}, \varrho_i^+ \models M$
but
![]() $\mathfrak{H}, \varrho_i^+ \not \models M$
for some relational atom
$\mathfrak{H}, \varrho_i^+ \not \models M$
for some relational atom
![]() $M \in \mathsf{at}{(\Pi,\mathcal{D})}$
, which implies
$M \in \mathsf{at}{(\Pi,\mathcal{D})}$
, which implies
![]() $H_i \neq T_i$
. If
$H_i \neq T_i$
. If
![]() $i \leq 0$
, then
$i \leq 0$
, then
![]() $b'_j =1$
for all
$b'_j =1$
for all
![]() $j \leq i$
, and so
$j \leq i$
, and so
![]() $\mathcal{C}_{\mathcal{W}'_0}^\gets$
accepts
$\mathcal{C}_{\mathcal{W}'_0}^\gets$
accepts
![]() ${{{\overleftarrow{w}}}}$
, which contradicts Condition 2. Otherwise, let i be the least (positive) integer such that
${{{\overleftarrow{w}}}}$
, which contradicts Condition 2. Otherwise, let i be the least (positive) integer such that
![]() $\mathfrak{T}, \varrho_i^+ \models M$
but
$\mathfrak{T}, \varrho_i^+ \models M$
but
![]() $\mathfrak{H}, \varrho_i^+ \not \models M$
, for some relational atom
$\mathfrak{H}, \varrho_i^+ \not \models M$
, for some relational atom
![]() $M \in \mathsf{at}{(\Pi,\mathcal{D})}$
. Observe that this implies
$M \in \mathsf{at}{(\Pi,\mathcal{D})}$
. Observe that this implies
![]() $H'_j=T_j$
for each
$H'_j=T_j$
for each
![]() $j <i$
, and
$j <i$
, and
![]() $M@ \varrho_i^+ \in T_i \backslash H'_i$
. By construction,
$M@ \varrho_i^+ \in T_i \backslash H'_i$
. By construction,
![]() $H'_i$
coincides with
$H'_i$
coincides with
![]() $H'_{i-1}$
over
$H'_{i-1}$
over
![]() $[\varrho_i^-,\varrho_i^+-1]$
; however, since
$[\varrho_i^-,\varrho_i^+-1]$
; however, since
![]() $H'_{i-1}=T_{i-1}$
, and
$H'_{i-1}=T_{i-1}$
, and
![]() $T_{i-1}$
coincides with
$T_{i-1}$
coincides with
![]() $T_i$
over
$T_i$
over
![]() $[\varrho_i^-,\varrho_i^+-1]$
, we have that
$[\varrho_i^-,\varrho_i^+-1]$
, we have that
![]() $H'_i$
coincides with
$H'_i$
coincides with
![]() $T_i$
over this interval. To sum up, recall that
$T_i$
over this interval. To sum up, recall that
![]() $\mathcal{W}_i$
is of the form
$\mathcal{W}_i$
is of the form
![]() $(\varrho_i, T_i, T_i, 0)$
, whereas, by construction,
$(\varrho_i, T_i, T_i, 0)$
, whereas, by construction,
![]() $\mathcal{W}_i'$
is of the form
$\mathcal{W}_i'$
is of the form
![]() $(\varrho_i, H_i', T_i, 1)$
; furthermore,
$(\varrho_i, H_i', T_i, 1)$
; furthermore,
![]() $H_i'$
coincides with
$H_i'$
coincides with
![]() $T_i$
over
$T_i$
over
![]() $[\varrho_i^{-},\varrho_i^{+}-1]$
, and there exists a relational atom M with
$[\varrho_i^{-},\varrho_i^{+}-1]$
, and there exists a relational atom M with
![]() $M@\varrho^+ \in T_i \backslash H_i'$
. This, by Definition 5.15, implies that the automaton
$M@\varrho^+ \in T_i \backslash H_i'$
. This, by Definition 5.15, implies that the automaton
![]() $\mathcal{F}_{\mathcal{W}_0}^\to$
cannot have a transition to
$\mathcal{F}_{\mathcal{W}_0}^\to$
cannot have a transition to
![]() $\mathcal{W}_i$
, and so,
$\mathcal{W}_i$
, and so,
![]() $\mathcal{W}_0, \mathcal{W}_{1}, \dots$
is not an accepting run of
$\mathcal{W}_0, \mathcal{W}_{1}, \dots$
is not an accepting run of
![]() $\mathcal{F}_{\mathcal{W}_0}^\to$
on
$\mathcal{F}_{\mathcal{W}_0}^\to$
on
![]() ${{{\overrightarrow{w}}}}$
, which raises a contradiction.
${{{\overrightarrow{w}}}}$
, which raises a contradiction.
Next, we use Lemma 5.16 to establish a tight
![]() ${{\rm PS}{\small\rm PACE}}$
bound for reasoning in
${{\rm PS}{\small\rm PACE}}$
bound for reasoning in
![]() ${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
.
${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
.
Theorem 5.18 Checking whether a
![]() ${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
program and a bounded dataset have a stable model is
${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
program and a bounded dataset have a stable model is
![]() ${{\rm PS}{\small\rm PACE}}$
-complete with respect to data complexity.
${{\rm PS}{\small\rm PACE}}$
-complete with respect to data complexity.
Proof. For the lower bound, we observe that Wałęga et al. (Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2020a) showed
![]() ${{\rm PS}{\small\rm PACE}}$
-hardness in data complexity of checking existence of models for a class of programs which is strictly smaller than the class of positive
${{\rm PS}{\small\rm PACE}}$
-hardness in data complexity of checking existence of models for a class of programs which is strictly smaller than the class of positive
![]() ${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
programs. Their reduction can be modified in a straightforward way so that the involved dataset is bounded. Then, Theorem 3.7 directly implies that the same lower bound holds for all (i.e., not necessarily positive)
${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
programs. Their reduction can be modified in a straightforward way so that the involved dataset is bounded. Then, Theorem 3.7 directly implies that the same lower bound holds for all (i.e., not necessarily positive)
![]() ${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
programs, as required.
${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
programs, as required.
For the upper bound, by Lemma 5.16, it suffices to show that checking existence of a window
![]() $\mathcal{W}_0$
and words
$\mathcal{W}_0$
and words
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() ${{{\overrightarrow{w}}}}$
satisfying the properties described in the statement of the lemma is feasible in
${{{\overrightarrow{w}}}}$
satisfying the properties described in the statement of the lemma is feasible in
![]() ${{\rm PS}{\small\rm PACE}}$
. First, we observe that
${{\rm PS}{\small\rm PACE}}$
. First, we observe that
![]() $\mathcal{W}_0$
is over
$\mathcal{W}_0$
is over
![]() ${\varrho_0= [t^{\min}_{\mathcal{D}}-(t_\Pi +1), t^{\min}_{\mathcal{D}}-1]}$
, so its length does not depend on
${\varrho_0= [t^{\min}_{\mathcal{D}}-(t_\Pi +1), t^{\min}_{\mathcal{D}}-1]}$
, so its length does not depend on
![]() $\mathcal{D}$
. Hence,
$\mathcal{D}$
. Hence,
![]() $\mathcal{W}_0$
is polynomially large (in the size of the representation of
$\mathcal{W}_0$
is polynomially large (in the size of the representation of
![]() $\mathcal{D}$
), and so it can be guessed in
$\mathcal{D}$
), and so it can be guessed in
![]() ${{\rm PS}{\small\rm PACE}}$
; moreover, one can check in
${{\rm PS}{\small\rm PACE}}$
; moreover, one can check in
![]() ${{\rm PS}{\small\rm PACE}}$
whether
${{\rm PS}{\small\rm PACE}}$
whether
![]() $\mathcal{W}_0$
locally satisfies
$\mathcal{W}_0$
locally satisfies
![]() $\Pi$
and
$\Pi$
and
![]() $\mathcal{D}$
, and whether it mentions only constants and predicates from
$\mathcal{D}$
, and whether it mentions only constants and predicates from
![]() $\Pi$
. Next, we show how to verify existence of words
$\Pi$
. Next, we show how to verify existence of words
![]() ${{{\overleftarrow{w}}}}$
and
${{{\overleftarrow{w}}}}$
and
![]() ${{{\overrightarrow{w}}}}$
over
${{{\overrightarrow{w}}}}$
over
![]() $2^{\mathsf{at}{(\Pi,\mathcal{D})}}$
such that
$2^{\mathsf{at}{(\Pi,\mathcal{D})}}$
such that
![]() $\mathcal{W}_0$
,
$\mathcal{W}_0$
,
![]() ${{{\overleftarrow{w}}}}$
, and
${{{\overleftarrow{w}}}}$
, and
![]() ${{{\overrightarrow{w}}}}$
satisfy Conditions 1–3. To verify existence of a word
${{{\overrightarrow{w}}}}$
satisfy Conditions 1–3. To verify existence of a word
![]() ${{{\overleftarrow{w}}}}$
accepted by
${{{\overleftarrow{w}}}}$
accepted by
![]() $\mathcal{B}_{\mathcal{W}_0}^\gets$
(first part of Condition 1) which is not accepted by any
$\mathcal{B}_{\mathcal{W}_0}^\gets$
(first part of Condition 1) which is not accepted by any
![]() $\mathcal{C}_{\mathcal{W}'_0}^\gets$
(Condition 2) we can use the approach from the proof of Theorem 5.14. We observe that
$\mathcal{C}_{\mathcal{W}'_0}^\gets$
(Condition 2) we can use the approach from the proof of Theorem 5.14. We observe that
![]() $\mathcal{W}_0$
mentions only constants and predicates from
$\mathcal{W}_0$
mentions only constants and predicates from
![]() $\Pi$
, and so, the same holds for windows
$\Pi$
, and so, the same holds for windows
![]() $\mathcal{W}_0'$
from Condition 2. Moreover, by Condition 3,
$\mathcal{W}_0'$
from Condition 2. Moreover, by Condition 3,
![]() ${{{\overleftarrow{w}}}}$
also mentions only constants and predicates from
${{{\overleftarrow{w}}}}$
also mentions only constants and predicates from
![]() $\Pi$
, and so the above check can be performed independently of
$\Pi$
, and so the above check can be performed independently of
![]() $\mathcal{D}$
. It remains to be shown that checking existence of a word
$\mathcal{D}$
. It remains to be shown that checking existence of a word
![]() ${{{\overrightarrow{w}}}}$
accepted by
${{{\overrightarrow{w}}}}$
accepted by
![]() $\mathcal{F}_{\mathcal{W}_0}^\to$
(that is, the second part of Condition 1) is feasible in
$\mathcal{F}_{\mathcal{W}_0}^\to$
(that is, the second part of Condition 1) is feasible in
![]() ${{\rm PS}{\small\rm PACE}}$
. To this end, we check existence of an accepting run
${{\rm PS}{\small\rm PACE}}$
. To this end, we check existence of an accepting run
![]() $\mathcal{W}_0, \mathcal{W}_1, \dots$
of
$\mathcal{W}_0, \mathcal{W}_1, \dots$
of
![]() $\mathcal{F}_{\mathcal{W}_0}^\to$
in two steps. First, we guess windows
$\mathcal{F}_{\mathcal{W}_0}^\to$
in two steps. First, we guess windows
![]() $\mathcal{W}_1, \dots , \mathcal{W}_j$
one by one, where
$\mathcal{W}_1, \dots , \mathcal{W}_j$
one by one, where
![]() ${j= t^{\max}_{\mathcal{D}} - t^{\min}_{\mathcal{D}} + 2 t_{\Pi} +2}$
, and second, we check if
${j= t^{\max}_{\mathcal{D}} - t^{\min}_{\mathcal{D}} + 2 t_{\Pi} +2}$
, and second, we check if
![]() $\mathcal{F}_{\mathcal{W}_j}^\to$
has an accepting run. We observe that each of the windows
$\mathcal{F}_{\mathcal{W}_j}^\to$
has an accepting run. We observe that each of the windows
![]() $\mathcal{W}_1, \dots , \mathcal{W}_j$
is of polynomial size, and so guessing them one by one, as well as checking that
$\mathcal{W}_1, \dots , \mathcal{W}_j$
is of polynomial size, and so guessing them one by one, as well as checking that
![]() $\mathcal{F}_{\mathcal{W}_0}^\to$
has transitions between consecutive windows, is feasible in
$\mathcal{F}_{\mathcal{W}_0}^\to$
has transitions between consecutive windows, is feasible in
![]() ${{\rm PS}{\small\rm PACE}}$
. To check non-emptiness of the language of
${{\rm PS}{\small\rm PACE}}$
. To check non-emptiness of the language of
![]() $\mathcal{F}_{\mathcal{W}_j}^\to$
, we construct for it an automaton
$\mathcal{F}_{\mathcal{W}_j}^\to$
, we construct for it an automaton
![]() $\widetilde{\mathcal{F}}_{\mathcal{W}_j}^\to$
in a similar way as we constructed
$\widetilde{\mathcal{F}}_{\mathcal{W}_j}^\to$
in a similar way as we constructed
![]() $\widetilde{X}_{\mathcal{W}_j}^\to$
for
$\widetilde{X}_{\mathcal{W}_j}^\to$
for
![]() $X_{\mathcal{W}_j}^\to$
in the proof of Theorem 5.14. The difference, however, is that the set of states of
$X_{\mathcal{W}_j}^\to$
in the proof of Theorem 5.14. The difference, however, is that the set of states of
![]() $\widetilde{\mathcal{F}}_{\mathcal{W}_j}^\to$
is the quotient set of
$\widetilde{\mathcal{F}}_{\mathcal{W}_j}^\to$
is the quotient set of
![]() $\sim$
between only those states of
$\sim$
between only those states of
![]() $\mathcal{F}_{\mathcal{W}_j}^\to$
whose first elements are intervals located entirely to the right of
$\mathcal{F}_{\mathcal{W}_j}^\to$
whose first elements are intervals located entirely to the right of
![]() $t^{\max}_{\mathcal{D}} + t_\Pi$
. For any such state
$t^{\max}_{\mathcal{D}} + t_\Pi$
. For any such state
![]() ${\mathcal{W}_i = (\varrho_i,T_i,T_i,0)}$
, checking whether it locally satisfies
${\mathcal{W}_i = (\varrho_i,T_i,T_i,0)}$
, checking whether it locally satisfies
![]() $\mathcal{D}$
simply amounts to verifying that
$\mathcal{D}$
simply amounts to verifying that
![]() $M@t \in T_i$
for each
$M@t \in T_i$
for each
![]() $M \in \mathsf{at}{(\Pi,\mathcal{D})}$
such that
$M \in \mathsf{at}{(\Pi,\mathcal{D})}$
such that
![]() $M@\varrho_j^{-} \in T_j$
, and each
$M@\varrho_j^{-} \in T_j$
, and each
![]() $t \in \varrho_i$
. Indeed, this follows from two observations: first, for any atom
$t \in \varrho_i$
. Indeed, this follows from two observations: first, for any atom
![]() $M\in \mathsf{at}{(\Pi,\mathcal{D})}$
and two arbitrary time points
$M\in \mathsf{at}{(\Pi,\mathcal{D})}$
and two arbitrary time points
![]() $t,t' > t^{\max}_{\mathcal{D}} + t_\Pi$
,
$t,t' > t^{\max}_{\mathcal{D}} + t_\Pi$
,
![]() $\mathcal{D} \models M @t$
if and only if
$\mathcal{D} \models M @t$
if and only if
![]() $\mathcal{D} \models M @t'$
; second,
$\mathcal{D} \models M @t'$
; second,
![]() $\varrho_j^- > t^{\max}_{\mathcal{D}} + t_\Pi$
, by definition of j. Then, using an argument analogous to the proof of Lemma 5.10, we can show that
$\varrho_j^- > t^{\max}_{\mathcal{D}} + t_\Pi$
, by definition of j. Then, using an argument analogous to the proof of Lemma 5.10, we can show that
![]() $\mathcal{F}_{\mathcal{W}_j}^\to$
and
$\mathcal{F}_{\mathcal{W}_j}^\to$
and
![]() $\widetilde{\mathcal{F}}_{\mathcal{W}_j}^\to$
are equivalent. Hence, it remains to check if the language of the latter automaton is non-empty. By construction, each state of the automaton
$\widetilde{\mathcal{F}}_{\mathcal{W}_j}^\to$
are equivalent. Hence, it remains to check if the language of the latter automaton is non-empty. By construction, each state of the automaton
![]() $\widetilde{\mathcal{F}}_{\mathcal{W}_j}^\to$
can be represented in polynomial space, so the non-emptiness check is feasible in
$\widetilde{\mathcal{F}}_{\mathcal{W}_j}^\to$
can be represented in polynomial space, so the non-emptiness check is feasible in
![]() ${{\rm PS}{\small\rm PACE}}$
using a standard on-the-fly approach.
${{\rm PS}{\small\rm PACE}}$
using a standard on-the-fly approach.
The assumption that
![]() $\mathcal{D}$
is bounded has been used to ensure existence of a time point such that no fact of
$\mathcal{D}$
is bounded has been used to ensure existence of a time point such that no fact of
![]() $\mathcal{D}$
holds to the left of it. Thus, our results can be extended to show that reasoning is still
$\mathcal{D}$
holds to the left of it. Thus, our results can be extended to show that reasoning is still
![]() ${{\rm PS}{\small\rm PACE}}$
in data complexity for datasets where intervals are only bounded on the left. Furthermore, none of our results in this section depend on the direction of time. Indeed, we can define the backward-propagating fragment of
${{\rm PS}{\small\rm PACE}}$
in data complexity for datasets where intervals are only bounded on the left. Furthermore, none of our results in this section depend on the direction of time. Indeed, we can define the backward-propagating fragment of
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
(analogously to
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
(analogously to
![]() ${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
) as the set of programs where operators
${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
) as the set of programs where operators ![]() ,
,
![]() $\boxminus$
, and
$\boxminus$
, and
![]() $\mathcal{S}$
are disallowed in rule bodies, and operator
$\mathcal{S}$
are disallowed in rule bodies, and operator
![]() $\boxplus$
is disallowed in the head. Then, we can obtain an analogous set of results for the backward-propagating fragment and show that reasoning in such fragment is also
$\boxplus$
is disallowed in the head. Then, we can obtain an analogous set of results for the backward-propagating fragment and show that reasoning in such fragment is also
![]() ${{\rm PS}{\small\rm PACE}}$
in data complexity.
${{\rm PS}{\small\rm PACE}}$
in data complexity.
6 Related work
Positive
![]() ${\textrm{DatalogMTL}}$
(Brandt et al. Reference Brandt, Kalayc, Ryzhikov, Xiao and Zakharyaschev2018) has been studied over both the rational (Brandt et al. Reference Brandt, Kalayc, Ryzhikov, Xiao and Zakharyaschev2018) and the integer (Włęga et al. 2020a) timelines. In both cases, the main reasoning tasks are
${\textrm{DatalogMTL}}$
(Brandt et al. Reference Brandt, Kalayc, Ryzhikov, Xiao and Zakharyaschev2018) has been studied over both the rational (Brandt et al. Reference Brandt, Kalayc, Ryzhikov, Xiao and Zakharyaschev2018) and the integer (Włęga et al. 2020a) timelines. In both cases, the main reasoning tasks are
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
-complete for combined complexity (Brandt et al. Reference Brandt, Kalayc, Ryzhikov, Xiao and Zakharyaschev2018) and
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
-complete for combined complexity (Brandt et al. Reference Brandt, Kalayc, Ryzhikov, Xiao and Zakharyaschev2018) and
![]() ${{\rm PS}{\small\rm PACE}}$
-complete for data complexity (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019). Low complexity fragments (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2020b; 2021) and alternative semantics (Ryzhikov et al. Reference Ryzhikov, Wałęga and Zakharyaschev2019) have also been studied. Practical reasoning algorithms for positive
${{\rm PS}{\small\rm PACE}}$
-complete for data complexity (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019). Low complexity fragments (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2020b; 2021) and alternative semantics (Ryzhikov et al. Reference Ryzhikov, Wałęga and Zakharyaschev2019) have also been studied. Practical reasoning algorithms for positive
![]() ${\textrm{DatalogMTL}}$
have been recently proposed and implemented in the MeTeoR system (Wang et al. Reference Wang, Hu, Wałęga and Cuenca Grau2022).
${\textrm{DatalogMTL}}$
have been recently proposed and implemented in the MeTeoR system (Wang et al. Reference Wang, Hu, Wałęga and Cuenca Grau2022).
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
is an extension of
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
is an extension of
![]() ${\textrm{DatalogMTL}}$
; therefore, it also extends other prominent temporal rule languages captured by
${\textrm{DatalogMTL}}$
; therefore, it also extends other prominent temporal rule languages captured by
![]() ${\textrm{DatalogMTL}}$
such as
${\textrm{DatalogMTL}}$
such as
![]() $\mbox{Datalog}_{1S}$
(Chomicki and Imieliński 1988; 1989) and Templog (Abadi and Manna Reference Abadi and Manna1989). In turn,
$\mbox{Datalog}_{1S}$
(Chomicki and Imieliński 1988; 1989) and Templog (Abadi and Manna Reference Abadi and Manna1989). In turn,
![]() ${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
generalises the forward-propagating fragment of
${\textrm{DatalogMTL}}^\neg_{\mathsf{FP}}$
generalises the forward-propagating fragment of
![]() ${\textrm{DatalogMTL}}$
introduced by Wałęga et al. (Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019), and it is thus related to other forward-propagating temporal logics proposed in the literature (Baldor and Niu Reference Baldor and Niu2012; Ronca et al. Reference Ronca, Kaminski, Cuenca Grau and Horrocks2018; Basin et al. Reference Basin, Klaedtke and Zălinescu2018). Our stable model semantics (Wałęga et al. Reference Wałęga, Tena Cucala, Kostylev and Cuenca Grau2021) extends the semantics for stratified
${\textrm{DatalogMTL}}$
introduced by Wałęga et al. (Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019), and it is thus related to other forward-propagating temporal logics proposed in the literature (Baldor and Niu Reference Baldor and Niu2012; Ronca et al. Reference Ronca, Kaminski, Cuenca Grau and Horrocks2018; Basin et al. Reference Basin, Klaedtke and Zălinescu2018). Our stable model semantics (Wałęga et al. Reference Wałęga, Tena Cucala, Kostylev and Cuenca Grau2021) extends the semantics for stratified
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
programs (Tena Cucala et al. Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021).
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
programs (Tena Cucala et al. Reference Tena Cucala, Wałęga, Cuenca Grau and Kostylev2021).
Our approach is closely related to a recently proposed family of non-monotonic temporal logics which simultaneously support ASP and modal temporal operators. TEL (Cabalar and Vega Reference Cabalar and Vega2007; Aguado et al. Reference Aguado, Cabalar, Diéguez, Pérez and Vidal2013; Cabalar et al. Reference Cabalar, Kaminski, Schaub and Schuhmann2018) combines propositional ASP with operators from linear temporal logic (Pnueli Reference Pnueli1977). Metric equilibrium logic (MEL) (Cabalar et al. Reference Cabalar, Dieguez, Schaub and Schuhmann2020) extends TEL with metric temporal operators that are roughly equivalent to our past operators
![]() $\mathcal{S}_{[0,k]}$
and
$\mathcal{S}_{[0,k]}$
and
![]() $\boxminus_{k}$
, and their future counterparts. Both logics introduce non-monotonic semantics for negation based on stable models, which are defined – as in our work – analogously to the models of equilibrium logic. However, TEL and MEL differ from our approach. First, they allow formulas supporting all Boolean connectives; therefore, they can represent disjunction between propositions, as well as ‘existential’ formulas using diamond operators; in contrast, in
$\boxminus_{k}$
, and their future counterparts. Both logics introduce non-monotonic semantics for negation based on stable models, which are defined – as in our work – analogously to the models of equilibrium logic. However, TEL and MEL differ from our approach. First, they allow formulas supporting all Boolean connectives; therefore, they can represent disjunction between propositions, as well as ‘existential’ formulas using diamond operators; in contrast, in
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
the use of logical connectives and temporal operators is restricted so that all formulas are shaped as rules similar in spirit to those of Datalog (see Definition 3.1). Second, they are propositional logics, so they do not allow universally quantified variables. Finally, the semantics of TEL and MEL are defined on integer timelines with a least time point, whereas we consider both the full integer timeline as well as the dense rational timeline. In terms of complexity, checking whether a formula has a stable model is known to be
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
the use of logical connectives and temporal operators is restricted so that all formulas are shaped as rules similar in spirit to those of Datalog (see Definition 3.1). Second, they are propositional logics, so they do not allow universally quantified variables. Finally, the semantics of TEL and MEL are defined on integer timelines with a least time point, whereas we consider both the full integer timeline as well as the dense rational timeline. In terms of complexity, checking whether a formula has a stable model is known to be
![]() ${{\rm PS}{\small\rm PACE}}$
-hard for both TEL and MEL, and feasible in
${{\rm PS}{\small\rm PACE}}$
-hard for both TEL and MEL, and feasible in
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
for TEL.
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
for TEL.
Our approach is also related to the LARS language (Beck et al. Reference Beck, Dao-Tran and Eiter2018) for stream reasoning. LARS is also a rule-based language allowing for negation interpreted under stable model semantics. The differences between
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
and LARS are as follows. First, conjuncts in the body of LARS rules are formulas constructed using temporal operators and unrestricted combinations of Boolean connectives; in contrast, body conjuncts in
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
and LARS are as follows. First, conjuncts in the body of LARS rules are formulas constructed using temporal operators and unrestricted combinations of Boolean connectives; in contrast, body conjuncts in
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
are metric atoms, which do not mention Boolean operators. Second, LARS does not allow for metric operators (only LTL-style boxes and diamonds), but it allows for window operators that have no counterpart in
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
are metric atoms, which do not mention Boolean operators. Second, LARS does not allow for metric operators (only LTL-style boxes and diamonds), but it allows for window operators that have no counterpart in
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
. Third, LARS rules are meant to be interpreted at individual time points, so the notion of a stable model in LARS is always relative to a time point (e.g., a LARS interpretation can be a stable model of a program at t, but not at
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
. Third, LARS rules are meant to be interpreted at individual time points, so the notion of a stable model in LARS is always relative to a time point (e.g., a LARS interpretation can be a stable model of a program at t, but not at
![]() $t+1$
); in contrast, a stable model of a
$t+1$
); in contrast, a stable model of a
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program satisfies each rule at every time point in the timeline (see Definition 3.2). Finally, LARS interpretations are defined over bounded intervals of the integer timeline, whereas
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
program satisfies each rule at every time point in the timeline (see Definition 3.2). Finally, LARS interpretations are defined over bounded intervals of the integer timeline, whereas
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
interpretations are defined over the full integer or rational timeline. Checking whether a LARS program and dataset have a stable model at a time point t is
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
interpretations are defined over the full integer or rational timeline. Checking whether a LARS program and dataset have a stable model at a time point t is
![]() ${{\rm PS}{\small\rm PACE}}$
-complete.
${{\rm PS}{\small\rm PACE}}$
-complete.
The use of ASP for temporal reasoning has been intensively explored, especially in the context of stream reasoning. Streamlog (Zaniolo Reference Zaniolo2012) introduces a variant of Datalog with negation where atoms are “time-stamped,” in the sense that the first term of an atom is a natural number representing the time point where the atom holds. Rules in Streamlog must be forward-propagating in time; furthermore, programs must be locally stratified, which ensures that they have a unique stable model. Do et al. (Reference Do, Loke and Liu2011) present an approach which combines a general-purpose ASP solver with a monotonic stream reasoner to support ASP in stream reasoning; in this approach, both systems are treated as black boxes. Another approach that supports ASP on a temporal setting is time-decaying reasoning (Gebser et al. Reference Gebser, Grote, Kaminski, Obermeier, Sabuncu and Schaub2013), which relies on programs similar to Datalog, but where each fact and rule need to hold only over a fixed time interval; this behaviour is used to capture changing information from a sliding window over a sequence of temporal data. More recently, negation-free
![]() ${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
has been applied in the context of monotonic stream reasoning (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019), and we see our current work as providing the foundations for extending this approach with support for ASP.
${\textrm{DatalogMTL}}^{\mkern-2mu \neg}$
has been applied in the context of monotonic stream reasoning (Wałęga et al. Reference Wałęga, Cuenca Grau, Kaminski and Kostylev2019), and we see our current work as providing the foundations for extending this approach with support for ASP.
7 Conclusion and future work
We extended
![]() ${\textrm{DatalogMTL}}$
with negation-as-failure under stable model semantics and shown that reasoning in this language is undecidable over the rational timeline but
${\textrm{DatalogMTL}}$
with negation-as-failure under stable model semantics and shown that reasoning in this language is undecidable over the rational timeline but
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
in data complexity over the integers. We also studied the forward-propagating fragment and shown that, although reasoning remains undecidable over the rational timeline, it is becomes
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
in data complexity over the integers. We also studied the forward-propagating fragment and shown that, although reasoning remains undecidable over the rational timeline, it is becomes
![]() ${{\rm PS}{\small\rm PACE}}$
-complete in data complexity over the integers (thus no harder than in the negation-free case).
${{\rm PS}{\small\rm PACE}}$
-complete in data complexity over the integers (thus no harder than in the negation-free case).
We see many avenues for future work. The more immediate challenge is to provide tight data complexity bounds for reasoning in the full language over the integer timeline, where we currently have an
![]() ${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
upper bound and a lower bound for data complexity. We also plan to consider combined complexity and identify fragments of the language where reasoning becomes decidable over the rational timeline. Finally, we are planning to develop practical algorithms and implement them as an extension the MeTeoR reasoner, that is currently allows for reasoning with positive
${{\rm E}{\small\rm XP}{\rm S}{\small\rm PACE}}$
upper bound and a lower bound for data complexity. We also plan to consider combined complexity and identify fragments of the language where reasoning becomes decidable over the rational timeline. Finally, we are planning to develop practical algorithms and implement them as an extension the MeTeoR reasoner, that is currently allows for reasoning with positive
![]() ${\textrm{DatalogMTL}}$
programs only (Wang et al. Reference Wang, Hu, Wałęga and Cuenca Grau2022).
${\textrm{DatalogMTL}}$
programs only (Wang et al. Reference Wang, Hu, Wałęga and Cuenca Grau2022).