Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-07T21:21:22.177Z Has data issue: false hasContentIssue false
  • English
  • Français

The Probabilistic Description Logic

Published online by Cambridge University Press:  11 December 2020

LEONARD BOTHA ,
THOMAS MEYER Open the ORCID record for THOMAS MEYER [Opens in a new window]  and
RAFAEL PEÑALOZA Open the ORCID record for RAFAEL PEÑALOZA [Opens in a new window]
LEONARD BOTHA
Affiliation:
University of Cape Town and CAIR, South Africa
THOMAS MEYER
Affiliation:
University of Cape Town and CAIR, South Africa
RAFAEL PEÑALOZA
Affiliation:
University of Milano-Bicocca, Italy (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Description logics (DLs) are well-known knowledge representation formalisms focused on the representation of terminological knowledge. Due to their first-order semantics, these languages (in their classical form) are not suitable for representing and handling uncertainty. A probabilistic extension of a light-weight DL was recently proposed for dealing with certain knowledge occurring in uncertain contexts. In this paper, we continue that line of research by introducing the Bayesian extension 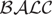of the propositionally closed DL 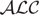. We present a tableau-based procedure for deciding consistency and adapt it to solve other probabilistic, contextual, and general inferences in this logic. We also show that all these problems remain ExpTime-complete, the same as reasoning in the underlying classical .

Keywords

knowledge representation and nonmonotonic reasoningdatabases and semantic web reasoning
Type
Original Article
Information
Theory and Practice of Logic Programming , Volume 21 , Issue 4: TPLP Special Issue from the 16th European Conference on Logics in Artificial Intelligence (JELIA 2019) , July 2021 , pp. 404 - 427
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

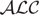Part of this work was carried out while this author was at the Free University of Bozen-Bolzano, Italy.

References

Artale, A., Calvanese, D., Kontchakov, R. and Zakharyaschev, M. 2009. The DL-Lite family and relations. Journal of Artificial Intelligence Research 36, 1–69.Google Scholar
Baader, F., Brandt, S. and Lutz, C. 2005. Pushing the EL envelope. In Proceedings of the Nineteenth International Joint Conference on Artificial Intelligence (IJCAI 2005), Kaelbling, L. P. and Saffiotti, A., Eds. Professional Book Center, 364–369.Google Scholar
Baader, F., Calvanese, D., McGuinness, D., Nardi, D., and Patel-Schneider, P., Eds. 2007. The Description Logic Handbook: Theory, Implementation, and Applications, 2nd ed. Cambridge University Press.CrossRefGoogle Scholar
Baader, F. and Hollunder, B. 1995. Embedding defaults into terminological knowledge representation formalisms. Journal of Automated Reasoning 14, 1, 149–180.CrossRefGoogle Scholar
Baader, F., Horrocks, I., Lutz, C. and Sattler, U. 2017. An Introduction to Description Logic. Cambridge University Press.CrossRefGoogle Scholar
Baader, F. and Peñaloza, R. 2007. Axiom pinpointing in general tableaux. In Proceedings of the 16th International Conference on Analytic Tableaux and Related Methods (TABLEAUX 2007), N. Olivetti, Ed. Notes, Lecture in Artificial Intelligence, vol. 4548. Springer-Verlag, Aix-en-Provence, France, 11–27.Google Scholar
Baader, F. and Peñaloza, R. 2010. Axiom pinpointing in general tableaux. Journal of Logic and Computation 20, 1 (February), 5–34. Special Issue: Tableaux and Analytic Proof Methods.CrossRefGoogle Scholar
Biere, A., Heule, M., van Maaren, H. and Walsh, T. 2009. Handbook of Satisfiability: Volume 185 Frontiers in Artificial Intelligence and Applications. IOS Press, Amsterdam, The Netherlands.Google Scholar
Botha, L. 2018. The Bayesian description logic ALC. M.S. thesis, University of Cape Town, South Africa.Google Scholar
Botha, L., Meyer, T. and Peñaloza, R. 2018. The Bayesian description logic BALC. In Proceedings of the 31st International Workshop on Description Logics (DL 2018), Ortiz, M. and Schneider, T., Eds. CEUR Workshop Proceedings, vol. 2211. CEUR-WS.org.Google Scholar
Botha, L., Meyer, T. and Peñaloza, R. 2019. A Bayesian extension of the description logic ALC. In Proceedings of the 16th European Conference on Logics in Artificial Intelligence (JELIA 2019), Calimeri, F., Leone, N., and Manna, M., Eds. Lecture Notes in Computer Science, vol. 11468. Springer, 339–354.Google Scholar
Brace, K. S., Rudell, R. L. and Bryant, R. E. 1990. Efficient implementation of a BDD package. In Proceedings of the 27th ACM/IEEE Design Automation Conference, DAC 1990. ACM, New York, NY, USA, 40–45.Google Scholar
Ceylan, İ. İ. 2018. Query answering in probabilistic data and knowledge bases. Ph.D. thesis, Dresden University of Technology, Germany.Google Scholar
Ceylan, İ. İ. and Lukasiewicz, T. 2018. A tutorial on query answering and reasoning over probabilistic knowledge bases. In 14th International Summer School on Reasoning Web, d’Amato, C. and Theobald, M., Eds. Lecture Notes in Computer Science, vol. 11078. Springer, 35–77.Google Scholar
Ceylan, İ. İ. and Peñaloza, R. 2014. The Bayesian description logic BEL. In Proceedings of the 7th International Joint Conference on Automated Reasoning (IJCAR 2014), Demri, S., Kapur, D., and Weidenbach, C., Eds. Lecture Notes in Computer Science, vol. 8562. Springer, 480–494.Google Scholar
Ceylan, İ. İ. and Peñaloza, R. 2014. Tight complexity bounds for reasoning in the description logic BEL. In Proceedings of the 14th European Conference on Logics in Artificial Intelligence (JELIA 2014), Fermé, E. and Leite, J., Eds. Lecture Notes in Computer Science, vol. 8761. Springer, 77–91.Google Scholar
Ceylan, İ. İ. and Peñaloza, R. 2017. The Bayesian ontology language BEL. Journal of Automated Reasoning 58, 1, 67–95.Google Scholar
d’Amato, C., Fanizzi, N. and Lukasiewicz, T. 2008. Tractable reasoning with Bayesian description logics. In Proceedings of the Second International Conference on Scalable Uncertainty Management, Greco, S. and Lukasiewicz, T., Eds. Lecture Notes in Computer Science, vol. 5291. Springer, 146–159.Google Scholar
Darwiche, A. 2009. Modeling and Reasoning with Bayesian Networks. Cambridge University Press.CrossRefGoogle Scholar
Donini, F. M. and Massacci, F. 2000. Exptime tableaux for . Artificial Intelligence 124, 1, 87–138.CrossRefGoogle Scholar
Gottlob, G., Lukasiewicz, T., Martinez, M. V. and Simari, G. I. 2013. Query answering under probabilistic uncertainty in datalog +/- ontologies. Annals of Mathematics and Artificial Intelligence 69, 1, 37–72.CrossRefGoogle Scholar
Gutiérrez-Basulto, V., Jung, J. C., Lutz, C., and Schröder, L. 2017. Probabilistic description logics for subjective uncertainty. Journal of Artificial Intelligence Research 58, 1–66.Google Scholar
Halpern, J. Y. 1990. An analysis of first-order logics of probability. Artificial Intelligence 46, 3, 311–350.CrossRefGoogle Scholar
Lee, C. Y. 1959. Representation of switching circuits by binary-decision programs. The Bell System Technical Journal 38, 985–999.Google Scholar
Lee, K., Meyer, T. A., Pan, J. Z. and Booth, R. 2006. Computing maximally satisfiable terminologies for the description logic ALC with cyclic definitions. In Proceedings of the 2006 International Workshop on Description Logics (DL2006), Parsia, B., Sattler, U., and Toman, D., Eds. CEUR Workshop Proceedings, vol. 189. CEUR-WS.org.Google Scholar
Lukasiewicz, T. and Straccia, U. 2008. Managing uncertainty and vagueness in description logics for the semantic web. Journal of Web Semantics 6, 4, 291–308.CrossRefGoogle Scholar
Meyer, T. A., Lee, K., Booth, R. and Pan, J. Z. 2006. Finding maximally satisfiable terminologies for the description logic ALC. In Proceedings of the Twenty-First National Conference on Artificial Intelligence and the Eighteenth Innovative Applications of Artificial Intelligence Conference. AAAI Press, 269–274.Google Scholar
Pearl, J. 1985. Bayesian networks: A model of self-activated memory for evidential reasoning. In Proceedings of Cognitive Science Society (CSS-7), 329–334.Google Scholar
Peñaloza, R. 2009. Axiom-Pinpointing in description logics and beyond. Ph.D. thesis, Dresden University of Technology, Germany.Google Scholar
Schild, K. 1991. A correspondence theory for terminological logics: Preliminary report. In Proceedings of the 12th International Joint Conference on Artificial Intelligence (IJCAI 1991), Mylopoulos, J. and Reiter, R., Eds. Morgan Kaufmann, 466–471.Google Scholar
Schmidt-Schauß, M. and Smolka, G. 1991. Attributive concept descriptions with complements. Artificial Intelligence 48, 1, 1–26.Google Scholar
Zese, R., Bellodi, E., Riguzzi, F., Cota, G. and Lamma, E. 2018. Tableau reasoning for description logics and its extension to probabilities. Annals of Mathematics and Artificial Intelligence 82, 1–3, 101–130.CrossRefGoogle Scholar