Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T11:14:32.644Z Has data issue: false hasContentIssue false
  • English
  • Français

Modular action language 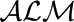${\mathcal ALM}$

Published online by Cambridge University Press:  06 July 2015

DANIELA INCLEZAN  and
MICHAEL GELFOND
DANIELA INCLEZAN
Affiliation:
Department of Computer Science and Software Engineering, Miami University Oxford, OH 45056, USA (e-mail: [email protected])
MICHAEL GELFOND
Affiliation:
Department of Computer Science, Texas Tech University Lubbock, TX 79409, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper introduces a new modular action language, 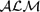${\mathcal ALM}$, and illustrates the methodology of its use. It is based on the approach of Gelfond and Lifschitz (1993, Journal of Logic Programming 17, 2–4, 301–321; 1998, Electronic Transactions on AI 3, 16, 193–210) in which a high-level action language is used as a front end for a logic programming system description. The resulting logic programming representation is used to perform various computational tasks. The methodology based on existing action languages works well for small and even medium size systems, but is not meant to deal with larger systems that require structuring of knowledge. 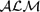$\mathcal{ALM}$ is meant to remedy this problem. Structuring of knowledge in 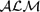${\mathcal ALM}$ is supported by the concepts of module (a formal description of a specific piece of knowledge packaged as a unit), module hierarchy, and library, and by the division of a system description of 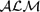${\mathcal ALM}$ into two parts: theory and structure. A theory consists of one or more modules with a common theme, possibly organized into a module hierarchy based on a dependency relation. It contains declarations of sorts, attributes, and properties of the domain together with axioms describing them. Structures are used to describe the domain's objects. These features, together with the means for defining classes of a domain as special cases of previously defined ones, facilitate the stepwise development, testing, and readability of a knowledge base, as well as the creation of knowledge representation libraries.

Keywords

logic programmingreasoning about actions and changeaction language
Type
Regular Papers
Information
Theory and Practice of Logic Programming , Volume 16 , Issue 2 , March 2016 , pp. 189 - 235
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akman, V., Erdogan, S. T., Lee, J., Lifschitz, V. and Turner, H. 2004. Representing the zoo world and the traffic world in the language of the causal calculator. Artificial Intelligence 153, 1–2 (March), 105–140.CrossRefGoogle Scholar
Balai, E., Gelfond, M. and Zhang, Y. 2012. SPARC – sorted ASP with consistency restoring rules. In Proc. of Answer Set Programming and Other Computing Paradigms (ASPOCP 2012), Fink, M. and Lierler, Y., Eds. Proceedings published online in arXiv at http://arxiv.org/html/1301.2215v1, 19–33.Google Scholar
Balduccini, M. 2004. USA-smart: Improving the quality of plans in answer set planning. In Proc. PADL'04, Jayaraman, B., Ed. Lecture Notes in Artificial Intelligence (LNCS). Springer, Berlin, 135–147.Google Scholar
Balduccini, M. 2007. CR-MODELS: An inference engine for CR-prolog. In Proc. of LPNMR-07, Baral, C., Brewka, G. and Schlipf, J. S., Eds., Springer, Berlin, 18–30.Google Scholar
Balduccini, M. 2013. ASP with non-Herbrand partial functions: A language and system for practical use. Theory and Practice of Logic Programming 13, 4–5, 547–561.CrossRefGoogle Scholar
Balduccini, M. and Gelfond, M. 2003a. Diagnostic reasoning with A-prolog. Theory and Practice of Logic Programming 3, 425–461.CrossRefGoogle Scholar
Balduccini, M. and Gelfond, M. 2003b. Logic programs with consistency-restoring rules. In International Symposium on Logical Formalization of Commonsense Reasoning, Doherty, P., McCarthy, J. and Williams, M.-A., Eds., AAAI 2003 Spring Symposium Series, Palo Alto, CA, 9–18.Google Scholar
Balduccini, M. and Gelfond, M. 2012. Language ASP{f} with arithmetic expressions and consistency-restoring rules. In Proc. of Answer Set Programming and Other Computing Paradigms (ASPOCP 2012), Fink, M. and Lierler, Y., Eds. Proceedings published online in arXiv at http://arxiv.org/pdf/1301.1387v1.pdf, 35–49.Google Scholar
Baral, C. 2003. Knowledge Representation, Reasoning, and Declarative Problem Solving. Cambridge University Press.CrossRefGoogle Scholar
Baral, C., Dzifcak, J. and Takahashi, H. 2006. Macros, macro calls and use of ensembles in modular answer set programming. In Logic Programming, Etalle, S. and Truszczyski, M., Eds. Lecture Notes in Computer Science, vol. 4079. Springer, Berlin Heidelberg, 376–390.CrossRefGoogle Scholar
Baral, C. and Gelfond, M. 2000. Reasoning Agents in Dynamic Domains. Kluwer Academic Publishers, Norwell, MA, 257–279.Google Scholar
Bartholomew, M. and Lee, J. 2013. On the stable model semantics for intensional functions. Journal of Theory and Practice of Logic Programming (TPLP) 13, 4–5, 863–876.CrossRefGoogle Scholar
Blount, J., Gelfond, M. and Balduccini, M. 2014. Towards a theory of intentional agents. In AAAI 2014 Spring Symposium Series, Sridharan, M., Yang, F., Ramamoorthy, S., Patoglu, V. and Erdem, E., Eds. AAAI Press, Palo Alto, CA.Google Scholar
Cabalar, P. 2011. Functional answer set programming. Journal of Theory and Practice of Logic Programming (TPLP) 11, 2–3, 203–233.CrossRefGoogle Scholar
Calimeri, F. and Ianni, G. 2006. Template programs for disjunctive logic programming: An operational semantics. AI Communications 19, 3, 193–206.Google Scholar
Chintabathina, S. 2012. Planning and scheduling in hybrid domains. Frontiers in Artificial Intelligence and Applications 241, 59–70.Google Scholar
Chintabathina, S., Gelfond, M. and Watson, R. 2005. Modeling hybrid domains using process description language. In Proc. of ASP '05 Answer Set Programming: Advances in Theory and Implementation, De Vos, M. and Provetti, A., Eds., CEUR-WS, CEUR-WS.org/ Aachen, 303–317.Google Scholar
Desai, N. and Singh, M. P. 2007. A modular action description language for protocol composition. In Proc. of the 22nd AAAI Conference on Artificial Intelligence, July 22–26, 2007, Vancouver, British Columbia, Canada, AAAI Press, Palo Alto, CA, 962–967.Google Scholar
Dovier, A., Formisano, A. and Pontelli, E. 2007. Multivalued action languages with constraints in CLP(FD). Logic Programming: Lecture Notes in Computer Science 4670, 255–270.CrossRefGoogle Scholar
Eiter, T., Erdem, E., Fink, M. and Senko, J. 2010. Updating action domain descriptions. Artif. Intell. 174, 15 (October), 1172–1221.CrossRefGoogle ScholarPubMed
Eiter, T., Faber, W., Leone, N., Pfeifer, G. and Polleres, A. 2004. Approach to knowledge-state planning: Semantics and complexity. ACM Transactions on Computational Logic 5, 206–263.CrossRefGoogle Scholar
Eiter, T., Ianni, G., Lukasiewicz, T., Schindlauer, R. and Tompits, H. 2008. Combining answer set programming with description logics for the semantic web. Artificial Intelligence 172, 12–13 (August), 1495–1539.CrossRefGoogle Scholar
Erdogan, S. and Lifschitz, V. 2006. Actions as special cases. In Principles of Knowledge Representation and Reasoning: Proceedings of the International Conference, Doherty, P., Mylopoulos, J. and Welty, C. A., Eds., AAAI Press, Palo Alto, CA, 377–387.Google Scholar
Erdogan, S. T. 2008. A Library of General-Purpose Action Descriptions. Ph.D. thesis, University of Texas at Austin, Austin, TX, USA.Google Scholar
Fodor, P. and Kifer, M. 2011. Modeling hybrid domains using process description language. In Proc. of the 27th International Conference on Logic Programming (ICLP), Gallagher, J. P. and Gelfond, M., Eds., Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, Wadern, 162–174.Google Scholar
Gebser, M., Grote, T., Kaminski, R. and Schaub, T. 2011. Reactive answer set programming. In LPNMR, Delgrande, J. P. and Faber, W., Eds. Lecture Notes in Computer Science, vol. 6645. Springer, Berlin, 54–66.Google Scholar
Gebser, M., Kaminski, R., Kaufmann, B. and Schaub, T. 2012. Answer Set Solving in Practice. Synthesis Lectures on Artificial Intelligence and Machine Learning. Morgan and Claypool Publishers.Google Scholar
Gebser, M., Sabuncu, O. and Schaub, T. 2011. An incremental answer set programming based system for finite model computation. AI Commun. 24, 2, 195–212.CrossRefGoogle Scholar
Gelfond, M. and Inclezan, D. 2009. Yet another modular action language. In Proc. of SEA-09. University of Bath Opus: Online Publications Store, 64–78.Google Scholar
Gelfond, M. and Inclezan, D. 2013. Some properties of system descriptions in ALd. Journal of Applied Non-Classical Logics 23, 105–120.CrossRefGoogle Scholar
Gelfond, M. and Kahl, Y. 2014. Knowledge Representation, Reasoning, and the Design of Intelligent Agents. Cambridge University Press.CrossRefGoogle Scholar
Gelfond, M. and Lifschitz, V. 1988. The stable model semantics for logic programming. In Proc. of ICLP-88, Kowalski, R. A. and Bowen, K. A., Eds., MIT Press, Cambridge, MA, 1070–1080.Google Scholar
Gelfond, M. and Lifschitz, V. 1991. Classical negation in logic programs and disjunctive databases. New Generation Computing 9, 3–4, 365–386.CrossRefGoogle Scholar
Gelfond, M. and Lifschitz, V. 1993. Representing action and change by logic programs. Journal of Logic Programming 17, 2–4, 301–321.CrossRefGoogle Scholar
Gelfond, M. and Lifschitz, V. 1998. Action languages. Electronic Transactions on AI 3, 16, 193–210.Google Scholar
Giunchiglia, E., Lee, J., Lifschitz, V., McCain, N. and Turner, H. 2004a. Nonmonotonic causal theories. Artificial Intelligence 153, 1–2, 105–140.CrossRefGoogle Scholar
Giunchiglia, E., Lee, J., Lifschitz, V., McCain, N. and Turner, H. 2004b. Nonmonotonic causal theories. Artificial Intelligence 153, 105–140.CrossRefGoogle Scholar
Giunchiglia, E. and Lifschitz, V. 1998. An action language based on causal explanation: Preliminary report. In Proc. of National Conference on Artificial Intelligence (AAAI), Mostow, J. and Rich, C., Eds., AAAI Press, Palo Alto, CA, 623–630.Google Scholar
Grosof, B., Dean, M. and Kifer, M. 2009. The SILK system: Scalable higher-order defeasible rules. In International RuleML Symposium on Rule Interchange and Applications. Available online at: http://silk.semwebcentral.org/talk-ruleml2009-silk-demo.pdf Google Scholar
Gunning, D., Chaudhri, V. K., Clark, P., Barker, K., Chaw, S.-Y., Greaves, M., Grosof, B., Leung, A., McDonald, D., Mishra, S., Pacheco, J., Porter, B., Spaulding, A., Tecuci, D. and Tien, J. 2010. Project Halo–progress toward digital aristotle. AI Magazine 31, 3, 33–58.CrossRefGoogle Scholar
Gustafsson, J. and Kvarnstróm, J. 2004. Elaboration tolerance through object-orientation. Artificial Intelligence 153, 239–285.CrossRefGoogle Scholar
Hanus, M. 1994. The integration of functions into logic programming: From theory to practice. Journal of Logic Programming 19–20, Supplement 1, 583–628.CrossRefGoogle Scholar
Henschel, A. and Thielscher, M. 2000. The LMW Traffic world in the fluent calculus. Linkóping Electronic Articles in Computer and Information Science 5 (14). Available at http://www.ep.liu.se/ea/cis/2000/014/.Google Scholar
Inclezan, D. 2010. Computing trajectories of dynamic systems using ASP and Flora-2. Paper presented at NonMon@30: Thirty Years of Nonmonotonic Reasoning Conference, Lexington, Kentucky, 22–25 October. Brewka, G., Marek, V. and Truszczynski, M., Eds., Available at http://www.depts.ttu.edu/cs/research/krlab/pdfs/papers/di10.pdf Google Scholar
Inclezan, D. and Gelfond, M. 2011. Representing biological processes in modular action language ALM. In Proc. of the 2011 AAAI Spring Symposium on Formalizing Commonsense. AAAI Press, Palo Alto, CA, 49–55.Google Scholar
Kakas, A. and Miller, R. 1997. A simple declarative language for describing narratives with actions. Journal of Logic Programming 31, 1–3, 157–200.CrossRefGoogle Scholar
Leone, N., Pfeifer, G., Faber, W., Eiter, T., Gottlob, G., Perri, S. and Scarcello, F. 2006. The DLV system for knowledge representation and reasoning. ACM Transactions on Computational Logic 7, 3, 499–562.CrossRefGoogle Scholar
Lierler, Y. and Truszczynski, M. 2013. Modular answer set solving. In Proc. of the 27th AAAI Conference on Artificial Intelligence (AAAI-13), AAAI Press, Palo Alto, CA, 68–70.Google Scholar
Lifschitz, V. 2012. Logic programs with intensional functions. In Proc. of International Conference on Principles of Knowledge Representation and Reasoning (KR), Brewka, G., Eiter, T. and McIlraith, S. A., Eds., AAAI Press, Palo Alto, CA, 24–31.Google Scholar
Lifschitz, V. and Ren, W. 2006. A modular action description language. In Proc. of the 21st National Conference on Artificial Intelligence (AAAI), AAAI Press, Palo Alto, CA, 853–859.Google Scholar
Marek, V. W. and Truszczynski, M. 1999. Stable models and an alternative logic programming paradigm. In The Logic Programming Paradigm: A 25-Year Perspective, Springer, Verlag, Berlin, 375–398.CrossRefGoogle Scholar
McCarthy, J. 1963. Situations, actions, and causal laws. Tech. Rep. Memo 2, Stanford University.CrossRefGoogle Scholar
McCarthy, J. 1968. Programs with common sense. In Semantic Information Processing, MIT Press, 403–418.Google Scholar
McCarthy, J. 1998. Elaboration tolerance. In Proceedings of Commonsense Reasoning. Available online at: http://www-formal.stanford.edu/jmc/elaboration/elaboration.html Google Scholar
Niemelä, I. 1998. Logic programs with stable model semantics as a constraint programming paradigm. Annals of Mathematics and Artificial Intelligence 25, 72–79.Google Scholar
Niemelä, I. and Simons, P. 1997. Smodels - an implementation of the stable model and well-founded semantics for normal logic programs. In Proc. of the 4th International Conference on Logic Programming and Non-Monotonic Reasoning (LPNMR-97). Lecture Notes in Artificial Intelligence (LNCS), Dix, J., Furbach, U. and Nerode, A., Eds., vol. 1265. Springer, Berlin, 420–429.Google Scholar
Oikarinen, E. and Janhunen, T. 2006. Modular equivalence for normal logic programs. In Proceedings of 17th European Conference on Artificial Intelligence(ECAI), Brewka, G., Coradeschi, S., Perini, A. and Traverso, P., Eds., IOS Press, Amsterdam, 412–416.Google Scholar
Pfenning, F., Ed. 1992. Types in Logic Programming. MIT Press.Google Scholar
Sandewall, E. 1999. Logic modelling workshop: Communicating axiomatizations of actions and change. URL: http://www.ida.liu.se/ext/etai/lmw.Google Scholar
Strass, H. and Thielscher, M. 2012. A language for default reasoning about actions. In Correct Reasoning: Essays in Honor of Vladimir Lifschitz, Erdem, E., Lee, J., Lierler, Y., and Pearce, D., Eds. Lecture Notes in Computer Science, vol. 7265. Springer, 527–542.CrossRefGoogle Scholar
Turner, H. 1997. Representing actions in logic programs and default theories: A situation calculus approach. Journal of Logic Programming 31, 1–3 (June), 245–298.CrossRefGoogle Scholar
Turner, H. 1999. A logic of universal causation. Artificial Intelligence 113, 87–123.CrossRefGoogle Scholar
Van Gelder, A., Ross, K. A. and Schlipf, J. S. 1991. The well-founded semantics for general logic programs. Journal of the ACM 38, 619–649.CrossRefGoogle Scholar
Wirth, N. 1971. Program development by stepwise refinement. Communications of the ACM 14, 4 (April), 221–227.CrossRefGoogle Scholar
Supplementary material: PDF

Inclezan and Gelfond supplementary material

Appendix

Download Inclezan and Gelfond supplementary material(PDF)
PDF 293.7 KB