1 Introduction and motivation
The motivation of the work presented in this paper stems from automatic static cost analysis and verification of logic programs (Debray et al., Reference Debray, Lin and Hermenegildo1990; Debray and Lin, Reference Debray and Lin1993; Debray et al., Reference Debray, Lopez-Garcia, Hermenegildo and Lin1997; Navas et al., Reference Navas, Mera, Lopez-Garcia and Hermenegildo2007; Serrano et al., Reference Serrano, Lopez-Garcia and Hermenegildo2014; Lopez-Garcia et al., Reference Lopez-Garcia, Klemen, Liqat and Hermenegildo2016, Reference Lopez-Garcia, Darmawan, Klemen, Liqat, Bueno and Heremenegildo2018). The goal of such analysis is to infer information about the resources used by programs without actually running them with concrete data and present such information as functions of input data sizes and possibly other (environmental) parameters. We assume a broad concept of resource as a numerical property of the execution of a program, such as number of resolution steps, execution time, energy consumption, memory, number of calls to a predicate, and number of transactions in a database. Estimating in advance the resource usage of computations is useful for a number of applications, such as automatic program optimization, verification of resource-related specifications, detection of performance bugs, helping developers make resource-related design decisions, security applications (e.g., detection of side channel attacks), or blockchain platforms (e.g., smart-contract gas analysis and verification).
The challenge we address originates from the established approach of setting up recurrence relations representing the cost of predicates, parameterized by input data sizes (Wegbreit, Reference Wegbreit1975; Rosendahl, Reference Rosendahl1989; Debray et al., Reference Debray, Lin and Hermenegildo1990; Debray and Lin, Reference Debray and Lin1993; Debray et al., Reference Debray, Lopez-Garcia, Hermenegildo and Lin1997; Navas et al., Reference Navas, Mera, Lopez-Garcia and Hermenegildo2007; Albert et al., Reference Albert, Arenas, Genaim and Puebla2011; Serrano et al., Reference Serrano, Lopez-Garcia and Hermenegildo2014; Lopez-Garcia et al., Reference Lopez-Garcia, Klemen, Liqat and Hermenegildo2016), which are then solved to obtain closed forms of such recurrences (i.e., functions that provide either exact, or upper/lower bounds on resource usage in general). Such approach can infer different classes of functions (e.g., polynomial, factorial, exponential, summation, or logarithmic).
The applicability of these resource analysis techniques strongly depends on the capabilities of the component in charge of solving (or safely approximating) the recurrence relations generated during the analysis, which has become a bottleneck in some systems.
A common approach to automatically solving such recurrence relations consists of using a Computer Algebra System (CAS) or a specialized solver. However, this approach poses several difficulties and limitations. For example, some recurrence relations contain complex expressions or recursive structures that most of the well-known CASs cannot solve, making it necessary to develop ad-hoc techniques to handle such cases. Moreover, some recurrences may not have the form required by such systems because an input data size variable does not decrease, but increases instead. Note that a decreasing-size variable could be implicit in the program, that is it could be a function of a subset of input data sizes (a ranking function), which could be inferred by applying established techniques used in termination analysis (Podelski and Rybalchenko, Reference Podelski and Rybalchenko2004). However, such techniques are usually restricted to linear arithmetic.
In order to address this challenge we have developed a novel, general method for solving arbitrary, constrained recurrence relations. It is a guess and check approach that uses machine learning techniques for the guess stage and a combination of an SMT-solver and a CAS for the check stage (see Figure 1). To the best of our knowledge, there is no other approach that does this. The resulting closed-form function solutions can be of different kinds, such as polynomial, factorial, exponential or logarithmic.
Our method is parametric in the guess procedure used, providing flexibility in the kind of functions that can be inferred, trading off expressivity with efficiency and theoretical guarantees. We present the results of two instantiations, based on sparse linear regression (with non-linear templates) and symbolic regression. Solutions to our equations are first evaluated on finite samples of the input space, and then, the chosen regression method is applied. In addition to obtaining exact solutions, the search and optimization algorithms typical of machine learning methods enable the efficient discovery of good approximate solutions in situations where exact solutions are too complex to find. These approximate solutions are particularly valuable in certain applications of cost analysis, such as granularity control in parallel/distributed computing. Furthermore, these methods allow exploration of model spaces that cannot be handled by complete methods such as classical linear equation solving (Table 1).
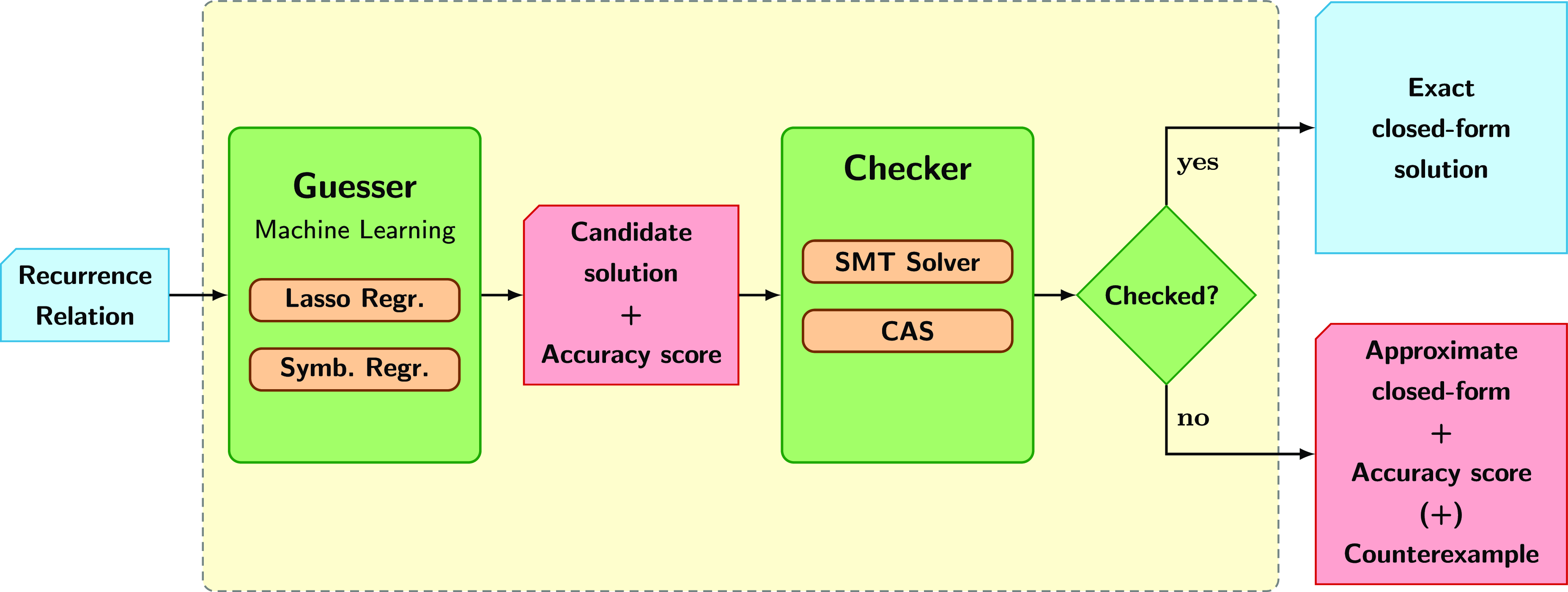
Fig 1. Architecture of our novel machine learning-based recurrence solver.
The rest of this paper is organized as follows. Section 2 gives and overview of our novel guess and check approach. Then, Section 3 provides some background information and preliminary notation. Section 4 presents a more detailed, formal and algorithmic description of our approach. Section 5 describes the use of our approach in the context of static cost analysis of (logic) programs. Section 6 comments on our prototype implementation as well as its experimental evaluation and comparison with other solvers. Finally, Section 7 discusses related work, and Section 8 summarizes some conclusions and lines for future work. Additionally, Appendix B provides complementary data to the evaluation of Section 6 and Table 2.
2 Overview of our approach
We now give an overview of our approach and its two stages already mentioned, illustrated in Figure 1: guess a candidate closed-form function, and check whether such function is actually a solution of the recurrence relation.
Given a recurrence relation for a function
![]() $f(\vec{x})$
, solving it means to find a closed-form expression
$f(\vec{x})$
, solving it means to find a closed-form expression
![]() $\hat{f}(\vec{x})$
defining a function, on the appropriate domain, that satisfies the relation. We say that
$\hat{f}(\vec{x})$
defining a function, on the appropriate domain, that satisfies the relation. We say that
![]() $\hat{f}$
is a closed-form expression whenever it does not contain any subexpression built using
$\hat{f}$
is a closed-form expression whenever it does not contain any subexpression built using
![]() $\hat{f}$
(i.e.,
$\hat{f}$
(i.e.,
![]() $\hat{f}$
is not recursively defined), although we will often additionally aim for expressions built only on elementary arithmetic functions, for example constants, addition, subtraction, multiplication, division, exponential, or perhaps rounding operators and factorial. We will use the following recurrence as an example to illustrate our approach.
$\hat{f}$
is not recursively defined), although we will often additionally aim for expressions built only on elementary arithmetic functions, for example constants, addition, subtraction, multiplication, division, exponential, or perhaps rounding operators and factorial. We will use the following recurrence as an example to illustrate our approach.
2.1 The “guess” stage
As already stated, our method is parametric in the guess procedure utilized, and we instantiate it with both sparse linear and symbolic regression in our experiments. However, for the sake of presentation, we initially focus on the former to provide an overview of our approach. Subsequently, we describe the latter in Section 3. Accordingly, any possible model we can obtain through sparse linear regression (which constitutes a candidate solution) must be an affine combination of a predefined set of terms that we call base functions. In addition, we aim to use only a small number of such base functions. That is, a candidate solution is a function
![]() $\hat{f}(\vec{x})$
of the form
$\hat{f}(\vec{x})$
of the form
where the
![]() $t_i$
are arbitrary functions on
$t_i$
are arbitrary functions on
![]() $\vec{x}$
from a set
$\vec{x}$
from a set
![]() $\mathcal{F}$
of candidate base functions, which are representative of common complexity orders, and the
$\mathcal{F}$
of candidate base functions, which are representative of common complexity orders, and the
![]() $\beta _i$
’s are the coefficients (real numbers) that are estimated by regression, but so that only a few coefficients are nonzero.
$\beta _i$
’s are the coefficients (real numbers) that are estimated by regression, but so that only a few coefficients are nonzero.
For illustration purposes, assume that we use the following set
![]() $\mathcal{F}$
of base functions:
$\mathcal{F}$
of base functions:
where each base function is represented as a lambda expression. Then, the sparse linear regression is performed as follows.
-
1. Generate a training set
 $\mathcal{T}$
. First, a set
$\mathcal{T}$
. First, a set
 $\mathcal{I} = \{ \vec{x}_1, \ldots ,\vec{x}_{n} \}$
of input values to the recurrence function is randomly generated. Then, starting with an initial
$\mathcal{I} = \{ \vec{x}_1, \ldots ,\vec{x}_{n} \}$
of input values to the recurrence function is randomly generated. Then, starting with an initial
 $\mathcal{T} = \emptyset$
, for each input value
$\mathcal{T} = \emptyset$
, for each input value
 $\vec{x}_i \in \mathcal{I}$
, a training case
$\vec{x}_i \in \mathcal{I}$
, a training case
 $s_i$
is generated and added to
$s_i$
is generated and added to
 $\mathcal{T}$
. For any input value
$\mathcal{T}$
. For any input value
 $\vec{x} \in \mathcal{I}$
, the corresponding training case
$\vec{x} \in \mathcal{I}$
, the corresponding training case
 $s$
is a pair of the formwhere
$s$
is a pair of the formwhere \begin{equation*} s = \big (\langle b_1, \ldots , b_{p} \rangle ,\,r\big ), \end{equation*}
\begin{equation*} s = \big (\langle b_1, \ldots , b_{p} \rangle ,\,r\big ), \end{equation*}
 $b_i ={\lbrack \hspace{-0.3ex}\lbrack } t_i{\rbrack \hspace{-0.3ex}\rbrack }_{\vec{x}}$
for
$b_i ={\lbrack \hspace{-0.3ex}\lbrack } t_i{\rbrack \hspace{-0.3ex}\rbrack }_{\vec{x}}$
for
 $1 \leq i \leq p$
, and
$1 \leq i \leq p$
, and
 ${\lbrack \hspace{-0.3ex}\lbrack } t_i{\rbrack \hspace{-0.3ex}\rbrack }_{\vec{x}}$
represents the result (a scalar) of evaluating the base function
${\lbrack \hspace{-0.3ex}\lbrack } t_i{\rbrack \hspace{-0.3ex}\rbrack }_{\vec{x}}$
represents the result (a scalar) of evaluating the base function
 $t_i \in \mathcal{F}$
for input value
$t_i \in \mathcal{F}$
for input value
 $\vec{x}$
, where
$\vec{x}$
, where
 $\mathcal{F}$
is a set of
$\mathcal{F}$
is a set of
 $p$
base functions, as already explained. The (dependent) value
$p$
base functions, as already explained. The (dependent) value
 $r$
(also a constant number) is the result of evaluating the recurrence
$r$
(also a constant number) is the result of evaluating the recurrence
 $f(\vec{x})$
that we want to solve or approximate, in our example, the one defined in Eq. (1). Assuming that there is an
$f(\vec{x})$
that we want to solve or approximate, in our example, the one defined in Eq. (1). Assuming that there is an
 $\vec{x} \in \mathcal{I}$
such that
$\vec{x} \in \mathcal{I}$
such that
 $\vec{x} = \langle 5 \rangle$
, its corresponding training case
$\vec{x} = \langle 5 \rangle$
, its corresponding training case
 $s$
in our example will be
$s$
in our example will be \begin{equation*} \begin {array}{r@{\quad}l@{\quad}l} s &=& \big (\langle {\lbrack \hspace {-0.3ex}\lbrack } x {\rbrack \hspace {-0.3ex}\rbrack }_{5}, {\lbrack \hspace {-0.3ex}\lbrack } x^2 {\rbrack \hspace {-0.3ex}\rbrack }_{5}, {\lbrack \hspace {-0.3ex}\lbrack } x^3 {\rbrack \hspace {-0.3ex}\rbrack }_{5}, {\lbrack \hspace {-0.3ex}\lbrack } \lceil \log _2(x) \rceil {\rbrack \hspace {-0.3ex}\rbrack }_{5}, \ldots \rangle ,\, \mathbf {f(5)}\big ) \\[5pt] &=& \big (\langle 5, 25, 125, 3, \ldots \rangle ,\, \mathbf {5}\big ). \\[5pt] \end {array} \end{equation*}
\begin{equation*} \begin {array}{r@{\quad}l@{\quad}l} s &=& \big (\langle {\lbrack \hspace {-0.3ex}\lbrack } x {\rbrack \hspace {-0.3ex}\rbrack }_{5}, {\lbrack \hspace {-0.3ex}\lbrack } x^2 {\rbrack \hspace {-0.3ex}\rbrack }_{5}, {\lbrack \hspace {-0.3ex}\lbrack } x^3 {\rbrack \hspace {-0.3ex}\rbrack }_{5}, {\lbrack \hspace {-0.3ex}\lbrack } \lceil \log _2(x) \rceil {\rbrack \hspace {-0.3ex}\rbrack }_{5}, \ldots \rangle ,\, \mathbf {f(5)}\big ) \\[5pt] &=& \big (\langle 5, 25, 125, 3, \ldots \rangle ,\, \mathbf {5}\big ). \\[5pt] \end {array} \end{equation*}
-
2. Perform sparse regression using the training set
 $\mathcal{T}$
created above in order to find a small subset of base functions that fits it well. We do this in two steps. First, we solve an
$\mathcal{T}$
created above in order to find a small subset of base functions that fits it well. We do this in two steps. First, we solve an
 $\ell _1$
-regularized linear regression to learn an estimate of the non-zero coefficients of the base functions. This procedure, also called lasso (Hastie et al., Reference Hastie, Tibshirani and Wainwright2015), was originally introduced to learn interpretable models by selecting a subset of the input features. This happens because the
$\ell _1$
-regularized linear regression to learn an estimate of the non-zero coefficients of the base functions. This procedure, also called lasso (Hastie et al., Reference Hastie, Tibshirani and Wainwright2015), was originally introduced to learn interpretable models by selecting a subset of the input features. This happens because the
 $\ell _1$
(sum of absolute values) penalty results in some coefficients becoming exactly zero (unlike an
$\ell _1$
(sum of absolute values) penalty results in some coefficients becoming exactly zero (unlike an
 $\ell ^2_2$
penalty, which penalizes the magnitudes of the coefficients but typically results in none of them being zero). This will typically discard most of the base functions in
$\ell ^2_2$
penalty, which penalizes the magnitudes of the coefficients but typically results in none of them being zero). This will typically discard most of the base functions in
 $\mathcal{F}$
, and only those that are really needed to approximate our target function will be kept. The level of penalization is controlled by a hyperparameter
$\mathcal{F}$
, and only those that are really needed to approximate our target function will be kept. The level of penalization is controlled by a hyperparameter
 $\lambda \ge 0$
. As commonly done in machine learning (Hastie et al., Reference Hastie, Tibshirani and Wainwright2015), the value of
$\lambda \ge 0$
. As commonly done in machine learning (Hastie et al., Reference Hastie, Tibshirani and Wainwright2015), the value of
 $\lambda$
that generalizes optimally on unseen (test) inputs is found via cross-validation on a separate validation set (generated randomly in the same way as the training set). The result of this first sparse regression step are coefficients
$\lambda$
that generalizes optimally on unseen (test) inputs is found via cross-validation on a separate validation set (generated randomly in the same way as the training set). The result of this first sparse regression step are coefficients
 $\beta _1,\dots ,\beta _{p}$
(typically many of which are zero), and an independent coefficient
$\beta _1,\dots ,\beta _{p}$
(typically many of which are zero), and an independent coefficient
 $\beta _0$
. In a second step, we keep only those coefficients (and their corresponding terms
$\beta _0$
. In a second step, we keep only those coefficients (and their corresponding terms
 $t_i$
) for which
$t_i$
) for which
 $|\beta _i|\geq \epsilon$
(where the value of
$|\beta _i|\geq \epsilon$
(where the value of
 $\epsilon \ge 0$
is determined experimentally). We find that this post-processing results in solutions that better estimate the true non-zero coefficients.
$\epsilon \ge 0$
is determined experimentally). We find that this post-processing results in solutions that better estimate the true non-zero coefficients. -
3. Finally, our method performs again a standard linear regression (without
 $\ell _1$
regularization) on the training set
$\ell _1$
regularization) on the training set
 $\mathcal{T}$
, but using only the base functions selected in the previous step. In our example, with
$\mathcal{T}$
, but using only the base functions selected in the previous step. In our example, with
 $\epsilon = 0.05$
, we obtain the model
$\epsilon = 0.05$
, we obtain the model \begin{equation*} \begin {array}{r@{\quad}l} \hat {f}(x) = 1.0 \cdot x. & \end {array} \end{equation*}
\begin{equation*} \begin {array}{r@{\quad}l} \hat {f}(x) = 1.0 \cdot x. & \end {array} \end{equation*}
A final test set
![]() $\mathcal{T}_{\text{test}}$
with input set
$\mathcal{T}_{\text{test}}$
with input set
![]() $\mathcal{I}_{\text{test}}$
is then generated (in the same way as the training set) to obtain a measure
$\mathcal{I}_{\text{test}}$
is then generated (in the same way as the training set) to obtain a measure
![]() $R^2$
of the accuracy of the estimation. In this case, we obtain a value
$R^2$
of the accuracy of the estimation. In this case, we obtain a value
![]() $R^2 = 1$
, which means that the estimation obtained predicts exactly the values for the test set. This does not prove that the
$R^2 = 1$
, which means that the estimation obtained predicts exactly the values for the test set. This does not prove that the
![]() $\hat{f}$
is a solution of the recurrence, but this makes it a candidate solution for verification. If
$\hat{f}$
is a solution of the recurrence, but this makes it a candidate solution for verification. If
![]() $R^2$
were less than
$R^2$
were less than
![]() $1$
, it would mean that the function obtained is not a candidate (exact) solution, but an approximation (not necessarily a bound), as there are values in the test set that cannot be exactly predicted.
$1$
, it would mean that the function obtained is not a candidate (exact) solution, but an approximation (not necessarily a bound), as there are values in the test set that cannot be exactly predicted.
Currently, the set of base functions
![]() $\mathcal{F}$
is fixed; nevertheless, we plan to automatically infer better, more problem-oriented sets by using different heuristics, as we comment on in Section 8. Alternatively, as already mentioned, our guessing method is parametric and can also be instantiated to symbolic regression, which mitigates this limitation by creating new expressions, that is new “templates”, beyond linear combinations of
$\mathcal{F}$
is fixed; nevertheless, we plan to automatically infer better, more problem-oriented sets by using different heuristics, as we comment on in Section 8. Alternatively, as already mentioned, our guessing method is parametric and can also be instantiated to symbolic regression, which mitigates this limitation by creating new expressions, that is new “templates”, beyond linear combinations of
![]() $\mathcal{F}$
. However, only shallow expressions are reachable in acceptable time by symbolic regression’s exploration strategy: timeouts will often occur if solutions can only be expressed by deep expressions.
$\mathcal{F}$
. However, only shallow expressions are reachable in acceptable time by symbolic regression’s exploration strategy: timeouts will often occur if solutions can only be expressed by deep expressions.
2.2 The “check” stage
Once a function that is a candidate solution for the recurrence has been guessed, the second step of our method tries to verify whether such a candidate is actually a solution. To do so, the recurrence is encoded as a first order logic formula where the references to the target function are replaced by the candidate solution whenever possible. Afterwards, we use an SMT-solver to check whether the negation of such formula is satisfiable, in which case we can conclude that the candidate is not a solution for the recurrence. Otherwise, if such formula is unsatisfiable, then the candidate function is an exact solution. Sometimes, it is necessary to consider a precondition for the domain of the recurrence, which is also included in the encoding.
To illustrate this process, Expression (2) below
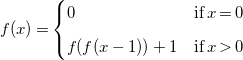 \begin{equation} \begin{array}{l@{\quad}l} f(x) = \begin{cases} 0 & \textrm{if}\; x = 0 \\[5pt] f(f(x-1)) + 1 & \textrm{if}\; x \gt 0 \end{cases} \end{array} \end{equation}
\begin{equation} \begin{array}{l@{\quad}l} f(x) = \begin{cases} 0 & \textrm{if}\; x = 0 \\[5pt] f(f(x-1)) + 1 & \textrm{if}\; x \gt 0 \end{cases} \end{array} \end{equation}
shows the recurrence we target to solve, for which the candidate solution obtained previously using (sparse) linear regression is
![]() $\hat{f}(x) = x$
(for all
$\hat{f}(x) = x$
(for all
![]() $x\geq 0$
). Now, Expression (3) below shows the encoding of the recurrence as a first order logic formula.
$x\geq 0$
). Now, Expression (3) below shows the encoding of the recurrence as a first order logic formula.
Finally, Expression (4) below shows the negation of such formula, as well as the references to the function name substituted by the definition of the candidate solution. We underline both the subexpressions to be replaced, and the subexpressions resulting from the substitutions.
It is easy to see that Formula (4) is unsatisfiable. Therefore,
![]() $\hat{f}(x) = x$
is an exact solution for
$\hat{f}(x) = x$
is an exact solution for
![]() $f(x)$
in the recurrence defined by Eq. (1).
$f(x)$
in the recurrence defined by Eq. (1).
For some cases where the candidate solution contains transcendental functions, our implementation of the method uses a CAS to perform simplifications and transformations, in order to obtain a formula supported by the SMT-solver. We find this combination of CAS and SMT-solver particularly useful, since it allows us to solve more problems than only using one of these systems in isolation.
3 Preliminaries
3.1 Notations
We use the letters
![]() $x$
,
$x$
,
![]() $y$
,
$y$
,
![]() $z$
to denote variables and
$z$
to denote variables and
![]() $a$
,
$a$
,
![]() $b$
,
$b$
,
![]() $c$
,
$c$
,
![]() $d$
to denote constants and coefficients. We use
$d$
to denote constants and coefficients. We use
![]() $f, g$
to represent functions, and
$f, g$
to represent functions, and
![]() $e, t$
to represent arbitrary expressions. We use
$e, t$
to represent arbitrary expressions. We use
![]() $\varphi$
to represent arbitrary boolean constraints over a set of variables. Sometimes, we also use
$\varphi$
to represent arbitrary boolean constraints over a set of variables. Sometimes, we also use
![]() $\beta$
to represent coefficients obtained with (sparse) linear regression. In all cases, the symbols can be subscribed.
$\beta$
to represent coefficients obtained with (sparse) linear regression. In all cases, the symbols can be subscribed.
![]() $\mathbb{N}$
and
$\mathbb{N}$
and
![]() $\mathbb{R}^+$
denote the sets of non-negative integer and non-negative real numbers, respectively, both including
$\mathbb{R}^+$
denote the sets of non-negative integer and non-negative real numbers, respectively, both including
![]() $0$
. Given two sets
$0$
. Given two sets
![]() $A$
and
$A$
and
![]() $B$
,
$B$
,
![]() $B^A$
is the set of all functions from
$B^A$
is the set of all functions from
![]() $A$
to
$A$
to
![]() $B$
. We use
$B$
. We use
![]() $\vec{x}$
to denote a finite sequence
$\vec{x}$
to denote a finite sequence
![]() $\langle x_1,x_2,\ldots ,x_{p}\rangle$
, for some
$\langle x_1,x_2,\ldots ,x_{p}\rangle$
, for some
![]() $p\gt 0$
. Given a sequence
$p\gt 0$
. Given a sequence
![]() $S$
and an element
$S$
and an element
![]() $x$
,
$x$
,
![]() $\langle x| S\rangle$
is a new sequence with first element
$\langle x| S\rangle$
is a new sequence with first element
![]() $x$
and tail
$x$
and tail
![]() $S$
. We refer to the classical finite-dimensional
$S$
. We refer to the classical finite-dimensional
![]() $1$
-norm (Manhattan norm) and
$1$
-norm (Manhattan norm) and
![]() $2$
-norm (Euclidean norm) by
$2$
-norm (Euclidean norm) by
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
, respectively, while
$\ell _2$
, respectively, while
![]() $\ell _0$
denotes the “norm” (which we will call a pseudo-norm) that counts the number of non-zero coordinates of a vector.
$\ell _0$
denotes the “norm” (which we will call a pseudo-norm) that counts the number of non-zero coordinates of a vector.
3.2 Recurrence relations
In our setting, a recurrence relation (or recurrence equation) is just a functional equation on
![]() $f:{\mathcal{D}}\to{\mathbb{R}}$
with
$f:{\mathcal{D}}\to{\mathbb{R}}$
with
![]() ${\mathcal{D}} \subset{\mathbb{N}}^{m}$
,
${\mathcal{D}} \subset{\mathbb{N}}^{m}$
,
![]() $m \geq 1$
, that can be written as
$m \geq 1$
, that can be written as
where
![]() $\Phi :{\mathbb{R}}^{\mathcal{D}}\times{\mathcal{D}}\to{\mathbb{R}}$
is used to define
$\Phi :{\mathbb{R}}^{\mathcal{D}}\times{\mathcal{D}}\to{\mathbb{R}}$
is used to define
![]() $f(\vec{x})$
in terms of other values of
$f(\vec{x})$
in terms of other values of
![]() $f$
. In this paper we consider functions
$f$
. In this paper we consider functions
![]() $f$
that take natural numbers as arguments but output real values, for example, corresponding to costs such as energy consumption, which need not be measured as integer values in practice. Working with real values also makes optimizing for the regression coefficients easier. We restrict ourselves to the domain
$f$
that take natural numbers as arguments but output real values, for example, corresponding to costs such as energy consumption, which need not be measured as integer values in practice. Working with real values also makes optimizing for the regression coefficients easier. We restrict ourselves to the domain
![]() $\mathbb{N}^{m}$
because in our motivating application, cost/size analysis, the input arguments to recurrences represent data sizes, which take non-negative integer values. Technically, our approach may be easily extended to recurrence equations on functions with domain
$\mathbb{N}^{m}$
because in our motivating application, cost/size analysis, the input arguments to recurrences represent data sizes, which take non-negative integer values. Technically, our approach may be easily extended to recurrence equations on functions with domain
![]() $\mathbb{Z}^{m}$
.
$\mathbb{Z}^{m}$
.
A system of recurrence equations is a functional equation on multiple
![]() $f_i:{\mathcal{D}}_i\to{\mathbb{R}}$
, that is
$f_i:{\mathcal{D}}_i\to{\mathbb{R}}$
, that is
![]() $\forall i,\,\forall{\vec{x}\in{\mathcal{D}}_i},\; f_i(\vec{x}) = \Phi _i(f_1,\ldots \!,f_r,\vec{x})$
. Inequations and non-deterministic equations can also be considered by making
$\forall i,\,\forall{\vec{x}\in{\mathcal{D}}_i},\; f_i(\vec{x}) = \Phi _i(f_1,\ldots \!,f_r,\vec{x})$
. Inequations and non-deterministic equations can also be considered by making
![]() $\Phi$
non-deterministic, that is
$\Phi$
non-deterministic, that is
![]() $\Phi :{\mathbb{R}}^{\mathcal{D}}\times{\mathcal{D}}\to{\mathcal{P}}({\mathbb{R}})$
and
$\Phi :{\mathbb{R}}^{\mathcal{D}}\times{\mathcal{D}}\to{\mathcal{P}}({\mathbb{R}})$
and
![]() $\forall{\vec{x}\in{\mathcal{D}}},\;f(\vec{x}) \in \Phi (f,\vec{x})$
. In general, such equations may have any number of solutions. In this work, we focus on deterministic recurrence equations, as we will discuss later.
$\forall{\vec{x}\in{\mathcal{D}}},\;f(\vec{x}) \in \Phi (f,\vec{x})$
. In general, such equations may have any number of solutions. In this work, we focus on deterministic recurrence equations, as we will discuss later.
Classical recurrence relations of order
![]() $k$
are recurrence relations where
$k$
are recurrence relations where
![]() ${\mathcal{D}}={\mathbb{N}}$
,
${\mathcal{D}}={\mathbb{N}}$
,
![]() $\Phi (f,n)$
is a constant when
$\Phi (f,n)$
is a constant when
![]() $n \lt k$
and
$n \lt k$
and
![]() $\Phi (f,n)$
depends only on
$\Phi (f,n)$
depends only on
![]() $f(n-k),\ldots \!,f(n-1)$
when
$f(n-k),\ldots \!,f(n-1)$
when
![]() $n \geq k$
. For example, the following recurrence relation of order
$n \geq k$
. For example, the following recurrence relation of order
![]() $k=1$
, where
$k=1$
, where
![]() $\Phi (f,n)= f(n-1) + 1$
when
$\Phi (f,n)= f(n-1) + 1$
when
![]() $n \geq 1$
, and
$n \geq 1$
, and
![]() $\Phi (f,n)= 1$
when
$\Phi (f,n)= 1$
when
![]() $n \lt 1$
(or equivalently,
$n \lt 1$
(or equivalently,
![]() $n = 0$
), that is
$n = 0$
), that is
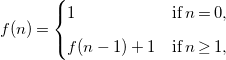 \begin{equation} f(n) = \begin{cases} 1 & \textrm{if}\; n = 0, \\[5pt] f(n-1) + 1 & \textrm{if}\; n \geq 1, \end{cases} \end{equation}
\begin{equation} f(n) = \begin{cases} 1 & \textrm{if}\; n = 0, \\[5pt] f(n-1) + 1 & \textrm{if}\; n \geq 1, \end{cases} \end{equation}
has the closed-form function
![]() $f(n) = n + 1$
as a solution.
$f(n) = n + 1$
as a solution.
Another example, with order
![]() $k=2$
, is the historical Fibonacci recurrence relation, where
$k=2$
, is the historical Fibonacci recurrence relation, where
![]() $\Phi (f,n)=f(n-1)+f(n-2)$
when
$\Phi (f,n)=f(n-1)+f(n-2)$
when
![]() $n\geq 2$
, and
$n\geq 2$
, and
![]() $\Phi (f,n)= 1$
when
$\Phi (f,n)= 1$
when
![]() $n \lt 2$
:
$n \lt 2$
:
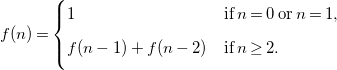 \begin{equation} f(n) = \begin{cases} 1 & \textrm{if}\; n = 0\; \textrm{or}\; n = 1, \\[5pt] f(n-1) + f(n-2) & \textrm{if}\; n \geq 2. \\[5pt] \end{cases} \end{equation}
\begin{equation} f(n) = \begin{cases} 1 & \textrm{if}\; n = 0\; \textrm{or}\; n = 1, \\[5pt] f(n-1) + f(n-2) & \textrm{if}\; n \geq 2. \\[5pt] \end{cases} \end{equation}
![]() $\Phi$
may be viewed as a recursive definition of “the” solution
$\Phi$
may be viewed as a recursive definition of “the” solution
![]() $f$
of the equation, with the caveat that the definition may be non-satisfiable or partial (degrees of freedom may remain). We define below an evaluation strategy
$f$
of the equation, with the caveat that the definition may be non-satisfiable or partial (degrees of freedom may remain). We define below an evaluation strategy
![]() $\mathsf{EvalFun}$
of this recursive definition, which, when it terminates for all inputs, provides a solution to the equation. This will allow us to view recurrence equations as programs that can be evaluated, enabling us to easily generate input-output pairs, on which we can perform regression to attempt to guess a symbolic solution to the equation.
$\mathsf{EvalFun}$
of this recursive definition, which, when it terminates for all inputs, provides a solution to the equation. This will allow us to view recurrence equations as programs that can be evaluated, enabling us to easily generate input-output pairs, on which we can perform regression to attempt to guess a symbolic solution to the equation.
This setting can be generalized to partial solutions to the equation, that is partial functions
![]() $f:{\mathcal{D}}\rightharpoonup{\mathbb{R}}$
such that
$f:{\mathcal{D}}\rightharpoonup{\mathbb{R}}$
such that
![]() $f(\vec{x}) = \Phi (f,\vec{x})$
whenever they are defined at
$f(\vec{x}) = \Phi (f,\vec{x})$
whenever they are defined at
![]() $\vec{x}$
.
$\vec{x}$
.
We are interested in constrained recurrence relations, where
![]() $\Phi$
is expressed piecewise as
$\Phi$
is expressed piecewise as
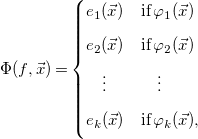 \begin{equation} \Phi (f,\vec{x}) = \begin{cases} e_1(\vec{x}) & \textrm{if}\; \varphi _1(\vec{x}) \\[5pt] e_2(\vec{x}) & \textrm{if}\; \varphi _2(\vec{x}) \\[5pt] \quad \vdots & \quad \vdots \\[5pt] e_k(\vec{x}) & \textrm{if}\; \varphi _k(\vec{x}), \\[5pt] \end{cases} \end{equation}
\begin{equation} \Phi (f,\vec{x}) = \begin{cases} e_1(\vec{x}) & \textrm{if}\; \varphi _1(\vec{x}) \\[5pt] e_2(\vec{x}) & \textrm{if}\; \varphi _2(\vec{x}) \\[5pt] \quad \vdots & \quad \vdots \\[5pt] e_k(\vec{x}) & \textrm{if}\; \varphi _k(\vec{x}), \\[5pt] \end{cases} \end{equation}
with
![]() $f:{\mathcal{D}}\to{\mathbb{R}}$
,
$f:{\mathcal{D}}\to{\mathbb{R}}$
,
![]() ${\mathcal{D}} = \{\vec{x}\,|\,\vec{x} \in{\mathbb{N}}^k \wedge \varphi _{\text{pre}}(\vec{x})\}$
for some boolean constraint
${\mathcal{D}} = \{\vec{x}\,|\,\vec{x} \in{\mathbb{N}}^k \wedge \varphi _{\text{pre}}(\vec{x})\}$
for some boolean constraint
![]() $\varphi _{\text{pre}}$
, called the precondition of
$\varphi _{\text{pre}}$
, called the precondition of
![]() $f$
, and
$f$
, and
![]() $e_i(\vec{x})$
,
$e_i(\vec{x})$
,
![]() $\varphi _i(\vec{x})$
are respectively arbitrary expressions and constraints over both
$\varphi _i(\vec{x})$
are respectively arbitrary expressions and constraints over both
![]() $\vec{x}$
and
$\vec{x}$
and
![]() $f$
. We further require that
$f$
. We further require that
![]() $\Phi$
is always defined, that is,
$\Phi$
is always defined, that is,
![]() $\varphi _{\text{pre}} \models \vee _i\,\varphi _i$
. A case such that
$\varphi _{\text{pre}} \models \vee _i\,\varphi _i$
. A case such that
![]() $e_i,\,\varphi _i$
do not contain any call to
$e_i,\,\varphi _i$
do not contain any call to
![]() $f$
is called a base case, and those that do are called recursive cases. In practice, we are only interested in equations with at least one base case and one recursive case.
$f$
is called a base case, and those that do are called recursive cases. In practice, we are only interested in equations with at least one base case and one recursive case.
A challenging class of recurrences that can be tackled with our approach is that of “nested” recurrences, where recursive cases may contain nested calls
![]() $f(f(\ldots ))$
.
$f(f(\ldots ))$
.
We assume that the
![]() $\varphi _i$
are mutually exclusive, so that
$\varphi _i$
are mutually exclusive, so that
![]() $\Phi$
must be deterministic. This is not an important limitation for our motivating application, cost analysis, and in particular the one performed by the CiaoPP system. Such cost analysis can deal with a large class of non-deterministic programs by translating the resulting non-deterministic recurrences into deterministic ones. For example, assume that the cost analysis generates the following recurrence (which represents an input/output size relation).
$\Phi$
must be deterministic. This is not an important limitation for our motivating application, cost analysis, and in particular the one performed by the CiaoPP system. Such cost analysis can deal with a large class of non-deterministic programs by translating the resulting non-deterministic recurrences into deterministic ones. For example, assume that the cost analysis generates the following recurrence (which represents an input/output size relation).
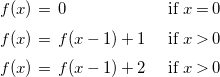 \begin{equation*} \begin {array}{l@{\quad}l} f(x) \, = \; 0 & \text { if } x = 0 \\[5pt] f(x) \, = \; f(x-1) + 1 & \text { if } x \gt 0 \\[5pt] f(x) \, = \; f(x-1) + 2 & \text { if } x \gt 0 \end {array} \end{equation*}
\begin{equation*} \begin {array}{l@{\quad}l} f(x) \, = \; 0 & \text { if } x = 0 \\[5pt] f(x) \, = \; f(x-1) + 1 & \text { if } x \gt 0 \\[5pt] f(x) \, = \; f(x-1) + 2 & \text { if } x \gt 0 \end {array} \end{equation*}
Then, prior to calling the solver, the recurrence is transformed into the following two deterministic recurrences, the solution of which would be an upper or lower bound on the solution to the original recurrence. For upper bounds:
and for lower bounds:
Our regression technique correctly infers the solution
![]() $f(x) = 2 x$
in the first case, and
$f(x) = 2 x$
in the first case, and
![]() $f(x) = x$
in the second case. We have access to such program transformation, that recovers determinism by looking for worst/best cases, under some hypotheses, outside of the scope of this paper, on the kind of non-determinism and equations that are being dealt with.
$f(x) = x$
in the second case. We have access to such program transformation, that recovers determinism by looking for worst/best cases, under some hypotheses, outside of the scope of this paper, on the kind of non-determinism and equations that are being dealt with.
We now introduce an evaluation strategy of recurrences that allows us to be more consistent with the termination of programs than the more classical semantics consisting only of maximally defined partial solutions. Let
![]() $\mathsf{def}(\Phi )$
denote a sequence
$\mathsf{def}(\Phi )$
denote a sequence
![]() $\langle (e_1(\vec{x}),\varphi _1(\vec{x})),\ldots ,(e_k(\vec{x}),\varphi _k(\vec{x}))\rangle$
defining a (piecewise) constrained recurrence relation
$\langle (e_1(\vec{x}),\varphi _1(\vec{x})),\ldots ,(e_k(\vec{x}),\varphi _k(\vec{x}))\rangle$
defining a (piecewise) constrained recurrence relation
![]() $\Phi$
on
$\Phi$
on
![]() $f$
, where each element of the sequence is a pair representing a case. The evaluation of the equation for a concrete value
$f$
, where each element of the sequence is a pair representing a case. The evaluation of the equation for a concrete value
![]() $\vec{{d}}$
, denoted
$\vec{{d}}$
, denoted
![]() $\mathsf{EvalFun}(f(\vec{{d}}))$
, is defined as follows.
$\mathsf{EvalFun}(f(\vec{{d}}))$
, is defined as follows.
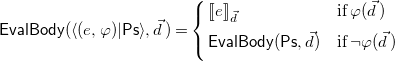 \begin{equation*} \mathsf {EvalBody}\big (\langle (e,\varphi )|\mathsf {Ps}\rangle , \vec {{d}}\,\big ) = \left\{\begin {array}{l@{\quad}l} {\lbrack \hspace {-0.3ex}\lbrack } e {\rbrack \hspace {-0.3ex}\rbrack }_{\vec {{d}}} & \textrm{if}\; \varphi \big (\vec {{d}}\,\big ) \\[5pt] \mathsf {EvalBody}(\mathsf {Ps}, \vec {{d}}) & \textrm{if}\; \neg \varphi \big (\vec {{d}}\,\big ) \\[5pt] \end {array}\right. \end{equation*}
\begin{equation*} \mathsf {EvalBody}\big (\langle (e,\varphi )|\mathsf {Ps}\rangle , \vec {{d}}\,\big ) = \left\{\begin {array}{l@{\quad}l} {\lbrack \hspace {-0.3ex}\lbrack } e {\rbrack \hspace {-0.3ex}\rbrack }_{\vec {{d}}} & \textrm{if}\; \varphi \big (\vec {{d}}\,\big ) \\[5pt] \mathsf {EvalBody}(\mathsf {Ps}, \vec {{d}}) & \textrm{if}\; \neg \varphi \big (\vec {{d}}\,\big ) \\[5pt] \end {array}\right. \end{equation*}
The goal of our regression strategy is to find an expression
![]() $\hat{f}$
representing a function
$\hat{f}$
representing a function
![]() ${\mathcal{D}}\to{\mathbb{R}}$
such that, for all
${\mathcal{D}}\to{\mathbb{R}}$
such that, for all
![]() $\vec{{d}} \in{\mathcal{D}}$
,
$\vec{{d}} \in{\mathcal{D}}$
,
-
•
 $\text{ If }\mathsf{EvalFun}(f(\vec{{d}})) \text{ terminates, then } \mathsf{EvalFun}(f(\vec{{d}})) ={\lbrack \hspace{-0.3ex}\lbrack } \hat{f}{\rbrack \hspace{-0.3ex}\rbrack }_{\vec{{d}}}$
, and
$\text{ If }\mathsf{EvalFun}(f(\vec{{d}})) \text{ terminates, then } \mathsf{EvalFun}(f(\vec{{d}})) ={\lbrack \hspace{-0.3ex}\lbrack } \hat{f}{\rbrack \hspace{-0.3ex}\rbrack }_{\vec{{d}}}$
, and -
•
 $\hat{f}$
does not contain any recursive call in its definition.
$\hat{f}$
does not contain any recursive call in its definition.
If the above conditions are met, we say that
![]() $\hat{f}$
is a closed form for
$\hat{f}$
is a closed form for
![]() $f$
. In the case of (sparse) linear regression, we are looking for expressions
$f$
. In the case of (sparse) linear regression, we are looking for expressions
where
![]() $\beta _i \in{\mathbb{R}}$
, and
$\beta _i \in{\mathbb{R}}$
, and
![]() $t_i$
are expressions over
$t_i$
are expressions over
![]() $\vec{x}$
, not including recursive references to
$\vec{x}$
, not including recursive references to
![]() $\hat{f}$
.
$\hat{f}$
.
For example, consider the following Prolog program which does not terminate for a call q(X) where X is bound to a positive integer.
The following recurrence relation for its cost (in resolution steps) can be set up.
A CAS will give the closed form
![]() $\mathtt{C}_{\mathtt{q}}(x) = 1 - x$
for such recurrence, however, the cost analysis should give
$\mathtt{C}_{\mathtt{q}}(x) = 1 - x$
for such recurrence, however, the cost analysis should give
![]() $\mathtt{C}_{\mathtt{q}}(x) = \infty$
for
$\mathtt{C}_{\mathtt{q}}(x) = \infty$
for
![]() $x\gt 0$
.
$x\gt 0$
.
3.3 (Sparse) linear regression
Linear regression (Hastie et al., Reference Hastie, Tibshirani and Friedman2009) is a statistical technique used to approximate the linear relationship between a number of explanatory (input) variables and a dependent (output) variable. Given a vector of (input) real-valued variables
![]() $X = (X_1,\ldots ,X_{p})^T$
, we predict the output variable
$X = (X_1,\ldots ,X_{p})^T$
, we predict the output variable
![]() $Y$
via the model
$Y$
via the model
which is defined through the vector of coefficients
![]() $\vec{\beta } = (\beta _0,\ldots ,\beta _{p})^T \in \mathbb{R}^{p+1}$
. Such coefficients are estimated from a set of observations
$\vec{\beta } = (\beta _0,\ldots ,\beta _{p})^T \in \mathbb{R}^{p+1}$
. Such coefficients are estimated from a set of observations
![]() $\{(\langle x_{i1},\ldots ,x_{ip}\rangle ,y_i)\}_{i=1}^{n}$
so as to minimize a loss function, most commonly the sum of squares
$\{(\langle x_{i1},\ldots ,x_{ip}\rangle ,y_i)\}_{i=1}^{n}$
so as to minimize a loss function, most commonly the sum of squares
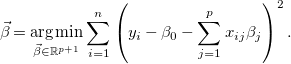 \begin{equation} \vec{\beta } = \underset{\vec{\beta } \in \mathbb{R}^{p+1}}{\textrm{arg min}}\sum _{i=1}^{n}\left(y_i - \beta _0 - \sum _{j=1}^{p} x_{ij}\beta _j\right)^2. \end{equation}
\begin{equation} \vec{\beta } = \underset{\vec{\beta } \in \mathbb{R}^{p+1}}{\textrm{arg min}}\sum _{i=1}^{n}\left(y_i - \beta _0 - \sum _{j=1}^{p} x_{ij}\beta _j\right)^2. \end{equation}
Sometimes (as is our case) some of the input variables are not relevant to explain the output, but the above least-squares estimate will almost always assign nonzero values to all the coefficients. In order to force the estimate to make exactly zero the coefficients of irrelevant variables (hence removing them and doing feature selection), various techniques have been proposed. The most widely used one is the lasso (Hastie et al., Reference Hastie, Tibshirani and Wainwright2015), which adds an
![]() $\ell _1$
penalty on
$\ell _1$
penalty on
![]() $\vec{\beta }$
(i.e., the sum of absolute values of each coefficient) to Expression 11, obtaining
$\vec{\beta }$
(i.e., the sum of absolute values of each coefficient) to Expression 11, obtaining
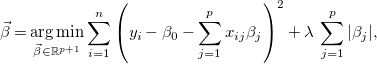 \begin{equation} \vec{\beta } = \underset{\vec{\beta } \in \mathbb{R}^{p+1}}{\textrm{arg min}}\sum _{i=1}^{n}\left(y_i - \beta _0 - \sum _{j=1}^{p} x_{ij}\beta _j\right)^2 + \lambda \,\sum _{j=1}^{p}|\beta _j|, \end{equation}
\begin{equation} \vec{\beta } = \underset{\vec{\beta } \in \mathbb{R}^{p+1}}{\textrm{arg min}}\sum _{i=1}^{n}\left(y_i - \beta _0 - \sum _{j=1}^{p} x_{ij}\beta _j\right)^2 + \lambda \,\sum _{j=1}^{p}|\beta _j|, \end{equation}
where
![]() $\lambda \ge 0$
is a hyperparameter that determines the level of penalization: the greater
$\lambda \ge 0$
is a hyperparameter that determines the level of penalization: the greater
![]() $\lambda$
, the greater the number of coefficients that are exactly equal to
$\lambda$
, the greater the number of coefficients that are exactly equal to
![]() $0$
. The lasso has two advantages over other feature selection techniques for linear regression. First, it defines a convex problem whose unique solution can be efficiently computed even for datasets where either of
$0$
. The lasso has two advantages over other feature selection techniques for linear regression. First, it defines a convex problem whose unique solution can be efficiently computed even for datasets where either of
![]() $n$
or
$n$
or
![]() $p$
are large (almost as efficiently as a standard linear regression). Second, it has been shown in practice to be very good at estimating the relevant variables. In fact, the regression problem we would really like to solve is that of Expression 11 but subject to the constraint that
$p$
are large (almost as efficiently as a standard linear regression). Second, it has been shown in practice to be very good at estimating the relevant variables. In fact, the regression problem we would really like to solve is that of Expression 11 but subject to the constraint that
![]() $\left \lVert (\beta _1,\ldots ,\beta _{p})^T\right \rVert _0 \le K$
, that is, that at most
$\left \lVert (\beta _1,\ldots ,\beta _{p})^T\right \rVert _0 \le K$
, that is, that at most
![]() $K$
of the
$K$
of the
![]() $p$
coefficients are non-zero, an
$p$
coefficients are non-zero, an
![]() $\ell _0$
-constrained problem. Unfortunately, this is an NP-hard problem. However, replacing the
$\ell _0$
-constrained problem. Unfortunately, this is an NP-hard problem. However, replacing the
![]() $\ell _0$
pseudo-norm with the
$\ell _0$
pseudo-norm with the
![]() $\ell _1$
-norm has been observed to produce good approximations in practice (Hastie et al., Reference Hastie, Tibshirani and Wainwright2015).
$\ell _1$
-norm has been observed to produce good approximations in practice (Hastie et al., Reference Hastie, Tibshirani and Wainwright2015).
3.4 Symbolic regression
Symbolic regression is a regression task in which the model space consists of all mathematical expressions on a chosen signature, that is expression trees with variables or constants for leaves and operators for internal nodes. To avoid overfitting, objective functions are designed to penalize model complexity, in a similar fashion to sparse linear regression techniques. This task is much more ambitious: rather than searching over the vector space spanned by a relatively small set of base functions as we do in sparse linear regression, the search space is enormous, considering any possible expression which results from applying a set of mathematical operators in any combination. For this reason, heuristics such as evolutionary algorithms are typically used to search this space, but runtime still remains a challenge for deep expressions.
The approach presented in this paper is parametric in the regression technique used, and we instantiate it with both (sparse) linear and symbolic regression in our experiments (Section 6). We will see that symbolic regression addresses some of the limitations of (sparse) linear regression, at the expense of time. Our implementation is based on the symbolic regression library PySR (Cranmer, Reference Cranmer2023), a multi-population evolutionary algorithm paired with classical optimization algorithms to select constants. In order to avoid overfitting and guide the search, PySR penalizes model complexity, defined as a sum of individual node costs for nodes in the expression tree, where a predefined cost is assigned to each possible type of node.
In our application context, (sparse) linear regression searches for a solution to the recurrence equation in the affine space spanned by candidate functions, that is
![]() $\hat{f} = \beta _0 + \sum _i \beta _i t_i$
with
$\hat{f} = \beta _0 + \sum _i \beta _i t_i$
with
![]() $t_i\in \mathcal{F}$
, while symbolic regression may choose any expression built on the chosen operators. For example, consider equation exp3 of Table 1, whose solution is
$t_i\in \mathcal{F}$
, while symbolic regression may choose any expression built on the chosen operators. For example, consider equation exp3 of Table 1, whose solution is
![]() $(x,y)\mapsto 2^{x+y}$
. This solution cannot be expressed using (sparse) linear regression and the set of candidates
$(x,y)\mapsto 2^{x+y}$
. This solution cannot be expressed using (sparse) linear regression and the set of candidates
![]() $\{\lambda xy.x,\lambda xy.y,\lambda xy.x^2,\lambda xy.y^2,\lambda xy.2^x,\lambda xy.2^y\}$
, but can be found with symbolic regression and operators
$\{\lambda xy.x,\lambda xy.y,\lambda xy.x^2,\lambda xy.y^2,\lambda xy.2^x,\lambda xy.2^y\}$
, but can be found with symbolic regression and operators
![]() $\{+(\cdot ,\cdot ), \times (\cdot ,\cdot ), 2^{(\cdot )}\}$
.
$\{+(\cdot ,\cdot ), \times (\cdot ,\cdot ), 2^{(\cdot )}\}$
.
4 Algorithmic description of the approach
In this section we describe our approach for generating and checking candidate solutions for recurrences that arise in resource analysis.
4.1 A first version
Algorithms1 and 2 correspond to the guesser and checker components, respectively, which are illustrated in Figure 1. For the sake of presentation, Algorithm1 describes the instantiation of the guess method based on lasso linear regression. It receives a recurrence relation for a function
![]() $f$
to solve, a set of base functions, and a threshold to decide when to discard irrelevant terms. The output is a closed-form expression
$f$
to solve, a set of base functions, and a threshold to decide when to discard irrelevant terms. The output is a closed-form expression
![]() $\hat{f}$
for
$\hat{f}$
for
![]() $f$
, and a score
$f$
, and a score
![]() $\mathcal{S}$
that reflects the accuracy of the approximation, in the range
$\mathcal{S}$
that reflects the accuracy of the approximation, in the range
![]() $[0,1]$
. If
$[0,1]$
. If
![]() $\mathcal{S} \approx 1$
, the approximation can be considered a candidate solution. Otherwise,
$\mathcal{S} \approx 1$
, the approximation can be considered a candidate solution. Otherwise,
![]() $\hat{f}$
is an approximation (not necessarily a bound) of the solution.
$\hat{f}$
is an approximation (not necessarily a bound) of the solution.
Algorithm 1. Candidate Solution Generation (Guesser).

4.1.1 Generate
In line 1 we start by generating a set
![]() $\mathcal{I}$
of random inputs for
$\mathcal{I}$
of random inputs for
![]() $f$
. Each input
$f$
. Each input
![]() $\vec{x_i}$
is an
$\vec{x_i}$
is an
![]() $m$
-tuple verifying precondition
$m$
-tuple verifying precondition
![]() $\varphi _{\text{pre}}$
, where
$\varphi _{\text{pre}}$
, where
![]() $m$
is the number of arguments of
$m$
is the number of arguments of
![]() $f$
. In line 2 we produce the training set
$f$
. In line 2 we produce the training set
![]() $\mathcal{T}$
. The (explanatory) inputs are generated by evaluating the base functions in
$\mathcal{T}$
. The (explanatory) inputs are generated by evaluating the base functions in
![]() $\mathcal{F} = \langle t_1, t_2, \ldots , t_{p} \rangle$
with each tuple
$\mathcal{F} = \langle t_1, t_2, \ldots , t_{p} \rangle$
with each tuple
![]() $\vec{x} \in \mathcal{I}$
. This is done by using function
$\vec{x} \in \mathcal{I}$
. This is done by using function
![]() $E$
, defined as follows.
$E$
, defined as follows.
We also evaluate the recurrence equation for input
![]() $\vec{x}$
, and add the observed output
$\vec{x}$
, and add the observed output
![]() $f(\vec{x})$
as the last element in the corresponding training case.
$f(\vec{x})$
as the last element in the corresponding training case.
4.1.2 Regress
In line 3 we generate a first linear model by applying function
![]() $\mathsf{CVLassoRegression}$
to the generated training set, which performs a sparse linear regression with lasso regularization. As already mentioned, lasso regularization requires a hyperparameter
$\mathsf{CVLassoRegression}$
to the generated training set, which performs a sparse linear regression with lasso regularization. As already mentioned, lasso regularization requires a hyperparameter
![]() $\lambda$
that determines the level of penalization for the coefficients. Instead of using a single value for
$\lambda$
that determines the level of penalization for the coefficients. Instead of using a single value for
![]() $\lambda$
,
$\lambda$
,
![]() $\mathsf{CVLassoRegression}$
uses a range of possible values, applying cross-validation on top of the linear regression to automatically select the best value for that parameter, from the given range. In particular,
$\mathsf{CVLassoRegression}$
uses a range of possible values, applying cross-validation on top of the linear regression to automatically select the best value for that parameter, from the given range. In particular,
![]() $k$
-fold cross-validation is performed, which means that the training set is split into
$k$
-fold cross-validation is performed, which means that the training set is split into
![]() $k$
parts or folds. Then, each fold is taken as the validation set, training the model with the remaining
$k$
parts or folds. Then, each fold is taken as the validation set, training the model with the remaining
![]() $k-1$
folds. Finally, the performance measure reported is the average of the values computed in the
$k-1$
folds. Finally, the performance measure reported is the average of the values computed in the
![]() $k$
iterations. The result of this function is the vector of coefficients
$k$
iterations. The result of this function is the vector of coefficients
![]() $\vec{\beta ^{\prime }}$
, together with the intercept
$\vec{\beta ^{\prime }}$
, together with the intercept
![]() $\beta _0^{\prime }$
. These coefficients are used in line 4 to decide which base functions are discarded before the last regression step. Note that
$\beta _0^{\prime }$
. These coefficients are used in line 4 to decide which base functions are discarded before the last regression step. Note that
![]() $\mathsf{RemoveTerms}$
removes the base functions from
$\mathsf{RemoveTerms}$
removes the base functions from
![]() $\mathcal{F}$
together with their corresponding output values from the training set
$\mathcal{F}$
together with their corresponding output values from the training set
![]() $\mathcal{T}$
, returning the new set of base functions
$\mathcal{T}$
, returning the new set of base functions
![]() $\mathcal{F}^{\prime }$
and its corresponding training set
$\mathcal{F}^{\prime }$
and its corresponding training set
![]() $\mathcal{T}^{\prime }$
. In line 5, standard linear regression (without regularization or cross-validation) is applied, obtaining the final coefficients
$\mathcal{T}^{\prime }$
. In line 5, standard linear regression (without regularization or cross-validation) is applied, obtaining the final coefficients
![]() $\vec{\beta }$
and
$\vec{\beta }$
and
![]() $\beta _0$
. Additionally, from this step we also obtain the score
$\beta _0$
. Additionally, from this step we also obtain the score
![]() $\mathcal{S}$
of the resulting model. In line 6 we set up the resulting closed-form expression, given as a function on the variables in
$\mathcal{S}$
of the resulting model. In line 6 we set up the resulting closed-form expression, given as a function on the variables in
![]() $\vec{x}$
. Note that we use the function
$\vec{x}$
. Note that we use the function
![]() $E$
to bind the variables in the base functions to the arguments of the closed-form expression. Finally, the closed-form expression and its corresponding score are returned as the result of the algorithm.
$E$
to bind the variables in the base functions to the arguments of the closed-form expression. Finally, the closed-form expression and its corresponding score are returned as the result of the algorithm.
4.1.3 Verify
Algorithm 2. Solution Checking (Checker).

Algorithm2 mainly relies on an SMT-solver and a CAS. Concretely, given the constrained recurrence relation on
![]() $f:{\mathcal{D}} \to{\mathbb{R}}$
defined by
$f:{\mathcal{D}} \to{\mathbb{R}}$
defined by
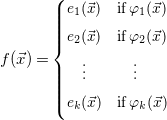 \begin{equation*} f(\vec {x}) = \small \begin {cases} e_1(\vec {x}) & \textrm{if}\; \varphi _1(\vec {x}) \\[5pt] e_2(\vec {x}) & \textrm{if}\; \varphi _2(\vec {x}) \\[5pt] \quad \vdots & \quad \vdots \\[5pt] e_k(\vec {x}) & \textrm{if}\; \varphi _k(\vec {x}) \\[5pt] \end {cases} \end{equation*}
\begin{equation*} f(\vec {x}) = \small \begin {cases} e_1(\vec {x}) & \textrm{if}\; \varphi _1(\vec {x}) \\[5pt] e_2(\vec {x}) & \textrm{if}\; \varphi _2(\vec {x}) \\[5pt] \quad \vdots & \quad \vdots \\[5pt] e_k(\vec {x}) & \textrm{if}\; \varphi _k(\vec {x}) \\[5pt] \end {cases} \end{equation*}
our algorithm constructs the logic formula
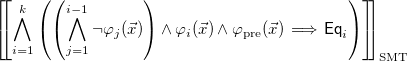 \begin{equation} \left[\hspace{-0.7ex}\left[ \bigwedge \limits _{i=1}^k \left (\left (\bigwedge \limits _{j=1}^{i-1} \neg \varphi _j(\vec{x}) \right ) \wedge \varphi _i(\vec{x}) \wedge \varphi _{\text{pre}}(\vec{x}) \implies \mathsf{Eq}_i \right )\right]\hspace{-0.7ex}\right]_{\text{SMT}} \end{equation}
\begin{equation} \left[\hspace{-0.7ex}\left[ \bigwedge \limits _{i=1}^k \left (\left (\bigwedge \limits _{j=1}^{i-1} \neg \varphi _j(\vec{x}) \right ) \wedge \varphi _i(\vec{x}) \wedge \varphi _{\text{pre}}(\vec{x}) \implies \mathsf{Eq}_i \right )\right]\hspace{-0.7ex}\right]_{\text{SMT}} \end{equation}
where operation
![]() ${\lbrack \hspace{-0.3ex}\lbrack } e{\rbrack \hspace{-0.3ex}\rbrack }_{\text{SMT}}$
is the translation of any expression
${\lbrack \hspace{-0.3ex}\lbrack } e{\rbrack \hspace{-0.3ex}\rbrack }_{\text{SMT}}$
is the translation of any expression
![]() $e$
to an SMT-LIB expression, and
$e$
to an SMT-LIB expression, and
![]() $\mathsf{Eq}_i$
is the result of replacing in
$\mathsf{Eq}_i$
is the result of replacing in
![]() $f(\vec{x}) = e_i(\vec{x})$
each occurrence of
$f(\vec{x}) = e_i(\vec{x})$
each occurrence of
![]() $f$
(a priori written as an uninterpreted function) by the definition of the candidate solution
$f$
(a priori written as an uninterpreted function) by the definition of the candidate solution
![]() $\hat{f}$
(by using
$\hat{f}$
(by using
![]() $\mathsf{replaceCalls}$
in line 4), and performing a simplification (by using
$\mathsf{replaceCalls}$
in line 4), and performing a simplification (by using
![]() $\mathsf{simplifyCAS}$
in line 6). The function
$\mathsf{simplifyCAS}$
in line 6). The function
![]() $\mathsf{replaceCalls}(\mathsf{expr},f(\vec{x}^\prime ),\hat{f},\varphi _{\text{pre}},\varphi )$
replaces every subexpression in
$\mathsf{replaceCalls}(\mathsf{expr},f(\vec{x}^\prime ),\hat{f},\varphi _{\text{pre}},\varphi )$
replaces every subexpression in
![]() $\mathsf{expr}$
of the form
$\mathsf{expr}$
of the form
![]() $f(\vec{x}^\prime )$
by
$f(\vec{x}^\prime )$
by
![]() $\hat{f}(\vec{x}^\prime )$
, if
$\hat{f}(\vec{x}^\prime )$
, if
![]() $\varphi \implies \varphi _{\text{pre}}(\vec{x}^\prime )$
. When checking Formula 13, all variables are assumed to be integers. As an implementation detail, to work with Z3 and access a large arithmetic language (including rational division), variables are initially declared as reals, but integrality constraints
$\varphi \implies \varphi _{\text{pre}}(\vec{x}^\prime )$
. When checking Formula 13, all variables are assumed to be integers. As an implementation detail, to work with Z3 and access a large arithmetic language (including rational division), variables are initially declared as reals, but integrality constraints
![]() $\large (\bigwedge _i \vec{x}_i = \lfloor \vec{x}_i \rfloor \large )$
are added to the final formula. Note that this encoding is consistent with the evaluation (
$\large (\bigwedge _i \vec{x}_i = \lfloor \vec{x}_i \rfloor \large )$
are added to the final formula. Note that this encoding is consistent with the evaluation (
![]() $\mathsf{EvalFun}$
) described in Section 3.
$\mathsf{EvalFun}$
) described in Section 3.
The goal of
![]() $\mathsf{simplifyCAS}$
is to obtain (sub)expressions supported by the SMT-solver. This typically allows simplifying away differences of transcendental functions, such as exponentials and logarithms, for which SMT-solvers like Z3 currently have extremely limited support, often dealing with them as if they were uninterpreted functions. For example, log2 is simply absent from SMT-LIB, although it can be modelled with exponentials, and reasoning abilities with exponentials are very limited: while Z3 can check that
$\mathsf{simplifyCAS}$
is to obtain (sub)expressions supported by the SMT-solver. This typically allows simplifying away differences of transcendental functions, such as exponentials and logarithms, for which SMT-solvers like Z3 currently have extremely limited support, often dealing with them as if they were uninterpreted functions. For example, log2 is simply absent from SMT-LIB, although it can be modelled with exponentials, and reasoning abilities with exponentials are very limited: while Z3 can check that
![]() $2^x - 2^x = 0$
, it cannot check (without further help) that
$2^x - 2^x = 0$
, it cannot check (without further help) that
![]() $2^{x+1}-2\cdot 2^x=0$
. Using
$2^{x+1}-2\cdot 2^x=0$
. Using
![]() $\mathsf{simplifyCAS}$
, the latter is replaced by
$\mathsf{simplifyCAS}$
, the latter is replaced by
![]() $0=0$
which is immediately checked.
$0=0$
which is immediately checked.
Finally, the algorithm asks the SMT-solver for models of the negated formula (line 17). If no model exists, then it returns
![]() $\mathsf{true}$
, concluding that
$\mathsf{true}$
, concluding that
![]() $\hat{f}$
is an exact solution to the recurrence, that is
$\hat{f}$
is an exact solution to the recurrence, that is
![]() $\hat{f}(\vec{x}) = f(\vec{x})$
for any input
$\hat{f}(\vec{x}) = f(\vec{x})$
for any input
![]() $\vec{x} \in{\mathcal{D}}$
such that
$\vec{x} \in{\mathcal{D}}$
such that
![]() $\mathsf{EvalFun}(f(\vec{x}))$
terminates. Otherwise, it returns
$\mathsf{EvalFun}(f(\vec{x}))$
terminates. Otherwise, it returns
![]() $\mathsf{false}$
. Note that, if we are not able to express
$\mathsf{false}$
. Note that, if we are not able to express
![]() $\hat{f}$
using the syntax supported by the SMT-solver, even after performing the simplification by
$\hat{f}$
using the syntax supported by the SMT-solver, even after performing the simplification by
![]() $\mathsf{simplifyCAS}$
, then the algorithm finishes returning
$\mathsf{simplifyCAS}$
, then the algorithm finishes returning
![]() $\mathsf{false}$
.
$\mathsf{false}$
.
4.2 Extension: Domain splitting
For the sake of exposition, we have only presented a basic combination of Algorithms1 and 2, but the core approach generate, regress and verify can be generalized to obtain more accurate results. Beyond the use of different regression algorithms (replacing lines 3–6 in Algorithm1, for example, with symbolic regression as presented in Section 3), we can also decide to apply Algorithm1 separately on multiple subdomains of
![]() $\mathcal{D}$
: we call this strategy domain splitting. In other words, rather than trying to directly infer a solution on
$\mathcal{D}$
: we call this strategy domain splitting. In other words, rather than trying to directly infer a solution on
![]() $\mathcal{D}$
by regression, we do the following.
$\mathcal{D}$
by regression, we do the following.
-
• Partition
 $\mathcal{D}$
into subdomains
$\mathcal{D}$
into subdomains
 ${\mathcal{D}}_i$
.
${\mathcal{D}}_i$
. -
• Apply (any variant of) Algorithm1 on each
 ${\mathcal{D}}_i$
, that is generate input-output pairs, and regress to obtain candidates
${\mathcal{D}}_i$
, that is generate input-output pairs, and regress to obtain candidates
 $\hat{f}_i:{\mathcal{D}}_i\to \mathbb{R}$
.
$\hat{f}_i:{\mathcal{D}}_i\to \mathbb{R}$
. -
• This gives a global candidate
 $\hat{f} : x \mapsto \{\hat{f}_i \text{ if } x\in{\mathcal{D}}_i\}$
, that we can then attempt to verify (Algorithm2).
$\hat{f} : x \mapsto \{\hat{f}_i \text{ if } x\in{\mathcal{D}}_i\}$
, that we can then attempt to verify (Algorithm2).
A motivation for doing so is the observation that it is easier for regression algorithms to discover expressions of “low (model) complexity”, that is expressions of low depth on common operators for symbolic regression and affine combinations of common functions for (sparse) linear regression (note that model complexity of the expression is not to be confused with the computational complexity of the algorithm whose cost is represented by the expression, that is, the asymptotic rate of growth of the corresponding function). We also observe that our equations often admit solutions that can be described piecewise with low (model) complexity expressions, where equivalent global expressions are somehow artificial: they have high (model) complexity, making them hard or impossible to find. In other words, equations with “piecewise simple” solutions are more common than those with “globally simple” solutions, and the domain splitting strategy is able to decrease complexity for this common case by reduction to the more favorable one.
For example, consider equation merge in Table 1, representing the cost of a merge function in a merge-sort algorithm. Its solution is
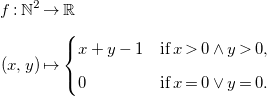 \begin{align*} f : \mathbb{N}^2 &\to \mathbb{R}\\[5pt] (x,y) &\mapsto \begin{cases} x+y-1 & \textrm{if}\; x\gt 0 \land y\gt 0, \\[5pt] 0 & \textrm{if}\; x=0 \lor y=0. \end{cases} \end{align*}
\begin{align*} f : \mathbb{N}^2 &\to \mathbb{R}\\[5pt] (x,y) &\mapsto \begin{cases} x+y-1 & \textrm{if}\; x\gt 0 \land y\gt 0, \\[5pt] 0 & \textrm{if}\; x=0 \lor y=0. \end{cases} \end{align*}
It admits a piecewise affine description, but no simple global description as a polynomial, although we can admittedly write it as
![]() $\min (x,1)\times \min (y,1)\times (x+y-1)$
, which is unreachable by (sparse) linear regression for any reasonable set of candidates, and of challenging depth for symbolic regression.
$\min (x,1)\times \min (y,1)\times (x+y-1)$
, which is unreachable by (sparse) linear regression for any reasonable set of candidates, and of challenging depth for symbolic regression.
To implement domain splitting, there are two challenges to face: (1) partition the domain into appropriate subdomains that make regression more accurate and (2) generate random input points inside each subdomain.
In our implementation (Section 6), we test a very simple version of this idea, were generation is handled by a trivial rejection strategy, and where the domain is partitioned using the conditions
![]() $\varphi _i(\vec{x})\wedge \bigwedge _{j=1}^{i-1}\neg \varphi _j(\vec{x})$
that define each clause of the input equation.
$\varphi _i(\vec{x})\wedge \bigwedge _{j=1}^{i-1}\neg \varphi _j(\vec{x})$
that define each clause of the input equation.
In other words, our splitting strategy is purely syntactic. More advanced strategies could learn better subdomains, for example by using a generalization of model trees, and are left for future work. However, as we will see in Section 6, our naive strategy already provides good improvements compared to Section 4.1. Intuitively, this seems to indicate that a large part of the “disjunctive behavior” of solutions originates from the “input disjunctivity” in the equation (which, of course, can be found in other places than the
![]() $\varphi _i$
, but this is a reasonable first approximation).
$\varphi _i$
, but this is a reasonable first approximation).
Finally, for the verification step, we can simply construct an SMT formula corresponding to the equation as in Section 4.1, using an expression defined by cases for
![]() $\hat{f}$
, for example with the ite construction in SMT-LIB.
$\hat{f}$
, for example with the ite construction in SMT-LIB.
5 Our approach in the context of static cost analysis of (logic) programs
In this section, we describe how our approach could be used in the context of the motivating application, Static Cost Analysis. Although it is general, and could be integrated into any cost analysis system based on recurrence solving, we illustrate its use in the context of the CiaoPP system. Using a logic program, we first illustrate how CiaoPP sets up recurrence relations representing the sizes of output arguments of predicates and the cost of such predicates. Then, we show how our novel approach is used to solve a recurrence relation that cannot be solved by CiaoPP.
Example 1. Consider predicate q/2 in Figure 2, and calls to it where the first argument is bound to a non-negative integer and the second one is a free variable.Footnote 1 Upon success of these calls, the second argument is bound to an non-negative integer too. Such calling mode, where the first argument is input and the second one is output, is automatically inferred by CiaoPP (see Hermenegildo et al. (Reference Hermenegildo, Puebla, Bueno and Garcia2005) and its references).

Fig 2. A program with a nested recursion.
The CiaoPP system first infers size relations for the different arguments of predicates, using a rich set of size metrics (see Navas et al. (Reference Navas, Mera, Lopez-Garcia and Hermenegildo2007); Serrano et al. (Reference Serrano, Lopez-Garcia and Hermenegildo2014) for details). Assume that the size metric used in this example, for the numeric argument X is the actual value of it (denoted int(X)). The system will try to infer a function
![]() $\mathtt{S}_{\mathtt{q}}(x)$
that gives the size of the output argument of q/2 (the second one), as a function of the size (
$\mathtt{S}_{\mathtt{q}}(x)$
that gives the size of the output argument of q/2 (the second one), as a function of the size (
![]() $x$
) of the input argument (the first one). For this purpose, the following size relations for
$x$
) of the input argument (the first one). For this purpose, the following size relations for
![]() $\mathtt{ S}_{\mathtt{q}}(x)$
are automatically set up (the same as the recurrence in Eq. (1) used in Section 2 as example).
$\mathtt{ S}_{\mathtt{q}}(x)$
are automatically set up (the same as the recurrence in Eq. (1) used in Section 2 as example).
The first and second recurrence correspond to the first and second clauses respectively (i.e., base and recursive cases). Once recurrence relations (either representing the size of terms, as the ones above, or the computational cost of predicates, as the ones that we will see later) have been set up, a solving process is started.
Nested recurrences, as the one that arise in this example, cannot be handled by most state-of-the-art recurrence solvers. In particular, the modular solver used by CiaoPP fails to find a closed-form function for the recurrence relation above. In contrast, the novel approach that we propose obtains the closed form
![]() $\hat{\mathtt{S}}_{\mathtt{q}}(x) = x$
, which is an exact solution of such recurrence (as shown in Section 2).
$\hat{\mathtt{S}}_{\mathtt{q}}(x) = x$
, which is an exact solution of such recurrence (as shown in Section 2).
Once the size relations have been inferred, CiaoPP uses them to infer the computational cost of a call to q/2. For simplicity, assume that in this example, such cost is given in terms of the number of resolution steps, as a function of the size of the input argument, but note that CiaoPP’s cost analysis is parametric with respect to resources, which can be defined by the user by means of a rich assertion language, so that it can infer a wide range of resources, besides resolution steps. Also for simplicity, we assume that all builtin predicates, such as arithmetic/comparison operators have zero cost (in practice there is a “trust” assertion for each builtin that specifies its cost as if it had been inferred by the analysis).
In order to infer the cost of a call to q/2, represented as
![]() $\mathtt{C}_{\mathtt{q}}(x)$
, CiaoPP sets up the following cost relations, by using the size relations inferred previously.
$\mathtt{C}_{\mathtt{q}}(x)$
, CiaoPP sets up the following cost relations, by using the size relations inferred previously.
We can see that the cost of the second recursive call to predicate p/2 depends on the size of the output argument of the first recursive call to such predicate, which is given by function
![]() $\mathtt{S}_{\mathtt{q}}(x)$
, whose closed form
$\mathtt{S}_{\mathtt{q}}(x)$
, whose closed form
![]() $\mathtt{S}_{\mathtt{q}}(x) = x$
is computed by our approach, as already explained. Plugging such closed form into the recurrence relation above, it can now be solved by CiaoPP, obtaining
$\mathtt{S}_{\mathtt{q}}(x) = x$
is computed by our approach, as already explained. Plugging such closed form into the recurrence relation above, it can now be solved by CiaoPP, obtaining
![]() $\mathtt{C}_{\mathtt{q}}(x) = 2^{x+1} - 1$
.
$\mathtt{C}_{\mathtt{q}}(x) = 2^{x+1} - 1$
.
6 Implementation and experimental evaluation
We have implemented a prototype of our novel approach and performed an experimental evaluation in the context of the CiaoPP system, by solving recurrences similar to those generated during static cost analysis, and comparing the results with the current CiaoPP solver as well as with state-of-the-art cost analyzers and recurrence solvers. Our experimental results are summarized in Table 2 and Figure 3, where our approach is evaluated on the benchmarks of Table 1, and where we compare its results with other tools, as described below and in Section 7. Beyond these summaries, additional details on chosen benchmarks are given in paragraph Evaluation and Discussion, and full outputs are included in Appendix B.
Table 1. Benchmarks
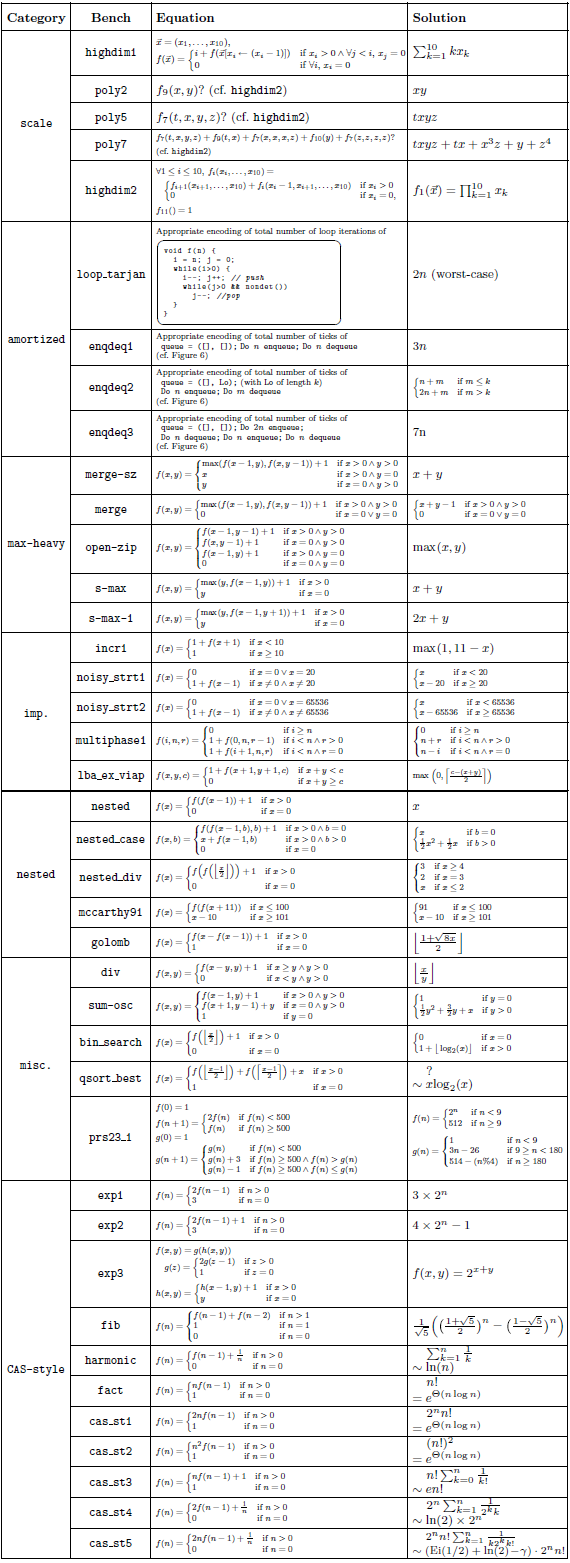
Table 2. Experimental evaluation and comparison
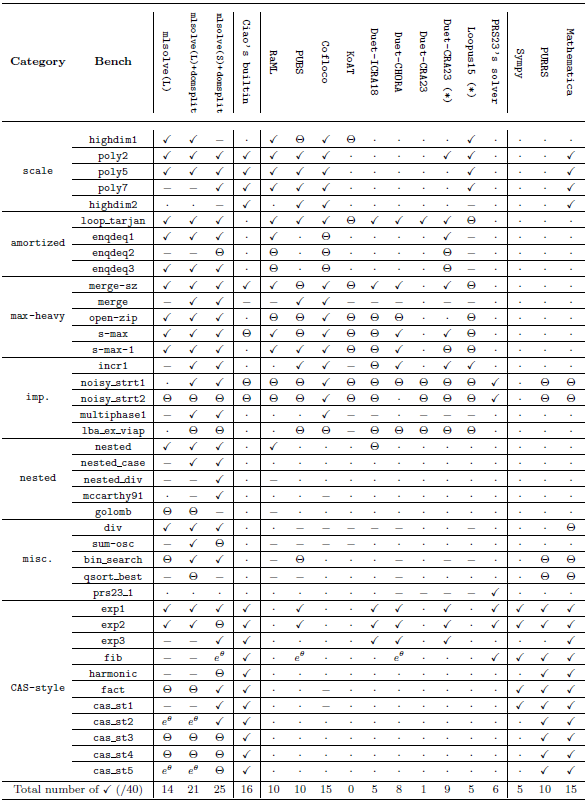
6.1 Prototype
As mentioned earlier, our approach is parameterized by the regression technique employed, and we have instantiated it with both (sparse) linear and symbolic regression. To assess the performance of each individually, as well as their combinations with other techniques, we have developed three versions of our prototype, which appear as the first three columns (resp. bars) of Table 2 (resp. Figure 3, starting from the top). The simplest version of our approach, as described in Section 4.1, is mlsolve(L). It uses linear regression with lasso regularization and feature selection. mlsolve(L)+domsplit is the same tool, adding the domain splitting strategy described in Section 4.2. Finally, mlsolve(S)+domsplit replaces (sparse) linear regression with symbolic regression.
The overall architecture, input and outputs of our prototypes were already illustrated in Figure 1 and described in Sections 2 and 4. The implementation is written in Python 3.6/3.7, using Sympy (Meurer et al., Reference Meurer, Smith, Paprocki, Čertík, Kirpichev, Rocklin, Kumar, Ivanov, Moore, Singh, Rathnayake, Vig, Granger, Muller, Bonazzi, Gupta, Vats, Johansson, Pedregosa and Scopatz2017) as CAS, Scikit-Learn (Pedregosa et al., Reference Pedregosa, Varoquaux, Gramfort, Michel, Thirion, Grisel, Blondel, Prettenhofer, Weiss, Dubourg, Vanderplas, Passos, Cournapeau, Brucher, Perrot and Duchesnay2011) for regularized linear regression and PySR (Cranmer, Reference Cranmer2023) for symbolic regression. We use Z3 (de Moura and Bjørner, Reference De Moura, Bjoner, Ramakrishnan and Rehof2008) as SMT-solver, and Z3Py (Z3Py, Reference Zuleger, Gulwani, Sinn and Veith2023) as interface.
6.2 Legend
Columns
![]() $3$
–
$3$
–
![]() $19$
of Table 2 are categorized, from left to right, as (1) the prototypes of this paper’s approach, (2) CiaoPP builtin solver, (3) other program analysis tools, and (4) computer algebra systems (CAS) with recurrence solvers. Such solvers also appear in the
$19$
of Table 2 are categorized, from left to right, as (1) the prototypes of this paper’s approach, (2) CiaoPP builtin solver, (3) other program analysis tools, and (4) computer algebra systems (CAS) with recurrence solvers. Such solvers also appear in the
![]() $y$
-axis of Figure 3, and there is a horizontal bar (among a-q) for each of them.
$y$
-axis of Figure 3, and there is a horizontal bar (among a-q) for each of them.
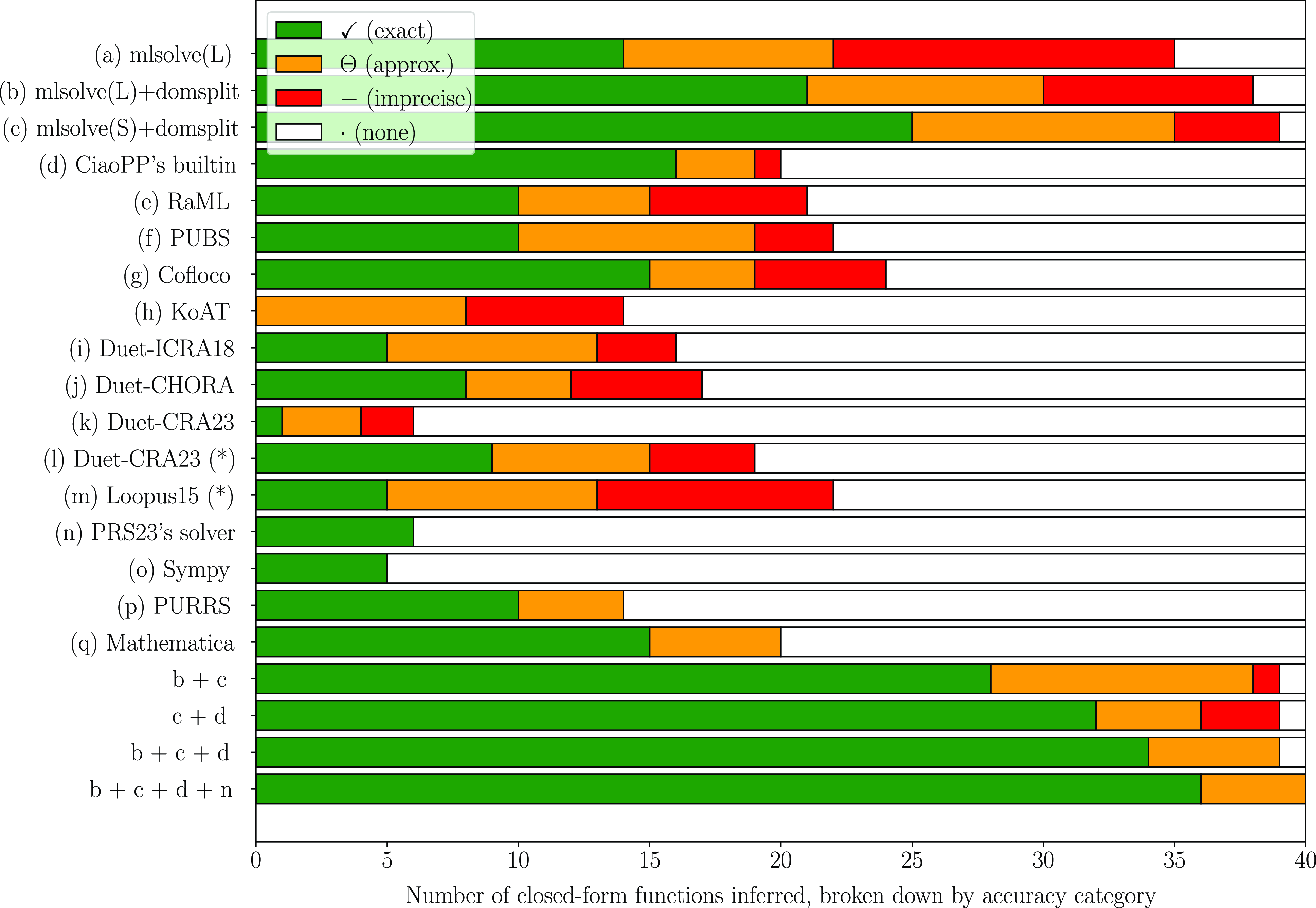
Fig 3. Comparison of solver tools by accuracy of the result.
From top to bottom, our benchmarks are organized by category reflecting some of their main features. Benchmarks are manually translated into the input language of each tool, following a best-effort approach. The symbol “(*)” corresponds to help provided for certain imperative-oriented tools. More comments will be given in tools and benchmarks paragraphs below.
For the sake of simplicity, and for space reasons, we report the accuracy of the results by categorizing them using only
![]() $4$
symbols. “
$4$
symbols. “
![]() $\checkmark$
” corresponds to an exact solution, “
$\checkmark$
” corresponds to an exact solution, “
![]() $\Theta$
” to a “precise approximation” of the solution, “
$\Theta$
” to a “precise approximation” of the solution, “
![]() $-$
” to another non-trivial output, and “
$-$
” to another non-trivial output, and “
![]() $\cdot$
” is used in all remaining cases (trivial infinite bound, no output, error, timeout, unsupported). Nevertheless, the concrete functions output are included in Appendix B. Figure 3 also shows the number of closed-form functions inferred broken down by these four accuracy categories, in the form of stacked horizontal bars. In addition, when a solution
$\cdot$
” is used in all remaining cases (trivial infinite bound, no output, error, timeout, unsupported). Nevertheless, the concrete functions output are included in Appendix B. Figure 3 also shows the number of closed-form functions inferred broken down by these four accuracy categories, in the form of stacked horizontal bars. In addition, when a solution
![]() $f$
has superpolynomial growth, we relax our requirements and may write “
$f$
has superpolynomial growth, we relax our requirements and may write “
![]() $e^\theta$
” whenever
$e^\theta$
” whenever
![]() $\hat{f}$
is not a precise approximation of
$\hat{f}$
is not a precise approximation of
![]() $f$
, but
$f$
, but
![]() $\log{\hat{f}}$
is a precise approximation of
$\log{\hat{f}}$
is a precise approximation of
![]() $\log{f}$
.Footnote 2 We include “
$\log{f}$
.Footnote 2 We include “
![]() $e^\theta$
” in the “
$e^\theta$
” in the “
![]() $\Theta$
” category in Figure 3. Given the common clash of definitions when using
$\Theta$
” category in Figure 3. Given the common clash of definitions when using
![]() $O$
notation on several variables, we make explicit the notion of approximation used here.
$O$
notation on several variables, we make explicit the notion of approximation used here.
We say that a function
![]() $\hat{f}$
is a precise approximation of
$\hat{f}$
is a precise approximation of
![]() $f:{\mathcal{D}}\to \mathbb{R}$
with
$f:{\mathcal{D}}\to \mathbb{R}$
with
![]() ${\mathcal{D}}\subset \mathbb{N}^m$
whenever
${\mathcal{D}}\subset \mathbb{N}^m$
whenever
where
![]() $\Theta$
is the usual uncontroversial one-variable big theta, and
$\Theta$
is the usual uncontroversial one-variable big theta, and
![]() $\Vert \cdot \Vert$
is any norm on
$\Vert \cdot \Vert$
is any norm on
![]() $\mathbb{R}^k$
. In other words, a precise approximation is a function which is asymptotically within a constant factor of the approximated function, where “asymptotically” means that some of the input values tend to infinity, but not necessarily all of them. Note that
$\mathbb{R}^k$
. In other words, a precise approximation is a function which is asymptotically within a constant factor of the approximated function, where “asymptotically” means that some of the input values tend to infinity, but not necessarily all of them. Note that
![]() $\max (x,y)$
and
$\max (x,y)$
and
![]() $x+y$
belong to the same class, but
$x+y$
belong to the same class, but
![]() $(x,y)\mapsto x+y-1$
is not a precise approximation of the solution of the merge benchmark (set
$(x,y)\mapsto x+y-1$
is not a precise approximation of the solution of the merge benchmark (set
![]() $u_n = (n,0)$
): the approximations we consider give “correct asymptotic class in all directions”.
$u_n = (n,0)$
): the approximations we consider give “correct asymptotic class in all directions”.
Hence, bounds that end up in the “
![]() $-$
” category may still be precise enough to be useful in the context of static analysis. We nevertheless resort to this simplification to avoid the presentation of an inevitably complex lattice of approximations. It may also be noted that different tools do not judge quality in the same way. CAS typically aim for exact solutions only, while static analysis tools often focus on provable bounds (exact or asymptotic), which the notion of approximation used in this table does not require. Once again, we use a single measure for the sake of simplicity.
$-$
” category may still be precise enough to be useful in the context of static analysis. We nevertheless resort to this simplification to avoid the presentation of an inevitably complex lattice of approximations. It may also be noted that different tools do not judge quality in the same way. CAS typically aim for exact solutions only, while static analysis tools often focus on provable bounds (exact or asymptotic), which the notion of approximation used in this table does not require. Once again, we use a single measure for the sake of simplicity.
6.3 Experimental setup
Chosen hyperparameters are given for the sake of completeness.
For regularized linear regression (Algorithm1), we set
![]() $\epsilon = 0.05$
for feature selection,
$\epsilon = 0.05$
for feature selection,
![]() $k=2$
for cross-validation, which will be performed to choose the value of
$k=2$
for cross-validation, which will be performed to choose the value of
![]() $\lambda$
in a set
$\lambda$
in a set
![]() $\Lambda$
of
$\Lambda$
of
![]() $100$
values taken from the interval
$100$
values taken from the interval
![]() $[0.001, 1]$
. (It is also possible to construct the entire regularization path for the lasso, which is piecewise linear, and obtain the solution for every value of
$[0.001, 1]$
. (It is also possible to construct the entire regularization path for the lasso, which is piecewise linear, and obtain the solution for every value of
![]() $\lambda \in{\mathbb{R}}$
(Hastie et al., Reference Hastie, Tibshirani and Wainwright2015), but here we opted to provide an explicit set of possible values
$\lambda \in{\mathbb{R}}$
(Hastie et al., Reference Hastie, Tibshirani and Wainwright2015), but here we opted to provide an explicit set of possible values
![]() $\Lambda$
.) If we use domain splitting, the choice of regression domain is as described in Section 4.2 (fit separately on the subdomains corresponding to each clause), but if we do not, we choose
$\Lambda$
.) If we use domain splitting, the choice of regression domain is as described in Section 4.2 (fit separately on the subdomains corresponding to each clause), but if we do not, we choose
![]() $\mathcal{D}$
to be (a power of)
$\mathcal{D}$
to be (a power of)
![]() $\mathbb{N}_{\gt 0}$
(this avoids the pathological behavior in
$\mathbb{N}_{\gt 0}$
(this avoids the pathological behavior in
![]() $0$
of some candidates). Verification is still performed on the whole domain of the equation, that is
$0$
of some candidates). Verification is still performed on the whole domain of the equation, that is
![]() $\varphi _{pre}=\vee _i \varphi _i$
. For each run of Algorithm1,
$\varphi _{pre}=\vee _i \varphi _i$
. For each run of Algorithm1,
![]() $n=100$
input values in
$n=100$
input values in
![]() $\mathcal{D}$
are generated, with each variable in
$\mathcal{D}$
are generated, with each variable in
![]() $[0,b]$
, where
$[0,b]$
, where
![]() $b\in \{20,10,5,3\}$
is chosen so that generation ends within a timeout of
$b\in \{20,10,5,3\}$
is chosen so that generation ends within a timeout of
![]() $2$
seconds.Footnote 3
$2$
seconds.Footnote 3
Candidate functions are selected as follows. For each number
![]() $m$
of input variables we choose sets
$m$
of input variables we choose sets
![]() $\mathcal{F}_{\mathrm{small}}$
,
$\mathcal{F}_{\mathrm{small}}$
,
![]() $\mathcal{F}_{\mathrm{medium}}$
,
$\mathcal{F}_{\mathrm{medium}}$
,
![]() $\mathcal{F}_{\mathrm{large}}$
representative of common complexities encountered in cost analysis. They are chosen explicitly for
$\mathcal{F}_{\mathrm{large}}$
representative of common complexities encountered in cost analysis. They are chosen explicitly for
![]() $m=1$
and
$m=1$
and
![]() $2$
, and built as combinations of base functions for
$2$
, and built as combinations of base functions for
![]() $m\geq 3$
. Regression is performed for each set, with a timeout of
$m\geq 3$
. Regression is performed for each set, with a timeout of
![]() $10$
s,Footnote
4
and the best solution is chosen. Chosen sets are indicated in Figures 4 and 5.
$10$
s,Footnote
4
and the best solution is chosen. Chosen sets are indicated in Figures 4 and 5.
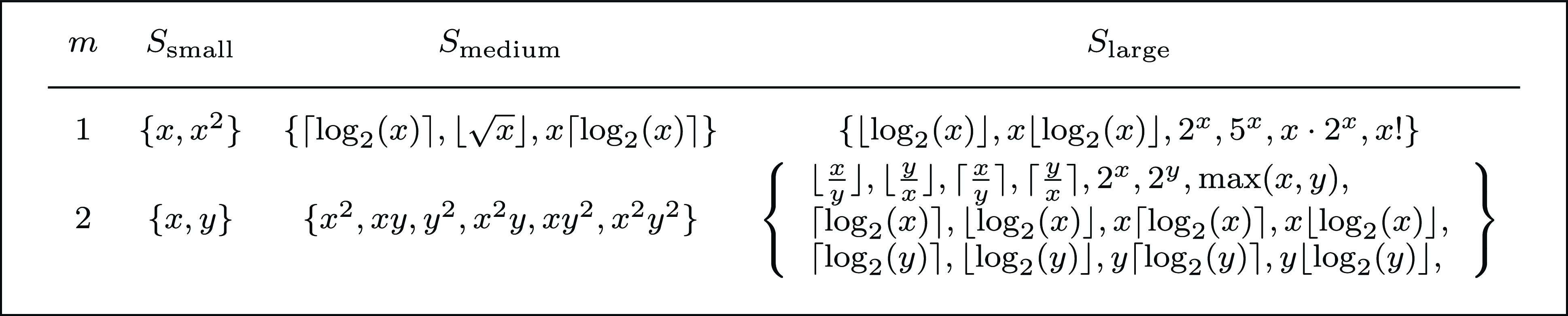
Fig 4. Candidate functions for linear regression in dimension
![]() $\leq 2$
.
$\leq 2$
.
![]() $\mathcal{F}_{\mathrm{small}}=S_{\mathrm{small}}$
,
$\mathcal{F}_{\mathrm{small}}=S_{\mathrm{small}}$
,
![]() $\mathcal{F}_{\mathrm{medium}}=\mathcal{F}_{\mathrm{small}}\cup S_{\mathrm{medium}}$
,
$\mathcal{F}_{\mathrm{medium}}=\mathcal{F}_{\mathrm{small}}\cup S_{\mathrm{medium}}$
,
![]() $\mathcal{F}_{\mathrm{large}}=\mathcal{F}_{\mathrm{medium}}\cup S_{\mathrm{large}}$
. Lambdas omitted for conciseness.
$\mathcal{F}_{\mathrm{large}}=\mathcal{F}_{\mathrm{medium}}\cup S_{\mathrm{large}}$
. Lambdas omitted for conciseness.
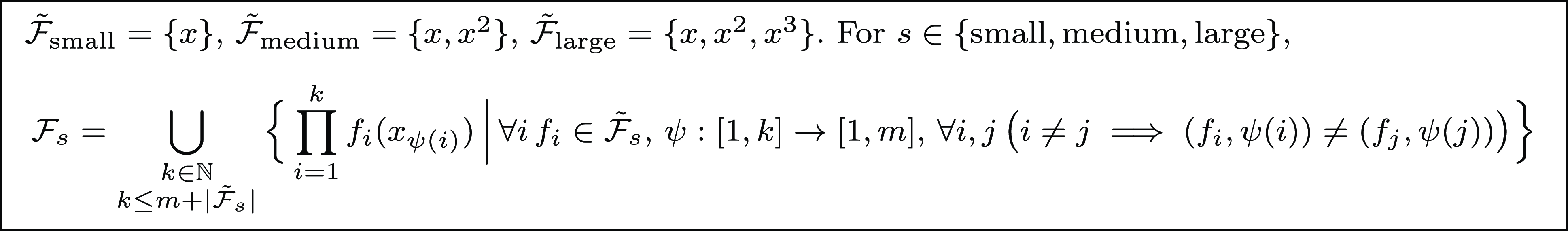
Fig 5. Candidate functions for linear regression in dimension
![]() $\geq 3$
.
$\geq 3$
.
![]() $\mathcal{F}_{s}$
is defined by combination of simpler base functions, as bounded products of applications of base functions to individual input variables. For example, with
$\mathcal{F}_{s}$
is defined by combination of simpler base functions, as bounded products of applications of base functions to individual input variables. For example, with
![]() $m=3$
,
$m=3$
,
![]() $\mathcal{F}_{\text{small}}=\{x,y,z,xy,xz,yz,xyz\}$
.
$\mathcal{F}_{\text{small}}=\{x,y,z,xy,xz,yz,xyz\}$
.
In the case of symbolic regression, instead of candidates, we need to choose operators allowed in expression trees. We choose binary operators
![]() $\{+, -, \max , \times , \div , (\cdot )^{(\cdot )}\}$
and unary operators
$\{+, -, \max , \times , \div , (\cdot )^{(\cdot )}\}$
and unary operators
![]() $\{\lfloor \cdot \rfloor , \lceil \cdot \rceil , (\cdot )^2, (\cdot )^3, \log _2(\cdot ), 2^{(\cdot )}, (\cdot )!\}$
. Nodes, including leaves, have default cost
$\{\lfloor \cdot \rfloor , \lceil \cdot \rceil , (\cdot )^2, (\cdot )^3, \log _2(\cdot ), 2^{(\cdot )}, (\cdot )!\}$
. Nodes, including leaves, have default cost
![]() $1$
. Ceil and floor have cost
$1$
. Ceil and floor have cost
![]() $2$
and binary exponentiation has cost
$2$
and binary exponentiation has cost
![]() $3$
. We have
$3$
. We have
![]() $45$
populations of
$45$
populations of
![]() $33$
individuals, and run PySR for
$33$
individuals, and run PySR for
![]() $40$
iterations and otherwise default options.
$40$
iterations and otherwise default options.
In all cases, to account for randomness in the algorithms, experiments are run twice and the best solution is kept. Variability is very low when exact solutions can be found.
Experiments are run on a small Linux laptop with 1.1 GHz Intel Celeron N4500 CPU, 4 GB, 2933MHz DDR4 memory. Lasso regression takes 1.4s to 8.4s with mean 2.5s (on each candidate set, each benchmark, excluding equation evaluation and regression timeoutsFootnote 5), showing that our approach is reasonably efficient. Symbolic regression (on each subdomain, no timeout, without early exit conditions) takes 56s to 133s with mean 66s. It may be noted that these results correspond to initial prototypes, and that experiments focus on testing the accuracy of our approach: many avenues for easy optimizations are left open, for example stricter (genetic) resource management in symbolic regression.
6.4 Benchmarks
We present 40 benchmarks, that is (systems of) recurrence equations, extracted from our experiments and organized in 7 categories that test different features. We believe that such benchmarks, evenly distributed among the categories considered, are reasonably representative and capture the essence of a much larger set of benchmarks, including those that arise in static cost analysis, and that their size and diversity provide experimental insight on the scalability of our approach.
Category scale tests how well solvers can handle increasing dimensions of the input space, for simple linear or polynomial solutions. The intuition for this test is that (global and numerical) machine learning methods may suffer more from the curse of dimensionality than (compositional and symbolic) classical approaches. We also want to evaluate when the curse will start to become an issue. Here, functions are multivariate, and most benchmarks are systems of equations, in order to easily represent nested loops giving rise to polynomial cost.
Category amortized contains examples inspired by the amortized resource analysis line of work illustrated by RaML. Such problems may be seen as situations in which the worst-case cost of a function is not immediately given by the sum of worst-case costs of called functions, requiring some information on intermediate state of data structures, which is often tracked using a notion of potential (Tarjan, Reference Tarjan1985). For the sake of comparison, we also track those intermediate states as sizes, and encode the corresponding benchmarks in an equivalent way as systems of equations on cost and size, following an approach basedFootnote 6 on Debray and Lin (Reference Debray and Lin1993). loop_tarjan comes from Sinn et al. (Reference Sinn, Zuleger and Veith2017), whereas enqdeq1-3 are adapted from Hoffmann (Reference Hoffmann2011). In each example, the cost function of the entry predicate admits a simple representation, whereas the exact solutions for intermediate functions are more complicated.
Category max-heavy contains examples where either the equation or (the most natural expression of) the solution contain
![]() $\max$
operators. Such equations may typically arise in the worst-case analysis of non-deterministic programs (or complex deterministic programs simplified to simple non-deterministic programs during analysis), but may also appear naturally in size equations of programs with tests.
$\max$
operators. Such equations may typically arise in the worst-case analysis of non-deterministic programs (or complex deterministic programs simplified to simple non-deterministic programs during analysis), but may also appear naturally in size equations of programs with tests.
Category imp. tests features crucial to the analysis of imperative programs, that tend to be of lesser criticality in other paradigms. Those features can be seen as features of loops (described as challenges in recent work including Flores-Montoya (Reference Flores-Montoya2017) and Sinn et al. (Reference Sinn, Zuleger and Veith2017)), such as increasing variables (corresponds to recursive call with increasing arguments), noisy/exceptional behavior (e.g., early exit), resets and multiphase loops.
Category nested contains examples with nested recursion, a class of equations known for its difficulty (Tanny, Reference Tanny2013), that can even be used to prove undecidability of existence of solutions for recurrence equations (Celaya and Ruskey, Reference Celaya and Ruskey2012). Such equations are extremely challenging for “reasoning-based” approaches that focus on the structure of the equation itself. However, focusing on the solution rather than the problem (to put it another way, on semantics rather than syntax), we may notice that several of these equations admit simple solutions, that may hence be guessed via regression or template methods. We include the famous McCarthy 91 function (Manna and McCarthy, Reference Manna and Mccarthy1970).
Category misc. features examples with arithmetic (euclidean division), sublinear (logarithmic) growth, deterministic divide-and-conquer, and alternating activation of equations’ clauses. We are not aware of simple closed-forms for the solution of qsort_best, although its asymptotic behavior is known. Hence, we do not expect tools to be able to infer exact solutions, but rather to aim for good approximations and/or bounds. Example prs23_1 is given as a motivating example in Wang and Lin (Reference Wang and Lin2023) for studying eventually periodic conditional linear recurrences, and displays a particular difficulty: cases are defined by conditions on results of recursive calls rather than simply on input values.
Finally, category CAS-style contains several examples from CAS’s problem domain, that is that can be reduced to unconditional single variable equations with a single recursive case of shape
![]() $f(n) = a(n)\times f(n-1) + b(n)$
, with
$f(n) = a(n)\times f(n-1) + b(n)$
, with
![]() $a$
and
$a$
and
![]() $b$
potentially complicated, for example hypergeometric. This is quite different from the application case of program cost analysis, where we have multiple variables, conditionals are relevant, but recursive cases are closer to (combinations of)
$b$
potentially complicated, for example hypergeometric. This is quite different from the application case of program cost analysis, where we have multiple variables, conditionals are relevant, but recursive cases are closer to (combinations of)
![]() $f(n) = a\times f(\phi (n)) + b(n)$
, with
$f(n) = a\times f(\phi (n)) + b(n)$
, with
![]() $a$
constant but
$a$
constant but
![]() $\phi (n)$
non-trivial.
$\phi (n)$
non-trivial.
In the case of a system of equations, we only evaluate the solution found for the topmost predicate (the entry function). It may be noted that all of our equations admit a single solution
![]() $f:{\mathcal{D}}\to \mathbb{R}$
where
$f:{\mathcal{D}}\to \mathbb{R}$
where
![]() ${\mathcal{D}}\subset \mathbb{N}^m$
is defined by
${\mathcal{D}}\subset \mathbb{N}^m$
is defined by
![]() $\varphi _{pre}=\vee _i\varphi _i$
, and that the evaluation strategy (defined in Section 3) terminates everywhere on
$\varphi _{pre}=\vee _i\varphi _i$
, and that the evaluation strategy (defined in Section 3) terminates everywhere on
![]() $\mathcal{D}$
. Precise handling and evaluation of partial solutions and non-deterministic equations is left for future work.
$\mathcal{D}$
. Precise handling and evaluation of partial solutions and non-deterministic equations is left for future work.
6.5 Tools and benchmark translation
Obtaining meaningful comparisons of static analysis tools is a challenge. Different tools analyze programs written in different languages, discrepancies from algorithms to implementations are difficult to avoid, and tools are particularly sensitive to representation choices: multiple programs, resp., equations, may have the same (abstract) semantics, resp., solutions, but be far from equally easy to analyze. In order to compare tools anyway, a common choice is to use off-the-shelf translators to target each input language, despite inevitable and unequal accuracy losses caused by those automated transformations. In this paper, we adopt a different approach: each benchmark is written separately in the input format of each tool, aiming for representations adapted to each of them, following a best-effort approach. This is motivated by the lack of available translation tools, by the loss of accuracy observed for those we could find, and by the desire to nonetheless offer a broad comparison with related work.
We cannot list all choices made in the translation process, and only present the most important ones. As a guiding principle, we preserve as much as possible the underlying numerical constraints and control-flow defined by each benchmark, whether the problem is being encoded as a program or a recurrence equation. In principle, it should be straightforward to translate between these representations: a system of recurrence equations may directly be written as a numerical program with recursive functions. However, there is an obstruction, caused by missing features in the tools we evaluated. When it is sufficiently easy to rewrite a benchmark in order to avoid the missing feature, we do so, but otherwise we have to deem the problem unsupported.
Main missing features include support for systems of equations, multiprocedural programs, multivariate equations, loop structures beyond a single incremented index variable, non-determinism, complex numerical operations (polynomials, divisions, rounding functions, but also maximum and minimum), and finally support for general recursion, including nested calls and non-linear recursion.
For tools focusing on loops, with limited support for multiprocedural programs, we perform the mechanical translation of linear tail-recursion to loops when possible, even if this might be seen as a non-trivial help. Such cases are indicated by “(*)” in our table. This includes Loopus, which analyzes C and LLVM programs without recursive functions, and Duet-CRA23, that is the 2023 version of duet’s cra analysis.Footnote 7 Since Duet-CRA23 is still able to perform some interprocedural analysis, we report its results on recursive-style benchmarks (column without “(*)”), but it gives better results when this imperative translation is applied.Footnote 8 We sometimes attempt less mechanical transformations to loops, for example for fib. The transformation discussed in this paragraph could also have been applied to KoAT,Footnote 9 , Footnote 10 but we do not report full results for conciseness.
When support for explicit
![]() $\max$
operators is limited or absent, we transform deterministic programs with
$\max$
operators is limited or absent, we transform deterministic programs with
![]() $\max$
into non-deterministic programs, in a way that preserves upper bounds, but in general not lower bounds.Footnote 11 This transformation is not needed for mlsolve, which accepts any nested expression with
$\max$
into non-deterministic programs, in a way that preserves upper bounds, but in general not lower bounds.Footnote 11 This transformation is not needed for mlsolve, which accepts any nested expression with
![]() $\max$
and
$\max$
and
![]() $\min$
, but is required for Ciao,Footnote
12
PUBS, Cofloco, Loopus and all versions of duet. It is applied for RaML too, using a trick, as we did not find a native construct for non-determinism. Finally, this cannot be applied or does not help to obtain results for PRS23, Sympy, PURRS and Mathematica.
$\min$
, but is required for Ciao,Footnote
12
PUBS, Cofloco, Loopus and all versions of duet. It is applied for RaML too, using a trick, as we did not find a native construct for non-determinism. Finally, this cannot be applied or does not help to obtain results for PRS23, Sympy, PURRS and Mathematica.
6.6 Evaluation and discussion
Overall, the experimental results are quite promising, showing that our approach is accurate and efficient, as well as scalable. We first discuss the stacked horizontal bar chart in Figure 3, which offers a graphical and comprehensive overview of the accuracy of our approach in comparison to state-of-the-art tools. We then provide comments on Table 2, which presents more detailed information.
As mentioned earlier, bars a-c (the first three from the top) of Figure 3 represent the three implemented versions of our approach. We can see that in general, for the benchmark set considered, which we believe is reasonably representative, each of these versions individually outperforms any of the other state-of-the-art solvers (included in either cost analyzers or CASs), which are represented by bars d-q. Bar b
![]() $+$
c represents the full version of our approach, which combines both regression methods, lasso (b) and symbolic (c), and the domain splitting strategy. The three bars at the bottom of the chart are included to assess how the combination of our machine learning-based solver with other solvers would potentially improve the accuracy of the closed-forms obtained. The idea is to use it as a complement of other back-end solvers in a higher-level combined solver in order to obtain further accuracy improvements. We can see that the combination (bar b
$+$
c represents the full version of our approach, which combines both regression methods, lasso (b) and symbolic (c), and the domain splitting strategy. The three bars at the bottom of the chart are included to assess how the combination of our machine learning-based solver with other solvers would potentially improve the accuracy of the closed-forms obtained. The idea is to use it as a complement of other back-end solvers in a higher-level combined solver in order to obtain further accuracy improvements. We can see that the combination (bar b
![]() $+$
c
$+$
c
![]() $+$
d) of CiaoPP’s builtin solver with the full version of our approach mentioned above would obtain exact solutions for
$+$
d) of CiaoPP’s builtin solver with the full version of our approach mentioned above would obtain exact solutions for
![]() $85\%$
of the benchmarks, and accurate approximations for the rest of them, except for one benchmark. As shown in Table 2, this benchmark is prs23_1, which can only be solved by PRS23’s solver. For our set of benchmarks, the best overall accuracy would be achieved by the combination represented by the bottom bar, which adds PRS23’s solver to the combination above.
$85\%$
of the benchmarks, and accurate approximations for the rest of them, except for one benchmark. As shown in Table 2, this benchmark is prs23_1, which can only be solved by PRS23’s solver. For our set of benchmarks, the best overall accuracy would be achieved by the combination represented by the bottom bar, which adds PRS23’s solver to the combination above.
We now comment on the experimental results of Table 2, category by category.
For category scale, we notice that mlsolve can go up to dimension
![]() $4$
without much trouble (actually up to
$4$
without much trouble (actually up to
![]() $7$
, that is, querying for
$7$
, that is, querying for
![]() $f_4$
in highdim2, and failing after that). The impact of the curse of dimensionality on our machine learning approach thus appears tolerable, and comparable to that on the template-based RaML, which timeouts reaching dimension
$f_4$
in highdim2, and failing after that). The impact of the curse of dimensionality on our machine learning approach thus appears tolerable, and comparable to that on the template-based RaML, which timeouts reaching dimension
![]() $7$
, that is for
$7$
, that is for
![]() $f_4$
in highdim2, allowing potentials to be polynomials of degree
$f_4$
in highdim2, allowing potentials to be polynomials of degree
![]() $7$
. PUBS and Cofloco perform well and quickly in this category, showing the value of compositional and symbolic methods. Surprisingly, Loopus performs well only until dimension
$7$
. PUBS and Cofloco perform well and quickly in this category, showing the value of compositional and symbolic methods. Surprisingly, Loopus performs well only until dimension
![]() $10$
where an approximation is performed, and duet gives nearly no non-trivial answer. The benchmarks being naturally presented in a multivariate recursive or nested way, they are difficult to encode in PRS23, Sympy and PURRS. The polynomial (locally monovariate) benchmarks are solved by Mathematica, if we provide the order in which subequations must be solved. The benchmarks are similarly difficult to encode in (cost-based) KoAT, and helping it with manual control-flow linearization did not suffice to get “
$10$
where an approximation is performed, and duet gives nearly no non-trivial answer. The benchmarks being naturally presented in a multivariate recursive or nested way, they are difficult to encode in PRS23, Sympy and PURRS. The polynomial (locally monovariate) benchmarks are solved by Mathematica, if we provide the order in which subequations must be solved. The benchmarks are similarly difficult to encode in (cost-based) KoAT, and helping it with manual control-flow linearization did not suffice to get “
![]() $\Theta$
” results.
$\Theta$
” results.
For category amortized, RaML performs well, but perhaps not as well as could have been imagined. For enqdeq1,2,3, it outputs bounds
![]() $[2n,3n]$
,
$[2n,3n]$
,
![]() $[n+m,2n+m]$
and
$[n+m,2n+m]$
and
![]() $[5n,8n]$
, respectively. The simplicity of the solutions allows mlsolve to perform well (using the full size and cost recurrence equation encoding discussed above, cf. Debray and Lin (Reference Debray and Lin1993), Footnote 6 and Figure 6). This performance can be attributed to the fact that mlsolve does not need to find and use the complicated cost expressions of the intermediate predicates: only full execution traces starting from the entry point are considered. Note that Cofloco also obtains reasonable results, making use of its disjunctive analysis features (visible with the -conditional_ubs option), although it loses accuracy in several places, and outputs linear bounds with incorrect constants. After simplification of its output, Duet-CRA23 obtains
$[5n,8n]$
, respectively. The simplicity of the solutions allows mlsolve to perform well (using the full size and cost recurrence equation encoding discussed above, cf. Debray and Lin (Reference Debray and Lin1993), Footnote 6 and Figure 6). This performance can be attributed to the fact that mlsolve does not need to find and use the complicated cost expressions of the intermediate predicates: only full execution traces starting from the entry point are considered. Note that Cofloco also obtains reasonable results, making use of its disjunctive analysis features (visible with the -conditional_ubs option), although it loses accuracy in several places, and outputs linear bounds with incorrect constants. After simplification of its output, Duet-CRA23 obtains
![]() $3n$
,
$3n$
,
![]() $2n+m$
and
$2n+m$
and
![]() $8n$
on enqdeq, but it may be noted that writing such benchmarks in an imperative fashion may be seen as unreasonable help to the control-flow analysis. Loopus obtains only quadratic bounds on the enqdeq, and no other tool obtains non-trivial bounds. loop_tarjan is handled by nearly all code analysis tools; however, surprisingly, Loopus loses a minor amount of accuracy and outputs
$8n$
on enqdeq, but it may be noted that writing such benchmarks in an imperative fashion may be seen as unreasonable help to the control-flow analysis. Loopus obtains only quadratic bounds on the enqdeq, and no other tool obtains non-trivial bounds. loop_tarjan is handled by nearly all code analysis tools; however, surprisingly, Loopus loses a minor amount of accuracy and outputs
![]() $2n+1$
instead of
$2n+1$
instead of
![]() $2n$
. It may be noted that no tool gets the exact solution for enqdeq2. For mlsolve, this hints at the fact that improved domain splitting strategies may be beneficial, as they may allow it to discover the
$2n$
. It may be noted that no tool gets the exact solution for enqdeq2. For mlsolve, this hints at the fact that improved domain splitting strategies may be beneficial, as they may allow it to discover the
![]() $m\leq k$
constraint, which is not directly visible in the equations.
$m\leq k$
constraint, which is not directly visible in the equations.

Fig 6. Prolog encoding of the enqdeq benchmarks, inspired from Section 2.1 of Hoffmann (Reference Hoffmann2011) introducing amortized analysis, where a queue datastructure is implemented as two lists that act as stacks. We encode the enqdeq problems for each tool following a best-effort approach. Recurrence equations are set up in terms of compositions of cost and size functions.
For category max-heavy, we simply observe that support for
![]() $\max$
operators is rare, although some disjunctive analysis and specific reasoning can be enough to get exact results after the
$\max$
operators is rare, although some disjunctive analysis and specific reasoning can be enough to get exact results after the
![]() $\max \to \mathtt{nondet}$
transformation, as is the case for Cofloco. Many tools can infer linear bounds for these benchmarks, without being able to get the correct coefficients. More challenging benchmarks could be created using nested
$\max \to \mathtt{nondet}$
transformation, as is the case for Cofloco. Many tools can infer linear bounds for these benchmarks, without being able to get the correct coefficients. More challenging benchmarks could be created using nested
![]() $\min$
-
$\min$
-
![]() $\max$
expressions and non-linear solutions to separate more tools.
$\max$
expressions and non-linear solutions to separate more tools.
In category imp., where examples are inspired from imperative problems, we notice that the domsplit extension is crucial to allow mlsolve to deal with even basic for loops (benchmark incr1, which also encodes the classical difficulty of recurrence-based methods with increasing arguments). Cofloco performs best in this category thanks to its control-flow refinement features. For noisy_strt*, several tools notice the two regimes but struggle to combine them correctly and precisely. PRS23 gets the exact solution, a testimony to its precise (but monovariate) phase separation. As expected, mlsolve + domsplit fails on noisy_strt2 even when it succeeds on noisy_strt1, misled by the late change of behavior, invisible to naive input generation, although counter-examples to the
![]() $x$
solution are produced. Such counter-examples may be used in future work to guide the regression process and learn better subdomains. Given the known limitations of RaML on integers, some inequalities that are natural in an imperative setting are difficult to encode without accuracy loss. For tools that solve lba_ex_viap,Footnote
13
small rounding errors appear.
$x$
solution are produced. Such counter-examples may be used in future work to guide the regression process and learn better subdomains. Given the known limitations of RaML on integers, some inequalities that are natural in an imperative setting are difficult to encode without accuracy loss. For tools that solve lba_ex_viap,Footnote
13
small rounding errors appear.
Category nested is composed of particularly challenging problems for which no general solving method is known, although low (model) complexity solutions exist for particular cases, giving a strong advantage to the mlsolve approach. It may be noted that RaML also gets the exact solution for the nested benchmark and that Duet-ICRA18 obtains the nearly exact
![]() $\max (1,x)$
solution. mlsolve(S)+domsplit performs best. It sometimes uses non-obvious expressions to fit the solution, such as
$\max (1,x)$
solution. mlsolve(S)+domsplit performs best. It sometimes uses non-obvious expressions to fit the solution, such as
![]() $\mathrm{ceil}(2.75 - 2.7/x)$
for the
$\mathrm{ceil}(2.75 - 2.7/x)$
for the
![]() $x\gt 0$
subdomain on nested_div. Although no tool solves the golomb recurrence in our experimental setup, it may be noted that mlsolve(S) finds the exact solution when
$x\gt 0$
subdomain on nested_div. Although no tool solves the golomb recurrence in our experimental setup, it may be noted that mlsolve(S) finds the exact solution when
![]() $\sqrt{\cdot }$
is added to the list of allowed operators, showing the flexibility of the approach.
$\sqrt{\cdot }$
is added to the list of allowed operators, showing the flexibility of the approach.
In category misc., division, logarithm, and complex control-flow, which are typically difficult to support, give an advantage to the mlsolve approach, as control-flow has low impact and operators can easily be included. It must be noted that our definition of “precise approximation” makes linear bounds insufficient for the division and logarithm benchmarks, and forces the
![]() $f(x,0)=1$
line to be considered in sum-osc. For bin_search, both PUBS and PURRS are able to obtain
$f(x,0)=1$
line to be considered in sum-osc. For bin_search, both PUBS and PURRS are able to obtain
![]() $1+\log _2(x)$
bounds on the
$1+\log _2(x)$
bounds on the
![]() $x\gt 0$
subdomain, close to the exact solution
$x\gt 0$
subdomain, close to the exact solution
![]() $1+\lfloor \log _2(x)\rfloor$
. Closed-form solutions are not available for qsort_best, and the
$1+\lfloor \log _2(x)\rfloor$
. Closed-form solutions are not available for qsort_best, and the
![]() $x\log _2(x)$
asymptotic behavior is only recovered by mlsolve(L)+domsplit,Footnote 14 as well as PURRS and Mathematica if helped by preprocessing, although other tools do infer quadratic bounds. Interestingly, prs23_1 is only solved by PRS23 (Wang and Lin, Reference Wang and Lin2023), because of the particular difficulty of using recursive calls in update conditions, even though this naturally encodes imperative loops with conditional updates.
$x\log _2(x)$
asymptotic behavior is only recovered by mlsolve(L)+domsplit,Footnote 14 as well as PURRS and Mathematica if helped by preprocessing, although other tools do infer quadratic bounds. Interestingly, prs23_1 is only solved by PRS23 (Wang and Lin, Reference Wang and Lin2023), because of the particular difficulty of using recursive calls in update conditions, even though this naturally encodes imperative loops with conditional updates.
Finally, as could be expected, CAS-style is the only category in which CAS obtain good results. All monovariate benchmarks are solved by PURRS and Mathematica, but unlike PURRS, Mathematica solves exp3 (with hints on resolution order). Surprisingly, Sympy fails for harmonic and cas_st2-5, but still generally obtains good results. It may be noted that for the last three benchmarks, Mathematica represents solutions as special functions while PURRS and Ciao’s builtin solver choose summations. These representations are equivalent and none can be obviously preferred to the other. The category is challenging for code analysis tools, but several deal or partly deal with the case of exponential bounds and of fib. In the latter case, the exponential part of the bound obtained is
![]() $2^x$
for PUBS and Duet-CHORA and
$2^x$
for PUBS and Duet-CHORA and
![]() $1.6169^x$
for mlsolve(S), closer to the golden ratio (
$1.6169^x$
for mlsolve(S), closer to the golden ratio (
![]() $\varphi \approx 1.6180\ldots$
) expected at infinity. Interestingly, while the exact solutions of the last cas_st* are too complex to be expressed by mlsolve(S) in our experimental setting, it is still able to obtain very good approximations of the asymptotic behavior, returning
$\varphi \approx 1.6180\ldots$
) expected at infinity. Interestingly, while the exact solutions of the last cas_st* are too complex to be expressed by mlsolve(S) in our experimental setting, it is still able to obtain very good approximations of the asymptotic behavior, returning
![]() $x! \times 2.71828$
,
$x! \times 2.71828$
,
![]() $2^x \times 0.69315$
and
$2^x \times 0.69315$
and
![]() $2^x\times x! \times 0.5701515$
for cas_st3,4,5 respectively, with coefficients close to the constants
$2^x\times x! \times 0.5701515$
for cas_st3,4,5 respectively, with coefficients close to the constants
![]() $e \approx 2.71828\ldots$
,
$e \approx 2.71828\ldots$
,
![]() $\ln (2)\approx 0.693147\ldots$
and
$\ln (2)\approx 0.693147\ldots$
and
![]() $\mathrm{Ei}(1/2)+\mathrm{ln}(2)\!-\!\gamma \approx 0.57015142\ldots$
, showing its ability to get good approximations, even in the case of complex equations with complex solutions.
$\mathrm{Ei}(1/2)+\mathrm{ln}(2)\!-\!\gamma \approx 0.57015142\ldots$
, showing its ability to get good approximations, even in the case of complex equations with complex solutions.
The results presented in the mlsolve columns correspond to the accuracy of the proposed candidates. We now say a few words on their verification. It must be noted that while the mlsolve version presented in Section 4 easily handles regression for systems of equations, verification has only been implemented for single equations. The verification strategy can be extended to systems of equations, but the naive approach has the disadvantage of requiring candidates for all subfunctions. More subtle solutions are left for future work.
Among the 40 benchmarks, mlsolve(L) finds the exact solution for 14, 9 of which come from single function problems. It is able to prove correctness of all of those 9 candidates, using the translation described in Eq. (13).
As mentioned at the end of Section 4.2, verification can be performed in a similar way in the domsplit cases. This translation has not yet been fully integrated in our prototype, but has been tested manually on a few examples, showing that Z3 can provide valuable insights for those piecewise candidates (verification of the noisy_start1 candidate, counter-examples, etc.), but is not strong enough to directly work with complex expressions involving factorials, logarithms, or difficult exponents.
6.7 Additional experiment: comparison with symbolic (linear) equation solving
To further justify our choice of methods, we conducted an additional experiment comparing numerical linear regression (used in the case of mlsolve(L)) with symbolic linear equation solving in terms of efficiency.
As mentioned in the introduction, efficiency is not the primary reason we choose search and optimization algorithms typical of machine learning methods over more classical exact symbolic methods. Instead, we prioritize expressivity and flexibility. While symbolic linear equation solving is limited to situations where an exact solution can be expressed as an affine combination of base functions, our approach enables the discovery of approximate solutions (particularly valuable in certain cost analysis applications) when closed-form solutions are too complex to find. Moreover, our modular approach allows the exploration of model spaces more complex than affine ones, which cannot be handled by complete methods (e.g., compare mlsolve(S) with mlsolve(L)).
Nevertheless, in situations where an exact solution can be expressed as an affine combination of base functions, we may choose to use exact, symbolic linear equation solvers instead of (float-based, iterative) linear regression solvers to infer template coefficients, as we have done in this paper. While this alternative approach is limited to cases where an exact solution exists within the model space, it has the advantage of providing exact, symbolic coefficients rather than imprecise floating-point numbers. However, aside from the limitation to exact solutions, such infinite-precision symbolic methods do not scale as well to large problems as the approximate, iterative methods used in linear regression. To evaluate this scalability issue, we conducted experiments comparing these methods within the Mathematica and Sympy CAS, using the Fibonacci (fib) benchmark,
![]() $22$
base functions (including powers of the golden ratio
$22$
base functions (including powers of the golden ratio
![]() $\varphi$
and its conjugate
$\varphi$
and its conjugate
![]() $\overline{\varphi }$
to enable an exact solution), and
$\overline{\varphi }$
to enable an exact solution), and
![]() $n\in [10,100]$
data points. It is worth noting that this example is intended solely to provide orders of scale of computation time: it is small enough to allow the use of exact symbolic methods and, for the same reason, employs handpicked base functions that may not be available in practice (Table 3).
$n\in [10,100]$
data points. It is worth noting that this example is intended solely to provide orders of scale of computation time: it is small enough to allow the use of exact symbolic methods and, for the same reason, employs handpicked base functions that may not be available in practice (Table 3).
Table 3. Comparison of linear regression and symbolic linear equation solvers for coefficient search on the fib benchmark, with
![]() $22$
base functions and
$22$
base functions and
![]() $n$
training points. Legend: underdetermined systems (und.), timeouts (T.O.), and out-of-memory errors (O.M.)
$n$
training points. Legend: underdetermined systems (und.), timeouts (T.O.), and out-of-memory errors (O.M.)

For Mathematica, we use the LinearSolve function on symbolic inputs, which returns one of the possible solutions when the system is underdetermined (other functions can be used to compute the full set of solutions). For
![]() $n=10$
input points, we observe that the solution it proposes (possibly chosen for its parsimony) corresponds to the exact closed form for the fib benchmark, although it obtains it at a
$n=10$
input points, we observe that the solution it proposes (possibly chosen for its parsimony) corresponds to the exact closed form for the fib benchmark, although it obtains it at a
![]() $\mathtt{\gt\,100}\times$
overhead compared to
$\mathtt{\gt\,100}\times$
overhead compared to
![]() $\mathtt{mlsolve(L)}$
. In fact, this CAS obtains O.M./T.O. errors for
$\mathtt{mlsolve(L)}$
. In fact, this CAS obtains O.M./T.O. errors for
![]() $n\geq 20$
and is not able to reach the stage where the systems become fully determined. Investigating this issue shows that it is caused by an inappropriate symbolic simplification strategy, where Mathematica conserves large polynomial coefficients in
$n\geq 20$
and is not able to reach the stage where the systems become fully determined. Investigating this issue shows that it is caused by an inappropriate symbolic simplification strategy, where Mathematica conserves large polynomial coefficients in
![]() ${\mathbb{Q}}[\sqrt{5}]$
during computation, without simplifying them to
${\mathbb{Q}}[\sqrt{5}]$
during computation, without simplifying them to
![]() $0$
early enough when possible, leading to wasted computational resources (note that this only happens for symbolic and not for float-based linear equation solving).
$0$
early enough when possible, leading to wasted computational resources (note that this only happens for symbolic and not for float-based linear equation solving).
The CAS Sympy does not display this performance issue and is able to obtain the exact symbolic solution as soon as the system is fully determined, although at a
![]() $\mathtt{\gt\,10}\times$
overhead compared to numerical iterative methods.
$\mathtt{\gt\,10}\times$
overhead compared to numerical iterative methods.
mlsolve(L) obtains a numerical approximation (with the correct features) of the expected solution, spending less than
![]() $0.2s$
in regression for all chosen values of
$0.2s$
in regression for all chosen values of
![]() $n$
, suggesting that this time is mostly spent in bookkeeping tasks rather than the core of regression itself. Note that mlsolve(L)’s focus on sparse candidates allows to obtain the correct solution even for underdetermined benchmarks.
$n$
, suggesting that this time is mostly spent in bookkeeping tasks rather than the core of regression itself. Note that mlsolve(L)’s focus on sparse candidates allows to obtain the correct solution even for underdetermined benchmarks.
Nonetheless, symbolic linear equation solving can be utilized in certain cases to achieve exact symbolic regression, albeit at the expense of time. As a direction for future work, it could be integrated with our method and applied selectively when a solution is deemed feasible, focusing on a subset of base functions identified by Lasso and a subset of data points for efficiency.
7 Related work
7.1 Exact recurrence solvers
Centuries of work on recurrence equations have created a large body of knowledge, whose full account is a matter of mathematical history (Dickson, Reference Dickson1919), with classical results such as closed forms of C-recursive sequences, that is of solutions of linear recurrence equations with constant coefficients (Kauers and Paule, Reference Kauers and Paule2010; Petkovšek and Zakrajšek, Reference Petkovsek and Zakrajsek2013).
Despite important decision problems remaining open (Ouaknine and Worrell, Reference Ouaknine, Worrell, Finkel, Leroux and Potapov2012), the field of symbolic computation now offers multiple algorithms to obtain solutions and/or qualitative insights on various classes of recurrence equations. For (monovariate) linear equations with polynomial coefficients, whose solutions are named P-recursive sequences, computing all their polynomial, rational and hypergeometric solutions, whenever they exist, is a closed problem (Petkovšek, Reference Petkovsek1992; Petkovšek et al., Reference Petkovsek, Wilf and Zeilberger1997; Abramov, Reference Abramov1995).
Several of the algorithms available in the literature have been implemented in popular CAS such as Sympy (Meurer et al., Reference Meurer, Smith, Paprocki, Čertík, Kirpichev, Rocklin, Kumar, Ivanov, Moore, Singh, Rathnayake, Vig, Granger, Muller, Bonazzi, Gupta, Vats, Johansson, Pedregosa and Scopatz2017), Mathematica (Mathematica, 2023), Maple (Heck and Koepf, Reference Heck and Koepf1993) and Matlab (Higham and Higham, Reference Higham and Higham2016). These algorithms are built on insights coming from mathematical frameworks including
-
• Difference Algebra (Karr, Reference Karr1981; Bronstein, Reference Bronstein2000; Levin, Reference Levin2008; Abramov et al., Reference Abramov, Bronstein, Petkovsek and Schneider2021), which considers wide classes of sequences via towers of
 $\Pi \Sigma ^*$
-extensions, and creates analogies between recurrence equations and differential equations,
$\Pi \Sigma ^*$
-extensions, and creates analogies between recurrence equations and differential equations, -
• Finite Calculus (Gleich, Reference Gleich2005), used in parts of Ciao’s builtin solver, partly explaining its good results in the CAS category of our benchmarks,
-
• Operational Calculus (Berg, Reference Berg1967; Kincaid et al., Reference Kincaid, Cyphert, Breck and Reps2018), and
-
• Generating Functions (Wilf, Reference Wilf1994; Flajolet and Sedgewick, Reference Flajolet and Sedgewick2009),
which may be mixed with simple template-based methods, for example finding polynomial solutions of degree
![]() $d$
by plugging such polynomial in the equation and solving for coefficients.
$d$
by plugging such polynomial in the equation and solving for coefficients.
Importantly, all of these techniques have in common the central role given to the relation between a sequence
![]() $f(n)$
and the shifted sequence
$f(n)$
and the shifted sequence
![]() $f(n-1)$
, via, for example a shift operator
$f(n-1)$
, via, for example a shift operator
![]() $\sigma$
, or multiplication by the formal variable of a generating function. As discussed before, it turns out that this simple observation highlights an important obstacle to the application of CAS to program analysis via generalized recurrence equations: these techniques tend to focus on monovariate recurrences built on finite differences, that is on recursive calls of shape
$\sigma$
, or multiplication by the formal variable of a generating function. As discussed before, it turns out that this simple observation highlights an important obstacle to the application of CAS to program analysis via generalized recurrence equations: these techniques tend to focus on monovariate recurrences built on finite differences, that is on recursive calls of shape
![]() $f(n-k)$
with
$f(n-k)$
with
![]() $k$
constant, instead of more general recursive calls
$k$
constant, instead of more general recursive calls
![]() $f(\phi (n))$
. Generalizations of these approaches exist, to handle multivariate “partial difference equations”, or “
$f(\phi (n))$
. Generalizations of these approaches exist, to handle multivariate “partial difference equations”, or “
![]() $q$
-difference equations” with recursive calls
$q$
-difference equations” with recursive calls
![]() $f(q\cdot n)$
with
$f(q\cdot n)$
with
![]() $q\in \mathbb{C}$
,
$q\in \mathbb{C}$
,
![]() $|q|\lt 1$
, but this is insufficient to deal with recurrences arising in static cost analysis, which may contain inequations, difficult recursive calls that cannot be discarded via change of variables, piecewise definitions, or non-determinism.
$|q|\lt 1$
, but this is insufficient to deal with recurrences arising in static cost analysis, which may contain inequations, difficult recursive calls that cannot be discarded via change of variables, piecewise definitions, or non-determinism.
CAS hence tend to focus on exact resolution of a class of recurrence equations that is quite different from those that arise in static cost analysis and do not provide bounds or approximations for recurrences they are unable to solve.
In addition to classical CAS, we have tested PURRS (Bagnara et al., Reference Bagnara, Pescetti, Zaccagnini and Zaffanella2005), which shares similarities with these solvers. PURRS is however more aimed at automated complexity analysis, which is why it provides some support for approximate resolution, as well as handling of some non-linear, multivariate, and divide-and-conquer equations.
7.2 Recurrence solving for invariant synthesis and verification
Another important line of work uses recurrence solving as a key ingredient in generation and verification of program invariants, with further applications such as loop summarization and termination analysis. Much effort in this area has been put on improving complete techniques for restricted classes of programs, usually without recursion and built on idealized numerical loops with abstracted conditionals and loop conditions. These techniques can nevertheless be applied to more general programs, yielding incomplete approaches, via approximations and abstractions.
This line is well-illustrated by the work initiated in Kovács (Reference Kovacs2007, Reference Kovács2008), where all polynomial invariants on program variables are generated for a subclass of loops introduced in Rodríguez-Carbonell and Kapur (Reference Rodriguez-Carbonell and Kapur2004), using recurrence-solving methods in addition to the ideal-theoretic approach of Rodríguez-Carbonell and Kapur (Reference Rodriguez-Carbonell and Kapur2007). Recent work on the topic enabled inference of polynomial invariants on combinations of program variables for a wider class of programs with polynomial arithmetic (Humenberger et al., Reference Humenberger, Jaroschek and Kovacs2018; Amrollahi et al., Reference Amrollahi, Bartocci, Kenison, Kovacs, Moosbrugger and Stankovic2022). A recommended overview can be found in the first few sections of Amrollahi et al. (Reference Amrollahi, Bartocci, Kenison, Kovacs, Moosbrugger and Stankovic2023).
This approach is also key to the compositional recurrence analysis line of work (Farzan and Kincaid, Reference Farzan and Kincaid2015; Kincaid et al., Reference Kincaid, Breck, Boroujeni and Reps2017; Breck et al., Reference Breck, Cyphert, Kincaid and Reps2020; Kincaid et al., Reference Kincaid, Koh and Zhu2023; Kincaid et al., Reference Kincaid, Koh and Zhu2023), implemented in various versions of duet, with a stronger focus on abstraction-based techniques (e.g., the wedge abstract domain), ability to discover some non-polynomial invariants, and some (discontinued) support for non-linear recursive programs, although the approach is still affected by limited accuracy in disjunctive reasoning.
Idealized numerical loops with precise conditionals are tackled by Wang and Lin (Reference Wang and Lin2023), tested in this paper under the name PRS23, which builds upon the work developed in VIAP and its recurrence solver Rajkhowa and Lin (Reference Rajkhowa and Lin2017, Reference Rajkhowa and Lin2019). PRS23 focuses on restricted classes of loops, with ultimately periodic case application. Hence, the problem of precise invariant generation, with fully-considered branching and loop conditions, for extended classes of loops and recursive programs, is still left largely open.
In addition, it may be noted that size analysis, although typically encountered in the context of static cost analysis, can sometimes be seen as a form of numerical invariant synthesis, as illustrated by Lommen and Giesl (Reference Lommen and Giesl2023), which exploits closed form computations on triangular weakly non-linear loops, presented, for example in Frohn et al. (Reference Frohn, Hark and Giesl2020).
7.3 Cost analysis via (generalized) recurrence equations
Since the seminal work of Wegbreit (Reference Wegbreit1975), implemented in Metric, multiple authors have tackled the problem of cost analysis of programs (either logic, functional, or imperative) by automatically setting up recurrence equations, before solving them, using either generic CAS or specialized solvers, whose necessity were quickly recognized. Beyond Metric, applied to cost analysis of Lisp programs, other important early work include ACE (Le Metayer, Reference Le Metayer1988), and Rosendahl (Reference Rosendahl1989) in an abstract interpretation setting.
We refer the reader to previous publications in the Ciao line of work for further context and details (Debray et al., Reference Debray, Lin and Hermenegildo1990; Debray and Lin, Reference Debray and Lin1993; Debray et al., Reference Debray, Lopez-Garcia, Hermenegildo and Lin1997; Navas et al., Reference Navas, Mera, Lopez-Garcia and Hermenegildo2007; Serrano et al., Reference Serrano, Lopez-Garcia and Hermenegildo2014; Lopez-Garcia et al., Reference Lopez-Garcia, Klemen, Liqat and Hermenegildo2016, Reference Lopez-Garcia, Darmawan, Klemen, Liqat, Bueno and Heremenegildo2018).
We also include tools such as PUBS Footnote 15 (Albert et al., Reference Albert, Arenas, Genaim and Puebla2011, Reference Albert, Genaim and Masud2013) and Cofloco Footnote 16 (Flores-Montoya, Reference Flores-Montoya2017) in this category. These works emphasize the shortcomings of using too simple recurrence relations, chosen as to fit the limitations of available CAS solvers, and the necessity to consider non-deterministic (in)equations, piecewise definitions, multiple variables, possibly increasing variables, and to study non-monotonic behavior and control flow of the equations. They do so by introducing the vocabulary of cost relations, which may be seen as systems of non-deterministic (in)equations, and proposing new coarse approximate resolution methods.
It may be noted that duet, mentioned above, also proposes an option for resource bound analysis, as a specialization of its numerical analysis. Additionally, recent work in the cost analyzer KoAT has given a greater importance to recurrence solving, for example in Lommen and Giesl (Reference Lommen and Giesl2023).
7.4 Other approaches to static cost analysis
Automatic static cost analysis of programs is an active field of research, and many approaches have been proposed, using different abstractions than recurrence relations.
For functional programs, type systems approaches have been studied. This includes the concept of sized types (Vasconcelos and Hammond, Reference Vasconcelos and Hammond2003; Vasconcelos, Reference Vasconcelos2008), but also the potential method implemented in RaML (Hoffmann, Reference Hoffmann2011; Hoffmann et al., Reference Hoffmann, Aehlig and Hofmann2012).
The version of RaML (1.5) tested in this paper is limited to potentials (and hence size and cost bounds) defined by multivariate polynomials of bounded degrees. One of the powerful insights of RaML is to represent polynomials, not in the classical basis of monomials
![]() $x^k$
, but in the binomial basis
$x^k$
, but in the binomial basis
![]() $\binom{x}{k}$
, leading to much simpler transformations of potentials when type constructors are applied. Thanks to this idea, the problem of inference of non-linear bounds can be reduced to a linear programming problem. A promising extension of RaML to exponential potentials has recently been presented (Kahn and Hoffmann, Reference Kahn and Hoffmann2020), using Stirling numbers of the second kind instead of binomial coefficients, but, at the time of writing this paper, no implementation is available to the best of the authors’ knowledge.
$\binom{x}{k}$
, leading to much simpler transformations of potentials when type constructors are applied. Thanks to this idea, the problem of inference of non-linear bounds can be reduced to a linear programming problem. A promising extension of RaML to exponential potentials has recently been presented (Kahn and Hoffmann, Reference Kahn and Hoffmann2020), using Stirling numbers of the second kind instead of binomial coefficients, but, at the time of writing this paper, no implementation is available to the best of the authors’ knowledge.
Other important approaches include those implemented in Loopus, via size-change graphs (Zuleger et al., Reference Zuleger, Gulwani, Sinn and Veith2011) and difference constraints (Sinn et al., Reference Sinn, Zuleger and Veith2017), as well as those implemented in AProve (Giesl et al., Reference Giesl, Aschermann, Brockschmidt, Emmes, Frohn, Fuhs, Hensel, Otto, Plucker, Schneider-KAMP, Stroder, Swiderski and Thiemann2017), KoAT (Giesl et al., Reference Giesl, Lommen, Hark and Meyer2022) and LoAT (Frohn and Giesl, Reference Frohn and Giesl2022), which translate programs to (extensions of) Integer Transition Systems (ITS) and use, among other techniques, automated inference of ranking functions, summarization, and alternate cost and size inference (Frohn and Giesl, Reference Frohn and Giesl2017).
7.5 Dynamic inference of invariants/Recurrences
Our approach is related to the line of work on dynamic invariant analysis, which proposes to identify likely properties over variables from observed program traces. Pioneer work on this topic is exemplified by the tool Daikon (Ernst, Reference Ernst2000; Ernst et al., Reference Ernst, Cockrell, Griswold and Notkin2001), which is able to infer some linear relationships among a small number of explicit program variables, as well as some template “derived variables”, although it is limited in expressivity and scalability. Further work on dynamic invariant analysis made it possible to discover invariants among the program variables that are polynomial (Nguyen et al., Reference Nguyen, Kapur, Weimer, Forrest, Glinz, Murphy and Pezzè2012) and tropical-linear (Nguyen et al., Reference Nguyen, Kapur, Weimer, Forrest, Jalote, Briand and Van der Hoek2014), that is a subclass of piecewise affine functions. More recently, Nguyen et al. (Reference Nguyen, Nguyen and Dwyer2022) added symbolic checking to check/remove spurious candidate invariants and obtain counterexamples to help inference, in a dynamic, iterative guess and check method, where the checking is performed on the program code. Finally, making use of these techniques, an approach aimed at learning asymptotic complexities, by dynamically inferring linear and divide-and-conquer recurrences before extracting complexity orders from them, is presented in (Ishimwe et al., Reference Ishimwe, Nguyen and Nguyen2021).
While these works are directly related to ours, as they take advantage of sample traces to infer invariants, there are several, important differences from our work. A key difference is that, instead of working directly on the program code, our method processes recurrence relations, which may be seen as abstractions of the program obtained by previous static analyses, and applies regression to training sets obtained by evaluating the recurrences on input “sizes” instead of concrete data.Footnote 17 Hence, we apply dynamic inference techniques on already abstracted programs: this allows complex invariants to be represented by simple expressions, which are thus easier to discover dynamically.
Moreover, our approach differs from these works in the kind of invariants that can be inferred, and in the regression techniques being used. The approach presented in Nguyen et al. (Reference Nguyen, Kapur, Weimer, Forrest, Glinz, Murphy and Pezzè2012) discovers polynomials relations (of bounded degree) between program variables. It uses an equation solving method to infer equality invariants – which correspond to exact solutions in our context – although their work recovers some inequalities by other means. Similarly to one instantiation of our guess method (but not both), they generate templates that are affine combinations of a predefined set of terms, which we call base functions. However, unlike Nguyen et al. (Reference Nguyen, Kapur, Weimer, Forrest, Glinz, Murphy and Pezzè2012) we obtain solutions that go beyond polynomials using both of our guessing methods, as well as approximations. These approximations can be highly beneficial in certain applications, as discussed in Section 1 and further elaborated on in the following section.
The Dynaplex (Ishimwe et al., Reference Ishimwe, Nguyen and Nguyen2021) approach to dynamic complexity inference has different goals than ours: it aims at asymptotic complexity instead of concrete cost functions, and, in contrast to our approach, does not provide any soundness guarantees. Dynaplex uses linear regression to find recurrences, but applies the Master theorem and pattern matching to obtain closed-form expressions representing asymptotic complexity bounds, unlike our approach, which uses a different solving method and obtains concrete cost functions (either exact or approximated), instead of complexity orders.
Nevertheless, it must be noted that all of these works are complementary to ours, in the sense that they can be used as part of our general framework. Indeed, we could represent recurrence relations as programs (with input arguments representing input data sizes and one output argument representing the cost) and apply, for example, Nguyen et al. (Reference Nguyen, Kapur, Weimer, Forrest, Glinz, Murphy and Pezzè2012) to find polynomial closed-forms of the recurrences. Similarly, we could apply the approach in Nguyen et al. (Reference Nguyen, Kapur, Weimer, Forrest, Jalote, Briand and Van der Hoek2014), which is able to infer piecewise affine invariants using tropical polyhedra, in order to extend/improve our domain splitting technique.
8 Conclusions and future work
We have developed a novel approach for solving or approximating arbitrary, constrained recurrence relations. It consists of a guess stage that uses machine learning techniques to infer a candidate closed-form solution, and a check stage that combines an SMT-solver and a CAS to verify that such candidate is actually a solution. We have implemented a prototype and evaluated it within the context of CiaoPP, a system for the analysis of logic programs (and other languages via Horn clause tranformations). The guesser component of our approach is parametric w.r.t. the machine learning technique used, and we have instantiated it with both sparse (lasso) linear regression and symbolic regression in our evaluation.
The experimental results are quite promising, showing that in general, for the considered benchmark set, our approach outperforms state-of-the-art cost analyzers and recurrence solvers. It also can find closed-form solutions for recurrences that cannot be solved by them. The results also show that our approach is reasonably efficient and scalable.
Another interesting conclusion we can draw from the experiments is that our machine learning-based solver could be used as a complement of other (back-end) solvers in a combined higher-level solver, in order to obtain further significant accuracy improvements. For example, its combination with CiaoPP’s builtin solver will potentially result in a much more powerful solver, obtaining exact solutions for
![]() $88\%$
of the benchmarks and accurate approximations for the rest of them, except for one benchmark (which can only be solved by PRS23’s solver).
$88\%$
of the benchmarks and accurate approximations for the rest of them, except for one benchmark (which can only be solved by PRS23’s solver).
Regarding the impact of this work on logic programming, note that an improvement in a recurrence solver can potentially result in arbitrarily large accuracy gains in cost analysis of (logic) programs. Not being able to solve a recurrence can cause huge accuracy losses, for instance, if such a recurrence corresponds to a predicate that is deep in the control flow graph of the program, and such accuracy loss is propagated up to the main predicate, inferring no useful information at all.
The use of regression techniques (with a randomly generated training set by evaluating the recurrence to obtain the dependent value) does not guarantee that a solution can always be found. Even if an exact solution is found in the guess stage, it is not always possible to prove its correctness in the check stage. Therefore, in this sense, our approach is not complete. However, note that in the case where our approach does not obtain an exact solution, the closed-form candidate inferred by the guess stage, together with its accuracy score, can still be very useful in some applications (e.g., granularity control in parallel/distributed computing), where good approximations work well, even though they are not upper/lower bounds of the exact solutions.
As a proof of concept, we have considered a particular deterministic evaluation for constrained recurrence relations, and the verification of the candidate solution is consistent with this evaluation. However, it is possible to implement different evaluation semantics for the recurrences, to support, for example, non-deterministic or probabilistic programs, adapting the verification stage accordingly. Note that termination of the recurrence evaluation needs to be required as a precondition for verifying the obtained results. This is partly due to the particular evaluation strategy of recurrences that we are considering. In practice, non-terminating recurrences can be discarded in the guess stage, by setting a timeout. Our approach can also be combined with a termination prover in order to guarantee such a precondition.
As a future work, we plan to fully integrate our novel solver into the CiaoPP system, combining it with its current set of back-end solvers (referred to as CiaoPP’s builtin solver in this paper) in order to improve the static cost analysis. As commented above, the experimental results encourage us to consider such a potentially powerful combination, which, as an additional benefit, would allow CiaoPP to avoid the use of external commercial solvers.
We also plan to further refine and improve our algorithms in several directions. As already explained, the set
![]() $\mathcal{F}$
of base functions is currently fixed, user-provided. We plan to automatically infer it by using different heuristics. We may perform an automatic analysis of the recurrence we are solving, to extract some features that allow us to select the terms that most likely are part of the solution. For example, if the system of recurrences involves a subproblem corresponding to a program with doubly nested loops, we can select a quadratic term, and so on. Additionally, machine learning techniques may be applied to learn a suitable set of base functions from selected recurrence features (or the programs from which they originate). Another interesting line for future work is to extend our solver to deal (directly) with non-deterministic recurrences.
$\mathcal{F}$
of base functions is currently fixed, user-provided. We plan to automatically infer it by using different heuristics. We may perform an automatic analysis of the recurrence we are solving, to extract some features that allow us to select the terms that most likely are part of the solution. For example, if the system of recurrences involves a subproblem corresponding to a program with doubly nested loops, we can select a quadratic term, and so on. Additionally, machine learning techniques may be applied to learn a suitable set of base functions from selected recurrence features (or the programs from which they originate). Another interesting line for future work is to extend our solver to deal (directly) with non-deterministic recurrences.
Finally, we plan to use the counterexamples found by the checker component to provide feedback (to the guesser) and help refine the search for better candidate solutions, such as by splitting the recurrence domains. Although our current domain splitting strategy already provides good improvements, it is purely syntactic. We also plan to develop more advanced strategies, for example, by using a generalization of model trees.
A New contributions w.r.t. our previous work
This work is an extended and revised version of our previous work presented at ICLP 2023 as a Technical Communication (Klemen et al., Reference Klemen, Carreira-Perpiñán, Lopez-Garcia, Pontelli, Costantini, Dodaro, Gaggl, Calegari, Garcez, Fabiano, Mileo, Russo and Toni2023). The main additions and improvements include:
-
• We report on a much more extensive experimental evaluation using a larger, representative set of increasingly complex benchmarks and compare our approach with recurrence solving capabilities of state-of-the-art cost analyzers and CASs. In particular, we compare it with RaML, PUBS, Cofloco, KoAT, Duet, Loopus, PRS23, Sympy, PURRS, and Mathematica.
-
• Since our guess-and-check approach is parametric in the regression technique used, in (Klemen et al., Reference Klemen, Carreira-Perpiñán, Lopez-Garcia, Pontelli, Costantini, Dodaro, Gaggl, Calegari, Garcez, Fabiano, Mileo, Russo and Toni2023) we instantiate it to (sparse) linear regression, but here we also instantiate it to symbolic regression, and compare the results obtained with both regression methods.
-
• In Section 4.2, we introduce a technique that processes multiple subdomains of the original recurrence separately, which we call domain splitting. This strategy is orthogonal to the regression method used and improves the results obtained, as our experimental evaluation shows.
-
• In Section 7, we include a more extensive discussion on related work.
-
• In general, we have made some technical improvements, including a better formalization of recurrence relation solving.
B Extended experimental results – Full outputs
In Table 2, to provide a more comprehensive overview within the constraints of available space, only a few symbols are used to categorize the outputs of the tools. For the sake of completeness, we include here full outputs of the tools in cases where approximate solutions were obtained (symbols “
![]() $\Theta$
” and “
$\Theta$
” and “
![]() $-$
”). We do not include exact outputs (symbol “
$-$
”). We do not include exact outputs (symbol “
![]() $\checkmark$
”), since they are simply equivalent to those in Table 1. We neither include details and distinctions in case where we obtained errors, trivial
$\checkmark$
”), since they are simply equivalent to those in Table 1. We neither include details and distinctions in case where we obtained errors, trivial
![]() $+\infty$
bounds, timeouts, nor were deemed unsupported, as they are better suited for direct discussions with tool authors.
$+\infty$
bounds, timeouts, nor were deemed unsupported, as they are better suited for direct discussions with tool authors.




























