No CrossRef data available.
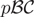 $p{\cal BC}$+
$p{\cal BC}$+Published online by Cambridge University Press: 23 December 2020
We extend probabilistic action language 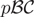 $p{\cal BC}$+ with the notion of utility in decision theory. The semantics of the extended
$p{\cal BC}$+ with the notion of utility in decision theory. The semantics of the extended 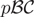 $p{\cal BC}$+ can be defined as a shorthand notation for a decision-theoretic extension of the probabilistic answer set programming language LPMLN. Alternatively, the semantics of
$p{\cal BC}$+ can be defined as a shorthand notation for a decision-theoretic extension of the probabilistic answer set programming language LPMLN. Alternatively, the semantics of 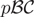 $p{\cal BC}$+ can also be defined in terms of Markov decision process (MDP), which in turn allows for representing MDP in a succinct and elaboration tolerant way as well as leveraging an MDP solver to compute a
$p{\cal BC}$+ can also be defined in terms of Markov decision process (MDP), which in turn allows for representing MDP in a succinct and elaboration tolerant way as well as leveraging an MDP solver to compute a  $p{\cal BC}$+ action description. The idea led to the design of the system pbcplus2mdp, which can find an optimal policy of a
$p{\cal BC}$+ action description. The idea led to the design of the system pbcplus2mdp, which can find an optimal policy of a  $p{\cal BC}$+ action description using an MDP solver.
$p{\cal BC}$+ action description using an MDP solver.
We are grateful to the anonymous referees for their useful comments and to Siddharth Srivastava, Zhun Yang, and Yu Zhang for helpful discussions. This work was partially supported by the National Science Foundation under Grant IIS-1815337.