Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Leone, Nicola
and
Faber, Wolfgang
2008.
Logic Programming.
Vol. 5366,
Issue. ,
p.
53.
Eiter, Thomas
Ianni, Giovambattista
and
Krennwallner, Thomas
2009.
Reasoning Web. Semantic Technologies for Information Systems.
Vol. 5689,
Issue. ,
p.
40.
Gebser, Martin
Kaminski, Roland
Ostrowski, Max
Schaub, Torsten
and
Thiele, Sven
2009.
Logic Programming and Nonmonotonic Reasoning.
Vol. 5753,
Issue. ,
p.
502.
Drabent, Włodzimierz
Eiter, Thomas
Ianni, Giovambattista
Krennwallner, Thomas
Lukasiewicz, Thomas
and
Małuszyński, Jan
2009.
Semantic Techniques for the Web.
Vol. 5500,
Issue. ,
p.
1.
Shen, Yi-Dong
and
You, Jia-Huai
2009.
Logic Programming and Nonmonotonic Reasoning.
Vol. 5753,
Issue. ,
p.
277.
Costantini, S.
and
Formisano, A.
2010.
Answer Set Programming with Resources.
Journal of Logic and Computation,
Vol. 20,
Issue. 2,
p.
533.
Truszczyński, Miroslaw
2010.
Reducts of propositional theories, satisfiability relations, and generalizations of semantics of logic programs.
Artificial Intelligence,
Vol. 174,
Issue. 16-17,
p.
1285.
Cakmak, Duygu
Erdem, Esra
and
Erdogan, Halit
2011.
Computing weighted solutions in ASP: representation-based method vs. search-based method.
Annals of Mathematics and Artificial Intelligence,
Vol. 62,
Issue. 3-4,
p.
219.
Woltran, Stefan
2011.
Datalog Reloaded.
Vol. 6702,
Issue. ,
p.
106.
Brewka, Gerhard
Eiter, Thomas
and
Truszczyński, Mirosław
2011.
Answer set programming at a glance.
Communications of the ACM,
Vol. 54,
Issue. 12,
p.
92.
CATTAFI, MASSIMILIANO
GAVANELLI, MARCO
NONATO, MADDALENA
ALVISI, STEFANO
and
FRANCHINI, MARCO
2011.
Optimal placement of valves in a water distribution network with CLP(FD).
Theory and Practice of Logic Programming,
Vol. 11,
Issue. 4-5,
p.
731.
Gebser, Martin
and
Schaub, Torsten
2013.
Tableau Calculi for Logic Programs under Answer Set Semantics.
ACM Transactions on Computational Logic,
Vol. 14,
Issue. 2,
p.
1.
Liu, Qian
Gao, Zhiqiang
Liu, Bing
and
Zhang, Yuanlin
2013.
A Logic Programming Approach to Aspect Extraction in Opinion Mining.
p.
276.
Zhang, Zhizheng
Zhao, Kaikai
and
Cui, Rongcun
2013.
ESmodels: An Inference Engine of Epistemic Specifications.
p.
769.
Wittocx, Johan
Denecker, Marc
and
Bruynooghe, Maurice
2013.
Constraint Propagation for First-Order Logic and Inductive Definitions.
ACM Transactions on Computational Logic,
Vol. 14,
Issue. 3,
p.
1.
Caprin, Edward
Zhang, Yan
and
Khan, Khaled M.
2013.
Social access control language (SocACL).
p.
261.
Zhang, Yuanlin
and
Zhang, Zhizheng
2014.
Knowledge Representation for Health Care.
Vol. 8903,
Issue. ,
p.
14.
Bomanson, Jori
Gebser, Martin
and
Janhunen, Tomi
2014.
Logics in Artificial Intelligence.
Vol. 8761,
Issue. ,
p.
166.
Zhang, Zhizheng
and
Zhang, Shutao
2015.
Logic Programming and Nonmonotonic Reasoning.
Vol. 9345,
Issue. ,
p.
517.
Shkapsky, Alexander
Yang, Mohan
and
Zaniolo, Carlo
2015.
Optimizing recursive queries with monotonic aggregates in DeALS.
p.
867.
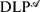 ), and illustrate how it can be profitably used for representingknowledge. Furthermore, we analyze the computational complexity of
), and illustrate how it can be profitably used for representingknowledge. Furthermore, we analyze the computational complexity of 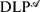 , showing that the addition of aggregates does not bring a highercost in that respect. Finally, we provide an implementation of
, showing that the addition of aggregates does not bring a highercost in that respect. Finally, we provide an implementation of 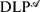 in DLV—a state-of-the-art DLP system—andreport on experiments which confirm the usefulness of the proposed extensionalso for the efficiency of computation.
in DLV—a state-of-the-art DLP system—andreport on experiments which confirm the usefulness of the proposed extensionalso for the efficiency of computation.