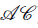Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-09T01:21:55.623Z Has data issue: false hasContentIssue false
  • English
  • Français

ASP ($\mathcal A \mathcal C$): Answer Set Programming with Algebraic Constraints

Published online by Cambridge University Press:  22 September 2020

THOMAS EITER Open the ORCID record for THOMAS EITER [Opens in a new window]  and
RAFAEL KIESEL Open the ORCID record for RAFAEL KIESEL [Opens in a new window]
THOMAS EITER
Affiliation:
Technical University Vienna, Vienna, Austria (e-mail: [email protected], [email protected])
RAFAEL KIESEL
Affiliation:
Technical University Vienna, Vienna, Austria (e-mail: [email protected], [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Weighted Logic is a powerful tool for the specification of calculations over semirings that depend on qualitative information. Using a novel combination of Weighted Logic and Here-and-There (HT) Logic, in which this dependence is based on intuitionistic grounds, we introduce Answer Set Programming with Algebraic Constraints (ASP(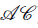$\mathcal A \mathcal C$)), where rules may contain constraints that compare semiring values to weighted formula evaluations. Such constraints provide streamlined access to a manifold of constructs available in ASP, like aggregates, choice constraints, and arithmetic operators. They extend some of them and provide a generic framework for defining programs with algebraic computation, which can be fruitfully used e.g. for provenance semantics of datalog programs. While undecidable in general, expressive fragments of ASP(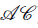$\mathcal A \mathcal C$) can be exploited for effective problem solving in a rich framework.

Keywords

Weighted LogicHere-and-There LogicAnswer Set ProgrammingConstraints
Type
Original Article
Information
Theory and Practice of Logic Programming , Volume 20 , Issue 6: 36th International Conference on Logic Programming Special Issue II , November 2020 , pp. 895 - 910
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Aziz, R. A., Chu, G., and Stuckey, P. J. 2013. Stable model semantics for founded bounds. Theory Pract. Log. Program. 13, 4-5, 517–532.Google Scholar
Balai, E., Gelfond, M., and Zhang, Y. 2013. Sparc-sorted asp with consistency restoring rules. arXiv preprint arXiv:1301.1386.Google Scholar
Bartholomew, M. and Lee, J. 2019. First-order stable model semantics with intensional functions. Artificial Intelligence 273, 56–93.Google Scholar
Bistarelli, S., Montanari, U., and Rossi, F. 1997. Semiring-based constraint logic programming. In Proc. IJCAI’97. 352–357.Google Scholar
Cabalar, P. 2011. Functional answer set programming. Theory and Practice of Logic Programming 11, 2-3, 203–233.Google Scholar
Cabalar, P., Fandinno, J., Schaub, T., and Wanko, P. 2020a. An ASP semantics for constraints involving conditional aggregates. arXiv preprint arXiv:2002.06911.Google Scholar
Cabalar, P., Fandinno, J., Schaub, T., and Wanko, P. 2020b. A uniform treatment of aggregates and constraints in hybrid ASP. arXiv preprint arXiv:2003.04176.Google Scholar
Cassaigne, J., Halava, V., Harju, T., and Nicolas, F. 2014. Tighter undecidability bounds for matrix mortality, zero-in-the-corner problems, and more. CoRR abs/1404.0644.Google Scholar
Dantsin, E., Eiter, T., Gottlob, G., and Voronkov, A. 2001. Complexity and expressive power of logic programming. ACM Comput. Surv. 33, 3, 374–425.Google Scholar
Droste, M. and Gastin, P. 2007. Weighted automata and weighted logics. Theor.Comp.Sci. 380, 1, 69.Google Scholar
Eiter, T. and Kiesel, R. 2020. Weighted lars for quantitative stream reasoning. In Proc. ECAI’20.Google Scholar
Faber, W., Pfeifer, G., and Leone, N. 2011. Semantics and complexity of recursive aggregates in answer set programming. Artificial Intelligence 175, 1, 278–298.Google Scholar
Ferraris, P. 2011. Logic programs with propositional connectives and aggregates. ACM TOCL 12, 4, 25.Google Scholar
Ferraris, P. and Lifschitz, V. 2010. On the stable model semantics of first-order formulas with aggregates. In Proc. International Workshop on Nonmonotonic Reasoning (NMR’10).Google Scholar
Gelfond, M. and Zhang, Y. 2014. Vicious circle principle and logic programs with aggregates. Theory and Practice of Logic Programming 14, 4-5, 587–601.Google Scholar
Green, T. J., Karvounarakis, G., and Tannen, V. 2007. Provenance semirings. In Proc. ACM PODS’07. ACM, 31–40.Google Scholar
Janhunen, T. 2018. Answer set programming related with other solving paradigms. KI 32, 2-3, 125–131.Google Scholar
Kimmig, A., Van den Broeck, G., and De Raedt, L. 2011. An algebraic prolog for reasoning about possible worlds. In Proc. AAAI’11.Google Scholar
Lierler, Y. 2014. Relating constraint answer set programming languages and algorithms. Artificial Intelligence 207, 1–22.Google Scholar
Lierler, Y. and Lifschitz, V. 2009. One more decidable class of finitely ground programs. In Proc. ICLP’09. Springer, 489–493.Google Scholar
Lifschitz, V., Pearce, D., and Valverde, A. 2001. Strongly equivalent logic programs. ACM TOCL 2, 4, 526–541.Google Scholar
Lifschitz, V., Tang, L. R., and Turner, H. 1999. Nested expressions in logic programs. Annals of Mathematics and Artificial Intelligence 25, 3-4, 369–389.Google Scholar
Littman, M. L., Goldsmith, J., and Mundhenk, M. 1998. The computational complexity of probabilistic planning. J. Artificial Intelligence Research 9, 1–36.Google Scholar
Marek, V. W., Niemela, I., et al. 2006. Logic programs with monotone abstract constraint atoms. arXiv preprint cs/0608103.Google Scholar
Niemelä, I., Simons, P., and Soininen, T. 1999. Stable model semantics of weight constraint rules. In Proc. LPNMR’99. Springer, 317–331.Google Scholar
Pearce, D. and Valverde, A. 2008. Quantified equilibrium logic and foundations for answer set programs. In Proc. ICLP’08, Garcia de la Banda, M. and Pontelli, E., Eds. Springer, 546–560.Google Scholar
Son, T. C., Pontelli, E., and Tu, P. H. 2007. Answer sets for logic programs with arbitrary abstract constraint atoms. Journal of Artificial Intelligence Research 29, 353–389.Google Scholar
Supplementary material: PDF

Eiter and Kiesel supplementary material

Eiter and Kiesel supplementary material 1

Download Eiter and Kiesel supplementary material(PDF)
PDF 188.6 KB
Supplementary material: File

Eiter and Kiesel supplementary material

Eiter and Kiesel supplementary material 2

Download Eiter and Kiesel supplementary material(File)
File 186.4 KB