In this paper, we present a simple model of
Fowler-Nordheim (FN) current of metal/ultra-thin oxide/semiconductor (MOS)
structures biased in the inversion mode ($V_{g }> 0$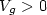 ) (injection of
electrons from the semiconductor). The oxide thickness varies from 45 Å
to 110 Å, the gate is in chrome and the semiconductor is of P type. From
the general models of the conduction by FN effect and by assuming a
continuum energy in the inversion layer, we have shown by using the
Wentzel-Kramers-Brillouin (WKB) approximation that the modeling of the FN
current, cannot be made by using the classical model generally used in the
case of electrons injection from the metal ($V_{g }< 0$
) (injection of
electrons from the semiconductor). The oxide thickness varies from 45 Å
to 110 Å, the gate is in chrome and the semiconductor is of P type. From
the general models of the conduction by FN effect and by assuming a
continuum energy in the inversion layer, we have shown by using the
Wentzel-Kramers-Brillouin (WKB) approximation that the modeling of the FN
current, cannot be made by using the classical model generally used in the
case of electrons injection from the metal ($V_{g }< 0$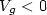 ). However, it
requires to introduce in the classical model a corrective term due to the
effects of the temperature, the oxide/semiconductor interface degeneracy
(the Fermi energy is localized in the semiconductor conduction band) and the
Schottky effect. The results obtained from the numerical simulation show
that these effects, at the ambient temperature, on the potential barrier at
the oxide/semiconductor interface is lower than 4% and the conduction
pre-exponential value (K1) is higher than that obtained in the
classical model ($K_1^o =10^{-6}$
). However, it
requires to introduce in the classical model a corrective term due to the
effects of the temperature, the oxide/semiconductor interface degeneracy
(the Fermi energy is localized in the semiconductor conduction band) and the
Schottky effect. The results obtained from the numerical simulation show
that these effects, at the ambient temperature, on the potential barrier at
the oxide/semiconductor interface is lower than 4% and the conduction
pre-exponential value (K1) is higher than that obtained in the
classical model ($K_1^o =10^{-6}$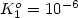 A/V2) [J. Appl. Phys. 40, 278 (1969)]. These results are
validated experimentally by modeling the current-voltage characteristics of
MOS structures where the oxide thickness is 109 Å. For oxide thickness
lower than 100 Å, we have found that the results of simulation disagree
with those experimental. We have attributed this disagreement to the
degradation of the conduction parameters by the presence of leakage current
before stressing the MOS structure (LCBS). This leakage current is
attributed to defects localized in the oxide layer. We have shown that the
leakage current is of FN type and deduced the effective barrier of defects.
By taking account of this barrier value and the corrective term due to the
temperature, the oxide/semiconductor interface degeneracy and the Schottky
effects (TDSEs), we have determined the defects effective area. From the
comparison between these results and those obtained in the case of electrons
injection from the metal ($V_{g} < 0$
A/V2) [J. Appl. Phys. 40, 278 (1969)]. These results are
validated experimentally by modeling the current-voltage characteristics of
MOS structures where the oxide thickness is 109 Å. For oxide thickness
lower than 100 Å, we have found that the results of simulation disagree
with those experimental. We have attributed this disagreement to the
degradation of the conduction parameters by the presence of leakage current
before stressing the MOS structure (LCBS). This leakage current is
attributed to defects localized in the oxide layer. We have shown that the
leakage current is of FN type and deduced the effective barrier of defects.
By taking account of this barrier value and the corrective term due to the
temperature, the oxide/semiconductor interface degeneracy and the Schottky
effects (TDSEs), we have determined the defects effective area. From the
comparison between these results and those obtained in the case of electrons
injection from the metal ($V_{g} < 0$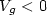 ) [Eur. Phys. J. Appl. Phys. 9, 239 (2000)], we have concluded that the
defects depth in the oxide layer is identical to the oxide thickness.
) [Eur. Phys. J. Appl. Phys. 9, 239 (2000)], we have concluded that the
defects depth in the oxide layer is identical to the oxide thickness.