Over the last two decades, advances in fabrication have led to significant progress in creating patterned heterostructures that support either carriers, such as electrons or holes, with specific band structure or electromagnetic waves with a given mode structure and dispersion. In this article, we review the properties of light in coupled optical waveguides that support specific energy spectra, with or without the effects of disorder, that are well-described by a Hermitian tight-binding model. We show that with a judicious choice of the initial wave packet, this system displays the characteristics of a quantum particle, including transverse photonic transport and localization, and that of a classical particle. We extend the analysis to non-Hermitian, parity and time-reversal ( PT $ \mathcal{PT}$ 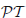) symmetric Hamiltonians which physically represent waveguide arrays with spatially separated, balanced absorption or amplification. We show that coupled waveguides are an ideal candidate to simulate PT $ \mathcal{PT}$ 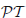-symmetric Hamiltonians and the transition from a purely real energy spectrum to a spectrum with complex conjugate eigenvalues that occurs in them.

We compared the performances of polymer-based photovoltaic devices prepared from different formulations of poly(3,4-ethylenedioxythiophene):poly(4-styrenesulfonate) (PEDOT:PSS). The PEDOT:PSS buffer layer is incorporated between the indium tin oxide (ITO) electrode and the active layer, which is composed of a blend of poly(3-hexylthiophene) (P3HT) and [6,6]-phenyl-C61-butyric acid methyl ester (PCBM). A highest efficiency of 3.86% (under AM1.5 solar illumination) was achieved for device prepared from a PEDOT:PSS trade-named high conductivity grade. However, annealing devices at a temperature over 120 °C results in decreased photovoltaic performance. This study shows that attention has to be paid to chemicals used to formulate high conductive PEDOT:PSS to become compatible with the production of solar cells involving thermal processing.

The characteristic properties, the critical surface transverse field Ωsc and the Curie temperature Tc, for an N-layer ferroelectric thin film with epitaxy surface layers Ns described by the transverse field Ising model have been studied by the differential operator technique within the framework of effective-field theory with correlations. The analytical equation for the phase diagrams of ferroelectric thin films is derived. The surface transverse field Ωs dependence of the Curie temperature Tc in the ferroelectric thin film with different epitaxy surface layers is calculated. Meanwhile the epitaxy surface layer number Ns dependence of the critical surface transverse field Ωsc and the Curie temperature Tc is also examined. The results show that the critical properties depend heavily on modifications of interchange interactions and transverse fields in the epitaxy surface layer.

Highly crystalline core-shell FeCo-CoFe2O4 nanowires were obtained from a three step process. Initially, CoFe2O4 nanowires were grown using electrospinning and annealing at higher temperatures. Through a thermal reduction under controlled conditions, CoFe2O4 nanostructures were converted to FeCo alloy nanowires. Then by natural oxidation, a highly crystalline shell of CoFe2O4 formed over the FeCo core structure. Structural and magnetic characterizations revealed the presence of highly crystalline FeCo-Co2FeO4 core-shell structure. Magnetically, the soft FeCo phase switches at a lower magnetic field compared to the hard CoFe2O4 phase, yielding an irregular hysteresis loop with a squeezed loop in the middle. The FeCo/CoFe2O4 core-shell is stable and it retains its structure for a prolonged duration.

Combining with the self-consistent condition and extended 5 × 5 matrix, we theoretically analyzed the polarization properties of the eigenmodes throughout the nonplanar ring resonators with different structures. According to the satisfactory cross section size of the eigenmodes, a comparative study of the stability properties of these nonplanar ring resonators is also provided, and the three dimensions stability space of these resonators are presented for the first time as far as our knowledge goes. The results show that the major and minor axes of the cross section change with the propagation distance and have a symmetrical point for resonators with two different structures, and the area of the stable region for these resonators can be extended by changing the incident angles of the laser beam or the radii of mirror surfaces in the resonator. These interesting results are important for designing and arranging the diaphragm in ring resonators with a nonplanar structure, as well as optimizing the structure of the resonators themselves.

It is well known that the interactions between a coherent light and a scattering medium produce a speckle pattern. But, even if intensity and phase statistics have been already well described for a long time, the statistics of the increments of the phase spectrum have never been explored. In this paper, we firstly introduce these concepts before demonstrate that phase spectrum increments contain informations on the medium observed. Moreover, we show that phase spectrum increments allow reaching informations on the media which are not present in the classical approaches based on the intensity. Monte Carlo simulations are used to this aim.

This paper deals with the development of a new generation of electric motors (7.5–15 kW) for automotive powertrains. The target is a full electric direct drive vehicle, for the particular application to heavy quadricycles. An original axial flux PM structure is proposed due to the simplicity of its manufacturing. However it leads to a 3D structure, difficult to study. The paper deals with analytical models that can be used to achieve the analysis and the sizing of the motor. The electromagnetic behavior is modeled using a simple magnetic equivalent network and the thermal behavior is analyzed with a thermal network. Finally, the analytical results are compared to those experimentally obtained and it proves the interest of the proposed structure: the construction is simple and the performances are satisfying.

Near-field radiative transfer is a promising way to significantly and simultaneously enhance both thermo-photovoltaic (TPV) devices power densities and efficiencies. A parametric study of Drude and Lorentz models performances in maximizing near-field radiative heat transfer between two semi-infinite planes separated by nanometric distances at room temperature is presented in this paper. Optimal parameters of these models that provide optical properties maximizing the radiative heat flux are reported and compared to real materials usually considered in similar studies, silicon carbide and heavily doped silicon in this case. Results are obtained by exact and approximate (in the extreme near-field regime and the electrostatic limit hypothesis) calculations. The two methods are compared in terms of accuracy and CPU resources consumption. Their differences are explained according to a mesoscopic description of nearfield radiative heat transfer. Finally, the frequently assumed hypothesis which states a maximal radiative heat transfer when the two semi-infinite planes are of identical materials is numerically confirmed. Its subsequent practical constraints are then discussed. Presented results enlighten relevant paths to follow in order to choose or design materials maximizing nano-TPV devices performances.