Plant fibers with nonzero microfibril angle show no plane reflection symmetries, the groups of spatial symmetry transformations consisting of rotations only. The spatial point symmetry group of any material made of such fibers is of order which is half of the order of the symmetry group of the corresponding orthotropic material. However, materials consisting of fibers show similar degeneracies of stiffness eigenvalues as the non-fibrous materials. Stiffness degeneracies appear to be controlled by the integer exponents of dicycle conditions applied on products of vectors generating symmetry groups. It is found that flat orthotropic sheets always retain their planar shape in eigen deformations, whereas those made of fibers with microfibrils do not. Features of the out-of-plane deformations are clarified. Orthotropic material elements experience normal on-axis eigen strains only, whereas fibrous bodies with orthotropic fiber alignment may experience on-axis shear strains as eigen strains.

Note to the reader:

On page 10402-p12, four mistakes have been corrected on September 7, 2009:

The following commands: " $\backslash$ 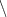overline{pq}" ( $\overline{pq}$ 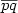) and " $\backslash$ 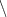overline{number}" have been replaced respectively by " $\backslash$ 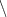overline{p} $\backslash$ 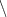overline{q}" ( $\overline{p}$ 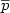$\overline{q}$ 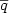) and " $\backslash$ 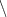overline{number} $\backslash$ overline{number}".