The aim of model reduction is to obtain the simplest model while reflecting as far as possible the dynamic behaviour of a system. First, we present the reduction method based on a complex admittance matrix [Y(s)] of the whole initial model. From which we obtain by two inversions, the matrix $[Y_{\rm red}(s)]$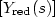, which can be interpreted as a reduced network. We give an example of application of the numeric reduction method. The same method is applied with success to analytical expression of impedances kept from the quadrupole representation of heat conduction. In order to simulate easily the transient responses of analytical models, we present the development of analytical impedance in the form of an equivalent network, which is proved to be very efficient during simulations. The first application is done with a heterogeneous system made of two bars of different materials, one is made of copper and the other is made of steel. The second application is done with a more complex thermal system constituting a cooler with 7 branches. This cooler is reduced to 1, 2 and 3 nodes to obtain the simplest model while reflecting as far as possible the dynamic behaviour. This document presents a generalisation of the method of network reduction in the case where the models' impedances have analytical expressions. In this case, we show that contrary to the numerical reduction, which approximates admittances to the first order, we are free to choose the model order, whatever the kept nodes, in such a manner that the model's bandwidth is considered as sufficient. The resulting equivalent networks allow easy simulations of the transient responses thanks to standard electric network softwares. Beyond the dealt examples of analytical reduction, for industrial systems non analytically calculable but governed by an equation of heat diffusion, the structures (topologies) of the reduced models would be the same. That opens prospects to obtain thermal reduced models from an automated networking realised in CAD.