Article contents
Nonlinear response of superconductor bolometer to phonon fluxes
Published online by Cambridge University Press: 07 April 2004
Abstract
A superconducting metallic film bolometer in contact
with thermal bath of temperature T0, is biased by a (i)
constant current $I_{\mathrm{b} }$ , or by (ii) the constant
voltage $U_{\mathrm{b}}$
, or by (ii) the constant
voltage $U_{\mathrm{b}}$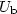 . The absorption of the time-dependent
power of a phonon beam W(t) elevates temperature of the film to
$T(t)>T_{\mathrm{0}}$
. The absorption of the time-dependent
power of a phonon beam W(t) elevates temperature of the film to
$T(t)>T_{\mathrm{0}}$ . The thermal contact of the bolometer with
the environment is characterized by the thermal conductance G,
and it depends on $[T^{n}(t)-T_{\mathrm{0}}^{n}]$
. The thermal contact of the bolometer with
the environment is characterized by the thermal conductance G,
and it depends on $[T^{n}(t)-T_{\mathrm{0}}^{n}]$ ($n=4{-}6$
($n=4{-}6$ ). For
both above methods of bias, we derive ordinary
nonautonomous nonlinear differential equations of the first order.
These equations are numerically solved. The knowledge of W(t)
allows one to calculate (i) $U_{\mathrm{b} }(t)$
). For
both above methods of bias, we derive ordinary
nonautonomous nonlinear differential equations of the first order.
These equations are numerically solved. The knowledge of W(t)
allows one to calculate (i) $U_{\mathrm{b} }(t)$ or (ii)
$I_{\mathrm{b}}(t)$
or (ii)
$I_{\mathrm{b}}(t)$ . The inverse problem of calculation of W(t)
from known (i) $U_{\mathrm{b}}(t)$
. The inverse problem of calculation of W(t)
from known (i) $U_{\mathrm{b}}(t)$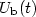 or (ii) $I_{\mathrm{b}}(t)$
or (ii) $I_{\mathrm{b}}(t)$ is
also solved. Using W(t) calculated in computer experiments, we
obtained the bolometer signal, and compared it with results of
real experiments performed on GaAs in which $I_{\mathrm{b}}$
is
also solved. Using W(t) calculated in computer experiments, we
obtained the bolometer signal, and compared it with results of
real experiments performed on GaAs in which $I_{\mathrm{b}}$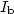 is
fixed, and U is measured. Comparison of calculated results with
results obtained for the linearized model shows that the
nonlinearity is essential for the correct description of metallic
superconducting film bolometer response.
is
fixed, and U is measured. Comparison of calculated results with
results obtained for the linearized model shows that the
nonlinearity is essential for the correct description of metallic
superconducting film bolometer response.
- Type
- Research Article
- Information
- The European Physical Journal - Applied Physics , Volume 26 , Issue 3: 14th International Colloquium on Plasma Processes (CIP 2003) , June 2004 , pp. 151 - 159
- Copyright
- © EDP Sciences, 2004
References
- 1
- Cited by


