Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-07-05T02:09:23.742Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinite 2D square network of identical capacitors with two missing bonds

Published online by Cambridge University Press:  13 December 2007

J. H. Asad ,
R. S. Hijjawi ,
A. J. Sakaji  and
J. M. Khalifeh
J. H. Asad*
Affiliation:
Tabuk University, Teachers' College, Department of Sciences (Physics), PO Box 1144, Tabuk, Saudi Arabia
R. S. Hijjawi
Affiliation:
Department of Physics, Mutah University, Jordan
A. J. Sakaji
Affiliation:
Department of Physics, Ajman University, UAE
J. M. Khalifeh
Affiliation:
Department of Physics, University of Jordan, 11942 Amman, Jordan
*
[email protected]
Get access

Abstract

The capacitance between any two arbitrary lattice sites of an infinite square network consisting of identical capacitors is studied analytically and numerically for a perturbed network. The perturbation is as a result of removing the bonds $(i_{0} j_{0})$ 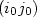and $(k_{0} l_{0})$ 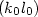from the perfect network. The equivalent capacitance is expressed in terms of the Lattice Green's Function (LGF) of the perturbed network. Solving Dyson's equation we express the LGF and the capacitance of the perturbed network in terms of those of the infinite perfect network. The asymptotic behavior of the perturbed capacitance is also studied. Finally, some numerical results are presented for the perturbed infinite square lattice, and a comparison is carried out for those of the perturbed and perfect infinite square network.

Keywords

Type
Research Article
Information
The European Physical Journal - Applied Physics , Volume 40 , Issue 3 , December 2007 , pp. 257 - 264
Copyright
© EDP Sciences, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Kirchhoff, G., Ann. Phys. und Chime 72, 497 (1847) CrossRef
B. Van der Pol, H. Bremmer, Operational Calculus Based on the Two-Sided Laplace Integral (Cambridge University Press, England, 1955)
Aitchison, R.E., Am. J. Phys. 32, 566 (1964) CrossRef
Bartis, F.J., Am. J. Phys. 35, 354 (1967) CrossRef
Atkinson, D., Van Steenwijk, F.J., Am. J. Phys. 67, 486 (1999) CrossRef
Venezian, G., Am. J. Phys. 62, 11 (1994) CrossRef
Jeng, M., Am. J. Phys. 68, 1 (2000) CrossRef
Lavatelli, L., Am. J. Phys. 40, 1246 (1972) CrossRef
Trier, P.E., Bull. Inst. Math. Appl. 21, 58 (1985)
Camermon, D., Math. Scientists 11, 75 (1986)
Van Steenwijk, F.J., Am. J. Phys. 66, 90 (1998) CrossRef
Cserti, J., Am. J. Phys. 68, 896 (2000) CrossRef
Cserti, J., David, G., Piroth, A., Am. J. Phys. 70, 153 (2002) CrossRef
J.H. Asad, Ph.D. thesis, University of Jordan (2004) (unpublished)
Asad, J.H., Hijjawi, R.S., Sakaji, A.J., Khalifeh, J.M., Int. J. Theo. Phys. 43, 2223 (2004) CrossRef
Asad, J.H., Hijjawi, R.S., Sakaji, A.J., Khalifeh, J.M., Int. J. Theo. Phys. 44, 471 (2005) CrossRef
Asad, J.H., Sakaji, A.J., Hijjawi, R.S., J.M. Khalifeh. Eur. Phys. J. B 52, 365 (2006) CrossRef
Wu, F.Y., J. Phys. A: Math. Gen. 37, 6653 (2004) CrossRef
Osterberg, P.M., Inan, A.S., Am. J. Phys. 72, 972 (2004) CrossRef
Van Enk, S.J., Am. J. Phys. 68, 854 (2000) CrossRef
Asad, J.H., Hijjawi, R.S., Sakaji, A.J., Khalifeh, J.M., Int. J. Mod. Phys. B 19, 3713 (2005) CrossRef
Asad, J.H., Hijjawi, R.S., Sakaji, A.J., Khalifeh, J.M., Eur. Phys. J. Appl. Phys. 32, 149 (2005) CrossRef
Tzenj, W.J., Wu, F.Y., J. Phys. A: Math. Gen. 39, 8579 (2006) CrossRef
Hijjawi, R.S., Asad, J.H., Sakaji, A.J., Khalifeh, J.M., Int. J. Mod. Phys. B 21, 199 (2007) CrossRef
E.N. Economou, Green's Function in Quantum Physics (Springer-Verlag, Berlin, 1983)
J.H. Asad, Mod. Phys. Lett. B 21, (2007)