Published online by Cambridge University Press: 15 November 2000
The toroidal technique is used in the determination of the complex, frequency dependent
magnetic susceptibility, $\chi (\omega) = \chi'(\omega) - {\rm i} \chi''(\omega)$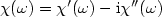 , of four magnetic fluids
consisting of colloidal suspensions of magnetite in water with corresponding saturation magnetisation of
134 G, 107 G, 90 G and 30 G. Plots of the susceptibility components against f (Hz) over the frequency
range 10 Hz to 1 MHz, are shown to have approximate Debye-type profiles with the presence of Brownian
relaxation being indicated by the frequency, fmax, of the maximum of the loss-peak in the
$\chi''(\omega)$
, of four magnetic fluids
consisting of colloidal suspensions of magnetite in water with corresponding saturation magnetisation of
134 G, 107 G, 90 G and 30 G. Plots of the susceptibility components against f (Hz) over the frequency
range 10 Hz to 1 MHz, are shown to have approximate Debye-type profiles with the presence of Brownian
relaxation being indicated by the frequency, fmax, of the maximum of the loss-peak in the
$\chi''(\omega)$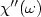 profiles. Corresponding calculations of particle hydrodynamic radius indicate the
presence of aggregation. An estimate of the aggregate size distribution in the samples is determined by
fitting the measured susceptibility profiles to susceptibility profiles generated by the Debye
equations modified by Frohlich, Cole-Cole, Normal and Lognormal distribution functions. The fits
obtained from the four fitting functions are found to be similar and thus it is concluded that none of
these functions offers any particular advantage over the other functions.
profiles. Corresponding calculations of particle hydrodynamic radius indicate the
presence of aggregation. An estimate of the aggregate size distribution in the samples is determined by
fitting the measured susceptibility profiles to susceptibility profiles generated by the Debye
equations modified by Frohlich, Cole-Cole, Normal and Lognormal distribution functions. The fits
obtained from the four fitting functions are found to be similar and thus it is concluded that none of
these functions offers any particular advantage over the other functions.