Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T17:58:29.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Theory of frequency response of magnetoelectric effects in radially polarized thin cylindrical composites

Published online by Cambridge University Press:  27 January 2014

Ru Zhang ,
Gaojian Wu ,
Li Zhang  and
Ning Zhang
Ru Zhang*
Affiliation:
Department of Applied Physics, Nanjing University of Technology, 210009, P.R. China Magnetoelectronic Lab, Nanjing Normal University, 210097, P.R. China
Gaojian Wu
Affiliation:
Department of Applied Physics, Nanjing University of Technology, 210009, P.R. China Magnetoelectronic Lab, Nanjing Normal University, 210097, P.R. China
Li Zhang
Affiliation:
Department of Applied Physics, Nanjing University of Technology, 210009, P.R. China
Ning Zhang
Affiliation:
Magnetoelectronic Lab, Nanjing Normal University, 210097, P.R. China
*
ae-mail: [email protected]
Get access

Abstract

A theoretical model for the frequency response of magnetoelectric (ME) effect in thin cylindrical piezoelectric-magnetostrictive composites is presented by using constitutive and elastodynamic equations. The calculated results show that there is a resonant enhancement peak of ME voltage coefficient in the electromechanical resonance region and the ME voltage coefficient at resonance frequency exceeds that at low frequency by one or two orders of magnitude. The resonance frequency is predicted to increase with decreasing average diameter D̅$ \bar{D}$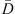 and increasing thickness of magnetostrictive layer tM of the cylindrical composite, which is in good agreement with the experimental results reported in literatures. The corresponding resonance ME voltage coefficient increases with increasing tM , but reaches to a peak value and then decreases with increasing D̅$ \bar{D}$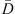. It is indicated that the ME effect of trilayered cylindrical composite is less than that of bilayered one, possibly due to its symmetric structure. Under clamped condition, the resonance frequency will shift to a very high value for both trilayered and bilayered cylindrical composites, while the ME effect has different performance, enhanced in bilayered but suppressed in trilayered cylindrical composite. Our model shows that one can obtain strong ME effect and proper resonance frequency by selecting suitable materials, optimizing its geometry structure and varying mechanical boundary conditions for the cylindrical composite structure

Type
Research Article
Information
The European Physical Journal - Applied Physics , Volume 65 , Issue 1 , January 2014 , 10602
Copyright
© EDP Sciences, 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Fiebig, M., J. Phys. D 38, R123 (2005)CrossRef
Dong, S.X., Li, J.F., Viehland, D., Appl. Phys. Lett. 83, 2265 (2003)CrossRef
Spaldin, N.A., Fiebig, M., Science 309, 391 (2005)CrossRefPubMed
Shi, Z., Nan, C.W., Zhang, J., Cai, N., Li, J.F., Appl. Phys. Lett. 87, 012503 (2005)CrossRef
Wan, J.G., Wang, X.W., Wu, Y.J., Zeng, M., Wang, Y., Jiang, H., Zhou, W.Q., Wang, G.H., Liu, J.-M., Appl. Phys. 86, 122501 (2005)
Nan, C.W., Liu, G., Lin, Y.H., Appl. Phys. Lett. 83, 4366 (2003)CrossRef
Dong, S.X., Zhai, J.Y., Xing, Z.P., Li, J.F., Viehland, D., Appl. Phys. Lett. 91, 022915 (2007)CrossRef
Wan, J.G., Li, Z.Y., Wang, Y., Zeng, M., Wang, G.H., Liu, J.M., Appl. Phys. Lett. 86, 202504 (2005)CrossRef
Li, L., Lin, Y.Q., Chen, X.M., J. Appl. Phys. 102, 064103 (2007)CrossRef
Wang, H.M., Pan, E., Chen, W.Q., J. Appl. Phys. 107, 093514 (2010)CrossRef
Pan, D.A., Bai, Y., Volinsky, A.A., Chu, W.Y., Qiao, L.J., Appl. Phys. Lett. 92, 052904 (2008)CrossRef
Wu, W., Bi, K., Wang, Y.G., J. Mater. Sci. 46, 1602 (2011)CrossRef
Li, L., Chen, X.M., Appl. Phys. A 98, 761 (2010)CrossRef
Bi, K., Wu, W., Gu, Q.L., Cui, H.N., Wang, Y.G., J. Alloys Compd. 509, 5163 (2011)CrossRef
Petrov, V.M., Srinivasan, G., Bichurin, M.I., Gupta, A., Phys. Rev. B 75, 224407 (2007)CrossRef
Li, L., Chen, X.M., Zhu, H.Y., J. Alloys Compd. 526, 116 (2012)CrossRef
Barker, B.D., Surf. Technol. 12, 77 (1981)CrossRef
Bi, K., Wang, Y.G., Solid. State Commun. 150, 248 (2010)CrossRef
Bi, K., Wang, Y.G., Wu, W., Pan, D.A., Phys, J., D, , Appl. Phys. 43, 132002 (2010)
Pan, D.A., Zhang, S.G., Volinsky, A.A., Qiao, L.J., J. Phys D: Appl. Phys. 41, 205008 (2008)CrossRef
Bichurin, M.I., Petrov, V.M., Averkin, S.V., Filippov, A.V., Phys. Solid State 52, 2116 (2012)CrossRef
Filippov, D.A., Laletsin, U., Srinivasan, G., J. Appl. Phys. 102, 093901 (2007)CrossRef
http://en.wikipedia.org/wiki/Nickel
Mandal, S.K., Sreenivasulu, G., Petrov, V.M., Bandekar, S., Srinivasan, G., Advances and Applications in Electroceramics, edited by Nair, K.M., Quanxi Jia, and Shashank Priya, , vol. 226 (Wiley, 2011)Google Scholar
Bichurin, M.I., Petrov, V.M., Srinivasan, G., Phys. Rev. B 68, 054402 (2003)CrossRef
Truell, R., Elbaum, C., Chick, B.B., Ultrasonic Methods in Solid State Physics (Academic Press, New York, 1969)Google Scholar
Pan, D.A., Zhang, S.G., Tian, J.J., Sun, J.S., Volinsky, A.A., Qiao, L.J., Appl. Phys. A 98, 449 (2010)CrossRef
Hong, H., Bi, K., Wang, Y.G., J. Alloys Comp. 545, 182 (2012)CrossRef
Guo, S.S., Lu, S.G., Xu, Z., Zhao, X.Z., Or, S.W., Appl. Phys. Lett. 88, 182906 (2006)CrossRef