The structural model discussed in Part I of the present work is applied to "true" behavior – i.e. shear thinning followed by shear thickening (sometimes followed by shear thinning) – very often observed in complex fluids as the applied shear is increased. This model states that the viscosity η of these fluids – described as concentrated dispersions of several classes of Structural Units (SUs) – is a unique function of a flow-dependent effective volume fraction, φeff. The latter is expressed in terms of Si = fraction of "aggregated" particles contained in all the SUis (as SUs of i-class) and Ci = (ϕi−1−1)= "compactness factor", directly related to the mean compactness ϕi of SUis. Shear induced flocculation (SIF) is the more obvious process capable to explain the shear thickening behavior of partially flocculated suspensions (obviously, another process should be required for stabilized dispersions). After progressive reduction of SUs submitted to shear forces (i.e. leading to a decrease of Si), such a behavior should be observed if SIF occurs beyond a critical shear rate ${\dot {\gamm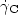a}_{\rm C}}$, then resulting in re-increase of Si, thus of φeff and η. The simplest "SIF-model" will introduce only one class of SUs, with only one variable S governed by a kinetic equation in which the kinetic rate for SU-formation increases with shear, thus giving the expected shear-thickening behavior if ${\dot {\gamma}}>{\dot {\gamma}_{\rm C}}$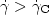. However, at high shear rates, SIF is limited by a (Smoluchowski-like) shear decreasing sticking probability. Effects of varying model parameters on predictions of the resulting SIF-model are discussed. Finally, this model is tested by comparison with observed rheological behavior, namely viscosity change vs. pH in aqueous styrene-ethylacrylate dispersions, from Laun's data [2].